Multi-Objective Short-Term Operation of Hydro–Wind–Photovoltaic–Thermal Hybrid System Considering Power Peak Shaving, the Economy and the Environment †
Abstract
1. Introduction
- A multi-objective, short-term operation model for the hydro–wind–PV–thermal hybrid system (MOHS) considering the peak shaving, operating costs and environmental impact is established.
- The hidden Markov regression method (HMR) and kernelized k-medoids clustering algorithm are applied to analyze the impact of energy uncertainty.
- A new cost value region search evolutionary algorithm (CVRSEA) is proposed to solve the MOHS problem and to demonstrated the flexible operation capability of hydroelectric power plants.
2. Methodology
2.1. Power Output Calculation
2.2. Multi-Objective Operation Model for a Hybrid System
2.2.1. Power Peak Shaving Objective
2.2.2. Economy Objective
2.2.3. Emission Objective
2.2.4. Constraints
- (1)
- In order to ensure the stability of the system, it is essential that the total power generated by hydroelectric stations, thermal generators, wind farms and solar power plants is equal to the system load demand for each time interval:where is the load demand of the wind–solar–hydro–thermal hybrid system during time t; Nh is the number of reservoirs; Nw is the number of wind farms; Ns is the number of solar power plants.
- (2)
- Power generation limits: The power generation capacity of hydropower stations, thermal generators, wind farms and solar power plants is subject to the maximum and minimum constraints of the generator:where and are the lower and upper generation limits of the i-th thermal generator, respectively; and are the lower and upper generation limits of the j-th reservoir, respectively; and are the lower and upper generation limits of the k-th wind farm, respectively; and are the lower and upper generation limits of the m-th solar power plant, respectively.
- (3)
- Water balance equation:where Ii,t is the inflow of the i-th reservoir during time t; Qi,t is the outflow of the i-th reservoir during time t; Δt is the time interval; Vi,t is the storage volume of i-th reservoir at time t.
- (4)
- Continuity equation for the cascade reservoirs:where qi,t is the interval runoff during time t; Nui is the number of upstream reservoirs above the i-th reservoir; Tki is the time delay from reservoir k to j.
- (5)
- Reservoir discharge constraints:where and are the lower and upper discharge limits of the i-th reservoir, respectively.
- (6)
- Reservoir storage volumes constraints:where and are the lower and upper limits of the volume of i-th reservoir, respectively.
- (7)
- The initial and terminal reservoir storage volume limits are as follows:where and are initial and terminal storage volume of i-th reservoir, respectively.
2.3. Representation of Uncertainty
2.3.1. Uncertainty Analysis
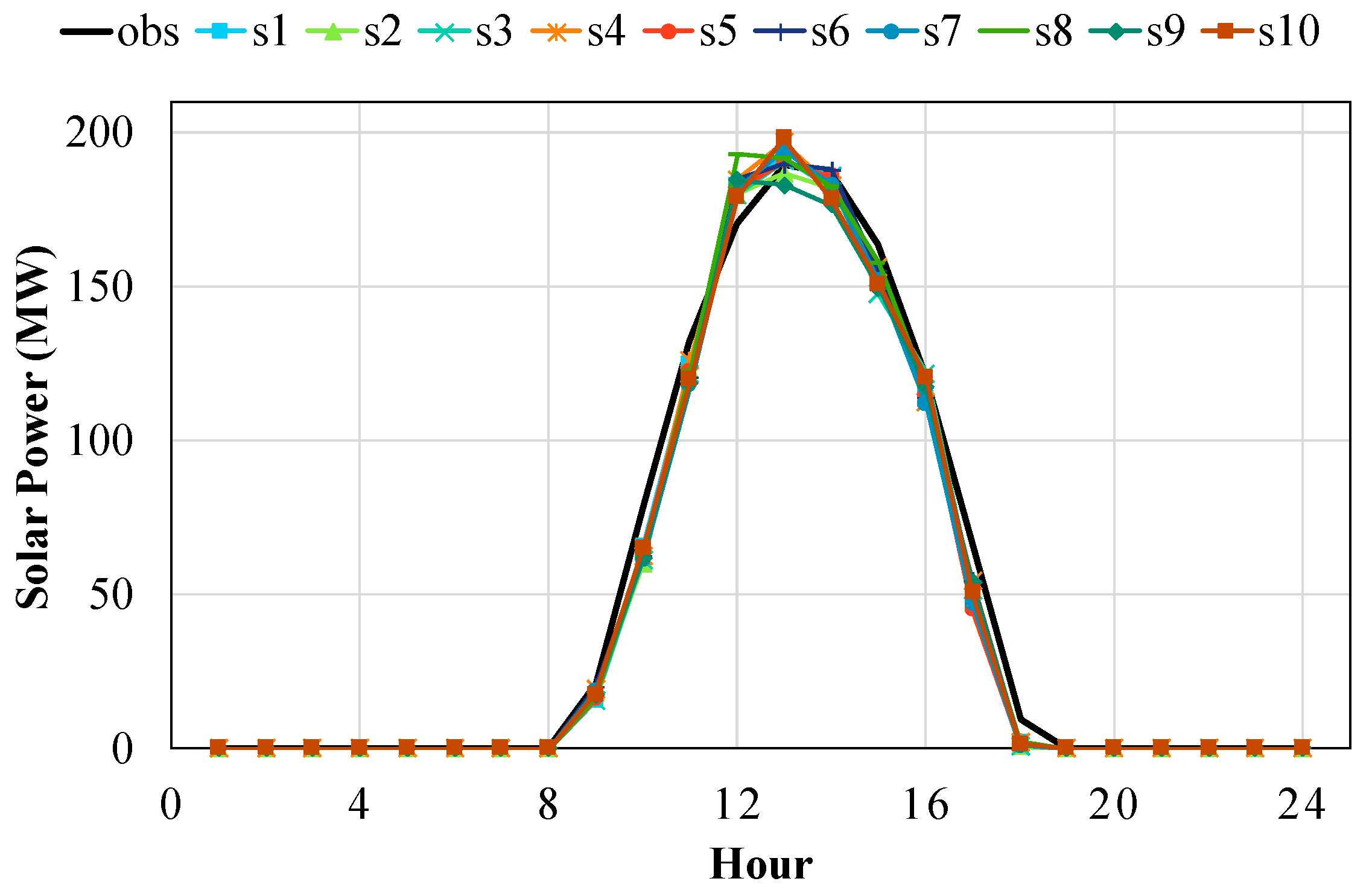
2.3.2. Simulation Scenarios
3. Cost Value Region Search Evolutionary Algorithm
3.1. Region Search Strategy
3.1.1. Regional Division and Identification
3.1.2. Regional Mating Selection and Regional Update
3.2. Cost Value Based Archive Set
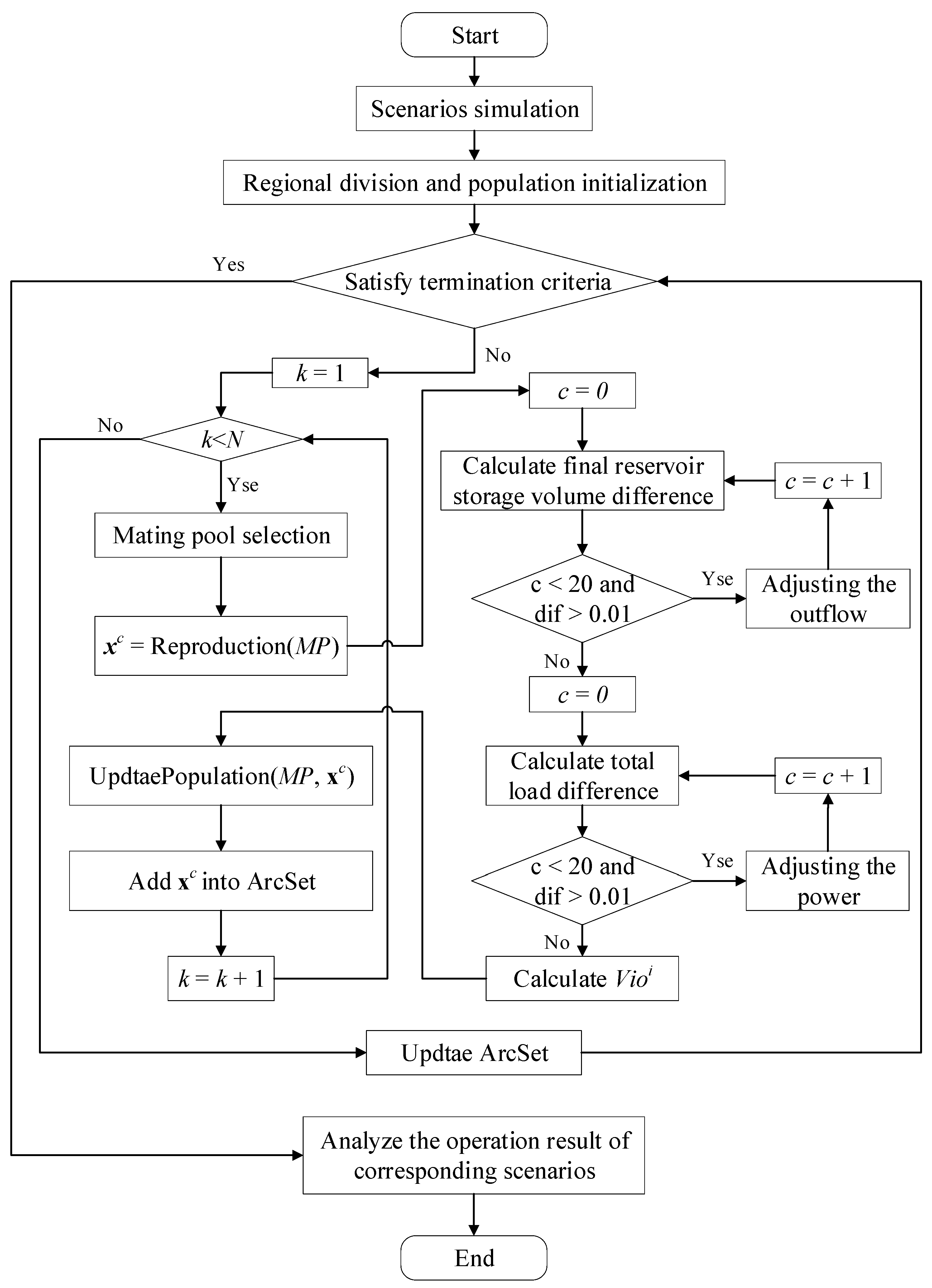
3.3. Framework for the Proposed Algorithm
| Algorithm 1: Framework for the CVRSEA |
| 1 (λ1, λ2,…, λN) = Initialization() 2 NR = InitializeNeighborRegions() 3 P = InitializePopulation() 4 while termination criteria is not satisfied do 5 for each region k = 1, 2, … , N do 6 // determine the mating pool 7 xc = Reproduction(MP) // xc is an offspring 8 P = UpdtaePopulation(MP, xc) 9 ArcSet = ArcSet {xc}; 10 end for 11 ArcSet = UpdtaeArcSet(ArcSet) 12 end while |
3.4. Constraint Handling Method
4. Results
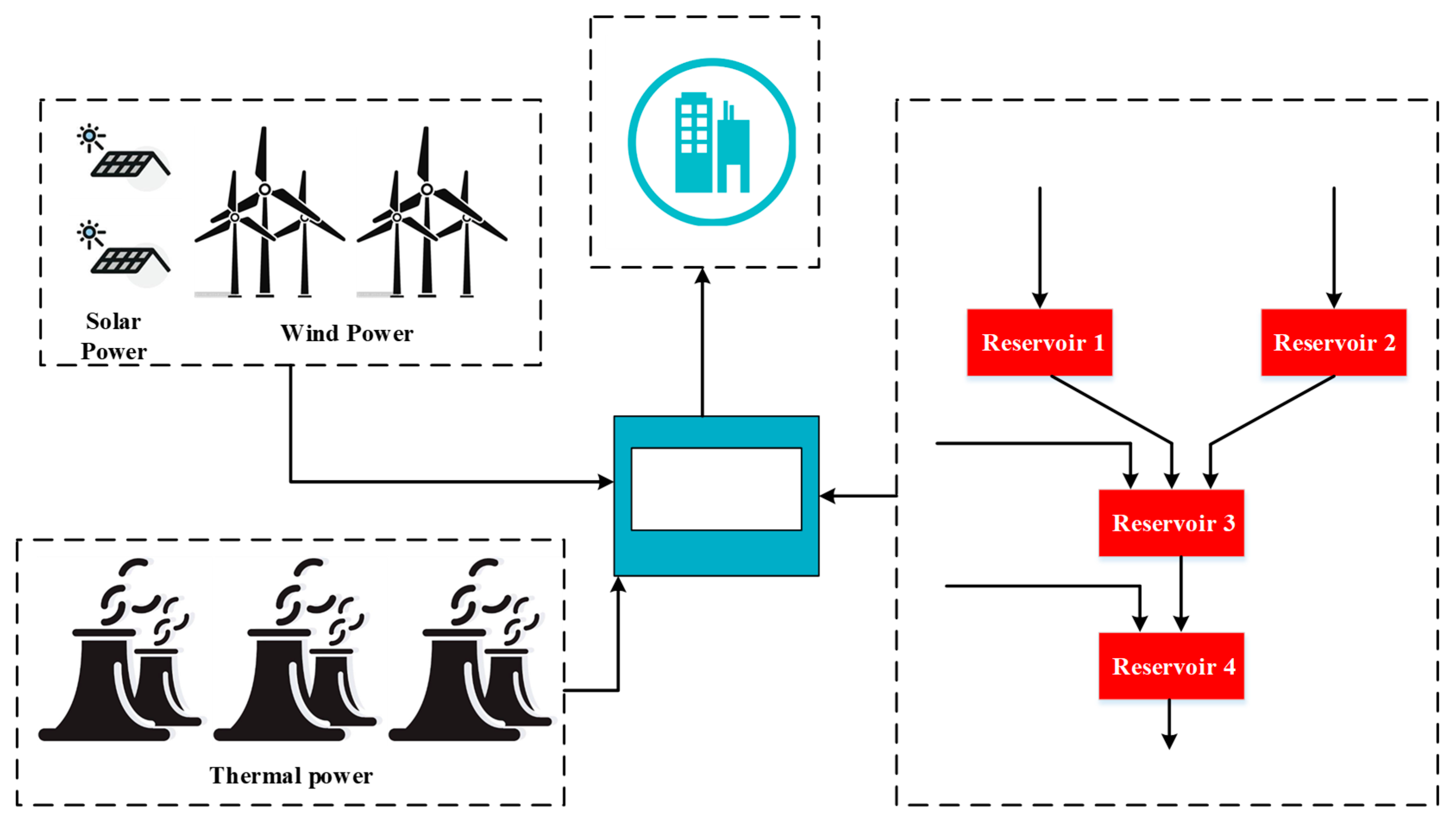
4.1. Simulation Data
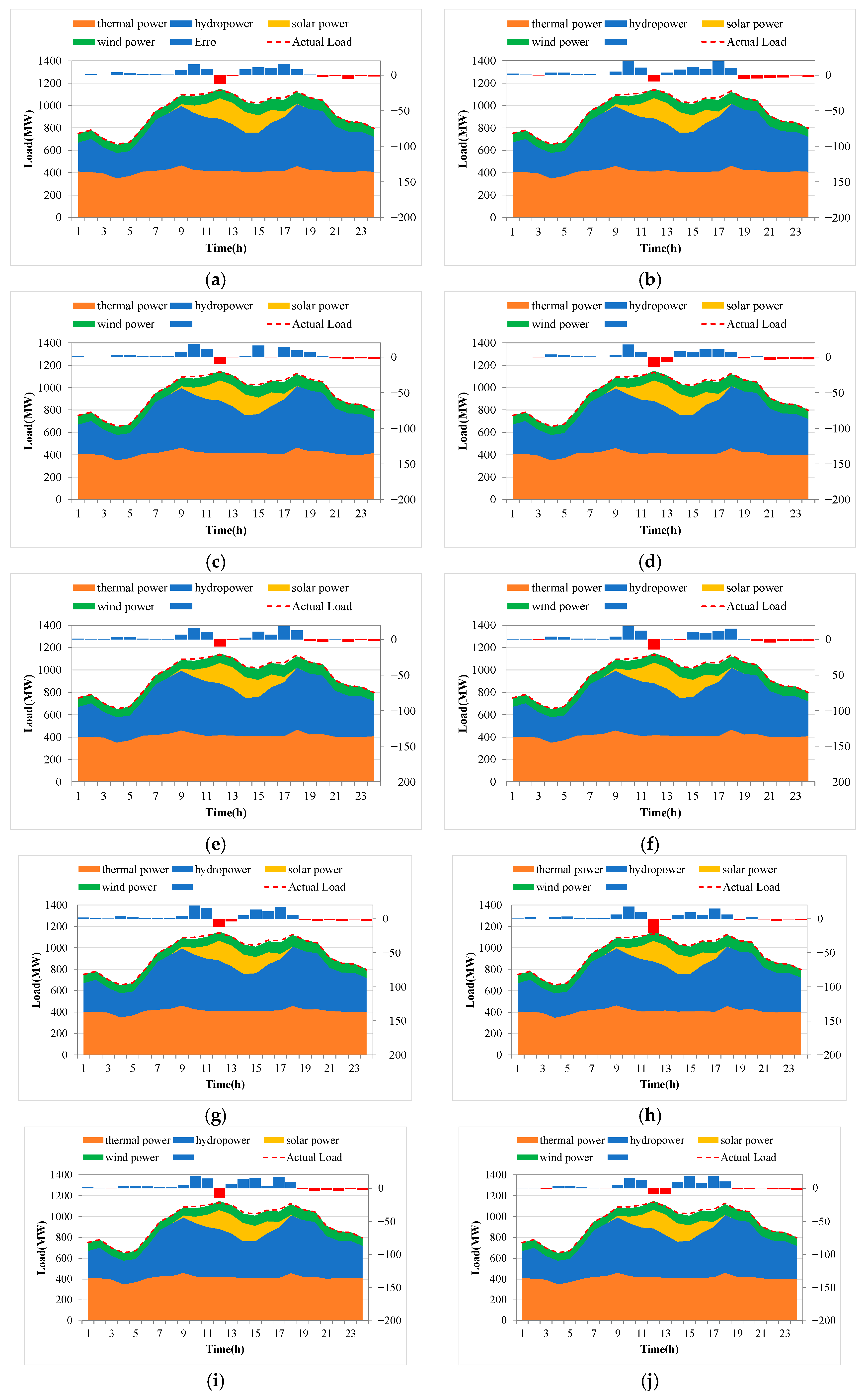
4.2. Results without Wind–Solar Energy
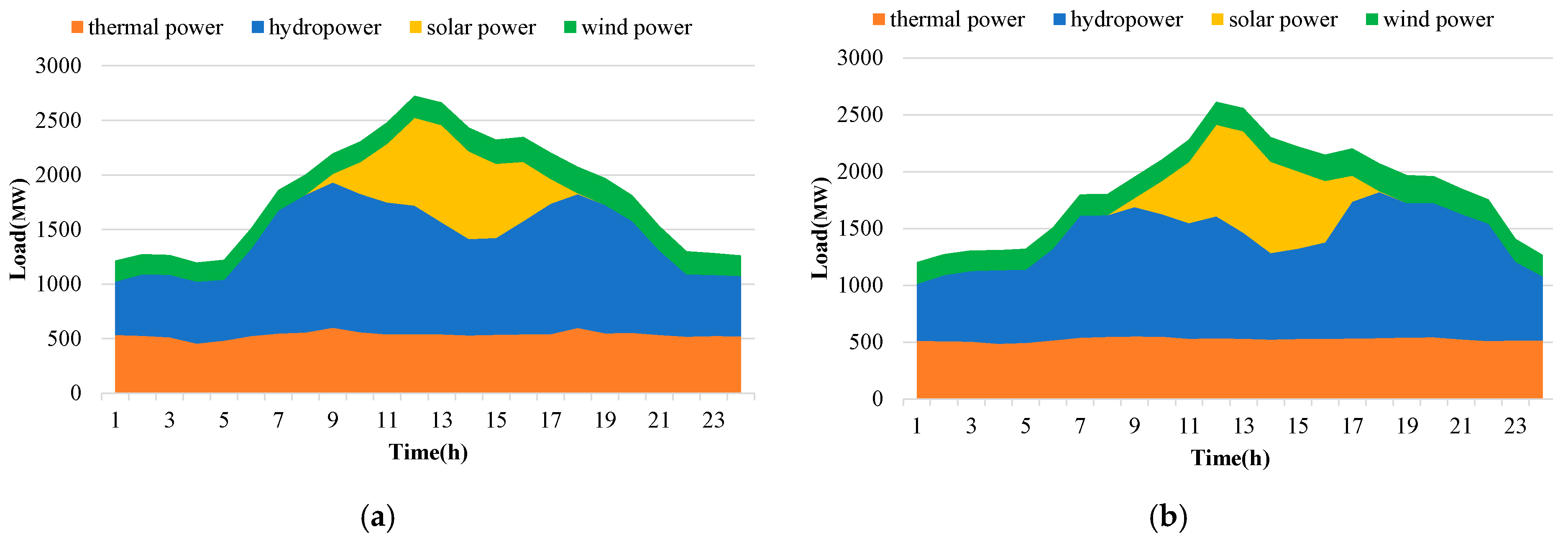
4.3. Results of Multi-Energy Hybrid System
4.4. Impacts of Uncertainty
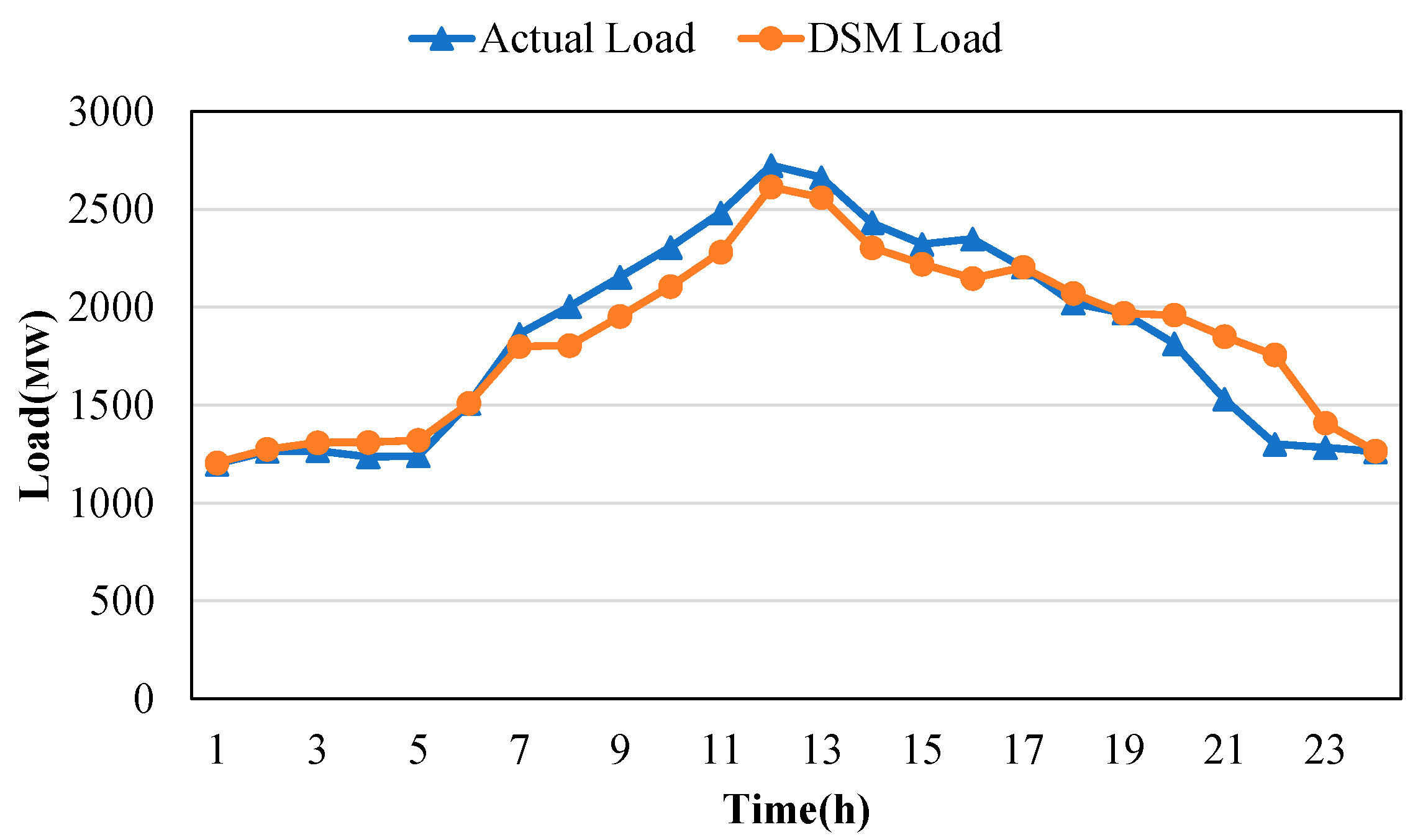
4.5. Results of a Realistic Model System Considering a Demand-Side Management Strategy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, Q.; Tapia, F.; Reith, A. Quantifying the influence of nature-based solutions on building cooling and heating energy demand: A climate specific review. Renew. Sustain. Energy Rev. 2023, 186, 113660. [Google Scholar] [CrossRef]
- Somoye, O.A. Energy crisis and renewable energy potentials in Nigeria: A review. Renew. Sustain. Energy Rev. 2023, 188, 113794. [Google Scholar] [CrossRef]
- Walmsley, T.G.; Philipp, M.; Picón-Núñez, M.; Meschede, H.; Taylor, M.T.; Schlosser, F.; Atkins, M.J. Hybrid renewable energy utility systems for industrial sites: A review. Renew. Sustain. Energy Rev. 2023, 188, 113802. [Google Scholar] [CrossRef]
- IRENA. Renewable Energy Statistics 2023; International Renewable Energy Agency: Masdar City, Abu Dhabi, 2023. [Google Scholar]
- Nowdeh, S.A.; Naderipour, A.; Davoudkhani, I.F.; Guerrero, J.M. Stochastic optimization—Based economic design for a hybrid sustainable system of wind turbine, combined heat, and power generation, and electric and thermal storages considering uncertainty: A case study of Espoo, Finland. Renew. Sustain. Energy Rev. 2023, 183, 113440. [Google Scholar] [CrossRef]
- Han, S.; He, M.; Zhao, Z.; Chen, D.; Xu, B.; Jurasz, J.; Zheng, H. Overcoming the uncertainty and volatility of wind power: Day-ahead scheduling of hydro-wind hybrid power generation system by coordinating power regulation and frequency response flexibility. Appl. Energy 2023, 333, 120555. [Google Scholar] [CrossRef]
- Kharrich, M.; Selim, A.; Kamel, S.; Kim, J. An effective design of hybrid renewable energy system using an improved Archimedes Optimization Algorithm: Acase study of Farafra, Egypt. Energy Convers. Manag. 2023, 283, 116907. [Google Scholar] [CrossRef]
- Bhandari, B.; Lee, K.-T.; Lee, C.S.; Song, C.-K.; Maskey, R.K.; Ahn, S.-H. A novel off-grid hybrid power system comprised of solar photovoltaic, wind, and hydro energy sources. Appl. Energy 2014, 133, 236–242. [Google Scholar] [CrossRef]
- Chen, Q.; Tang, Z.; Lei, Y.; Sun, Y.; Jiang, M. Feasibility analysis of nuclear–coal hybrid energy systems from the perspective of low-carbon development. Appl. Energy 2015, 158, 619–630. [Google Scholar] [CrossRef]
- Bao, X.; Li, F.; Sun, H.; Iglesias, G.; Shi, H. Performance characteristics and parameter analysis of a multi-DOF wave energy converter with hybrid power take-off systems. Energy Convers. Manag. 2023, 278, 116751. [Google Scholar] [CrossRef]
- Al Afif, R.; Ayed, Y.; Maaitah, O.N. Feasibility and optimal sizing analysis of hybrid renewable energy systems: A case study of Al-Karak, Jordan. Renew. Energy 2023, 204, 229–249. [Google Scholar] [CrossRef]
- Liu, Y.; Ye, L.; Qin, H.; Hong, X.; Ye, J.; Yin, X. Monthly streamflow forecasting based on hidden Markov model and Gaussian Mixture Regression. J. Hydrol. 2018, 561, 146–159. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, H.; Zhang, Z.; Pei, S.; Wang, C.; Yu, X.; Jiang, Z.; Zhou, J. Ensemble spatiotemporal forecasting of solar irradiation using variational Bayesian convolutional gate recurrent unit network. Appl. Energy 2019, 253, 13596. [Google Scholar] [CrossRef]
- Li, F.-F.; Qiu, J. Multi-objective optimization for integrated hydro–photovoltaic power system. Appl. Energy 2016, 167, 377–384. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Liu, Y.; Wang, Y.; Yao, L.; Li, Q.; Li, J.; Pei, S. Long Short-Term Memory Network based on Neighborhood Gates for processing complex causality in wind speed prediction. Energy Convers. Manag. 2019, 192, 37–51. [Google Scholar] [CrossRef]
- Yaghoubirad, M.; Azizi, N.; Farajollahi, M.; Ahmadi, A. Deep learning-based multistep ahead wind speed and power generation forecasting using direct method. Energy Convers. Manag. 2023, 281, 116760. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, H.; Zhang, Z.; Pei, S.; Jiang, Z.; Feng, Z.; Zhou, J. Probabilistic spatiotemporal wind speed forecasting based on a variational Bayesian deep learning model. Appl. Energy 2020, 260, 14259. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, G.; Huang, F.; Qin, H.; Wang, B.; Yi, L. Directed graph deep neural network for multi-step daily streamflow forecasting. J. Hydrol. 2022, 607, 127515. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, J.; Lu, Y.; Wang, Y.; Zhang, Y. Multi-objective differential evolution with adaptive Cauchy mutation for short-term multi-objective optimal hydro-thermal scheduling. Energy Convers. Manag. 2010, 51, 788–794. [Google Scholar] [CrossRef]
- Hamann, A.; Hug, G. Integrating Variable Wind Power Using a Hydropower Cascade. Energy Procedia 2016, 87, 108–115. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, P.; Ming, B.; Xu, W.; Huang, K.; Li, X. Deriving pack rules for hydro–photovoltaic hybrid power systems considering diminishing marginal benefit of energy. Appl. Energy 2021, 304, 117858. [Google Scholar] [CrossRef]
- Li, H.; Liu, P.; Guo, S.; Ming, B.; Cheng, L.; Yang, Z. Long-term complementary operation of a large-scale hydro-photovoltaic hybrid power plant using explicit stochastic optimization. Appl. Energy 2019, 238, 863–875. [Google Scholar] [CrossRef]
- Qi, Y.; Hu, W.; Dong, Y.; Fan, Y.; Dong, L.; Xiao, M. Optimal configuration of concentrating solar power in multienergy power systems with an improved variational autoencoder. Appl. Energy 2020, 274, 115124. [Google Scholar] [CrossRef]
- Li, H.; Mahmud, M.A.; Arzaghi, E.; Abbassi, R.; Chen, D.; Xu, B. Assessments of economic benefits for hydro-wind power systems: Development of advanced model and quantitative method for reducing the power wastage. J. Clean. Prod. 2020, 277, 123823. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Li, J.; Liu, Y.; Yao, L.; Wang, Y.; Zhou, J. Short-term optimal operation of wind-solar-hydro hybrid system considering uncertainties. Energy Convers. Manag. 2020, 205, 112405. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, G.; Wen, X.; Tan, Q.; Zhang, P.; Liu, Z. Coordinated operation of conventional hydropower plants as hybrid pumped storage hydropower with wind and photovoltaic plants. Energy Convers. Manag. 2023, 277, 116654. [Google Scholar] [CrossRef]
- Liu, Y.; Zhan, X.; Lyu, H.; Qin, H. Region search evolutionary algorithm with constraint handling for multi-objective short-term wind-solar-hydro-thermal scheduling. E3S Web Conf. 2021, 233, 01018. [Google Scholar] [CrossRef]
- Fan, J.-L.; Huang, X.; Shi, J.; Li, K.; Cai, J.; Zhang, X. Complementary potential of wind-solar-hydro power in Chinese provinces: Based on a high temporal resolution multi-objective optimization model. Renew. Sustain. Energy Rev. 2023, 184, 113566. [Google Scholar] [CrossRef]
- Yang, T.; Ma, C.; Pérez-Díaz, J.I.; Patelli, E.; Liu, C.; Chen, D.; Xu, B. Identifying the functional form and operation rules of energy storage pump for a hydro-wind-photovoltaic hybrid power system. Energy Convers. Manag. 2023, 296, 117700. [Google Scholar] [CrossRef]
- Ding, Z.; Fang, G.; Wen, X.; Tan, Q.; Mao, Y.; Zhang, Y. Long-term operation rules of a hydro–wind–photovoltaic hybrid system considering forecast information. Energy 2024, 288, 129634. [Google Scholar] [CrossRef]
- Li, Y.; Ming, B.; Huang, Q.; Wang, Y.; Liu, P.; Guo, P. Identifying effective operating rules for large hydro–solar–wind hybrid systems based on an implicit stochastic optimization framework. Energy 2022, 245, 123260. [Google Scholar] [CrossRef]
- Muhsen, D.H.; Ghazali, A.B.; Khatib, T. Multiobjective differential evolution algorithm-based sizing of a standalone photovoltaic water pumping system. Energy Convers. Manag. 2016, 118, 32–43. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM J. Optim. 1998, 8, 631–657. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, H.; Zhang, Z.; Yao, L.; Wang, C.; Mo, L.; Ouyang, S.; Li, J. A region search evolutionary algorithm for many-objective optimization. Inf. Sci. 2019, 488, 19–40. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, H.L.; Gu, F. A Cost Value Based Evolutionary Many-Objective Optimization Algorithm with Neighbor Selection Strategy. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]





| Time | Pd | R1 | R2 | R3 | R4 |
|---|---|---|---|---|---|
| 1 | 750 | 10 | 8 | 8.1 | 2.8 |
| 2 | 780 | 9 | 8 | 8.2 | 2.4 |
| 3 | 700 | 8 | 9 | 4 | 1.6 |
| 4 | 650 | 7 | 9 | 2 | 0 |
| 5 | 670 | 6 | 8 | 3 | 0 |
| 6 | 800 | 7 | 7 | 4 | 0 |
| 7 | 950 | 8 | 6 | 3 | 0 |
| 8 | 1010 | 9 | 7 | 2 | 0 |
| 9 | 1090 | 10 | 8 | 1 | 0 |
| 10 | 1080 | 11 | 9 | 1 | 0 |
| 11 | 1100 | 12 | 9 | 1 | 0 |
| 12 | 1150 | 10 | 8 | 2 | 0 |
| 13 | 1110 | 11 | 8 | 4 | 0 |
| 14 | 1030 | 12 | 9 | 3 | 0 |
| 15 | 1010 | 11 | 9 | 3 | 0 |
| 16 | 1060 | 10 | 8 | 2 | 0 |
| 17 | 1050 | 9 | 7 | 2 | 0 |
| 18 | 1120 | 8 | 6 | 2 | 0 |
| 19 | 1070 | 7 | 7 | 1 | 0 |
| 20 | 1050 | 6 | 8 | 1 | 0 |
| 21 | 910 | 7 | 9 | 2 | 0 |
| 22 | 860 | 8 | 9 | 2 | 0 |
| 23 | 850 | 9 | 8 | 1 | 0 |
| 24 | 800 | 10 | 8 | 0 | 0 |
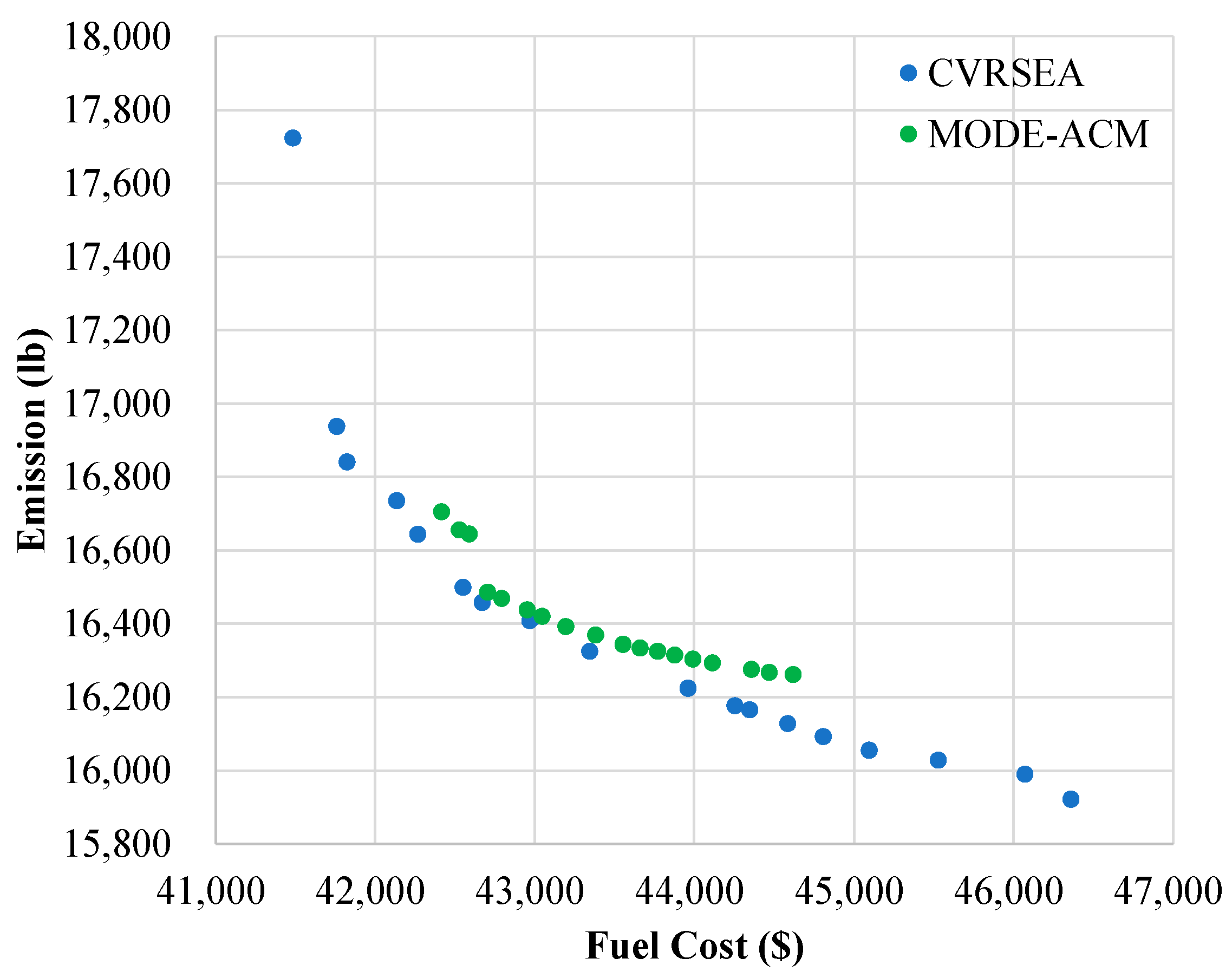
| Scheme | MODE-ACM | CVRSEA | ||
|---|---|---|---|---|
| Fuel Cost ($) | Emission (lb) | Fuel Cost ($) | Emission (lb) | |
| 1 | 42,417 | 16,706 | 41,485 | 17,723 |
| 2 | 42,432 | 16,688 | 41,623 | 17,527 |
| 3 | 42,479 | 16,672 | 41,659 | 16,980 |
| 4 | 42,529 | 16,656 | 41,760 | 16,938 |
| 5 | 42,590 | 16,645 | 41,825 | 16,841 |
| 6 | 42,609 | 16,523 | 41,968 | 16,822 |
| 7 | 42,650 | 16,500 | 42,001 | 16,733 |
| 8 | 42,705 | 16,486 | 42,136 | 16,735 |
| 9 | 42,793 | 16,469 | 42,268 | 16,644 |
| 10 | 42,870 | 16,455 | 42,408 | 16,556 |
| 11 | 42,952 | 16,439 | 42,551 | 16,499 |
| 12 | 43,046 | 16,421 | 42,672 | 16,458 |
| 13 | 43,125 | 16,407 | 42,834 | 16,431 |
| 14 | 43,196 | 16,393 | 42,970 | 16,409 |
| 15 | 43,289 | 16,382 | 43,150 | 16,360 |
| 16 | 43,382 | 16,370 | 43,345 | 16,326 |
| 17 | 43,474 | 16,358 | 43,569 | 16,292 |
| 18 | 43,553 | 16,344 | 43,960 | 16,225 |
| 19 | 43,660 | 16,334 | 44,254 | 16,177 |
| 20 | 43,770 | 16,326 | 44,346 | 16,166 |
| 21 | 43,878 | 16,315 | 44,585 | 16,129 |
| 22 | 43,991 | 16,304 | 44,707 | 16,143 |
| 23 | 44,113 | 16,294 | 45,095 | 16,056 |
| 24 | 44,249 | 16,286 | 45,248 | 16,045 |
| 25 | 44,357 | 16,276 | 45,529 | 16,029 |
| 26 | 44,470 | 16,268 | 46,172 | 15,991 |
| 27 | 44,619 | 16,262 | 46,359 | 15,922 |
| 28 | 44,724 | 16,253 | 46,501 | 15,949 |
| 29 | 44,842 | 16,249 | 47,049 | 15,883 |
| 30 | 44,962 | 16,242 | 47,872 | 15,829 |
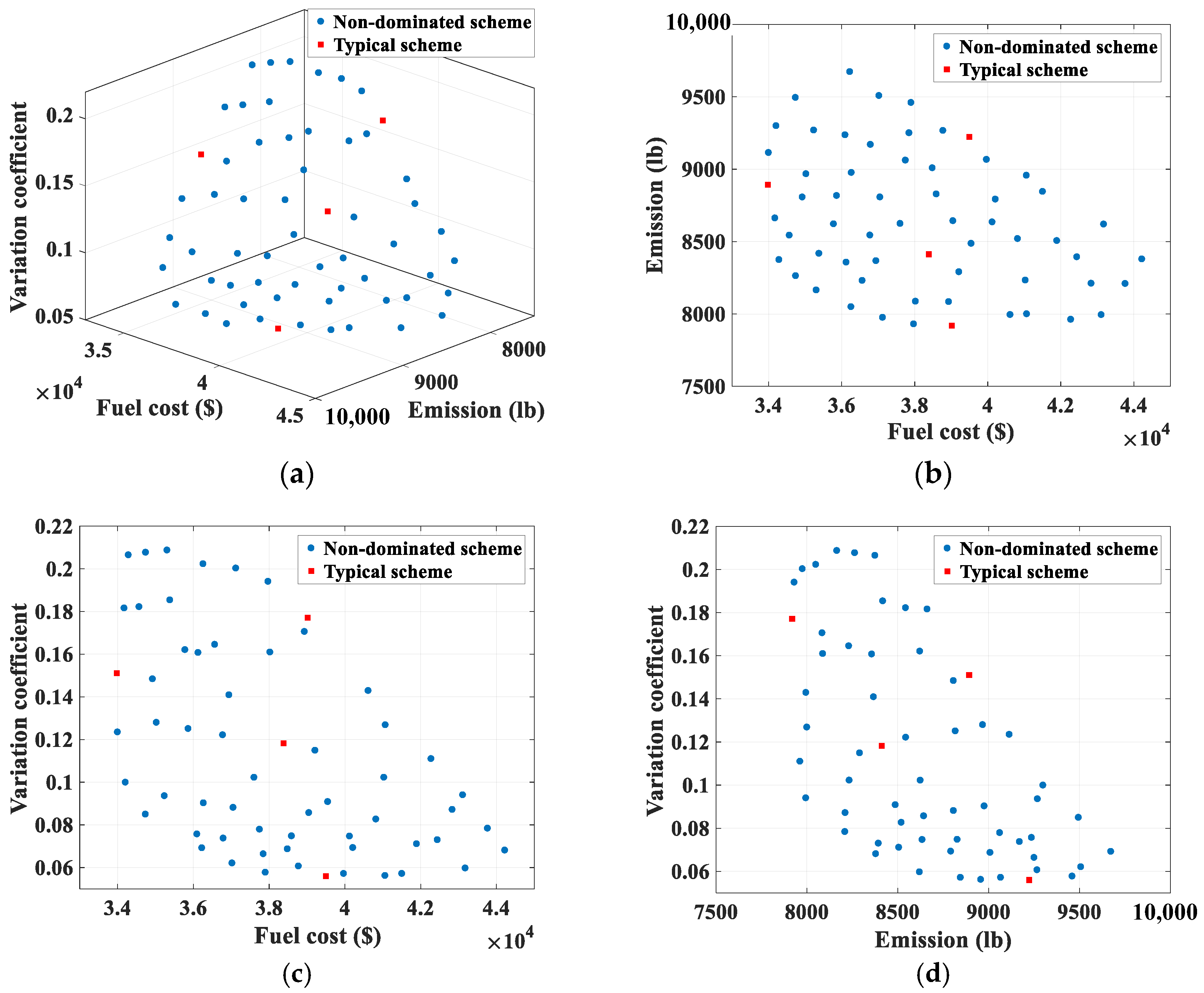
| Scheme | Fuel Cost ($) | Emission (lb) | CV | Scheme | Fuel Cost ($) | Emission (lb) | CV |
|---|---|---|---|---|---|---|---|
| 1 | 33,974 | 8893 | 0.151 | 31 | 37,901 | 9460 | 0.058 |
| 2 | 33,997 | 9114 | 0.123 | 32 | 37,972 | 7930 | 0.194 |
| 3 | 34,173 | 8662 | 0.182 | 33 | 38,023 | 8087 | 0.161 |
| 4 | 34,206 | 9299 | 0.100 | 34 | 38,384 | 8413 | 0.118 |
| 5 | 34,285 | 8375 | 0.206 | 35 | 38,484 | 9009 | 0.069 |
| 6 | 34,567 | 8543 | 0.182 | 36 | 38,593 | 8828 | 0.075 |
| 7 | 34,735 | 9495 | 0.085 | 37 | 38,775 | 9267 | 0.061 |
| 8 | 34,741 | 8263 | 0.208 | 38 | 38,933 | 8084 | 0.171 |
| 9 | 34,923 | 8807 | 0.148 | 39 | 39,019 | 7919 | 0.177 |
| 10 | 35,024 | 8968 | 0.128 | 40 | 39,049 | 8643 | 0.086 |
| 11 | 35,236 | 9269 | 0.094 | 41 | 39,213 | 8290 | 0.115 |
| 12 | 35,305 | 8165 | 0.209 | 42 | 39,497 | 9222 | 0.056 |
| 13 | 35,380 | 8418 | 0.185 | 43 | 39,548 | 8487 | 0.091 |
| 14 | 35,779 | 8622 | 0.162 | 44 | 39,967 | 9067 | 0.057 |
| 15 | 35,863 | 8817 | 0.125 | 45 | 40,123 | 8635 | 0.075 |
| 16 | 36,095 | 9237 | 0.076 | 46 | 40,211 | 8792 | 0.069 |
| 17 | 36,125 | 8357 | 0.161 | 47 | 40,615 | 7995 | 0.143 |
| 18 | 36,225 | 9673 | 0.069 | 48 | 40,819 | 8520 | 0.083 |
| 19 | 36,257 | 8049 | 0.202 | 49 | 41,030 | 8233 | 0.102 |
| 20 | 36,266 | 8976 | 0.090 | 50 | 41,060 | 8957 | 0.056 |
| 21 | 36,565 | 8231 | 0.165 | 51 | 41,068 | 8000 | 0.127 |
| 22 | 36,775 | 8544 | 0.122 | 52 | 41,504 | 8845 | 0.057 |
| 23 | 36,789 | 9170 | 0.074 | 53 | 41,893 | 8506 | 0.071 |
| 24 | 36,941 | 8367 | 0.141 | 54 | 42,276 | 7962 | 0.111 |
| 25 | 37,022 | 9508 | 0.062 | 55 | 42,442 | 8394 | 0.073 |
| 26 | 37,050 | 8807 | 0.088 | 56 | 42,834 | 8211 | 0.087 |
| 27 | 37,122 | 7975 | 0.200 | 57 | 43,111 | 7994 | 0.094 |
| 28 | 37,603 | 8624 | 0.102 | 58 | 43,177 | 8620 | 0.060 |
| 29 | 37,748 | 9062 | 0.078 | 59 | 43,766 | 8209 | 0.078 |
| 30 | 37,847 | 9251 | 0.066 | 60 | 44,223 | 8379 | 0.068 |
| Scheme | Fuel Cost ($) | Emissions (lb) | CV | Sum PT | Sum Ph | Sum Ps | Sum Pw | Total Load |
|---|---|---|---|---|---|---|---|---|
| Typical 1 | 33,974 | 8893 | 0.151 | 9372 | 10,079 | 1138 | 2061 | 22,650 |
| Typical 2 | 39,019 | 7919 | 0.177 | 9209 | 10,241 | 1138 | 2061 | 22,650 |
| Typical 3 | 39,497 | 9222 | 0.056 | 9812 | 9638 | 1138 | 2061 | 22,650 |
| Typical 4 | 38,384 | 8413 | 0.118 | 9420 | 10,030 | 1138 | 2061 | 22,650 |
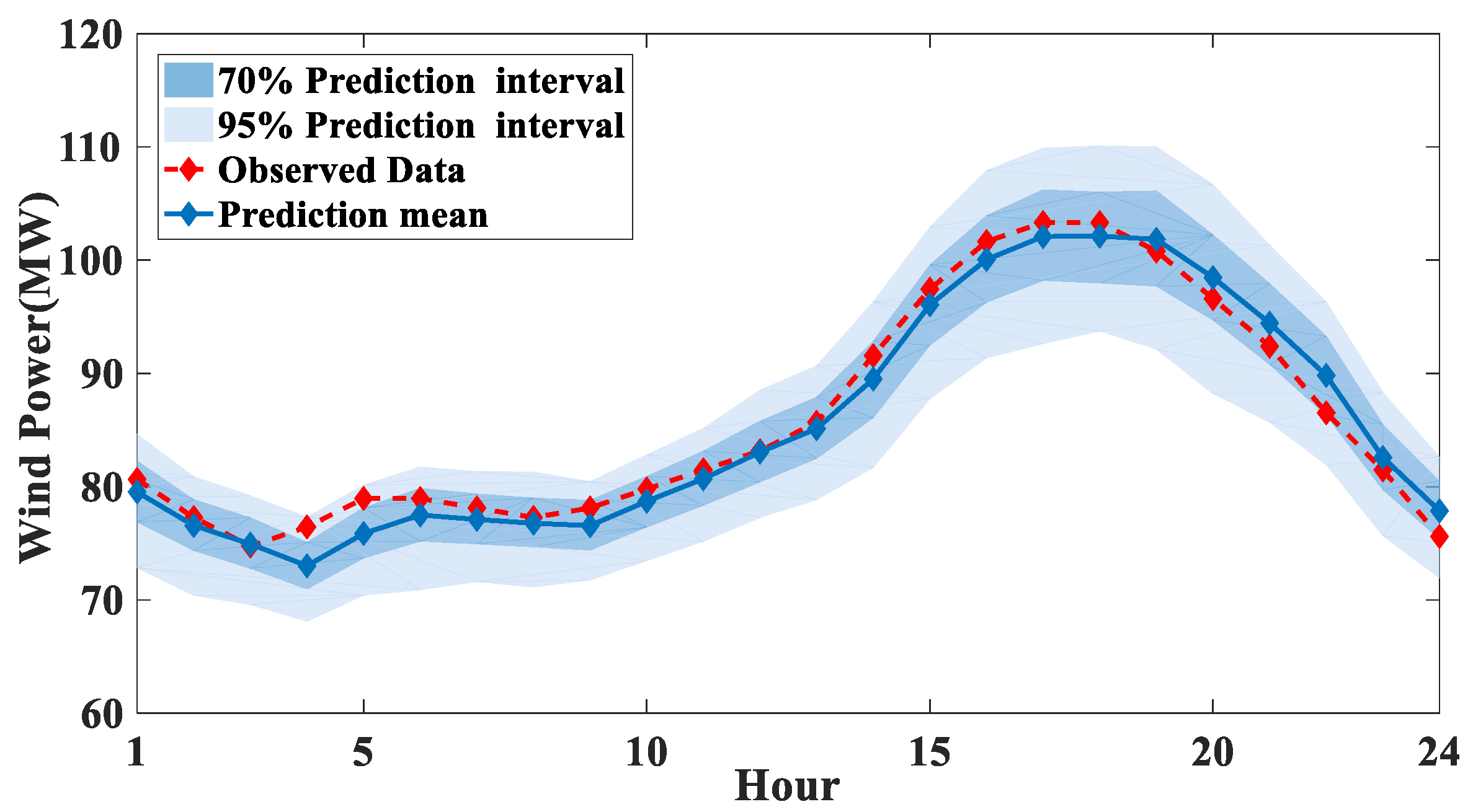
| Time (h) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wind power (MW) | obs | 81 | 77 | 75 | 76 | 79 | 79 | 78 | 77 | 78 | 80 | 81 | 83 |
| fore | 80 | 77 | 75 | 73 | 76 | 77 | 77 | 77 | 77 | 79 | 81 | 83 | |
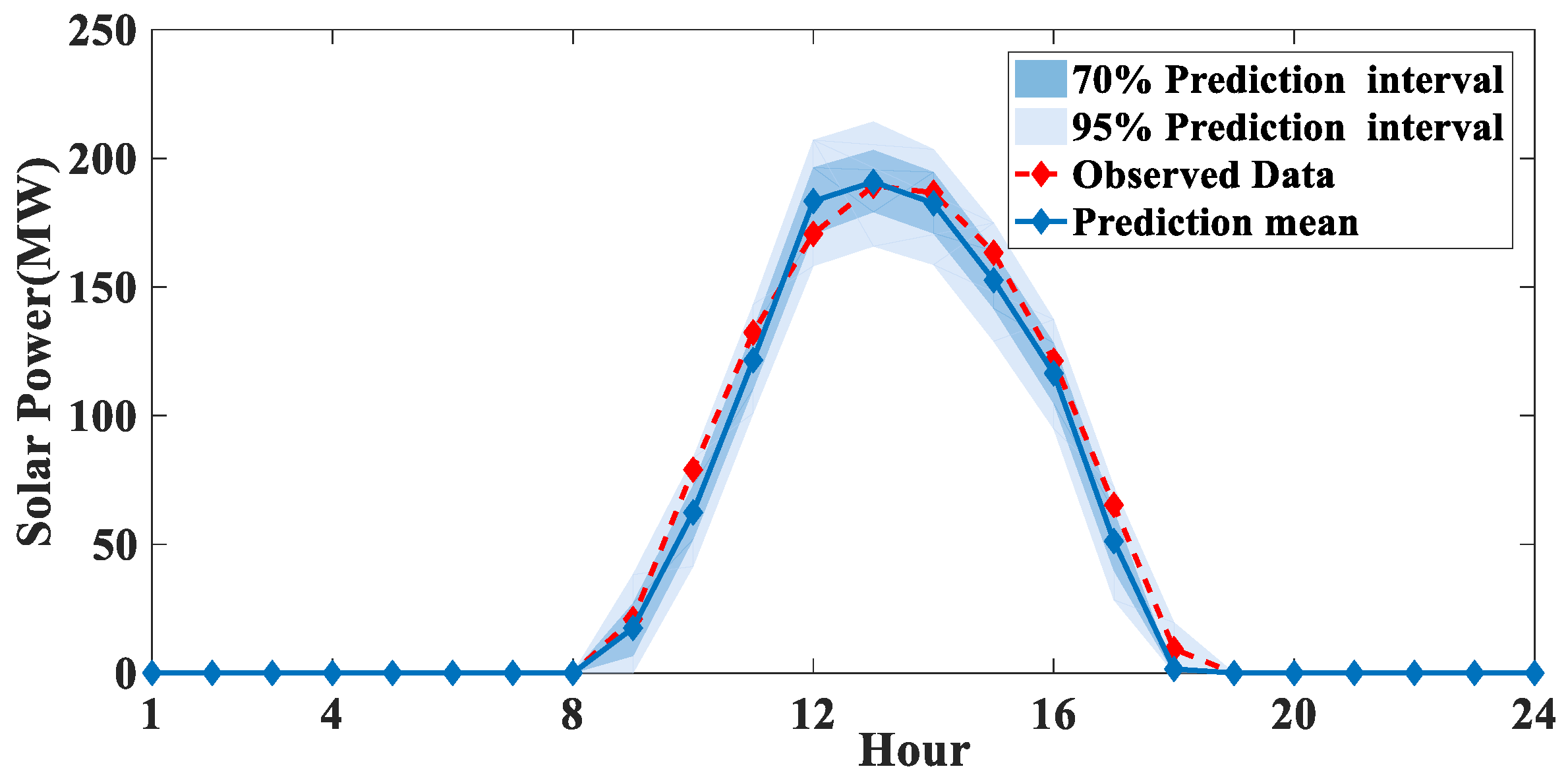
| Solar power (MW) | obs | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 21 | 79 | 132 | 171 |
| fore | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 17 | 62 | 122 | 183 | |
| Time (h) | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
| Wind power (MW) | obs | 86 | 92 | 97 | 102 | 103 | 103 | 101 | 97 | 92 | 87 | 81 | 76 |
| fore | 85 | 90 | 96 | 100 | 102 | 102 | 102 | 98 | 94 | 90 | 83 | 78 | |
| Solar power (MW) | obs | 189 | 187 | 163 | 121 | 65 | 9 | 0 | 0 | 0 | 0 | 0 | 0 |
| fore | 191 | 183 | 153 | 116 | 51 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, Y.; Hou, G.; Qin, H. Multi-Objective Short-Term Operation of Hydro–Wind–Photovoltaic–Thermal Hybrid System Considering Power Peak Shaving, the Economy and the Environment. Energies 2024, 17, 4698. https://doi.org/10.3390/en17184698
Liu Y, Li Y, Hou G, Qin H. Multi-Objective Short-Term Operation of Hydro–Wind–Photovoltaic–Thermal Hybrid System Considering Power Peak Shaving, the Economy and the Environment. Energies. 2024; 17(18):4698. https://doi.org/10.3390/en17184698
Chicago/Turabian StyleLiu, Yongqi, Yuanyuan Li, Guibing Hou, and Hui Qin. 2024. "Multi-Objective Short-Term Operation of Hydro–Wind–Photovoltaic–Thermal Hybrid System Considering Power Peak Shaving, the Economy and the Environment" Energies 17, no. 18: 4698. https://doi.org/10.3390/en17184698
APA StyleLiu, Y., Li, Y., Hou, G., & Qin, H. (2024). Multi-Objective Short-Term Operation of Hydro–Wind–Photovoltaic–Thermal Hybrid System Considering Power Peak Shaving, the Economy and the Environment. Energies, 17(18), 4698. https://doi.org/10.3390/en17184698






