Abstract
The dielectric constant of aviation turbine fuel is leveraged by aircraft fuel quantity indicator systems (FQISs) using the Clausius–Mossotti relation, which assumes no significant dipole moments. For fossil-derived jet fuel containing relatively consistent fractions of polar aromatic molecules, this is appropriate. However, the interest in sustainable aviation fuels (SAFs) to reduce the carbon intensity of commercial aviation has brought attention to the uncertainty of the FQISs’ compatibility for low- or zero-aromatic fuels exhibiting dielectric constant values outside of the conventional Jet-A range. A dielectric constant model accounting for the varying dipole moments of both aromatic and non-aromatic jet-range hydrocarbons improves the community’s understanding of fuel composition on FQISs’ operability and provides a tool suitable for fuel performance property optimizations while maintaining compatibility with current aircraft systems. Here, the Clausius–Mossotti relation is first evaluated against a training dataset of 240 dielectric constant and density measurements (48 neat hydrocarbons each measured at five temperatures). Then, the dipole moment is calculated for each species of interest using open-source computational chemistry software, and a second-degree binomial regression is performed over the training data to correct for the error in the Clausius–Mossotti relation. The Clausius–Mossotti relation exhibited an R2 value of 0.54, which increased to 0.92 when terms for the dipole correction were added to the model. The improved accuracy from this model establishes a computationally inexpensive framework for modeling theoretical fuel compositions that demonstrate improved performance characteristics (sooting propensity, thermal management, aircraft efficiency, etc.) while remaining within key limiting property constraints, such as the dielectric constant.
1. Introduction
Sustainable aviation fuel (SAF) has been identified as a leading prospect for meeting the decarbonization goals of commercial aviation [1]. To advance this technology, a joint effort by the United States’ Department of Energy, Department of Agriculture, Department of Transportation, and Federal Aviation Administration has put forth a number of domestic SAF production targets, including 3 billion gallons of SAF by 2030 and 35 billion by 2050 (10% and 100% of the United States’ projected fuel demand, respectively) [2]. Standing in the way of these goals are a number of obstacles, not the least of which is the compatibility of the current operational aircraft fleet with novel SAFs. Currently, in-flight fuel safety and performance characteristics are maintained by a maximum 50%v blending limit for SAF in conventional petroleum-based fuels [3]. Ensuring full fleet compatibility past this limit is a critical step towards meeting the stated industry targets.
Many SAF compositions significantly vary from those of conventional petroleum jet fuel (Jet-A), and ongoing regulatory efforts are in place to ensure safe operation for aircraft utilizing SAFs. Due to the high cost of developing novel fuels, the community benefits from reliable predictive methods for fuel properties critical to engine and fuel system function. One of these properties, the dielectric constant, is central to an empirical version of the Clausius–Mossotti relation (C-M) with density used in capacitance-based fuel quantity indicator systems (FQISs) [4]. If this relationship for a prospective SAF is far outside of the expected fuel values used by the system, then a significant error in density can occur as a result, potentially leading to an incorrect indicated fuel mass on board the aircraft [5,6]. All of the currently approved (up to 50%v) low-aromatic SAFs would fall into this category if they were to be allowed up to 100%v [7,8].
The conventional fuel dielectric constant is highly dependent upon aromatic content. Existing SAF technologies that contain little-to-no aromatics, such as synthetic paraffinic kerosene (SPK) or cycloparaffinic kerosene (CPK), do not match the conventional fuel experience range for density as a function of the dielectric constant [9]. Both density and the relationship between density and the dielectric constant restrict, to varying degrees, the blend fraction of low-aromatic synthetic fuels, which are otherwise viewed favorably in terms of LHV, sooting propensity, and thermal stability [10].
An O-ring seal swell is an additional fuel property of concern to engine and aircraft manufacturers that is driven largely by aromatics in conventional fuels [11]. The inclusion of cycloalkanes at larger fractions is currently seen as a low-sooting alternative to induce adequate seal swell and density [12,13], but cannot be used to improve fuel gauging relative to the Jet-A range [7]. Understanding how to improve the viability of low- or zero-aromatic SAFs in the entirety of current aircraft systems requires accurate prediction methods for the properties of aromatic species and potential substitutes, namely certain cycloalkanes.
Here, the dielectric constant is predicted using a two-part model. First, QSPR polarizability predictions from Wang et al. [14] and density measurements are applied to the theoretical version of the Clausius–Mossotti relation, which assumes no permanent molecular dipole moments [15,16], to demonstrate its efficacy in jet fuel applications. Second, the permanent dipole moments of 240 molecules are calculated from first principles and are used as an independent variable in a second-degree binomial regression to predict the difference between the empirical dielectric constant data of Yang et al. [7] and the Clausius–Mossotti dielectric calculation. Adding the terms of this regression to the theoretical Clausius–Mossotti relation results in a new, computationally inexpensive dielectric constant prediction method that, when used in tandem with the blending rules verified by Yang et al. [7], can be easily implemented into fuel-composition optimizations to effectively forecast fuels that will maintain compatibility with current aircraft fuel systems, including FQISs, while exhibiting advantageous performance properties [10,17,18].
2. Materials and Methods
The 230 dielectric constant and density measurements (46 molecules at 10, 15, 20, 25, and 30 °C) found in Yang et al. [7] are utilized here along with 10 additional data points, 1,3,5-trimethylcyclohexane (TCI America, Portland, OR, USA, Purity >98.0%) and cis-1,3-dimethylcyclohexane (TCI America, Portland, OR, USA, Purity >99.0%), each at the same 5 temperatures as the previous study, for model development. The 10 added measurements can be found in Tables S1 and S2 of the Supplementary Information (SI). The temperatures considered here cover a moderate fraction of the expected range for an in-service jet fuel. However, historical jet fuel dielectric constant data [19,20] indicate a linear relationship on the Clausius–Mossotti plot for each fuel over a more comprehensive temperature range, −35 to 70 °C. Although currently unavailable, single-species dielectric constant data over a wider temperature range, which will improve modeling efforts, will be a focus of future experimental work. To provide further context towards the dipole moments of jet-range hydrocarbons (C7 to C18), the permanent dipoles of 1827 molecules found in the NIST Web Thermo Tables Version 2-2012 [21] are computed and discussed.
Polarizability is a relatively easily predicted property, and multiple QSPR/QSAR models exist for this purpose [14,22]. Here, polarizability is predicted using Wang et al.’s Model 2E [14]. This is a simple QSPR model built with 420 experimental polarizability data points and has a coefficient of determination (R2) equal to 0.9978. While the present study employs quantum mechanical calculations for the dipole moment, this empirical model was favored for predicting polarizability values. In addition to added simplicity, this choice is based on Wang et al.’s [14] comparison of Model 2E to quantum mechanical molecular polarizabilities, which showed superior performance of Model 2E relative to the experimental values.
The dipole moment represents the solution to the dipole operator with respect to the electronic wave function of the molecule at its ground electronic energy state [23]. These two steps, optimizing a molecule’s atomic coordinates to its ground state and evaluating the wave function, are somewhat computationally expensive even for hydrocarbons. Additionally, molecules often have multiple electronic energy local minima, representing different electronic states for the same molecule. Accounting for all of these conformations requires additional iterations of an already time-consuming calculation.
Fortunately, easily accessible computational quantum chemistry software packages [24,25] exist for running calculations for the molecular dipole moment. With the species’ isomeric SMILES string [26] and a random number generator ‘seed’ as inputs, RDKit Version 2023.09.05 [27] was used for obtaining initial atomic coordinates. Then, the Psi4 software package Version 1.9.1 [24] was employed to handle the quantum mechanical calculations using the Hartree–Fock method [23] and 6-31G** basis set [28,29]. To account for the presence of multiple local electronic energy minima, this computation was repeated with 100 different atomic coordinate seeds for each species in the database. The average of the 100 dipole moment calculations for each molecule was then stored for use in property predictions. Additionally, it is important to note that the basis set and level of theory used here are simplistic and computationally inexpensive relative to what can be found in work dedicated to determining optimal dipole calculation methods [23,30,31]. Improved dipole calculations would, in all likelihood, lead to improved dielectric predictions, at the cost of computational time not afforded to the work shown here.
As mentioned, the prediction method for the dielectric constant described here consists of two parts. The first part stems from the Clausius–Mossotti relation (Equation (1)) for the dielectric constant () with Avogadro’s number (), molar volume (), and molecular polarizability () [15].
Solving Equation (1) for the dielectric constant results in Equation (2).
The original development of the Clausius–Mossotti relation was for applications to substances without a significant permanent dipole moment, such as noble gases or simple aliphatic hydrocarbons [15,16]. Hydrocarbons are generally considered non-polar due to the similar electronegativities of hydrogen and carbon (2.1 and 2.5, respectively). However, the hydrogen/carbon (H/C) ratio and structural differences between hydrocarbon classes (n-/iso-alkanes, cycloalkanes, aromatics, etc.) does introduce a small and varied dipole moment. This implies that Equation (2) may underrepresent the impact of dipole moments on the dielectric constant, or that, in other words, some hydrocarbons can have non-negligible permanent dipole moments. A more comprehensive overview of the Clausius–Mossotti relation in aviation applications can be found in the works of Yang et al. [7] and Kosir et al. [9].
Part two of the model presented here aims to address the potential impacts of the dipole moments of molecules. Using data for 48 neat molecules, the difference between the measured dielectric constant and the result of Equation (2) was calculated. A second-degree binomial regression was performed on this dataset with the dipole moment acting as the independent variable. Multiple forms of regression, with and without forcing the y-intercept term to zero, were considered. Ultimately, the second-degree binomial form with an intercept equal to zero was chosen for its high accuracy compared to the other forms considered and its semblance to the theoretical applications of dipole moments in dielectric constant calculations [32]. The results of the regression, including 5 k-fold cross-validation scores indicating no overfitting, can be found in Figure S1 and Table S3 of the SI. The dielectric constant prediction for a given species () was computed according to Equation (3) as the sum of the Equation (2) result () and the output of this regression with the dipole moment () as calculated by the method described above.
3. Results and Discussion
3.1. Dipole Moment Calculation
Figure 1 shows the results of the dipole moment calculations for the NIST database of 1827 jet-range hydrocarbons. While confirmation of these values remains difficult due to the lack of available dipole moment data in the archival literature, this self-consistent dataset is convenient for understanding molecular dipole moments relative to hydrocarbon class and carbon number, as well as the variance of dipoles within these descriptors. It is suitable for relating Equation (2) model error to the calculated dipole moment; however, the coefficients of the regression are specific to the dipole calculation method presented in this article.
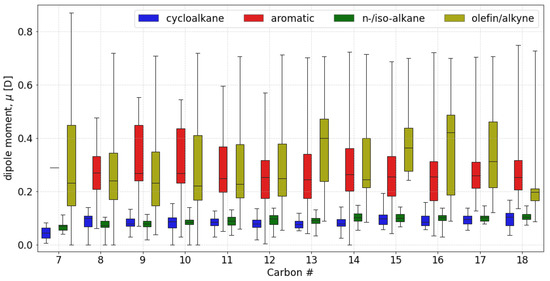
Figure 1.
Calculated dipole moments sorted by carbon number and general hydrocarbon class. Cycloalkanes include mono, di, and tricycloalkanes. Aromatics include alkylbenzenes, di-aromatics, and cyclo-aromatics. Olefins include linear and branched alkenes, alkynes, and dienes.
The most polar hydrocarbons common to aviation turbine fuels, di-aromatics, have dipole moments well below 1 Debye (D), which is often considered non-polar within the context of heteroatom-containing hydrocarbons, as well as most inorganic compounds. For clarity, dipole moments are discussed here in terms that are relative to the ranges shown in Figure 1. For example, a high dipole moment for a constituent fuel molecule would be 0.6 D.
As expected, n-, iso-, and cyclic alkanes all have a much lower mean dipole moment across all carbon numbers compared to unsaturates (aromatics, olefins, and alkynes). Unsaturated compounds also show a much higher variance within carbon number groups, with some species exhibiting lower dipole moments than many alkanes. This makes the identification of carbon-number trends among unsaturated compounds difficult. Alkanes show a slight increase in the dipole moment with higher carbon number, likely due to an increased opportunity for branching.
3.2. Model Performance
The dielectric constant measurements of 48 neat molecules at five temperatures were compared with values predicted from the Clausius–Mossotti relation (Equation (2)) using the measured density and QSPR-calculated polarizability [14] as inputs. As shown in Figure 2 and Table 1, the majority of n-, iso-, and cycloalkanes in the dataset show good agreement with this equation due to the relatively low dipole moments of most aliphatic hydrocarbons. However, the two additional cycloalkanes measured for this study, 1,3,5-trimethylcyclohexane and cis-1,3-dimethylcyclohexane, show a MARE nearly five times higher than the rest of the alkanes in the dataset and have the two largest dipole moments within the alkanes in the dataset. Since these molecules appear much nearer to the conventional fuel range compared to other alkanes, it is important to ensure that the dielectric constant can be correctly predicted for similar molecules. This is discussed further in Section 3.3. Additionally, for unsaturated molecules exhibiting higher dipole moments, Equation (2) consistently underestimated the dielectric constant leading to a poor overall R2 of 0.54 for the Clausius–Mossotti relation. Given the importance of aromatics for meeting the conventional jet fuel range for the dielectric constant, and the potential impact of certain cycloalkanes as higher-performing substitutes for aromatics in synthetic fuels, Equation (2) alone is not sufficient for accurate predictions.
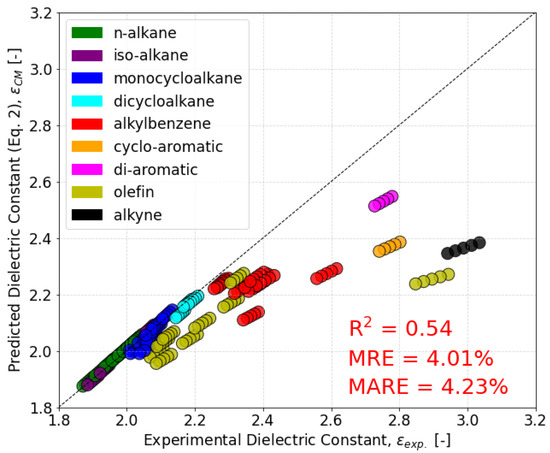
Figure 2.
Unity plot for dielectric predictions via the Clausius–Mossotti relation (Equation (2)) with accuracy metrics for the entire dataset. R2 = coefficient of determination, MRE = mean relative error, MARE = mean absolute relative error.

Table 1.
Error metrics for the two dielectric constant models presented here.
The results for the dipole-corrected C-M model described by Equation (3) are shown in Figure 3 below. The Equation (3) predictions for alkanes remain mostly consistent with those from the standalone C-M relation, while the predictions for aromatics and olefins are most affected by the inclusion of a weighted dipole moment term. This is supported by Table 1, where the accuracy increases significantly for alkylbenzenes, cyclo-aromatics, and di-aromatics. The correction of these groups is the main contributor to the much-improved R2 of 0.92 for the overall model.
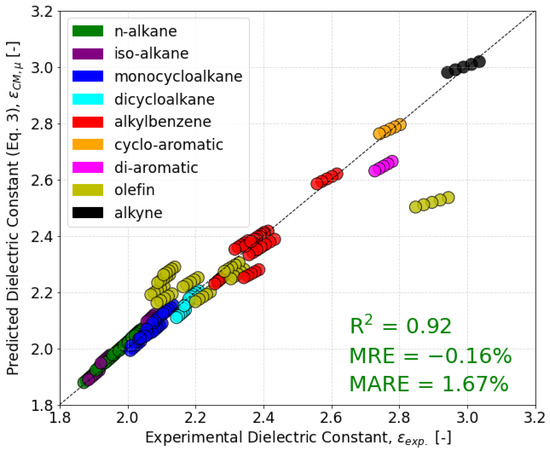
Figure 3.
Unity plot for dielectric predictions via the dipole-corrected Clausius–Mossotti model (Equation (3)) with accuracy metrics for the entire dataset.
Olefins did not show an obvious improvement with the dipole correction compared to the other hydrocarbon classes. While the MARE for these molecules slightly improved from 6.76% to 4.80% with the dipole moment correction, over half of the molecules see an overcorrection in the dielectric constant from the additional model term. This indicates that partial saturates, whether cyclic or linear, may have electronic or magnetic [9] properties that are beyond what is described by a singular dipole moment term. While this represents one limitation of the current work, it is of relatively low concern because jet fuel typically contains less than 2.5%v of olefins measured by ASTM D1319 [19,33].
Another impact of the dipole moment correction is the slight decrease in accuracy for n-alkanes, iso-alkanes, and dicycloalkanes. The change in accuracy between the two models in Table 1 correlates with the dipole moment calculations found in Figure 1. Specifically, these molecules all have small, but nonzero, dipole moments. When applied to Equation (3), this confounds what is otherwise a highly accurate prediction from the C-M relation (Equation (2)) where no dipole moments are assumed. The error for these molecules in the dipole-corrected model still appears reasonably close to the unity line, although its impact on the relationship with density is more pronounced and will be discussed in Section 3.3.
Most of the monocycloalkanes behave similarly with regard to the dipole correction; however, the group at large sees a slight improvement in accuracy due to the much-improved predictions for 1,3,5-trimethylcyclohexane and cis-1,3-dimethylcyclohexane. These molecules exhibit higher polarity than the rest of the cycloalkanes, and thus are not well characterized by the Clausius–Mossotti model alone (Equation (2)). Because cycloalkanes are seen as desirable for improving the density and seal swell characteristics of SPK SAFs, which are almost entirely composed of n- and iso-alkanes, it is important to accurately capture the dielectric behavior of the entire spectrum of cycloalkanes. Additionally, the disproportionate influence of aromatic molecules on fuels meeting the Jet-A experience range for the dielectric constant implies that cycloalkanes exhibiting higher dipole moments could actually contribute positively towards SAFs meeting this property constraint.
3.3. Impacts on Model Application
This work provides a method for predicting the dielectric constant of aviation turbine fuel. However, as mentioned before, aircraft FQISs function under the assumption that the onboard fuel resembles the conventional fuel range on the Clausius–Mossotti plot. Using historical dielectric constant data for 172 fuels at 10°, 15°, 20°, 25°, and 30 °C from ARINC 611-1 and CRC 647 [19,20], the Jet-A experience range is shown in Figure 4 and Figure 5 as a reference point to evaluate how the models presented here (Equations (2) and (3)) performed for each hydrocarbon class in a fuel-gauging application. The impact of hydrocarbon class in relation to the Clausius–Mossotti Jet-A range is discussed at length in previous work [7], so it will not be repeated. However, an important detail to point out in these plots is the close proximity in Figure 4b and Figure 5b of the two additional cycloalkane molecules measured, 1,3,5-trimethylcyclohexane (thin diamonds) and cis-1,3-dimethylcyclohexane (stars), to the conventional fuel range.
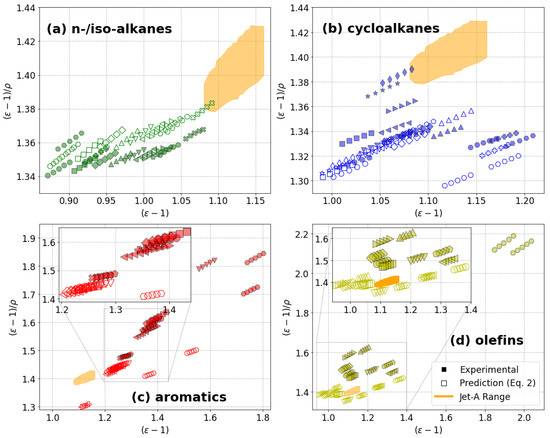
Figure 4.
Clausius–Mossotti plots containing experimental results (closed symbols) and predictions from the Clausius–Mossotti relation shown in Equation (2) (open symbols). Each subplot (and color) focuses on one general hydrocarbon class: n-/iso-alkanes (a), cycloalkanes (b), aromatics (c), olefins, and alkynes (d). Each molecule is identified by a unique shape. The Jet-A experience range, based on ARINC and CRC historical data, is shown in orange.
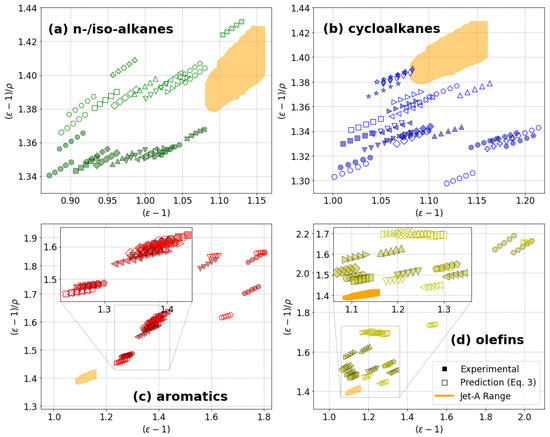
Figure 5.
Clausius–Mossotti plots containing experimental results (closed symbols) and predictions from the dipole-corrected Clausius–Mossotti relation shown in Equation (3) (open symbols). Each subplot (and color) focuses on one general hydrocarbon class: n- and iso-alkanes (a), cycloalkanes (b), aromatics (c), olefins, and alkynes (d). Each molecule is identified by a unique shape. The Jet-A experience range, based on ARINC and CRC historical data, is shown in orange.
Given the results shown in Figure 2, the results shown in Figure 4 are largely unsurprising. The placements of more polar hydrocarbons, aromatics (Figure 4c) and olefins (Figure 4d), are poorly predicted by the theoretical Clausius–Mossotti relation (Equation (2)). Barring the two additional cycloalkanes measured for this study, the cycloalkanes predictions from Equation (2) are found well below the Jet-A range, in general alignment with the experimental values. Figure 4a, on the other hand, demonstrates a consistent overprediction of the n-/iso-alkanes on the Clausius–Mossotti plot despite displaying low errors for Equation (2) predictions in Figure 1 and Table 1. Because these molecules have much lower density than the other hydrocarbon classes, errors in the dielectric constant are exacerbated on the Clausius–Mossotti plot. The small increase in dielectric error for n-/iso-alkanes in the dipole-corrected (Equation (3)) model further demonstrates this effect on the Clausius–Mossotti plot in Figure 5a. However, because these molecules display relatively little variance across species for FQIS implications (or O-ring seal swell, for that matter), they can be adequately represented in fuel-composition optimizations with the properties of a commercially available SPK or iso-paraffinic solvent.
Figure 5b–d show predictions more consistent with the experimental values for cycloalkanes and aromatics. The improved prediction capabilities for aromatics offer the opportunity for identifying the most desirable species for improving FQISs’ compatibility while taking the sooting impacts of the molecule into consideration. Additionally, the improvement in accuracy for 1,3,5-trimethylcyclohexane (thin diamonds) and cis-1,3-dimethylcyclohexane (stars) indicate this method’s potential to forecast the dielectric constant values for more polar cycloalkane species that may offer some benefit in reducing the need for aromatics in aviation fuel. The improvement in prediction accuracy for molecules near the Jet-A range comes at the cost of some cycloalkanes showing overpredictions on the y-axis of the Clausius–Mossotti plot. This underlines that there are other electromagnetic properties impacting the dielectric constant that are uncharacterized by this model. However, the range of species near the Jet-A range on the Clausius–Mossotti plot is fairly narrow, making experimental validation of these molecules for model applications much simpler than evaluating the entirety of jet-range hydrocarbons.
With this in mind, Figure 6b illustrates that certain cycloalkanes from the NIST database may positively contribute towards fulfilling the constraints of the Clausius–Mossotti Jet-A range when using the dipole-corrected model (Equation (3)) for dielectric constant prediction. Alternatively, Figure 6a shows that predictions made on the same database using only the Clausius–Mossotti relation (Equation (2)) significantly impact the solution space for modeling FQIS-compatible fuel compositions from this database.
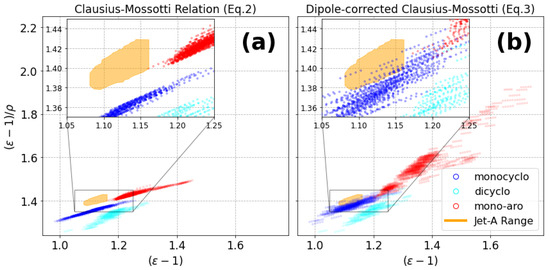
Figure 6.
Clausius–Mossotti plot displaying predictions from (a) the Clausius–Mossotti relation (Equation (2)) and (b) the dipole-corrected model (Equation (3)) for the NIST database molecules of interest for blending with current SPK products (monocycloalkanes, dicycloalkanes, and mono-aromatics). The Jet-A range is shown in orange as a reference point.
While not insignificant, the applications of the dipole-corrected model presented here are limited to research or production efforts at low fuel readiness levels [34] seeking to evaluate fuel compositions in relation to the Jet-A range on the Clausius–Mossotti plot. This model does not sufficiently capture the temperature dependence of the dielectric constant, which is leveraged in aircraft FQISs in the form of the gauging slope and intercept [9]. A closer look at Figure 3 shows that the slope of the temperature series for many molecules is not consistent with the unity line. This is likely the result of some temperature dependency that has not been assessed for some of the model inputs, namely polarizability and the dipole moment. Although some work has been performed to show the impact of temperature on the electronic properties of molecules [35,36], accurately calculating this dependency is beyond the scope of this work.
4. Conclusions
This work evaluated the Clausius–Mossotti relation (Equation (2)), which assumes negligible molecular dipole moments, for predicting the dielectric constant of aviation jet-range hydrocarbons and proposes Equation (3) as a more accurate prediction method using a simple correction for dipole moments calculated using open-source computational chemistry software. Both models (Equations (2) and (3)) were evaluated over a training dataset of density and dielectric constant measurements for 48 neat molecules at five temperatures each. The relatively high dipole moments of aromatic molecules led to poor prediction accuracy over the entirety of the dataset (R2 = 0.54, MRE = 4.01%, MARE = 4.23%) when Equation (2) was used. With the addition of model terms accounting for the dipole moment, Equation (3) showed significantly improved error metrics (R2 = 0.92, MRE = −0.16%, MARE = 1.67%) by more accurately capturing the behavior of aromatics and polar cycloalkane species. Both models showed low accuracy for olefins, which is of little concern due to their relatively low concentration in jet fuels. Predictions from both models had small error metrics for the dielectric constant values of n-/iso-alkanes, but presented exacerbated inaccuracies on the Clausius–Mossotti plot used in fuel-gauging applications, due to the low density of these molecules. More computationally intensive dipole moment calculations would likely improve these predictions and may be the subject of future work. Despite this, the authors suggest the current dipole-corrected model (Equation (3)) as appropriate for use in exploratory fuel-composition optimizations where the n-/iso-alkane fraction of the solutions can be represented with existing SPK products to highlight the influence of aromatics and cycloalkanes on fuel performance and operability properties, e.g., sooting propensity, energy density, volumetric density, elastomer O-ring seal swell, and dielectric constant-based FQISs, that are currently of high interest to the community.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/en17184700/s1, Tables of dielectric constant and density measurements added to the dataset of Yang et al. [7] for use in model development (Tables S1 and S2). Plot of regression performed to generate the dipole-correction term in Equation (3) (Figure S1). Cross-validation R2 scores for dipole moment regression (Table S3).
Author Contributions
C.F.: conceptualization, formal analysis, investigation, methodology, validation, visualization, writing (original draft), and writing (review and editing). D.C.B.: data curation, software, and writing (review and editing). R.B.: formal analysis, supervision, and writing (review and editing). J.H.: conceptualization, resources, funding acquisition, and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the United States Federal Aviation Administration (FAA) Office of Environment and Energy through ASCENT, the FAA Center of Excellence for Alternative Jet Fuels and the Environment, Project 65 through FAA Awards Number 13-C-AJFE-WASU-035 (PI: Joshua Heyne) under the supervision of Ana Gabrielan, and Project 66 through FAA Award Number 13-C-AJFE-WaSU-036 under the supervision of Bahman Habibzadeh, Ana Gabrielian, and Prem Lobo. Any opinions, findings, conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the FAA.
Data Availability Statement
Dielectric constant and density measurements for the two additional molecules measured for this study, 1,3,5-trimethylcyclohexane and cis-1,3-dimethylcyclohexane, can be found in the supporting material for this article. Readers are directed towards the work of Yang et al. [7] for the remaining 46 molecules used here. Molecular dipole moment data can be made available upon request.
Acknowledgments
The authors would also like to thank Harrison Yang of Washington State University for his assistance in collection of dielectric constant data and insights about the results.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| α | Molecular polarizability. |
| ASTM | ASTM International. |
| C-M (or CM) | Clausius–Mossotti relation. |
| CPK | Cycloparaffinic kerosene. |
| D | Debye. |
| ε | Dielectric constant. |
| FQIS | Fuel quantity indicator system. |
| μ | Permanent dipole moment. |
| Na | Avogadro’s number. |
| NIST | National Institute of Standards and Technology. |
| QSPR/QSAR | Quantitative structure property/activity relationship. |
| R2 | Coefficient of determination. |
| SAF | Sustainable aviation fuel. |
| SPK | Synthetic paraffinic kerosene |
| Vm | Molar volume. |
References
- Air Transport Action Group. Waypoint 2050: Balancing Growth in Connectivity with a Comprehensive Global Air Transport Response to the Climate Emergency: A Vision of Net-Zero Aviation by Mid-Century; Air Transport Action Group: Geneva, Switzerland, 2021; Available online: https://aviationbenefits.org/environmental-efficiency/climate-action/waypoint-2050/ (accessed on 16 June 2024).
- SAF Grand Challenge Roadmap Flight Plan for Sustainable Aviation Fuel; US Department of Energy: Washington, DC, USA, 2022. Available online: https://www.energy.gov/sites/default/files/2022-09/beto-saf-gc-roadmap-report-sept-2022.pdf (accessed on 25 January 2023).
- ASTM D7566-22a; Standard Specification for Aviation Turbine Fuel Containing Synthesized Hydrocarbons 1. ASTM: West Conshohocken, PA, USA, 2023. [CrossRef]
- Connors, M. A Systems Design Approach to Fuel Measurement in Hybrid-Electric Aircraft; Vertical Flight Society: Fairfax, VA, USA, 2020. [Google Scholar]
- Brasfield, R.G. Patent: Fuel Gaging System. WO1984001428A1, 12 April 1984. [Google Scholar]
- ASTM D924; JetDC 88500-0 Measurement of Dielectric Constant of Aviation Turbine Fuel IP PM-FC/21. ASTM: West Conshohocken, PA, USA. Available online: https://www.stanhope-seta.co.uk/ (accessed on 22 May 2024).
- Yang, Z.; Bell, D.C.; Boehm, R.C.; Fischer Marques, P.; Boze, J.A.; Kosilkin, I.V.; Heyne, J.S. Assessing the Effect of Composition on Dielectric Constant of Sustainable Aviation Fuel. Available online: https://ssrn.com/abstract=4700499 (accessed on 22 May 2024).
- ASTM D7566-23b; Standard Specification for Aviation Turbine Fuel Containing Synthesized Hydrocarbons 1. ASTM: West Conshohocken, PA, USA, 2024. [CrossRef]
- Kosir, S.; Landsaw, A.; Steinecker, W.H.; West, Z.J.; Zabarnick, S. Synthetic Blend Component Study: The Effects of Hydrocarbon Composition on Aviation Fuel Dielectric Constant. Energy Fuels 2024, 38, 16451–16457. [Google Scholar] [CrossRef]
- Boehm, R.C.; Faulhaber, C.; Behnke, L.; Heyne, J. The Effect of Theoretical SAF Composition on Calculated Engine and Aircraft Efficiency. Fuel 2024, 371, 132049. [Google Scholar] [CrossRef]
- Faulhaber, C.; Borland, C.; Boehm, R.; Heyne, J. Measurements of Nitrile Rubber Absorption of Hydrocarbons: Trends for Sustainable Aviation Fuel Compatibility. Energy Fuels 2023, 37, 9207–9219. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, Z.; Feng, M.; Cort, J.R.; Gieleciak, R.; Heyne, J.; Yang, B. Lignin-Based Jet Fuel and Its Blending Effect with Conventional Jet Fuel. Fuel 2022, 321, 124040. [Google Scholar] [CrossRef]
- Muldoon, J.A.; Harvey, B.G. Bio-Based Cycloalkanes: The Missing Link to High-Performance Sustainable Jet Fuels. ChemSusChem 2020, 13, 5777–5807. [Google Scholar] [CrossRef]
- Wang, J.; Xie, X.Q.; Hou, T.; Xu, X. Fast Approaches for Molecular Polarizability Calculations. J. Phys. Chem. A 2007, 111, 4443–4448. [Google Scholar] [CrossRef]
- Van Rysselberghe, P. Remarks Concerning the Clausius-Mossotti Law. J. Phys. Chem. 1932, 36, 1152–1155. [Google Scholar] [CrossRef]
- Talebian, E.; Talebian, M. A General Review on the Derivation of Clausius-Mossotti Relation. Optik 2013, 124, 2324–2326. [Google Scholar] [CrossRef]
- Kosir, S.; Stachler, R.; Heyne, J.; Hauck, F. High-Performance Jet Fuel Optimization and Uncertainty Analysis. Fuel 2020, 281, 118718. [Google Scholar] [CrossRef]
- Kroyan, Y.; Wojcieszyk, M.; Kaario, O.; Larmi, M. Modeling the Impact of Sustainable Aviation Fuel Properties on End-Use Performance and Emissions in Aircraft Jet Engines. Energy 2022, 255, 124470. [Google Scholar] [CrossRef]
- Hadaller, O.; Johnson, J. World Fuel Sampling Program; Coordinating Research Council: Alpharetta, GA, USA, 2006. [Google Scholar]
- ARINC611-1; ARINC Report 611-1 Guidance for the Design and Installation of Fuel Quantity Systems. ARINC: Annapolis, MD, USA, 1999.
- Kroenlein, K.; Muzny, C.; Kazakov, A.; Diky, V.; Chirico, R.; Magee, J.; Abdulagatov, I.; Frenkel, M. NIST Standard Reference 203: TRC Web Thermo Tables (WTT) Version 2-2012-1 Professional; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2012. [Google Scholar]
- Bosque, R.; Sales, J. Polarizabilities of Solvents from the Chemical Composition. J. Chem. Inf. Comput. Sci. 2002, 42, 1154–1163. [Google Scholar] [CrossRef] [PubMed]
- Szabo, A.; Ostlund, N. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory; Dover Publications: Mineola, NY, USA, 1996. [Google Scholar]
- Smith, D.G.A.; Burns, L.A.; Simmonett, A.C.; Parrish, R.M.; Schieber, M.C.; Galvelis, R.; Kraus, P.; Kruse, H.; Di Remigio, R.; Alenaizan, A.; et al. 1.4: Open-Source Software for High-Throughput Quantum Chemistry. J. Chem. Phys. 2020, 152, 184108. [Google Scholar] [CrossRef] [PubMed]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An Open Chemical Toolbox. J. Cheminform. 2011, 3, 33. [Google Scholar] [CrossRef] [PubMed]
- Weininger, D. SMILES, a Chemical Language and Information System. 1. Introduction to Methodology and Encoding Rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Landrum, G. RDKit: Open-Source Cheminformatics. Q2 2010. Version 2023.09.05. Available online: https://www.rdkit.org (accessed on 23 January 2024).
- Hariharan, P.C.; Pople, J.A. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theor. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Francl, M.M.; Pietro, W.J.; Hehre, W.J.; Binkley, J.S.; Gordon, M.S.; DeFrees, D.J.; Pople, J.A. Self-Consistent Molecular Orbital Methods. XXIII. A Polarization-Type Basis Set for Second-Row Elements. J. Chem. Phys. 1982, 77, 3654–3665. [Google Scholar] [CrossRef]
- Hait, D.; Head-Gordon, M. How Accurate Is Density Functional Theory at Predicting Dipole Moments? An Assessment Using a New Database of 200 Benchmark Values. J. Chem. Theory Comput. 2018, 14, 1969–1981. [Google Scholar] [CrossRef]
- Zapata, J.C.; McKemmish, L.K. On the Computation of Dipole Moments: A Recommendation on the Choice of the Basis Set and the Level of Theory. J. Phys. Chem. 2020, 124, 7538–7548. [Google Scholar] [CrossRef]
- Caleman, C.; Van Maaren, P.J.; Hong, M.; Hub, J.S.; Costa, L.T.; Van Der Spoel, D. Force Field Benchmark of Organic Liquids: Density, Enthalpy of Vaporization, Heat Capacities, Surface Tension, Isothermal Compressibility, Volumetric Expansion Coefficient, and Dielectric Constant. J. Chem. Theory Comput. 2012, 8, 61–74. [Google Scholar] [CrossRef]
- ASTM D1319-20a; Standard Test Method for Hydrocarbon Types in Liquid Petroleum Products by Fluorescent Indicator Adsorption 1. ASTM: West Conshohocken, PA, USA, 2020. [CrossRef]
- CAAFI. Fuel Readiness Level (FRL); CAAFI: Bristol, UK, 2010; Available online: https://www.caafi.org/information/pdf/FRL_CAAFI_Jan_2010_V16.pdf (accessed on 13 June 2024).
- Sharipov, A.S.; Loukhovitski, B.I.; Starik, A.M. The Influence of Vibrations of Polyatomic Molecules on Dipole Moment and Static Dipole Polarizability: Theoretical Study. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 165101. [Google Scholar] [CrossRef]
- Miller, T.M.; Bederson, B. Atomic and Molecular Polarizabilities—A Review of Recent Advances. Adv. At. Mol. Phys. 1978, 13, 1–55. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).