Transient Active Power in Two-Terminal Networks

Abstract

This article presents the hitherto unknown concept of transient active power in two-terminal networks. This phenomenon occurs when current and voltage signals are not sinusoidal but quasi-sinusoidal—in the case of an approximation of transient state. The modification of Parseval’s formula and the power–immittance relations are presented in this paper. To illustrate the phenomenon, a simulation is included for several types of transient states, and their influence on transient active power waveform is shown. The article also contains a comparison of transient active power and classical active power and highlights situations where it is impossible to use classical theory but where transient active power yields measurable results. In the article, an analysis of an idealized case and measurement data obtained from a modeled voltage sag in a laboratory setup is conducted. The impact of disturbance power on the total power in the case of disturbances that may occur in the real power network is demonstrated.

1. Introduction

In recent years, energy quality issues and methods for quality improvement have increased significantly. More and more scientific and technical works describe the issues of quality indicators—the active and non-active power, as well as the theory and construction of compensation systems to improve these indicators. Also, optimal control in terms of energy quality is an important topic.

Historically, one of the first people who worked on power theory was C. Budeanu, who proposed the unit electric reactive power (VAr) and introduced the concept of deformed power in electric networks [1]. However, the term “power theory” appeared in literature for the first time in S. Fryze’s paper in 1931 about optimal cooperation between the energy source and the energy receiver. Fryze determined the current with the minimum effective value that supplies the given active power to the terminals of an ideal voltage source [2]. His work provided a foundation for various power concepts developed by scientists who studied the power properties of electrical circuits, such as W. Shepherd and P. Zakikhani’s power theory [3]; N. Kusters and W. Moore’s power theory [4]; M. Depenbrock’s power theory, also known as the FDB method [5]; A. Nabae and H. Akagi’s instantaneous reactive power (IRP) p-q theory [6,7]; L. Czarnecki’s CPC power theory [8]; P. Tenti and E. Tedeschi’s conservative power theory [9]; and so on. The optimal source–load cooperation research that Fryze started was directly continued and extended by M. Brodzki, M. Pasko, M. Siwczyński and J. Walczak. The most recent publications on the optimal cooperation of a source–load system focus on minimizing the RMS value of the source current in a steady state for a given active power delivered to the load in the continuous time domain [10] and discrete time domain [11].

Nowadays, society relies heavily on the accessibility of electricity. Reliable power supply supports all economic and social endeavors. To meet this growing demand, the scale and intricacy of power systems incorporating renewable energy generation are expanding. This compels energy systems to function near the threshold of stability [12]. The growing proportion of generation by renewable energy sources or other distributed low-power energy resources (DERs) further exacerbates the issue of decreased system inertia, leading to energy systems experiencing reduced stability, security and reliability. This implies that stability (especially transient stability) serves as a crucial indicator of the resilience of energy systems, which are inherently vulnerable to failures and disruptions [13,14]. A lack of stability or prolonged transient states, such as those accompanying load changes in the system, can not only lead to exceeding the required quality parameters of electrical energy but also generate additional power losses, significantly reducing the efficiency of the system. Transient stability refers to a power system’s capability to return to a stable state after experiencing a significant disruption [15]. An analysis of transient stability assesses the dynamic response of a power system in the seconds immediately following a major disruption. If system instability is not detected in time to initiate corrective actions, a single-point failure can rapidly escalate into other failures, often leading to blackouts (local outages causing system separation and islanded operation, for which the isolated part of the system is not always adequately prepared in terms of the installed power generation units or the control systems themselves) or large-scale power outages. The rapid and accurate assessment of transient stability is crucial for safe and stable power system operation. To detect system instability before it occurs, transient stability assessment should shift from offline or day-forward calculations to a real-time operational environment. Conventional transient stability simulation methods depend on numerical techniques, like the Euler or Runge–Kutta methods, to solve equations describing the dynamic behavior of the power system. Such techniques are used in software with millisecond integration steps to fulfill the criteria [16]. These techniques, however, are resource-demanding, particularly in huge systems with many unforeseen circumstances. Researchers and the power industry are looking for more efficient cutting-edge tools for the real-time simulation of power system transient stability.

Power systems with high and medium power, commonly used in industry, adversely affect the parameters of the power supply network, decreasing the quality of energy delivered to different types of receivers. In turn, the presence of non-linear receivers causes the distortion of current and voltage waveforms, generating higher harmonics. In addition to absorbing active power, such receivers also consume inactive power. The extensive use of non-linear receivers in homes (the continuously increasing share of devices equipped with power electronic converters) and industry affects the quality of power. Devices ranging from small items like LED lights, chargers and laptops to industrial machinery like railway systems [17,18], arc furnaces and variable-frequency/speed motor drives causes harmonic distortion of the network’s current and voltage. If left uncompensated, such harmonics can cause numerous adverse effects on the power system, such as increased losses (even in power supply networks because of the skin effect), voltage sags, equipment overheating and excessive neutral currents, potentially leading to insulation breakdown. Power equipment can tolerate poor-quality energy for a certain period, but modern electronically controlled equipment is more sensitive to harmonic distortions [19]. The consumers are more and more concerned about the quality of power distributed from power plants [20]. An APF (active power filter), due to its reliability and response, provides a feasible solution for the compensation of harmonics [21,22,23]. Its purpose is to eliminate specific harmonics, improve the power factor and equalize the network. The term “active” comes from the real-time response of the filter to variable load, as opposed to “passive” filters, which are constructed to compensate selected harmonics of a given load [24]. On the one hand, APFs are more expensive, but on the other hand, their response to load changes ensures that the THD level remains within the IEEE required level. A shunt APF eliminates the harmonics of the source’s current by adding an equal but opposite compensating current [25]. The part of the filter responsible for reference signal extraction operates first, so the time required to obtain this signal is crucial for the performance of the APF. The most common methods in the time domain are the IRP p-q theory and SRF (synchronous reference frame), with the advantage of simple implementation [26,27]. Nevertheless, the use of a low-pass filter can cause large amplitude and phase errors and ultimately lead to poor harmonic compensation [28,29].

In power supply networks, there are transient states caused by disturbances inside sources and receivers. There are situations where these states occur regularly or even permanently. Ignoring their impact may contribute to increased energy losses. Therefore, the most advantageous solution is to adjust the source–receiver system not only in the steady state but also in the transition states occurring between steady states.

This article aims to expand the definition of active power and thus not only enable a mathematical description in the steady state but also show the changes in active power during the transient states. This issue is important from the point of view of optimal cooperation of the source–receiver system in a transient state because when the load of the source changes, voltage sags or swells can occur, which lead to the disturbance of power transmission, and without a mathematical description of this phenomenon, optimal source–receiver cooperation will yield false results. The concept presented in the article may provide a deeper understanding of power theory, i.e., what happens to active power during a transient state, system stability and reliability and power flow in the compensation process.

The rest of the paper is organized as follows. Section 2 provides the derivation of the transient active power and power–immittance formulas. Section 3 presents simulation results for several assumed disrupted voltage signals and shows how they affect the waveform of the transient active power. Section 4 extends the simulation research to tests based on signals measured in a real laboratory power system. Finally, Section 5 draws the conclusions of this work.

2. Analytical Analysis

The transient active power is expressed as a function in the time domain:

$$P\left(t\right)={\displaystyle \frac{1}{T}}{\displaystyle \underset{t}{\overset{t+T}{\int }}u\left(\tau \right)i\left(\tau \right)d\tau }={\displaystyle \frac{1}{T}}{\displaystyle \underset{0}{\overset{T}{\int }}u\left(t+\tau \right)i\left(t+\tau \right)d\tau }$$

(1)

where u(t) and i(t) are the quasi-harmonic voltage and current signals with time-dependent amplitudes and phases:

$$u\left(t\right)={\displaystyle \frac{1}{\sqrt{2}}}\left[U\left(t\right)e^{j\omega t}+U^{*}\left(t\right)e^{-j\omega t}\right]$$

(2)

$$i\left(t\right)={\displaystyle \frac{1}{\sqrt{2}}}\left[I\left(t\right)e^{j\omega t}+I^{*}\left(t\right)e^{-j\omega t}\right]$$

(3)

$$U\left(t\right)=\left|U\left(t\right)\right|e^{j\measuredangle U\left(t\right)}$$

(4)

$$I\left(t\right)=\left|I\left(t\right)\right|e^{j\measuredangle I\left(t\right)}$$

(5)

$$U^{*}\left(t\right)=\left|U\left(t\right)\right|e^{-j\measuredangle U\left(t\right)}$$

(6)

$$I^{*}\left(t\right)=\left|I\left(t\right)\right|e^{-j\measuredangle I\left(t\right)}$$

(7)

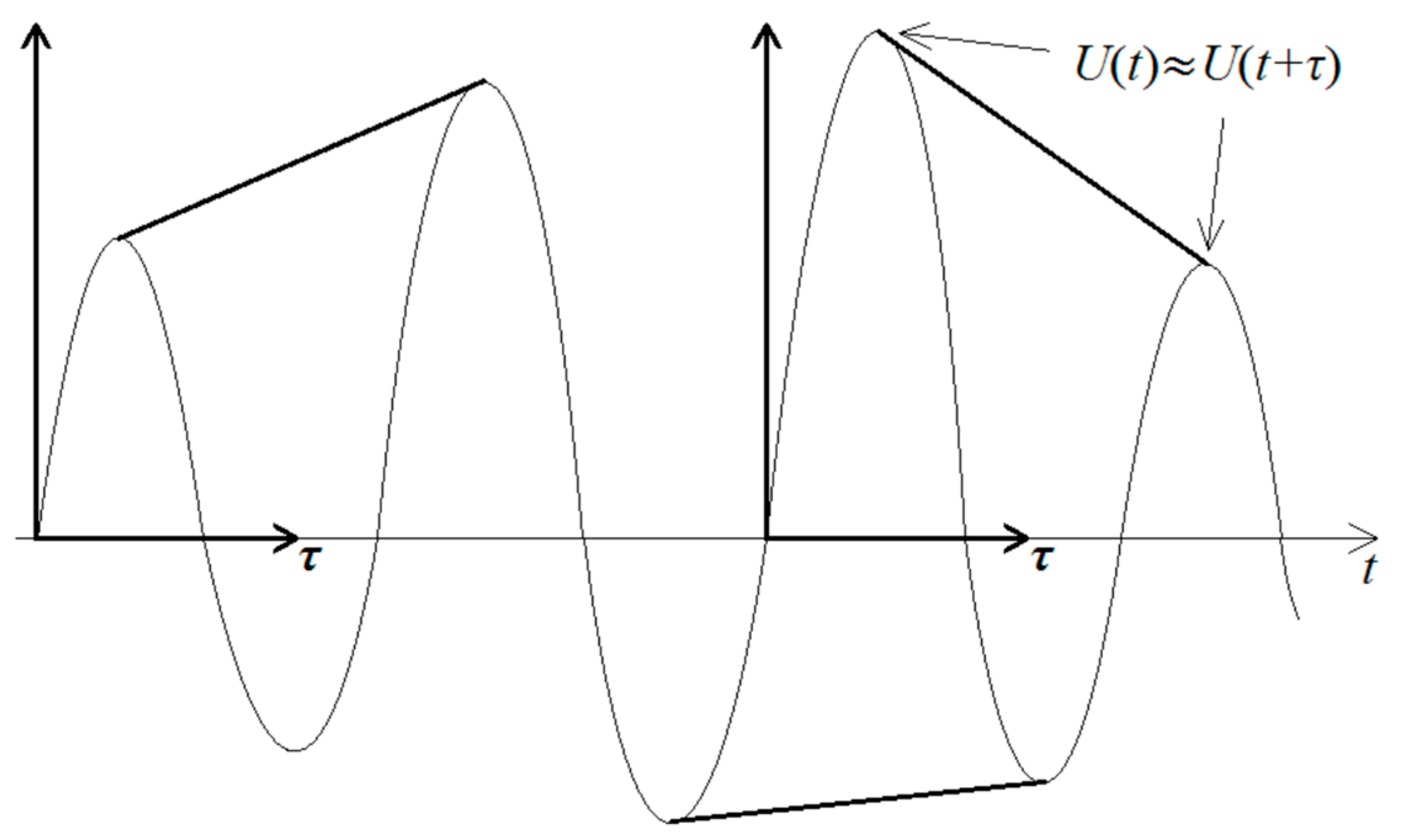
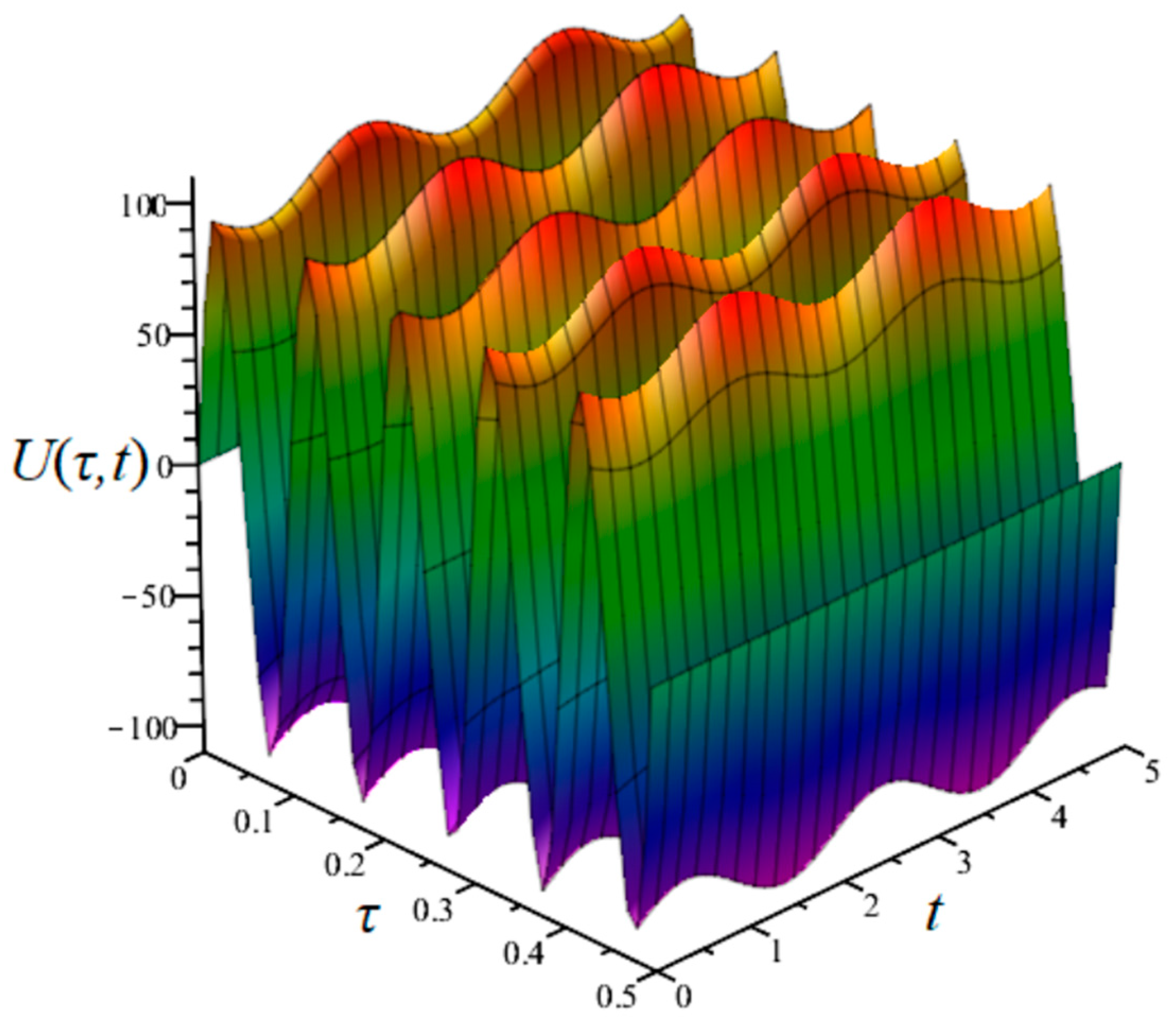
Figure 1 shows the above-mentioned T-periodic quasi-harmonic signal. Two timelines are visible. A fixed axis is shown for the time associated with the transient state −∞ < t < ∞ and a moving axis for the time associated with the harmonic signal period 0 < τ < T.

Both of these times take part in the integration process of the transient active power (1). Such large differences between the amplitudes shown in Figure 1 do not occur. For slow changes in the signal on the t axis, the subsequent amplitudes will differ slightly from each other, and this would not be visible in Figure 1; therefore, an “exaggerated” waveform is presented.

The instantaneous power is given by the following expression:

$$\begin{array}{ll}p\left(t\right)=& u\left(t\right)i\left(t\right)={\displaystyle \frac{1}{2}}\left[U\left(t\right)e^{j\omega t}+U^{*}\left(t\right)e^{-j\omega t}\right]\left[I\left(t\right)e^{j\omega t}+I^{*}\left(t\right)e^{-j\omega t}\right]=\\ & ={\displaystyle \frac{1}{2}}\left[U\left(t\right)I^{*}\left(t\right)+U^{*}\left(t\right)I\left(t\right)\right]+{\displaystyle \frac{1}{2}}\left[U\left(t\right)I\left(t\right)e^{j2\omega t}+U^{*}\left(t\right)I^{*}\left(t\right)e^{-j2\omega t}\right]=\\ & =\mathrm{Re}\left[U\left(t\right)I^{*}\left(t\right)\right]+\mathrm{Re}\left[U\left(t\right)I\left(t\right)e^{j2\omega t}\right]\end{array}$$

(8)

from which the transient active power is obtained through averaging (1):

$$P\left(t\right)={\displaystyle \frac{1}{T}}{\displaystyle \underset{0}{\overset{T}{\int }}p\left(t+\tau \right)d\tau }\approx \mathrm{Re}\left[U\left(t\right)I^{*}\left(t\right)\right]{\displaystyle \frac{1}{T}}{\displaystyle \underset{0}{\overset{T}{\int }}d\tau }+\mathrm{Re}\left[U\left(t\right)I\left(t\right)e^{j2\omega t}{\displaystyle \frac{1}{T}}{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{j2\omega \tau }d\tau }\right]=\mathrm{Re}\left[U\left(t\right)I^{*}\left(t\right)\right]$$

(9)

Expression (9) is approximated. It is assumed that the function U(t + τ) I(t + τ) in the averaging interval 0 < τ < T increases slightly so that the expression U (t) I (t) can be excluded from the integral as follows:

$$U\left(t+\tau \right)I\left(t+\tau \right)\approx U\left(t\right)I\left(t\right)$$

(10)

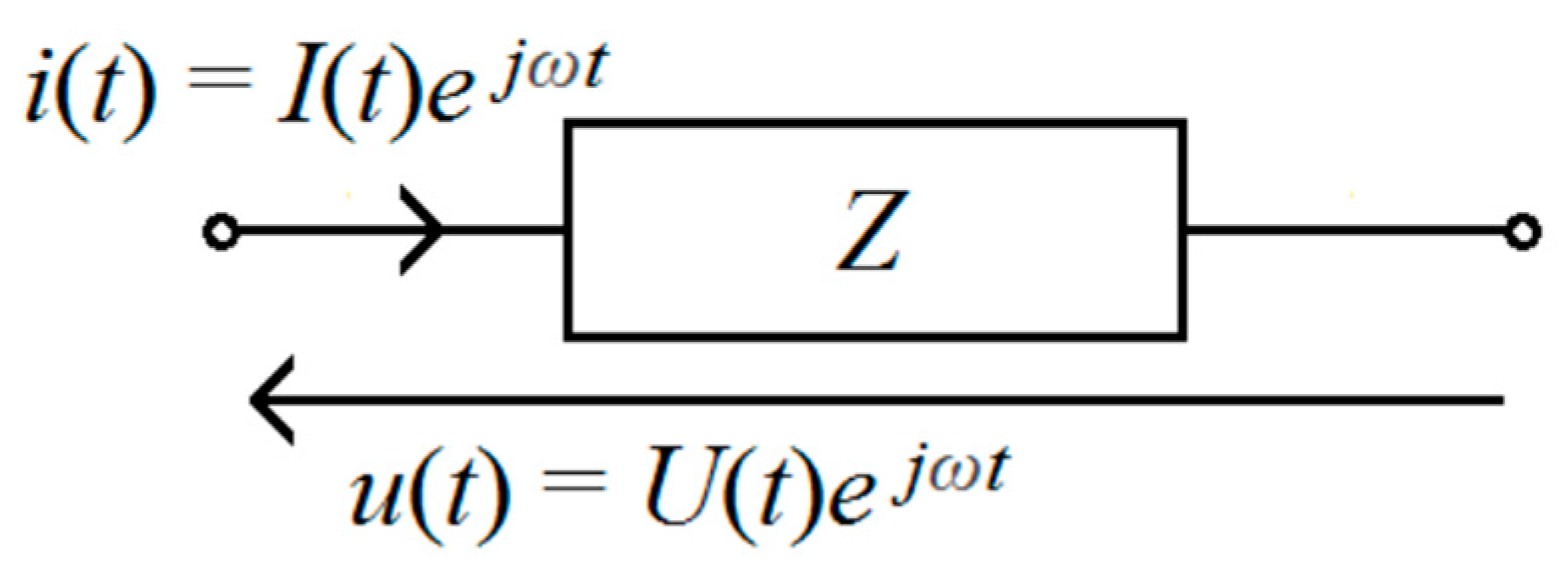
While expression (9) mathematically describes the generalized phenomenon of transient active power well, for practical reasons (simulation and laboratory tests), it is more convenient to use power–immittance formulas. In this case, the disturbance is also transferred to the operator describing the system. Therefore, the derivation of the formulas will start with a given impedance operator Z of a simple two-terminal network, as shown in Figure 2.

It is assumed that voltage and current signals in this description are represented by complex valued functions:

$$u\left(t\right)=U\left(t\right)e^{j\omega t}$$

(11)

$$i\left(t\right)=I\left(t\right)e^{j\omega t}$$

(12)

The mentioned signals should be assumed as vectors in the complex coordinate system, the arrowhead of which, depending on the type of distortion, is displacement. If the amplitude is distorted, the vector is shortened and/or lengthened. The distortion of the signal phase causes the vector angle to shift. In turn, the simultaneous distortion of the amplitude and phase of the signal causes the vector tip to move in a certain small area. The impact of assumed distortions on the vector is illustrated in Figure 3.

A direct relationship between the time-dependent envelopes of U(t) and I(t) should be found. Using the Laplace transformation, the relations between the signal transform and the envelope transform [30] are obtained:

$$\overline{u}\left(s\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}U\left(t\right)e^{j\omega t}{e}^{-st}dt}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}U\left(t\right)e^{-\left(s-j\omega \right)t}dt}=\overline{U}\left(s-j\omega \right)$$

(13)

From Ohm’s law, the following is derived:

$$\overline{u}\left(s\right)=Z\left(s\right)\overline{i}\left(s\right)$$

(14)

which can also be presented in the following form:

$$\overline{U}\left(s-j\omega \right)=Z\left(s\right)\overline{I}\left(s-j\omega \right)$$

(15)

And after changing the variable s to s + jω, the desired relationship between the transforms of the voltage and current envelopes is as follows:

$$\overline{U}\left(s\right)=Z\left(s+j\omega \right)\overline{I}\left(s\right)$$

(16)

This procedure causes the distortion to be transferred from the voltage and current signals to the operator describing the system. The impedance operator thus distorted can be expanded into a Taylor series, and for slow changes in the envelope of the signal, i.e., |s| << ω, the powers higher than one can be omitted:

$$Z\left(s+j\omega \right)\approx Z\left(j\omega \right)+{\displaystyle \frac{dZ\left(j\omega \right)}{dj\omega }}s=Z\left(j\omega \right)-j{\displaystyle \frac{dZ\left(j\omega \right)}{d\omega }}s$$

(17)

Then, by decomposing Z(jω) into the real part R(ω)—resistance and the imaginary part X(ω)—reactance, the following expression is obtained:

$$Z\left(s+j\omega \right)\approx R\left(\omega \right)+{\displaystyle \frac{dX\left(\omega \right)}{d\omega }}s+j\left[X\left(\omega \right)-{\displaystyle \frac{dR\left(\omega \right)}{d\omega }}s\right]$$

(18)

In Formula (18), R(ω), X(ω), dR(ω)/dω and dX(ω)/dω are real values of the functions R and X and their frequency derivatives at a given point ω (the carrier frequency of signals u(t) and i(t)).

The same decomposition can be applied to the distorted admittance operator:

$$Y\left(s+j\omega \right)\approx G\left(\omega \right)+{\displaystyle \frac{dB\left(\omega \right)}{d\omega }}s+j\left[B\left(\omega \right)-{\displaystyle \frac{dG\left(\omega \right)}{d\omega }}s\right]$$

(19)

where G(ω), B(ω), dG(ω)/dω and dB(ω)/dω are real values of the conductance G and susceptance B functions and their frequency derivatives at a given point ω.

The distorted impedance operator (18) directly affects the current envelope:

$$U\left(t\right)=R\left(\omega \right)I\left(t\right)+{\displaystyle \frac{dX\left(\omega \right)}{d\omega }}{\displaystyle \frac{dI\left(t\right)}{dt}}+j\left[X\left(\omega \right)I\left(t\right)-{\displaystyle \frac{dR\left(\omega \right)}{d\omega }}{\displaystyle \frac{dI\left(t\right)}{dt}}\right]$$

(20)

while the distorted admittance operator affects the voltage envelope:

$$I\left(t\right)=G\left(\omega \right)U\left(t\right)+{\displaystyle \frac{dB\left(\omega \right)}{d\omega }}{\displaystyle \frac{dU\left(t\right)}{dt}}+j\left[B\left(\omega \right)U\left(t\right)-{\displaystyle \frac{dG\left(\omega \right)}{d\omega }}{\displaystyle \frac{dU\left(t\right)}{dt}}\right]$$

(21)

Joule’s law describes the power–immittance relations for active power:

$$P=R{\left|I\right|}^2=G{\left|U\right|}^2$$

(22)

The distorted version of Formula (22) is obtained from the combination of transient complex power

$$S\left(t\right)=U\left(t\right)I^{*}\left(t\right)$$

(23)

and the distorted Ohm’s law from (20) and (21) and yields the following:

$$S\left(t\right)=R\left(\omega \right){\left|I\left(t\right)\right|}^2+jX\left(\omega \right){\left|I\left(t\right)\right|}^2+\left[{\displaystyle \frac{dX\left(\omega \right)}{d\omega }}-j{\displaystyle \frac{dR\left(\omega \right)}{d\omega }}\right]{\displaystyle \frac{dI\left(t\right)}{dt}}{I}^{*}\left(t\right)$$

(24)

$$S^{*}\left(t\right)=R\left(\omega \right){\left|I\left(t\right)\right|}^2-jX\left(\omega \right){\left|I\left(t\right)\right|}^2+\left[{\displaystyle \frac{dX\left(\omega \right)}{d\omega }}+j{\displaystyle \frac{dR\left(\omega \right)}{d\omega }}\right]{\displaystyle \frac{d{I}^{*}\left(t\right)}{dt}}I\left(t\right)$$

(25)

Therefore, the transient active power can be presented as follows:

$$\begin{array}{ll}P\left(t\right)=& {\displaystyle \frac{1}{2}}\left[S\left(t\right)+S^{*}\left(t\right)\right]=R\left(\omega \right){\left|I\left(t\right)\right|}^2+{\displaystyle \frac{1}{2}}{\displaystyle \frac{dX\left(\omega \right)}{d\omega }}\left[{\displaystyle \frac{dI\left(t\right)}{dt}}{I}^{*}\left(t\right)+{\displaystyle \frac{d{I}^{*}\left(t\right)}{dt}}I\left(t\right)\right]+\\ & +{\displaystyle \frac{1}{j2}}{\displaystyle \frac{dR\left(\omega \right)}{d\omega }}\left[{\displaystyle \frac{dI\left(t\right)}{dt}}{I}^{*}\left(t\right)-{\displaystyle \frac{d{I}^{*}\left(t\right)}{dt}}I\left(t\right)\right]\end{array}$$

(26)

Considering (5) and (7) the formulas in (26) are simplified to:

$${\displaystyle \frac{dI\left(t\right)}{dt}}{I}^{*}\left(t\right)+{\displaystyle \frac{d{I}^{*}\left(t\right)}{dt}}I\left(t\right)=2\left|I\left(t\right)\right|{\displaystyle \frac{d\left|I\left(t\right)\right|}{dt}}$$

(27)

$${\displaystyle \frac{dI\left(t\right)}{dt}}{I}^{*}\left(t\right)-{\displaystyle \frac{d{I}^{*}\left(t\right)}{dt}}I\left(t\right)=j2{\left|I\left(t\right)\right|}^2{\displaystyle \frac{d\measuredangle I\left(t\right)}{dt}}$$

(28)

and then the final power–impedance distorted version of Joule’s law takes the following form:

$$P\left(t\right)=\left[R\left(\omega \right)+{\displaystyle \frac{dR\left(\omega \right)}{d\omega }}{\displaystyle \frac{d\measuredangle I\left(t\right)}{dt}}\right]{\left|I\left(t\right)\right|}^2+{\displaystyle \frac{dX\left(\omega \right)}{d\omega }}\left|I\left(t\right)\right|{\displaystyle \frac{d\left|I\left(t\right)\right|}{dt}}$$

(29)

In the same way, the power–admittance distorted version of Joule’s law can be determined as follows:

$$P\left(t\right)=\left[G\left(\omega \right)-{\displaystyle \frac{dG\left(\omega \right)}{d\omega }}{\displaystyle \frac{d\measuredangle U\left(t\right)}{dt}}\right]{\left|U\left(t\right)\right|}^2-{\displaystyle \frac{dB\left(\omega \right)}{d\omega }}\left|U\left(t\right)\right|{\displaystyle \frac{d\left|U\left(t\right)\right|}{dt}}$$

(30)

The distorted Formulas (29) and (30) are universal and include every combination of distortions (amplitude, phase, both or none).

3. Simulation Research

This section includes the results of computer simulation for a few assumed transient states. First, let us consider the RL branch with the parameters

$$R=50,L=0.2$$

(31)

and a quasi-harmonic voltage signal containing a transient state in the form of an exponentially distorted amplitude:

$$u\left(\tau ,t\right)=100\left(1-e^{-5t}\right)\sin \left(62.8\tau \right)$$

(32)

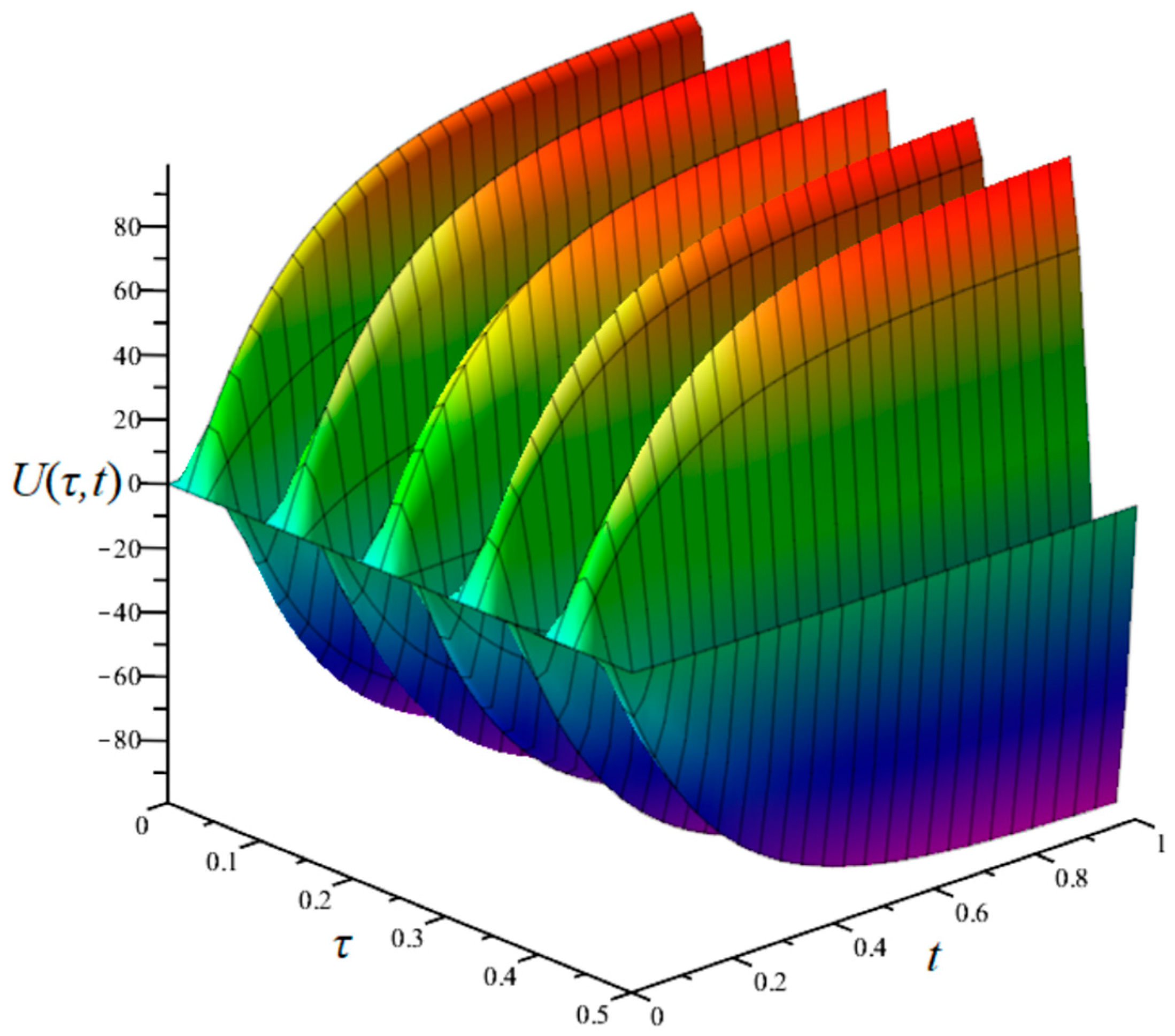
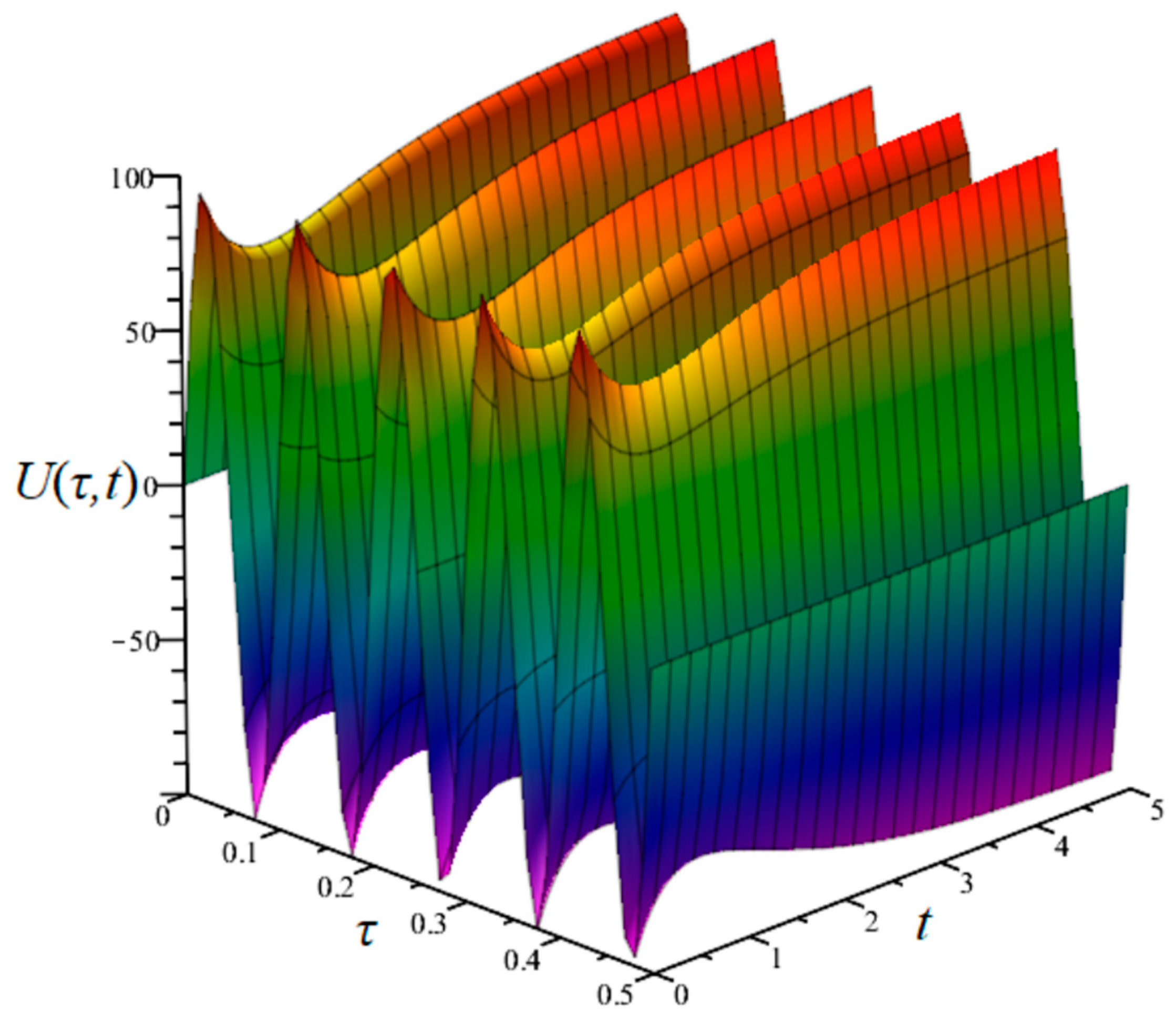
The voltage signal determined by Formula (32) depends on two times, the periodic 0 < τ ≤ T and the distorting −∞ < t < ∞, in which the signal envelope slowly changes. The 3D waveform of the assumed voltage signal is shown in Figure 4.

Such a three-dimensional signal can be simplified to a two-dimensional form by unifying the time axes (τ and t), as shown in Figure 5.

Despite the graphical simplification, the presented algorithm must be used in a form with separated times—harmonic τ and distorting t.

The admittance of the given RL load is as follows:

$$Y\left(j\omega \right)={\displaystyle \frac{R}{L^2{\omega }^2+R^2}}-j{\displaystyle \frac{\omega L}{L^2{\omega }^2+R^2}}=0.018813-j0.004726$$

(33)

Using the classic approach to active power, we must wait until system reaches a steady state, and then the following can be applied:

$$P=\mathrm{Re}\left[Y\left(j\omega \right)\right]{\left|U\right|}^2=188.13$$

(34)

However, in the classical form, during the transient state, there is no information available on the load’s active power usage. In such a situation, the concept presented in this paper is significant. First, the distorted admittance operator is calculated according to Formula (17):

$$\begin{array}{l}Y\left(j\omega +s\right)\approx Y\left(j\omega +s\right)-j{\displaystyle \frac{Y\left(j\omega \right)}{d\omega }}s=\\ =0.018813-j0.004726-0.000066s+j0.000036s\end{array}$$

(35)

where s is the envelope derivative with respect to distorting time t.

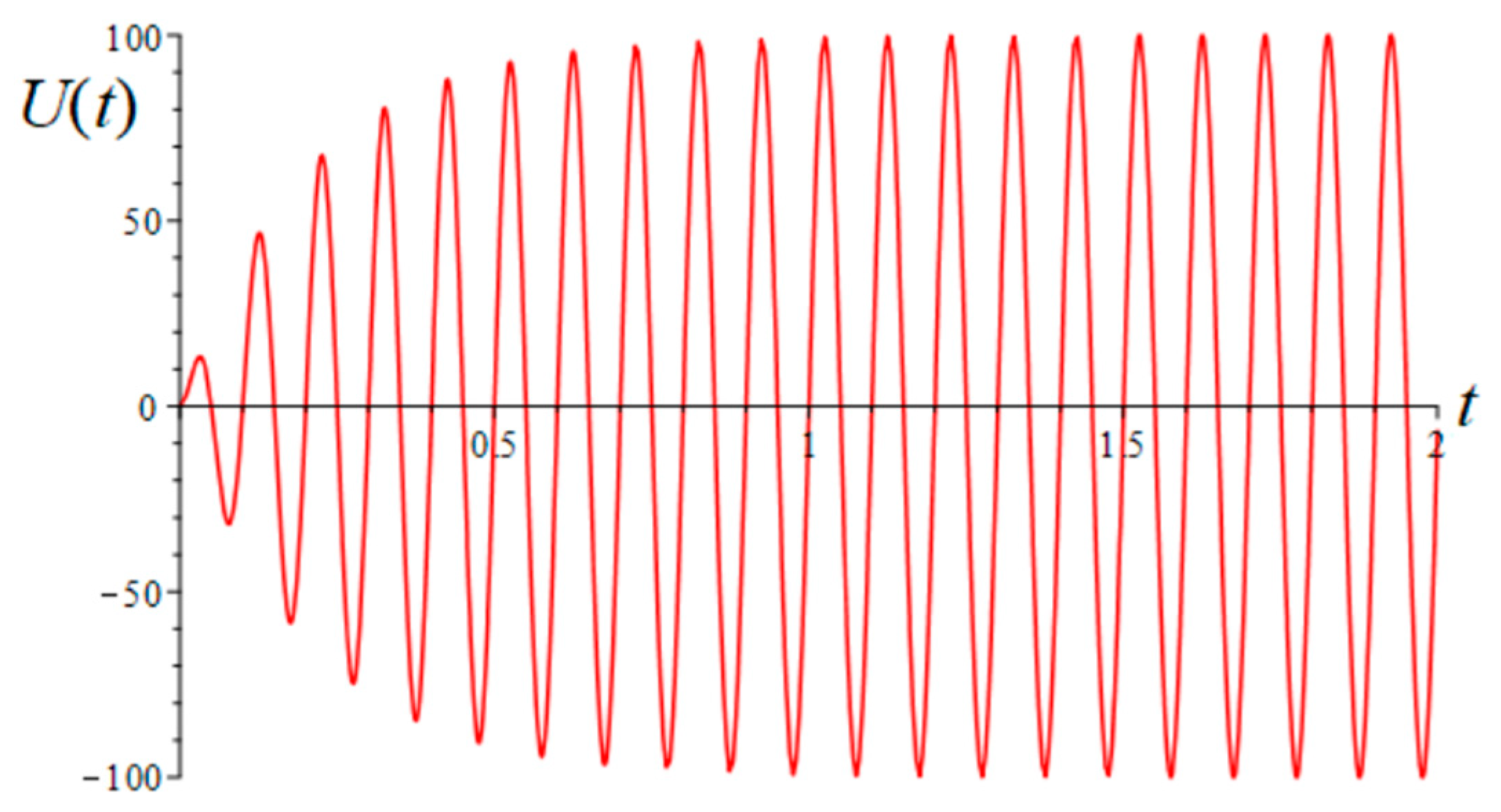
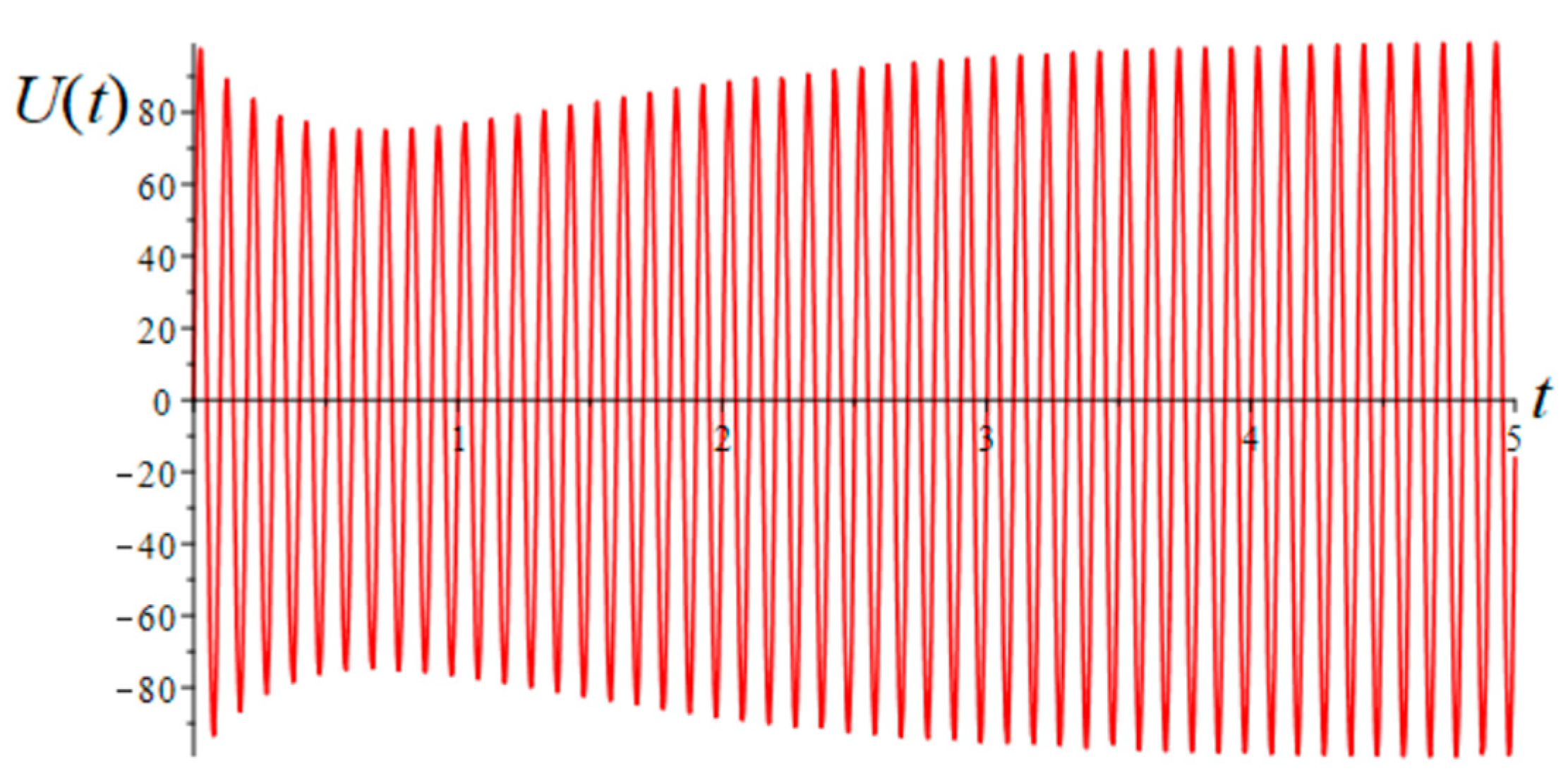
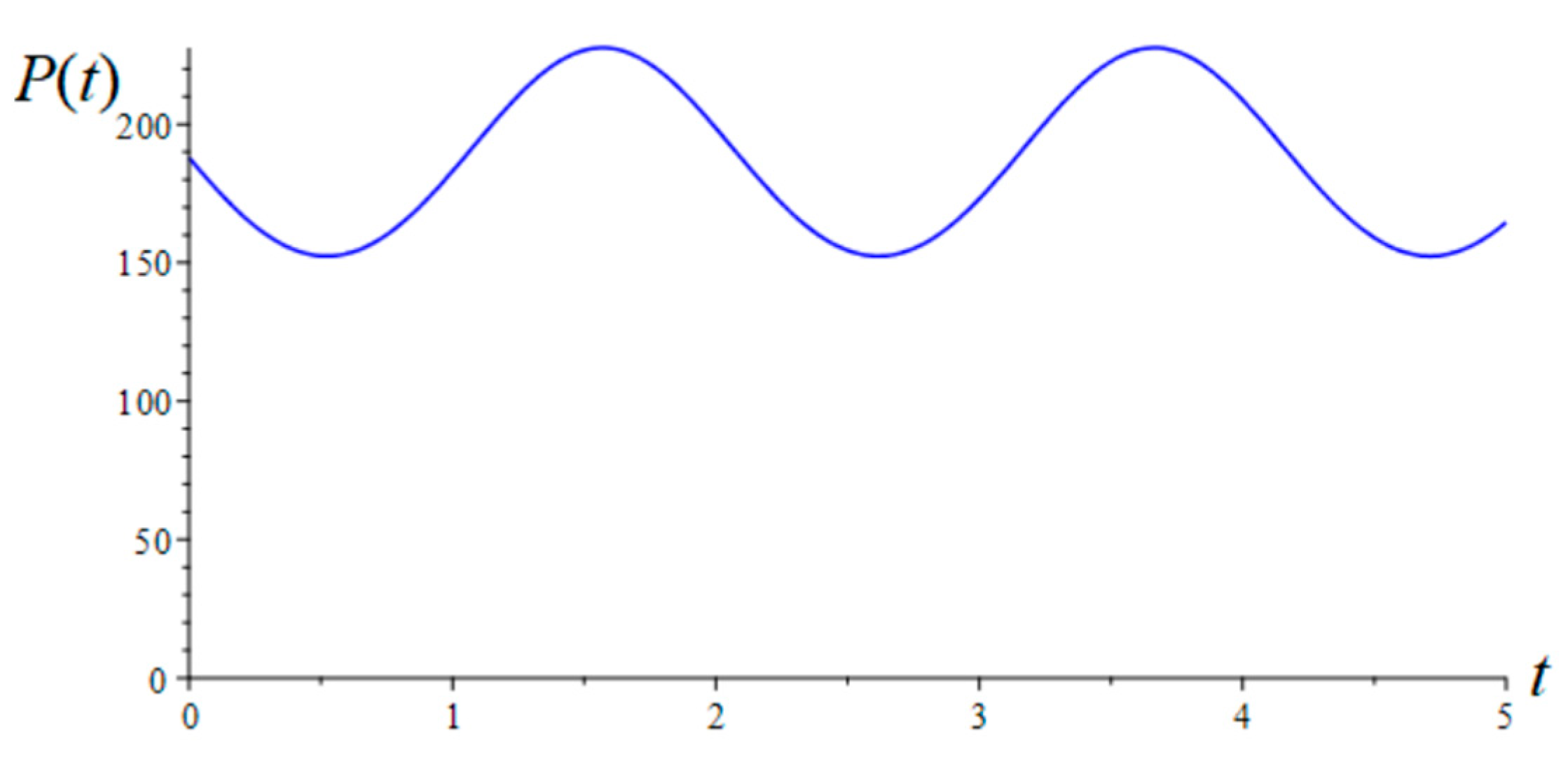
The transient active power is determined from Formula (30). In the assumed voltage signal, only the amplitude is distorted; then Equation (30) takes the following form:

$$\begin{array}{ll}P\left(t\right)=& G\left(\omega \right){\left|U\left(t\right)\right|}^2-{\displaystyle \frac{dB\left(\omega \right)}{d\omega }}\left|U\left(t\right)\right|{\displaystyle \frac{d\left|U\left(t\right)\right|}{dt}}=\\ & =188.13-372.96e^{-5t}+184.83e^{-10t}\end{array}$$

(36)

The signal determined by Equation (36) is shown in Figure 6. It is worth highlighting that when the signal reaches a steady state, both the active powers from (34) and (36) will have the same value.

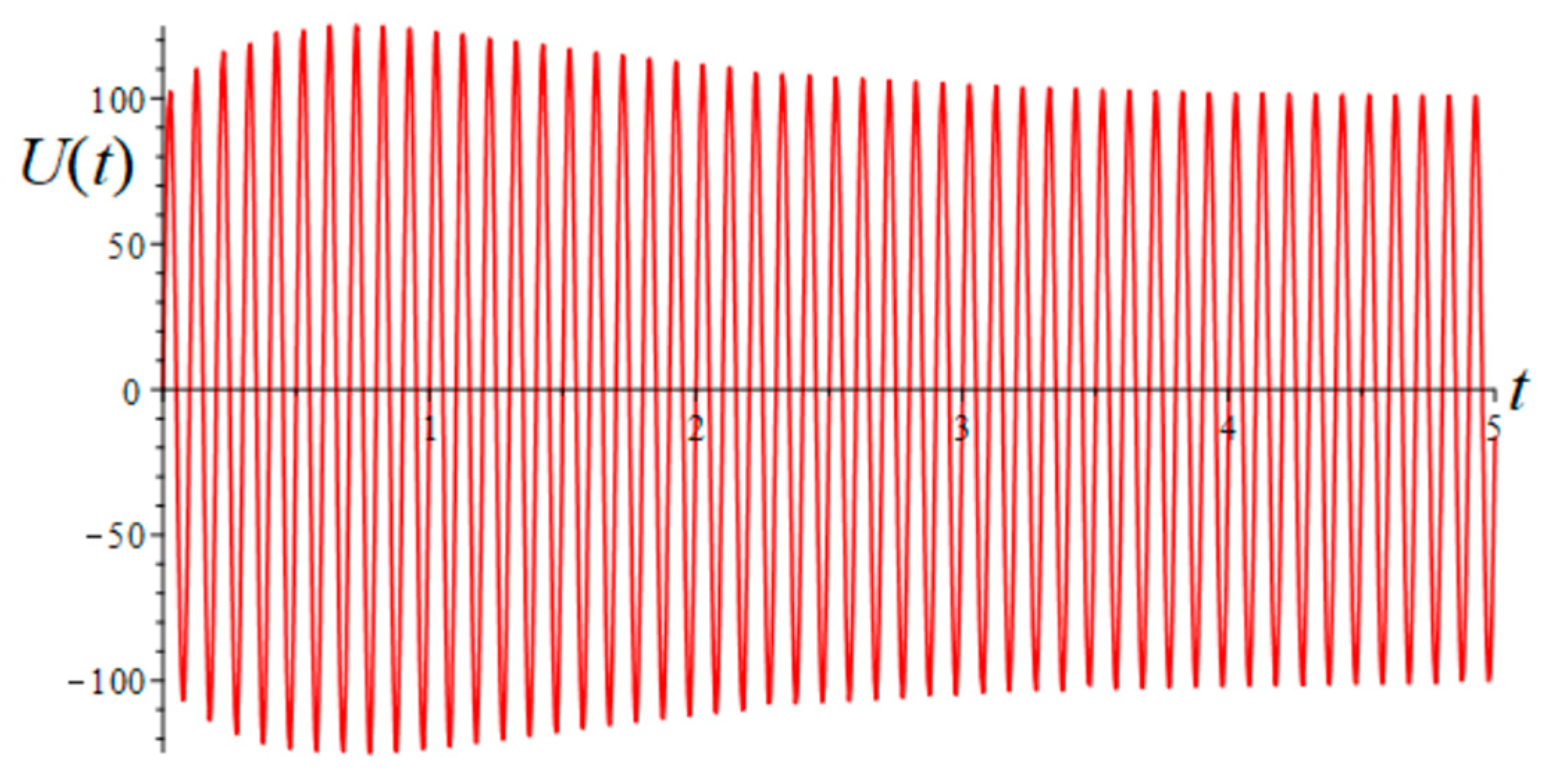
In the second case, the same RL branch is considered, but with a different voltage signal—amplitude distortion in the case of voltage sag (37) and volage swell (38):

$$u\left(\tau ,t\right)=100\left(1-e^{-t}+e^{-2t}\right)\sin \left(62.8\tau \right)$$

(37)

$$u\left(\tau ,t\right)=100\left(1-e^{-2t}+e^{-t}\right)\sin \left(62.8\tau \right)$$

(38)

The 3D and 2D waveforms for the voltage sag are shown in Figure 7 and Figure 8, while for the voltage swell is presented in Figure 9 and Figure 10.

The classic active power for a steady state can be determined in the same way as in the first case:

$$P=\mathrm{Re}\left[Y\left(j\omega \right)\right]{\left|U\right|}^2=188.13$$

(39)

while transient active power including a voltage sag yield results in a transient state:

$$\begin{array}{ll}P\left(t\right)=& G\left(\omega \right){\left|U\left(t\right)\right|}^2-{\displaystyle \frac{dB\left(\omega \right)}{d\omega }}\left|U\left(t\right)\right|{\displaystyle \frac{d\left|U\left(t\right)\right|}{dt}}=\\ & =188.13-375.6e^{-t}+562.41e^{-2t}-374.28e^{-3t}+186.81e^{-4t}\end{array}$$

(40)

and for voltage swell, the following is observed:

$$\begin{array}{ll}P\left(t\right)=& G\left(\omega \right){\left|U\left(t\right)\right|}^2-{\displaystyle \frac{dB\left(\omega \right)}{d\omega }}\left|U\left(t\right)\right|{\displaystyle \frac{d\left|U\left(t\right)\right|}{dt}}=\\ & =188.13+375.6e^{-t}-187.47e^{-2t}-374.28e^{-3t}+186.81e^{-4t}\end{array}$$

(41)

The waveforms of the transient active powers are presented in Figure 11 and Figure 12. After reaching a steady state, all calculated active powers in (39)–(41) have the same value.

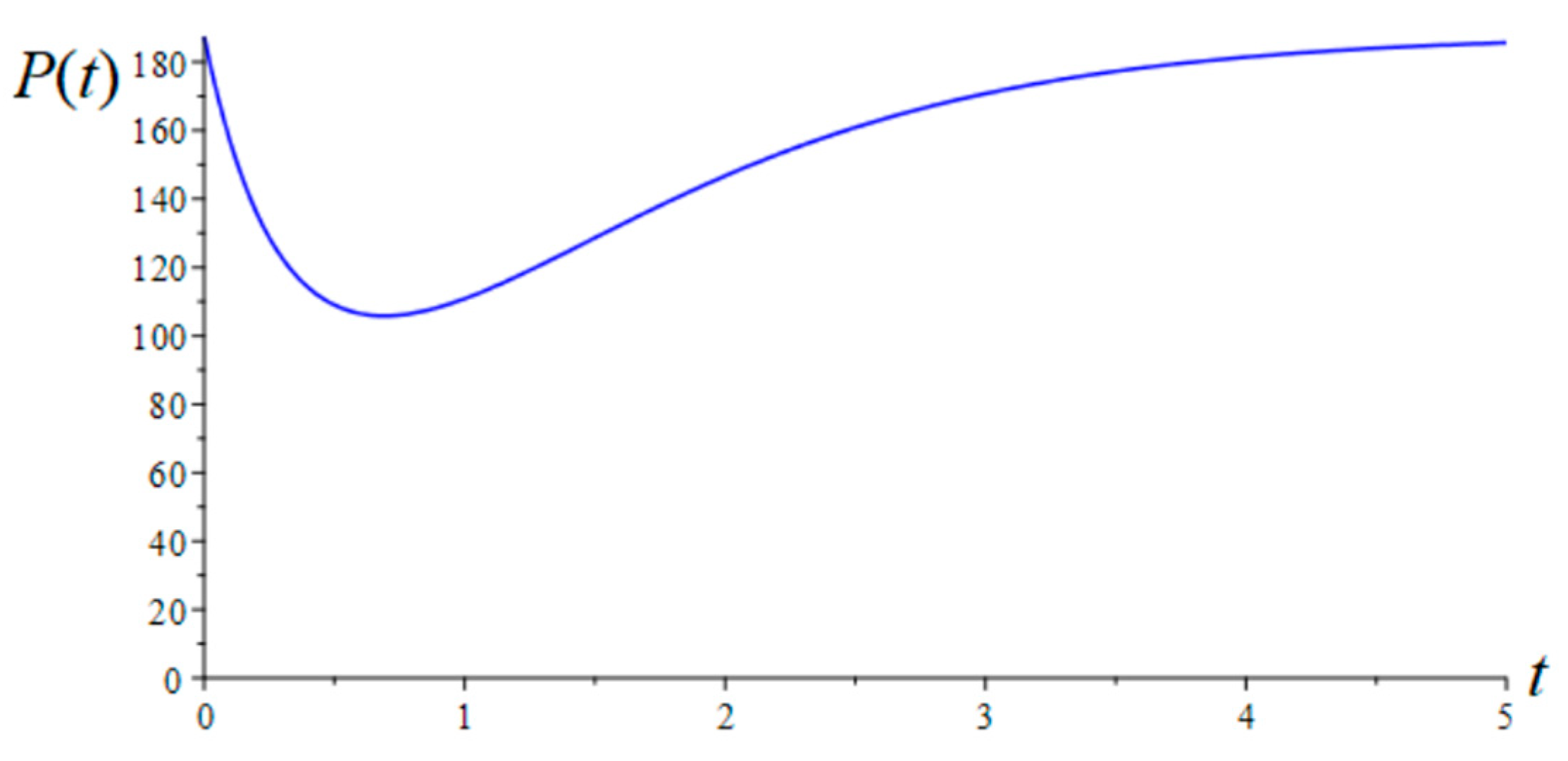
As the last analyzed case, the same RL branch is considered, but with a voltage signal that will never reach the steady state—the case including permanent voltage fluctuations:

$$u\left(\tau ,t\right)=100\left[1-0.1\sin \left(3t\right)\right]\sin \left(62.8\tau \right)$$

(42)

The 3D and 2D waveforms for the above voltage are shown in Figure 13 and Figure 14.

This case is different from the previously mentioned ones. The assumed voltage signal will never reach a steady state. Therefore, it is impossible to determine the exact value of the active power consumed by the RL branch. This limitation is not applicable for transient active power and yields the following result:

$$\begin{array}{l}P\left(t\right)=G\left(\omega \right){\left|U\left(t\right)\right|}^2-{\displaystyle \frac{dB\left(\omega \right)}{d\omega }}\left|U\left(t\right)\right|{\displaystyle \frac{d\left|U\left(t\right)\right|}{dt}}=\\ =189.07065-37.626\sin \left(3t\right)-0.198\cos \left(3t\right)+0.0099\sin \left(6t\right)-0.94065\cos \left(6t\right)\end{array}$$

(43)

which is shown in Figure 15.

4. Calculations Based on Laboratory Measured Signals

Voltage sags are a phenomenon that often appears in power systems after the sudden switching on of high-power loads. The percentage difference between the standard voltage value and the reduced voltage value depends on many parameters, including the moment of inertia of the generating units. This phenomenon will become more intense in hybrid networks operating on islands supplied by relatively small generating units. These systems will also experience short-term voltage increases (swells) during sudden load relief.

To verify the impact of disturbance losses on the total losses occurring during transient states in energy distribution systems, several scenarios of voltage sags were modeled in a laboratory five-node power system (compliant with IEEE standards) designed for the study of dynamic processes. The power system laboratory model set was described in detail in [31].

The laboratory setup was configured according to the diagram shown in Figure 16. The system was supplied by a LINZ E1S13M D/2 generator (LINZ ELECTRIC S.P.A., Verona, Italy) with rated power of 22 kVA propelled by a DC machine (MS1322 M32, made by Leroy-Somer, Angouleme, France) driven via a two-quadrant converter. The generator was coupled with a π-section power line (divided into five sections, each corresponding to a 30 km) using a block transformer with a 400 V/400 V ratio. At the beginning (before the first section of the line) and end (after the fifth section of the line) of the power line model, RL loads with adjustable active power (step adjustment ranging from 600 W to 9 kW) and reactive power (continuous adjustment ranging from 0 Var to 6 kVar) were connected. The load at the end of the line, which was permanently connected, was configured as a load representing 70% of the set operating power of the supplying generator. The load connected in steps at the beginning of the line (to model voltage sag) was set to 80% of the set operating power of the supplying generator.

The measurement of voltages and currents was performed at the end of the power line (as indicated in Figure 16). The measuring system featured a data acquisition set of current clamps FLUKE ac i1000s (measurement range 100 A (10 mV/A, accuracy 2% of reading ±5 mV) and 1000 A (1 mV/A, accuracy 1% of reading ±1 mV)) manufactured by Fluke Corporation (Everett, WA, USA) an NI USB-6259 measuring card and NI LabVIEW Signal Express software in ver. 15.0.0 (National Instruments Corp., Austin, TX, USA). The sampling frequency for all measurement signals was set to 50 kHz.

Voltage sags were modeled by suddenly connecting a load to the power system (operating in a single-generator configuration—unidirectional supply structure) with power higher than the power of the generator operating with constant torque control. The point of load connection (P, Q LOAD) is also marked in Figure 16.

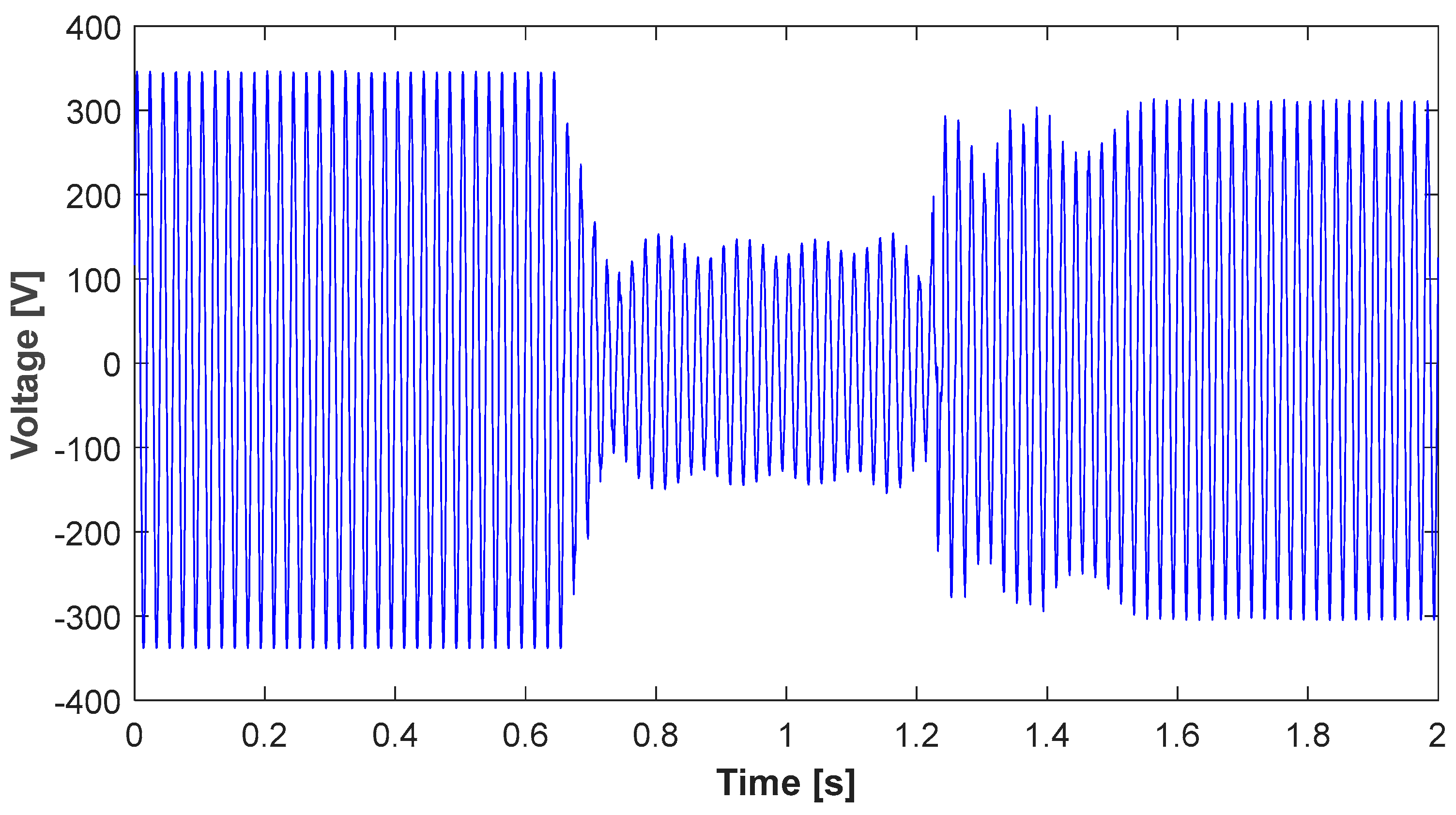
One of the time waveforms of the voltage sag measured during the laboratory tests is shown in Figure 17.

At the moment the extra load is connected to the system (by switch S1—Figure 16), the voltage at the receiver at the end of the supply line drops to about 40% of its nominal value (at 0.65 s of the simulation—Figure 17). After disconnecting the extra load (at 1.25 s of the simulation—Figure 17), the voltage at the end receiver rises again to the value it had before the voltage sag.

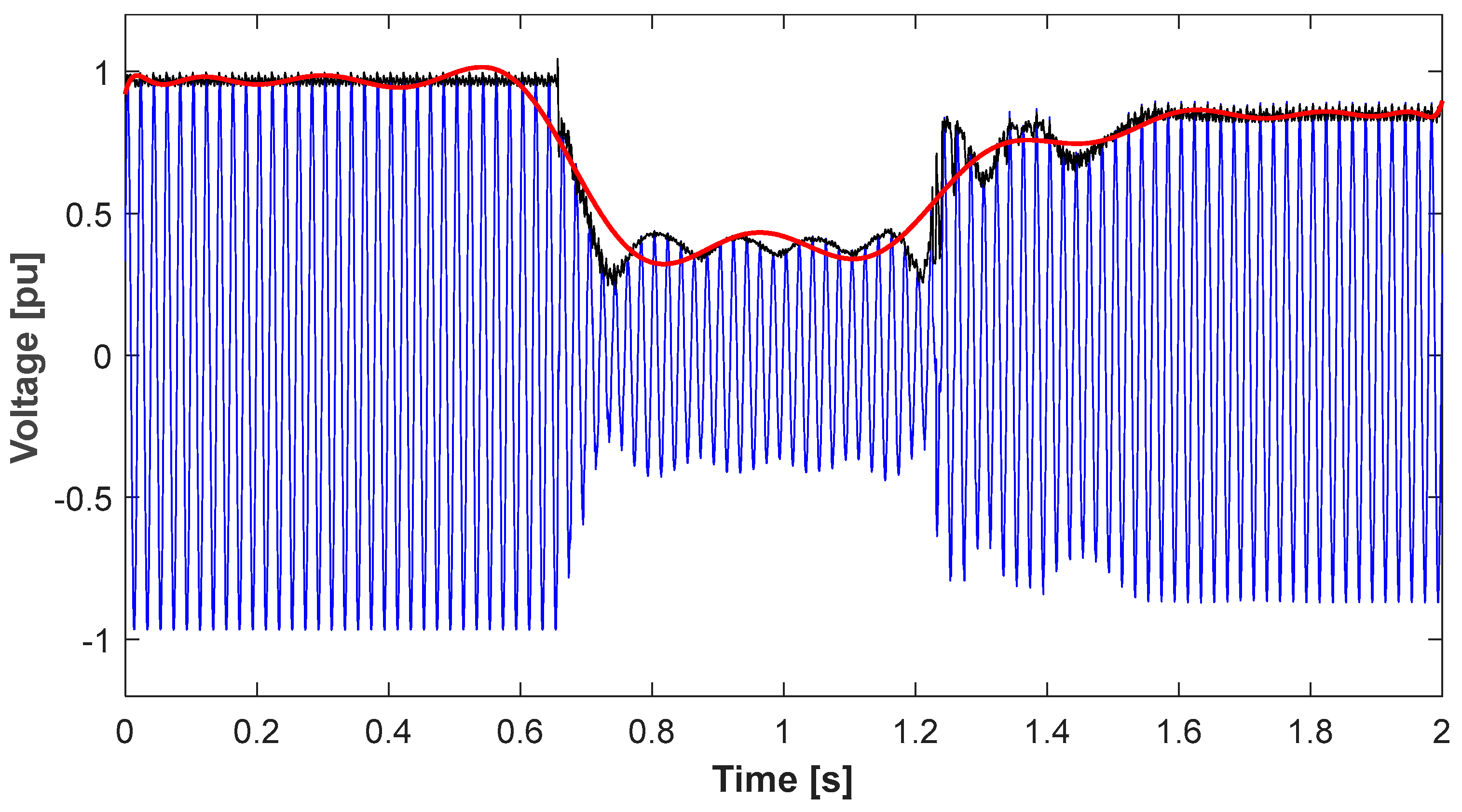
To determine disturbance losses, an envelope was applied to the voltage waveform at the receiver (Figure 18—black color). Then, an analytical polynomial function was used to map the voltage waveform envelope shown in Figure 18—red color. A 20th-degree polynomial was analytically determined (The units p.u. used for the axis labels on the graphs refer to the nominal values of voltage and power of the receiver).

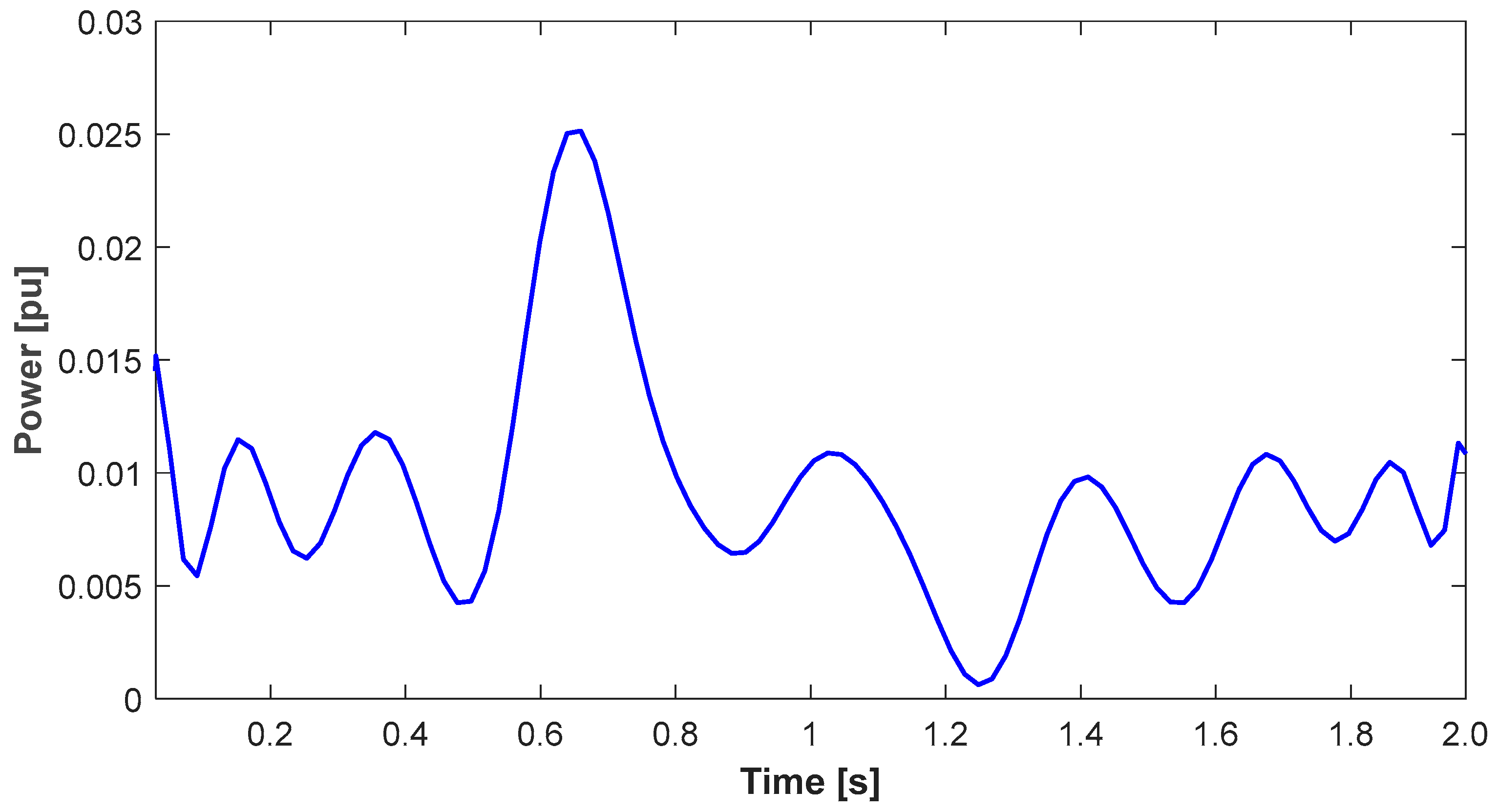
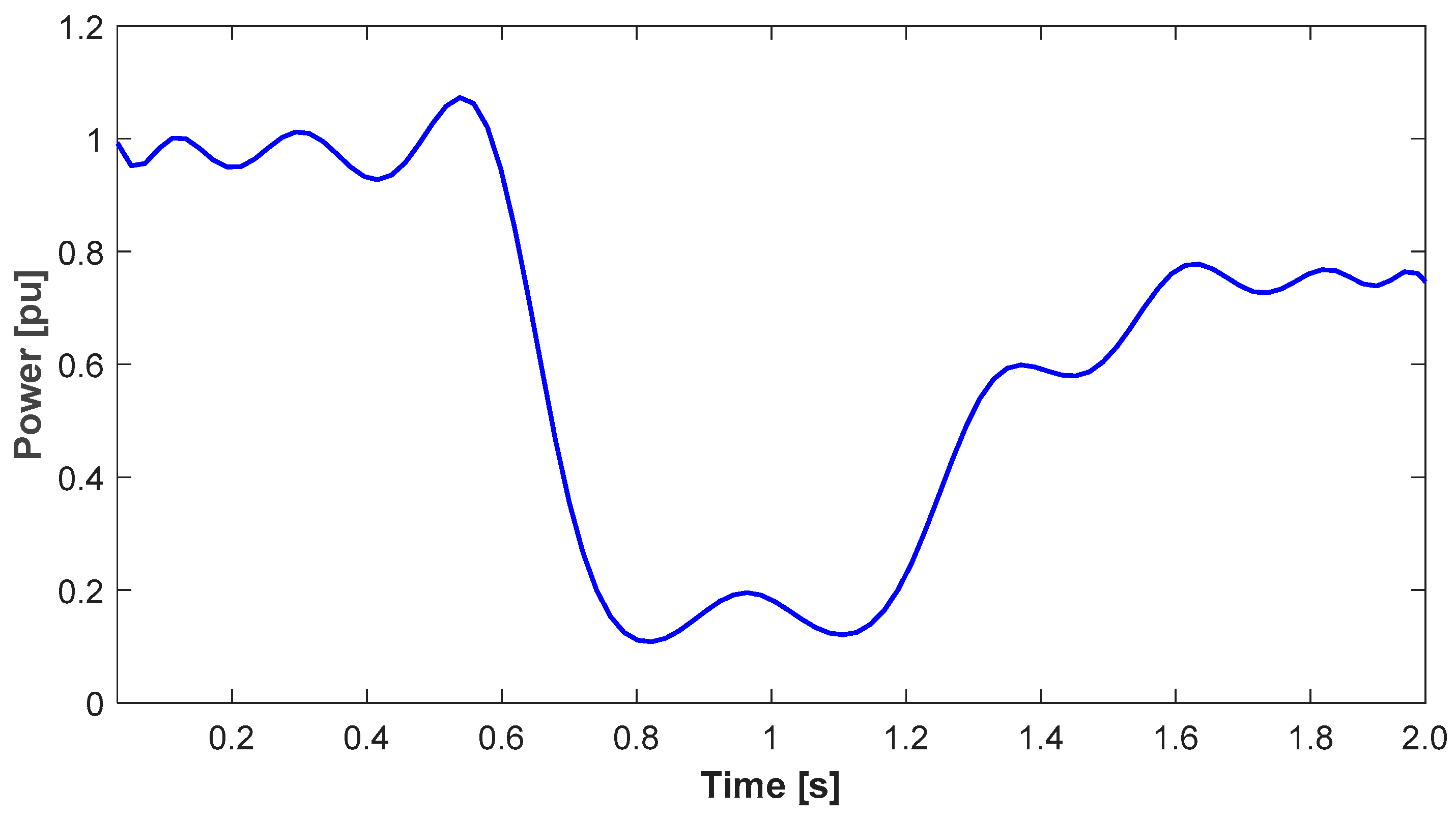
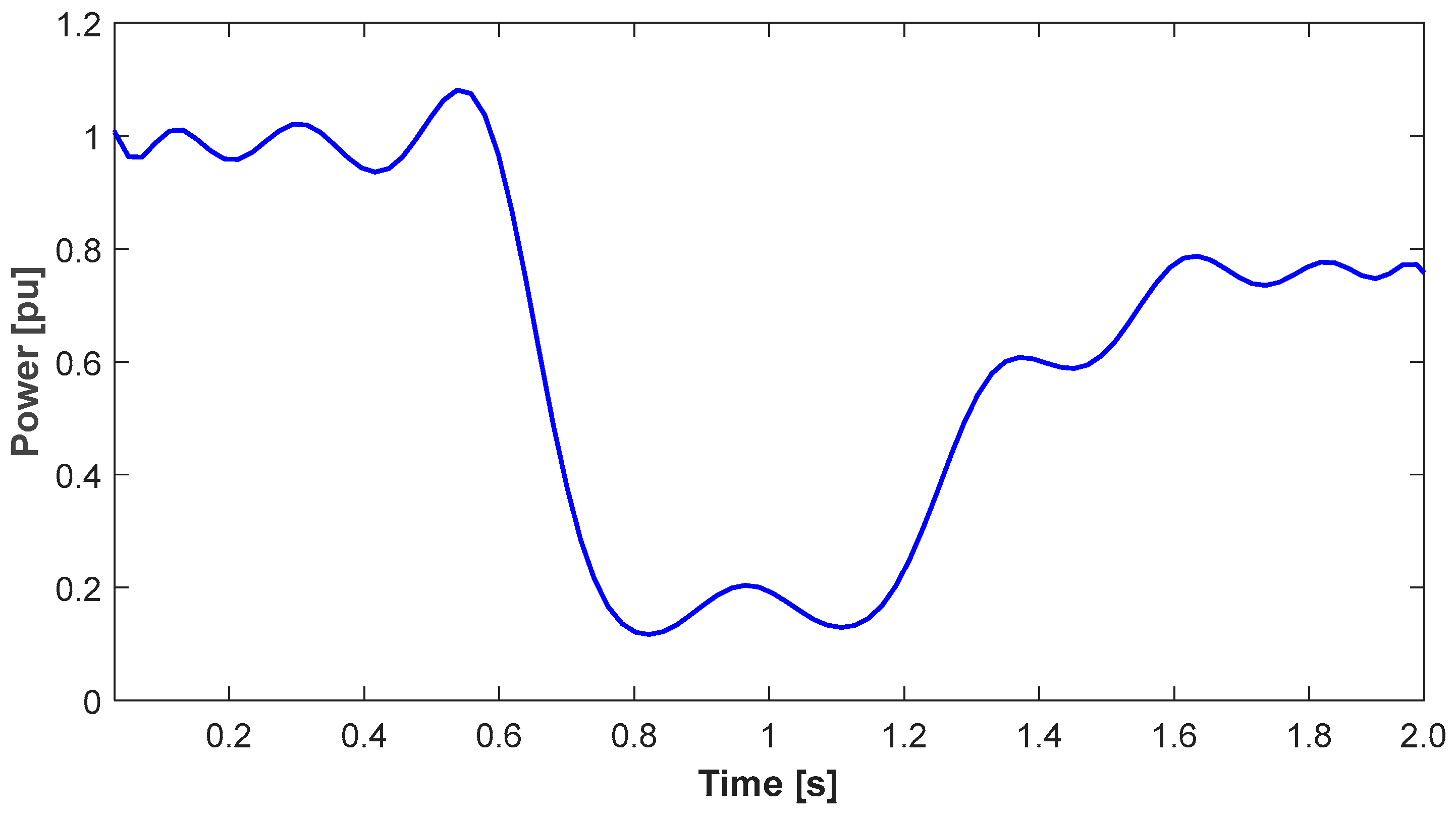
Based on the coefficients of the polynomial shown in Figure 18 and relationship (30), the disturbance active power waveform for the modeled voltage sag was determined and is shown in Figure 19. Meanwhile, the waveform of the main power load coefficient is presented in Figure 20. The total active power delivered to the receiver consists of the main coefficient and the disturbance coefficient, as shown in Figure 21.

The average value of the disturbance active power during the investigated case of voltage sag presented in Figure 19, Figure 20 and Figure 21 is 0.0092 p.u., while the maximum value reached is 0.025 p.u. In comparison to the average value of the primary component of active power delivered to the receiver (0.62 p.u.), these values represent 1.46% and 3.97%, respectively, considering that the disturbance component results in an approximately 1.5% increase in the average total active power compared to the active power without accounting for this component.

5. Conclusions

The concept of transient active power presented in this article enables its mathematical description in operating states that are different from normative states—during various variants of signal distortions caused by transient states. The simulation research section presents several of the most common variants of voltage changes and shows their impact on the active power.

This article shows the impact of disturbance power on the total power consumed by the load. In the presented case, it accounted for approximately 1.5% of the total power transmitted to the load (in relation to average values). The exclusion of disturbance power in the modeled voltage sag scenario does not pose a significant problem that could affect the operation of the power supply network. However, in the case of other types of disturbances, such as short circuits (in particular multiple short circuits), this component may not be negligible. For example, the additional small percentage of energy (which is often ignored) that dissipates in the conductor during a short circuit could raise its temperature. Therefore, the analysis of disturbance power during short circuits will be the subject of further research.

In future laboratory tests, the measured signals will be subjected to the envelope detection process, which is used to calculate transient active power. The laboratory tests performed so far have shown a potential limitation of the described method. The limitation is the requirement of differentiability of the given signal envelope. It is fulfilled in the case of polynomial approximation. Of course, this has its consequences, as the result will not be exact but approximated, especially in terms of the shape of the transient active power waveform. However, the assumed 20th-degree polynomial in the laboratory test section yields an error of 0.003% according to the average values in the given range (260.4069 V avg voltage and 260.4148 V avg polynomial).

The concept presented in this article will be used to solve one of the most important tasks of ensuring optimal cooperation between the energy source and energy receiver. This issue is related to minimizing the losses of transmitted energy, i.e., minimizing the effective value of the current transporting the required active power to the receiver. The problem is well known and solved for steady states [10] and is under development for transient states.