Independent Pitch Adaptive Control of Large Wind Turbines Using State Feedback and Disturbance Accommodating Control
Abstract
1. Introduction
2. Wind Turbine Model
3. Full State Feedback Control
3.1. LQR Control Design
3.2. Disturbance Accommodating Control Design
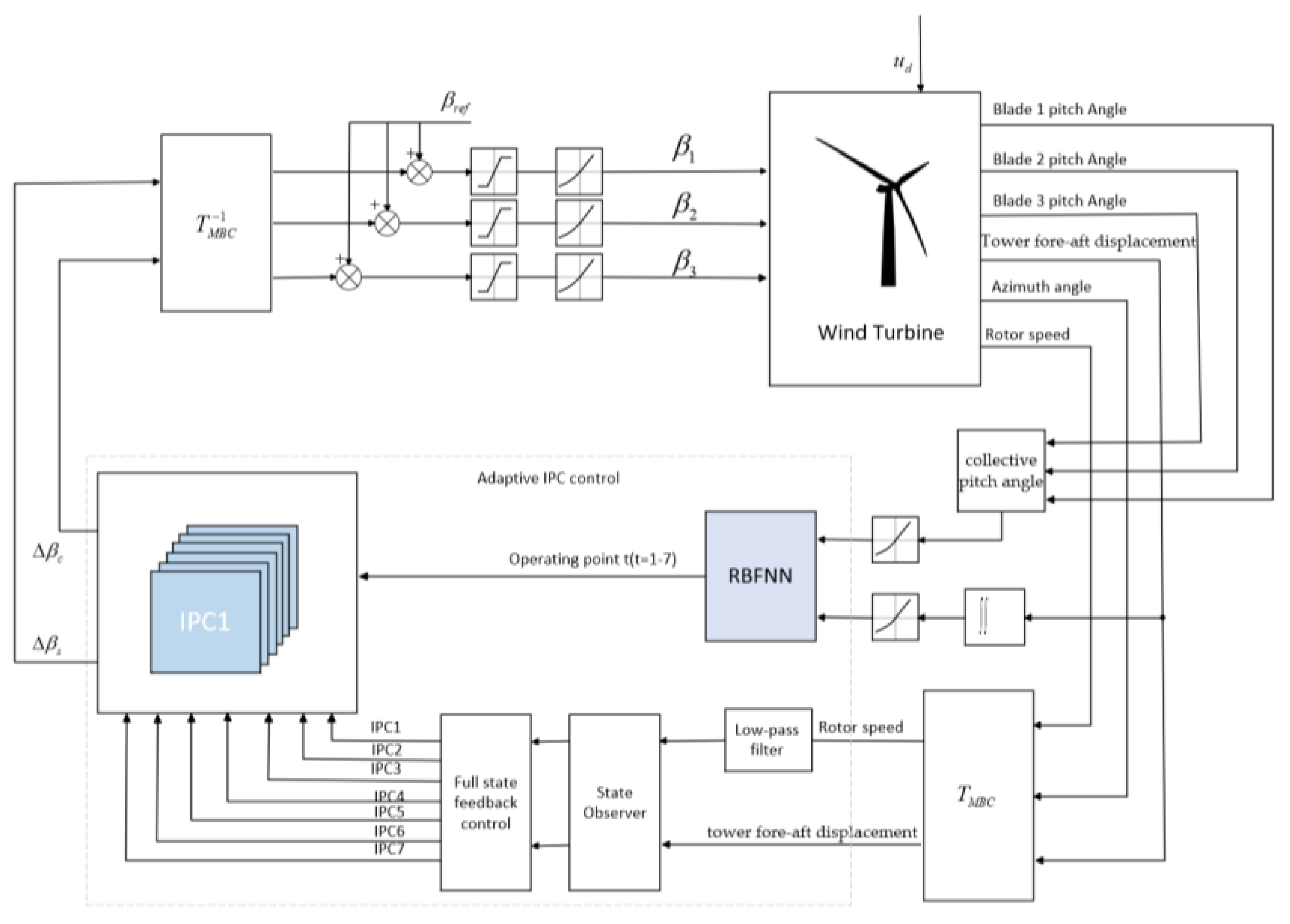
4. Adaptive Independent Pitch System Design
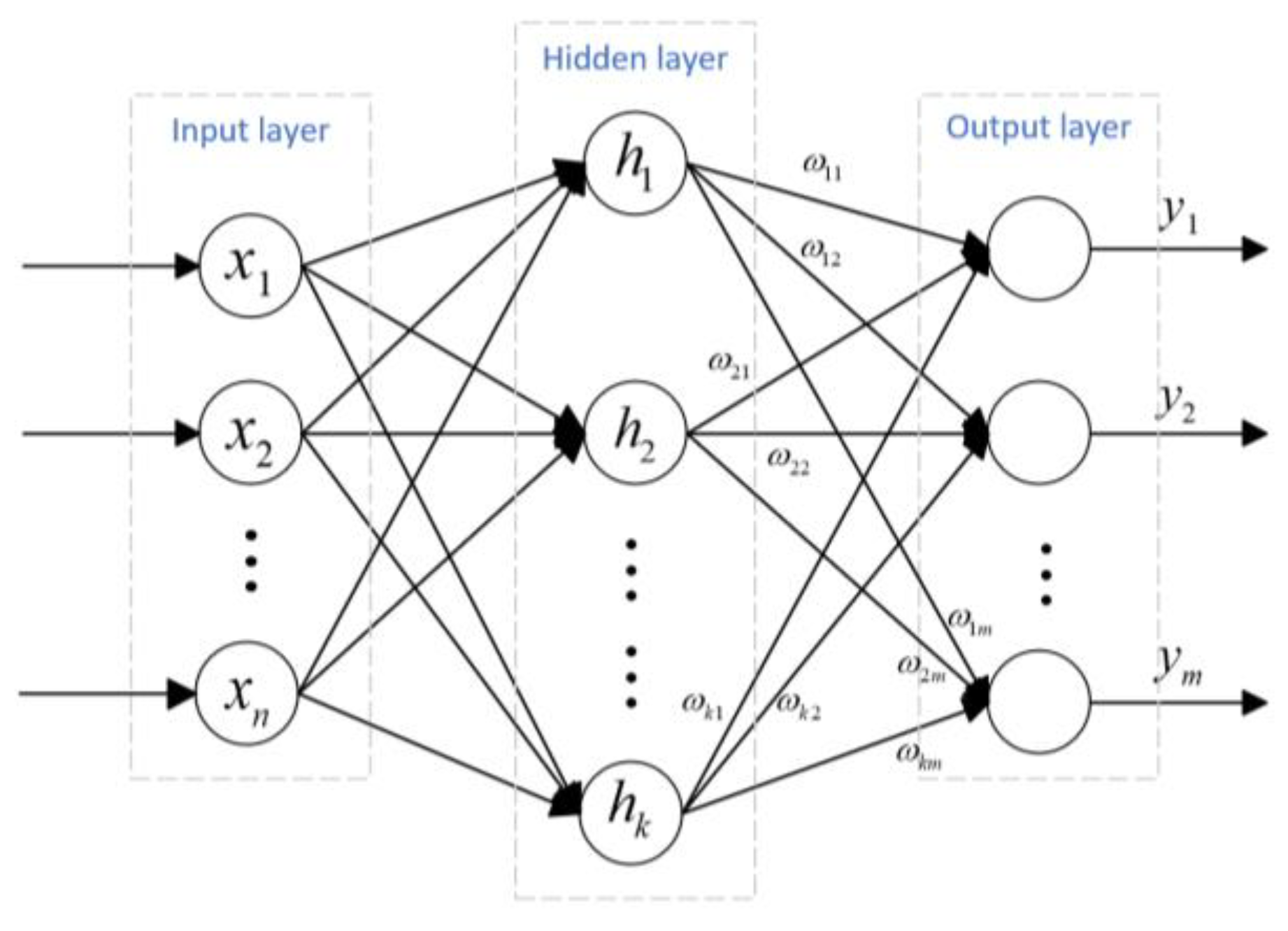
4.1. RBF Neural Network Architecture
4.2. Adaptive Independent Pitch Control System Design
5. Simulations Results
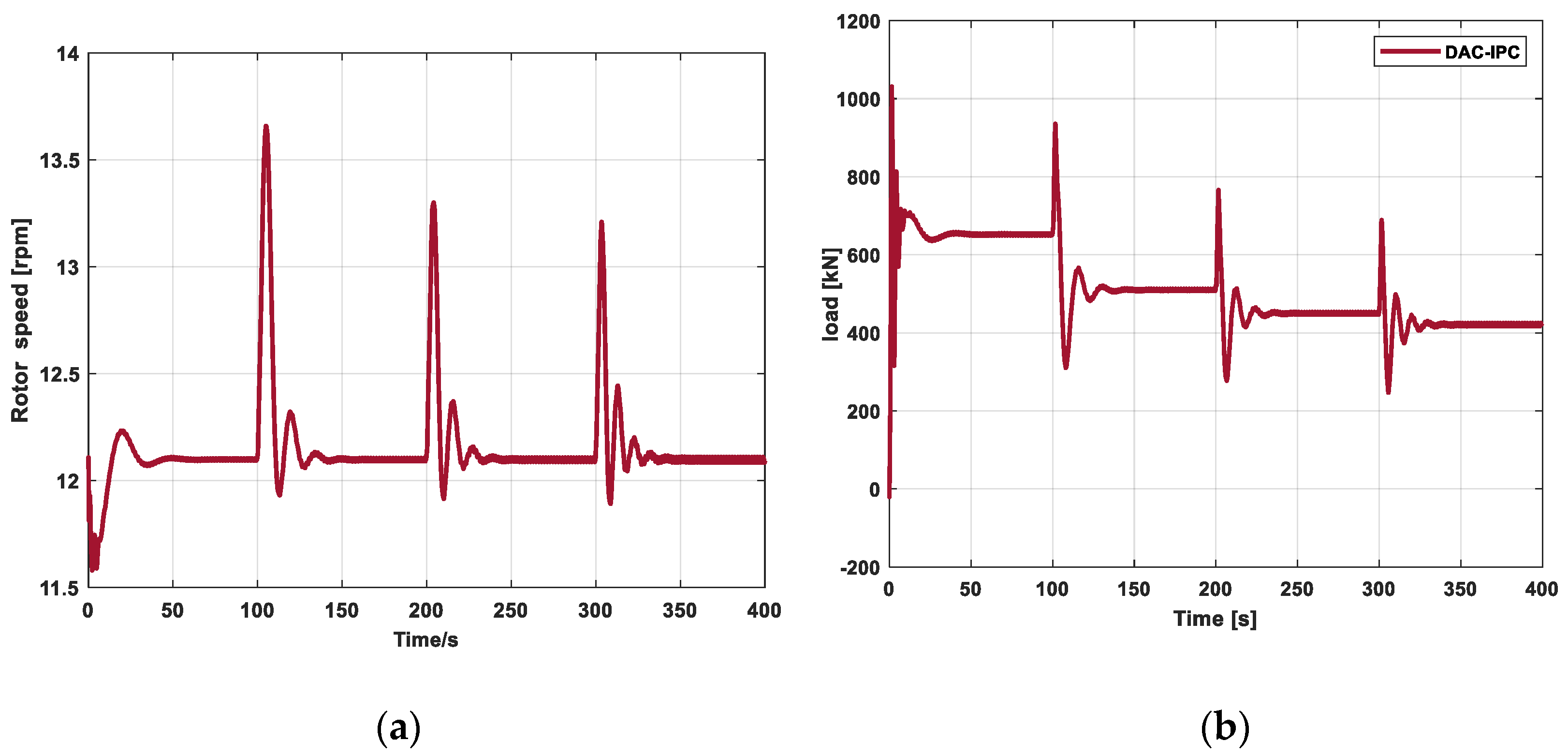
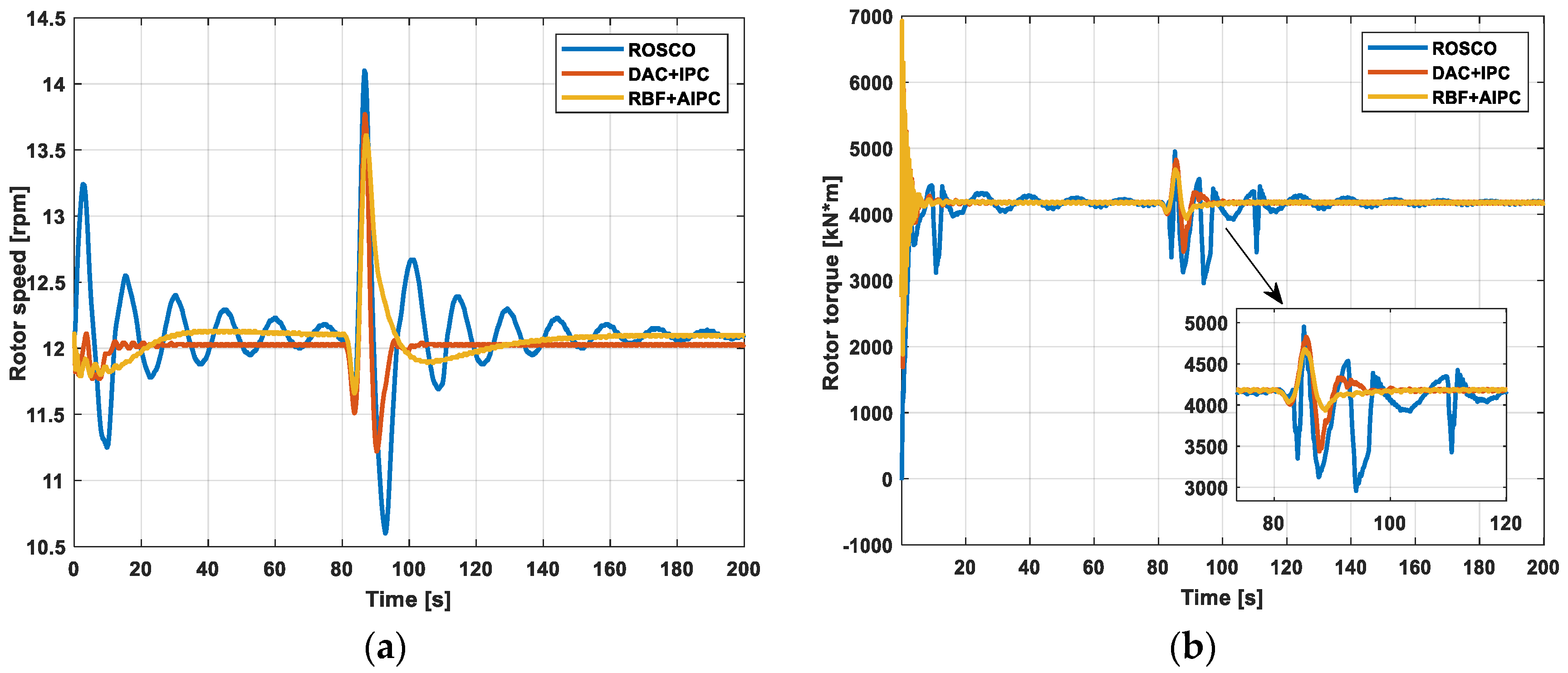
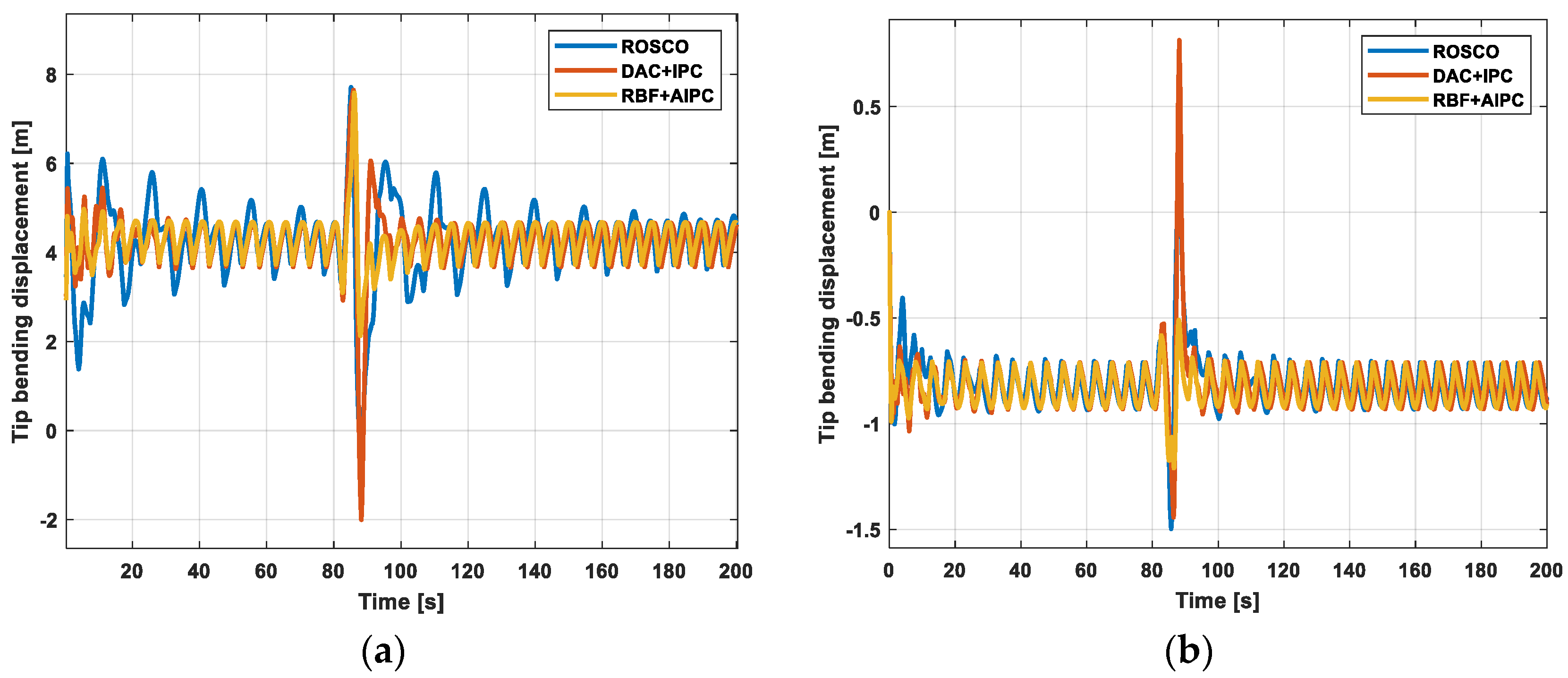
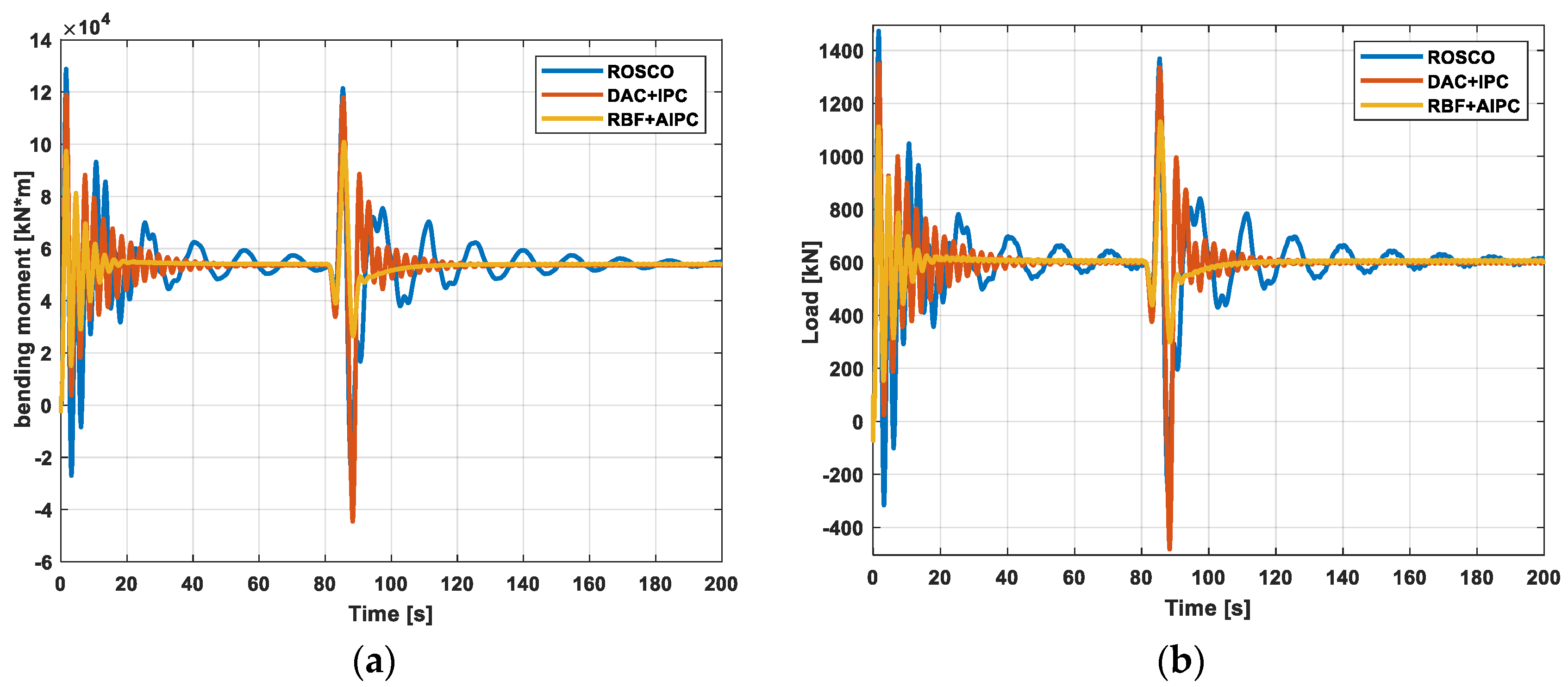
5.1. Adaptive Disturbance Control
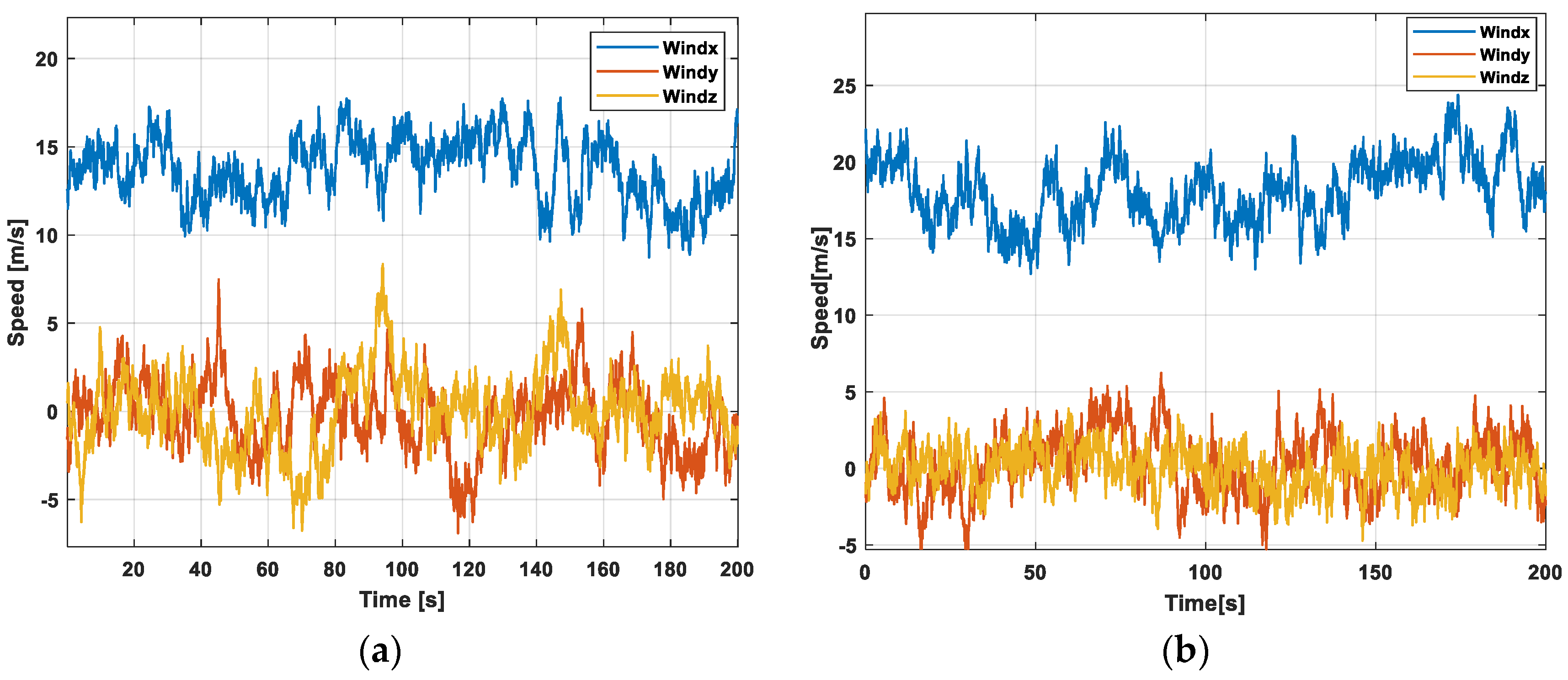
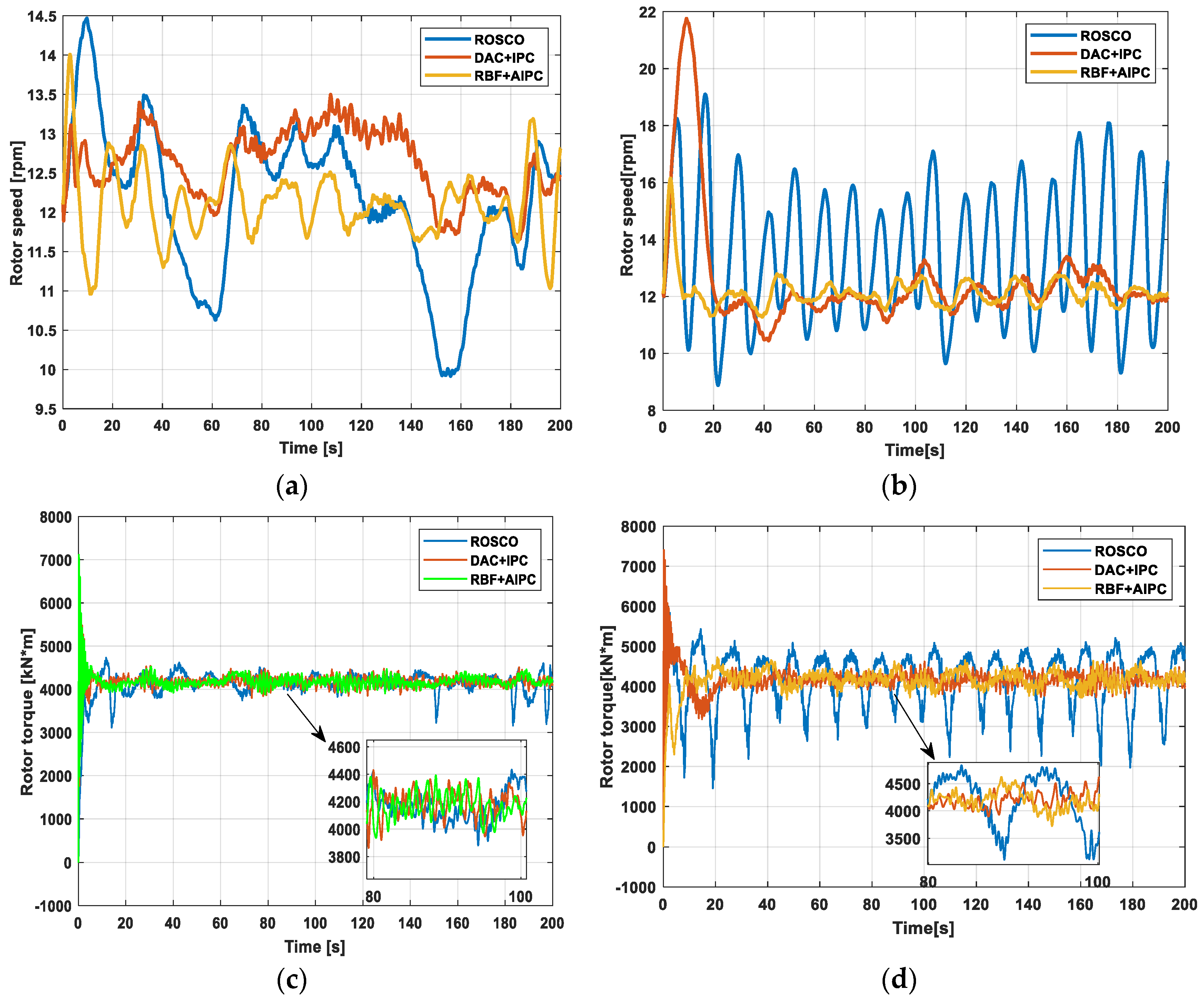
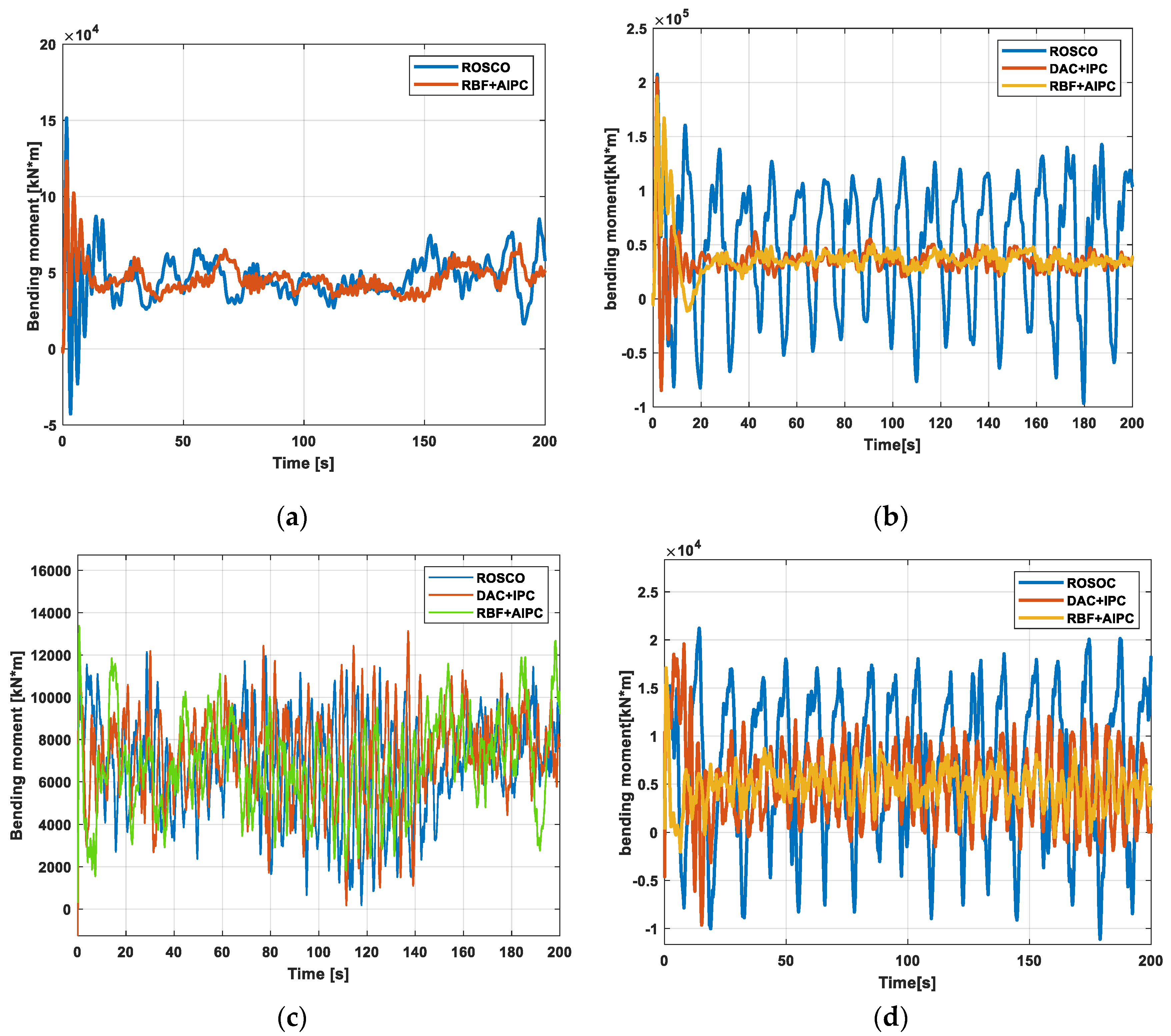
5.2. DLC1.1 Working Condition Analysis of RBF-AIPC
5.3. DLC1.3 Working Condition Analysis of RBF-AIPC
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gambier, A. Pitch control of three bladed large wind energy converters—A review. Energies 2021, 14, 8083. [Google Scholar] [CrossRef]
- Didier, F.; Liu, Y.-C.; Laghrouche, S.; Depernet, D. A comprehensive review on advanced control methods for floating offshore wind turbine systems above the rated wind speed. Energies 2024, 17, 2257. [Google Scholar] [CrossRef]
- Lio, W.H.; Jones, B.L.; Rossiter, J.A. Estimation and Control of Wind Turbine Tower Vibrations Based on Individual Blade-Pitch Strategies. IEEE Trans. Control Syst. Technol. 2019, 27, 1820–1828. [Google Scholar] [CrossRef]
- Lara, M.; Mulders, S.P.; van Wingerden, J.-W.; Vázquez, F.; Garrido, J. Analysis of Adaptive Individual Pitch Control Schemes for Blade Fatigue Load Reduction on a 15 MW Wind Turbine. Appl. Sci. 2023, 14, 183. [Google Scholar] [CrossRef]
- El Yaakoubi, A.; Bouzem, A.; El Alami, R.; Chaibi, N.; Bendaou, O. Wind turbines dynamics loads alleviation: Overview of the active controls and the corresponding strategies. Ocean. Eng. 2023, 278, 114070. [Google Scholar] [CrossRef]
- Hu, X.Q.; Tan, W.; Hou, G.L. PIDD2 Control of Large Wind Turbines Pitch Angle. Energies 2023, 16, 5096. [Google Scholar] [CrossRef]
- Lim, C.-W. A study of a gain-scheduled individual pitch controller for an NREL 5 MW wind turbine. Energies 2024, 17, 246. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, B. Pitch angle Control of Variable Speed Wind Turbine by using Fuzzy Logic. In Proceedings of the 2018 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 22–24 October 2018; pp. 56–60. [Google Scholar]
- Shawqran, A.M.; El-Marhomy, A.; Attia, M.A. Pitch angle Adaptive PI controller based on heuristics optimization algorithms. In Advanced Machine Learning Technologies and Applications: Proceedings of AMLTA 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 674–687. [Google Scholar]
- Brandetti, L.; Mulders, S.P.; Liu, Y.; Watson, S.; van Wingerden, J.-W. Analysis and multi-objective optimisation of wind turbine torque control strategies. Wind Energy Sci. 2023, 8, 1553–1573. [Google Scholar] [CrossRef]
- Lara, M.; Garrido, J.; Ruz, M.L.; Vázquez, F. Multi-objective optimization for simultaneously designing active control of tower vibrations and power control in wind turbines. Energy Rep. 2023, 9, 1637–1650. [Google Scholar] [CrossRef]
- Han, Y.; Liu, X. Collective pitch sliding mode control for large scale wind turbines considering load reduction. In Proceedings of the 2014 International Conference on Mechatronics and Control, Jinzhou, China, 3–5 July 2014. [Google Scholar]
- Fu, D.Y.; Kong, L.X.; Gong, L.C.; Wang, A.; Jia, H.; Zhao, N. Wind Turbine Load Optimization Control Strategy Based on LIDAR Feed-Forward Control for Primary Frequency Modulation Process with Pitch Angle Reservation. Energies 2023, 16, 510. [Google Scholar] [CrossRef]
- Sarkar, S.; Fitzgerald, B.; Basu, B. Individual blade pitch control of floating offshore wind turbines for load mitigation and power regulation. IEEE Trans. Control Syst. Technol. 2020, 29, 305–315. [Google Scholar] [CrossRef]
- Bashetty, S.; Guillamon, J.I.; Mutnuri, S.S.; Ozcelik, S. Design of a robust adaptive controller for the pitch and torque control of wind turbines. Energies 2020, 13, 1195. [Google Scholar] [CrossRef]
- Kipchirchir, E.; Do, M.H.; Njiri, J.G.; Soffker, D. Mixed-Sensitivity Robust Disturbance Accommodating Control for Load Mitigation and Speed Regulation of Wind Turbines. In Proceedings of the 2022 European Control Conference (ECC), London, UK, 12–15 July 2022; pp. 1012–1017. [Google Scholar]
- Kipchirchir, E.; Söffker, D. IPC-based robust disturbance accommodating control for load mitigation and speed regulation of wind turbines. Wind Energy 2024, 27, 382–402. [Google Scholar] [CrossRef]
- Wen, H.Y.; Liu, Y.; Lee, S.M.; Park, J.H. Optimal Power Regulating for Wind Turbine with LQR and Disturbance Accommodation Pitch Control. In Proceedings of the 2023 9th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 21–23 April 2023. [Google Scholar]
- Menezes, E.J.N.; Araújo, A.M.; Rohatgi, J.S.; del Foyo, P.M.G. Active load control of large wind turbines using state-space methods and disturbance accommodating control. Energy 2018, 150, 310–319. [Google Scholar] [CrossRef]
- Wang, N.; Wright, A.D.; Johnson, K.E. Independent Blade Pitch Controller Design for a Three-Bladed Turbine Using Disturbance Accommodating Control. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 2301–2306. [Google Scholar]
- Wang, N.; Wright, A.D.; Balas, M.J. Disturbance accommodating control design for wind turbines using solvability conditions. J. Dyn. Syst. Meas. Control 2017, 139, 41007. [Google Scholar] [CrossRef]
- Kipchirchir, E.; Do, M.H.; Njiri, J.G.; Söffker, D. Adaptive robust observer-based control for structural load mitigation and speed regulation in commercial wind turbines. IEEE Access 2024, 12, 38335–38350. [Google Scholar] [CrossRef]
- Fitzgerald, B.; Sarkar, S. Observer based pitch control for load mitigation and power regulation of floating offshore wind turbines. J. Phys. Conf. Ser. 2024, 2647, 032003. [Google Scholar] [CrossRef]
- Asgharnia, A.H.; Jamali, A.; Shahnazi, R.; Maheri, A. Load mitigation of a class of 5-MW wind turbine with RBF neural network based fractional-order PID controller. ISA Trans. 2020, 96, 272–286. [Google Scholar] [CrossRef]
- Routray, A.; Sivakumar, N.; Hur, S.H.; Bang, D.J. A comparative study of optimal individual pitch control methods. Sustainability 2023, 15, 10933. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Jonkman, B.J. FAST modularization framework for wind turbine simulation: Full-system linearization. J. Phys. Conf. Ser. 2016, 753, 082010. [Google Scholar] [CrossRef]
- Abbas, N.J.; Zalkind, D.S.; Pao, L.; Wright, A. A reference open-source controller for fixed and floating offshore wind turbines. Wind Energy Sci. 2022, 7, 53–73. [Google Scholar] [CrossRef]
- Wind Turbines—Part 1: Design Requirements. Available online: https://webstore.iec.ch/publication/64648 (accessed on 14 August 2024).
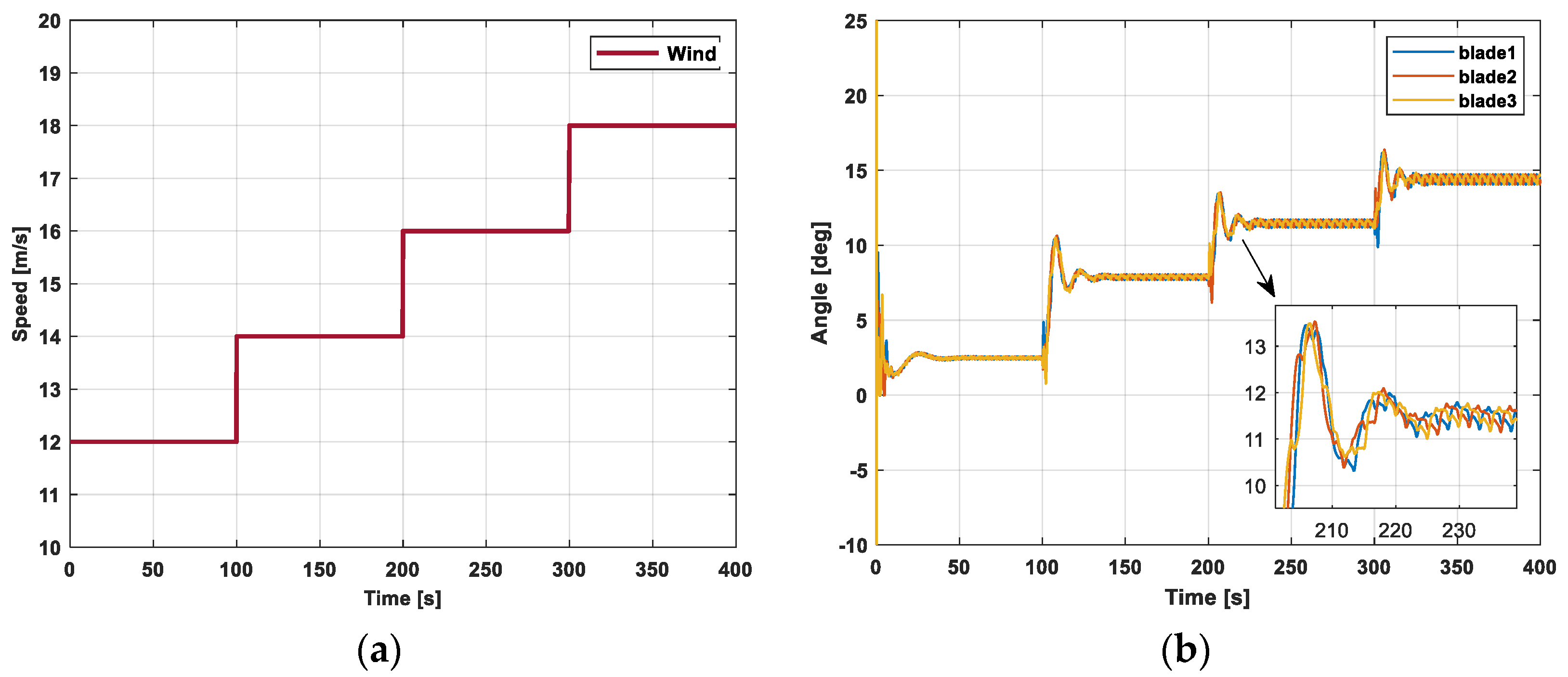

| IPC | Wind Speed (m/s) | Angle (Deg) | Rotor Speed (rpm) |
|---|---|---|---|
| 1 | 12 | 3.83 | 12.1 |
| 2 | 14 | 8.72 | 12.1 |
| 3 | 16 | 12.06 | 12.1 |
| 4 | 18 | 14.92 | 12.1 |
| 5 | 20 | 17.47 | 12.1 |
| 6 | 22 | 19.94 | 12.1 |
| 7 | 24 | 22.35 | 12.1 |
| Parameter | Value | Unit |
|---|---|---|
| Rated power | 5 | MW |
| Cut-in, rated, cut-out wind speed | 3, 11.4, 25 | m/s |
| Blade pitch range | 0–90 | ° |
| Cut-in, rated rotor speed | 6.9, 12.1 | rpm |
| Gearbox ratio | 1:97 | - |
| Rotor, hub radius | 63, 1.5 | m |
| Optimum pitch angle () | 0 | ° |
| Hub height | 90 | m |
| Maximum power coefficient () | 0.482 | - |
| Optimal tip-speed-ratio () | 7.55 | - |
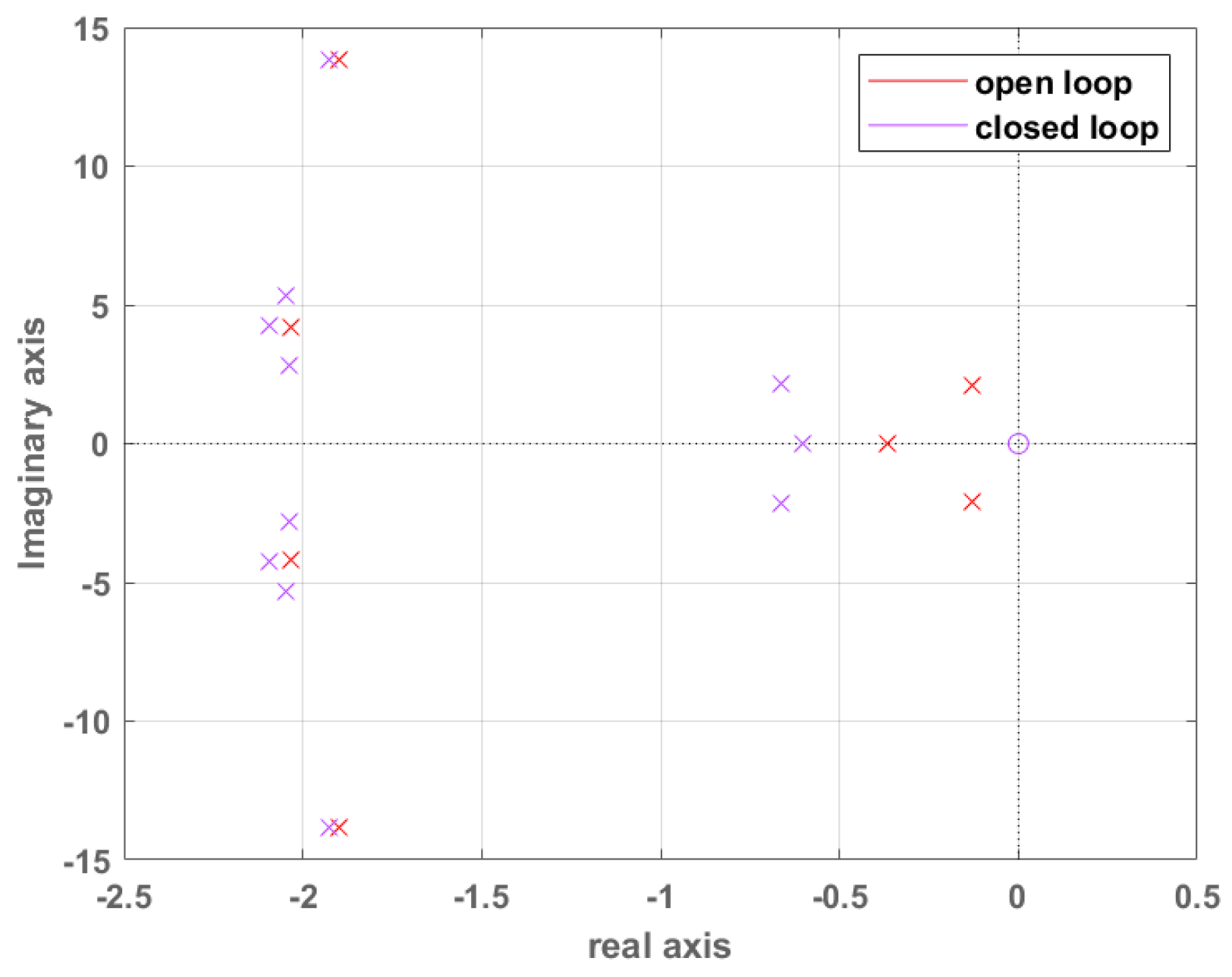
| System Mode | Open Loop Pole | LQR Pole Configuration after |
|---|---|---|
| Rotor speed | −0.37 | −0.6 |
| Drivetrain torsional mode | 1.9 ± 13.8i | −1.92 ± 13.86i |
| Blade 1 F-W mode | −2.03 ± 4.22i | −2.04 ± 2.79i |
| Blade 2 F-W mode | −2.04 ± 2.79i | −2.05 ± 5.32i |
| Blade 3 F-W mode | −2.05 ± 5.32i | −2.09 ± 4.25i |
| Tower F-A mode | −0.13 ± 2.08i | −0.67 ± 2.13i |
| Load Channel [kNm] | Controller | Avg (14 m/s) | Avg (18 m/s) | Std (14 m/s) | Std (18 m/s) |
|---|---|---|---|---|---|
| Tower F-A [104] | ROSCO | 4.7990 | 4.966 | 1.5974 | 4.885 |
| RBF + AIPC | 4.6041 | 3.506 | 1.0380 | 1.672 | |
| Blade F-W | ROSCO | 6619.2 | 7012.8 | 2311.1 | 4267.5 |
| DAC + IPC | 7188.7 | 5155.2 | 2116.4 | 3145.6 | |
| RBF + AIPC | 6619.4 | 4795.6 | 2126.8 | 1992.3 |
| Parameter | Controller | Std. | % |
|---|---|---|---|
| Rotor speed | ROSCO | 2.47 | - |
| DAC + IPC | 1.80 | −27.12 | |
| RBF + AIPC | 1.36 | −44.90 | |
| Rotor torque | ROSCO | 989.94 | - |
| DAC + IPC | 564.26 | −43.00 | |
| RBF + AIPC | 499.22 | −49.57 |
| Parameter | Controller | Std. | % |
|---|---|---|---|
| In plane | ROSCO | 3.52 | - |
| DAC + IPC | 4.22 | −19.88 | |
| RBF + AIPC | 2.33 | −33.80 | |
| Out of plane | ROSCO | 5.63 | - |
| DAC + IPC | 5.82 | 3.02 | |
| RBF + AIPC | 3.84 | −31.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wang, Y.; Wang, X. Independent Pitch Adaptive Control of Large Wind Turbines Using State Feedback and Disturbance Accommodating Control. Energies 2024, 17, 4619. https://doi.org/10.3390/en17184619
Liu Y, Wang Y, Wang X. Independent Pitch Adaptive Control of Large Wind Turbines Using State Feedback and Disturbance Accommodating Control. Energies. 2024; 17(18):4619. https://doi.org/10.3390/en17184619
Chicago/Turabian StyleLiu, Yingming, Yi Wang, and Xiaodong Wang. 2024. "Independent Pitch Adaptive Control of Large Wind Turbines Using State Feedback and Disturbance Accommodating Control" Energies 17, no. 18: 4619. https://doi.org/10.3390/en17184619
APA StyleLiu, Y., Wang, Y., & Wang, X. (2024). Independent Pitch Adaptive Control of Large Wind Turbines Using State Feedback and Disturbance Accommodating Control. Energies, 17(18), 4619. https://doi.org/10.3390/en17184619





