Packing Characteristics and Heat Transfer Performance of Non-Spherical Particles for Concentrated Solar Power Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. DEM Contact Model
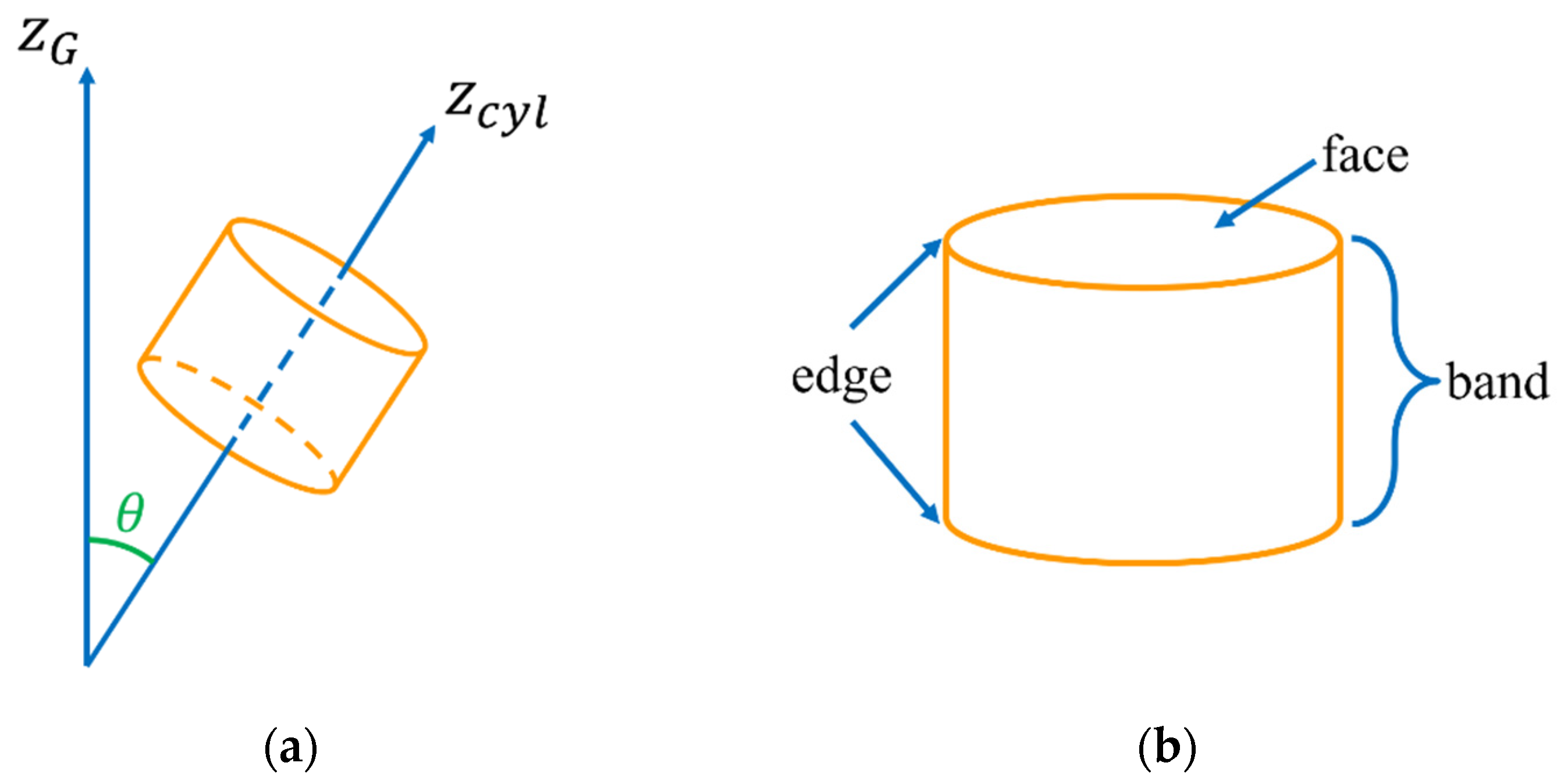
2.2. DEM Contact Detection for Superquadrics
2.3. Material Properties and Particle Geometry Characteristics
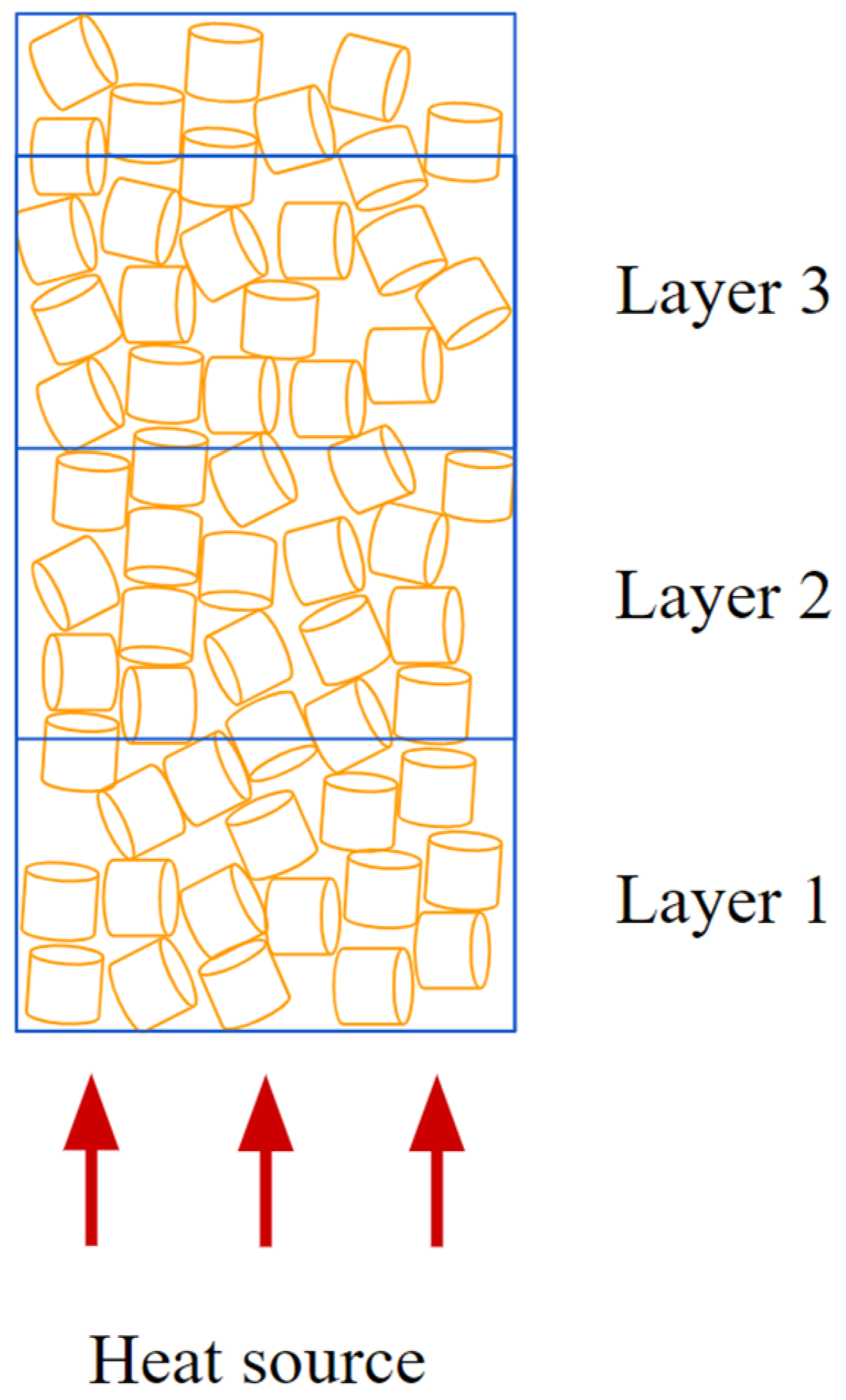
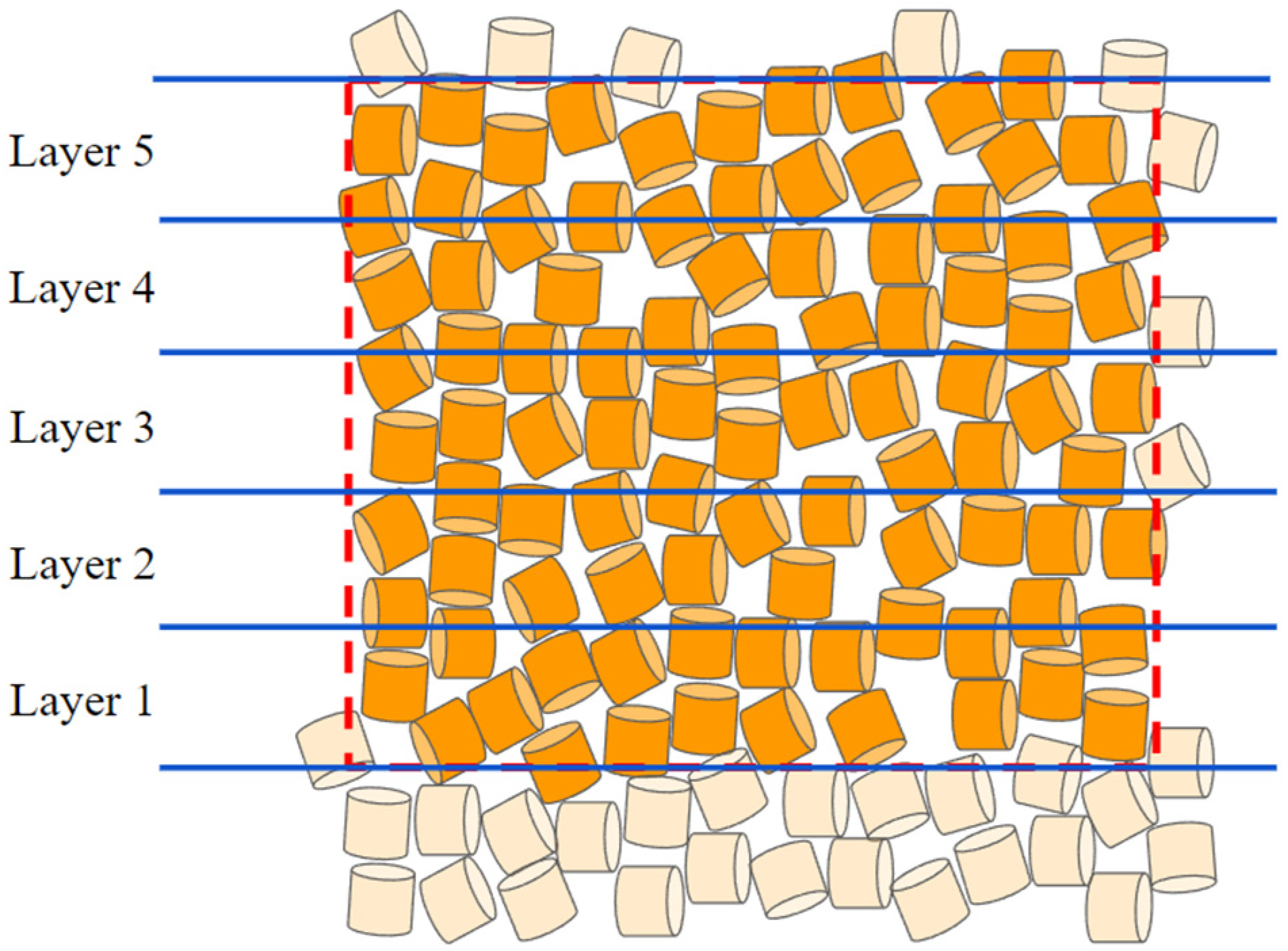
2.4. Modeling of Packed Bed and Heat Conduction
2.5. Packing Structure Analysis
2.6. Heat Transfer Evaluation
3. Results & Discussion
3.1. Comparison of Non-Spherical and Spherical Particles by Particle Sphericity
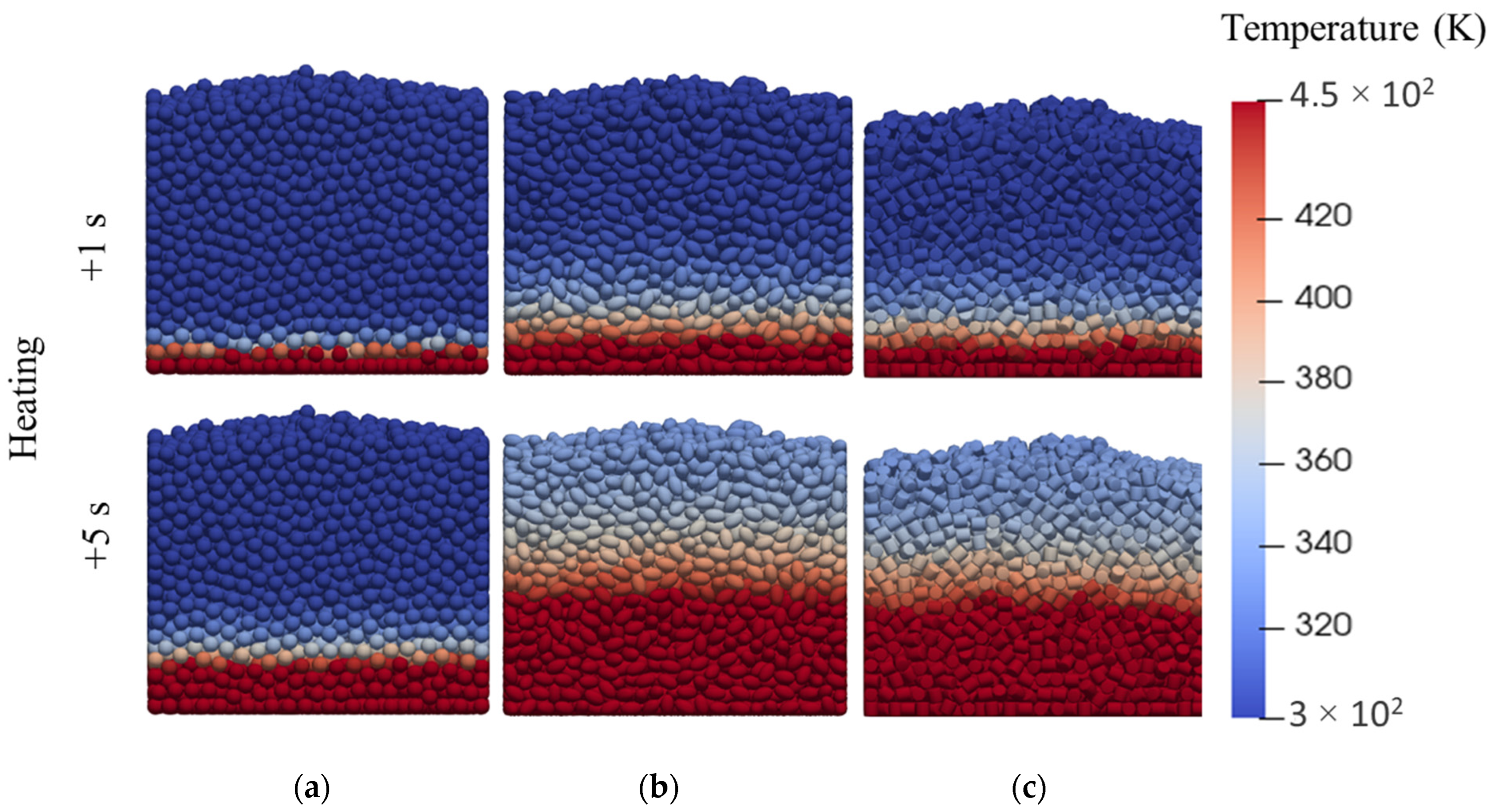
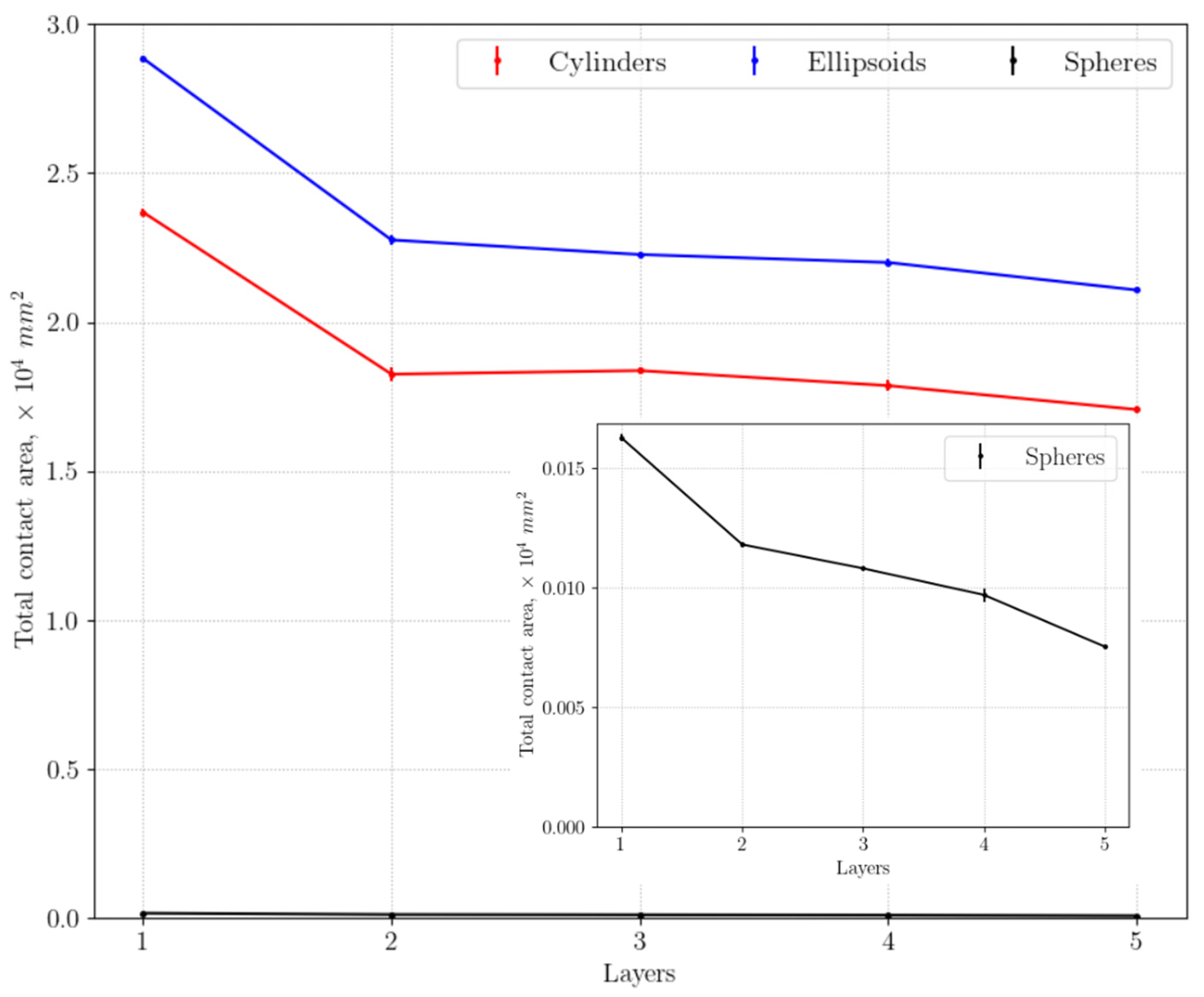
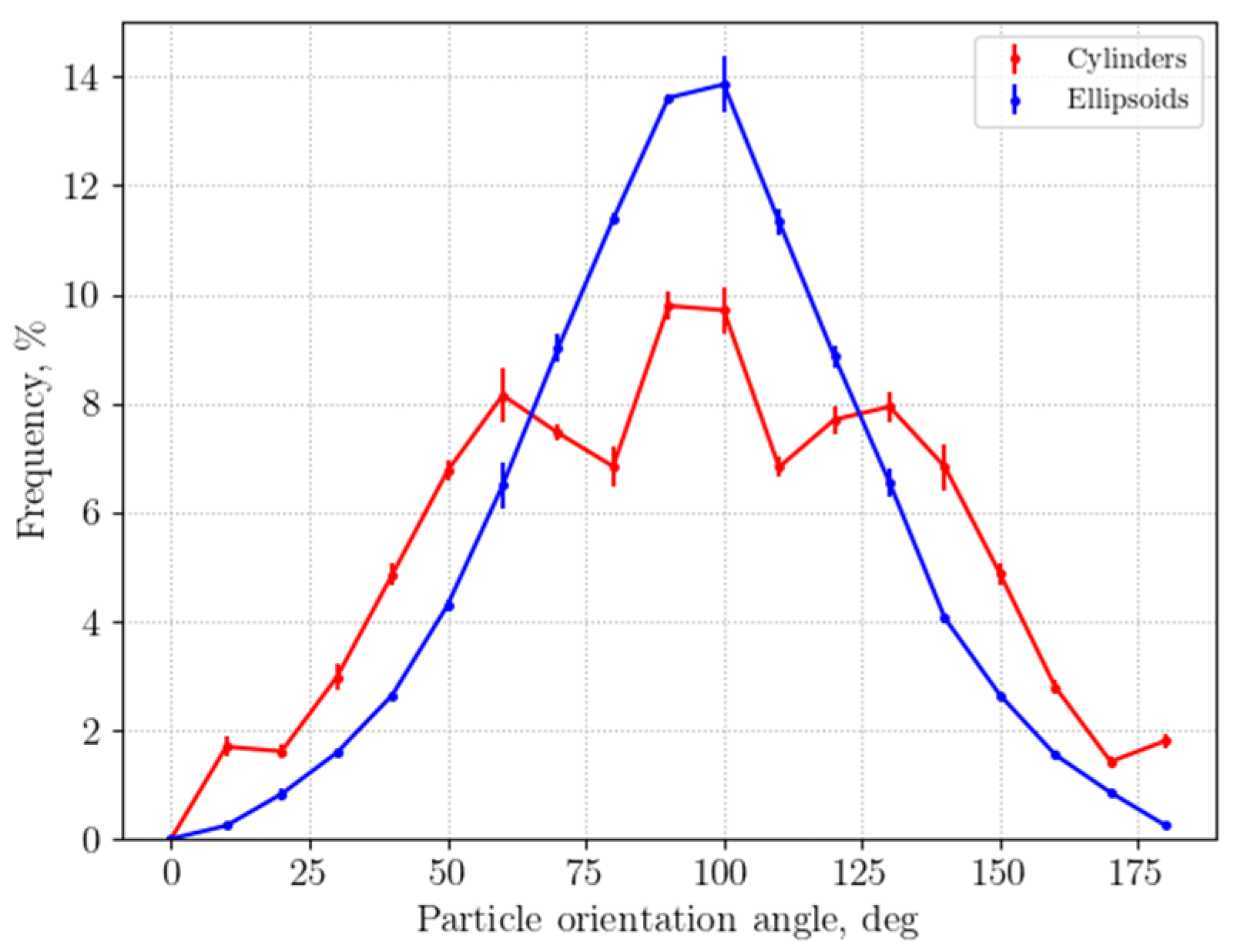
3.1.1. Packing Structure Analysis
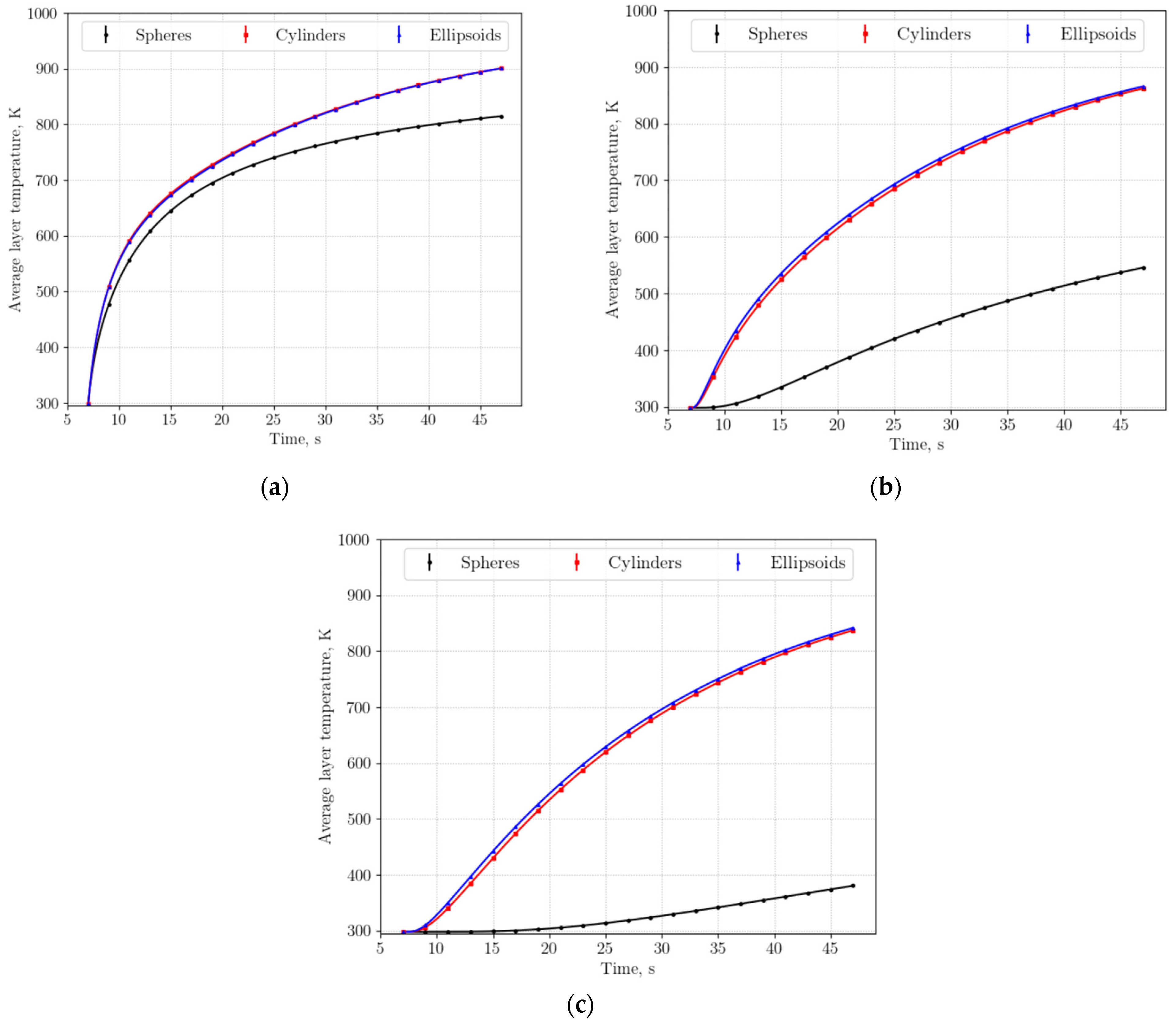
3.1.2. Heat Transfer Evaluation
3.2. Comparison of Cylindrical Particles with Different Aspect Ratios
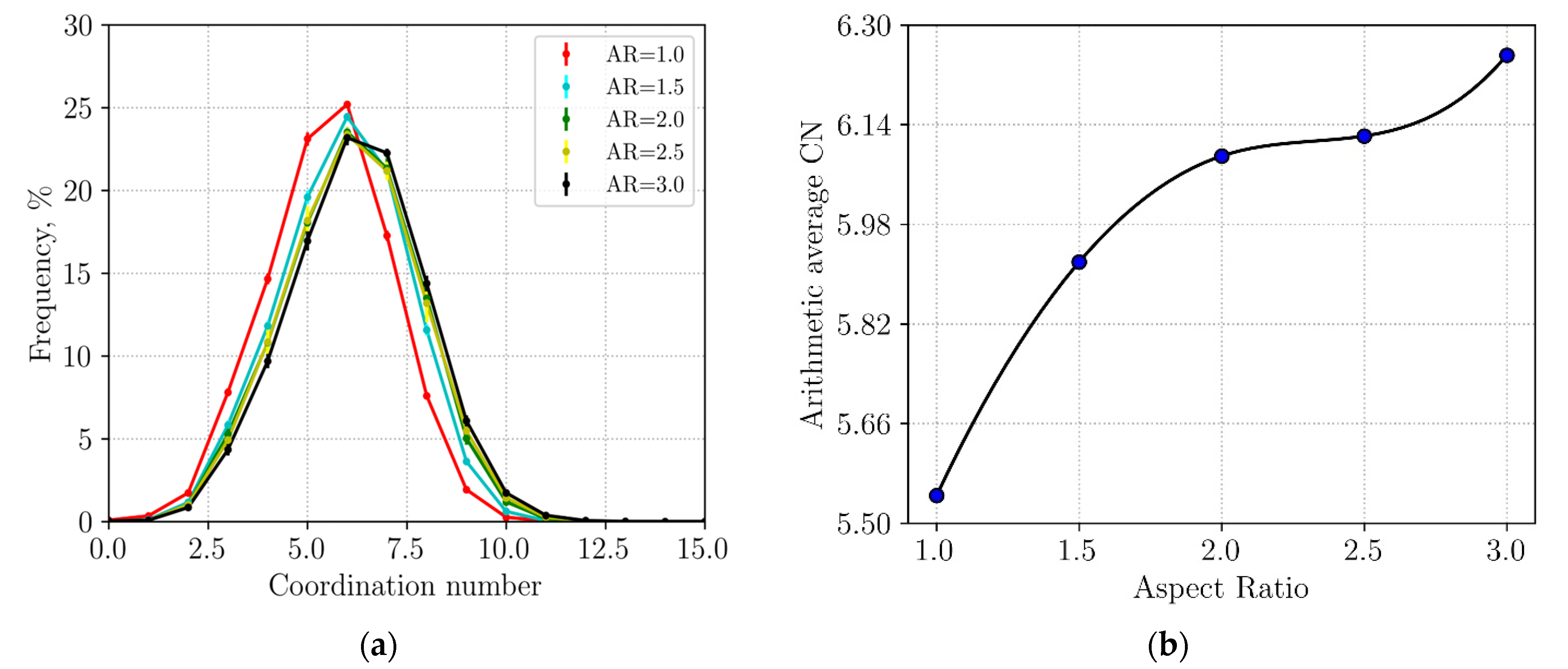
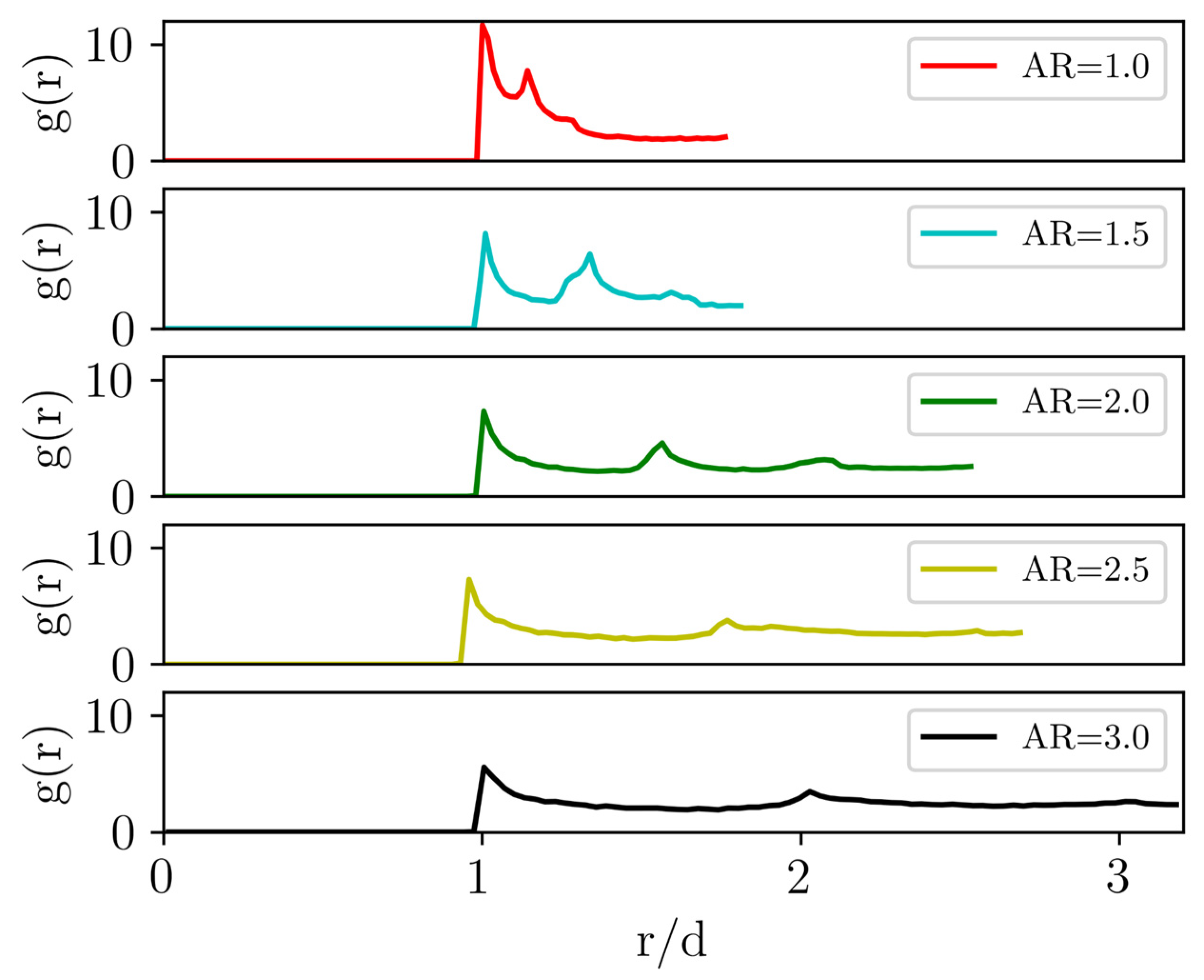
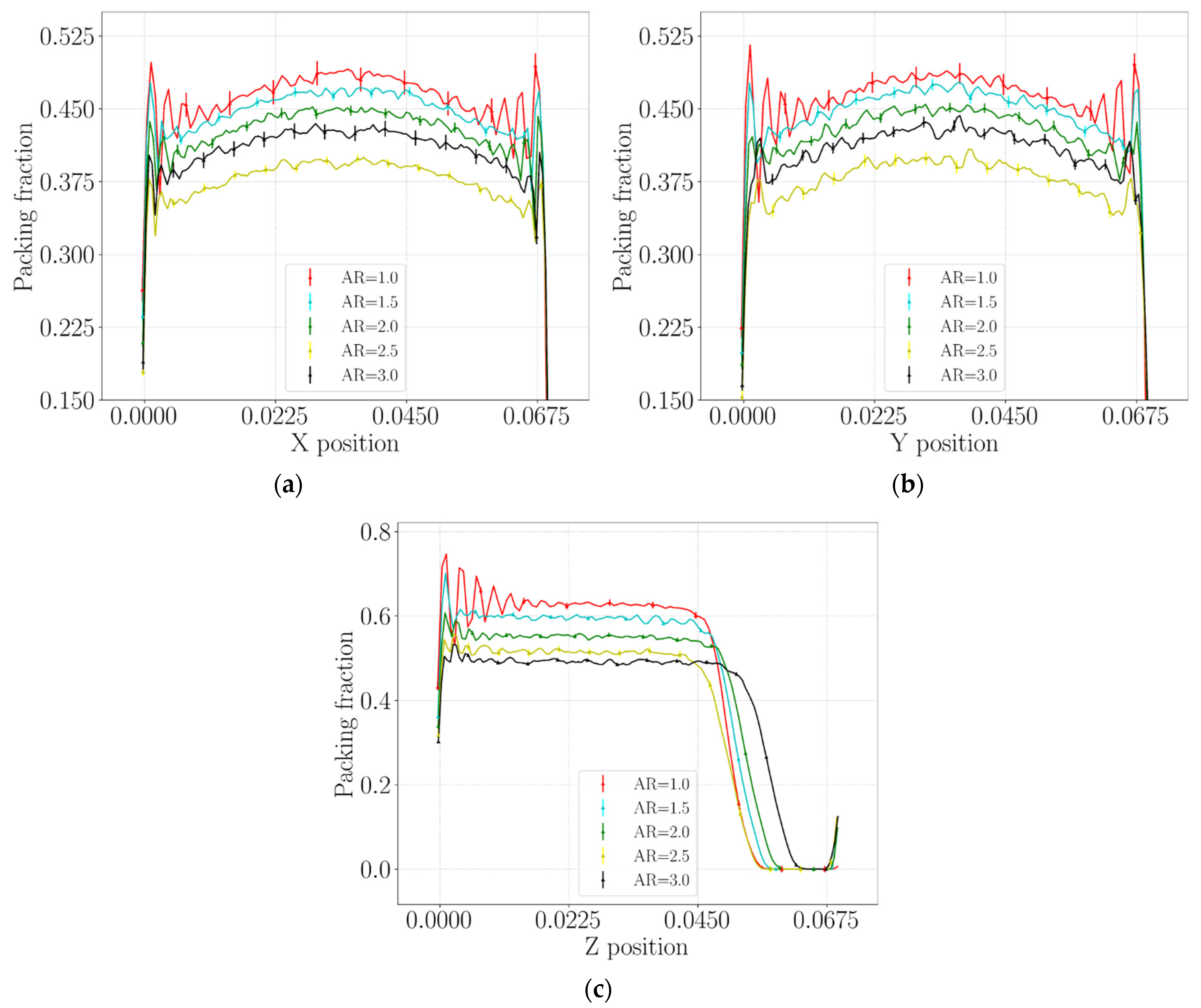
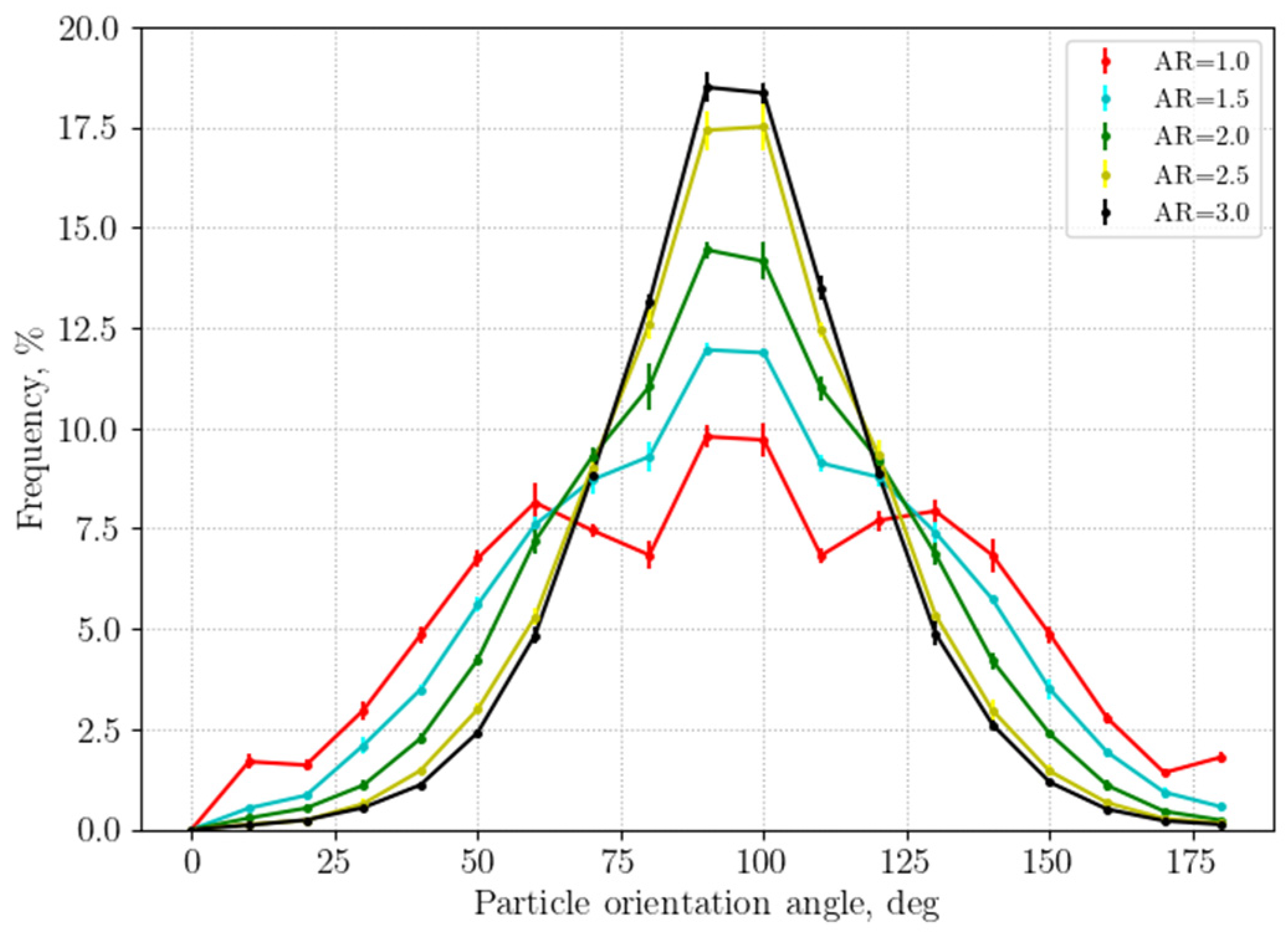
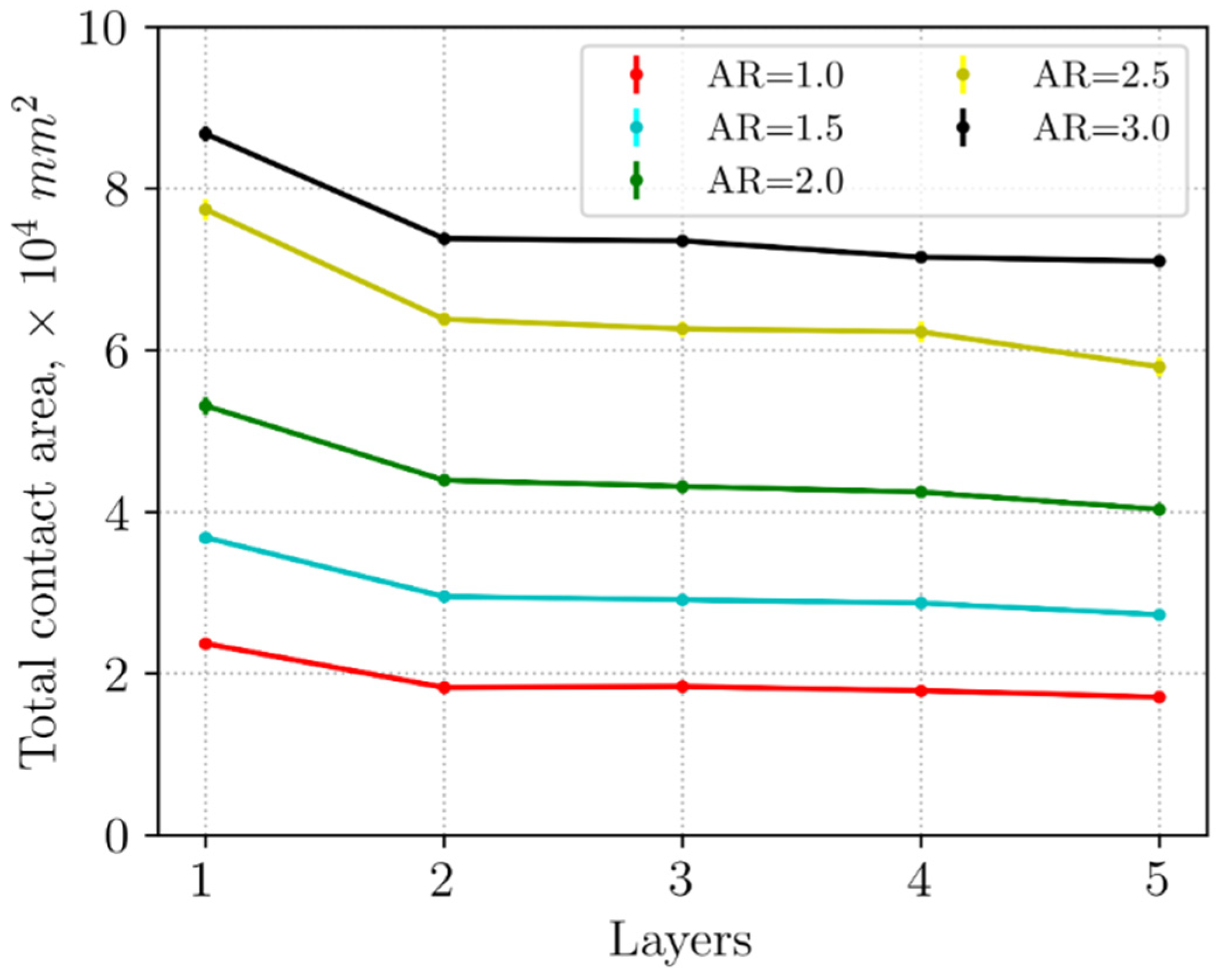
3.2.1. Packing Structure Analysis
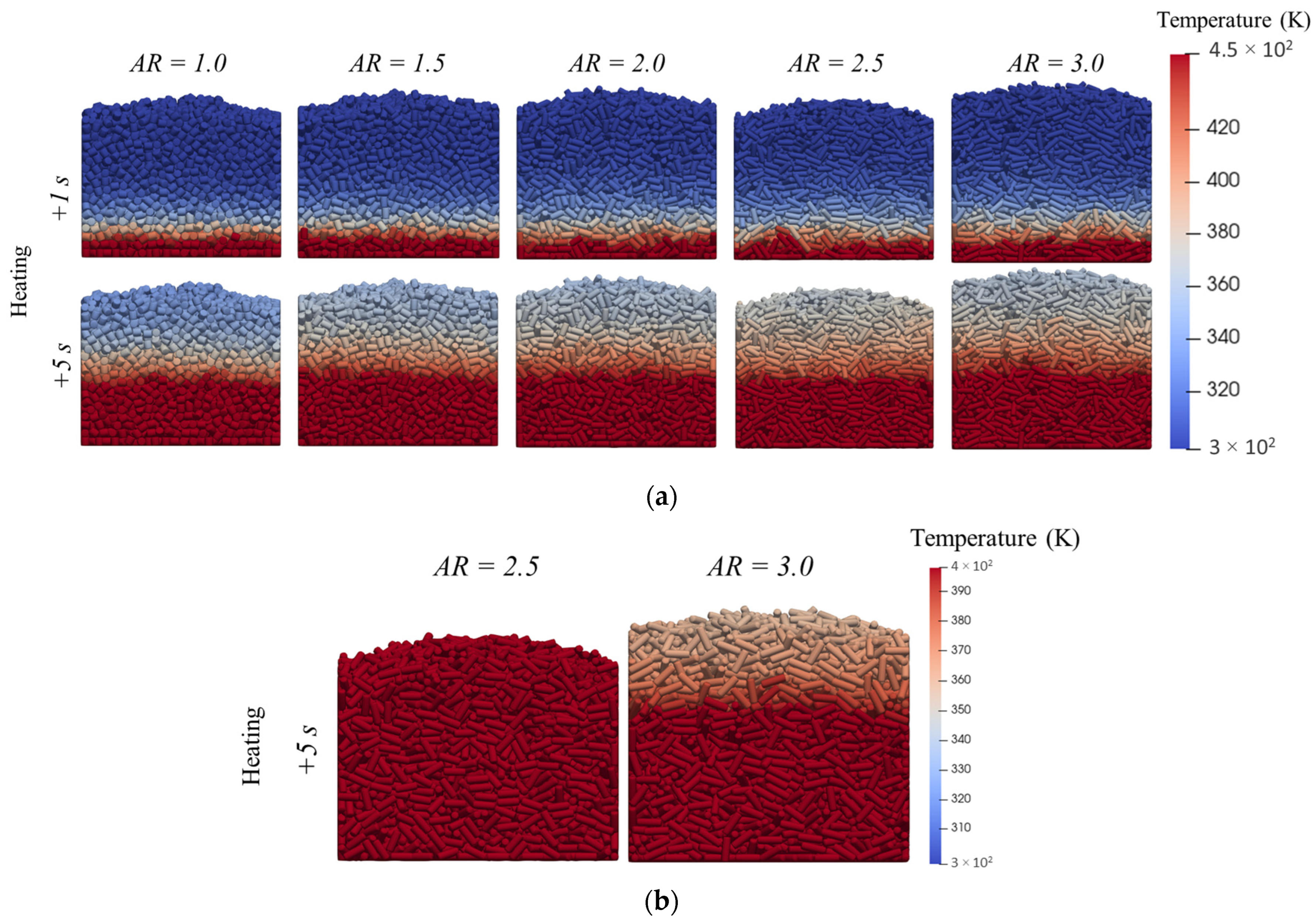
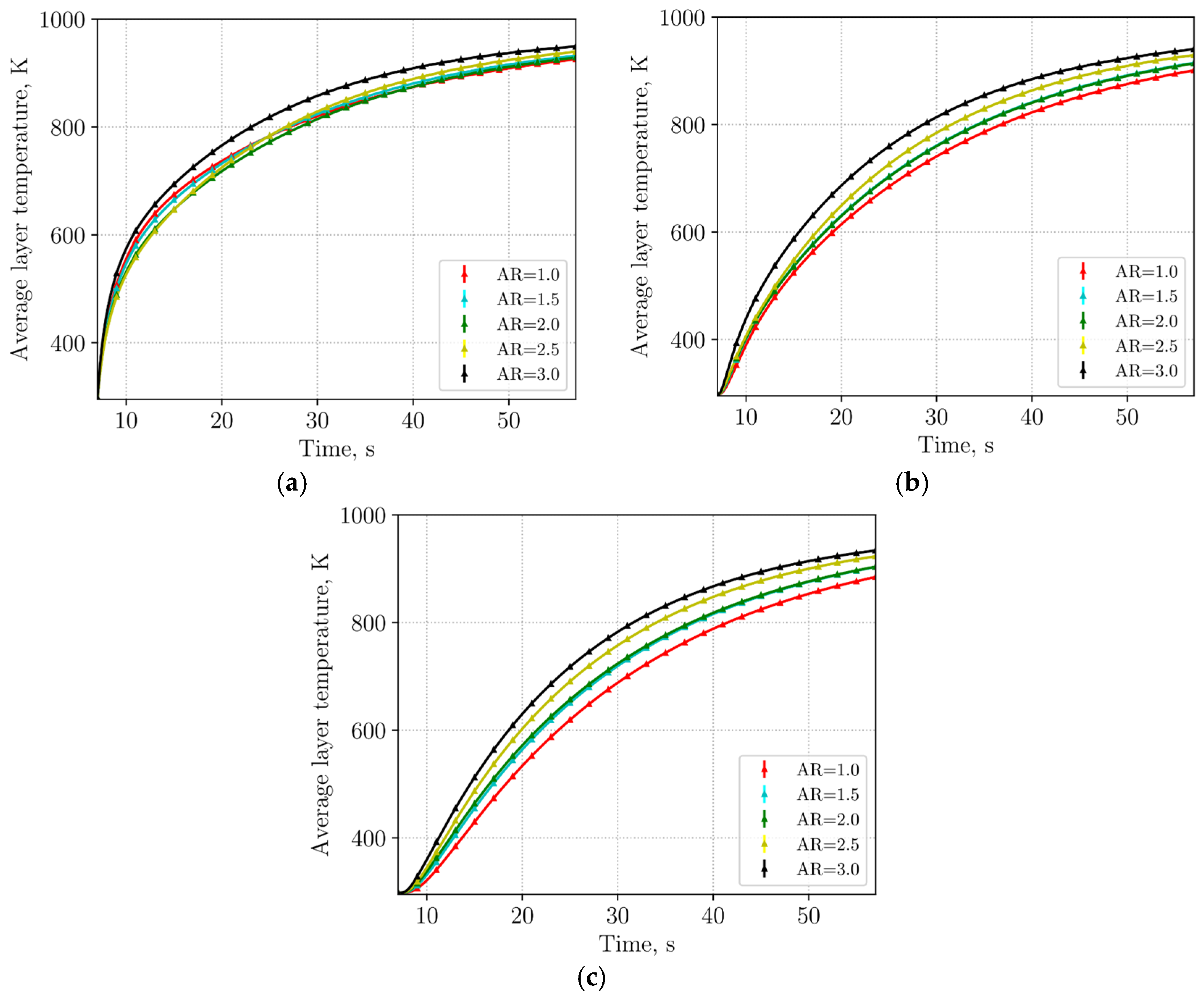
3.2.2. Heat Transfer Evaluation
4. Conclusions
- Differences in particle sphericity among spherical, ellipsoidal, and cylindrical particles significantly affect the morphology of the packing structure. Cylindrical particles show both short- and long-range structural patterns, while ellipsoidal particles lack these structures.
- The particle sphericity of non-spherical particles notably impacts heat transfer, as observed in the average temperature changes within the packed bed over time.
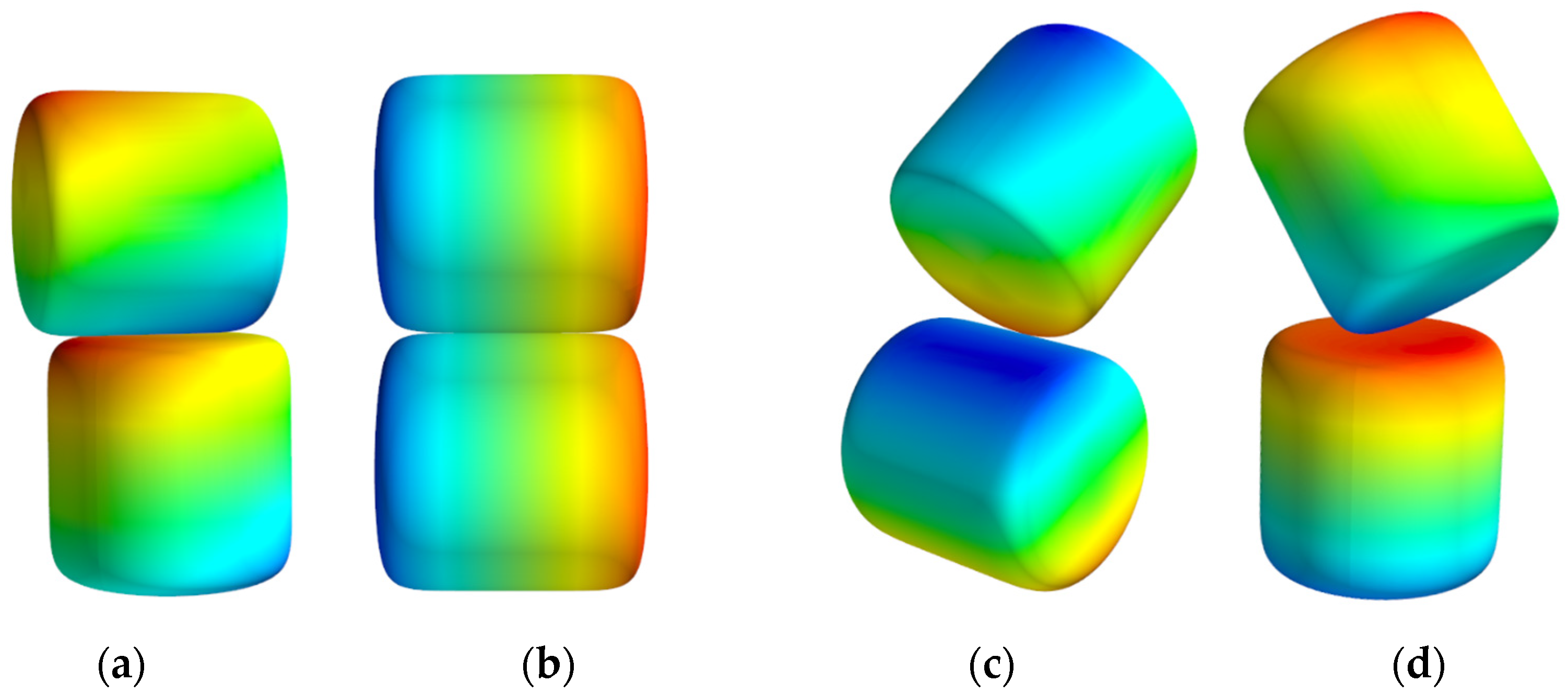
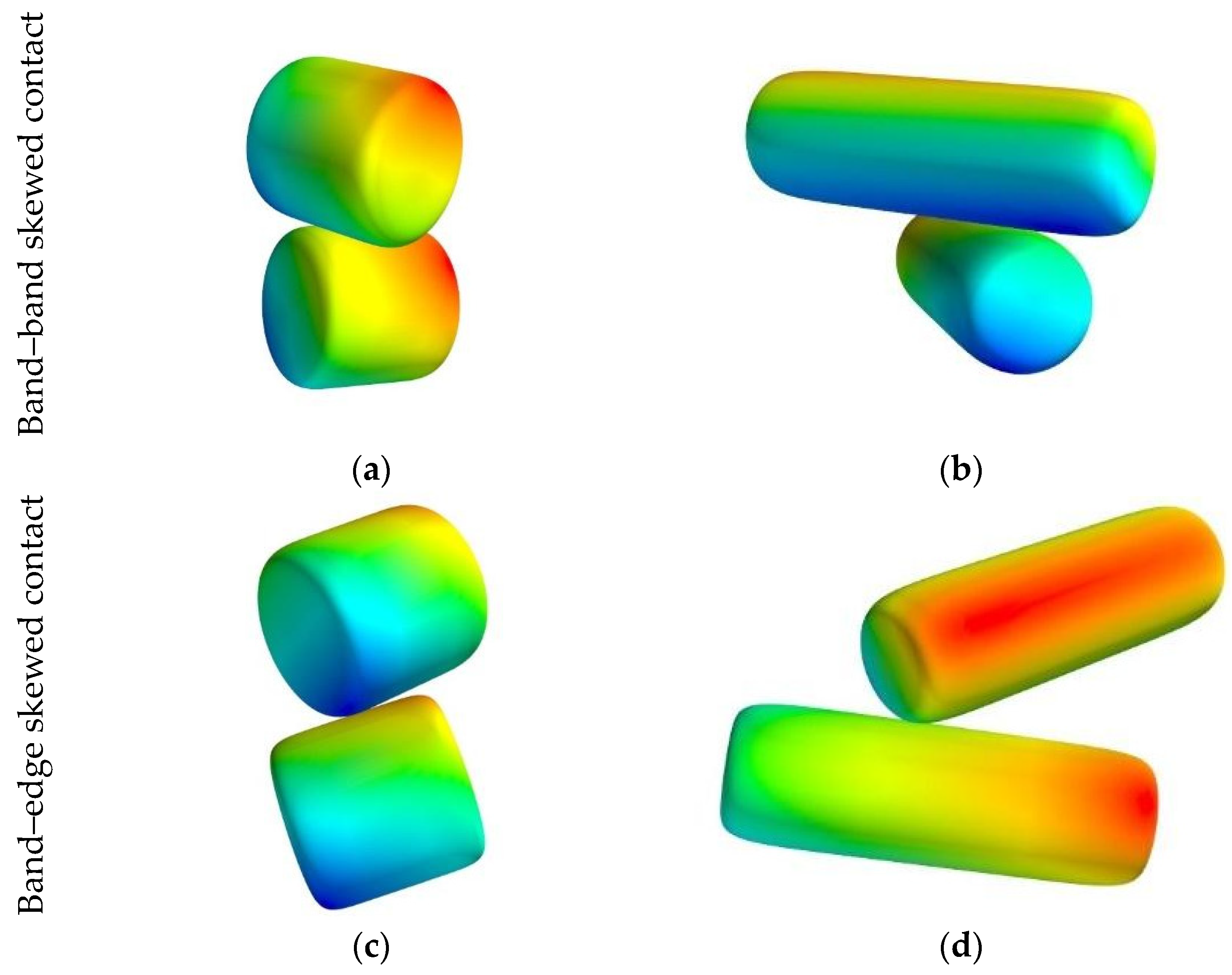
- Cylinders with higher ARs exhibit increased contact areas and coordination numbers. With the increasing AR, band–band skewed and band–edge contacts become more prevalent, significantly increasing the median contact area.
- Although higher-aspect ratio cylinders predominantly orient horizontally, opposing the heat flux direction, their larger contact areas and the increased number of contact points reduce the thermal resistance, leading to an enhanced heat transfer rate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, Y.L.; Qiu, Y.; Wang, K.; Yuan, F.; Wang, W.Q.; Li, M.J.; Guo, J.Q. Perspective of concentrating solar power. Energy 2020, 198, 117373. [Google Scholar] [CrossRef]
- Mubarrat, M.; Mashfy, M.M.; Farhan, T.; Ehsan, M.M. Research advancement and potential prospects of thermal energy storage in concentrated solar power application. Int. J. Thermofluids 2023, 20, 100431. [Google Scholar] [CrossRef]
- Le Roux, D.; Olivès, R.; Neveu, P. Multi-Objective optimisation of a thermocline thermal energy storage integrated in a concentrated solar power plant. Energy 2024, 300, 131548. [Google Scholar] [CrossRef]
- Baumann, T.; Zunft, S. Properties of granular materials as heat transfer and storage medium in CSP application. Sol. Energy Mater. Sol. Cells 2015, 143, 38–47. [Google Scholar] [CrossRef]
- Albrecht, K.J.; Ho, C.K. Heat transfer models of moving packed-bed particle-to-sCO2 heat exchangers. J. Sol. Energy Eng. 2019, 141, 031006. [Google Scholar] [CrossRef]
- Palacios, A.; Barreneche, C.; Navarro, M.E.; Ding, Y. Thermal energy storage technologies for concentrated solar power—A review from a materials perspective. Renew. Energy 2020, 156, 1244–1265. [Google Scholar] [CrossRef]
- Tian, X.; Yang, J.; Wang, T.; Tian, Y.; Zhou, Z.; Wang, Q. Effective waste heat recovery from industrial cohesive granular materials: A moving bed indirect heat exchanger with special flow control. J. Clean. Prod. 2024, 437, 140700. [Google Scholar] [CrossRef]
- El Alami, K.; Asbik, M.; Agalit, H. Identification of natural rocks as storage materials in thermal energy storage (TES) system of concentrated solar power (CSP) plants—A review. Sol. Energy Mater. Sol. Cells 2020, 217, 110599. [Google Scholar] [CrossRef]
- Bai, C.; Liu, Y.; Liu, Z.; Liu, P.; Deng, X.; Li, J.; Yang, J. Fabrication and properties of mullite-bonded porous SiC membrane supports using bauxite as aluminum source. Ceram. Int. 2015, 41, 4391–4400. [Google Scholar] [CrossRef]
- Johnson, E.F.; Tarı, İ.; Baker, D. Modeling heat exchangers with an open source DEM-based code for granular flows. Sol. Energy 2021, 228, 374–386. [Google Scholar] [CrossRef]
- Kiani-Oshtorjani, M.; Jalali, P. Thermal discrete element method for transient heat conduction in granular packing under compressive forces. Int. J. Heat Mass Transf. 2019, 145, 118753. [Google Scholar] [CrossRef]
- Moghaddam, E.M.; Foumeny, E.A.; Stankiewicz, A.I.; Padding, J.T. Multiscale modelling of wall-to-bed heat transfer in fixed beds with non-spherical pellets: From particle-resolved CFD to pseudo-homogenous models. Chem. Eng. Sci. 2021, 236, 116532. [Google Scholar] [CrossRef]
- Jeong, S.Y.; Bagepalli, M.V.; Brooks, J.D.; Ranjan, D.; Zhang, Z.M.; Loutzenhiser, P.G. Experimental and numerical analyses of gravity-driven granular flows between vertical parallel plates for solar thermal energy storage and transport. Int. J. Heat Mass Transf. 2023, 216, 124571. [Google Scholar] [CrossRef]
- Liu, S.Q.; Li, Y.B.; Liu, X.Y.; Zhu, B.J.; Tian, H.Q.; Shi, Y.L. Numerical Simulation on the Effective Thermal Conductivity of Porous Material. Adv. Mater. Res. 2012, 557, 2388–2395. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Yang, Z.X.; Wu, Y. Critical state for anisotropic granular materials: A discrete element perspective. Int. J. Geomech. 2017, 17, 04016054. [Google Scholar] [CrossRef]
- Nisar, F.; Rojek, J.; Nosewicz, S.; Kaszyca, K.; Chmielewski, M. Evaluation of effective thermal conductivity of sintered porous materials using an improved discrete element model. Powder Technol. 2024, 437, 119546. [Google Scholar] [CrossRef]
- Peng, Z.; Doroodchi, E.; Moghtaderi, B. Heat transfer modelling in Discrete Element Method (DEM)-based simulations of thermal processes: Theory and model development. Prog. Energy Combust. Sci. 2020, 79, 100847. [Google Scholar] [CrossRef]
- Yarrington, J.D.; Bagepalli, M.V.; Pathikonda, G.; Schrader, A.J.; Zhang, Z.M.; Ranjan, D.; Loutzenhiser, P.G. Numerical analyses of high temperature dense, granular flows coupled to high temperature flow property measurements for solar thermal energy storage. Sol. Energy 2021, 213, 350–360. [Google Scholar] [CrossRef]
- Soltanbeigi, B.; Podlozhnyuk, A.; Papanicolopulos, S.A.; Kloss, C.; Pirker, S.; Ooi, J.Y. DEM study of mechanical characteristics of multi-spherical and superquadric particles at micro and macro scales. Powder Technol. 2018, 329, 288–303. [Google Scholar] [CrossRef]
- Wei, G.; Zhang, H.; An, X.; Dianyu, E. Numerical investigation on the mutual interaction between heat transfer and non-spherical particle dynamics in the blast furnace raceway. Int. J. Heat Mass Transf. 2020, 153, 119577. [Google Scholar] [CrossRef]
- Korkerd, K.; Zhou, Z.; Zou, R.; Piumsomboon, P.; Chalermsinsuwan, B. Effect of immersed tubes configurations on mixing and heat transfer of mixed biomass and silica sand in a bubbling fluidized bed using CFD-DEM and statistical experimental design analysis. Powder Technol. 2024, 437, 119542. [Google Scholar] [CrossRef]
- Zou, R.P.; Yu, A.B. Evaluation of the packing characteristics of mono-sized non-spherical particles. Powder Technol. 1996, 88, 71–79. [Google Scholar] [CrossRef]
- Donev, A.; Cisse, I.; Sachs, D.; Variano, E.A.; Stillinger, F.H.; Connelly, R.; Torquato, S.; Chaikin, P.M. Improving the density of jammed disordered packings using ellipsoids. Science 2004, 303, 990–993. [Google Scholar] [CrossRef]
- Zhao, B.; An, X.; Wang, Y.; Zhao, H.; Shen, L.; Sun, X.; Zou, R. Packing of different shaped tetrahedral particles: DEM simulation and experimental study. Powder Technol. 2020, 360, 21–32. [Google Scholar] [CrossRef]
- Gerhardter, H.; Prieler, R.; Schluckner, C.; Knoll, M.; Hochenauer, C.; Mühlböck, M.; Tomazic, P.; Schröttner, H. Modelling convective heat transfer to non-spherical particles. Powder Technol. 2019, 343, 245–254. [Google Scholar] [CrossRef]
- Negotiates, P.; Durajski, A.P.; Rajca, P.; Gruszka, K.M.; Marek, M. Experimental and numerical study on the orientation distribution of cylindrical particles in random packed beds. Chem. Eng. J. 2022, 432, 134043. [Google Scholar]
- Zhang, M.; Dong, H.; Geng, Z. Computational study of flow and heat transfer in fixed beds with cylindrical particles for low tube to particle diameter ratios. Chem. Eng. Res. Des. 2018, 132, 149–161. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, L.; Umbanhowar, P.B.; Lueptow, R.M. Discrete element simulation of cylindrical particles using super-ellipsoids. Particuology 2019, 46, 55–66. [Google Scholar] [CrossRef]
- Gou, D.; Fan, W.; Zhou, B.; An, X.; Yang, R.; Dong, K.; Zou, R.; Fu, H.; Zhang, H.; Yang, X.; et al. CFD-DEM numerical study on air impacted packing densification of equiaxed cylindrical particles. Adv. Powder Technol. 2022, 33, 103641. [Google Scholar] [CrossRef]
- Qian, Q.; Wang, L.; An, X.; Wu, Y.; Wang, J.; Zhao, H.; Yang, X. DEM simulation on the vibrated packing densification of mono-sized equilateral cylindrical particles. Powder Technol. 2018, 325, 151–160. [Google Scholar] [CrossRef]
- Gan, J.; Yu, A. DEM simulation of the packing of cylindrical particles. Granul. Matter 2020, 22, 1–19. [Google Scholar] [CrossRef]
- Kodam, M.; Bharadwaj, R.; Curtis, J.; Hancock, B.; Wassgren, C. Cylindrical object contact detection for use in discrete element method simulations. Part I–Contact detection algorithms. Chem. Eng. Sci. 2010, 65, 5852–5862. [Google Scholar] [CrossRef]
- Guo, Y.; Wassgren, C.; Ketterhagen, W.; Hancock, B.; Curtis, J. Some computational considerations associated with discrete element modeling of cylindrical particles. Powder Technol. 2012, 228, 193–198. [Google Scholar] [CrossRef]
- Hertz, H.R. Über die Berührung fester elastischer Körper und über die Härte. In Verhandlungen des Vereins zur Beförderung des Gewerbfleißes; Verein zur Beförderung des Gewerbefleisses: Berlin, Germany, 1882; pp. 449–463. [Google Scholar]
- Mindlin, R.D. Compliance of elastic bodies in contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Podlozhnyuk, A.; Pirker, S.; Kloss, C. Efficient implementation of superquadric particles in discrete element method within an open-source framework. Comput. Part. Mech. 2017, 4, 101–118. [Google Scholar] [CrossRef]
- Barr, A.H. Superquadrics and angle-preserving transformations. IEEE Comput. Graph. Appl. 1981, 1, 11–23. [Google Scholar] [CrossRef]
- Boribayeva, A.; Gvozdeva, X.; Golman, B. Numerical Analysis of Non-Sphericity of Particles of Powder Material and their Effect on Packing Structure for Concentrated Solar Power Applications. Defect Diffus. Forum 2024, 432, 109–114. [Google Scholar] [CrossRef]
- Wadell, H. Volume, shape, and roundness of quartz particles. J. Geol. 1935, 43, 250–280. [Google Scholar] [CrossRef]
- Aspherix®; DCS Computing GmbH: Linz, Austria, 2021.
- Qi, F.; Wright, M.M. Particle scale modeling of heat transfer in granular flows in a double screw reactor. Powder Technol. 2018, 335, 18–34. [Google Scholar] [CrossRef]
- Schirck, J.; Morris, A. Heat transfer and flow analysis of a novel particle heater using CFD-DEM. Powder Technol. 2024, 442, 119858. [Google Scholar] [CrossRef]
- Peters, J.F.; Muthuswamy, M.; Wibowo, J.; Tordesillas, A. Characterization of force chains in granular material. Phys. Rev. E 2005, 72, 041307. [Google Scholar] [CrossRef] [PubMed]
- Pola, V.R.M.; Desu, R.K.; Annabattula, R.K. Voxelization based packing analysis for discrete element simulations of non-spherical particles. arXiv 2021, arXiv:2110.14151. [Google Scholar]
- Govender, N.; Cleary, P.W.; Kiani-Oshtorjani, M.; Wilke, D.N.; Wu, C.; Kureck, H. The effect of particle shape on the packed bed effective thermal conductivity based on DEM with polyhedral particles on the GPU. Chem. Eng. Sci. 2020, 219, 115584. [Google Scholar] [CrossRef]
- Wilke, D.N. Traction chain networks: Insights beyond force chain networks for non-spherical particle systems. Powder Technol. 2022, 402, 117362. [Google Scholar] [CrossRef]
- Yu, F.; Cui, D.; Zhang, Y.; Zhou, G. Effect of vibration direction on the packing of sphero-cylinders. Adv. Powder Technol. 2023, 34, 104138. [Google Scholar] [CrossRef]


| Units | Value | |
|---|---|---|
| Material density | 2.780 | |
| Young’s modulus | 10 | |
| Poisson ratio | - | |
| Thermal capacity | 1275 | |
| Bulk thermal conductivity | 200 | |
| Time step | s | |
| Gravity | 9.81 |
| Particle Shape | AR | n1 | n2 | |||
|---|---|---|---|---|---|---|
| Spherical | 3.434 | 3.434 | 1.000 | 1.000 | 2 | 2 |
| Ellipsoidal | 4.500 | 3.000 | 0.974 | 1.500 | 2 | 2 |
| Cylindrical 1 | 3.000 | 3.000 | 0.874 | 1.000 | 8 | 2 |
| Cylindrical 2 | 3.931 | 2.621 | 0.859 | 1.500 | 8 | 2 |
| Cylindrical 3 | 4.762 | 2.381 | 0.832 | 2.000 | 8 | 2 |
| Cylindrical 4 | 5.526 | 2.210 | 0.805 | 2.500 | 8 | 2 |
| Cylindrical 5 | 6.240 | 2.080 | 0.779 | 3.000 | 8 | 2 |
| Area per Contact, mm2 | |||||
|---|---|---|---|---|---|
| Contact Types | AR = 1.0 | AR = 1.5 | AR = 2.0 | AR = 2.5 | AR = 3.0 |
| Band–band skewed | 6.76 ± 0.01 | 11.40 ± 0.02 | 16.43 ± 0.03 | 21.15 ± 1.70 | 27.82 ± 0.02 |
| Band–edge | 6.13 ± 0.02 | 9.22 ± 0.06 | 14.28 ± 0.04 | 19.68 ± 0.07 | 25.24 ± 0.05 |
| Band–band parallel | 7.04 ± 0.01 | 11.95 ± 0.02 | 17.40 ± 0.05 | 23.18 ± 0.05 | 29.78 ± 0.10 |
| Edge–edge | 5.48 ± 0.08 | 8.11 ± 0.04 | 11.91 ± 0.09 | 16.47 ± 0.09 | 21.11 ± 0.12 |
| Special | 5.00 ± 0.04 | 7.84 ± 0.02 | 11.29 ± 0.06 | 15.08 ± 0.14 | 19.56 ± 0.55 |
| Face–edge | 6.09 ± 0.02 | 5.61 ± 0.06 | 6.65 ± 0.12 | 7.77 ± 0.17 | 9.14 ± 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boribayeva, A.; Gvozdeva, X.; Golman, B. Packing Characteristics and Heat Transfer Performance of Non-Spherical Particles for Concentrated Solar Power Applications. Energies 2024, 17, 4552. https://doi.org/10.3390/en17184552
Boribayeva A, Gvozdeva X, Golman B. Packing Characteristics and Heat Transfer Performance of Non-Spherical Particles for Concentrated Solar Power Applications. Energies. 2024; 17(18):4552. https://doi.org/10.3390/en17184552
Chicago/Turabian StyleBoribayeva, Aidana, Xeniya Gvozdeva, and Boris Golman. 2024. "Packing Characteristics and Heat Transfer Performance of Non-Spherical Particles for Concentrated Solar Power Applications" Energies 17, no. 18: 4552. https://doi.org/10.3390/en17184552
APA StyleBoribayeva, A., Gvozdeva, X., & Golman, B. (2024). Packing Characteristics and Heat Transfer Performance of Non-Spherical Particles for Concentrated Solar Power Applications. Energies, 17(18), 4552. https://doi.org/10.3390/en17184552








