Hybrid-Energy Storage Optimization Based on Successive Variational Mode Decomposition and Wind Power Frequency Modulation Power Fluctuation

Abstract

In order to solve the problem of frequency modulation power deviation caused by the randomness and fluctuation of wind power outputs, a method of auxiliary wind power frequency modulation capacity allocation based on the data decomposition of a “flywheel + lithium battery” hybrid-energy storage system was proposed. Firstly, the frequency modulation power deviation caused by the uncertainty of wind power is decomposed by the successive variational mode decomposition (SVMD) method, and the mode function is segmented and reconstructed by high and low frequencies. Secondly, a mathematical model is established to maximize the economic benefit of energy storage considering the frequency modulation mileage, and quantum particle swarm optimization is used to solve the target model considering the charging and discharging power of energy storage and the charging state constraints to obtain the optimal hybrid-energy storage configuration. Finally, the simulation results show that, in the step disturbance, the Δf_max of the hybrid-energy storage mode is reduced by 37.9% and 15.3%, respectively, compared with single-energy storage. Under continuous disturbance conditions, compared with the single-energy storage mode, the Δf_{p_v} is reduced by 52.73%, 43.72%, 60.71%, and 47.62%, respectively. The frequency fluctuation range is obviously reduced, and the frequency stability is greatly improved.

1. Introduction

With the increasing amount of global attention paid to sustainable development, the proportion of new energy in energy supply is constantly increasing. According to the statistics of the National Energy Administration, as of the end of February 2023, the cumulative installed power generation capacity of the country is about 2.60 billion kilowatts. Among them, the installed capacity of wind power is about 370 million kilowatts, with a year-on-year growth rate of 11.0% and rapid development [1]. However, due to the instability and intermittence of new energy generation, new energy cannot always meet the bidirectional power demand of the system when participating in FM [2]. Energy storage frequency modulation technology can respond quickly and provide stable adjustments when new energy power supply is insufficient or there is a sudden fluctuation in load to ensure the smooth operation of the power system [3,4].

At present, a large number of studies have examined the involvement of energy storage in frequency modulation. Refs. [5,6] uses dynamic control strategies to coordinate power sharing between batteries and fuel cells to adjust frequency fluctuations. Ref. [7] studied the benefits of batteries in participating in frequency modulation and wind power peaking and limiting the output slope rate of wind farms and concluded that the benefits were the highest when energy storage participated in the frequency modulation of power systems. Ref. [8] compared the operating costs and benefits of lead-acid batteries, nickel–cadmium batteries, and sodium–sulfur batteries participating in primary frequency modulation and found that within a certain range of energy storage capacity, battery energy storage has the greatest application potential in primary frequency modulation in the next 3 to 5 years. Ref. [9] demonstrates that the battery energy storage system can reduce the impact of wind forecasting errors, while extending the service life of the energy storage system and making the coordination between short-term energy storage systems and wind farms more flexible. Ref. [10] uses the difference between the grid-connected reference power and the original wind power output to decompose the reference power, obtains the time spectrum through Hilbert transform, determines the appropriate dividing frequency, and reconstructs the high- and low-frequency components. Then, combined with the output data of wind farms, an economic cost calculation model of an energy storage system based on the life cycle cost theory is established. The optimal configuration scheme is obtained. Ref. [11] considers the fluctuation of wind power output and the operational constraints of the battery system itself and proposes an energy storage capacity allocation strategy for the combined wind power system to save the system’s investment cost and operation and maintenance cost. Ref. [12] adopted the fully integrated empirical mode decomposition based on adaptive noise to realize time–frequency analysis of load power, established an optimization model of hybrid-energy storage capacity configuration aiming at lifetime economic costs, and determined the optimal filtering sequence and corresponding energy storage configuration scheme.

The commonly used methods for signal decomposition include wavelet analysis [13], first-order inertial filtering [14], and Kalman filtering [15]. Among them, wavelet analysis has a large amount of computation and a long calculation time, and the first-order inertial filter has a poor effect on the decomposition of low-frequency signals, while the accuracy of Kalman filter is low, so it is not suitable for the decomposition of primary frequency modulation power instructions. Variational mode decomposition (VMD) is essentially a quasi-orthogonal analysis method that is transformed into a frequency-mixed variational problem by Wiener filter and Hilbert transform [16]. VMD has unique advantages as a completely non-recursive signal processing algorithm. However, when decomposing VMD, it is affected by the IMF number K and the quadratic penalty factor α, which will greatly reduce the decomposition effect [17] if not properly set. SVMD does not need to determine the number of IMF and has better robustness compared with the initial value of the modal center frequency [18]. Therefore, this paper uses the SVMD algorithm to decompose the primary frequency modulation power instructions.

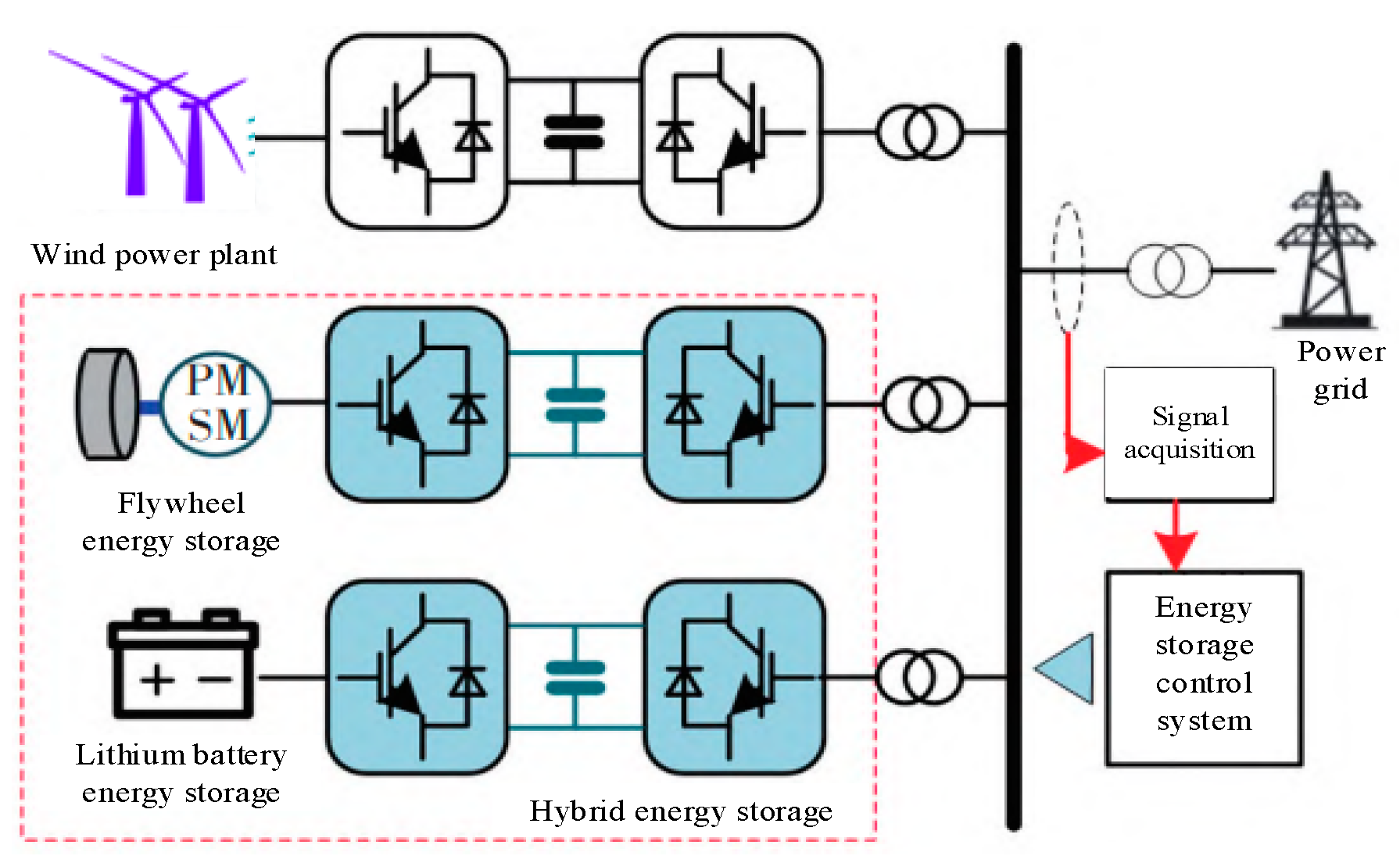
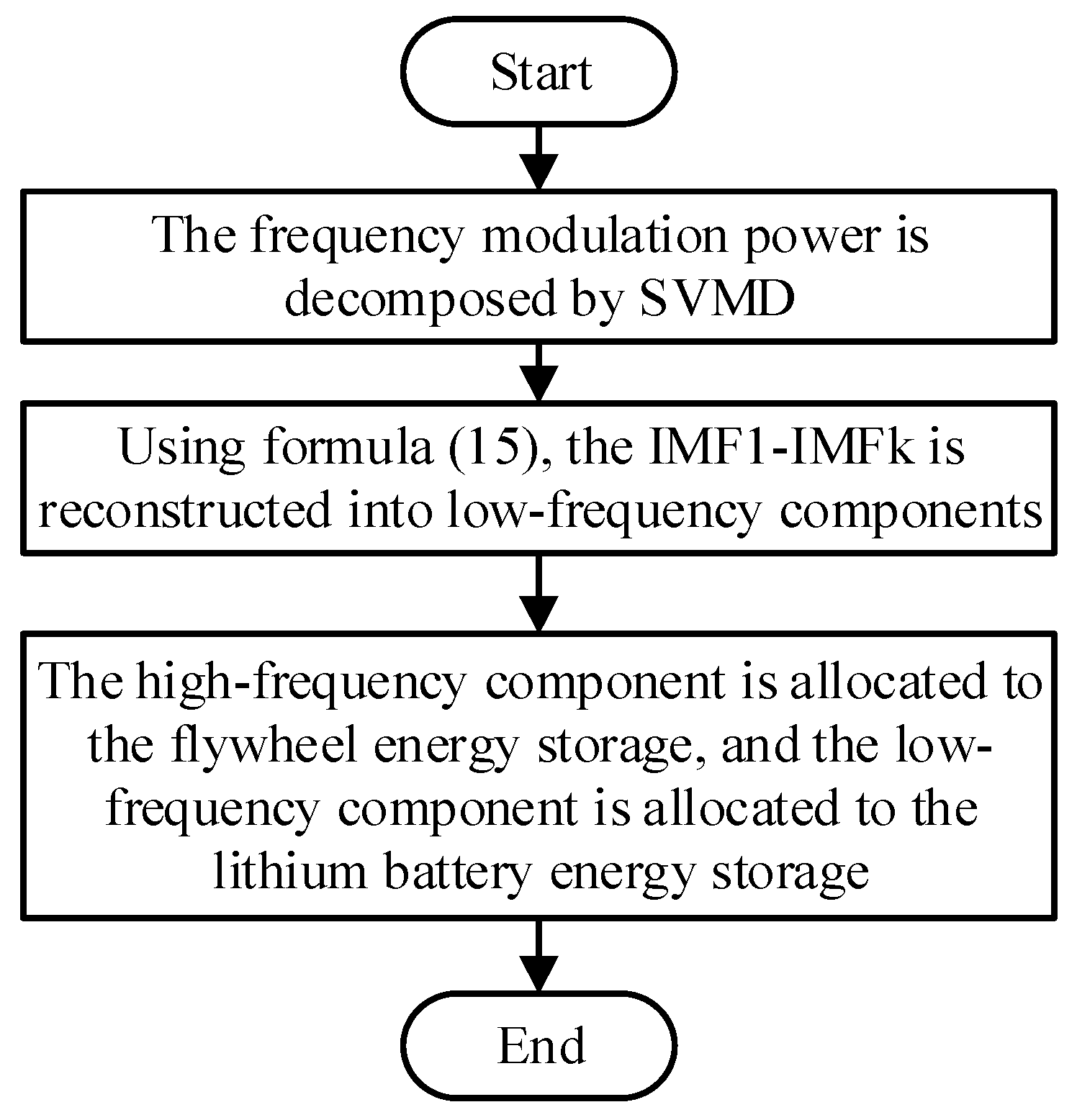
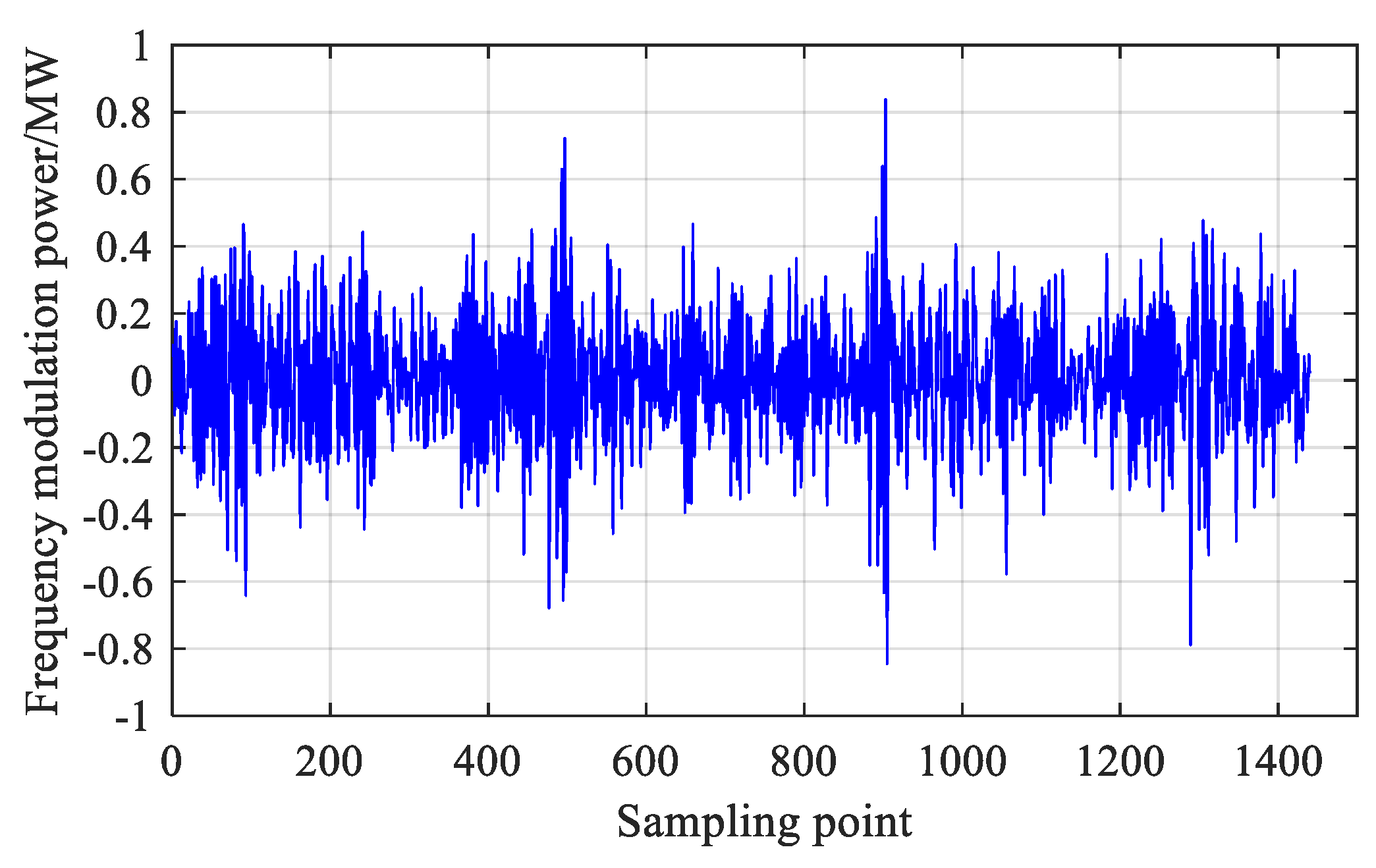
In order to solve the problem of frequency modulation power deviation caused by the randomness and volatility of wind power output, the main contributions of this paper are as follows: (1) the sequential variational mode decomposition method effectively solves the problem that VMD parameters cannot be selected adaptively, and the frequency modulation instruction is decomposed into high-frequency demand and low-frequency demand, which effectively solves the problem of the influence of boundary points on capacity allocation; (2) based on the characteristics of large flywheel energy storage output and high frequency, and small lithium battery energy storage output and low frequency, a frequency modulation power distribution strategy considering hybrid-energy storage characteristics was proposed. Flywheel energy storage undertook high-frequency tasks, and lithium battery energy storage undertook low-frequency components, fully playing into the advantages of flywheel energy storage with high life cycles and large power in a short period of time. At the same time, the frequent charge and discharge of lithium batteries are avoided.

2. Air Storage Joint Frequency Modulation Framework

2.1. Topology of the Air Storage System

The hybrid-energy storage composed of flywheel and lithium batteries can complement each other and effectively improve the effect of wind farm’s participation in primary frequency modulation. Figure 1 shows the topology of the mixed-air storage system.

It can be seen from Figure 1 that the flywheel–lithium battery hybrid-energy storage system installed at the connecting point of the wind farm participates in the primary frequency modulation of the power system. When the grid frequency drops, the hybrid-energy storage system can quickly release the stored electrical energy, convert it into the compensation power required by the grid through the DC/DC converter, and stabilize the grid frequency. When the frequency of the grid rises, the hybrid-energy storage system quickly stores the excess electricity required by the grid, preventing the wind farm from supplying excessive power to the grid, thus balancing the difference between supply and demand to maintain the stability of the frequency [19].

2.2. Energy Storage Characteristic Analysis

At present, electrochemical energy storage, pumped storage, supercapacitor energy storage, and flywheel energy storage are relatively established energy storage methods, and their parameter performances are shown in

Table 1. Characteristics of different types of energy storage technologies.

Type of Energy Storage	Power Class	Response Time	Conversion Efficiency	Cycle Life (Times)
Flywheel energy storage	0–250 KW	millisecond	80–95%.	200,000
Superconducting magnetic energy storage	10 KW–10 MW	Millisecond class	96%	≥10,000
supercapacitor	0–300 KW	Millisecond class	70–80%.	100,000
Lead-acid battery	0–20 MW	second	63–80%.	500–1000
Lithium-ion battery	1–10 MW	second	90–98%.	1000–10,000 s
Sodium battery	1 KW–10 MW	second	75–90%.	4500
Flow cell	1–10 MWW	second	65–85%.	12,000

. However, the above energy storage facilities all belong to single-power or single-capacity energy storage technologies, which cannot simultaneously meet the new adjustment requirements of “high capacity, high power and fast response” required by the grid under the conditions of a large number of new energy connections.

Analysis of the above table shows that electrochemical energy storage is a relatively mature high-capacity energy storage technology, but its service life is short, the efficiency gap between different types of batteries is large, and there are some environmental pollution problems. Superconducting magnetic energy storage has fast response speed, long service life, and high energy conversion efficiency, but it has a great impact on the surrounding production, life and ecological environment, and the technology is not mature. Supercapacitors have advantages in terms of efficiency and energy density, but they are difficult to apply on a large scale due to their short working time and high cost of high-performance materials. In contrast, flywheel energy storage technology can achieve fast and deep charge and discharge, with extremely high energy conversion efficiency and service life. Due to its pure mechanical structure, it does not produce pollution and can be completely recycled. At the same time, considering the construction cost, power density and energy density, response speed and cycle life, flywheel energy storage system is selected as a power-type energy storage component. The energy storage system has the working characteristics of high energy density.

2.3. Hybrid-Energy Storage Frequency Modulation Power Distribution Strategy

The traditional frequency modulation control strategy of combined wind storage does not fully consider the difference in the frequency modulation characteristics of different energy storage systems, such as the large difference in flywheel energy storage instantaneous charge and discharge power, fast response speed, and frequent charge and discharge. Lithium batteries have a large energy storage capacity and long discharge time, but frequent charge and discharge can seriously affect their service life. According to the above characteristics, the frequency modulation power deviation of wind power is decomposed by the successive variational mode decomposition (SVMD) method and reconstructed into high-frequency and low-frequency parts. The low-frequency part is borne from the lithium battery, and the high-frequency part is borne from the flywheel energy storage, fully playing into the advantages of the frequency modulation of the two kinds of energy storage. The allocation strategy is shown in Figure 2.

3. Frequency Modulation Power Distribution Model Based on SVMD

3.1. SVMD of Frequency Modulation Power

The primary frequency modulation power instruction P_G(t) is assumed to decompose into the L-th power instruction modal component u_L(t) and the residual power instruction component P_r(t), wherein the residual power instruction includes the first (L−1) power instruction modal component obtained after decomposition and the unprocessed partial power instruction P_u(t) [20].

$$P_G\left(t\right)=-K_G\left(1-\eta \right)\Delta f\left(t\right)$$

(1)

$$P_G\left(t\right)=u_L\left(t\right)+P_r\left(t\right)$$

(2)

$$P_r\left(t\right)={\displaystyle \sum _{i=1}^{L-1}{u}_i\left(t\right)+P_u\left(t\right)}$$

(3)

In order to determine u_L(t) and construct the first part of P_r(t), the following criteria are established.

(1) Each modal component obtained by decomposition is compact near the central frequency, so it is realized by minimizing the constraints as follows:

$$J_1={‖{\partial }_t\left[\left(\delta \left(t\right)+{\displaystyle \frac{j}{\pi t}}\right)\ast u_L\left(t\right)\right]e^{-j{\omega }_{L}t}‖}_2^2$$

(4)

where δ(t) is the Dirac distribution; * is the convolution operation; ω_L is the center frequency of the decomposition of the L-order modal component.

(2) The aliasing spectrum of P_r(t) in the decomposition process is minimal, which can be achieved by appropriate filters as follows:

$${\widehat{\beta }}_L\left(\omega \right)={\displaystyle \frac{1}{\alpha {\left(\omega -{\omega }_L\right)}^2}}$$

(5)

So, the minimum constraint of this criterion is

$$J_2={‖{\beta }_L\left(t\right)\ast P_r\left(t\right)‖}_2^2$$

(6)

where β_L(t) is the impulse response of the filter in Equation (6).

(3) In order to effectively distinguish the L-order modal component from the previous modal component, the center frequency energy of the L-order modal component should be minimized when compared with the previous modal component. According to the implementation scheme in (2), the filter frequency response can be increased as follows:

$${\widehat{\beta }}_i\left(\omega \right)={\displaystyle \frac{1}{\alpha {\left(\omega -{\omega }_i\right)}^2}},i=1,2,\cdots ,L-1$$

(7)

where ω_i is the center frequency of the decomposed (L − 1) mode component.

So, the minimum constraint of this criterion is

$$J_3={\displaystyle \sum _{i=1}^{L-1}{‖{\beta }_i\left(t\right)\ast u_L\left(t\right)‖}_2^2}$$

(8)

where β_L(t) is the impulse response of the filter in Equation (8).

(4) It is necessary to ensure that the signal can be completely reconstructed during decomposition, so the constraints are established as follows:

$$P_G\left(t\right)=u_L\left(t\right)+P_u\left(t\right)+{\displaystyle \sum _{i=1}^{L-1}{u}_i\left(t\right)}$$

(9)

The above criteria can be expressed as a minimization problem with constraints as follows:

$$\left\{\begin{array}{c}\underset{u_L,{\omega }_L,P_r}{\min }\left(a{J}_1+J_2+J_3\right)\\ s.t.\hspace{1em}\hspace{1em}{u}_L\left(t\right)+P_r\left(t\right)=P_G\left(t\right)\end{array}\right.$$

(10)

where a is the balance parameter.

The minimization problem is solved iteratively by alternating direction multiplier method. When the power instruction is decomposed by SVMD, the iterative expression is as follows:

$$\begin{array}{l}{\widehat{u}}_L^{n+1}\left(\omega \right)=\\ {\displaystyle \frac{{\widehat{P}}_G\left(\omega \right)+{\alpha }^2{\left(\omega -{\omega }_L^n\right)}^4{\widehat{u}}_L^n\left(\omega \right)+\frac{\widehat{\lambda }\left(\omega \right)}{2}}{\left[1+{\alpha }^2{\left(\omega -{\omega }_L^n\right)}^4\right]\left[1+2\alpha {\left(\omega -{\omega }_L^n\right)}^2+{\displaystyle \sum _{i=1}^{L-1}\frac{1}{{\alpha }^2{\left(\omega -{\omega }_i\right)}^4}}\right]}}\end{array}$$

(11)

In the above formula, α generally takes a large value and represents the balance parameter of the fidelity of the power instruction; Lambda is the Lagrange multiplier.

The corresponding iterative expression of the power instruction P_u(t) is

$$\begin{array}{l}{\widehat{P}}_u^{n+1}\left(\omega \right)=\\ {\displaystyle \frac{{\alpha }^2{\left(\omega -{\omega }_L^{n+1}\right)}^4\left({\widehat{P}}_G\left(\omega \right)-{\widehat{u}}_L^{n+1}\left(\omega \right)-{\displaystyle \sum _{i=1}^{L-1}{\widehat{u}}_i\left(\omega \right)}+\frac{\widehat{\lambda }\left(\omega \right)}{2}\right)}{1+{\alpha }^2{\left(\omega -{\omega }_L^{n+1}\right)}^4}}-{\displaystyle \frac{{\displaystyle \sum _{i=1}^{L-1}{\widehat{u}}_i\left(\omega \right)}}{1+{\alpha }^2{\left(\omega -{\omega }_L^{n+1}\right)}^4}}\end{array}$$

(12)

The iterative equation of ω_L can be approximated as follows:

$${\omega }_L^{n+1}={\displaystyle \frac{{\displaystyle {\int }_0^{\infty }\omega {\left|{\widehat{u}}_L^{n+1}\left(\omega \right)\right|}^{2}d\omega }}{{\displaystyle {\int }_0^{\infty }{\left|{\widehat{u}}_L^{n+1}\left(\omega \right)\right|}^{2}d\omega }}}$$

(13)

The iterative equation for λ obtained by the double ascending method and Equation (13) is as follows:

$${\widehat{\lambda }}^{n+1}={\widehat{\lambda }}^n+\tau \left[{\widehat{P}}_G\left(\omega \right)-\left({\widehat{u}}_L^{n+1}\left(\omega \right)+{\widehat{P}}_u^{n+1}\left(\omega \right)+{\displaystyle \sum _{i=1}^{L-1}{u}_i^{n+1}\left(\omega \right)}\right)\right]$$

(14)

where τ is the iterative parameter.

Through the SVMD process, the primary frequency modulation power instructions are decomposed step by step. When the power instruction reconstruction error is less than a certain threshold, the modal components with different characteristics can be obtained.

3.2. Frequency Modulation Power Frequency Division Model

When the frequency dividing point is too small, the flywheel energy storage system has high capacity due to its high power, resulting in a high capacity cost. When the boundary point is too large, the battery bears more power, the change range of the charge state increases, and the depth of charge and discharge of the battery increases, which seriously affects its operating life and leads to an increase in replacement cost. Therefore, multiple IMFs can be obtained through SVMD, and it is necessary to determine whether IMF is a low-frequency component. After the SVMD of an FM instruction, the following changes are noted: IMF1 marker indicator 1, IMF1 + IMF2 marker indicator 2, IMF1 + IMF2 + IMF3 marker indicator 3… In the same way, the first k of the IMF and marked index k. Then, calculate the mean of each indicator and test whether the mean is much greater than or much less than 0. The test statistic z is

$$z={\displaystyle \frac{\sqrt{m-1}\left({\overline{N}}_k-0\right)}{{\sigma }_k}}$$

(15)

where m is the number of IMF after decomposition; N_k is the mean value of indicator k; σ_k is the standard deviation of indicator k.

If z is much greater than or much less than 0, then k, k + 1, k + 2, …. The m IMF is a low-frequency component, so it can be determined that the low-frequency component is allocated to lithium battery energy storage.

$$P_{G\_L}={\displaystyle \sum _{i=k}^m{I}_{MFi}}$$

(16)

Then, the flywheel energy storage distribution power is

$$P_{G\_H}=-K_G\left(1-\eta \right)\Delta f-P_{G\_L}$$

(17)

4. Hybrid-Energy Storage Capacity Optimization Based on Quantum Particle Swarm Optimization

4.1. Objective Function

The objective function of the capacity optimization allocation of a hybrid-energy storage system with maximum economic benefit can be expressed as follows:

$$\begin{array}{c}{E}^N=\max \left(E^{RM}-C_{ESS}^H\right)\\ \hspace{1em} ={\displaystyle \sum _t\left(f_t^{mil}{P}_t^{mil}+f_t^{cap}{P}_t^{cap}\right)}{K}^P-C_{ESS}^F-C_{ESS}^L\end{array}$$

(18)

where $f_t^{cap}$ and $f_t^{mil}$ is the frequency modulation capacity and mileage price; $P_t^{cap}$ and $P_t^{mil}$ is the winning mileage and capacity; $K^p$ is the frequency modulation performance index; $C_{ESS}^F$ and $C_{ESS}^L$ is the flywheel and lithium battery costs.

The sum of FM power deviation caused by wind power uncertainty is

$$P_t^{mil}={\displaystyle \sum _{t=0}^n\left|P_t^{reg}-P_{t-1}^{reg}\right|}$$

(19)

where $P_t^{reg}$ and $P_{t-1}^{reg}$ are the actual frequency modulation power and predicted frequency modulation power, respectively.

$$K^p=k_1{K}^{cor}+k_2{K}^{del}+k_3{K}^{pre}$$

(20)

where $K^{del}$, $K^{pre}$, and $K^{\mathrm{co}r}$ are, respectively, delay, accuracy, and correlation, and k₁, k₂, and k₃ are the weighted parameters.

$$C_{ESS}^H=C_{ESS}^F+C_{ESS}^L$$

(21)

$$C_{ESS}=C_{inv}+C_{om}+C_{loss}+C_{rep}$$

(22)

where C_inv, C_om, C_loss, and C_rep are, respectively, investment, operation and maintenance, penalty, and wear and tear costs.

$$C_{inv}={\displaystyle \sum _{t=1}^{T_{LCC}}\left(u_{pc}{P}_{rat}+u_{ec}{E}_{rat}\right){\left(1+r\right)}^{-t}}$$

(23)

where u_pc and u_ec are unit power and capacity costs; P_rat and E_rat are rated power and capacity.

$$C_{om}=u_{pom}{P}_{rat}{\displaystyle \frac{{\left(1+r\right)}^{T_{LCC}}-1}{r{\left(1+r\right)}^{T_{LCC}}}}+{\displaystyle \sum _{t=1}^{T_{LCC}}{u}_{eom}{E}_{rat}{\left(1+r\right)}^{-t}}$$

(24)

where u_pom and u_eom are unit power and capacity maintenance costs; r is the discount rate; T_LCC is the life cycle.

$$C_{loss}={\displaystyle \sum _{t=1}^{T_{LCC}}{u}_{loss}{P}_{loss}\left(t\right){\left(1+r\right)}^{-t}}$$

(25)

where P_loss is the lost power.

$$C_{rep}={\displaystyle \sum _{t=0}^n{u}_{ec}{E}_{rep}{\left(1+r\right)}^{-\left[t{T}_{LCC}/\left(n_1+1\right)\right]}}$$

(26)

where n₁ is the number of replacement times, and E_rep is the replacement capacity.

4.2. Constraints

(1) Hybrid-energy storage charge and discharge power constraints

$$\left\{\begin{array}{c}{P}_{lb}^{rate}=\max \left\{\left|\max \left[\Delta P_{lb}\left(t\right)\right]\right|{\eta }_{lb}^{cha},{\displaystyle \frac{\left|\min \left[\Delta P_{lb}\left(t\right)\right]\right|}{{\eta }_{lb}^{dis}}}\right\}\\ -P_{lb}^{rate}<\Delta P_{lb}\left(t\right)<P_{lb}^{rate}\end{array}\right.$$

(27)

$$\left\{\begin{array}{c}{P}_{sc}^{rate}=\max \left\{\left|\max \left[\Delta P_{sc}\left(t\right)\right]\right|{\eta }_{sc}^{cha},{\displaystyle \frac{\left|\min \left[\Delta P_{sc}\left(t\right)\right]\right|}{{\eta }_{sc}^{dis}}}\right\}\\ -P_{sc}^{rate}<\Delta P_{sc}\left(t\right)<P_{sc}^{rate}\end{array}\right.$$

(28)

where ΔP_lb(t) is the charge and discharge power required by the lithium battery at time t. ΔP_sc(t) is the charge and discharge power required by the supercapacitor at time t. η^cha_lb and η^dis_lb are the charging and discharging efficiency of lithium batteries, respectively. η^cha_sc and η^dis_sc are the charging and discharging efficiency of the supercapacitor, respectively.

(2) Hybrid-energy storage SOC constraints

$$SO{C}_{lb\min }\le SO{C}_{lb}\left(t\right)\le SO{C}_{lb\max }$$

(29)

$$SO{C}_{sc\min }\le SO{C}_{sc}\left(t\right)\le SO{C}_{sc\max }$$

(30)

where SOC_lb(t) is the SOC value of the lithium battery at time t; SOC_lbmax and SOC_lbmin are, respectively, the upper and lower SOC limits for lithium batteries. SOC_sc(t) indicates the SOC value of the supercapacitor at time t. SOC_scmax and SOC_scmin indicate the upper and lower SOC limits of the supercapacitor, respectively.

(3) Power balance constraints

$$\Delta P_{te}\left(t\right)=\Delta P_{lb}\left(t\right)+\Delta P_{sc}\left(t\right)$$

(31)

4.3. Capacity Optimization Solution Method Based on QPSO

In the traditional particle swarm optimization algorithm [21], the particle trajectory in the search space is determined in each iteration, and it is easy to fall into the local optimal. Therefore, quantum particle swarm optimization is adopted in this paper.

In the quantum particle swarm algorithm, the update of a particle’s position has nothing to do with the previous motion of the particle, which increases the randomness of the particle’s position and makes it easier to find the global optimal value.

By solving the Schrodinger equation, using Monte Carlo simulation, the motion position of the particle can be expressed as

$$\left\{\begin{array}{l}{x}_{ij}(t+1)=p_i(t)+\beta |M{\mathrm{best}}_j(t)-x_{ij}(t)|\ln ({\displaystyle \frac{1}{u}}), k>0.5\\ x_{ij}(t+1)=p_i(t)-\beta |M{\mathrm{best}}_j(t)-x_{ij}(t)|\ln ({\displaystyle \frac{1}{u}}), k\le 0.5\end{array}\right.$$

(32)

where k and u are random numbers on 0 ~ 1; t is the number of iterations; x_ij(t + 1) is the i particle in the j dimension of space; β is the coefficient of shrinkage and expansion; p_i is the local attraction point; Mbest is the average optimal position.

The average best value is the average of the best solutions for all individuals of a population, calculated as

$$M{\mathrm{best}}_j(t)={\displaystyle \frac{1}{\lambda }}{\displaystyle \sum _{j=1}^{\lambda }{p}_{gj}(t)}$$

(33)

where g is the index of the best particle in the population; Lambda is the number of particles. In addition, the local attractor p_i guarantees the convergence of the algorithm and is defined as

$$p_i(t)={\displaystyle \frac{c_1{p}_{ki}+c_2{p}_{gj}}{c_1+c_2}}$$

(34)

where c₁ and c₂ are the acceleration factors; p_ki and p_gi are the “best” location of the i particle discovery and the location index of the corresponding particle swarm, respectively. According to the above principles, the specific optimization steps are as follows:

(1) Input the calculation example parameters and obtain the required output of each energy storage of the hybrid-energy storage system according to Section 3.2;

(2) Set t = 0, initialize particle population and particle position, and set the maximum number of iterations n and expansion coefficient β;

(3) Calculate the average optimal position of particles according to Equation (32) and the fitness of particles according to the objective function;

(4) t = t+1, update the particle position according to Equation (31);

(5) Determine whether t is greater than the maximum number of iterations n; if t < n, return to step (3), and if t ≥ n, the algorithm stops iteration and outputs the optimal rated capacity and rated power configuration scheme of the hybrid-energy storage system. The optimization process is shown in Figure 3.

5. Simulation Analysis

5.1. Fundamentals of Simulation

Taking the measured data of a 100 MW wind farm in a province of China as the research object, the frequency modulation deviation power of a wind farm on a typical day is shown in Figure 4 when load reduction d% = 10%. As can be seen from Figure 4, the maximum frequency modulation power demand is 0.85 MW, the minimum is −0.85 MW, and the average is 0.37 MW.

The QPSO algorithm adopted in this paper is used to configure the flywheel and lithium battery hybrid-energy storage. The iteration number is 500, the particle population size is 100, the inertia weight ω adaptively linearly decreases from 0.9 to 0.4 as the iteration number increases, the learning parameter c₁ = c₂ = 1.5, the scaling parameter F = 0.95, and the crossover probability C_R = 0.88. The parameters of the flywheel are shown in

Table 2. Flywheel parameters.

Main Parameter	Value
Stator winding resistance	0.097
Rotor flux	0.128
Damping coefficient	1100
Stator inductance	2.085
Logarithm of motor flux	2
The flywheel turns to inertia	24.2

, and the parameters of the calculation example are shown in

Table 3. Cost parameter settings.

Object	Index	Value
Lithium battery	Power cost/(10,000 CNY/MW)	200
	Capacity cost/(10,000 CNY/MWh)	150
	Operation and maintenance cost/(10,000 CNY/MW)	40
	Charge and discharge efficiency/%	90
	Cycle life	6000 times
	SOC limit	[0.2, 0.8]
Flywheel	Power cost/(10,000 CNY/MW)	600
	Capacity cost/(10,000 CNY/MWh)	1000
	Operation and maintenance cost/(10,000 CNY/MW)	20
	Charge and discharge efficiency/%	95
	Cycle life	160,000 times
	SOC limit	[0.1, 0.9]
Other	Discount rate/%	5
	PCS loss cost/(10,000 CNY/MW)	80
	Hybrid-energy storage life/a	20
	Capacity declaration price/(CNY/MWh)	[5, 10]
	Mileage declaration price/(CNY/MW)	[6, 15]

.

5.2. Capacity Optimization Configuration Analysis

5.2.1. Frequency Division Analysis

In order to verify the accuracy and stability of the SVMD of FM power, the VMD and SVMD of the FM deviation power instructions of wind turbines are, respectively, carried out. Since the number of modes of VMD needs to be determined in advance, according to Ref. [22], the optimal parameter combination is determined to be K = 6,1000, and the modal components of the two decomposition methods are obtained under the optimal fitness, as shown in Figure 5.

Figure 5a adopts the VMD method, and Figure 5b adopts the SVMD method. From the modal components obtained after decomposition, it can be seen that the high-frequency component obtained by VMD has a good effect, but the low-frequency effect is poor. For example, although the frequency of IMF1 is low, the modal component has small fluctuations at different times, and it is not suitable to be used as the reference power of the actual frequency modulation output of lithium battery energy storage. The low-frequency modal component obtained by SVMD is more prominent and less volatile than VMD, which is suitable for the actual reference value of lithium battery energy storage frequency modulation.

5.2.2. Capacity Optimization Configuration Results

With the goal of maximizing the net benefit of hybrid-energy storage, under the premise of meeting the constraints, the quantum particle swarm optimization algorithm is used to optimize the capacity and power of hybrid-energy storage. The PSO and genetic Algorithm (GA) were compared. The performance comparison data of different optimization algorithms are shown in

Table 4. Performance comparison of different optimization algorithms.

Method	Run Time/s	Number of Iterations
PSO	351.27	302
GA	301.77	174
QPSO	245.71	128

.

As can be seen from Table 4, compared with PSO and GA, the running time of QPSO is reduced by 30.05% and 18.58%, and the number of iterations is reduced by 174 and 46 times. It can be seen that QPSO can effectively improve iteration speed and reduce iteration times. The hybrid-energy storage capacity configuration results of different algorithms are shown in

Table 5. Results of configuration by different methods.

Method	Type of Energy Storage	Rated Power/MW	Rated Capacity/MWh	Cost/CNY	Net Benefit/CNY
PSO	Flywheel	0.48	1.26	7,325,542	673,689
	Lithium battery	0.41	0.21
GA	Flywheel	0.42	1.19	7,140,821	625,465
	Lithium battery	0.51	0.23
QPSO	Flywheel	0.24	0.54	5,575,218	814,283
	Lithium battery	0.55	0.24

.

It can be seen from Table 5 that using QPSO to optimize the capacity of hybrid-energy storage can effectively reduce the cost and improve the net benefit of the energy storage system while ensuring the effect of frequency modulation. Compared with PSO and GA, the benefit of the energy storage system is higher by 20.86% and 30.18%, and the cost is reduced by 23.89% and 21.92%, showing a good economic impact.

As can be seen from Table 5 and

Table 6. Benefits of single-energy storage frequency modulation.

Index	Flywheel	Lithium Battery
Rated power/MW	0.89	0.89
Rated capacity/MWh	1.47	1.47
Energy storage annual net income/yuan	412,346	595,612
Cost per/CNY	8,756,811	5,584,531

, the annual net income of the hybrid-energy storage system is much greater than that of a single flywheel or lithium battery, and the income of a single flywheel is only CNY 412,346, while the income of a lithium battery is CNY 595,612. The sum of the two is far less than that of hybrid-energy storage, mainly because the flywheel mainly deals with high-frequency components and has a poor processing effect on low-frequency components. The processing capacity of lithium batteries for high-frequency components is limited, so under the action of single-energy storage, the penalty cost of frequency modulation is significantly increased, and the benefit of frequency modulation is significantly decreased. This effectively shows the economic effectiveness and feasibility of hybrid-energy storage frequency modulation.

5.3. Analysis of Frequency Modulation Effect

In order to verify that hybrid-energy storage is superior to a separate energy storage system, three configuration schemes are selected according to the energy storage characteristics of lithium iron phosphate batteries and flywheel energy storage systems, which are battery-only energy storage, flywheel energy storage, battery and flywheel energy storage, and hybrid-energy storage.

5.3.1. Primary Frequency Modulation Specifications

In order to better evaluate the performance of frequency modulation, two evaluation indexes of frequency modulation are proposed according to the type of load disturbance. The first is the step disturbance, the absolute value of the maximum frequency deviation |Δf_max|, and the adjustment time |t_s|. The second is the continuous disturbance index.

$$\Delta f_{\mathrm{p}\_\mathrm{v}}=f_{\max }-f_{\min }$$

(35)

$$f_{RMS}=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{(f_i-f_0)}^2}}$$

(36)

where Δf_{p_v} is the frequency peak-valley difference; f_min, f_max, f_i, and f₀ are minimum frequency, maximum frequency, real-time frequency, and reference value; f_RMS is the frequency root mean square value.

5.3.2. Step Disturbance

When t = 5 s, the load increases by 30 MW, resulting in a decrease in system frequency. Under different modes, the frequency change curve is shown in Figure 6, and the frequency modulation index is shown in

Table 7. Comparison of effects of different methods.

Way	|Δfmax|	|ts|
Single flywheel	0.115 Hz	5.26
Single lithium battery	0.085 Hz	5.11
Hybrid-energy storage	0.071 Hz	4.17

.

According to Figure 6 and Table 7, compared with the single mode, the mixed-energy storage mode has the best frequency modulation effect, and Δf_max is reduced by 37.9% and 15.3%, respectively, which effectively indicates that mixed-energy storage has a better suppression effect and frequency modulation effect on frequency deviation.

5.3.3. Continuous Disturbance

In order to further analyze the frequency modulation effect of hybrid-energy storage, under the continuous frequency deviation condition, the frequency modulation effect is compared with that of a single flywheel with equal capacity and energy storage, as shown in Figure 7, and the frequency modulation index is shown in

Table 8. Continuous disturbance frequency modulation index.

Way	Δfp_v	fRMS
Single flywheel	0.256 Hz	0.028
Single lithium battery	0.215 Hz	0.021
Hybrid-energy storage	0.121 Hz	0.011

.

From the above frequency modulation simulation results, it is not difficult to find that under the continuous disturbance condition, when hybrid-energy storage participates in the combined primary frequency modulation of wind farms, Δf_{p_v} = 0.121 Hz, Δf_{p_v} = 0.011 Hz, compared with the single-energy storage mode, the Δf_{p_v} is reduced by 52.73%, 43.72%, 60.71%, and 47.62%, respectively. The frequency fluctuation range is obviously reduced, and the frequency stability is greatly improved. This further demonstrates the effectiveness and feasibility of hybrid-energy storage frequency modulation.

6. Conclusions

Aiming at the problems of slow power response and high long-term use cost of single-battery energy storage system in wind-storage system, a new hybrid flywheel-battery energy storage system is established in this paper. Through simulation analysis, the following conclusions can be drawn:

(1) By decomposing primary frequency modulation power instructions, lithium battery energy storage distributes low-frequency power instructions, which can effectively avoid the problem of frequent outputs during frequency modulation. At the same time, the flywheel energy storage responds to the high frequency part of a frequency modulation command, which can give full play to the advantages of more charge and discharge times of flywheel energy storage.

(2) Based on the typical daily frequency modulation power, the optimization result of flywheel energy storage capacity is 0.54 MWh and 0.24 MW, and the capacity of lithium battery is 0.24 MWh and 0.55 MW. The feasibility of this method is verified by comparing the frequency modulation effect of different allocation schemes.

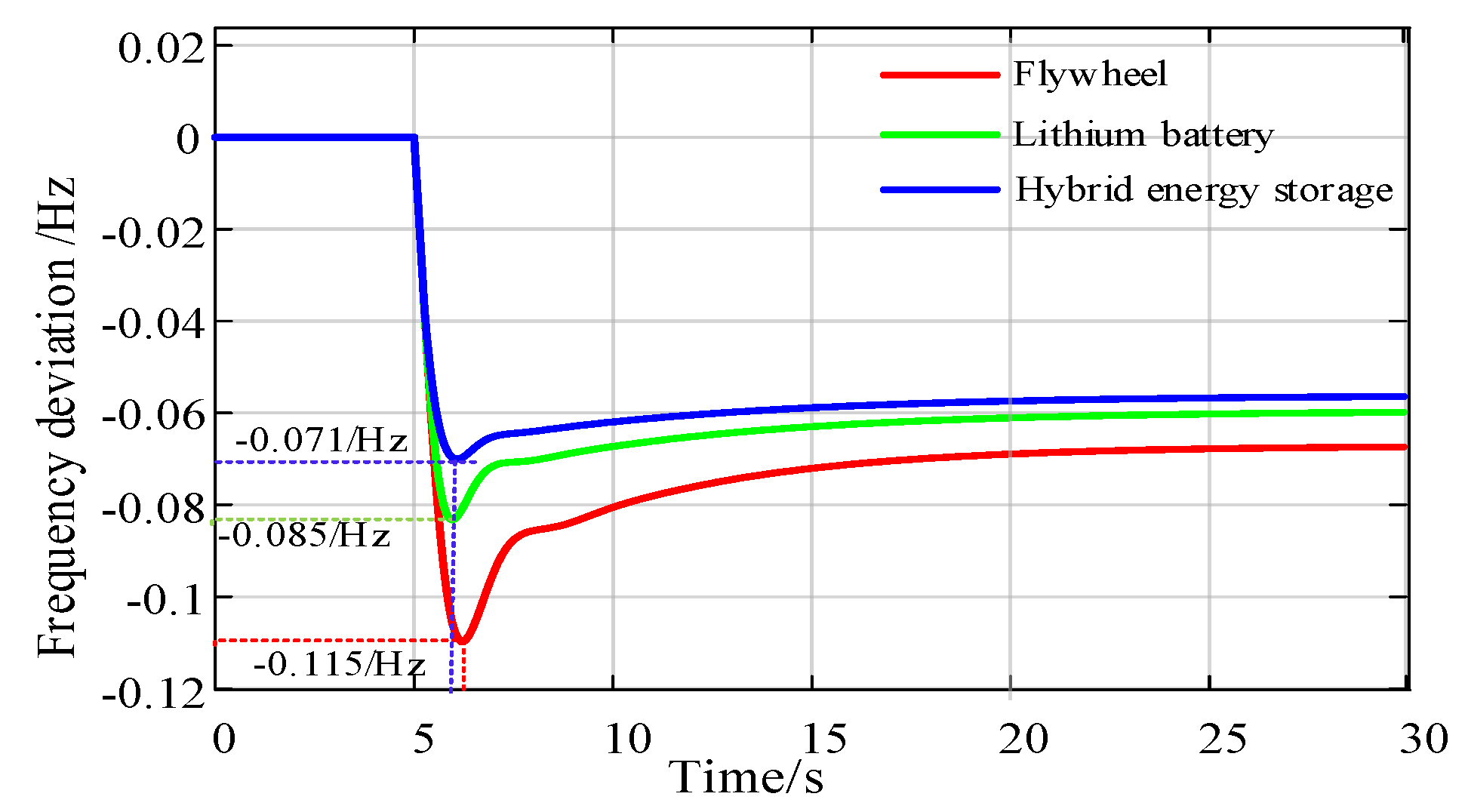
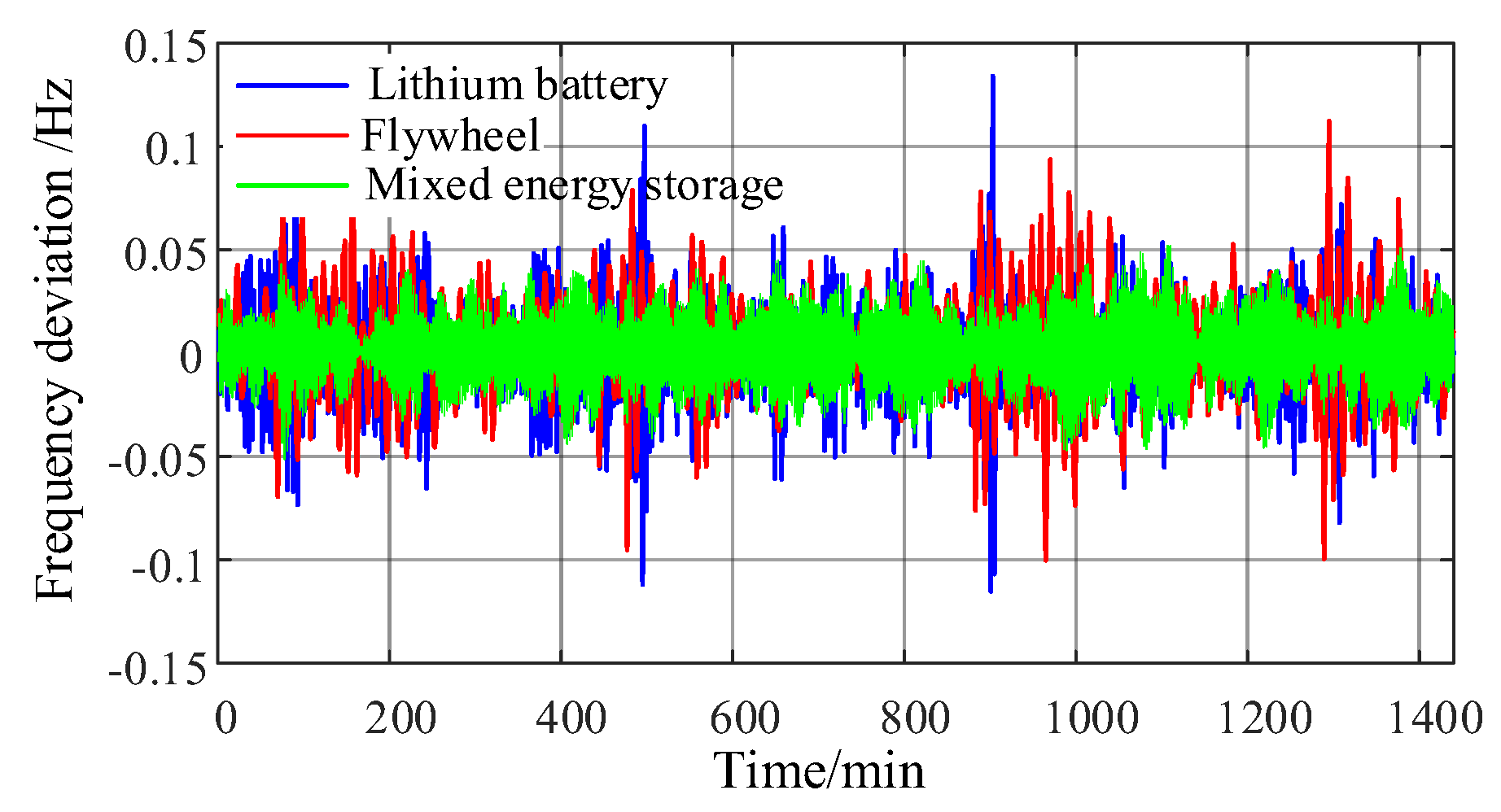
(3) Compared with a single flywheel and a single lithium battery, hybrid-energy storage can effectively improve the primary frequency modulation effect of photovoltaic power generation systems. Under the two scenarios of load step disturbance and continuous random disturbance, the frequency fluctuation range is smaller, and the frequency stability is greatly improved.

The focus of a future paper will be to test the proposed model and method in the real system, so as to improve its practical application value. In the model, the influence factors such as the service life and temperature of the energy storage system will be further considered to make it more perfect and fit the actual project.