Assessment of Municipal Waste Forecasting Methods in Poland Considering Socioeconomic Aspects
Abstract
1. Introduction
2. A Critical Bibliographic Analysis of Methods for Forecasting the Municipal Waste Accumulation Rate
3. Materials and Methods
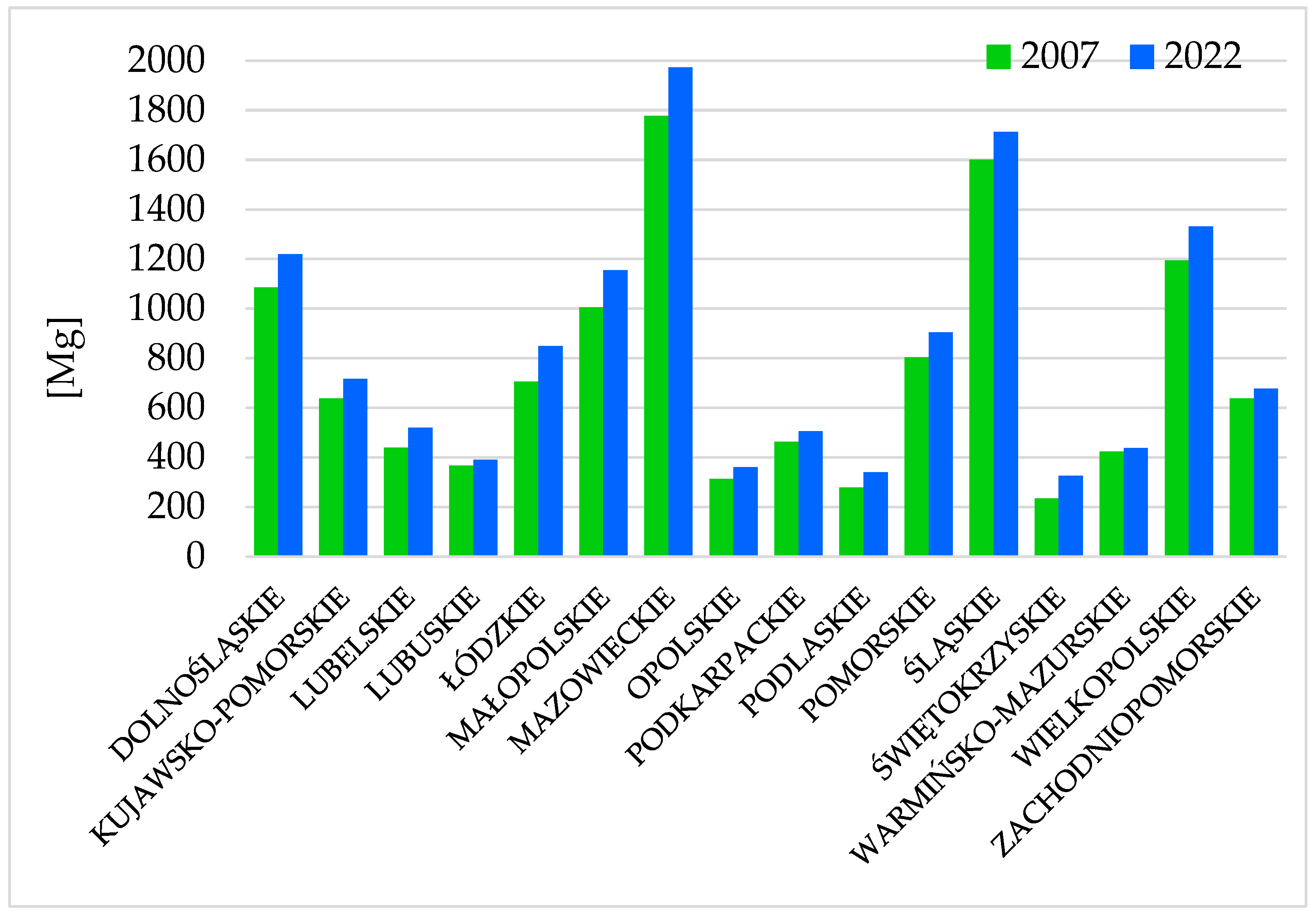
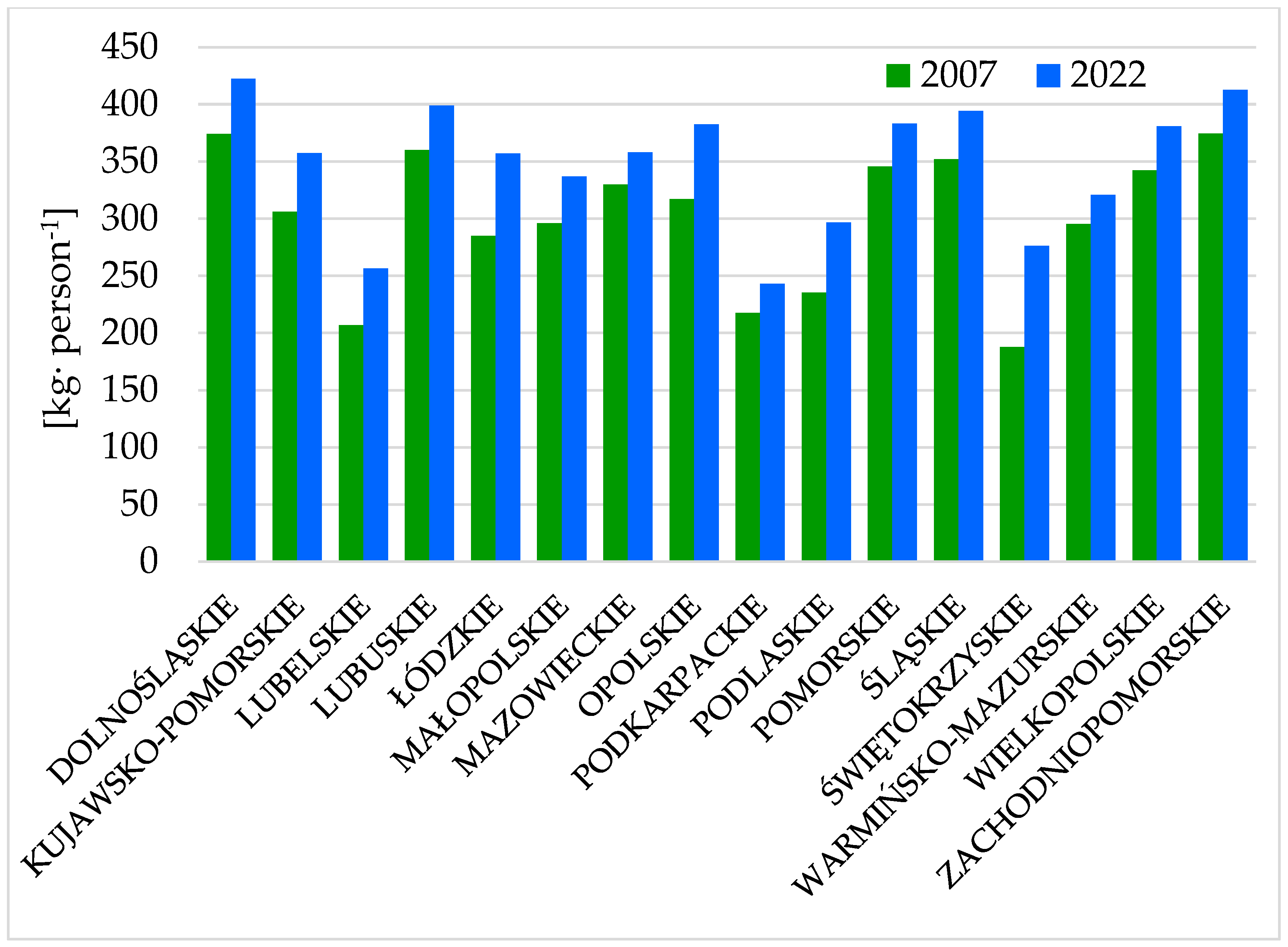
4. Characteristics of the Research Object
5. Research Results
6. Results and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Famielec, S.; Malinowski, M.; Tomaszek, K.; Wolny-Koładka, K.; Krilek, J. The effect of biological methods for MSW treatment on the physicochemical, microbiological and phytotoxic properties of used biofilter bed media. Waste Manag. 2024, 175, 276–285. [Google Scholar] [CrossRef] [PubMed]
- Izquierdo-Horna, L.; Kahhat, R.; Vázquez-Rowe, I. Reviewing the influence of sociocultural, environmental and economic variables to forecast municipal solid waste (MSW) generation. Sustain. Prod. Consum. 2022, 33, 809–819. [Google Scholar] [CrossRef]
- Abdallah, M.; Abu Talib, M.; Feroz, S.; Nasir, Q.; Abdalla, H.; Mahfood, B. Artificial intelligence applications in solid waste management: A systematic research review. Waste Manag. 2020, 109, 231–246. [Google Scholar] [CrossRef] [PubMed]
- Klimek, P. Ocena potencjału energetycznego odpadów komunalnych w zależności od zastosowanej technologii ich utylizacji. Nafta-Gaz 2013, 12, 909–914. Available online: http://www.archiwum.inig.pl/INST/nafta-gaz/nafta-gaz/Nafta-Gaz-2013-12-05.pdf (accessed on 6 March 2024). (In Polish).
- Wielgosinski, G. Wybór technologii termicznego przekształcania odpadów komunalnych. Nowa Energ. 2012, 1, 66–80. Available online: https://scholar.google.com/scholar_lookup?title=Wyb%C3%B3r+technologii+termicznego+przekszta%C5%82cania+odpad%C3%B3w+komunalnych&author=Wielgosinski,+G.&publication_year=2012&journal=Nowa+Energ.&volume=1&pages=66%E2%80%9380 (accessed on 1 April 2024). (In Polish).
- de Morais Vieira, V.H.A.; Matheus, D.R. The impact of socioeconomic factors on municipal solid waste generation in São Paulo, Brazil. Waste Manag. Res. 2018, 36, 79–85. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, M.; Hanandeh, A.E. Forecasting municipal solid waste generation using artificial intelligence modelling approaches. Waste Manag. 2016, 56, 13–22. [Google Scholar] [CrossRef]
- Khan, A.H.; López-Maldonado, E.A.; Khan, N.A.; Villarreal-Gómez, L.J.; Faris, M.; Munshi, F.M.; Alsabhan, A.H.; Kahkashan Perveen, K. Current solid waste management strategies and energy recovery in developing countries—State of art review. Chemosphere 2022, 291, 133088. [Google Scholar] [CrossRef]
- Przydatek, G. Recognition of systemic differences in municipal waste management in selected cities in Poland and the United States. Environ. Sci. Pollut. Res. 2023, 30, 76217–76226. [Google Scholar] [CrossRef]
- Nęcka, K.; Szul, T.; Knaga, J. Identification and Analysis of Sets Variables for of Municipal Waste Management Modelling. Geosciences 2019, 9, 458. [Google Scholar] [CrossRef]
- Kundariya, N.; Mohanty, S.S.; Varjani, S.; Hao Ngo, H.; Wong, J.W.C.; Taherzadeh, M.J.; Chang, J.-S.; Yong Ng, H.; Kim, S.-H.; Bui, X.-T. A review on integrated approaches for municipal solid waste for environmental and economical relevance: Monitoring tools, technologies, and strategic innovations. Bioresour. Technol. 2021, 342, 125982. [Google Scholar] [CrossRef] [PubMed]
- Sinha, R.; Prabhudev, B.C. Impact of socio-cultural challenges in solid waste management. Int. J. Eng. Res. Technol. (IJERT) 2016, 4, 1–3. Available online: https://www.ijert.org/research/impact-of-socio-cultural-challenges-in-solid-waste-management-IJERTCONV4IS27036.pdf (accessed on 10 April 2024).
- Lebersorger, S.; Beigl, P. Municipal solid waste generation in municipalities: Quantifying impacts of household structure, commercial waste and domestic fuel. Waste Manag. 2011, 31, 1907–1915. [Google Scholar] [CrossRef]
- Trang, P.T.T.; Dong, H.Q.; Toan, D.Q.; Hanh, N.T.X.; Thu, N.T. The Effects of Socio-economic Factors on Household Solid Waste Generation and Composition: A Case Study in Thu Dau Mot, Vietnam. Energy Procedia 2017, 107, 253–258. [Google Scholar] [CrossRef]
- Ali Abdoli, M.; Falah Nezhad, M.; Salehi Sede, R.; Behboudian, S. Longterm forecasting of solid waste generation by the artificial neural networks. Environ. Prog. Sustain. Energy 2012, 31, 628–636. [Google Scholar] [CrossRef]
- Namlis, K.G.; Komilis, D. Influence of four socioeconomic indices and the impact of economic crisis on solid waste generation in Europe. Waste Manag. 2019, 89, 190–200. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, M.; Rastgoo, M.N.; Nakisa, B. Monthly and seasonal modeling of municipal waste generation using radial basis function neural network. Environ. Prog. Sustain. Energy 2018, 38, e13033. [Google Scholar] [CrossRef]
- Johnson, N.E.; Ianiuk, O.; Cazap, D.; Liu, L.; Starobin, D.; Dobler, G.; Ghandehari, M. Patterns of waste generation: A gradient boosting model for short-term waste prediction in New York City. Waste Manag. 2017, 62, 3–11. [Google Scholar] [CrossRef]
- Shah, A.V.; Srivastava, V.K.; Mohanty, S.S.; Varjani, S. Municipal solid waste as a sustainable resource for energy production: State-of-the-art review. J. Environ. Chem. Eng. 2021, 9, 105717. [Google Scholar] [CrossRef]
- Han, Z.; Liu, Y.; Zhong, M.; Shi, G.; Li, Q.; Zeng, D.; Zhang, Y.; Fei, Y.; Xie, Y. Influencing factors of domestic waste characteristics in rural areas of developing countries. Waste Manag. 2018, 72, 45–54. [Google Scholar] [CrossRef]
- Vu, H.L.; Ng, K.T.W.; Bolingbroke, D. Time-lagged effects of weekly climatic and socio-economic factors on ANN municipal yard waste prediction models. Waste Manag. 2019, 84, 129–140. [Google Scholar] [CrossRef] [PubMed]
- Cárdenas-Mamani, Ú.; Kahhat, R.; Vázquez-Rowe, I. District-level analysis for household-related energy consumption and greenhouse gas emissions: A case study in Lima, Peru. Sustain. Cities Soc. 2022, 77, 103572. [Google Scholar] [CrossRef]
- Giampietro, M.; Mayumi, K.; Sorman, A. The Metabolic Pattern of Societies: Where Economists Fall Short, 1st ed.; Routledge: London, UK, 2012. [Google Scholar] [CrossRef]
- Kaza, S.; Yao, L.; Bhada-Tata, P.; Van Woerden, F. What a Waste 2.0: A Global Snapshot of Solid Waste Management to 2050; World Bank Publications: Washington, DC, USA, 2018; Available online: https://books.google.pl/books?hl=pl&lr=&id=bnN_DwAAQBAJ&oi=fnd&pg=PP13&ots=faNcyx50M8&sig=f_x48AAFyWRJScWTxyOsZxwEIsI&redir_esc=y#v=onepage&q&f=false (accessed on 11 April 2024).
- de Souza Melaré, V.A.; Montenegro González, S.; Faceli, K.; Casadei, V. Technologies and decision support systems to aid solid-waste management: A systematic review. Waste Manag. 2017, 59, 567–584. [Google Scholar] [CrossRef] [PubMed]
- Chhay, L.; Reyad, M.A.H.; Suy, R.; Islam, M.R.; Mian, M.M. Municipal solid waste generation in China: Influencing factor analysis and multi-model forecasting. J. Mater. Cycles Waste Manag. 2018, 20, 1761–1770. [Google Scholar] [CrossRef]
- Nguyen, X.C.H.; Nguyen, T.T.H.; La, D.D.; Kumar, G.; Rene, E.R.; Nguyen, D.D.; Chang, S.W.; Chung, W.J.; Nguyen, X.H.; Nguyen, V.K. Development of machine learning—Based models to forecast solid waste generation in residential areas: A case study from Vietnam. Conserv. Recycl. 2021, 167, 105381. [Google Scholar] [CrossRef]
- Popli, K.; Park, C.; Han, S.-M.; Kim, S. Prediction of Solid Waste Generation Rates in Urban Region of Laos Using Socio-Demographic and Economic Parameters with a Multi Linear Regression Approach. Sustainability 2021, 13, 3038. [Google Scholar] [CrossRef]
- Azadi, S.; Karimi-Jashni, A. Verifying the performance of artificial neural network and multiple linear regression in predicting the mean seasonal municipal solid waste generation rate: A case study of Fars province, Iran. Waste Manag. 2016, 48, 14–23. [Google Scholar] [CrossRef] [PubMed]
- Sunayana; Kumar, S.; Kumar, R. Forecasting of municipal solid waste generation using non-linear autoregressive (NAR) neural models. Waste Manag. 2021, 121, 206–214. [Google Scholar] [CrossRef] [PubMed]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. Available online: https://www.jmlr.org/papers/volume3/guyon03a/guyon03a.pdf?ref=driverlayer.com/web (accessed on 11 April 2024).
- Lin, K.; Zhao, Y.; Kuo, J.-H.; Deng, H.; Cui, F.; Zhang, Z.; Zhang, M.; Zhao, C.; Gao, X.; Zhou, T.; et al. Toward smarter management and recovery of municipal solid waste: A critical review on deep learning approaches. J. Clean. Prod. 2022, 346, 130943. [Google Scholar] [CrossRef]
- Orsoni, A.; Karadimas, N.V.; Loumos, V. Municipal Solid Waste Generation Modelling Based on Fuzzy Logic; European Council for Modeling and Simulation ECMS: Caserta, Italy, 2006; pp. 309–314. [Google Scholar] [CrossRef]
- Szul, T.; Nęcka, K.; Lis, S. Application of the Takagi-Sugeno Fuzzy Modeling to Forecast Energy Efficiency in Real Buildings Undergoing Thermal Improvement. Energies 2021, 14, 1920. [Google Scholar] [CrossRef]
- Chen, H.W.; Chang, N.-B. Prediction analysis of solid waste generation based on grey fuzzy dynamic modeling. Resour. Conserv. Recycl. 2000, 29, 1–18. [Google Scholar] [CrossRef]
- Intharathirat, R.; Salam, P.A.; Kumar, S.; Untong, A. Forecasting of municipal solid waste quantity in a developing country using multivariate grey models. Waste Manag. 2015, 39, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Mwenda, A.; Kuznetsov, D.; Mirau, S. Time series forecasting of solid waste generation in Arusha city-Tanzania. Math. Theory Model. 2014, 4, 29–39. Available online: https://core.ac.uk/download/pdf/234679771.pdf (accessed on 15 April 2024).
- Owusu-Sekyere, E.; Harris, E.; Bonyah, E. Forecasting and Planning for Solid Waste Generation in the Kumasi Metropolitan Area of Ghana: An ARIMA Time Series Approach. Int. J. Sci. 2013, 2, 69–83. [Google Scholar] [CrossRef]
- Ayeleru, O.O.; Fajimi, L.I.; Oboirien, B.O.; Olubambi, P.A. Forecasting municipal solid waste quantity using artificial neural network and supported vector machine techniques: A case study of Johannesburg, South Africa. J. Clean. Prod. 2021, 289, 125671. [Google Scholar] [CrossRef]
- Ghinea, C.; Drăgoi, E.N.; Comăniţă, E.-D.; Gavrilescu, M.; Câmpean, T.; Curteanu, S.; Gavrilescu, M. Forecasting municipal solid waste generation using prognostic tools and regression analysis. J. Environ. Manag. 2016, 182, 80–93. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, M.; Abduli, M.A.; Omidvar, B.; Baghvand, A. Results uncertainty of support vector machine and hybrid of wavelet transform-support vector machine models for solid waste generation forecasting. Environ. Prog. Sustain. Energy 2014, 33, 220–228. [Google Scholar] [CrossRef]
- Cubillos, M. Multi-site household waste generation forecasting using a deep learning approach. Waste Manag. 2020, 115, 8–14. [Google Scholar] [CrossRef]
- Shuyan Wan, S.; Nik-Bakht, M.; Tsun Wai Ng, K.; Tian, X.; An, C.; Sun, H.; Yue, R. Insights into the urban municipal solid waste generation during the COVID-19 pandemic from machine learning analysis. Sustain. Cities Soc. 2024, 100, 105044. [Google Scholar] [CrossRef]
- Younes, M.K.; Nopiah, Z.M.; Basri, N.E.A.; Basri, H.; Maulud, K.N.A. Prediction of municipal solid waste generation using nonlinear autoregressive network. Environ. Monit. Assess. 2015, 187, 753. [Google Scholar] [CrossRef] [PubMed]
- Xu, A.; Chang, H.; Xu, Y.; Li, R.; Li, X.; Zhao, Y. Applying artificial neural networks (ANNs) to solve solid waste-related issues: A critical review. Waste Manag. 2021, 124, 385–402. [Google Scholar] [CrossRef] [PubMed]
- Dyson, B.; Chang, N.-B. Forecasting municipal solid waste generation in a fast-growing urban region with system dynamics modeling. Waste Manag. 2005, 25, 669–679. [Google Scholar] [CrossRef] [PubMed]
- Kursa, M.B.; Rudnicki, W.R. Wybór funkcji z pakietem Boruta. J. Stat. Oprogramowanie 2010, 36, 1–13. [Google Scholar] [CrossRef]
- efg’s R Notes: Boruta Package. 2015. Available online: https://earlglynn.github.io/RNotes/package/Boruta/index.html (accessed on 2 May 2024). (In Polish).
- The R Project for Statistical Computing. Available online: https://cloud.r-project.org. (accessed on 2 April 2024).
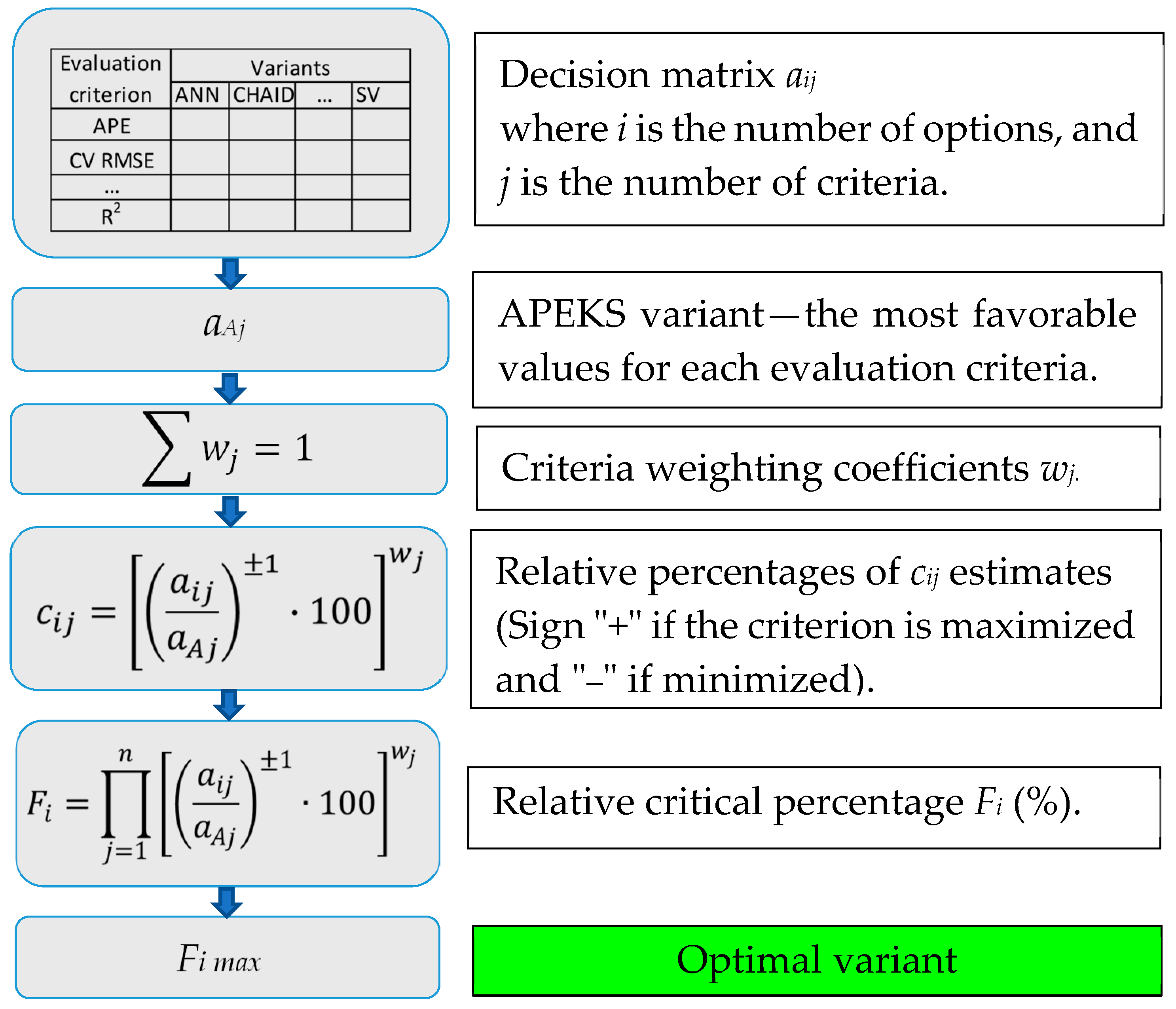
- Szybka, J.; Pabian, S. APEKS—A method of decision making. Sci. Technol. Innov. 2021, 12, 45–50. [Google Scholar] [CrossRef]
- Statistics Poland. Central Statistical Office. Local Data Bank. 2024. Available online: https://bdl.stat.gov.pl/.BDL/start (accessed on 15 March 2024).
- Bański, J. Contemporary typologies of rural areas in Poland—An overview of methodological approaches. Przegląd Geogr. 2014, 86, 441–470. Available online: http://www.rcin.org.pl/Content/51257/WA51_70537_r2014-t86-z4_Przeg-Geogr-Banski.pdf (accessed on 15 March 2024). (In Polish). [CrossRef]
- Ruiz, G.R.; Bandera, C.R. Validation of Calibrated Energy Models: Common Errors. Energies 2017, 10, 1587. [Google Scholar] [CrossRef]
- von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1947. [Google Scholar]
- Churchman, C.W.; Ackoff, R.L.; Arnoff, E.L. Introduction to Operations Research; Wiley: New York, NY, USA, 1957. [Google Scholar]


| No. | Independent Variables | Reference | |
|---|---|---|---|
| 1. | Socio-cultural | age cultural factors demographic conditions education | [6,8,10,11,12,13,14,15,16] |
| 2. | Environmental | energy consumption precipitation temperature | [1,17,18,19,20,21,22,23] |
| 3. | Economic | economic trends employment rate household income work and occupation | [10,12,17,24,25,26,27,28,29] |
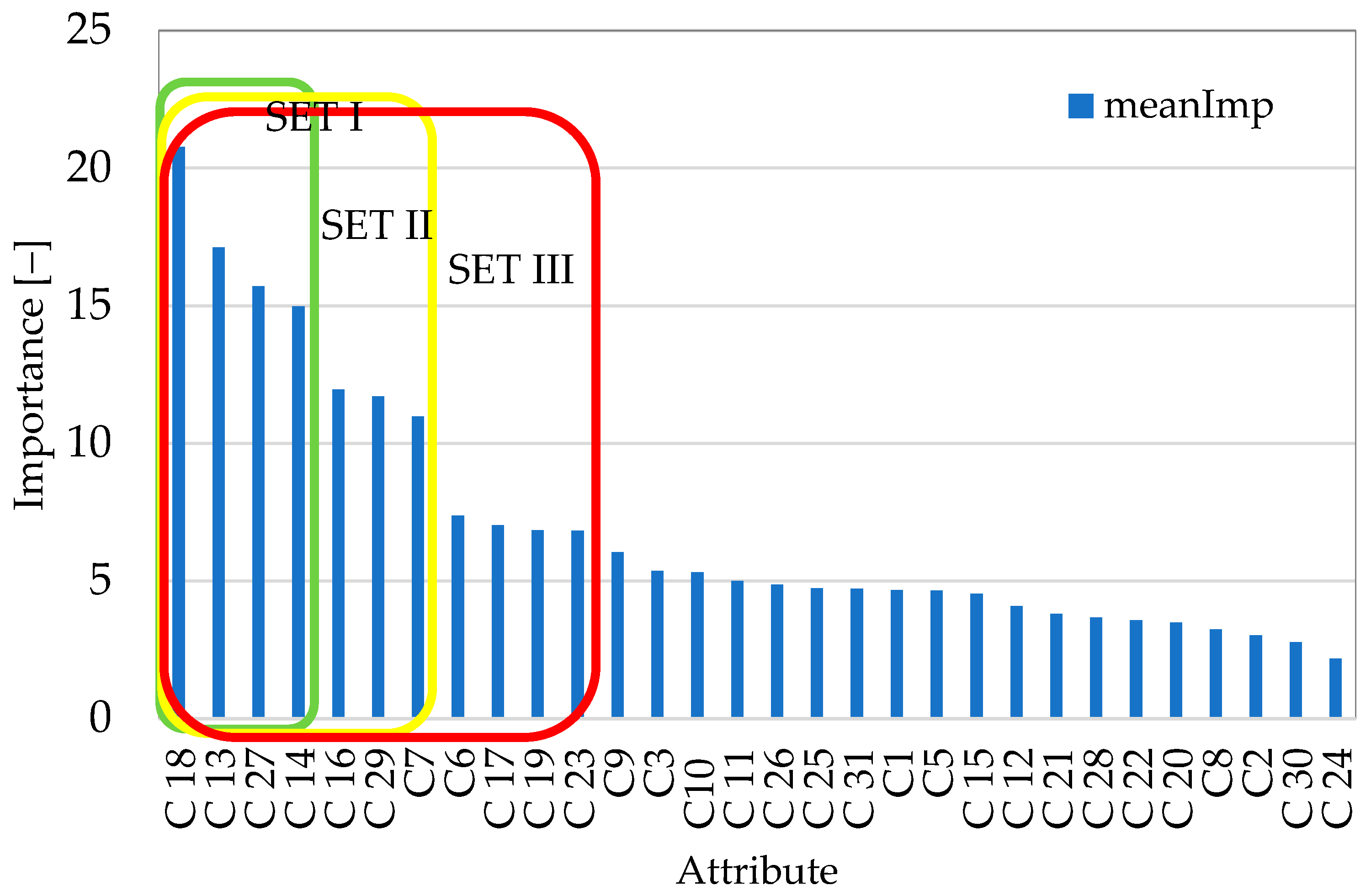
| Symbol Attribute | Name of Independent Variable | Unit |
|---|---|---|
| C1 | voivodeship | — |
| C2 | municipality administrative type | — |
| C3 | functional structure of communes | — |
| C4 | typology of municipalities according to the scope of impact | — |
| C5 | population density | per·km−2 |
| C6 | building occupancy rate | per·apartment−1 |
| C7 | average agricultural area | ha |
| C8 | percentage of apartments heated with natural gas | % |
| C9 | average gas consumption for residential heating by household | MWh·apartment−1 |
| C10 | share of apartments equipped with water supply | % |
| C11 | share of apartments equipped with sewage systems | % |
| C12 | share of apartments equipped with a gas installation | % |
| C13 | share of apartments equipped with a flush toilet | % |
| C14 | share of apartments equipped with a bathroom | % |
| C15 | share of farms deriving income from agricultural activities | % |
| C16 | personal income tax | PLN·per−1 |
| C17 | corporate income tax | PLN·per−1 |
| C18 | municipal waste management expenses | PLN·per−1 |
| C19 | feminization ratio (number of women per 100 men) | person |
| C20 | persons of non-working age per 100 persons of working age | person |
| C21 | persons of post-working age per 100 persons of pre-working age | person |
| C22 | persons of post-working age per 100 persons of working age | person |
| C23 | migration balance per 1000 population | person |
| C24 | indicator of enterprises carrying out collection of mixed municipal waste | % |
| C25 | rate of provision of municipal waste collection services from residential properties | % |
| C26 | rate of provision of municipal waste collection services from unoccupied properties | % |
| C 27 | cost efficiency ratio of total services of municipal waste collected | PLN·Mg−1 |
| C28 | total registered unemployed in population | % |
| C29 | number of apartments in the building | pcs |
| C30 | number of live births per 1000 people | — |
| C31 | natural increase per 1000 inhabitants | % |
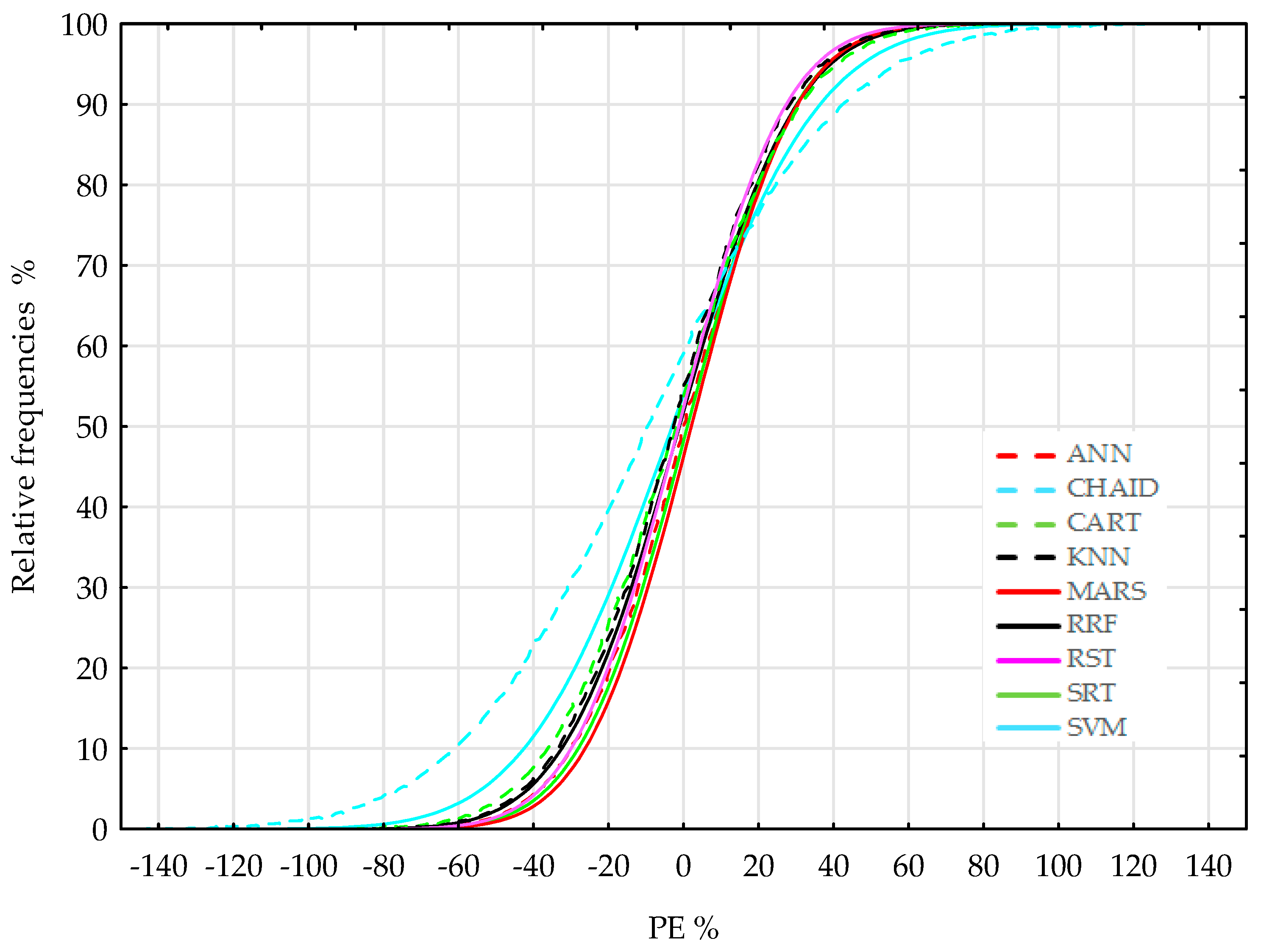
| 4 Variables | ANN | CHAID | CART | KNN | MARS | RRF | RST | SRT | SVM |
|---|---|---|---|---|---|---|---|---|---|
| CVRMSE | 20.1 | 30.7 | 22.8 | 21 | 20.9 | 21.2 | 20 | 21.7 | 26.9 |
| MAE | 37.4 | 63.8 | 46.2 | 43.2 | 40.4 | 42.7 | 38.8 | 42.1 | 52.4 |
| MAPE | 14.7 | 28.1 | 18.9 | 17.9 | 15.6 | 17.4 | 15.4 | 16.5 | 21.9 |
| MBE | 5.1 | 2.1 | 3.8 | 4.6 | 6.8 | 4.0 | 1.3 | 6.3 | 4.6 |
| ME | 13.6 | 5 | 9.9 | 12.3 | 18.1 | 10.4 | 3.5 | 16.8 | 12.1 |
| MPE | 0.3 | −9.4 | −2.4 | −1.1 | 2.1 | −2.7 | −1.3 | 1 | −3.1 |
| R2 | 0.77 | 0.41 | 0.69 | 0.74 | 0.76 | 0.76 | 0.76 | 0.74 | 0.56 |
| 7 Variables | ANN | CHAID | CART | KNN | MARS | RRF | RST | SRT | SVM |
|---|---|---|---|---|---|---|---|---|---|
| CVRMSE | 30.6 | 33.2 | 30.4 | 27.4 | 26.1 | 28.5 | 18.8 | 25.9 | 25.3 |
| MAE | 48.9 | 53.4 | 48.8 | 41.4 | 31.2 | 43 | 37.6 | 35.3 | 49 |
| MAPE | 19.4 | 20.7 | 19.3 | 16.2 | 11.8 | 17.2 | 14.8 | 13.8 | 20.5 |
| MBE | 3.8 | 3.9 | 1.7 | 3.6 | 2.1 | 2.4 | 1.8 | 1.4 | 3.1 |
| ME | 10.2 | 10.6 | 4.6 | 9.6 | 5.6 | 6.6 | 4.8 | 3.8 | 8.4 |
| MPE | −2 | −3.4 | −4.6 | −1.5 | −0.9 | −4.3 | −0.7 | −2.4 | −3.7 |
| R2 | 0.56 | 0.48 | 0.56 | 0.65 | 0.68 | 0.63 | 0.78 | 0.68 | 0.71 |
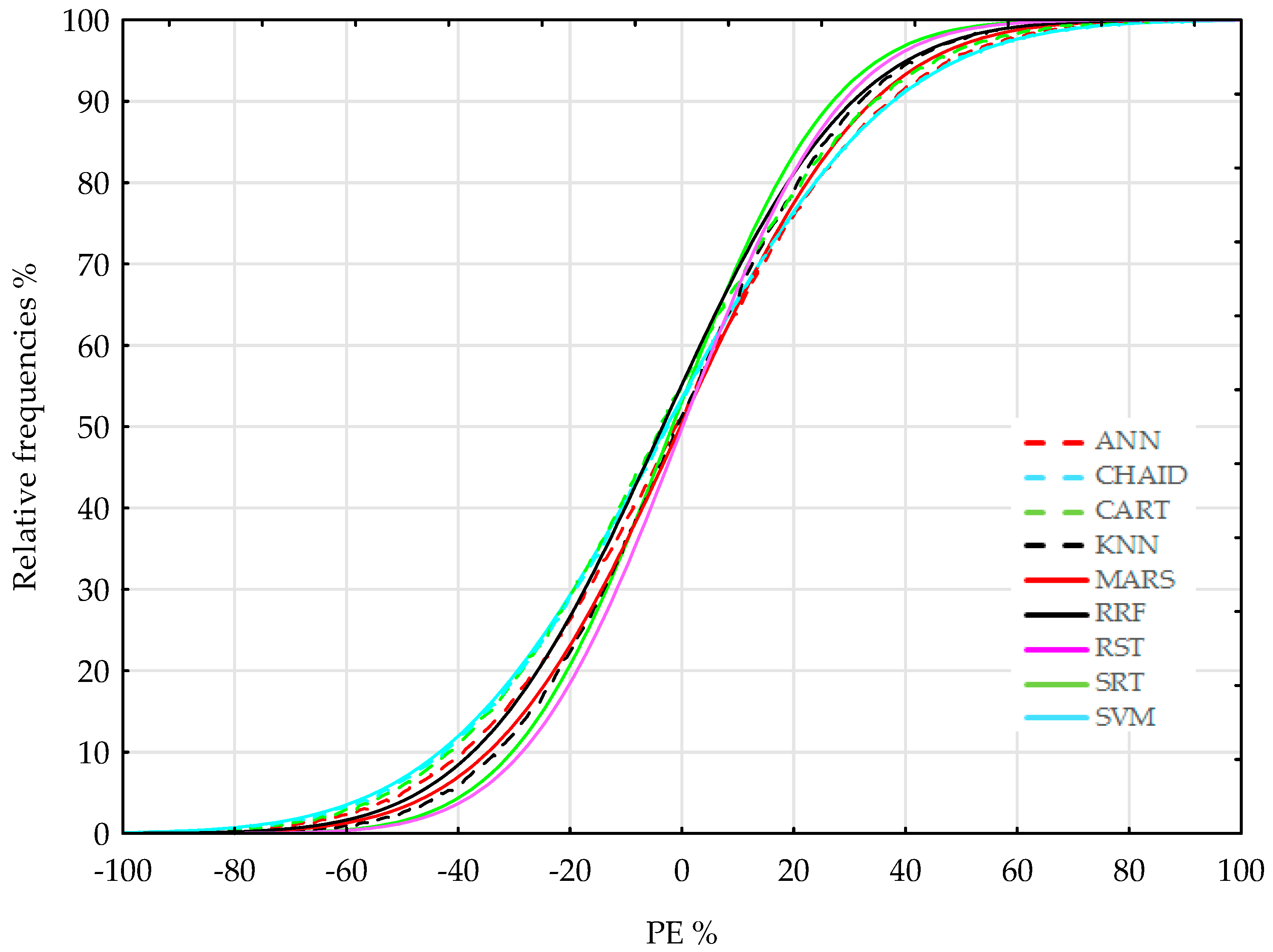
| 11 Variables | ANN | CHAID | CART | KNN | MARS | RRF | RST | SRT | SVM |
|---|---|---|---|---|---|---|---|---|---|
| CVRMSE | 19.2 | 26.3 | 21.4 | 20.2 | 19.1 | 20.4 | 19.6 | 16.5 | 21.5 |
| MAE | 38.2 | 54.8 | 42.6 | 41.3 | 29.4 | 41.3 | 38.3 | 32.8 | 44.6 |
| MAPE | 15.4 | 24.3 | 17.6 | 16.9 | 11.7 | 17.6 | 14.8 | 13.5 | 18.7 |
| MBE | 4.1 | 0.2 | 0.9 | 3.4 | 1.3 | 1.2 | 2.9 | 0.6 | 2.5 |
| ME | 10.9 | 0.6 | 2.5 | 9 | 3.5 | 3.2 | 7.7 | 1.6 | 6.8 |
| MPE | −0.9 | −7.9 | −4.1 | −1.4 | −0.9 | −5.2 | 0.4 | −2.7 | −3.1 |
| R2 | 0.79 | 0.57 | 0.72 | 0.76 | 0.78 | 0.76 | 0.77 | 0.83 | 0.72 |
| Relative Critical Percentages | Types of Forecasting Models | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ANN | CHAID | CART | KNN | MARS | RRF | RST | SRT | SVM | |
| Fi (%) SET I | 68 | 39 | 50 | 54 | 46 | 50 | 80 | 51 | 41 |
| Fi (%) SET II | 50 | 44 | 56 | 58 | 81 | 55 | 88 | 75 | 51 |
| Fi (%) SET III | 34 | 48 | 40 | 33 | 51 | 36 | 43 | 55 | 31 |
| SET III | SET III | SET III | SET II | SET I | SET II | |
|---|---|---|---|---|---|---|
| Relative critical percentages | SRT | MARS | CHAID | RST | RST | MARS |
| Fi (%) | 52.36 | 49.36 | 45.80 | 43.68 | 42.84 | 40.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nęcka, K.; Szul, T.; Piotrowska-Woroniak, J.; Pancerz, K. Assessment of Municipal Waste Forecasting Methods in Poland Considering Socioeconomic Aspects. Energies 2024, 17, 3524. https://doi.org/10.3390/en17143524
Nęcka K, Szul T, Piotrowska-Woroniak J, Pancerz K. Assessment of Municipal Waste Forecasting Methods in Poland Considering Socioeconomic Aspects. Energies. 2024; 17(14):3524. https://doi.org/10.3390/en17143524
Chicago/Turabian StyleNęcka, Krzysztof, Tomasz Szul, Joanna Piotrowska-Woroniak, and Krzysztof Pancerz. 2024. "Assessment of Municipal Waste Forecasting Methods in Poland Considering Socioeconomic Aspects" Energies 17, no. 14: 3524. https://doi.org/10.3390/en17143524
APA StyleNęcka, K., Szul, T., Piotrowska-Woroniak, J., & Pancerz, K. (2024). Assessment of Municipal Waste Forecasting Methods in Poland Considering Socioeconomic Aspects. Energies, 17(14), 3524. https://doi.org/10.3390/en17143524







