Data-Driven Distributionally Robust Optimization for Day-Ahead Operation Planning of a Smart Transformer-Based Meshed Hybrid AC/DC Microgrid Considering the Optimal Reactive Power Dispatch
Abstract
1. Introduction
| Ref. | Year | Type System | Type Problem | ST | PQ Power Dispatch | Uncertainties | DDDRO Approach | Solution Algorithm | Subproblem |
|---|---|---|---|---|---|---|---|---|---|
| [23] | 2018 | DS | OP | - | Y | PVG—DM | Y | - | - |
| [31] | 2018 | HMG | OP | - | - | PVG—DM | Y | C&CG | nested-C&CG |
| [32] | 2018 | DS | OP | Y | Y | - | - | PSO | - |
| [33] | 2018 | DS | OP | Y | Y | - | - | - | - |
| [27] | 2019 | TS | UC | - | - | WT—DM | Y | C&CG | DFD |
| [34] | 2019 | TS | UC | - | - | WT—DM | - | BD | DT |
| [29] | 2019 | MG | UC | - | - | WT | Y | C&CG | DFD |
| [35] | 2019 | DS | UC | - | - | WT—DM | - | BD | DT |
| [36] | 2019 | HMG | OP | - | - | PVG—DM | - | C&CG | DT |
| [37] | 2019 | TS | UC | - | - | WT | - | C&CG | DT |
| [26] | 2019 | TS | PL | - | - | WT—PVG | Y | C&CG | DT |
| [6] | 2020 | MG | OP | Y | Y | - | - | - | - |
| [38] | 2020 | MG | PL | - | Y | WT—PVG—DM | Y | - | DT |
| [28] | 2020 | MG | OP | - | Y | WT—PVG—DM | Y | C&CG | DFD |
| [12] | 2020 | DS | PL | - | Y | PVG—DM | Y | C&CG | DF |
| [39] | 2020 | MG | OP | Y | Y | - | - | GA | - |
| [40] | 2021 | TS | UC | - | - | WT—DM | Y | C&CG | DT |
| [41] | 2021 | TS | PL | - | Y | PVG | Y | C&CG | DT |
| [42] | 2021 | TS | UC | - | - | WT | Y | C&CG | DT |
| [8] | 2021 | DS | OP | Y | Y | - | - | - | - |
| [43] | 2021 | HMG | OP | Y | Y | - | - | - | - |
| [44] | 2021 | HMG | OP | Y | Y | - | - | GA | - |
| [45] | 2021 | HMG | OP | Y | Y | - | - | - | - |
| [46] | 2021 | HMG | OP | Y | - | - | - | GA | - |
| [47] | 2021 | HMG | OP | Y | Y | - | - | GA | - |
| [48] | 2021 | DS | PL | - | - | PVG—DM | - | C&CG | DT |
| [19] | 2021 | TS | OP | - | - | WT | Y | C&CG | DFD |
| [49] | 2022 | MG | OP | - | Y | EV—PVG | Y | C&CG | DT |
| [50] | 2022 | HMG | OP | Y | Y | WT—PVG—DM—EV | - | PSO | PSO |
| [51] | 2022 | DS | OP | - | Y | WT | Y | C&CG | DT |
| [52] | 2022 | HMG | OP | Y | - | - | - | - | - |
| [10] | 2023 | DS | OP | Y | Y | WT—PVG—DM—EV | - | PSO | - |
| [53] | 2023 | DS | OP | Y | Y | WT—PVG—DM—EV | - | PSO | - |
| [30] | 2023 | MG | OP | - | - | PVG—DM | Y | C&CG | DFD |
| Proposed | 2023 | HMG | OP | Y | Y | PVG—DM | Y | C&CG | DFD |
- ✓
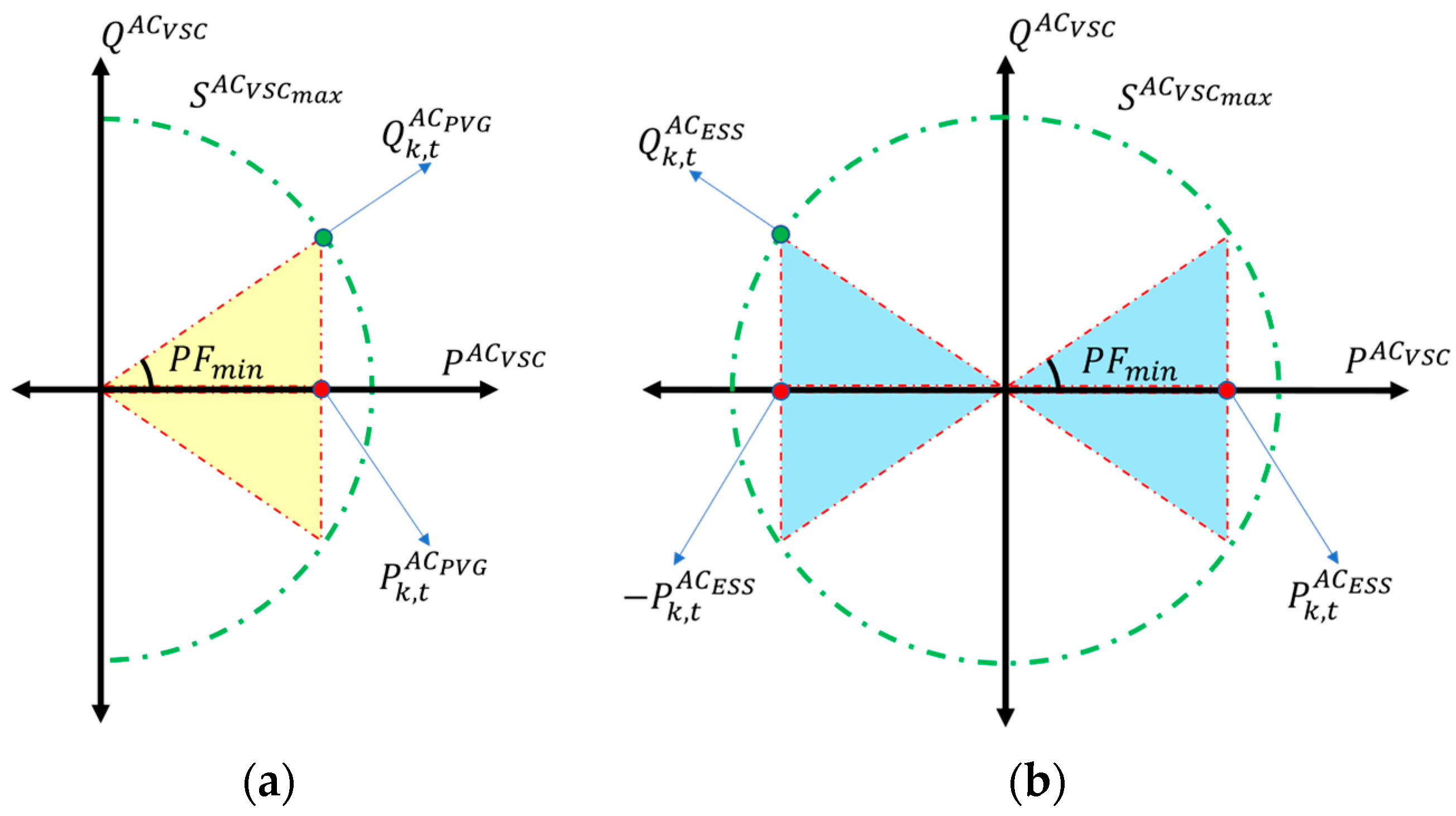
- An equivalent ST and Voltage-Sourced Converter (VSC) model is formulated to determine the impact of reactive power regulation from variable power factors on voltage deviation and loss minimization in a ST-based MHM in an optimal power-flow problem under uncertainty;
- ✓
- For day-ahead operation planning of the ST-based MHM, a DDDRO is proposed to consider the DG’s active and reactive power dispatch, the uncertainty of photovoltaic generators (PVGs), and demand;
- ✓
- A tri-level master–subproblem framework based on the DFD method and the C&CG algorithm is developed to solve the day-ahead operation planning of a ST-based MHM.
2. Deterministic Optimization Model
2.1. Constraints
2.1.1. Voltage-Sourced Converter
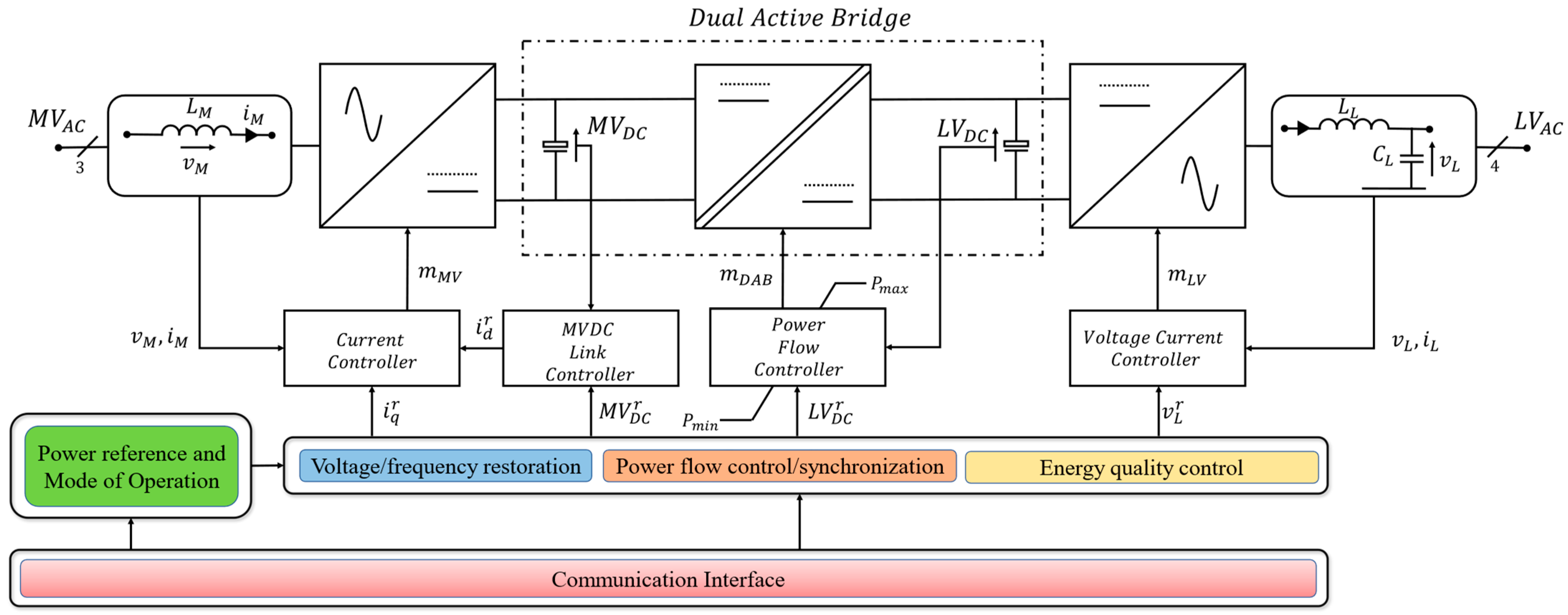
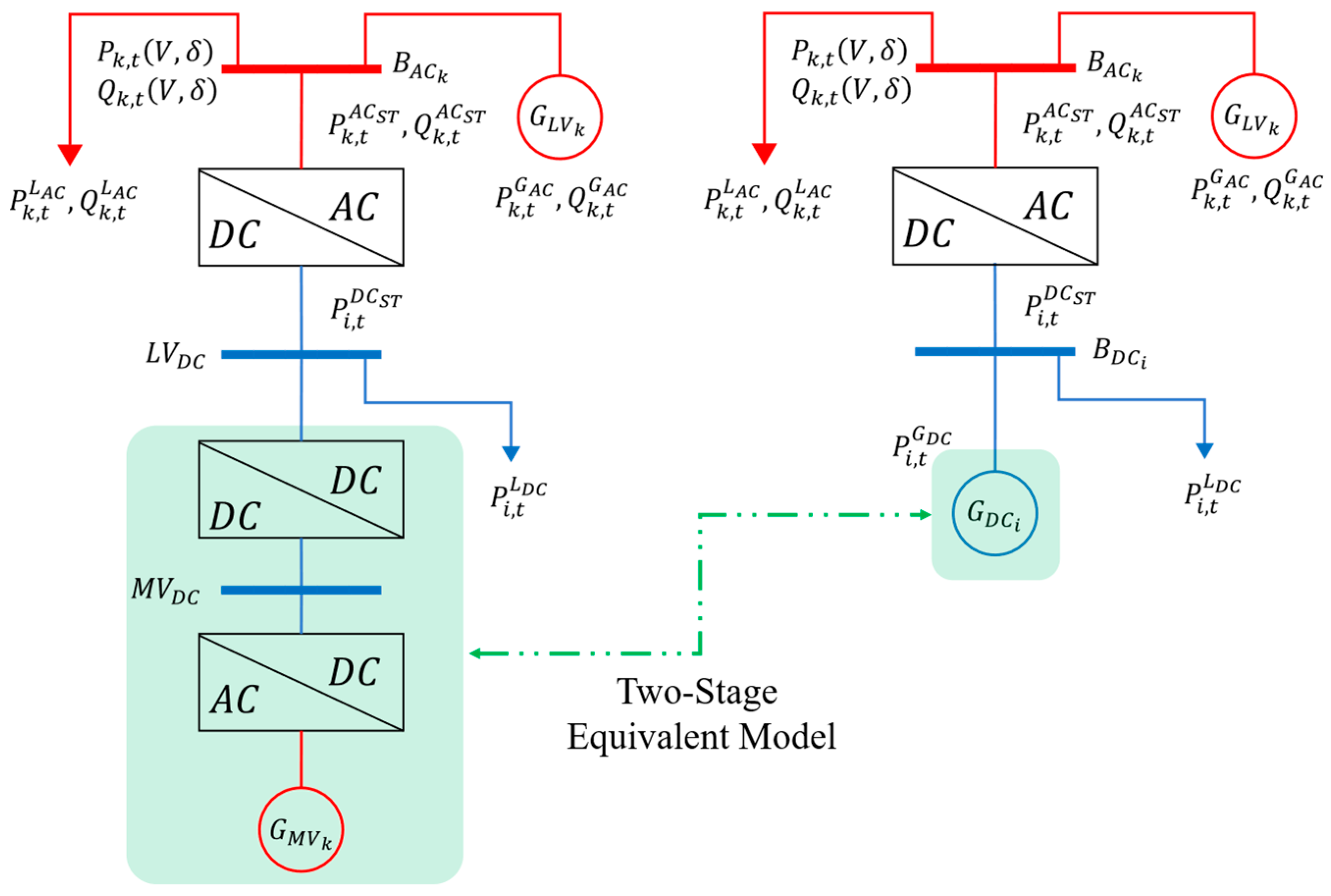
2.1.2. ST Equivalent Power-Flow Model
2.1.3. Battery Energy Storage System
2.1.4. Power-Flow Constraints
2.2. Objective Functions
2.3. Second-Order Cone Relaxation and Positive Octagonal Constraint Method
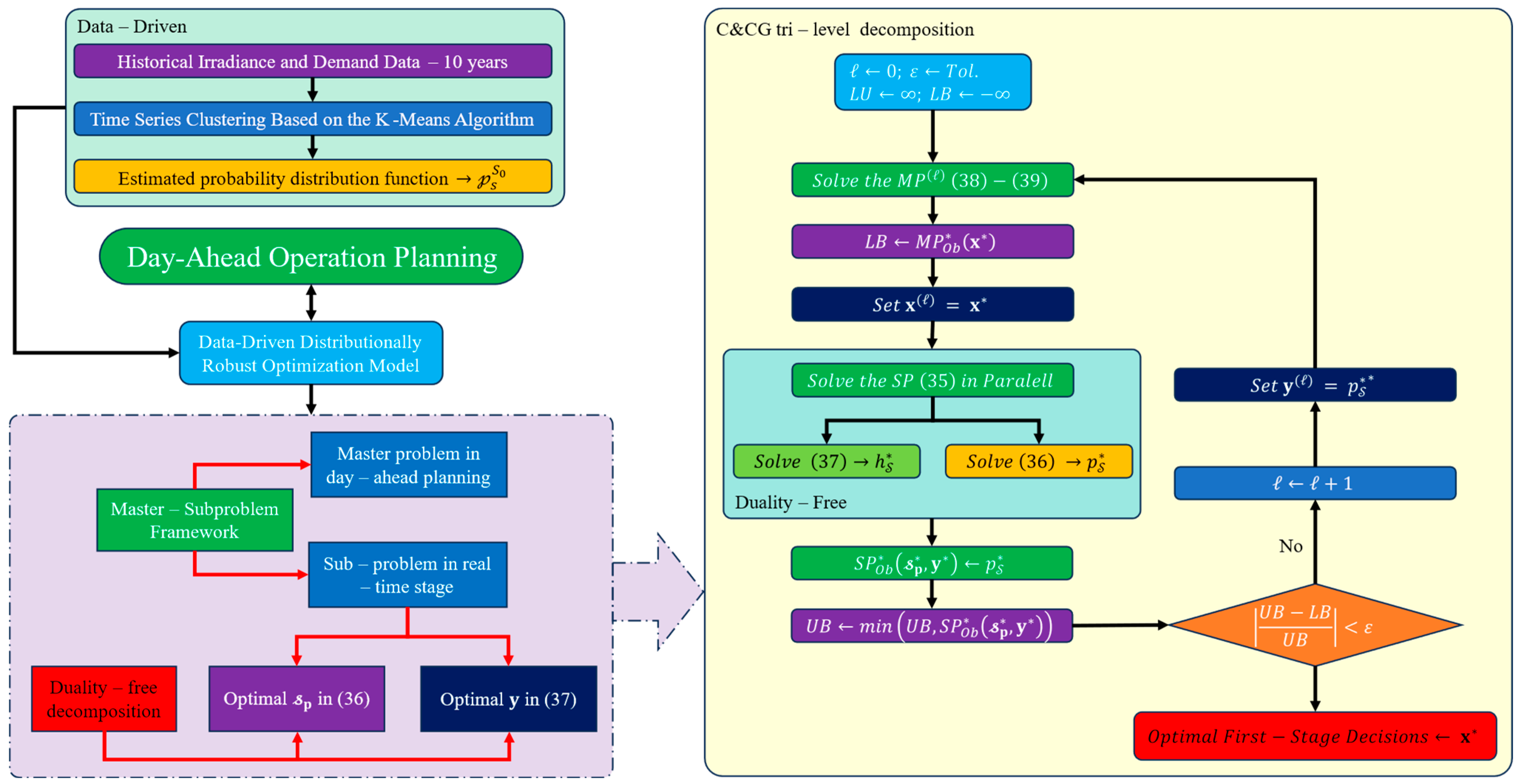
3. Modeling and Solution under Uncertainty by DDDRO
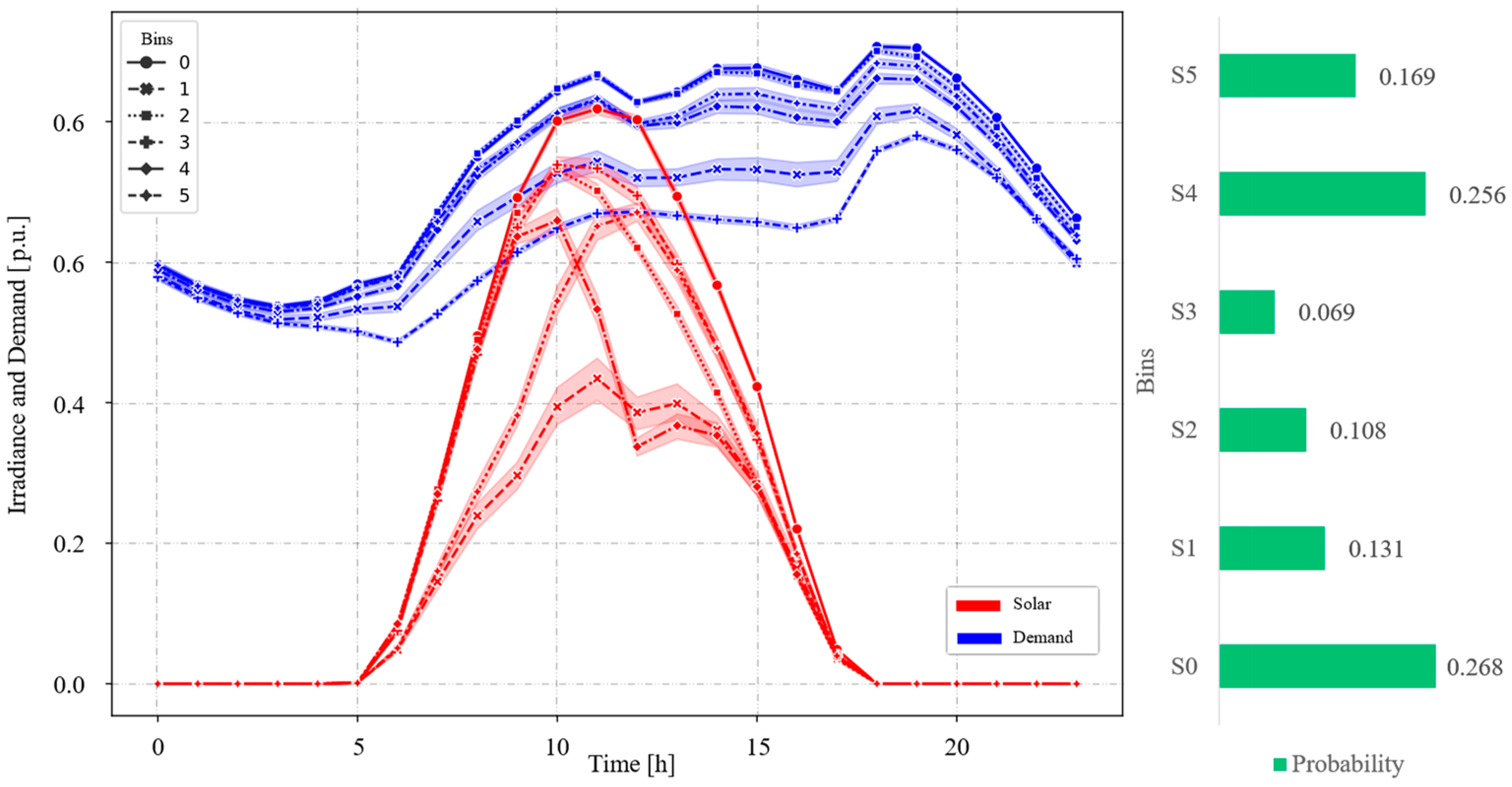
3.1. Ambiguity Set for Uncertainties
3.2. The Two-Stage Robust Optimization Model
3.3. Duality-Free Decomposition Method
3.3.1. Subproblem
3.3.2. Master Problem
4. Case Studies and Results
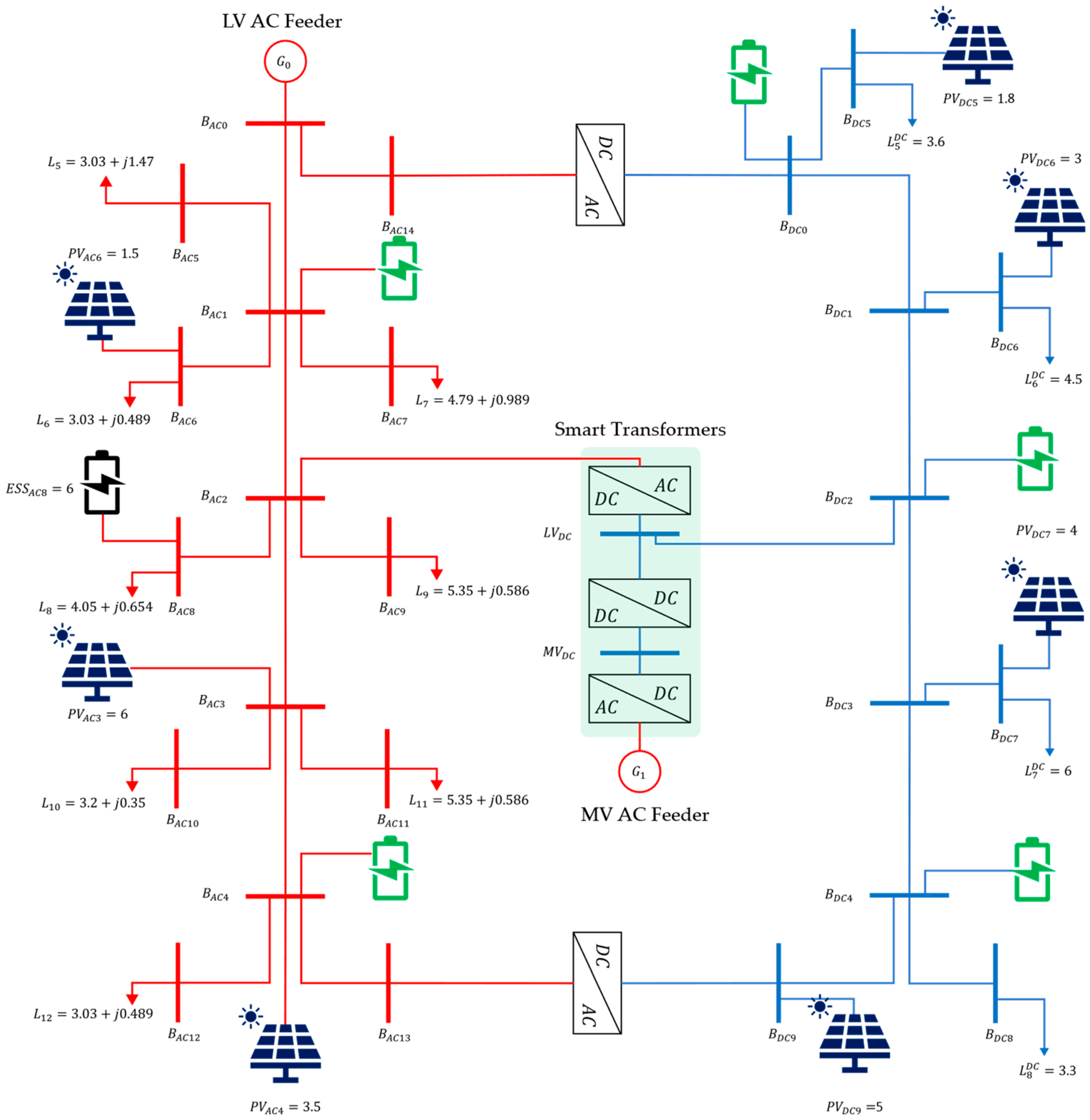
4.1. Benchmark Test System
4.2. Tests Cases and Results
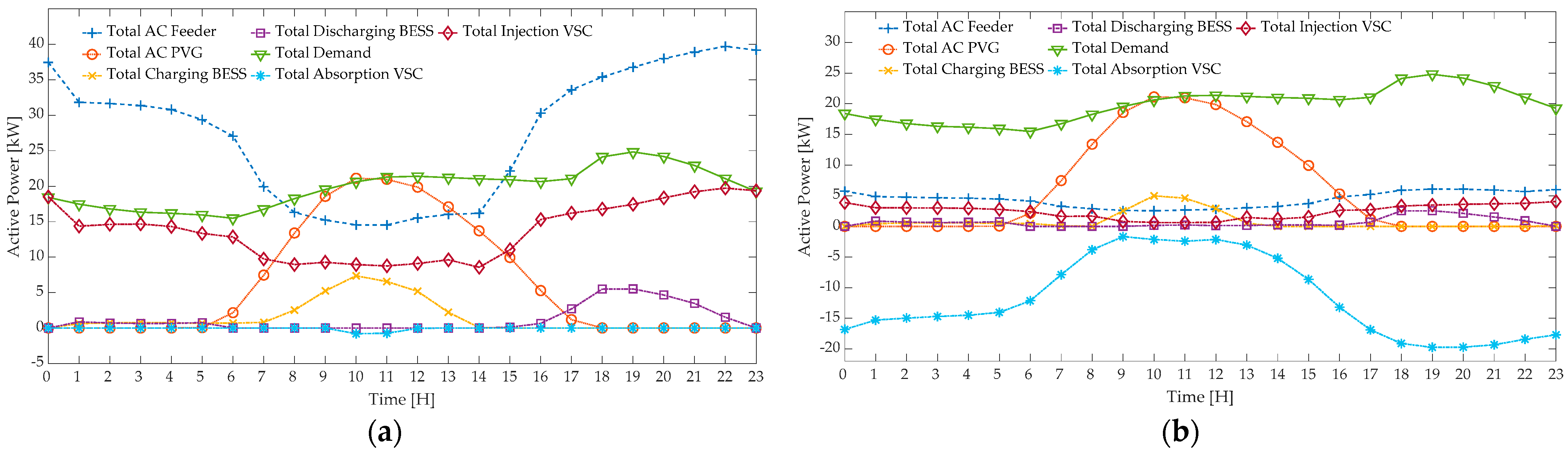
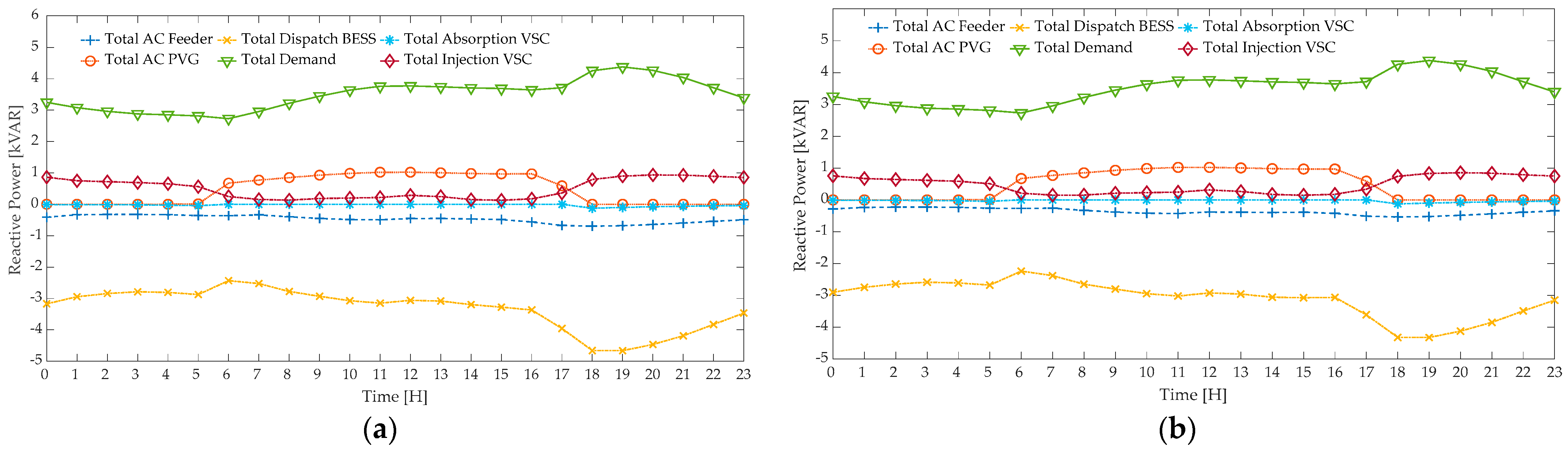
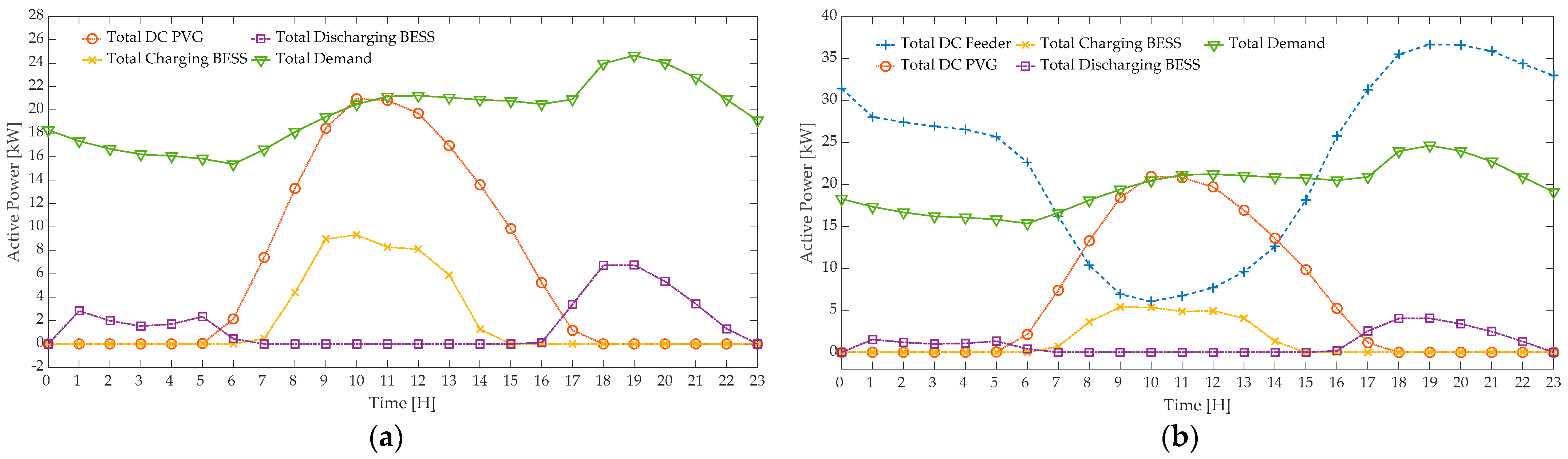
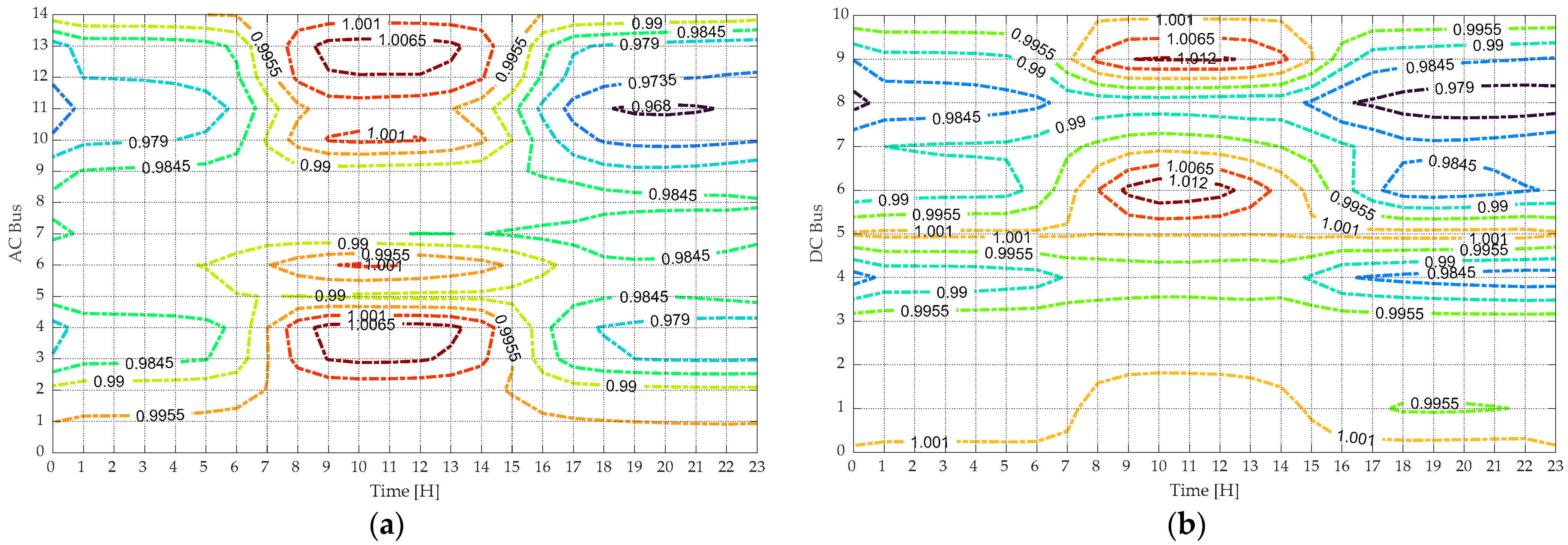
4.2.1. Case I
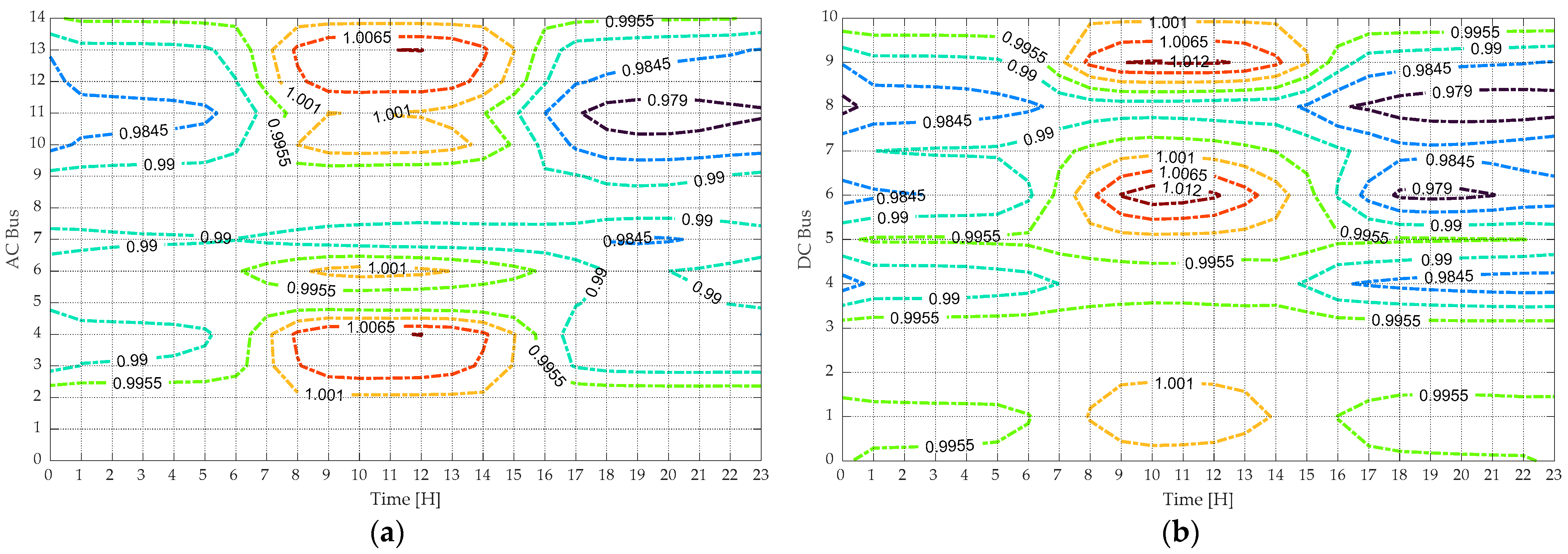
4.2.2. Case II
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| List of acronyms. | |
| Symbol | Meaning |
| BESS | Battery Energy Storage System |
| DG | Distributed Generation |
| MG | Microgrids |
| DER | Distributed Energy Resource |
| DS | Distribution System |
| HMG | Hybrid AC/DC Microgrid |
| IC | Interlinking Converter |
| MHM | ST-based Meshed Hybrid AC/DC Microgrid |
| ER | Energy Router |
| PEI | Power Electronic Interface |
| EMS | Energy Management System |
| SP | Stochastic Programming |
| RO | Robust Optimization |
| DDDRO | Data-Driven Distributionally Robust Optimization |
| C&CG | Column-and-Constraint Generation |
| BD | Bender’s Decomposition |
| DFD | Duality-Free Decomposition |
| TS | Transmission System |
| UC | Unit commitment |
| OP | Operation |
| PL | Planning |
| WT | Wind turbine |
| DM | Demand |
| EV | Electric vehicle |
| PSO | Particle Swarm Optimization |
| GA | Generic Algorithm |
| VSC | Voltage-Sourced Converter |
| PVG | Photovoltaic generators |
| SoC | State of charge |
| MPPT | Maximum Power Point Tracking |
| LFT | Low-frequency transformers |
| SOCP | Second-Order Cone Programming |
| E-PDF | Estimated probability distribution function |
| T-PDF | True probability distribution function |
| MP | Master problem |
| SP | Subproblem |
| UB | Upper bound |
| LB | Lower bound |
| List of symbols. | |
| Abbreviation | Meaning |
| Index for DC side | |
| Index for AC side | |
| Index for time | |
| Scenario index | |
| Low voltage on the AC side | |
| Low voltage on the DC side | |
| Voltage and phase on bus on AC side | |
| Bus on AC side | |
| Voltage at bus on DC side | |
| Bus on DC side | |
| VSC active power on AC side | |
| Active power of VSC on DC side | |
| Bidirectional power transfer losses | |
| Loss coefficient | |
| VSC’s reactive power | |
| VSC’s apparent power rating | |
| Active power of the BESS on the AC side | |
| Maximum active power BESS on AC side | |
| Reactive power of the BESS on the AC side | |
| PVG active power on AC side | |
| PVG reactive power on the AC side | |
| VAS phasing for a minimum power factor | |
| Minimum power factor | |
| DC generator | |
| Binary variable indicating charging | |
| Binary variable indicating discharging | |
| & | Efficiency of charging and discharging, respectively |
| State of charge | |
| Series admittance of the line | |
| Shunt susceptance on the AC side | |
| Conductance on DC side | |
| Active power through the AC line | |
| Reactive power through the AC line | |
| Objective function | |
| Operation cost | |
| Network losses | |
| Voltage deviation AC and DC side | |
| The respective weights of operational costs, network losses, and voltage deviations | |
| Costs of energy exchange with the main medium voltage grid and the operating costs of the BESS on both AC and DC sides | |
| The generator set, BESS set, PVG set, and load set on the AC and DC sides | |
| Demand profile | |
| Set scenarios | |
| Number of data bins | |
| Norm H-1 | |
| Norm H-Inf | |
| True probability distribution function | |
| Estimated probability distribution function | |
| Tolerance coefficients to define the confidence levels | |
| Sample size | |
| Confidence levels | |
| Probability error | |
| Decision variables of the first stage | |
| Decision variables of the third level in the second stage | |
| Decision variables of the second level in the second stage | |
| Convergence tolerance | |
References
- Judge, M.A.; Khan, A.; Manzoor, A.; Khattak, H.A. Overview of smart grid implementation: Frameworks, impact, performance and challenges. J. Energy Storage 2022, 49, 104056. [Google Scholar] [CrossRef]
- Chicco, G.; Ciocia, A.; Colella, P.; Di Leo, P.; Mazza, A.; Musumeci, S.; Spertino, F. Introduction—Advances and Challenges in Active Distribution Systems. In Planning and Operation of Active Distribution Networks; Lecture Notes in Electrical Engineering; Springer Science and Business Media Deutschland GmbH: Cham, Switzerland, 2022; Volume 826, pp. 1–42. [Google Scholar]
- Sahoo, S.K.; Sinha, A.K.; Kishore, N.K. Control Techniques in AC, DC, and Hybrid AC-DC Microgrid: A Review. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 738–759. [Google Scholar] [CrossRef]
- Debouza, M.; Al-Durra, A.; EL-Fouly, T.H.M.; Zeineldin, H.H. Survey on microgrids with flexible boundaries: Strategies, applications, and future trends. Electr. Power Syst. Res. 2022, 205, 107765. [Google Scholar] [CrossRef]
- Jia, L.; Zhu, Y.; Wang, Y. Architecture design for new AC-DC hybrid micro-grid. In Proceedings of the 2015 IEEE 1st International Conference on Direct Current Microgrids, ICDCM, Atlanta, GA, USA, 7–10 June 2015; pp. 113–118. [Google Scholar] [CrossRef]
- Zhu, R.; Liserre, M.; Langwasser, M.; Kumar, C. Operation and Control of Smart Transformer in Meshed and Hybrid Grids. IEEE Ind. Electron. Mag. 2020, 15, 43–57. [Google Scholar] [CrossRef]
- Kumar, C.; Gao, X.; Liserre, M. Smart Transformer Based Loop Power Controller in Radial Power Distribution Grid. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018. [Google Scholar] [CrossRef]
- Das, D.; Hrishikesan, V.M.; Kumar, C.; Liserre, M. Smart Transformer-Enabled Meshed Hybrid Distribution Grid. IEEE Trans. Ind. Electron. 2021, 68, 282–292. [Google Scholar] [CrossRef]
- Zhu, R.; de Carne, G.; Andresen, M.; Liserre, M. Control of Smart Transformer in Different Electric Grid Configurations. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019-ECCE Asia), Busan, Republic of Korea, 27–30 May 2019; pp. 1668–1675. [Google Scholar]
- Singh, A.; Maulik, A.; Maheshwari, A. Probabilistic multi-objective energy management of a distribution system considering reactive power injection by voltage source converters. Electr. Eng. 2023, 105, 2107–2136. [Google Scholar] [CrossRef]
- Guo, H.; Wang, F.; Luo, J.; Zhang, L. Review of energy routers applied for the energy internet integrating renewable energy. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1997–2003. [Google Scholar] [CrossRef]
- Gao, H.; Wang, R.; Liu, Y.; Wang, L.; Xiang, Y.; Liu, J. Data-driven distributionally robust joint planning of distributed energy resources in active distribution network. IET Gener. Transm. Distrib. 2020, 14, 1653–1662. [Google Scholar] [CrossRef]
- Wang, X.; Yang, W.; Liang, D. Multi-Objective Robust Optimization of Hybrid AC/DC Distribution Networks Considering Flexible Interconnection Devices. IEEE Access 2021, 9, 166048–166057. [Google Scholar] [CrossRef]
- Rangu, S.K.; Lolla, P.R.; Dhenuvakonda, K.R.; Singh, A.R. Recent trends in power management strategies for optimal operation of distributed energy resources in microgrids: A comprehensive review. Int. J. Energy Res. 2020, 44, 9889–9911. [Google Scholar] [CrossRef]
- Qiu, H.; Gu, W.; Liu, P.; Sun, Q.; Wu, Z.; Lu, X. Application of two-stage robust optimization theory in power system scheduling under uncertainties: A review and perspective. Energy 2022, 251, 123942. [Google Scholar] [CrossRef]
- Yang, J.; Su, C. Robust optimization of microgrid based on renewable distributed power generation and load demand uncertainty. Energy 2021, 223, 120043. [Google Scholar] [CrossRef]
- Claeys, S.; Vanin, M.; Geth, F.; Deconinck, G. Applications of optimization models for electricity distribution networks. Wiley Interdiscip. Rev. Energy Environ. 2021, 10, e401. [Google Scholar] [CrossRef]
- Zhang, Y.; Le, J.; Zheng, F.; Zhang, Y.; Liu, K. Two-stage distributionally robust coordinated scheduling for gas-electricity integrated energy system considering wind power uncertainty and reserve capacity configuration. Renew. Energy 2019, 135, 122–135. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Shu, S.; Zheng, F.; Huang, Z. A data-driven distributionally robust optimization model for multi-energy coupled system considering the temporal-spatial correlation and distribution uncertainty of renewable energy sources. Energy 2021, 216, 119171. [Google Scholar] [CrossRef]
- Zhao, C.; Guan, Y. Data-Driven Stochastic Unit Commitment for Integrating Wind Generation. IEEE Trans. Power Syst. 2016, 31, 2587–2596. [Google Scholar] [CrossRef]
- Li, P.; Song, L.; Qu, J.; Huang, Y.; Wu, X.; Lu, X.; Xia, S. A Two-Stage Distributionally Robust Optimization Model for Wind Farms and Storage Units Jointly Operated Power Systems. IEEE Access 2021, 9, 111132–111142. [Google Scholar] [CrossRef]
- Pinto, R.S.; Unsihuay-Vila, C.; Tabarro, F.H. Coordinated operation and expansion planning for multiple microgrids and active distribution networks under uncertainties. Appl. Energy 2021, 297, 117108. [Google Scholar] [CrossRef]
- Mieth, R.; Dvorkin, Y. Data-Driven Distributionally Robust Optimal Power Flow for Distribution Systems. IEEE Control. Syst. Lett. 2018, 2, 363–368. [Google Scholar] [CrossRef]
- Zeng, B.; Zhao, L. Solving two-stage robust optimization problems using a column-and-constraint generation method. Oper. Res. Lett. 2013, 41, 457–461. [Google Scholar] [CrossRef]
- Paredes, M.; Martins, L.S.A.; Soares, S.; Ye, H. Benders’ decomposition of the unit commitment problem with semidefinite relaxation of AC power flow constraints. Electr. Power Syst. Res. 2021, 192, 106965. [Google Scholar] [CrossRef]
- Wu, T.; Xie, K.; Hu, B.; Lu, H.; Ding, J.; Shen, W. Data-Driven Approach based Tri-Level Generation and Transmission Expansion Planning Model with High Wind Penetration. In Proceedings of the iSPEC 2019—2019 IEEE Sustainable Power and Energy Conference, Beijing, China, 21–23 November 2019; Volume 58, pp. 2607–2618. [Google Scholar] [CrossRef]
- Ding, T.; Yang, Q.; Liu, X.; Huang, C.; Yang, Y.; Wang, M.; Blaabjerg, F. Duality-Free Decomposition Based Data-Driven Stochastic Security-Constrained Unit Commitment. IEEE Trans. Sustain. Energy 2019, 10, 82–93. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, C.; Gong, K.; Si, R.; Shao, H.; Liu, W. Data-driven distributionally robust economic dispatch for distribution network with multiple microgrids. IET Gener. Transm. Distrib. 2020, 14, 5816–5822. [Google Scholar] [CrossRef]
- Ning, C.; You, F. Data-driven adaptive robust unit commitment under wind power uncertainty: A Bayesian nonparametric approach. IEEE Trans. Power Syst. 2019, 34, 2409–2418. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, T.; Liu, Y.; Feng, Y.; Wang, R.; Huang, S. Optimal design and operation of islanded multi-microgrid system with distributionally robust optimization. Electr. Power Syst. Res. 2023, 221, 109437. [Google Scholar] [CrossRef]
- Qiu, H.; Gu, W.; Pan, J.; Xu, B.; Xu, Y.; Fan, M.; Wu, Z. Multi-interval-uncertainty constrained robust dispatch for AC/DC hybrid microgrids with dynamic energy storage degradation. Appl. Energy 2018, 228, 205–214. [Google Scholar] [CrossRef]
- Syed, I.; Khadkikar, V.; Zeineldin, H.H. Loss Reduction in Radial Distribution Networks Using a Solid-State Transformer. IEEE Trans. Ind. Appl. 2018, 54, 5474–5482. [Google Scholar] [CrossRef]
- de Carne, G.; Buticchi, G.; Zou, Z.; Liserre, M. Reverse Power Flow Control in a ST-Fed Distribution Grid. IEEE Trans. Smart Grid 2018, 9, 3811–3819. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Y.; Ma, J.; Liu, X.; Wang, W. Two-Stage Robust Security Constrained Unit Commitment Considering the Spatiotemporal Correlation of Uncertainty Prediction Error. IEEE Access 2019, 7, 22891–22901. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Y.; Liu, X.; Wang, W. Two-Stage Robust Security-Constrained Unit Commitment Model Considering Time Autocorrelation of Wind/Load Prediction Error and Outage Contingency Probability of Units. IEEE Access 2019, 7, 25398–25408. [Google Scholar] [CrossRef]
- Qiu, H.; Gu, W.; Xu, Y.; Wu, Z.; Zhou, S.; Wang, J. Interval-Partitioned Uncertainty Constrained Robust Dispatch for AC/DC Hybrid Microgrids with Uncontrollable Renewable Generators. IEEE Trans. Smart Grid 2019, 10, 4603–4614. [Google Scholar] [CrossRef]
- Yuan, S.; Dai, C.; Guo, A.; Chen, W. A novel multi-objective robust optimization model for unit commitment considering peak load regulation ability and temporal correlation of wind powers. Electr. Power Syst. Res. 2019, 169, 115–123. [Google Scholar] [CrossRef]
- Dehghan, S.; Nakiganda, A.; Aristidou, P. A data-driven two-stage distributionally robust planning tool for sustainable Microgrids. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020. [Google Scholar] [CrossRef]
- Kumar, C.; Manojkumar, R.; Ganguly, S.; Liserre, M. Power Loss Minimization in Smart Transformer Based Meshed Hybrid Distribution Network. In Proceedings of the IECON 2020—The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 1670–1675. [Google Scholar] [CrossRef]
- Le, L.; Fang, J.; Zhang, M.; Zeng, K.; Ai, X.; Wu, Q.; Wen, J. Data-driven stochastic unit commitment considering commercial air conditioning aggregators to provide multi-function demand response. Int. J. Electr. Power Energy Syst. 2021, 129, 106790. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, L.; Cheng, H.; Liu, D.; Zhang, J.; Li, G. Data-driven distributionally robust transmission expansion planning considering contingency-constrained generation reserve optimization. Int. J. Electr. Power Energy Syst. 2021, 131, 106973. [Google Scholar] [CrossRef]
- Wang, C.; Gong, Z.; He, C.; Gao, H.; Bi, T. Data-Driven Adjustable Robust Unit Commitment of Integrated Electric-Heat Systems. IEEE Trans. Power Syst. 2021, 36, 1385–1398. [Google Scholar] [CrossRef]
- Hrishikesan, V.M.; Kumar, C. Operation of Meshed Hybrid Microgrid During Adverse Grid Conditions with Storage Integrated Smart Transformer. IEEE Open J. Ind. Electron. Soc. 2021, 2, 315–325. [Google Scholar] [CrossRef]
- Kumar, C.; Manojkumar, R.; Ganguly, S.; Liserre, M. Impact of Optimal Control of Distributed Generation Converters in Smart Transformer Based Meshed Hybrid Distribution Network. IEEE Access 2021, 9, 140268–140280. [Google Scholar] [CrossRef]
- Hrishikesan, V.M.; Kumar, C.; Liserre, M. An MVDC Based Meshed Hybrid Microgrid Enabled Using Smart Transformers. IEEE Trans. Ind. Electron. 2021, 69, 3722–3731. [Google Scholar] [CrossRef]
- Das, D.; Manojkumar, R.; Kumar, C.; Ganguly, S. Optimal Power Management for Islanded Operation of ST-based Meshed Hybrid LV Microgrid. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 183–188. [Google Scholar] [CrossRef]
- Kumar, C.; Manojkumar, R.; Ganguly, S. Optimal Placement of Smart Transformer Low Voltage Converter in Meshed Hybrid Distribution Network. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 1795–1800. [Google Scholar] [CrossRef]
- De Lara Filho, M.O.; Pinto, R.S.; De Campos, A.C.; Vila, C.U.; Tabarro, F.H. Day-ahead robust operation planning of microgrids under uncertainties considering DERs and demand response. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Conference—Latin America, ISGT Latin America 2021, Lima, Peru, 15–17 September 2021; Volume 15, pp. 1–5. [Google Scholar] [CrossRef]
- Feizi, M.R.; Khodayar, M.E.; Li, J. Data-driven distributionally robust unbalanced operation of distribution networks with high penetration of photovoltaic generation and electric vehicles. Electr. Power Syst. Res. 2022, 210, 108001. [Google Scholar] [CrossRef]
- Gupta, S.; Maulik, A.; Das, D.; Singh, A. Coordinated stochastic optimal energy management of grid-connected microgrids considering demand response, plug-in hybrid electric vehicles, and smart transformers. Renew. Sustain. Energy Rev. 2022, 155, 111861. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, Y.; Xie, S. Data-adaptive robust coordinated optimization of dynamic active and reactive power flow in active distribution networks. Renew. Energy 2022, 188, 164–183. [Google Scholar] [CrossRef]
- Das, D.; Kumar, C. Partial Startup Scheme for Smart Transformer in Meshed Hybrid Islanded Grid Operation. IEEE Trans. Ind. Appl. 2022, 58, 142–151. [Google Scholar] [CrossRef]
- Singh, A.; Maulik, A. Energy Management of an Active Distribution Network Considering Correlation Between Uncertain Input Variables. Arab. J. Sci. Eng. 2023, 48, 6377–6398. [Google Scholar] [CrossRef]
- Zhao, Q.; García-González, J.; Gomis-Bellmunt, O.; Prieto-Araujo, E.; Echavarren, F.M. Impact of converter losses on the optimal power flow solution of hybrid networks based on VSC-MTDC. Electr. Power Syst. Res. 2017, 151, 395–403. [Google Scholar] [CrossRef]
- Mohammadi, F.; Nazri, G.-A.; Saif, M. An Improved Mixed AC/DC Power Flow Algorithm in Hybrid AC/DC Grids with MT-HVDC Systems. Appl. Sci. 2019, 10, 297. [Google Scholar] [CrossRef]
- Núñez-Rodríguez, R.A.; Unsihuay-Vila, C.; Posada, J.; Pinzón-Ardila, O.; Aoki, A.R.; Bueno-Otto, R. Real-Time Testing Optimal Power Flow in Smart-Transformer-Based Meshed Hybrid Microgrids: Design and Validation. Energies 2024, 17, 1950. [Google Scholar] [CrossRef]
- Lachovicz, F.J.; Fernandes, T.S.P.; Junior, J.A.V. Impacts of PV-STATCOM Reactive Power Dispatch in the Allocation of Capacitors Bank and Voltage Regulators on Active Distribution Networks. J. Control. Autom. Electr. Syst. 2023, 34, 796–807. [Google Scholar] [CrossRef]
- Jeyapradha, R.B.; Rajini, V. Investigations on Service Extensions of Solid State Transformer. In Proceedings of the 2019 Fifth International Conference on Electrical Energy Systems (ICEES), Chennai, India, 21–22 February 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Jakka, V.N.; Acharya, S.; Anurag, A.; Prabowo, Y.; Kumar, A.; Parashar, S.; Bhattacharya, S. Protection design considerations of a 10 kV SiC MOSFET enabled mobile utilities support equipment based solid state transformer (muse-SST). In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 5559–5565. [Google Scholar] [CrossRef]
- Zhu, R.; Andresen, M.; Langwasser, M.; Liserre, M.; Lopes, J.P.; Moreira, C.; Rodrigues, J.; Couto, M. Smart transformer/large flexible transformer. CES Trans. Electr. Mach. Syst. 2021, 4, 264–274. [Google Scholar] [CrossRef]
- Zhu, R.; Buticchi, G.; Liserre, M. Investigation on Common-Mode Voltage Suppression in Smart Transformer-Fed Distributed Hybrid Grids. IEEE Trans. Power Electron. 2018, 33, 8438–8448. [Google Scholar] [CrossRef]
- González-Castellanos, A.; Pozo, D.; Bischi, A. Distribution System Operation with Energy Storage and Renewable Generation Uncertainty. In Handbook of Optimization in Electric Power Distribution Systems; Resener, M., Rebennack, S., Pardalos, P.M., Haffner, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 69–120. [Google Scholar]
- Pinto, R.S. Computational Models for Expansion Planning of Electric Power Distribution Systems Containing Multiple Microgrids and Distributed Energy Resources under Uncertainties. Ph.D. Thesis, Universidade Federal do Paraná, Curitiba, Brazil, 2022. [Google Scholar]
- Bernal, D.E.; Chen, Q.; Gong, F.; Grossmann, I.E. Mixed-Integer Nonlinear Decomposition Toolbox for Pyomo (MindtPy). Comput. Aided Chem. Eng. 2018, 44, 895–900. [Google Scholar] [CrossRef]
- XM. Curva de Demanda Promedio en Colombia. 2019. Available online: https://sinergox.xm.com.co/dmnd/Paginas/Informes/DemandaRealPerdidas.aspx (accessed on 15 April 2023).
- SolarCast Historical and TMY. Time Series. 2022. Available online: https://toolkit.solcast.com.au/historical (accessed on 15 April 2023).
- Strunz, K.; Abbey, C.; Andrieu, C.; Campbell, R.C.; Fletcher, R. Benchmark Systems for Network Integration of Renewable and Distributed Energy Resources—TF C6.04.02. 2014. Available online: https://www.e-cigre.org/publications/detail/575-benchmark-systems-for-network-integration-of-renewable-and-distributed-energy-resources.html (accessed on 15 April 2023).
- Zhang, M.; Ai, X.; Fang, J.; Yao, W.; Zuo, W.; Chen, Z.; Wen, J. A systematic approach for the joint dispatch of energy and reserve incorporating demand response. Appl. Energy 2018, 230, 1279–1291. [Google Scholar] [CrossRef]
- Goerigk, M.; Khosravi, M. Optimal scenario reduction for one- and two-stage robust optimization with discrete uncertainty in the objective. Eur. J. Oper. Res. 2023, 310, 529–551. [Google Scholar] [CrossRef]

| Cases | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Case I | 661.84 | −11.35 | 0 | 34.21 | 27.64 | 46.69 | 37.82 | 11.45 | −79.50 |
| Case II | 105.58 | −8.75 | 552.36 | 18.89 | 15.30 | 30.30 | 24.54 | 10.60 | −74.12 |
| Case | Operation Cost [USD/kW] | Losses [kW] | Deviation Voltage AC [p.u.] | Deviation Voltage DC [p.u.] | BESS’s Cost [USD/kW] |
|---|---|---|---|---|---|
| Case I | 66,184.54 | 14.26 | 0.07031 | 0.02327 | 15.49334 |
| Case II | 65,795.18 | 10.37 | 0.03279 | 0.02527 | 8.76482 |
| Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | Test 6 | |
|---|---|---|---|---|---|---|
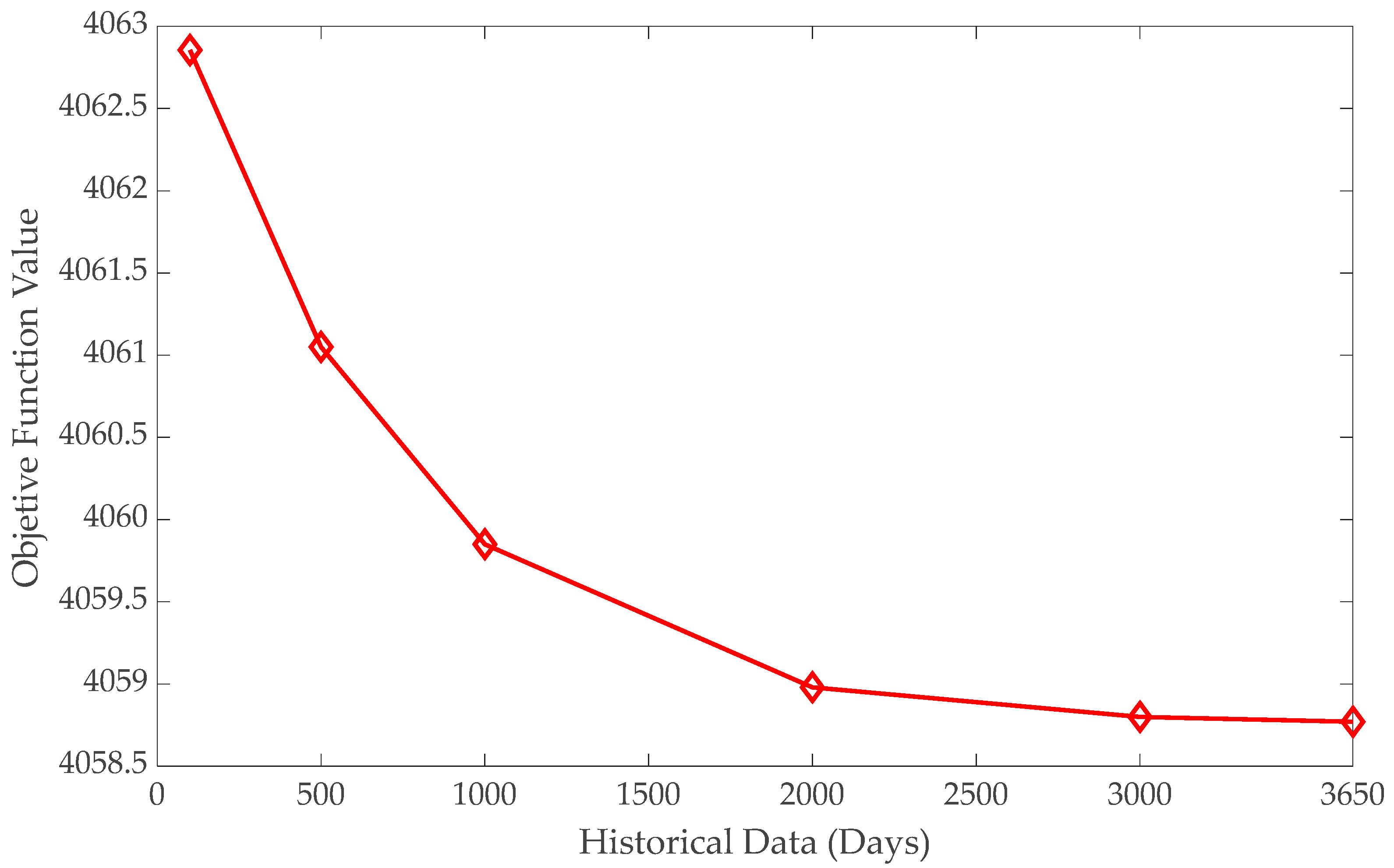
| Size sample (days) | 100 | 500 | 1000 | 2000 | 3000 | 3650 |
| Objective function | 4062.856 | 4061.05 | 4059.85 | 4058.98 | 4058.8 | 4058.77 |
| 0.5 | 0.8 | 0.99 | |
|---|---|---|---|
| 0.5 | 4057.22 | 4058.40 | 4058.35 |
| 0.8 | 4057.21 | 4058.03 | 4058.55 |
| 0.99 | 4057.22 | 4058.40 | 4058.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Núñez-Rodríguez, R.A.; Unsihuay-Vila, C.; Posada, J.; Pinzón-Ardila, O. Data-Driven Distributionally Robust Optimization for Day-Ahead Operation Planning of a Smart Transformer-Based Meshed Hybrid AC/DC Microgrid Considering the Optimal Reactive Power Dispatch. Energies 2024, 17, 4036. https://doi.org/10.3390/en17164036
Núñez-Rodríguez RA, Unsihuay-Vila C, Posada J, Pinzón-Ardila O. Data-Driven Distributionally Robust Optimization for Day-Ahead Operation Planning of a Smart Transformer-Based Meshed Hybrid AC/DC Microgrid Considering the Optimal Reactive Power Dispatch. Energies. 2024; 17(16):4036. https://doi.org/10.3390/en17164036
Chicago/Turabian StyleNúñez-Rodríguez, Rafael A., Clodomiro Unsihuay-Vila, Johnny Posada, and Omar Pinzón-Ardila. 2024. "Data-Driven Distributionally Robust Optimization for Day-Ahead Operation Planning of a Smart Transformer-Based Meshed Hybrid AC/DC Microgrid Considering the Optimal Reactive Power Dispatch" Energies 17, no. 16: 4036. https://doi.org/10.3390/en17164036
APA StyleNúñez-Rodríguez, R. A., Unsihuay-Vila, C., Posada, J., & Pinzón-Ardila, O. (2024). Data-Driven Distributionally Robust Optimization for Day-Ahead Operation Planning of a Smart Transformer-Based Meshed Hybrid AC/DC Microgrid Considering the Optimal Reactive Power Dispatch. Energies, 17(16), 4036. https://doi.org/10.3390/en17164036






