Abstract
Porosity assessment is a vital component for reservoir evaluation in the oil and gas sector, and with technological advancement, reliance on conventional methods has decreased. In this regard, this research aims to reduce reliance on well logging, purposing successive machine learning (ML) techniques for precise porosity measurement. So, this research examines the prediction of the porosity curves in the Sui main and Sui upper limestone reservoir, utilizing ML approaches such as an artificial neural networks (ANN) and fuzzy logic (FL). Thus, the input dataset of this research includes gamma ray (GR), neutron porosity (NPHI), density (RHOB), and sonic (DT) logs amongst five drilled wells located in the Qadirpur gas field. The ANN model was trained using the backpropagation algorithm. For the FL model, ten bins were utilized, and Gaussian-shaped membership functions were chosen for ideal correspondence with the geophysical log dataset. The closeness of fit (C-fit) values for the ANN ranged from 91% to 98%, while the FL model exhibited variability from 90% to 95% throughout the wells. In addition, a similar dataset was used to evaluate multiple linear regression (MLR) for comparative analysis. The ANN and FL models achieved robust performance as compared to MLR, with R2 values of 0.955 (FL) and 0.988 (ANN) compared to 0.94 (MLR). The outcomes indicate that FL and ANN exceed MLR in predicting the porosity curve. Moreover, the significant R2 values and lowest root mean square error (RMSE) values support the potency of these advanced approaches. This research emphasizes the authenticity of FL and ANN in predicting the porosity curve. Thus, these techniques not only enhance natural resource exploitation within the region but also hold broader potential for worldwide applications in reservoir assessment.
1. Introduction
Porosity examination is crucial in the comprehensive estimation of rock formations for accurate assessment [1]. It characterizes the storage capacity for oil and natural gas in the proposed zone [2]. In this regard, earth science exploration encounters obstacles as a consequence of uncertainties, errors, and unproven associations between datasets in geophysical logs [3,4,5]. These challenges are deep-rooted in matters like inadequate logging in long-standing boreholes, imprecisions in estimations owing to hole circumstances, and technical glitches that lead to unreliable log suites [6,7,8]. Hence, the current research scrutinized the fuzzy logic (FL) approach utilizing Gaussian-shaped membership functions and the artificial neural network (ANN) method to achieve precise prediction and analysis of the porosity curve among five well log dataset. Machine learning (ML) methods like federated learning (FL) and ANN have been demonstrated to be competent in handling intricate challenges exemplified via environmental impulsiveness and evidence uncertainty [9,10,11]. The current research makes a substantial contribution by producing a porosity curve from the well log dataset. Furthermore, it examines how an ML technique can efficiently evaluate hydrocarbon-bearing reservoir parameters in the absence of a core dataset [12,13]. Earlier research has implicated forecasting the porosity curve, exploring the appropriateness of ANN and FL procedures in the Fahlian limestone reservoir in Iran, utilizing DT, GR, NPHI, and RHOB well logs [14]. Wood, David A. documented that ANN trained with the DT log and the GR log was capable of predicting porosity cure [15].
ML practices in recent times have delivered real solutions for several operational and predictive tasks across the oil and gas sector, encompassing areas, for instance, drilling, reservoir performance, and geo-mechanical assessment [16,17,18]. ML tactics excel in addressing problems exhibited by numerous variables, nonlinear relations, and complicated dispersions of values [19,20,21]. FL and ANN, mainly rooted in regression relationships, have confirm extremely effective in considerably enhancing the accuracy of predicting variables related to the oil and gas sector [22].
FL is a logic system proficient to understand values over true either false [23,24]. Cuddy presented FL concepts for both estimating as well as predicting output curves employing a chosen set of input curves [25]. Furthermore, FL was applied in the calculation of reservoir rock properties [26]. Saggaf utilized fuzzy logic (FL) in predicting lithofacies and applying it to geological circumstances via well logs [27]. A further inclusive exploration of FL within the oil and gas area was presented by Modestus Okechukwu [28].
The ANN algorithm exploits several basic calculation units referenced as neurons [29]. Every neuron process inbounds data and generates an output, establishing acquaintances with different neurons within the network [30]. The practice of ANN is meticulously recognized in numerous studies [31,32,33]. ANN could fabricate models on the basis of multidimensional, nonlinear, as well as intricate data, discovering various applications in the examination of data from fields, industries, and laboratories [34]. ANN have been trained for the recognitions of zones, facies assessment, as well as the valuation of porosity and permeability [35]. Applying geophysical well logs, predictions of rock features have been productively attained through ANN, neuro-fuzzy models, as well as knowledge-based tactics [36].
Several scholars have undertaken extensive efforts to evaluate the Sui main and Sui upper limestone reservoir in the Middle Indus Basin of Pakistan [37,38]. These efforts include petrophysical analysis, seismic interpretation, exploration of geophysical aspects, static reservoir modeling, deliberations of tectonics, and the investigation of many structural styles [39,40]. Nonetheless, the vigorous predictive techniques of FL and ANN have not yet been implemented in the present research area in favor of reservoir modeling applying geophysical log. To expand reservoir classification, this research uses FL and ANN to create an advanced porosity curve. The curve was established by applying four input logs, which includes DT, NPHI, RHOB and GR. The research also examines the impact of input features and the authenticity of well logs. The outcomes gained from the FL as well as ANN were correlated with the coefficient of determination (R2) resulting from the MLR for the resemblance. The robust performance of ANN and FL in the present research emphasizes their pivotal role in optimizing porosity curve prediction, offering a promising direction for advancing hydrocarbon exploration and exploitation techniques on a global scale.
2. Geologic Setting and Stratigraphy
The Indus Basin in Pakistan stands out as among the most extensive basins formed by the Himalayan tectonic event [41,42,43,44]. It is partitioned into three distinct sections, namely, the Upper Indus Basin, Middle Indus Basin, and Lower Indus Basin, each delineated by its structural characteristics, depositional environments, and geological compositions, as shown in Figure 1 [45,46]. The current research area is positioned in the Middle Indus Basin (MIB). The Qadirpur region’s source rocks comprise the Sember shale, Mughalkot shale, and Ranikot shale [47]. Moreover, the Sirki Formation was scrutinized for its potentiality as a source. In Pakistan, nowhere else the Sui Main Limestone is detected. The Pirkoh as well as Habib Rahi Limestones are contemplated secondary reservoirs, whereas the key reservoir and gas source is ascribed to the Sui Main Limestone and Sui Upper Limestone, correspondingly [47]. The cap rock within the current study consists of Gazij shale and Sirki shale, as shown in Figure 2. The Indian Shield is positioned east of the Middle Indus Basin, with the borderline of the Indian Plate to the west and the Sukkar Rifle originates from the south [48,49]. The prime tectonic activity formatting the structural drifts and sedimentary shapes in the Middle Indus Basin, from Jurassic to Early Cretaceous, corresponds to the Indian plate’s separation from Gondwanaland [50]. Aside from rifting, the creation of a new ocean caused isostatic uplift along its borders, resulting in uplift and slanting to the east during the early Cretaceous period. During this period, the dynamic movement of Cretaceous plate tectonics could have instigated sinistral strike-slip faulting, as well as the emergence of hot spots and thermal doming lengthwise to the boundary among Madagascar and Indian plate [51]. Subsequently, uplift occurred within the Deccan flood basalts along with NNW striking normal faults [37].
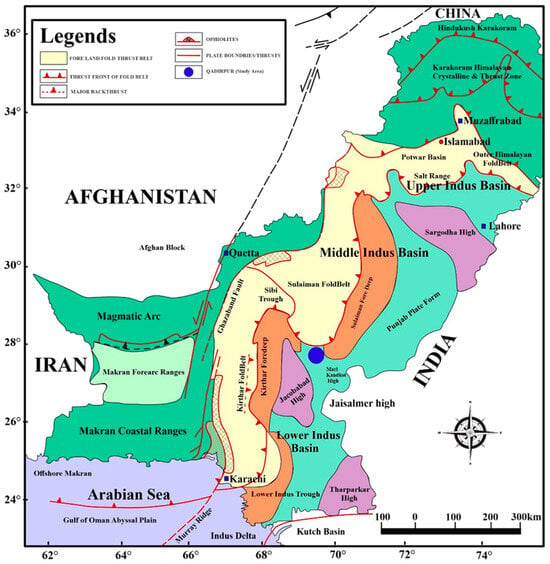
Figure 1.
Geological map of the preset study area.
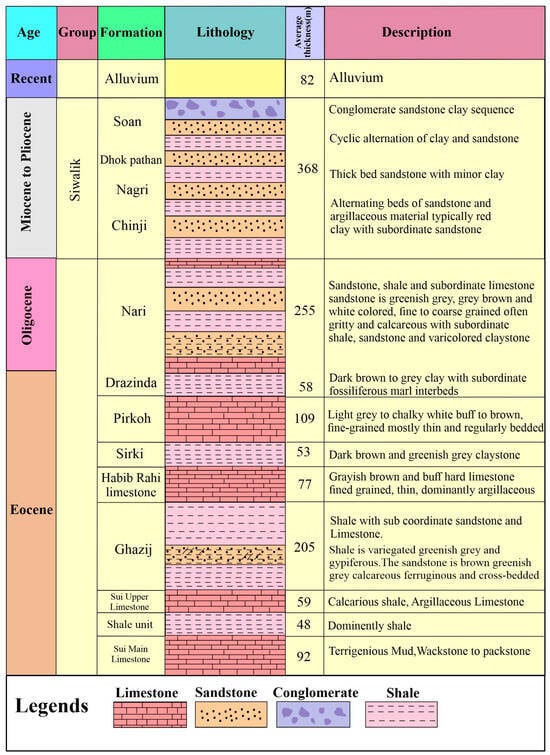
Figure 2.
Stratigraphic chart of the Middle Indus basin.
The impact of the Himalayas during the Oligocene period and up to the current time proceeded in sinistral transgression in the western zone of the MIB. This collision led to the surprinting of fold-thrust characteristics with sinistral flower features [52]. The principal structural forces in the area were the inclining fault blocks across the horst–graben morphological pattern. The geological as well as tectonic procedures in MIB could be considered to pre-separation and post-separation epochs [53]. Prior to the parting of the Indian peninsula from Gondwanaland, it remained a portion of this supercontinent. The Afghanistan–Iranian geological units separated from Gondwanaland amidst the Triassic period. Mesozoic sedimentation happened in the platform area, with disruptions in sedimentation resulting after the displacement of orogenic plates [47]. Facies dissimilarities within the MIB are largely controlled by three elements: tectonic motion, sea level vacillations, and sedimentation rates, documented in descending command of significance [54]. In the examined region, rifting triggered rapid marine transgression, influencing marine sedimentation. The Paleocene era trails the incidence of tectonic events within the Sulaiman Fold Belt [55]. During the Eocene epoch, a geological period characterized by substantial tectonic activity, a succession of thrust faults developed along the eastern perimeter of the Sulaiman region. These faults, revealing strong geological forces, extended further southward, crossing over the Marri-Bugti sector. The disruption of the Indian plate and the tectonic events exerted by the Afghan block culminated in the creation of the Sulaiman-Foredeep [56]. The stable unit of the Punjab Platform is placed within the eastern zone of the Sulaiman-Foredeep.
3. Materials and Methods
The porosity curve was predicted by employing well logs from five boreholes (QGF-03, 11, 15, 16, and 17) over the formulation of ANN and FL approaches (Figure 3). The systematic workflow is presented in Figure 4, which summarizes the procedure for assessing the efficacy of ANN and FL in predicting the porosity curve.
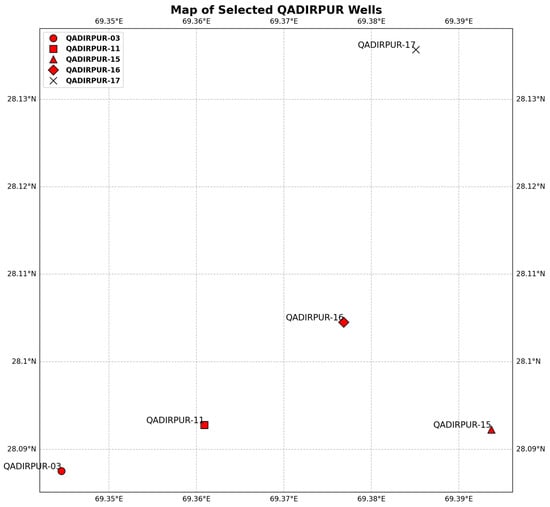
Figure 3.
Base map of the Qadirpur gas field demonstrating well locations.
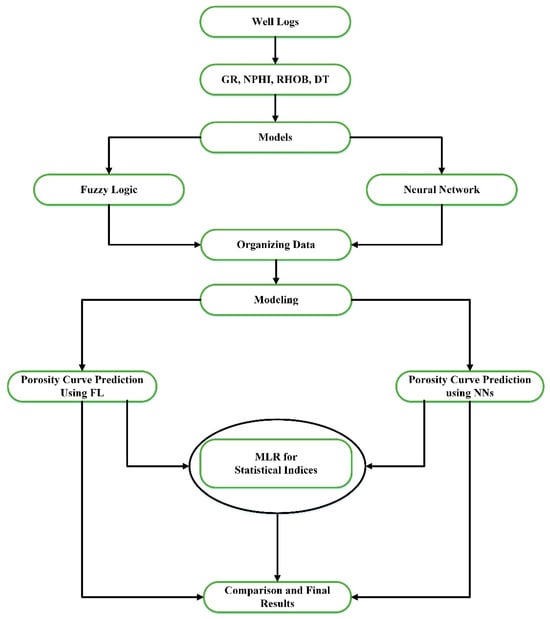
Figure 4.
Workflow for NNs and FL modeling for porosity curve prediction.
3.1. Input Curves and Their Descriptions
The prediction of porosity cure contained the usage of four input well log curves: sonic, density, gamma-ray, and neutron log. The gamma ray log defined electromagnetic radiation originated inherently via radioactive materials existing within rock formations, for instance, thorium, uranium, as well as potassium [57,58]. The intrinsic radioactivity of rocks was resolute by its arrangement, assisting as an indication for the depositional setting as well as paragenesis of rock formations [59,60]. Rocks that had a higher clay content often manifest the highest gamma-ray value [61]. GR logs sake valuable claims in defining lithology, discriminating among shale and sand intervals, and estimating shaliness association between wells [62,63]. The neutron log utilized the neutron device, operational on the framework in which the radioactive causes constantly discharged maximum energy neutrons [64]. These neutrons loss energy when they collided with nuclei of similar mass for instance, hydrogen atoms [65]. When water or hydrocarbons are present within the formation, along with porosity of the rock and presuming a full fluid saturation, resulted neutrons diminish the pace, resulting in energy loss [66].
The density log, utilized for elucidating lithology and classifying areas with oil or gas depended on the gamma-ray dispersal impression within a formation comprehending the radioactive emitter [67]. It evaluated the replicated (Compton scattered) gamma rays, supplying information about the formation’s density and helping as a key predictor of the porosity curve [68]. Precise determination of porosity was enabled by determining the density of the matrix [69]. The DT log measured the time occupied by an acoustic pulse aimed to navigate a rock configuration [70]. The DT log is supported in assessing the porosity as well as secondary porosity of non-clastic reservoirs [71]. When composite with the density log or neutron log, the sonic log was exploited to determine lithology [72]. Moreover, it is employed in building synthetic seismograms and developing the connection among well data and seismic data.
3.2. The Artificial Neural Network (ANN)
ANN and FL approaches have uncovered widespread applications in ML across geological sciences [73]. The fundamental ANN is comprised of an input layer, an output layer, as well as additional hidden layers [74]. The initial layer comprised unrefined data, which is specified to the network, and the values in this layer remained unchanged [74]. Each input to the system was replicated and supplied to the nodes in the hidden layer. The hidden layer obtained data from the input layer, altering those with explicit weight values to yield new values [75]. These recently obtained values are then conveyed to the output layer. Afterward, the output layer operated the data acquired from the hidden layer and created the ultimate output. The data operated for evaluating the ANN were characterized among three sets: training, validation, and testing. Data for training encompassed altering the interior structure of the network, whereas validation involved evaluating the network’s performance throughout its training segment. A testing dataset was employed to assess the reliable potency of the trained network. To lessen errors and accomplish optimal output, ANN training was carried out on reservoir zones across each iteration showing a training sequence for the ANN. An epoch, or training cycle, encompasses displaying all the training datasets onto the network across the training progression [76]. The term “epochs as per step” states the frequency at which the training data are strained from the training sets and fed throughout the ANN across every training session. To validate the training results, the dataset endured K-fold cross-validation [77]. In the current study, both random subsampling as well as K-fold cross-validation approaches were applied to increase the robustness of the porosity curve prediction and decrease uncertainty. The existing dataset comprised numerous wells, which were arbitrarily divided into a 70% training dataset and a 30% testing dataset. To avoid overfitting and assess multiple candidate ML models, K-fold cross-validation was applied, with a four-fold size selected to resemble the number of samples in the final valuation testing set. Figure 5 demonstrates the overall ML workflow, including the implemented K-fold cross-validation procedure.
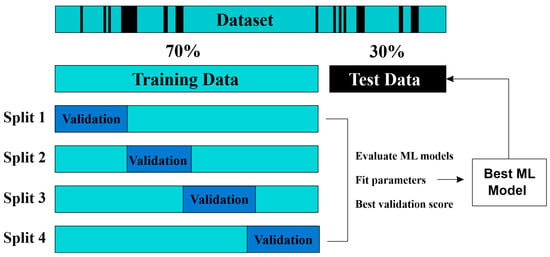
Figure 5.
Demonstration of data partitioning of ML models.
The modeling procedure exploits the training dataset, and predictions were consequently made employing the test dataset. This tactic confirmed peripheral prediction and boosted assurance in the predictions, predominantly when challenged with varied datasets portioning similar parameters [78]. For every single well, five dissimilar training sections were chosen. The concept of training zones refers to the portioning of the log dataset into multiple subsets aimed at simplifying the training procedure in ML [79]. Essentially, these training sections are comprised of pairs of input parameters and their equivalent targeted output patterns, helping as initial units for training iterations. During the network training, a similar dataset was subjected to numerous evaluations to acquire suitable weights as well as outputs. The purpose of training neural network (NN) models was to accomplish an appropriate low-error resolution for the specified problem. Several ANN learning algorithms, for instance, Gradient Descent, Quasi Newton’s Method, Levenberg, Marquardt as well as Conjugate Gradient, could be exploited for this aim, with the selection influenced by variables like the numeral of training cycles, constraints, and dataset [80]. In the current research, backpropagation (BP) has been applied to train the neural network model [81]. The BP algorithm utilized the chain rule to determine the effect of every weight inside the network structure on the variations in the error function. The principles for culminating the training procedure were constructed across the number of training cycles, also termed epochs. In the current study, an absolute of one hundred epochs were preferred for model training. The selection of this explicit number was vital, as opting for a complex value may result in the assimilation of patterns that become complicated to simplify [82].
3.3. Fuzzy Logic (FL)
The FL framework, which used numerical values between 0 and 1 fuzzy set examination, was operated to portray decisions or make conclusions [83]. For the current research, the Mamdani and Assilian model, incorporating explicit input data as well as membership functions, was selected due to its common application as a fuzzy technique [84]. The fuzzy scheme of implication is explained as follows:
µA (x): X → [0, 1]
In this framework, μA(x) signifies the membership grade of component x within the fuzzy set A, whereas X signifies the general set demarcated in the exact obstacle [85,86]. The vital phases of FL handling comprised of the fuzzification of inputs, perused by the implementation of FL rules (such as “and, or, not”) [85]. Afterward, the fitness was measured at the third level, and the consequences were accumulated with a single fuzzy set. Lastly, the defuzzification phase produced the decisive output. FL presented a level of uncertainty or probability to the valuation of individual rock property, for instance, shaliness, color, as well as porosity [87]. Each fuzzy set was signified by a membership function, which could yield arrangements such as trapezoidal, sigmoid, trapezoidal, triangular, Gaussian, S-shape, either Z-shape [87].
During the modeling progression, the selected data endured the obligation of bin boundaries by fuzzy sets [88]. Porosity readings were dispersed over cross-bin boundaries, wherein Gaussian disseminations were fitted to each bin. Quantization either binning of data aided as the extensive mechanism for numeric value processing in ML. In this setting, the dataset was characterized through bins stranded on log curves, signifying appropriate bin spots, including widths to consistently allocate the equivalent number of samples (Figure 6, Figure 7 and Figure 8). The estimation of a bin’s probability integrated the number of samples confined within it. In the building of the FL model, the sum of 409 data values from individual bins has been used.
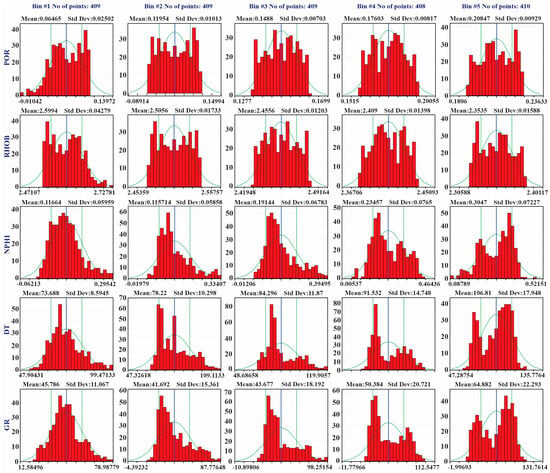
Figure 6.
QGF-well 03 Bin histograms (bins 1–5) depict the fitting of the Gaussian membership function to the POR/predicted porosity curve, GR, NPHI and DT logs. Mean values and SD are indicated by the blue line.
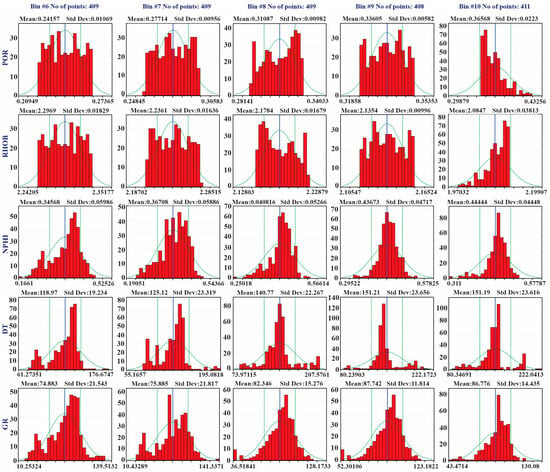
Figure 7.
QGF-well 03 Bin histograms (bins 6–10) depict the fitting of the Gaussian membership function to the POR/predicted porosity curve, GR, NPHI and DT logs. Mean values and SD are indicated by the blue line.
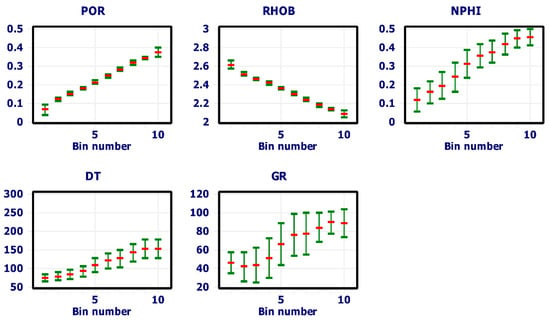
Figure 8.
Demonstrates curve bin distribution visualized via cross plots depicting bin mean values versus bin numbers for each input.
The FL model was employed on the well log dataset, using the training statistics. Afterward, a probability estimate was derived for the fitting of porosity curves for each individual well [89]. Consequently, the solution, represented as the final probability (Pi), was resolute by choosing the result with the maximum possibility. The subsequent output curves contained the most possible setting, depicted the outcome with the maximum probability; the following utmost likely setting delineated the outcome with the second-highest probability; and the weighted typical second most probable situation, which was a weighted mean of the two utmost possible decisions [89]. The closeness of fit (Cfit) readings portrayed in the output curves aided as a reliable measure of the quality and accuracy of the outcomes. The curve contrasted the outcome and the original curve applied in creating the model using bin distance as a metric [89]. The percentage deviation from the elected result operated for generating the low and high probability outcomes was 25%. This research utilized 10 bins, and all bins were evenly sampled. Class interval or bin is an approach to arrange or classify datasets within a histogram. The prime of 10 bins was completed to lodge the comprehensive well log dataset of the Sui main limestone reservoir zone of interest whereas keeping equal-sized bins in clusters of ten. Evenly sampled bins were utilized to initiate data maximums along with minimums for each curve founded upon the input information. The modification of bin arrangement confirmed an identical extent of data in each bin, although it is possible that this procedure might not constantly produce an identical value in each bin.
3.4. Multiple Linear Regression (MLR)
MLR computation was executed on a dataset derived from five wells to contrast the potency and accuracy of the MLR method with FL as well as ANN models. Regression assessment involves the usage of statistical processes in evaluating the link among variables exhibiting causal relationships. The estimation could involve either multilinear or univariate. Univariate scrutinizes the connection between a reliant variable and an independent variable, estimating the linear relationship comparison among them [90,91]. The R2 value signified the squared correlation coefficient, which has been operated to calculate the efficacy of models, extending from 0 to 1. The correlation coefficient was estimated using the subsequent equation:
In the specified equation, where Yi signified the Y value at the ith sample, indicated the root mean squared deviation of predicted values samples, Y mean represented the mean value of whole Y samples, and Y was the outcome at the ith sample intended from the regression formula. The MLR investigation was calculated using the subsequent equation:
1.60606061 − 0.60606061 × RHOB − 2.38672341 × 10−9 × NPHI + 1.69721625 × 10−11 × DT + 4.94700197 × 10−12 × GR
3.5. Evaluation Metrics
To improve the estimation of the accuracy accomplished by the FL and ANN methods, an additional calculation was executed applying root mean square error (RMSE) upon the similar data. That metric was an arithmetical measure which counted the anticipated square of the disparity between the observed and predicted values of the porosity curve. RMSE assisted as an extensively implemented criterion for determining the prediction authenticity of any model [92]. The RMSE value could be employed in the following formula:
In the provided framework, where denoted the actual data points while X (Model, i) implied the predicted data points, n represented the total of recorded data points, and i specified variable i.
4. Results
This section represented the results obtained from examining the dataset sourced from wells QGF-03, 11, 15, 16, and QGF well-17, focusing on ANN and FL. The implementation of FL and ANN approaches intended to scrutinize porosity log within the Eocene reservoir sequence, evaluating log uniformity and precision. Comprehensive statistics obtained from the FL model, integrating curve data from the reservoir intervals of the five wells assembled into 10 bins, were represented in Figure 6 and Figure 7. Moreover, the standard-deviation (SD) as well as means for individual curves were presented. Based on FL statics illustrated in Figure 8, it was observed that the FL predictions for NPHI revealed an underestimation of actual values at five distinct points. Figure 8 demonstrated that NPHI values fell within the range between approximately 0.10 and 0.22 v/v. In spite of this extant, FL outcomes constantly underestimated the accurate values of NPHI.
Assessment of FL predictions for RHOB revealed that merely three data points had underestimated authentic values (RHOB approximately 2.50 g/cm3, while the real range for clastic rock stood at 2.65 g/cm3. The depiction of the Gaussian-shaped membership function, signified by a uniform green curve, which is shown in Figure 6 and Figure 7, was generally applied to fit the well log data. The preference of the Gaussian-shaped membership function for building the fuzzy model aligned with the universal principle valid to natural data is frequently categorized across the standard (Gaussian-shaped) distribution. The actual input curve was overlapped with a standard Gaussian-shaped distribution line, and the vertical green lines specify one standard deviation on each side of the arithmetic mean value (shown in the blue line).
The usage of input curves for every data bin encompassed a succession of cross-plots that represented the bin arithmetic mean value in contradiction of the bin number (as revealed in Figure 8) for individual input curves. The green vertical lines delineated the standard deviation on both sides of the bin’s arithmetic mean, which was displayed via the red horizontal line. These approaches relied on commonly accessible electronic logs like porosity and density, instead of involving the usage of advanced logging systems. The comparative assessment between genuine and predicted well log data through ANN highlights the proficiency of ANN methods in assessing porosity from the assembling of logs, as shown in Figure 9.
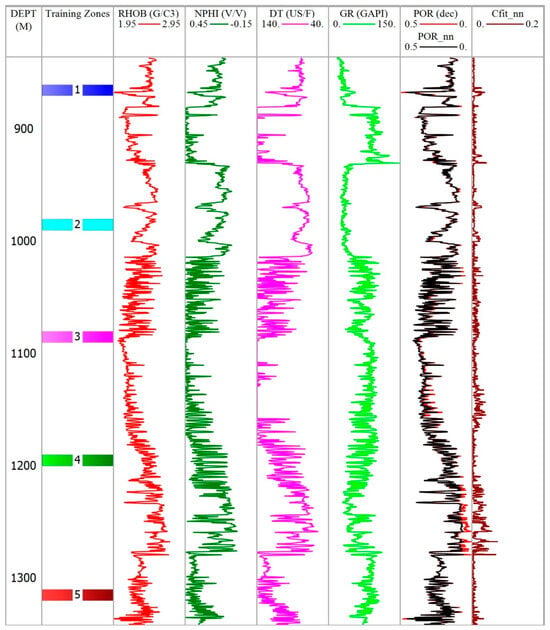
Figure 9.
Log plot highlighting training zones used in ANN for porosity curve prediction.
Figure 10 demonstrated the actual porosity in track two, trailed by sets of curves illustrating the highest probable (mL), subsequent probable (2 mL), as well, as the weighted mean value. The probabilities linked with these values are portrayed in track 3, although track 4 reveals C-fit (closeness-fit) curves.
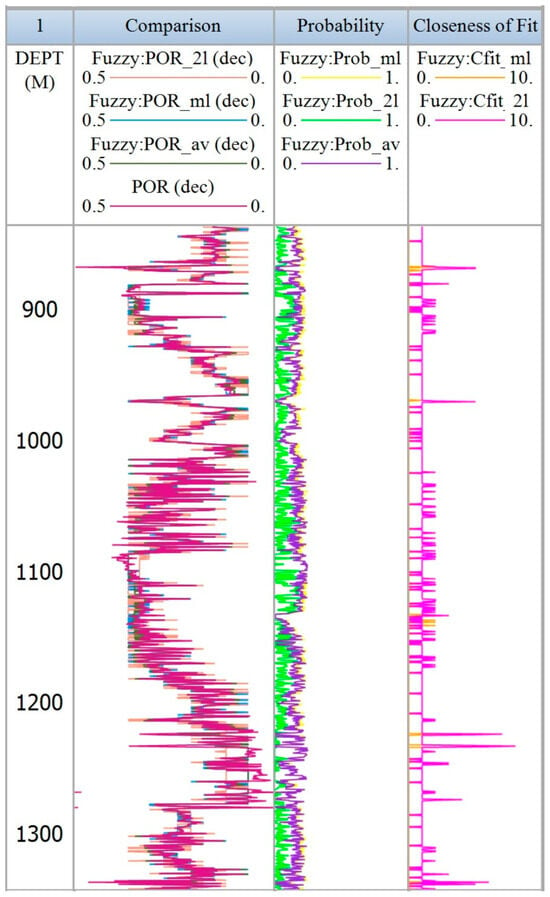
Figure 10.
Displays the porosity curve and closeness of fit curves for QGF well-03.
In assessing ANN, the data underwent preliminary fitting on training data to conduct predictions on test data, enabling an assessment of internal prediction accuracy. Following this, predictions were made using similar well data or from different wells. Figure 11, Figure 12 and Figure 13 display the cross-plot featuring the association between the initial as well as predicted porosity of ANN, FL and MLR models. Utilizing the ANN model, the calculation of the correlation coefficient yielded a significant precision of 0.988. The effectiveness of both the ANN and FL models was displayed through plotting predicted versus initial porosity values. This visualization clarified the distribution of data clusters along the mean line. The predicted and initial porosity results using ANN, MLR, and FL approaches are shown in Table 1. The SD stats in Table 1 indicated that the data points are closely clustered near the arithmetic means, enhancing the reliability of the outcomes. The outcomes of MLR, integrating DT, RHOB, NPHI, GR, and associated coefficients, are shown in Table 2.
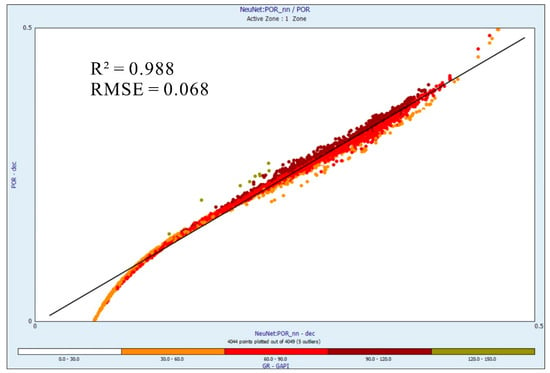
Figure 11.
Demonstrates the R2 between the actual curve and the predicted porosity curve applying ANN.
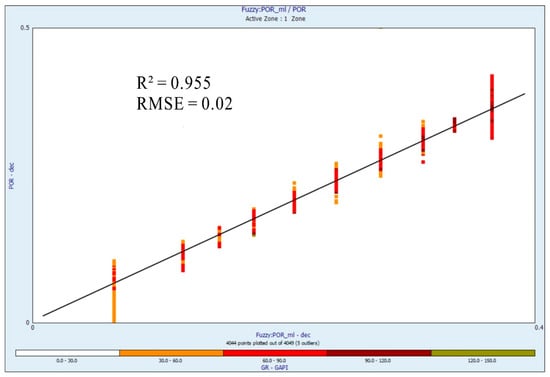
Figure 12.
Demonstrates the R2 between the actual curve and the predicted porosity curve applying FL.
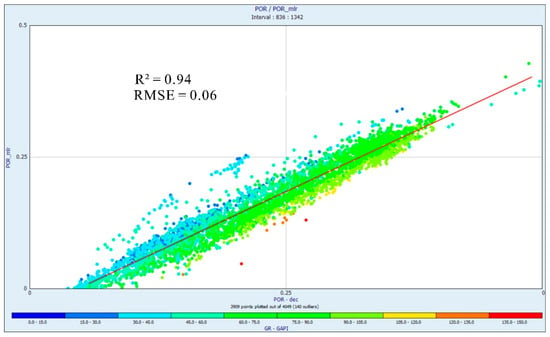
Figure 13.
Demonstrates the R2 between the actual curve and the predicted porosity curve applying MLR.

Table 1.
Porosity prediction outcomes using ANN, FL, and MLR.

Table 2.
MLR regression outcomes of all wells.
In comparison to the FL and NNs methods, the SD derived from MLR analysis exhibited the highest values, indicating a broader distribution of data and subsequently less reliability. The numerical MLR values for the QGF-well-3, investigation was accounted as 0.94 (Figure 13), which was comparatively lower than the estimates provided by ANN and FL as mentioned previously.
The present investigation emphasized the consistency of ANN as well as FL for the wells considered across the QGF. Nevertheless, ANN offered a more precise alignment with genuine and predicted porosity curve. The FL model recommended a minimal variance between real and predicted values. In general, the ranges of DT and GR values exhibited consistent patterns without significant variations across the dataset. The porosity curve predicted by the FL model exhibited a close correlation, though with a minor tendency to overestimate. The prime objective of this regression assessment was to scrutinize the connection between a response variable and a predictor variable. The R2 value obtained from MLR scrutiny of the porosity curve was 0.94. Meanwhile, FL model R2 values were recorded 0.955, as well as ANN model R2 values were notably higher 0.988. These R2 values were derived by cross-plotting the real and predicted porosity curve across the FL, ANN and MLR. The suggested models ANN and FL exhibited adequate authenticity, resulted in a robust alignment between the predicted and real porosity curve. The consistency of this alignment was further validated through the RMSE assessment, illustrated in Figure 11, Figure 12 and Figure 13. Although ANN and FL algorithms have not been broadly discussed in the literature regarding their pros and cons, integrating these techniques aimed to harness the benefits of a neuro-fuzzy framework, thereby enhancing outcomes in resource exploitation and development [30,64,69]. Figure 14 graphically characterized the definite and predicted porosity curve of ANN, FL and ML, and demonstrated excellent precision alongside a vigorous correlation with the predicted and observed data. In situations with incomplete datasets, these methods exhibited robustness and were effective for reservoir modeling. These results proposed convincing indications concerning the efficiency of the predictive models, signifying their potency as substantial tools for forthcoming applications. The flexibility and usefulness of these practices in modeling geological well log data were manifest, predominantly in circumstances with inadequate information.
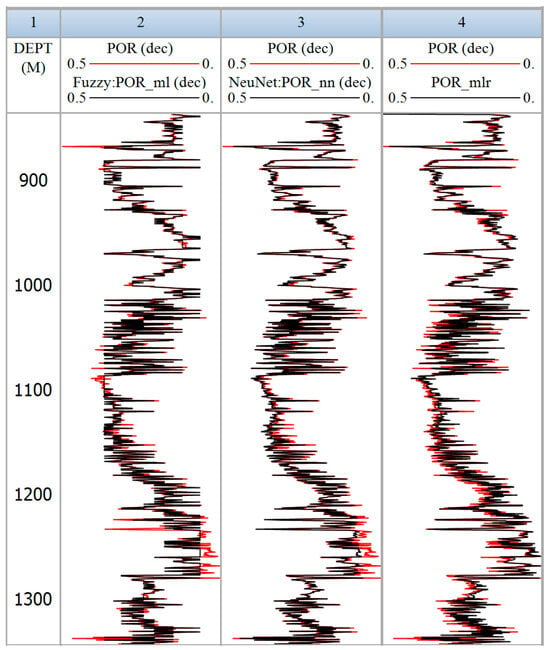
Figure 14.
Illustrates the original porosity curve and predicted porosity curve employing FL, MLR and NNs.
The research reveals that strategically synthesizing logs and comparing them with initial data could aid as proof of the precise synthesis of well logs. In these methods, the proximity between the initial porosity curve and the estimate derived from the models exceeded 95%, with median correlation values spanning from 94% to 98%. Comparative examination of predicted and real parameters applying two discrete techniques, it was apparent that both methodologies yielded almost similar precision; nevertheless, ANN exhibited greater precision in predicting the porosity curve, transcending the competencies of FL. Utilization of both ANN and FL methods offered viable options for developing models across various reservoirs and prospecting wells. However, the R2 values obtained from NNs outperformed the FL approach. Insignificant changes detected in the predicted porosity values linked to the actual values applying FL and ANN models could be assigned to dissimilarities in mineralogical configuration, modeling imprecisions, test data disagreements, as well as variances in fluid composition and saturation level.
5. Discussion
The prediction of the porosity curve is a crucial feature of reservoir characterization in the petroleum sector. The present research aimed to employ ML approaches, such as ANN and FL, to predict porosity curves grounded on geophysical logs from QGF. It highlighted the eminence of precise porosity predictions, the validity of ANN and FL techniques, their comparison with conventional models, and the wider effects for reservoir characterization and hydrocarbon exploration. Explicit porosity predictions are crucial for geologists and reservoir engineers as they deliver perceptions into reservoir quality, energy resource potential, and optimum well location strategies. The capability of ANN and FL to generate accurate porosity values, as proved by R2 values of 0.988 and 0.955 correspondingly, underscored their significance in reservoir modeling. By exploiting intricate computational algorithms, ANN exceeded in capturing complex patterns and associations among the data, allowing them to yield extensively accurate predictions. In the same manner, FL, with its potency to deal with fuzziness and uncertainties within the dataset, provided vigorous predictions of the porosity curve. ANN and FL comparing performance with conventional MLR assessment uncover their dominance in predicting porosity curves. Although MLR adopts a linear relationship between input and output parameters, ANN and FL techniques could encapsulate nonlinear reliance and compound relationships, resulting in more precise predictions.
Earlier studies have also examined the use of ANN and FL for predicting porosity curves in numerous geological formations. For instance, A. Sridi et al. utilized an FL-based method for porosity prediction within a shaly Triassic reservoir, emphasizing the efficiency of fuzzy interference in predicting porosity and permeability [93]. AN Okon et al. employed ANN to model the association between well log data and prediction of petrophysical parameters, porosity, water saturation, and permeability in the Niger Delta region, emphasizing the capability of ANN to deal with nonlinear and complex data patterns [94]. Furthermore, Tahar Aifa et al. proposed a novel technique for porosity permeability prediction in a shaly sand reservoir by applying a hybrid neuro-fuzzy model. Their method revealed the efficacy of combining ANN and FL approaches in reservoir valuation [95]. Based upon these perceptions gained from the literature, the current study encompasses the application of ANN and FL approaches to predict the porosity curve in the QGF reservoir interval, offering the progression of predictive modeling methods in reservoir assessment. Furthermore, the functional significance of precise porosity predictions amplified reservoir regulation as well as production enhancement. Accurate porosity measurements helped reservoir engineers fabricate knowledge-based decisions relating to well placement, reservoir exploitation and development. Applying ANN and FL methods, the researcher could explore reservoir heterogeneity and fluid dispersion, resulting in enhanced reservoir performance and significant hydrocarbon recovery. Nonetheless, it is crucial to acknowledge the constraints and challenges linked with ANN and FL approaches. Factors, for instance, the quality of data, the complexity of the model as well as variable selection, can impact prediction accuracy and model performance. Vigorous validation methods such as sensitivity analysis and cross-validation are vital to evaluate model performance and assure precise predictions. The performance of the model particularly relies on the quality and range of the input well logs curve, which could differ across several reservoir fields. Although the models exhibited extreme accuracy for the QGF limestone reservoir zone, their applicability to other natural reservoirs requires further authentication. In addition, continuing developments in ML algorithms provide robust possibilities to enhance the effectiveness and accuracy of porosity prediction models.
6. Conclusions
The comprehensive dataset of the Eocene reservoir was assembled to predict the advanced porosity curve. The outcomes revealed the robust performance of the tested tactics across numerous models, with noteworthy conclusions strained from the subsequent facts:
- ➢
- Among the predicted models applied, the ANN model demonstrated superior accuracy in predicting the porosity curve, evidenced by the R2 value of 0.988 and RMSE values of 0.068. The FL model also achieved a strong, dependable prediction for porosity, showcasing R2 values of 0.955 and RMSE value of 0.02. Moreover, the precision of the predicted outcomes was used to compare with the MLR model, which exhibited lower accuracy, indicated via an R2 value of 0.94 and RMSE values of 0.06.
- ➢
- The outcomes recommended that ML approaches provided higher accuracy and consistency in predicting reservoir constraints than conventional methods. Both the FL and ANN methods have shown promising outcome measures, emphasizing the effectiveness of reservoir variable assessment.
- ➢
- The notable predictive accuracy concluded that the ANN model and the FL model developed from the well log dataset could be excellently employed for predicting the porosity curve in various oil and gas fields.
- ➢
- The proposed models could assist geologists in examining the reservoir characteristics within the exploratory wells via well logs, which were susceptible to error and ambiguity. These widely applied algorithms emerged as prevailing tools for unfolding reservoirs stranded on well logs, predominantly in the framework of oil and gas expansion plans.
- ➢
- Processing of well data validated the techniques’ capability to evaluate porosity exactly. The outcomes proposed that FL and ANN rigorous algorithms have the competence to correctly synthesize petrophysical well logs, viably substituting substitute to traditional approaches such as multiple regression.
Author Contributions
Conceptualization, N.A.; data curation, X.F., J.H., W.H., N.R., S.M.I. and A.A.; formal analysis, N.A., J.H. and S.M.I.; funding acquisition, A.A.; investigation, X.F., J.C., W.H. and A.A.; methodology, N.A. and W.H.; project administration, X.F. and J.C.; resources, X.F., J.C. and A.A.; software, N.A., J.H., W.H. and S.M.I.; supervision, X.F. and J.C.; validation, N.A., J.H., W.H., N.R., S.M.I. and A.A.; visualization, J.H., N.R., S.M.I. and A.A.; writing—original draft, N.A.; writing—review and editing, N.A., X.F., J.C., J.H., W.H., N.R., S.M.I. and A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This Research work was funded by Institutional Fund Projects under grant no. (IFPIP: 210-611-1443). The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Data Availability Statement
The study data can be obtained by contacting the first and corresponding authors. However, they are not currently public due to their use in an ongoing thesis.
Acknowledgments
Nafees Ali is an awardee for the ANSO Scholarship 2021-PhD. The authors of the current research would like to pay their gratitude to the Directorate General of Petroleum Concession (DGPC) for providing the well logging data employed in this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sharifi, J.; Moghaddas, N.H.; Saberi, M.R.; Mondol, N.H. A Novel Approach for Fracture Porosity Estimation of Carbonate Reservoirs. Geophys. Prospect. 2023, 71, 664–681. [Google Scholar] [CrossRef]
- Stadtműller, M.; Jarzyna, J.A. Estimation of Petrophysical Parameters of Carbonates Based on Well Logs and Laboratory Measurements, a Review. Energies 2023, 16, 4215. [Google Scholar] [CrossRef]
- Iqbal, S.M.; Hussain, A.; Ali, N.; Hussain, W.; Hussain, H.; Hussain, S.; Shah, S.Y.A.; Nyakilla, E.E. Experimental Evaluation of Different Influencing Parameters on Cutting Transport Performance (CTP) in Deviated Wells. Geosyst. Geoenviron. 2023, 2, 100110. [Google Scholar] [CrossRef]
- Hussain, W.; Ali, N.; Sadaf, R.; Hu, C.; Nykilla, E.E.; Ullah, A.; Iqbal, S.M.; Hussain, A.; Hussain, S. Petrophysical Analysis and Hydrocarbon Potential of the Lower Cretaceous Yageliemu Formation in Yakela Gas Condensate Field, Kuqa Depression of Tarim Basin, China. Geosyst. Geoenviron. 2022, 1, 100106. [Google Scholar] [CrossRef]
- Ermakov, A.I.; Park, R.S.; Roa, J.; Castillo-Rogez, J.C.; Keane, J.T.; Nimmo, F.; Kite, E.S.; Sotin, C.; Lazio, T.J.W.; Steinbrügge, G. A Recipe for the Geophysical Exploration of Enceladus. Planet. Sci. J. 2021, 2, 157. [Google Scholar] [CrossRef]
- Ali, N.; Chen, J.; Fu, X.; Hussain, W.; Ali, M.; Hussain, M.; Anees, A.; Rashid, M.; Thanh, H.V. Prediction of Cretaceous Reservoir Zone through Petrophysical Modeling: Insights from Kadanwari Gas Field, Middle Indus Basin. Geosyst. Geoenviron. 2022, 1, 100058. [Google Scholar] [CrossRef]
- Lemière, B.; Harmon, R.S. XRF and LIBS for Field Geology. Portable Spectrosc. Spectrom. 2021, 455–497. [Google Scholar] [CrossRef]
- Hashan, M.; Jahan, L.N.; Imtiaz, S.; Hossain, M.E. Modelling of Fluid Flow through Porous Media Using Memory Approach: A Review. Math. Comput. Simul. 2020, 177, 643–673. [Google Scholar] [CrossRef]
- Shi, X.; Wang, J.; Liu, G.; Yang, L.; Ge, X.; Jiang, S. Application of Extreme Learning Machine and Neural Networks in Total Organic Carbon Content Prediction in Organic Shale with Wire Line Logs. J. Nat. Gas Sci. Eng. 2016, 33, 687–702. [Google Scholar] [CrossRef]
- Ashraf, U.; Zhang, H.; Thanh, H.V.; Anees, A.; Ali, M.; Duan, Z.; Mangi, H.N.; Zhang, X. A Robust Strategy of Geophysical Logging for Predicting Payable Lithofacies to Forecast Sweet Spots Using Digital Intelligence Paradigms in a Heterogeneous Gas Field. Nat. Resour. Res. 2024, 33, 1741–1762. [Google Scholar] [CrossRef]
- Hu, K.; Li, Y.; Xia, M.; Wu, J.; Lu, M.; Zhang, S.; Weng, L. Federated Learning: A Distributed Shared Machine Learning Method. Complexity 2021, 2021, 8261663. [Google Scholar] [CrossRef]
- Hussain, W.; Ehsan, M.; Pan, L.; Wang, X.; Ali, M.; Din, S.U.; Hussain, H.; Jawad, A.; Chen, S.; Liang, H. Prospect Evaluation of the Cretaceous Yageliemu Clastic Reservoir Based on Geophysical Log Data: A Case Study from the Yakela Gas Condensate Field, Tarim Basin, China. Energies 2023, 16, 2721. [Google Scholar] [CrossRef]
- Lawal, A.; Yang, Y.; He, H.; Baisa, N.L. Machine Learning in Oil and Gas Exploration—A Review. IEEE Access 2024, 12, 19035–19058. [Google Scholar] [CrossRef]
- Rezaee, M.R.; Kadkhodaie-Ilkhchi, A.; Alizadeh, P.M. Intelligent Approaches for the Synthesis of Petrophysical Logs. J. Geophys. Eng. 2008, 5, 12–26. [Google Scholar] [CrossRef]
- Wood, D.A. Predicting Porosity, Permeability and Water Saturation Applying an Optimized Nearest-Neighbour, Machine-Learning and Data-Mining Network of Well-Log Data. J. Pet. Sci. Eng. 2020, 184, 106587. [Google Scholar] [CrossRef]
- Ali, N.; Chen, J.; Fu, X.; Hussain, W.; Ali, M.; Iqbal, S.M.; Anees, A.; Hussain, M.; Rashid, M.; Thanh, H.V. Classification of Reservoir Quality Using Unsupervised Machine Learning and Cluster Analysis: Example from Kadanwari Gas Field, SE Pakistan. Geosyst. Geoenviron. 2023, 2, 100123. [Google Scholar] [CrossRef]
- Salem, A.M.; Yakoot, M.S.; Mahmoud, O. Addressing Diverse Petroleum Industry Problems Using Machine Learning Techniques: Literary Methodology—Spotlight on Predicting Well Integrity Failures. ACS Omega 2022, 7, 2504–2519. [Google Scholar] [CrossRef] [PubMed]
- Sircar, A.; Yadav, K.; Rayavarapu, K.; Bist, N.; Oza, H. Application of Machine Learning and Artificial Intelligence in Oil and Gas Industry. Pet. Res. 2021, 6, 379–391. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, P.; Lyu, F.; Zhu, S.; Zhou, R.; Li, B.; He, T.; Lin, Y.; Gao, Y.; Song, W. Machine Learning (ML) for Fluvial Lithofacies Identification from Well Logs: A Hybrid Classification Model Integrating Lithofacies Characteristics, Logging Data Distributions, and ML Models Applicability. Geoenergy Sci. Eng. 2024, 233, 212587. [Google Scholar] [CrossRef]
- Ashraf, U.; Zhang, H.; Anees, A.; Ali, M.; Mangi, H.N.; Zhang, X. An Ensemble-Based Strategy for Robust Predictive Volcanic Rock Typing Efficiency on a Global-Scale: A Novel Workflow Driven by Big Data Analytics. Sci. Total Environ. 2024, 937, 173425. [Google Scholar] [CrossRef]
- Ashraf, U.; Shi, W.; Zhang, H.; Anees, A.; Jiang, R.; Ali, M.; Mangi, H.N.; Zhang, X. Reservoir Rock Typing Assessment in a Coal-Tight Sand Based Heterogeneous Geological Formation through Advanced AI Methods. Sci. Rep. 2024, 14, 5659. [Google Scholar] [CrossRef] [PubMed]
- Hussain, W.; Luo, M.; Ali, M.; Hussain, S.M.; Ali, S.; Hussain, S.; Naz, A.F.; Hussain, S. Machine Learning-a Novel Approach to Predict the Porosity Curve Using Geophysical Logs Data: An Example from the Lower Goru Sand Reservoir in the Southern Indus Basin, Pakistan. J. Appl. Geophys. 2023, 214, 105067. [Google Scholar] [CrossRef]
- Ansari, A.; Bakar, A.A. A Comparative Study of Three Artificial Intelligence Techniques: Genetic Algorithm, Neural Network, and Fuzzy Logic, on Scheduling Problem. In Proceedings of the 2014 4th International Conference on Artificial Intelligence with Applications in Engineering and Technology, Kota Kinabalu, Malaysia, 3–5 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 31–36. [Google Scholar]
- Godo, L.; Jacas, J.; Valverde, L. Fuzzy Values in Fuzzy Logic. Int. J. Intell. Syst. 1991, 6, 199–212. [Google Scholar] [CrossRef]
- Cuddy, S.J.; Glover, P.W.J. The Application of Fuzzy Logic and Genetic Algorithms to Reservoir Characterization and Modeling. In Soft Computing for Reservoir Characterization and Modeling; Springer: Berlin/Heidelberg, Germany, 2002; pp. 219–241. [Google Scholar]
- Lim, J.-S. Reservoir Properties Determination Using Fuzzy Logic and Neural Networks from Well Data in Offshore Korea. J. Pet. Sci. Eng. 2005, 49, 182–192. [Google Scholar] [CrossRef]
- Saggaf, M.M.; Nebrija, E.L. A Fuzzy Logic Approach for the Estimation of Facies from Wire-Line Logs. Am. Assoc. Pet. Geol. Bull. 2003, 87, 1223–1240. [Google Scholar] [CrossRef]
- Okwu, M.O.; Nwachukwu, A.N. A Review of Fuzzy Logic Applications in Petroleum Exploration, Production and Distribution Operations. J. Pet. Explor. Prod. Technol. 2019, 9, 1555–1568. [Google Scholar] [CrossRef]
- Iturrarán-Viveros, U.; Parra, J.O. Artificial Neural Networks Applied to Estimate Permeability, Porosity and Intrinsic Attenuation Using Seismic Attributes and Well-Log Data. J. Appl. Geophys. 2014, 107, 45–54. [Google Scholar] [CrossRef]
- Otchere, D.A.; Ganat, T.O.A.; Gholami, R.; Ridha, S. Application of Supervised Machine Learning Paradigms in the Prediction of Petroleum Reservoir Properties: Comparative Analysis of ANN and SVM Models. J. Pet. Sci. Eng. 2021, 200, 108182. [Google Scholar] [CrossRef]
- Adibifard, M.; Tabatabaei-Nejad, S.A.R.; Khodapanah, E. Artificial Neural Network (ANN) to Estimate Reservoir Parameters in Naturally Fractured Reservoirs Using Well Test Data. J. Pet. Sci. Eng. 2014, 122, 585–594. [Google Scholar] [CrossRef]
- Ali, M.; Zhu, P.; Jiang, R.; Huolin, M.; Ashraf, U.; Zhang, H.; Hussain, W. Data-Driven Lithofacies Prediction in Complex Tight Sandstone Reservoirs: A Supervised Workflow Integrating Clustering and Classification Models. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 70. [Google Scholar] [CrossRef]
- Ali, M.; Zhu, P.; Huolin, M.; Pan, H.; Abbas, K.; Ashraf, U.; Ullah, J.; Jiang, R.; Zhang, H. A Novel Machine Learning Approach for Detecting Outliers, Rebuilding Well Logs, and Enhancing Reservoir Characterization. Nat. Resour. Res. 2023, 32, 1047–1066. [Google Scholar] [CrossRef]
- Kuo, J.-T.; Hsieh, M.-H.; Lung, W.-S.; She, N. Using Artificial Neural Network for Reservoir Eutrophication Prediction. Ecol. Modell. 2007, 200, 171–177. [Google Scholar] [CrossRef]
- Saikia, P.; Baruah, R.D.; Singh, S.K.; Chaudhuri, P.K. Artificial Neural Networks in the Domain of Reservoir Characterization: A Review from Shallow to Deep Models. Comput. Geosci. 2020, 135, 104357. [Google Scholar] [CrossRef]
- Moghadasi, L.; Ranaee, E.; Inzoli, F.; Guadagnini, A. Petrophysical Well Log Analysis through Intelligent Methods. In Proceedings of the SPE Norway Subsurface Conference, Bergen, Norway, 1–5 April 2017; SPE: Treasure Island, FL, USA, 2017; p. D011S001R002. [Google Scholar]
- Ahmad, W.; Ma, X.; ul Islam, F. Reservoir Characterization of Qadirpur Gas Field, Central Indus Basin, Pakistan. In Proceedings of the International Field Exploration and Development Conference 2018 8th, Xi’an, China, 18–20 September 2018; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1073–1081. [Google Scholar]
- Khan, M.; Arif, M.; Ali, N.; Yaseen, M.; Ahmed, A.; Siyar, S.M. Petrophysical Parameters and Modelling of the Eocene Reservoirs in the Qadirpur Area, Central Indus Basin, Pakistan: Implications from Well Log Analysis. Arab. J. Geosci. 2016, 9, 425. [Google Scholar] [CrossRef]
- Ali, A.; Younas, M.; Ullah, M.; Hussain, M.; Toqeer, M.; Bhatti, A.S.; Khan, A. Characterization of Secondary Reservoir Potential via Seismic Inversion and Attribute Analysis: A Case Study. J. Pet. Sci. Eng. 2019, 178, 272–293. [Google Scholar] [CrossRef]
- Siddiqui, N.K. Sui Main Limestone: Regional Geology and the Analysis of Original Pressures of a Closed-System Reservoir in Central Pakistan. Am. Assoc. Pet. Geol. Bull. 2004, 88, 1007–1035. [Google Scholar] [CrossRef]
- Ali, N.; Fu, X.; Ashraf, U.; Chen, J.; Thanh, H.V.; Anees, A.; Riaz, M.S.; Fida, M.; Hussain, M.A.; Hussain, S.; et al. Remote Sensing for Surface Coal Mining and Reclamation Monitoring in the Central Salt Range, Punjab, Pakistan. Sustainability 2022, 14, 9835. [Google Scholar] [CrossRef]
- Hussain, J.; Zhang, J.; Iqbal, S.M.; Hussain, J.; Fitria, F.; Lina, X.; Ali, N.; Hussain, S.; Akram, W.; Ali, M. Exploring the Potential of Late Permian Aggregate Resources for Utilization in Engineering Structures through Geotechnical, Geochemical and Petrographic Analyses. Sci. Rep. 2023, 13, 5088. [Google Scholar] [CrossRef]
- Hussain, J.; Zhang, J.; Saleem, A.; Luo, Y.; Afaq Hussain, M.; Hussain, J.; Fitria, F.; Akram, W.; Arifullah; Hussain, H. Suitability Assessment Constraints of Potential Aggregate Resources Using an Integrated GIS Approach. J. Mater. Civ. Eng. 2023, 35, 4023307. [Google Scholar] [CrossRef]
- Ehsan, M.; Chen, R.; Latif, M.A.U.; Abdelrahman, K.; Ali, A.; Ullah, J.; Fnais, M.S. Unconventional Reservoir Characterization of Patala Formation, Upper Indus Basin, Pakistan. ACS Omega 2024, 9, 15573–15589. [Google Scholar] [CrossRef]
- Daud, H.; Tanoli, J.I.; Asif, S.M.; Qasim, M.; Ali, M.; Khan, J.; Bhatti, Z.I.; Jadoon, I.A.K. Modelling of Debris-Flow Susceptibility and Propagation: A Case Study from Northwest Himalaya. J. Mt. Sci. 2024, 21, 200–217. [Google Scholar] [CrossRef]
- Ashraf, U.; Zhang, H.; Anees, A.; Ali, M.; Zhang, X.; Shakeel Abbasi, S.; Nasir Mangi, H. Controls on Reservoir Heterogeneity of a Shallow-Marine Reservoir in Sawan Gas Field, SE Pakistan: Implications for Reservoir Quality Prediction Using Acoustic Impedance Inversion. Water 2020, 12, 2972. [Google Scholar] [CrossRef]
- Zeb, R.A.; Khan, M.H.; Naseem, W.; Awais, M.; Zaheen, H.; Khalid, A. Reservoir Characterization of Eocene Carbonates of Central Indus Basin, Pakistan. Indones. J. Earth Sci. 2022, 2, 64–77. [Google Scholar] [CrossRef]
- Cook, M.A. Annexation and the Unhappy Valley: The Historical Anthropology of Sindh’s Colonization. In Annexation and the Unhappy Valley; Brill: Leiden, The Netherlands, 2015; ISBN 9004293671. [Google Scholar]
- Hussain, W.; Luo, M.; Ali, M.; Hussain, H.; Ali, S.; Iqbal, J.; Nyakilla, E.E.; Asghar, A. Rock Physics Modeling to Evaluate Clastic Reservoirs: A Case Study from the Lower Goru Formation, Middle Indus Basin, Pakistan. Environ. Earth Sci. 2024, 83, 383. [Google Scholar] [CrossRef]
- Khan, M.; Liu, Y. Geodynamic Evolution of the Offshore Indus Basin Pakistan: The Western Indian Plate Passive Continental Margin. Geophys. J. Int. 2019, 217, 1366–1386. [Google Scholar] [CrossRef]
- Hussain, W.; Ali, M.; Sadaf, R.; Al-Khafaji, H.F.; Sadiq, I.; Hu, C.; Daud, H.; Ahmed, S.A.A. Advanced AI Approach for Enhanced Predictive Modeling in Reservoir Characterization within Complex Geological Environments. Model. Earth Syst. Environ. 2024, 1–19. [Google Scholar] [CrossRef]
- Khalid, P.; Ehsan, M.I.; Khurram, S.; Ullah, I.; Ahmad, Q.A. Reservoir Quality and Facies Modeling of the Early Eocene Carbonate Stratigraphic Unit of the Middle Indus Basin, Pakistan. Front. Earth Sci. 2022, 10, 1063877. [Google Scholar] [CrossRef]
- Ali, A.; Alves, T.M.; Amin, Y. Integrated Geophysical Analysis of the Sembar Formation, Central Indus Basin, as an Unconventional Resource. J. Nat. Gas Sci. Eng. 2022, 101, 104507. [Google Scholar] [CrossRef]
- Shah, F.; Miraj, M.A.F.; Ali, A.; Ahsan, N.; Mehmood, T.; Sajid, M.; Salaam, A.; Fazal, A.G. Tectonics of Jacobabad–Khairpur High and Its Impact on Petroleum Fields of the Region, Southern Indus Basin, Pakistan: A Case Study. Geotectonics 2023, 57, 346–358. [Google Scholar] [CrossRef]
- Ahmad, W.; Zeb, S.F.; Ali, N.; Latif, K.; Siyar, S.M.; Khan, S. Petrophysical Modelling of the Cretaceous Lower Goru Formation, Lower Indus Basin, Pakistan. J. Himal. Earth Sci. 2022, 55, 57–67. [Google Scholar]
- Jamil, A.; Waheed, A.; Sheikh, R.A. Pakistan’s Major Petroleum Plays–An Overview of Dwindling Reserves. Search Discov. Artic. 2012, 1–2. [Google Scholar]
- Adams, J.A.S.; Gasparini, P. Gamma-Ray Spectrometry of Rocks; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 1483257347. [Google Scholar]
- Hernandez, G.M.; Figueiredo, F.T.; Janikian, L.; do Nascimento Santana, M.; Gomes, P.V.O. Facies Prediction in a Mature Oil Field of Cretaceous Age in the Calumbi Formation (Sergipe-Alagoas Basin, Brazil) by Using an Outcrop Analogue Approach. Mar. Pet. Geol. 2024, 162, 106738. [Google Scholar] [CrossRef]
- Yan, H.; Pi, D.-H.; Jiang, S.-Y.; Mao, J.; Xu, L.; Yang, X.; Hao, W.; Mänd, K.; Li, L.; Konhauser, K.O. Mineral Paragenesis in Paleozoic Manganese Ore Deposits: Depositional versus Post-Depositional Formation Processes. Geochim. Cosmochim. Acta 2022, 325, 65–86. [Google Scholar] [CrossRef]
- Ali, N.; Jamil, S.; Zaheer, M.; Hussain, W.; Hussain, H.; Muhammad Iqbal, S.; Ullah, H. Exploration and Development of Shale Gas in China: A Review. Iran. J. Earth Sci. 2022, 14, 87–103. [Google Scholar]
- Day-Stirrat, R.J.; Hillier, S.; Nikitin, A.; Hofmann, R.; Mahood, R.; Mertens, G. Natural Gamma-Ray Spectroscopy (NGS) as a Proxy for the Distribution of Clay Minerals and Bitumen in the Cretaceous McMurray Formation, Alberta, Canada. Fuel 2021, 288, 119513. [Google Scholar] [CrossRef]
- Ismail, A.; Raza, A.; Gholami, R.; Rezaee, R. Reservoir Characterization for Sweet Spot Detection Using Color Transformation Overlay Scheme. J. Pet. Explor. Prod. Technol. 2020, 10, 2313–2334. [Google Scholar] [CrossRef]
- Ehsan, M.; Latif, M.A.U.; Ali, A.; Radwan, A.E.; Amer, M.A.; Abdelrahman, K. Geocellular Modeling of the Cambrian to Eocene Multi-Reservoirs, Upper Indus Basin, Pakistan. Nat. Resour. Res. 2023, 32, 2583–2607. [Google Scholar] [CrossRef]
- Xu, L.; Schultz, W.; Huiszoon, C. A Comprehensive Investigation of Source Effects on Neutron Porosity Response for Logging-While-Drilling Measurements. In Proceedings of the SPWLA Annual Logging Symposium, The Woodlands, TX, USA, 21–24 June 2009; SPWLA: Houston, TX, USA, 2009. [Google Scholar]
- Chen, G.; Dang, L.; Cai, W.; Li, J.; Dong, J.; Chen, Z.; Deng, R. Study on Monitoring Reservoir Gas Density by Pulsed Neutron Logging. Int. J. Energy Res. 2023, 2023, 1363145. [Google Scholar] [CrossRef]
- Munther, A.; Sahaab, A.M. Well Logs Analysis and Reservoir Evaluation of Hartha Formation in the East Baghdad Oil Field Central Iraq. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Ramadi, Iraq, 13–15 December 2023; IOP Publishing: Bristol, UK, 2024; Volume 1300, p. 12028. [Google Scholar]
- Lyu, Q.; Luo, S.; Guan, Y.; Fu, J.; Niu, X.; Xu, L.; Feng, S.; Li, S. A New Method of Lithologic Identification and Distribution Characteristics of Fine-Grained Sediments: A Case Study in Southwest of Ordos Basin, China. Open Geosci. 2019, 11, 17–28. [Google Scholar] [CrossRef]
- ShadSanjabad, M.; Feghhi, A.; Ghaderi, R. Regime Independent Flow Rate Prediction in a Gas-Liquid Two-Phase Facility Based on Gamma Ray Technique and One Detector Using Multi-Feature Extraction. Flow Meas. Instrum. 2023, 92, 102388. [Google Scholar] [CrossRef]
- Sang, W.; Yuan, S.; Han, H.; Liu, H.; Yu, Y. Porosity Prediction Using Semi-Supervised Learning with Biased Well Log Data for Improving Estimation Accuracy and Reducing Prediction Uncertainty. Geophys. J. Int. 2023, 232, 940–957. [Google Scholar] [CrossRef]
- Saxena, V.; Krief, M.; Adam, L. Handbook of Borehole Acoustics and Rock Physics for Reservoir Characterization; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 012812332X. [Google Scholar]
- Elmahdy, M.; Radwan, A.A.; Nabawy, B.S.; Abdelmaksoud, A.; Nastavkin, A. V Integrated Geophysical, Petrophysical and Petrographical Characterization of the Carbonate and Clastic Reservoirs of the Waihapa Field, Taranaki Basin, New Zealand. Mar. Pet. Geol. 2023, 151, 106173. [Google Scholar] [CrossRef]
- Serra, O. Advanced Interpretation of Wireline Logs; Schlumberger: Houston, TX, USA, 1986. [Google Scholar]
- Arabi Aliabad, F.; Shojaei, S.; Zare, M.; Ekhtesasi, M.R. Assessment of the Fuzzy ARTMAP Neural Network Method Performance in Geological Mapping Using Satellite Images and Boolean Logic. Int. J. Environ. Sci. Technol. 2019, 16, 3829–3838. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial Neural Networks: Fundamentals, Computing, Design, and Application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef] [PubMed]
- Rolon, L.; Mohaghegh, S.D.; Ameri, S.; Gaskari, R.; McDaniel, B. Using Artificial Neural Networks to Generate Synthetic Well Logs. J. Nat. Gas Sci. Eng. 2009, 1, 118–133. [Google Scholar] [CrossRef]
- Saljooghi, B.S.; Hezarkhani, A. Comparison of WAVENET and ANN for Predicting the Porosity Obtained from Well Log Data. J. Pet. Sci. Eng. 2014, 123, 172–182. [Google Scholar] [CrossRef]
- Abdulaziz, A.M.; Mahdi, H.A.; Sayyouh, M.H. Prediction of Reservoir Quality Using Well Logs and Seismic Attributes Analysis with an Artificial Neural Network: A Case Study from Farrud Reservoir, Al-Ghani Field, Libya. J. Appl. Geophys. 2019, 161, 239–254. [Google Scholar] [CrossRef]
- Aliouane, L.; Ouadfeul, S.-A.; Djarfour, N.; Boudella, A. Lithofacies Prediction from Well Logs Data Using Different Neural Network Models. In Proceedings of the Special Session on Pattern Recognition in Geosciences: Theory and Applications, Lisbon, Portugal, 22–24 February 2023; SCITEPRESS: Setúbal, Portugal, 2013; Volume 2, pp. 702–706. [Google Scholar]
- Chaki, S.; Verma, A.K.; Routray, A.; Jenamani, M.; Mohanty, W.K.; Chaudhuri, P.K.; Das, S.K. Prediction of Porosity and Sand Fraction from Well Log Data Using ANN and ANFIS: A Comparative Study. In Proceedings of the 10th Biennial International Conference & Exposition of SPG, Kochi, India, 23–25 November 2013. [Google Scholar]
- Mukherjee, I.; Routroy, S. Comparing the Performance of Neural Networks Developed by Using Levenberg–Marquardt and Quasi-Newton with the Gradient Descent Algorithm for Modelling a Multiple Response Grinding Process. Expert Syst. Appl. 2012, 39, 2397–2407. [Google Scholar] [CrossRef]
- Asadisaghandi, J.; Tahmasebi, P. Comparative Evaluation of Back-Propagation Neural Network Learning Algorithms and Empirical Correlations for Prediction of Oil PVT Properties in Iran Oilfields. J. Pet. Sci. Eng. 2011, 78, 464–475. [Google Scholar] [CrossRef]
- Cigizoglu, H.K.; Kişi, Ö. Flow Prediction by Three Back Propagation Techniques Using K-Fold Partitioning of Neural Network Training Data. Hydrol. Res. 2005, 36, 49–64. [Google Scholar] [CrossRef]
- Zadeh, L.A. The Role of Fuzzy Logic in the Management of Uncertainty in Expert Systems. Fuzzy Sets Syst. 1983, 11, 199–227. [Google Scholar] [CrossRef]
- Mohd Adnan, M.R.H.; Sarkheyli, A.; Mohd Zain, A.; Haron, H. Fuzzy Logic for Modeling Machining Process: A Review. Artif. Intell. Rev. 2015, 43, 345–379. [Google Scholar] [CrossRef]
- Zerrouki, A.A.; Aïfa, T.; Baddari, K. Prediction of Natural Fracture Porosity from Well Log Data by Means of Fuzzy Ranking and an Artificial Neural Network in Hassi Messaoud Oil Field, Algeria. J. Pet. Sci. Eng. 2014, 115, 78–89. [Google Scholar] [CrossRef]
- Ehsan, M.; Gu, H. An Integrated Approach for the Identification of Lithofacies and Clay Mineralogy through Neuro-Fuzzy, Cross Plot, and Statistical Analyses, from Well Log Data. J. Earth Syst. Sci. 2020, 129, 101. [Google Scholar] [CrossRef]
- Zhou, Z.; Shi, S.; Ma, S.; Fu, J. Application of Fuzzy Comprehensive Evaluation Method for Reservoir Well Logging Interpretation While Drilling. In Proceedings of the Mobile Networks and Management: 9th International Conference, MONAMI 2017, Melbourne, Australia, 13–15 December 2017; Proceedings 9. Springer: Berlin/Heidelberg, Germany, 2018; pp. 79–86. [Google Scholar]
- Vardian, M.; Nasriani, H.R.; Faghihi, R.; Vardian, A.; Jowkar, S. Porosity and Permeability Prediction from Well Logs Using an Adaptive Neuro-Fuzzy Inference System in a Naturally Fractured Gas-Condensate Reservoir. Energy Sources Part A Recover. Util. Environ. Eff. 2016, 38, 435–441. [Google Scholar] [CrossRef]
- Wang, X.; Yang, S.; Wang, Y.; Zhao, Y.; Ma, B. Improved Permeability Prediction Based on the Feature Engineering of Petrophysics and Fuzzy Logic Analysis in Low Porosity–Permeability Reservoir. J. Pet. Explor. Prod. Technol. 2019, 9, 869–887. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J. Integrating Well Log Interpretations for Lithofacies Classification and Permeability Modeling through Advanced Machine Learning Algorithms. J. Pet. Explor. Prod. Technol. 2017, 7, 1023–1033. [Google Scholar] [CrossRef]
- Zoveidavianpoor, M.; Samsuri, A.; Shadizadeh, S.R. Prediction of Compressional Wave Velocity by an Artificial Neural Network Using Some Conventional Well Logs in a Carbonate Reservoir. J. Geophys. Eng. 2013, 10, 45014. [Google Scholar] [CrossRef]
- Ali, M.; Zhu, P.; Jiang, R.; Huolin, M.; Ehsan, M.; Hussain, W.; Zhang, H.; Ashraf, U.; Ullaah, J. Reservoir Characterization through Comprehensive Modeling of Elastic Logs Prediction in Heterogeneous Rocks Using Unsupervised Clustering and Class-Based Ensemble Machine Learning. Appl. Soft Comput. 2023, 148, 110843. [Google Scholar] [CrossRef]
- Sridi, A.; Aliouane, L.; Doghmane, M.Z.; Ouadfeul, S.-A.; Boudella, A. Porosity and Permeability Prediction in Shaly Triassic Reservoirs of the Hassi R’mel Field (Algeria) from Well Log Data Using Fuzzy Logic. Bull. Geophys. Oceanogr. 2023, 64, 175–191. [Google Scholar]
- Okon, A.N.; Adewole, S.E.; Uguma, E.M. Artificial Neural Network Model for Reservoir Petrophysical Properties: Porosity, Permeability and Water Saturation Prediction. Model. Earth Syst. Environ. 2021, 7, 2373–2390. [Google Scholar] [CrossRef]
- Aïfa, T.; Baouche, R.; Baddari, K. Neuro-Fuzzy System to Predict Permeability and Porosity from Well Log Data: A Case Study of Hassi R’ Mel Gas Field, Algeria. J. Pet. Sci. Eng. 2014, 123, 217–229. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).