Numerical Study on the Influence of Various Design Variables on the Behavior Characteristics of Oil and Gas in Internal Floating Roof Tanks
Abstract
1. Introduction
2. Model Analysis
2.1. Governing Equations
2.2. Turbulence Equations
2.3. Meshing
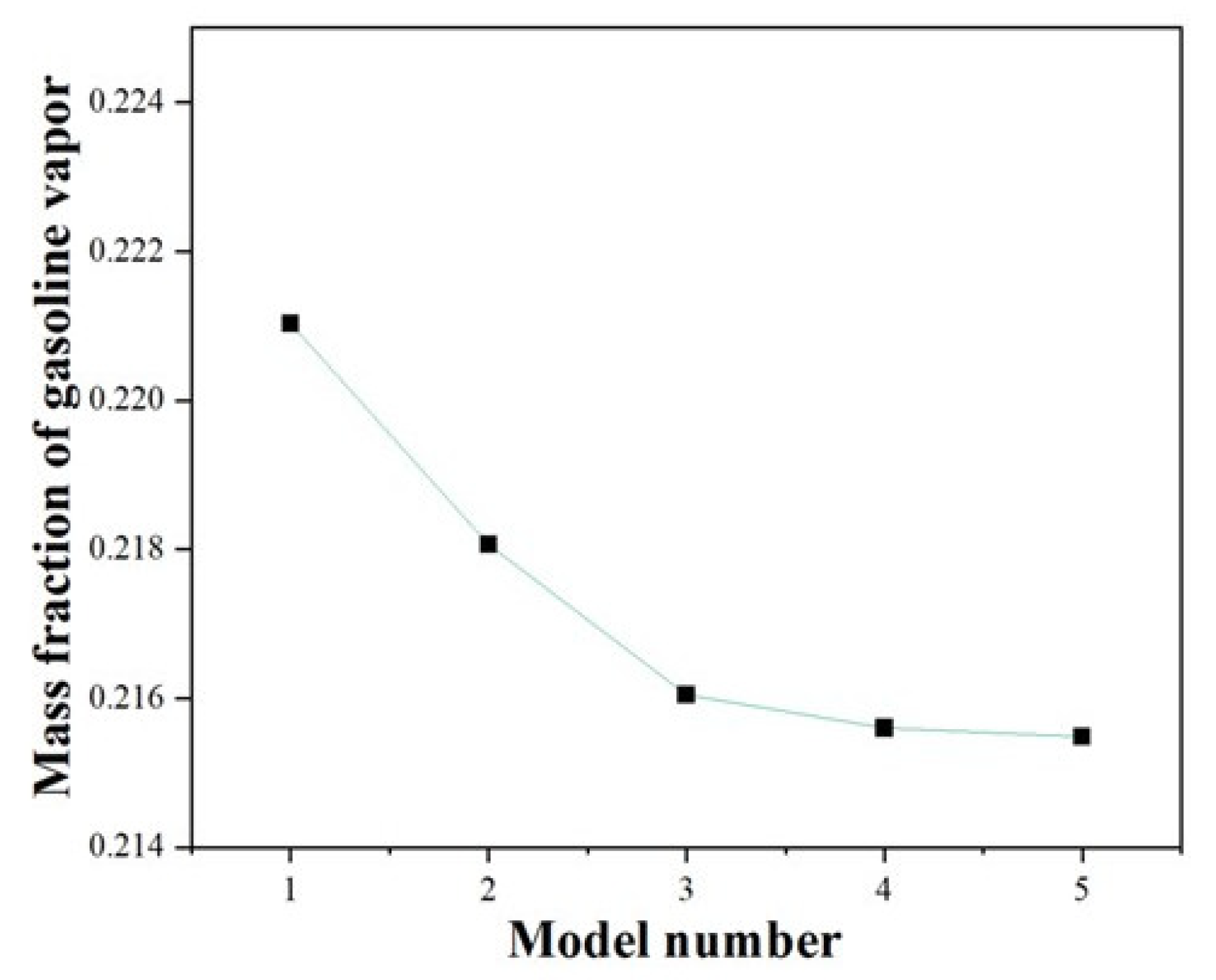
2.4. Mesh Independence Verification
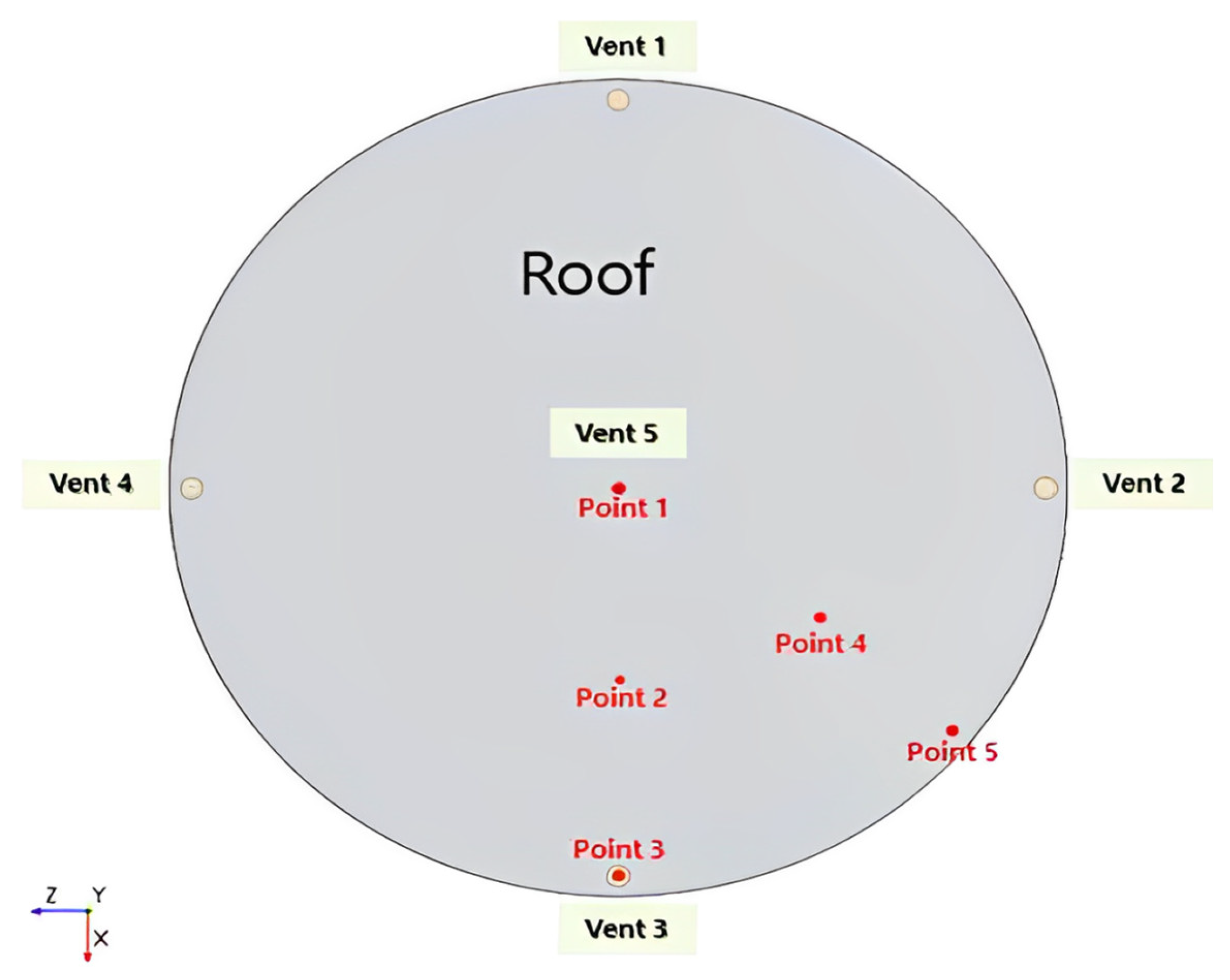
2.5. Boundary Conditions
3. Results and Discussion
3.1. Behavioral Characteristics of Gasoline Vapor in the Baseline Model
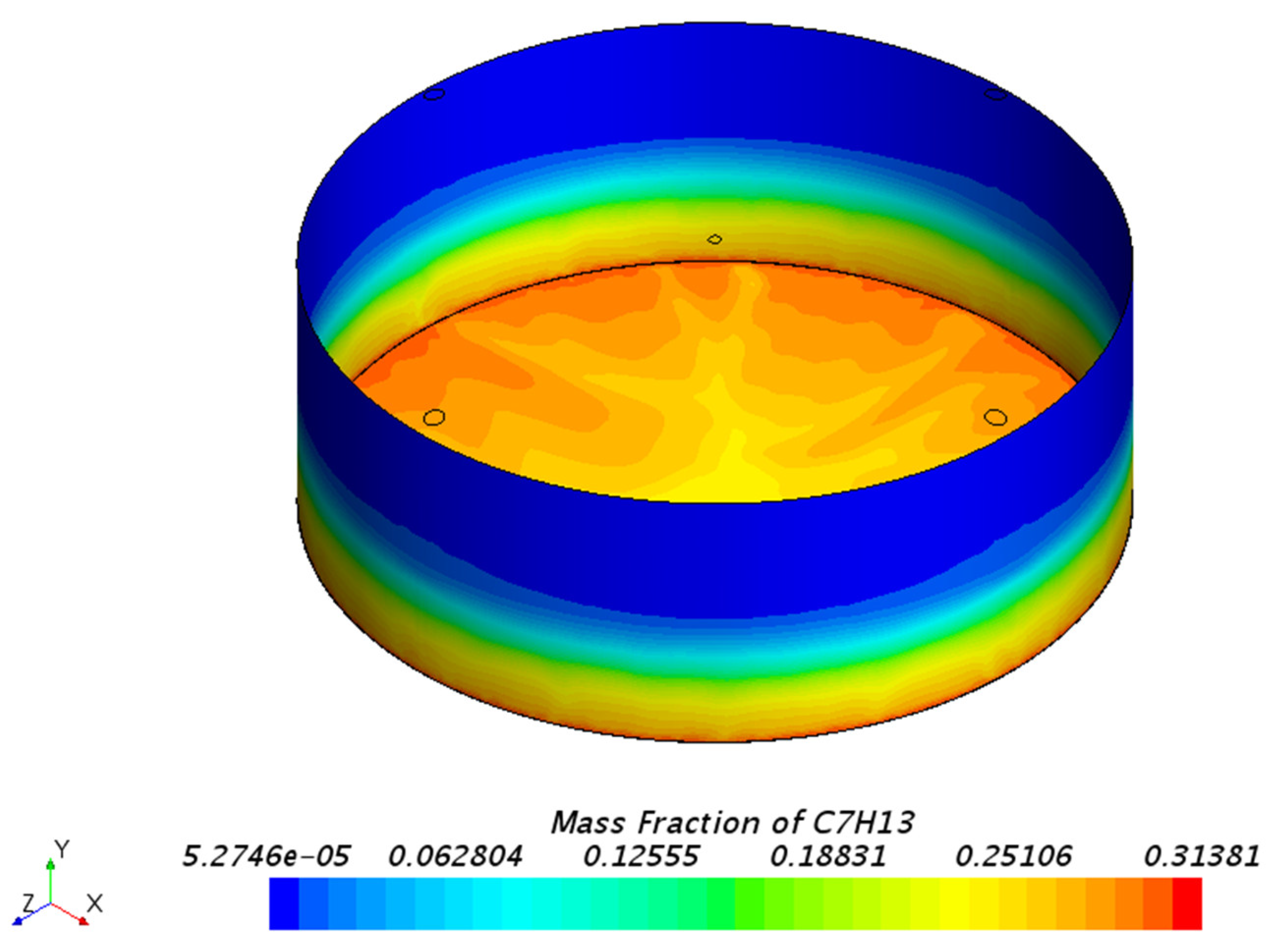
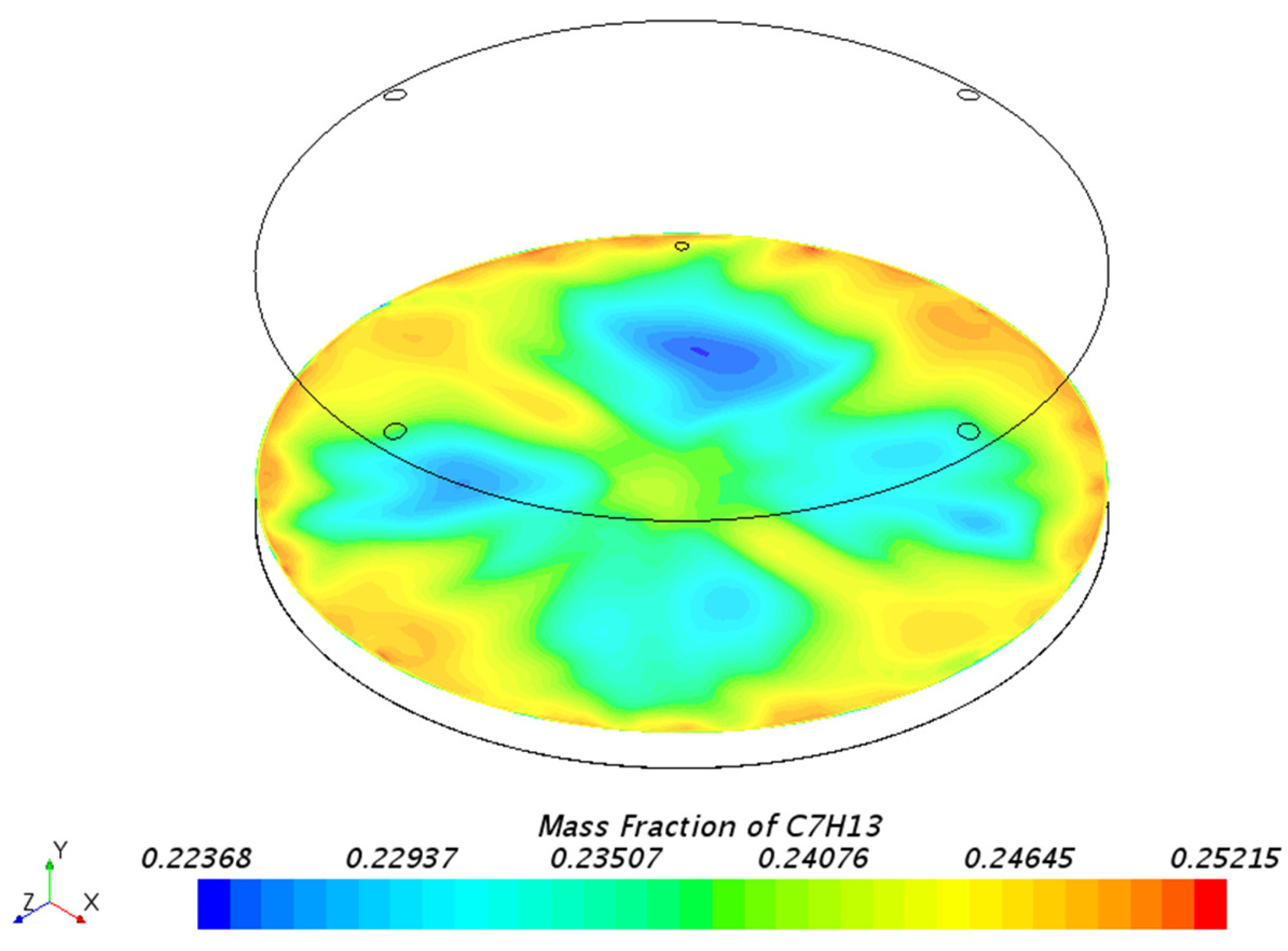
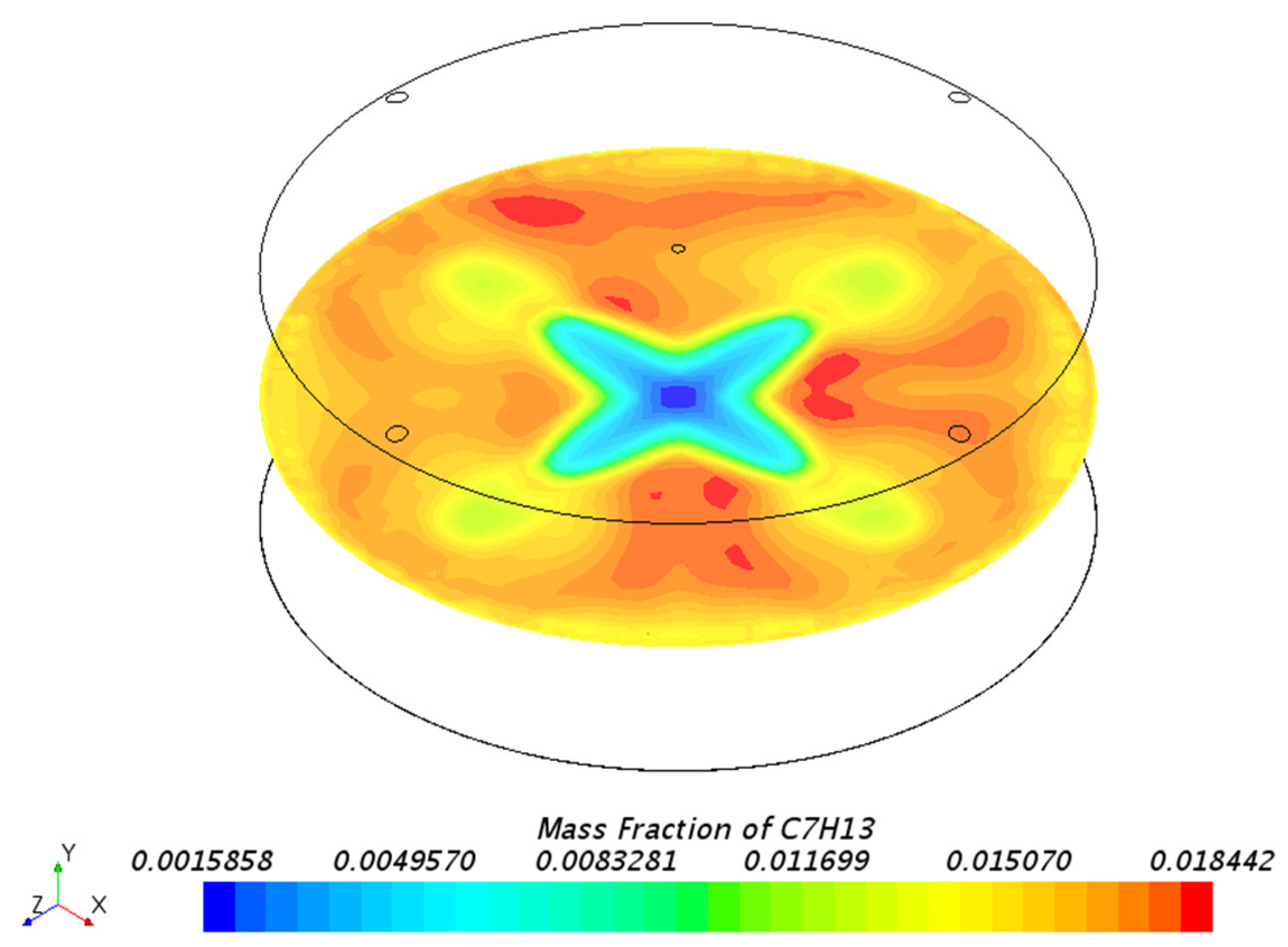
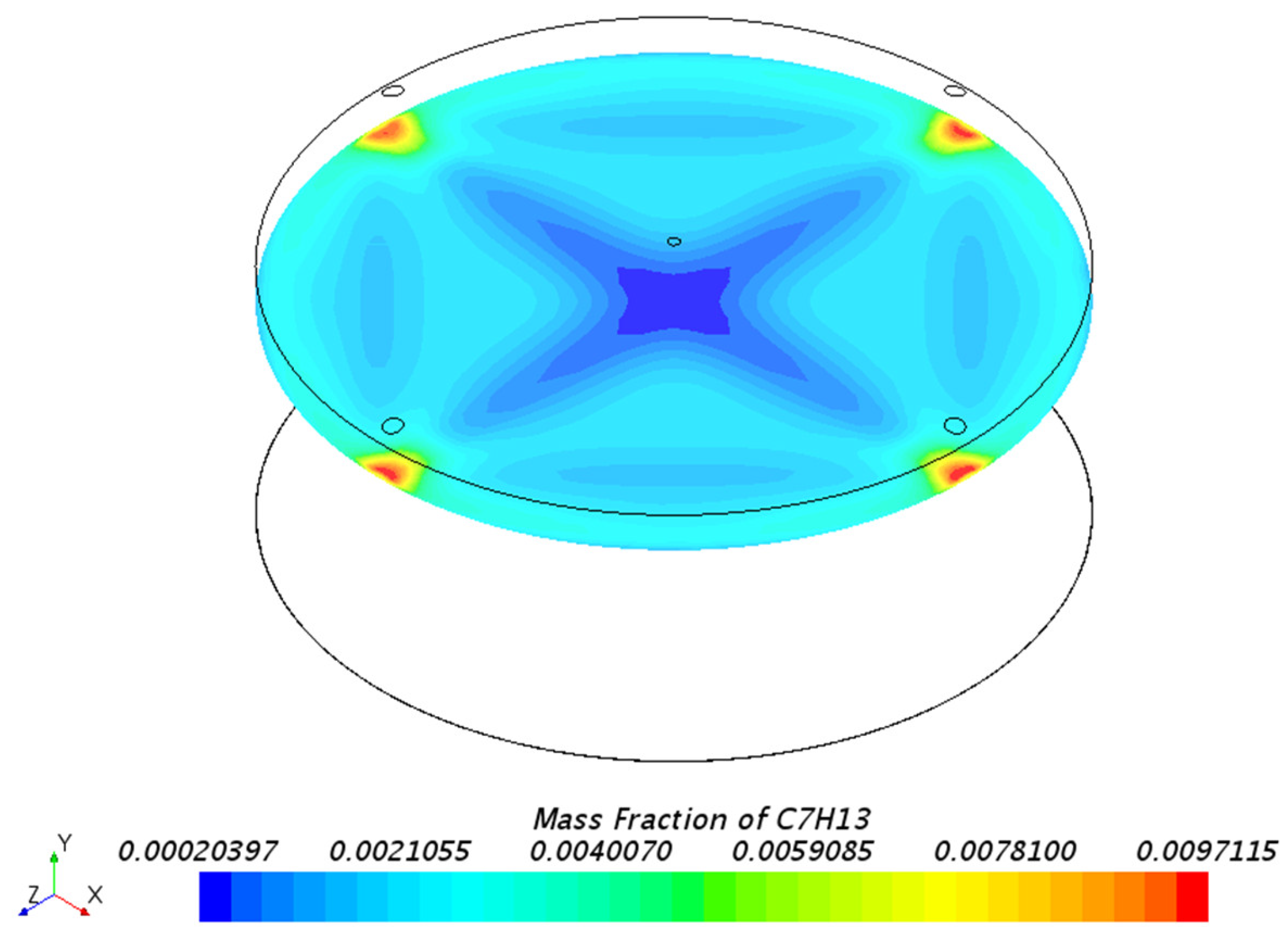
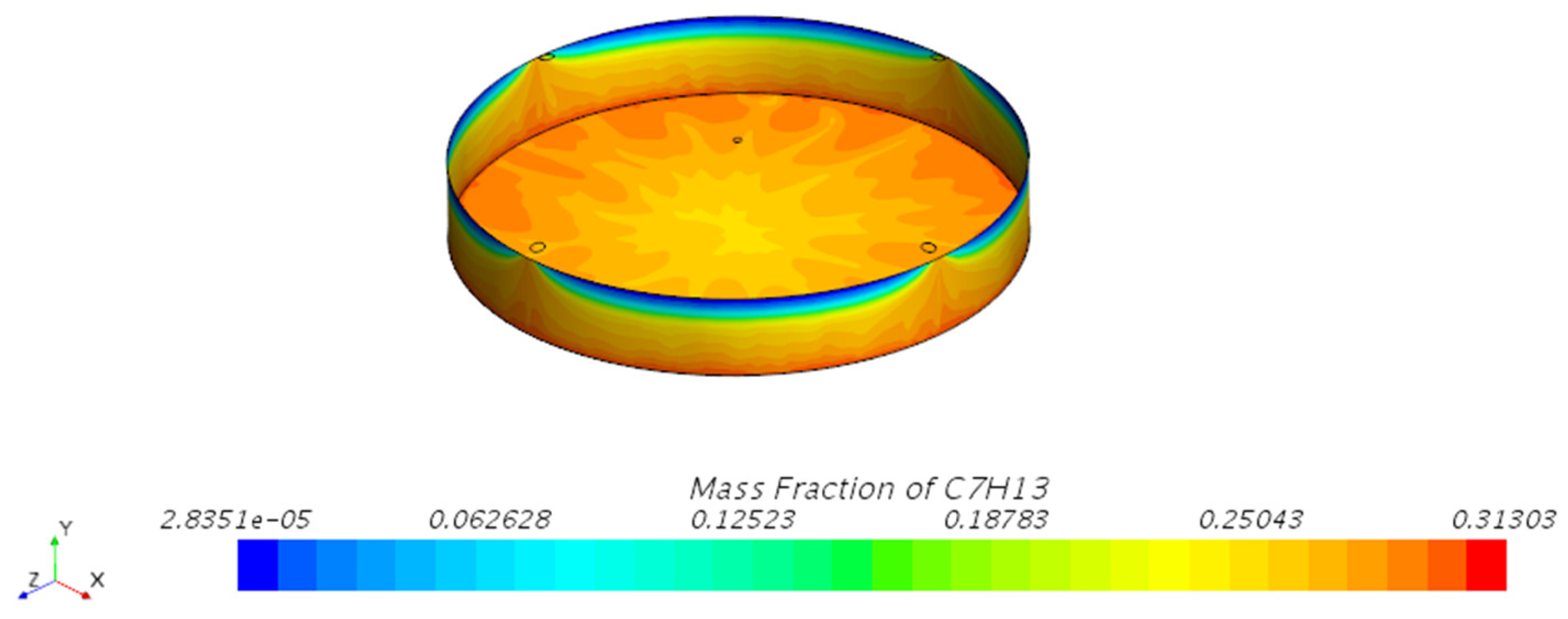
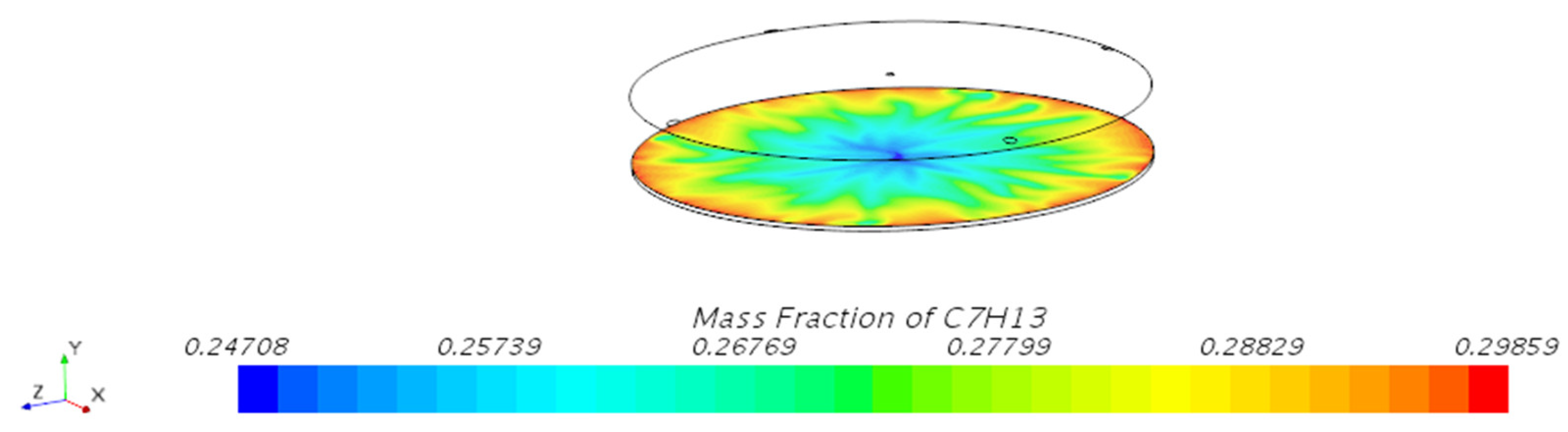
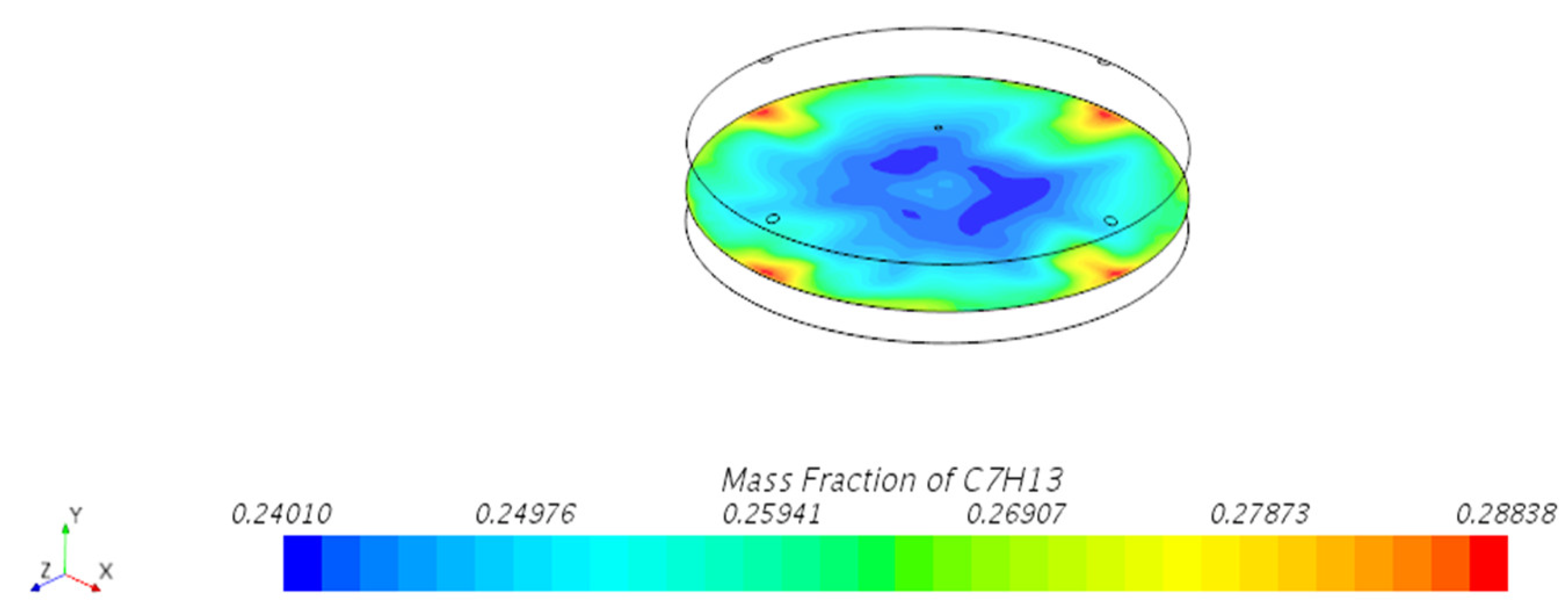
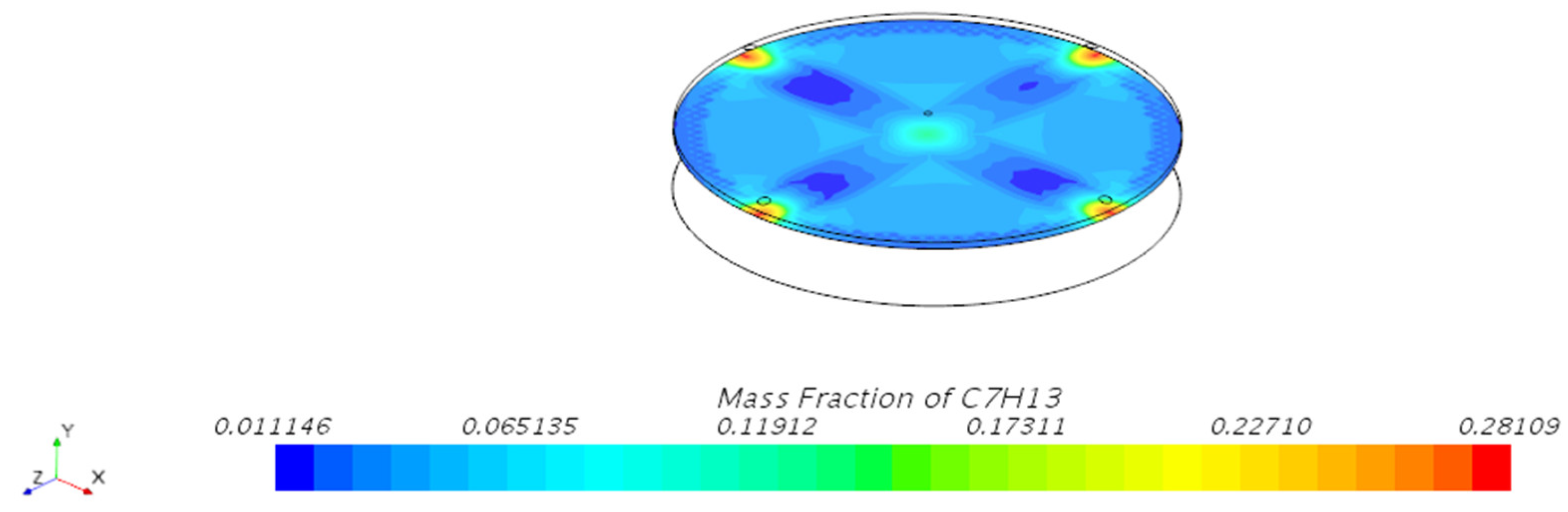
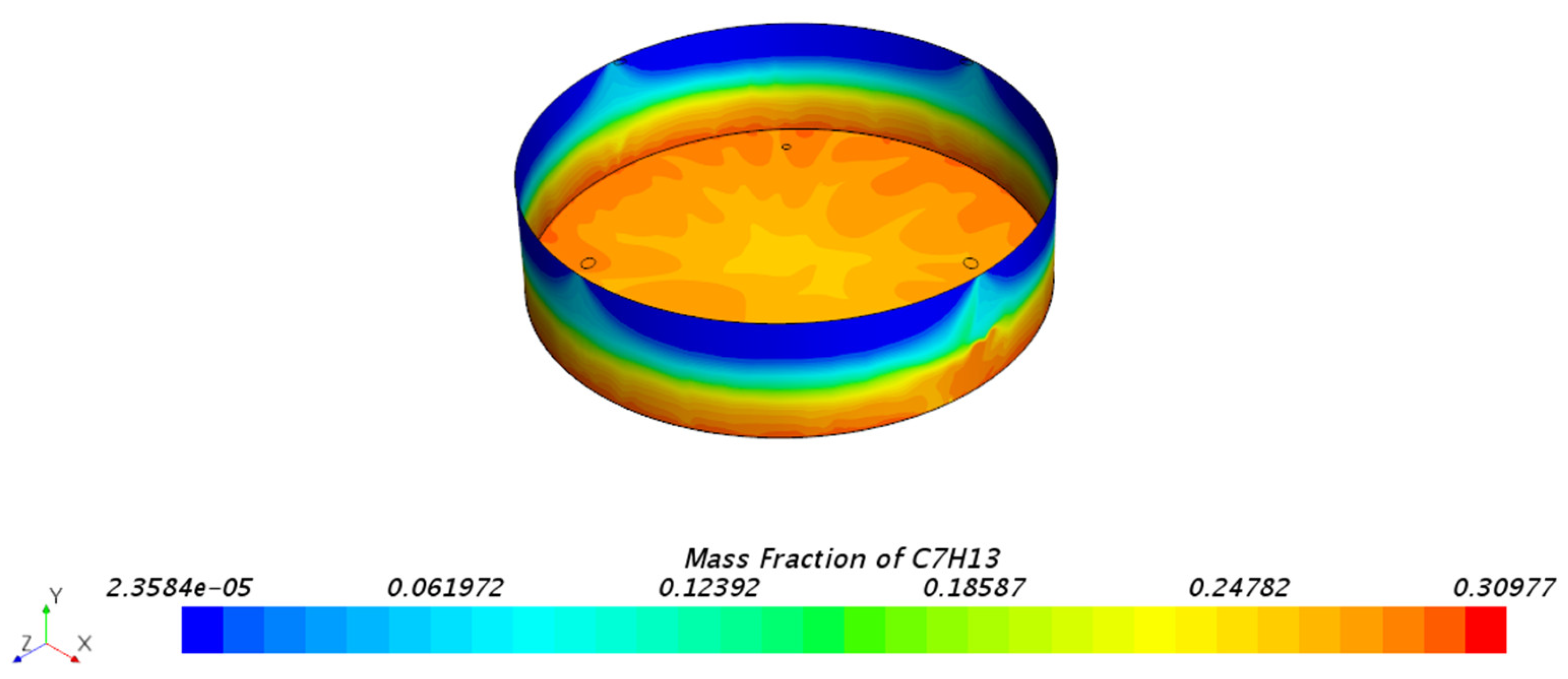
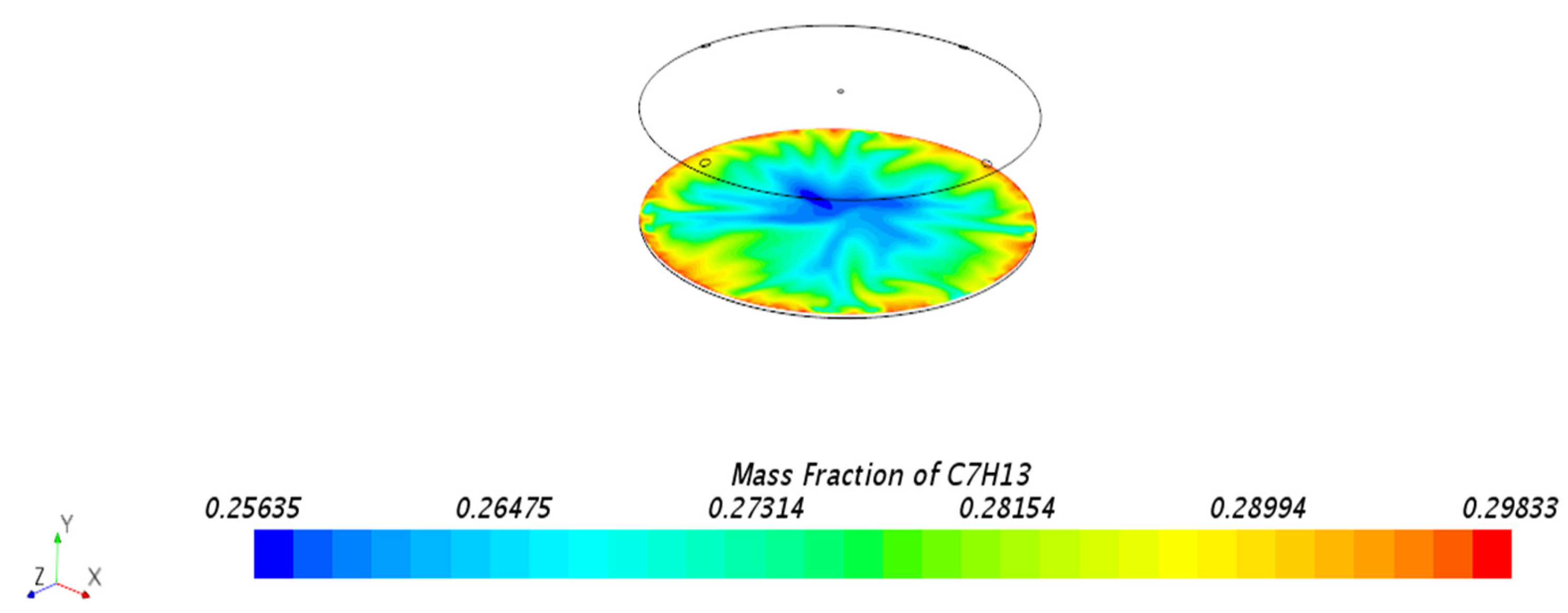
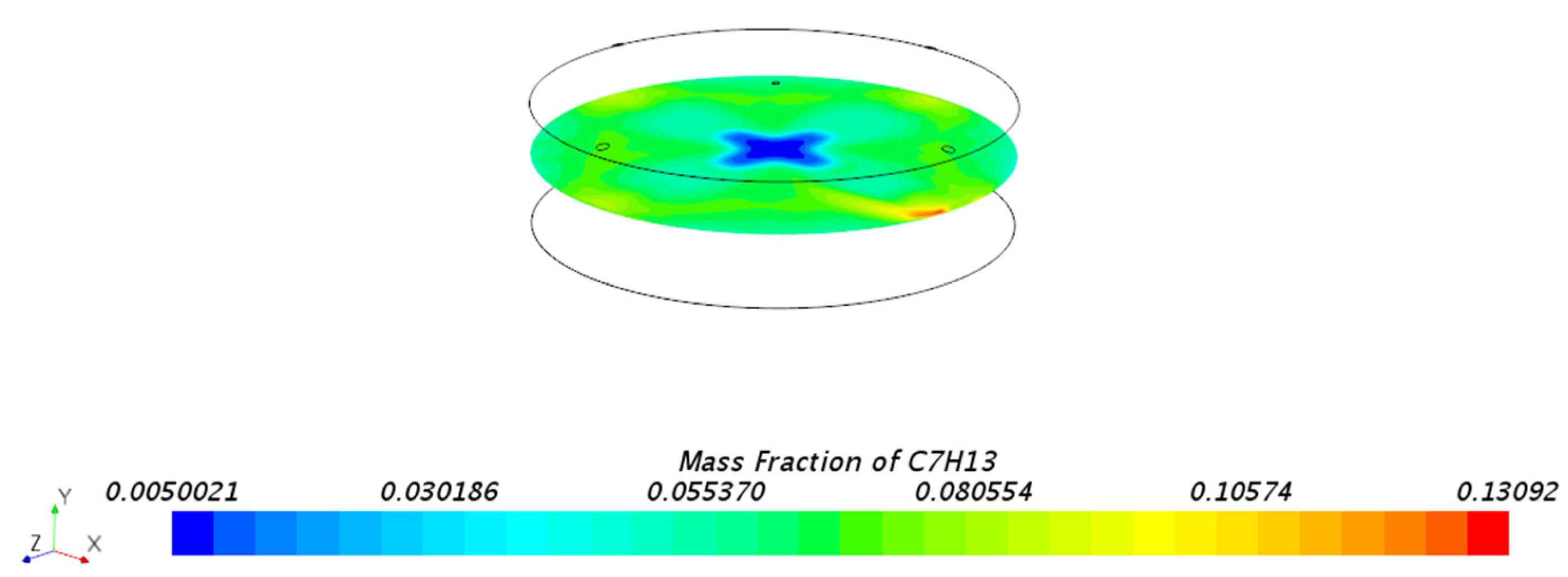
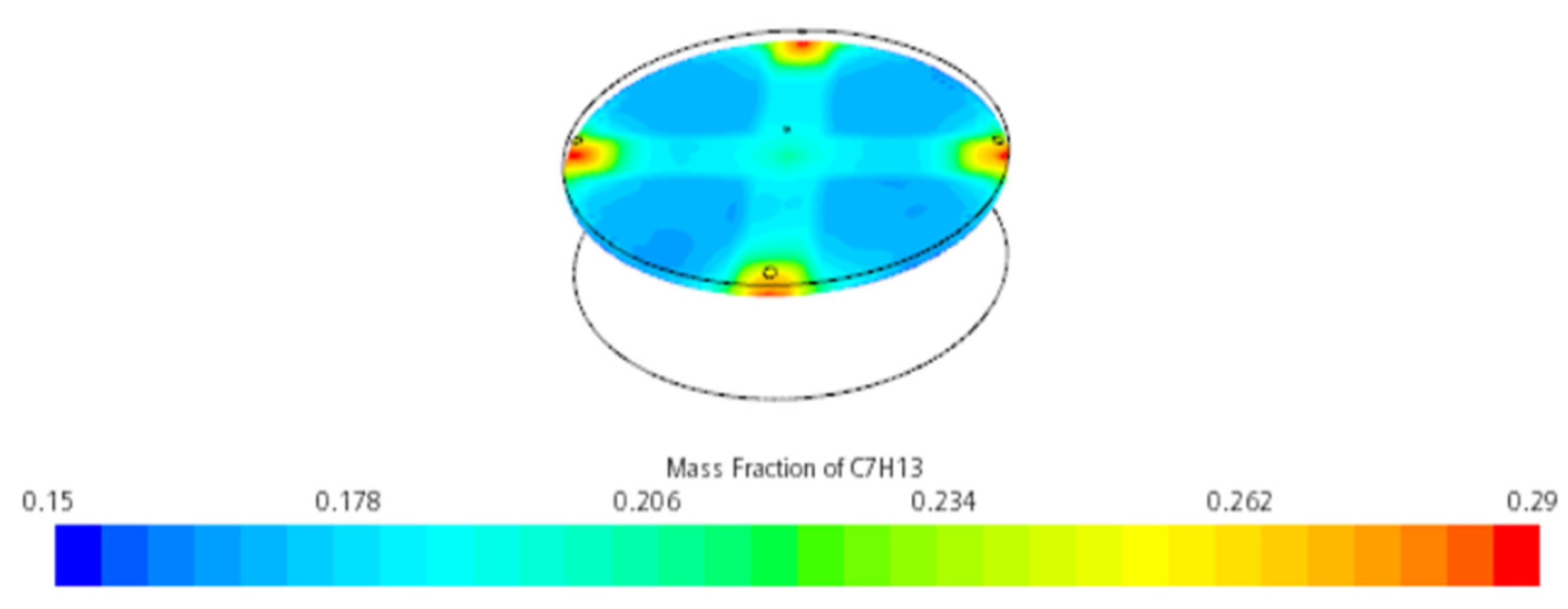
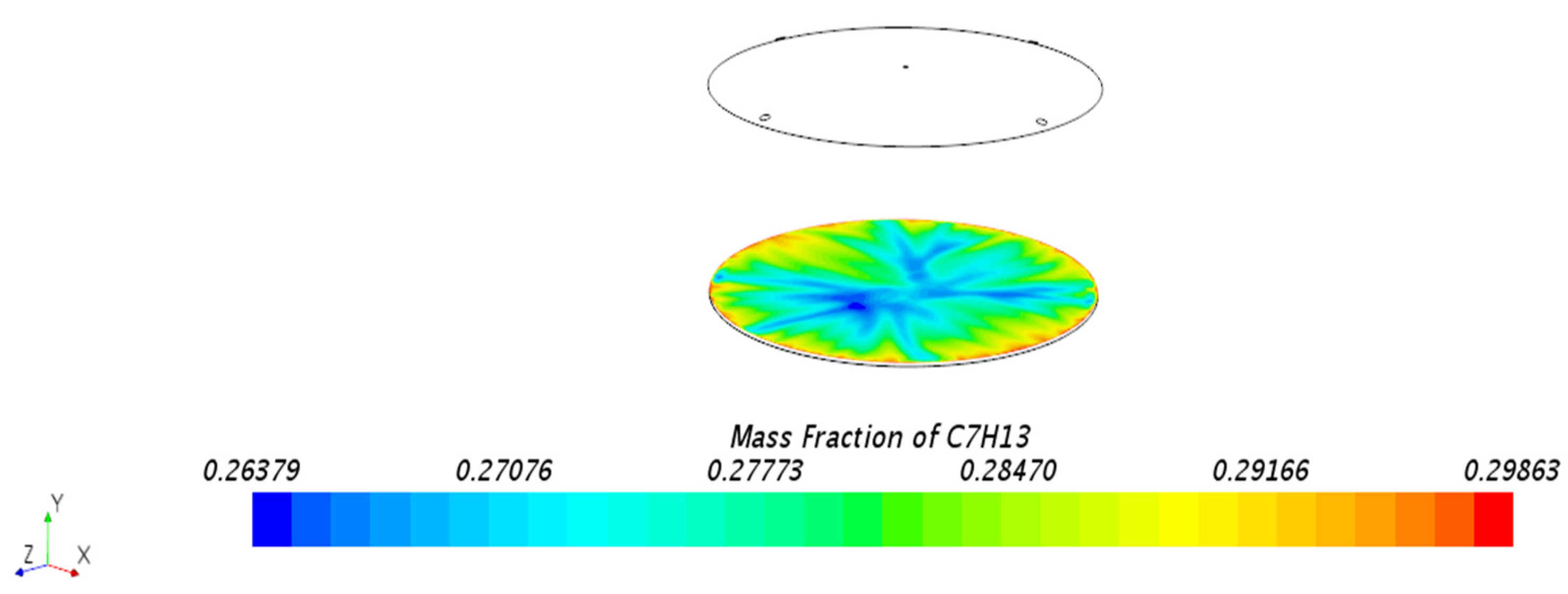
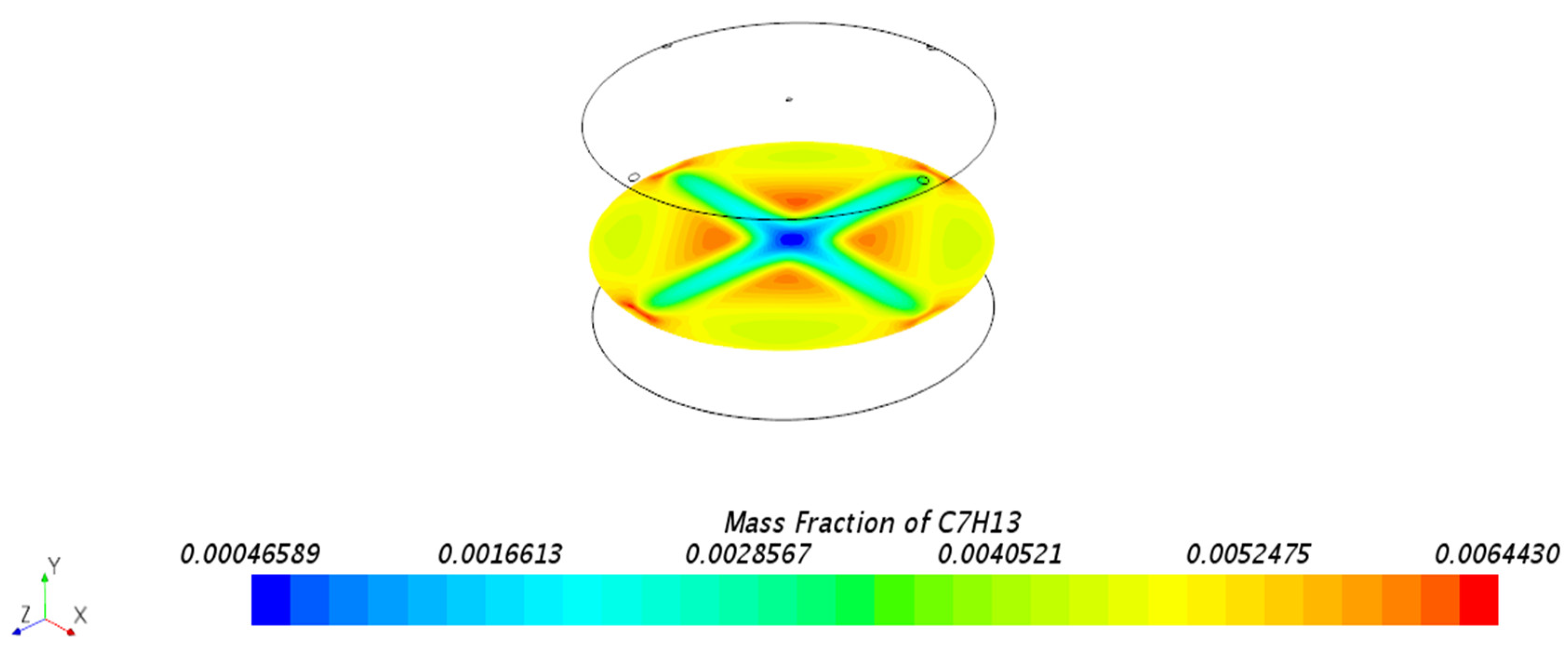
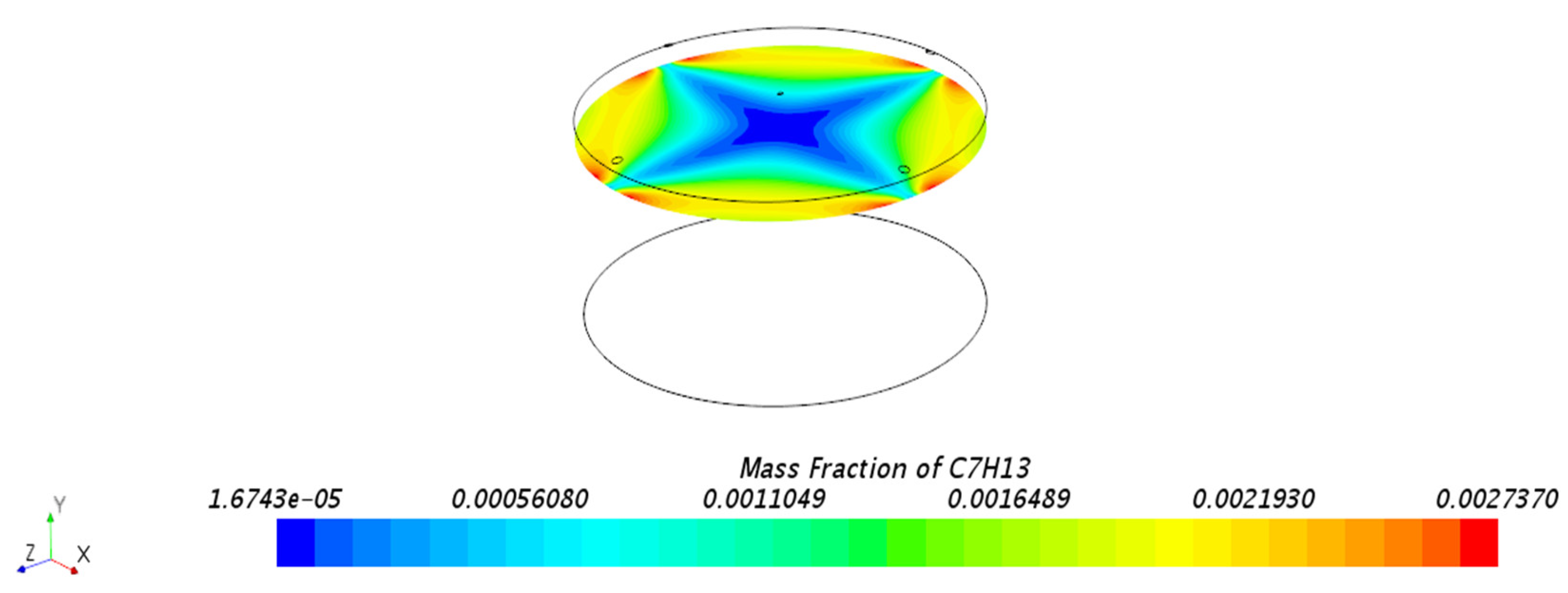
3.1.1. Mass Fraction Distribution
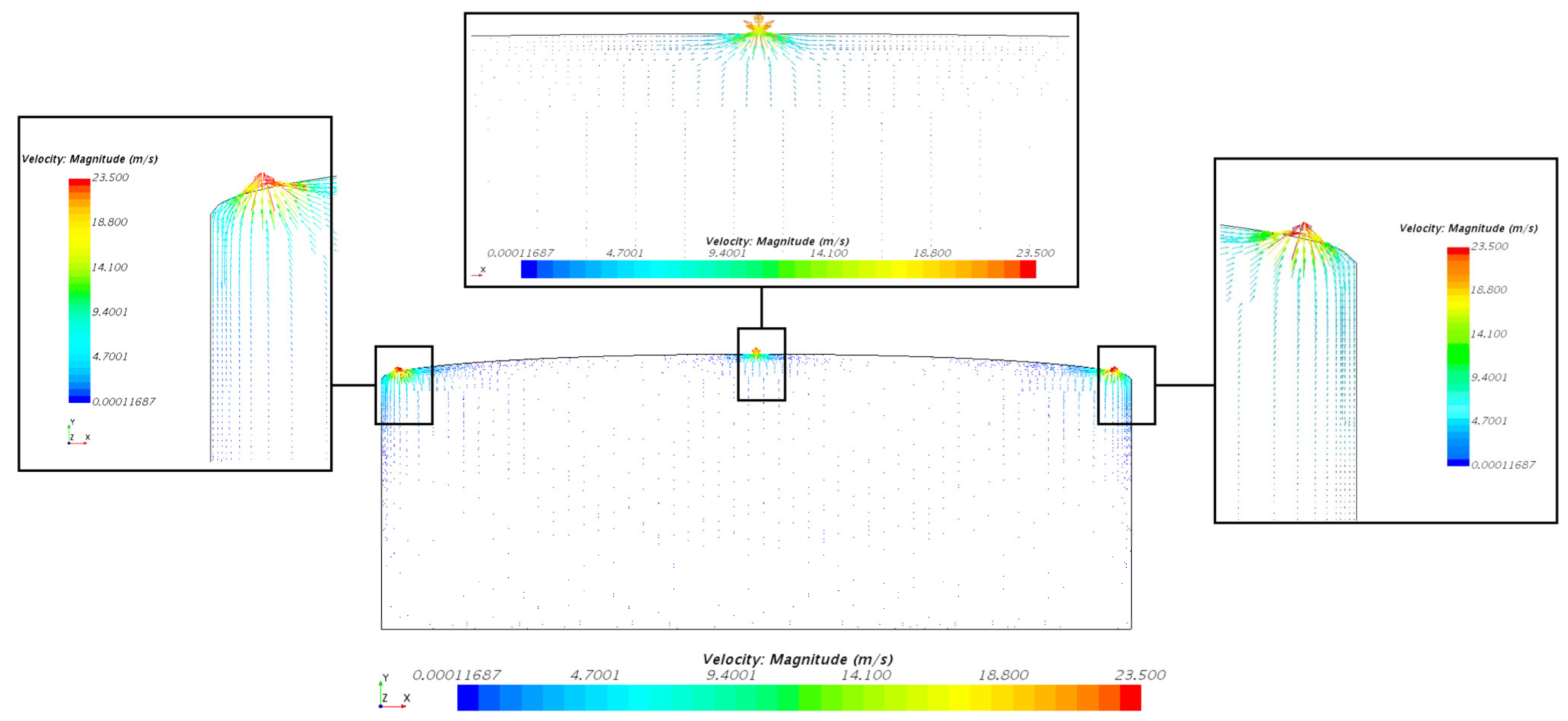
3.1.2. Velocity Distribution
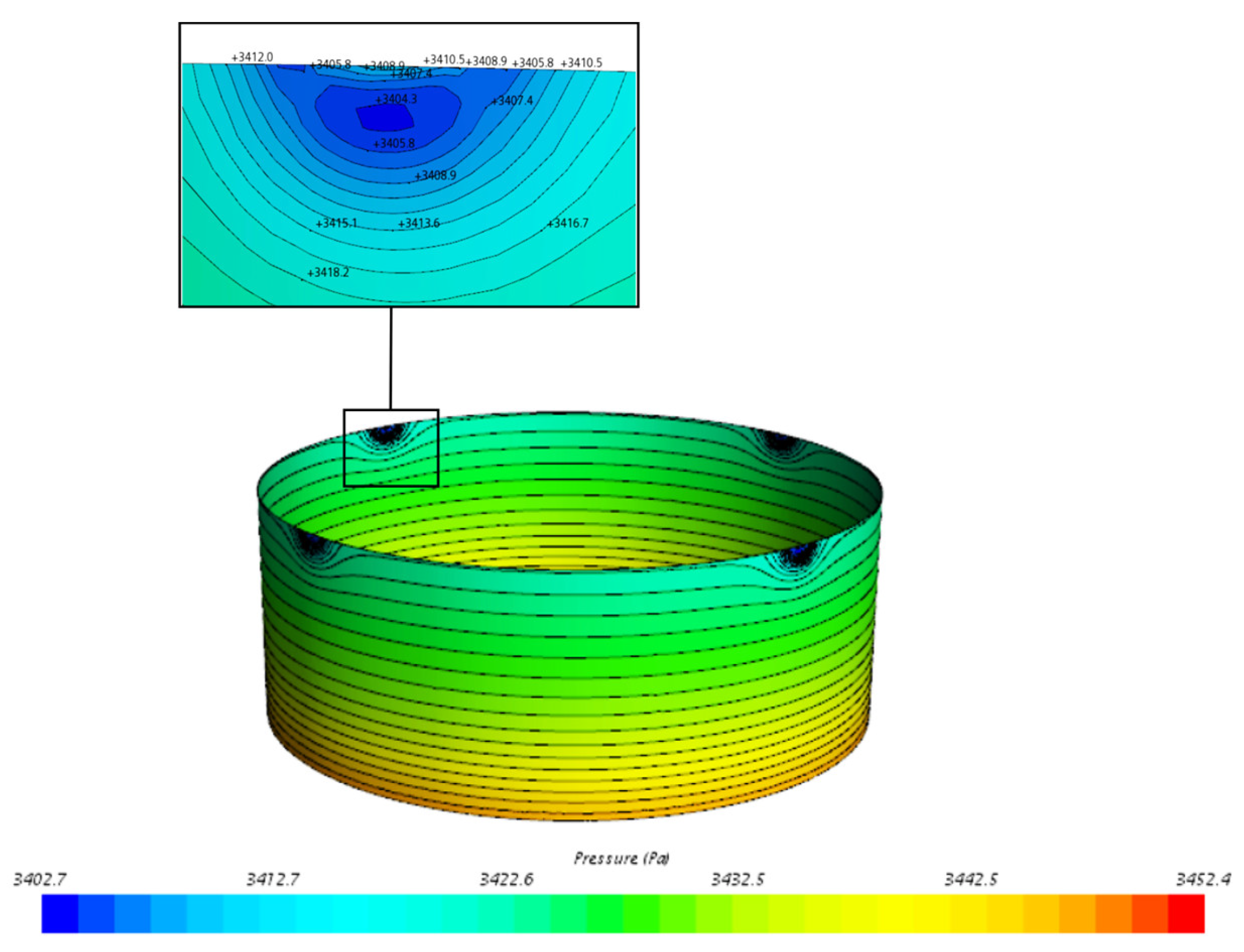
3.1.3. Pressure Distribution
3.1.4. Evaluation of Explosion Stability Caused by Oil Vapor inside Oil Tank
3.2. Behavior Characteristics of Oil Vapor in Tanks at Different Float Heights
3.2.1. Gasoline Vapor Behavior Characteristics of CASE 1
3.2.2. Gasoline Vapor Behavior Characteristics of CASE 2
3.2.3. Gasoline Vapor Behavior Characteristics of CASE 4
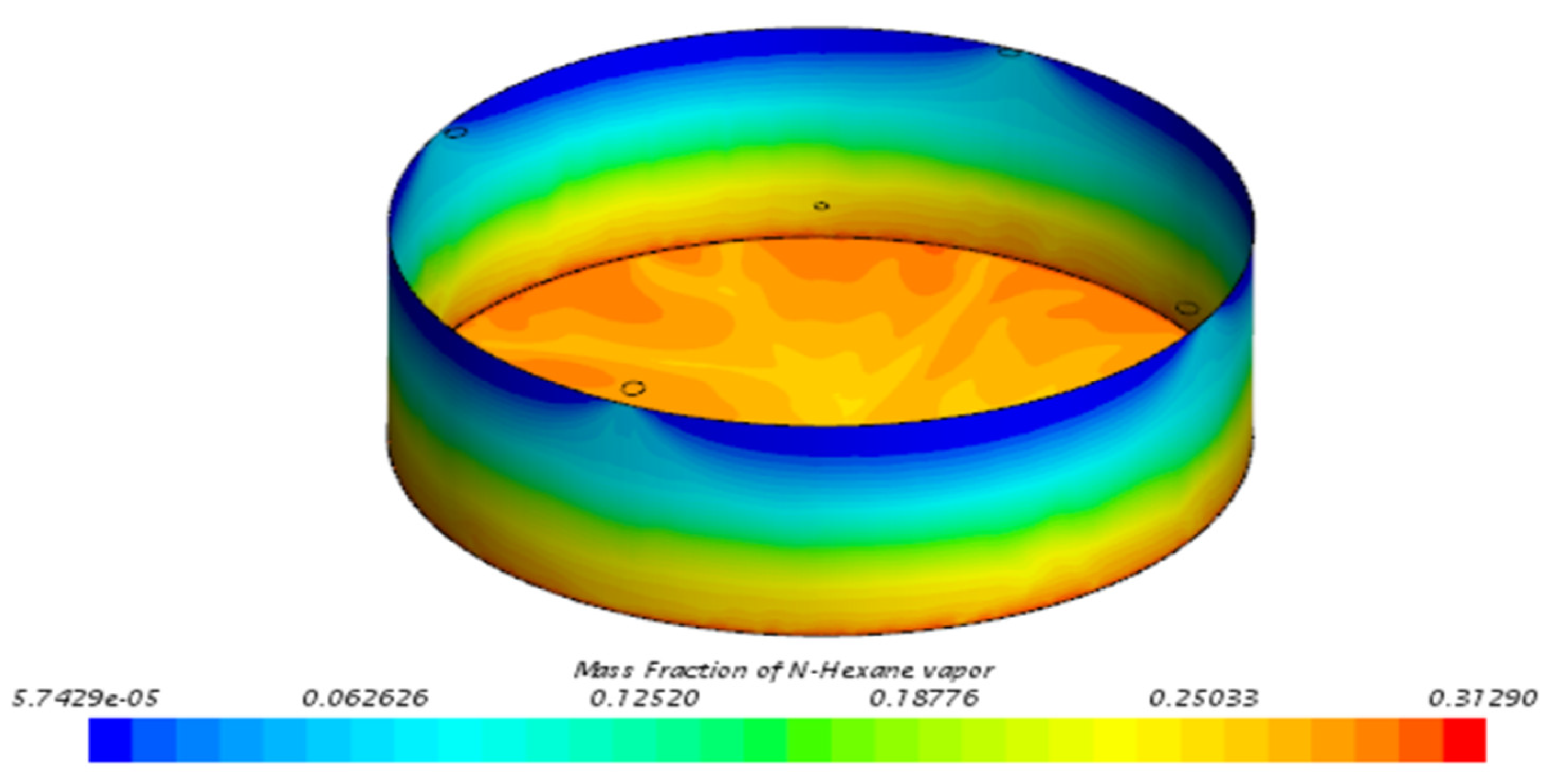
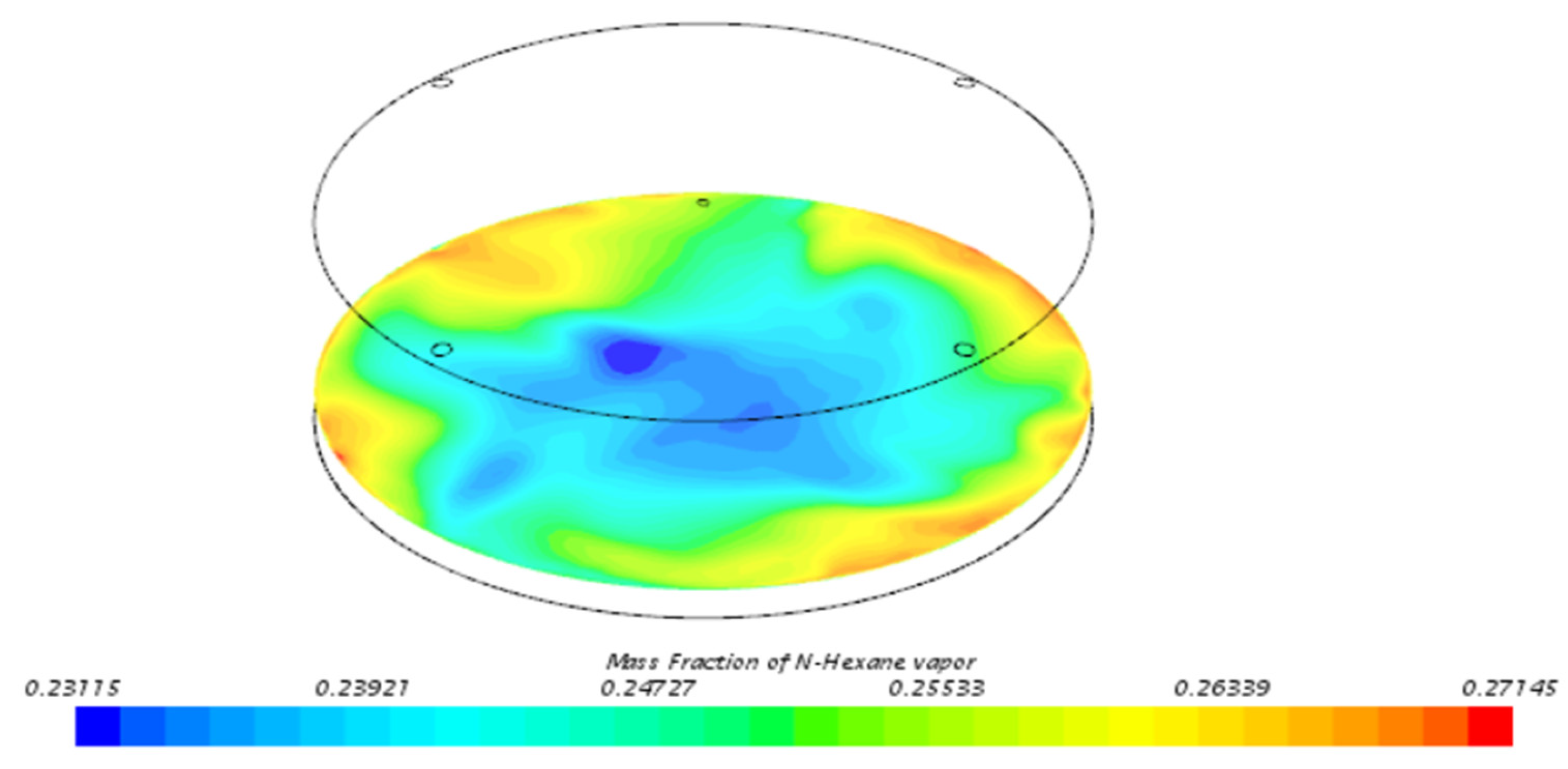
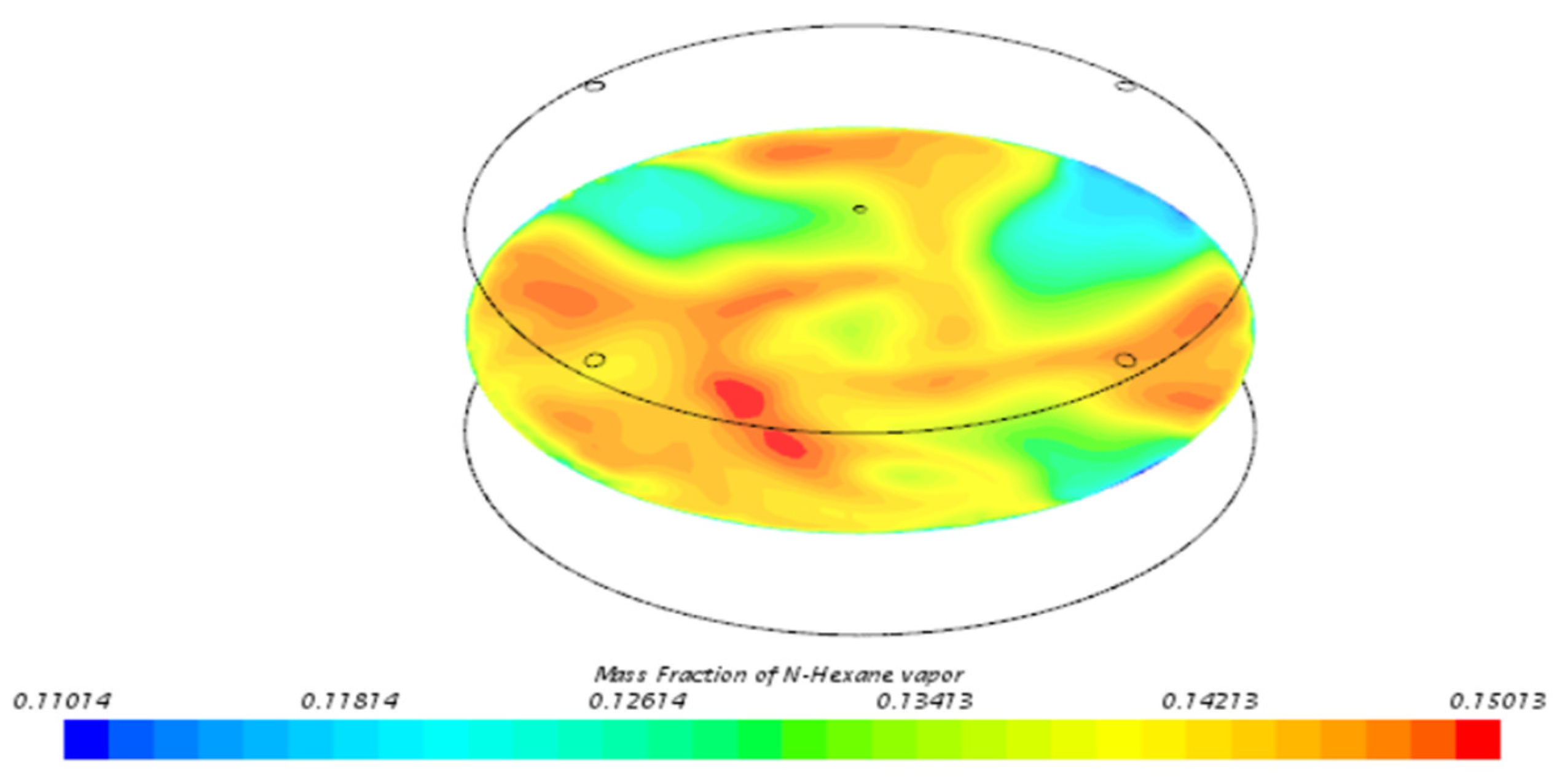
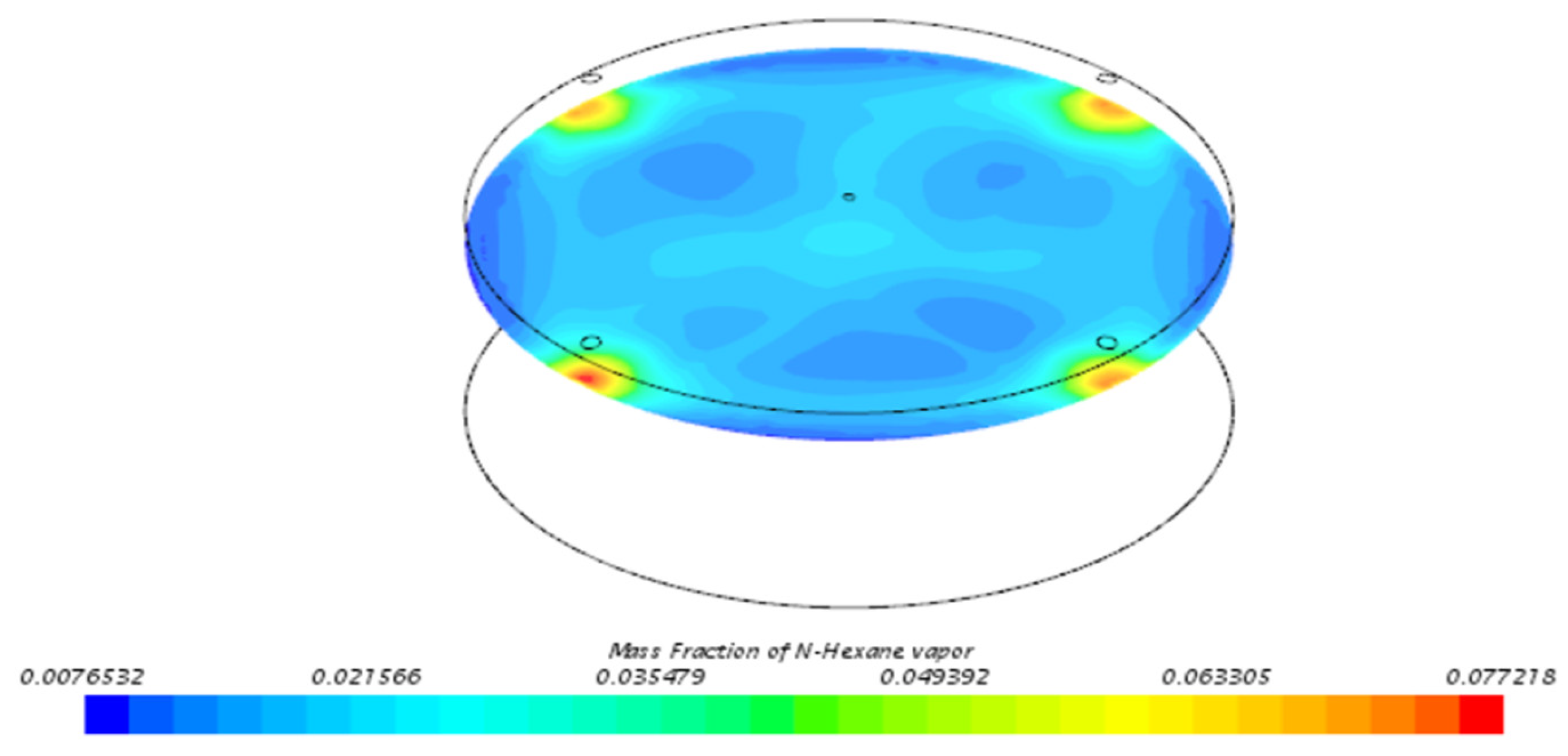
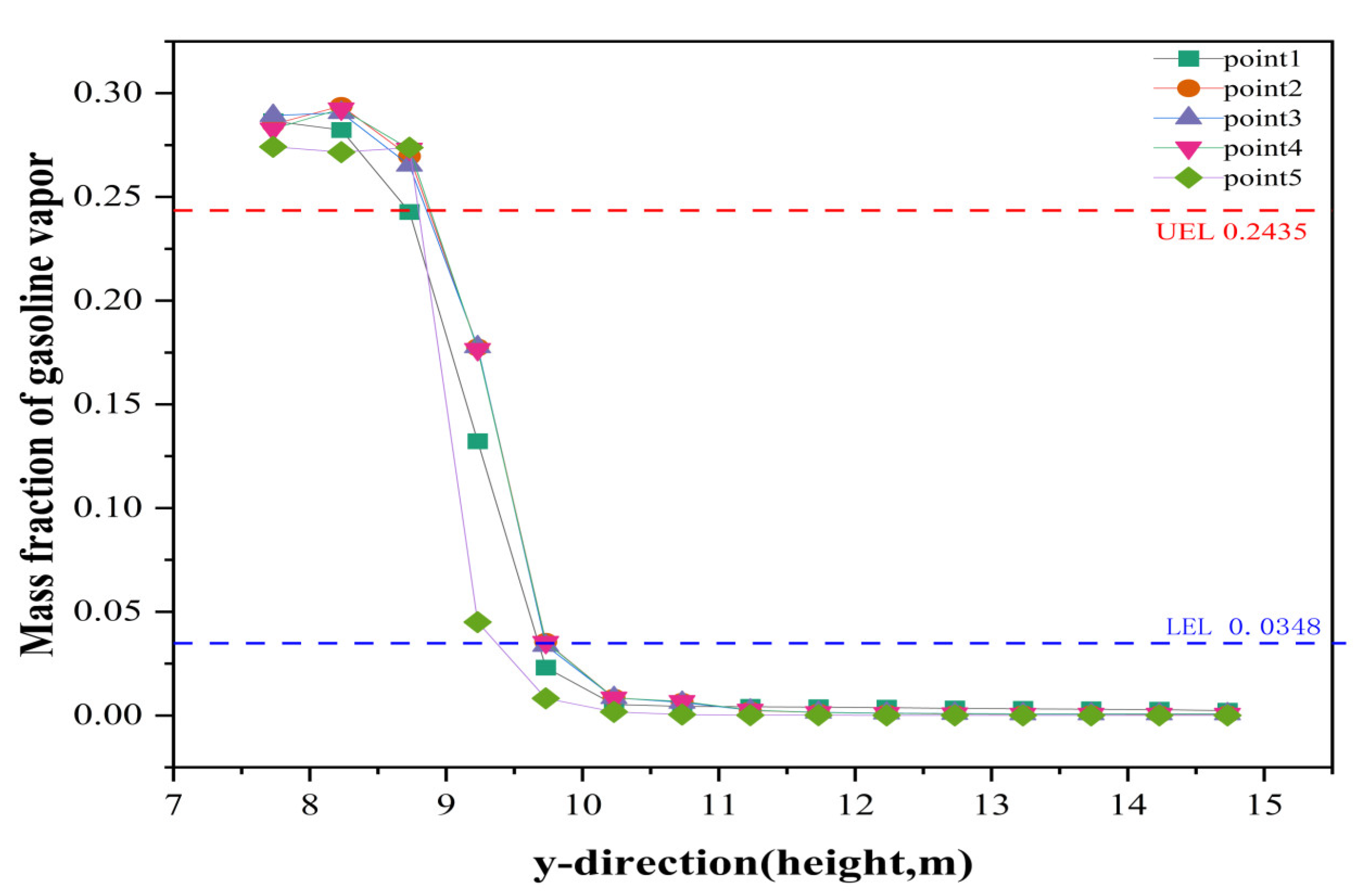
3.3. Behavior of n-Hexane in the Benchmark Model
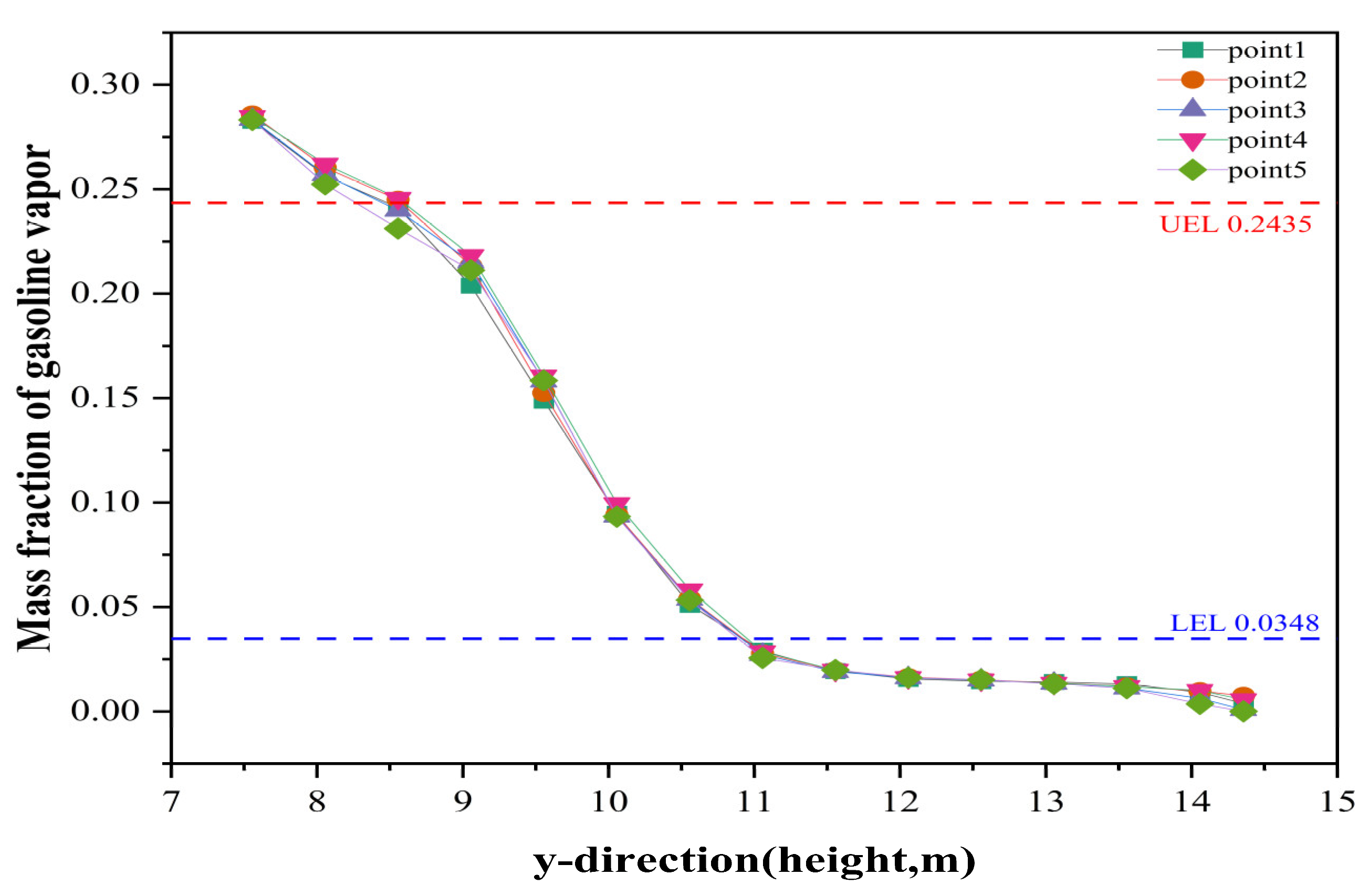
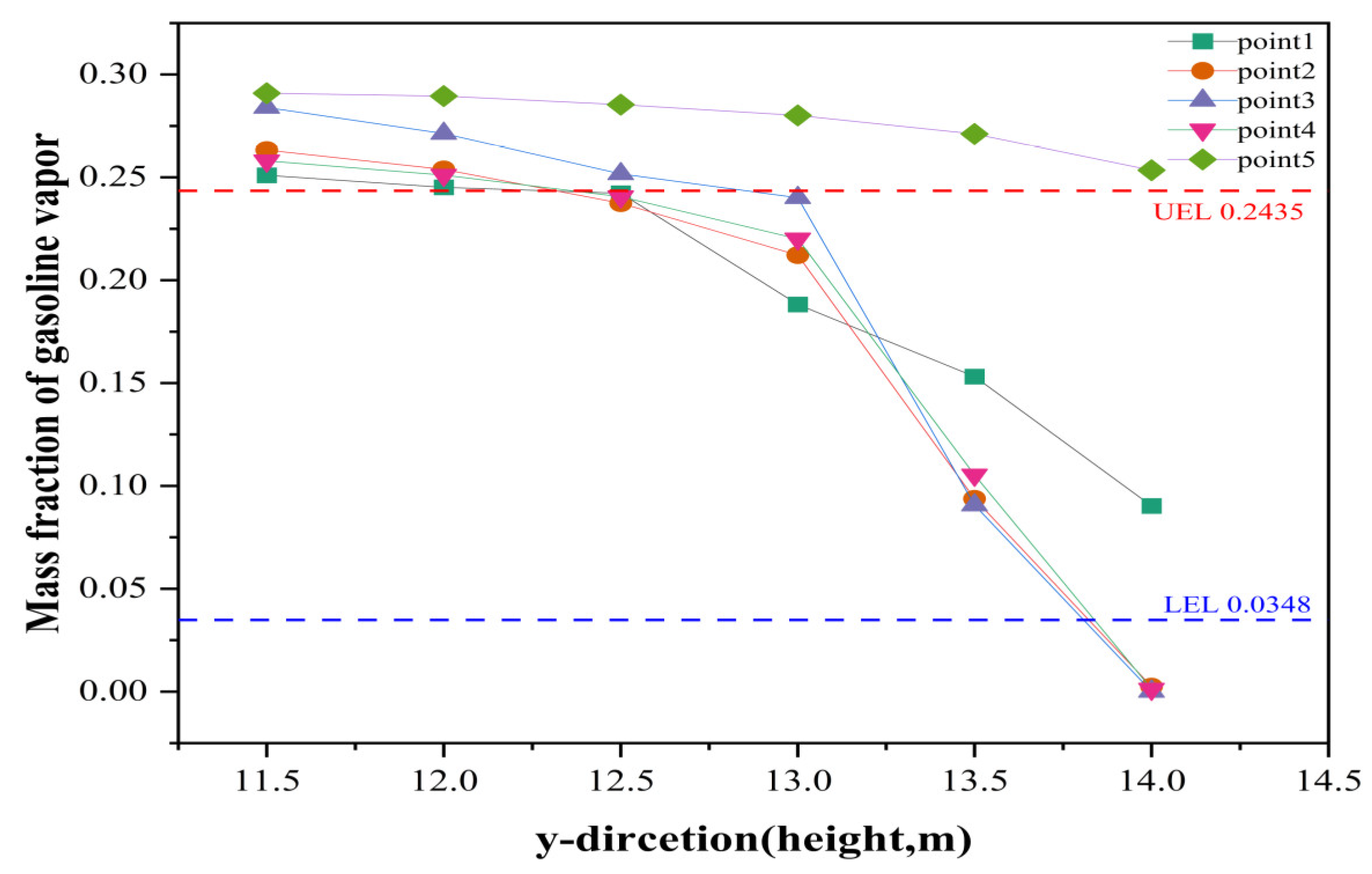
3.4. Prediction of (Gasoline) UEL and LEL by Floating Roof Height
4. Conclusions
- Impact of Floating Roof Height: Based on numerical simulations, the significant impact of floating roof height on the diffusion phenomenon of oil vapor in IFRT was confirmed. The simulation results showed that the lower the floating roof height, the lower the oil vapor mass fraction in the mixed gas region, with higher oil vapor mass fractions near the vent locations.
- Vapor Diffusion Characteristics: In the internal floating roof tank, the evaporated oil vapor primarily diffuses horizontally under the influence of gravity and exhibits a distinct vertical stratification characteristic. This characteristic is particularly evident near the vents, indicating that the vent locations significantly impact the diffusion of oil vapor.
- Tank Stability: By predicting the impact of floating roof height on oil vapor behavior, the study demonstrated the influence of the amount of oil inside the tank on the stability of the tank. Changes in floating roof height and the amount of oil inside the tank directly affect the diffusion and evaporation processes of oil vapor, thereby impacting the overall stability of the tank.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Karavaichenko, M.G.; Fathiev, N.M. Natural ventilation of gas space in reservoir with internal floating roof. Записки Гoрнoгo Института 2018, 234, 637–642. [Google Scholar]
- Pouyakian, M.; Jafari, M.J.; Laal, F.; Nourai, F.; Zarei, E. A comprehensive approach to analyze the risk of floating roof storage tanks. Process. Saf. Environ. Prot. 2020, 146, 811–836. [Google Scholar] [CrossRef]
- Wu, D.; Chen, Z. Quantitative risk assessment of fire accidents of large-scale oil tanks triggered by lightning. Eng. Fail. Anal. 2016, 63, 172–181. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, Z.; Jiang, A.; Liu, Q.; Liu, B. FDTD analysis of the effects of indirect lightning on large floating roof oil tanks. Electr. Power Syst. Res. 2016, 139, 81–86. [Google Scholar] [CrossRef]
- Tauseef, S.; Abbasi, T.; Pompapathi, V.; Abbasi, S. Case studies of 28 major accidents of fires/explosions in storage tank farms in the backdrop of available codes/standards/models for safely configuring such tank farms. Process. Saf. Environ. Prot. 2018, 120, 331–338. [Google Scholar] [CrossRef]
- Huang, W.; Huang, F.; Fang, J.; Fu, L. A calculation method for the numerical simulation of oil products evaporation and vapor diffusion in an internal floating-roof tank under the unsteady operating state. J. Pet. Sci. Eng. 2020, 188, 106867. [Google Scholar] [CrossRef]
- Saufi, A.; Calabria, R.; Chiariello, F.; Frassoldati, A.; Cuoci, A.; Faravelli, T.; Massoli, P. An experimental and CFD modeling study of suspended droplets evaporation in buoyancy driven convection. Chem. Eng. J. 2019, 375, 122006. [Google Scholar] [CrossRef]
- Afshar-Mohajer, N.; Fox, M.A.; Koehler, K. The human health risk estimation of inhaled oil spill emissions with and without adding dispersant. Sci. Total. Environ. 2018, 654, 924–932. [Google Scholar] [CrossRef]
- Parvini, M.; Gharagouzlou, E. Gas leakage consequence modeling for buried gas pipelines. J. Loss Prev. Process. Ind. 2015, 37, 110–118. [Google Scholar] [CrossRef]
- Siddiqui, M.; Jayanti, S.; Swaminathan, T. CFD analysis of dense gas dispersion in indoor environment for risk assessment and risk mitigation. J. Hazard. Mater. 2012, 209–210, 177–185. [Google Scholar] [CrossRef]
- Giannissi, S.; Hoyes, J.; Chernyavskiy, B.; Hooker, P.; Hall, J.; Venetsanos, A.; Molkov, V. CFD benchmark on hydrogen release and dispersion in a ventilated enclosure: Passive ventilation and the role of an external wind. Int. J. Hydrogen Energy 2015, 40, 6465–6477. [Google Scholar] [CrossRef]
- Giannissi, S.; Shentsov, V.; Melideo, D.; Cariteau, B.; Baraldi, D.; Venetsanos, A.; Molkov, V. CFD benchmark on hydrogen release and dispersion in confined, naturally ventilated space with one vent. Int. J. Hydrogen Energy 2015, 40, 2415–2429. [Google Scholar] [CrossRef]
- Li, X.; Chen, G.; Zhu, H.; Xu, C. Gas dispersion and deflagration above sea from subsea release and its impact on offshore platform. Ocean Eng. 2018, 163, 157–168. [Google Scholar] [CrossRef]
- Stamoudis, N.; Chryssakis, C.; Kaiktsis, L. A two-component heavy fuel oil evaporation model for CFD studies in marine Diesel engines. Fuel 2014, 115, 145–153. [Google Scholar] [CrossRef]
- Hassanvand, A.; Hashemabadi, S.; Bayat, M. Evaluation of gasoline evaporation during the tank splash loading by CFD techniques. Int. Commun. Heat Mass Transf. 2010, 37, 907–913. [Google Scholar] [CrossRef]
- Galeev, A.; Salin, A.; Ponikarov, S. Numerical simulation of evaporation of volatile liquids. J. Loss Prev. Process. Ind. 2015, 38, 39–49. [Google Scholar] [CrossRef]
- Huang, W.; Fang, J.; Li, F.; Ji, H.; Wang, H. Numerical simulation and applications of equivalent film thickness in oil evaporation loss evaluation of internal floating-roof tank. Process. Saf. Environ. Prot. 2019, 129, 74–88. [Google Scholar] [CrossRef]
- Kim, E.; Park, J.; Cho, J.H.; Moon, I. Simulation of hydrogen leak and explosion for the safety design of hydrogen fueling station in Korea. Int. J. Hydrogen Energy 2013, 38, 1737–1743. [Google Scholar] [CrossRef]
- Hata, H.; Yamada, H.; Kokuryo, K.; Okada, M.; Funakubo, C.; Tonokura, K. Estimation model for evaporative emissions from gasoline vehicles based on thermodynamics. Sci. Total. Environ. 2018, 618, 1685–1691. [Google Scholar] [CrossRef]
- Hai-Juan PA, N.; Jun-Bo ZH, O.U.; Liang-Chao CH, E.N.; Jian-Feng YA, N.G.; Xin-Yuan, L.U. Study on leakage and diffusion law of “large breathing” loss of gasoline storage tank based on PHAST. In Proceedings of the 2018 International Conference on Energy Development and Environmental Protection (EDEP 2018), Nanjing, China, 17–19 August 2018; Atlantis Press: Amsterdam, The Netherlands, 2018; pp. 134–140. [Google Scholar]
- Zhang, G.; Huang, F.; Huang, W.; Zhu, Z.; Fang, J.; Ji, H.; Fu, L.; Sun, X. Analysis of Influence of Floating-Deck Height on Oil-Vapor Migration and Emission of Internal Floating-Roof Tank Based on Numerical Simulation and Wind-Tunnel Experiment. Processes 2020, 8, 1026. [Google Scholar] [CrossRef]
- Hou, Y.; Chen, J.; Zhu, L.; Sun, D.; Li, J.; Jie, P. Numerical simulation of gasoline evaporation in refueling process. Adv. Mech. Eng. 2017, 9, 1687814017714978. [Google Scholar] [CrossRef]
- Sun, W.; Cheng, Q.; Zheng, A.; Gan, Y.; Gao, W.; Liu, Y. Heat flow coupling characteristics analysis and heating effect evaluation study of crude oil in the storage tank different structure coil heating processes. Int. J. Heat Mass Transf. 2018, 127, 89–101. [Google Scholar] [CrossRef]
- Du, L.; Zhao, W.; Yan, H.; Liu, D. Stability and Strength Analysis of Internal Floating Roof Atmospheric Tank. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kazimierz Dolny, Poland, 21–23 November 2019; Volume 592. [Google Scholar]
- Pasley, H.; Clark, C. Computational fluid dynamics study of flow around floating-roof oil storage tanks. J. Wind Eng. Ind. Aerodyn. 2000, 86, 37–54. [Google Scholar] [CrossRef]
- Zhao, C.L.; Huang, W.Q.; Zhong, J.; Wang, W.J.; Xu, X.Y.; Wang, Y.X. Numerical simulation of oil vapor leakage from external floating-roof tank. CIESC J. 2014, 65, 4203–4209. [Google Scholar]
- Uematsu, Y.; Koo, C.; Yasunaga, J. Design wind force coefficients for open-topped oil storage tanks focusing on the wind-induced buckling. J. Wind Eng. Ind. Aerodyn. 2014, 130, 16–29. [Google Scholar] [CrossRef]
- Uematsu, Y.; Yasunaga, J.; Koo, C. Design wind loads for open-topped storage tanks in various arrangements. J. Wind Eng. Ind. Aerodyn. 2015, 138, 77–86. [Google Scholar] [CrossRef]
- Hassanvand, A.; Hashemabadi, S.H. Direct numerical simulation of interphase mass transfer in gas-liquid multiphase systems. Int. Commun. Heat Mass Transf. 2011, 7, 943–950. [Google Scholar] [CrossRef]
- Hao, Q.F.; Huang, W.Q.; Jing, H.B. Numerical simulation of oil vapor leakage and diffusion from different pores of external floating-roof tank. Chem. Ind. Eng. Prog. 2019, 38, 1226–1235. [Google Scholar]



| Mesh Tpye | Polyhedral Mesher |
|---|---|
| Base Size | 400 mm |
| Number of Prism Layer | 7 |
| Prism Layer Stretching | 1.2 |
| Prism Layer Thickness | 20% |
| Volumetric Relative size | 30 |
| Volumetric Controls | 120 mm |
| Number of Volume Mesh Cells | 530,000 |
| Number of Model | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Number of Meshes | 443,776 | 496,334 | 523,536 | 657,442 | 704,625 |
| Boundary | Condition |
|---|---|
| Space | There-dimensional |
| Fluid | Multi-component gas |
| Flow solver | Segregated |
| Equation of state | Constant Density |
| Viscous regime | Turbulence |
| Reynolds-averaged turbulence | Realizable k-ε |
| Reynolds Number | 5.5 × 10⁶ |
| Prandtl Number | 0.9 |
| Schmidt Number | 1 |
| Locations/States | Parameters | Comments | |
|---|---|---|---|
| Inlet (Air) | Speed entrance | 2.5 m/s, 4.5 m/s, 6.5 m/s | Velocity Inlet |
| Inlet | Gap between the floating deck and tank wall | m/s | Velocity |
| Outlet | Free exit | 101.325 kPa | Pressure Outlet |
| Wall | Tank bottom, wall, floating deck | 0 | No-slip |
| Mass fraction | saturated concentration of N-hexane | 0.3 | gap of the floating deck |
| Ambient | Outside of the tank | 303 K | Temperature |
| LEL | UEL | |||
|---|---|---|---|---|
| [vol %] | [Mass Fraction] | [vol %] | [Mass Fraction] | |
| Gasoline | 1.4 | 0.0530 | 7.6 | 0.2447 |
| n-Hexane | 1.2 | 0.0348 | 7.6 | 0.2435 |
| Height of Floating Deck | Height of Mixed Gas | Computational Domain | |
|---|---|---|---|
| CASE 1 | 11 | 3.7 | 3.7 |
| CASE 2 | 9 | 5.7 | 5.7 |
| CASE 3 [Basic Model] | 7 | 7.7 | 7.7 |
| CASE 4 | 5 | 9.7 | 9.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.-C.; Liu, M.; Dang, S.-W.; Hu, L.-C.; Chen, G.; Zhang, S.-D.; Kong, X.-H.; Xu, H. Numerical Study on the Influence of Various Design Variables on the Behavior Characteristics of Oil and Gas in Internal Floating Roof Tanks. Energies 2024, 17, 4336. https://doi.org/10.3390/en17174336
Li J-C, Liu M, Dang S-W, Hu L-C, Chen G, Zhang S-D, Kong X-H, Xu H. Numerical Study on the Influence of Various Design Variables on the Behavior Characteristics of Oil and Gas in Internal Floating Roof Tanks. Energies. 2024; 17(17):4336. https://doi.org/10.3390/en17174336
Chicago/Turabian StyleLi, Ji-Chao, Ming Liu, Shi-Wang Dang, Ling-Chong Hu, Guang Chen, Sheng-Dong Zhang, Xiang-Hu Kong, and Heng Xu. 2024. "Numerical Study on the Influence of Various Design Variables on the Behavior Characteristics of Oil and Gas in Internal Floating Roof Tanks" Energies 17, no. 17: 4336. https://doi.org/10.3390/en17174336
APA StyleLi, J.-C., Liu, M., Dang, S.-W., Hu, L.-C., Chen, G., Zhang, S.-D., Kong, X.-H., & Xu, H. (2024). Numerical Study on the Influence of Various Design Variables on the Behavior Characteristics of Oil and Gas in Internal Floating Roof Tanks. Energies, 17(17), 4336. https://doi.org/10.3390/en17174336






