Fast Terminal Sliding-Mode Predictive Speed Controller for Permanent-Magnet Synchronous Motor Drive Systems
Abstract
1. Introduction
2. Dynamic Model of PMSM
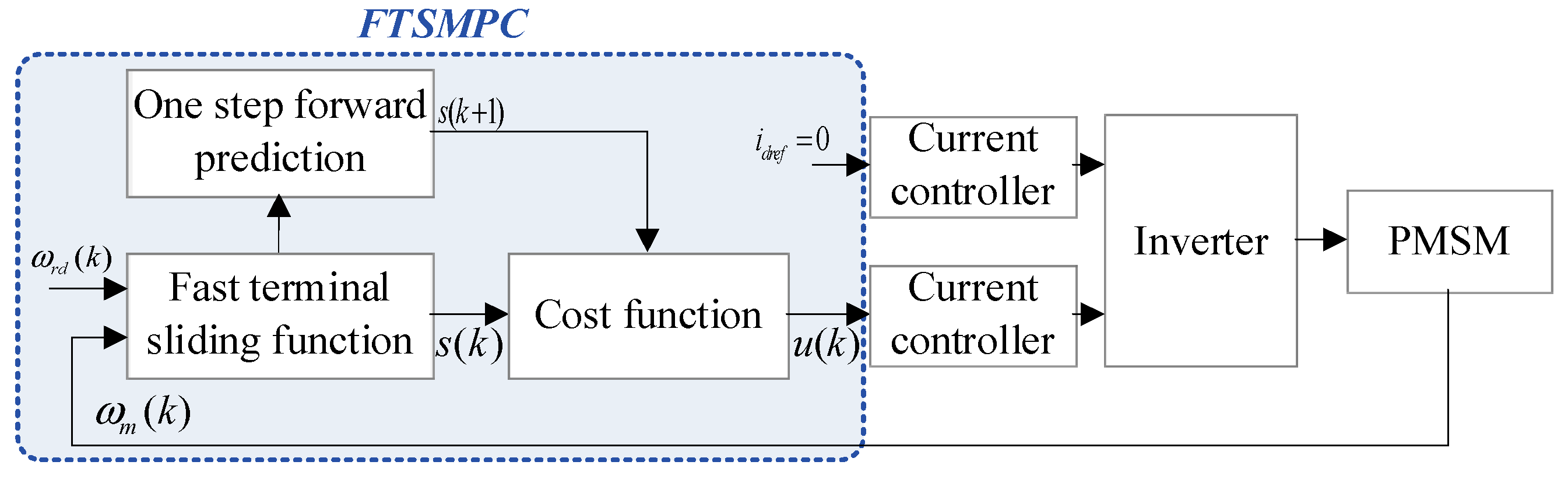
3. Proposed FTSMPC
3.1. Proposed FTSMPC for Speed Control
3.2. Stability and Convergence Analysis
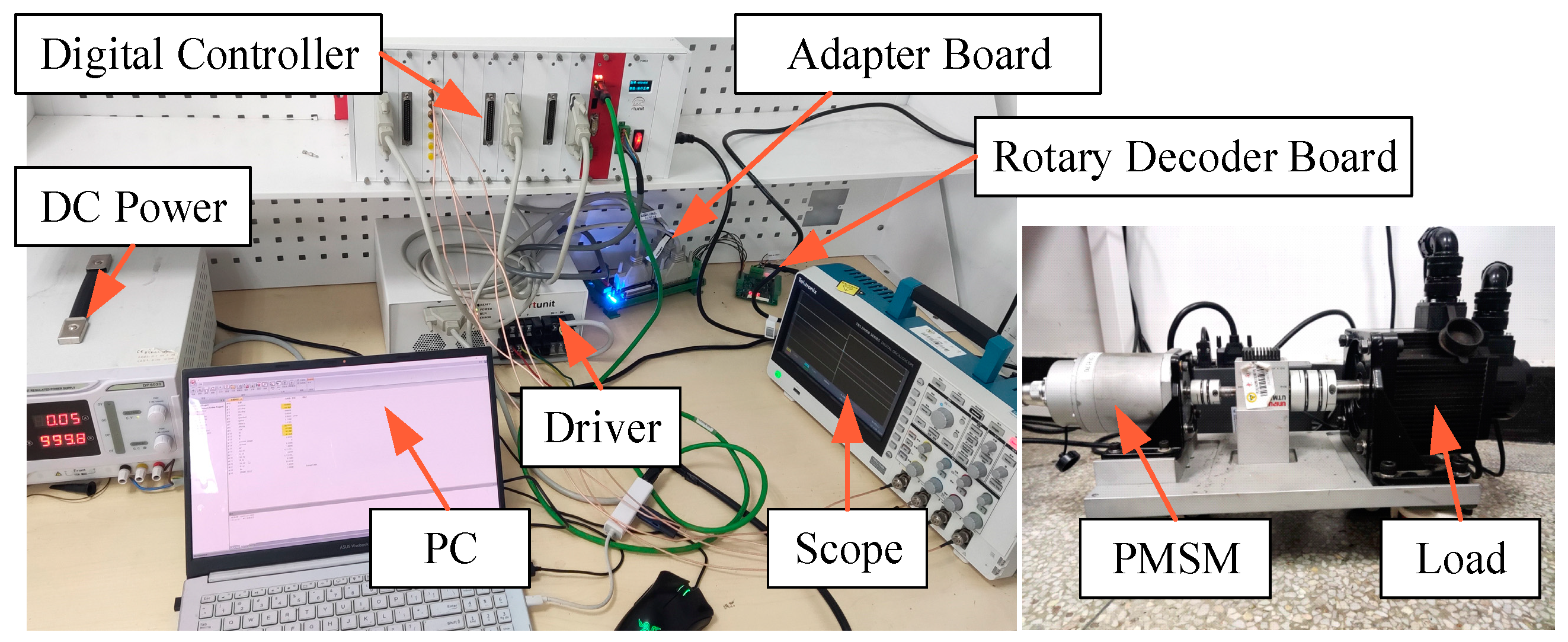
4. Simulation and Experimental Analysis
4.1. Design of PI and LSMPC Speed Controller
4.1.1. Design of PI Speed Controller
4.1.2. Design of LSMPC Speed Controller
4.2. Simulations and Experiments
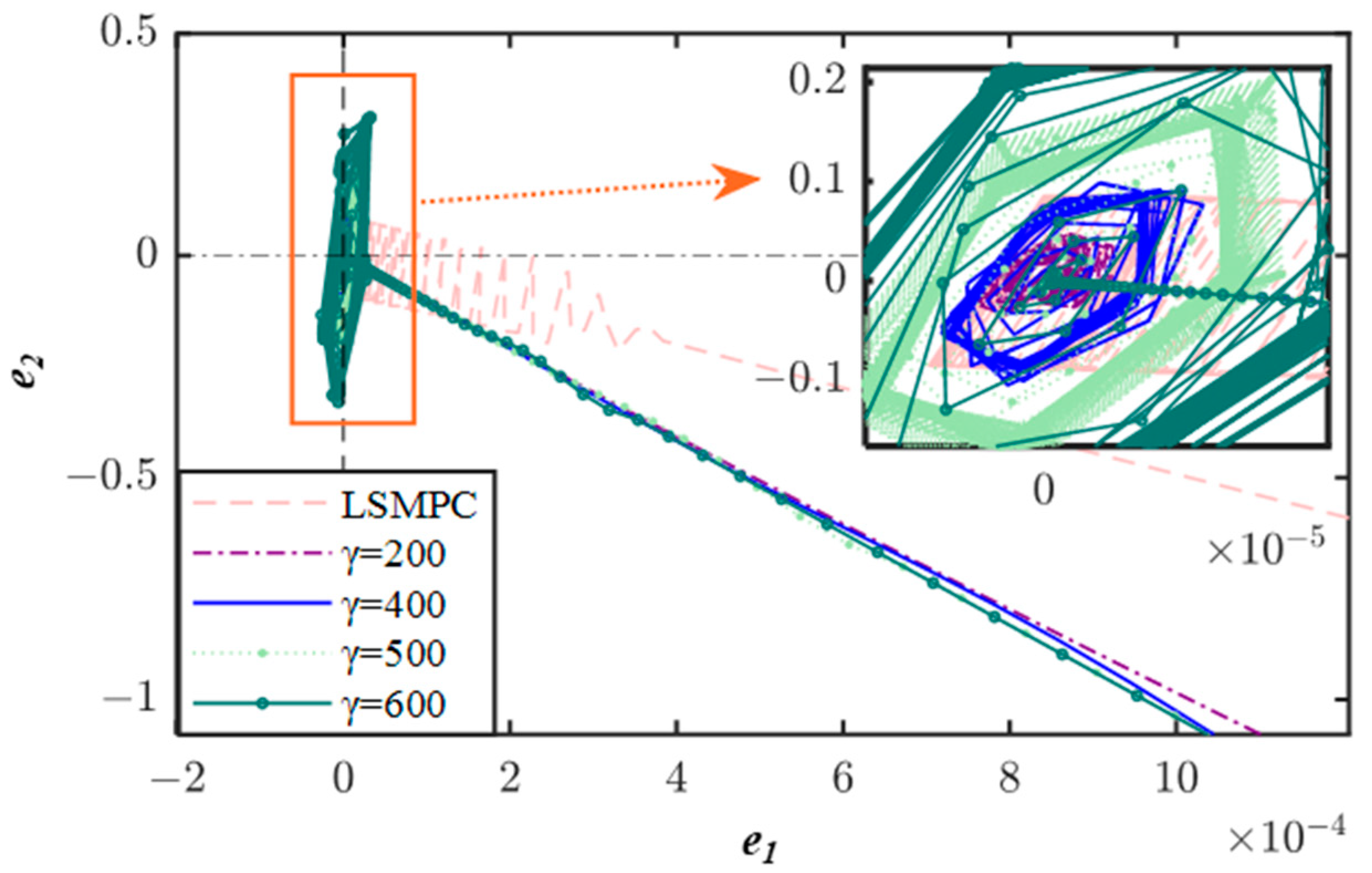
4.2.1. Parameter Tuning
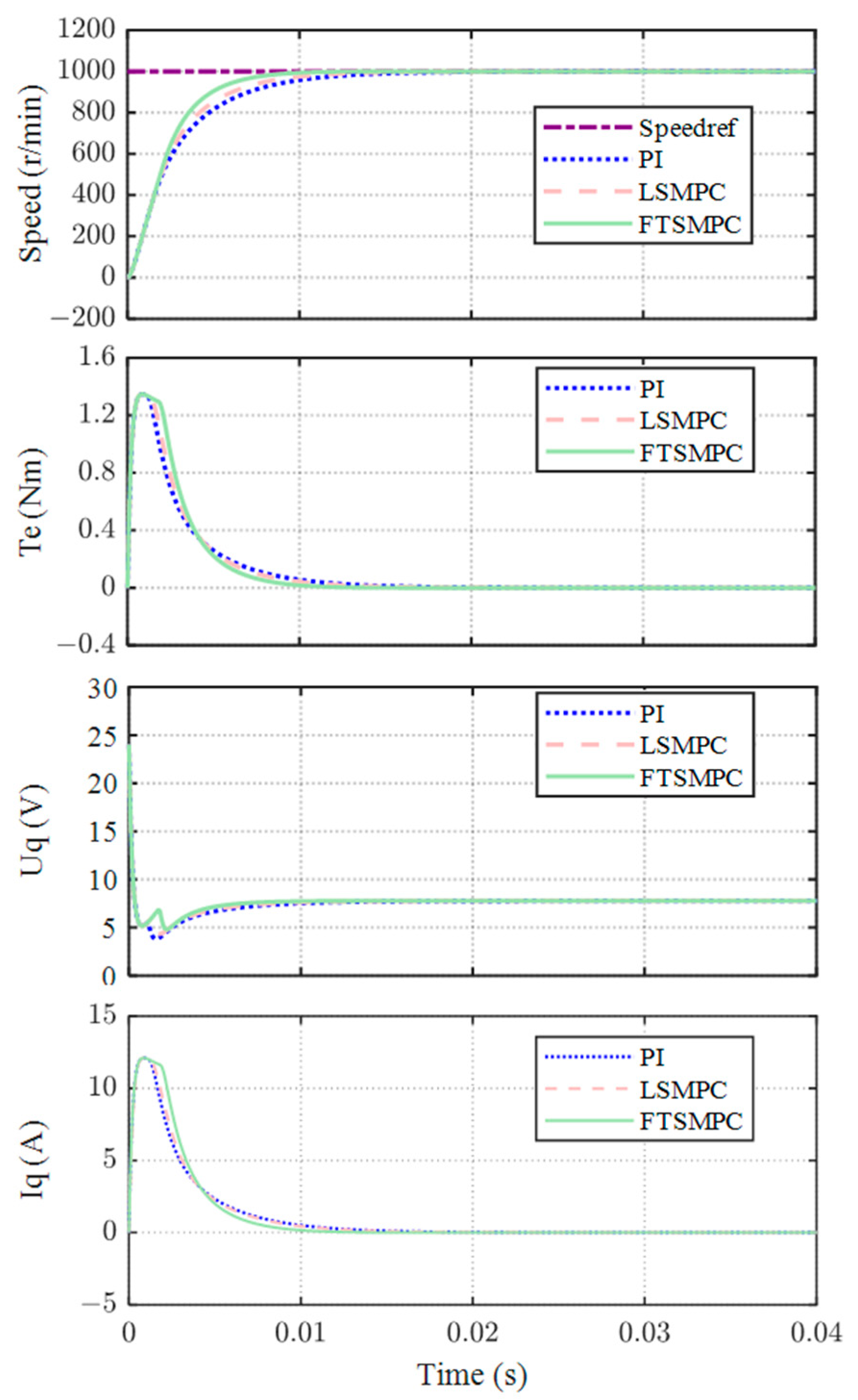
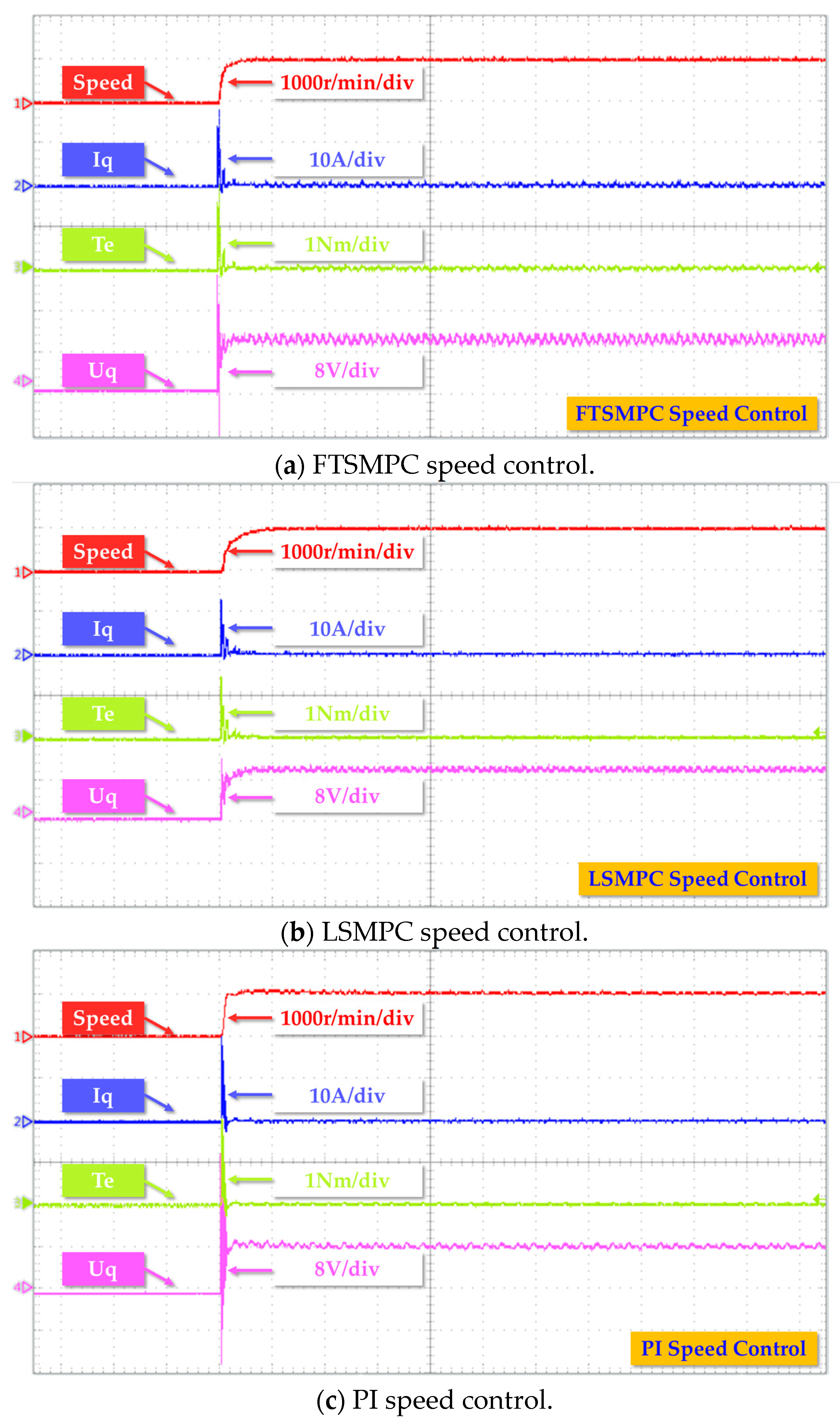
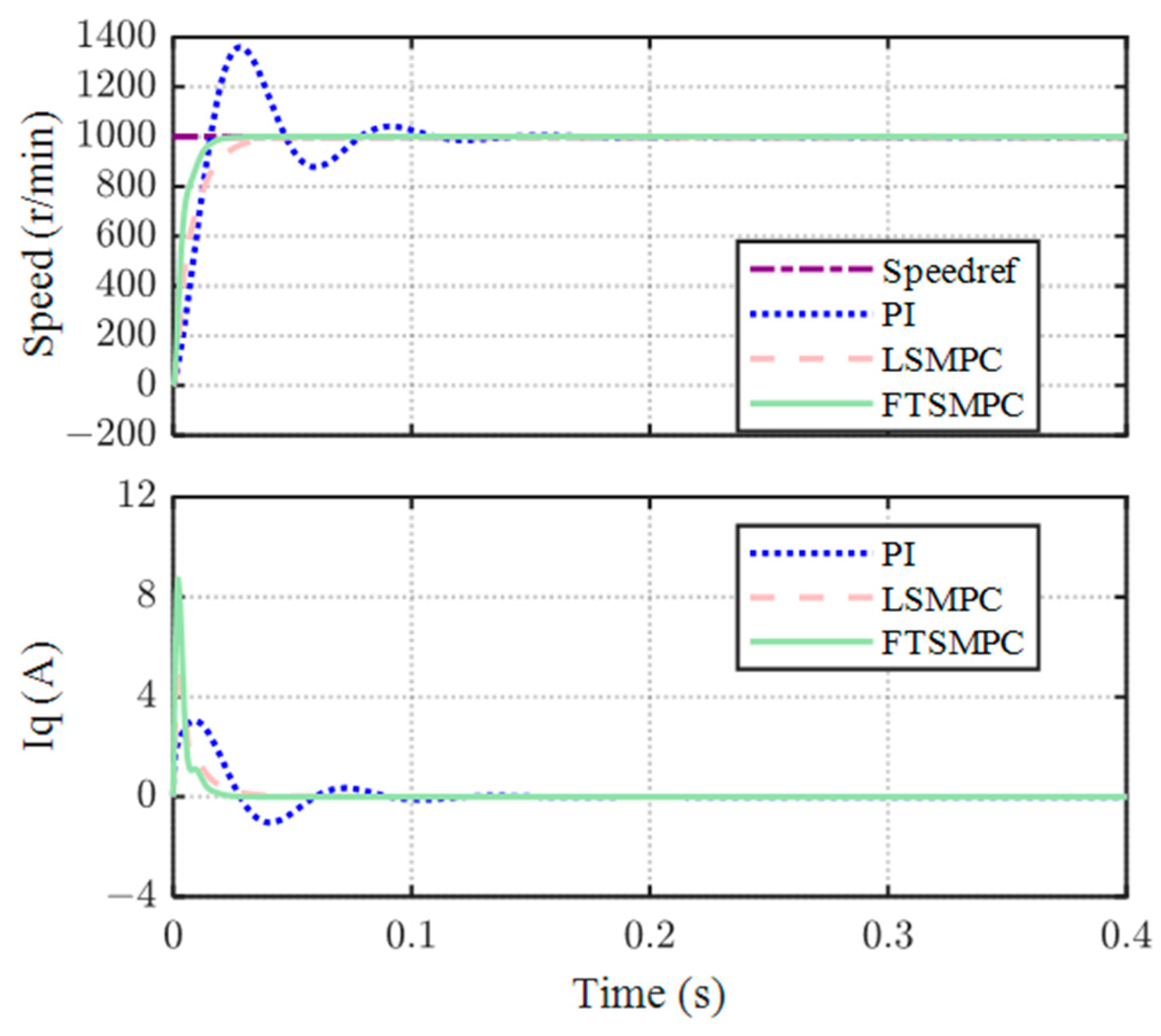
4.2.2. Step Response Performance
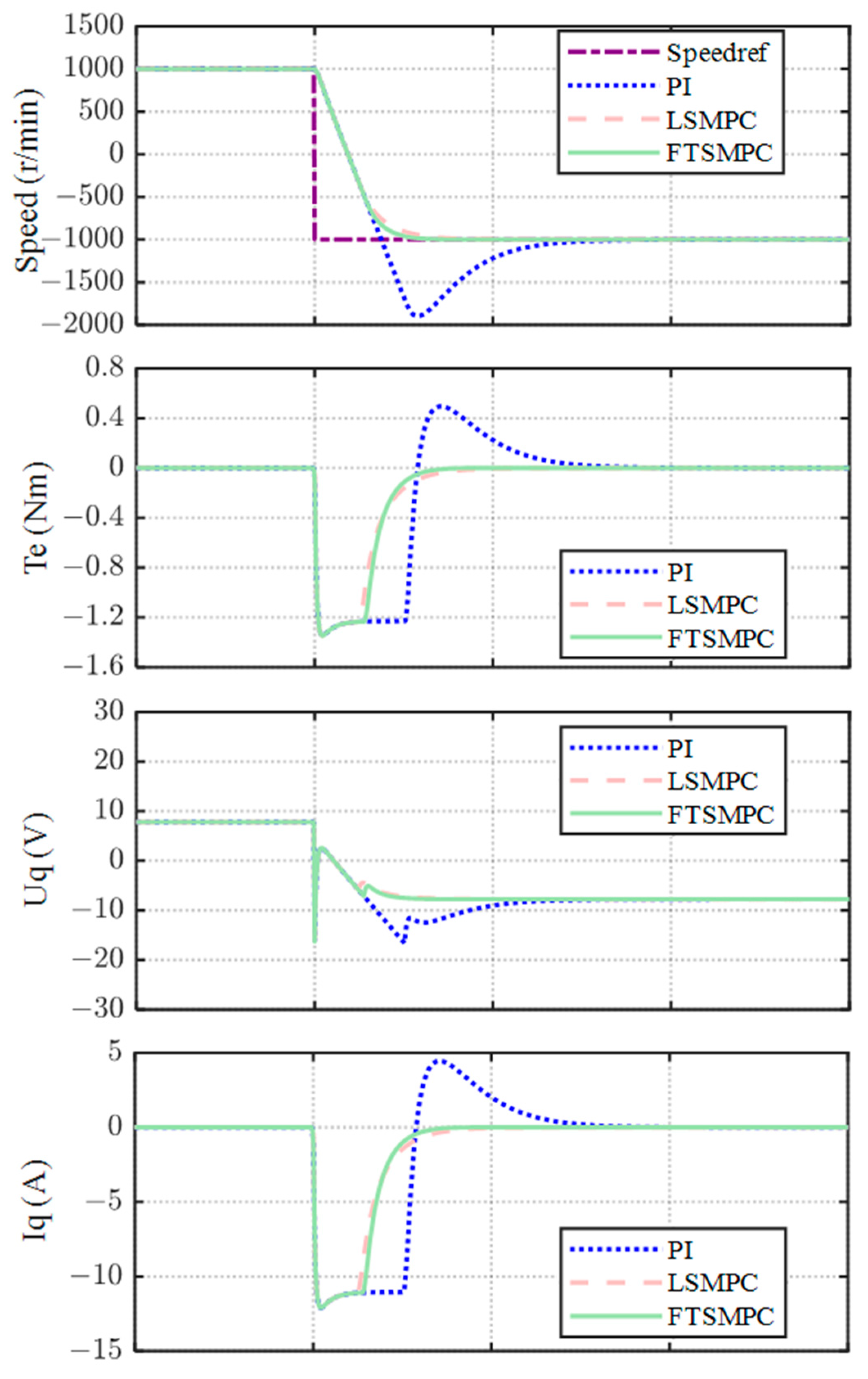
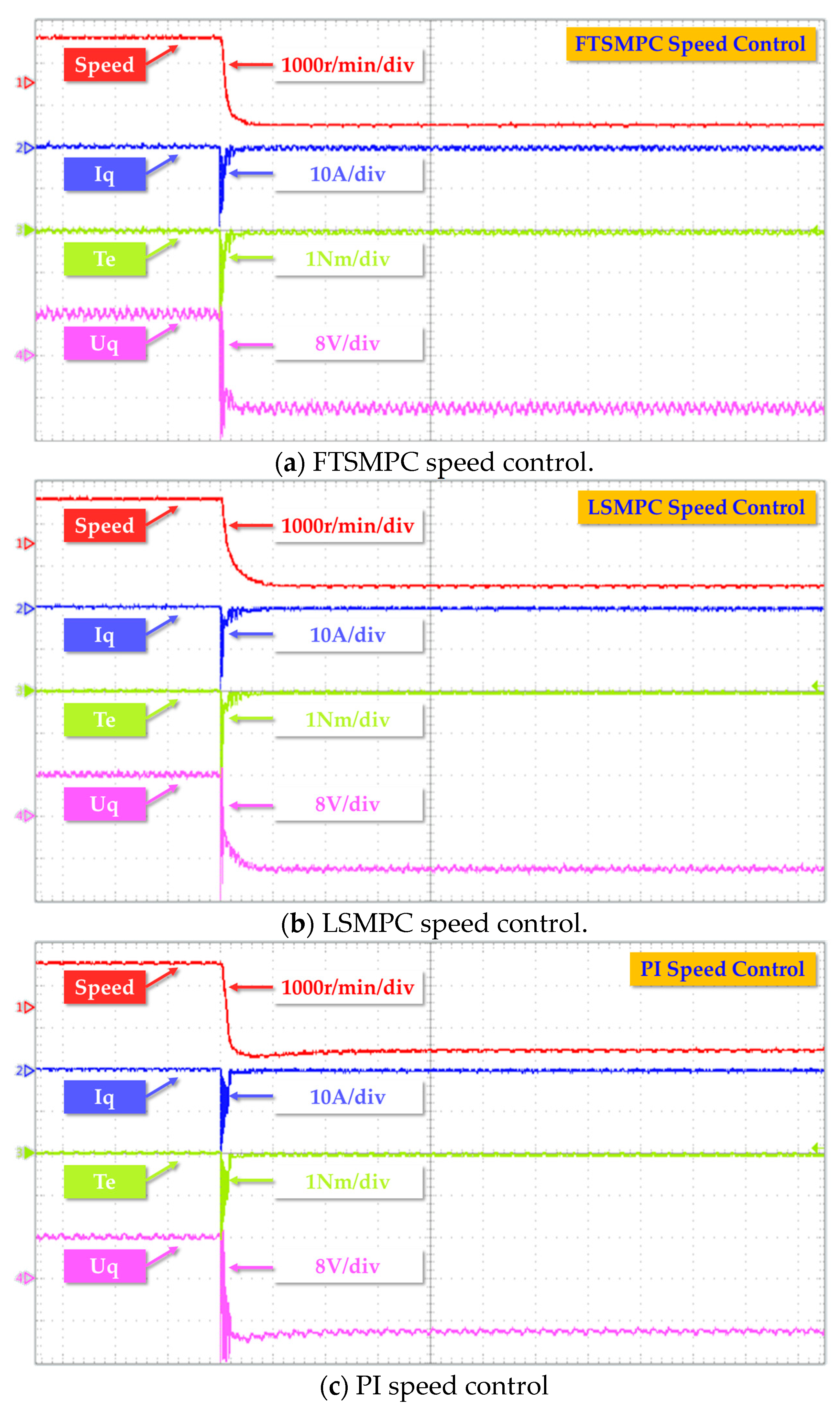
4.2.3. Speed Revisal Performance
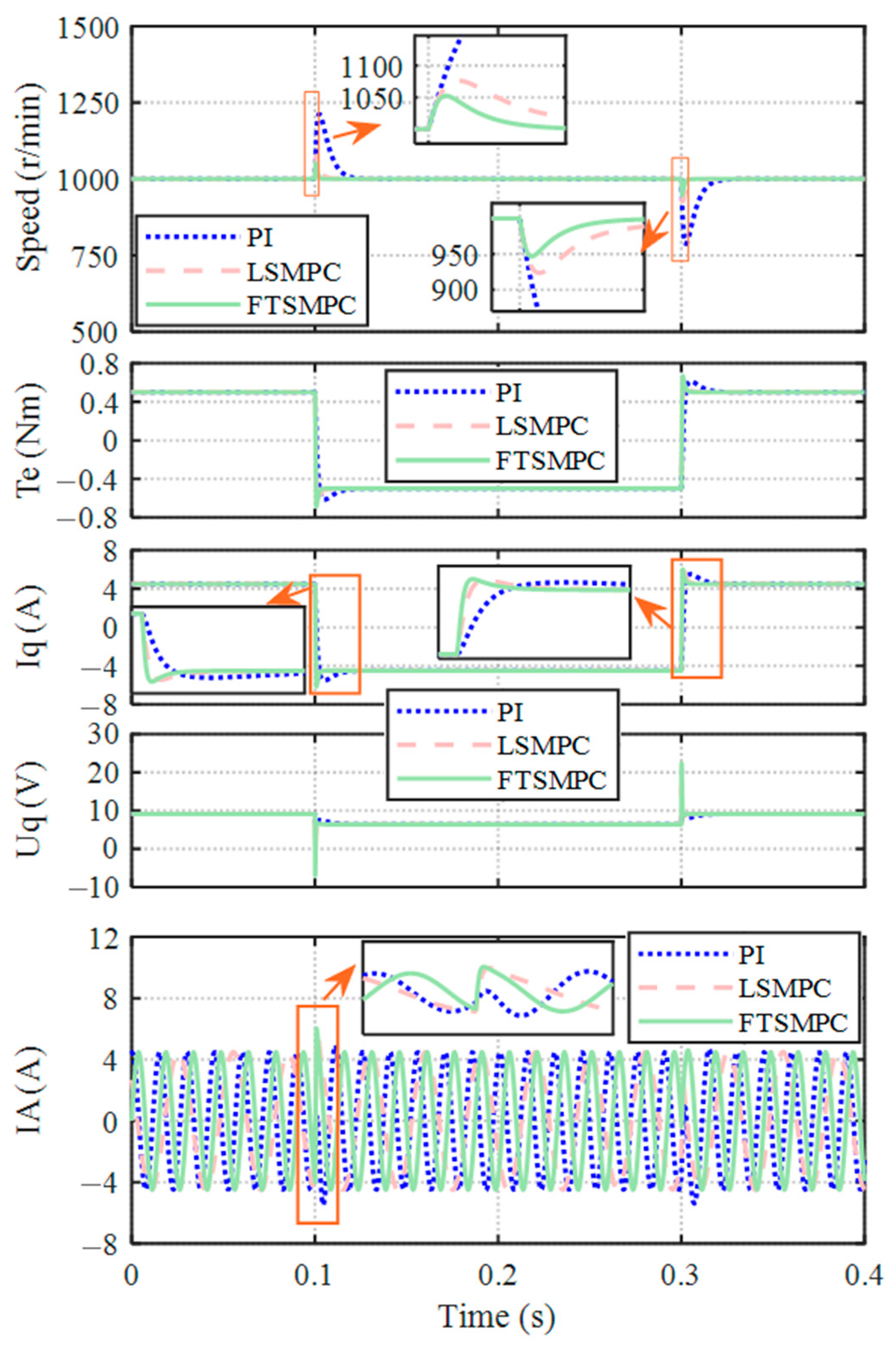
4.2.4. Load Disturbance Performance
4.2.5. Parameter Variation Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Jiao, T.; Xing, X.; Yang, Y. Speed Regulation of PMSM Systems Based on a New Sliding Mode Reaching Law. IEEE Access 2024, 12, 24062–24070. [Google Scholar] [CrossRef]
- Rovere, L.; Formentini, A.; Zanchetta, P. FPGA Implementation of a Novel Oversampling Deadbeat Controller for PMSM Drives. IEEE Trans. Ind. Electron. 2019, 66, 3731–3741. [Google Scholar] [CrossRef]
- Zuo, Y.; Lai, C.; Iyer, K.L.V. A Review of Sliding Mode Observer Based Sensorless Control Methods for PMSM Drive. IEEE Trans. Power Electron. 2023, 38, 11352–11367. [Google Scholar] [CrossRef]
- Lara, J.; Xu, J.; Chandra, A. Effects of Rotor Position Error in the Performance of Field Oriented Controlled PMSM Drives for Electric Vehicle Traction Applications. IEEE Trans. Ind. Electron. 2016, 63, 4738–4751. [Google Scholar] [CrossRef]
- Seok, J.K.; Lee, J.K.; Lee, D.C. Sensorless speed control of nonsalient permanent-magnet synchronous motor using rotor-position-tracking PI controller. IEEE Trans. Ind. Electron. 2006, 53, 399–405. [Google Scholar] [CrossRef]
- Li, X.; Tian, W.; Gao, X.; Yang, Q.; Kennel, R. A Generalized Observer-Based Robust Predictive Current Control Strategy for PMSM Drive System. IEEE Trans. Ind. Electron. 2022, 69, 1322–1332. [Google Scholar] [CrossRef]
- Yim, J.; You, S.; Lee, Y.; Kim, W. Chattering Attenuation Disturbance Observer for Sliding Mode Control: Application to Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2023, 70, 5161–5170. [Google Scholar] [CrossRef]
- Garduno, D.; Rivas, J.J.; Castillo, O.; Ortega Gonzalez, R.; Gutierrez, F.E. Current Distortion Rejection in PMSM Drives Using an Adaptive Super-Twisting Algorithm. IEEE Trans. Energy Convers. 2022, 37, 927–934. [Google Scholar] [CrossRef]
- Nguyen, N.-D.; Nam, N.N.; Yoon, C.; Lee, Y.I. Speed Sensorless Model Predictive Torque Control of Induction Motors Using a Modified Adaptive Full-Order Observer. IEEE Trans. Ind. Electron. 2022, 69, 6162–6172. [Google Scholar] [CrossRef]
- Li, L.; Pei, G.; Liu, J.; Du, P.; Pei, L.; Zhong, C. 2-DOF Robust H∞ Control for Permanent Magnet Synchronous Motor with Disturbance Observer. IEEE Trans. Ind. Electron. 2021, 36, 3462–3472. [Google Scholar] [CrossRef]
- Shao, M.; Deng, Y.; Li, H.; Liu, J.; Fei, Q. Robust Speed Control for Permanent Magnet Synchronous Motors Using a Generalized Predictive Controller with a High-Order Terminal Sliding-Mode Observer. IEEE Access 2019, 7, 121540–121551. [Google Scholar] [CrossRef]
- Tian, M.; Wang, T.; Yu, Y.; Dong, Q.; Wang, B.; Xu, D. Integrated Observer-Based Terminal Sliding-Mode Speed Controller for PMSM Drives Considering Multisource Disturbances. IEEE Trans. Ind. Electron. 2024, 39, 7968–7979. [Google Scholar] [CrossRef]
- Wang, C.; Liu, F.; Xu, J.; Pan, J. An SMC-Based Accurate and Robust Load Speed Control Method for Elastic Servo System. IEEE Trans. Ind. Electron. 2024, 71, 2300–2308. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Z.; Yu, X.; Yang, J.; Li, S. Sliding-Mode-Based Robust Output Regulation and Its Application in PMSM Servo Systems. IEEE Trans. Ind. Electron. 2023, 70, 1852–1860. [Google Scholar] [CrossRef]
- Tian, Z.; Yuan, J.; Zhang, X.; Kong, L.; Wang, J. Modeling and sliding mode predictive control of the ultra-supercritical boiler-turbine system with uncertainties and input constraints. ISA Trans. 2018, 76, 43–56. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Wang, F.; Ke, D. FPGA-Based Sliding-Mode Predictive Control for PMSM Speed Regulation System Using an Adaptive Ultralocal Model. IEEE Trans. Ind. Electron. 2021, 36, 5784–5793. [Google Scholar] [CrossRef]
- Ma, Y.; Li, D.; Li, Y.; Yang, L. A Novel Discrete Compound Integral Terminal Sliding Mode Control with Disturbance Compensation For PMSM Speed System. IEEE/ASME Trans. Mechatron. 2022, 27, 549–560. [Google Scholar] [CrossRef]
- Du, H.; Chen, X.; Wen, G.; Yu, X.; Lu, J. Discrete-Time Fast Terminal Sliding Mode Control for Permanent Magnet Linear Motor. IEEE Trans. Ind. Electron. 2018, 65, 9916–9927. [Google Scholar] [CrossRef]
- Xu, Q. Digital Integral Terminal Sliding Mode Predictive Control of Piezoelectric-Driven Motion System. IEEE Trans. Ind. Electron. 2016, 63, 3976–3984. [Google Scholar] [CrossRef]
- Kang, S.; Wu, H.; Yang, X.; Li, Y.; Yao, J.; Chen, B.; Lu, H. Discrete-Time Predictive Sliding Mode Control for a Constrained Parallel Micropositioning Piezostage. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3025–3036. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Bai, H. Sliding-Mode-Based Deadbeat Predictive Current Control for PMSM Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 962–969. [Google Scholar] [CrossRef]
- Yang, S.-M.; Lin, K.-W. Automatic Control Loop Tuning for Permanent-Magnet AC Servo Motor Drives. IEEE Trans. Ind. Electron. 2016, 63, 1499–1506. [Google Scholar] [CrossRef]

| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Stator resistance | 0.3 Ω | Rotor inertia | 4.4109 × 10−5 kg·m2 |
| Stator inductance | 4.6 × 10−4 H | Rated torque | 1 Nm |
| Pole pairs | 2 | Rated speed | 3000 r/min |
| PM flux | 0.0371 Vs | DC link voltage | 50 V |
| Rate current | 9 A | Max. current (peak) | 12.73 A |
| Simulations/Experiments | Controllers | Methods | Parameters |
|---|---|---|---|
| Simulations | Speed controllers | PI | kpω = 0.159, kiω = 50.727 |
| LSMPC | c1 = 500, λ1 = 0.5, λ2 = 0.4, α = 2/3 | ||
| FTSMPC | c1 = 500, γ= 400, λ1 = 0.8, λ2 = 0.8, α = 2/3 | ||
| Current controllers | PI | kp = 1.889, ki = 1231.995 | |
| Experiments | Speed controllers | PI | kpω = 0.158, kiω = 15.823 |
| LSMPC | c1 = 200, λ1 = 0.7, λ1 = 0.6, α = 2/3 | ||
| FTSMPC | c1 = 200, γ = 400, λ1 = 0.8, λ1 = 0.8, α = 2/3 | ||
| Current controllers | PI | kp = 1.889, ki = 1231.995 |
| Simulations /Experiments | Performance Index | PI | LSMPC | FTSMPC |
|---|---|---|---|---|
| Simulations | Rise time (s) | 0.0065 | 0.0060 | 0.0044 |
| Settling time (s) (0.5%) | 0.0153 | 0.0137 | 0.0085 | |
| Overshoot (%) | 0 | 0 | 0 | |
| Experiments | Rise time (s) | 0.0071 | 0.0482 | 0.0250 |
| Settling time (s) (2%) | 0.2382 | 0.075698 | 0.0465 | |
| Overshoot (%) | 5.51% | 0 | 0 |
| Simulations /Experiments | Performance Index | PI | LSMPC | FTSMPC |
|---|---|---|---|---|
| Simulations | Rise time (s) | 0.0059 | 0.0075 | 0.0064 |
| Settling time (s) (0.5%) | 0.0366 | 0.0138 | 0.0086 | |
| Undershoot (%) | 896.16 | 0 | 0 | |
| Experiments | Rise time (s) | 0.0134 | 0.0461 | 0.0250 |
| Settling time (s) (2%) | 0.3207 | 0.0732 | 0.0409 | |
| Undershoot (%) | 11.52% | 0 | 0 |
| Performance Index | PI | LSMPC | FTSMPC |
|---|---|---|---|
| Overshoot (r/min) | 212.79 | 76.31 | 52.56 |
| Recovery time (s) (0.5%) | 0.0206 | 0.0071 | 0.0026 |
| Undershoot (r/min) | 212.70 | 76.44 | 53.24 |
| Recovery time (s) (0.5%,) | 0.0206 | 0.0071 | 0.0031 |
| Performance Index | PI | LSMPC | FTSMPC |
|---|---|---|---|
| Rise time (s) | 0.0117 | 0.0173 | 0.0095 |
| Settling time (s) (0.5%) | 0.1036 | 0.0388 | 0.0190 |
| Overshoot (r/min) | 359.68 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, D.; Cai, H.; Zeng, W. Fast Terminal Sliding-Mode Predictive Speed Controller for Permanent-Magnet Synchronous Motor Drive Systems. Energies 2024, 17, 3767. https://doi.org/10.3390/en17153767
Kong D, Cai H, Zeng W. Fast Terminal Sliding-Mode Predictive Speed Controller for Permanent-Magnet Synchronous Motor Drive Systems. Energies. 2024; 17(15):3767. https://doi.org/10.3390/en17153767
Chicago/Turabian StyleKong, Delin, Haiwei Cai, and Wenkai Zeng. 2024. "Fast Terminal Sliding-Mode Predictive Speed Controller for Permanent-Magnet Synchronous Motor Drive Systems" Energies 17, no. 15: 3767. https://doi.org/10.3390/en17153767
APA StyleKong, D., Cai, H., & Zeng, W. (2024). Fast Terminal Sliding-Mode Predictive Speed Controller for Permanent-Magnet Synchronous Motor Drive Systems. Energies, 17(15), 3767. https://doi.org/10.3390/en17153767








