Decentralized Multi-Area Economic Dispatch in Power Systems Using the Consensus Algorithm
Highlights
- A three-level consensus algorithm is proposed to study multi-area economic dispatch.
- Breadth‐first search is used to identify the leader agent to reduce the iteration number.
- The tie-line flows and system losses are taken into account.
- The CPU time required is only 0.307 s for a realistic 64-generator system.
Abstract
1. Introduction
- (i)
- (ii)
- (iii)
- (iv)
- (v)
- (i)
- (ii)
- (iii)
- (iv)
2. Background
2.1. Graph Theory
2.2. First-Order Consensus Algorithm
2.3. Security-Constrained Economic Dispatch
3. Proposed Method
3.1. Leader in the Consensus Algorithm
| Algorithm 1. Pseudo-code of BFS. |
| Initialization: queue=[] state=root_node; While (true); if goal is (state), then return SUCCESS; else, add_to_back_of_queue (successors (state)); if queue is [], then report FAILURE; state=queue [0]; remove_first_item from (queue); End while. |
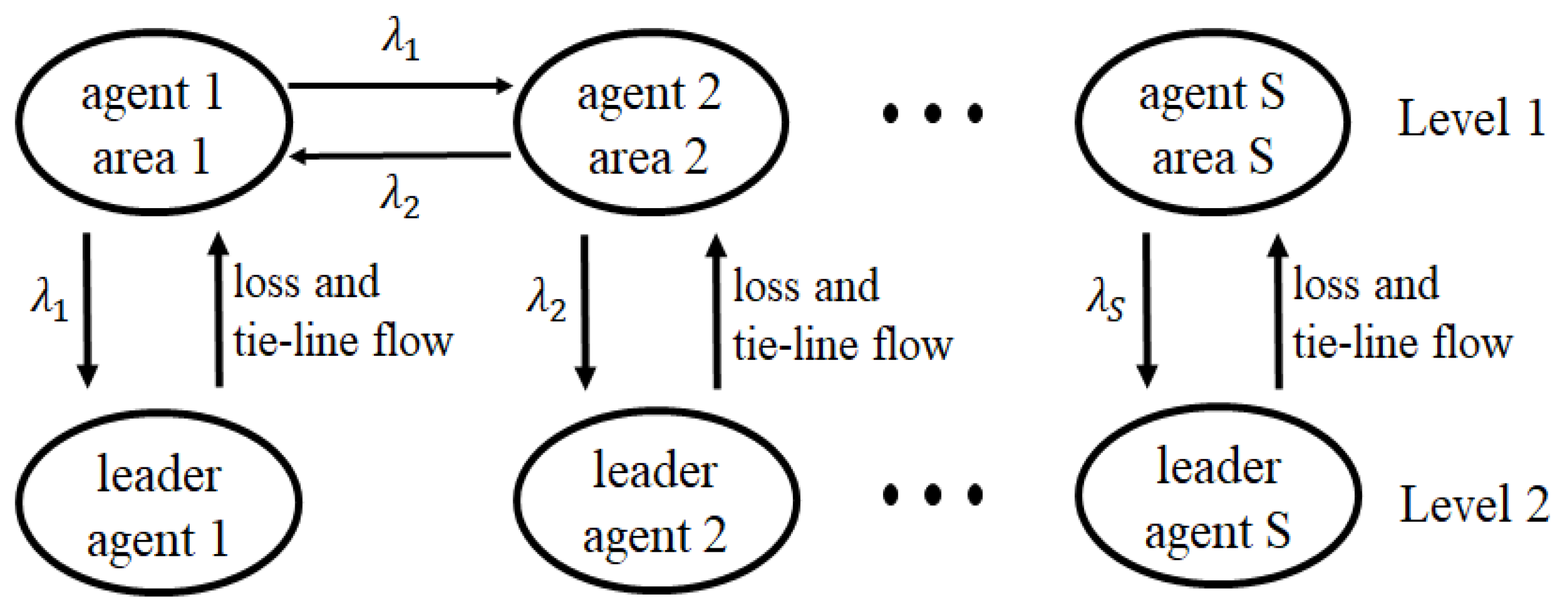
3.2. Three-Level Hierarchical CA
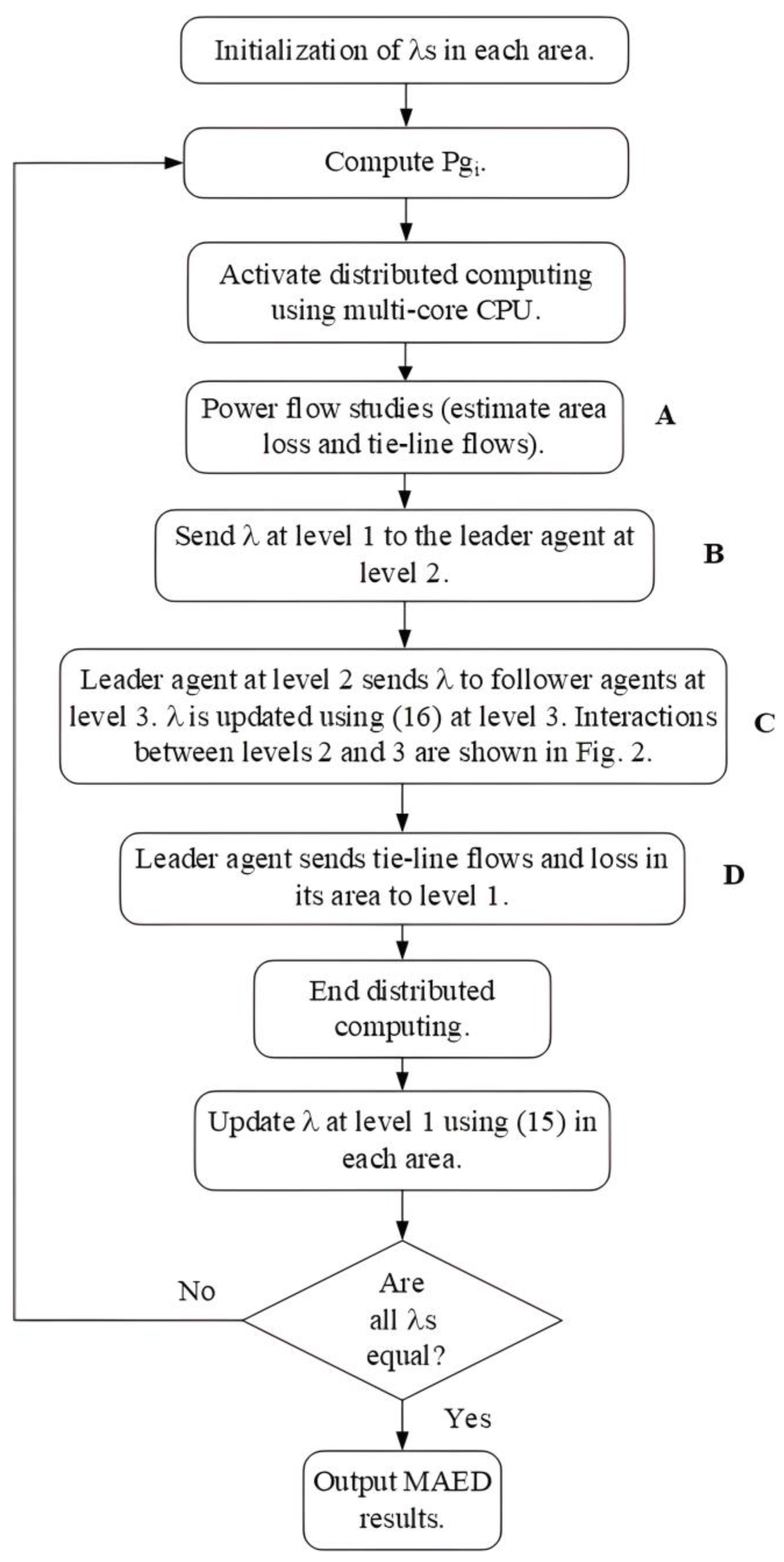
3.3. Flowchart and Implementation of the Proposed Method
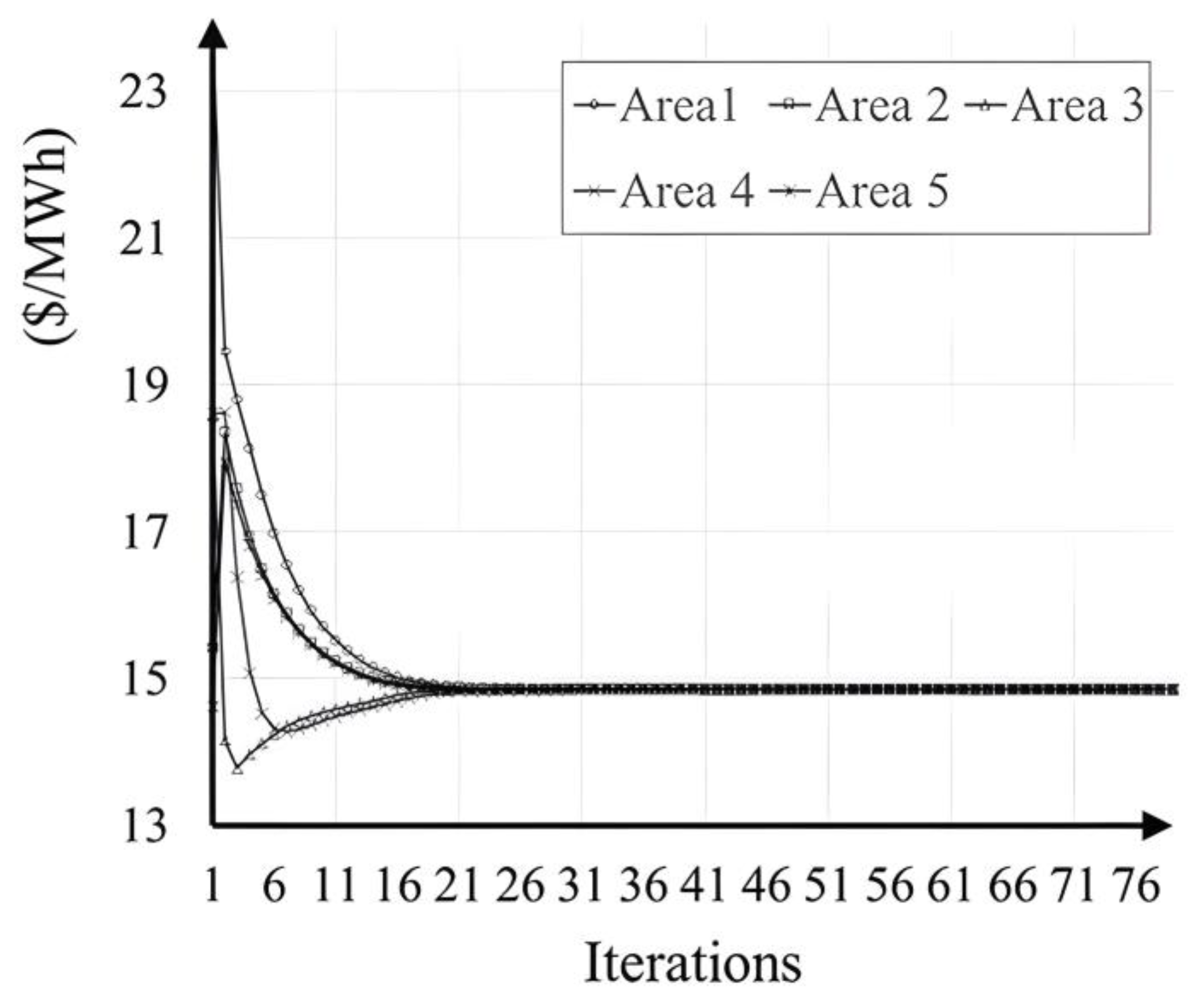
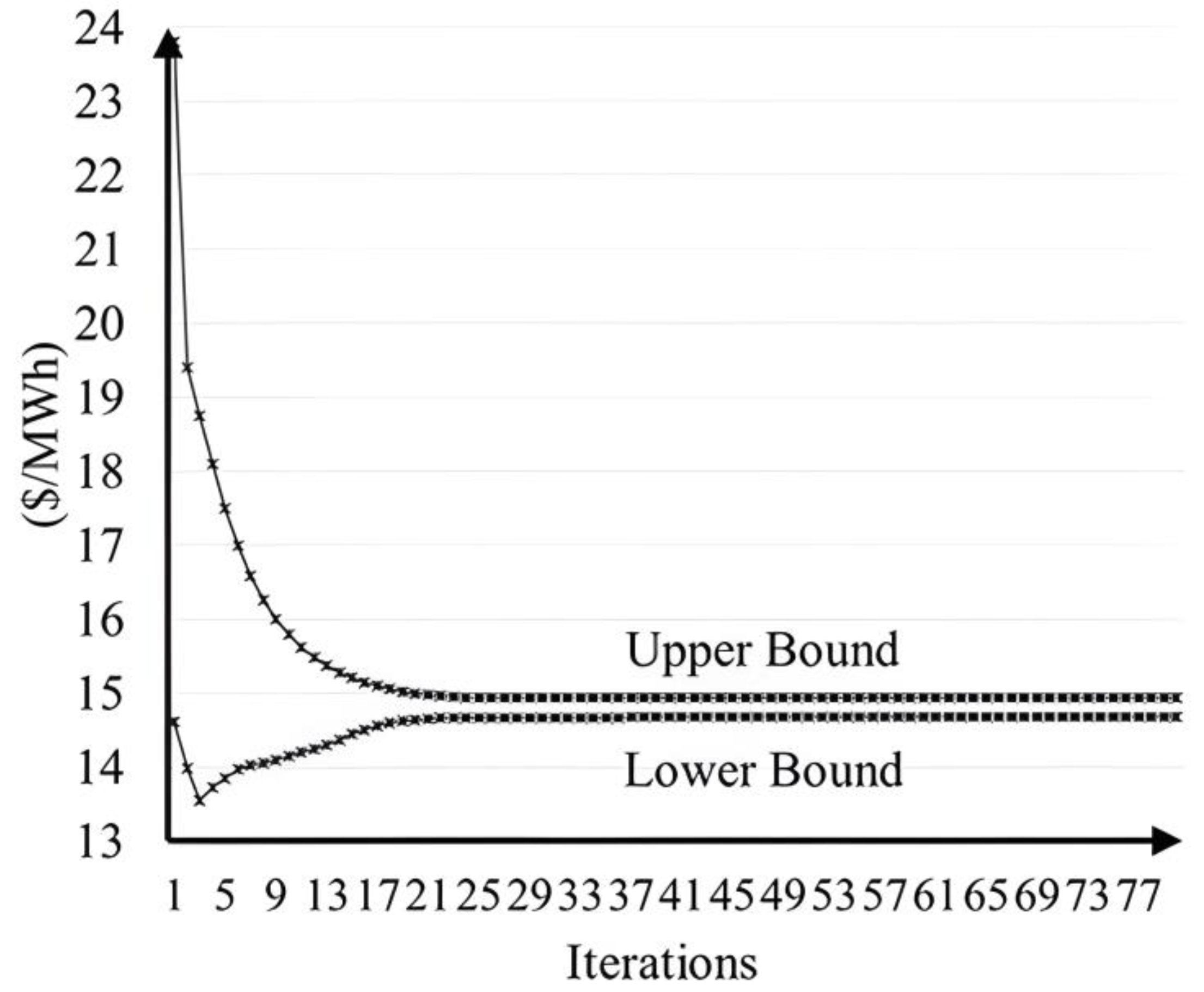
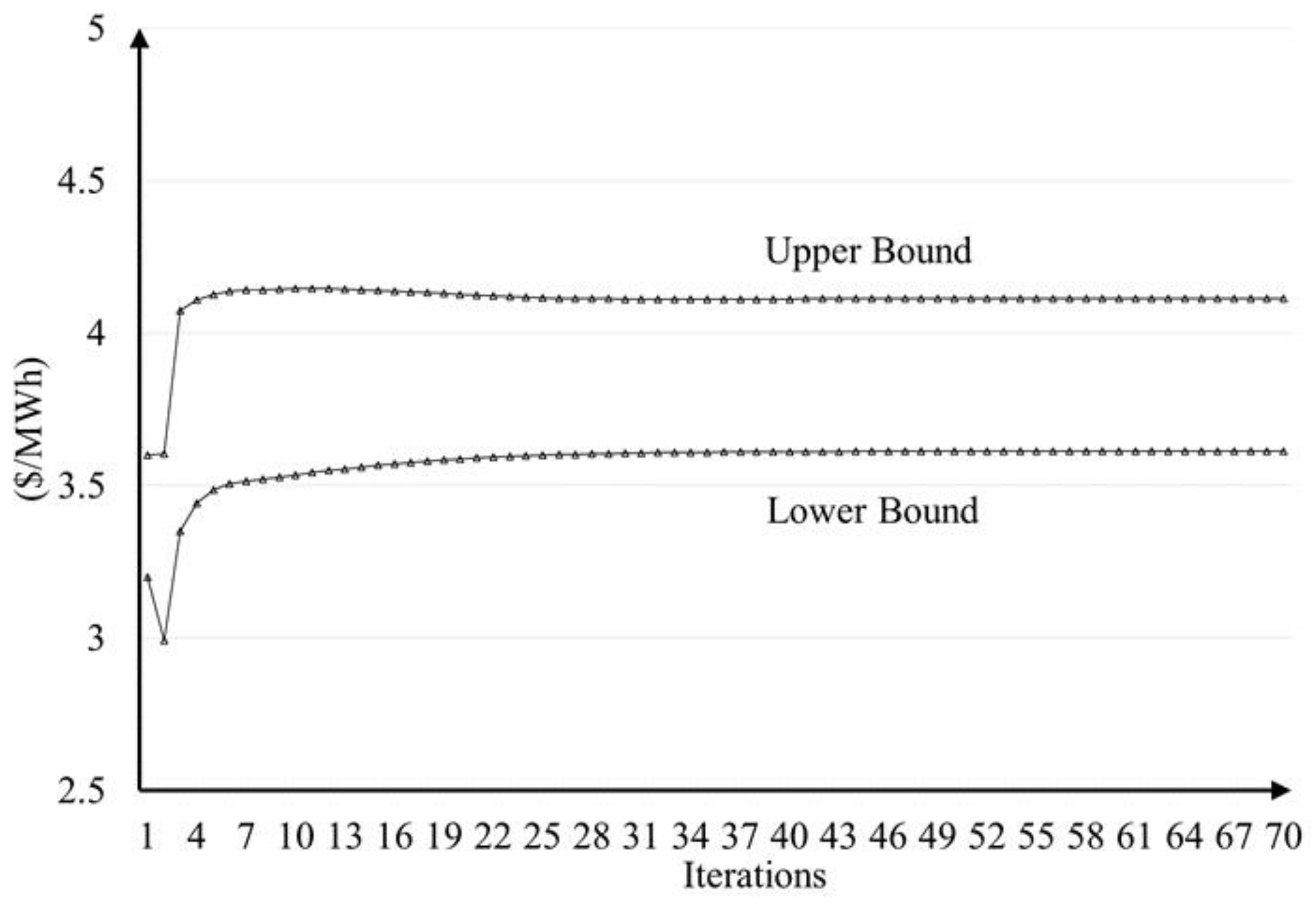
4. Simulation Results
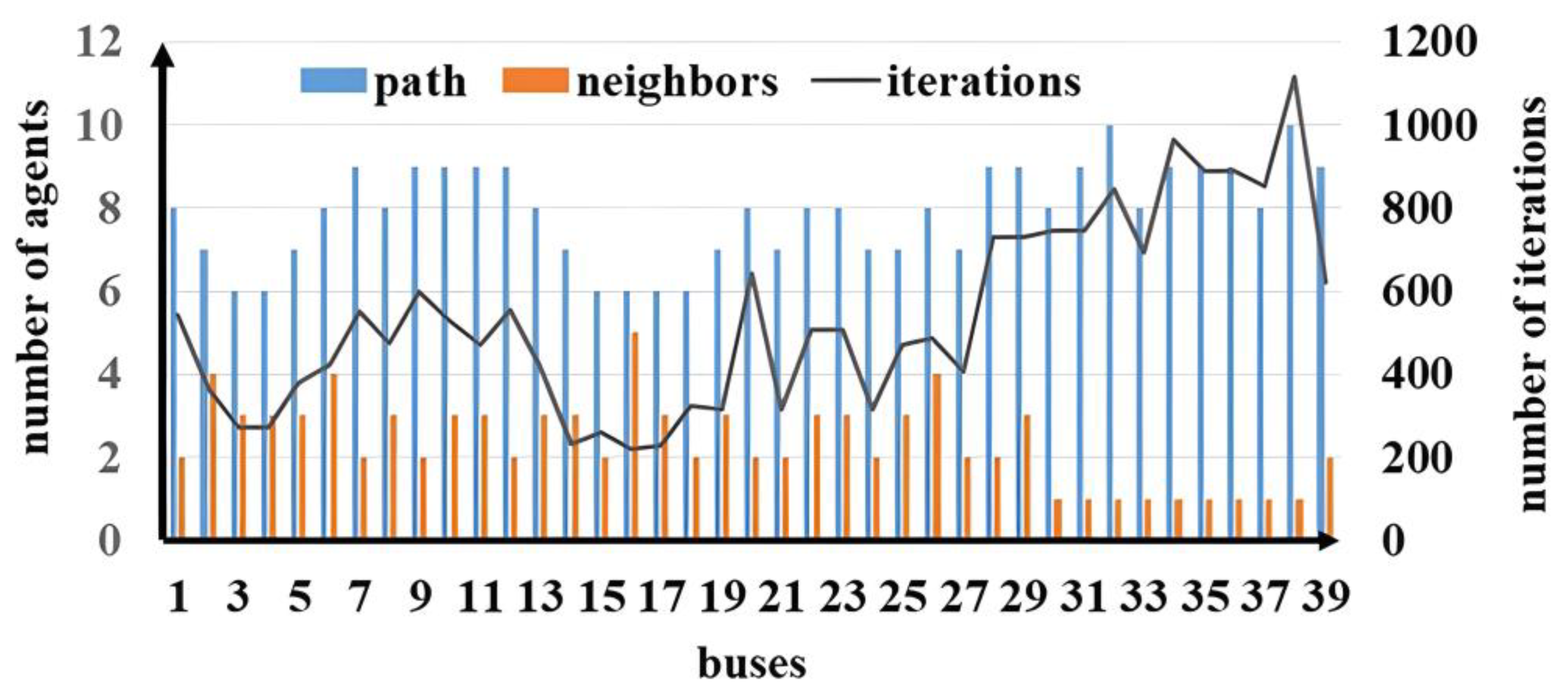
4.1. Identification of Leader Agent Using BFS
4.2. Verification of B-Coefficients in Loss Formula
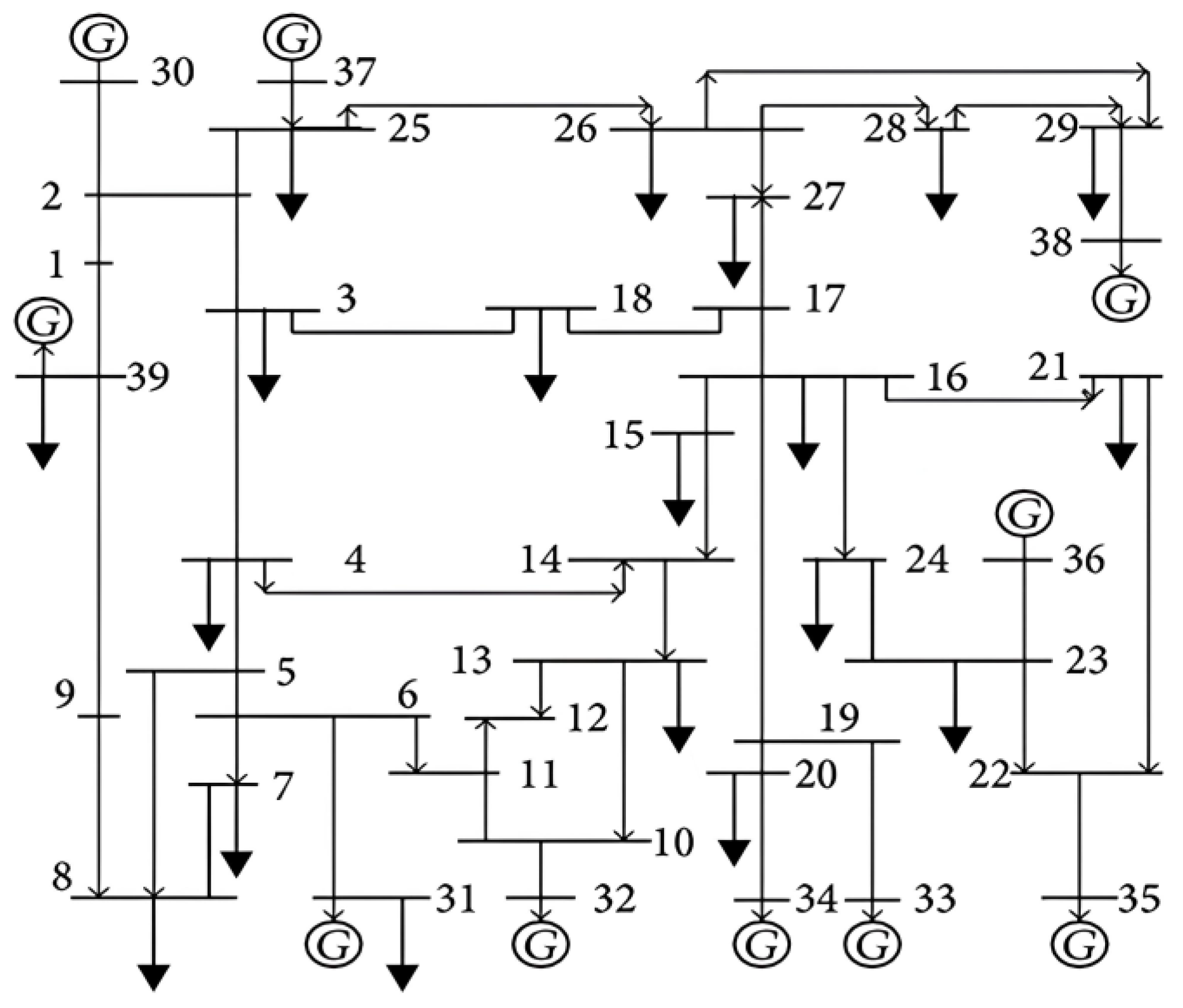
4.3. Simulation Results of the IEEE 118-Bus System
4.4. Simulation Results of the Taiwan Power System
4.5. Uncertainty in Loads and Renewables
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lai, X.; Xie, L.; Xia, Q.; Zhong, H.; Kang, C. Decentralized multi-area economic dispatch via dynamic multiplier-based Lagrangian relaxation. IEEE Trans. Power Syst. 2015, 30, 3225–3233. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Zhang, B.; Wang, B. Decentralized multi-area dynamic economic dispatch using modified generalized Benders decomposition. IEEE Trans. Power Syst. 2016, 31, 526–538. [Google Scholar] [CrossRef]
- Guo, Y.; Tong, L.; Wu, W.; Zhang, B.; Sun, H. Coordinated multi-area economic dispatch via critical region projection. IEEE Trans. Power Syst. 2017, 32, 3736–3746. [Google Scholar] [CrossRef]
- Wu, L. A transformation-based multi-area dynamic economic dispatch approach for preserving information privacy of individual areas. IEEE Trans. Smart Grid 2019, 10, 722–731. [Google Scholar] [CrossRef]
- Xue, X.; Fang, J.; Ai, X.; Cui, S.; Jiang, Y.; Yao, W.; Wen, J. A fully distributed ADP algorithm for real-time economic dispatch of microgrid. IEEE Trans. Smart Grid 2024, 15, 513–528. [Google Scholar]
- Yan, X.; Zhong, H.; Tan, Z.; Lian, J. Fast tuning-free distributed algorithm for solving the network-constrained economic dispatch. IEEE Trans. Smart Grid 2024, 15, 595–606. [Google Scholar] [CrossRef]
- Elsayed, W.T.; El-Saadany, E.F. A fully decentralized approach for solving the economic dispatch problem. IEEE Trans. Power Syst. 2015, 30, 2179–2189. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, H.; Yu, T.; Yang, B.; Xu, M. Robust collaborative consensus algorithm for decentralized economic dispatch with a practical communication network. Electr. Power Syst. Res. 2016, 140, 597–610. [Google Scholar] [CrossRef]
- Yang, T.; Wu, D.; Sun, Y.; Lian, J. Minimum-time consensus-based approach for power system applications. IEEE Trans. Ind. Electron. 2016, 63, 1318–1328. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, W.; Zhang, B. A fully distributed power dispatch method for fast frequency recovery and minimal generation cost in autonomous microgrids. IEEE Trans. Smart Grid 2016, 7, 19–31. [Google Scholar] [CrossRef]
- Yang, Z.; Xiang, J.; Li, Y. Distributed consensus based supply–demand balance algorithm for economic dispatch problem in a smart grid with switching graph. IEEE Trans. Ind. Electron. 2017, 64, 1600–1610. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, L.; Wang, S. A fully-decentralized consensus-based ADMM approach for DC-OPF with demand response. IEEE Trans. Smart Grid 2017, 8, 2637–2647. [Google Scholar] [CrossRef]
- Hamdi, M.; Chaoui, M.; Idoumghar, L.; Kachouri, A. Coordinated consensus for smart grid economic environmental power dispatch with dynamic communication network. IET Gener. Transm. Distrib. 2018, 12, 2603–2613. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, Z. Delay effects on consensus-based distributed economic dispatch algorithm in microgrid. IEEE Trans. Power Syst. 2018, 33, 602–612. [Google Scholar] [CrossRef]
- Hao, R.; Lu, T.; Wu, Q.; Chen, X.; Ai, Q. Distributed piecewise approximation economic dispatch for regional power systems under non-ideal communication. IEEE Access 2019, 7, 45533–45543. [Google Scholar] [CrossRef]
- Liu, W.J.; Chi, M.; Liu, Z.W.; Guan, Z.H.; Chen, J.; Xiao, J.W. Distributed optimal active power dispatch with energy storage units and power flow limits in smart grids. Electr. Power Energy Syst. 2019, 105, 420–428. [Google Scholar] [CrossRef]
- Liu, Z.; Yi, Y.; Yang, J.; Tang, W.; Zhang, Y.; Xie, X.; Ji, T. Optimal planning and operation of dispatchable active power resources for islanded multi-microgrids under decentralized collaborative dispatch framework. IET Gener. Transm. Distrib. 2020, 14, 408–422. [Google Scholar] [CrossRef]
- Wang, R.; Li, Q.; Zhang, B.; Wang, L. Distributed consensus based algorithm for economic dispatch in a microgrid. IEEE Trans. Smart Grid 2019, 10, 3630–3640. [Google Scholar] [CrossRef]
- Wang, A.; Liu, W. Distributed incremental cost consensus-based optimization algorithms for economic dispatch in a microgrid. IEEE Access 2020, 8, 12933–12941. [Google Scholar] [CrossRef]
- Cheng, Z.; Chow, M.Y. Resilient collaborative distributed energy management system framework for cyber-physical DC microgrids. IEEE Trans. Smart Grid 2020, 11, 4637–4649. [Google Scholar] [CrossRef]
- Fu, Y.; Guo, X.; Mi, Y.; Yuan, M.; Ge, X.; Su, X.; Li, Z. The distributed economic dispatch of smart grid based on deep reinforcement learning. IET Gener. Transm. Distrib. 2021, 15, 2645–2658. [Google Scholar] [CrossRef]
- Ya, Y.; Chen, Z.; Varadharajan, V.; Hossain, M.J.; Town, G.E. Distributed consensus-based economic dispatch in power grids using the Paillier cryptosystem. IEEE Trans. Smart Grid 2021, 12, 3493–3502. [Google Scholar]
- Bai, L.; Ye, M.; Sun, C.; Hu, G. Distributed economic dispatch control via saddle point dynamics and consensus algorithms. IEEE Trans. Control Syst. Technol. 2019, 27, 898–905. [Google Scholar] [CrossRef]
- Sharifian, Y.; Abdi, H. Multi-area economic dispatch problem: Methods, uncertainties, and future directions. Renew. Sustain. Energy Rev. 2024, 191, 114093. [Google Scholar] [CrossRef]
- Kunya, A.B.; Abubakar, A.S.; Yusuf, S.S. Review of economic dispatch in multi-area power system: State-of-the-art and future prospective. Electr. Power Syst. Res. 2023, 217, 109089. [Google Scholar] [CrossRef]
- Samende, C.; Bhagavathy, S.M.; McCulloch, M. Power loss minimisation of off-grid solar DC nano-grids—Part II: A quasi-consensus-based distributed control algorithm. IEEE Trans. Smart Grid 2022, 13, 38–46. [Google Scholar] [CrossRef]
- Martinez-Gomez, M.; Orchard, M.E.; Bozhko, S. Dynamic average consensus with anti-windup applied to interlinking converters in AC/DC microgrids under economic dispatch and delays. IEEE Trans. Smart Grid 2023, 14, 4137–4140. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, S.; Li, W.; Luo, X. A Consensus-based distributed temperature priority control of air conditioner clusters for voltage regulation in distribution networks. IEEE Trans. Smart Grid 2023, 14, 290–301. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Chen, Z. A marginal cost consensus scheme with reset mechanism for distributed economic dispatch in BESSs. IEEE Trans. Smart Grid 2024, 15, 2898–2908. [Google Scholar] [CrossRef]
- Lyu, J.; Zhang, S.; Cheng, H.; Yuan, K.; Song, Y. A graph theory-based optimal configuration method of energy hub considering the integration of electric vehicles. Energy 2022, 243, 123078. [Google Scholar] [CrossRef]
- Morro-Mello, I.; Padilha-Feltrin, A.; Melo, J.D.; Heymann, F. Spatial connection cost minimization of EV fast charging stations in electric distribution networks using local search and graph theory. Energy 2021, 235, 121380. [Google Scholar] [CrossRef]
- Balaji, K.; Rabiei, M. Carbon dioxide pipeline route optimization for carbon capture, utilization, and storage: A case study for North-Central USA. Sustain. Energy Technol. Assess. 2022, 51, 101900. [Google Scholar] [CrossRef]
- Filho Vinicius, G.T.; Silvia, C.; Aleksandar, D.; Massimo, B.; Marco, M. Rural electrification planning based on graph theory and geospatial data: A realistic topology oriented approach. Sustain. Energy Grids Netw. 2021, 28, 100525. [Google Scholar] [CrossRef]
- Khan, I.; Xu, Y.; Sun, H.; Bhattacharjee, V. Distributed optimal reactive power control of power systems. IEEE Access 2018, 6, 7100–7111. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Kim, H.M. Cluster-based predictive PCC voltage control of large-scale offshore wind farm. IEEE Access 2021, 9, 4630–4641. [Google Scholar] [CrossRef]
- Chen, S.; Gong, Q.; Lu, X.; Lai, J. Distributed cooperative control for economic dispatch and SOC balance in DC microgrids with vanadium redox batteries. Sustain. Energy Grids Netw. 2021, 28, 100534. [Google Scholar] [CrossRef]
- Zheng, S.; Liao, K.; Yang, J.; He, Z. Droop-based consensus control scheme for economic dispatch in islanded microgrids. IET Gener. Transm. Distrib. 2020, 14, 4529–4538. [Google Scholar] [CrossRef]
- Ambia, M.N.; Meng, K.; Xiao, W.; Al-Durra, A.; Dong, Z.Y. Adaptive droop control of multi-terminal HVDC network for frequency regulation and power sharing. IEEE Trans. Power Syst. 2021, 36, 566–578. [Google Scholar] [CrossRef]
- Kim, S.; Hyon, S.; Kim, C. Distributed virtual negative-sequence impedance control for accurate imbalance power sharing in islanded microgrids. Sustain. Energy Grids Netw. 2018, 16, 28–36. [Google Scholar] [CrossRef]
- Winston, P.H. Artificial Intelligence, 2nd ed.; Addison-Wesley Publishing Company: Reading, MA, USA, 1984. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence—A Modern Approach, 2nd ed.; Pearson Education, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Coppin, B. Artificial Intelligence Illuminated; Jones and Bartlett Publishers: Sudbury, MA, USA, 2004. [Google Scholar]
- Power Systems Test Case Archive. Available online: https://labs.ece.uw.edu/pstca/ (accessed on 27 May 2024).
- Wood, A.J.; Wollenberg, B.F.; Sheblé, G.B. Power Generation, Operation, and Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Li, Z.; Xu, Y.; Wang, P.; Xiao, G. Restoration of a multi-energy distribution system with joint district network reconfiguration via distributed stochastic programming. IEEE Trans. Smart Grid 2024, 15, 2667–2680. [Google Scholar] [CrossRef]
- Huang, H.; Li, Z.; Sampath, L.P.M.I.; Yang, J.; Nguyen, H.D.; Gooi, H.B.; Liang, R.; Gong, D. Blockchain-enabled carbon and energy trading for network-constrained coal mines with uncertainties. IEEE Trans. Sustain. Energy 2023, 14, 1634–1647. [Google Scholar] [CrossRef]
- Breve, M.M.; Bohnet, B.; Michalke, G.; Kowal, J.; Strunz, K. Flow-network-based method for the reliability analysis of decentralized power system topologies with a sequential Monte-Carlo simulation. IEEE Trans. Reliab. 2024, 73, 1005–1019. [Google Scholar] [CrossRef]



| Method | Proposed Method | Traditional SCED Method [44] |
|---|---|---|
| System load (MW) | 6097.1 | |
| Total loss (MW) | 46.8995 | 46.8985 |
| Incremental cost ($/MWh) | 17.5443 | 17.5436 |
| Generation cost ($/h) | 66,268.34 | 66,266.62 |
| Total generation (MW) | 6143.9995 | 6143.9985 |
| Bus | Proposed Method (MW) | Traditional SCED Method (MW) [44] |
|---|---|---|
| 30 | 800 | 800 |
| 31 | 720.69 | 720.65 |
| 32 | 501.04 | 501.01 |
| 33 | 560 | 560 |
| 34 | 412.27 | 412.24 |
| 35 | 700 | 700 |
| 36 | 600 | 600 |
| 37 | 550 | 550 |
| 38 | 550 | 550 |
| 39 | 750 | 750 |
| Percentage | Load (MW) | MW Loss by PSS/E | MW Loss By B coefficient | Error (%) |
|---|---|---|---|---|
| 105% | 41704 | 583.4 | 591.6 | 1.41 |
| 103% | 40910 | 555.8 | 559.9 | 0.73 |
| 100% | 39718 | 516.5 | 516.7 | 0.04 |
| 97% | 38527 | 480.9 | 475.2 | −1.12 |
| 95% | 37733 | 455.0 | 446.2 | −1.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, Y.-Y.; Zeng, H. Decentralized Multi-Area Economic Dispatch in Power Systems Using the Consensus Algorithm. Energies 2024, 17, 3609. https://doi.org/10.3390/en17153609
Hong Y-Y, Zeng H. Decentralized Multi-Area Economic Dispatch in Power Systems Using the Consensus Algorithm. Energies. 2024; 17(15):3609. https://doi.org/10.3390/en17153609
Chicago/Turabian StyleHong, Ying-Yi, and Hao Zeng. 2024. "Decentralized Multi-Area Economic Dispatch in Power Systems Using the Consensus Algorithm" Energies 17, no. 15: 3609. https://doi.org/10.3390/en17153609
APA StyleHong, Y.-Y., & Zeng, H. (2024). Decentralized Multi-Area Economic Dispatch in Power Systems Using the Consensus Algorithm. Energies, 17(15), 3609. https://doi.org/10.3390/en17153609







