A Novel Hybrid Harris Hawk Optimization–Sine Cosine Algorithm for Congestion Control in Power Transmission Network
Abstract
1. Introduction
1.1. Literature Survey
1.2. Research Contribution
- A CM strategy has been developed to optimally manage rescheduled real power deliveries from the system generators.
- An enhanced hybrid Harris Hawk Optimization–Sine Cosine Algorithm (hHHO-SCA) is proposed as an efficient optimization technique aimed at minimizing congestion costs by optimal adjustments in the real power deliveries of the generators.
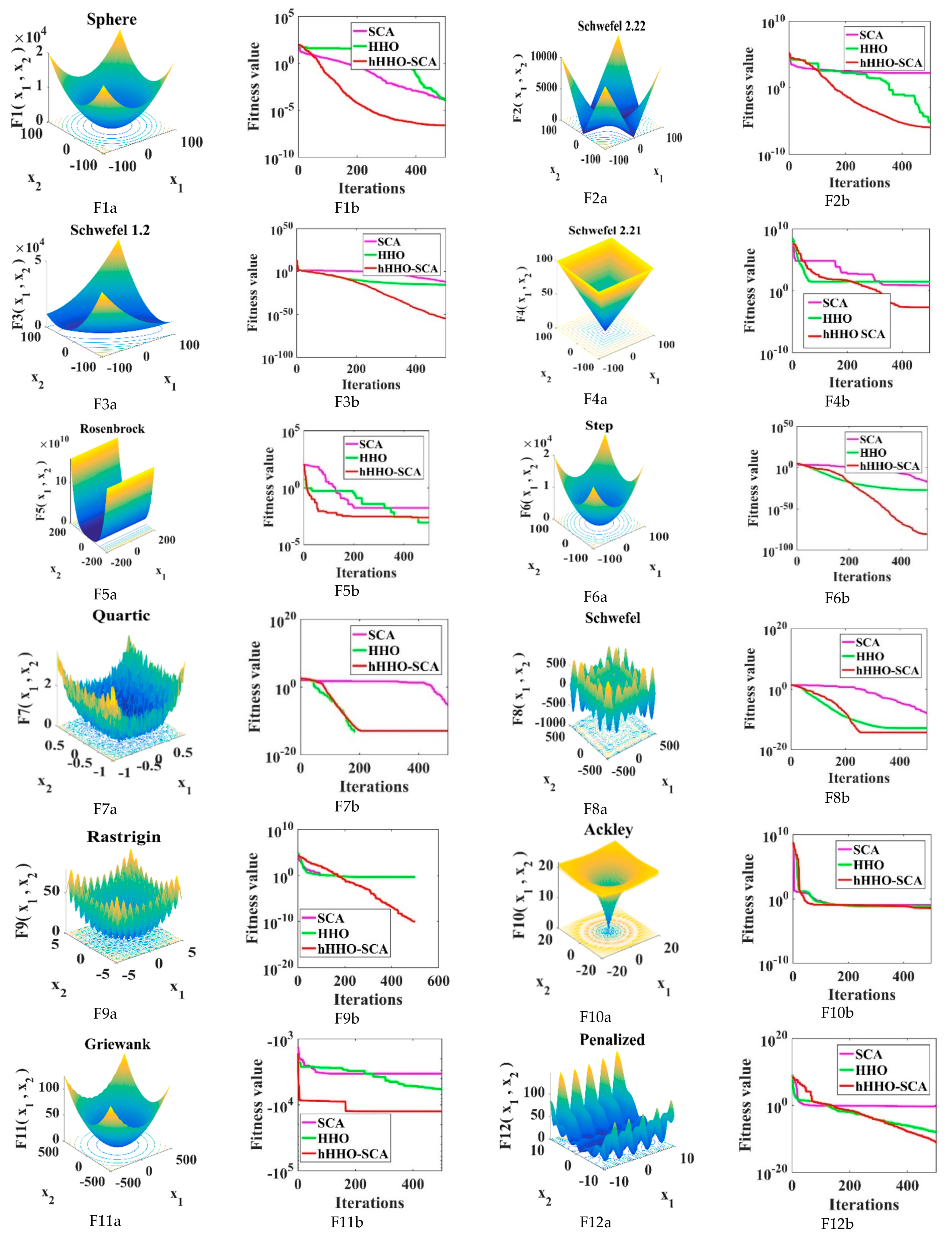
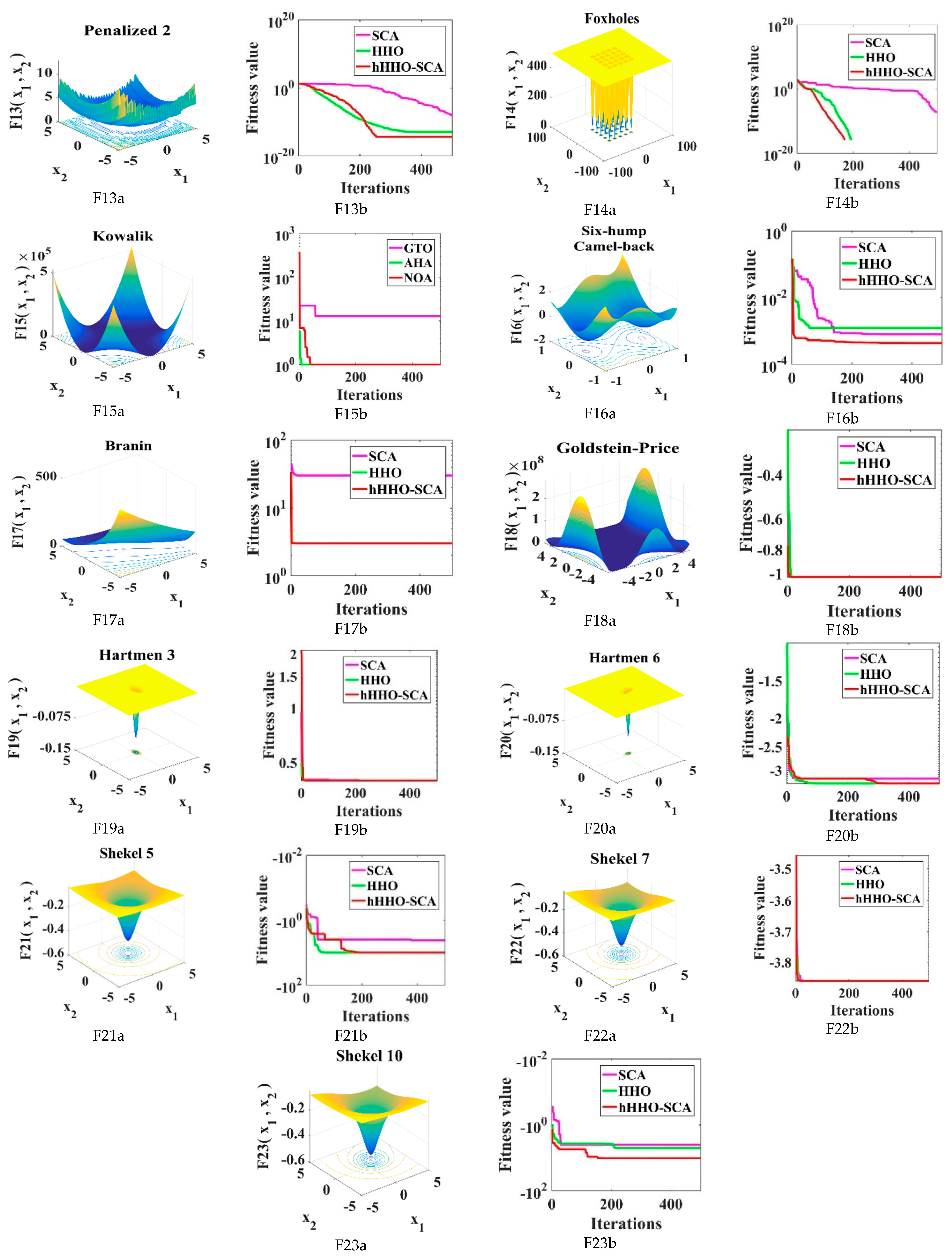
- Conventional benchmark functions have been employed to evaluate the performance of HHO-SCA and its application has been implemented on the IEEE 30-bus system and 118-bus system, demonstrating congestion mitigation with minimum rescheduling cost.
- Comparisons have been established to highlight the effectiveness of HHO-SCA with other recent optimization algorithms based on congestion cost, voltage profile, and system loss.
2. Problem Formulation
2.1. Inequality Constraints
2.2. Equality Constraints
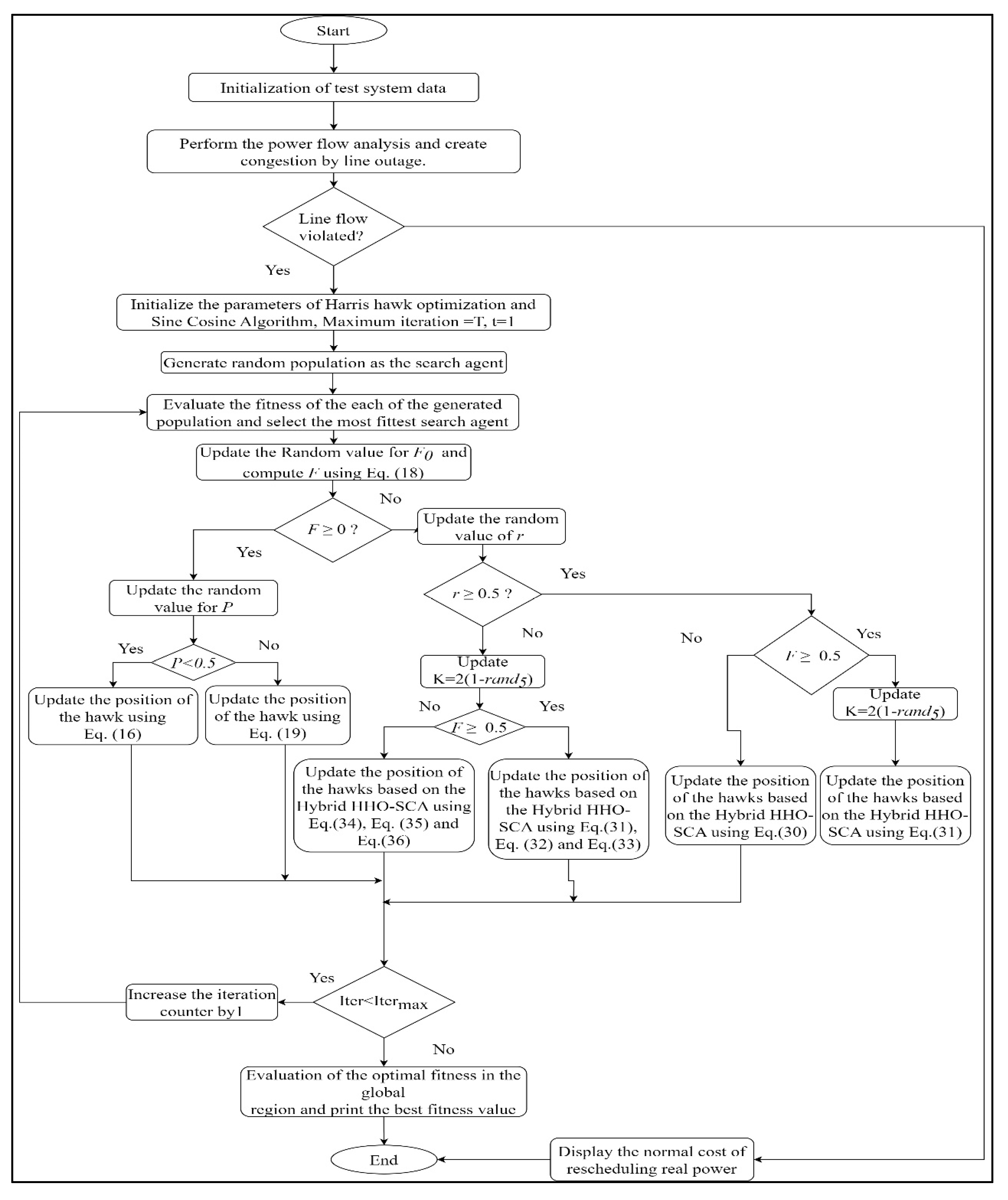
3. Hybrid Harris Hawk Optimization–Sine Cosine Algorithm (hHHO-SCA)
3.1. Sine Cosine Algorithm (SCA)
3.2. Harris Hawk Optimization (HHO)
3.2.1. Exploration Phase
3.2.2. Exploitation Phase
3.2.3. Soft Besiege
3.2.4. Hard Besiege
3.2.5. Soft Besiege with Gradual Brisk Dives
3.2.6. Hard Besiege with Progressive Rapid Dives
4. Formulation of hHHO-SCA
- Soft-Besiege [( and ()]
- Hard-Besiege [( and ()]
- Soft-Besiege with rapid drive [( and ()]
- Hard Besiege with progressive rapid dive [( and ()]
Performance Analysis of hHHO-SCA
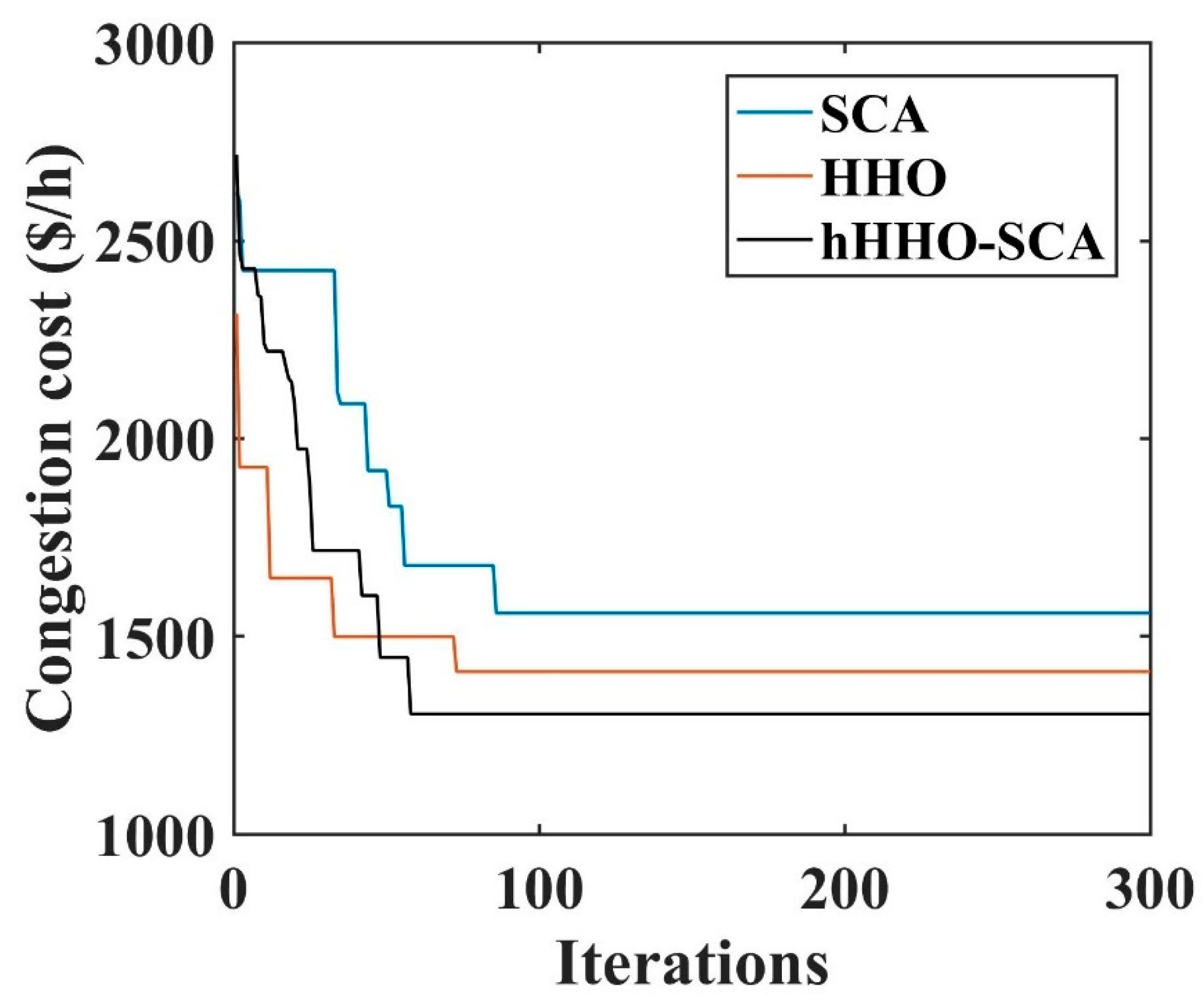
5. Results and Discussions
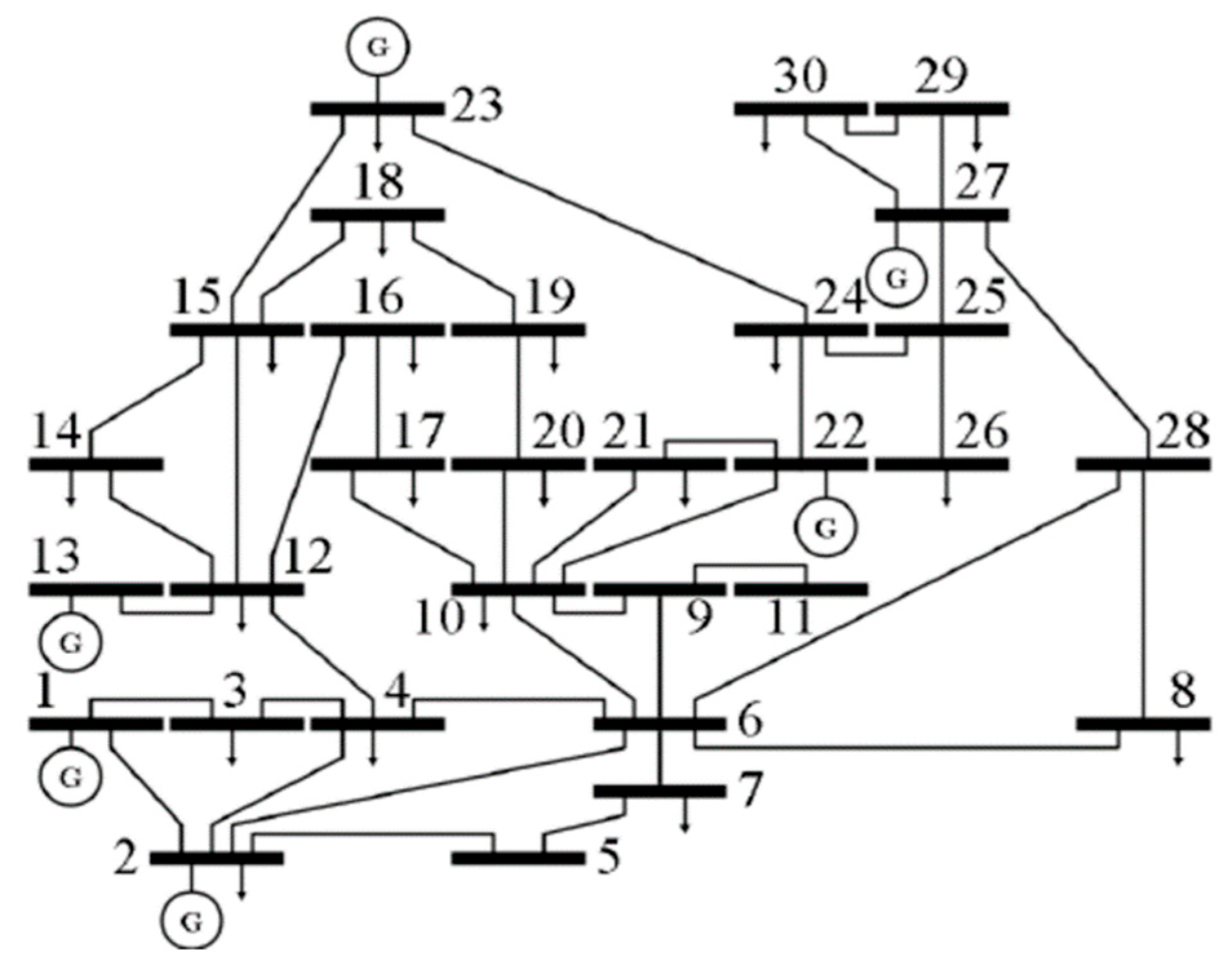
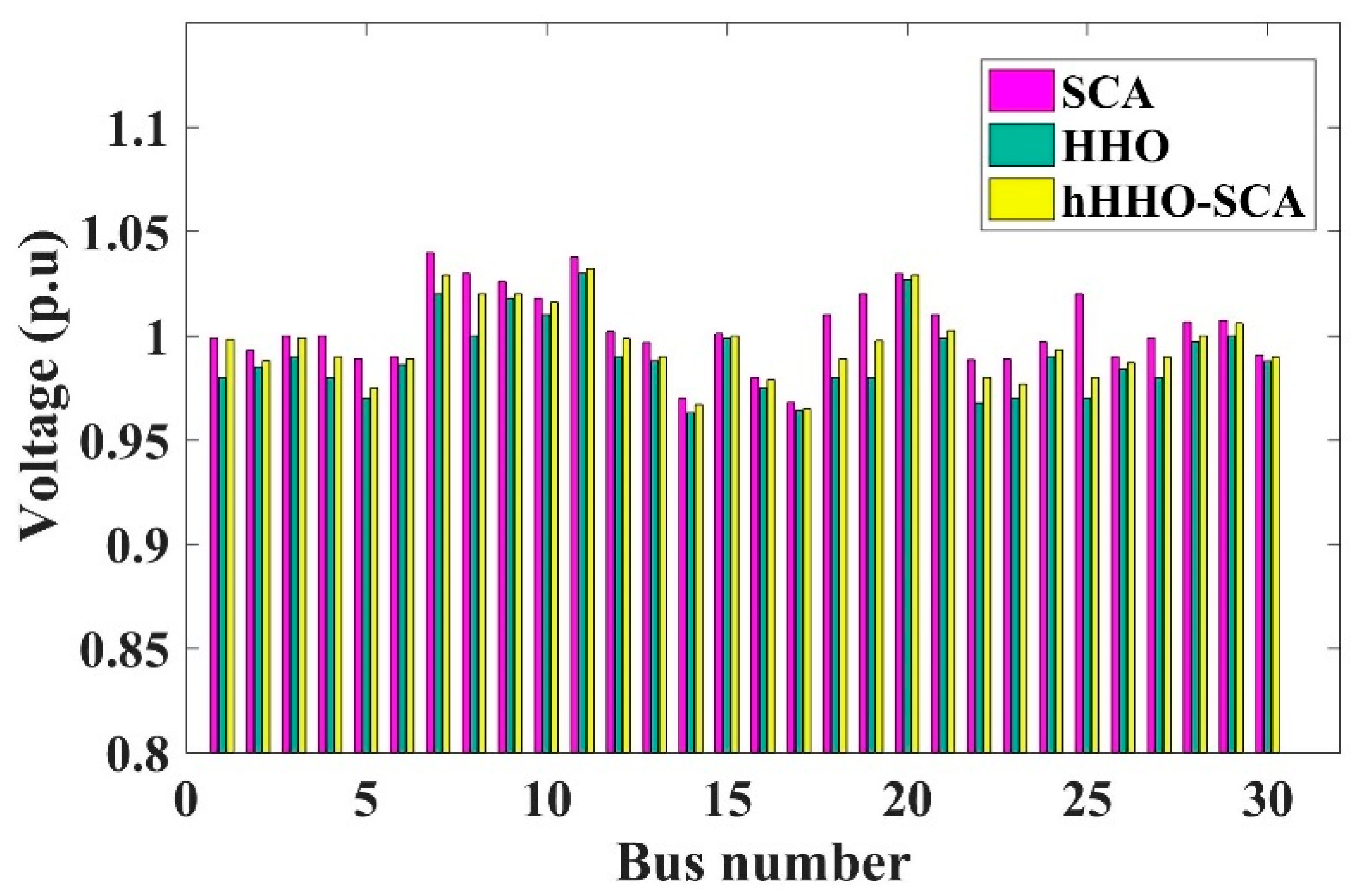
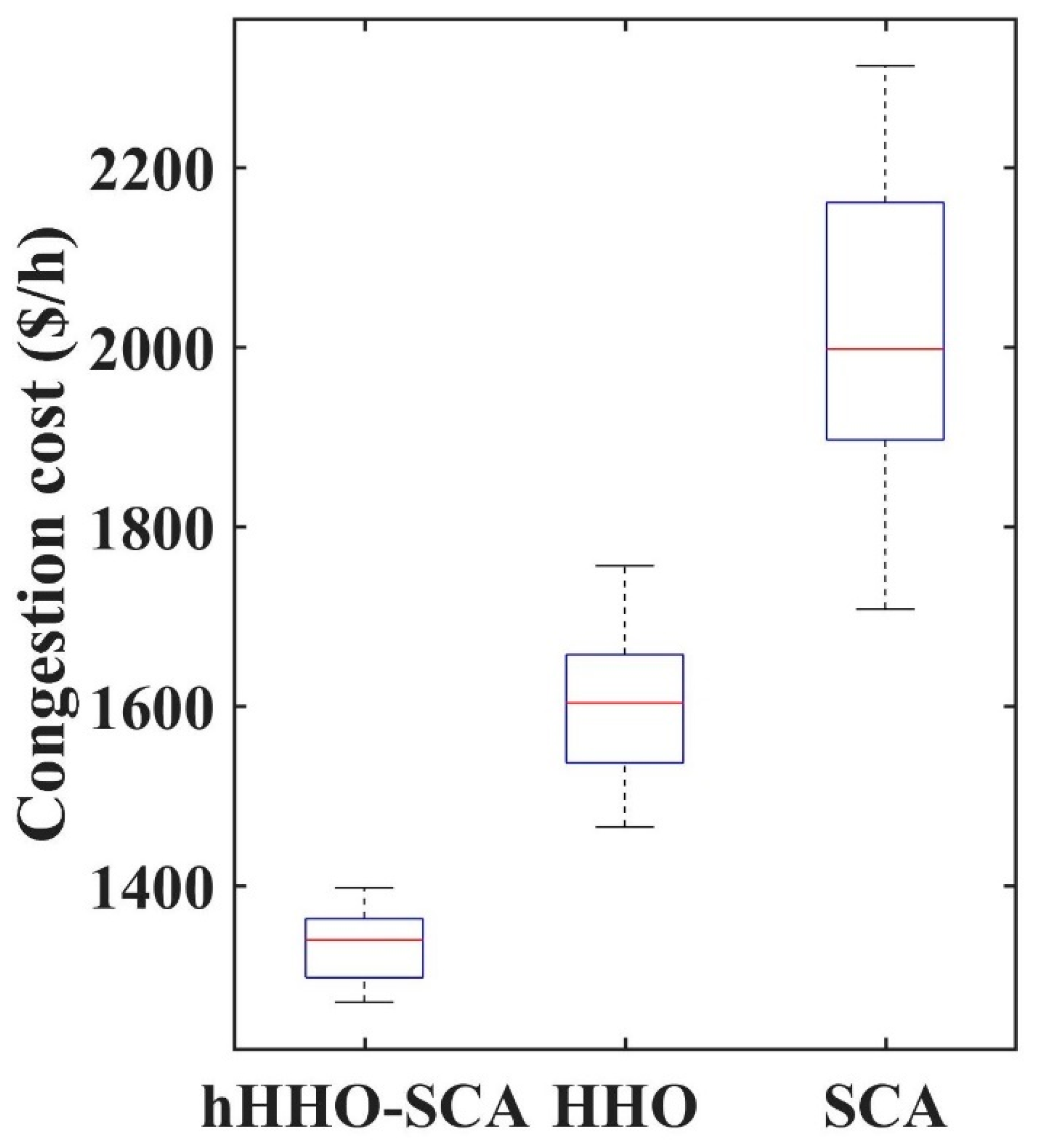
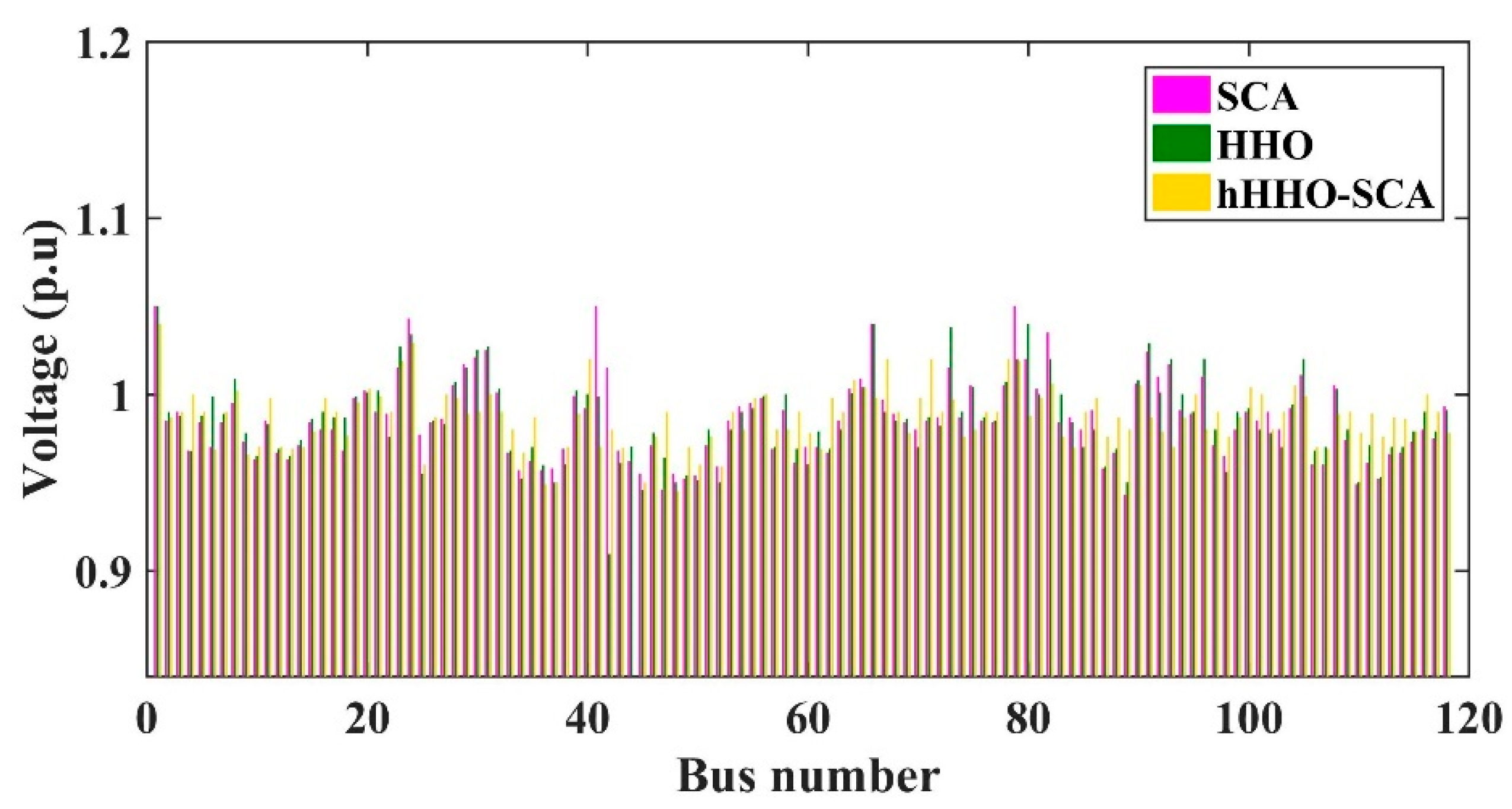
5.1. IEEE 30-Bus System
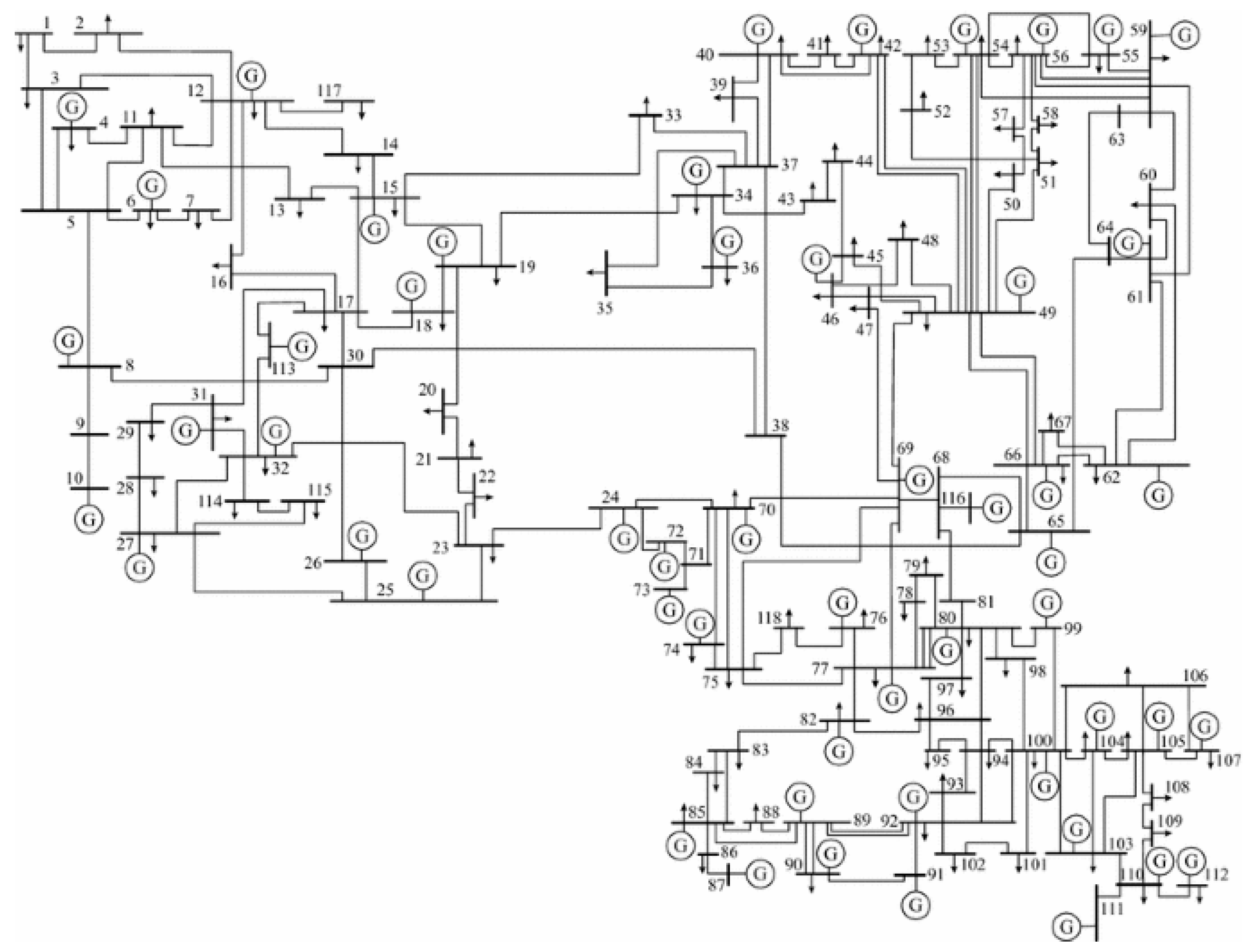
5.2. IEEE 118-Bus System
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bouhouras, A.S.; Kelepouris, N.S.; Koltsaklis, N.; Oureilidis, K.; Christoforidis, G.C. Congestion Management in coupled TSO and DSO networks. Electr. Power Syst. Res. 2024, 229, 110145. [Google Scholar] [CrossRef]
- Alavijeh, N.M.; Steen, D.; Le, A.T.; Nyström, S. Capacity limitation based local flexibility market for congestion management in distribution networks: Design and challenges. Int. J. Electr. Power Energy Syst. 2024, 156, 109742. [Google Scholar] [CrossRef]
- Zhou, H.; Lu, L.; Wei, M.; Shen, L.; Liu, Y. Robust Scheduling of a Hybrid Hydro/photovoltaic/Pumped-Storage System for Multiple Grids Peak-Shaving and Congestion Management. IEEE Access 2023, 12, 22230–22242. [Google Scholar] [CrossRef]
- Dehnavi, E.; Akmal, A.A.S.; Moeini-Aghtaie, M. Developing a novel zonal congestion management based on demand response programs considering dynamic transmission ratings. Int. J. Electr. Power Energy Syst. 2023, 146, 108779. [Google Scholar] [CrossRef]
- Majeed Rashid Zaidan, S.I.T. Emergency congestion management of power systems by static synchronous series compensator. Indones. J. Electr. Eng. Comput. Sci. 2022, 25, 1258–1265. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, T.; Parisio, A. Frequency regulation and congestion management by Virtual Storage Plants. Sustain. Energy Grids Netw. 2022, 29, 100586. [Google Scholar] [CrossRef]
- Hobbie, H.; Mehlem, J.; Wolff, C.; Weber, L.; Flachsbarth, F.; Möst, D.; Moser, A. Impact of model parametrization and formulation on the explorative power of electricity network congestion management models-Insights from a grid model comparison experiment. Renew. Sustain. Energy Rev. 2022, 159, 112163. [Google Scholar] [CrossRef]
- Zakaryaseraji, M.; Ghasemi-Marzbali, A. Evaluating congestion management of power system considering the demand response program and distributed generation. Int. Trans. Electr. Energy Syst. 2022, 2022, 5818757. [Google Scholar] [CrossRef]
- Shaikh, M.S.; Raj, S.; Babu, R.; Kumar, S.; Sagrolikar, K. A hybrid moth–flame algorithm with particle swarm optimization with application in power transmission and distribution. Decis. Anal. J. 2023, 6, 100182. [Google Scholar] [CrossRef]
- Roustaei, M.; Letafat, A.; Sheikh, M.; Sadoughi, R.; Ardeshiri, M. A cost-effective voltage security constrained congestion management approach for transmission system operation improvement. Electr. Power Syst. Res. 2022, 203, 107674. [Google Scholar] [CrossRef]
- Mishra, S.; Samal, S.K. Impact of electrical power congestion and diverse transmission congestion issues in the electricity sector. Energy Syst. 2023, 15, 767–779. [Google Scholar] [CrossRef]
- Paul, K. Modified grey wolf optimization approach for power system transmission line congestion management based on the influence of solar photovoltaic system. Int. J. Energy Environ. Eng. 2022, 13, 751–767. [Google Scholar] [CrossRef]
- Sarwar, M.; Siddiqui, A.S.; Ghoneim, S.S.; Mahmoud, K.; Darwish, M.M. Effective transmission congestion management via optimal DG capacity using hybrid swarm optimization for contemporary power system operations. IEEE Access 2022, 10, 71091–71106. [Google Scholar] [CrossRef]
- Subramaniyan, V.; Gomathi, V. A Soft Computing-Based Analysis of Congestion Management in Transmission Systems. Teh. Vjesn. 2023, 30, 274–281. [Google Scholar] [CrossRef]
- Agrawal, A.; Pandey, S.N.; Srivastava, L.; Walde, P.; Singh, S.; Khan, B.; Saket, R. Hybrid Deep Neural Network-Based Generation Rescheduling for Congestion Mitigation in Spot Power Market. IEEE Access 2022, 10, 29267–29276. [Google Scholar] [CrossRef]
- Chakravarthi, K.; Bhui, P.; Sharma, N.K.; Pal, B.C. Real Time Congestion Management Using Generation Re-dispatch: Modeling and Controller Design. IEEE Trans. Power Syst. 2022, 38, 2189–2203. [Google Scholar] [CrossRef]
- Srivastava, J.; Yadav, N.K. Rescheduling-based congestion management by metaheuristic algorithm: Hybridizing lion and moth search models. Int. J. Numer. Model. Electron. Netw. Devices Fields 2021, 35, e2952. [Google Scholar] [CrossRef]
- Ogunwole, E.I.; Krishnamurthy, S. Transmission Congestion Management Using Generator Sensitivity Factors for Active and Reactive Power Rescheduling Using Particle Swarm Optimization Algorithm. IEEE Access 2022, 10, 122882–122900. [Google Scholar] [CrossRef]
- Prajapati, V.K.; Mahajan, V. Demand response based congestion management of power system with uncertain renewable resources. Int. J. Ambient Energy 2022, 43, 103–116. [Google Scholar] [CrossRef]
- Thiruvel, A.; Thiruppathi, S.; Chidambararaj, N.; Aravindhan, K. In Modern Power System Operations in Effective Transmission Congestion Management via Optimal DG Capacity Using Firefly Algorithms. In Proceedings of the 2023 9th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 23–25 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 360–365. [Google Scholar] [CrossRef]
- Kamaraj, N. Transmission congestion management using particle swarm optimization. J. Electr. Syst. 2011, 7, 54–70. [Google Scholar] [CrossRef]
- Saravanan, C.; Anbalagan, P. An intelligent hybrid technique for optimal generator rescheduling for congestion management in a deregulated power market. J. Intell. Fuzzy Syst. 2022, 43, 1331–1345. [Google Scholar] [CrossRef]
- Sharma, V.; Walde, P. A novel optimisation technique based on swarm intelligence for congestion management in transmission lines. Int. J. Power Energy Convers. 2022, 13, 1–23. [Google Scholar] [CrossRef]
- Haq, F.U.; Bhui, P.; Chakravarthi, K. Real time congestion management using plug in electric vehicles (PEV’s): A game theoretic approach. IEEE Access 2022, 10, 42029–42043. [Google Scholar] [CrossRef]
- Verma, S.; Mukherjee, V. Optimal real power rescheduling of generators for congestion management using a novel ant lion optimiser. IET Gener. Transm. Distrib. 2016, 10, 2548–2561. [Google Scholar] [CrossRef]
- Paul, K.; Kumar, N.; Agrawal, S.; Paul, K. Optimal rescheduling of real power to mitigate congestion using gravitational search algorithm. Turk. J. Electr. Eng. Comput. Sci. 2019, 27, 2213–2225. [Google Scholar] [CrossRef]
- Qu, K.; Zheng, X.; Li, X.; Lv, C.; Yu, T. Stochastic Robust Real-Time Power Dispatch with Wind Uncertainty using Difference-of-Convexity Optimization. IEEE Trans. Power Syst. 2022, 37, 4497–4511. [Google Scholar] [CrossRef]
- Paul, K.; Dalapati, P.; Kumar, N. Optimal Rescheduling of Generators to Alleviate Congestion in Transmission System: A Novel Modified Whale Optimization Approach. Arab. J. Sci. Eng. 2021, 47, 3255–3279. [Google Scholar] [CrossRef]
- Verma, S.; Mukherjee, V. Firefly algorithm for congestion management in deregulated environment. Eng. Sci. Technol. Int. J. 2016, 19, 1254–1265. [Google Scholar] [CrossRef]
- Meddeb, A.; Amor, N.; Abbes, M.; Chebbi, S. A novel approach based on crow search algorithm for solving reactive power dispatch problem. Energies 2018, 11, 3321. [Google Scholar] [CrossRef]
- Fan, X.; Liu, Y.; Gu, Z.; Yao, Q. A double-loop adaptive relevant vector machine combined with Harris Hawks optimization-based importance sampling. Eng. Comput. 2024. [Google Scholar] [CrossRef]
- Dey, P.; Marungsri, B. Modified Harris Hawk algorithm-based optimal photovoltaics for Voltage Stability and Load Flow Analysis. Int. J. Green Energy 2024, 21, 2378–2392. [Google Scholar] [CrossRef]
- Almousa, M.T.; Gomaa, M.R.; Ghasemi, M.; Louzazni, M. Single-Sensor Global MPPT for PV System Interconnected with DC Link Using Recent Red-Tailed Hawk Algorithm. Energies 2024, 17, 3391. [Google Scholar] [CrossRef]
- Peng, L.; Li, X.; Yu, L.; Heidari, A.A.; Chen, H.; Liang, G. Q-learning guided mutational Harris hawk optimizer for high-dimensional gene data feature selection. Appl. Soft Comput. 2024, 161, 111734. [Google Scholar] [CrossRef]
- Belazzoug, M.; Touahria, M.; Nouioua, F.; Brahimi, M. An improved sine cosine algorithm to select features for text categorization. J. King Saud Univ. Comput. Inf. Sci. 2020, 32, 454–464. [Google Scholar] [CrossRef]
- Mirjalili, S.M.; Mirjalili, S.Z.; Saremi, S.; Mirjalili, S. Sine cosine algorithm: Theory, literature review, and application in designing bend photonic crystal waveguides. In Nature-Inspired Optimizers: Theories, Literature Reviews and Applications; Springer: Cham, Switzerland, 2020; pp. 201–217. [Google Scholar] [CrossRef]
- Mittal, U.; Nangia, U.; Jain, N.K.; Gupta, S. Optimal power flow solution using a learning-based sine–cosine algorithm. J. Supercomput. 2024, 80, 15974–16012. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Sharma, P.; Batish, N.; Khan, S.; Arya, S. Power flow analysis for IEEE 30 bus distribution system. WSEAS Trans. Power Syst. 2018, 13, 48–59. [Google Scholar]
- Dash, S.; Mohanty, S. In Multi-objective economic emission load dispatch with nonlinear fuel cost and noninferior emission level functions for IEEE-118 bus system. In Proceedings of the 2015 2nd International Conference on Electronics and Communication Systems (ICECS), Coimbatore, India, 26–27 February 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1371–1376. [Google Scholar] [CrossRef]
- Verma, S.; Saha, S.; Mukherjee, V. Optimal rescheduling of real power generation for congestion management using teaching-learning-based optimization algorithm. J. Electr. Syst. Inf. Technol. 2018, 5, 889–907. [Google Scholar] [CrossRef]
| Functions | HHO | SCA | hHHO-SCA | |
|---|---|---|---|---|
| F1 | AVG | 2.77 × 10−27 | 1.62 × 10−42 | 0.00 × 100 |
| SD | 8.68 × 10−27 | 1.8 × 10−42 | 0.00 × 100 | |
| Med | 2.27 × 10−29 | 1.32 × 10−44 | 0.00 × 100 | |
| Worst | 4.59 × 10−26 | 8.9 × 10−44 | 0.00 × 100 | |
| F2 | AVG | 1.27 × 10−19 | 8.61 × 10−27 | 0.00 × 100 |
| SD | 3.05 × 10−20 | 6.12 × 10−27 | 0.00 × 100 | |
| Med | 7.67 × 10−23 | 7.19 × 10−27 | 0.00 × 100 | |
| Worst | 7.94 × 10−20 | 3.72 × 10−27 | 0.00 × 100 | |
| F3 | AVG | 4.58 × 10−8 | 0.286 | 0.00 × 100 |
| SD | 0.000000128 | 0.213 | 0.00 × 100 | |
| Med | 3.95 × 10−12 | 0.241 | 0.00 × 100 | |
| Worst | 0.000000407 | 0.221 | 0.00 × 100 | |
| F4 | AVG | 2.54 × 10−9 | 0.000000312 | 0.00 × 100 |
| SD | 5.46 × 10−9 | 8.48 × 10−10 | 0.00 × 100 | |
| Med | 4.81 × 10−11 | 0.00000028 | 0.00 × 100 | |
| Worst | 0.000000168 | 0.000000229 | 0.00 × 100 | |
| F5 | AVG | 7.118 | 4.3 | 821.1151 |
| SD | 0.25018 | 3.3 | 3296.2251 | |
| Med | 8.6281 | 3.76 | 225.2106 | |
| Worst | 8.3662 | 7.58 | 8810.2357 | |
| F6 | AVG | 0.4417 | 0.00 × 100 | 0.00 × 100 |
| SD | 0.3336 | 0.00 × 100 | 0.00 × 100 | |
| Med | 0.3883 | 0.00 × 100 | 0.00 × 100 | |
| Worst | 0.57389 | 0.00 × 100 | 0.00 × 100 | |
| F7 | AVG | 0.0008288 | 0.0028 | 0.0000157 |
| SD | 0.0006801 | 0.00103 | 0.0000141 | |
| Med | 0.0005445 | 0.0026 | 0.000012 | |
| Worst | 0.0040891 | 0.00478 | 0.0000531 | |
| F8 | AVG | −3323.231 | −4170 | −3365.415 |
| SD | 348.3505 | 50 | 333.7271 | |
| Med | −3187.4255 | −4190 | −3534.859 | |
| Worst | −3137.601 | −4070 | −3300.079 | |
| F9 | AVG | 2.4967 | 0.00 × 100 | 0.00 × 100 |
| SD | 6.1494 | 0.00 × 100 | 0.00 × 100 | |
| Med | 7.55 × 10−11 | 0.00 × 100 | 0.00 × 100 | |
| Worst | 14.5679 | 0.00 × 100 | 0.00 × 100 | |
| F10 | AVG | 2.52−16 | 5.55 × 10−16 | 7..99 × 10−18 |
| SD | 3.25 × 10−16 | 0.00 × 100 | 0.00 × 100 | |
| Med | 7.0707 × 10−16 | 5.55 × 10−15 | 9.89 × 10−15 | |
| Worst | 3 × 10−14 | 5.55 × 10−15 | 8.99 × 10−15 | |
| F11 | AVG | 0.080791 | 0.00074 | 0.00 × 100 |
| SD | 0.29872 | 0.00234 | 0.00 × 100 | |
| Med | 0.00000087 | 0.00 × 100 | 0.00 × 100 | |
| Worst | 0.52624 | 0.0074 | 0.00 × 100 | |
| F12 | AVG | 0.080838 | 4.71 × 10−32 | 0.32412 |
| SD | 0.03070 | 2.26 × 10−48 | 0.5869 | |
| Med | 0.076773 | 5.81 × 10−33 | 0.0000939 | |
| Worst | 0.007228 | 5.81 × 10−33 | 3.248 | |
| F13 | AVG | 0.32412 | 1.35 × 10−32 | 0.020908 |
| SD | 0.07336 | 3.90 × 10−49 | 0.037983 | |
| Med | 0.45525 | 2.46 × 10−33 | 0.008320 | |
| Worst | 0.52125 | 2.46 × 10−33 | 0.071273 | |
| F14 | AVG | 1.6935 | 0.998 | 0.896 |
| SD | 0.84822 | 0.00 × 100 | 0.00 × 100 | |
| Med | 0.9456 | 0.772 | 0.699 | |
| Worst | 1.8321 | 0.772 | 0.699 | |
| F15 | AVG | 0.000988 | 0.000382 | 0.0002927 |
| SD | 0.000223 | 0.000202 | 0.000348 | |
| Med | 0.000885 | 0.000829 | 0.0006074 | |
| Worst | 0.002435 | 0.00122 | 0.0050304 | |
| F16 | AVG | −1.0123 | −1.03 | −2.04151 |
| SD | 0.000017 | 0.00 × 100 | 0.00 × 100 | |
| Med | −1.6554 | −1.03 | −3.23271 | |
| Worst | −1.9987 | −1.03 | −3.24271 | |
| F17 | AVG | 0.4231 | 0.398 | 0.30991 |
| SD | 0.002234 | 0.00 × 100 | 0.00 × 100 | |
| Med | 0.6789 | 0.502 | 0.40870 | |
| Worst | 0.5438 | 0.402 | 0.50990 | |
| F18 | AVG | 3 | 3 | 3 |
| SD | 0.0000457 | 2.96 × 10−16 | 0.00 × 100 | |
| Med | 3 | 3 | 3 | |
| Worst | 3.0001 | 3 | 3 | |
| F19 | AVG | −4.7891 | −4.97 | −5.1735 |
| SD | 0.0008651 | 9.47 × 10−17 | 0.00 × 100 | |
| Med | −6.8761 | −5.63 | −5.5718 | |
| Worst | −6.8612 | −5.13 | −5.0719 | |
| F20 | AVG | −2.9654 | −4.56 | −4.2862 |
| SD | 0.2367 | 4.68 × 10−16 | 0.037421 | |
| Med | −3.1365 | −3.32 | −4.123 | |
| Worst | −1.8767 | −3.32 | −4.1031 | |
| F21 | AVG | −4.0077 | −10.1 | −11.0432 |
| SD | 3.1012 | 0.078 | 0.00 × 100 | |
| Med | −4.1738 | −10.2 | −11.0431 | |
| Worst | −0.5881 | −9.91 | −11.1231 | |
| F22 | AVG | −5.2501 | −10.4 | −11.2028 |
| SD | 2.3107 | 2.43 × 10−16 | 3.39 × 10−15 | |
| Med | −3.708 | −10.4 | −11.3028 | |
| Worst | −0.80836 | −10.4 | −11.3021 | |
| F23 | AVG | −5.5371 | −8.45 | −11.3362 |
| SD | 0.88747 | 3.43 | 2.58 × 10−16 | |
| Med | −4.5678 | −10.5 | −11.6362 | |
| Worst | −1.9867 | −1.86 | −11.6265 |
| Scenarios | Standard Power System Network | Overloading Conditions |
|---|---|---|
| 1 | IEEE 30-bus system [39] | Tripping of lines 1–2 |
| 2 | IEEE 118-bus system [40] | Increment in load of 57% at buses 11 and 20, outage of lines 8–5 |
| Congested/Overload Lines | Power Flow (MW) | Excess Power Flow (MW) | Power Flow Limit (MW) | Overload (%) | |
|---|---|---|---|---|---|
| Outage of lines 1–2 | 1–3 | 147.46 | 17.46 | 130 | 13.43 |
| 6–8 | 136.29 | 6.29 | 130 | 4.84 |
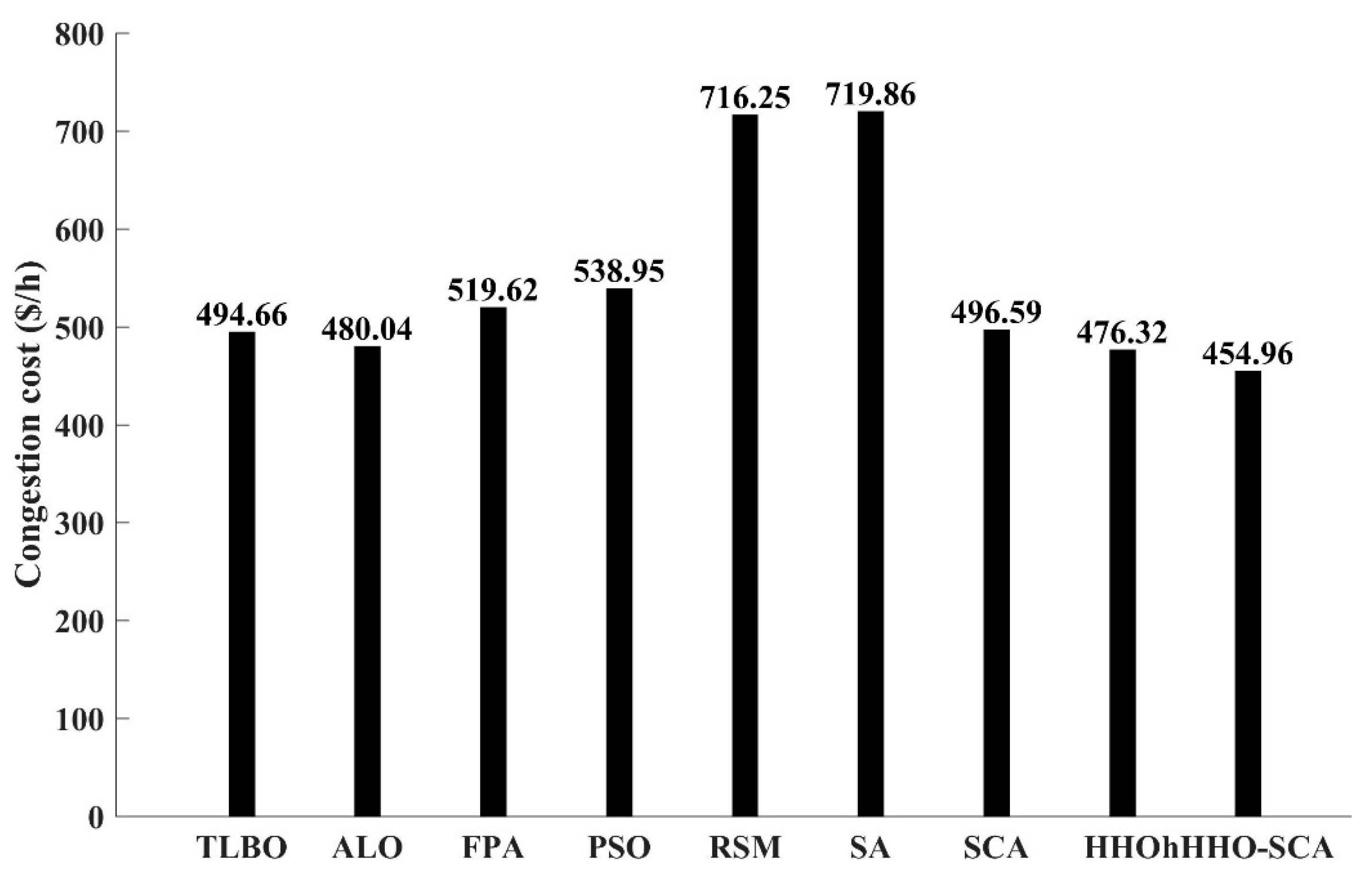
| TLBO [41] | ALO [25] | FPA [25] | PSO [21] | RSM [21] | SA [21] | SCA [Solved] | HHO [Solved] | hHHO-SCA [Proposed] | |
|---|---|---|---|---|---|---|---|---|---|
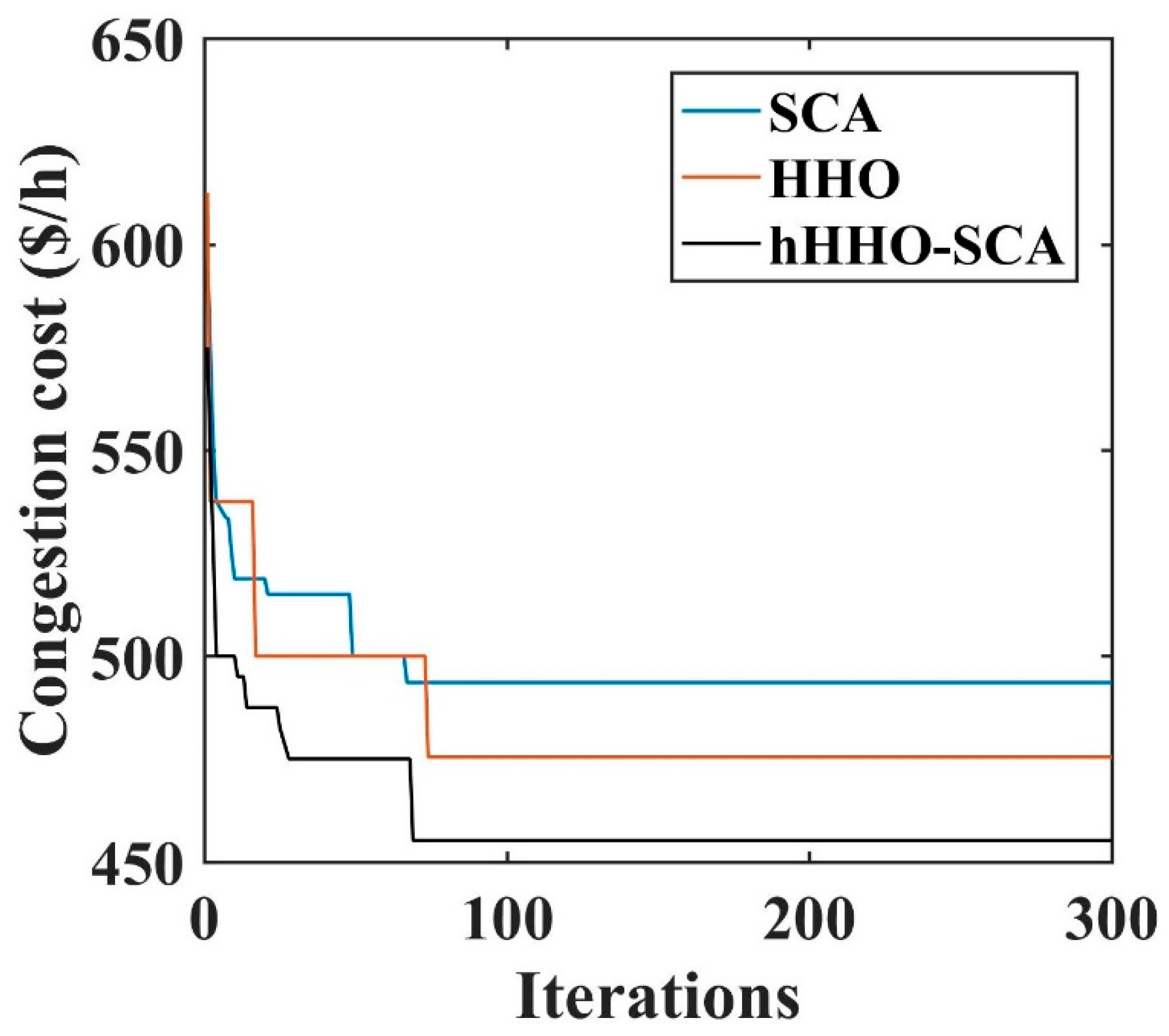
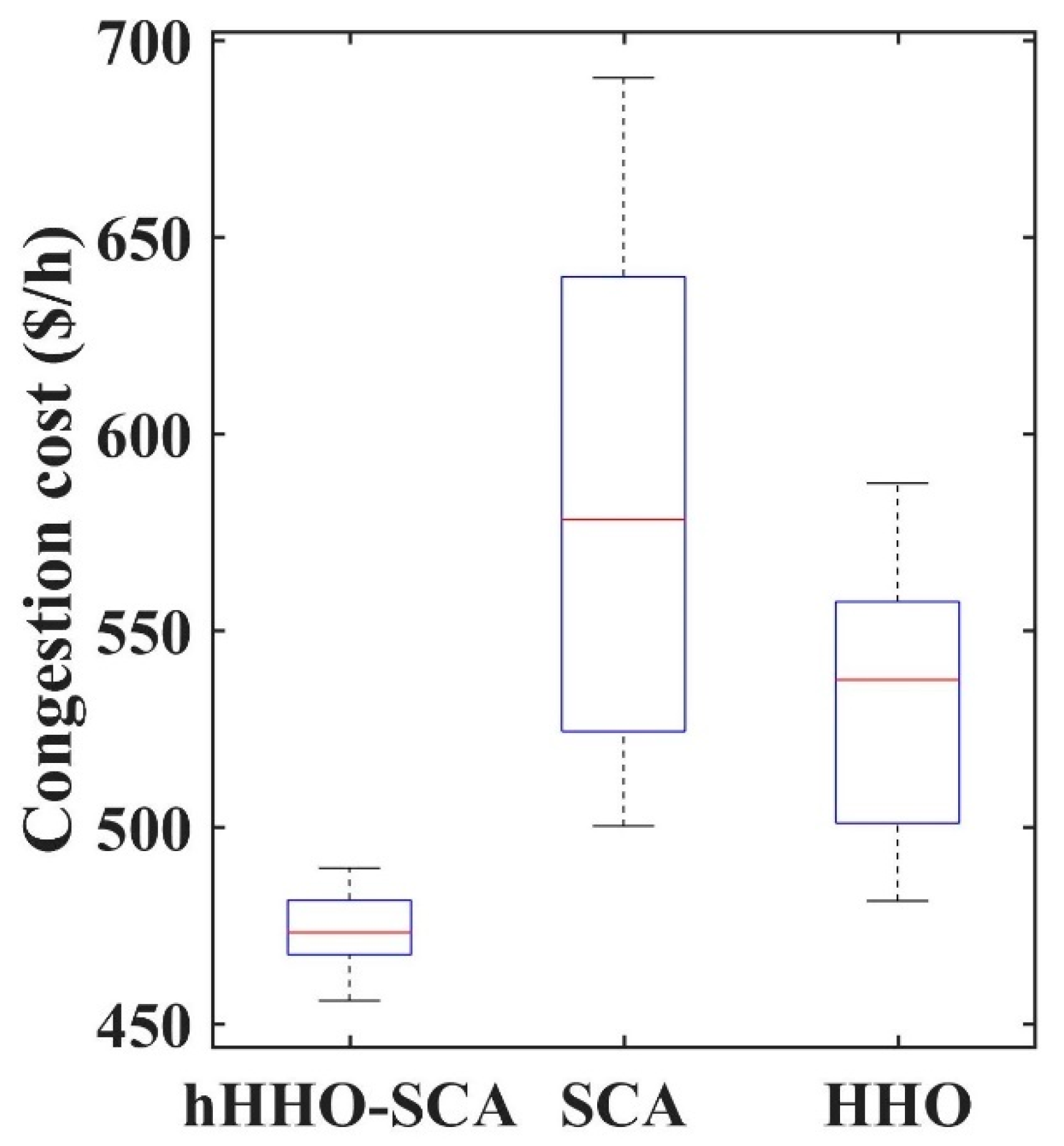
| Congestion cost ($/h) | 494.66 | 480.04 | 519.62 | 538.95 | 716.25 | 719.86 | 496.59 | 476.32 | 454.96 |
| Best congestion cost ($/h) | * NR | * NR | * NR | * NR | * NR | * NR | 496.59 | 476.32 | 454.96 |
| Worst congestion cost ($/h) | * NR | * NR | * NR | * NR | * NR | * NR | 801.58 | 596.12 | 490.24 |
| Line (1–3) power flow (post-CM) | 130.00 | 129.5 | 129.60 | 129.97 | 129.78 | 129.51 | 129.69 | 129.98 | 129.65 |
| Line (6–8) power flow (post-CM) | 120.78 | 120.79 | 120.58 | 120.62 | 120.60 | 120.35 | 120.38 | 120.65 | 120.03 |
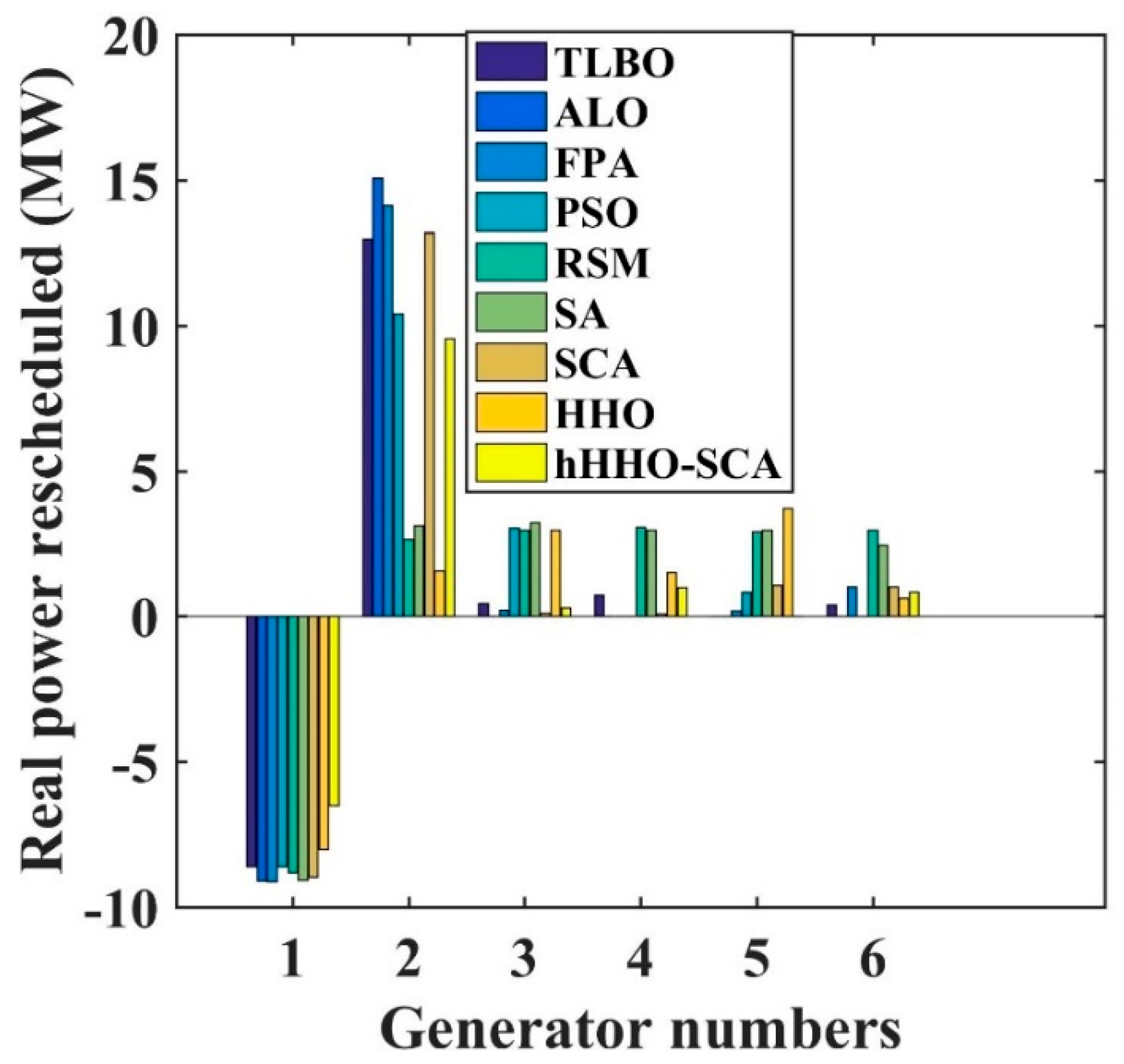
| ∆P1 (MW) | −8.5876 | −9.0880 | −9.127 | −8.61 | −8.808 | −9.076 | −8.97 | −8.004 | −6.491 |
| ∆P2 (MW) | 12.9855 | 15.0668 | 14.14 | 10.40 | 2.647 | 3.133 | 13.20 | 1.568 | 9.5519 |
| ∆P3 (MW) | 0.4598 | 0.0198 | 0.206 | 3.03 | 2.953 | 3.234 | 0.109 | 2.96 | 0.2854 |
| ∆P4 (MW) | 0.7289 | 0.0001 | 0.0188 | 0.02 | 3.063 | 2.968 | 0.074 | 1.519 | 0.9962 |
| ∆P5 (MW) | 0.0093 | 0.0002 | 0.189 | 0.85 | 2.913 | 2.954 | 1.065 | 3.719 | 0.0034 |
| ∆P6 (MW) | 0.3988 | 0.0001 | 1.013 | 0.01 | 2.952 | 2.443 | 1.007 | .628 | 0.8476 |
| Total amount (MW) | 23.169 | 24.1552 | 24.703 | 22.93 | 23.33 | 23.80 | 23.619 | 20.111 | 19.4734 |
| Congested/Overload Lines (MW) | Power Flow (MW) | Excess Power Flow (MW) | Line Limit (MW) | % Overload | |
|---|---|---|---|---|---|
| Tripping of lines 8–5 with increase in load at buses 11–20 by 57% | 16–17 | 209.14 | 34.14 | 175 | 12.83 |
| 30–17 | 568.73 | 13.16 | 500 | 37.6 | |
| 8–30 | 380.59 | 205.59 | 175 | 54.01 |
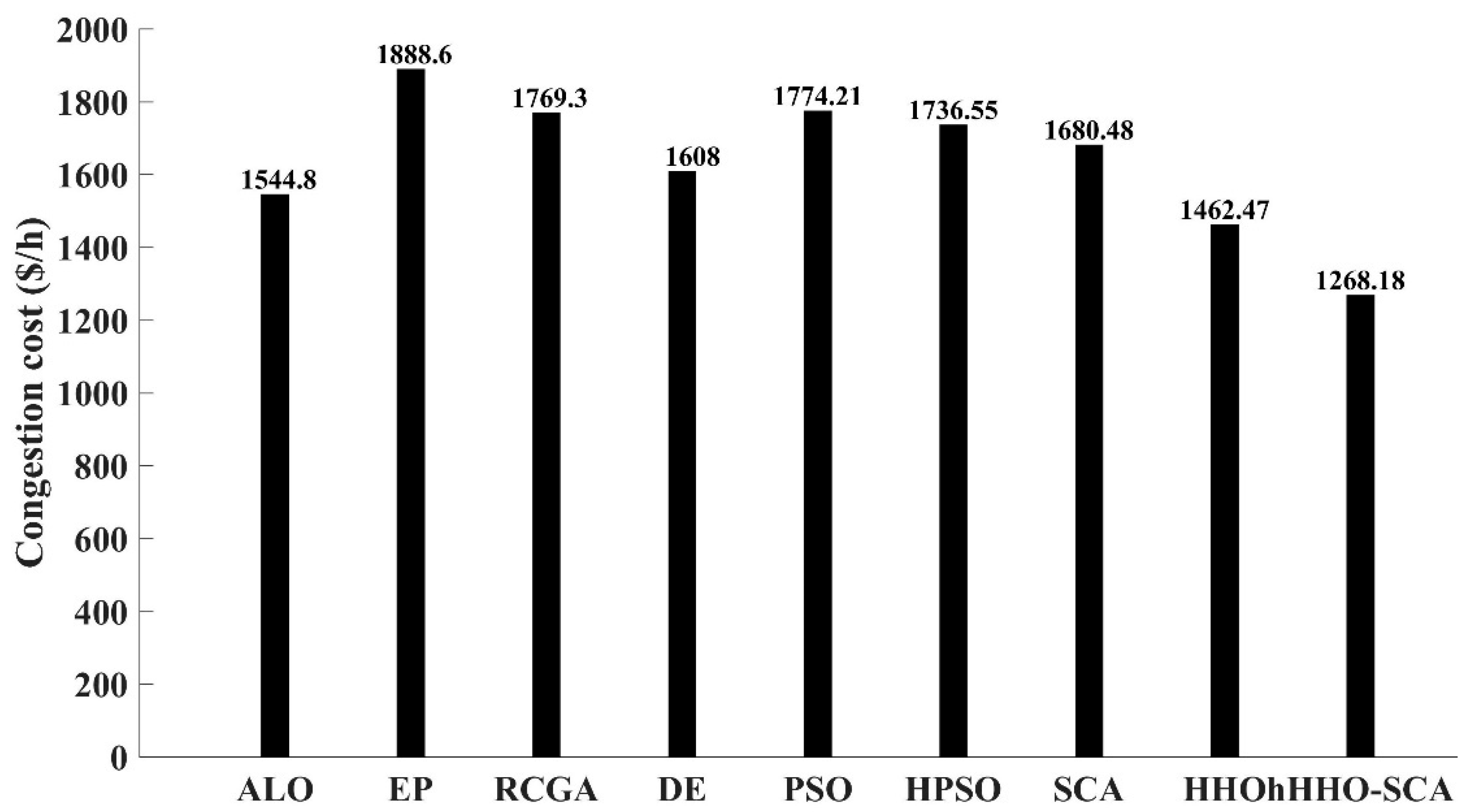
| ALO [41] | EP [21] | RCGA [21] | DE [21] | PSO [25] | HPSO [25] | SCA [Solved] | HHO [Solved] | hHHO-SCA [Proposed] | |
|---|---|---|---|---|---|---|---|---|---|
| Congestion cost ($/h) | 1544.8 | 1888.60 | 1769.3 | 1608.0 | 17,742 | 17,365 | 1680.48 | 1462.47 | 1268.18 |
| Best congestion cost ($/h) | * NR | * NR | * NR | * NR | * NR | * NR | 1680.48 | 1462.47 | 1268.18 |
| Worst congestion cost ($/h) | * NR | * NR | * NR | * NR | * NR | * NR | 2318.67 | 1762.78 | 1398.56 |
| Line (16–17) power flow (post-CM) | 174.20 | 173.89 | 174.26 | 174.37 | 174.15 | 174.62 | 174.23 | 174.87 | 173.18 |
| Line (30–17) power flow (post-CM) | 497.94 | 498.14 | 499.09 | 496.88 | 496.09 | 495.42 | 496.36 | 497.30 | 495.42 |
| Line (8–30) power flow (post-CM) | 174.76 | 174.54 | 174.68 | 174.20 | 174.82 | 174.59 | 174.48 | 174.00 | 174.02 |
| ∆PG1 | 0.0177 | 38.11 | 26.274 | 6.4705 | 24.502 | 11.59 | 0 | 0.0426 | 0.125 |
| ∆PG2 | 0.0362 | 0 | 0 | 0 | 0 | 0 | 0.0177 | 0.0001 | 3.0727 |
| ∆PG3 | 17.266 | 63.06 | 31.422 | 12.295 | 1.0259 | 6.568 | −0.2312 | 0.014 | 0 |
| ∆PG4 | −0.0031 | −7.48 | 11.349 | −0.056 | 1.3148 | −0.046 | 7.4155 | −0.0004 | 0 |
| ∆PG5 | −207.83 | −200.6 | −219.3 | −208.1 | −21.82 | −207.7 | 0.0655 | 0.0002 | 1.7508 |
| ∆PG6 | 105.32 | 48.58 | 101.42 | 105.32 | 105.32 | 80.126 | 0.1504 | 0.0237 | 0 |
| ∆PG7 | 0.002 | 0 | 0 | 0 | 0 | 0 | 89.669 | 0.004 | 104.93 |
| ∆PG8 | 4.6839 | 49.17 | 0.0029 | 1.9946 | 16.815 | 6.0059 | 0 | 0.0036 | 0.0731 |
| ∆PG9 | 2.597 | 64.056 | 8.0582 | 1.2884 | 23.665 | −0.239 | 3.0092 | 0.0051 | 11.165 |
| ∆PG10 | 0.0042 | 0 | 0 | 0 | 0 | 0 | −0.125 | 0.0023 | 15.742 |
| ∆PG11 | 0.0915 | 121.51 | 114.69 | 49.697 | 121.51 | 121.51 | 98.0354 | 17.745 | 0 |
| ∆PG12 | 28.186 | 25.918 | 116.31 | 113.29 | 116.31 | 108.06 | 28.186 | 0.0006 | 113.4 |
| ∆PG13 | −0.0024 | 85.370 | 7.4155 | 0.8125 | 3.0092 | 10.752 | 0.4916 | −0.0005 | 1.6977 |
| ∆PG14 | 0.0678 | 32.857 | −0.0019 | 2.1836 | 0.0177 | −0.536 | 22.78 | 0.0223 | −10.03 |
| ∆PG15 | 89.765 | 31.616 | 28.095 | 89.669 | 8.8665 | 11.254 | −0.0024 | −0.0141 | 1.665 |
| ∆PG16 | 0.0025 | 39.071 | 1.7508 | 0.7819 | 7.1475 | 0.0731 | 49.17 | 8.1664 | 9.6558 |
| ∆PG17 | 0.004 | 37.552 | 0.0004 | −0.041 | 0.4916 | −0.394 | −0.0141 | −0.0273 | −0.092 |
| ∆PG18 | 0.0426 | 0 | 0 | 0 | 0 | 0 | 64.056 | 0.0177 | 4.9421 |
| ∆PG19 | 0.0036 | 0 | 0 | 0 | 0 | 0 | 25.114 | 116.12 | −0.5718 |
| ∆PG20 | 0.1504 | 89.001 | 1.7478 | −0.089 | 6.0792 | 4.3096 | 0.0036 | 0.2261 | 0.0087 |
| ∆PG21 | 25.114 | 96.075 | 18.528 | 102.85 | 19.359 | 77.661 | 1.5098 | 2.3777 | 0 |
| ∆PG22 | 8.6749 | 93.828 | 33.426 | 7.3786 | 36.798 | 72.901 | 0.0025 | 0.2974 | 0.7567 |
| ∆PG23 | −0.0141 | 0 | 0 | 0 | 0 | 0 | 1.2884 | 0.0035 | 18.528 |
| ∆PG24 | 0.0059 | 0 | 0 | 0 | 0 | 0 | 0.7819 | 8.8665 | −0.536 |
| ∆PG25 | 17.745 | 0 | 0 | 0 | 0 | 0 | 75.1407 | 116.31 | 8.3874 |
| ∆PG26 | 8.1664 | 0 | 0 | 0 | 0 | 0 | 113.29 | 0.0276 | −207.3 |
| ∆PG27 | −0.0024 | 0 | 0 | 0 | 0 | 0 | 48.58 | 9.1758 | 0 |
| ∆PG28 | 33.28 | 0 | 0 | 0 | 0 | 0 | 7.1475 | 8.6749 | 1.53 |
| ∆PG29 | 9.1758 | 0 | 0 | 0 | 0 | 0 | 0.0087 | 33.28 | 10.752 |
| ∆PG30 | 0.6717 | −450.9 | 0 | 4.904 | 10.702 | 0.6525 | 49.697 | 0.9068 | 0.8256 |
| ∆PG31 | 0.0173 | 0 | 0 | 0 | 0 | 0 | −0.4218 | 46.1738 | 0.3837 |
| ∆PG32 | 0.0032 | 0 | 0 | 0 | 0 | 0 | 28.095 | 4.8963 | 28.095 |
| ∆PG33 | 0.0218 | 0 | 0 | 0 | 0 | 0 | −0.0019 | −0.0024 | 0.0023 |
| ∆PG34 | 0.0024 | 0 | 0 | 0 | 0 | 0 | 13.317 | 0.0052 | 71.938 |
| ∆PG35 | 0.1945 | 0 | 0 | 0 | 0 | 0 | 8.8665 | 16.815 | −0.394 |
| ∆PG36 | 0.0013 | 0 | 0 | 0 | 0 | 0 | 2.1836 | 0.0001 | 0 |
| ∆PG37 | 39.667 | 0 | 0 | 0 | 0 | 0 | 32.857 | 121.51 | 0.0004 |
| ∆PG38 | 0.0372 | 0 | 0 | 0 | 0 | 0 | 5.777 | 0.1654 | 0.0023 |
| ∆PG39 | 2.7964 | 0 | 0 | 0 | 0 | 0 | 0.7567 | 0.0059 | 0.9656 |
| ∆PG40 | 0.0031 | 0 | 0 | 0 | 0 | 0 | 121.51 | 0.0748 | 1.7478 |
| ∆PG41 | 0.0033 | 0 | 0 | 0 | 0 | 0 | 8.6749 | 0.2949 | 101.12 |
| ∆PG42 | 0.0151 | 0 | 0 | 0 | 0 | 0 | 116.31 | 0 | 2.1221 |
| ∆PG43 | 0.4569 | 0 | 0 | 0 | 0 | 0 | 0.0426 | 0.1504 | 4.409 |
| ∆PG44 | 0.0073 | 0 | 0 | 0 | 0 | 0 | 85.37 | 69.115 | 11.254 |
| ∆PG45 | 0.196 | 0 | 0 | 0 | 0 | 0 | 3.7627 | 205.114 | 0 |
| ∆PG46 | 3.2218 | 1574.9 | 719.8998 | 707.3281 | 717.7839 | 720.4816 | 0 | 0.0019 | 13.317 |
| ∆PG47 | −0.0015 | 0 | 0 | 0 | 0 | 0 | 1.4716 | 3.0092 | 22.78 |
| ∆PG48 | −0.0013 | 0 | 0 | 0 | 0 | 0 | 3.0727 | 23.665 | 72.901 |
| ∆PG49 | 0.0039 | 0 | 0 | 0 | 0 | 0 | 12.6412 | 0.0001 | 4.3096 |
| ∆PG50 | 0.0012 | 0 | 0 | 0 | 0 | 0 | 0.8125 | 42.198 | 33.426 |
| ∆PG51 | 100.433 | 0 | 0 | 0 | 0 | 0 | 25.918 | 0.0004 | 11.934 |
| ∆PG52 | −0.0045 | 0 | 0 | 0 | 0 | 0 | 2.5903 | 0.4916 | −0.0018 |
| ∆PG53 | 7.3507 | 0 | 0 | 0 | 0 | 0 | 0.4368 | 0.0452 | 0 |
| ∆PG54 | 0.0009 | 0 | 0 | 0 | 0 | 0 | 0.004 | 7.1475 | 77.661 |
| Total amount (MW) | 713.3677 | 2149.654 | 1439.6913 | 1414.5492 | 1242.5373 | 1440.8597 | 988.32 | 971.18 | 913.828 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, V.; Rao, R.N.; Ansari, M.F.; Shekher, V.; Paul, K.; Sinha, P.; Alkuhayli, A.; Khaled, U.; Mahmoud, M.M. A Novel Hybrid Harris Hawk Optimization–Sine Cosine Algorithm for Congestion Control in Power Transmission Network. Energies 2024, 17, 4985. https://doi.org/10.3390/en17194985
Kumar V, Rao RN, Ansari MF, Shekher V, Paul K, Sinha P, Alkuhayli A, Khaled U, Mahmoud MM. A Novel Hybrid Harris Hawk Optimization–Sine Cosine Algorithm for Congestion Control in Power Transmission Network. Energies. 2024; 17(19):4985. https://doi.org/10.3390/en17194985
Chicago/Turabian StyleKumar, Vivek, R. Narendra Rao, Md Fahim Ansari, Vineet Shekher, Kaushik Paul, Pampa Sinha, Abdulaziz Alkuhayli, Usama Khaled, and Mohamed Metwally Mahmoud. 2024. "A Novel Hybrid Harris Hawk Optimization–Sine Cosine Algorithm for Congestion Control in Power Transmission Network" Energies 17, no. 19: 4985. https://doi.org/10.3390/en17194985
APA StyleKumar, V., Rao, R. N., Ansari, M. F., Shekher, V., Paul, K., Sinha, P., Alkuhayli, A., Khaled, U., & Mahmoud, M. M. (2024). A Novel Hybrid Harris Hawk Optimization–Sine Cosine Algorithm for Congestion Control in Power Transmission Network. Energies, 17(19), 4985. https://doi.org/10.3390/en17194985







