Electrical Power Systems Reinforcement through Overall Contingency Index Analysis and Improvement

Abstract

This paper analyzes the behavior of an electrical power system when N-1 contingencies occur in the transmission stage, which can be produced by incorrect operation of the protection relays, phenomena of natural origin, or increased loadability, which affect the operation and reliability of the electrical system. The operation output of a transmission line results in the variation of the nominal values of the electrical parameters involved because they disturb the stability of the generation, transmission systems, and the supply of electrical energy to the loads, such as voltages and angles of the nodes and the active and reactive power of the system. The proposed methodology was based on analyzing the different electrical parameters of the power system, quantifying the contingency index in a state of regular operation, and comparing it to operation in contingency N-1, with which the most severe contingency was determined and, therefore, achieved; identifying contingencies that can cause system collapses; improving the contingency index from 23.08555 to 22.9276624 for the L16–19 contingency and to 22.9795235 for the L21–22 contingency, which are the most severe contingencies determined with the proposed methodology. To test the proposed methodology, the IEEE 39 bus-bar test system was considered, and the elements that should be implemented to avoid the vulnerability of the power system to N-1 contingencies were determined.

1. Introduction

The continued growth of electricity users [1] leads to an increase in the demand for electrical energy, making it necessary to expand generation, transmission, and distribution systems [2]. The growth of demand for electrical energy worldwide will increase; in Ecuador, it will be 4.7% [3]. Every year, it is analyzed whether it is necessary to build new generation plants or transmission lines, in addition to the environmental problems and the costs of executing the TEP to take action in the short, medium, and long term. The transmission liens and generation plants are established and must be built or re-powered to supply the new consumers of electrical energy [4]. The continuous increase in loads demands quality service and modifies the flow of power in the existing network electricity, causing considerable problems in reliability due to overloads and effects on the stability of the EPS and indicates that a contingency is the operation output of a transmission line or a generator; when it is out of service it causes the electrical parameters of the system to suffer. Alterations occur when their values vary, and when these events occur, an alert must be given so that the operator knows how to act so as not to allow the EPS to collapse  [5].

When a failure or contingency occurs in the transmission system of an electrical power system (EPS) [6], the electrical protections will act and put the transmission line out of service, causing an increase in load capacity and due to the overload, the remaining transmission line will be disconnected, upon which the SIL establishes the capacity of a transmission line and this numerical value defines the limits of the power flow in a transmission line to maintain the electrical power system in the range of stability and expected operation. In this way, before starting the construction of the transmission system, the short-term planning is related to the operating limits of the system, the medium term refers to the re-powering of the EPS to increase reliability, and the long term includes the construction of new transmission lines according to the projected increase in demand.

The transmission system [7] must be reliable, safe, stable, and cost-effective to operate successfully and reduce expansion costs; these factors are important for optimized transmission expansion planning. Hence, it is necessary to consider the behavior of the electricity market in the expansion plans, as proposed in [8], which considers grid congestion and renewable generation dispatch.

The transmission expansion planning (TEP) [9] allows one to know the expansion plan with a minimum investment cost of the electricity transmission and generation system equipment. In [10], the cascading failures of an EPS lead to affecting the operation of transmission lines and factors such as reliability and economy. In [11], the primary solution is to determine the exact location to build transmission lines that are missing or that must be re-powered.

The TEP is a decision problem for constructing transmission lines and increasing the system’s capacity, thus reducing operating and investment costs in the future while maintaining an optimal level of reliability and operability. The study in [12] considers distributed generation in sub-transmission and distribution systems; focusing on the technical–economic results for the solution of the TEP covers the TEP based on the risk of wind generation by reducing the investment of the transmission system using the convex relaxation method for a deterministic TEP and with restricted proposals [13,14].

To solve the problem of TEP, Ref. [1] proposes a meta-heuristic algorithm inspired by nature; it is the Cuco search algorithm, which solves optimization problems in different fields of engineering. In this case, it increases the stability of the transmission lines and reduces the power loss uses a Constructive Heuristic Algorithm, detailed as follows. (a) For EPS expansion through heuristic optimization, it considers a line outage for contingency N-1; (b) a new performance index evaluates expansion decisions; (c) it obtains several possible solutions of greater sensitivity and quality.

Another way to solve the TEP in [4] verifies the behavior of the EPS according to each operating condition using OPF, the indices of economy, reliability, flexibility, the investment decision, and the control variables when simulating blackouts. Redistributing the generation and disconnecting the load is considered in [5]. The model is based on contingencies hlN-1, N-k and the severity of equipment failure, and researchers propose the deep network Q algorithm using interactive learning characteristics and the sequence when building transmission lines from a static TEP model that finally carries out the adaptation planning of transmission lines in a flexible way, adjusting to the already-planned scheme according to needs.

The load ability of the transmission line is one of the most critical problems to consider in an EPS [6] when specifying the capacity of the power transmission system in the face of maximum power flow situations and the operation. The planning of the EPS increases the difficulty due to the need a more complex analysis by specifying the maximum power that a transmission line can transmit in the face of maximum demand.

A robust method [7] with nonlinear mathematical optimization and the DC power flow, obtaining an optimization model that is solved sequentially [9], is proposed, called the Resilient TEP model; it optimizes system expansion based on safety and resilience criteria. The research in [12] uses the Benders Decomposition algorithm, managing safety and resilience constraints, and an iterative algorithm that is based on outage distribution factors, with the line determining the most damaging contingency in each year. It must be considered in the TEP to add safety criteria, demonstrating that the investment provisions in the transmission system can vary the flexibility restrictions.

The reliability index is the numerical result of the performance of an EPS [15], there being two situations: operation and failure, being safe if it supports the interruption of one of its elements and guarantees the supply of demand.

A heuristic model for the transmission system using N-1 and OPF-AC contingencies is proposed by [16]. It adds a damping capacity factor in the transmission lines, being characterized by robustness, approach, and solutions to solve the problem of TEP.

This article seeks to solve the problem of EPS expansion. The 39 bus-bar IEEE model was chosen to develop the analysis. The tool to be used is the OPF-AC, applied under normal conditions and with N-1 contingencies to determine the values of the electrical parameters V, $\delta$, in bars and P, Q in transmission lines.

The OPF-AC method is applied when a transmission line in the EPS is out of operation. The values acquired from V, $\delta$, P, and Q are used to calculate J heuristically for each case. The calculation results are then arranged from highest to lowest to identify transmission lines that could lead to instability and increased loadability when out of operation. Such a situation could cause all or part of the EPS to be out of service. J values in normal conditions and with N-1 contingencies are compared to facilitate the transmission line selection. The transmission line with the worst J values is chosen, and the new transmission line is implemented. The OPF-AC is then reapplied in the new EPS with contingency N-1. The J values of the selected transmission lines are verified to have improved remarkably.

The main contributions of the present research are as follows:

• Establish a ranking of contingencies from the most severe to the least severe by calculating the contingency index J considering the node voltages, the voltage angle at the nodes, and the real and reactive power flows circulating through the transmission lines when applying N-1 contingencies.
• Identification of transmission lines to be reinforced or even identification of when to implement new links, and in addition to the restrictions established in the scientific literature, the behavior of some electrical parameters is considered, and such behavior is quantified by employing a global index.
• The proposed TEP methodology based on the global J-index can improve the performance of the electrical parameters under various operating conditions, including the worst contingencies detected.

Next, the article is organized as follows: in Section 2, the proposals to solve the TEP and the formulation of the problem; in Section 3, the analysis of the results obtained; and in Section 4 the main conclusions of the work.

2. Problem Formulation and Methodology

In all electrical power systems, due to their construction condition, geographic location, existence, and the development of natural events such as atmospheric discharges, landslides, floods, tree falls, and terrorist activities, the operation of the generation, transmission, and distribution systems will at some point suffer failures that leave part or all of the EPS inoperative, causing load shedding, losses in a generation, activation of electrical protections. With this background, for the development of this work, the N-1 contingencies will be used in the transmission system to take each TL out of service and evaluate the behavior of the EPS through an OPF-AC, obtaining the voltage data, active power voltage angle, and reactive voltage, which will be compared with the same parameters of the EPS operating under normal conditions.

2.1. Transmission Expansion Planning

To find a solution to the problem of TEP, Ref. [17] proposes the improved genetic algorithm; it is an evolutionary meta-heuristic that solves the TEP through heuristic performance and is related to the power flow of the transmission system through sensitivity indices, obtaining a remedial tool. This results in system expansion with various size and topology characteristics.

An optimal power flow (OPF) [18] is a fundamental tool used to evaluate the operation of the EPS, the objective being to obtain optimal results and low costs in the face of uncertainties in the elements, system, so robust optimization modeling is proposed, adjustable for OPF when N-1 contingencies exist.

By using the OPF-AC in an EPS, the values of the power generated by each generation unit are obtained [11], as well as active and reactive powers [13], losses in the system [19], and this includes the maximum charge ability. The researchers in [20] carried out the charge ability analysis and ranking of contingencies, while [21] obtained the magnitude of the voltage, currents in buses and TL, the flow through the elements of the EPS, losses, voltage profile, and angular deviation; the parameters used to find solutions are [4] voltage profiles and angular deviation. The research in [22] adds transient stability restrictions for N-1 contingencies of the EPS using volt/var controllers through a mixed integer linear programming model for the optimization and stability of the system.

The definition of contingency [23] is the operation output of elements individually N-1 or several outputs N-k when operating an EPS false contingency related to voltages, state of transmission lines, generation dispatch, and activation of electrical protections, if the operator assumes that these parameters are not correct; that is why the J must efficiently evaluate the system.

When new transmission lines are going to be built, Ref. [24] defines a set of new reinforcements for the EPS that allow an adequate link between generation and demand of electrical energy; in the case of the long-term TEP, it uses the model of linear DC network. The research in [11] transforms a non-linear model of the TEP into a linear one by proposing Mixed Integer Linear Programming, which proves to be effective, accurate, and assumes that the voltage magnitude is known in the EPS. The voltage phase angle difference between the i-j bars is sufficiently small under normal operating conditions, considering that the value of the voltage magnitude is approximately 1 pu, which is a requirement to maintain the safety and stability of the system.

The reliability of the EPS [15] is guaranteed by the security provided by each of the elements that make it up; analyzing the distribution of operation and failure time, types of failure, and load priorities is established by the failures that may occur over some time, and the EPS will ensure that there are no variations in voltage, frequency, or power, because reliability is based on the frequency and permanence of the failure. If the system does not stabilize within the established time, a collapse in operation and control would occur.

The research in [25], for planning decisions, decreases the search space and uses the modified bat algorithm, which considers essential points such as active transmission losses and safety restrictions. Other research develops the gravitational search algorithm and the transmission line load index [26]. The contingencies are determined by maximizing the load index of the transmission line and solving the operation problem according to the most severe contingency.

Applying the N-1 safety criterion consists of disconnecting an element in the EPS, whether a generator or a TL; Ref. [27] leaves a TL of the system inoperative, preparing a list of contingencies to confirm the effectiveness of the resulting design and guarantee generation dispatch by obtaining a linearized power flow from each disconnected circuit and the N-1 safety criterion for the transmission network is taken into account as a need to be satisfied by estimating the ohmic losses.

The TEP modeling is based on non-linear OPF-AC equations as a Non-Linear Mixed Integer Programming problem, linear as a Mixed Integer Linear Programming problem, and the sequential solution of the TEP optimization model is executed in four steps that can be reviewed in [28].

The OPF-AC is used to determine the functioning and operation of the EPS and to study the electrical parameters. Below are the [4,20] equations used in the OPF-AC. The objective function (1) reduces generation costs and is restricted by (2), (3) to determine the balance of active and reactive power of generation, transmission, and demand; (4), (5) can be used to obtain the flow of active and reactive power that is transported by the transmission line according to the conductance, susceptance; (6), (7) restrict the active and reactive power limits of the generation system; (8) limits the voltages on the bars and (9) limits the voltage angle.

Objective Function:

$$\mathrm{Min}\mathrm{Z}=\sum _{i=1}^n{P}_{ij};C_{gi}$$

(1)

Constraints:

$$P_g-P_D=\sum _{i=1}^{n_{barra}}{P}_{ij};\forall i,j\in n_{barra}$$

(2)

$$Q_g-Q_D=\sum _{i=1}^{n_{barra}}{Q}_{ij};\forall i,j\in n_{barra}$$

(3)

$$P_{ij}={\left|V_i\right|}^2{G}_{ij}-\left|V_i\right|\left|V_j\right|[G_{ij}cos({\delta }_i-{\delta }_j)+B_{ij}sin({\delta }_i-{\delta }_j)];\forall i,j\in n_{barra}$$

(4)

$$Q_{ij}={\left|V_i\right|}^2{G}_{ij}-\left|V_i\right|\left|V_j\right|[G_{ij}sin({\delta }_i-{\delta }_j)-B_{ij}cos({\delta }_i-{\delta }_j)];\forall i,j\in n_{barra}$$

(5)

$$P_g^{min}\le P_g\le P_g^{max};\forall g\in n_G$$

(6)

$$Q_g^{min}\le Q_g\le Q_g^{max};\forall g\in n_G$$

(7)

$$\left|V_i^{min}\right|\le \left|V_i\right|\le \left|V_i^{max}\right|;\forall i\in n_{barra}$$

(8)

$${\delta }_{ij}^{min}\le {\delta }_{ij}\le {\delta }_{ij}^{max};\forall i,j\in n_{barra}$$

(9)

2.2. Contingency Index Analysis

When a contingency occurs in the EPS [4], all electrical parameters change their nominal values. For this reason, the rigor of the contingency must be quantified, a ranking must be prepared, and the element that causes the most damage to the EPS must be identified by N-1 contingency analysis, obtaining several results for each electrical parameter to be studied [23]. The overloads are determined using an OPF-AC, being necessary to analyze the results after the failures [24]. J examines the contingencies and defines those that would cause overloads in the TL or violations of the voltage limits, guaranteeing the operation of the EPS because it detects emergencies and gives warning signals so that operators can make decisions to control failures or know what operations to carry out to stabilize the system.

When considering sensitivity indices in the context of N-1 contingency analysis, the load on the transmission system is observed during the study without any contingency. This load is then compared with the overload and load restrictions evaluated with N-1 contingencies. This comparison helps understand the system’s response to different scenarios and the potential risks it may face [17].

When a TL stops operating [29], it causes a considerable increase in the changeability and electrical parameters; the J is necessary for the evaluation of the capacity of the EPS to return to the contingency state after making variations in the system topology when a TL stops operating.

The J establishes the state of the EPS when operating normally or when contingencies occur. If the state is expected, the generation and transmission systems operate within the expected limits, and J will be minimal; when disconnections occur in EPS elements, the J will increase [30].

The usual and emergency state of the EPS can be determined using J if, when calculating it, a low value is obtained, which indicates that the EPS is operating in a normal state and that the generation and transmission systems are operating within the established ranges. If a high value of J is obtained, this determines which external events have caused the disconnection of parts of the SEP. With the already-calculated values of J, they are ordered from highest to lowest and serve to identify which element, when it stops operating, causes the most damage in the system; it is known that the first values of J are the worst possible results because they exceed both the capacity and voltage restrictions on the bus.

To weight the values of J, (10) is used, and the functioning of the EPS is evaluated when N-1 contingencies are developed, a method also used by [4,28] in their research, which contributes to the obtention of results, as well as optimal TEP solutions. The values of $W_i$ and m are assigned, assuming that the TL can contribute to not increasing the loadability of the system. It is established that it has a value of 1 and 2, respectively, for each TL of the system, being applicable to optimize the ordering of the contingencies N-1, since $f_i$ will represent the voltage and voltage angle in the bars and the active and reactive power of the transmission lines. The maximum values of the electrical parameters can be seen in (11).

$$J=\sum _{i=1}^N\frac{W_i}{m}{\left(\frac{f_i}{f_{i_{max}}}\right)}^m$$

(10)

$$J=\frac{1}{2}\left(\sum _{i=1}^{n_{bus}}{\left(\frac{V_i}{1.05}\right)}^2+\sum _{i=1}^{n_{bus}}{\left(\frac{{\delta }_i}{0.6}\right)}^2+\sum _{i=1}^{n_{bus}}\sum _{j=1}^{n_{bus}}{\left(\frac{P_{i-j}}{600}\right)}^2+\sum _{i=1}^{n_{bus}}\sum _{j=1}^{n_{bus}}{\left(\frac{Q_{i-j}}{600}\right)}^2\right)$$

(11)

Algorithm 1 represents the heuristic methodology used to solve the problem of TEP based on the OPF-AC, N-1 contingencies, and contingency index. In step 1, the EPS information is entered, and OPF-AC is applied, obtaining the results of the selected electrical parameters; in step 2, the EPS is evaluated under standard conditions using OPF-AC to determine the J; in step 3, N-1 contingencies are executed for each case, an OPF-AC is applied, and the Total J is obtained that allows determining which TL would cause problems in the EPS when it goes out of operation; in step 4, it is decided to subjectively select the two worst cases of the TL with $J_{con{t}_{case}}⩾25$, and the decision is made to strengthen the EPS by building new TLs that meet this condition, J is applied again, and it is observed how the electrical parameters improve. In this way, the problem of TEP is solved.

Algorithm 1 TEP considering contingency index J

Step: 1 Imput Data EPS Parameters Lines: $r,x,b$ and $SIL$ Generators: $P{g}_{min}$ and $P{g}_{max}$ Loads: $L_i$ Step: 2 Determination of initial conditions by OPF-AC $V_i, {\delta }_i, P_{i-j}, Q_{i-j}$ $J_{bas{e}_{cont}}=\frac{1}{2}\left({\sum }_{i=1}^{n_{bus}}{\left(\frac{V_i}{1.05}\right)}^2+{\sum }_{i=1}^{n_{bus}}{\left(\frac{{\delta }_i}{0.6}\right)}^2+{\sum }_{i=1}^{n_{bus}}{\sum }_{j=1}^{n_{bus}}{\left(\frac{P_{i-j}}{600}\right)}^2+{\sum }_{i=1}^{n_{bus}}{\sum }_{j=1}^{n_{bus}}{\left(\frac{Q_{i-j}}{600}\right)}^2\right)$ Save$J_{bas{e}_{cont}}$ Step: 3 N-1 Contingency analysis for  $case c=1:n_{linea}$ $$  Apply OPF-AC $$$V_{i_c}, {\delta }_{i_c}, P_{i-j_c}, Q_{i-j_c}$ $$$J_{con{t}_{case}}\left(c\right)=\frac{1}{2}\left({\sum }_{c=1}^{n_{bus}}{\left(\frac{V_c}{1.05}\right)}^2+{\sum }_{c=1}^{n_{bus}}{\left(\frac{{\delta }_c}{0.6}\right)}^2+{\sum }_{c=1}^{n_{bus}}{\sum }_{j=1}^{n_{bus}}{\left(\frac{P_{{i-j}_c}}{600}\right)}^2+{\sum }_{c=1}^{n_{bus}}{\sum }_{j=1}^{n_{bus}}{\left(\frac{Q_{{i-j}_c}}{600}\right)}^2\right)$ end for Save$J_{con{t}_{case}}$ Step: 4 New TL Determination for  $case=1:n_{line}$     If  $J_{bas{e}_{cont}}\le J_{con{t}_{case}}$ $$$$Select 2 worst cases of $J_{con{t}_{case}}$ $$$$$J_{con{t}_{case}}$$⩾ 25$ $$$$Save worst TL     End if  end for

3. Analysis of Results

The algorithm simulation was developed in the IEEE 39 bus-bar test system, comprised of 34 TLs. It was selected to carry out the J analysis and verify the effectiveness of the heuristic methodology for expansion planning in an EPS. The following electrical parameters will be considered: voltage, voltage angle, and active and reactive power, which were developed in MATLAB R2023b. Subsequently, OTS was performed in the GAMS 27.3 environment, considering the above-mentioned contingencies. This simulation ran on a computer with the following parameters: Intel(R) Xeon(R) W-11955M CPU @ 2.60 GHz 2.61 GHz, 64 GB of RAM, and Windows 11 Pro for Workstations. And the simulation was made by Digsilent Power Factory.

3.1. Contingency Index and Heuristic Methodology

The Power Factory DigSilent program was used through the OPF-AC tool that is executed in the EPS operating under normal conditions without the existence of contingencies; as a result, the values of V, $\delta$ for the bars, and P, Q for the TL were used. The information on these parameters allows us to verify that the system operates correctly because the V, $\delta$, P, and Q do not exceed the values of 1.05 p.u, 0.6 radians, 600 MW, and 600 Mvar, respectively, which are established for proper operation, guaranteeing the reliability, safety, and loadability of the SEP. The values of J are indicated in

Table 1. J Base and Overall J for IEEE 39 bus-bar without N-1 contingency.

V	$\mathit{\delta }$	P	Q	J Total
18.6172814	0.69128497	3.59904093	0.17794617	23.08555

and it is confirmed that the operation is correct.

For the analysis of J, the N-1 contingency criterion is applied in the SEP, leaving each of the 34 TLs that comprise it out of service; the OPF-AC is executed every time a TL is not operational. The heuristic methodology to be used is based on Equation (1) and determines the value of J that is dimensionless, resulting in 34 values of J for V, $\delta$, P, and Q. This information will be used to know which TL(s), when they stop working, cause changes in load capacity in the transmission system, overload, or loss of service of the generation units, and also the increase or decrease in the nominal values of the electrical parameters analyzed.

The Total J is obtained by obtaining all the J values for V, $\delta$, P, and Q for each contingency, represented in

Table 2. Overall J values for IEEE 39 bus-bar system without N-1 contingency.

N°	Out Service TL	Overall J	N°	Out Service TL	Overall J	N°	Out Service TL	Overall J
1	1–2	23.43392519	13	7–8	23.37427702	25	17–18	23.44630421
2	1–39	23.42413163	14	8–9	23.02869457	26	17–27	23.06087266
3	2–3	23.53415515	15	9–39	23.00177978	27	21–22	25.2405899
4	2–25	23.71899354	16	10–11	23.31187489	28	22–23	23.13730751
5	3–4	23.06334879	17	10–13	23.9948808	29	23–24	24.49106131
6	3–18	23.09281749	18	13–14	24.3393066	30	25–26	23.075422
7	4–5	23.25425096	19	14–15	23.06006623	31	26–27	23.70054855
8	4–14	23.71535086	20	15–16	23.90703507	32	26–28	23.03055128
9	5–6	23.98262775	21	16–17	23.92647995	33	26–29	23.38005293
10	5–8	23.51184165	22	16–19	26.97603398	34	28–29	23.44981054
11	6–7	24.36525498	23	16–21	23.56102874
12	6–11	23.56595881	24	16–24	23.16181901

. Then, the values obtained from each TL are organized from highest to lowest. Thus, the TLs that must be analyzed are known, and through the TEP, it is determined whether new TLs are built or re-powered; all of this is carried out according to the geographical location, characteristics of electrical techniques, and the behavior of the EPS in a state of contingency and post-contingency.

When analyzing the J Total values for the thirty-four TLs of the SEP, it was verified that two TLs had the highest values compared to the rest of the transmission system. This indicates that TL 16–19 and TL 21–22 should be analyzed and studied to determine the action to be taken in case they go out of operation so that they do not significantly affect the SEP. In such a case, it stops operating or operates in abnormal conditions.

3.2. Contingency Ranking

The values of the Total J are presented in Figure 1; they are ordered from highest to lowest to identify the TL that would have a more severe impact on the EPS when going out of operation due to an N-1 contingency.

Figure 1 shows that TL 16–19 and TL 21–22, when they go out of operation due to an N-1 contingency, would damage the transmission and generation system and increase loadability in the remaining TLs of the EPS, variations in power flow, and electrical parameter values. The values of Total J are 26.97603398 and 25.2405899 for the mentioned lines, respectively, the highest values obtained.

For the development of this study, an OPF-AC is used, an essential tool for the design and planning of the future expansion of an EPS; the data obtained are the magnitude of the voltage, phase angle of the voltage, and active and reactive power. With the information received, the EPS expansion planning is carried out by building the TL 16–19N and TL 21–22N with similar technical and electrical characteristics to the existing ones, executing the optimal expansion of the transmission system so that it is robust, reliable, and is not affected by the existence of N-1 contingencies. The construction of the new TL in the 39 bus-bar IEEE test system can be seen in Figure 2 [31].

The expansion of the EPS is carried out based on the value of J Total. The solution is obtained from developing the heuristic methodology, and TL 16–19N and TL 21–22N are implemented. After the new TLs are constructed, the OPF-AC is executed to verify the behavior of the electrical parameters, observing that these values improve compared with the results obtained before the new TLs were constructed. The IEEE 39 bus-bar EPS, after carrying out the TEP, will comprise 36 TLs.

Figure 2 shows the topology of the EPS. It is also possible to visually determine that if an N-1 contingency occurs that takes TL 16–19 out of service, it will cause more significant damage to the EPS because an island would form in bars 19, 20, 33, and 34, because there is no TL that allows the power generated by Units G4 and G5 to be supplied to bus 16. On the other hand, with TL 21–22, when it stops operating, it would restrict the EPS so that the power of units G6 and G7 can only be transported by TL 23–24 to bus 24, losing the direct supply to bus 21 and resulting in increased load capacity in the aforementioned TL.

Figure 3, Figure 4, Figure 5 and Figure 6 demonstrate the results obtained from the parameters V, $\delta$, P, and Q when the EPS operates under normal conditions, under normal conditions plus expansion, with N-1 contingencies, and with N-1 contingencies plus expansion. These values are used to analyze and compare the results and thus verify how they improve when expanding the EPS by constructing two new TLs.

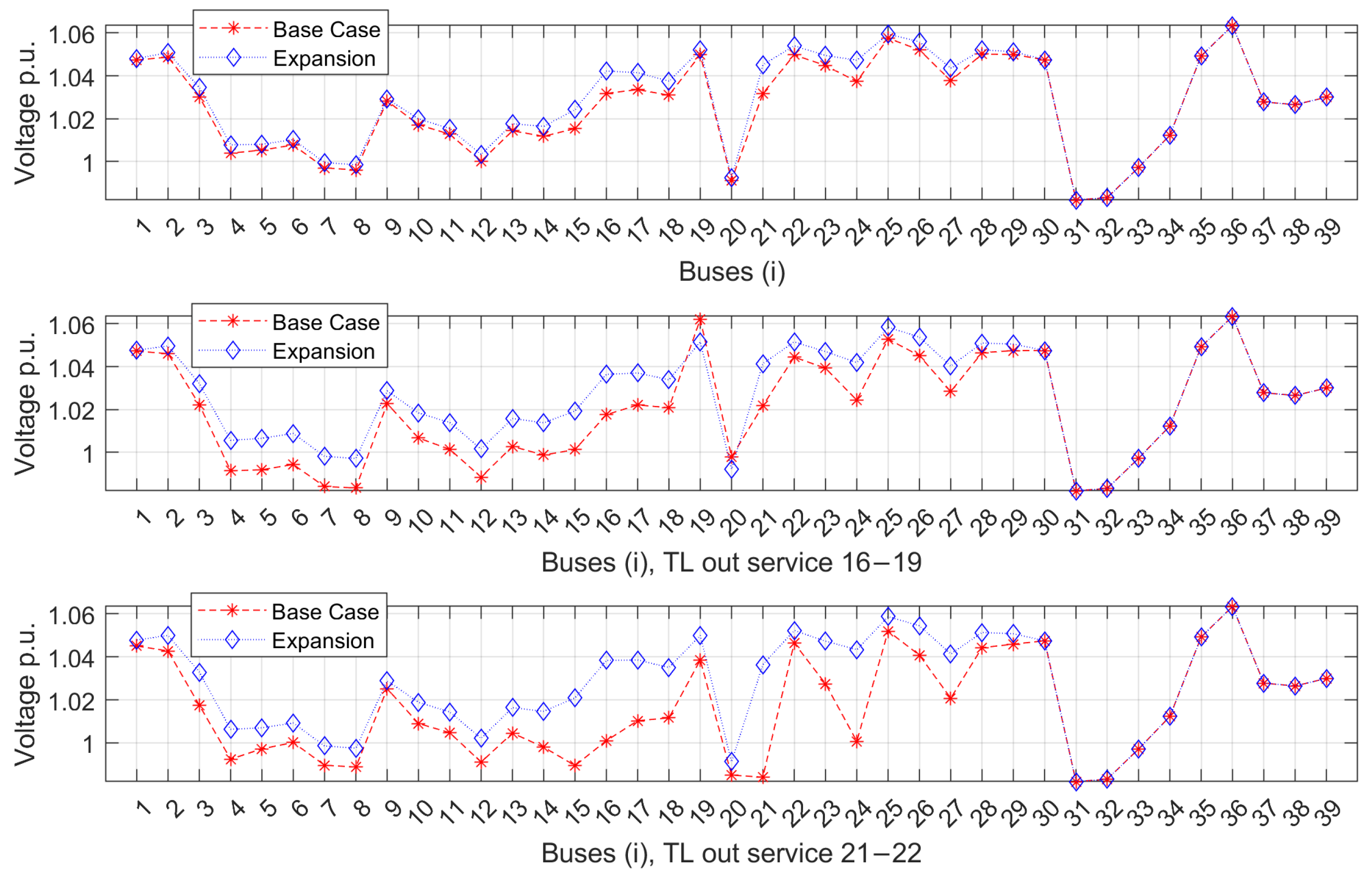
Figure 3 shows the voltage behavior in all the EPS nodes under the different scenarios analyzed, and all of them show an improvement in the voltage profile compared to the base case. In the case of the contingency of line 21–22, a significant improvement can be seen with the expansion that the model gives as a result.

The results obtained for the voltage are shown in Figure 3, and the main effects are as follows:

• Base case: By performing the optimal expansion of the EPS, running an OPF-AC without contingencies, and comparing it with the Base Case EPS, it is determined that voltage improves in bars 21, 16, 24, 15, 17, 18.
• Case of out-of-service TL 16–19: When performing the optimal expansion of the EPS, run an OPF-AC with the TL 16–19 without operating and compare it with the values obtained from the EPS Base Case with contingency N-1; it is determined that voltage improves in bars 21, 16, 15, 24, 14, 17, 5, 6, 4, 7, 8, 12, 13, 18, 11, 27, 10.
• Case of out-of-service TL 21–22: When performing the optimal expansion of the SEP, run an OPF-AC with the TL 21–22 without operating and compare it with the values obtained from the EPS Base Case with contingency N-1; it is determined that voltage improves in bars 21, 24, 16, 15, 17.

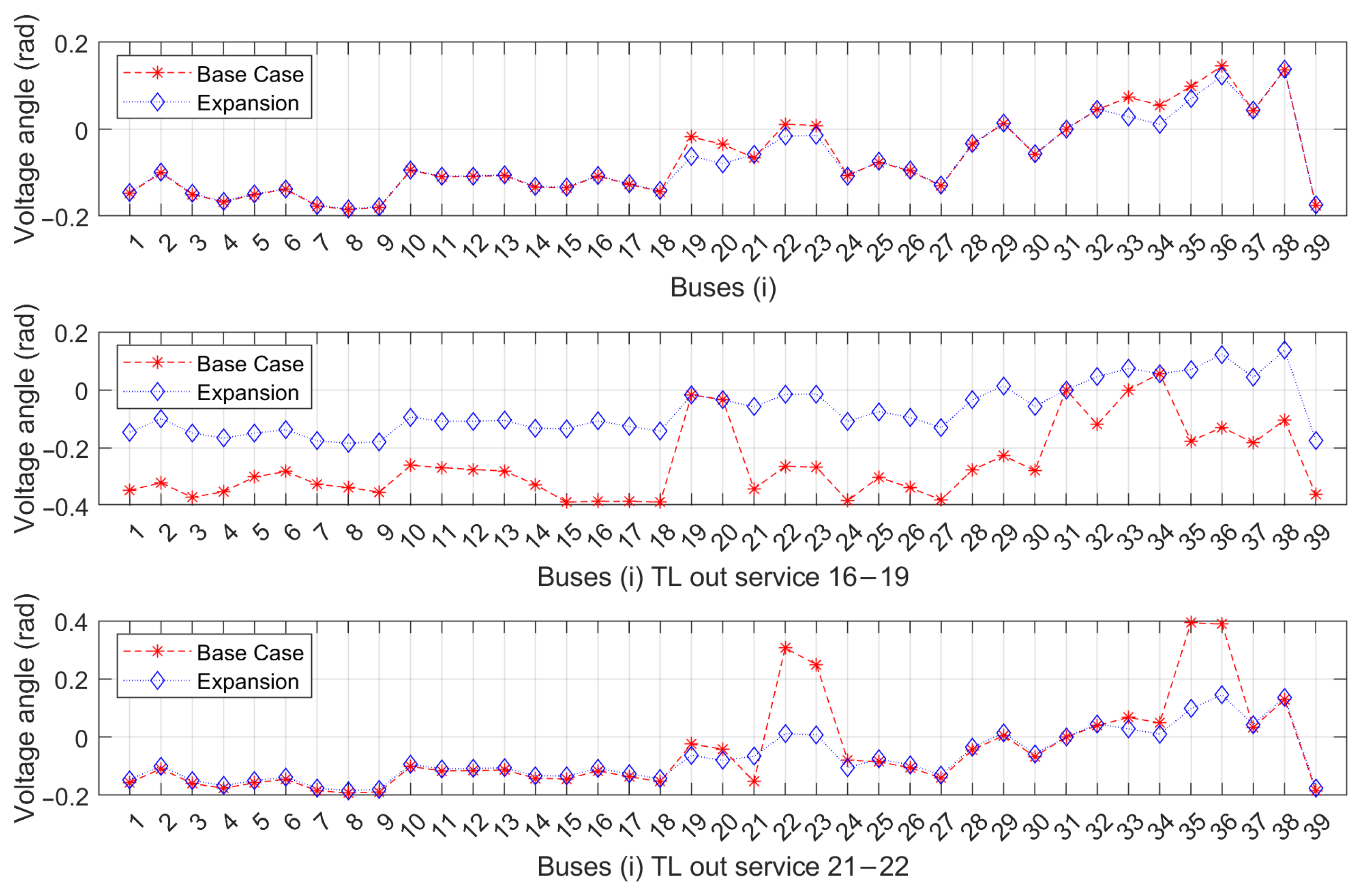
Similarly, in Figure 4, the behavior of the voltage angle in each node of the EPS is analyzed. It is known from previous studies that when a contingency occurs, the voltage degrades, and sometimes, it can even reach states of angle instability; therefore, it is necessary to improve the power systems [32]. It can be seen that in the case of the contingency on line 16–19, the deviation improvement is considerable. In the case of a contingency on line 21–22, when the expansion is already in place, the behavior is similar to that of the base case.

The results obtained for the voltage angle are shown in Figure 4, and the main effects are as follows:

• Base case: By performing the optimal expansion of the SEP, running an OPF-AC without contingencies, and comparing it with the Base Case SEP, it is determined that $\delta$ improves in bars 21, 3, 39, 1, 18, 27, 9, 4, 25, 2, 26, 15, 30, 8.
• Case of out-of-service TL 16–19: When performing the optimal expansion of the SEP, run an OPF-AC with the TL 16–19 without operating and compare it with the values obtained from the EPS Base Case with contingency N-1; it is determined that $\delta$ improves in bars 21, 16, 24, 17, 15, 23, 36, 27, 22, 35, 18, 26, 28, 29, 38.
• Case of out-of-service TL 21–22: When performing the optimal expansion of the SEP, run an OPF-AC with the TL 21–22 without operating and compare it with the values obtained from the EPS Base Case with contingency N-1; it is determined that $\delta$ improves on bars 21, 27, 18, 3, 15, 1, 17, 25, 26.

Figure 5 shows the behavior of the active power flows through the transmission lines, in which it can be seen that the new lines implemented in the EPS carry the power flows that are naturally redirected. A similar situation occurs for reactive power, as shown in Figure 6.

The results obtained for the real power flow are shown in Figure 5, and the main effects are as follows:

• Base Case: By performing the optimal expansion of the SEP, running an OPF-AC without contingencies, and comparing it with the Base Case SEP, it is determined that the active power improves in TL 21–22N, 21–22, 16–19N, 16–19, and TL 16–24.
• Case of out-of-service TL 16–19: When performing the optimal expansion of the SEP, run an OPF-AC with the TL 16–19 without operating and compare it with the values obtained from the EPS Base Case with contingency N-1; it is determined that P improves in TL 16–19N, 21–22N, 21–22, 5–6, 4–5,16–17, 17–18, 10–11, and 03–04.
• Case of out-of-service TL 21–22: When performing the optimal expansion of the SEP, run an OPF-AC with the TL 21–22 without operating and compare it with the values obtained from the EPS Base Case with contingency N-1; it is determined that P improves in TL 21–22N, 16–24, 16–19N, and 16–19.

The results obtained for the reactive power flow are shown in Figure 6, and the main effects are as follows:

• Base case: By performing the optimal expansion of the SEP, running an OPF-AC without contingencies, and comparing it with the Base Case SEP, it is determined that Q improves in TL 21–22N, 21–22, 16–17, 16–19N, 17–18, and 17–27.
• Case of out-of-service TL 16–19: When performing the optimal expansion of the SEP, run an OPF-AC with the TL 16–19 without operating and compare it with the values obtained from the EPS Base Case with contingency N-1; it is determined that Q improves in TL 21–22, 21–22N, 16–19N, and 06–11.
• Case of out-of-service TL 21–22: When performing the optimal expansion of the SEP, run an OPF-AC with the TL 21–22 without operating and compare it with the values obtained from the EPS Base Case with contingency N-1; it is determined that Q improves in TL 16–17, 21–22N, and 16–19.

All modeling and optimization results were validated through simulation. By constructing two TLs with similar technical characteristics to the two TLs with the highest value of J Total obtained from the heuristic methodology developed through Equation (1), it is guaranteed that when an N-1 contingency occurs, the reliability and operation of the SEP would not be affected, solving the TEP problem. Finally, the new values of J, as detailed in

Table 3. J values for each case.

J	Out Service TL 16–19	Out Service TL 16–19 with Expansion	Out Service TL 21–22	Out Service TL 21–22 with Expansion
V	18.4041295	18.6725573	18.2673522	18.6837946
$\delta$	4.44982758	0.67016988	1.37391558	0.68539697
P	3.86841102	3.40758685	5.28512963	3.42972771
Q	0.25366587	0.17734835	0.31419249	0.18060424
J Total	26.9760340	22.9276624	25.2405899	22.9795235

, are obtained.

The values of the EPS parameters improve when N-1 contingencies exist; it is verified that the planning of the expansion of the transmission system through the application of the heuristic equation meets the expectations raised in the work developed.

Table 4. Comparative analysis of previous TEP models.

Previous Investigations	Year	OPF-DC	OPF-AC	Loadability	Contingencies N-1 and N-m	Contingency Index
Khandelwal [33]	2017	✓			✓
Ploussard [34]	2018	✓		✓
De Oliveira [25]	2018		✓	✓	✓
Gutierrez [12]	2020	✓			✓
Qorbani [9]	2021	✓		✓	✓
Assis [17]	2021	✓		✓	✓
Espinel [6]	2023	✓		✓	✓
This proposal	2024		✓	✓	✓	✓

shows previous works that also focused on TEP considering different methodologies; many authors use OPF-DC as the basis of their methodologies to reduce the computational effort based on simplifications in voltage and reactive power, a situation that does not happen with OPF-AC. In addition to the constraints of the OPF-DC and OPF-AC models, loadability and contingency constraints are also considered in the literature for the planning of power systems. In the present investigation, the identification of the worst operating conditions through the J-index considering all the electrical parameters obtained from the power flow analysis is added to the above.

4. Conclusions

The methodology proposed for expanding the power systems allowed for the identification of the needs of the EPS based on the evaluation of the contingency index, which allows for cataloging the severity of the contingencies that may occur in the electric system. The methodology used the OPF-AC constraints as a basis. The methodology was applied to the IEEE 39 bus-bar test system, and based on the proposed methodology, the two worst conditions that could occur in the system were identified; based on this, the decision to reinforce the system was made, for this EPS, TL 16–19 and TL 21–22.

Since the proposed methodology is based on the value of the contingency index J, it was necessary to compare the value of J in the initial state of the EPS (J = 23.08555) and thus identify the worst contingencies, which were the contingency in TL 16–19 in which J = 26.976034 and the contingency in TL 21–22 in which J = 25.2405899; as can be seen, there was a growth in the J index, and this is due to the degradation of some of the electrical parameters that were quantified to calculate J.

For the most severe contingency TL 16–19, after expanding the EPS, the J index was reduced to 22.927662, improving the EPS by about 15% in this operating condition and even performing better than the original system. Something similar happens with the contingency in TL 21–22, where J was improved to 22.9795265, which is an 8.9% improvement in J.