Transformer-Based Deep Learning Models for State of Charge and State of Health Estimation of Li-Ion Batteries: A Survey Study
Abstract
1. Introduction
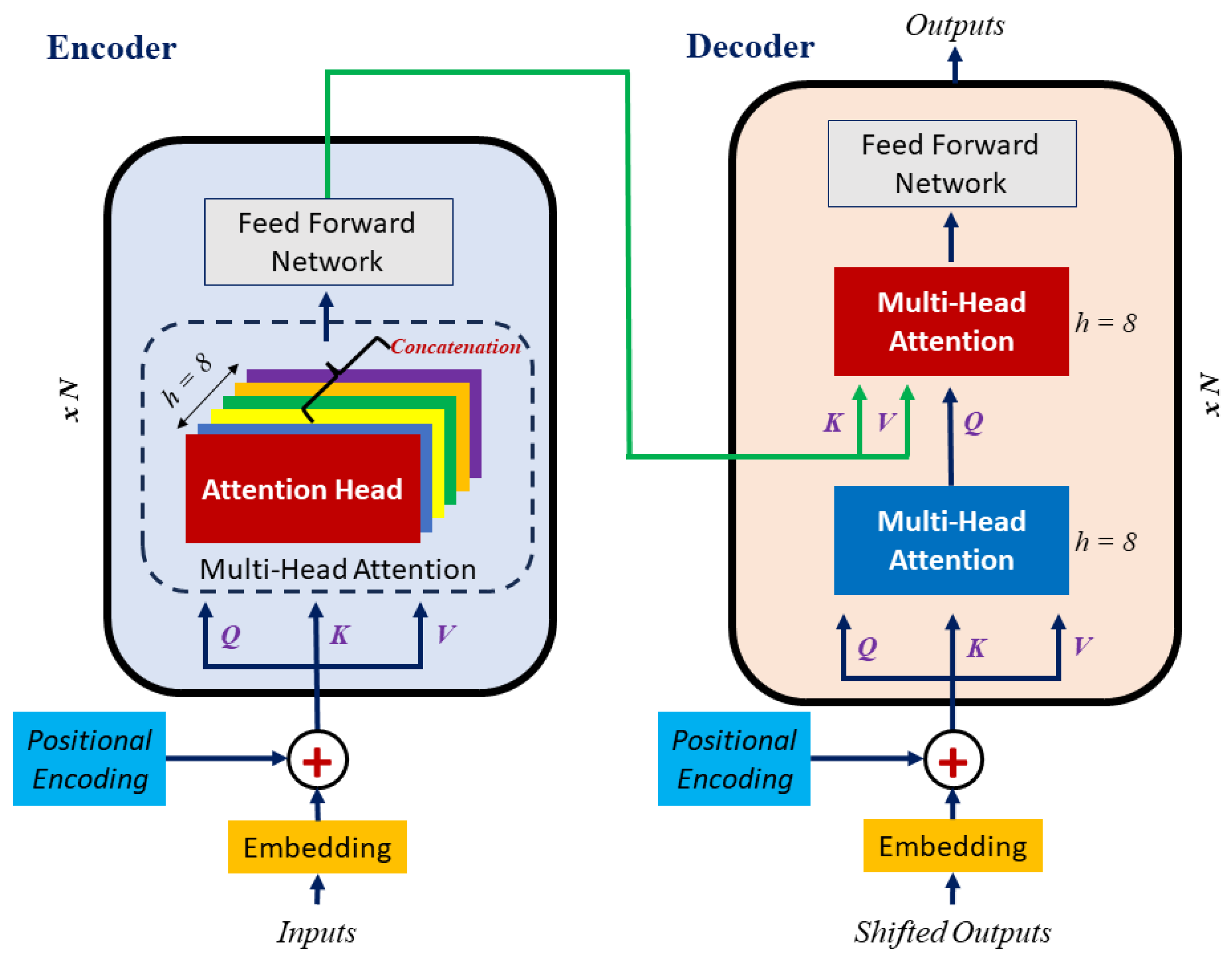
2. An Overview of the Transformer Model
3. Datasets
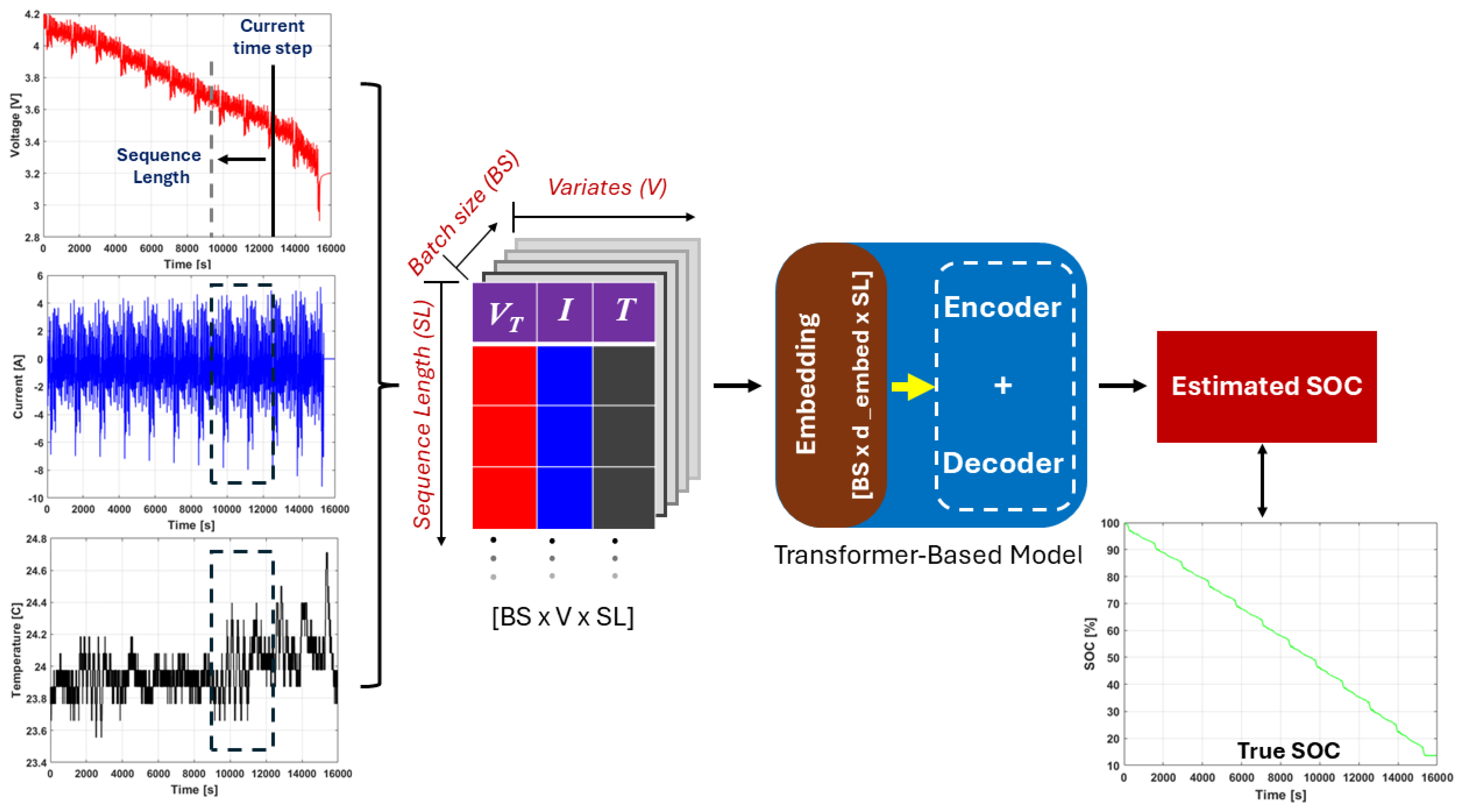
4. State of Charge Estimation
| Methodology | Dataset | RMSE | MAE |
|---|---|---|---|
| Transformer with SSL [35] | LG 18650HG2 [33] | 1.9%: 20% of training data 0.9%: constant temperature 1.19%: varying temperature | 0.44%: constant temperature 1.7%: varying temperature |
| 2-Encoder Transformer + I&I Observer [36] | LiFeO4 chemistry-based battery [37] | <1% | —— |
| Convolutional Transformer network (CTN) + SPKF [38] | Panasonic 18650PF [39] | 0.93% | 0.81% |
| CNN-Informer [40] | Panasonic 18650PF [39] and INR [42] | 0.86% | 0.77% |
| BERTtery [43] | 5 large-scale NMC cells and a battery pack serviced for 8 months in an EV | 0.5% | 2% |
| Transformer with SPMe [44] | CALCE [45] | <2% | —— |
| TTSNet + Kalman filter (post-processing) [46] | —— | 0.69% | 0.5% |
| Comparative Study [47]: Transformer, LSTM, Bi-LSTM, and SVR | NASA [34], BMW i3 [48], Stanford University [49], and Musoshi electric vehicles. | 0.99%: Transformer | —— |
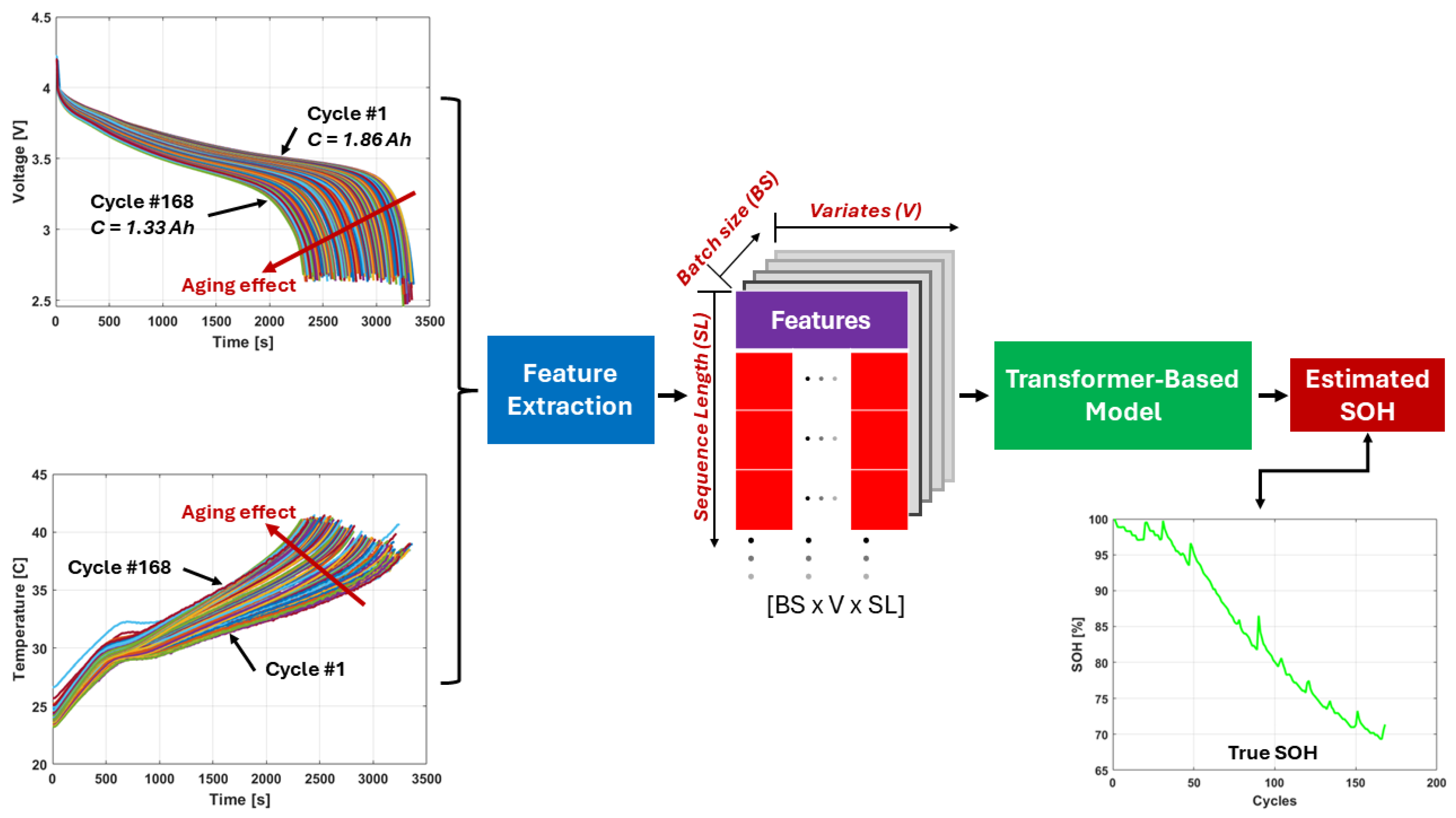
5. State of Health Estimation
| Methodology | Dataset | RMSE | MAE |
|---|---|---|---|
| DAE -> Transformer (DeTramsformer) [50] | NASA [34] and CALCE [45] | 8% 7% | 7% 6% |
| [PCA, PCC, and feature scaling] + CNN–Transformer [51] | NASA [34] | ≈0.55% | ≈0.55% |
| CNN-MVIP-Trans [52] | NASA [34] and Oxford [53] | 0.5% 0.3% | —— |
| PCC + encoder-only Transformer [54] | NASA [34] | 2.9% | 2.6% |
| Vision Transformer (ViT) [55] | NASA [34] and CALCE [45] | 0.46% 0.47% | 0.36% 0.37% |
| Transformer with EIS analysis [56] | CLUC [57] | 0.64% | 0.51% |
| Transformer–GRU [58] | NASA [34] | 1.19% | 0.62% |
| 1D-CNN + T-LSTM [59] | Aging experiment on 7 Prospower ICR18650P batteries, and CLUC [57] | 0.66% | 0.53% |
| ITFT (Bi-LSTM) [60] | MIT [61] | SOH: 0.13% RUL: 0.67% | —— |
| MCC + Informer [62] | MIT [61] CALCE [45] | 0.2% 1.8% | 0.2% 1.0% |
| SGEformer [63] | NASA [34] and CALCE [45] | 0.96% | 0.01% |
| Encoder-only Transformer [66] | The study used a dataset that was generated specifically for this work based on measurements from 3 real EVs in 3 years. | 1.31% | —— |
| PCA -> Stacked DAE -> Transformer for RUL [67] | NASA [34] | 0.2% | 0.17% |
| DAE -> KF-Transformer [68] | NASA [34] and CALCE [45] | 3.45%2.52% | —— |
6. Conclusions
- For SOC estimation, it is obvious that in most of the studies, there is a need to utilize post-processing methods to attenuate the severe fluctuations in the output predictions of the Transformer-based model; this is carried out using filters and state observers.
- For the SOH, there is always a need for preprocessing feature extraction to extract the features from the raw aging datasets to be passed to the Transformer model to infer the SOH; CNNs, DAEs, and correlation analysis methods may be used for this.
- It is evident from the reviewed manuscripts that Transformer-based models can achieve impressive estimation accuracy, with an RMSE below 1% for both states.
- Nevertheless, with more than a million learnable parameters, the computational complexity of these models results in daunting processing.
- Addressing the implementation of Transformer-based models in real time on microcontrollers is crucial in future work, to demonstrate the feasibility of deploying this approach in the BMS of an EV.
Funding
Conflicts of Interest
Abbreviations
| BEV | Battery electric vehicle |
| LIB | Lithium-ion battery |
| SOC | State of charge |
| SOH | State of health |
| FNN | Feedforward neural network |
| RNN | Recurrent neural network |
| LSTM | Long–short-term memory |
| NLP | Natural language processing |
| UDDS | Urban Dynamometer Driving Schedule |
| I&I | Immersion and invariance |
| CTN | Convolutional Transformer network |
| CNN | Convolutional neural network |
| BERT | Bidirectional encoder representation from Transformers |
| SPMe | Single-particle model with electrolyte dynamics |
| TTSNet | Temporal Transformer-based sequence network |
| SVR | Support vector regression |
| RUL | Remaining useful life |
| DAE | Denoising Auto-Encoder |
| PCA | Principal component analysis |
| PCC | Pearson correlation coefficient |
| MVIP | Multiview information perception framework |
| ViT | Vision Transformer |
| CLUC | Cavendish Laboratory of the University of Cambridge |
| EIS | Electrochemical impedance spectroscopy |
| GRU | Gated recurrent unit |
| VMD | Variational mode decomposition |
| PSO | Particle swarm optimization |
| ITFT | Improved temporal fusion Transformer |
| TPE | Tree-structure Parzen estimator |
| MCC | Multiple correlation coefficient |
| SGE | Seasonal and growth embedding |
| KF | Kalman filter |
| MLP | Multilayer perceptron |
References
- Swarnkar, R.; Ramachandran, H.; Ali, S.H.M.; Jabbar, R. A Systematic Literature Review of State of Health and State of Charge Estimation Methods for Batteries Used in Electric Vehicle Applications. World Electr. Veh. J. 2023, 14, 247. [Google Scholar] [CrossRef]
- Watari, T.; McLellan, B.C.; Ogata, S.; Tezuka, T. Analysis of potential for critical metal resource constraints in the international energy agency’s long-term low-carbon energy scenarios. Minerals 2018, 8, 156. [Google Scholar] [CrossRef]
- Maizland, L. Global Climate Agreements: Successes and Failures. 2023. Available online: https://www.cfr.org/backgrounder/paris-global-climate-change-agreements#chapter-title-0-2 (accessed on 9 July 2024).
- The Government of Canada. Net-Zero Emissions by 2050; The Government of Canada: Ottawa, ON, USA, 2024.
- The Government of Canada. Building a Green Economy: Government of Canada to Require 100% of Car and Passenger Truck Sales Be Zero-Emission by 2035 in Canada; The Government of Canada: Ottawa, ON, USA, 2021.
- Ng, K.S.; Moo, C.S.; Chen, Y.P.; Hsieh, Y.C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Yan, J.; Xu, G.; Qian, H.; Xu, Y. Robust state of charge estimation for hybrid electric vehicles: Framework and algorithms. Energies 2010, 3, 1654–1672. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for electric vehicle batteries using unscented kalman filtering. Microelectron. Reliab. 2013, 53, 840–847. [Google Scholar] [CrossRef]
- Belt, J.; Utgikar, V.; Bloom, I. Calendar and PHEV cycle life aging of high-energy, lithium-ion cells containing blended spinel and layered-oxide cathodes. J. Power Sources 2011, 196, 10213–10221. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Hu, C.; Youn, B.D.; Chung, J. A multiscale framework with extended Kalman filter for lithium-ion battery SOC and capacity estimation. Appl. Energy 2012, 92, 694–704. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Rahimifard, S.; Habibi, S.; Tjong, J. Dual estimation strategy for new and aged electric vehicles batteries. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; pp. 579–583. [Google Scholar]
- Rahimifard, S.; Habibi, S.; Goward, G.; Tjong, J. Adaptive smooth variable structure filter strategy for state estimation of electric vehicle batteries. Energies 2021, 14, 8560. [Google Scholar] [CrossRef]
- Wang, L.; Ma, J.; Zhao, X.; Li, X.; Zhang, K. Online estimation of state-of-charge inconsistency for lithium-ion battery based on SVSF-VBL. J. Energy Storage 2023, 67, 107657. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, B.; Vachtsevanos, G.; Orchard, M. Machine condition prediction based on adaptive neuro–fuzzy and high-order particle filtering. IEEE Trans. Ind. Electron. 2010, 58, 4353–4364. [Google Scholar] [CrossRef]
- Ahmed, R.; Sayed, M.E.; Arasaratnam, I.; Tjong, J.; Habibi, S. Reduced-Order Electrochemical Model Parameters Identification and SOC Estimation for Healthy and Aged Li-Ion Batteries Part I: Parameterization Model Development for Healthy Batteries. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 659–677. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.; Li, D.; Cui, X.; Wang, L.; Li, L.; Wang, K. Electrochemical Impedance Spectroscopy: A New Chapter in the Fast and Accurate Estimation of the State of Health for Lithium-Ion Batteries. Energies 2023, 16, 1599. [Google Scholar] [CrossRef]
- Tran, M.K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Tao, Z.; Zhao, Z.; Wang, C.; Huang, L.; Jie, H.; Li, H.; Hao, Q.; Zhou, Y.; See, K.Y. State of charge estimation of lithium Batteries: Review for equivalent circuit model methods. Measurement 2024, 236, 115148. [Google Scholar] [CrossRef]
- Ahmed, D.M.; Hassan, M.M.; Mstafa, R.J. A Review on Deep Sequential Models for Forecasting Time Series Data. Appl. Comput. Intell. Soft Comput. 2022, 2022, 1–19. [Google Scholar] [CrossRef]
- Li, Y.; Du, M.; He, S. Attention-Based Sequence-to-Sequence Model for Time Series Imputation. Entropy 2022, 24, 1798. [Google Scholar] [CrossRef]
- Eleftheriadis, P.; Giazitzis, S.; Leva, S.; Ogliari, E. Data-Driven Methods for the State of Charge Estimation of Lithium-Ion Batteries: An Overview. Forecasting 2023, 5, 576–599. [Google Scholar] [CrossRef]
- Lucaferri, V.; Quercio, M.; Laudani, A.; Riganti Fulginei, F. A Review on Battery Model-Based and Data-Driven Methods for Battery Management Systems. Energies 2023, 16, 7807. [Google Scholar] [CrossRef]
- Vieira, R.N.; Kollmeyer, P.; Naguib, M.; Emadi, A. Feedforward and NARX Neural Network Battery State of Charge Estimation with Robustness to Current Sensor Error. In Proceedings of the 2023 IEEE Transportation Electrification Conference & Expo (ITEC), Chiang Mai, Thailand, 28 November–1 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Wand, M.; Koutník, J.; Schmidhuber, J. Lipreading with long short-term memory. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 6115–6119. [Google Scholar]
- Vidal, C.; Malysz, P.; Naguib, M.; Emadi, A.; Kollmeyer, P.J. Estimating battery state of charge using recurrent and non-recurrent neural networks. J. Energy Storage 2022, 47, 103660. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long short-term memory networks for accurate state-of-charge estimation of Li-ion batteries. IEEE Trans. Ind. Electron. 2017, 65, 6730–6739. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Google Scholar. Search Engine. Available online: https://scholar.google.com/ (accessed on 15 March 2024).
- Engineering Village. Search Engine. Available online: https://www.engineeringvillage.com/home.url?redir=t (accessed on 15 March 2024).
- Kollmeyer, P.; Vidal, C.; Naguib, M.; Skells, M. LG 18650HG2 Li-ion Battery Data and Example Deep Neural Network xEV SOC Estimator Script. 2020. Available online: https://data.mendeley.com/datasets/cp3473x7xv/3 (accessed on 10 December 2023).
- Saha, B.; Goebel, K. Battery Data Set. NASA AMES Prognostics Data Repository. 2007. Available online: https://data.nasa.gov/dataset/Li-ion-Battery-Aging-Datasets/uj5r-zjdb/about_data (accessed on 15 January 2024).
- Hannan, M.A.; How, D.N.; Lipu, M.H.; Mansor, M.; Ker, P.J.; Dong, Z.; Sahari, K.; Tiong, S.K.; Muttaqi, K.M.; Mahlia, T.I.; et al. Deep learning approach towards accurate state of charge estimation for lithium-ion batteries using self-supervised transformer model. Sci. Rep. 2021, 11, 19541. [Google Scholar] [CrossRef]
- Shen, H.; Zhou, X.; Wang, Z.; Wang, J. State of charge estimation for lithium-ion battery using Transformer with immersion and invariance adaptive observer. J. Energy Storage 2022, 45, 103768. [Google Scholar] [CrossRef]
- Chin, C.; Gao, Z. A123’s Lithium Iron Phosphate (ANR26650M1-B) Battery Cell Data 2019. Available online: https://ieee-dataport.org/documents/a123s-lithium-iron-phosphate-anr26650m1-b-battery-cell-data (accessed on 10 May 2024).
- Duan, Y.; Zou, R. A Novel State-of-Charge Estimation Method for Lithium-ion Batteries Using Convolutional Transformer Network and Sigma-point Kalman Filter. In Proceedings of the 2022 4th International Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 27–30 October 2022; pp. 1850–1855. [Google Scholar]
- Kollmeyer, P. Panasonic 18650PF Li-Ion Battery Data 2018. Available online: https://data.mendeley.com/datasets/wykht8y7tg/1 (accessed on 10 May 2024).
- Zou, R.; Duan, Y.; Wang, Y.; Pang, J.; Liu, F.; Sheikh, S.R. A novel convolutional informer network for deterministic and probabilistic state-of-charge estimation of lithium-ion batteries. J. Energy Storage 2023, 57, 106298. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Zheng, F.; Xing, Y.; Jiang, J.; Sun, B.; Kim, J.; Pecht, M. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries. Appl. Energy 2016, 183, 513–525. [Google Scholar] [CrossRef]
- Shi, D.; Zhao, J.; Wang, Z.; Zhao, H.; Wang, J.; Lian, Y.; Burke, A.F. Spatial-temporal self-attention transformer networks for battery state of charge estimation. Electronics 2023, 12, 2598. [Google Scholar] [CrossRef]
- Ahn, H.; Shen, H.; Zhou, X.; Kung, Y.C.; Wang, J. State of Charge Estimation of Lithium-Ion Batteries Using Physics-Informed Transformer for Limited Data Scenarios. ASME Lett. Dyn. Syst. Control 2023, 3, 041002. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. Int. J. Electr. Power Energy Syst. 2014, 62, 783–791. [Google Scholar] [CrossRef]
- Bao, Z.; Nie, J.; Lin, H.; Gao, K.; He, Z.; Gao, M. TTSNet: State-of-Charge Estimation of Li-ion Battery in Electrical Vehicles with Temporal Transformer-based Sequence Network. IEEE Trans. Veh. Technol. 2024, 73, 7838–7851. [Google Scholar] [CrossRef]
- Yılmaz, M.; Çinar, E.; Yazici, A. A Novel Transformer-Based Model for State of Charge Estimation of Electrical Vehicle Batteries. Available at SSRN 4736082. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4736082 (accessed on 9 April 2024).
- Steinstraeter, M.; Buberger, J.; Trifonov, D. Battery and heating data in real driving cycles. IEEE Dataport 2020, 10. [Google Scholar] [CrossRef]
- Catenaro, E.; Onori, S. Experimental data of lithium-ion batteries under galvanostatic discharge tests at different rates and temperatures of operation. Data Brief 2021, 35, 106894. [Google Scholar] [CrossRef]
- Chen, D.; Hong, W.; Zhou, X. Transformer Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Access 2022, 10, 19621–19628. [Google Scholar] [CrossRef]
- Gu, X.; See, K.W.; Li, P.; Shan, K.; Wang, Y.; Zhao, L.; Lim, K.C.; Zhang, N. A novel state-of-health estimation for the lithium-ion battery using a convolutional neural network and transformer model. Energy 2023, 262, 125501. [Google Scholar] [CrossRef]
- Bai, T.; Wang, H. Convolutional Transformer-Based Multiview Information Perception Framework for Lithium-Ion Battery State-of-Health Estimation. IEEE Trans. Instrum. Meas. 2023, 72, 2523312. [Google Scholar] [CrossRef]
- Birkl, C. Oxford Battery Degradation Dataset 1. 2017. Available online: https://ora.ox.ac.uk/objects/uuid:03ba4b01-cfed-46d3-9b1a-7d4a7bdf6fac (accessed on 15 April 2024).
- Zhao, Y.; Behdad, S. State of Health Estimation of Electric Vehicle Batteries Using Transformer-Based Neural Network. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers, Boston, MA, USA, 20–23 August 2023; Volume 87332, p. V005T05A017. [Google Scholar]
- Chen, L.; Xie, S.; Lopes, A.M.; Bao, X. A vision transformer-based deep neural network for state of health estimation of lithium-ion batteries. Int. J. Electr. Power Energy Syst. 2023, 152, 109233. [Google Scholar] [CrossRef]
- Luo, K.; Zheng, H.; Shi, Z. A simple feature extraction method for estimating the whole life cycle state of health of lithium-ion batteries using transformer-based neural network. J. Power Sources 2023, 576, 233139. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Liang, X.; Li, F.; Zhang, Z. Battery health state estimation of combined Transformer-GRU based on modal decomposition. Energy Storage Sci. Technol. 2023, 12, 2927. [Google Scholar]
- Fan, Y.; Li, Y.; Zhao, J.; Wang, L.; Yan, C.; Wu, X.; Zhang, P.; Wang, J.; Gao, G.; Wei, L. Online State-of-Health Estimation for Fast-Charging Lithium-Ion Batteries Based on a Transformer–Long Short-Term Memory Neural Network. Batteries 2023, 9, 539. [Google Scholar] [CrossRef]
- Gomez, W.; Wang, F.K.; Chou, J.H. Li-ion battery capacity prediction using improved temporal fusion transformer model. Energy 2024, 296, 131114. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
- Gao, M.; Shen, H.; Bao, Z.; Deng, Y.; He, Z. A Correlation-Augmented Informer-Based Method for State-of-Health Estimation of Li-Ion Batteries. IEEE Sens. J. 2024, 24, 3342–3353. [Google Scholar] [CrossRef]
- Fauzi, M.R.; Yudistira, N.; Mahmudy, W.F. State-of-Health Prediction of Lithium-Ion Batteries Using Exponential Smoothing Transformer With Seasonal and Growth Embedding. IEEE Access 2024, 12, 14659–14670. [Google Scholar] [CrossRef]
- Woo, G.; Liu, C.; Sahoo, D.; Kumar, A.; Hoi, S. Etsformer: Exponential smoothing transformers for time-series forecasting. arXiv 2022, arXiv:2202.01381. [Google Scholar]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar]
- Nakano, K.; Tanaka, K. Transformer-Based Online Battery State of Health Estimation from Electric Vehicle Driving Data. Available online: https://www.enerarxiv.org/thesis/1704194360.pdf (accessed on 9 April 2024).
- Zhang, W.; Jia, J.; Pang, X.; Wen, J.; Shi, Y.; Zeng, J. An Improved Transformer Model for Remaining Useful Life Prediction of Lithium-Ion Batteries under Random Charging and Discharging. Electronics 2024, 13, 1423. [Google Scholar] [CrossRef]
- Huang, Y.; Liang, H.; Xu, L. Kalman Filter Optimize Transformer Method for State of Health Prediction on Lithium-Ion Battery. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4718095 (accessed on 9 April 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guirguis, J.; Ahmed, R. Transformer-Based Deep Learning Models for State of Charge and State of Health Estimation of Li-Ion Batteries: A Survey Study. Energies 2024, 17, 3502. https://doi.org/10.3390/en17143502
Guirguis J, Ahmed R. Transformer-Based Deep Learning Models for State of Charge and State of Health Estimation of Li-Ion Batteries: A Survey Study. Energies. 2024; 17(14):3502. https://doi.org/10.3390/en17143502
Chicago/Turabian StyleGuirguis, John, and Ryan Ahmed. 2024. "Transformer-Based Deep Learning Models for State of Charge and State of Health Estimation of Li-Ion Batteries: A Survey Study" Energies 17, no. 14: 3502. https://doi.org/10.3390/en17143502
APA StyleGuirguis, J., & Ahmed, R. (2024). Transformer-Based Deep Learning Models for State of Charge and State of Health Estimation of Li-Ion Batteries: A Survey Study. Energies, 17(14), 3502. https://doi.org/10.3390/en17143502






