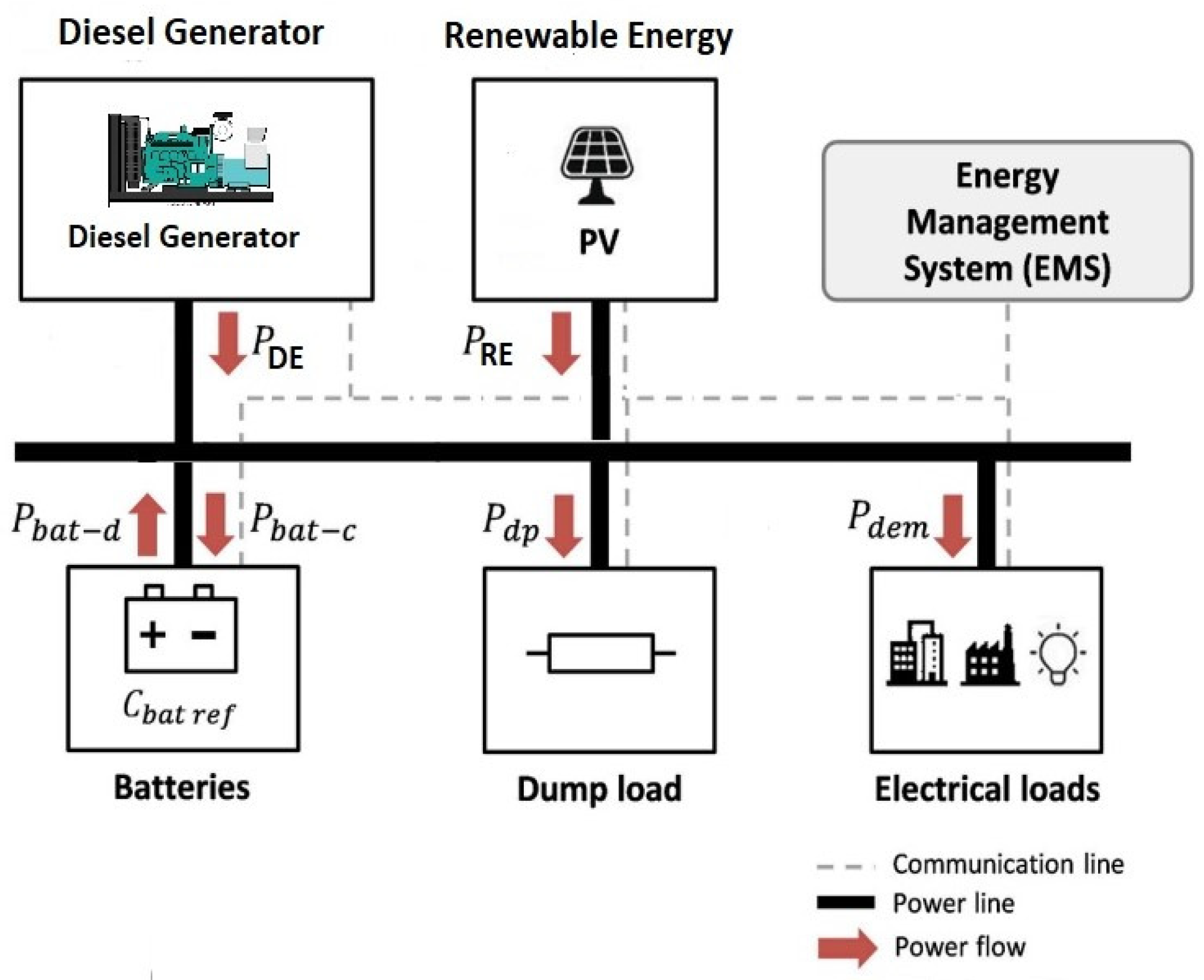
1. Introduction
The imperative to address climate change has fueled a growing emphasis on designing microgrids that operate with minimal greenhouse gas (GHG) emissions. As the world transitions towards sustainable energy solutions, the design of microgrids plays a pivotal role in achieving this environmental goal [
1]. The optimal sizing of microgrids and energy management were investigated in several studies as a way to decrease GHG emissions and costs [
2,
3,
4,
5,
6,
7]. In our previous study [
1], a new modeling approach was used to optimize sizing, considering CO
2 emissions and costs. A real-time energy management system (EMS) was implemented using mixed integer linear programming (MILP) to ensure minimal life cycle emissions. In the rapidly evolving field of energy systems, the optimal placement of energy sources is influenced by a multitude of interrelated factors. Our study’s focus on the transmission loss within a microgrid of 20 residential units highlights a key aspect of energy efficiency. By addressing transmission loss, we aim to highlight a critical factor that directly influences the operational costs and energy efficiency of the system. Transmission loss not only represents a significant portion of energy waste but also impacts the overall performance and sustainability of the microgrid. Reducing transmission loss is essential for optimizing energy distribution, minimizing financial expenditure, and enhancing the reliability and effectiveness of the energy system. This focus underscores the importance of efficient energy management practices, which are crucial for the long-term viability and scalability of microgrid solutions [
8].
While our study focuses specifically on transmission loss, it is crucial to acknowledge that a comprehensive approach should incorporate various economic and technical elements that were tackled in our previous study [
1]. These include installation costs, maintenance, grid stability, and the integration of renewable energy sources, especially in the context of a medium-sized microgrid consisting of 20 residential units. Installation costs are a significant consideration since they vary based on the scale of the microgrid, the type of energy sources used, and local economic conditions [
9]. Maintenance costs are another vital factor, representing the ongoing expenses required to ensure the system operates efficiently over time. In a microgrid setup, the ease of maintenance and the availability of technical support can significantly impact overall cost-effectiveness [
10]. Grid stability is essential for ensuring a reliable and uninterrupted power supply within the microgrid. For a network of 20 residential units, maintaining stability involves managing demand fluctuations, ensuring proper load distribution, and integrating backup systems to handle unexpected outages or peak demands [
11]. The integration of renewable energy sources is particularly relevant in modern microgrids. Utilizing solar panels, wind turbines, or other renewable technologies can reduce the dependency on traditional energy sources, lower operational costs, and enhance sustainability. However, the variable nature of renewables requires advanced management strategies to balance supply and demand effectively [
12].
A major part of these techno-economic challenges, as well as environmental objectives, were tackled in our previous study [
1], where the DC microgrid sizing considered satisfied the load demand at 100 percent while respecting the source-load balance. Sizing was done through a double loop: an outer loop used a genetic algorithm to provide sizing for the inner loop, consisting of mixed-integer linear programming and an economic function. The inner loop minimizes economic and environmental objectives. The minimum emissions were computed for a defined budget that took into consideration investment (CAPEX) and operational (OPEX) costs.
The current study is a continuation of the previous study, while it focuses on reducing emissions through minimizing distribution losses. Consequently, emissions will be reduced at the design and operation levels in a holistic approach.
The optimization of sources’ placement has been developed in many studies that align with reducing line losses and decreasing GHG emissions. Ref. [
13] proposes a technique for determining the size and optimal locations of grid-connected solar PV in primary distribution systems, using a multi-objective index for voltage profile improvement, demonstrating that multi-solar PV placement reduces power losses and enhances voltage profiles more effectively than single-PV placement. The research paper [
14] utilizes particle swarm optimization to determine the optimal sizing and placement of various distributed generators in a microgrid, with a focus on minimizing costs and meeting reliability constraints in both grid-connected and islanded modes. The study [
15] presents a non-linear programming approach with an optimal AC power flow for the ideal placement and sizing of distributed generators in active distribution networks, demonstrating superior performance in reducing total energy losses compared to existing methods using real-world distribution systems. Ref. [
16] suggests a modified analytical method for optimizing the location and size of solar photovoltaic-based distributed generation in medium-voltage distribution lines, validated on an IEEE 33-bus distribution system, showing improvements in the loss reduction and voltage profile. The research article [
17] utilizes load flow methods and a genetic algorithm to determine the best location for distributed generation in distribution systems, considering the high R/X of the transmission-system load flow, and it validates the approach with both 33-bus and 69-bus radial distribution systems. The paper [
18] introduces a methodology for determining the location and size of renewable energy sources in microgrid networks, considering system dynamics and stability and using a modified microgrid load flow model, and it experimentally verifies the proposed methodology on a microgrid testbed. [
19] proposes a method for the optimal placement of distributed generators in distribution networks, using the Brute Force search algorithm and a Backward Forward Sweep method for optimization and load flow, validating the approach with an IEEE 33-bus radial distribution test system through case studies.
All of these previous studies consider radial distribution, which is a special case of mesh network distribution. The foundation of the current research lies in the acknowledgment of the advantages of mesh network topologies within islanded microgrids. Recently, mesh networks (MNs) have gained prominence as a compelling alternative to radial distribution, showcasing a set of key strengths that distinguish them, which are mainly as follows:
Reliability: MNs decentralize communication and coordination among devices [
20,
21,
22], which ensures reliable communication even if some nodes experience disruptions.
Resilience: MNs are inherently resilient, as they can adapt to changes in the network topology or the failure of individual nodes without causing a complete system breakdown [
22].
Scalability: MNs can be easily scaled by adding more nodes, making them suitable for microgrid systems that may grow or evolve over time. Loads could also share power from available sources in other nodes [
23].
Flexibility: The decentralized nature of MN allows for increased flexibility in managing and controlling various devices within the microgrid [
23].
Efficiency: Mesh networks can optimize distribution routes, leading to more energy efficiency. Loads search for a supply from the nearest available sources [
23].
On the other hand, DC microgrids are more and more considered a viable alternative to AC microgrids, demonstrating significant potential. Despite their promising features, there remains ample room for further research and exploration in the field of DC microgrids, indicating a growing interest in uncovering their full capabilities and applications. In this study, DC microgrids are explored for their high potential to deliver the following:
Renewable energy integration: Many renewable energy sources, such as solar panels and batteries, inherently produce or store electricity in DC. A DC microgrid may simplify the integration of these renewable sources without the need for frequent conversions between AC and DC [
24,
25].
Control and stability: DC systems may offer better controllability and stability, especially in islanded microgrid scenarios. The absence of reactive power in DC systems simplifies control mechanisms, making it potentially easier to manage and optimize the power flow [
24,
25]. Additionally, there is no frequency to control in DC microgrids [
26].
Voltage stability: DC systems generally exhibit better voltage stability compared to AC systems. This can be advantageous in islanded microgrids, where maintaining stable voltage levels is crucial for the proper functioning of electrical loads [
24,
25].
Easy supply for DC loads: It is easier to implement a DC distribution system in order to supply electronic devices like computers and LED lighting without the need for inverters. This allows for a reduction in conversion losses and an improvement in overall efficiency [
24,
25].
This study concentrates on the dynamic aspects of DC islanded microgrids using mesh network topologies. This involves addressing distribution networks that differ from the usual radial designs, enabling the existence of multiple paths between nodes.
The non-radial nature of the distribution network, with multiple paths between nodes, necessitates a comprehensive evaluation of the network’s efficiency [
27]. By leveraging Dijkstra’s algorithm, traditionally used for finding the shortest path between nodes [
27], we explore its application to minimize power losses and enhance overall microgrid efficiency. Dijkstra’s algorithm is a popular method for finding the shortest path in a weighted graph from a single source vertex to all other vertices. It works by iteratively selecting the vertex with the smallest known distance from the source and updating the distances to its adjacent vertices [
28]. Implementing Dijkstra’s algorithm is very convenient and suitable when multiple paths exist between available sources and loads, unlike algorithms used in previous studies for radial distribution (where only one path exists between a source and a load).
In this context, the focus shifts to the strategic placement of microgrid electric sources (a diesel generator, PV panels, and batteries) to minimize distribution losses and enhance overall performance. Dijkstra’s algorithm is applied not only to optimize cable resistances dynamically but also to determine the optimal placement of these components, ensuring a synergistic approach to efficiency and reliability [
29].
Our research paper unfolds a comprehensive framework that harmonizes source placement at multiple positions and dynamic considerations of mesh network topologies within islanded microgrids. It represents a continuation of our earlier research, which focused on determining the optimal placement of energy sources within a single position in a DC islanded mesh network [
30]. By addressing sources’ optimal placement, we aim to minimize distribution losses and increase mesh network efficiency.
This paper addresses gaps in prior research, and its primary contributions can be summarized as follows:
Specifying optimal multiple sources positions in the DC islanded microgrid with a mesh network topology.
Validating the use of Dijkstra’s algorithm in sources’ placement through a comparison of the model using MATPOWER.
Developing a techno-economic study to evaluate the profitability of adopting sources’ placement at multiple positions in a mesh network topology compared to single-position source placement.
Our study serves as a foundational step in optimizing distribution losses within mesh-type electric microgrids. While previous optimization techniques have primarily focused on reducing transmission losses in radial distribution networks, our research is pioneering in addressing the complexities of mesh-type microgrids. In essence, this research is akin to the Google Maps of mesh-type microgrids, offering innovative guidance and precision in navigating and enhancing their efficiency.
This paper is organized as follows:
Section 2 defines the studied microgrid. The optimization of lines’ losses and lines’ total weight, corresponding to all sources placed in one node, is developed in
Section 3.
Section 4 defines the optimal source placement at multiple positions with the corresponding mesh network topology.
Section 5 validates Dijkstra’s model by comparing it to the power flow computed in MATPOWER.
Section 6 develops a techno-economic perspective that assesses the profitability of placing sources at multiple positions compared to a single position.
Section 7 concludes the paper with a discussion.
3. Dijkstra’s Model of the Microgrid Network
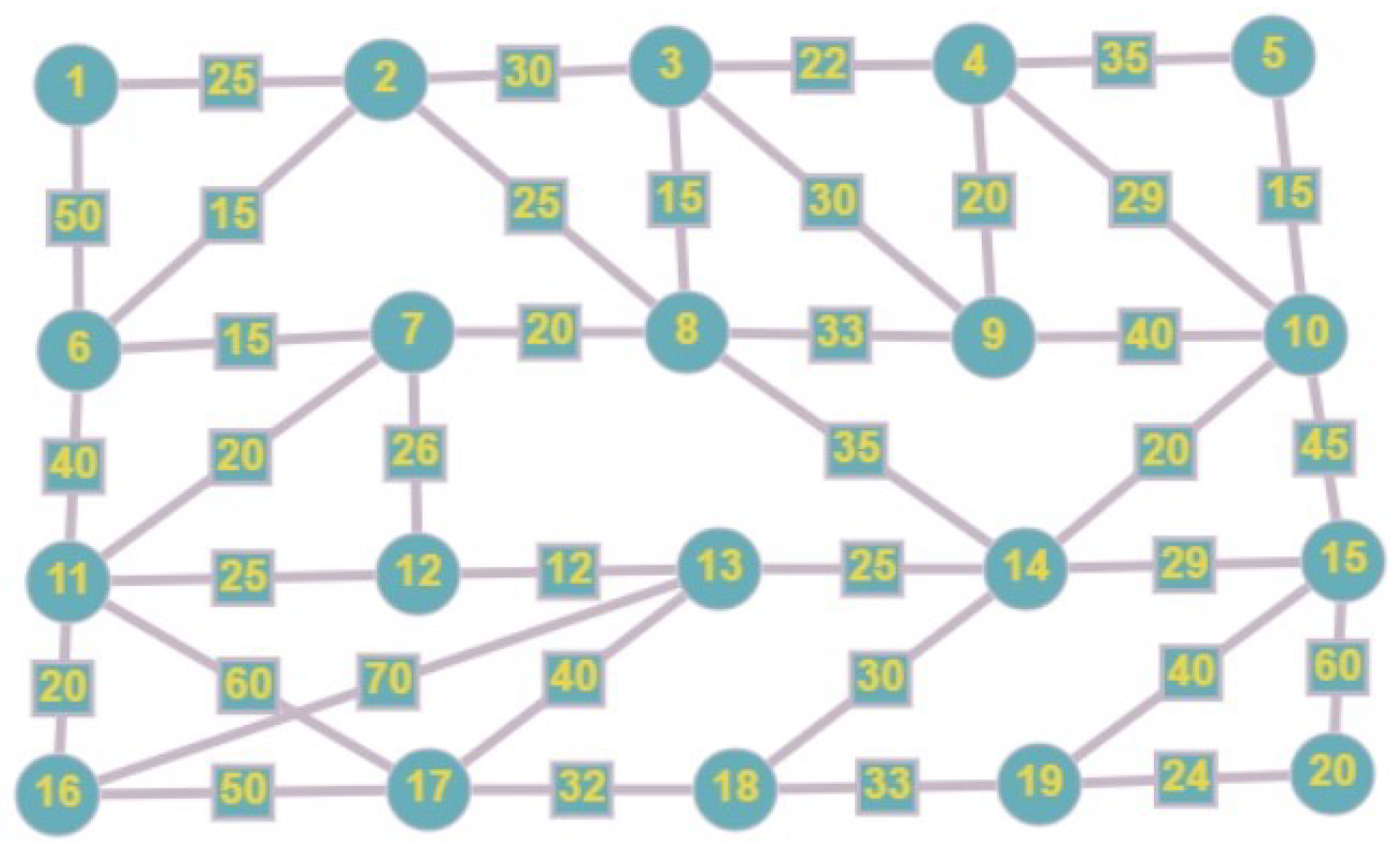
The detailed mesh network topology of the studied microgrid is presented in
Figure 3. It represents a realistic power distribution network of a residential compound composed of 20 residential units (20 buses). In this section, it is supposed that all sources are placed in the same position. The objective is to rank single sources’ positions from positions with the fewest line losses to the most line losses [
30]. This section serves to prepare the optimization of sources’ placement at multiple positions in
Section 4, while the main concern is to reduce the microgrid’s emissions.
3.1. Microgrid and Distribution Network Representation
This section employs Dijkstra’s algorithm as an optimization technique to identify the best location to place sources in the considered DC islanded microgrid. The optimization considers both the optimal line losses and the cable weight to enhance the efficiency of the system. To compute minimal distribution losses in a mesh-type microgrid, determining the shortest path is essential. Dijkstra’s algorithm serves as a tool, not the objective, for finding these shortest paths. Utilizing different algorithms, such as the Bellman–Ford algorithm or A-star algorithm, would yield the same shortest paths and, consequently, the same results. Thus, the choice of algorithm does not impact the final outcomes of our study, as it is known that the structure of our nodes and edges is not considered complex. In fact, for more complex structures, the A-star algorithm is faster than Dijkstra’s algorithm in terms of computation time.
In
Figure 3, each node represents a load; it is assumed that all the electric sources are placed in one of these nodes before sources’ placement at multiple positions is considered (as detailed in
Section 4). We aimed to find the best location for power sources by evaluating and ranking each source node based on the amount of energy lost in the distribution power lines. Loads are connected with branches whose length is defined in a rectangle. Despite having a predetermined structure, the distribution network’s resistance and line weight are computed according to the sources’ position, which can be situated at any predefined node. This study introduces a novel method for assessing network configurations, emphasizing optimal line losses and minimizing the cable weight [
30].
3.2. Initializing the Dijkstra Graph Matrix
The initial step involves constructing the Dijkstra graph using a 20 × 20 matrix (as represented in
Figure 4), corresponding to the 20 possible source nodes. This matrix represents the distances (in meters) between directly connected source nodes
. For example, if the distance between source nodes 1 and 2 is 25 m, both positions (1,2) and (2,1) in the Dijkstra graph matrix are set to 25. When nodes
i and
j are not connected, the matrix value at position
is 0. Additionally, the value at position
of the initial matrix is set to 0 [
30].
3.3. Determining the Best Location for Placing Sources
Given the existence of multiple paths from a source to a load, Dijkstra’s algorithm is employed to compute the shortest path connecting these nodes. The algorithm outlined in this paper follows these steps [
30]:
Step 1 involves determining the current required for each load in the DC microgrid. To calculate the DC current, given the active power profile, P, of the loads and the DC voltage, U (assumed to be 120 V), the formula is applied. The average current over the four representative days is used to calculate line losses, while cable sizing considers the maximum current.
Step 2 involves initiating iteration 0, where all branches are assumed to possess equal linear resistance. Each node is individually considered as the source node supplying power to all other loads. The Dijkstra graph matrix is configured as shown in
Figure 4. Dijkstra’s algorithm is then executed to determine the shortest path between a source and all other loads. Subsequently, the current flowing through each branch is computed, utilizing the power relation outlined in step 1. The cable specifications, obtained from [
32], are utilized to determine the cable resistance (in Ohm/km) and the corresponding cable weight (in kg/km), based on the computed current. Line losses attributed to a branch connecting two nodes are calculated using the following equation:
where the line losses in the connected branch
, denoted as
, are measured in Watts.
represents the resistance of line
in Ohm/km. The distance between nodes
i and
j, if they are connected, is provided by
and measured in kilometers. The term
represents the total current circulating in branch
from a source to a load node.
In fact, first, the matrix of the cable specification is filled, defining the linear resistance and weight for the corresponding current. The load of 20 nodes during 4 days at a step time of 1 h is filled in a (96 × 20) matrix. The average and maximum current of each load is then determined to, respectively, compute line losses and cables’ size. The Dijkstra graph, which represents distances between connected nodes, is multiplied by linear resistances since the least resistance is considered the shortest path (not necessarily the shortest distance). At this stage, the unique source is placed consecutively at each node. For each source position, the shortest paths from the source to each load are detected, allowing for the computation of the current circulating in each branch (i, j) and storing it in a corresponding current (20 × 20) matrix. As the current circulating in each branch is known, the cables are sized accordingly, allowing for the computation of the total line losses for each source position. The algorithm coded using Matlab is not complex since the computation time is a few seconds. However, for more complex topologies, the computation time might increase.
Step 3 involves initiating a new iteration to ensure the absence of the newly created shortest paths, given that cable linear resistances are no longer considered equal for all lines as in iteration 0. Line resistances are adjusted based on the current circulating in the respective branch, which was computed in the previous iteration. This adjustment results in the generation of potential new paths connecting nodes, calculated as . A new Dijkstra matrix representing the new paths between connected nodes is created. Dijkstra’s algorithm is then applied to identify the shortest path between a source and all other loads, with the source’s position ranging from node 1 to node 20. The value of the current circulating between connected nodes could change if new shortest paths are identified. Consequently, the line resistance and weight are once again updated. The placement of the source can be ranked based on positions with the lowest to highest line losses.
Step 4: Step 3 is repeated until the cable resistances of all branches converge to a constant value (no more shorter paths are detected due to lines’ linear resistance update).
In the following subsection, the results of applying Dijkstra’s algorithm to compute the optimal line losses of a DC islanded microgrid distribution network are presented.
3.4. Simulation Results
As already seen, the study focuses on a DC islanded microgrid comprising 20 residential units, employing a mesh network with an average total load power of 32.4 kW. The connected nodes are illustrated in the Dijkstra matrix (
Figure 4). In this regard, it is worth recalling that Dijkstra’s algorithm calculates the shortest path between a source located at a specified node and all other load nodes, which makes this algorithm crucial when multiple paths exist within a mesh network. During its execution, the algorithm determines the current flowing in each line connecting two nodes, taking into account the active power of each load and the optimal path from the source to the load. It is important to note that average current values are utilized to compute line losses, while maximal current values are considered for cable sizing.
3.4.1. Implementation of Dijkstra’s Algorithm
In this research, a Dijkstra function was employed from Mathworks, as detailed in [
33], which contains Matlab M-files for implementing Dijkstra’s algorithm. Utilizing the distance graph matrix of directly connected nodes, we can find the shortest distance and its corresponding path between a source node and a destination node using the following command:
In this context, the distance represents the minimum resistance between a source node and a destination node. The path indicates the optimal route from each source to the destination, and the graph represents the matrix of resistances between two directly connected nodes. Matrices storing currents flowing between nodes, losses, resistances, and cable weights were computed using Dijkstra’s algorithm.
3.4.2. Minimal Line Losses and Cables’ Weight Considering Optimized Cable Sizing
Optimal sources’ placement for minimizing line losses can be approached from different angles. Initially, placing sources in a designated node involves computing currents in each branch, sizing cables using a datasheet [
32], and assessing optimal line losses for the network configuration. Once branch currents are calculated, cable sizing and line resistances are determined. A subsequent iteration may generate new optimal paths,
. Iterations persist until the resistances of the cables within the mesh network reach convergence, signifying the establishment of the network configuration. In
Table 1, the sources are all placed at each node, and the corresponding optimal line losses and total network cable weight are calculated.
Table 1 ranks the single-position placement of sources based on node position, from the least to the maximum line losses. Minimal line losses are obtained when these sources are placed at node 16.
3.4.3. Minimal Line Losses Considering an Optimized Network’s Total Cable Weight
Examining optimal source placement and network optimization from another angle involves considering the importance of cables’ weight in evaluating line losses (i.e., when two resistances are in parallel, the equivalent resistance decreases by half, while the cables’ weight doubles). This underscores the significance of cables’ weight as a crucial factor in assessing line losses. To illustrate this ratio’s importance, a comparison is made between placing the sources at node 16 and node 14.
Table 1 shows that placing the sources at node 16 results in 529 W of line losses, whereas placing it at node 14 incurs 638 W of losses. Despite node 14 having higher total line losses, placing all the electric sources there results in a lower optimal total cable weight (57 kg vs. 112 kg). This indicates that, by doubling the cables’ weight at node 14, line losses can be halved (319 W). Considering the minimal line weight per kW of losses (as depicted in
Table 2) underscores the efficiency of placing the sources at node 14 in terms of the optimal cable weight.
It is important to note that, in this study, the weight of the cables represents their price. This approach introduces a techno-economic perspective, as the market price of the copper used in the cables can fluctuate. By focusing on cable weight instead of price, the study integrates both technical and economic considerations in evaluating optimal source placement and network optimization.
4. Optimal Placement of Sources at Multiple Positions
In
Section 3, we analyzed the optimal positioning of sources within a single node. In this section, we will explore the optimal placement of sources at multiple positions within the microgrid under examination. The EMS defining the total load share power profile is summarized in
Table 3, where the portion of each electric source supplying the different loads is defined. Our strategy to reduce distribution losses is to place batteries next to loads, to put PV panels at node 14 (the source with the least line weight per kW of losses), and finally to put the diesel generator at node 8. In fact, PV panels have priority for node 14 since they deliver more power to electric loads and batteries than the diesel generator (
Table 3). Since it is known that batteries are placed next to each load, the distribution losses related to batteries’ discharge when supplying the loads are almost negligible. However, additional currents are incurred due to charging batteries from PV panels and a diesel generator. In fact, for a considered battery associated with a load, charging and discharging are not done simultaneously. This is the reason why the maximum power that should be supplied to each node (load + battery) increases, which directly impacts the cable sizing that takes into consideration the maximum currents in each branch. On the other hand, line losses are contingent upon the average power (rather than the maximum power) supplied to each node over the course of the four-day period.
Consequently, each load causing line losses could be written as follows:
While the maximum load (for the 4 days) considered for cable sizing of each branch is as follows:
is the electric residential load at a defined node,
is the charging power, and
is the discharging power of batteries placed at each node. The EMS defining the power profile was taken from [
1]. The Dijkstra-based algorithm developed in
Section 3 is now applied for the new loads (20 residences where each of them is paired with its dedicated battery pack to efficiently manage its power requirements). Dynamic matrices are used to store new cables’ resistances, weights, and losses based on average and maximum currents circulating between two nodes. Placing batteries next to loads implies higher maximum currents due to the fact that PV arrays and a diesel generator should cover the electric load plus charging batteries. This means that the new optimal mesh network topology based on optimal source placement at multiple positions requires heavier cables, which decreases line resistance. Consequently, line losses decrease since the average power,
, is almost the same as
in each node, as it is known that the average powers
and
are nearly identical for the 4 days, as shown in
Table 3, thus respecting batteries’ charge-sustaining operation.
Table 4 shows the new line losses associated with the new load. As expected, line losses have considerably decreased compared to
Table 2.
In this study, a constraint related to energy reliability was added; PV panels and the diesel generator should be able to supply all loads alone in the case of the failure of one of these sources. This implies that each cable should be sized based on the maximum current that could circulate in the corresponding connected nodes. For this reason, we considered the following two cases leading to the highest possible currents in all branches:
The maximum current circulating in each cable for cases 1 and 2 is stored in a matrix. The cables connecting two nodes in the new network configuration (sources at multiple positions) should allow the maximum possible current (comparing case 1 and case 2) to circulate. Consequently, a new distribution network is created by superposing both network structures by choosing, when nodes are connected, the cable with the least resistance (the biggest cable section supporting the highest current). When superposing the network topology of single sources’ positions placed at nodes 14 and 8, the new total network weight becomes 358 kg, and line losses are equal to 120 W for both sources placed at nodes 14 and 8. Considering the optimal placement of multiple source positions, the total energy lost in cables during the 4 days is 11.5 kWh, which is equal to 0.65 percent of the total load. The energy lost when considering single sources’ optimal position placement represents 3.41 percent of the load. The losses are divided by 5.3, while the line weight is multiplied by 3.9, which highlights the advantage of considering sources’ placement at multiple positions instead of single-position placement.
The following section presents a techno-economic study that shows the advantages and disadvantages of considering optimal sources’ placement at multiple positions in a mesh network topology for a DC islanded microgrid while focusing mainly on line losses and the converter price.
5. Line Losses Comparison between Dijkstra Hypothesis and MATPOWER
The previous part of this study considered optimal line losses while using Dijkstra’s algorithm. Our main approach to compute approximate losses was based on a hypothesis where currents circulate through lines with the least resistance (the shortest path). In reality, currents’ flow in a mesh network is determined according to electricity laws. In this section, we validate whether Dijkstra’s algorithm could be used to approximately compute power flow, line resistances, and losses.
MATPOWER is a package of MATLAB used to solve optimal power flow problems while computing bus voltages and line losses. In order to run the power flow study in MATPOWER, we used line resistance values computed through Dijkstra’s algorithm for five source positions to be compared (sources, respectively, at nodes 16, 7, 14, 4, and 18). For each source position, a new network topology was coded where 20 buses is generated with their corresponding loads, voltages, and branch resistances. In order to compute line losses, the average load power of each node was used.
Table 5 shows the ranking of sources’ placement based on the optimal current flow while putting batteries next to loads.
Table 6 shows the power flow results obtained using MATPOWER while placing a source at node 16. The total line losses obtained are equal to 235 W. Power flows corresponding to sources placed, respectively, at positions 7, 14, 4, and 18 were also computed after the data related to branches’ resistances (sized using Dijkstra’s algorithm) were changed. The line losses for these source placements are, respectively, as follows: 210 W, 217 W, 247 W, and 257 W.
After comparing the line loss values obtained using Dijkstra’s algorithm approximation (
Table 5) with those derived from MATPOWER, it is evident that the values differ by approximately 60 percent between the two methods. This discrepancy was expected, as Dijkstra’s algorithm approximates the power flow by assuming that currents travel along the shortest path between a source and a load. In contrast, electricity laws account for current distribution across multiple paths, not limited to the path of least resistance. Consequently, this results in higher power loss calculations in MATPOWER. However, the ranking of these losses remains the same for both methods except for the source placed at position 16.
Table 7 shows the comparison of branches’ loss rankings while using both methods. Five source positions were studied only through MATPOWER due to the amount of information to enter for 20 buses.
We can conclude, for this specific case study, that Dijkstra’s algorithm could be used as an approximation method for defining and ranking source positions from the least to the highest line losses. A future study could investigate whether this method could be generalized to any mesh-type DC microgrid.
7. Conclusions, Discussion, and Perspectives
This paper used our previous study [
1] to select the optimal sizing of the microgrid used in the current study. The sizing with the fewest emissions for a specified budget was computed. This article maintains its commitment to reducing greenhouse gas emissions by exploring the most effective positioning of power sources in an isolated DC microgrid using a mesh network topology. The primary goal is to minimize losses in distribution lines. The study employed Dijkstra’s algorithm to identify the shortest paths between a source node and all other load nodes, accounting for multiple pathways within the microgrid. Notably, the network’s line resistance was not predetermined. The article investigated two perspectives for optimal source placement.
The initial approach involved assessing sources’ placements based on line losses, taking into account cable resistance, which is influenced by the circulating current. The second perspective introduced an innovative method to evaluate the optimal network configuration by comparing various topologies, considering the weight of cables used per kilowatt of losses.
This study’s significance lies in its capacity to rank nodes according to their line losses and recommend corresponding network structures for each source’s placement.
A key contribution of this research is the validation of Dijkstra’s algorithm as a reliable method to estimate sources’ placement in a mesh-type DC microgrid. We compared line losses calculated using Dijkstra’s algorithm and MATPOWER. Dijkstra’s algorithm, which assumes currents follow paths of the least resistance, was tested against the more comprehensive MATPOWER analysis, which adheres to electricity laws. Despite a 60-percent difference in the absolute values of line losses between the two methods, the ranking of losses for different source positions was largely consistent, except for one case. This suggests, in our case study, that while Dijkstra’s algorithm may not provide precise loss values, it can effectively approximate and rank line losses, making it a potentially useful tool for preliminary power flow analysis in complex network topologies. A future study will validate whether this hypothesis could be generalized to all mesh-type DC microgrids.
In this article, the best way to position multiple energy sources was also explored. Batteries were placed close to the loads, which increased the power demand, converter power, and cable weight. Photovoltaic panels (PVs) and the diesel generator were positioned in the two most optimal locations, minimizing line losses.
A techno-economic analysis was conducted to evaluate the profitability of optimizing multiple-source-position placement compared to single-source position placement. The analysis revealed interesting economic outcomes, particularly with a short payback period achieved through the optimal placement of sources at multiple positions, compared to a single-source position. Additionally, a substantial reduction in greenhouse gas (GHG) emissions was observed during this payback period.
Using the optimized source placement at multiple positions appears to be beneficial, especially when considering the microgrid size, based on our previous study [
1], in which residential areas had a very long lifespan.
The topology of the studied microgrid, shown in
Figure 3, corresponds to the Dijkstra graph matrix in
Figure 4. For each study, the specific topology must be defined. If a different topology is considered, the Dijkstra graph matrix should be updated to reflect the new configuration, resulting in a different ranking of losses among the nodes. However, the techno-economic findings of our study are generalizable and remain applicable to various topologies.
Future research will include sensitivity analysis to assess the impact of varying parameters such as cable weight, converter power, and network topology configuration on the results of the optimal source placement strategy. This approach would offer a more reliable understanding of the system’s behavior under different scenarios. Additionally, incorporating uncertainty analysis into the methodology is essential to account for variations in parameters such as load profiles, renewable energy generation, and equipment efficiency. This will provide valuable insights into the robustness of the optimal siting strategy under conditions of uncertainty.
In conclusion, our study has shown that the Dijkstra algorithm plays a key role in optimizing sources’ placement in a DC microgrid. We aimed to validate the approximation of electricity laws using the Dijkstra algorithm and found it suitable for this purpose. While we focused on Dijkstra’s approach due to its efficiency and reliability, we recognize the need to explore other algorithms. In future research, we will compare Dijkstra’s approach with other algorithms, like A-star and Bellman–Ford. This will help us determine which algorithms are best for different scenarios, potentially improving our model’s accuracy and effectiveness. We also plan to test our model on more complex scenarios beyond the simple graph of 20 residential units used in this study. By applying our model to larger and more intricate microgrid systems, we aim to better understand its robustness and scalability. This will include testing with diverse types of units and conducting sensitivity analyses to see how changes in input parameters affect performance. This work will help refine our model, making it more applicable to real-world microgrid optimization.