Improved MTPA and MTPV Optimal Criteria Analysis Based on IPMSM Nonlinear Flux-Linkage Model
Abstract
1. Introduction
2. Conventional Linear Motor Model and Operating Criteria
2.1. Flux, Voltage, and Electromagnetic Torque Equations
2.2. Current and Voltage Limits
2.3. MTPA and MTPV Criteria Based on the Linear Motor Model
3. Improved MTPA and MTPV Criteria Based on Nonlinear Flux-Linkage Model
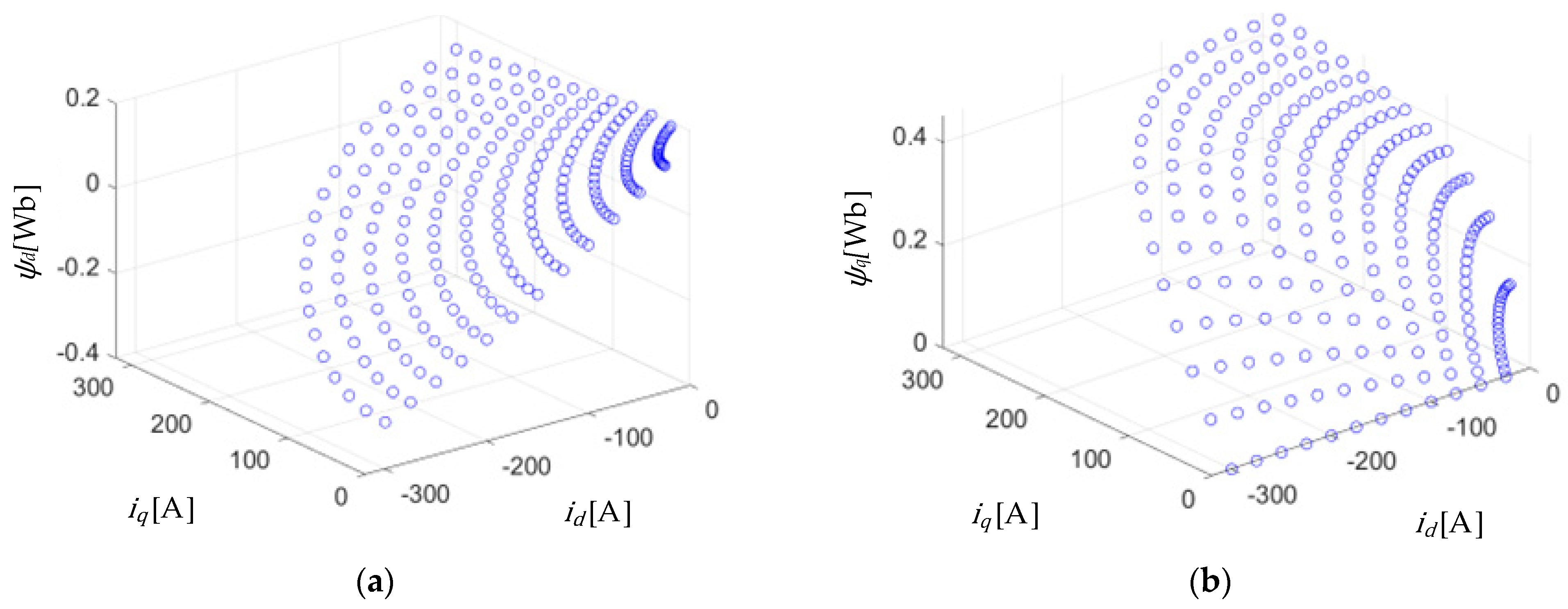
3.1. Nonlinear Flux-Linkage Model
3.2. Analysis of Improved MTPA Criteria Based on the Nonlinear Flux-Linkage Model
3.3. Analysis of Improved MTPV Criteria Based on the Nonlinear Flux-Linkage Model
4. Experiments
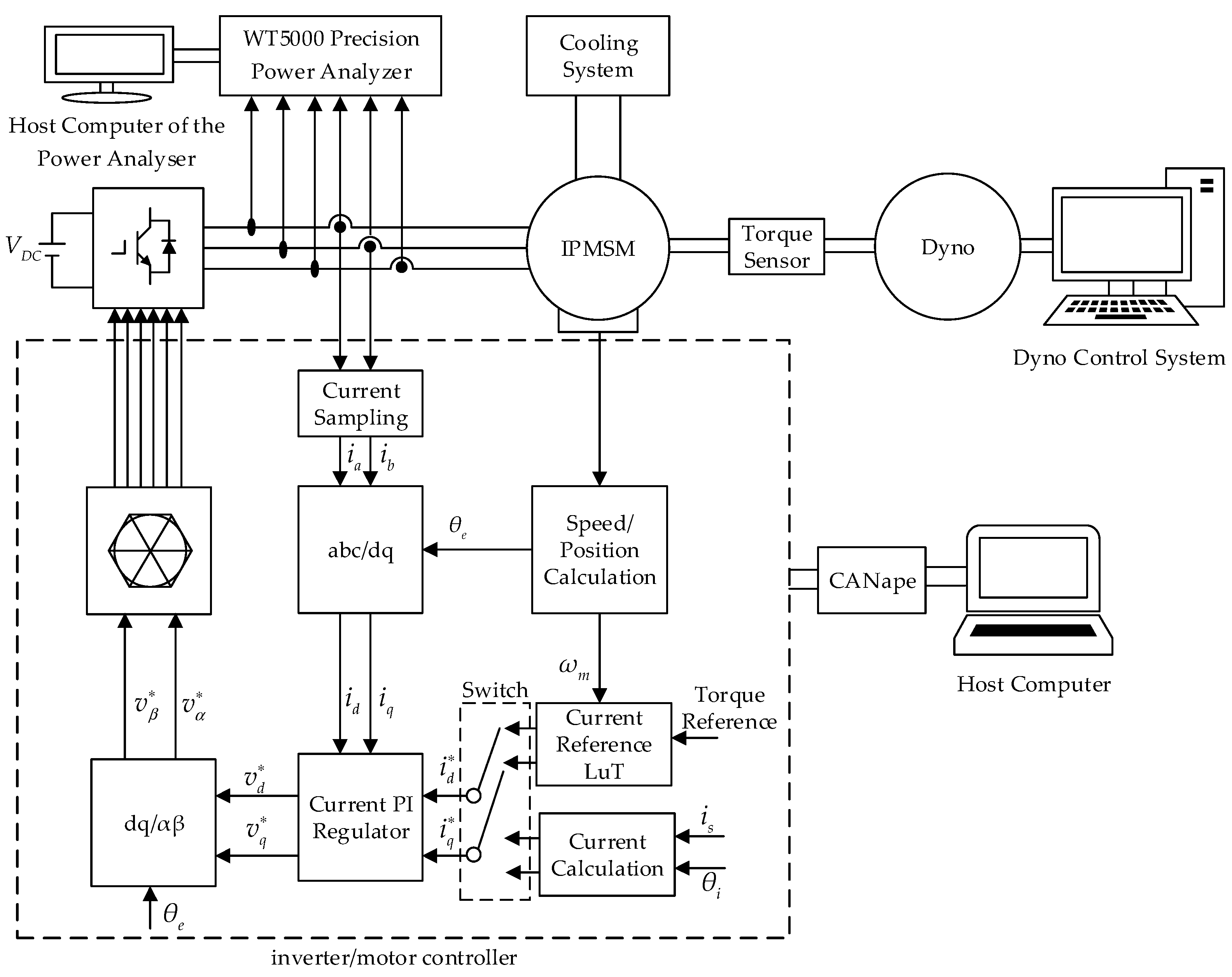
4.1. Experiment Platform
4.2. Experimental Identification of Nonlinear Flux-Linkage Model
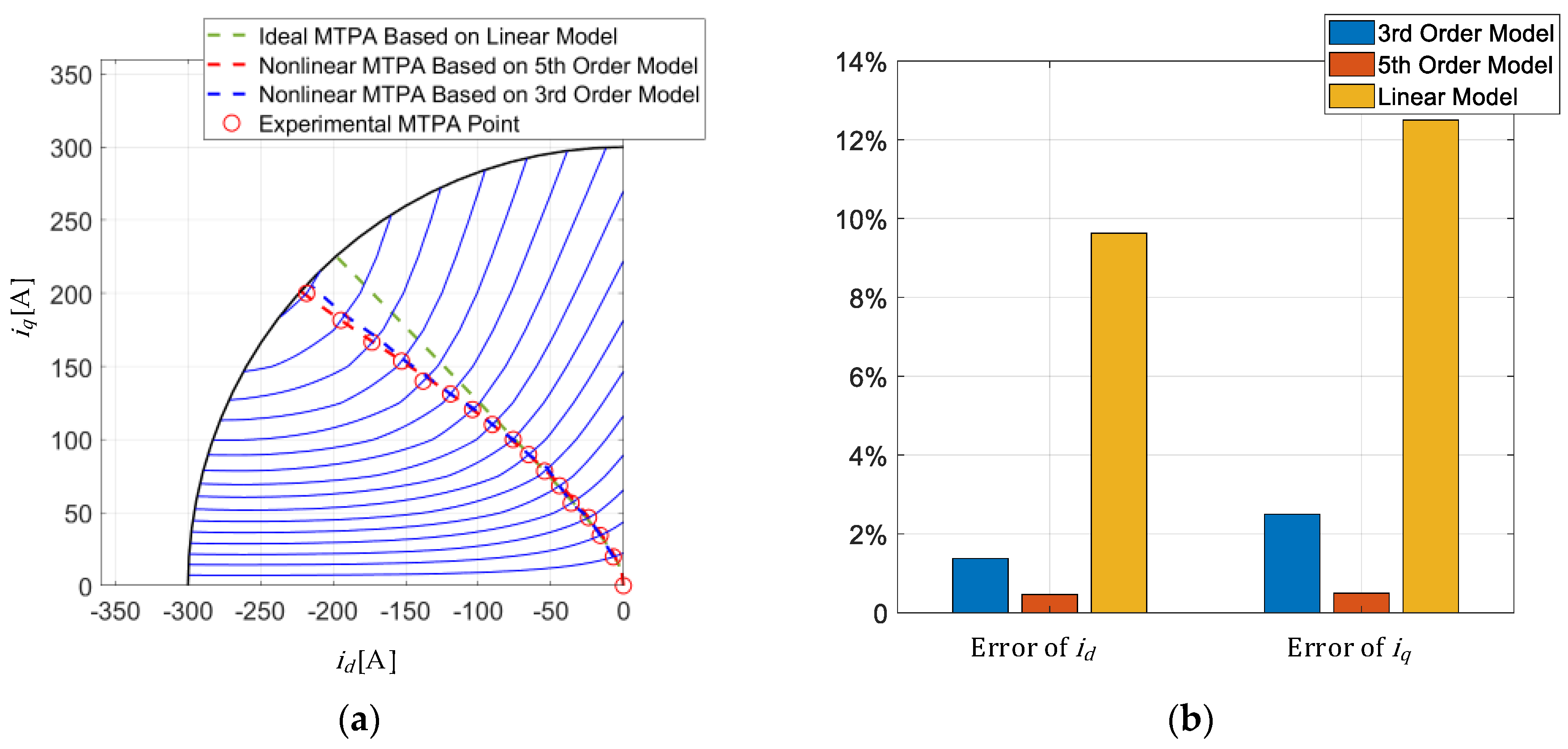
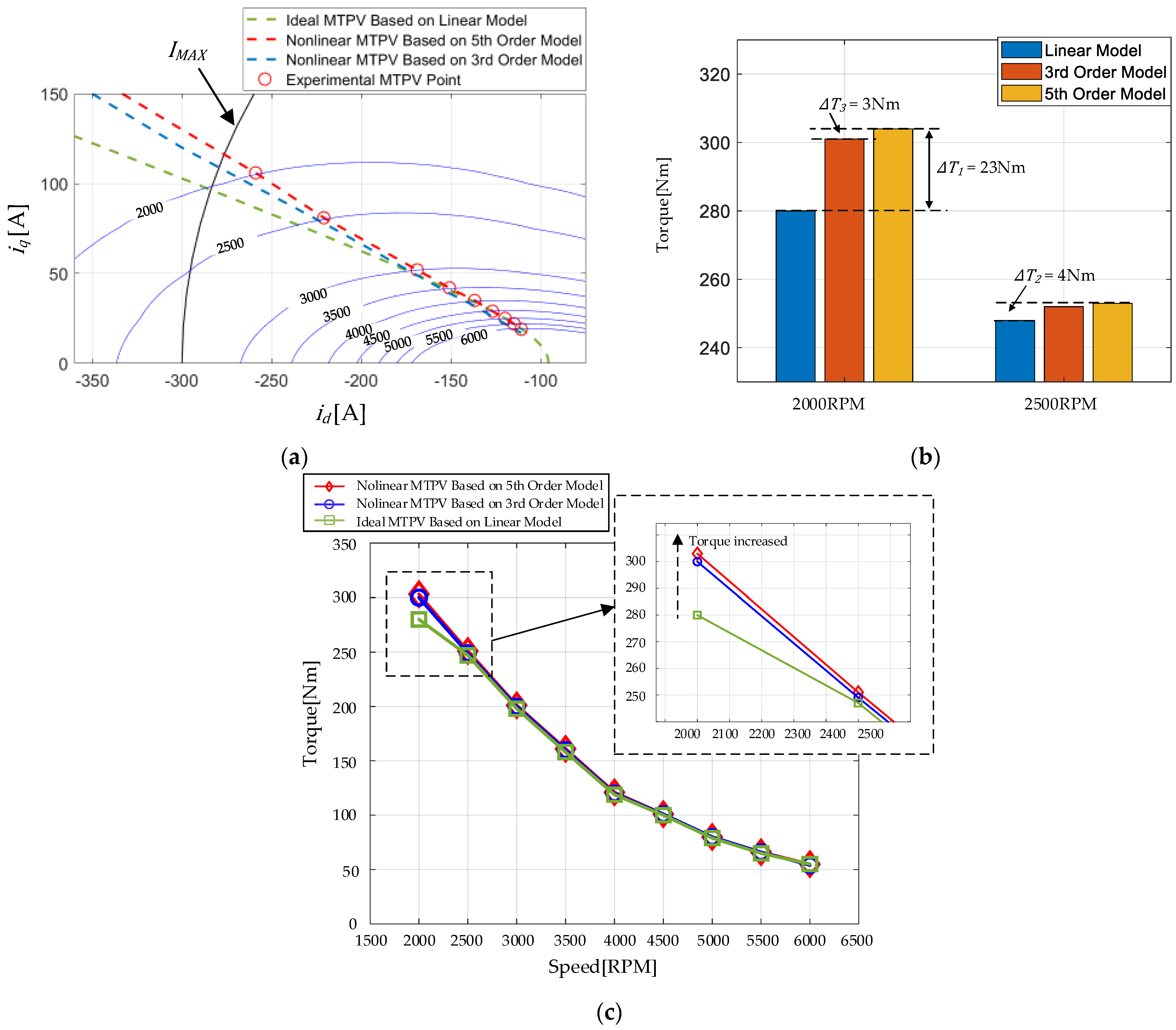
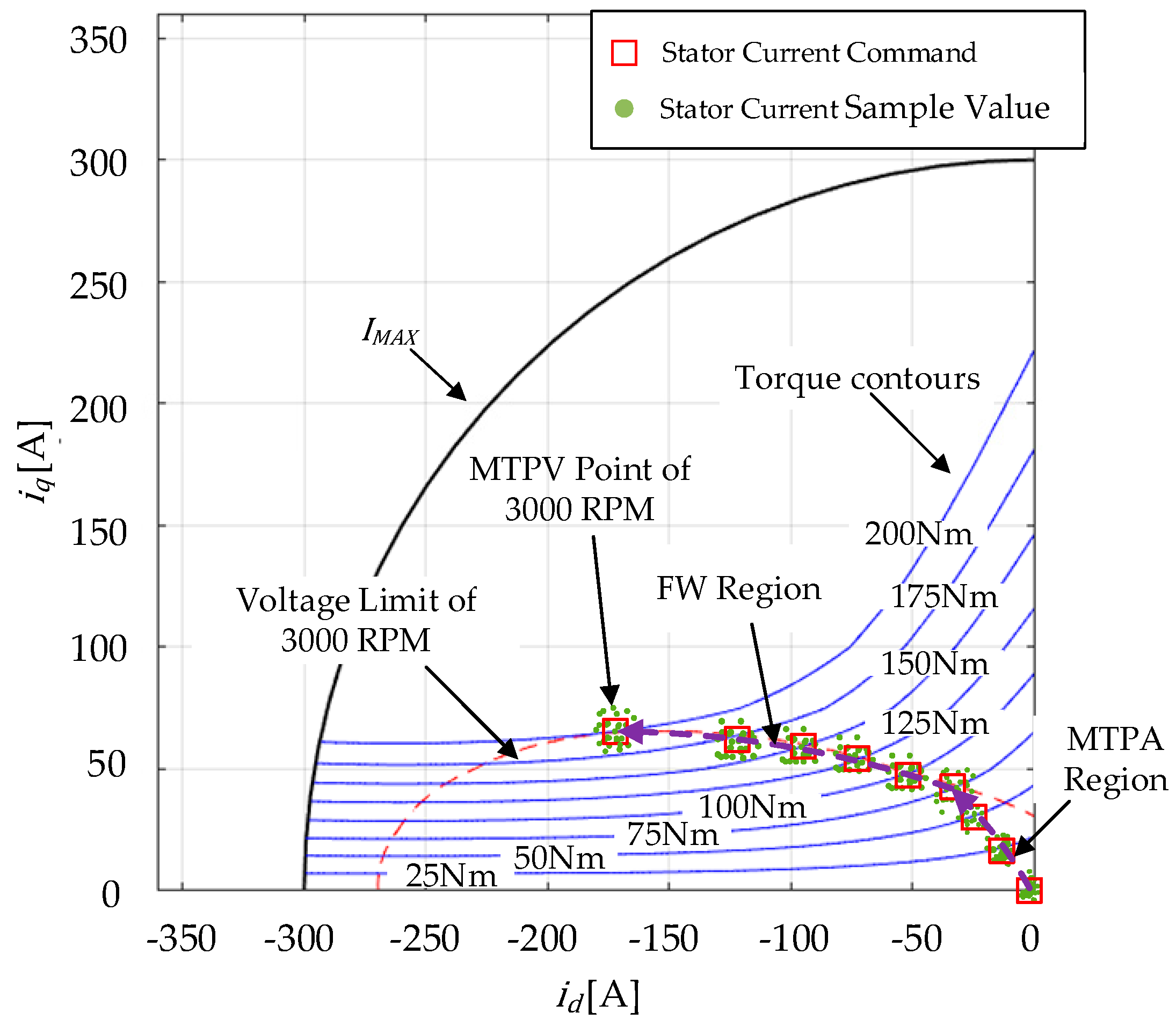
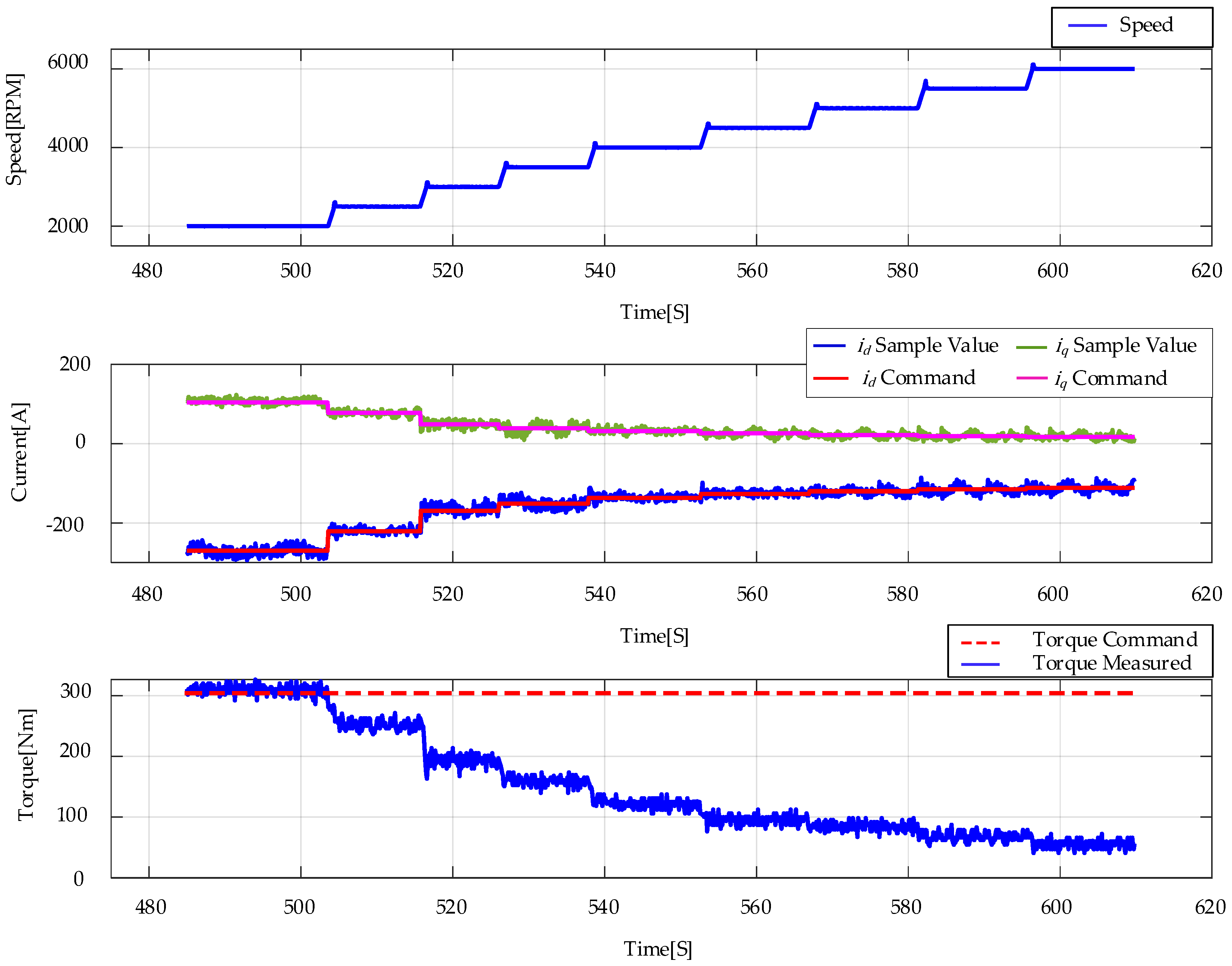
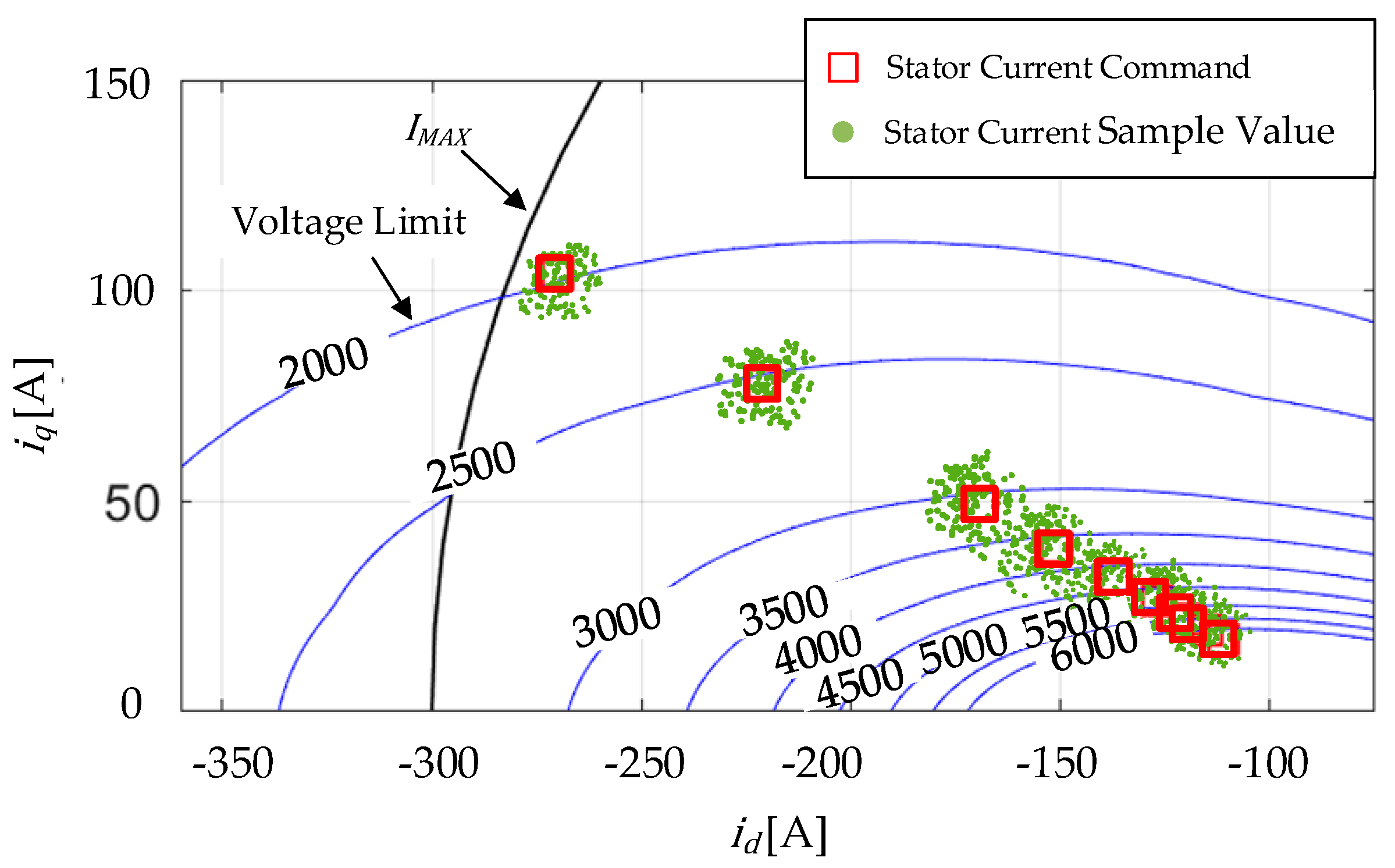
4.3. Experimental Identification of MTPA, FW, and MTPV Current Trajectory
4.4. Experimental Results of the Improved MTPA and MTPV Criteria
5. Conclusions
- (1)
- The nonlinear flux-linkage model of the IPMSM under test was established through the experimental test method. The principle, procedure, and precautions of the experimental test method were explained in detail.
- (2)
- The MTPA and MTPV optimal criteria were then analyzed by constructing and solving different optimal problems to obtain their closed-form solutions. The analysis results showed that the nonlinear current criteria can achieve a good matching effect with the actual current trajectory compared to the linear current criteria.
- (3)
- The current command LuT suitable for IPMSM control was constructed based on the improved MTPA and MTPV optimal criteria proposed in this paper. The optimal criteria proposed in this paper and their control performance were validated through experimental testing.
- (4)
- The experimental results showed that the maximum current error between the improved MTPA criteria and the experimental MTPA points was reduced to 3% in the MTPA region. Considering the current ripple inherent in FOC, this is an almost negligible current error. In contrast, the maximum current error of the linear MTPA criteria could be up to 12.5%. In the high-speed region, the performance difference between the nonlinear criteria and the linear current criteria was not significant due to the low influence of magnetic saturation and cross-coupling factors. Nevertheless, in the 2000 RPM to 2500 RPM speed range, the nonlinear standard achieved a notable torque enhancement effect, with a maximum torque increase of 23 Nm.
- (5)
- In addition to saturation and cross-coupling factors, the temperature factor can also influence the performance of IPMSMs. In this paper, the research was performed only on the saturation and cross-coupling factors. The temperature of the experiments was controlled by an external water-cooling equipment in order to ensure that all experiments were performed at approximately the same temperature, thus eliminating the effect of temperature on the errors in this research. In the subsequent stage of the investigation, it would be beneficial to introduce the effect of the temperature factor.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Terms | Units | Meaning |
| Ω | Stator winding resistance | |
| Wb | Permanent-magnet flux-linkage | |
| Number of pole pairs | ||
| mH | d- and q-axis inductance | |
| A | d- and q-axis stator current | |
| Wb | d- and q-axis stator flux-linkage | |
| V | d- and q-axis stator voltage | |
| rad/s | Electrical rotor speed | |
| Nm | Electromagnetic torque | |
| A | Maximum stator current | |
| V | Maximum stator voltage | |
| V | DC-link voltage of inverter | |
| A | Characteristic current | |
| d-axis stator flux-linkage function | ||
| q-axis stator flux-linkage function | ||
| Polynomial degree of flux-linkage fitting model | ||
| Coefficients in the flux-linkage fitting model |
| Terms | Units | Meaning |
| Objective function in improved MTPA criteria analysis | ||
| Lagrange function in improved MTPA criteria analysis | ||
| Lagrange multiplier in improved MTPA criteria analysis | ||
| Objective function in improved MTPV criteria analysis | ||
| Lagrange function in improved MTPV criteria analysis | ||
| Lagrange multiplier in improved MTPV criteria analysis | ||
| V | Stator voltage | |
| A | Stator current | |
| Wb | Stator flux-linkage |
| Terms | Units | Meaning |
| A | A and B phase current | |
| A | d- and q-axis current command | |
| V | d- and q-axis voltage command | |
| V | α- and β-axis voltage command | |
| RPM | Mechanical rotor speed | |
| rad | Electrical rotor position angle | |
| rad | Stator voltage vector angle | |
| rad | Stator current vector angle | |
| °C | Initial ambient temperature | |
| °C | The set and maintained experimental temperature | |
| 1/°C | Temperature coefficient of resistance | |
| Ω | Stator winding resistance measured at the initial ambient temperature | |
| ° | Stator current angle scanning step | |
| A | Stator current magnitude scanning step |
References
- Inventory of U.S. Greenhouse Gas Emissions and Sinks: 1990–2022. Available online: https://www.epa.gov/system/files/documents/2024-04/us-ghg-inventory-2024-main-text_04-18-2024.pdf (accessed on 11 April 2024).
- Aiso, K.; Akatsu, K. Performance Comparison of High-Speed Motors for Electric Vehicle. World Electr. Veh. J. 2022, 13, 57. [Google Scholar] [CrossRef]
- Yang, Z.; Shang, F.; Brown, I.P.; Krishnamurthy, M. Comparative Study of Interior Permanent Magnet, Induction, and Switched Reluctance Motor Drives for EV and HEV Applications. IEEE Trans. Transp. Electrif. 2015, 1, 245–254. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Chu, W.Q.; Guan, Y. Quantitative comparison of electromagnetic performance of electrical machines for HEVs/EVs. CES Trans. Electr. Mach. Syst. 2017, 1, 37–47. [Google Scholar] [CrossRef]
- Krishnan, R. Permanent magnet synchronous and brushless DC motor drives; CRC press: 2017.
- Novotny, D.W.; Lipo, T.A. Vector Control and Dynamics of AC Drives; Oxford University Press: Oxford, UK, 1996; Volume 41. [Google Scholar]
- Morimoto, S.; Takeda, Y.; Hirasa, T.; Taniguchi, K. Expansion of operating limits for permanent magnet motor by current vector control considering inverter capacity. IEEE Trans. Ind. Appl. 1990, 26, 866–871. [Google Scholar] [CrossRef]
- Bianchini, C.; Bisceglie, G.; Torreggiani, A.; Davoli, M.; Macrelli, E.; Bellini, A.; Frigieri, M. Effects of the Magnetic Model of Interior Permanent Magnet Machine on MTPA, Flux Weakening and MTPV Evaluation. Machines 2023, 11, 77. [Google Scholar] [CrossRef]
- Tinazzi, F.; Bolognani, S.; Calligaro, S.; Kumar, P.; Petrella, R.; Zigliotto, M. Classification and review of MTPA algorithms for synchronous reluctance and interior permanent magnet motor drives. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE’19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. P.1–P.10. [Google Scholar]
- Miguel-Espinar, C.; Heredero-Peris, D.; Villafafila-Robles, R.; Montesinos-Miracle, D. Review of Flux-Weakening Algorithms to Extend the Speed Range in Electric Vehicle Applications with Permanent Magnet Synchronous Machines. IEEE Access 2023, 11, 22961–22981. [Google Scholar] [CrossRef]
- Hackl, C.M.; Kullick, J.; Eldeeb, H.; Horlbeck, L. Analytical computation of the optimal reference currents for MTPC/MTPA, MTPV and MTPF operation of anisotropic synchronous machines considering stator resistance and mutual inductance. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.10. [Google Scholar]
- Jahns, T.M.; Kliman, G.B.; Neumann, T.W. Interior Permanent-Magnet Synchronous Motors for Adjustable-Speed Drives. IEEE Trans. Ind. Appl. 1986; IA-22, 738–747. [Google Scholar] [CrossRef]
- Morimoto, S.; Sanada, M.; Takeda, Y. Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator. IEEE Trans. Ind. Appl. 1994, 30, 920–926. [Google Scholar] [CrossRef]
- Xia, Z.; Nalakath, S.; Tarvirdilu-Asl, R.; Sun, Y.; Wiseman, J.; Emadi, A. Online Optimal Tracking Method for Interior Permanent Magnet Machines with Improved MTPA and MTPV in Whole Speed and Torque Ranges. IEEE Trans. Power Electron. 2020, 35, 9753–9769. [Google Scholar] [CrossRef]
- Xia, Z.; Filho, S.R.; Xiao, D.; Fang, G.; Sun, Y.; Wiseman, J.; Emadi, A. Computation-Efficient Online Optimal Tracking Method for Permanent Magnet Synchronous Machine Drives for MTPA and Flux-Weakening Operations. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5341–5353. [Google Scholar] [CrossRef]
- Cheng, B.; Tesch, T.R. Torque Feedforward Control Technique for Permanent-Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2010, 57, 969–974. [Google Scholar] [CrossRef]
- Ge, H.; Miao, Y.; Bilgin, B.; Nahid-Mobarakeh, B.; Emadi, A. Speed Range Extended Maximum Torque Per Ampere Control for PM Drives Considering Inverter and Motor Nonlinearities. IEEE Trans. Power Electron. 2017, 32, 7151–7159. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, X.; Wang, J.; Niu, F.; Zhang, J.; Fang, Y.; Wu, L. Improved Flux-Weakening Control of IPMSMs Based on Torque Feedforward Technique. IEEE Trans. Power Electron. 2018, 33, 10970–10978. [Google Scholar] [CrossRef]
- Dianov, A.; Tinazzi, F.; Calligaro, S.; Bolognani, S. Review and Classification of MTPA Control Algorithms for Synchronous Motors. IEEE Trans. Power Electron. 2022, 37, 3990–4007. [Google Scholar] [CrossRef]
- Hu, D.; Alsmadi, Y.; Xu, L. High fidelity nonlinear IPM modeling based on measured stator winding flux linkage. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), 14–18 September 2014; pp. 3199–3205. [Google Scholar]
- Bolognani, S.; Petrella, R.; Prearo, A.; Sgarbossa, L. Automatic Tracking of MTPA Trajectory in IPM Motor Drives Based on AC Current Injection. IEEE Trans. Ind. Appl. 2011, 47, 105–114. [Google Scholar] [CrossRef]
- Kim, S.; Yoon, Y.; Sul, S.; Ide, K. Maximum Torque per Ampere (MTPA) Control of an IPM Machine Based on Signal Injection Considering Inductance Saturation. IEEE Trans. Power Electron. 2013, 28, 488–497. [Google Scholar] [CrossRef]
- Antonello, R.; Carraro, M.; Zigliotto, M. Maximum-Torque-Per-Ampere Operation of Anisotropic Synchronous Permanent-Magnet Motors Based on Extremum Seeking Control. IEEE Trans. Ind. Electron. 2014, 61, 5086–5093. [Google Scholar] [CrossRef]
- Liu, G.; Wang, J.; Zhao, W.; Chen, Q. A Novel MTPA Control Strategy for IPMSM Drives by Space Vector Signal Injection. IEEE Trans. Ind. Electron. 2017, 64, 9243–9252. [Google Scholar] [CrossRef]
- Lai, C.; Feng, G.; Mukherjee, K.; Tjong, J.; Kar, N.C. Maximum Torque Per Ampere Control for IPMSM Using Gradient Descent Algorithm Based on Measured Speed Harmonics. IEEE Trans. Ind. Inform. 2018, 14, 1424–1435. [Google Scholar] [CrossRef]
- Lai, C.; Feng, G.; Tjong, J.; Kar, N.C. Direct Calculation of Maximum-Torque-Per-Ampere Angle for Interior PMSM Control Using Measured Speed Harmonic. IEEE Trans. Power Electron. 2018, 33, 9744–9752. [Google Scholar] [CrossRef]
- Dianov, A.; Kim, Y.-K.; Lee, S.-J.; Lee, S.-T. Robust self-tuning MTPA algorithm for IPMSM drives. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 1355–1360. [Google Scholar]
- Windisch, T.; Hofmann, W. A Novel Approach to MTPA Tracking Control of AC Drives in Vehicle Propulsion Systems. IEEE Trans. Veh. Technol. 2018, 67, 9294–9302. [Google Scholar] [CrossRef]
- Xia, J.; Guo, Y.; Li, Z.; Jatskevich, J.; Zhang, X. Step-Signal-Injection-Based Robust MTPA Operation Strategy for Interior Permanent Magnet Synchronous Machines. IEEE Trans. Energy Convers. 2019, 34, 2052–2061. [Google Scholar] [CrossRef]
- Dianov, A.; Anuchin, A. Adaptive Maximum Torque Per Ampere Control for IPMSM Drives with Load Varying Over Mechanical Revolution. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 10, 3409–3417. [Google Scholar] [CrossRef]
- Kwon, Y.C.; Kim, S.; Sul, S.K. Voltage Feedback Current Control Scheme for Improved Transient Performance of Permanent Magnet Synchronous Machine Drives. IEEE Trans. Ind. Electron. 2012, 59, 3373–3382. [Google Scholar] [CrossRef]
- Jacob, J.; Bottesi, O.; Calligaro, S.; Petrella, R. Design Criteria for Flux-Weakening Control Bandwidth and Voltage Margin in IPMSM Drives Considering Transient Conditions. IEEE Trans. Ind. Appl. 2021, 57, 4884–4900. [Google Scholar] [CrossRef]
- Uddin, M.N.; Chy, M.M.I. Online Parameter-Estimation-Based Speed Control of PM AC Motor Drive in Flux-Weakening Region. IEEE Trans. Ind. Appl. 2008, 44, 1486–1494. [Google Scholar] [CrossRef]
- Wang, H.; Li, C.; Zhang, G.; Geng, Q.; Shi, T. Maximum Torque Per Ampere (MTPA) Control of IPMSM Systems Based on Controller Parameters Self-Modification. IEEE Trans. Veh. Technol. 2020, 69, 2613–2620. [Google Scholar] [CrossRef]
- Hoffmann, S.; Schrott, M.; Huber, T.; Kruse, T. Model-based Methods for the Calibration of Modern Internal Combustion Engines. MTZ Worldw. 2015, 76, 24–29. [Google Scholar] [CrossRef]
- Stumberger, B.; Stumberger, G.; Dolinar, D.; Hamler, A.; Trlep, M. Evaluation of saturation and cross-magnetization effects in interior permanent-magnet synchronous motor. IEEE Trans. Ind. Appl. 2003, 39, 1264–1271. [Google Scholar] [CrossRef]
- Li, S.; Han, D.; Sarlioglu, B. Modeling of Interior Permanent Magnet Machine Considering Saturation, Cross Coupling, Spatial Harmonics, and Temperature Effects. IEEE Trans. Transp. Electrif. 2017, 3, 682–693. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Griffo, A. A High-Fidelity and Computationally Efficient Electrothermally Coupled Model for Interior Permanent-Magnet Machines in Electric Vehicle Traction Applications. IEEE Trans. Transp. Electrif. 2015, 1, 336–347. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Sen, B.; Lazari, P.; Sun, T. A High-Fidelity and Computationally Efficient Model for Interior Permanent-Magnet Machines Considering the Magnetic Saturation, Spatial Harmonics, and Iron Loss Effect. IEEE Trans. Ind. Electron. 2015, 62, 4044–4055. [Google Scholar] [CrossRef]
- Hu, D.; Alsmadi, Y.M.; Xu, L. High-Fidelity Nonlinear IPM Modeling Based on Measured Stator Winding Flux Linkage. IEEE Trans. Ind. Appl. 2015, 51, 3012–3019. [Google Scholar] [CrossRef]
- Scheer, R.; Bergheim, Y.; Heintges, D.; Rahner, N.; Gries, R.; Andert, J. An FPGA-Based Real-Time Spatial Harmonics Model of a PMSM Considering Iron Losses and the Thermal Impact. IEEE Trans. Transp. Electrif. 2022, 8, 1289–1301. [Google Scholar] [CrossRef]
- Miao, Y.; Ge, H.; Preindl, M.; Ye, J.; Cheng, B.; Emadi, A. MTPA Fitting and Torque Estimation Technique Based on a New Flux-Linkage Model for Interior-Permanent-Magnet Synchronous Machines. IEEE Trans. Ind. Appl. 2017, 53, 5451–5460. [Google Scholar] [CrossRef]
- Calculation of Orthogonal Coordinate System DQ-Axis Parameters of Permanent Magnet Synchronous Motor (PMSM) Using Clarke & Park Transform with the Precision Power Analyzer and the Waveform Measuring Instrument’s High-speed Math Function. Available online: https://cdn.tmi.yokogawa.com/1/9729/files/WP_WT5000_dqCalc-01EN_r2.pdf (accessed on 5 December 2023).


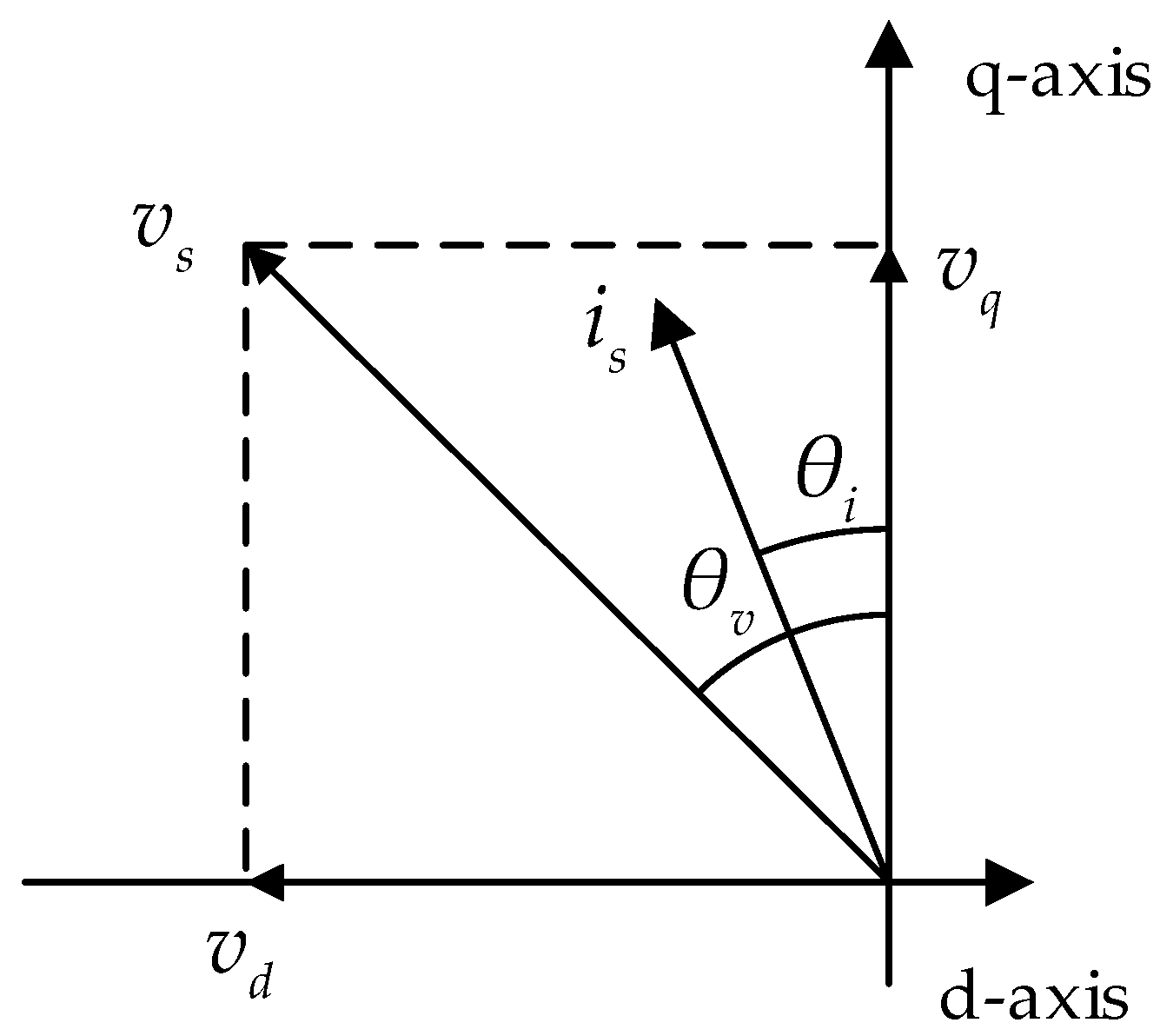
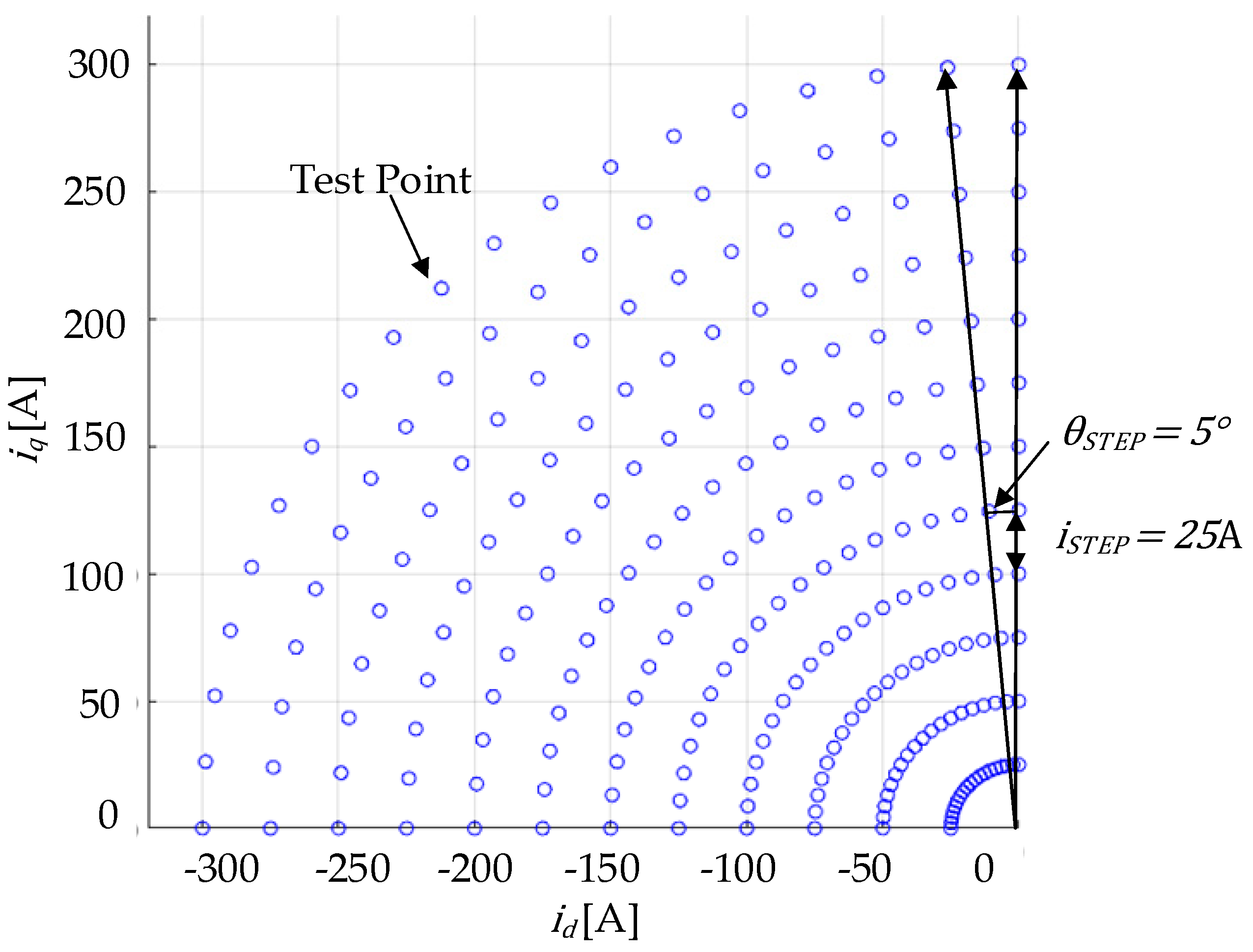
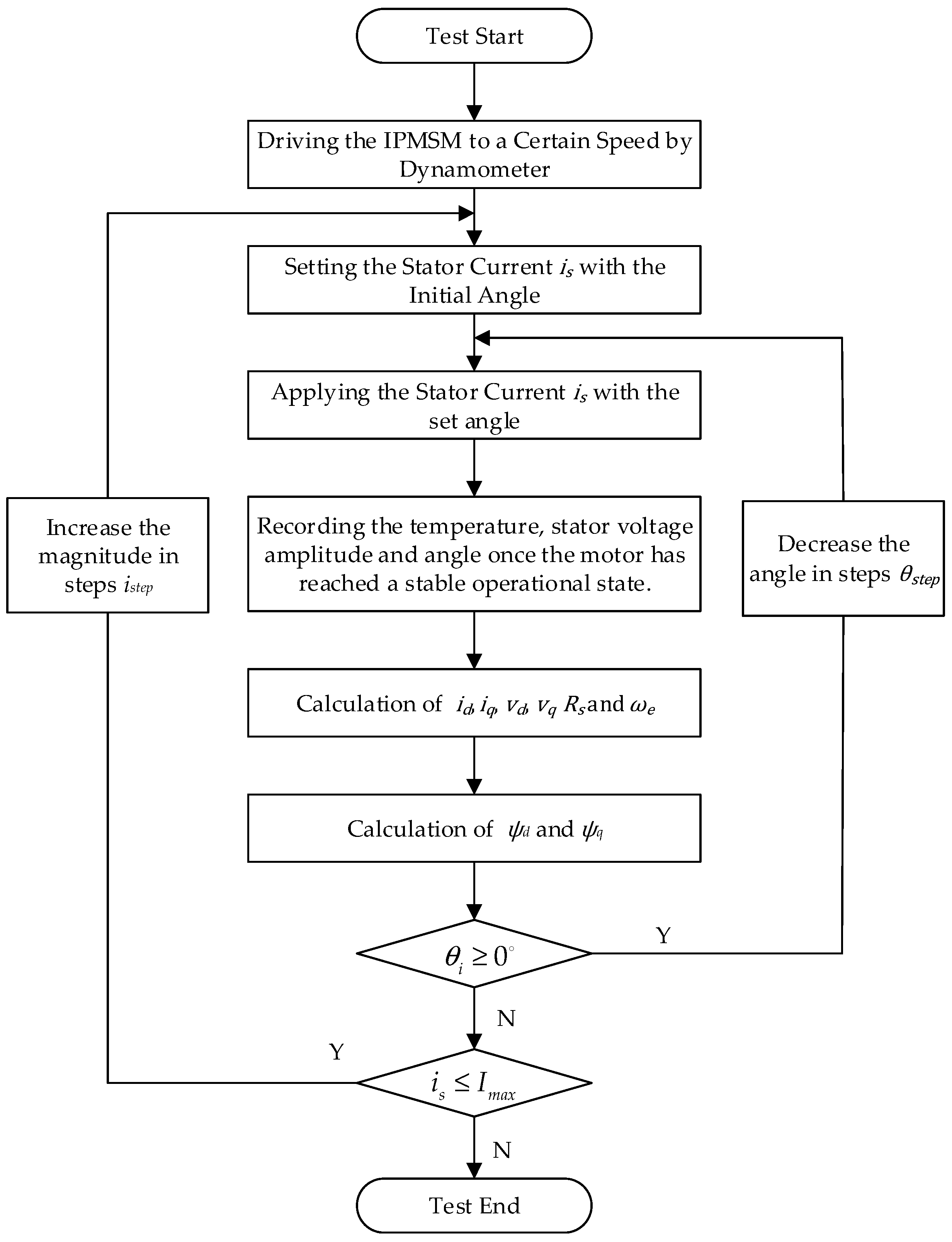
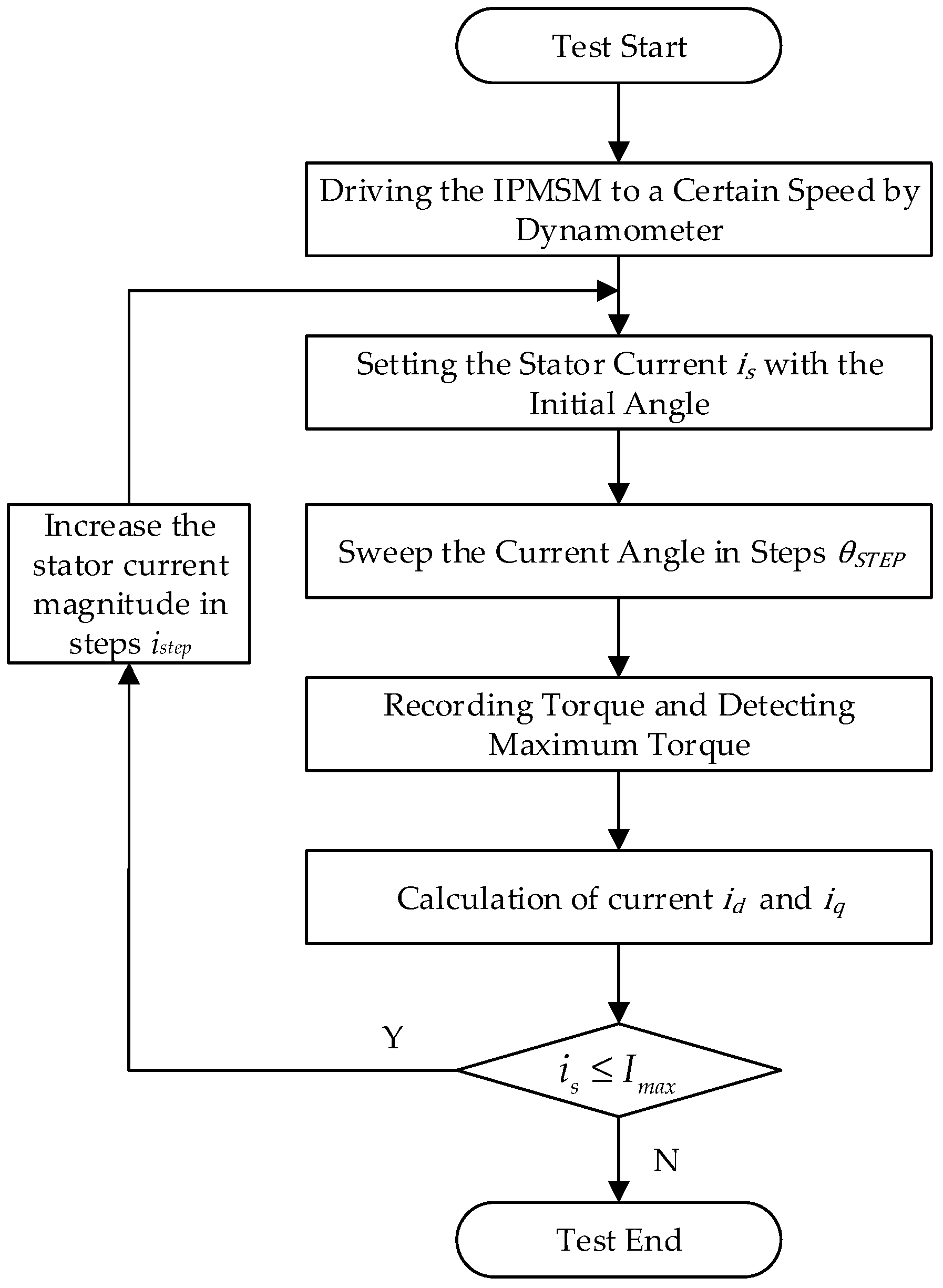

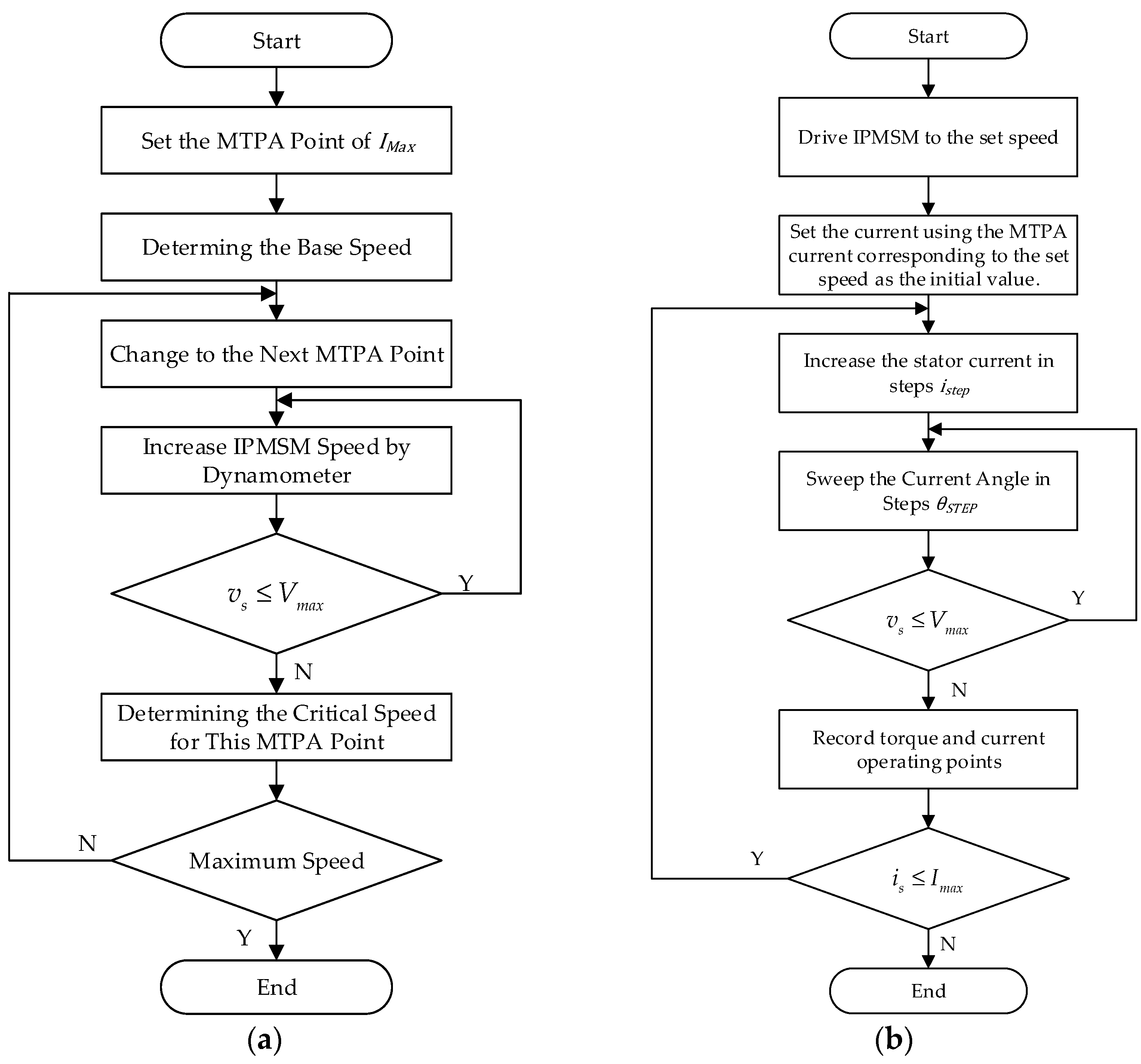
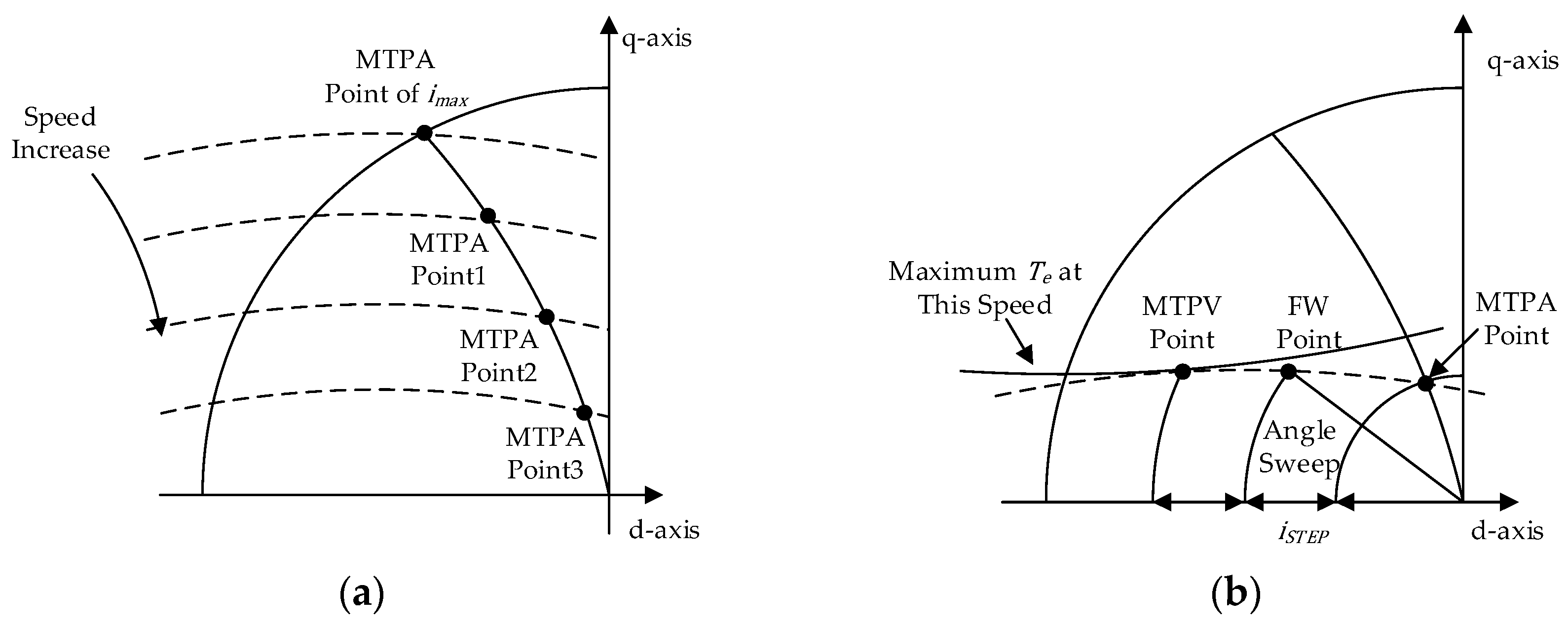
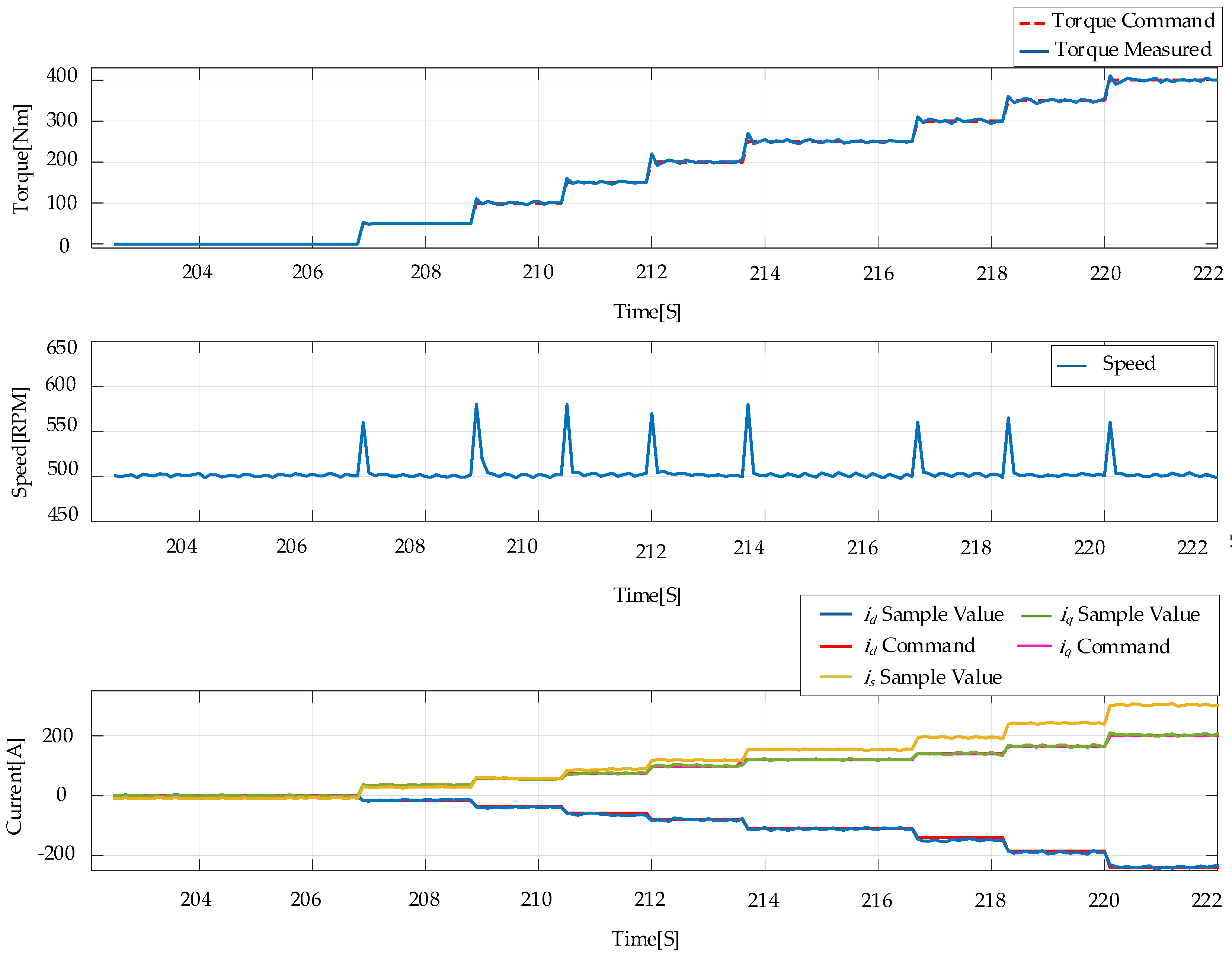
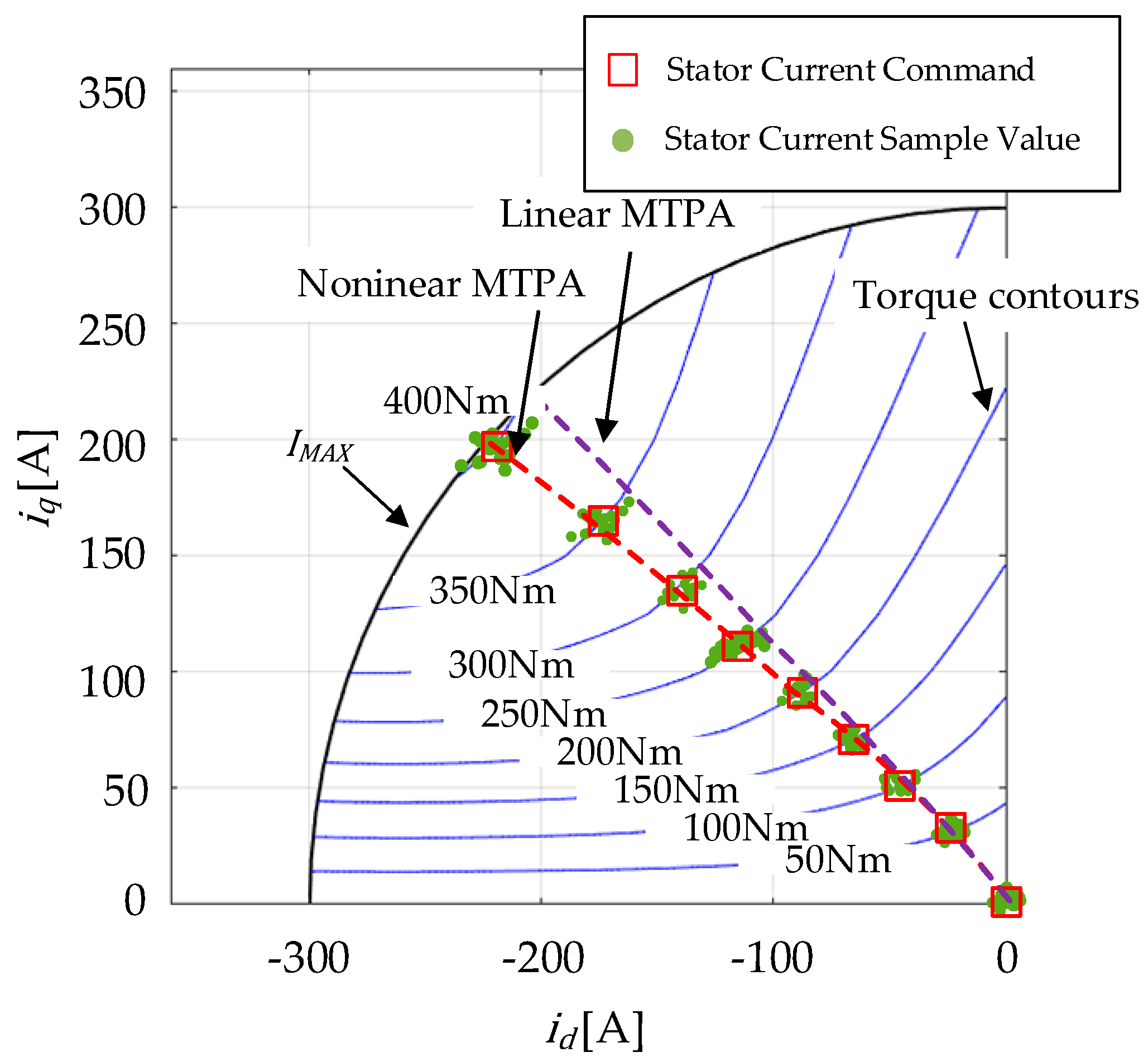

| Parameters | Value |
|---|---|
| Number of pole pairs | 4 |
| Stator winding resistance | 0.058 Ω |
| Permanent-magnet flux-linkage | 0.182 Wb |
| d-axis inductance based on static measurements | 1.9 mH |
| q-axis inductance based on static measurements | 5 mH |
| Rated speed | 1500 RPM |
| Maximum speed | 6000 RPM |
| Rated torque | 400 Nm |
| Rated power | 60 kW |
| DC bus voltage | 500 V |
| Maximum current | 300 A |
| Experimental Equipment | Vendor |
|---|---|
| IPMSM under test | A 60 kW IPMSM with the parameters shown in Table 1 |
| Dynamometer | A 200 kW AC asynchronous motor with a control system developed by Wuxi Langdi Measurement and Control Technology Co., Ltd. (Wuxi, China). |
| Inverter/motor controller | A 100 kW inverter/motor controller developed by VEPCO Technologies Inc. (Los Angeles, CA, USA). |
| DC Power | A 1000 V/600 A battery simulator provided by Shandong Wocen Power Equipment Co., Ltd. (Jinan, China). |
| CAN Communication | CANape, developed by Vector Informatik GmbH (Stuttgart, Germany). |
| Power Analyzer | Yokogawa WT5000 Precision Power Analyzer (Tokyo, Japan) |
| Cooling System | Water-cooling system developed by Wuxi Langdi Measurement and Control Technology Co., Ltd. (Wuxi, China). |
| Torque Sensor | T40B from Hottinger Brüel and Kjaer GmbH (Darmstadt, Germany) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Ma, H.; Zhu, G.; Luo, J. Improved MTPA and MTPV Optimal Criteria Analysis Based on IPMSM Nonlinear Flux-Linkage Model. Energies 2024, 17, 3494. https://doi.org/10.3390/en17143494
Fan Y, Ma H, Zhu G, Luo J. Improved MTPA and MTPV Optimal Criteria Analysis Based on IPMSM Nonlinear Flux-Linkage Model. Energies. 2024; 17(14):3494. https://doi.org/10.3390/en17143494
Chicago/Turabian StyleFan, Yingpeng, Hongtai Ma, Guoqing Zhu, and Jian Luo. 2024. "Improved MTPA and MTPV Optimal Criteria Analysis Based on IPMSM Nonlinear Flux-Linkage Model" Energies 17, no. 14: 3494. https://doi.org/10.3390/en17143494
APA StyleFan, Y., Ma, H., Zhu, G., & Luo, J. (2024). Improved MTPA and MTPV Optimal Criteria Analysis Based on IPMSM Nonlinear Flux-Linkage Model. Energies, 17(14), 3494. https://doi.org/10.3390/en17143494






