Energy Consumption Prediction in Residential Buildings—An Accurate and Interpretable Machine Learning Approach Combining Fuzzy Systems with Evolutionary Optimization
Abstract
1. Introduction
2. Related Work
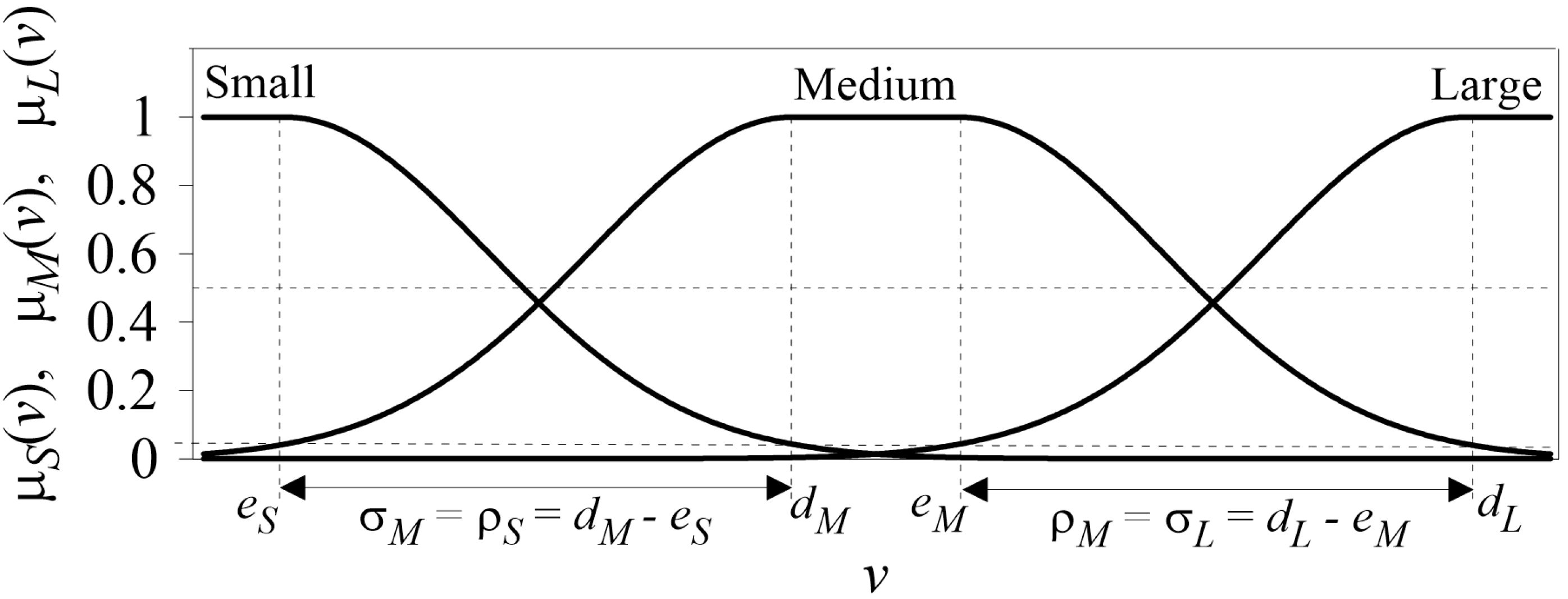
3. Methodology: Designing Fuzzy Rule-Based Prediction Systems (FRBPSs) from Data Using Multi-Objective Evolutionary Optimization Algorithms (MOEOAs)
- (i)
- in (5) represents conditional inclusion of into a considered rule if and only if is fulfilled,
- (ii)
- return the absolute value,
- (iii)
- , , are switch-parameters (set and modified by an MOEOA) that control the presence/absence of the ith input attribute in the rth fuzzy rule. , where is the earlier-defined number of fuzzy sets (and the corresponding linguistic terms) that represent the ith input attribute. are defined as follows:
- -
- for , the ith input attribute is excluded from (not active in) the rth rule,
- -
- for , the component () is included in the rth rule,
- -
- for , the component () is included in the rth rule (not and ; and are membership functions of fuzzy sets and , respectively).
- (i)
- (ii)
- (iii)
4. Energy Consumption Prediction Data Set Considered
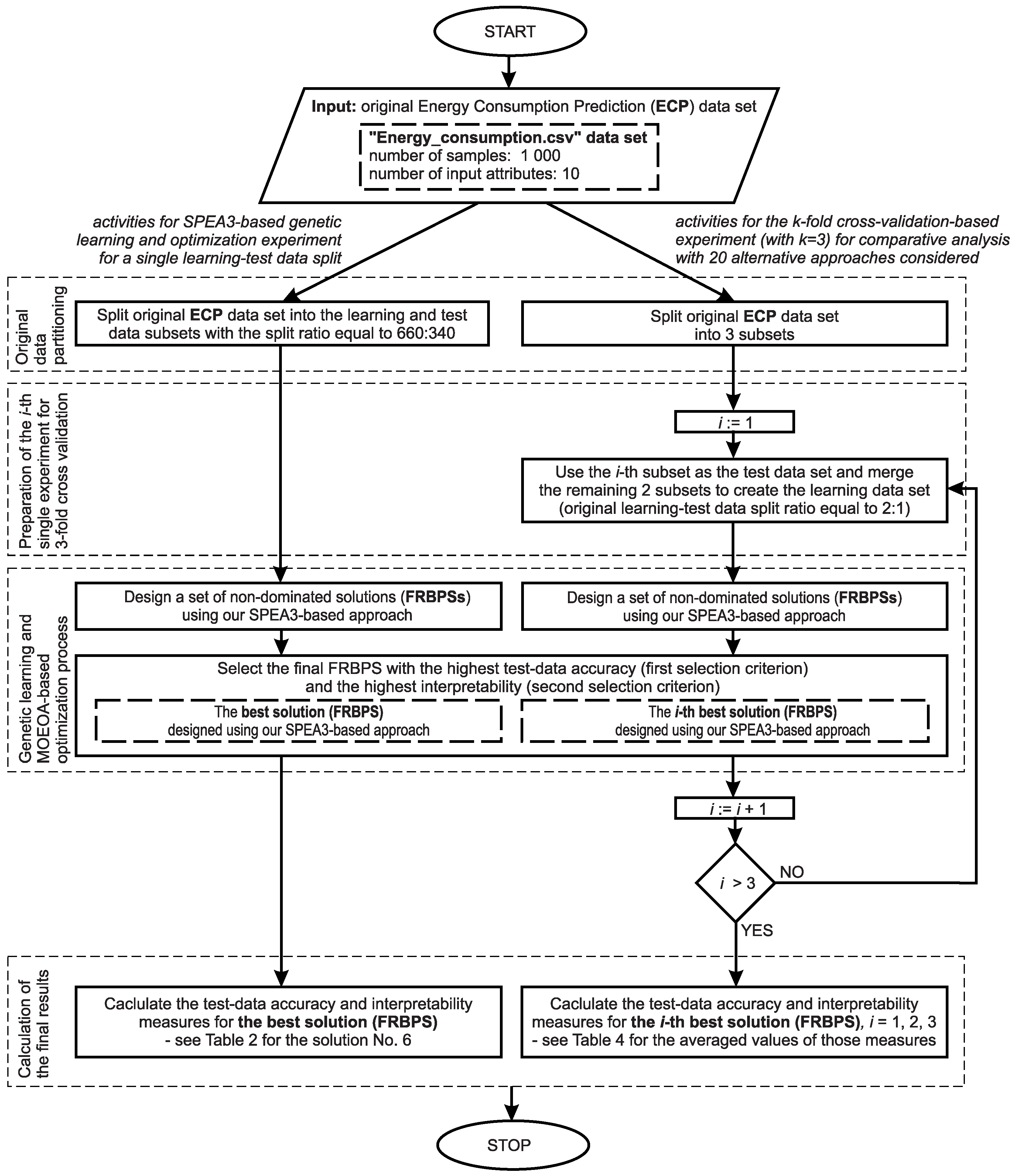
5. Experiments (Application of Our Approach to Prediction of Building Energy Consumption) and Comparative Analysis
- If temperature is small, then energy consumption is slightly smaller than average.
- If temperature increases slightly but the number of occupants is small and if HVAC and lighting systems are turned off, then energy consumption is still slightly smaller than average (as in the case of rule No. 1).
- If the lighting system is turned on but the number of occupants is relatively small, the HVAC system is turned off, and renewable energy sources provide a small amount of energy, then energy consumption is still slightly smaller than average (as in the case of rule No. 1).
- If temperature is still low (as in the case of rule No. 1) but the HVAC system is turned on or the number of occupants is relatively large, then energy consumption increases slightly (in comparison with the case of rule No. 1).
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Seem, J. Using intelligent data analysis to detect abnormal energy consumption in buildings. Energy Build. 2007, 39, 52–58. [Google Scholar] [CrossRef]
- Spertino, F.; Leo, P.D.; Cocina, V. Which are the constraints to the photovoltaic grid-parity in the main European markets? Sol. Energy 2014, 105, 390–400. [Google Scholar] [CrossRef]
- Zhao, P.; Suryanarayanan, S.; Simoes, M. An energy management system for building structures using a multi-agent decision-making control methodology. IEEE Trans. Ind. Appl. 2013, 49, 322–330. [Google Scholar] [CrossRef]
- Candanedo, J.; Dehkordi, V.; Stylianou, M. Model-based predictive control of an ice storage device in a building cooling system. Appl. Energy 2013, 111, 1032–1045. [Google Scholar] [CrossRef]
- MrSimple07. Energy-Consumption-Prediction. 2024. Available online: https://www.kaggle.com/dsv/7436840 (accessed on 15 April 2024).
- Samuel, A.L. Some Studies in Machine Learning Using the Game of Checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- What Is Computational Intelligence? Available online: https://cis.ieee.org/about/what-is-ci (accessed on 15 April 2024).
- Dubois, D.; Prade, H. What are fuzzy rules and how to use them. Fuzzy Sets Syst. 1996, 84, 169–185. [Google Scholar] [CrossRef]
- Fazzolari, M.; Alcala, R.; Nojima, Y.; Ishibuchi, H.; Herrera, F. A review of the application of multiobjective evolutionary fuzzy systems: Current status and further directions. IEEE Trans. Fuzzy Syst. 2013, 21, 45–65. [Google Scholar] [CrossRef]
- Gorzałczany, M.B.; Piekoszewski, J.; Rudziński, F. A Modern Data-Mining Approach Based on Genetically Optimized Fuzzy Systems for Interpretable and Accurate Smart-Grid Stability Prediction. Energies 2020, 13, 2559. [Google Scholar] [CrossRef]
- Khalil, M.; McGough, A.; Pourmirza, Z.; Pazhoohesh, M.; Walker, S. Machine Learning, Deep Learning and Statistical Analysis for forecasting building energy consumption—A systematic review. Eng. Appl. Artif. Intell. 2022, 115, 105287. [Google Scholar]
- Klyuev, R.; Morgoev, I.; Morgoeva, A.; Gavrina, O.; Martyushev, N.; Efremenkov, E.; Mengxu, Q. Methods of Forecasting Electric Energy Consumption: A Literature Review. Energies 2022, 15, 8919. [Google Scholar] [CrossRef]
- Al-Shargabi, A.; Almhafdy, A.; Ibrahim, D.; Alghieth, M.; Chiclana, F. Buildings’ energy consumption prediction models based on buildings’ characteristics: Research trends, taxonomy, and performance measures. J. Build. Eng. 2022, 54, 104577. [Google Scholar] [CrossRef]
- Han-Yun, C.; Ching-Hung, L. Electricity consumption prediction for buildings using multiple adaptive network-based fuzzy inference system models and gray relational analysis. Energy Rep. 2019, 5, 1509–1524. [Google Scholar]
- Zheng, S.; Xu, H.; Mukhtar, A.; Hizam Md Yasir, A.S.; Khalilpoor, N. Estimating residential buildings’ energy usage utilising a combination of Teaching-Learning-Based Optimization (TLBO) method with conventional prediction techniques. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2276347. [Google Scholar] [CrossRef]
- Fayaz, M.; Kim, D. A Prediction Methodology of Energy Consumption Based on Deep Extreme Learning Machine and Comparative Analysis in Residential Buildings. Electronics 2018, 7, 222. [Google Scholar] [CrossRef]
- Nsangou, J.C.; Kenfack, J.; Nzotcha, U.; Salomon, P.; Ekam, N.; Voufo, J.; Tamo, T.T. Explaining household electricity consumption using quantile regression, decision tree and artificial neural network. Energy 2022, 250, 123856. [Google Scholar] [CrossRef]
- Lazzari, F.; Mor, G.; Cipriano, J.; Gabaldon, E.; Grillone, B.; Chemisana, D.; Solsona, F. User behaviour models to forecast electricity consumption of residential customers based on smart metering data. Energy Rep. 2022, 8, 3680–3691. [Google Scholar] [CrossRef]
- Adegoke, M.; Hafiz, A.; Ajayi, S.; Olu-Ajayi, R. Application of Multilayer Extreme Learning Machine for Efficient Building Energy Prediction. Energies 2022, 15, 9512. [Google Scholar] [CrossRef]
- Aliev, R.; Kacprzyk, J.; Pedrycz, W.; Jamshidi, M.; Babanli, M.; Sadikoglu, F. (Eds.) Prediction of Energy Consumption in Residential Buildings Using Type-2 Fuzzy Wavelet Neural Network; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2023; Volume 610. [Google Scholar]
- Chujie, L.; Sihui, L.; Zhengjun, L. Building energy prediction using artificial neural networks: A literature survey. Energy Build. 2022, 262, 111718. [Google Scholar]
- Olu-Ajayi, R.; Alaka, H.; Sulaimon, I.; Sunmola, F.; Ajayi, S. Building energy consumption prediction for residential buildings using deep learning and other machine learning techniques. J. Build. Eng. 2022, 45, 103406. [Google Scholar] [CrossRef]
- Lei, L.; Wei, C.; Bing, W.; Chao, C.; Wei, L. A building energy consumption prediction model based on rough set theory and deep learning algorithms. Energy Build. 2021, 240, 110886. [Google Scholar] [CrossRef]
- Wei, C.; Xiaodong, W.; Chaoen, L.; Jingjing, S.; Jianguo, X. Predicting the energy consumption in buildings using the optimized support vector regression model. Energy 2023, 273, 127188. [Google Scholar]
- Khajavi, H.; Rastgoo, A. Improving the prediction of heating energy consumed at residential buildings using a combination of support vector regression and meta-heuristic algorithms. Energy 2023, 272, 127069. [Google Scholar] [CrossRef]
- Deng, H.; Fannon, D.; Eckelman, M. Predictive modeling for US commercial building energy use: A comparison of existing statistical and machine learning algorithms using CBECS microdata. Energy Build. 2018, 163, 34–43. [Google Scholar] [CrossRef]
- Olu-Ajayi, R.; Alaka, H.; Sulaimon, I.; Sunmola, F.; Ajayi, S. Machine learning for energy performance prediction at the design stage of buildings. Energy Sustain. Dev. 2022, 66, 12–25. [Google Scholar] [CrossRef]
- Pandarasamy, A.; Kameshwar, P.; Clayton, M. BEEM: Data-driven building energy benchmarking for Singapore. Energy Build. 2022, 260, 111869. [Google Scholar]
- Dinmohammadi, F.; Han, Y.; Shafiee, M. Predicting Energy Consumption in Residential Buildings Using Advanced Machine Learning Algorithms. Energies 2023, 16, 3748. [Google Scholar] [CrossRef]
- Anam Nawaz, K.; Naeem, I.; Rashid, A.; Do-Hyeun, K. Ensemble Prediction Approach Based on Learning to Statistical Model for Efficient Building Energy Consumption Management. Symmetry 2021, 13, 405. [Google Scholar] [CrossRef]
- Priyadarshini, I.; Sahu, S.; Kumar, R.; Taniar, D. A machine-learning ensemble model for predicting energy consumption in smart homes. Internet Things 2022, 20, 100636. [Google Scholar] [CrossRef]
- Guimei, W.; Azfarizal, M.; Hossein, M.; Nima, K.; Quynh, T. Application and evaluation of the evolutionary algorithms combined with conventional neural network to determine the building energy consumption of the residential sector. Energy 2024, 298, 131312. [Google Scholar]
- Mohsen, A.; Soofiabadi, M.; Nikpour, M.; Naderi, H.; Abdullah, L.; Arandian, B. Developing a Deep Neural Network with Fuzzy Wavelets and Integrating an Inline PSO to Predict Energy Consumption Patterns in Urban Buildings. Mathematics 2022, 10, 1270. [Google Scholar] [CrossRef]
- Lize, W.; Dong, X.; Lifeng, Z.; Zixuan, Z. Application of the hybrid neural network model for energy consumption prediction of office buildings. J. Build. Eng. 2023, 72, 106503. [Google Scholar]
- Suqin, X.; Yang, L.; Qiuyang, L.; Zhishan, Y.; Somayeh, P. Energy consumption prediction by modified fish migration optimization algorithm: City single-family homes. Appl. Energy 2024, 353, 122065. [Google Scholar]
- Moldovan, D.; Slowik, A. Energy consumption prediction of appliances using machine learning and multi-objective binary grey wolf optimization for feature selection. Appl. Soft Comput. 2021, 111, 107745. [Google Scholar] [CrossRef]
- Seyedzadeh, S.; Rahimian, F.P.; Oliver, S.; Glesk, I.; Kumar, B. Data driven model improved by multi-objective optimisation for prediction of building energy loads. Autom. Constr. 2020, 116, 103188. [Google Scholar] [CrossRef]
- Mystakidis, A.; Koukaras, P.; Tsalikidis, N.; Ioannidis, D.; Tjortjis, C. Energy Forecasting: A Comprehensive Review of Techniques and Technologies. Energies 2024, 17, 1662. [Google Scholar] [CrossRef]
- Cordón, O.; Herrera, F.; Hoffman, F.; Magdalena, L. Genetic Fuzzy Systems: Evolutionary Tuning and Learning of Fuzzy Knowledge Bases; Advances in Fuzzy Systems—Applications and Theory; World Scientific: Singapore, 2001; Volume 19. [Google Scholar]
- Herrera, F. Genetic fuzzy systems: Taxonomy, current research trends and prospects. Evol. Intell. 2008, 1, 27–46. [Google Scholar] [CrossRef]
- Baczyński, M.; Jayaram, B. Fuzzy Implications; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gorzałczany, M.B. Computational Intelligence Systems and Applications: Neuro-Fuzzy and Fuzzy Neural Synergisms; Studies in Fuzziness and Soft Computing; Physica-Verlag: New York, NY, USA, 2002. [Google Scholar]
- Gacto, M.J.; Alcala, R.; Herrera, F. Interpretability of linguistic fuzzy rule-based systems: An overview of interpretability measures. Inf. Sci. 2011, 181, 4340–4360. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm for multi-objective optimization. In Proceedings of the Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems, Barcelona, Spain, 19–21 September 2001; pp. 95–100. [Google Scholar]
- Rudziński, F. Finding sets of non-dominated solutions with high spread and well-balanced distribution using generalized strength Pareto evolutionary algorithm. In Proceedings of the 2015 Conference International Fuzzy Systems Association and Europ. Society for Fuzzy Logic and Technology (IFSA-EUSFLAT-15), Gijón, Spain, 30 June–3 July 2015; José, M.A., Humberto, B., Marek, R., Eds.; Volume 89, pp. 178–185. [Google Scholar]
- Gorzałczany, M.B.; Rudziński, F.; Piekoszewski, J. Business Intelligence in Airline Passenger Satisfaction Study—A Fuzzy-Genetic Approach with Optimized Interpretability-Accuracy Trade-Off. Appl. Sci. 2021, 11, 5098. [Google Scholar] [CrossRef]
- Miller, G. The magical number seven plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81–97. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. Available online: https://scikit-learn.org (accessed on 15 April 2024).
- Arrieta, A.B.; Diaz-Rodriguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; Garcia, S.; Gil-Lopez, S.; Molina, D.; Benjamins, R.; et al. Explainable artificial intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Samek, W.; Montavon, G.; Vedaldi, A.; Hansen, L.; Müller, K.R. (Eds.) Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Lecture Notes in Artificial Intelligence; Springer Nature Switzerland AG: Cham, Switzerland, 2019. [Google Scholar]
- Monar, C. Interpretable Machine Learning. A Guide for Making Black Box Models Explainable. Under the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. 2020, pp. 1–318. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 15 April 2024).
- Escalante, H.J.; Escalera, S.; Guyon, I.; Baró, X.; Güçlütürk, Y.; Güçlü, U.; Gerven, M. (Eds.) Explainable and Interpretable Models in Computer Vision and Machine Learning; The Springer Series on Challenges in Machine Learning; Springer Nature Switzerland AG: Cham, Switzerland, 2018. [Google Scholar]



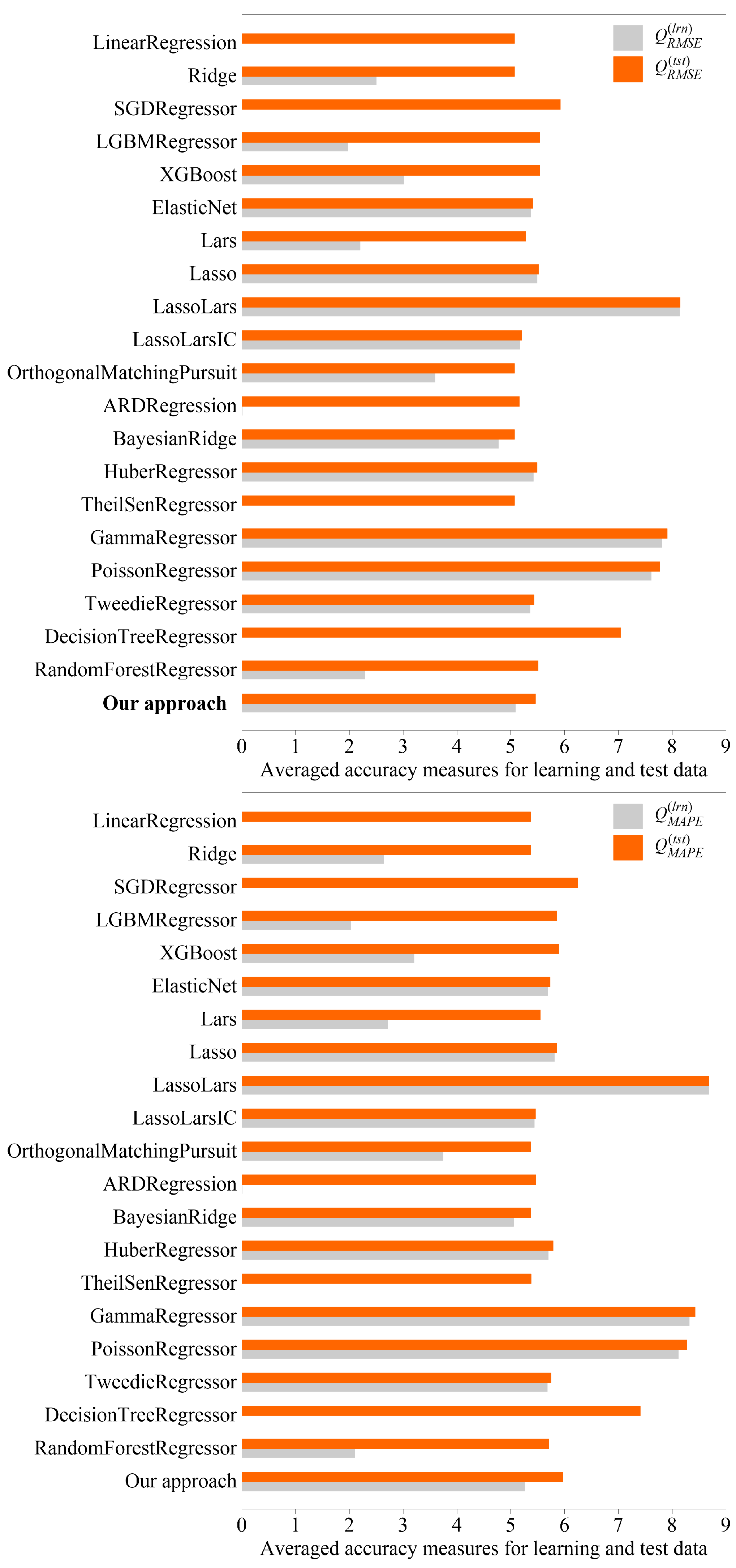

| No. | Attribute Name | Attribute Type | Attribute Domain | Attribute Description | |
|---|---|---|---|---|---|
| 1. | input attributes | Timestamp | date, time | [1 January 2022, 11 February 2022] | The chronological record of each data point, providing a time-based context. |
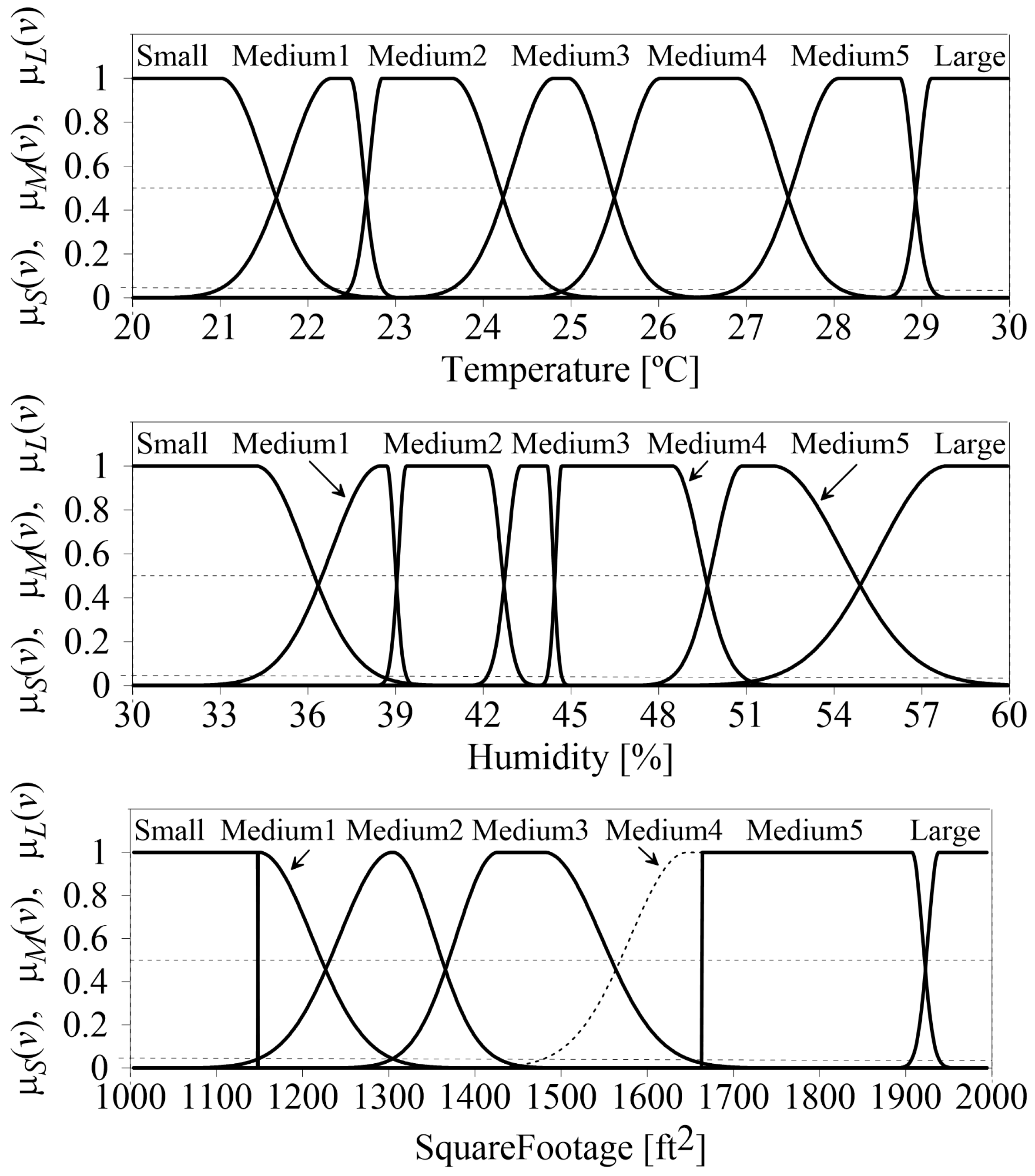
| 2. | Temperature | numerical-real | [20, 30] | Randomly generated values representing ambient temperatures in degrees Celsius. | |
| 3. | Humidity | numerical-real | [30, 60] | Randomly generated values reflecting the humidity level as a percentage. | |
| 4. | SquareFootage | numerical-real | [1000, 2000] | Simulated values representing the size of the environment in square footage. | |
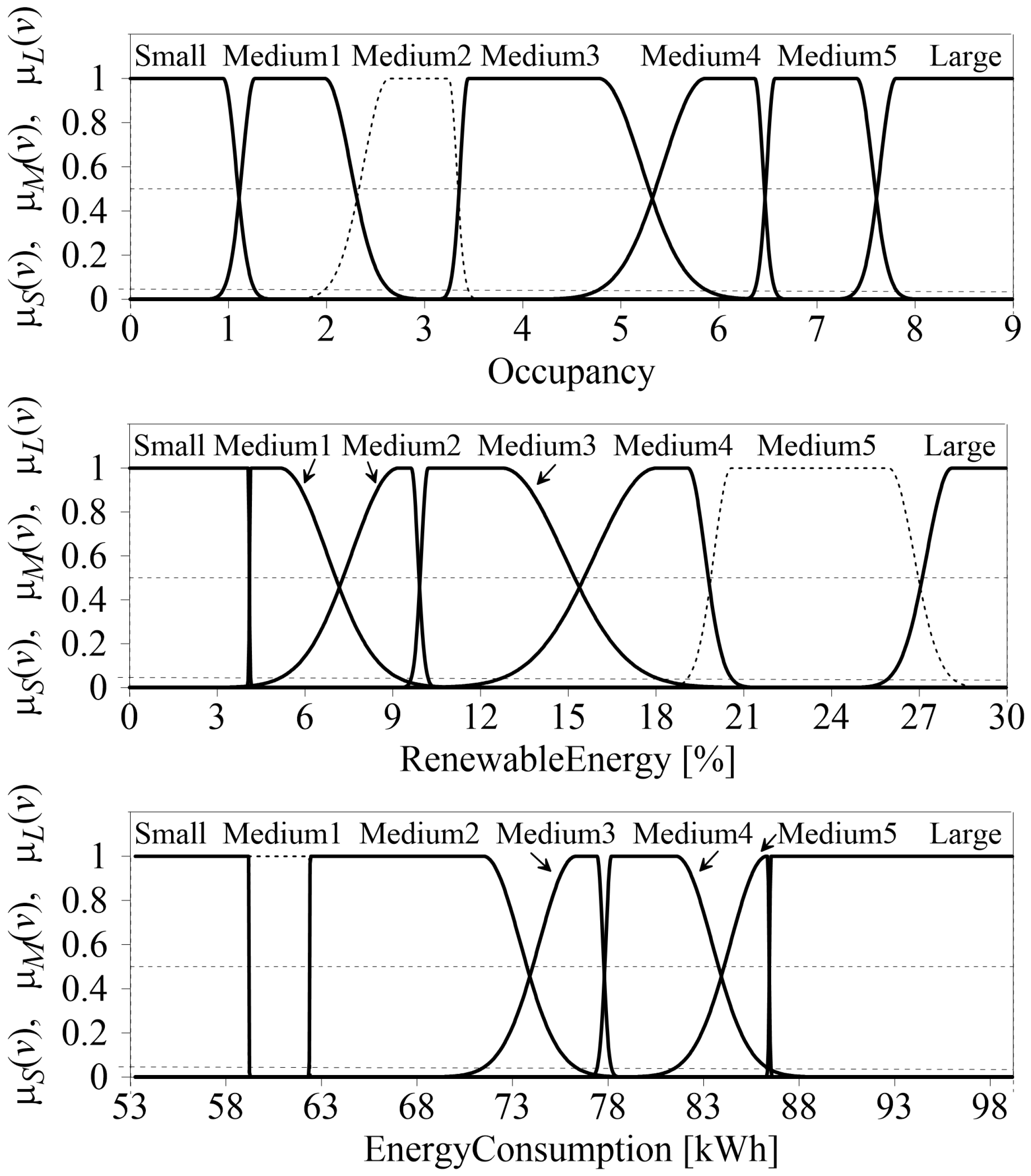
| 5. | Occupancy | numerical-integer | [0, 9] | Randomly generated integer values indicating the number of occupants. | |
| 6. | HVACUsage | categorical | On, Off | Categorical variable denoting the HVAC system’s operational state (‘On’ or ‘Off’). | |
| 7. | LightingUsage | categorical | On, Off | Categorical variable indicating the lighting system’s operational state (‘On’ or ‘Off’). | |
| 8. | RenewableEnergy | numerical-real | [0.01, 30] | Randomly generated values representing the contribution of renewable energy sources as a percentage. | |
| 9. | DayOfWeek | categorical | Monday, …, Sunday | Categorical variable indicating the day of the week. | |
| 10. | Holiday | categorical | Yes, No | Categorical variable denoting whether the day is a holiday (‘Yes’ or ‘No’). | |
| 11. | output attribute | Energy Consumption | numerical-real | [53.2, 99.2] | Output (target) attribute. |
| No. | Objective Function Complements | MAPE-Based Accuracy Measures | Interpretability Measures | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1. | 0.0062 | 5.841 | 5.973 | 6.25% | 6.38% | 1 | 1 | 2 | 1 |
| 2. | 0.0810 | 5.706 | 5.637 | 6.14% | 6.12% | 2 | 2 | 4 | 1.5 |
| 3. | 0.0802 | 5.454 | 5.551 | 5.95% | 6.09% | 3 | 2 | 5 | 1.3 |
| 4. | 0.1219 | 5.269 | 5.498 | 5.50% | 6.06% | 3 | 3 | 5 | 1.3 |
| 5. | 0.2203 | 5.142 | 5.494 | 5.31% | 6.04% | 4 | 4 | 8 | 2.2 |
| 6. | 0.3117 | 5.073 | 5.459 | 5.24% | 5.96% | 5 | 5 | 11 | 3.2 |
| 7. | 0.4021 | 4.956 | 5.520 | 5.19% | 6.02% | 7 | 6 | 16 | 3.4 |
| 8. | 0.4942 | 4.875 | 5.600 | 5.08% | 6.10% | 8 | 7 | 22 | 3.7 |
| 9. | 0.6768 | 4.791 | 5.592 | 4.97% | 6.06% | 10 | 9 | 31 | 4.8 |
| 10. | 0.8498 | 4.624 | 5.718 | 4.84% | 6.14% | 21 | 9 | 49 | 6.3 |
| No. | Fuzzy Prediction Rules | |
|---|---|---|
| Solution No. 1: | ||
| 1. | IF | Temperature is Small THEN EnergyConsumption is Medium2 |
| Solution No. 2: | ||
| 1. | IF | Temperature is Small THEN EnergyConsumption is Medium2 |
| 2. | IF | Temperature is Small AND HVACUsage is On THEN EnergyConsumption is Medium4 |
| Solution No. 3: | ||
| 1. | IF | Temperature is Small THEN EnergyConsumption is Medium2 |
| 2. | IF | Temperature is Small AND HVACUsage is On THEN EnergyConsumption is Medium4 |
| 3. | IF | Temperature is Medium1 THEN EnergyConsumption is Medium2 |
| Solution No. 4: | ||
| 1. | IF | Temperature is Small THEN EnergyConsumption is Medium2 |
| 2. | IF | Temperature is Small AND HVACUsage is On THEN EnergyConsumption is Medium4 |
| 3. | IF | Occupancy is Medium5 THEN EnergyConsumption is Medium4 |
| Solution No. 5: | ||
| 1. | IF | Temperature is Small THEN EnergyConsumption is Medium2 |
| 2. | IF | Temperature is Small AND HVACUsage is On THEN EnergyConsumption is Medium4 |
| 3. | IF | Temperature is Small AND Occupancy is Medium5 THEN EnergyConsumption is Medium4 |
| 4. | IF | Temperature is Medium2 AND Occupancy is Small AND HVACUsage is Off AND LightingUsage is Off THEN EnergyConsumption is Medium2 |
| Solution No. 6: | ||
| 1. | IF | Temperature is Small THEN EnergyConsumption is Medium2 |
| 2. | IF | Temperature is Small AND HVACUsage is On THEN EnergyConsumption is Medium4 |
| 3. | IF | Temperature is Small AND Occupancy is Medium5 THEN EnergyConsumption is Medium4 |
| 4. | IF | Temperature is Medium2 AND Occupancy is Small AND HVACUsage is Off AND LightingUsage is Off THEN EnergyConsumption is Medium2 |
| 5. | IF | Occupancy is Medium1 AND HVACUsage is Off AND LightingUsage is On AND RenewableEnergy is Small THEN EnergyConsumption is Medium2 |
| Solution No. 7: | ||
| 1. | IF | Temperature is Small THEN EnergyConsumption is Medium2 |
| 2. | IF | Temperature is Small AND HVACUsage is On THEN EnergyConsumption is Medium4 |
| 3. | IF | Temperature is Small AND Occupancy is Medium5 THEN EnergyConsumption is Medium4 |
| 4. | IF | Temperature is Medium2 AND Occupancy is Small AND HVACUsage is Off AND LightingUsage is Off THEN EnergyConsumption is Medium2 |
| 5. | IF | Occupancy is Medium1 AND HVACUsage is Off AND LightingUsage is On AND RenewableEnergy is Small THEN EnergyConsumption is Medium2 |
| 6. | IF | Temperature is Small AND Humidity is not Medium5 AND HVACUsage is On AND LightingUsage is On THEN EnergyConsumption is Medium4 |
| 7. | IF | Temperature is Small AND Humidity is Small AND Occupancy is Large AND HVACUsage is On AND RenewableEnergy is Large THEN EnergyConsumption is Large |
| Solution No. 8: | ||
| 1. | IF | Temperature is Small THEN EnergyConsumption is Medium2 |
| 2. | IF | Temperature is Small AND SquareFootage is not Medium2 AND HVACUsage is On THEN EnergyConsumption is Medium4 |
| 3. | IF | Temperature is Small AND Occupancy is Medium5 AND RenewableEnergy is Large THEN EnergyConsumption is Medium4 |
| 4. | IF | Temperature is Medium2 AND SquareFootage is not Large AND Occupancy is Small AND HVACUsage is Off AND LightingUsage is Off AND RenewableEnergy is not Large THEN EnergyConsumption is Medium2 |
| 5. | IF | Occupancy is Medium1 AND HVACUsage is Off AND LightingUsage is On AND RenewableEnergy is Small THEN EnergyConsumption is Medium2 |
| 6. | IF | Temperature is Small AND Humidity is not Medium5 AND HVACUsage is On AND LightingUsage is On THEN EnergyConsumption is Medium4 |
| 7. | IF | Temperature is Small AND Humidity is Small AND Occupancy is Large AND HVACUsage is On AND RenewableEnergy is Large THEN EnergyConsumption is Large |
| 8. | IF | Temperature is Medium1 AND Humidity is Medium1 AND SquareFootage is not Medium5 THEN EnergyConsumption is Medium3 |
| Solution No. 9: | ||
| 1. | IF | Temperature is Small THEN EnergyConsumption is Medium2 |
| 2. | IF | Temperature is Small AND SquareFootage is not Medium2 AND Occupancy is not Medium1 AND HVACUsage is On THEN EnergyConsumption is Medium4 |
| 3. | IF | Temperature is Small AND Occupancy is Medium5 AND RenewableEnergy is Large THEN EnergyConsumption is Medium4 |
| 4. | IF | Temperature is Medium2 AND Humidity is not Medium5 AND SquareFootage is not Large AND Occupancy is Small AND HVACUsage is Off AND LightingUsage is Off AND RenewableEnergy is not Large THEN EnergyConsumption is Medium2 |
| 5. | IF | Occupancy is Medium1 AND HVACUsage is Off AND LightingUsage is On AND RenewableEnergy is Small THEN EnergyConsumption is Medium2 |
| 6. | IF | Temperature is Small AND Humidity is not Medium2 AND SquareFootage is not Small AND LightingUsage is On AND RenewableEnergy is not Medium2 AND DayOfWeek is Friday THEN EnergyConsumption is Medium5 |
| 7. | IF | Temperature is Small AND Humidity is Small AND Occupancy is Large AND HVACUsage is On AND RenewableEnergy is Large THEN EnergyConsumption is Large |
| 8. | IF | Temperature is Medium2 AND Humidity is Medium4 AND HVACUsage is On AND RenewableEnergy is Medium4 AND DayOfWeek is Tuesday AND Holiday is No THEN EnergyConsumption is Medium2 |
| 9. | IF | Temperature is Small AND Humidity is not Small AND SquareFootage is not Small AND Occupancy is not Large AND HVACUsage is Off AND DayOfWeek is Wednesday AND Holiday is No THEN EnergyConsumption is Small |
| 10. | IF | Humidity is Medium3 AND Occupancy is Small AND LightingUsage is Off AND RenewableEnergy is Medium2 AND DayOfWeek is not Friday THEN EnergyConsumption is Medium2 |
| No. | Method | Averaged Accuracy Measures for Learning and Test Data | Averaged Interpretability Measures | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Clasical linear regressors | LinearRegression | 5.5 × 10−12 ± 2.3 × 10−12 | 5.07 ± 0.16 | 5.38 × 10−12 ± 2.9 × 10−12 | 5.37 ± 0.17 | n/ap | 10 | n/ap | n/ap |
| 2. | Ridge | 2.50 ± 0.02 | 5.07 ± 0.16 | 2.64 ± 0.02 | 5.37 ± 0.17 | n/ap | 10 | n/ap | n/ap | |
| 3. | SGDRegressor | 3.6 × 10−4 ± 1.1 × 10−5 | 5.92 ± 0.9 | 3.63 × 10−4 ± 3.5 × 10−6 | 6.25 ± 0.18 | n/ap | 10 | n/ap | n/ap | |
| 4. | LGBMRegressor | 1.97 ± 0.05 | 5.54 ± 0.30 | 2.02 ± 0.06 | 5.86 ± 0.42 | 3046.4 ± 12.8 | 15 ± 0.0 | n/ap | 7.91 ± 0.52 | |
| 5. | XGBoost | 3.01 ± 0.09 | 5.54 ± 0.30 | 3.20 ± 0.11 | 5.89 ± 0.43 | 556.4 ± 19.8 | 15 ± 0.0 | n/ap | 5.87 ± 0.02 | |
| 6. | Regressors with variable selection | ElasticNet | 5.37 ± 0.04 | 5.41 ± 0.15 | 5.69 ± 0.05 | 5.73 ± 0.19 | n/ap | 10 | n/ap | n/ap |
| 7. | Lars | 2.20 ± 0.06 | 5.28 ± 0.21 | 2.71 ± 0.09 | 5.55 ± 0.25 | n/ap | 10 | n/ap | n/ap | |
| 8. | Lasso | 5.49 ± 0.05 | 5.52 ± 0.16 | 5.81 ± 0.06 | 5.85 ± 0.21 | n/ap | 10 | n/ap | n/ap | |
| 9. | LassoLars | 8.14 ± 0.05 | 8.15 ± 0.21 | 8.68 ± 0.06 | 8.69 ± 0.26 | n/ap | 10 | n/ap | n/ap | |
| 10. | LassoLarsIC | 5.17 ± 0.07 | 5.21 ± 0.17 | 5.44 ± 0.08 | 5.46 ± 0.18 | n/ap | 10 | n/ap | n/ap | |
| 11. | Orthogonal-MatchingPursuit | 3.59 ± 0.02 | 5.07 ± 0.17 | 3.74 ± 0.02 | 5.37 ± 0.16 | n/ap | 10 | n/ap | n/ap | |
| 12. | Bayesian regressors | ARDRegression | 9.65 × 10−3 ± 2.8 × 10−3 | 5.16 ± 0.19 | 7.78 × 10−3 ± 3.4 × 10−3 | 5.47 ± 0.20 | n/ap | 10 | n/ap | n/ap |
| 13. | BayesianRidge | 4.77 ± 0.05 | 5.07 ± 0.16 | 5.05 ± 0.05 | 5.37 ± 0.16 | n/ap | 10 | n/ap | n/ap | |
| 14. | Outlier-robust regressors | HuberRegressor | 5.42 ± 0.06 | 5.49 ± 0.25 | 5.70 ± 0.06 | 5.79 ± 0.28 | n/ap | 10 | n/ap | n/ap |
| 15. | TheilSenRegressor | 3.3 × 10−12 ± 1.1 × 10−12 | 5.07 ± 0.17 | 4.01 × 10−12 ± 1.4 × 10−12 | 5.38 ± 0.17 | n/ap | 10 | n/ap | n/ap | |
| 16. | Generalized linear models | GammaRegressor | 7.81 ± 0.64 | 7.91 ± 0.56 | 8.32 ± 0.72 | 8.43 ± 0.51 | n/ap | 10 | n/ap | n/ap |
| 17. | PoissonRegressor | 7.61 ± 1.04 | 7.77 ± 0.81 | 8.12 ± 1.14 | 8.27 ± 0.81 | n/ap | 10 | n/ap | n/ap | |
| 18. | TweedieRegressor | 5.36 ± 0.06 | 5.43 ± 0.13 | 5.68 ± 0.06 | 5.75 ± 0.16 | n/ap | 10 | n/ap | n/ap | |
| 19. | Decision trees and random forests | DecisionTree-Regressor | 0.0 ± 0.0 | 7.04 ± 0.28 | 0.0 ± 0.0 | 7.41 ± 0.37 | 800.0 ± 0.0 | 17.8 ± 0.4 | n/ap | 11.7 ± 0.1 |
| 20. | RandomForest-Regressor | 2.29 ± 0.03 | 5.51 ± 0.28 | 2.10 ± 0.03 | 5.71 ± 0.35 | 505.2 ± 6.4 | 17.9 ± 0.24 | n/ap | 10.9 ± 0.24 | |
| 21. | Our approach | 5.091 ± 0.15 | 5.46 ± 0.21 | 5.26 ± 0.16 | 5.97 ± 0.23 | 5.3 ± 0.6 | 5.6 ± 0.6 | 11.6 ± 0.6 | 3.3 ± 0.06 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorzałczany, M.B.; Rudziński, F. Energy Consumption Prediction in Residential Buildings—An Accurate and Interpretable Machine Learning Approach Combining Fuzzy Systems with Evolutionary Optimization. Energies 2024, 17, 3242. https://doi.org/10.3390/en17133242
Gorzałczany MB, Rudziński F. Energy Consumption Prediction in Residential Buildings—An Accurate and Interpretable Machine Learning Approach Combining Fuzzy Systems with Evolutionary Optimization. Energies. 2024; 17(13):3242. https://doi.org/10.3390/en17133242
Chicago/Turabian StyleGorzałczany, Marian B., and Filip Rudziński. 2024. "Energy Consumption Prediction in Residential Buildings—An Accurate and Interpretable Machine Learning Approach Combining Fuzzy Systems with Evolutionary Optimization" Energies 17, no. 13: 3242. https://doi.org/10.3390/en17133242
APA StyleGorzałczany, M. B., & Rudziński, F. (2024). Energy Consumption Prediction in Residential Buildings—An Accurate and Interpretable Machine Learning Approach Combining Fuzzy Systems with Evolutionary Optimization. Energies, 17(13), 3242. https://doi.org/10.3390/en17133242








