Changes in Gross Nuclear Electricity Production in the European Union

Abstract

Economic development requires a constant supply of energy. The utilization of fossil fuels causes environmental pollution and greenhouse gas emissions. The effects of fossil fuel use have impacted global warming, which may affect the world. The problem of environmental degradation can be decreased by using renewable energy sources and nuclear energy. The role of nuclear energy is increasing. More than 10% of electric energy is now produced from nuclear energy worldwide. However, the share varies by country. For example, in France, it is 70%, in Slovakia, it is 55%, and in Ukraine, it is 53%. Many countries do not have nuclear energy at all. This study aims to investigate the development of gross nuclear electricity production both in the world and in the European Union (EU) in terms of stationarity and prognosis. To achieve the goal of this study, the authors utilized descriptive statistics. The time range included the period 1990–2022. This long time period enabled us to conduct the ADF (Augmented Dickey Fuller) test. According to our analysis, gross nuclear electricity production in the European Union (EU) was stationary. We also evaluated future prognosis using the ARIMA (Autoregressive Moving Average) model. We also used the Vector Autoregressive (VAR) model to evaluate changes within nuclear electricity production. Based on our research, we can conclude that the data were stationary. Finally, we concluded that gross nuclear electricity production in the European Union (EU) will increase in eight countries. In 2022, countries such as Belgium, Bulgaria, Czechia, Spain, France, Hungary, the Netherlands, Romania, Slovenia, Slovakia, and Finland increased their gross nuclear electricity production compared to 1990. Based on the ARIMA model prognosis, the following countries will increase their gross nuclear electricity production in the period 2023–2032: Belgium, Bulgaria, Czechia, Finland, Hungary, the Netherlands, Romania, Slovakia, and Slovenia. Based on the VAR model, we elaborated the prognosis, according to which countries such as France, Romania, Spain, and Sweden will increase their gross nuclear electricity production in the period 2023–2032.

1. Introduction

Nuclear energy is the future of energy and will help reduce carbon emissions, which are the most important problem worldwide. Carbon emissions are responsible for climate change and temperature increases [1]. Nuclear energy can increase the efficiency of energy use worldwide and shrink the environmental footprint of radioactive waste by using new inventions such as fast neutron reactors [2]. However, nuclear energy requires investments in nuclear plants. Generally, nuclear plans can be divided into two kinds: single-modular nuclear plants and multinodular nuclear plants. Single-modular nuclear plants are the most commonly adopted worldwide because of lower costs and less reliance on water resources to cool the reactor [3].

Nuclear energy meets global energy needs worldwide and plays an important role in creating long-term environmental strategies. Economic growth creates energy demand, which can adversely impact the environment, sources of energy, energy consumption, economic growth, nuclear energy consumption, and renewable energy sources [4].

The consumption of nuclear energy has risen in the world, leading to about 437 nuclear power reactors being built worldwide, which produce 378 GW of installed capacity [5]. In 2019, there were 417 nuclear power units worldwide (in 31 countries), with a total capacity of 370 GWE. In 2015, 391 nuclear reactors with 336.5 GWE were in operation [6].

In China, the consumption of nuclear energy increased from 0.4 Mtoe in 1993 to 48.2 Mtoe in 2016. The country is a leader not only in nuclear energy consumption but also in renewable energy acquisition [7]. If fossil fuel consumption in China decreases, the utilization of nuclear and renewable energy sources will increase. Nuclear energy is recommended even after the Fukushima nuclear accidents, proving this country’s high demand for clean and cheap energy sources. Even though China has large coal resources, this country has recommended programs through which to reduce environmental pollution and decrease the use of coal [8].

Nuclear energy has advantages and disadvantages. Generally speaking, nuclear power can be used in electricity production, which carries benefits and risks. It is cheap in the long run and reduces dependence on fossil fuels, but it can be a potential risk for nuclear catastrophes [9]. It can make up the energy deficit and is considered to be cheap and safe. It can be a powerful source of energy, and it is also clean energy. However, it requires more water to cool the reactor and can be risky during earthquakes and wars. There is also a problem with waste after using the nuclear units, and they are also radioactive [10]. The most important problem with nuclear energy pertains to the short supply of uranium and its radioactivity. Moreover, greenhouse gases (GHG) are produced during the nuclear cycle [11]. Nuclear energy plays a key role in energy solutions but may also result in the buildup of nuclear weapons. These weapons are very dangerous for humanity and can degrade the environment for many years. Using nuclear weapons is forbidden. The location of nuclear power plants requires stable water content for cooling the reactors. Nuclear power plants can also cause global catastrophes, such as those in Three Mile Island in the United States (US) in 1979, Chernobyl in 1986 in Ukraine, and Fukushima in 2011 in Japan, the consequences of which are visible today [12].

The development of nuclear energy requires capital for the implementation of nuclear technologies. However, investments pay off because, over a long time, nuclear energy for electricity has significantly lower costs than other sources such as fossil fuels and renewable energy sources [13]. Nuclear power plants (NPPs) are increasing their energy capacity more safely. The security systems are safer, and plants are not unexpectedly shut down. The energy crisis has encouraged governments to invest in NPPs [14]. Some nuclear accidents have been caused by human mistakes, which can be avoided by good training of the staff and training with qualified producers [15,16]. Nuclear power programs should be consistent with the development of human resources, and proper training can reduce the risk of catastrophes [17]. Investment in NPPs should be based on plant computer systems (PCS), which are useful and can calculate the efficiency of the heat supply side and the power conversion side and the state of the reactor, turbines, steam, pumps, and other appliances [18].

The literature on nuclear energy is rich. Khodaverdi [19] prepared a graduate thesis concerning future energy production using a hybrid artificial neural network and ARiMA. Wu et al. [20] elaborated on China’s predicted energy consumption using a novel gray Riccati model. Lee and Tong [21] forecasted energy consumption using the gray model. Gao et al. [22] estimated Chinese CO₂ emissions based on a discrete fractional accumulation gray model. Ma et al. [23] used a new fractional time-delayed gray model with a gray wolf optimizer to forecast the natural gas and coal consumption in China. Ding et al. [24] applied a novel structure-adaptive gray model with adjustable time-power items for nuclear energy consumption forecasting. In the literature, we found a research gap concerning nuclear energy and its prognosis.

The contribution of this study is as follows: First, we discuss strengths, weaknesses, opportunities, and threats to the development of nuclear energy. Second, we use different methods to analyze the changes in nuclear energy development using traditional unit root tests and prepared the ADF test, ARiMA model, and VAR model for the stationarity analysis. This test, when confirmed by the stationarity of the time series, obtains accurate results [25]. Third, we elaborate on the prognosis of gross nuclear electricity production, which can be useful for policymakers and EU governments (Figure 1). The authors of the paper use the vector autoregressive (VAR) model to complete the evaluation of changes that take place in nuclear electricity production. We also describe the negative consequences of nuclear catastrophes.

This study aims to investigate the development of gross nuclear electricity production in the world and in the European Union (EU) in terms of stationarity and prognosis. The following research questions were asked:

• Is nuclear energy developing and is this energy prognostic?
• What are the trends in the development of nuclear energy?

The following hypothesis was elaborated.

Hypothesis 1 (H1).

Nuclear energy has stagnated due to catastrophes in the USA, Ukraine, Japan, and other countries.

1.1. Problems of Nuclear Energy Development in the European Union (EU) Energy Policy

Nuclear power plants are more environmentally friendly compared to fossil fuels. This helps to preserve the integrity of the environment and decrease global warming. What is more, nuclear power plants can produce significant amounts of electricity [26].

Nuclear energy is one of the most promising energies in the world. This source of energy is responsible for carbon emission mitigation. However, the problem with nuclear energy is radioactive waste and the dangers of nuclear accidents [1]. Nuclear energy is derived from the fission of uranium and platinum (transmuted from U-238), and it can replace fossil-fuel-derived energy. This kind of energy can deliver clean, economical, and reliable energy based on uranium deposits [11].

Nuclear energy is capital-intensive and less vulnerable to changes in fuel, coal, and gas prices. Countries acquiring energy from nuclear plants are less dependent on energy deliveries from other countries. Countries that build nuclear power plants are less dependent on the price volatility of different energy sources, which reduces economic risk. However, the most important problems pertaining to nuclear energy development include radioactive waste disposal, operational safety, and other risks [27].

Nuclear energy can cause disasters on a global scale. The first catastrophe was at Three Mile Island in the United States (US) in 1979. The reactor had deteriorated dramatically, and the contamination of radioactive pollutants started the debate regarding the use of nuclear energy not only in America but also around the world [28].

The most dangerous nuclear disaster was the Chernobyl disaster, a nuclear accident that occurred on 26 April 1986, in the No. 4 reactor at the Chernobyl Nuclear Power Plant, near the city of Pripyat [29]. The radioactive catastrophe caused global pollution with radioactive particles. The Swedish government identified a radioactive cloud and notified the global community. Children in schools in Poland were required to drink Lugol’s iodine liquid to help prevent thyroid damage. The thyroid gland attracts iodine and is responsible for the functioning of the entire organism. A huge number of people died because of radioactive particle ingestion, and many people suffered from thyroid problems as a result of this accident. All nuclear power plants in Ukraine and Slovakia were built during the Soviet era. At that time, the construction of nuclear power plants in the Union of Soviet Socialist Republics (USSR) was carried out only for political reasons and was mainly a by-product of the large production of atomic weapons.

Another catastrophe that took place was in Fukushima on 11 March 2011. This dangerous accident was the result of an earthquake, which caused a huge tsunami and damaged power plants. Radioactive pollution was emitted into the environment, including iodine-131, cesium-134, and cesium-137. Radioactive isotopes were released into the Pacific Ocean and into the atmosphere, leading to radiation as far away as North America and Europe. The Fukushima Daiichi Nuclear Power Plant (FDNPP) released large amounts of radioactivity. Additionally, the earthquake created a tsunami, which flooded over 500 km² of land, resulting in destruction and fatalities in the population [30,31]. The International Atomic Energy Agency (IAEA) evaluated the Fukushima accident as very dangerous, in which approximately 8000 people were missing and 15,000 were killed [32,33]. The catastrophe led to many impacts, including protests in many places and other economic, environmental, and political issues [8,34].

Such accidents have had an impact on nuclear policies in many countries. Japan, for example, halted its plans to build more nuclear reactors. Germany announced the shutdown of 17 power reactors. Switzerland decided to phase out its reactors over the next 25 years, and Italy explored excluding nuclear energy [12,35]. Moreover, the International Atomic Energy Agency (IAEA) controls the world’s reactors and is the global auditor of nuclear reactors [26].

Fukushima and other catastrophes have had an impact on countries’ strategies regarding nuclear energy. The first group of countries plans to develop nuclear power (South America, South Asia, the Middle East, and North America). The second group of countries increased security precautions and slowed the development of nuclear plants (Western European Union countries, the United States, China, Canada, and India). The third group maintains their present conditions (Portugal, Spain, and Japan). The fourth group consists of countries reducing their share of nuclear power (Germany and Sweden) [5].

The above-mentioned catastrophes are not the only ones that have taken place. In the USSR, more than 10 nuclear submarines have been involved in accidents. It is worth mentioning that the K-19 submarine has had many accidents with reactors. Moreover, the K-27 submarine has also had several accidents [36].

Another problem with nuclear energy production is nuclear waste. Some of the waste from France was exported to Russia for re-enriching uranium. However, only part of this waste was returned to France and reused.

1.2. Use of Nuclear Power Plants (NPPs) in Countries with a Significant Reliance on Nuclear Energy

Many countries in the European Union depend on nuclear energy. This reliance causes problems with the use of nuclear power plants. Nuclear energy also has its disadvantages. The most important can be catastrophes involving explosions in nuclear power plants. However, the production of nuclear energy and electricity also creates economic, organizational, and environmental problems. Nuclear energy should play an important role in reducing carbon usage and CO₂ emissions. However, taking into account uranium mining, milling, conversion, and enrichment, nuclear energy is not free from emissions or environmentally friendly [37].

Nuclear energy also has its disadvantages. One of them is the lack of flexibility in operation due to thermal cycling constraints. Small modular reactors (SMRs) also have their problems. New reactors should be competitive in the market, enabling constant usage [38]. Modern Generation III nuclear reactors are more flexible in terms of operations and load-following capabilities and have increased capabilities compared to existing reactors (Generations I and II) [39].

In these regions, NPPs often operate in a load-following mode, which leads to several downsides, such as increased fuel costs. It includes unequally distributed resources that cause uncertainty in the market [40]. Increases in fuel costs are the result of logistics, storage, and the reuse of uranium.

Shorter fuel cycles are also a problem in nuclear energy production. This means that the reactors and fuel need to be changed more often, creating more problems regarding waste. The development of nuclear energy depends on shorter fuel cycles and future fuel cycle characteristics. After the Fukushima accident, only a few countries phased out nuclear energy. Most countries generating nuclear energy have decided to further increase production. Fuel cycle choices are important in terms of safety issues regarding nuclear energy. Fuel cycles with fast reactors are performed with homogenous and heterogenous approaches. In open cycles, there is predicted to be pressure on the uranium market at the end of the current century. Unequally distributed resources can cause uncertainty in the market, even higher than uranium cost considerations [40]. This is why suitable fuel cycle infrastructure should be built [40].

The increasing wear of components is also a problem in nuclear electricity and heat production. The production of nuclear energy depends on the supply of water used for cooling the reactor. However, wear problems may occur as the result of vibrations induced by high water flow rates and when tubes impact their guides [41]. Water-cooled reactors use ceramic fuel pellets, which consist of UO₂ and produce heat. The ceramic pellet transfers the nuclear heat to the flowing water coolant and is a barrier containing volatile radioactive fission byproducts [42]. Wear appears because of vibration and heat transfer.

Additionally, a shorter service life is a feature of nuclear electricity and heat production. The issue of a shorter service life is the result of the aging of the installation. Most of the reactors were completed in the 1970s and 1980s and are over 30 years old [42]. As we know, the core of a nuclear reactor is dangerous for the environment because of intense radiation fluxes. Nuclear power plants have great problems pertaining to their steam generators, which are based on tube heat exchangers. Flow-induced vibration (FIV) is the reason for replacing, removing, and repairing the steam generators. Therefore, an important issue in nuclear power plants is the service life of steam generators.

Moreover, higher maintenance expenses appear in the functioning of nuclear power plants. The maintenance cost includes repair costs and labor costs. Such costs are important in running a nuclear factory because not all mechanics can repair the item failure. The costs mainly include planned and corrective costs. They include labor costs (manpower costs), the cost of new parts, and emergency orders for expensive items [43]. Nuclear power reactors have relatively large investment costs and flexible electricity production. The safety requirements are also expensive [44].

However, the most important problems are operational issues at nuclear power plants. Operational issues also exist in nuclear electricity production. The high cost of nuclear power plants enhances the need to look for new solutions. Small modular reactor (SMR) designs are the answer for safer energy. This reactor is easier to operate and does not need as extensive water resources for cooling. Moreover, these reactors reduce capital costs and serve as alternatives to conventional large reactors, suiting different needs. The cost of fabrication depends on the type of fuel assembly chosen for the reactor. Moreover, the costs of enrichment, conversion, and uranium determine the efficiency of nuclear power plants too [45]. Additionally, small nuclear reactors (SNRs) are also offered on the market. They are characterized by lower initial investments and lower expertise in operations. They have more benefits than disadvantages. First of all, such reactors reduce capital costs. SNRs are located close to local residences, so they are cheaper and independent from the electricity grid system. They can also provide heat for local residents [44,46].

Many issues appear in the process of nuclear energy installation and operation and the utilization of waste. To solve these problems, hybrid systems are offered on the market. Hybrid systems are based on thermal energy storage (TES) support as the base load. The process can enhance the NPPs’ operational flexibility and profitability throughout their lifespan.

2. Materials and Methods

2.1. Data Sources

The main sources of information used in this paper were Eurostat and world statistics. These sources of information included yearly data from the period 2005–2021. The main source of data was Eurostat [47].

Table 1. Gross nuclear electricity production (GWH).

Time	Belgium	Bulgaria	Czechia	Germany	Spain	France	Lithuania	Hungary	Netherlands	Romania	Slovenia	Slovakia	Finland	Sweden
1990	42,722.000	14,665.000	12,585.000	152,468.000	54,268.000	314,081.000	17,033.000	13,731.000	3502.000	0.000	4622.000	12,036.000	19,216.000	68,185.000
1991	42,861.000	13,184.000	12,132.000	147,229.000	55,578.000	331,340.000	17,000.000	13,726.000	3329.000	0.000	4952.000	11,689.000	19,511.000	76,761.000
1992	43,456.000	11,552.000	12,250.000	158,804.000	55,782.000	338,445.000	14,638.000	13,964.000	3800.000	0.000	3971.000	11,050.000	19,260.000	63,544.000
1993	41,927.000	13,973.000	12,627.000	153,276.000	56,060.000	368,188.000	12,260.000	13,796.000	3948.000	0.000	3956.000	11,486.000	19,928.000	61,395.000
1994	40,624.000	15,335.000	12,977.000	150,703.000	55,313.000	359,981.000	7706.000	14,049.000	3967.000	0.000	4609.000	12,595.000	19,427.000	73,156.000
1995	41,356.000	17,261.000	12,230.000	153,091.000	55,455.000	377,231.000	11,822.000	14,026.000	4018.000	0.000	4779.000	11,437.000	19,216.000	69,935.000
1996	43,336.000	18,082.000	12,850.000	160,016.000	56,330.000	397,340.000	13,942.000	14,180.000	4160.000	1386.000	4647.000	11,249.000	19,476.000	74,274.000
1997	47,408.000	17,751.000	12,494.000	170,328.000	55,298.000	395,483.000	12,024.000	13,968.000	2408.000	5400.000	5019.000	11,073.000	20,894.000	69,928.000
1998	46,165.000	16,899.000	13,178.000	161,644.000	58,993.000	387,990.000	13,554.000	13,949.000	3814.000	5307.000	5042.000	11,394.000	21,853.000	73,583.000
1999	49,017.000	15,814.000	13,357.000	170,004.000	58,852.000	394,244.000	9862.000	14,096.000	3832.000	5198.000	4696.000	13,117.000	22,974.000	73,188.000
2000	48,157.000	18,178.000	13,590.000	169,606.000	62,206.000	415,162.000	8419.000	14,180.000	3926.000	5456.000	4761.000	16,494.000	22,479.000	57,316.000
2001	46,349.000	19,553.000	14,749.000	171,305.000	63,708.000	421,076.000	11,362.000	14,126.000	3976.000	5446.000	5257.000	17,103.000	22,773.000	72,109.000
2002	47,360.000	20,222.000	18,738.000	164,842.000	63,016.000	436,760.000	14,142.000	13,953.000	3915.000	5513.000	5528.000	17,953.000	22,295.000	68,111.000
2003	47,379.000	17,280.000	25,872.000	165,060.000	61,875.000	441,070.000	15,484.000	11,013.000	4018.000	4906.000	5207.000	17,864.000	22,731.000	67,415.000
2004	47,312.000	16,815.000	26,325.000	167,065.000	63,606.000	448,241.000	15,102.000	11,915.000	3822.000	5548.000	5459.000	17,026.000	22,716.000	77,486.000
2005	47,595.000	18,653.000	24,728.000	163,055.000	57,539.000	451,529.000	10,337.000	13,834.000	3997.000	5555.000	5884.000	17,727.000	23,271.000	72,377.000
2006	46,645.000	19,493.000	26,046.000	167,269.000	60,126.000	450,191.000	8651.000	13,461.000	3469.000	5632.000	5548.000	18,012.000	22,906.000	66,977.000
2007	48,227.000	14,643.000	26,172.000	140,534.000	55,103.000	439,730.000	9833.000	14,677.000	4200.000	7709.000	5695.000	15,334.000	23,423.000	66,969.000
2008	45,568.000	15,765.000	26,551.000	148,495.000	58,973.000	439,447.000	9894.000	14,818.000	4169.000	11,226.000	6273.000	16,703.000	22,958.000	63,889.000
2009	47,222.000	15,256.000	27,208.000	134,932.000	52,761.000	409,736.000	10,852.000	15,426.000	4248.000	11,752.000	5739.000	14,081.000	23,526.000	52,173.000
2010	47,944.000	15,249.000	27,998.000	140,556.000	61,990.000	428,521.000	0.000	15,761.000	3969.000	11,623.000	5657.000	14,574.000	22,800.000	57,828.000
2011	48,234.000	16,314.000	28,283.000	107,971.000	57,718.000	442,387.763	0.000	15,685.000	4141.000	11,747.000	6215.000	15,411.000	23,187.000	60,475.000
2012	40,295.000	15,785.000	30,324.000	99,460.000	61,470.000	425,406.017	0.000	15,793.000	3915.000	11,466.000	5528.000	15,495.000	22,987.000	64,037.000
2013	42,644.000	14,171.000	30,745.000	97,290.000	56,726.000	423,684.671	0.000	15,370.000	2891.000	11,618.000	5300.000	15,720.000	23,606.000	66,457.000
2014	33,703.000	15,867.000	30,325.000	97,129.000	57,305.000	436,479.009	0.000	15,649.000	4091.000	11,676.000	6370.000	15,499.000	23,580.000	64,877.000
2015	26,103.000	15,383.000	26,841.000	91,786.000	57,196.000	437,427.808	0.000	15,834.000	4078.041	11,640.000	5648.000	15,146.000	23,245.000	56,348.000
2016	43,523.000	15,776.000	24,104.000	84,634.000	58,633.000	403,195.482	0.000	16,054.000	3960.278	11,286.000	5715.000	14,774.000	23,203.000	63,101.000
2017	42,226.800	15,545.499	28,339.600	76,324.000	58,039.000	398,359.129	0.000	16,098.000	3402.478	11,508.865	6285.272	15,081.000	22,477.000	65,696.000
2018	28,597.000	16,125.281	29,921.311	76,005.000	55,766.000	412,941.812	0.000	15,733.000	3514.770	11,377.435	5776.439	14,843.000	22,793.000	68,549.000
2019	43,523.600	16,555.288	30,246.209	75,071.000	58,349.000	399,011.587	0.000	16,288.000	3909.748	11,280.167	5821.257	15,282.000	23,870.000	66,130.000
2020	34,434.700	16,625.765	30,043.280	64,382.000	58,299.000	353,832.867	0.000	16,055.000	4087.363	11,466.404	6352.766	15,444.000	23,291.000	49,198.000
2021	50,326.200	16,486.894	30,731.180	69,130.000	56,564.000	379,361.292	0.000	15,990.000	3827.956	11,284.320	5705.951	15,730.000	23,598.000	52,965.000
2022	43,879.000	16,462.000	31,022.000	34,709.000	58,590.000	294,731.000	0.000	15,812.000	4156.000	11,089.000	5606.000	15,920.000	25,336.000	51,944.000

Source: own elaborations based on Eurostat [47].

shows the gross nuclear electricity production. The data are the most important part of the analysis because they enable the conduct of analysis and prognosis. The time scope included the period 1990–2022, a total of 33 years. The long period of analysis was helpful in conducting analysis, tests, and other methods. We obtained data for 14 countries in the European Union. However, the data concerning Lithuania were not complete for the period 1990–2009. The data for Romania included the period 1996–2022. The data proved the changes in gross nuclear electricity production. Some countries, such as Lithuania, discontinued the use of nuclear power, while others, such as Romania, made the decision to begin nuclear production.

Lithuania produced nuclear energy at the Ignalina Nuclear Power Plant, which was finally closed. Unit 1 of the power plant was closed in December 2004 and Unit 2 on 31 December 2009. The decommissioning was expensive, but finally, the European Union (EU) covered the costs of this process [48]. Countries such as Belgium, Bulgaria, Czechia, Spain, Hungary, the Netherlands, Romania, Slovenia, Slovakia, and Finland increased gross nuclear electricity production in 2022 compared to 1990.

2.2. Methods

We used different methods for this study. First, we used a normal unit root test to analyze changes in an individual time series. The use of prognostic models depends on data availability. The factors influencing the choice of prognostic models include [49]:

-

type of data time series;

-

amount of available data;

-

statistic characteristics of the data;

-

prognostic objectives.

There are many unit tests, among which the Dickey-Fuller (DF) and Philips-Perron (PP) tests are mostly used in the evaluation of the normality of analyzed variables [50,51]. The stationarity of time series is an important topic in various fields, including commodity markets, the environment, and climate. The time series should be a stochastic process with stationary oscillations around means [52].

We used different methods to analyze the collected data. First, we conducted the Augmented Dickey-Fuller test (ADF test). The test helped to verify if the gross nuclear electricity production in the European Union is stationary. Stationarity is important in the process of forecasting variables. Stationarity is better because traditional econometric methods are better suited for such a process. Regression can be spurious when the time series are nonstationary [53]. If a variable is not stationary, the first difference must be studied. If the first difference is stationary, the multiple regression technique can be applied [54]. However, some problems may appear when analyzing the panel time series if one is strongly stationary [55].

The data generation process of time series described in the ADF test (Augmented Dickey-Fuller test) xt (t − 1, …, T) can be characterized by a simple first-order autoregressive model (AR(1) process [56]:

xt = u + ρxt − 1 + εt,

(1)

where:

x0 = 0

u is a constant

and {εt} is a sequence of independent normal random variables with zero mean and variance σ2 (i.e., εt ∼ i.i.d(0,σ2)).

Our next step was to elaborate on the Autoregressive Moving Average model (ARiMA model). The ARiMA model belongs to the time series model group and is very useful in verifying data and preparing for prognosis. This is a typical econometric method and is organized in a simple linear way, and the forecast using this model is a function of previous data and random errors [56,57].

The generalized univariate ARIMA model with p, d, and q processes can be described by the following equation [58]:

Yt = μ + α1Yt − 1 + … + αpYt − p − θ1et − 1 − … − θqet − q

(2)

where: Yt is the differenced time series value,

α and θ are unknown parameters and

e are independent, identically distributed error terms with zero mean. The lagged autoregressive (AR) process is symbolized by p and that of a moving average (MA) process is symbolized by q [58].

Our final step was the elaboration of the prognosis. The prognosis can be very useful because it can show future trends in the analyzed data. An analysis of the use of nuclear energy in the future elucidates the reliability and alleviation of degradation issues with this type of energy. However, it is difficult to analyze because of the nonlinearity and uncertainty of the data [24,59]. Forecasting can help the government develop future regulations to shift toward nuclear energy [19].

To improve the analysis, the authors used the vector autoregressive (VAR) model, which is widely used in econometric analysis [60]. VAR models are generally used to analyze uncertainty in the underlying distribution [61]. Other authors have claimed that VAR models are used to analyze the relationship between different variables over time [62]. It is widely believed that there is greater use of VAR models. VAR models are used to summarize data interdependences and test hypotheses [63]. The model analyzes the quantile of distribution [64]. Moreover, VAR models have greater application in risk management and evaluate the performance of risk-takers and regulatory requirements [65]. The application of VAR models is mainly in financial market risk, such as time-varying distributions of portfolio returns [66]. Additionally, this model is widely used in forecasting by bank companies to examine statistical accuracy [67]. In addition, VAR models are a function of volatility forecasts [68]. VAR models are used as a standard criterion for assessing risk in the financial industry [69].

The classic form of the vector-autoregressive model is as follows:

$$\mathrm{Z}\mathrm{t}={\sum }_{\mathrm{i}=1}^{\mathrm{k}}\mathrm{A}\mathrm{i} \mathrm{Z}\mathrm{t}-1+\mathsf{\epsilon }\mathrm{t}, \mathrm{t}=\mathrm{1,2},\dots \mathrm{n}$$

(3)

where:

Zt—vector of observations of the current values of all n model variables;

Ai—matrix of autoregressive operators of individual processes in which no zero elements are assumed a priori;

εt—vector of residual processes for which it is assumed that individual components are simultaneously correlated with each other, but do not contain autocorrelation;

k—order of the VAR model.

VAR models have big applications and are widely used to analyze time-series research. They are also used in the process of examining the dynamic relationships that exist between variables that interact with one another. Such models are also used in forecasting processes. They have wide applications in the economic sciences, policy-making, social sciences, agricultural sciences, and technical sciences too.

3. Results

3.1. Nuclear Energy Production in the World

Nuclear energy is clean and environmentally friendly, but it can also be dangerous if accidents occur. Electricity is critical for delivering products and services to consumers and improving standards of living, education, and health. Electric power stations are transforming, and more and more electricity is derived from renewable energy sources and nuclear power stations than from fossil fuels. These changes are the effects of decarbonization. Nuclear energy plays an important role in the production of electricity because it reduces pollution, improves fuel diversification, and has a positive impact on the whole economy. Moreover, the development of this sector, which creates electricity from nuclear energy, creates new jobs [70]. Each country in the world has its own conditions that have an impact on the use of nuclear energy for electricity generation [71]. Nuclear energy is most popular in medium- to highly-developed countries with a high demand for electricity [6].

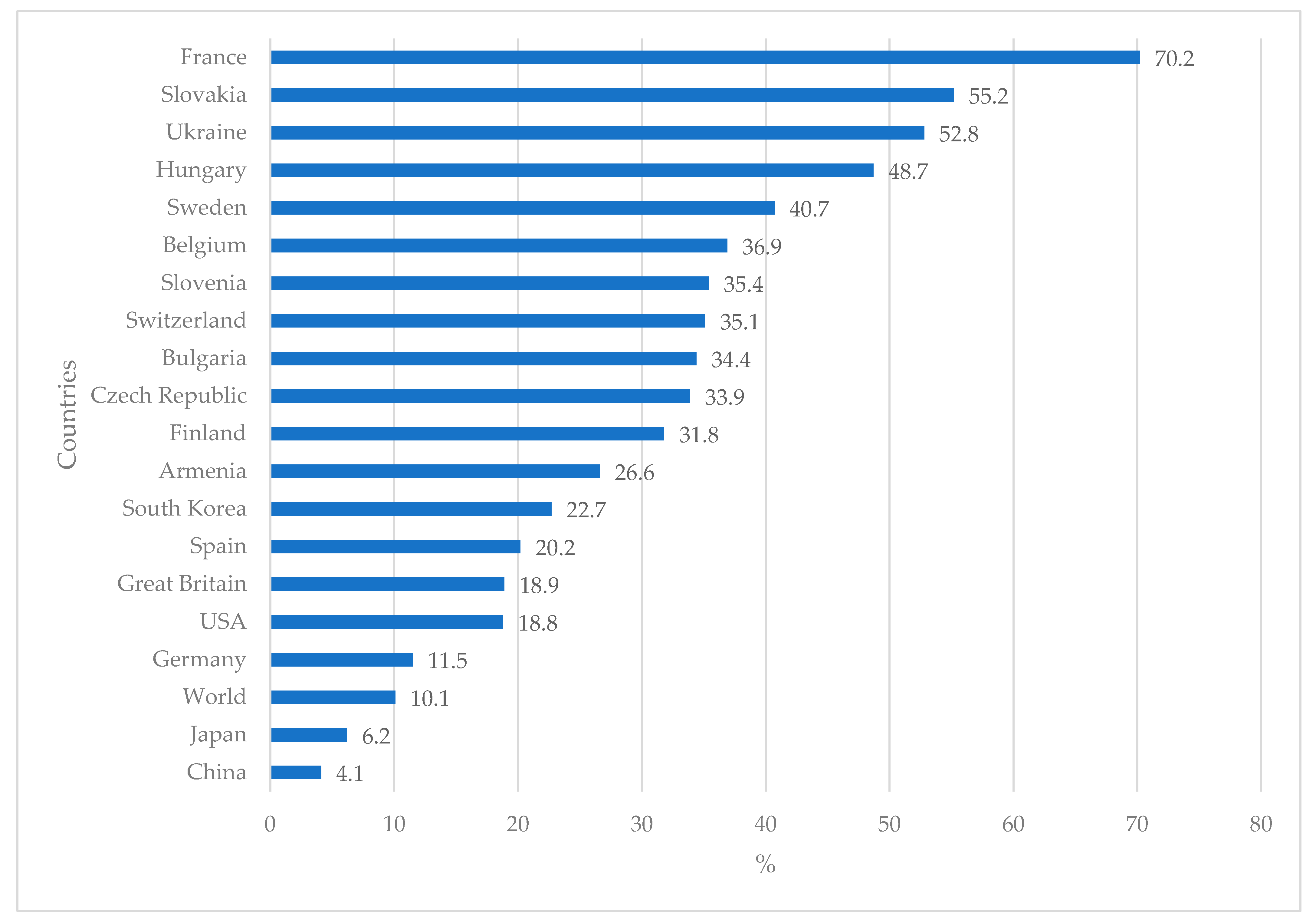
Nuclear power is important and accounts for about 16% of the world’s electricity supply [72]. The share of nuclear energy in electricity production is diversified regionally. France (70.2%), Slovakia (55.2%), Ukraine (52.8%), Hungary (48.7%), and Sweden (40.7%) are countries with the highest share of nuclear energy in electricity production (Figure 2). The data demonstrate the importance of this kind of energy. This energy will undoubtedly be a significant part of the total energy in the future for various reasons, such as availability, decreased greenhouse gas emissions, and other characteristics [72]. The production of nuclear energy is complicated and includes processes such as uranium mining, the production of heat and electricity, cooling the reactor, and, finally, waste disposal. The controversial production leads to the high production of heat and electricity and is safer for the environment compared to fossil fuels [73].

The world’s production of electricity from nuclear plants is stable. The consumption of electricity plays an important role in economic growth. The relationship between electricity and energy consumption has been analyzed. Higher economic development requires higher consumption of electricity [75]. The production of electricity and energy affects human well-being and is important for sustainability and development [71]. The production of electricity from nuclear energy in the future will likely grow because this energy is clean and environmentally friendly. There are no emissions as with fossil fuels, and nuclear energy is cheaper than fossil fuels [76].

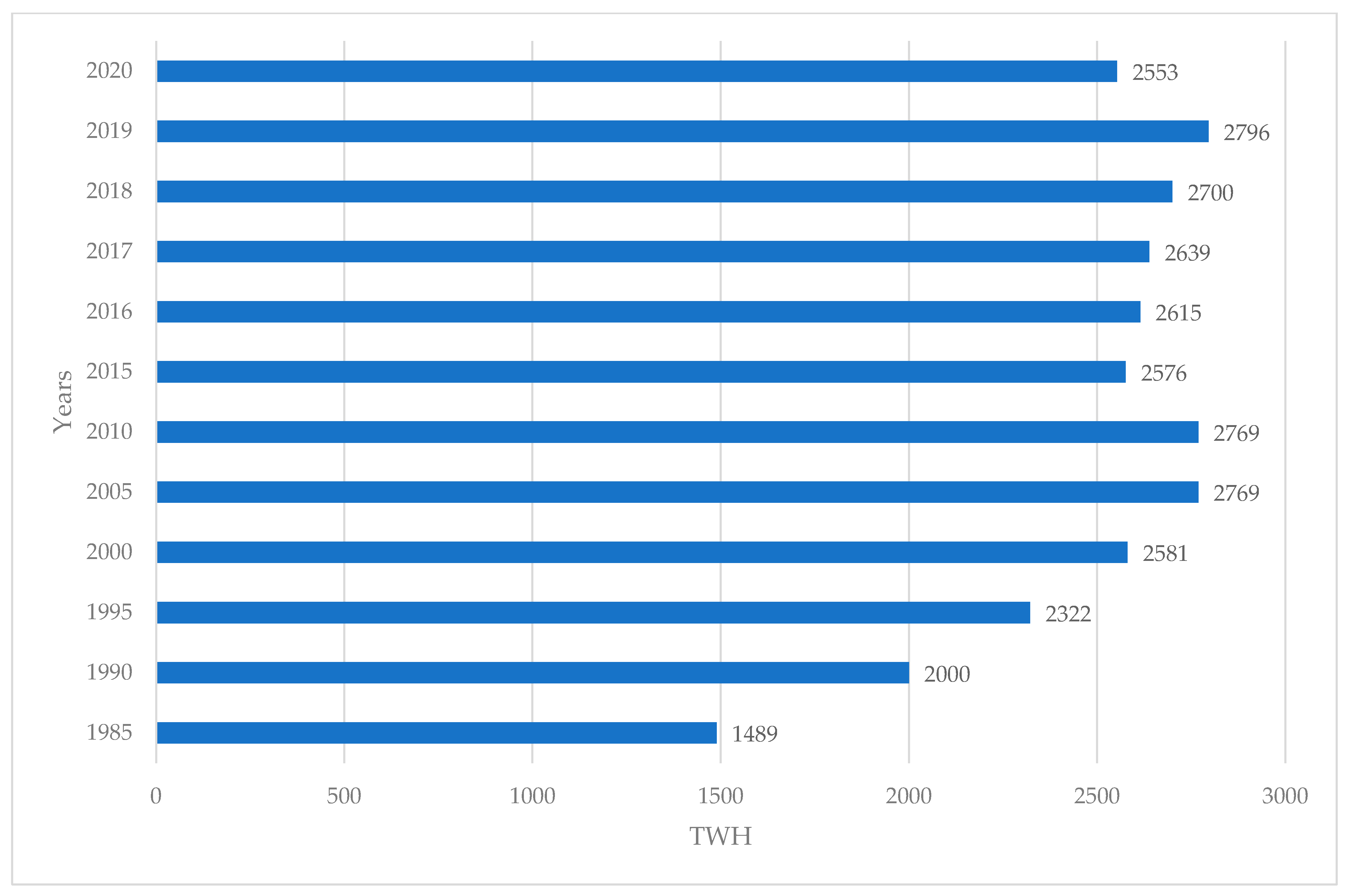
The production of nuclear energy requires a constant supply of technology and its development. Nuclear energy is a key technical challenge, particularly for countries that do not have such technology [77]. According to the data presented in Figure 3, the world’s production of electricity in nuclear plants in 2020 was 2553 TWH. It had decreased compared to 2019 by 9.5%. This decrease may be the result of the COVID-19 pandemic, which decreased the demand for electricity, particularly in factories.

The production of nuclear energy has an impact on the development of each country. It has been proven in the literature that countries producing nuclear energy have a Gross Domestic Product (GDP) per capita increase. Moreover, nuclear countries recorded an increase in the production and use of renewable energy sources. Countries producing nuclear energy use more energy than others and import resources [71]. In 2019, nuclear power plants produced 2796 TWH of electricity. Countries such as the USA, France, China, and Russia together produce over 65% of the total amount of electricity generated in nuclear power plants [6].

The USA is the biggest producer of nuclear energy. The most important feature of the US nuclear market is its complexity. The US has the longest history of nuclear energy, and the market is mature and efficient. The technology is new, and the US is exporting it worldwide [78].

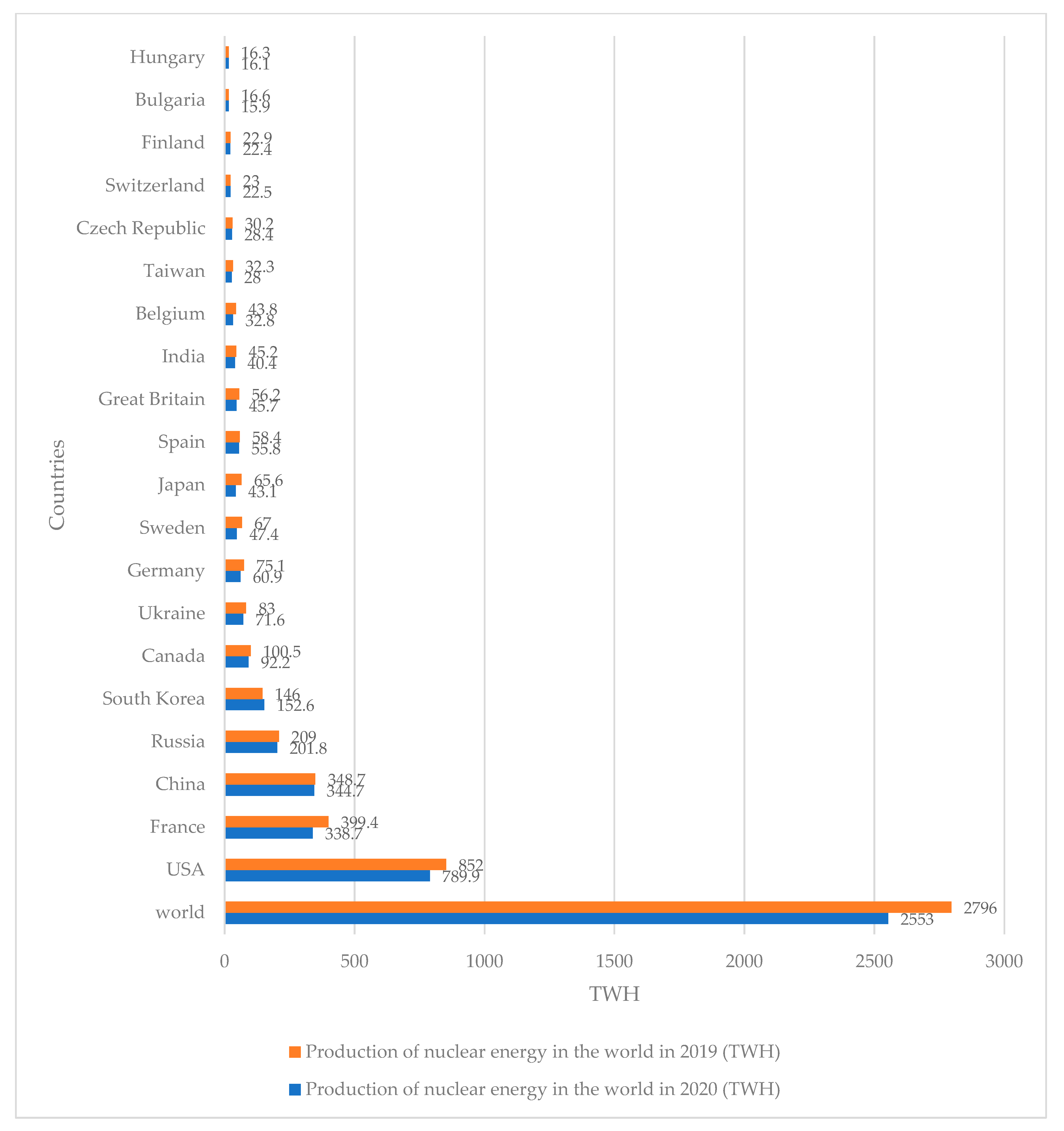
The production of nuclear energy decreased in 2020 compared to 2019. As we can see from Figure 4, the decrease was noted in most countries. Only South Korea increased the production of nuclear energy in 2020 compared to 2019. The biggest producer was undoubtedly the USA. It accounts for more than 30% of the worldwide nuclear generation of electricity [79]. The US generates about 98 GWe from 103 reactors, representing 20% of electricity, whereas world production is 370 GW of electricity from 436 nuclear power reactors [80].

The European Union is a big producer of nuclear energy. However, the biggest producer of nuclear energy in the EU is France. Since Great Britain left the European Union, France has been the leader in nuclear energy production and consumption. Nuclear power plants such as Nord, Paluel, and Cattenom are the biggest French plants. These power plants have a capacity of more than 5200 MN each [81]. Germany, Sweden, Spain, and Belgium are also big producers of nuclear energy in the European Union (EU). However, countries in the European Union have different strategies concerning nuclear energy. Some want to increase nuclear power production, and others, such as Germany and Belgium, wish to phase out nuclear power in the future, as they consider it very dangerous [82]. There are 46 power units under construction in over 15 countries worldwide, most of them in China and India. Countries planning to increase the production of electricity should take into account the high costs of production. The high costs of building a nuclear power plant include a large amount of water for cooling the reactor, the protection of the environment against radiation, and the disposal of unprotected radioactive waste [6]. 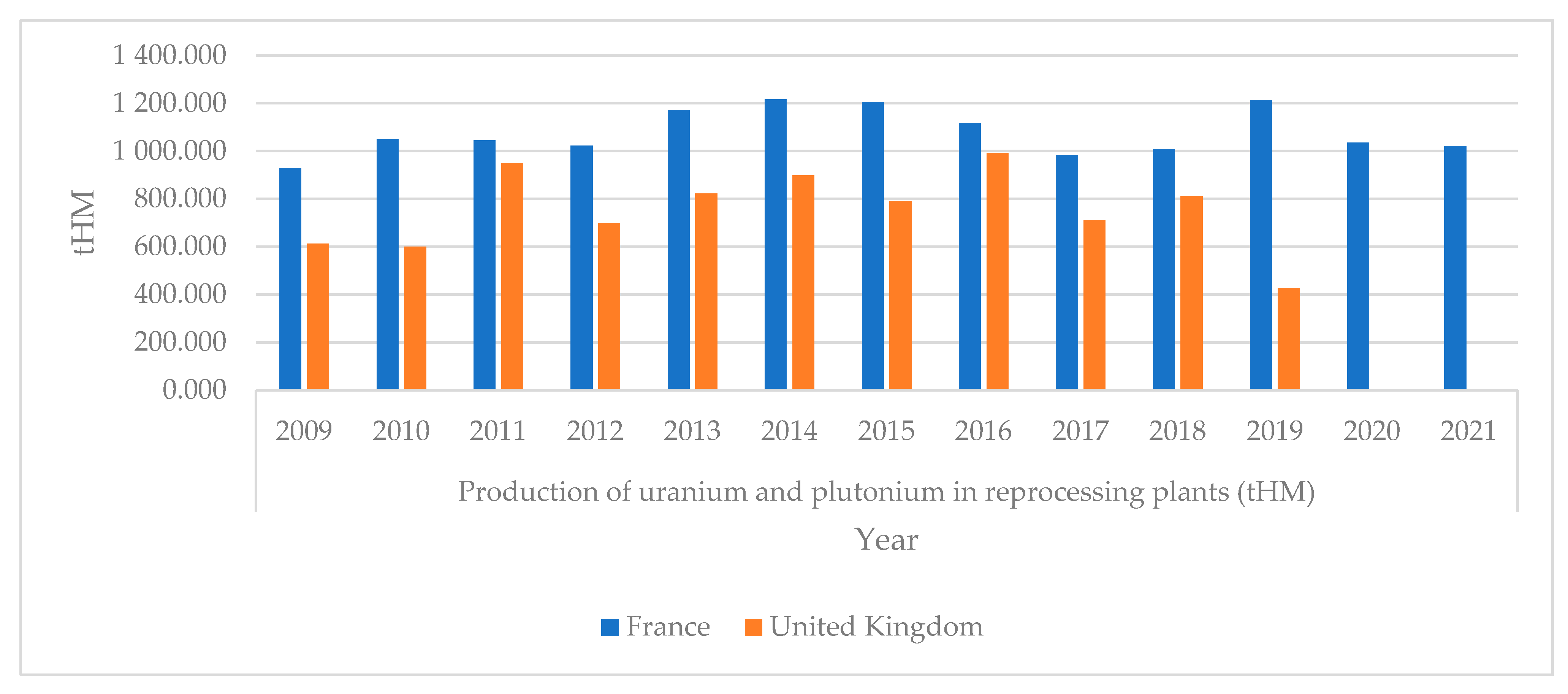Low greenhouse gas emissions put nuclear energy in the position of modern electricity technology [83]. The main chemical elements for nuclear energy production are uranium and plutonium. France is the biggest producer of uranium and plutonium in Europe, and production was 1,021,100 tons of heavy metal (tHM) (Figure 5).

Nuclear fuels consist of uranium and thorium. From 1 kg of uranium, 235 times as much energy is obtained as in thermal power plants from 2500 tons of coal or 1800 tons of petroleum products [6]. Processes pertaining to the extraction and conversion of uranium ore are long. They also need energy that can also emit greenhouse gases (GHG) that are attributed to nuclear power [84].

3.2. Gross Nuclear Electricity Production in the European Union (EU)

The European Union is also a big and meaningful producer of nuclear energy. In some countries, nuclear energy production is the main source of energy, such as France, Slovakia, Ukraine, and Hungary.

To analyze the changes in gross nuclear electricity production, we conducted descriptive statistics (

Table 2. Discriptive statistics of gross nuclear electricity production in the period 1990–2021 (in GWH—gigawatt-hour).

Variable	Average	Mediana	Minimal	Maximal	Std. Dev.	Coefficient of Variation	Skewedness	Kurtosis
Belgium	43,519.0	43,879.0	26,103.0	50,326.0	5632.1	0.12942	−1.6115	2.2635
Bulgaria	16,264.0	16,125.0	11,552.0	20,222.0	1825.5	0.11224	−0.021593	0.43123
Czechia	22,290.0	26,046.0	12,132.0	31,022.0	7578.7	0.34000	−0.33589	−1.6618
Germany	12,9820	148,505	34,709.0	171,305	40,085.	0.30876	−0.71676	−0.85680
Spain	58,106.0	57,718.0	52,761.0	63,708.0	2827.4	0.048659	0.46032	−0.59718
France	401,590	409,740	294,731	451,529	41,060.0	0.10224	−0.90247	0.075409
Lithuania	7391.4	9833.0	0.0000	17,033.0	6426.8	0.86949	−0.095011	−1.6040
Hungary	14,637.0	14,180.0	11,013.0	16,288.0	1238.7	0.084631	−0.79520	0.66812
Netherlands	3832.2	3948.0	2408.0	4248.0	388.5	0.10137	−2.0062	4.2820
Romania	7124.1	5632.0	0.0000	11,752.0	4513.4	0.63354	−0.40511	−1.2875
Slovenia	5382.6	5528.0	3956.0	6370.0	636.92	0.11833	−0.44234	−0.36316
Slovakia	14,677.0	15,282.0	11,050.0	18,012.0	2235.7	0.15233	−0.32217	−1.0763
Finland	22,267.0	22,800.0	19,216.0	25,336.0	1647.0	0.073965	−0.81569	−0.43058
Sweden	65,345.0	66,457.0	49,198.0	77,486.0	7380.9	0.11295	−0.49045	−0.48700

Source: own elaborations based on Eurostat [47].

). The highest average gross nuclear electricity production in the period 1990–2021 was achieved by France (401,590 GWH), Germany (129,820 GWH), and Sweden (65,345 GWH). The smallest gross nuclear electricity production was in the Netherlands (3832.2 GWH), Slovenia (5382.6 GWH), and Romania (7124.1 GWH).

The coefficient of variation describes the changes in the analyzed variables, and the highest was noted in Lithuania (0.86949) and Romania (0.63354). This informs the changes. For example, Romania started with zero production in 1990 and ended with a production of 11,752 GWH. Lithuania, for example, started with a production of 17,033 GWH and ended with zero production.

Skewedness and kurtosis describe the changes in variables. In terms of skewedness, in most cases, the data were negative, so the data were left-handed compared to the average. Kurtosis was positive in the following examples: Belgium, Bulgaria, Hungary, and the Netherlands. The data are right-handed.

3.3. Stationarity Analysis of the Gross Nuclear Electricity Production in the EU

The energy time series analysis is based on its stationarity or nonstationarity analysis, linerality and nonlinerality, complexity, and seasonality analysis. The nature and pattern characteristics of time series concerning nuclear energy market development can be used to explore perspectives [85].

In

Table 3. ADF test for gross nuclear electricity production.

Countries	Free Expression Test				Test with Intercept and Linear Trend				First Differences for Free Expression Test				First Differences for Test with Intercept and Linear Trend
	Estimated Value (a − 1)	Test Stat: tau_ct(1)	Asymptomatic p-Value	Autocorrelation of First-Order Residuals	Estimated Value (a − 1)	Test Stat: tau_ct(1)	Asymptomatic p-Value	Autocorrelation of First-Order Residuals	Estimated Value (a − 1)	Test Stat: tau_ct(1)	Asymptomatic p-Value	Autocorrelation of First-Order Residuals	Estimated Value (a − 1)	Test Stat: tau_ct(1)	Asymptomatic p-Value	Autocorrelation of First-Order Residuals
Belgium	−1.243	−3.103	0.026	0.017	−0.737	−3.825	0.015	−0.084	−2.039	−5.824	0.000	−0.004	−2.040	−5.684	0.000	−0.005
Bulgaria	−0.589	−2.147	0.226	−0.068	−0.624	−1.887	0.661	−0.051	−1.653	−4.356	0.000	−0.034	−4.501	0.001	−0.030	2.038
Czech Republic	−0.043	−0.876	0.796	0.007	−0.267	−2.370	0.395	0.084	−0.972	−4.418	0.000	0.005	−0.975	−4.348	0.003	0.003
Germany	−0.101	−1.493	0.537	−0.000	−0.318	−3.306	0.065	−0.057	−0.420	−1.062	0.733	0.069	−0.552	−0.818	0.963	0.080
Spain	−0.393	−2.217	0.200	−0.047	−0.662	−2.463	0.347	−0.058	−1.718	−12.993	0.000	0.197	−1.727	−13.017	0.000	0.188
France	−0.198	−1.761	0.400	0.067	−0.088	0.561	0.981	−0.080	−0.476	−1.229	0.664	0.074	−3.874	−3.414	0.049	−0.062
Lithuania	−0.108	−1.379	0.594	0.015	−0.357	−2.454	0.351	0.120	−1.025	−5.425	0.000	−0.000	−1.026	−5.340	0.000	0.001
Hungary	−0.164	−1.544	0.511	−0.022	−0.348	−2.464	0.346	0.040	−1.113	−5.925	0.000	−0.022	−1.115	−5.827	0.000	−0.023
The Netherlands	−1.017	−5.538	0.001	−0.039	−1.030	−5.487	0.001	−0.030	−2.479	−5.195	0.000	−0.093	−7.056	−3.660	0.025	0.122
Romania	−0.062	−1.478	0.545	0.044	−0.267	−2.198	0.489	0.007	−0.703	−3.885	0.002	0.064	−0.722	−3.932	0.011	0.056
Slovenia	−0.208	−2.429	0.133	−0.109	−0.755	−2.064	0.565	−0.021	−1.842	−3.880	0.002	0.047	−2.309	−11.450	0.000	0.037
Slovakia	−0.548	−3.759	0.003	−0.132	−0.446	−3.156	0.093	−0.204	−1.356	−2.521	0.110	−0.068	−1.941	−3.018	0.127	−0.145
Finland	−0.649	−4.303	0.000	−0.084	−0.617	−2.989	0.135	−0.088	−1.180	−6.345	0.000	0.046	−1.214	−6.415	0.000	0.042
Sweden	−0.566	−3.163	0.022	−0.014	−0.809	−4.302	0.003	0.048	−2.381	−3.961	0.002	−0.075	−1.343	−7.541	0.000	−0.050

Source: own elaborations based on Eurostat [47].

, we present the augmented Dickey-Fuller test for gross nuclear electricity production. We tested two hypotheses. The null hypothesis was that the series has a unit root, and the alternative was that the series does not contain a unit root [86].

We evaluated the gross nuclear electricity production by p-value. This value was quite high, which suggests that the data are not stationary. Only in five countries, Belgium (0.026), the Netherlands (0.001), Slovakia (0.003), Finland (0.000), and Sweden (0.022), were they lower than 0.05, which suggests the stationarity of the gross nuclear electricity production time series.

When describing the data using the test with intercept and linear trends, we achieved similar results, and five countries’ data describing gross nuclear electricity production achieved stationarity. Our time series were transformed from non-stationary to stationary for applying the ARiMA model. Using statistical techniques, we used the ARiMA model, which is a simple tool for analyzing time series [87].

For the process called nuclear electricity production, the Dickey-Fuller test was performed to test its stationarity. The significance of the delay up to order 5 was checked based on the AIC criterion.

Null hypothesis: The gross nuclear electricity production process was assumed to have a unit root, implying non-stationarity, and was therefore an I(1) process.

Free expression test characteristics (no trend):

Model: (1 − L)y = b0 + (a − 1) × y(−1) + e

The estimated value of (a − 1) is negative for all countries.

The (1)tauc(1) test statistic is also negative for all countries.

The asymptotic p-value is high for most countries which indicates that we cannot reject the null hypothesis at the 5% significance level for this model.

Only Finland, Slovakia, Sweden, and the Netherlands achieved the low value of p and the null hypothesis for these countries can be rejected.

The autocorrelation of the residuals for the first lag is quite low for all countries, which may indicate some dependence in the residuals.

Test with intercept and linear trend:

Model: (1 − L)y = b0 + b1 × t + (a − 1) × y(−1) + e

The estimated value of (a − 1) for all countries has a negative value.

The tauct(1) test statistic is negative for most countries, except France (0.561).

The asymptotic p-value is high for most countries, which means that we definitely cannot reject the null hypothesis for this model. Only for Germany, the Netherlands, Slovakia, and Sweden, can the null hypothesis be rejected.

The autocorrelation of the residuals for the first lag is high, which may also indicate a pattern in the residuals.

Based on the results obtained, we cannot reject the null hypothesis for any of the models, which suggests that the gross nuclear electricity production process is probably non-stationary.

After differentiation, the gross nuclear electricity production process appears to be non-stationary, especially when we consider a model with a linear trend. However, the autocorrelation values of the residuals indicate that the model may not be perfect, which is worth considering in further analysis.

Table 4. ARIMA model of gross nuclear electricity production in the EU.

Country	Test Doornika-Hansena	p	AR				MA
			Coefficient	Std. Error	Z	p Value	Coefficient	Std. Error	Z	p Value
Belgium	21.895	0.000	0.789	0.207	3.811	0.000	−0.504	0.239	−2.111	0.034
Bulgaria	2.512	0.285	0.547	0.216	2.528	0.012	0.194	0.316	0.615	0.539
Czechia	20.599	0.003	0.942	0.078	11.990	0.000	0.510	0.191	2.674	0.007
Finland	10.270	0.006	0.931	0.058	15.890	0.000	−0.139	0.224	−0.622	0.534
France	8.013	0.018	0.879	0.128	6.881	0.000	−0.163	0.411	−0.398	0.690
Germany	13.172	0.001	0.982	0.021	45.750	0.000	−0.122	0.145	−0.841	0.400
Hungary	4.026	0.134	0.847	0.126	6.738	0.000	−0.045	0.383	−0.116	0.907
Lithuania	10.956	0.004	0.890	0.254	3.496	0.000	0.022	0.258	0.086	0.931
Netherlands	28.050	0.008	0.781	0.139	5.603	0.000	−1.000	0.090	−11.100	0.000
Romania	9.357	0.009	0.931	0.078	11.980	0.000	0.447	0.209	2.142	0.032
Slovakia	4.063	0.131	0.862	0.081	10.590	0.000	0.008	0.183	0.049	0.961
Slovenia	1.549	0.461	0.953	0.044	21.340	0.000	−0.788	0.174	−4.507	0.000
Spain	2.489	0.288	0.749	0.234	3.189	0.001	−0.457	0.291	−1.573	0.116
Sweden	2.406	0.300	0.741	0.383	1.935	0.053	−0.316	0.454	−0.696	0.486

Source: own elaboration based on Eurostat [37].

and

Table 5. ARIMA model characteristics for gross nuclear electricity production.

Country	Arithmetic Mean of the Dependent Variable	Mean of Random Perturbations	R-Squared Determination Coefficient	Likelihood Logarithm	Critical Bayesian Schwarz Criterion	Standard Deviation of Dependent Variable	Standard Deviation of Random Disturbances	Corrected R-Square	Critical Information Akaike Criterion	Critical Hannan–Quinn Criterion
Belgium	43,543	−6.700	0.179	−318.595	651.053	5720.338	5100.833	0.151	645.190	647.134
Bulgaria	16,314	10.441	0.436	−276.146	566.156	1831.624	1353.757	0.417	560.293	562.236
Czechia	22,593	26.892	0.648	−283.219	580.302	7493.739	1688.625	0.946	574.439	576.382
Finland	22,362	−0.830	0.848	−250.430	514.722	1578.079	606.066	0.843	508.859	510.803
France	404,329	32.774	0.673	−364.926	743.714	38,542.750	21,678.200	0.662	737.851	739.795
Germany	129,823	−3032.524	0.932	−356.315	726.616	40,084.590	11,280.970	0.930	720.630	722.644
Hungary	14,664	−0.272	0.689	−254.314	522.492	1247.648	684.299	0.679	516.629	518.573
Lithuania	7090	0.508	0.824	−296.979	607.820	6288.352	2595.782	0.818	601.957	603.900
Netherlands	3832	−41.077	0.133	−242.004	497.995	388.473	361.383	0.105	492.009	494.022
Romania	7346	9.649	0.956	−263.453	540.769	4397.675	910.478	0.954	534.906	536.849
Slovakia	14,759	0.219	0.774	−267.670	549.204	2219.795	1038.749	0.766	543.342	545.285
Slovenia	5406	−23.669	0.658	−234.363	482.589	632.072	366.833	0.647	476.726	478.669
Spain	58,225	−4.850	0.236	−294.410	602.684	2786.027	2395.600	0.211	596.821	598.764
Sweden	65,255	75.812	0.236	−326.029	665.921	7481.127	6434.755	0.211	660.058	662.002

Source: own elaboration based on Eurostat [47].

present the ARiMA model for gross nuclear electricity production in EU countries. We evaluated the model based on p-value. The p-value describing the AR part of the model was quite low, which confirms the stationarity of the time series. The ARiMA model to forecast the gross nuclear electricity production in the EU showed favorable forecasting performance. Similar results were achieved by Ding et al. [24], who found a similar prognosis for US nuclear power consumption. Nuclear energy represents the future and is described as a zero-emissions source. Its role in future energy demand cover is enormous, and it provides options for governments [88].

Taking into account observations from the period 1990–2022 (N = 33 observations in total), the ARIMA model was estimated (after eliminating the need for an integrated component). For the nuclear electricity production variable, an analysis was performed using the AS 197 method, suitable for estimation using the maximum likelihood (ML) method. The following results were obtained from the estimation of the ARIMA model for the constant biomass variable:

Autoregressive coefficient (phi_1): The estimate for the first lag is quite high for all countries with low standard errors. Excellently statistically significant (high z; p ≈ 0), this indicates a strong autoregressive influence of past values of nuclear electricity on its current values.

Moving average coefficient (theta_1): The estimate for the first lag is relatively high for all countries with low standard errors. Even though the value of the z statistic is also relatively high, this coefficient is not statistically significant (high p value).

Additionally, the analysis of AR and MA elements suggests the stability of the models. Specifically, the AR root demonstrates the stability of the autoregression for all countries, while the MA root highlights the inverse relationship in the moving average for gross nuclear electricity production.

The analysis of ARMA models for total energy from 2005 to 2020 showed strong autoregression, which indicates the influence of past gross nuclear electricity energy production values on its current levels. Key statistics, such as the high coefficient of determination R2, confirm the model’s ability to explain variability in the data. Moreover, the stability of the model was verified by AR and MA root analyses, highlighting its reliability.

Forecasts for the period 2023–2032 suggest relatively stable gross nuclear electricity production, despite growing uncertainty in the longer term. Estimates indicate diversified development of the nuclear sector in the EU, with minor fluctuations in production and increasing forecast error. This means that although some stabilization of production can be expected, it will be important to monitor market and technological changes affecting the nuclear sector.

In summary, the presented analysis provides an in-depth look at gross nuclear electricity production in the EU, relying on solid statistical and econometric methods. This enables a better understanding of trends and potential changes in the sector, which is crucial for planning and implementing nuclear energy strategies.

The key statistics of the models are as follows:

• The coefficient of determination R2 is quite high for all countries, which indicates the high ability of the model to explain the variability in nuclear electricity production data.
• The log likelihood of the model is relatively high for all countries, which is important for comparisons with other potential models for gross nuclear electricity production.

3.4. Prognosis of the Gross Nuclear Electricity Production in the EU Using ARIMA Model

Nuclear energy is the future; however, it is also the most debatable and controversial energy. The construction boom has been particularly noticeable in Asia. The importance of this energy is increasing worldwide. It is believed that nuclear energy can replace conventional fuels and will improve energy security [89].

Predicting the nuclear energy market is important because policymakers, planners, and producers can obtain useful information for nuclear energy development. Numerous factors affect the prognosis of the nuclear market, such as nuclear accidents, investment supports, technology improvements, and political bias [90].

Our research enables us to elaborate on the prognosis (

Table 6. Prognosis of gross nuclear electricity production in the EU (GWH—gigawatt-hour).

Year	Prediction/std. Error	Belgium	Bulgaria	Czechia	Finland	France	Germany	Hungary	Netherlands	Romania	Slovakia	Slovenia	Spain	Sweden
2023	Pred.	43,665.400	16,421.717	30,925.279	25,069.420	321,913.361	40,097	15,693.370	3778.223	11,090.641	15,866.590	5948.479	58,256.930	56,745.660
	Error	5100.8	1353.8	1688.6	606.1	21,698.2	11,280.9	684.3	361.4	910.5	1038.7	366.8	2395.6	6434.7
2024	Pred.	43,666.300	16,391.506	30,941.468	25,054.110	331,773.451	41,177	15,591.660	3792.872	11,141.516	15,818.600	5967.422	58,342.430	58,576.200
	Error	5304.2	1684.9	2976.7	772.9	26,674.1	14,888.2	877.4	370.0	1550.9	1377.7	371.8	2495.4	6991.3
2025	Pred.	43,667.100	16,374.983	30,956.719	25,039.870	340,439.485	42,239	15,505.490	3804.307	11,189.189	15,777.230	5985.490	58,406.500	59,932.570
	Error	5427.1	1772.1	3767.5	892.7	29,957.2	17,687.5	993.2	375.1	1942.6	1583.3	376.3	2549.7	7278.8
2026	Pred.	43,667.700	16,365.947	30,971.087	25,026.600	348,056.065	0.00	15,432.480	3813.233	11,233.600	15,741.550	6002.726	58,454.500	60,937.590
	Error	5502.4	1797.3	4350.5	984.8	32,265.4	20,023.5	1068.6	378.2	2227.4	1720.3	380.3	2579.6	7431.9
2027	Pred.	43,668.200	16,361.005	309,840.623	25,014.250	354,750.278	0.00	15,370.620	3820.201	11,274.973	15,710.790	6019.166	58,490.470	61,682.270
	Error	5548.8	1804.7	4809.1	1058.1	33,941.1	23,265.9	1119.6	380.1	2447.8	1815.5	383.9	2596.3	7514.7
2028	Pred.	43,668.500	16,358.302	30,997.374	25,002.750	360,633.824	0.00	15,318.220	3825.640	11,313.515	15,684.260	6034.847	58,517.420	62,234.060
	Error	5577.5	1806.9	5182.3	1117.8	35,180.9	20,023.5	1154.8	381.2	2624.1	1883.1	387.2	2605.6	7559.7
2029	Pred.	43,668.800	16,356.823	31,009.386	24,992.050	365,804.873	0.00	15,273.820	3829.889	11,349.421	15,661.390	6049.806	58,537.610	62,642.910
	Error	5595.4	1807.6	5492.2	1167.1	36,109.6	20,023.5	1179.4	381.9	2768.0	1931.9	390.2	2610.9	7584.3
2030	Pred.	43,669.100	16,356.015	31,020.703	24,982.080	370,349.710	0.00	15,236.200	3833.200	11,382.870	15,641.660	6064.074	58,552.740	62,945.850
	Error	5606.5	1807.8	5735.3	1208.1	36,810.9	20,023.5	1196.8	382.3	2887.1	1967.4	392.8	2613.8	7597.8
2031	Pred.	43,669.200	16,355.573	31,031.364	24,972.800	374,344.167	0.00	15,204.330	3835.787	11,414.030	15,624.660	6077.683	58,564.080	63,170.330
	Error	5613.4	1807.9	5975.5	1242.7	37,343.6	20,023.5	1209.1	382.6	2986.6	1993.4	395.2	2615.4	7605.2
2032	Pred.	43,669.400	16,355.331	31,041.408	24,964.160	377,854.897	0.00	15,177.330	3837.807	11,443.059	15,610.000	6090.665	58,572.570	63,336.650
	Error	5617.7	1807.9	6166.0	1271.8	37,749.9	20,023.5	1217.8	382.7	3070.4	2012.5	397.4	2616.3	7609.2

Source: own elaboration based on Eurostat [47].

). The research is quite optimistic. Eight countries in the EU will record an increase in gross nuclear electricity production. Based on the ARIMA model, the following countries will increase gross nuclear electricity production: for example, Belgium, Czechia, France, the Netherlands, Romania, Slovenia, Spain, and Sweden. We did not elaborate on the prognosis for Lithuania because this country stopped using nuclear energy in 2010. Countries such as Bulgaria, Finland, Hungary, and Slovakia will record a decrease in gross nuclear electricity production in the period 2023–2032. Germany will stop producing nuclear energy in the future. Energy concerns, which are a global challenge, show that nuclear energy prediction can enhance positive energy security and also reduce the emission of greenhouse gases (GHG). The future prognosis depends on policy too. Future gross nuclear electricity production depends on information about the upcoming modernization or decommissioning of a unit. However, the current situation and war in Ukraine have forced European Union countries to treat gross nuclear electricity production as a priority. Some countries, such as Poland, which does not produce electricity from nuclear resources, will introduce it in the future to replace fossil fuels and ensure a stable energy supply.

The prognosis for nuclear energy is very promising because this sector can deliver many benefits for the European Union’s economy. The first benefit is increased energy security and the development of almost all sectors of the economy and technology [91].

The analysis of the forecasts shows that gross nuclear electricity production will remain at a stable level, with minor fluctuations. Nevertheless, there is a noticeable increase in forecast error in subsequent years, which indicates increasing uncertainty in long-term forecasts.

The 95% confidence intervals for subsequent years also widen, highlighting the increasing uncertainty of future forecasts. Nevertheless, these forecasts provide important information about potential trends and can serve as an auxiliary tool in planning development strategies for the nuclear sector.

3.5. Prognosis of the Gross Nuclear Electricity Production in the EU Using the VAR Model

To diversify the analysis, we used the Vector Autoregressive model (VAR) model. As previously mentioned, this method is widely used in forecasting and deep analysis.

In the next step, the order of variable delays was examined (

Table 7. VAR model of gross nuclear electricity production in the EU.

Country	AIC	BIC	HQC	Constant				Model
				Coefficient	Std. Error	t-Student	p Value	Coefficient	Std. Error	t-Student	p Value
Belgium	20.116	20.208	20.147	28,998.2	7546.6	3.843	0.000	0.334	0.172	1.944	0.061
Bulgaria	17.397	17.488	17.427	5796.3	2229.5	2.600	0.014	0.650	0.136	4.747	0.000
Czechia	17.998	18.089	18.028	1384.8	1052.6	1.316	0.198	0.963	0.045	21.260	0.000
Finland	15.792	15.884	15.822	1961.5	1596.6	1.229	0.229	0.920	0.072	12.810	0.000
France	22.956	23.048	22.987	59,224.0	44,883.7	1.320	0.197	0.852	0.110	7.720	0.000
Germany	21.503	21.595	21.533	−11,636.5	7356.9	−1.582	0.124	1.059	0.053	19.830	0.000
Hungary	16.021	16.112	16.051	2471.3	1500.3	1.647	0.110	0.835	0.102	8.156	0.000
Lithuania	18.686	18.778	18.717	279.6	744.8	0.375	0.710	0.893	0.075	11.850	0.000
Netherlands	14.864	14.955	14.893	3505.1	700.9	5.571	0.000	−0.016	0.182	−0.090	0.929
Romania	16.734	16.826	16.764	724.3	332.6	2.178	0.037	0.946	0.040	23.610	0.000
Slovakia	16.855	16.946	16.885	2111.5	1262.4	1.673	0.105	0.864	0.085	10.130	0.000
Slovenia	15.088	15.180	15.119	1600.6	667.8	2.397	0.023	0.708	0.123	5.738	0.000
Spain	18.604	18.752	18.691	38,161.1	9628.33	3.963	0.000	0.345	0.166	2.086	0.046
Sweden	20.518	20.609	20.548	32,400.3	11,222.5	2.887	0.007	0.500	0.170	2.944	0.006

Source: own elaboration based on Eurostat [47].

). The VAR model successfully passed the verification process (the random component of the model was not normally distributed). The choice of the order of variable lags depends on the researcher, but several criteria indicate to econometricians the best order of lags, and the most popular of them includes Akaike’s information criterion AIC, Schwarz BIC, and Hannan and Quinn HQ.

All criteria indicated the first order of lags of the vector-autoregressive model; therefore, the parameters of the VAR model were estimated. Both the Akaike information criterion and the Hannan and Quinn information criterion indicated the order of lags equal to I (the smallest value of the information criterion). Because most criteria indicated the order of lags equal to I, as well as the fact that we estimated the model based on quarterly data, the authors decided to choose this order of variable lags.

The adjusted coefficient of determination R² for the individual equations is very high for all countries. The model has been successfully verified and can be used to predict gross nuclear electricity production. KMNK was used to estimate the parameters of the VAR model. The estimated parameters are presented in

Table 8. VAR model characteristics for gross nuclear electricity production.

Country	Test Parmanteau LB(8)	Df = 7	Arithmetic Mean of the Dependent Variable	Sum of Square Rest	R-Squared Determination Coefficient	F	Autocorrelation of Rests	Standard Deviation of Dependent Variable	Standard Deviation Error	Corrected R-Square	p Value for F Test	Durbin-Watson Statistics
Belgium	5.485	0.601	43,543.7	0.009	0.111	3.777	−0.096	5720.338	5480.124	0.082	0.061	2.187
Bulgaria	5.204	0.635	16,314.2	5938	0.429	22.537	0.059	1831.624	1406.964	0.410	0.000	1.808
Czechia	6.154	0.522	22,593.7	0.012	0.937	452.026	0.286	7493.739	1900.397	0.936	0.000	1.411
Finland	10.753	0.150	22,362.2	1193	0.845	164.071	−0.144	1578.079	630.710	0.840	0.000	1.989
France	4.024	0.777	404,328.9	0.015	0.665	59.594	−0.265	28,542.750	22,671.710	0.654	0.000	1.764
Germany	13.090	0.070	129,115.8	0.361	0.929	393.338	−0.453	40,516.020	10,963.870	0.927	0.000	2.521
Hungary	2.566	0.922	14,644.9	1499	0.689	66.516	−0.022	1247.648	707.086	0.679	0.000	2.041
Lithuania	9.551	0.215	7090.1	0.216	0.824	140.503	0.014	6288.352	2681.343	0.818	0.758	1.961
Netherlands	2.653	0.915	3842.5	4715	0.000	0.008	−0.040	390.068	396.462	−0.033	0.929	2.000
Romania	9.155	0.242	7346.8	3062	0.948	557.307	0.294	4397.675	1010.349	0.947	0.000	1.393
Slovakia	8.841	0.264	14,759.6	3453	0.774	102.707	0.011	2219.795	1072.866	0.766	0.000	1.958
Slovenia	32.748	0.000	5406.3	5904	0.523	32.929	−0.177	632.072	443.629	0.507	0.000	2.353
Spain	32.675	0.000	58,225.9	0.210	0.127	4.352	−0.229	2786.027	2646.575	0.097	0.045	2.444
Sweden	4.253	0.750	65,255.9	0.135	0.224	8.667	−0.052	7481.127	6698.444	0.198	0.006	1.986

Source: own elaboration based on Eurostat [47].

. As previously stated, the parameters of the VAR model were estimated for the first differences of the variables. P-values less than 0.05 indicate a significant multiple correlation coefficient. The next step was to examine the autocorrelation of the random components of the individual model equations (Table 8) and to check whether the individual random components had a normal distribution.

The p values in Table 8 indicate the lack of autocorrelation of the random components and prove that the residuals of the individual equations are normally distributed. VAR models have successfully passed the verification process and can be used to determine forecasts for the studied variables.

We used the Portmanteau test to analyze the VAR model. This is a widely used model to evaluate the adequacy of the model’s fit. This statistical test is constructed based on the squared residual autocorrelation function. Based on the achieved results, we can conclude that the model is well-fitted in most countries of the European Union (EU).

Table 9. Prognosis of gross nuclear electricity production in the EU based on VAR model (GWH—gigawatt-hour).

Year	Prediction/Std. Error	Belgium	Bulgaria	Czechia	Finland	France	Germany	Hungary	Netherlands	Romania	Slovakia	Slovenia	Spain	Sweden
2023	Pred.	43,667.900	16,446.150	31,267.446	25,274.530	310,408.681	25,152.100	15,677.270	3837.016	11,214.891	15,867.100	5569.461	58,398.110	58,351.700
	Error	5306.1	1362.3	1840.1	610.7	21,951.8	10,615.7	684.6	383.9	978.3	1038.8	429.4	2562.5	6485.7
2024	Pred.	43,597.300	16,435.897	31,503.877	25,217.980	323,769.993	15,022.590	15,564.740	3842.243	11,333.988	15,821.400	5543.593	58,331.830	61,553.010
	Error	5594.8	1622.5	2554.9	829.9	28,842.4	15,469.2	892.0	383.9	1346.7	1372.9	526.3	2711.1	7250.1
2025	Pred.	43,573.700	16,429.263	31,731.624	25,165.930	335,157.178	4286.160	15,470.760	3842.159	11,446.659	15,781.910	5525.279	58,308.940	63,152.390
	Error	5626.1	1719.8	3072.9	977.8	32,956.1	19,532.6	1011.8	383.9	1606.3	1576.8	568.6	2728.3	7428.7
2026	Pred.	43,565.800	16,424.972	31,951.007	25,118.050	344,861.913	0.00	15,392.270	3842.159	11,553.250	15,747.790	5512.313	58,301.030	63,951.450
	Error	5629.6	1758.9	3485.3	1087.4	35,647.6	23,265.9	1087.6	383.9	1807.2	1713.2	588.7	2730.3	7472.6
2027	Pred.	43,563.100	16,422.195	32,162.333	25,073.980	353,132.778	0.00	15,326.710	3842.159	11,654.089	15,718.300	5503.134	58,298.300	64,350.660
	Error	5630.0	1774.9	3828.5	1172.2	37,481.6	23,265.9	1137.4	383.9	1969.8	1808.4	598.5	2730.6	7483.5
2028	Pred.	43,562.300	16,420.399	32,365.897	25,033.440	360,181.627	0.00	15,271.960	3842.159	11,749.486	15,692.830	5496.635	58,297.360	64,550.110
	Error	5630.0	1791.7	4121.4	1239.5	38,759.3	23,265.9	1170.9	383.9	2104.7	1876.4	603.3	2730.6	7486.2
2029	Pred.	43,562.000	16,419.237	32,561.985	24,996.130	366,189.012	0.00	15,226.240	3842.159	11,839.735	15,670.820	5492.034	58,297.030	64,649.760
	Error	5630.1	1784.5	4375.8	1293.7	39,661.5	23,265.9	1193.8	383.9	2218.5	1925.5	605.8	2730.6	7486.9
2030	Pred.	43,561.900	16,418.485	32,750.871	24,961.800	371,308.809	0.00	15,188.050	3842.159	11,925.115	15,651.800	5488.777	58,296.920	64,699.540
	Error	5630.1	1785.7	4599.2	1337.9	40,304.1	23,265.9	1209.5	383.9	2315.5	1961.4	606.9	2730.6	7487.1
2031	Pred.	43,561.800	16,417.999	32,932.820	24,930.210	375,672.159	0.00	15,156.150	3842.159	12,005.887	15,635.370	5486.471	58,296.880	64,724.840
	Error	5630.1	1786.2	4797.2	1374.2	40,764.6	23,265.9	1220.3	383.9	2399.1	1987.7	607.6	2730.6	7487.1
2032	Pred.	43,561.800	16,417.685	33,108.086	24,901.150	379,390.826	0.00	15,129.510	3842.159	12,082.300	15,621.170	5484.839	58,296.870	64,736.8
	Error	5630.1	1786.4	4973.9	1404.2	41,095.8	23,265.9	1227.8	383.9	2471.5	2007.2	607.9	2730.6	7487.1

Source: own elaboration on the basis of Eurostat [37].

shows point forecasts, ex-ante forecast errors, 95% confidence intervals for forecasts, and actual values of gross nuclear electricity production in the EU.

All statistics refer to the first differences between both variables. The presented analysis shows that the 95% confidence interval of the forecasts covered the actual value of the forecast variable in the period for which the forecast was calculated. It should be remembered that the forecast interval depends on the average forecast error, so the larger the error, the wider the confidence interval, and vice versa; i.e., the smaller the error, the narrower the confidence interval.

After verifying the model, the forecasts of all variables used for vector autoregressive modeling were calculated. Both point and interval forecasts for two consecutive quarters were counted, and then the forecasts were compared with the actual values of the studied variables in these periods. All predictions concern the first differences between the studied variables. The vast majority of forecasts were accurate. Based on the VAR model, we elaborated the prognosis according to which countries, such as France, Romania, Spain, and Sweden, will increase gross nuclear electricity production in the period 2022–2026.

Based on our prognosis using the VAR model, we can state that five countries will increase gross nuclear electricity production in the period 2023–2032; for example, Czechia, France, the Netherlands, Romania, and Sweden. According to our prognosis, more countries will record a decrease in gross nuclear electricity production in the period 2023–2032; for example, Belgium, Bulgaria, Finland, Hungary, Slovakia, Slovenia, and Spain. Based on our prognosis using the VAR model, Germany will not produce gross nuclear electricity in the coming future.

When comparing the two prognoses based on the ARiMA and VAR models, we can state that the forecasts based on ARIMA models are more optimistic. This is the reason why ARiMA models are used worldwide for predictions. The VAR models are stricter, and the prognosis has more errors. However, these are the limitations of research and prognosis, which depend on data sources. However, global documents and prognosis elaborated by the International Energy Association suggest that nuclear energy in the European Union will deliver 11% of total energy supply in 2050, compared to 10% in 2020. Moreover, in the electricity and heat sectors, nuclear energy will have a share of 13%, compared to 15% in 2020 [92].

3.6. Prognosis of Nuclear Power in the United States of America

The United States of America is the main nuclear electricity producer and consumer. The prognosis presented in Figure 6 delivers interesting information. Total energy consumption will stagnate in the period 2022–2033. It means that, with the increase in demand, more and more energy should be delivered to fulfill energy demand. Nuclear power has great potential and is still the second-largest source of low-emission electricity. The United States of America undertook the Civil Nuclear Credit Program in 2022, and invested USD 6 billion to help preserve the existing US reactor fleet. Moreover, it allocated USD 8 billion to demonstrate clean hydrogen hubs, including at least one hub dedicated to the production of hydrogen with nuclear energy. In addition, this country elaborated the Advanced Reactor Demonstration Program, investing a total of USD 3.2 billion over seven years on two nuclear projects [93]. At present, the United States has 92 reactors, and they will be used in the future. The prognosis suggests that, in 2050, the number of reactors in the USA will be the same. Existing nuclear power plants are struggling to cover their costs, and the prospects of new nuclear power plants being able to make a profit under current market conditions are even less promising [94].

4. Discussion

The development of the nuclear energy market in the European Union, the United States of America, and other parts of the world depends on this policy. France is the biggest producer of gross nuclear electricity. The France 2030 investment has been announced to extend the lifetime of all nuclear reactors that can be extended while ensuring safety. The country plans to build six new large reactors starting in 2028, which will cost EUR 50 billion. Moreover, the possibility of building eight more by 2050 was recently announced. In addition, France is going to use EUR 1 billion for investment in small modular reactors by 2030 [93].

Belgium, for example, does not want to resign from nuclear reactors and wants to extend the lifetime of the two existing ones through 2035. This decision was taken in March 2022 [93].

The Netherlands also led a discussion to build two new nuclear stations [93].

Poland is a country that does not have nuclear electricity but plans to build reactors in the European Union. The Polish Nuclear Power Program plans to construct two reactors between 6 GW and 9 GW. These power plants will be built by the United States of America and South Korea Industries. Additionally, small modular reactors based on US technology will be deployed to replace coal plants [93].

Germany, which is also a big producer of nuclear energy, is going to phase out coal and nuclear energy. The reason for this is the catastrophe in Fukushima, which forced Germans to react when the plant was struck by an earthquake [95]. All nuclear power plants for commercial use will be closed. The problem with lower energy supply will be solved by expanding the energy mix, including increasing renewable source share [96].

The depletion of coal, oil, and natural gas, and the deterioration of ecosystems are occurrences that have forced society to look towards nuclear energy [97]. Nuclear energy is useful for biodiversity conservation, can eliminate fossil fuel dependency, and can help in the process of reducing global energy power [98].

Nuclear energy is considered to be clean energy; however, the use of this energy should be discussed from an economic, government policy, and ecological point of view, as there is international concern about possible catastrophes. This energy has a large supply capacity, and it is a promising technology. Rapid economic growth requires a stable supply of energy to cover needs [99,100,101,102]. Nuclear energy has many advantages because it can improve sustainability, produce low-carbon electricity, benefit human well-being, and affect ecosystems [103].

Apart from its advantages, nuclear energy requires a controlled approach and a stable policy that will protect humanity against nuclear accidents. This kind of energy can be very dangerous if not appropriately used. Moreover, the proper storage of radioactive isotopes is also important [104].

Policymakers should consider many precautions in elaborating the policy. The nuclear catastrophes were not only the results of human mistakes but also of natural earthquakes. This should encourage better recognition of the placement of nuclear power plants and better education for nuclear employees. Both renewable energy sources and nuclear energy should replace fossil fuels. However, it is common that renewable energy sources are used to replace nuclear energy for example, in Lithuania. This process may decrease the pace of replacing fossil fuels [105]. In countries such as Sweden, renewable energy sources, mainly wind energy, are being used to displace nuclear energy. This has led to an increase in wind power installations [106].

Our research proved that gross nuclear electricity production data can be classified as stationary, which confirmed the ADF test and ARiMA model. This means that the values in the time series depend on each other. Production in one year impacts production in the following years.

Our prognosis based on the ARIMA model proves that gross nuclear electricity production will increase in the European Union. Eight countries in the EU will record an increase in gross nuclear electricity production. Based on our prognosis, we can predict nuclear supply and demand, which will be important in ensuring a stable, clear energy supply that can help achieve the goals of the environment [24]. Using the VAR model, we concluded that four countries will increase gross nuclear electricity production (France, Romania, Spain, and Sweden).

5. Conclusions

Renewable energy sources such as wind and photovoltaics are not stable and predictable. This obstacle can be overcome by utilizing nuclear energy to fill the gaps in energy needs [10].

This study aimed to investigate the development of gross nuclear electricity production in the world and in the European Union (EU) in terms of stationarity and prognosis. Our research proved that the development of nuclear electricity production is diversified in the European Union (EU). The economic development of the world and nuclear energy consumption are linked together. Policies of the European Union (EU) and other parts of the world have impacted the consumption of nuclear energy and its growth [107].

Our research proved that France (70.2%), Slovakia (55.2%), Ukraine (52.8%), Hungary (48.7%), and Sweden (40.7%) were countries with the highest share of nuclear energy in electricity production in 2018. In contrast, China (4.1%), Japan (6.2%), Germany (11.5%), and the USA (18.8%) were countries with the lowest reliance on nuclear energy in 2018.

In 2019, electricity produced by nuclear power plants amounted to 2796 TWH. This production was mainly located (65% of the total amount of electricity) in the USA, France, China, and Russia.

Hypothesis 1 (H1), which assumed that Nuclear energy has stagnated due to catastrophes in the USA, Ukraine, Japan, and other countries, was not verified positively. Countries around the world have started to consider whether nuclear energy is safe enough. Only Germany, Spain, Lithuania, and Sweden decreased their gross nuclear electricity production in the period 1990–2022. Other countries in the European Union (EU) have increased their gross nuclear electricity production in the period 1990–2022. However, the need to replace fossil fuels will increase the dependence on nuclear energy. Such countries as Poland will introduce and produce electricity from nuclear energy. This process requires large investments.

Our forecast established the development of nuclear energy in most countries of the EU. Based on the ARiMA model, we determined that gross nuclear electricity production will increase. Our results can be very useful for policymakers and nuclear power plant (NPP) management. The information we provide can be part of the information to improve knowledge of nuclear energy development and unexpected situations [108].

Using ARIMA and VAR models, we prepared a prognosis for gross nuclear electricity production. The ARIMA model showed that eight countries would record the development of gross nuclear electricity production in the period 2023–2032. The VAR model was less optimistic, and showed that only five countries would record an increase in gross nuclear electricity production. The differences in prognosis can be explained by the fact that the ARIMA model is less optimistic and able to elaborate on gross nuclear electricity production. The elaborated prognosis can be useful for policymakers, who should take into account different methods and compare results. Based on both models, ARiMA and VAR, Germany will phase out nuclear energy in the wake of Fukushima. The electricity production in Germany will depend very much on its nuclear energy policy, which foresees the abolition of nuclear electricity production.

There are some countries that do not produce gross nuclear electricity, but plan to do so in the future. Some countries have decided to build new nuclear power plants. In Poland, for example, one nuclear power plant will be built by the United States of America and the second by South Korea. Countries whose energy sectors are based on coal and do not have nuclear electricity are considering the implementation of nuclear energy production. Nuclear energy seems to be relatively cheap, safe, and efficient, and the technology is developing in Europe.

Finland may depend on the condition of its new nuclear power plant, but it is increasing renewable energy sources too. Only a mix of energy sources, including nuclear electricity and renewable energy sources, can fulfill the increasing future demand for energy.

Policy Implications

Policymakers should understand both problems pertaining to energy use. First, the need to ban or limit fossil fuels is essential. They contaminate the environment. Second, the world should look for other energy sources, such as renewable energy sources (RES) and nuclear energy. Nuclear energy is very useful, but it carries the risk of radioactive contamination when accidents occur. That is why international policies should be established for the safe use of nuclear energy. The negative consequences for society should be decreased with safer radioactive isotope storage. Proper education, including in regard to the advantages and disadvantages of nuclear energy, should be introduced. This education can help increase global acceptance of this clean, useful, but also potentially dangerous energy source. Education should be introduced to schools at different levels [104].

The energy policy of the EU includes the transformation of the sector that is needed to limit the extent of climate change to 2 °C above preindustrial temperatures [109]. Nuclear energy will play a key role in this process because countries need more cheap and clean energy to satisfy the increasing demand, reduce CO₂ emissions and other greenhouse gases (GHG), and reduce imports of energy [110,111].

Nuclear energy production and consumption depend on consumer acceptance of this form of energy source. Moreover, the lower cost of fuel may have an impact on increasing gross nuclear electricity production. Additionally, the development of technology in the nuclear sector is important because it may increase efficiency, safety, and reliance on this energy.