Abstract
The increasing demand for power quality in modern power supply facilities and the deepening changes in the power market have led to frequent power quality events, making the assessment of power quality a necessity. In view of the complexity of the model and the sensitivity of the parameters of the existing power quality assessment system, as well as the shortcomings of the traditional hierarchical analysis method, this paper proposes a data-driven power quality assessment system based on the improved determinant-valued extension hierarchical analysis, which makes the factors affecting power quality hierarchical, and enhances the conservatism of the matrix while reducing the human subjective factors, so as to analyze the main power quality problems in a clearer and more intuitive way. The evaluation system is validated and analyzed, and the corresponding evaluation result is “excellent”, which proves that the system effectively evaluates the power quality in real scenarios, and has a good prospect in power quality evaluation.
1. Introduction
With the development of modern industrial technology, the types of electrical loads have become more and more diversified, and the capacity and number of power grids are increasing, together with voltage and frequency fluctuations as well as other factors, all of which are deteriorating the quality of power supply. The increasing prominence of power quality issues, more complex power systems, and diverse power usage scenarios have led to a significant focus on power quality assessment. As power quality is affected by a number of factors, separate analysis and evaluation are often difficult to reflect the actual situation. The establishment of a comprehensive power quality assessment system will help to carry out a comprehensive assessment and governance of power quality. Currently, the research on power quality assessment is divided into two main categories: (1) analyzing single power quality indicators, such as harmonics, voltage dips, three-phase imbalance, long-time interruption, etc., and proposing new research methods and establishing a power quality assessment system; (2) establishing a comprehensive assessment system for power quality indicators.
In the above context, in order to be able to analyze the economics of power quality management more scientifically and rationally, Guo J. et al. [1] proposed a comprehensive assessment method for power quality based on the variable fuzzy set idea, used the power quality standard cloud model and sample data cloud model, calculated the cloud similarity, and derived the power quality evaluation level based on the results, but the model was more complex. Tymchuk S et al. [2] proposed an estimation method for power quality which utilized fuzzy set theory to assess the consistency of power quality indicators with power quality limits, but it was not possible to accurately analyze the more precise weights of the indicators. Shi H. [3] proposed a comprehensive power quality evaluation method based on CRITIC and dynamic coefficients, which could reflect both the intrinsic characteristics of the data series and the relationship between different data series, but there were shortcomings in terms of generalizability and accessibility. Barros, J. et al. [4] addressed power quality in DC distribution grids, but they did not consider power quality in AC grids. Dong H. et al. [5] used a comprehensive power quality evaluation method based on the fuzzy soft set theory of time series interval value, but there were problems with high data requirements. Milanović J et al. [6] proposed a methodology inspired by the analytic hierarchy process (AHP), which evaluated the overall power quality (PQ) performance on the bus based on several different PQ phenomena considered simultaneously. But the limitations of the hierarchical analysis method have not been well taken into account. Chen et al. [7] proposed a combination of AHP and S-Transform for power quality assessment, but there was a problem that the judgment matrix was not flexible. Lu Y. [8], on the other hand, introduced the extension hierarchical analysis method to analyze the power data, thus providing a comprehensive evaluation of power quality. But there were problems with subjective factors that tended to influence the judgment matrix.
Some machine learning methods have also been used for power quality assessment [9]. For example, Huang H. [10] proposed a power quality assessment method based on a graph convolutional network and established a power quality assessment system with index grading. However, there was a problem of insufficient model interpretability. Jia X. [11] proposed a five-level classification method and a deep belief network (DBN) model using deep learning algorithms to establish a power quality assessment model, but there were issues such as parameter sensitivity. In addition to this, methods for assessing the quality of electrical energy include the use of the random forest method [12], the extension theory method [13], and the theory of evidence method [14,15].
Combining the above studies, the traditional hierarchical analysis method is selected as the main body of the power quality assessment system for the deep learning method with model complexity, and parameter sensitivity, etc. However, it still has the problem of subjective factors easily affecting the judgment matrix as well as the elasticity of the judgment matrix. In order to address the above issues, the main contributions of this paper are as following.
- (1)
- We propose a data-driven power quality assessment system based on the improved determinant value of the extension hierarchical analysis method.
- (2)
- The evaluation system is validated and analyzed by using simulation data, and the final evaluation index stands at 0.9286, aligning with the “excellent” rating as defined by the evaluation standard.
2. Basic Theory
2.1. Power Quality Assessment Indicators
Power quality is affected by multiple factors [16]. In the process of analyzing and researching power quality, we can start from a single indicator, and then integrate from the perspective of multiple indicators, and then establish a perfect power quality assessment system. The metrics for assessing power quality are described below.
(1) Voltage deviation [17]: Voltage deviation refers to the difference between the actual voltage and the rated voltage, including those caused by the working mode of the power supply and distribution control system or load changes.
where Ure indicates the measured voltage and UN indicates the system standard voltage.
(2) Harmonic [18,19,20]: With the progress of science and technology, the power system will access more and more nonlinear loads, which makes the power system inject a large number of harmonics, resulting in problems with electrical equipment, affecting the stable operation of the power system, but also leads to relays, and automatic protection devices cannot act in accordance with the original settings, which leads to inaccurate measurement results. With the increased application of power electronics in the power grid, harmonics will be more likely to be superimposed. The superimposed harmonics will cause serious harm to the human body.
(3) Flicker: In the power system, due to voltage fluctuation, it will cause various electrical equipment to work abnormally. Table 1 demonstrates the prescribed limits of voltage flicker for different voltage levels in international standards, where Pst denotes the short-time flash value and Plt denotes the long-time flash value.

Table 1.
Voltage flicker limit system voltage level under each voltage level.
(4) Voltage transient dips and voltage interruptions: Voltage transient dips and voltage interruptions can cause short-circuit faults and even affect the normal operation of sensitive equipment, and there is a correlation between the two. A voltage transient drop is a sudden drop in voltage caused by a grid fault or large load access [21], and voltage interruption is a voltage transient value infinitely close to zero.
(5) Transient pulse: A transient is a very short duration voltage surge or spike in the shape of a sine wave. It is a non-stationary power quality event that may occur at any time of the day due to switching activity in the distribution system. A transient caused by lightning is called a transient pulse. It is a non-stationary event that usually occurs during a direct lightning strike near a transmission line. The transient pulse can be modeled numerically using an exponential function as shown in Equation (2).
where t1 is the transient start-up time, tm is the transient amplitude, and ρ is the pulse transient attenuation factor.
(6) Three-phase imbalance [21]: Three-phase imbalance refers to the power supply system in which the three-phase current amplitude is not the same, and the amplitude difference beyond the rule area. Due to the uneven load added to each phase of the power supply, it is the base wave load configuration problems. Caused by three-phase imbalance and user load characteristics closely related, it was also closely related to the power supply system planning and load distribution.
2.2. Extension Theory
The extension theory [22,23] is mainly used to study the expansion laws of the characteristics of things. While the theory of matter-element is mainly used to collect information within things, extension sets undertake the task of describing and quantifying the properties of things.
The model is based on the concept of matter-element, which describes objective things, characteristics, and data values as the basic unit of the matter-element model. The concept of matter-element can be expressed as follows.
Definition 1
where (c, v) is the matter-element M-related feature element.
(One-dimensional Matter-element). If we form a triad with the objective with N, c as physical characteristics and v as a quantity, we have,
M = (N, c, v)
In order to better represent the different features, a multidimensional matter-element approach is usually used for the analysis.
Definition 2
(Multidimensional Matter-element). If c1, c2, … cn are the n eigenvalues corresponding to a thing N, then M is said to be a multidimensional matter-element.
Definition 3
(Covariate Matter-element). If the characteristic element (c, v) has a measure v about the feature c that varies with the parameter t, then it is called a covariate matter-element.
M(t) = (n, c, v(t)),
In the category of extension, the correlation function describes changes in the nature of things. In the field of mathematics, it is generally all real numbers. Because of the rules for taking values of the characteristic function, it takes values in the range [0, 1].
Simple correlation functions are generally used in the case of intervals degenerating into single intervals in the following ways:
- The positive domain is a finite interval X = <a, b>, M ∈ X,
Then k(x) satisfies the following properties.
(a) k(x) attains its maximum value at x = M and k(M) = l;
(b) x ∈ X, and x ≠ a, b when k(x) > 0;
(c) x ∉ X and x ≠ a, b when k(x) < 0;
(d) x = a or x = b ⇔ k(x) = 0. The published results.
- 2.
- The positive domain is an infinite interval X = <a, +∞>, M ∈ X,
- 3.
- The universe is an infinite interval X = <−∞, b>, M ∈ X,
- 4.
- The universe is an infinite domain X = <−∞, +∞>, M ∈ X,
3. Data-Driven Power Quality Assessment System
3.1. Power Quality Assessment Framework
Using the extension theory combined with the relevant indicators of power quality, an improved hierarchical analysis method is used to establish a power quality evaluation system so that the quality of power supply can be effectively guaranteed. Each evaluation index in the system should be in line with the objective facts of power quality, and at the same time, the computational complexity and time should be considered. Considering the above factors, the assessment system in this study selects five main power quality indicators and constructs a data-driven power quality assessment system based on them, and Figure 1 shows the framework of the assessment system [24].
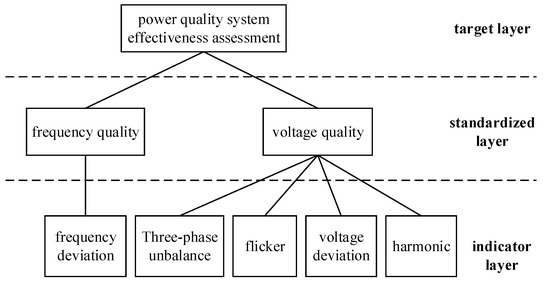
Figure 1.
Electricity quality system effectiveness assessment index system.
3.2. Power Quality Indicator Evaluation Objective
Extension theory is a mathematical theory based on matter-element analysis, which defines an matter-element as a set consisting of three basic elements, namely R = (N,C,V), where N is the name of the evaluation target, C is the characteristic index, and V is the index value. There are three kinds of matter-elements: classical domain, section domain, and matter-element to be evaluated.
1. Classical domain. In power quality evaluation, the classical domain is the range of values corresponding to the evaluation level of each index. Its calculation is shown in Equation (10).
where Nj denotes the jth power quality assessment level; <a1, b1> is the range of values of the indexes under the jth assessment level and c1–c5 are the corresponding indexes of the index layer in Figure 1 in order. c1 is the three-phase imbalance, c2 is the flicker, c3 is the harmonic, c4 is the voltage deviation, and c5 is the frequency deviation.
2. Section domain. The section domain is the concatenation of all the value ranges of the classical domain, which generally indicates all the value ranges of the indicators in the power quality assessment system, as shown in Equation (11).
where N is the power quality impact level; <d1, e1> denotes the range of values for all assessment levels of c1.
3. Matter-element to be evaluated. When carrying out the evaluation of power quality factors, it is necessary to convert all the power data in the event into matter-element with the following Equation (12).
where N0 is the codename of the event affecting power quality to be evaluated; x1 is the value of c1.
3.3. Assessment Process of the Power Quality Assessment System
The specific process of the power quality assessment system proposed in this paper is as follows:
Step 1: Establish a judgment matrix U for evaluating the indicator system, substitute the corresponding eigenvectors with its maximum characteristic root, and after normalization, an individual weight for each indicator can be obtained.
Step 2: Consistency detection. In order to solve the problem of imperfect judgment matrix consistency criterion in the AHP method, this paper modifies the judgment matrix consistency criterion to solve the defects of the AHP method: that is, to find out the value of the corresponding determinant, if its value is 0, then it means that it is with complete consistency; if the absolute value of the determinant is less than 1, it means that it is in good consistency. Then, for the judgment matrix consistency test, if it meets the requirements, you can continue to pass; if it does not meet the requirements, for the input values in the judgment matrix to adjust, re-execute the consistency check until the conditions are met. In addition, the number of intervals instead of the number of point values can reduce the error brought by subjective judgment. On this basis, by calculating the weight vector of each sub-indicator, a uniform comparability and scale between the sub-indicators is realized.
a. For quantitative indicators, a method of calculating mathematical expectations is used to calculate the degree of affiliation of the indicator. If the underlying index value is x, ideally this factor value is f, and the minimum value of this factor is gi, if it meets the actual demand, then its degree of affiliation R(J) is able to refer to the following Equations (13) and (14) to normalize:
For extremely large metrics, larger xj, and correspondingly higher system performance, there is:
For very small metrics, systems with smaller xj that have correspondingly higher integrated assessment values, there is:
b. For qualitative indicators, the confidence interval method is used to evaluate the degree of affiliation of the indicator. Let n experts rating, given that an expert on (0, 1) of this indicator score is x, its confidence level is a, so get n pairs of numbers (x, a), j = 1, 2,…, n. Then, there will be:
Step 3: System energy efficiency determination. The energy efficiency of the power quality evaluation system is equivalent to the linear weighting of the product of the weights of each sub-indicator and the corresponding affiliation degree. Reference can be made to the expert system energy efficiency evaluation criteria assessment criteria to judge the advantages and disadvantages. The specific judging criteria are shown in Table 2.

Table 2.
Evaluation standards of system performance.
In summary, the flowchart for evaluating the system using the data-driven extension hierarchy analysis based on improved determinant values is shown in Figure 2.
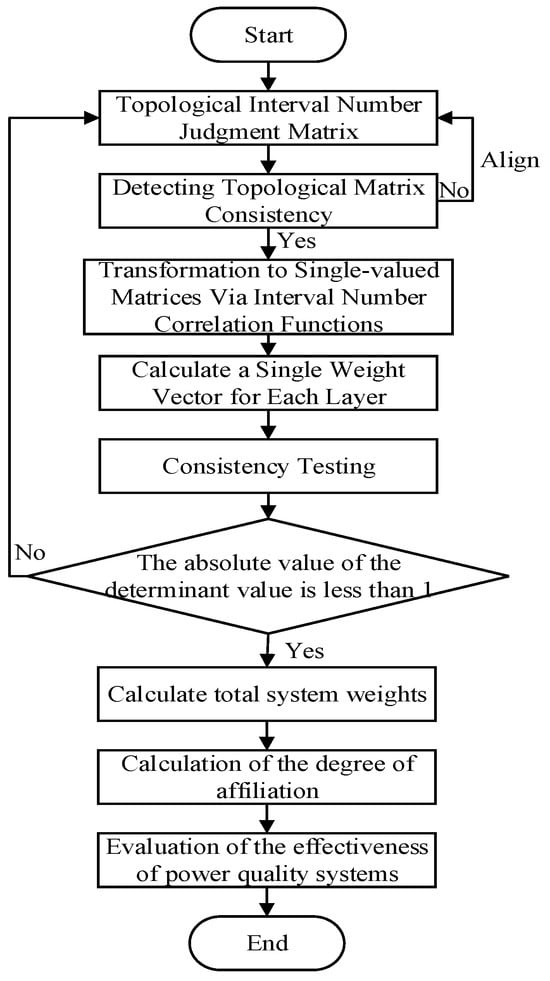
Figure 2.
Power quality system efficiency evaluation flowchart.
4. Results and Discussion
4.1. Example Analysis
The main configuration of the computer platform is win10 system, Intel(R) Core(TM) i5-9300H, RAM 8 GB. And the name of the manufacturer is Lenovo, sourced from Beijing, China. This paper is mainly completed by using python3.9 language programming.
Regarding the data source, we have sampled ideal data and conducted random simulations to generate experimental data. Specifically, we have extracted key parameters from existing theoretical models and performed random sampling to generate experimental data. Firstly, we have extracted pivotal parameters such as voltage deviation, harmonic content, and frequency deviation from well-established theoretical models of power quality. Subsequently, leveraging random sampling techniques, we have replicated the natural range and distribution of these parameters in real-world scenarios. Ultimately, based on these sampled values, we have utilized SPSS v28.0.1.1 analysis software to generate a series of realistic and representative experimental datasets.
For the power quality system evaluation system proposed in this paper, the CR values and their corresponding determinant values that meet the judgment conditions are given in Table 2, Figure 3, and Figure 4, respectively. From Table 3, as well as Figure 3 and Figure 4, it can be seen that the determinant values of its judgment matrix are stable on the interval (−1, 1), but the determinant values of other intervals are very different, so that the selection of the determinant values that meet the judgment criteria and its judgment matrix can be distinguished within the range of (−1, 1).
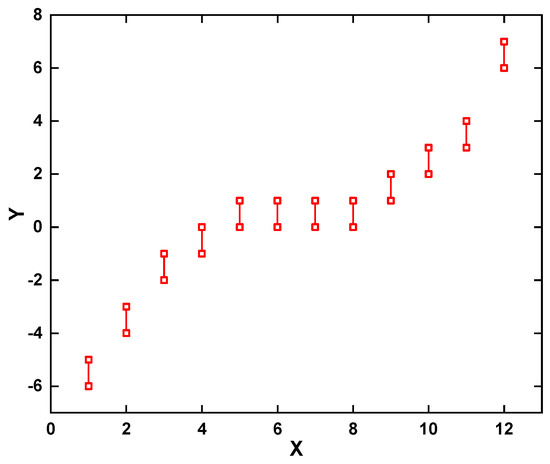
Figure 3.
The value of the consistency index CR of the judgment matrix.
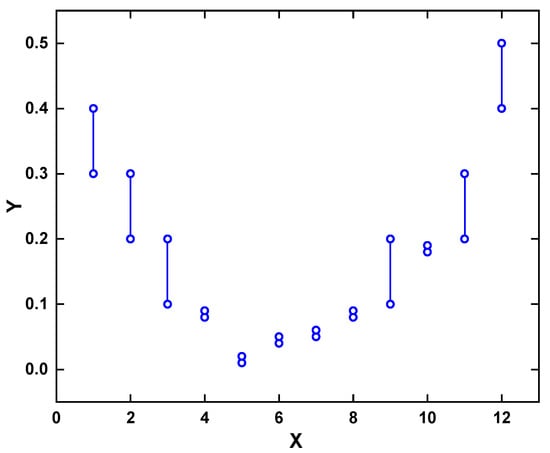
Figure 4.
The value of the consistency index CR corresponding to the determinant.

Table 3.
Evaluation standards of system performance.
Assuming that the absolute value of the determinant is at (−1, 1), the matrix consistency is better or worse depending on the size of the absolute value of the determinant. For the determinant less than 1, the matrix consistency is good; the opposite is poor. If it is greater than 1, the internal elements of the matrix need to be analyzed to detect whether the order consistency is satisfied; if so, the criteria are acceptable; otherwise, the input values need to be adjusted. The results show that the method proposed in this paper is compatible with the traditional matrix consistency determination criterion CR < 0.10.
For the decision-making problem, in order to determine the importance of each indicator, it can be generally categorized into three levels: the target level, the criterion level, and the indicator level. Table 3 demonstrates the values of the extension intervals of the criterion layer derived by two groups of experts with reference to the assessment system constructed in this paper.
As can be seen from Table 4, the plasticity of the extension intervals obtained by the method of this paper performs well. At this point, the computation of the matrix eigenvectors consisting of the lower endpoints of the interval has:

Table 4.
Contribution of criterion layer to target layer.
Computing the eigenvectors of the matrix consisting of the endpoints on the interval has:
From Equation (16), we get k = 0.976 < m = 1.057, so the judgment matrix is in good agreement.
From S = (S1, S2,…, Snk)T = <kx−, kx+>, the weights S1 = <0.759, 0.853>, S2 = <0.203, 0.217> are found; thus, there is V(S1 ≥ S2). Then we have:
Based on Equation (17), we can get P1 = 2.64, P2 = 1.1. At this time, we have the two evaluation indicators to the target layer of the ranking of P = (0.855, 0.456)T. Similarly, the indicator weights of the indicator layer of the evaluation system are calculated as 0.602, 0.451, 0.224, and 0.199.
Based on Wk = (W1k, W2k,…, Wnkk)T = PkWk−1, the synthetic ranking of indicators of the indicator layer to the target layer can be calculated as W3 = {0.413, 0.207, 0.121, 0.156, 0.377}.
The data are used as an example to verify the evaluation method of this paper. According to various national standards, including GB/T 12325-2008 [25], GB/T 15945-2008 [26], GB/T 15543-2008 [27], GB/T 12326-2008 [28], and GB/T 24337-2009 [29], detailed data are shown in Table 5, where five grades of excellent, good, moderate, qualified, and poor are used to indicate the grade of power quality.

Table 5.
Evaluation parameters of system performance.
Referring to the data in Table 5, we construct the matter-element model, and we have:
- Classical domain matter-element
The classical domain matter-element Rj denotes the power quality matter-element of the jth class.
where Ri denotes the matter-element form of the evaluation result, Ni denotes the assessment interval, and c denotes the characterization of the power quality.
- 2.
- Section domain matter-element
The overall assessment interval for power quality can be expressed using Rp.
- 3.
- Matter-element to be evaluated
R is the matter-element to be evaluated that consists of the monitoring data. Taking the measured values in Table 5 as an example, we have:
The above three matter-elements are substituted into the following equation for the correlation value. The optimal value A is:
- 4.
- Calculate the correlation value
Assuming that the three-phase voltage unbalance values are distributed in the domain of rank superiority, we have:
The optimal value is obtained at a, so we have ρ(x, x0, X) = x − b = −0.133, D(x, x0, X) = ρ(x, X) − ρ(x, X0). At this time, we have:
Similarly, all the correlation values are calculated and integrated into a correlation matrix K. Then we have:
A positive correlation value means that the assessment result is within a reasonable range, and the higher it is, the closer the assessment result is to the optimal value. A negative correlation value means that the assessment result is out of range, and the higher the absolute value, the more it is outside this range.
The final result of the evaluation can be obtained by synthesizing the target weights W3 and the associated value matrix K, as shown in Equation (19).
The P factor comprehensively evaluates the degree of association of each power quality class, “∘” indicates the weighted summation after vector dot-multiplication. Substituting the correlation matrix and target weights of measured data into Equation (19), and utilizing the linear weighting result, we can get P = 0.9286. According to Table 1, we can see that the power quality rating result of this measured data is “excellent”.
4.2. Discussion
In this paper, the study focuses on a rated power of 16 kW and a rated voltage of 220 V. Depending on the primary impact indicators in a given voltage event, both HVDC (high-voltage direct current) and HVAC (high-voltage alternating current) systems can be utilized. Additionally, the same methodology is applicable to both low-voltage and high-voltage power systems. The frequency range under investigation spans from 50 Hz to 50 ± 1 Hz.
The research in this paper aims to combine the principle of extension and the hierarchical analysis method with improved determinant values based on the data-driven basis, which can better evaluate the power quality data while reducing the influence of subjective factors on the judgment matrix. In the example analysis, firstly, the CR value and its corresponding determinant value that meet the judgment conditions are analyzed, and it is found that this paper’s method can be compatible with the traditional matrix consistency judgment standard CR < 0.10. And later, using the values of extension intervals of the criterion layer given by the expert system combined with the data of electric energy in a laboratory, and utilizing the electric energy evaluation system proposed in this paper, we get the final evaluation index of 0.9286 and the evaluation result is “excellent” according to the evaluation standard, which proves the effectiveness of the evaluation system proposed in this paper.
5. Conclusions
The power quality problem is becoming more and more serious, which causes huge economic losses, and it is necessary to assess the power quality. Therefore, this paper proposes a data-driven power quality assessment system based on the improved determinant value of the extension hierarchical analysis method, which can better carry out the assessment of power quality, ensure the stable operation of the power system, improve the efficiency of the utilization of electric energy, prevent equipment failures, and help to formulate a scientific governance program.
Certainly, the power quality assessment system proposed in this paper has good effectiveness, but there are still some shortcomings, not comprehensively considering all the indicators affecting power quality, while not taking into account the intrinsic connection between the indicators. Therefore, we believe that it is important to rationally utilize a larger number of indicators and indicator-related information. For example, graph models can be used to define the correlation between indicators through relevant knowledge and experience, and the increase in the number of nodes representing the evaluation indicators will not have a large impact on the complexity of the graph, which may be used to combine for power quality assessment.
In the future work, we will further improve the proposed power quality assessment system, and more real data will be used to test the assessment system. Furthermore, the potential practical applications studied in this paper are mainly focused on areas such as hospital energy management, new energy grid connection detection and substation detection. Meanwhile, we will consider the economic cost of power quality to explore the intrinsic connection between power quality and economic cost, and then provide appropriate suggestions for subsequent decision-making on power quality event management.
Author Contributions
Conceptualization, J.Z. and T.S.; data curation, T.S. and M.Y.; formal analysis, P.G. and J.B.; funding acquisition, J.S.; investigation, P.G.; methodology, P.G. and J.B.; resources, J.Z.; supervision, M.Y.; validation, J.Z., T.S. and P.G.; writing—original draft, H.W.; writing—review and editing, M.Y., H.W. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Graduate Student Innovation Program of Beijing University of Civil Engineering and Architecture, grant number PG2024147.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Jingyi Zhang, Pan Gu and Jinming Bao was employed by the State Grid Economic and Technological Research Institute Co., Ltd. And author Tongtian Sheng was employed by the State Grid Corporation of China. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Guo, J.; Jiang, J. Comprehensive Evaluation of Power Quality with Variable Fuzzy Cloud Model. J. Zhengzhou Univ. (Nat. Sci. Ed.) 2021, 53, 110–118. [Google Scholar] [CrossRef]
- Tymchuk, S.; Miroshnyk, O.; Shendryk, S.; Shendryk, V. Integral fuzzy power quality assessment for decision support system at management of power network with distributed generation. In Proceedings of the International Conference on Information and Software Technologies, Sevilla, Spain, 29 August 2018. [Google Scholar] [CrossRef]
- Shi, H.; Li, Y.; Jiang, Z.; Zhang, J. Comprehensive power quality evaluation method of microgrid with dynamic weighting based on CRITIC. Meas. Control 2021, 54, 1097–1104. [Google Scholar] [CrossRef]
- Barros, J.; de Apráiz, M.; Diego, R.I. Power Quality in DC Distribution Networks. Energies 2019, 12, 848. [Google Scholar] [CrossRef]
- Dong, H.; Tian, Y.; Chen, J.; Wang, Y.; Zhao, B. Comprehensive Evaluation of Power Quality Based on Time-series Interval Valued Fuzzy Soft Set. Adv. Technol. Electr. Eng. Energy 2022, 41, 46–54. [Google Scholar]
- Milanović, J.; Abdelrahman, S.; Liao, H. Compound index for power quality evaluation and benchmarking. IET Gener. Transm. Distrib. 2018, 12, 4269–4275. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, Z.; Weng, X.; He, M.; Zhang, G.; Yuan, D.; Jin, T. A Novel Approach for Evaluating Power Quality in Distributed Power Distribution Networks Using AHP and S-Transform. Energies 2024, 17, 411. [Google Scholar] [CrossRef]
- Lu, Y. Power Quality Integrated Evaluation Based on the lmproved AHP. Software 2019, 40, 16–20. [Google Scholar]
- Rodrigues, N.M.; Janeiro, F.M.; Ramos, P.M. Power Quality Transient Detection and Characterization Using Deep Learning Techniques. Energies 2023, 16, 1915. [Google Scholar] [CrossRef]
- Huang, H.; Ni, D.; Liu, X. Comprehensive Evaluation of Power Quality Based on Graph Convolutional Network. Electron. Sci. Technol. 2023, 1–6. [Google Scholar] [CrossRef]
- Jia, X.; Li, X.; Yan, S.; Wang, S.; Xu, S. Power Quality Assessment of SESN Power Supply Network Based on Deep Learning. Control Eng. China 2021, 28, 2052–2059. [Google Scholar] [CrossRef]
- Wan, X.; Wang, H. Classification and Evaluation of Power Quality Disturbance Based on SVM Machine Learning Algorithm. Electr. Eng. 2021, 96–99. [Google Scholar] [CrossRef]
- Li, S.; Chen, D.; Qiu, Q.; Shi, J.; Xu, W.; Song, X.; Chen, Z. Comprehensive Assessment of Power Quality Based on Random Forest. Mod. Electr. Power 2019, 36, 81–87. [Google Scholar] [CrossRef]
- Yu, H.; Liu, Y.; Huang, T.; Wu, Z.; Luo, Y.; Chen, X.; Xiong, W.; Yuan, X. Power Quality Evaluation Based on Extension Cloud Model and Fuzzy Proximity Degree. Smart Power 2022, 50, 23–29+52. [Google Scholar]
- Li, L.; Liu, J.; Ling, Y.; Zhou, X.; Zhang, Y. Power Quality Comprehensive Evaluation Based on Matter-Element Theory and Evidence Theory. Trans. China Electrotech. Soc. 2015, 30, 383–391. [Google Scholar] [CrossRef]
- Liao, J.; Liu, Y.; Guo, C.; Zhou, N.; Wang, Q.; Kang, W.; Vasquez, J.; Guerrero, J. Power quality of DC microgrid: Index classification, definition, correlation analysis and cases study. Int. J. Electr. Power Energy Syst. 2024, 156, 109782. [Google Scholar] [CrossRef]
- Ostrowska, A.; Michalec, Ł.; Skarupski, M.; Jasiński, M.; Sikorski, T.; Kostyła, P.; Lis, R.; Mudrak, G.; Rodziewicz, T. Power Quality Assessment in a Real Microgrid-Statistical Assessment of Different Long-Term Working Conditions. Energies 2022, 15, 8089. [Google Scholar] [CrossRef]
- Zheng, J.; Huang, J.; Chen, Y.; Hu, X. Research on Control Strategy of Multifunctional Voltage Sag Treatment Equipment. Electr. Drive 2023, 53, 71–78. [Google Scholar] [CrossRef]
- Michalec, Ł.; Jasiński, M.; Sikorski, T.; Leonowicz, Z.; Jasiński, Ł.; Suresh, V. Impact of Harmonic Currents of Nonlinear Loads on Power Quality of a Low Voltage Network—Review and Case Study. Energies 2021, 14, 3665. [Google Scholar] [CrossRef]
- Wang, N.; Zheng, S.; Gao, W. Microgrid Harmonic Mitigation Strategy Based on the Optimal Allocation of Active Power and Harmonic Mitigation Capacities of Multi-Functional Grid-Connected Inverters. Energies 2022, 15, 6109. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, X.; Liu, Y.; Zhu, Y.; Chen, J. Control Strategy of Clustered Micro-Grids for Grid Voltage Unbalance Compensation without Communications. IET Gener. Transm. Distrib. 2020, 14, 4410–4415. [Google Scholar] [CrossRef]
- Xiao, Y.; Lu, W.; Li, Y.; Zhong, Y.; Qi, Y.; Peng, J. Research on index system and its evaluation methods of urban distribution network development form. Power Syst. Prot. Control 2021, 49, 62–71. [Google Scholar] [CrossRef]
- Shang, J.; Xu, Q.; Yang, J.; Guo, M. Study on quantitative estimation method of energy saving and emission reduction of renewable energy system based on fuzzy matter-element method. Sustain. Energy Grids Netw. 2024, 38, 101223. [Google Scholar] [CrossRef]
- Zhang, J.; Sheng, T.; Gu, P.; Yu, M.; Yan, J.; Sun, J.; Liu, S. Dynamics Power Quality Cost Assessment Based on a Gradient Descent Method. Energies 2024, 17, 2104. [Google Scholar] [CrossRef]
- GB/T 12325-2008; Power Quality—Deviation of Supply Voltage. National Standards of the People’s Republic of China: Beijing, China, 2008.
- GB/T 15945-2008; Power Quality—Frequency Deviation for Power System. National Standards of the People’s Republic of China: Beijing, China, 2008.
- GB/T 15543-2008; Power Quality—Three-Phase Voltage Unbalance. National Standards of the People’s Republic of China: Beijing, China, 2008.
- GB/T 12326-2008; Power Quality—Voltage Fluctuation and Flicker. National Standards of the People’s Republic of China: Beijing, China, 2008.
- GB/T 24337-2009; Power Quality—Interharmonics in Public Supply Network. National Standards of the People’s Republic of China: Beijing, China, 2009.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).