A Survey of Quantitative Techniques in Electricity Consumption—A Global Perspective

Abstract

This study uses the Scopus and Web of Science databases to review quantitative methods to forecast electricity consumption from 2015 to 2024. Using the PRISMA approach, 175 relevant publications were identified from an initial set of 821 documents and subsequently subjected to bibliometric analysis. This analysis examined publication trends, citation metrics, and collaboration patterns across various countries and institutions. Over the period analyzed, the number of articles has steadily increased, with a more rapid rise observed after 2020. Although China dominates this research field, strong bibliographic coupling worldwide indicates significant international collaboration. The study suggests that no single method consistently outperforms others across all contexts and that forecasting methods should be adapted to regional contexts, considering specific economic, social, and environmental factors. Furthermore, we emphasize that review papers should compare methods and results regarding both time horizon and temporal resolution, as these aspects are crucial for the accuracy and applicability of the forecasts.

1. Introduction

In the 21st century, the world has faced numerous challenges, but the energy crisis is particularly prominent because without sustainable supply and efficient energy management, the world cannot solve the current severe energy supply–demand gap. The pressing issues around climate change and the simultaneous demands of economic stability and energy security have elevated the global dialogue regarding the future of our energy sources. The transition to renewable energy is a central theme in this conversation, as it is increasingly recognized as a substitute for conventional power sources and a critical component in radically altering our connection with the environment, our economy, and broader societal values [1].

Renewable energy sources such as solar, wind, hydro, geothermal, and biomass play a critical role in guiding the course of this global energy revolution. These sources signify a profound shift in the production and consumption of energy, reflecting a broader commitment to sustainability, resilience, and a more harmonious balance with the natural world. They go beyond simple technological substitutes. Fossil fuels—coal, oil, and natural gas—have historically played a crucial role in creating and maintaining the world’s energy infrastructure, supporting many of the advancements in economics and technology. By 2024, the world’s energy consumption will have increased by 1.8%, primarily due to Asia’s robust demand. The demand for fossil fuels will hit historic highs despite persistently high costs and unresolved supply chain issues, while the demand for renewable energy will increase by 11% (Energy Outlook 2024 [2]).

These non-renewable resources have been crucial for advancing technology, promoting urban development, and boosting economic progress, but their widespread usage has hurt the environment. One of the leading causes of the rising carbon dioxide emissions that underpin global climate change is the burning of fossil fuels. The production and use of fossil fuels have also resulted in significant pollution and biodiversity loss, endangering the stability and well-being of the planet’s ecosystems.

Several factors have significantly impacted these transitions: shifting economic environments, including market structures and resource availability; sociopolitical dynamics, such as public opinion and policy decisions; worldwide events, like wars or environmental crises, which can significantly alter priorities and resources; and shifting consumer demands, which are influenced by shifts in lifestyle, awareness, and economic capabilities [3].

The electrical industry is evolving rapidly, which creates more opportunities and requires empirical research like forecasting. Numerous novel techniques and areas of application have emerged in recent years. The fragmented scientific work must be merged and structured as research expands and becomes more specialized and diverse. It is critical to balance the production and consumption of electricity. Its implementation primarily depends on the strategies and tactics used to plan electricity production. Since having an accurate prediction increases the validity of management decisions, forecasting is essentially one of the planning instruments. Probabilistic and contemporary forecasting techniques employ classical and deep machine learning algorithms, the rank analysis methodology, fuzzy set theory, singular spectral analysis, wavelet transformations, grey models, and other methods. Classical forecasting techniques are grounded in the theory of regression and statistical analysis (regression, autoregressive models).

For over 33 years, the global patterns of electricity consumption growth have been sustained (Figure 1). Since electricity is a vital resource in the current stage of human development and is necessary for household and professional activities, there are no requirements for cutting back on energy consumption in the future. Enerdata, a global energy and climate portal, reports statistics for 2024 that show that, at 25,759 TWh, electricity consumption in 2023 was 10.08% and 9.75% higher than in 2020 and 2019, respectively. Data on the electrification of final consumption worldwide also support the increase in electricity consumption. The global electrification trend is still increasing; the indicator increased by 31.21% from 2010 to 2023 (https://www.enerdata.net/publications/reports-presentations/world-energy-trends.html, (accessed on 15 July 2024)).

In Figure 2, as per the global energy and climate data provided by Enerdata, Asia had the highest growth rate of electricity consumption from 2000 to 2023, with a rate of 286.09%. Comparably, for the Middle East, Africa, Latin America, CIS, Pacific, North America, and Europe throughout this time, the growth rates for electricity are 199.01%, 103.75%, 91.31%, 39.26, 33.39%, 14.32%, and 9.18%, respectively. However, if we look at the data on the top 10 countries’ electricity consumption in 2023, we can see that China consumed the most, with 8391.78 TWh. After this, the USA, India, Brazil, Canada, South Korea, Germany, and France were the countries with the highest electricity consumption. The USA has the second most electricity consumption user country with 4065.29 TWh, with similar figures for India (1406.66 TWh), Russia (996.59 TWh), Japan (908.65 TWh), Brazil (594.30 TWh), Canada (557.56 TWh), South Korea (557.56 TWh), Germany (557.56 TWh), and France (557.56 TWh). Figure 2 displays the dynamic pattern of power use in the eight regions from 2010 to 2023.

Quantitative research is distinguished by its use of deductive methods in the research process to establish, refute, or enhance the validation of established hypotheses. This research methodology entails the quantification of variables and the examination of the associations between variables with the aim of uncovering patterns, correlations, or causal connections. Researchers may utilize linear techniques for gathering and analyzing data, which yield statistical data. The fundamental principles that underpin quantitative research are impartiality, objectivity, and the attainment of a substantial breadth of information (e.g., a statistical summary from a significant sample). This method is usually suitable when your main objective is to elucidate or critically assess (Leavy [4], p. 9).

There is a plethora of research on electricity consumption/load/demand forecasting based on geographical regions, time, nature of datasets, and methodology. Quantitative methods encompass a variety of statistical, econometric, and machine-learning techniques, each tailored to address specific forecasting horizons and accuracy requirements. Traditional methods such as regression analysis, autoregressive models, and time series analysis have been foundational in this field, providing a basis for understanding consumption patterns and trends. Numerous researchers have compared different techniques for forecasting electricity consumption. In this context, studies have compared several methods based on quantitative methods, including time series econometrics, machine learning, deep learning, hybrid models, and optimized models, e.g., [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27].

On the other hand, some studies focus on time horizons, e.g., [28,29,30,31,32,33,34,35,36,37,38,39,40]. Although the definitions of the time horizon differ by author, typically, they are divided into three distinct categories: (1) short-term forecasts, which cover up to one week ahead; (2) mid-term forecasts, spanning from one to several months; and (3) long-term forecasts, extending beyond 1 year up to 30 years. Each of these time horizons serves different operational and strategic purposes. Short-term forecasts are used for day-to-day operational planning of the power system, including solving unit commitment and economic dispatch problems, electricity trading, security constraints, and power flow analysis. Mid-term forecasts are essential for activities such as maintenance scheduling, estimation of electricity losses in the networks, and minor infrastructure modifications. Long-term forecasts are primarily utilized for strategic planning of infrastructure expansion, encompassing investments in new generation facilities, energy storage systems, and power grid development [41].

Short-term forecasting is essential for Distribution System Operators (DSOs), electricity retailers, energy communities and clusters, industry, and Virtual Power Plants (VPPs). Most of the electricity for these consumers is purchased on the day-ahead market based on consumption forecasts. Any deviations between the forecast and actual demand are then managed in the real-time balancing market, where prices have become increasingly volatile in recent years. Higher volumes in the balancing market result in more significant financial losses due to forecasting errors.

Ref. [42] examined that a 1% reduction in the MAPE results in an average retailer profit gain of EUR 0.72 per year per household. For a major electricity supplier like British Gas, this equates to approximately EUR 3.9 million per year. In the experiment described in [43], seven algorithms were tested using different look-ahead windows (i.e., 1, 6, 12, and 24 h). The experiment was conducted on a Virtual Power Plant (VPP) composed of ten manufacturing factories: two cement plants, two forges, three metal factories, one paper mill, and two steel plants. The study proved that energy demand forecasting benefits VPPs in planning and optimizing energy dispatching strategies to meet user power demand.

Mid-term electricity demand forecasting is crucial for grid operators and utility companies. Besides helping them schedule maintenance and planning minor infrastructure modifications, mid-term forecasts can also impact their economic performance. For instance, the study of [44] describes how mid-term forecasting using multiple regression (MR) and time series models could support Dutch DSOs in purchasing the right amount of electricity one year ahead with hourly intervals to offset transmission losses via forward contracts with a fixed price and fixed volume.

Short- and mid-term forecasting also contributes to reducing GHG emissions by optimizing the use of storage assets and demand-side response actions. This allows for the most efficient generation dispatch, including natural gas-fired units. Long-term forecasting helps policymakers, TSOs, and energy utilities make informed decisions regarding future electricity needs and optimize resource allocation to ensure the adequacy and reliability of the electricity supply. They constitute the critical input to elaborate Long-Term Low Emission Development Strategies (LT-LEDS) to guide countries in aligning their developmental goals with the Paris Agreement’s objective to limit global warming to below 2 °C [45].

Electricity consumption is shaped by various factors, causing variations in consumption patterns across different time scales, such as days, weeks, months, seasons, and years. Changes in weather conditions, economic activity, technological advancements, and social behavior drive these variations. In temperate regions, the daytime during winter is much shorter than in summer, directly impacting heating/cooling needs and people’s daily activities.

Researchers have employed univariate and multivariate analysis techniques to forecast electricity consumption. Univariate analysis focuses on forecasting future consumption based solely on past consumption data, assuming that future temporal patterns are primarily derived from past behavior. The development of smart metering allows consumption time series data to be composed of observations at different time intervals: the minute-level, hourly, daily, weekly, monthly, quarterly, and annual, depending on the purpose of the study and the desired forecasting time horizon.

In contrast, multivariate analysis incorporates additional external variables, such as weather, economic indicators, and demographic trends, providing a more comprehensive approach to understanding and forecasting electricity demand.

In multivariate analysis for short- and mid-term forecasts, the most significant independent variables often include calendar data, time variables, meteorological factors, and certain dummy variables to capture trends. For example, in Ref. [46], the authors used variables such as temperature, categorical variables representing the day of the week and national holidays, a numerical variable indicating the current day of the year, and a time of day index. In Ref. [47], the meteorological data considered included temperature, humidity, wind speed, and rainfall. Ref. [48] examines the relationship between electricity consumption and weather variables such as temperature, precipitation, relative humidity, wind speed, cloud cover, and sun duration during different periods (morning, peak, evening, and night).

The findings of a study at the household level in Ireland [49] revealed that, in addition to weather conditions, socio-demographic factors such as occupation and employment status, which influence lifestyle, play a significant role in shaping electricity usage. Moreover, dwelling characteristics were also found to impact household electricity consumption strongly.

In long-term forecasting, which spans decades, socioeconomic factors are fundamental in shaping electricity consumption behavior. Key variables include demographic trends like population growth and urbanization, which directly influence energy demand. Economic growth, measured by GDP, and the economy’s structure—i.e., whether it is heavily industrial, service-oriented, or balanced—are also significant. Additionally, macroeconomic policies, such as energy pricing and regulation, drive technological choices, investments, and efficiency improvements.

For instance, a case study referenced in [50], which employed Multivariate Regression and End-Use Methods, identified GDP, population, electrification ratio, and electricity price as the most significant influence on long-term demand forecasting. In a study employing an enhanced artificial neural network (ANN) model [51], the authors reported a correlation coefficient of approx. 0.9 or higher between electricity consumption and influencing factors such as GDP, Value Added of Economic Sectors, GDP per Capita, Population, Per Capita Consumption Expenditure, and Total Retail Sales of Consumer Goods. A review of key independent variables in long-term forecasting is presented in [52]. This list is further expanded to include environmental factors such as temperature, Cooling Degree Days (CDDs), and Heating Degree Days (HDDs).

In a study conducted in Thailand [53] using monthly data from 2002 to 2020, the authors identified the industrial production index, electricity price, and an energy policy dummy variable as the critical demand drivers of electricity consumption.

Industry transformation, high-resolution data availability, and advancements in data processing capabilities have significantly influenced the evolution of electricity demand forecasting methods and models.

In the past, traditional methods such as regression analysis, autoregressive models, and time series analysis were sufficient for short- and mid-term forecasting to address the relatively stable and predictable nature of electricity demand. These methods provided a foundation for understanding consumption patterns and trends, supporting the industry in making informed operational and strategic decisions.

However, as the power industry has become more dynamic—characterized by the integration of intermittent renewable energy sources, increased decentralization, and more volatile consumption patterns—there has been a corresponding need for more sophisticated forecasting techniques. Currently, the most widely adopted methods can be categorized into three primary types: deep learning models, hybrid models, and ensemble methods. Ref. [54] confirms this, which indicates that based on articles published between 2012 and 2022, the most commonly used short-term forecasting methods in the residential sector are machine learning (approximately 58%), statistical methods (approximately 24%), and a combination of both (approximately 18%).

Hybrid models, which integrate multiple forecasting approaches, are gaining popularity due to their enhanced predictive accuracy.

These modern techniques can handle more extensive and complex datasets, capture nonlinear relationships, and adapt to real-time changes in consumption behavior, which are critical in today’s power systems. They also significantly enhance the ability to forecast electricity consumption with greater accuracy and granularity.

Long-term forecasting relies heavily on traditional statistical approaches, such as trend analysis and end-use models. According to a study conducted in 2015 [55], nearly 60% of the forecasting models reviewed were statistical in nature, with end-use models accounting for approximately 4% and AI-based models constituting about 24%. A subsequent literature review covering the period from 2015 to 2021 [52] revealed that 50% of the papers surveyed employed exclusively statistical models, 25% utilized only AI-based models, and the remaining studies adopted hybrid or other approaches.

Our study aims to systematically review the existing quantitative methods used in forecasting electricity consumption, specifically focusing on 2015 to 2024. Based on a bibliometric analysis of 175 papers, this paper explores the rapid growth in electricity demand forecasting research. It examines the global research landscape by analyzing publication trends, key contributors, leading journals, methodological advancements, research interconnectivity, and international research collaborations. A comprehensive summary of 33 selected papers details the study’s authors, sample periods, focus countries, target variables, methodologies employed, and key empirical findings.

The present work makes the following contributions to the literature on energy modeling:

• This paper provides an extensive and in-depth evaluation of earlier cutting-edge research on electricity consumption forecasting, considering the methodologies employed, the time framework including period and frequency, and the accuracy metrics utilized in the forecast.
• This study provides a succinct synopsis of the practical features of the compared methods for forecasting electricity consumption/loading/demand.
• This study determines the obstacles and prospects for additional research in forecasting electricity consumption/load/demand.

In other similar review papers on electricity consumption forecasting, methods have been described and compared, but they often lack a clear connection to the time framework. This omission can create the mistaken impression that some methods are universally effective, regardless of the scale and temporal resolution. In our work, we emphasize that these aspects are vital, demonstrating that review papers should compare methods and results regarding both time horizon and temporal resolution. Additionally, given the rapid evolution of forecasting methods, our publication is up-to-date and incorporates the most recent literature.

The remainder of the paper is organized as follows: Section 2 reports the relevant materials and methods. Section 3 provides a comprehensive literature review of the most recent advancements in forecasting methods. Section 4 presents and discusses the results. Section 5 provides the conclusions.

2. Material and Methods

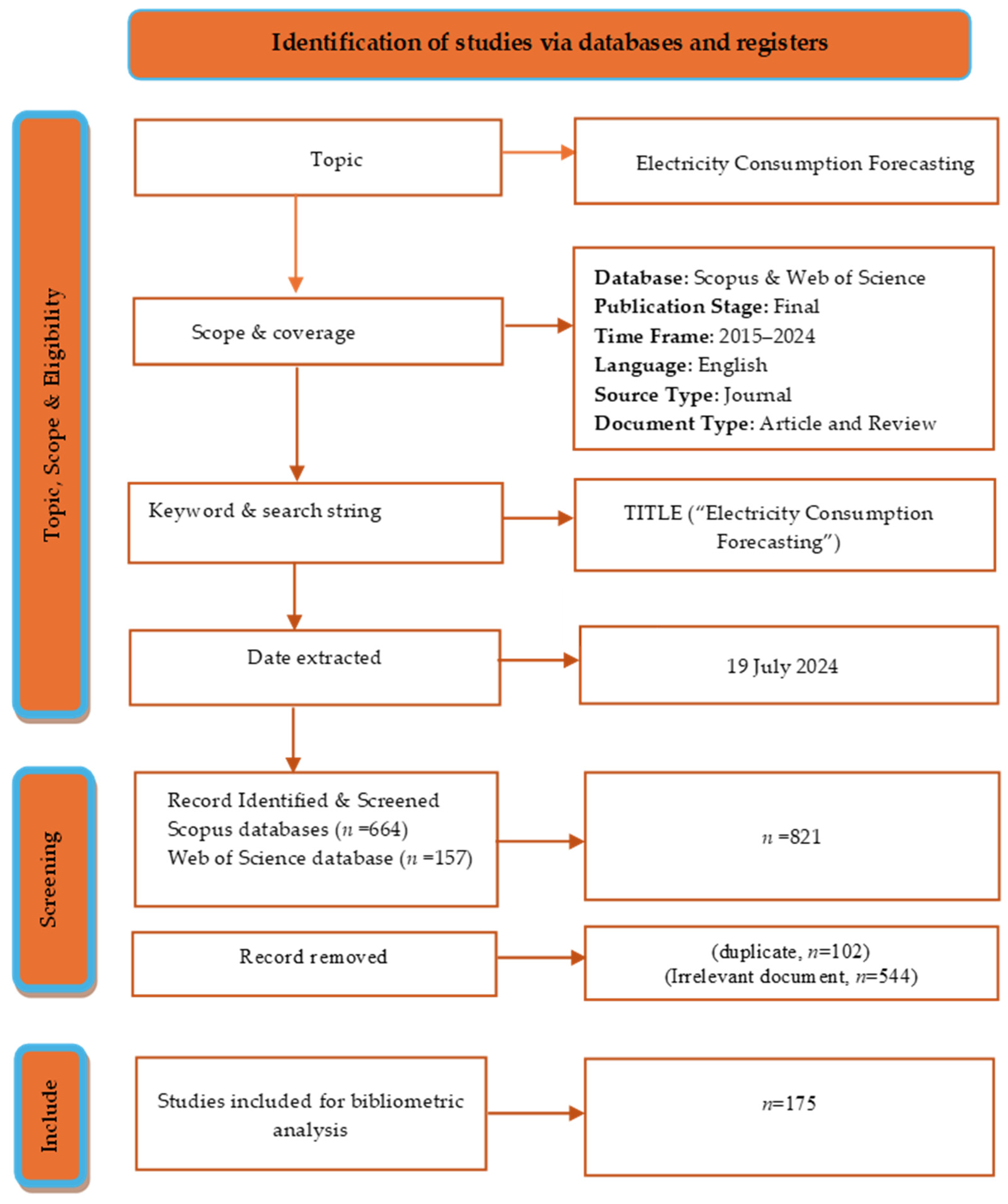
2.1. Information Extraction

Figure 3 shows our search strategy. To avoid double counting in this investigation, we deleted erratum documents and withdrawn papers that would have produced false-positive results. Every document was examined using bibliometrics. Using Microsoft Excel 2016, we produced the pertinent charts and graphs and calculated the citation metrics. Har-zing’s Publish and Perish software (https://harzing.com/resources/publish-or-perish, accessed on 25 July 2024) was used to calculate the frequencies and percentages of the published materials. VOSviewer (version 1.6.20) created and visualized the bibliometric networks [56].

2.2. Data Analysis

The current study examined previous research on electricity consumption forecasting using several quantitative methods (e.g., time series models, grey forecasting, machine learning methods, deep learning approaches, and hybrid forecasting methods). The study considered research and review studies from 2015 and earlier during the review. In the last five years, the dynamics of research have changed, and in applied research work, many researchers have adopted artificial intelligence methods for predicting the accuracy of electricity consumption. However, we also focused on earlier research that reflected the primary advancement paths in electricity consumption forecasting. From 2015 to 2024, bibliometric analysis was carried out using the Web of Science and the Scopus database.

The study extracted the data from the Web of Science by using the query (https://www.webofscience.com/wos/woscc/summary/f590ae0f-6d99-4f0a-b591-df580686e2fc-fc9b44bc/relevance/1, accessed on 17 July 2024). The study ensured the validity of the data by focusing on the most reliable and prominent research journals (e.g., Elsevier, Springer Nature, Taylor & Francis, Wiley, Emerland, etc.). Similarly, the study selected the research area most related to electricity consumption forecasting (focused on areas like energy fuels, engineering, business economics, operation research management science, computer science, ecology, environmental science, mathematics, etc.). The search queries in both databases were created with Boolean operators like electricity AND usage AND forecasts.

Scopus and the Web of Science are two of the most comprehensive and widely respected databases in academic research. Both databases index peer-reviewed articles from reputable journals such as Elsevier and IEEE, ensuring that the studies included in the review are of high quality and have undergone rigorous academic scrutiny.

Additionally, these databases are particularly valuable for bibliometric analysis, as they provide detailed citation data crucial for examining publication trends, authorship patterns, and collaboration networks. The search term “electricity consumption forecasting”, which appears in the article’s title, abstract, and keywords, was used to find pertinent English-language publications with research on the subject. This study only included articles and review documents and excluded conference and book chapters. Because it is easy for readers to follow up on the pertinent information, the current study concentrated on the article titles. It is a pertinent subject that is important to this study’s goal and research field. This study eliminated and retracted document kinds to prevent multiple or fraudulent document counts (false-positive data) [58].

Using keywords and terms like artificial intelligence (AI), electricity consumption forecasting (ECF), time series (TS), machine learning (ML), and combinations of AI and ECP, ML and ECF, ML and ECF, and ML and ECF, the current study selected 175 cutting-edge research works out of 821 documents from Scopus and the Web of Science. Following a thorough analysis, each downloaded research work was divided into two categories for electricity consumption forecasting: engineering approaches and data-driven (artificial intelligence) methods.

The study extracted the data from Scopus by using the keywords: TITLE-ABS-KEY (electricity AND consumption AND forecasting) AND PUBYEAR > 2014 AND PUBYEAR < 2025 AND (LIMIT-TO (LANGUAGE, “English”)) AND (LIMIT-TO (DOCTYPE, “ar”) OR LIMIT-TO (DOCTYPE, “re”)) AND (LIMIT-TO (PUBSTAGE, “final”)) AND (LIMIT-TO (SUBJAREA, “ENER”) OR LIMIT-TO (SUBJAREA, “ENGI”) OR LIMIT-TO (SUBJAREA, “ENVI”) OR LIMIT-TO (SUBJAREA, “ECON”) OR LIMIT-TO (SUBJAREA, “MULT”) OR LIMIT-TO (SUBJAREA, “DECI”)) AND (LIMIT-TO (SRCTYPE, “j”)) AND (LIMIT-TO (EXACTKEYWORD, “Machine Learning”) OR LIMIT-TO (EXACTKEYWORD, “Forecasting Method”) OR LIMIT-TO (EXACTKEYWORD, “Electricity”) OR LIMIT-TO (EXACTKEYWORD, “Electricity Consumption”) OR LIMIT-TO (EXACTKEYWORD, “Electricity Consumption Forecasting”) OR LIMIT-TO (EXACTKEYWORD, “Times Series”) OR LIMIT-TO (EXACTKEYWORD, “Forecasting Models”)).

2.3. Study Framework

According to Ref. [59], every systematic review’s quality depends on its building protocol, which describes the study’s purpose, theory, and techniques. Only a small number of systematic reviews, though, provide their framework’s report. A comprehensive and articulated framework for systemic reviews aids in comprehending and assessing the employed techniques. As shown in Figure 3, this investigation used the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) model [57].

The PRISMA technique enhances objectivity and enables the researcher to assess the quality of the review [59]. In addition, the PRISMA standards allow for rapid and precise exploration of large databases, making it easier to conduct thorough and accurate investigations [59].

The PRISMA analysis was utilized as a framework for this systematic literature review (SLR) investigation. This approach uses a literature review (LR) guideline of superior quality due to its comprehensive data collection and rather stringent and meticulous process. PRISMA has the benefit of integrating precise protocols that enhance uniformity, clarity, and adherence to rigorous criteria in producing qualitative research reports. This methodology is called a systematic process because it adheres to a well-defined procedure for production and encompasses all relevant and reusable resources (replicate) that previous researchers who have adopted a similar approach to the topic have utilized to examine it. This approach enables the utilization of keywords to precisely establish the extent and constraints of the investigation. These standards additionally prohibit writers from wasting time and doubting whether the highlights of their work are adequate. PRISMA facilitates the author in locating the relevant literature that aligns with the study’s objectives by employing four steps: identification, screening, eligibility, and inclusion [60].

Moreover, the PRISMA 2020 protocol provides a solid guideline for reviewing users, such as policymakers, guideline developers, healthcare practitioners, patients, other stakeholders, authors, editors, and peer reviewers of systematic reviews. Similarly, PRISMA provides a smooth way for researchers to implement the guidelines, producing results in more accurate, thorough, and transparent reporting of systematic reviews, which facilitates the use of evidence in decision-making [61].

As seen in Figure 3, the PRISMA flow diagram has five (5) phases. Phase 1 comprises the review’s scope, questions, and inclusion/exclusion criteria.

Phase 2 searches the literature with keywords to identify potential studies. Phase 3 includes determining the addition of a paper by screening its abstracts to see if it meets the inclusion criteria. Phase 4 provides the characterization of the paper for mapping by keywords. This review aimed to document an overview of the research on electricity consumption forecasting to make way for future studies. As a result, a fifth (5) step is used, which offers an in-depth quantitative synthesis (meta-analysis) of studies included in the review. Phase 2 looks for possible research by using keywords to search the literature. Phase 3 involves evaluating a paper’s abstract to check if it fits the inclusion requirements before adding it. Phase 4 consists of characterizing the paper and mapping it using keywords. To provide a precise view of the study, this review aims to compile an overview of the literature on electricity consumption forecasts. Thus, a comprehensive quantitative synthesis (meta-analysis) of the papers included in the review is provided in the fifth phase.

The current research extracted 821 documents (articles and reviews) from Scopus and the Web of Science (see Figure 3). During the identification and screening process, six hundred and sixty-four (664) documents were extracted from Scopus, and one hundred and fifty-seven (157) articles were extracted from the Web of Science out of eight hundred and twenty-one (821) articles. Of the eight hundred and twenty-one (821) records, one hundred and two (102) were duplicates, and five hundred and forty-four (544) documents were irrelevant to the study’s objective; hence, they were removed, leaving one hundred and seventy-five (175) records shortlisted in the screening stage.

3. Comprehensive Review for Electricity Consumption Forecasting

The current section provides a comprehensive literature review of the most recent advancements in the forecasting methods considering time (e.g., short-term, long-term, and long-term). These include quantitative methods such as time series modelling, grey prediction models, machine learning models, deep learning models, probabilistic models, regression analysis, etc. Lastly, this study also reviews the comparative studies based on mixed approaches.

3.1. Review of Electricity Consumption Based on Time Span

3.1.1. Short-Term Forecasting

This subsection is based on a review of electricity consumption forecasting based on short-term periods. Many researchers have explored this topic in different regions and have used quantitative methods [28,29,30,31,32,33,34,35,36,37,38,39,40]. A vital part of an energy management system is that STLF manages time zones that can vary by a few minutes, hours, or days. It plays a major role in a power company’s daily operations and planning. The short-term forecasting strategy directly impacts savings by effectively lowering operational risks and financial expenses. As a result, the cutthroat energy market is being paid a lot of attention and is considered a severe issue [33].

Ref. [31] analyzed short-term electricity consumption by transmitting the Internet of Things (IOTs). This work focuses on forecasting an office building’s electricity consumption using a small-scale dataset of 117 daily building electricity consumption values, of which 89 are designated as the training dataset and the remaining 28 as the testing dataset. With varying prediction horizons ranging from one day to twenty-eight days, the hybrid model ARIMA (Autoregression Integrated Moving Average)–SVR (support vector regression) is presented to predict electricity used. The ARIMA, ARIMA-GBR (gradient boosting regression), long short-term memory (LSTM), and gated recurrent unit (GRU) models are compared with the suggested model, ARIMA-SVR. The experiment results indicate that the ARIMA-SVR model performs better when the prediction horizon is between 20 and 28 days, and the ARIMA model performs better when the prediction horizon is less than 20 days. With its increased flexibility, the suggested method ARIMA-SVR is a fantastic option for a more accurate electricity consumption forecast.

Ref. [32] examined the development of statistical and machine learning methods for forecasting hourly electricity demand in Ontario. This study presents several novelties, including six features, namely snow depth, cloud cover, precipitation, temperature, irradiance at the top of the atmosphere, and surface irradiance, which were identified as significant. The MAPE is a statistical measure used to assess the accuracy of a forecasting method. The hybrid BOA-NARX achieves an accuracy of approximately 3% for five consecutive weekdays across all seasons, whereas significant variation is noted in the hybrid BOA-SARIMAX. BOA-NARX offers an overall Relative Error (RE) that remains steady across all seasons, ranging from 1% to 6.56%, whereas BOA-SARIMAX exhibits instability. The results indicate a range of 0.73% to 2.98% for fall and 8.41% to 14.44% for summer. The R² values for both models exhibit a performance greater than 0.96. The overall results indicate that both models exhibit strong performance; however, the hybrid model demonstrates additional advantages. BOA-NARX demonstrates a consistent capability in managing day-ahead electricity load forecasts.

To study the short-term power load, Ref. [36] created a novel short-term load forecasting model that combines several machine learning techniques, including random forest (RF), grey catastrophe (GC (1,1)), and support vector regression (SVR). RF’s superior optimization capabilities are employed to maximize forecasting performance. The researcher used electric loads from the Australian Energy- Market Operator; the suggested SVR-GC-RF model has a higher forecasting accuracy (the MAPE values are 6.35% and 6.21%, respectively); it can offer analytical support to anticipate electricity consumption accurately.

Ref. [37] examined several algorithms and a novel hybrid deep learning model that combines LSTM and convolutional neural network (CNN) models to evaluate their effectiveness for short-term load forecasting. The suggested model is PLCNet, which is short for parallel LSTM-CNN. The proposed models are tested and compared using two real-world datasets: the “hourly load consumption of Malaysia” and the “daily power electric consumption of Germany”. R², MAPE, and RMSE were used to assess the performance of the tested models. The findings demonstrate the suitability of deep neural network (DNN) models—PLCNet in particular—as short-term prediction instruments. PLCNet greatly succeeded in load forecasting, increasing the accuracy from 83.17% to 91.18% for the German data and achieving 98.23% accuracy for the Malaysian data.

To estimate the short-term power consumption for an enterprise’s daily power consumption data, Ref. [38] observed the time series prediction model based on the EMD-Fbprophet-LSTM approach. The time series was split into a residual component and a multisong intrinsic mode function (IMF) using the EMD model. The study reported that the time series prediction model based on the EMD-Fbprophet-LSTM approach has higher forecast accuracy than the single time series prediction model. This method may substantially increase the accuracy of short-term regional power consumption prediction.

Ref. [62] used the BPNN model to analyze the short-term forecasting performance and projected sample generation helped to improve it. The accuracy of the BPNN model was improved by increasing both the number of training samples and the amount of information gleaned from the dataset—two essential components for building a robust model. The utilization of the latent information function in the projected sample generation demonstrated by the results made the upgraded BPNN model superior to the original BPNN model. The study concluded that small time series forecasts can be effectively performed using the BPNN model with projected samples.

Ref. [63] devised a two-stage approach to model electricity usage in Germany. The first phase involved formulating the average daily use, while the second step involved modeling each hourly variance from this average. Both models include temperature, industrial output, daylight hours, and numerical dummies representing days of the week and months of the year as explanatory variables. Our findings indicate that the first model, albeit less complex, provides a more accurate prediction of hourly electricity demand. The study used data from the European Network of Transmission System Operators for Electricity (ENTSO-E) from 1 January 2008 to 1 January 2014. Through a comprehensive comparison of the performance of these two models, we observe that the simpler model is based on Ranaweera et al. [64]. The more complex model based on Sotiropoulos’s thesis regularly outperforms it (available at: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=9aac3bfa9580c1541e62a9dfb393dc4a14a1d259, accessed on 10 September 2024). This is true for the overall performance and different days of the week, months of the year, and hours of the day. The findings of our study suggest that electricity consumption at different periods of the day corresponds to different commodities and should be analyzed individually for each hour.

3.1.2. Medium-Term Forecasting

This subsection is based on the reviews of the most crucial studies on medium-term forecasting for electricity consumption, e.g., [65,66]. Ref. [65] developed and compared district-level models for electrical load demand prediction based on deep learning techniques like LSTM and nonlinear autoregressive exogenous (NARX) neural networks and machine learning techniques like support vector machines (SVMs) and RF. After completing the preprocessing and cleaning steps, the models are trained using a dataset that includes nine years of historical load demand for Bruce County, Ontario, Canada, fused with the climatic information (temperature and wind speed). With an R² of roughly 0.93–0.96 and a MAPE of approximately 4–10%, the results demonstrate that the model could forecast the load demand more correctly using deep learning than SVM and RF.

Ref. [66] combines the GRU model, which is appropriate for long-term forecasting, with the Prophet model, which is appropriate for seasonality and event handling, to offer a short- and medium-term power consumption prediction algorithm. The researchers preprocessed the data to anticipate seasonality and event management and put forth the Prophet model. Seven multivariate data were tested using GRU in the second step. Additionally, projections of electricity consumption were provided for both short- and medium-term periods (2 days and 7 days) and (15 days and 30 days). The suggested method works better than the Prophet and GRU models, lowering prediction errors and providing insightful information about electricity consumption patterns.

Ref. [67] employed a Seasonal Autoregressive Integrated Moving Average (SARIMA) model for medium- and long-term forecasting built by simulating Yunnan Province’s entire society’s electricity consumption data from 2008 to 2018. The analysis results indicate that the experimental data have strong autocorrelation, a continuous upward trend, and strong seasonality. Lastly, the model’s parameters were optimized and tested using the test set. Ultimately, the model obtained a MAPE of 6.05%.

Ref. [68] analyzed the mid-term monthly electricity consumption using ARIMA and ETS in several developed and developing countries, namely Canada, France, Italy, Japan, Brazil, Mexico, and Turkey. The authors applied decomposition and Bootstrap aggregating (Bagging) techniques to improve univariate monthly electric energy demand forecasts. A novel variation of an existing bagging approach is proposed, termed Remainder Sieve Bootstrap (RSB). The results indicate that the proposed methodologies enhance forecast accuracy. Furthermore, the methods employing the RSB procedure for simulation, forecasting, and aggregation yielded the most favorable outcomes, particularly regarding MAPE, in most instances.

3.1.3. Long-Term Forecasting

This subsection is based on reviews of the most significant studies on long-term forecasting for electricity consumption [52,67,69]. Ref. [67] analyzed the forecasting of medium- and long-term electric consumption for Yunnan Province of China. The operation and planning of power systems are significantly influenced by medium- and long-term load forecasting (M-LTLF), which is complex and nonlinear, posing challenges for traditional and long-term forecasting models to yield reliable outcomes. This study selects the SARIMA model for M-LTLF, and the model parameters are optimized. The electricity consumption data from 2008 to 2018 serve as a training sample for fitting and analysis, while predictions for the entire province’s electricity consumption are made for 2019 to 2020. The results indicate the viability and efficacy of the SARIMA model for M-LTLF with a 6.05% MAPE value. Moreover, the study used the comparative analysis and found that the MAPE values for the SARIMA, Holt-Winters (HW), LSTM, and ARIMA models are 6.05%, 9.18%, 10.67%, and 13.87%, respectively.

Ref. [69] estimated Sierra Leone’s electricity consumption from 2023 to 2050 using MAED-D (version 2.0.0) demand software. The researchers used technical and socioeconomic factors to study three new scenarios—baseline, high, and low demand. The high-demand scenario looks at an ambitious development future with increasing economic diversification and mechanization, while the low-demand scenario looks at more restrained future development. The baseline scenario treats the current electrical sector as if it were business as usual. The base case, high-demand, and low-demand scenarios show a rise in power demand by 2050 of 7.32 PJ, 12.23 PJ, and 5.53 PJ, respectively, according to the results of the modeled scenario.

Among various data-driven techniques, Ref. [52] found the most effective one for estimating the effects of socioeconomic and climatic shifts on Hong Kong’s long-term monthly electricity demand in the future. First, these models are trained and validated using 40 years of historical data on socioeconomic conditions, climate, and electricity consumption. Second, as future climate changes are anticipated, three percentiles of the results from 24 global circulation models and several representative concentration pathway (RCP) scenarios are used. For future socioeconomic uncertainty, however, five common socioeconomic routes are considered. According to the findings, the ANN approach has the lowest accuracy and the least capacity for generalization, while the GBDT method offers the highest accuracy, time series stability, and generalization.

3.2. Review of Electricity Consumption Based on Quantitative Methods

This subsection is based on a review of the most prominent studies, which exhibit the types, impact, scope, and significance of quantitative methods used in electricity consumption forecasting. In this section, the study mentions the most important and frequently used quantitative methods (e.g., time series econometrics modeling, grey forecasting models, machine learning models, deep learning models, optimization-based models, top-down and bottom-up models, and hybrid models).

3.2.1. Time Series Econometric Forecast Models

This subsection reviews the most prominent studies based on time series econometrics approaches. Most of the studies used the traditional forecasting methods (e.g., Autoregressive Integrated Moving Average (ARIMA), SARIMA, SARIMAX, HW, decomposition methods, Autoregressive Conditional Heteroscedasticity (ARCH), Generalized ARCH (GARCH), exponential smoothing (ETS)). Generally, researchers adopted the ARIMA forecasting methods as a benchmark to measure forecasting accuracy. Researchers often used solely ARIMA methods; however, some studies compared ARIMA predicting performance with other quantitative methods. The studies used the ARIMA models [68,70,71,72,73,74,75,76,77,78,79,80,81], SARIMA models [82,83,84], regression analysis [85,86,87,88,89], SARIMAX [90], ETS [13,33,91], and decomposition methods [68,73,81].

Using a spatial model, Ref. [72] examined the regional electricity consumption in Brazil and produced a spatial pattern of regional dissimilarity. After applying the suggested method to the regional power demand in Brazil, it was discovered that there is a spatial dependence on the region’s regional electricity consumption, resulting in a spatial pattern of dissimilarity between areas. By lowering the MAPE of forecasts, the ARIMASp model—presented in this paper—performed better predictively than the ARIMA model. In terms of numbers, the ARIMA forecast showed a shortfall of 1317.30 GW, but the ARIMASp model overestimated the electricity demand by 214.68 GW.

Ghana’s electricity consumption by 2030 was predicted using the ARIMA model, employed in Ref. [75]. Ghana’s electricity consumption is expected to increase from 8.5210 billion kWh in 2012 to 9.5597 billion kWh in 2030 under the predicted scenario, from 8.5210 billion kWh in 2012 to 4.7839 billion kWh in 2030 under the low-growth scenario, and from 8.5210 billion kWh in 2012 to 17.3267 billion kWh in 2030 under the high-growth scenario, according to data from the ARIMA forecast using a time series spanning from 1980 to 2013. Moreover, the empirical findings show the accuracy of the forecast; the study employed goodness-of-fit measures such as R² (0.931), stationary R² (0.894), RMSE (0.419), MAPE (5.34%), MAE (0.297), MaxAPE (13%), and MaxAE (0.793).

Ref. [81] analyzed the monthly electricity consumption forecasting from January 2007 to October 2009 in Sichuan Province, China. This paper presents a decomposition-based combination forecasting model that employs dynamic adaptive entropy-based weighting for forecasting total electricity demand at the engineering level. This article involved an analysis of variance and an orthogonal approach to solving the least squares equations, incorporating classical individual models, a combination forecasting model, and a decomposition-based combination forecasting model. The proposed method demonstrated satisfactory overall performance, exhibiting favorable verification and validation results compared to the ARIMA and ANN. The proposed method effectively integrates multiple forecasting models and demonstrates the ability to decompose and adapt to diverse characteristic datasets, resulting in accurate and stable forecasting performance. Consequently, it may be widely utilized for predicting electricity demand and formulating electricity generation strategies and associated energy policies.

To create forecasting models of the amount of electricity consumption, Ref. [82] examined the various forecasting techniques, including the hybrid SARIMA-ANN and hybrid model by SARIMA–Gaussian Processes (GPs) with the coupled Kernel Function methodology. Utilizing data on electricity consumption, the study examined how well the two systems performed. The research computed the SARIMA model’s forecast values and Thailand’s electricity consumption between 2005 and 2015. With a MAPE of 4.7072 × 10⁻⁹ and 4.8623, respectively, the hybrid model by SARIMA-GP with an integrated Kernel Function approach performed better than the SARIMA-ANN model.

Using a novel framework, the panel quantile regression neural network (PQRNN) is created by incorporating an artificial neural network structure into a panel quantile regression model; Ref. [85] examined the prediction of electricity consumption for China. An empirical examination of China’s province panel dataset from 1999 to 2017 is used to assess the prediction accuracy and demonstrate the effectiveness of the PQRNN-based electricity consumption forecast. Lastly, using the PQRNN model, the province’s electricity consumption for the following five years (2018–2022) is estimated. The empirical study assesses accuracy using MAE, RMSE, MAPE, RRMSE, total RMAE, total RMSE, total MAPE, and total RRMSE. The data become increasingly spread, as evidenced by the Mean ± standard deviation of power consumption, which is 411:5 ± 247:7 in 1999, 1219:2 ± 892:4 in 2009, and 2100:6 ± 1500:7 in 2017.

3.2.2. Grey Forecasting Forecast Models

This subsection reviews the most prominent studies based on grey forecasting methods. The literature investigates several approaches to electricity consumption forecasting using grey prediction models. The main advantage of the grey model is that it is best suited for predicting with a small data span. Many researchers have explored the issue of electricity consumption forecasting on an hourly, daily, monthly, quarterly, and annual basis, e.g., [92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119].

Ref. [92] examined the predictive accuracy for residential electricity consumption in China from 2015 to 2022 using the novel discrete grey model (DTGFM (1,1, N)). The study compared the ARIMA, DNN, and four grey models, e.g., SGM (1,1), GMP (1,1), GFM (1,1,6), and proposed model DTGFM (1,1, N). The results indicate that the proposed model captures the dynamic amplitude variations of the time series and has better prediction performances than other benchmark grey prediction models and non-grey prediction models. The results show that the MAPE of the test dataset is 3.26%, 4.4.6%, 12.89%, 4.29%, 6.73%, and 11.26% for the DTGFM (1,1, N), GFM (1,1,6), GMP (1,1); SGM (1,1), DNN, and ARIMA models respectively.

Ref. [96] creates a novel discrete grey model (abbreviated as DGM (2,1,kn)) for predicting China’s per capita electricity consumption. The research employed in this work predicts China’s per capita electricity consumption using the DGM(2,1,kn) model. The CPR, BPNN, NDGM(1,1,k), and DGM(2,1) models are contrasted with the results. The raw data were China’s per-person electricity consumption (kilowatt-hours) between 1997 and 2017. The MAPEs of five models were empirically numerically determined between 1997 and 2017. The MAPEs of the CPR, BPNN, NDGM(1,1,k), DGM(2,1), and DGM(2,1,kn) models were observed to be 3.01%, 5.29%, 6.02%, 6.70%, and 3.03% during the simulation stage, and 9.75%, 14.40%, 8.47%, 8.12%, and 2.72% at the verification stage, respectively.

Ref. [104] analyzed three different grey forecasting models to predict yearly net electricity consumption in Turkey. The study applied three models, which were compared to find the best model using performance criteria. The non-homogeneous discrete grey model (NDGM) is the best approach to forecast electricity consumption from 2014 to 2030. The study proposed that the NDGM grey model delivers better forecasting performance. The results indicate that the MAPE values of the DGM, ODGM, and NDGM models are 22.39%, 11.45%, and 6.38% respectively.

Ref. [115] proposed a novel unbiased fractional nonlinear grey Bernoulli model [i.e., UFNGBM (1,1)] to forecast China’s annual electricity consumption based on the nonlinear grey Bernoulli model [i.e., NGBM (1,1)]. The experimental results demonstrate that our proposed model is significantly superior to nine alternative models in terms of the electricity consumption data of Jilin and Jiangsu. The performance of our novel method is close to the state-of-the-art deep learning method on the electricity consumption data of Shandong. It is noticed that our method [as an extended version of NGBM (1,1)] is significantly better than NGBM (1,1) on these three real-world datasets, which further shows the effectiveness of our proposed algorithm. The UFNGBM (1,1) models show the best predictive performance with the smallest MAPE values of 2.94% and 3.04% for the Jiangsu and Jilian Provinces, respectively.

3.2.3. Machine Learning Forecast Models

There is a plethora of electricity consumption forecasting using machine learning approaches, e.g., [5,91,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146]. On the one hand, some researchers examined the forecasting issue based on single machine learning methods; some used a comparison of machine learning methods, and similarly, some used a comparison of machine learning and other well-known methods.

Using historical time series data from January 1975 to December 2021 and suitable estimation techniques, Ref. [6] investigated gross electricity consumption (GEC) forecasting models. To anticipate GEC in Türkiye, a machine-learning model utilizing a deep-learning technique based on an LSTM neural network was employed in this study. The SARIMA model was compared to the LSTM model to calculate the total amount of electricity consumption. Despite the results being near one another, the LSTM model fared better overall than the SARIMA model. It had the highest R² value (0.9992) and the lowest values of MAPE (2.42%), MAE (215.35 GWh), and RMSE (329.9 GWh).

Ref. [23] forecasted the electricity consumption of an administration building in London, the United Kingdom, to compare the prediction abilities of five distinct intelligent system methodologies. These approaches are SVM, ANN, DNN, Genetic Programming (GP), and MR. Five years’ worth of observed data for five distinct parameters—solar radiation, temperature, wind speed, humidity, and weekday index—were used to build the prediction models. The weekday index is an essential metric to distinguish between working and non-working days. The first four years’ data are used to generate prediction data for the fifth year and train the models. Lastly, a comparison is made between each model’s estimated and actual electricity consumption for the fifth year. The results show that, with a MAPE of 6%, the ANN outperforms the other four techniques, MR, GP, SVM, and DNN, having MAPEs of 8.5%, 8.7%, 9%, and 11%, respectively.

Overall, the application of machine learning in electricity consumption forecasting holds great promise for enhancing energy management, reducing costs, and supporting the integration of renewable energy sources into the grid. In Singapore, a hybrid approach combining building characteristics and urban landscape variables with the XGboost model has outperformed other models like Geographically Weighted Regression (GWR) and RF, achieving an R² value of 0.9 in forecasting residential electricity consumption [146]. In Saudi Arabia, a hybrid model combining a Bayesian optimization algorithm (BOA) with SVR and NARX has shown high accuracy in long-term electricity consumption forecasting, with R² values exceeding 0.98 [147]. Machine learning in electricity consumption forecasting is not limited to large-scale applications; it also extends to individual households, where models can predict electricity bills based on historical consumption patterns, helping consumers manage their energy expenses better [148].

A model for estimating power consumption in Agartala, Tripura, India, was proposed by Ref. [145]. This model can accurately anticipate the load for the following 24 h and can estimate the load for a week or a month. Furthermore, the current work demonstrates how an ensemble machine-learning procedure can significantly increase prediction accuracy. We showed how RF and XGBoost performed both individually and collectively. The accuracy achieved by the RF and XGBoost ensemble was improved by 15–29%.

3.2.4. Deep Learning Forecast Models

This subsection reviews the most prominent studies based on deep-learning approaches [104,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177]. A novel convolutional neural network (CNN) technique using an input signal decomposition algorithm was presented in Ref. [155]. Hourly electricity consumption data for Turkey’s COVID-19 period were used as input data, and the short-term electricity consumption was projected using the suggested CNN architecture. Empirical Mode Decomposition (EMD), a signal decomposition technique, was used to break the input data into smaller components. All input data were converted into 2D feature maps to extract the deep features and fed into CNN. The pre-trained models GoogleNet, AlexNet, SqueezeNet, and ResNet18 were used to compare the outcomes. According to model-wise comparisons, the suggested approach exhibited the best R², the lowest MAE, and the lowest RMSE values for the 1, 2, and 3 h periods. For one hour, two hours, and three hours ahead, the suggested method’s mean R² values were 95.6%, 95.2%, and 94.0%, respectively.

Ref. [159] used a deep belief network (DBN) based on multiple layers of restricted Boltzmann machines to investigate Macedonia’s electricity consumption forecasting. Short-term electrical load forecasting using the suggested DBN model used hourly electricity consumption data from 2008 to 2014. The results are compared with the most recent real data, the Macedonian system operator (MEPSO) data, and the predicted data from a conventional feed-forward multi-layer perceptron neural network. The comparisons demonstrate that the used model outcome has better results than those produced with conventional techniques and is appropriate for the Macedonian electric power system’s hourly electricity load forecasts. When utilizing the DBN instead of MEPSO data for 24-h forward forecasting, the mean MAPE is lowered by 8.6%, and the MAPE for daily peak forecasting is reduced by up to 21%.

Ref. [173] adopted a panel semiparametric quantile regression neural network (PSQRNN) developed by combining an ANN and semiparametric quantile regression for panel data. By embedding penalized quantile regression with the least absolute shrinkage and selection operator (LASSO), ridge regression, and backpropagation, PSQRNN keeps the flexibility of nonparametric models and the interpretability of parametric models simultaneously. The prediction accuracy is evaluated based on a study of 30 provinces’ panel datasets from 1999 to 2018 in China under three different scenarios. The results indicate that with the lowest MAPE value, PSQRNN with 0.1364 performs better compared with three benchmark methods, including the BP neural network (BP) with 0.2621, SVM with 0.2345, and quantile regression neural network (QRNN) with 0.2559.

Ref. [177] analyzed the sample data to remove the volatility of the electricity consumption data by denoising it using a wavelet transform. The multi-layer LSTM model is trained using the pre-processed samples, and the suggested model is validated and projected to consume daily power consumption based on the area controlled by the U.S. electric power company. The experimental findings demonstrate that this model outperforms bidirectional and conventional LSTM in terms of prediction performance. The coefficient of determination (R²) is as high as 0.997, and the MSE is 0.019.

3.2.5. Hybrid Forecast Models

This subsection is based on reviews of the most critical studies on hybrid models forecasting electricity consumption [101,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195].

Ref. [180] looked at Türkiye’s forecasting model for electricity consumption. This involves comparing the predicting abilities of single and hybrid electricity consumption models; SARIMA is the time series model, ANNs and MLPs are single machine learning models, and SARIMA-ANNs and SARIMA-MLPs are hybrid models. Using novel hybrid models, this study investigates whether Zhang’s hybrid model—often employed as the ARIMA hybrid model with well-known flaws—is better than the multiplicative model of Wang et al. or the combination model of Khashei and Bijari. The findings indicate that when it comes to predicting Turkish electricity consumption, hybrid models outperform single-time series and machine learning models in terms of accuracy. Furthermore, it was shown that the Khashei and Bijari hybrid models performed better than the others and were the most accurate in predicting Turkey’s electricity consumption, respectively.

Ref. [183] uses hourly data from Ukraine from 2013 to 2020 to forecast the country’s electricity demand using an innovative hybrid approach combining traditional statistics and machine learning. The hourly, daily, and annual time series of electricity consumption were examined in the study, along with their underlying structures. Macroeconomic regression analysis assesses the annual trend in the long term. The mid-term model describes the error term by combining ARIMA and LSTM “black-box” pattern-based techniques, while the underlying structure is defined by integrating temperature and calendar regressors. The short-term model captures the hourly seasonality using several ARMA models for the residual and calendar regressors. According to the results, the best forecasting model combines an LSTM hybrid model for residual prediction with MR models. On an hourly level, our hybrid model performs exceptionally well in predicting long-term electricity consumption. For LM, LM+ARIMA, LM+LSTM, and LM+ARIMA+LSTM, the corresponding RMSE values in megawatts (MW) are 552.8 MW, 533.4 MW, 500.6 MW, and 504 MW.

In order to estimate energy consumption in China’s primary sector, Ref. [183] proposed the Fourier-modified grey forecasting model (FDSGM (1, 1, x(β), γ)) based on seasonal fluctuation features and starting condition optimization. This study compares grey forecasting models based on the seasonal index (SGM (1,1)), grey correlation seasonal index (RSGM (1,1)), and dynamic seasonal index (DSGM (1,1)) with empirical data on seasonal electricity consumption in China’s primary industry. In the training set, the MAPEs of the SGM, RSGM, and DSGM models were 2.89%, 2.92%, and 1.08%, respectively; in the testing set, they were 6.13%, 6.16%, and 6.09%. The FDSGM (1, 1, x(β), γ) model’s prediction accuracy is superior to three prior prediction models combined. The training and testing sets’ MAPEs decreased to 0.2% and 6.02%, respectively. The dynamic seasonal factor-constructed model has been demonstrated to outperform the previous two seasonal models in terms of accuracy and suitability for electricity consumption prediction.

Ref. [187] created a hybrid model based on the Extreme Learning Machine (ELM) network and the HW approach for ultra-short-term Chinese residential electricity consumption forecasts. The suggested HW-ELM model was applied to various training set sizes and seasons to forecast results for 15 min of electricity consumption. The suggested model frequently showed reduced inaccuracy in forecasting residential electricity consumption compared to HW, ELM, and LSTM. The RMSE values were decreased by 87.98%, 64.89%, and 53.39%, respectively, for a training set size of 50 days in the spring. The trials’ findings demonstrate that the suggested HW-ELM model performs more exceptionally than the established models created using other techniques.

3.3. Advantages and Disadvantages of Selected Quantitative Models

The study of Velasquez [73] explained the advantages and disadvantages of time series and machine learning models.

3.3.1. Time Series Models

Regression and Seasonality (RS): The advantage of this method is its consistently low % mistake rate in most scenarios and sophisticated estimation. On the other hand, the disadvantage of the RS method is that it is prone to drastic fluctuations in data, as exemplified by the north scenario.

Exponential smoothing (ES): One advantage of ES is its ability to decrease forecasting noise when it deviates significantly from the baseline. An inherent drawback is that the accuracy of the predictions is significantly influenced by the most recent years of the employed historical data. The aspect is very delicate, and incorrect considerations may result in a delay in the prediction.

ARIMA: One advantage of ARIMA is the utilization of correlations to replicate historical data. The degree of approximation can be determined by considering the time delay in the data; it exhibits excellent ability to adapt. A disadvantage is that the forecasts lack sufficient accuracy beyond six years from the first reference.

3.3.2. Grey Models

Grey: (1) One advantage of the grey forecasting model is that it has a flexible structure and is efficient for small sample datasets [196]. (2) Grey models do not rely on restrictive statistical assumptions and are simple to use [197]. (3) Grey prediction does not necessitate the utilization of many related variables. The time and expense of gathering data are greatly decreased by the ease of access to data. (4) The accuracy of grey prediction is very high [198]. On the other hand, a grey forecasting model may occasionally provide predicting mistakes that are too great [199].

3.3.3. Machine Learning Models

One advantage of machine learning is its superior level of approximation for short-term and mid-term forecasts. The shape of the curve precisely corresponds to the peaks and valleys in electricity demand. Conversely, a drawback of machine learning is the requirement for a substantial amount of data to train and acquire knowledge about the characteristics of the curves.

Similarly, the studies of Refs. [200,201] mentioned several advantages and disadvantages of machine learning models.

Support vector machines (SVMs): The advantages of SVMs include the ability to (1) model complex and nonlinear data behavior, (2) model noisy or incomplete datasets, and (3) model with little to no prior data knowledge. However, the drawbacks of SVMs are as follows: (1) difficult to interpret; (2) trial-and-error model architecture design; (3) lack of guidance for tweaking model hyperparameters; and (4) susceptibility to overfitting.

Bayesian: The Bayesian model offers the following advantages: (1) it can be used to represent stochastic systems and allows for probabilistic inference; (2) it can show the causal linkages between variables; (3) it is effective at preventing data overfitting; (4) it can handle missing data; and (5) it can make use of prior knowledge. However, the disadvantages of the Bayesian model are as follows: (1) it is more arbitrary and subjective than classical probability; (2) the number of potential network topologies can increase quickly as the number of nodes increases; and (3) it is computationally expensive.

Hidden Markov: The Hidden Markov model has the following advantages: (1) it is a probabilistic model with a strong statistical basis; (2) it can handle time series data; and (3) it can handle inputs with varying lengths. However, the disadvantages of Hidden Markov include (1) a computationally costly training procedure and (2) difficulties arising from the large size of the training data.

3.3.4. Deep Learning Models

Artificial neural network (ANN): The ANN model has the following advantages: (1) it can model complicated and nonlinear data behavior; (2) it can model datasets with noisy or incomplete data; and (3) it can model with little to no prior knowledge of the data. However, the disadvantages of the ANN are as follows: (1) it is difficult to interpret; (2) it has a trial-and-error model architecture design; (3) it lacks advice for tweaking model hyperparameters; and (4) it is prone to overfitting. [200,201].

Convolutional neural network (CNN): The CNN model has the following advantages: (1) it eliminates the need for feature engineering, a laborious and time-consuming process that is typically required in image processing; (2) the models are thought to be robust under a variety of challenging conditions, such as complex backgrounds, system orientation and size, different resolutions, and illumination; (3) after training, the testing time efficiency is significantly higher than that of other approaches, including SVMs; (4) it requires less time for classification; (5) it can automatically detect critical parameters without human supervision; and (6) it has excellent accuracy in image recognition tasks. However, the disadvantages of CNNs are as follows: (1) inadequate data labeling can drastically lower system performance and accuracy; (2) relatively larger training datasets are needed, and accurate annotation necessitates domain expertise; (3) there are difficulties with optimization brought on by hardware constraints and model complexity; (4) they occasionally require more time to train data; (5) they have a high computational cost; and (6) they require more time to train when utilizing a defective GPU [202].

Recurrent neural network (RNN): Advantages of the RNN model include the following: (1) extending the effective pixel neighborhood by using RNNs in conjunction with convolutional layers; (2) forecasting time series because the highlight point serves as a recall of earlier inputs; (3) training an RNN for computational problems is time-consuming; (4) RNNs can manage both long-term correlations and nonlinear dynamics when they are fed time series inputs; (5) the weight of an RNN stays constant throughout all layers, reducing the number of parameters the network must learn; (6) RNNs can process input of any length; and (7) when the input dimension is increased, the model dimension does not change. However, the disadvantages of RNNs include the following: (1) the problem of gradient and exploding vanishing, which restricts the length of longer sequences; (2) they are incapable of stacking; (3) they have complex and slow training processes; (4) the RNN is not as strong as the CNN; (5) Relu or Tanh cannot manage very lengthy sequences when employed as an activation feature; (6) the assignment is terrifying because the information flows across the layers and levels; (7) without understanding the tree’s structure for every input sample, it cannot proceed; and (8) because the computation is repeated or recurrent, it proceeds somewhat slowly [202].

3.3.5. Hybrid Models

Ref. [203] mentioned several hybrid forecasting models. Ref. [204] has outlined several benefits and drawbacks of particular hybrid models. Neuro-fuzzy (NF): NF hybrid models have the benefit of being based on data characterization; however, they also have the disadvantage of having an unidentified ideal number of clusters. The benefit of ANN-k-shape clustering is its ability to extract features through an unsupervised process; the drawback is its inability to determine the ideal number of clusters. The benefit of ANN-WT lies in its input selection foundation, whereas its drawback stems solely from its frequency resolution limitations. SVM-FOA: this method has the benefit of being quick to search, but it also has the drawback of being built on a complex architecture. SVM-HS: this method has the benefit of being faster in computing and appropriate for small samples; nevertheless, its complex design is a downside.

3.4. The Accuracy Metrics

The accuracy metrics of electricity consumption forecasting models found in the papers include the following:

• Mean Absolute Error (MAE);
• Mean Squared Error (MSE);
• Root Mean Squared Error (RMSE);
• Mean Absolute Percentage Error (MAPE);
• R-squared (R²).

These metrics provide a comprehensive understanding of the model’s predictive performance and ability to accurately capture the underlying patterns in the data. Almost every study mentioned the accuracy metrics MAE, MSE, RMSE, MAPE, and R²; however, for the reader, Ref. [33] mentioned different values of MAPE in the previous studies. Moreover, Fan et al. discussed forecasting accuracy (MAPE, RMSE, MAE) in detail and the trend of several time series, machine, and deep learning models (see Tables 6 and 7 in ref. [36]). Similarly, Alharbi discussed the forecasting accuracy of previous empirical models (See Table 2 in ref. [90]).

3.5. Role of ChatGPT and Generative AI in Forecasting

ChatGPT and AI have several advantages in forecasting and other existing empirical research work, including (1) the role of ChatGPT in aiding data scientists by automating key workflow components, such as data cleaning and preprocessing, model training, and result interpretation; (2) ChatGPT’s potential to yield new insights and enhance decision-making processes through the analysis of unstructured data; (3) ChatGPT’s capacity for fine-tuning across various language-related tasks and its capability to generate synthetic data; (4) ChatGPT’s significant potential to enhance productivity and accuracy in data science workflows; and (5) ChatGPT’s support in various natural language processing tasks in data science, such as language translation, sentiment analysis, and text classification [205]. Some studies compared ChatGPT with the existing parametric and non-parametric forecasting methods (seasonal naive (SNAIVE), HW, ARIMA, ETS, trigonometric seasonality, Box-Cox transformations, ARMA errors, trend and seasonal components (TBATS), and seasonal–trend decomposition using LOESS (STL), and the Theta method) provided via the forecast package in R (Package ‘Forecast’, 2024. Available online: https://cran.r-project.org/web/packages/forecast/forecast.pdf (accessed on 10 September 2024) [206,207]. Ref. [206] found that predictions made by Gen-AI models can occasionally perform noticeably better than predictions made by well-known benchmarks.

On the other hand, ChatGPT has some limitations and issues that are examined: (1) the bias and plagiarism in ChatGPT; (2) the output of ChatGPT may be challenging to interpret; (3) ChatCPT is potentially complicated decision-making in data science applications [205].

3.6. Obstacles to Additional Research in Forecasting Electricity Consumption

Forecasting models are heavily dependent on the quality and availability of historical data, and therefore, inconsistent, incomplete, or outdated data significantly hinder the development and validation of effective forecasting models. The lack of historical data series with high time granularity limits the ability to perform accurate short-term forecasts. In the case of mid- and long-term forecasts, a particular challenge is incorporating the impact of energy and climate policy goals, which influence the dynamics of the energy transition and lead to the diffusion of new electric end-use technologies that substitute the fossil-fuel status quo. Another difficulty is to account for the impact of climate change and unforeseen events (e.g., pandemics and natural disasters). This creates problems for models that rely on historical data. The inability to accurately predict or incorporate such variables into models could limit their long-term forecasting accuracy.

As forecasting models become more complex, especially with the integration of machine learning and deep learning techniques, their interpretability decreases. This complexity can create challenges in understanding the underlying factors driving electricity consumption.

Furthermore, advanced forecasting models require substantial computational resources, particularly machine learning and deep learning. This can be a barrier for researchers or institutions with limited access to high-performance computing facilities.

4. Results and Discussion

The study highlights the most significant quantitative forecasting approaches and their forecasting performance. As previously mentioned, one hundred and seventy-five (175) papers were included in the quantitative analysis. This work makes significant contributions to the literature on energy modeling. The bibliometric R package was employed to estimate the empirical findings of this study [208].

Figure 4 illustrates the number of articles published annually from 2014 to 2024. The trend reveals two distinct phases of research activity. From 2014 to 2020, there was a steady increase in the number of articles published each year, indicating growing interest in the research topic. Between 2020 and 2022, the number of publications doubled annually, peaking in 2022. Although 2023 saw a slight decrease, the number of publications remained more than double compared to the years before 2020, indicating sustained research interest in electricity demand forecasting. It is challenging to comment on the most recent trend, as 2024 has not yet concluded, and additional publications could still influence the final count.

Figure 5 displays the cumulative number of papers by the major producing countries for the same period. China has demonstrated a significant increase in article production over the years, especially after 2020, reaching the highest count among all the countries by 2024. Brazil and the USA have a steady increase in article production but at a slower rate compared to China. Turkey and Pakistan have relatively lower and more stable production rates, with minor increases over the observed period.

A network visualization map of bibliographic coupling among countries depicted in Figure 6 confirms that the countries presented in Figure 6 play a significant role in shaping the global research landscape in fields related to electricity demand forecasting. There are dense connections between China, Turkey, the United States, and other countries, highlighting that the research conducted in these nations is strongly interconnected. China has the highest volume of coupled publications. Furthermore, a few distinct research hubs, built upon strong bibliographic coupling, have formed across the following countries: (i) China and Turkey, (ii) Germany and Italy, (iii) the United States and France, and (iv) India, Spain, and Denmark.

Table 1. Top 10 most productive authors in 2015–2024.

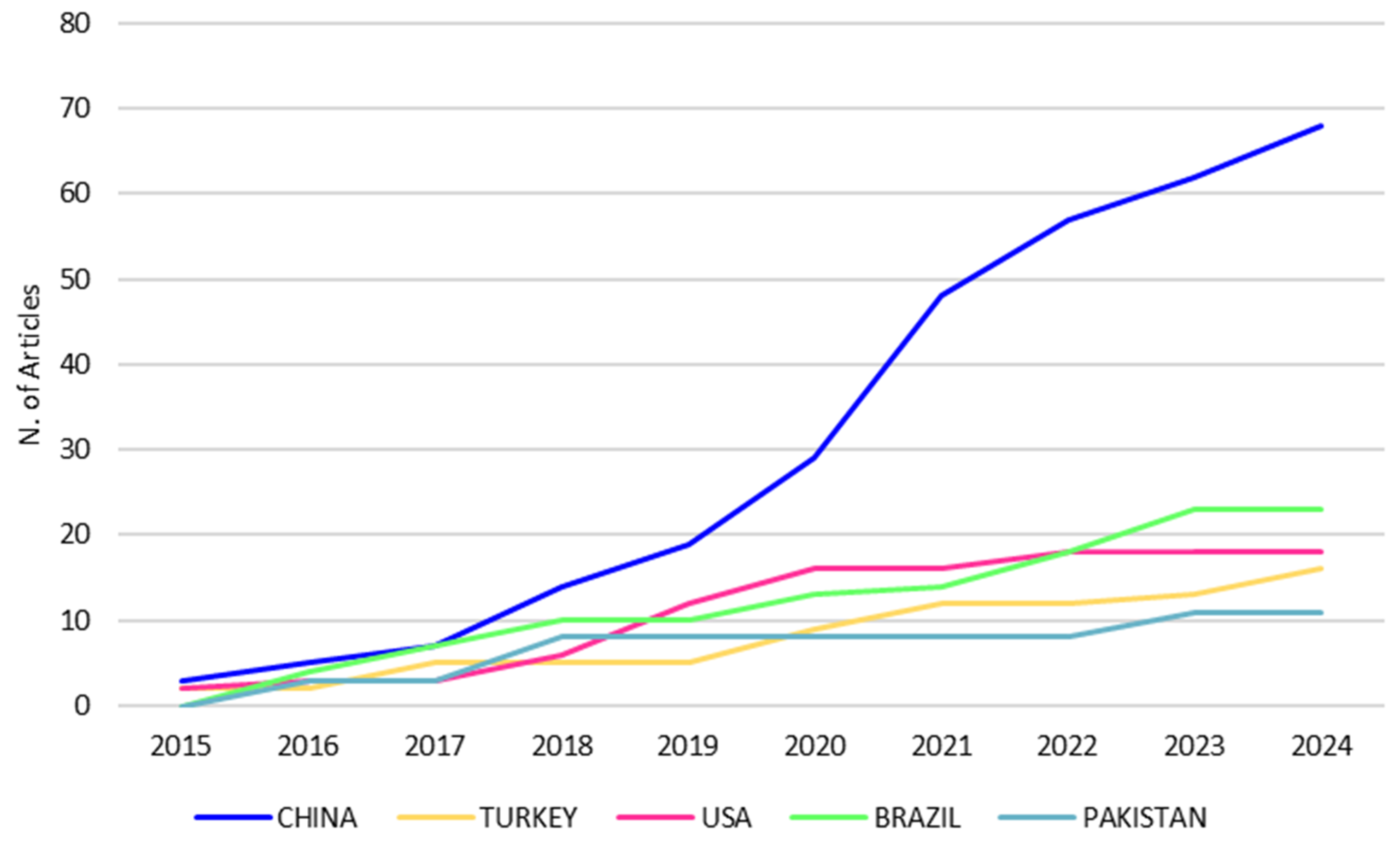
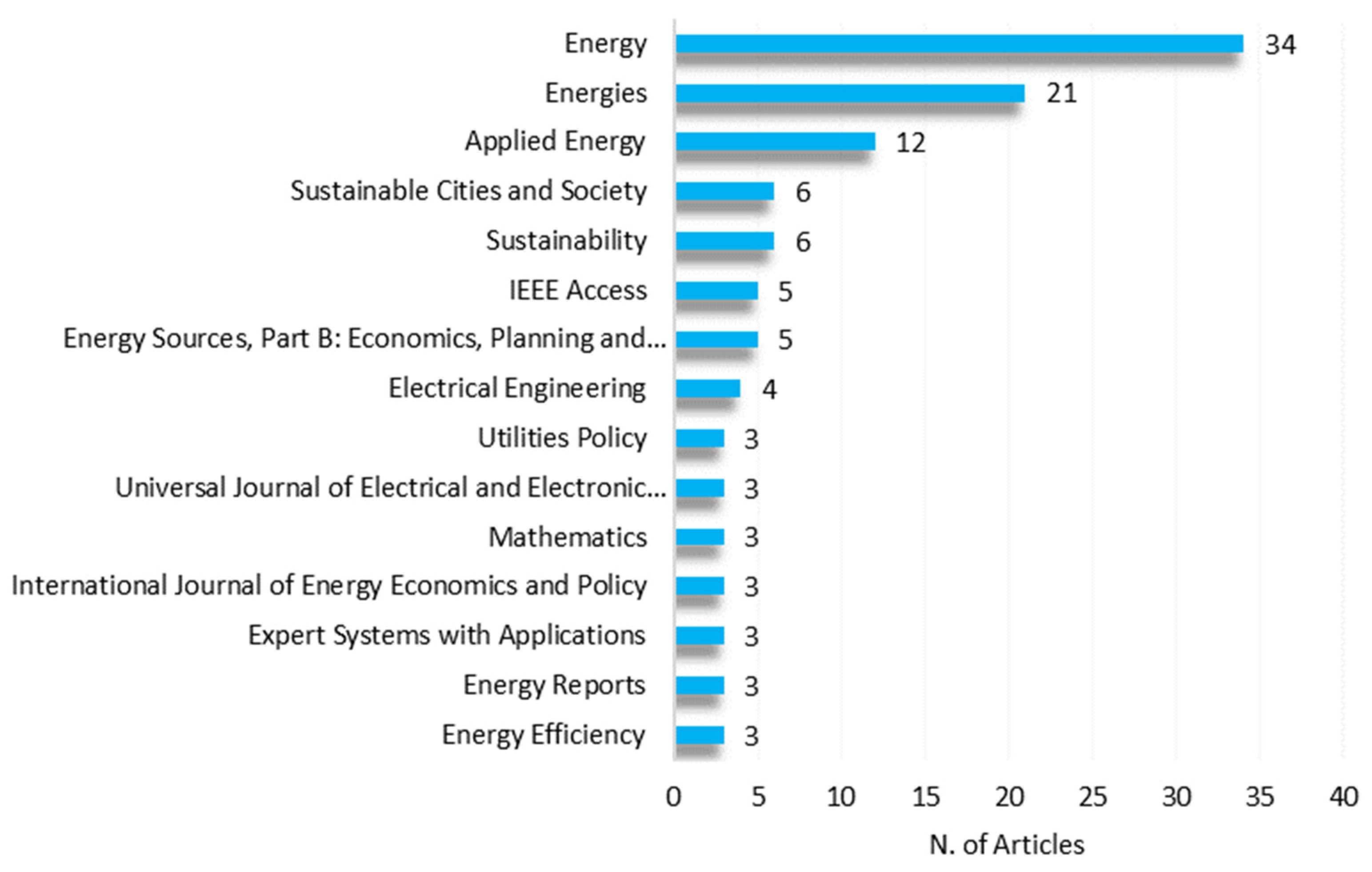
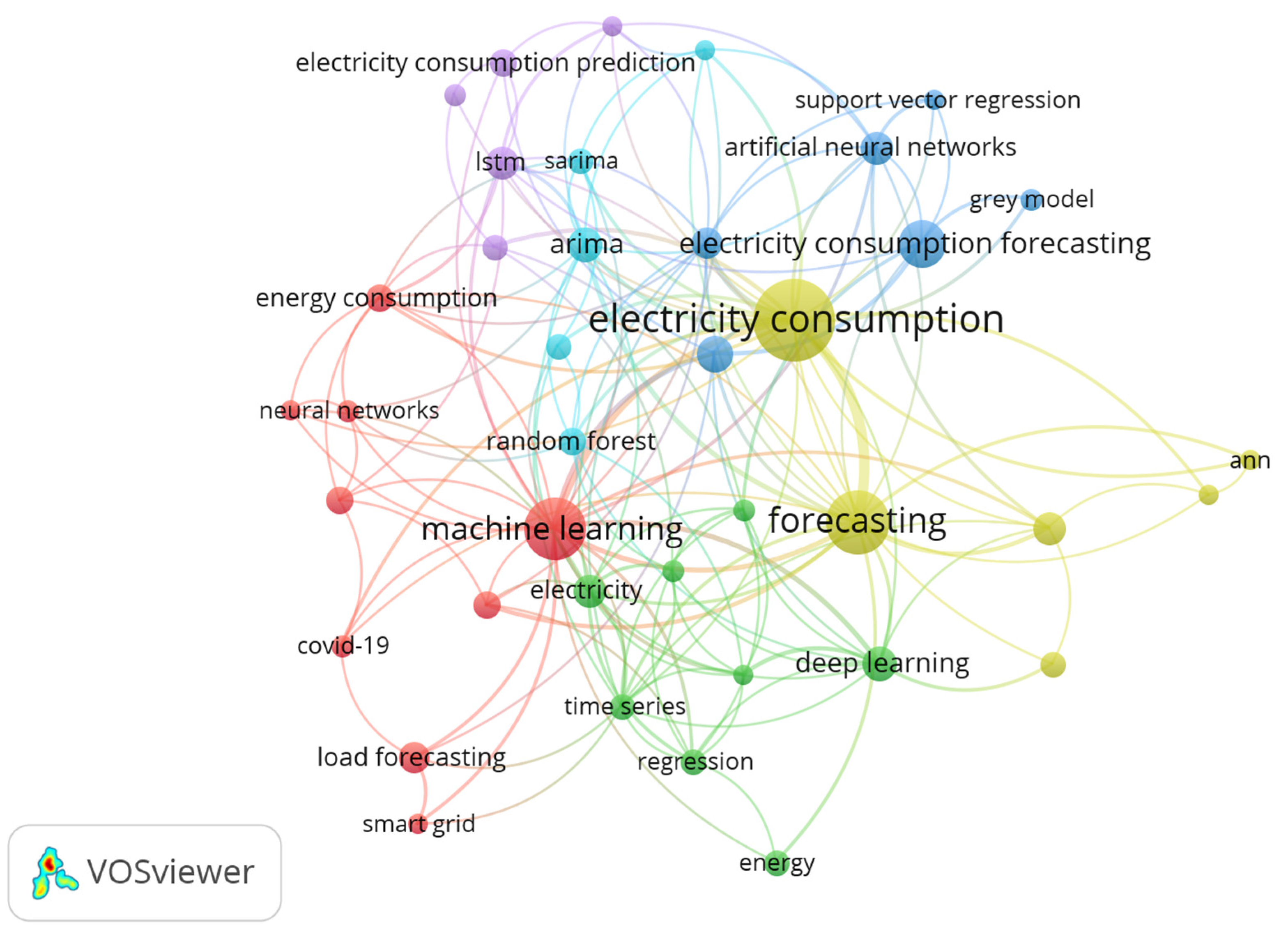
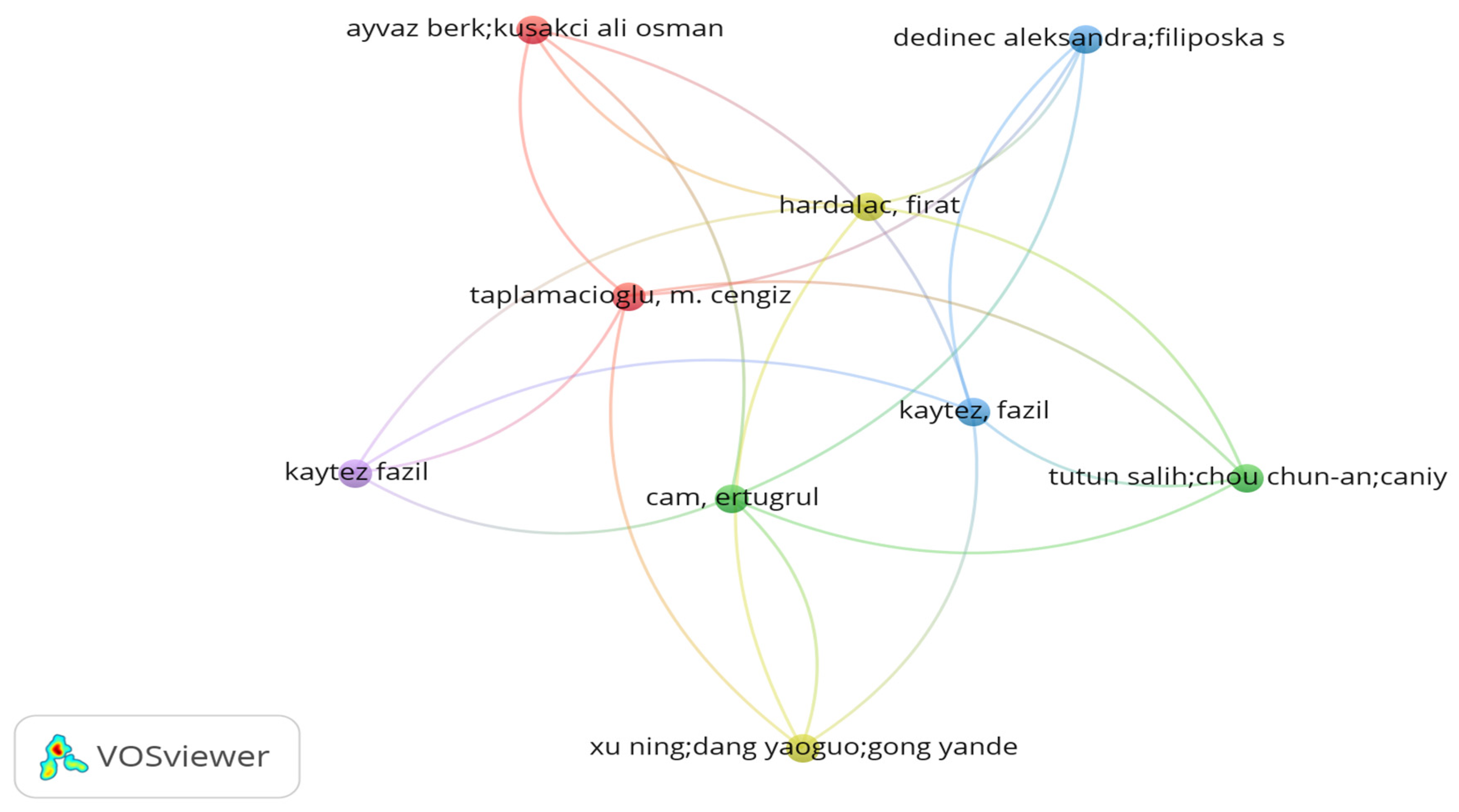
Author’s Name	Affiliation	Country	P	h	g	m	C	C/P
Dang, Y.	College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing	China	4	4	4	0.50	502	125.5
Liu, C.	College of Sciences, Northeastern University, Shenyang	China	3	3	3	0.60	186	62.0
Wu, L.	School of Economics and Business Administration, Central China Normal University, Wuhan	China	3	3	3	0.33	344	114.7
Yang, L.	Big Data Research Center, University of Electronic Science and Technology of China	China	3	3	3	0.50	22	7.3
Almuhaini, S.	Department of Computer Science, Imam Abdulrahman Bin Faisal University	Saudi Arabia	2	2	2	0.67	26	13.0
Chen, L.	Faculty of Civil Aviation and Aeronautics, Kunming University of Science and Technology, Kunming	China	2	2	2	1.00	6	3.0
Ddeinec, A.	Faculty of Computer Science and Engineering, Ss. Cyril and Methodius University, Skopje	North Macedonia	2	2	2	0.22	488	244.0
Ding, S.	College of Economics and Management, Nanjing University of Aeronautics and Astronautics	China	2	2	2	0.29	352	176.0
Fan, G.	School of Mathematics & Statistics, Pingdingshan University, Pingdingshan	China	2	2	2	0.40	169	84.5
Gao, F.	Institutes of Science and Development, Chinese Academy of Sciences	China	2	2	2	0.20	65	32.5

Note: P: number of publications; h: h_index; g: g_index; m:m_index; C: Total number of citations; C/P: average citations per publication.

lists the top 10 most productive authors between 2015 and 2024 whose research focused on forecasting electricity consumption. The table ranks these authors based on several bibliometric indicators. The table reveals a notable concentration of productive authors from China, which shows that universities in China have become key centers for research in electricity consumption forecasting. The h-index values indicate that these authors publish frequently and produce well-cited work, suggesting a high impact within the research community. For example, with an h-index of 4 and 502 total citations, Dang Y stands out as having a particularly strong influence. Ddeinec A and Ding S have a lower publication count, but their work is highly cited on average, with C/P values of 244 and 176, respectively, indicating that their publications are highly valued.

Figure 7 shows the top 15 relevant scientific journals. Among all sources, Energy has the most published papers, with 34 out of 175, accounting for ca. 30% of all retrieval collections. Energies is second with 21 publications, accounting for more than 18%. Applied Energy is in third place with 12 publications, accounting for ca. 10%.

Figure 8 shows the growth trends for the first five journals—Energy, Energies, Applied Energy, Sustainable Cities and Society, and Sustainability—which account for almost 70% of the total articles in the collection. The highest growth is observed in the Energy Journal, which has consistently increased publications, especially from 2018 onwards. The significant rise in Energies is highly visible, particularly after 2019, which allowed this journal to enter second place, surpassing Applied Energy.

Figure 9 depicts the network visualization map of the co-occurrence of authors’ keywords. The most central and prominent keywords are electricity consumption and forecasting. The keywords that frequently co-occur include (i) machine learning together with neural networks, load forecasting, and smart grid; (ii) deep learning, time series, and regression; (iii) ANN, grey model, and SVR; and (iv) ARIMA, SARIMA, and RF. This suggests that research in electricity consumption forecasting commonly employs statistical methods and AI techniques, focusing on integrating these approaches, including hybrid models.

Table 2. Summary of previous studies on quantitative techniques in electricity consumption.

S. NO	Author(s)	Sample(s)	Time/Frequency	Country(s)	Target Variable(s)	Methodology	Empirical Findings
1	[5]	2007 m1–2016 m12	2016 m1–2016 m12 (SR&LR)	7 countries	EC	ANN, ANFIS, LSSVM, FTS	The FTS model performed well.
2	[6]	January 1975–December 2021	January 2022–December 2031	Turkie	EC	SARIMA, LSTM	The LSTM model generally outperformed the SARIMA model, with the lowest MAPE (2.42%) values and the most excellent R2 (0.9992).
3	[7]	1970–2009	2010–2011	Turkey	EC	SVM; LSSVM; ANN	The proposed LSSVM model is an accurate prediction method.
4	[8]	Daily 2009–2018 (3652 obs)	January 2018–December 2018 (SR)	Thailand	EC	ANN, MLR, SVM, hybrid models (NFL theorem)	The forecasting performance of ANNs and MLR is the best.
5	[9]	January 1990–December 2010	January 2011–December 2020	Turkey	EC	SARIMA, NARANN, LADES, RADES	LADES and RADES are more robust and reliable forecasts.
6	[10]	January 1999–December 2019	2009–2019 (annual data) 2018–2019 (daily data) 1 January 2009–31 December 2014 1 January 2021–31 December 2025	Brazil	ED	RS, ES, ARIMA, RS-ES, AFT, AWT, ANN	AWT performs better with a 3% average percent error in most cases.
7	[62]	2000–2019	2020–2026	Rwanda	EC	ARIMA, MLR	ARIMA (1,1,1) was the best model to forecast EC.
8	[71]	January 2000–January 2014	January 2012–December 2014	China	EC	SAS-SVECM, X-12-ARIMA	The results verify that SAS-SVECM achieves better forecasting.
9	[72]	January 2003–December 2013	July 2013–December 2013	Brazil	REC	ARIMA, ARIMAspa	ARIMASp shows better predictive performance than ARIMA.
10	[73]	January 2002–December 2020 January 2002–December 2014 January 2002–December 2019 January 2002–December 2014 January 2002–December 2015 January 2002–December 2014 January 2010–December 2020 January 2010–December 2014 January 2009–December 2019 January 2009–December 2014	January 2021–December 2025 January 2015–December 2019 January 2020–December 2025 January 2015–December 2019 January 2016–December 2025 January 2015–December 2019 January 2021–December 2025 January 2015–December 2019 January 2020–December 2025 January 2015–December 2019	Brazilian Regions	ED	RS, ES, ARIMA, RS + ES + ARIMA, ARIMA + RS, RS + ES	RS, RS + ES has the best forecasting performance.
11	[82]	January 2005–December 2015	January 2016–December 2025	Thailand	EC	SARIMA-ANNs and SARIMA-GP (with combined Kernel Functions)	SARIMA-GP with the combined Kernel Function technique outperformed the SARIMA-ANN model with a MAPE of 4.7072 × 10−9 and 4.8623, respectively.
12	[85]	1999–2017	2018–2022	China	EC	PQRNN, BPNN, GRNN, ELM, SVM	PQRNN has advantages over both CQR and ANN.
13	[90]	1990–2018	2021–2050	Saudia Arabia	EC	SARIMAX	SARIMAX has the best performance.
14	[92]	1 January 2017–31 December 2020 1 January 2010–31 December 2021	2022	Qatar	EC	XGBoost, RF, SVM	The XGBoost algorithm’s performance is the best.
15	[92]	January 2015–December 2022	January 2022–December 2022	China	REC	ARIMA, DNN, GM (1,1), DGM (1,1), SGM (1,1), GMP (1,1,1), GFM (1,1,n), DTFGM(1,1,N)	The proposed model performs better than benchmark grey and non-grey prediction models.
16	[93]	2003–2013	2014–2020	China	EC	GM, NP-GM, OICGM, IRGM	The forecasting performance of the IRGM (1,1) model is the best.
17	[94]	1999–2018	2019–2023	China	EC	GM, DGM, CFGM, CFGOM	CFGOM shows the best forecasting performance with a minimum MAPE of 1.54% and 0.65% for Fujian and Shandong, respectively.
18	[95]	2010–2020	2021–2030	China (Jiangsu)	EC	GM, FDGM, HES	GM (1,Nr) is the best performer.
19	[120]	January 2010–December 2015 January 1994–December 2014	January 2014–December 2014 January 2015–December 2015	China	EC	SARIMA, BPNN, SVR, PSOSVR, FOASVR, SPSOSVR, SFOASVR	The SFOASVR hybrid model has a better forecasting performance.
20	[121]	January 1990–December 2010	–	Türkiye	EC	XGBoost-Based hybrid models (XGBoost-GWO, XGBoost-PPSO, XGBoost-SSA), CatBoost-Based hybrid models (CatBoost-GWO, CatBoost-PPSO, CatBoost-SSA)	The XGBoost-SSA model has superior forecasting performance with a MAPE of 0.00229.
21	[122]	2005–2020	2021–2024	Saudi Arabia	EC; weather parameters, demographics, and economic variables	ARIMA AIM, MLR	ARIMA:APE = 3.8%, MAE = 0.1308; AIM: APE = 8.1%, MAE = 0.1308; MLR: APE = 5.6%, MAE = 0.2264.
22	[149]	January 2007–June 2016	next 4 h	Spain	EC	LSTM, CVOA	The LSTM network obtains the smallest errors.
23	[150]	1980–2012	2013–2015 2013–2018 2013–2021 2013–2025	OPEC	EC	ANN, PSO, ABCA, GA, CSA	The cuckoo search neural network is effective, efficient, robust, consistent, and reliable.
24	[151]	January 1979–December 2020	next 24 h	Brazil	IEC	HW, SARIMA, DLM, TBATS, ARMA, ANN, ARNN, MLP	The MLP model obtains the best forecasting performance.
25	[152]	1993–2019	2020	UK	EC	BPNN, MLR, LSSVM	The LS-SVM model has the best forecasting performance.
26	[172]	January 2008–December 2016	2 weeks Between 2 and 4 weeks Between 2 and 3 months Between 3 and 4 months	France	ELC	GA, LSTM, GA-LSTM, LSTM-RNN	The LSTM-RNN-based forecasting method has lower forecast errors with 339 (RMSE for 2 weeks).
27	[178]	2000–2009	–	China	REC	BPNN, SVM, ELM, Jaya-ELM, SARIMA	The forecasting performance of Jaya-ELM is better than that of BPNN, SVM, ELM, and SARIMA.
28	[179]	1970–2017	2019 –2022	Turkey	EC	ARIMA, MLR, ARIMA-LSSVM	The hybrid-based ARIMA-LSSVM can generate more realistic and reliable forecasts.
29	[180]	June 2013 –March 2020	–	Turkey	EC	SARIMA, ANNs, MLPs, SARIMA-ANNs, SARIMA-MLPs	The hybrid models are more accurate than single time series/machine learning models.
30	[181]	1999–2018	2019–2020	China	EC	IMGM, SFOGM, GMC, FOAGRNN, MGM	The forecasting performance of IMGM, SFOGM, GMC, and FOAGRNN is better than that of the MGM model.
31	[182]	2013–2020 (Hourly)	2019–2020 (17,520 h)	Ukraine	ED	MLR, MLR-ARIMA, MLR-LSTM, MLR-ARIMA-LSTM	The ARIMA-LSTM hybrid model has the best forecasting performance.
32	[183]	2010 Q1–2016 Q4	–	China	EC	GM, SGM, DSGM, RSGM, FDSGM	FDSGM has better forecasting performance with MAPE values of 0.2% and 6.02% for training and testing data, respectively.
33	[209]	January 2010–December 2018	–	China	EC	SI, MHW-default, FOASVR, GASVR GA-MHW, FOA-MHW	The FOA-MHW hybrid model has the best forecasting performance, with a MAPE of 3.58% and only 3 years of training data.

Note: Variables Abbreviations: EC: electricity consumption; ED: electricity demand; REC: regional electricity consumption; GEC: gross electricity consumption; NEC: net electricity consumption; EG: electricity generation; ELC: electricity load consumption; IEC: industrial electricity consumption; PCEC: per capita electricity consumption. Methods Abbreviations: ABCA: artificial bee colony algorithm; AIM: abductory induction mechanism; AFT: ARIMA with Fourier Transform; ARMA: Autoregressive Moving Average; ARIMA: Autoregressive Integrated Moving Average; ARIMAspa: Spatial ARIMA; ARNN: autoregressive neural network; ANFIS: adaptive neuro-fuzzy inference system with subtractive clustering; ANFIS with fuzzy cmeans (FCM); ANFIS with grid partition (GP); ANN: artificial neural network; AWT: ARIMA with wavelet transform; BPNN: back propagation neural network; CVOA: coronavirus optimization algorithm; CSA: cuckoo search algorithm; CFGM: conformable fractional grey model; CFGOM: conformable fractional grey model in opposite-direction; DES: double exponential smoothing; DGM: discrete grey model; DSGM: grey forecasting model based on dynamic seasonal index; DNN: deep neural network; DTFGM; discrete time-varying grey Fourier model with fractional order terms; DLM: dynamic linear model; DWT: Discrete Wavelet transformation; ETS: exponential smoothing state space; ELM: Extreme Learning Machine; ES: exponential smoothing; FDGM: fractional discrete grey model; FDSGM: Fourier-modified grey forecasting model; FFNN: Feedforward Neural Network; FTS: fuzzy time series; FOAGRNN: generalized regression neural network model with fly optimization algorithm; FOASVR: fruit fly optimization algorithm SVR model; FOA-MHW: fruit fly optimization algorithm–multiplicative holt–winters; GA: genetic algorithm; GA-MHW: genetic algorithm enhanced Holt–Winters exponential smoothing method; GASVR: genetic algorithm-based support vector regression model; GM; standard grey model; GMC: grey prediction model with convolution integral; GFM: grey Fourier model; GMP: grey prediction model; GRNN: general regression neural network; GWO: Grey Wolf Optimizer; HW: Holt–Winters; HES: Holt exponential smoothing; HD: Hybrid Decomposition; IMGM: improved multivariable grey model; IRGM: improved-response grey prediction model; k-NN: k-Nearest neighbour; LADES: LASSO-based adaptive evolutionary simulated annealing model; LSTM; long short-term memory; LSSVMd: least squares support vector machines; MA: Moving Average; MGM: original multivariable grey model; MLR: multiple linear regression; MLP: multilayer perceptron; MHW-Default: multiplicative HW model with default parameters; NARANN: nonlinear autoregressive artificial neural network method; NFL: No Free Lunch algorithm; NPGM: newly priority grey prediction model; PQRNN: panel quantile regression neural network; PPSO: Phasor particle swarm optimization; PSO: particle swarm optimization; PSOSVR: particle swarm optimization–support vector regression model; RADES: ridge-based adaptive evolutionary simulated annealing model; RS: regression with seasonality; RNN: recurrent neural network; RF: random forest; RSD: Regression Spline Decomposition; RSGM: grey forecasting model based on grey correlations seasonal index; SARIMA: Seasonal Autoregressive Integrated Moving Average; SI: seasonal index (SI) model; SPSOSVR: seasonal particle swarm optimization–support vector regression model; SSA: Sparrow Search Algorithm; SSD; Smoothed Spline Decomposition; SAS-SEVC: self-adaptive screening model based on vector error correction model; SFOASVR: seasonal fruit fly optimization algorithm SVR model; SFOGM: self-adaptive fractional weighted grey model; SVM: support vector machine; SVR: support vector regression; SES: single exponential smoothing; SGM; seasonal grey model; TBATS: trigonometric Box–Cox transform; TGMRM: trigonometric grey model with rolling mechanism; OICGM(1,1): optimized initial condition GM(1,1) model; XGBoost: Extreme gradient boosting; Data Sources Abbreviations: CBS: China statistics bureau; EIA: energy information administration; PBS: Pakistan bureau of statistics; TEIAS: Turkish electricity transmission company; TEDC: Turkish electricity distribution corporation; Q1: first quarter; Q4: fourth quarter; WDI: world development indicators.

provides a comprehensive summary of 33 selected papers indicating the study’s authors, sample periods, focus country, target variables, methodologies employed, and key empirical findings. Depending on the information provided in the papers, it also includes details on the forecasting horizon, which ranges from hourly to multi-decade predictions, and/or the frequency, which ranges from hourly to annual resolution.

Across the studies, several models have been highlighted as having superior forecasting performance. For instance, LSTM models frequently outperform traditional methods like SARIMA, especially in studies focusing on short-term forecasts. Many studies report that advanced models such as hybrid approaches and deep learning techniques offer the most accurate predictions. The most important observation from the table is the consistent finding that advanced machine learning models and hybrid approaches generally outperform traditional statistical methods. Specifically, models like LSTM, hybrid models combining various algorithms (e.g., ARIMA-LSTM, SARIMA-GP), and specialized techniques like XGBoost and SFOASVR frequently demonstrate superior accuracy across different contexts, countries, and timeframes. This underscores the increasing need for advanced, data-driven models to achieve more accurate and reliable electricity consumption forecasts.

Figure 10 visualizes citations and authors; in this analysis, the study selected at least 1 document and 40 citations. The results show that nine authors are connected.

5. Conclusions

This study has provided a comprehensive bibliometric analysis of electricity consumption forecasting research conducted from 2015 to 2024. By analyzing 175 documents from the Scopus and Web of Science databases, we have highlighted significant trends, compared different methodologies, revealed their strengths and weaknesses, and identified which models perform best under specific conditions. There has been a steady increase in publications on electricity consumption forecasting over the past decade. This growth underscores the critical role of accurate forecasting in planning power system operations and expansion. The variety of methods reflects the inherent complexity of electricity consumption and the ongoing pursuit of more precise forecasting models.

The analysis identified several emerging trends, including the use of big data analytics, the incorporation of socioeconomic factors, and the application of advanced optimization algorithms. Electricity consumption forecasting is particularly important for countries such as China, Brazil, the USA, Pakistan, Turkey, and various European nations. Most of the articles on this topic are produced in these countries. China has shown a significant increase in article production post-2020, which aligns with its broader economic and industrial growth. Although China dominates, significant international collaboration is essential for advancing research and sharing diverse perspectives. Countries like the United States and China have strong collaborative networks, which contribute to the high impact of their research outputs.

The study indicates that no single method consistently outperforms others across all contexts. Traditional statistical methods such as ARIMA and SARIMA remain commonly used due to their robustness and simplicity. However, machine learning (ML) and deep learning (DL) models have gained significant traction. These models, including XGBoost, LSTM, and hybrid approaches, have demonstrated superior accuracy in handling large and complex datasets. The shift towards ML and DL approaches signifies a broader movement towards leveraging advanced computational techniques to improve forecasting accuracy. Hybrid models are found to be more robust and reliable for long-term forecasting. The choice of model often depends on the specific characteristics of the data and the forecasting horizon.

One significant limitation discovered in the study is the difficulty in consistently and easily extracting detailed information on the forecasting temporal resolution of the models discussed in the reviewed articles. Temporal resolution plays a crucial role in determining the applicability and accuracy of different models. However, the variability in how this information is reported across studies makes it challenging to systematically compare and analyze the impact of temporal resolution on forecasting performance. This limitation could lead to an incomplete understanding of how well different models perform under various temporal resolutions, potentially affecting the generalizability of the study’s findings. Many models are trained and tested in specific contexts. This could reduce the applicability of the findings to different countries or under varying circumstances, such as rapid technological changes or shifts in energy policy. The increasing complexity of forecasting models, particularly those based on machine learning and deep learning, often comes at the cost of interpretability. This can make it difficult for stakeholders like policymakers and energy planners to identify the key factors influencing the forecast outcomes, potentially limiting the models’ practical application and acceptance.

Demand forecasting has far-reaching political implications. One of the main goals of energy policy is to ensure the reliability of electricity supply. Demand forecasting plays a fundamental role in ensuring system reliability across both key dimensions: system adequacy and operational security. Accurate electricity demand prediction enables decision-makers to make informed choices about infrastructure investments, ensuring that generation capacity and grid infrastructure are sufficient to balance future power demand. From an operational point of view, load forecasting is essential for managing the integration of variable renewable energy sources (VRESs). Wind and solar-based generation introduce variability in both supply and demand, and accurate load forecasts help manage this variability by allowing grid operators to optimize energy storage, adjust power output from dispatchable generators, and implement demand response measures to maintain grid stability. Operational studies, in which load forecasting is fundamental, enable policymakers to determine the optimal transition rate toward higher shares of VRESs, ensuring grid stability while meeting climate goals. In this way, demand forecasting also influences regulatory frameworks and market design, shaping policies that enhance system flexibility by introducing dynamic pricing models and consumer participation in demand response programs.

In this study, we reviewed, discussed, and compared numerous studies related to short-, mid-, and long-term forecasting. The use of advanced machine learning and hybrid forecasting models in short-term operational planning suggests the need for investment in data collection and processing technologies. Policymakers may need to establish frameworks that support the adoption of smart grids and IoT devices to capture high-resolution consumption data. The study also highlights the main socioeconomic factors that should be considered in mid- and long-term forecasting, which are crucial for ensuring system adequacy.

Future research should continue to explore these areas, with a particular emphasis on improving the accuracy and scalability of forecasting models. There is also a need for more region-specific studies that account for local economic, social, and environmental factors affecting electricity consumption. Lastly, research could focus on enhancing the interpretability of complex models to make them more accessible to policymakers and industry practitioners. It is necessary to conduct similar reviews systematically in the future because rapid advancements in energy technologies, high-resolution data collection from smart meters, socioeconomic factors, etc., may require new or adapted forecasting models. These advancements also provide an opportunity to use new modeling techniques and to share these developments with the research community.