Abstract
This paper concerns an economic and exergetic efficiency analysis of a plate heat exchanger placed in a solar installation with TiO2:SiO2/DI:EG nanofluid. This device separates the primary circuit—with the solar fluid—and the secondary circuit—in which domestic hot water flows (DHW). The solar fluid is TiO2:SiO2 nanofluid with a concentration in the range of 0.5–1.5%vol. and T = 60 °C. Its flow is maintained at a constant level of 3 dm3/min. The heat-receiving medium is domestic water with an initial temperature of 30 °C. This work records a DHW flow of = 3–6(12) dm3/min. In order to calculate the exergy efficiency of the system, first, the total exergy destruction, the entropy generation number Ns, and the Bejan number Be are determined. Only for a comparable solar fluid flow, DHW 3 dm3/min, and concentrations of 0 and 0.5%vol. is there no significant improvement in the exergy efficiency. In other cases, the presence of nanoparticles significantly improves the heat transfer. The TiO2:SiO2/DI:EG nanofluid is even a 13 to 26% more effective working fluid than the traditional solar fluid; at Re = 329, the exergy efficiency is = 37.29%, with a nanoparticle concentration of 0% and (1.5%vol.) = 50.56%; with Re = 430, (0%) = 57.03% and (1.5%) = 65.9%.
1. Introduction
Heat exchangers (HXs) are used to transfer heat between two fluids with different thermodynamic parameters in a noncontact manner, also involving mono and hybrid nanofluids of different concentrations. They allow the efficiency of the heating or cooling system to be improved by, for example, using waste heat and transferring it to other parts of the installation [1]. The most famous and tested heat exchangers that cooperate with new-generation working fluids, such as nanofluids, include double-tube heat exchangers [2], plate heat exchangers [3], and shell and tube heat exchangers [4]. Nowadays, when so much attention is paid to sustainability [5], environmental aspects, and energy efficiency, the role of heat exchangers is gaining importance. Undeniable evidence here may be the analysis of scientific works collected in the Elsevier Scopus citation database. By entering the two terms ‘nanofluids’ + ‘heat exchangers’ in the search engine on the ScienceDirect platform, a total of 13,685 publications of various types are obtained, starting from 1998 and extending until 26 January 2024 [6]. Among the types of publications available in Scopus, the most common are research articles at 78.5%, followed by review articles at 10%, short communications at 4.4%, and book chapters 4.5%; the remaining ones constitute approximately 2.5%, including conference abstracts, encyclopedia, case reports, editorials, mini reviews, correspondence, news, and other types (see Figure 1a). If the query is refined by typing ‘hybrid nanofluids’ + ‘heat exchangers’, the total number of publications since 1998, when the first one is recorded, is 6131 (see Figure 1b); and if it is asked for ‘nanofluids + plate heat exchangers’, it turns out that this type of heat exchanger covers as many as 63% of the publications. Figure 2 also shows the growth rate of interest in the topic related to the use of nanofluids in exchanger systems. The medium-term rate of change is between 42 and 44% for mono and hybrid nanofluids, respectively.
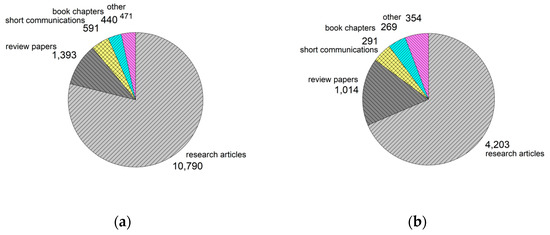
Figure 1.
Number of all publications registered in the Scopus database for the entry (a) ‘nanofluids’ + ‘heat exchangers’ from 1998 to 16 January 2024 and (b) ‘hybrid nanofluids’ + ‘heat exchangers’ from 1999 to 26 January 2024.
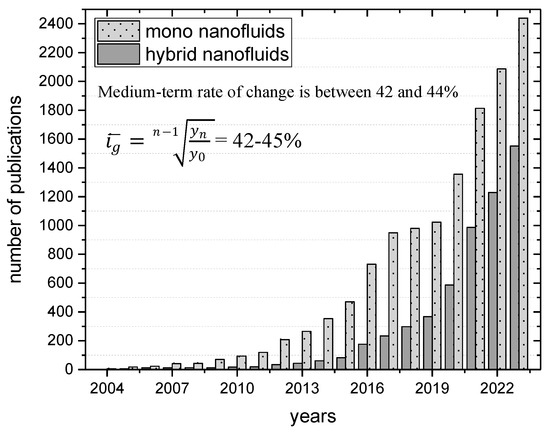
Figure 2.
Growth rate of publications registered in the Scopus database for the entry ‘nanofluids’/‘hybrid nanofluids’ + ‘heat exchangers’ from 2003 to 31 December 2023.
As can be seen, one of the most commonly used heat exchangers is compact plate heat exchangers consisting of a series of thin plates connected together. Due to the way they are connected, there are four main types: gasketed, brazed, semi-welded, or welded. The first systems of this type were used in 1923 for the pasteurization of dairy products [7]. Currently, due to their design enabling the provision of strictly defined hygienic conditions, their use is very wide, from the food and chemical industries to the HVAC, refrigeration, and cryogenic industries. Depending on the desired heat exchange effects, the amount of flowing fluid, and its parameters, the size of this type of exchanger can vary greatly. A single exchanger may consist of several hundred stacked, most often corrugated, plates with narrow channels between them; hot and cold fluids alternately flow through them, providing little resistance to heat transfer. Plate corrugations have a significant impact on the thermohydraulic performance of the device and can be performed in various ways. Figure 3c shows one of the most typical plate corrugations, the chevron. The herringbone angle is reversed in adjacent sheets so that when the boards are tightened, the corrugations provide multiple points of contact. Molded elastomer gaskets are most often installed at the ends of plates.
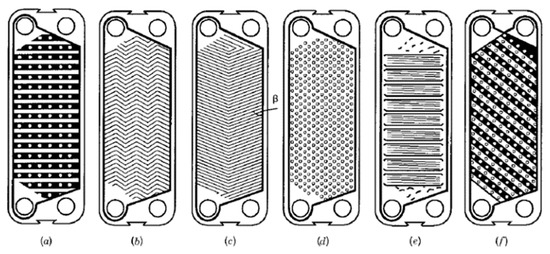
Figure 3.
The most common variations of plate heat exchangers (PHEs) and their corrugations: (a) washboard, (b) zigzag, (c) chevron or herringbone, (d) protrusions and depressions, (e) washboard with secondary corrugations, and (f) oblique washboard [8,9].
As far as the method of fluid flow inside the PHE is concerned, there are single-pass systems (1-1 single-pass arrangements) and co- or counter-current, in which the mutual position of the hot and cold channels is shaped in the form of a letter U, Z–U, or Z arrangement, appropriately. Moreover, in installations where there are very large differences in flows or speeds and we want an additional intensification of the heat exchange, multi-pass exchanger arrangements are also possible [8].
Scientists around the world conduct intensive research [10], as well as analytical and numerical work [11,12], to determine the effectiveness of using nanofluids with heat exchangers in closed-loop solar systems [3,13] and outside of them [14,15]. Solar collectors are relatively simple devices in construction, using the energy of solar radiation and transforming it into thermal energy (flat-plate collectors (FPCs), evacuated tube solar collectors (ETSCs), parabolic trough solar collectors (PTSCs), compound parabolic collectors (CPCs), and linear Fresnel reflectors (LFRs)) or electrical energy (photovoltaic thermal collectors (PVTs) [16]).
The most common flat solar collector is made of an absorber that receives solar radiation and converts it into heat, which, in turn, is transferred to the fluid flowing through a system of pipes located in solar panels. The heated fluid that circulates in the system flows through a heat exchanger or tank coil, where the heat is transferred to domestic water. The cooled liquid then returns to the collector, and the entire process is repeated. The conventional and most frequently used working fluids so far have been water or a mixture of water and glycols (ethylene or, less frequently, propylene), oils, and gases. Mono and hybrid nanofluids are new-generation working fluids which, due to their superior thermal properties, have potential use as working fluids in various systems with solar collectors. This was proven by Choudhary et al. in [17], where an improvement of over 16% in the thermal efficiency of an FPC operating with a working medium of 1.5% MnO EG/water-based nanofluid was shown compared to the pure base fluid of EG/water. The solution provided by Ahmadlouydarab et al. also turns out to be interesting and innovative. In [18], due to its high thermal capacity, 5% vol. TiO2–water-based nanofluid was used for the thermal insulation of a flat solar collector. In addition, the outer part of the absorber was covered with TiO2 nanoparticles to improve its self-cleaning properties. This made it possible to improve the overall efficiency of the solar collector by almost 50%. Saffarian et al. in [19] proved that the design of the piping and the route of the pipes inside the solar collector significantly affect the efficiency of the device and the quality of the heat transfer. By using corrugated pipes through which 4% vol. CuO nanofluid was pumped, an increase of over 78% in the heat transfer coefficient was achieved compared to a typical solution.
The efficiency of solar installations and fluids that cooperate with heat exchangers can be effectively assessed using the exergy method, as was performed, for example, in [20,21,22]. In many papers, the solar energy rate absorbed by the solar collector and the exergetic efficiency of the system are also determined, for example, by Mostafizur et al. in [23] and Zhai and Wu in [24]. Iranmanesh et al. in [10] used graphene nanoplatelet nanofluids in a plate heat exchanger system. The flow of solar fluid ranged from 0.5 to 1.5 dm3/min, and its mass concentration was 0.025, 0.5, 0.075, and 0.1% wt. The heat-receiving element was a 50 liter cooling water tank; however, no flow parameters were provided here. Due to the tropical weather conditions in which the experiment was carried out, the base liquid was distilled water (there was no need to use glycol admixtures). The basic parameters determining the efficiency of such a system were the Bejan’s number, entropy generation, and pumping power. Ultimately, it was concluded that the entropy generation was inversely proportional to the concentration of the nanofluid, and the Bejan number increased with concentration but decreased with a higher solar fluid flow. The best results were obtained with the highest flow of nanofluids (1.5 dm3/min) with a concentration of 0.1% wt. The exergy and thermal efficiency increased by approximately 40% and 20%, respectively, compared to distilled water.
Moghaieb H.S. et al. [15] drew attention to highly efficient direct-absorption solar collector installations based on nanofluids. Nanofluids as working fluids have been proven to represent an innovative approach to direct-absorption solar collectors for the efficient conversion of solar and thermal energy [25]. They also have better optical and thermal properties compared to regular working fluids. The improvement in the thermal and rheological properties of nanofluids results from their physical properties and observed phenomena, including thermophoresis, van der Waals, electrostatic double-layer forces, and Brownian motion. By selecting the appropriate type of nanoparticles, as shown in several studies [26], a more than 40% thermal conductivity enhancement can be achieved compared to the base fluid, which was proven by Akhgar et al. in [27]. There, various artificial neural networks (ANNs) were tested to predict the thermal conductivity of a 0.05–1% vol. MWCNT + TiO2 water–ethylene-glycol-based hybrid nanofluid. There are also dozens of correlations available in the literature that allow for determining the conductivity of nanofluids (including hybrid ones) depending on their molecular composition and the share of individual fractions [28].
Tong et al., in [21], performed a detailed energy and exergy analysis of the operation of a flat-plate solar collector using Al2O3 and CuO water-based nanofluids. The results were compared with those for pure water. The highest collector efficiency (approx. 22% higher than that for water) and the lowest entropy generation were achieved using 1% vol. Al2O3/water nanofluid. In turn, the exergy efficiency of the FPC was approximately 57% and 50% higher when using 1% vol. Al2O3 and 0.5% vol. CuO water-based nanofluids, respectively, compared to pure water. It should be noted here that the research was conducted in a warm climate (Gwangju, Korea), where pure water (without any additives) is used most often in typical solar installations. In the moderate or cold climate of Europe, outdoor solar installations are filled with a mixture of water and glycol, most often ethylene glycol, which prevents the working medium from freezing in winter, when temperatures drop to well below 0 °C. It is worth noting that the thermal conductivity coefficient of the mixture of ethylene glycol and water was approximately 30% higher than that in the case of pure water [29]. It turns out that, in the case of aqueous solutions of nanofluids, the effect of improving energy or exergy efficiency is usually more spectacular than in the case of ethylene glycol or oil [22]. Therefore, when comparing these two parameters, one should always take into account the operating conditions of the installation. So, Ehyaei M.A. et al. in [22] conducted research for a solar installation located in the capital of Iran, Tehran, where there is a steppe, Mediterranean climate and average annual temperatures reach 20 °C. This publication [22] presents a numerical analysis consisting of examining, among other factors, the energy and exergy efficiency of parabolic trough solar collectors (PTSCs) working with CuO and Al2O3 nanofluids in volumetric ratios of 1%, 3%, and 5%; the nanofluids were prepared on the basis of water and oil. The best effects were obtained for 5% vol. CuO/water nanofluid—with increases in the annual mean energy and exergy efficiency of dε = 0.09% and dηex = 0.93%, respectively—and for 5% vol. Al2O3/water nanofluid—dε = 0.03% and dηex = 1.98%. Moreover, it turned out that, in the case of aqueous solutions of nanofluids, the annual mean energy and exergy efficiencies of PTCs were higher than those of PTCs involving oil as a base fluid.
In turn, Lazarevikj M. et al. in [11] performed a CFD analysis of heat transfer during the flow of a water-based Al2O3 nanofluid with volume concentrations in the range of 0.5–3% through a plate heat exchanger. The final results showed an improvement in the thermal parameters considered, such as the overall heat transfer coefficient, U, the nanofluid heat transfer coefficient h, and the efficiency, ε, of the plate heat exchanger by 23%, 30%, and 12%, respectively.
In [14], Yashawantha et al. examined the energy efficiency of a plate heat exchanger that cooperated with a mono nanofluid of Al2O3 produced on the basis of ethylene glycol in the flow range of 11–19 dm3/min; the nanofluid with a concentration of 0.2–2% wt. worked as a coolant with an initial temperature of 5–10 °C. It was shown that the overall heat transfer coefficient, U, increased by a maximum of almost 15% (for nanofluids with a concentration of 2% wt. and an initial temperature T = 10 °C) compared to the base liquid. Additionally, an increase in pumping power of up to 14% was recorded.
Javadi F.S. et al. in [30] showed how the thermodynamic properties and concentration of liquid nitrogen-based nanofluids affect the mass flow and effective heat transfer in a PHE. For SiO2 with a concentration of 0.2% vol., the mass flow rate was 0.278 kg/s, and for a concentration of 2%, it was 2.079 kg/s. For the 0.2% volume fraction of TiO2, and Al2O3, the mass flow rate m = 0.459 kg/s and 0.439 kg/s, respectively; at a higher concentration of 2%, the mass flow rate was much higher and equaled 3.861 kg/s and 3.691 kg/s, respectively.
The upgrading of thermal conductivity for TiO2 and Al2O3 is observed to be comparable and significantly higher than that in the case of nanofluids with the addition of SiO2. Moreover, the heat transfer coefficient increases with thermal conductivity and the concentration of the nanofluid particle volume. It has also been noticed that the criterion number Pr is inversely proportional to the concentration and varies in a range from approximately 0.355 for 2% vol. TiO2 nanofluid to approximately 0.414 for 0.2% vol. SiO2 nanofluid. Entropy generation is directly proportional to the concentration of nanoparticles, and approximately 50% higher for TiO2 and Al2O3 than in the case of SiO2.
Hami et al. in [29] analyzed how the proportion of components of the base liquid (water in relation to ethylene glycol, W:EG) will affect the efficiency in heat transfer during turbulent flow and the forced convection of a TiO2 + SiO2 hybrid nanofluid with a concentration of 1% and an initial temperature of 30 °C, through a refrigeration system. Heat flux was constant and amounted to approximately 8 W/m2. Among the analyzed W:EG ratios (20:80, 50:50, and 80:20), the one containing 20% water and 80% glycol turned out to be the most effective. The decision criterion was a significant improvement in the heat transfer (almost 30%) with the smallest increase in friction factor, which amounted to 1.03. Moreover, the thermal conductivity coefficient, k, at maximum Re numbers up to 11,000 increased by up to 24% compared to the base liquid without nanoparticles.
The use of nanofluids in various heating and cooling layouts and processes is extremely effective because of their proven superior thermal properties. On the other hand, there are a number of basic limitations and requirements [31], which include, among others, economic considerations [32], problems with increasing pumping power [33], and suspension stability [34,35]. For example, the pumping power for the highest concentration analyzed in [10] of 0.1% wt. graphene nanoplatelets nanofluids and at a flow of 0.5 L/min increased by 6% compared to pure water. This increase in pumping power requirement applies to most nanofluids, whose density may be approximately 10% higher than that in the case of pure water [30]. Another problem is the nano-size of mineral particles that can potentially damage the pumping device. The necessity of developing a new and innovative pumping device has been suggested [23]. Other challenges, recommendations, or future perspectives are also presented in some of the recent publications of Mukherie et al. [5] and Moghaieb et al. [15].
Papers in which nanofluids cooperate with heat exchangers in solar systems to increase the intensification of heat transfer are the subject of many studies [17,18,19,21,22,23]. However, in most cases, the cooling efficiency, not heating efficiency, is tested, which is usually not the same, and the values differ by a few percent [36]. Therefore, nanofluids in exchanger systems are mainly used as coolants to check and/or increase cooling performance [14,26]. It is difficult to find a case in which the efficiency of a solar installation is determined and the temperature of the nanofluid is much higher than that of the working medium on the internal secondary side of the PHE, that is, the hot water installation. This is a typical situation faced by designers and users. This thesis is confirmed by the publication by Iranmanesh et al. [10], who highlight this problem. However, the efficiency of a solar installation working with an aqueous solution of GNPs in warm climate conditions was tested. In turn, the climate of central Europe forces the use of a base liquid in the form of a mixture of glycol and water, which protects the installation against possible freezing.
Bio-ethylene-glycol-based TiO2:SiO2 hybrid nanofluid has better thermal properties in comparison to typical solar fluids that are commonly used glycols, thus requiring more distinct study.
This paper concerns the determination of, among others, the exergetic and economic efficiency of a typical solar installation with a PHE separating the primary circuit—with the solar fluid—and the secondary circuit—in which domestic hot water flows (DHW). The solar fluid is a hybrid nanofluid TiO2:SiO2 (20:80) with a concentration in the range of 0.5–1.5% vol. and a temperature of 60 °C. The base fluid is a mixture of deionized water and bio ethylene glycol in a ratio of 60:40. The heat-receiving medium is domestic water with an initial temperature of 30 °C. The analysis is intended to demonstrate and confirm the effectiveness and profitability of using nanoadditives in this type of system. Moreover, this research expands the general knowledge base on the properties of hybrid nanofluids and their potential use in the heating industry.
The innovation of this work consists of the analysis of the economic and technical effectiveness of the use of an exemplary hybrid nanofluid in a solar system with a PHE. The working medium acts as a heating medium, not as a heated one. Most studies are related to the use of nanofluids as a coolant on the secondary side of the installation [9,14].
2. Materials and Methods
2.1. Hybrid Nanofluids Preparation and Stability
In this paper, TiO2 nanoparticles with a diameter of 4–8 nm (79.9 g/mol; density 3.9 g/mdm3) from ROTH and SiO2 with a diameter of 10–20 nm (60.08 g/mol; density 2.2–2.6 g/mdm3) from Aldrich Chemistry were used to prepare the hybrid nanofluid; they were mixed in a mixture ratio of 20:80. The base fluid was a mixture of deionized water and bio ethylene glycol (62.07 g/mol) in a 60:40 ratio. The nanofluids were prepared using a two-stage method. In the first step, without the presence of surfactants, using a mechanical stirrer—R14 CAT—and an ultrasonic cleaner—Proclean 0.7 M of the Ulsonix brand—mono nanoliquids of TiO2/DI + EG and SiO2/DI + EG with concentrations of 0.5, 1.0, and 1.5% vol. were prepared.
Then, to obtain stable hybrid nanofluids, they were mixed in a 20:80 ratio and exposed to ultrasound for 3 h and 15 min. The stability of the suspension for the 0.5, 1.0, and 1.5% nanofluids, after 14 days, was measured with the Nano ZS MPT-2 Zetameter from Malvern and measured at averages of 56.2 mV, 56.6 mV, and 55.9 mV, which, according to [37], gives a very good result that allows suspensions to be classified as very stable.
2.2. Hybrid Nanofluids Properties
To determine the basic physical properties of the suspension, such as the density and specific heat , the rule of mixture (according to Equations (1) and (2)) was used and the results are shown in Figure 4 and Figure 5; the results corresponding to the hybrid nanofluid TiO2:SiO2(20:80)/DI:EG(60:40) are marked with filled symbols, while data from the literature are marked with empty symbols.
where relete to the particle concentration, density, and specific heat of the base fluid (bf) and nanoparticles of specific types, respectively.
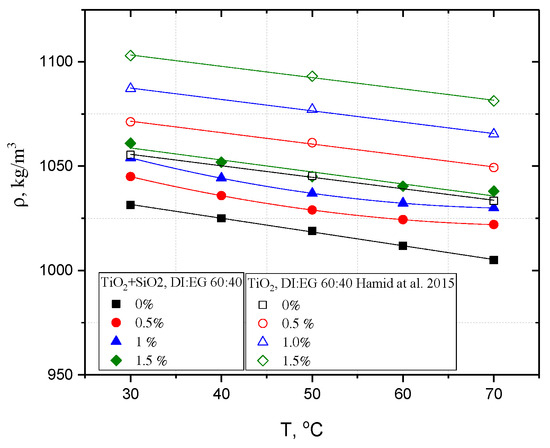
Figure 4.
Density of TiO2 + SiO2/DI:EG hybrid nanofluid as a function of its concentration in comparison with literature [38].
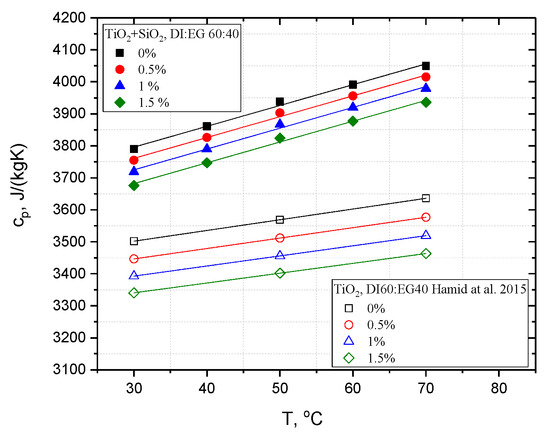
Figure 5.
Specific heat of TiO2:SiO2/DI:EG hybrid nanofluid as a function of the concentration concentration in comparison with literature [38].
In Equations (1) and (2), it is assumed that the mixture ratio of TiO2:SiO2 nanoparticles is 20:80.
A similar method was used in the works by Teng and Hung, Raja et al., Ahammed et al., Hormozi et al., and Sundar et al. [39,40,41,42,43], where the maximum measurement error was 2.53% for density and 5.88% for specific heat. Hamid et al. in [38] studied the effect of temperature on the heat transfer coefficient of titanium dioxide in ethylene-glycol-based nanofluid. The properties of TiO2/DI:EG 60:40 nanofluids with concentrations ranging from 0.5 to 1.5% vol. tested by the authors were compared with our own research, and it was noticed that, in each case, that is, for each concentration, the density of the hybrid nanofluid was ~3% lower than that in the case of the mono nanofluid. However, the specific heat was higher by ~10%.
The dynamic viscosity was assumed based on measurements [44] and is shown in Figure 6. Measurements were carried out using a RheolabQC rotational rheometer (Austria, 2015) in the temperature range from 30 to 70 °C. The angular resolution of the device was 2 µrad. In turn, the thermal conductivity coefficient was determined using a C-Therm TCi Thermal Analyzer (USA, 2015) with an accuracy of 5%. In most cases, the TiO2:SiO2/DI:EG hybrid nanofluid is characterized by a higher viscosity than the TiO2 mono-nanofluid [38]; depending on the concentration, these differences range from 1 to 58%. Additionally, using data developed by Apmann et al. in [45] for 1.5% vol. SiO2 DI:EG 60:40, it is noted that, at lower temperatures, that is, up to 40 °C, the results coincide with this analysis, but at higher temperatures, discrepancies of up to 18% are noted.
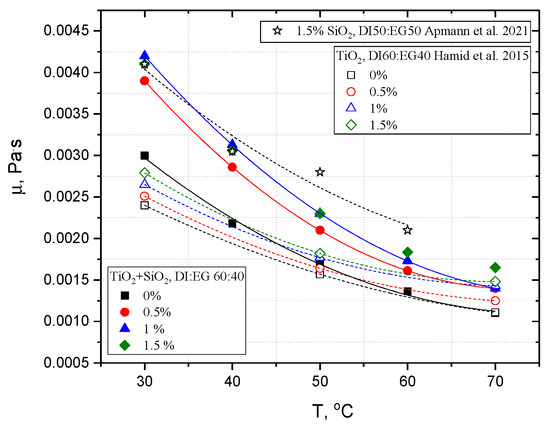
Figure 6.
Dynamic viscosity of TiO2:SiO2/DI:EG hybrid nanofluid versus its concentration in comparison with literature [38,45].
The thermodynamic properties of the obtained nanofluids (density, specific heat, dynamic viscosity, and thermal conductivity) were determined for the temperature range from 30 to 70 °C and are presented in Figure 4, Figure 5, Figure 6 and Figure 7. They were also compared with those available in the literature. The assumed thermal conductivity coefficient differed only by 0.5% from that given by Hamid et al. in [29], where slightly different proportions of the base liquid mixture were adopted, DI:EG 50:50 (here, 60:40). Furthermore, in Figure 7b, the accuracy error of the thermal conductivity k measurements is delineated.
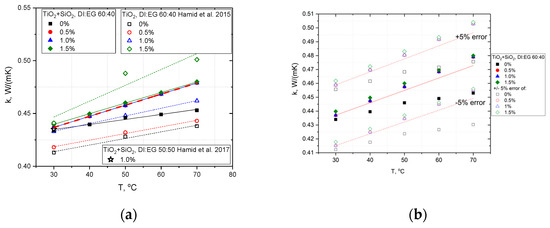
Figure 7.
Thermal conductivity of TiO2:SiO2/DI:EG hybrid nanofluid (a) versus its concentration in comparison with literature data and (b) with error analysis in comparison with literature [29,38].
The thermal conductivity coefficient k increases significantly with the temperature and concentration of the nanoparticles, and is approximately 6% higher in the case of the 1.5% TiO2:SiO2/DI:EG suspension at a temperature of 70 °C than that for the pure DI:EG 60:40 base fluid. However, the parameter k does not change significantly within the analyzed concentrations of 0.5–1.5% and correlates well with the results presented in [29]; for a 1% hybrid nanofluid with a slightly different base fluid mixing ratio DI50:EG50, the difference in value is 0.2%.
2.3. Numerical Modeling
This paper includes a numerical study of the operation of heat exchangers modeled in MATLAB. The analysis relates to determining the efficiency of the heat exchange with the counter-current flow of the working fluid heated by a plate heat exchanger. This device is installed in a solar system to prepare the DHW for a single-family residential building and is made of stainless steel, with the dimensions given in Table 1 and Figure 8. In this case, the solar fluid is a TiO2:SiO2 hybrid nanofluid with a concentration in the range of 0.5–1.5%; the base fluid is a mixture of deionized water and bio ethylene glycol in the DI:EG ratio of 60:40.

Table 1.
Technical parameters of the studied PHE.
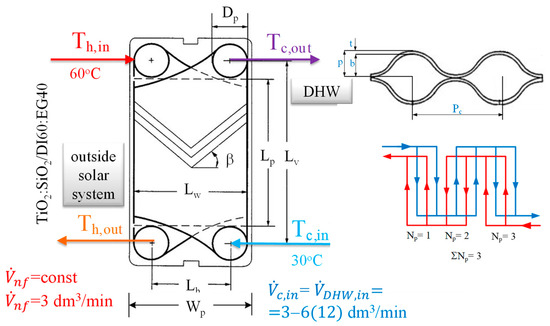
Figure 8.
Initial conditions of the solar system and basic dimensions of a chevron-type PHE with its cross-sectional dimensions normal to the direction of troughs.
Figure 9 shows a diagram of the solar installation to prepare the DHW for a residential building. The PHE visible there constitutes the division between the primary and secondary sides. In the primary part, the working medium is a hybrid nanofluid TiO2:SiO2/DI:EG, the flow of which is maintained at a constant level of 3 dm3/min, thanks to the use of rotameters and a solar pump. A constant and appropriate flow guarantees low heat losses in the installation, the effective operation of solar collectors without reducing their efficiency, the optimal ‘consumption’ of the solar fluid without the need for frequent replacement, long solar pump operation cycles, and the optimal electricity consumption.
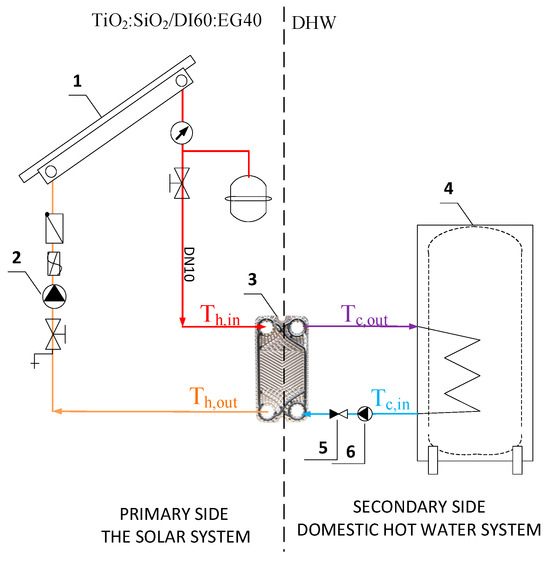
Figure 9.
Schematic test stand of a solar system with flat-plate collectors and TiO2:SiO2/DI:EG hybrid nanofluid as a working fluid: 1—flat-plate collectors, 2—pump unit, 3—a chevron-type PHE, 4—domestic hot water tank, 5—reversible valve, and 6—a pump.
The guidelines and design data recommended by Viessmann [46] for such installations assume that the flow speed of the solar fluid should be between 0.4 and 0.7 m/s. Therefore, the required flow should be between 20 and 40 dm3/h for each 1 m2 of active surface of flat-plate collector, and for vacuum collectors, 40–60 dm3/h.
The model installation includes two flat solar collectors, for which:
- the active area of a single collector is 3.0 m2,
- the required unit flow rate of solar fluid is .
Taking the above into account, the required solar fluid flow will be as follows:
.
For a given area of solar collectors used of 6 m2 and the required flow of 3 dm3/min, the appropriate pipe diameter to guarantee the velocity of the solar fluid in the range of 0.4–0.7 m/s will be DN10 (which is marked in Figure 9).
Hot domestic water flows in the coil located on the secondary side, i.e., on the right side of the heat exchanger (see Figure 9). The initial conditions assume that its temperature at the inlet to the heat exchanger is equal to , and its flow is conditioned by the consumption. This work analyzes the DHW flow varying in the range of = 3–6 dm3/min with a step of = 1 dm3/min and a much larger 12 dm3/min. It is also assumed that all the connecting pipes are well insulated in the case of minimizing the heat loss. The initial conditions assume that the temperature of the solar fluid is equal to .
For comparison, an analysis was carried out in [10] to determine the efficiency of a solar system cooperating with a graphene-based nanofluid and a panel with an active absorber area of 1.14 m2, for which the flow varied in the range from 0.5 to 1.5 dm3/min, which is proportional to the assumptions of this work and confirms their validity.
The studied PHE has an expanded heat transfer area of 0.3 m2 and a surface enhancement factor of 1.15. It is used with a Z-type arrangement, has a counter-current flow corrugation pattern, and consists of six plates. The total number of passes is three, as is shown in Figure 8.
2.4. Heat Transfer Study
The heat balance of the counter-current PHE system is carried out assuming that its external surface is very well insulated and that the heat flux transferred from the hot solar fluid is equal to the amount of heat transferred to the coolant, that is, to the DHW. To balance the heat of the discussed system, an auxiliary in Figure 10 was used, where 1 is the hot solar liquid with a temperature flowing into the exchanger and 2 is the colder liquid on the DHW installation side with much lower parameters , which receives heat.
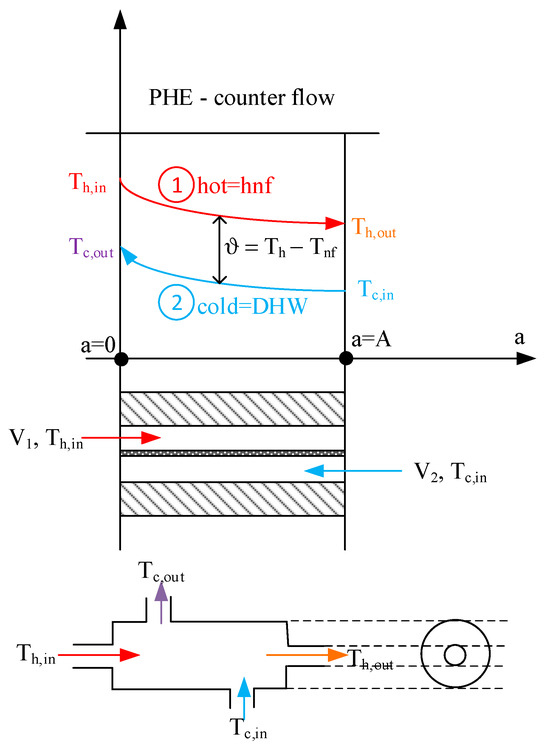
Figure 10.
Analysis of a counter-flow heat exchanger.
The heat transfer rate on the hot liquid side results from the following relationship:
where C is the heat capacity.
The heat quantity received by the cooler liquid is:
The heat capacities of the media (the so-called water equivalents) for liquids 1 and 2 (according to Figure 10) result from their fluxes and specific heat , and are calculated as follows:
Differentiating the above relationships:
Further, the elementary difference between fluids is:
where .
The average temperature difference for a counter-current PHE is:
which can be written as:
The above reasoning, with knowledge of both the heat transfer coefficient U and the inlet and outlet temperatures for both factors, allows for the calculation of the average heat flux (see Equations (13) and (14)) when the size of the heat exchange surface A between the factors is known, or allows for determining the area A when the size of the heat flux is known.
The method for determining the average logarithmic temperature can be used when the inlet and outlet temperatures of the media are known; or in the opposite situation, they can be determined from the energy balance. If only the inlet temperatures are known, the logarithmic mean temperature difference method (abbr. LMTD) requires an iterative procedure.
In order to determine the efficiency of the HE, we must introduce the concept of the maximum heat flux that can be exchanged, i.e., one that is a counter-current of infinite length. In this case, one of the factors will record the largest possible temperature drop, i.e., .
If the heat capacity of the cooling/heat-receiving fluid (here, DHW) is lower than the fluid from which heat is received, i.e., Cc < Ch, then |dTc| > |dTh|. The cold fluid will experience a greater temperature change and will be heated to the hot fluid inlet temperature (Tc,out = Th,in). For this assumption, the following statement is:
otherwise:
The following generalization can be made:
Knowledge of the actual and maximum heat flux and heat capacity ratio of fluids allows for determining the PHE efficiency, ε, which takes values from 0 to 1:
where are the real and maximum heat flux, respectively.
The effectiveness of the PHE depends also on its configuration, and the Number of Transfer Units (abbr. NTU), see Equation (21). The number of exchanges, NTU, is a dimensionless quantity, often used in the analysis of the size of heat exchangers and depending, among others, on their material parameters:
For the counter-current flow, the PHE effectiveness can be calculated on the basis of [47]:
Then, based on Formulas (4), (5), and (19), it is possible to determine the real average heat flow and the temperatures at the outlet from the exchanger :
Thus, the overall heat transfer coefficient U may be calculated as:
where, are the convective heat transfer coefficients of the hotter fluid and the coolant, respectively, and depend on the PHE geometry, fluid properties, and its flow, is the conductive heat transfer coefficient, and tPHE, relates to the plate thickness.
The convective heat transfer coefficients of the hotter fluid, in Equation (27), can be expressed as:
where is the conductive heat transfer coefficient of the hot fluid, is the Nusselt number for the description of the dynamic similarity phenomenon, and refers to the hydrodynamic channel diameter. The unknown parameters can be calculated from Equations (29)–(31).
For the laminar flow of the solar fluid, that is, 3 dm3/min, and for the 30° chevron angle of PHE, the Nusselt similarity number can be calculated based on the following correlation, [48]:
and for DHW 5250 > ReDHW > 450 [49]:
where C and m are constants adopted in accordance with [47], Re and Pr are the Reynolds and Prandtl nondimensional numbers, respectively, b is the mean channel gap, as shown in Figure 8, and is the enlargement factor of the plate area that, as in [8], is usually taken as 1.15–1.25 or a little bit higher for other heat exchangers [49]; detailed geometric data of the heat exchanger are also given in Table 1.
The Re and Pr numbers are then calculated as follows:
In Reynolds number mathematical expressions, are the hot and cold channels’ mass flow rates, respectively, and are the dynamic viscosities of the two fluids.
where refer to the two fluids’ mass and volume flows, respectively, and their densities, is the number of channels per pass (a channel is the space between two adjacent plates; the end plates are not taken into account, so the number of exchanger channels is the number of plates minus one; odd-numbered channels belong to side I and even-numbered channels belong to side II), and , is the plate width between gaskets in line with the dimensions in Figure 8 and Table 1.
where is the pass number (this is the number of changes in the direction of a specific stream inside the plate pack plus one) and is the total number of plates.
2.5. Entropy and Exergy Study of PHE
The total entropy generation of the fluid results from thermal and frictional entropy [50,51,52], thus, , respectively.
where is the density, f is the friction factor, and is the height of the PHE in line with Figure 8.
As the entropy of the system increases, its degree of disorder, reversibility, and dissipation also increase, and its exergy decreases. The entropy change is defined by its total differential:
where T is an absolute temperature and is a small amount of heat supplied to the system.
The friction factor, f, of the working hybrid nanofluid can be calculated from the expression that includes the pressure drop between the inlet and outlet channels at the PHE:
where v is the fluid velocity calculated from the mass flow, g is the gravity acceleration, H is the static pressure drop, Di is the inner diameter of the pipe, and L is its length, which is in good correlation with the Hagen–Poiseuille law:
and other friction factor relations [50] with a maximal variation of ±3%.
After determining the thermal and frictional entropy, it is possible to calculate the dimensionless Bejan number, which, in thermodynamics, is the ratio of thermal entropy to the total entropy generated of the system [53] (the ratio of heat transfer irreversibility to the summary entropy generation) and compares the energy lost as a result of friction (pressure drop) and transferred thermal energy:
Thereby, the total exergy destruction, in a heat plate exchanger results from the total entropy generation and on the basis of the Gouy–Stodola theorem [53], and can be calculated as follows:
where, are the thermal and frictional exergy destruction, respectively.
Further, the exergy efficiency of the PHE is defined as the ratio of the useful exergy output to the total exergy input [54] and can be written as:
where Ta and Tw,ex are the ambient and external surface temperatures of the PHE, respectively.
The reference temperature Ta can be estimated from the following energy equation:
The temperature of the outer surface of the heat exchanger, was calculated using the relationship of the heat transfer through a single-layer flat wall.
The relationship between the exergy destruction and the heat flux can be used to determine the irreversible losses of the installation and is defined as the entropy generation number Ns:
The entropy generation number is, thus, directly connected with Bejan, Be (see Equation (45)). Both of these quantities are inversely proportional to the heat transfer efficiency.
3. Results and Discussion
This section may be divided into subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.
This chapter discusses the thermohydraulic analysis of the solar system shown in Figure 9. A PHE separates the internal and external parts of the DHW installation. On the external side—thus, on the solar installation—TiO2:SiO2 hybrid nanofluid with various concentrations of 0.5–1.5% was used as a solar fluid; it was produced on the basis of a mixture of deionized water and ethylene glycol in a ratio of 60:40. Conditions of a constant flow and temperature of the solar fluid were assumed here as 3 dm3/min and 60 °C, respectively.
On the internal side, the initial temperature of the domestic water was 30 °C, and its flow was variable, ranging from 3 to 6 dm3/min with flow step of 1 dm3/min; additionally, the results for a much higher flow of 12 dm3/min are also shown.
Based on relationships (32) and (33), the Reynolds numbers were calculated separately for fluids in the cold and hot channels of the studied PHE. In the hot channel, due to the constant flow of the working medium of 3 dm3/min, the values of the Re numbers were slightly variable and depended primarily on the concentration of the nanofluid in the installation and its thermodynamic parameters, and were 430.25, 368.85, 345.90, and 328.67 for the concentrations of the TiO2:SiO2 nanofluid of 0%, 0.5%, 1.0%, and 1.5% vol., respectively.
In the cold channel, on the side of the DHW installation, the Re numbers varied from 719 for a flow of 3 dm3/min to 1438 for a flow of 6 dm3/min. Simulations were also performed for higher flows, corresponding to the water outflow from the intake valve of 12 dm3/min, for which the number Re = 2875.51.
When the corrugated PHE efficiency was analyzed, all of the calculated Re numbers indicated a laminar flow, except the last extreme value relating to the flow of 12 dm3/min. In this type of system, it is assumed that laminar flow can persist up to Re = 2000, as claimed by Kabeel et al. in the works of [55,56], or even up to Re = 2500, as proven by Goodarzi et al. in [57]. It is worth mentioning that, in the case of a microchannel heat exchanger, Jiang et al. in [58] observed a turbulent flow already at Re = 600, which, however, does not coincide with the scope of this study.
Figure 11a–c show how the Re number changes with the nanofluid concentration, flow, and Nu number. The results were compared with the data available in the literature (for similar flows) [50,59]. As it turns out, nanofluids consisting of two types of nanoparticles are characterized by a higher Nu number than mono nanofluids. Moreover, the Nu number is also proportional to the concentration of the suspension. An important observation is that ethylene-glycol-based nanofluids also increase the Nu number from 10 to 32% [60].
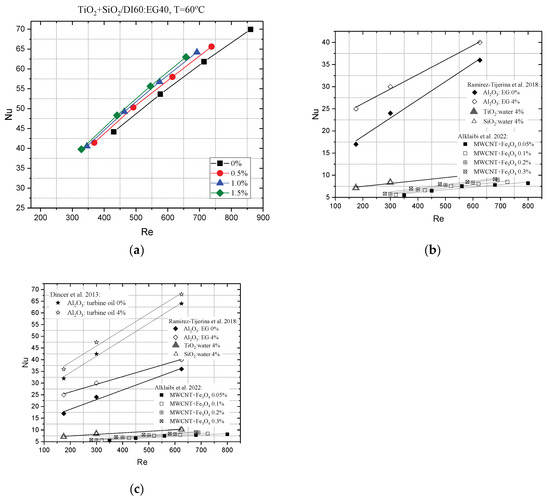
Figure 11.
Nusselt number of (a) studied TiO2:SiO2/water ethylene glycol 60:40—hybrid nanofluid and (b,c) [36,50,60] other nanofluids according to worldwide researchers versus low Reynold number.
In Figure 12 and Figure 13, the Nusselt number of the DHW is shown during the flow through the PHE system versus the Reynolds number for variable flows of 3–6 and 12 dm3/min. Our own results were compared with those obtained by Akturek F. et al. in [49], where the performance of a gasketed-plate heat exchanger with a surface extended area of A ≈ 0.14 m2 was tested; the average water temperatures on the hot side of the heat exchanger were Th,av = 71.5 °C, and on the cold side were Tc,av = 17 °C. The average difference between the Nusselt number values was Nu = 5.07, that is, approximately 12.7%. In turn, the average standard deviation between the obtained Nusselt number values was SD ± 3.59, i.e., approximately 9%. Despite the basic differences between the assumptions and the input data, the obtained result is very satisfactory, and the validation of the adopted methodology is positive.
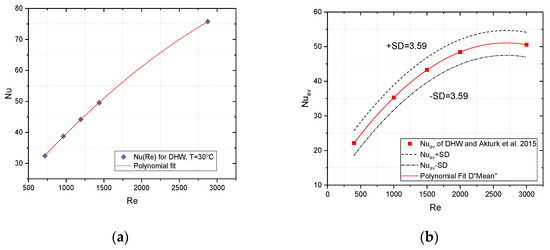
Figure 12.
Nusselt number validation of DHW during the flow through PHE system versus Reynolds number. (a) own research; (b) in comparison with literature [49].
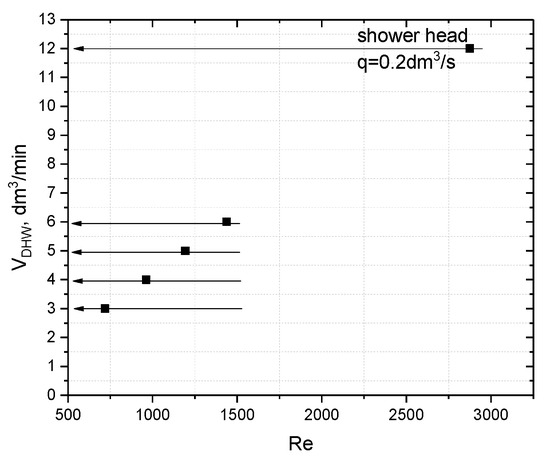
Figure 13.
Reynolds number versus DHW flow.
The friction factor for water was calculated on the basis of the Hagen–Poiseuille law (f = 64/Re), and then compared with the experimental results presented in [50] (see Figure 14a); the maximum discrepancies in the results reached ±7.0%, however, after interpolation with a second-degree polynomial (determination coefficient R2 = 0.99), the functions were convergent and the discrepancies reached less than ±0.5%.
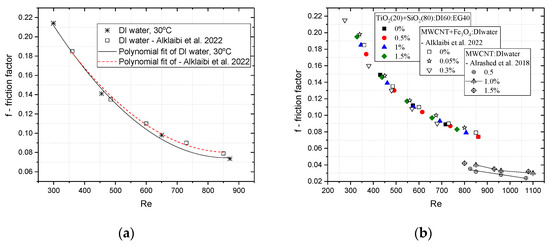
Figure 14.
Friction factor calculated in present study in comparison with the literature (a) for deionized water and [50] (b) nanofluids [50,61].
The friction factor for the TiO2 + SiO2/DI + EG hybrid nanofluid in the concentration range from 0 to 1.5% and the operating temperature of 60 °C is shown in Figure 14b. The f parameter depended on the flow and, in the case of the DI60 + EG40 base fluid, was from 0 to 4% lower than the base fluid used in the tests [50]. However, no discrepancies in the friction coefficient greater than ±1% were observed in the range of tested nanofluids and their concentrations and Re numbers, as was visible in the case of the 0.5- and 1.0%-MWCNT water-based nanofluids at higher flow values [61]. When comparing our own research with 0–0.3%-MWCNT + Fe3O4 water-based nanofluid [50], the differences between the f values ranged from 0 to ±7.7%. Therefore, it can be concluded that an increase in the concentration of nanofluids does not always translate directly into a reduction in the phenomenon of liquid friction against the pipeline walls, which should be analyzed more thoroughly.
An exergy analysis of the system with an economizer (in the form of a PHE) exchanging thermal energy between the internal hot water installation and the external solar installation with the working medium of a TiO2:SiO2/DI:EG hybrid nanofluid comes down to determining the exergy efficiency (also cold as the rational efficiency or the second-law efficiency), (see Equation (47)). This parameter determines the efficiency of the system under reversible conditions and is defined as the quotient of the useful work/exergy output of the system to the reversible work/exergy output for work/exergy-consuming systems. In order to calculate this rational efficiency, first, the total exergy destruction in the PHE was determined, and then, the entropy generation number Ns and the dimensionless Bejan number, Be, were calculated.
In Figure 15, the entropy generation number Ns of the solar research arrangement with a TiO2:SiO2 hybrid nanofluid of varying concentrations that influences the Reynolds numbers is extracted. The entropy generation numbers are presented for different DHW flows of 3–12 dm3/min. In turn, Figure 16 shows the variability of the Bejan number depending on the flow and concentration of nanoparticles. The smaller the values of entropy generation and the Bejan numbers (Ns and Be), the greater the efficiency of the system [53].
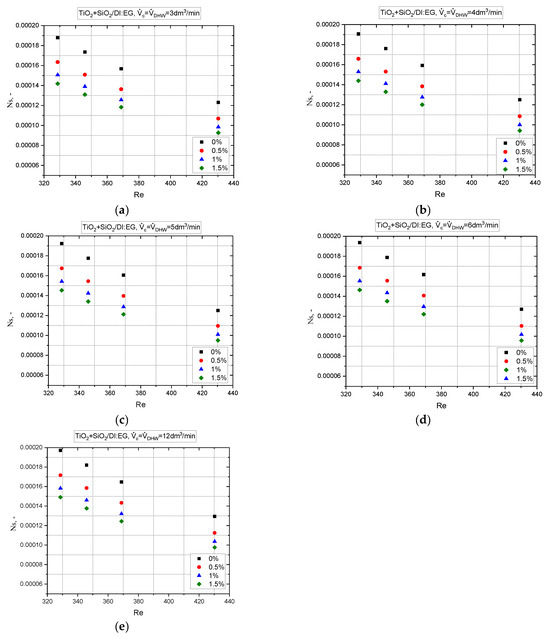
Figure 15.
Entropy generation number versus Reynolds numbers and volume concentrations of TiO2:SiO2/DI:EG hybrid nanofluid and different DHW flow from (a) 3 dm3/min, through (b) 4 dm3/min, (c) 5 dm3/min, (d) 6 dm3/min, up to (e) 12 dm3/min.
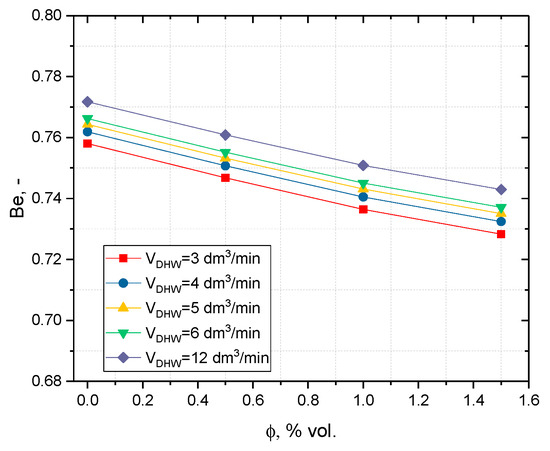
Figure 16.
Bejan number variation with volumetric flow of nanofluid and concentration.
The Be number was inversely proportional to the concentration of the nanofluid and increased with the DHW flow by approximately 25% on average, for each of the analyzed concentrations; however, it decreased with an increase in the flow of nanofluids through the exchanger on the primary side of the analyzed solar installation. The observed relationship was confirmed by research conducted by Alklaibi et al. [50], Sundar et al. [62], and Iranmanesh et al. [10].
Compared to the data presented in the literature, for a similar range of flows, the Ns and Be values calculated in this case were low; hence, the expected high efficiency of the solar installation, i.e., the thermal energy transferred to the DHW installation on the secondary, i.e., internal/user side, would be high, and the losses caused by friction would be slight. Ultimately, it is concluded that the presence of nanoparticles intensified the heat transfer in the plate heat exchanger.
The exergy efficiency of the PHE operating based on a base liquid, that is, a mixture of deionized water and ethylene glycol and a hybrid nanofluid of various concentrations, depending on the flow on the DHW side ranging from (a) 3 to (e) 12 dm3/min, is shown in Figure 17.
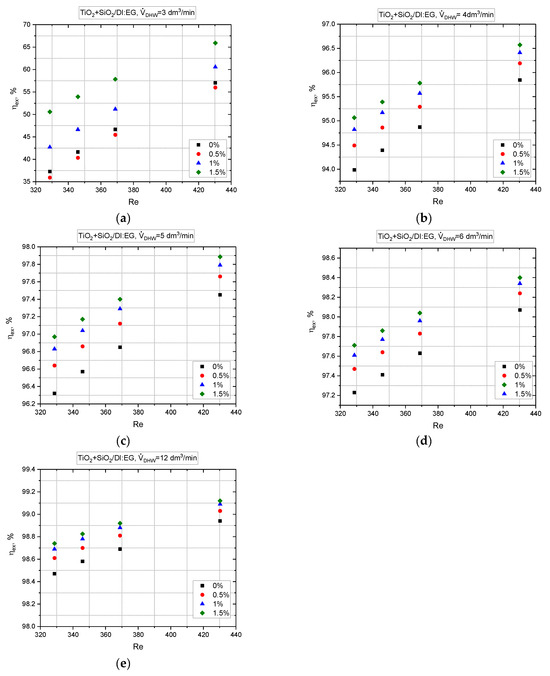
Figure 17.
The exergy efficiency of PHE with working fluids of different concentration versus Reynolds number and DHW flow of (a) 3 dm3/min; (b) 4 dm3/min; (c) 5 dm3/min; (d) 6 dm3/min; (e) 12 dm3/min.
Only for a comparable solar fluid flow, DHW 3 dm3/min (see Figure 17a), and concentrations of 0 and 0.5% vol. was there no significant improvement in the exergy efficiency. In other cases, the presence of nanoparticles significantly improved the heat transfer; the higher the concentration and the flow of hot water, the higher the exergy efficiency was. For example, based on Figure 17a, it is concluded that the TiO2:SiO2/DI:EG hybrid nanofluid was a 13 to 26% more effective working fluid than the traditional solar fluid; at Re = 329, the exergy efficiency was (0%) = 37.29%, with a nanoparticle concentration of 0% and (1.5%) = 50.56%; with Re = 430, (0%) = 57.03%, and (1.5%) = 65.9%. For comparison, work [10] showed a 20% increase in the exergy efficiency for graphene-based nanofluids compared to pure water.
For the highest flow analyzed on the DHW side, i.e., 12 dm3/min, the exergy efficiency of the PHE was, on average, 98.5%, but the difference between concentrations was not significant. The selection of the size of the solar installation, and, therefore, the flow of the solar fluid, should be closely related to the water consumption, and this should be carefully calculated, also taking into account the individual preferences of residents and the time of using sanitary utensils/frequency occurrence of flows with high normative values. Only in this way will the use of nanofluids be efficient and economically justified.
Figure 18 presents an overall heat transfer coefficient, U, W/m2K of the analyzed gasket PHE versus the hybrid nanofluid concentration, and the DHW flow is presented in Figure 18. This coefficient is directly proportional to the concentration and flow of the DHW. By adding nanoparticles in the amount of a 1.5% vol. fraction to the base liquid, the overall heat transfer coefficient increased by 100 W/m2K for VDHW = 3 dm3/min and by 177 W/m2K for VDHW = 12 dm3/min, which corresponded to an approx. 7% intensification of heat transfer and is a comparable value to that obtained by Okonkowo et al. in [31] for SiO2/Syltherm-800 based nanofluids at 4% vol. Additionally, when the flow in the DHW installation changed from 3 to 12 dm3/min, the presence of nanoparticles could cause a 30% increase in the overall heat transfer coefficient from 1700 to over 2400 W/m2K. The obtained results were also compared with those published by Yashawanth et al. in [14], where the thermal efficiency of a PHE was tested in the flow range of 11–19 dm3/min; the temperature difference between the working media, Al2O3 mono nanofluid produced on the basis of ethylene glycol, and water was ΔT = 50 °C; the nanofluid, in this case, worked as a coolant. The difference between the U values obtained in this work, for an example concentration of 1.5%, compared to the work [14], was 21%. Moreover, in [14], a maximum of a 9.8% increase in the U was recorded when comparing the base liquid and the Al2O3 nanofluid with a concentration of 1.5%. In this work, the difference was 7%, which confirms the same order of magnitude of the obtained parameters.
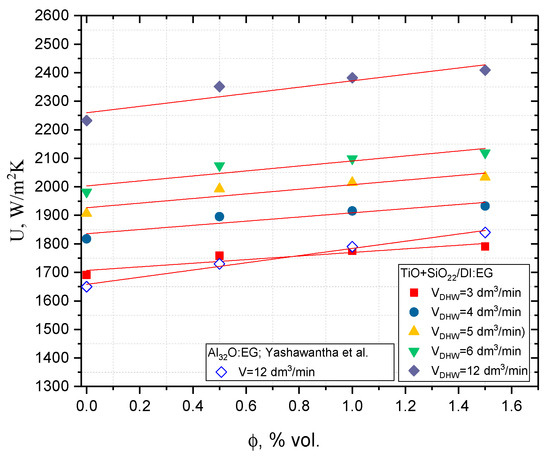
Figure 18.
The overall heat transfer coefficient of the hybrid nanofluid versus it % vol. concentration and DHW flow [14].
The overall heat transfer coefficient U derives from the enhancement of the hybrid nanofluid heat transfer coefficient hnf, which is presented in Figure 19. There were observed intensifications in the hnf by 6.6%, 7.7%, and 11.2% for the TiO2:SiO2/DI:EG hybrid nanofluid of concentrations of 0.5, 1, and 1.5% vol., respectively, compared to the base fluid. The obtained values for the laminar flow and low Reynolds numbers were of the same order of magnitude as those in Okonkowo et al. in [31] and in [14].
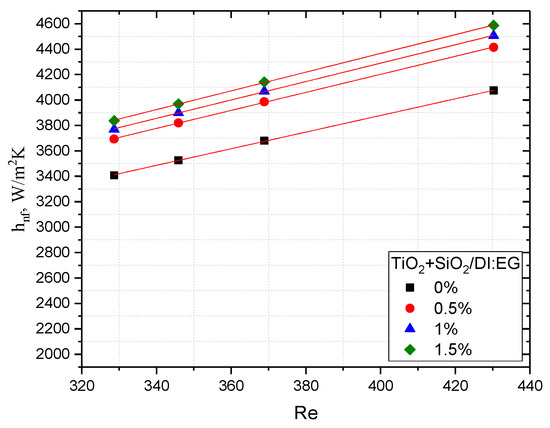
Figure 19.
The heat transfer coefficient of TiO2:SiO2/DI:EG hybrid nanofluid with Reynolds number.
In the next step, based on Equations (18)–(23), the effectiveness, ε, of the PHE was calculated for different concentrations of nanofluid, and the results are presented in Figure 20. The average difference in values observed between the base liquid and the highest of the analyzed concentrations (1.5%) within each of the analyzed DHW flows (from (a) to (e)) was approximately 2%, and it reached a maximum of 9%. The results obtained were, on average, approximately 10% higher than the research performed by Yashawanth et al. in [14], where Al2O3/DI:EG nanofluid with a flow of 12.5 dm3/min and similar concentrations was analyzed; the differences are shown in Figure 21. In [14], the effectiveness of the PHE, ε, was 3.5% higher for the 1.5% nanofluid than for the base liquid.
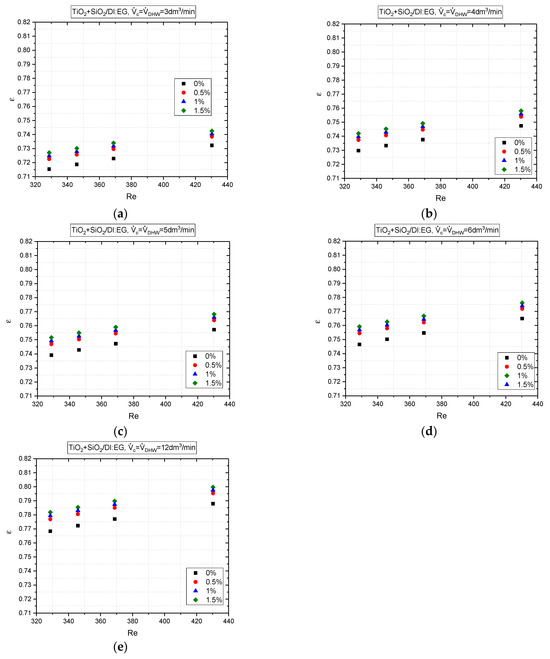
Figure 20.
The effectiveness of PHE versus Reynolds number and volume concentrations of TiO2:SiO2/DI:EG hybrid nanofluid and different DHW flow from (a) 3 dm3/min, through (b) 4 dm3/min, (c) 5 dm3/min, (d) 6 dm3/min, up to (e) 12 dm3/min.
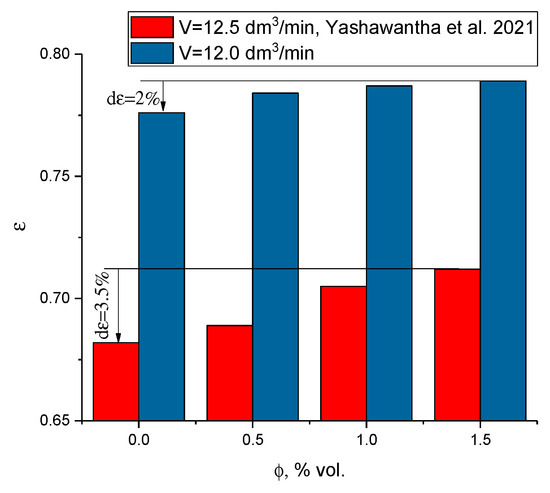
Figure 21.
The comparison of effectiveness of PHE with available literature data [14].
Next, the NTU method, discussed in the previous section, was used to analyze the effectiveness of the HE using thermal equations transformed into dimensionless form. As shown in Figure 22, the NTU value for the hybrid nanofluid was higher than that for the base liquid, and for Reynolds numbers in the range of Re = 329–430, it increased linearly and proportionally to the nanofluid concentration from 5% to 7%; for comparison, work [14] showed an average improvement of 12% in the quality of the PHE operation compared to the base liquid. When comparing the values obtained with those of Alklaibi et al. [50], it can be seen that the NTUs for water-based nanofluids were much lower than those for mixtures of ethylene glycol and deionized water. This difference was up to approximately 70%, as shown in the next Figure 23; the NTU for deionized water is shown as a solid line, which is 0.75; for the same flow of 3 dm3/min and the base liquid and ethylene glycol, the NTU is 2.6.
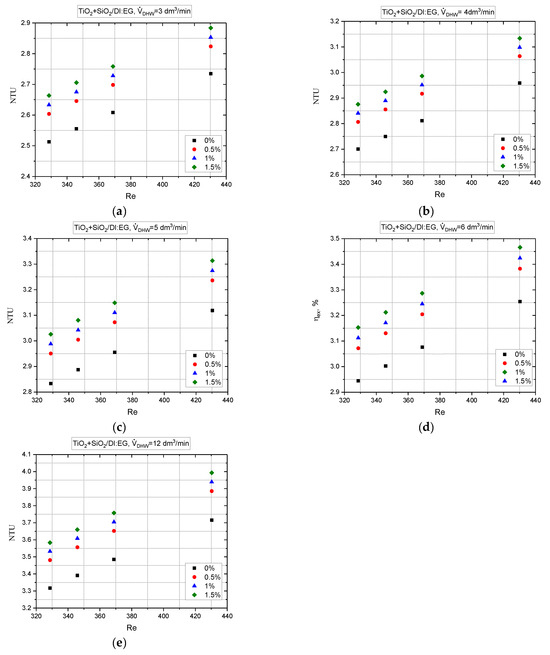
Figure 22.
The number of transfer units of PHE using TiO2:SiO2/DI:EG hybrid nanofluid hybrid nanofluid as a function of Reynolds number and different DHW flow from (a) 3 dm3/min, through (b) 4 dm3/min, (c) 5 dm3/min, (d) 6 dm3/min, up to (e) 12 dm3/min.
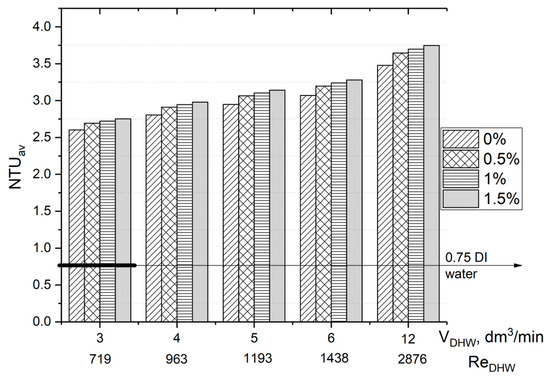
Figure 23.
An average number of transfer units of PHE using TiO2:SiO2/DI:EG hybrid nanofluid as a function of DHW and Reynolds number [2].
Further analysis shows how the average NTU value changes with a variable flow in the DHW installation and Re. A change in NTUav was observed in the range from 2.6 (for the base liquid) to 3.75 (for the 1.5% nanofluid). The higher the flow in the DHW installation, the proportionally higher the NTUav, and varied from 25% to 27% within a given number of ReDHW. The highest increase was recorded for 1% nanofluids.
Moreover, for assessing the total performance of the heat exchanger thermohydraulic performance index, THPI was evaluated in accordance with Equation (50) and is shown in Figure 24. The parameter explicitly depends on the Nu and f factor, therefore, the heat transfer and pumping power or the friction factor in laminar or turbulent flow. The higher the THPI index (preferably > 1), the more effective the heat transfer.
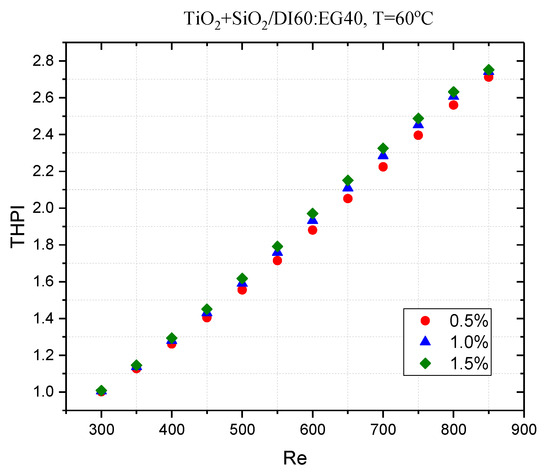
Figure 24.
THPI of TiO2:SiO2/DI:EG hybrid nanofluid at different Re and concentration.
It turned out that THPI increased with the flow and was much higher than 1 for nanofluids, but no significant differences were observed between the values of this indicator for nanoliquids with the analyzed concentrations.
The ability to assess the qualitative impact of data disturbance on the result is the basis for numerical calculations. The sensitivity of the solution to the initial data was determined by the so-called conditioning of the numerical task. A task is ill-conditioned if small (relative) changes in the initial data produce large (relative) changes in the results, which was almost not observed in this case. However, some of the input data came from measurements, which is why the assessment of measurement uncertainty, especially with respect to the key input parameters, was determined using Method B for estimating the uncertainty resulting from the precision of the measuring instrument. The measurement error is shown in Figure 17b. The maximum absolute error was 5%.
If the energy efficiency of the exchanger was determined in real conditions, the parameters measured in an indirect way and would be influenced by many measurement values. In this case, it was Equations (18) and (47), the solution to which, due to measured quantities, can be written in the following form:
The equation provides the basis for an uncertainty analysis, which, in real conditions, should be conducted with the total differential method, using the following dependence:
and a similar one for exergy efficiency.
According to previous research, the value of these errors does not exceed 5% [33].
4. Economic Analysis
Using simple mathematical formulas provided in the literature [32], the unit total cost of producing the TiO2:SiO2/DI:EG nanofluid was calculated (see Equations (52) and (53)). It was compared to the price of the ethylene glycol mixture that is standardly filled in solar installations, and the results are summarized in Table 2.
where CNano is cu, EUR/1g is the unit cost of purchasing nano particles, ρ is the density of the nanofluid, V is the volume, Cother accounts for the variable additional costs related to the preparation of the suspension like maintenance costs or stabilization, and CBase is the unit purchase price of the base liquid.

Table 2.
Total gross unit costs of the preparation of TiO2:SiO2/DI60:EG40 nanofluids with various nanoparticle concentrations.
Then, using the correlation proposed by Hsieh et al. in [63] (see Equation (54)), the heat transfer enhancement ratios of the studied hybrid nanofluids of the proposed concentrations were calculated, and the results are shown in Figure 25. The use of 1.5% TiO2:SiO2/DI:EG hybrid nanofluid in a flat solar collector system can contribute to approximately a 35% intensification in heat transfer compared to the base liquid.
where h is the heat transfer coefficient, q is the heat flux, and is the nanoparticle volume fraction.
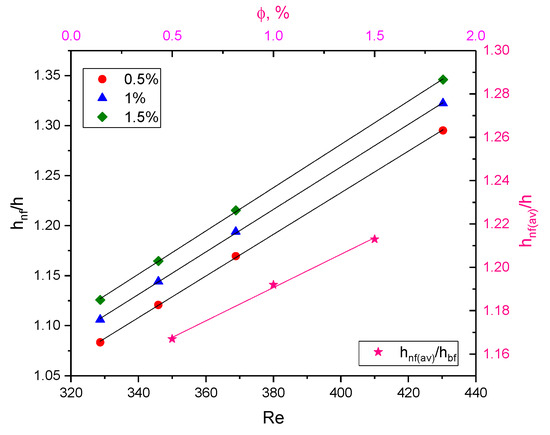
Figure 25.
Heat transfer enhancement ratios of TiO2:SiO2/DI:EG hybrid nanofluid versus Reynolds number.
Assuming that the solar installation is 3 dm3, the cost of 1.5% nanofluid is approximately EUR 3785, so the investment outlays are much higher than those in the case of using a mixture of water and ethylene glycol. However, if we take into account the 35% intensification of heat exchange, the outlays will pay off after approximately 7 years, SPBT = 7.37 years.
If we take pumping power as the profitability criterion, the operating cost required to maintain the flow through the solar channel is proportional to the pressure drop [49]:
where is the pumping power and Cel refers to the unit costs of electricity, Cel = 0.18 EUR/kWh.
where is the difference in pressure between the inlet and outlet of the solar fluid through the analyzed PHE, g is the gravity acceleration, and H is the vertical pressure height.
The power required to pump nanofluids and its associated costs increase in direct proportion with the suspension concentration, as shown in Figure 26. The power requirement for a circulation pump pumping only a pure working medium consisting of a mixture of water and glycol is 2.1 W and is 30% higher than that for 0.5% TiO2:SiO2/DI:EG nanofluids. Furthermore, the costs associated with the electrical energy required to pump the nanofluids are, therefore, negligible.
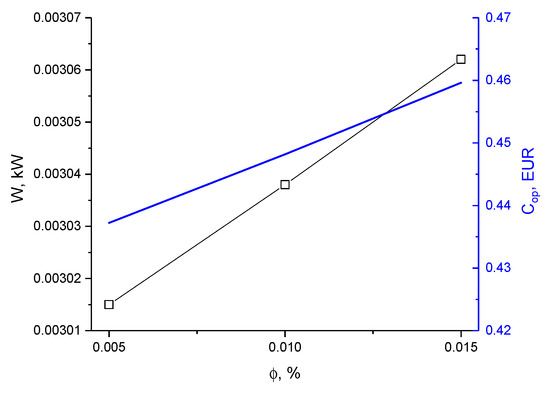
Figure 26.
The pumping power requirement of TiO2:SiO2/DI:EG hybrid nanofluid versus its concentration.
Using renewable energy sources in a diverse European climate [64] and other potential limitations and challenges in studying solar installation are broadly discussed in [65,66,67].
5. Conclusions
In this paper, water–ethylene (60:40)-glycol-based TiO2:SiO2 hybrid nanofluids were numerically studied as solar fluids in a domestic hot water installation. A plate heat exchanger was placed in the installation and separated the primary circuit—with the solar fluid—and the secondary circuit—in which domestic hot water flowed. The hybrid nanofluid TiO2:SiO2 (20:80) with a concentration in the range of 0.5–1.5% vol. and a temperature of 60 °C were prepared by two-step method and checked for their stability with a Nano ZS MPT-2 Zetameter. The properties of the suspensions were experimentally examined for their flow rates in the range = 3–6 dm3/min with a step of = 1 dm3/min, and much larger 12 dm3/min. The innovation in this work was to analyze the economic and technical effectiveness of the use of exemplary hybrid nanofluids with a PHE in the solar installation system. Working fluids acted as heating, not as heated medium. Most of the studies related to the use of nanofluid as a cooling agent on the secondary side of the installation.
In this study, many thermodynamic parameters were calculated and they indicated that TiO2:SiO2/DI:EG hybrid nanofluid enhanced the performance of the plate heat exchanger. The most significant conclusions are the following:
- -
- the thermal conductivity coefficient, k, increased significantly with the temperature and concentration of the nanoparticles of approximately 6%;
- -
- a change in NTUav was observed in the range from 2.6 (for the base liquid) to 3.75 (for the 1.5% nanofluid). The higher the flow in the DHW installation, the proportionally higher the NTUav; it varied from 25% to 27% within a given number of ReDHW;
- -
- ethylene-glycol-based nanofluids increased the Nu number from 10 to 32% depending on the suspension concentration; at Re = 657, the Nu of 1.5% TiO2:SiO2/DI:EG hybrid nanofluid in the PHE was 5% higher than that of the base fluid; but the friction factor, f, increased with the concentration and did not significantly exceed the base fluid friction factor—0 to 4% growth;
- -
- the entropy generation number, Ns, was lowered to ~15% using a 1.5% suspension compared to the base fluid;
- -
- the Bejan number, Be, was inversely proportional to the concentration of the nanofluid and increased with the DHW flow by approximately 25% on average, for each of the analyzed concentrations; it also decreased with the increase in the flow of nanofluids through the PHE on the primary side of the analyzed solar installation;
- -
- The TiO2:SiO2/DI:EG hybrid nanofluid was a 13 to 26% more effective working fluid than the traditional solar fluid; at Re = 329, the exergy efficiency was = 37.29%, with a nanoparticle concentration of 0% and (1.5% vol.) = 50.56%; with Re = 430, (0%) = 57.03% and (1.5%) = 65.9%;
- -
- the overall heat transfer coefficient, U, increased by 100 W/m2K for VDHW = 3 dm3/min and by 177 W/m2K for VDHW = 12 dm3/min, which corresponded to approx. a 7% intensification of the heat transfer;
- -
- based on the heat transfer enhancement ratios, it is concluded that the use of 1.5% TiO2:SiO2/DI:EG hybrid nanofluid in a flat solar collector system can contribute to approximately a 35% intensification of heat transfer compared to the base fluid;
- -
- the effectiveness, ε, of the PHE increased with the nanofluid concentration and the flow in the DHW system, and was 3.5% higher for the 1.5% nanofluid in comparison with the base fluid for each DHW flow;
- -
- using nanofluids, in some cases, will pay off after approximately 7 years.
Author Contributions
Conceptualization, S.W. and D.T.; methodology, S.W. and D.T.; validation, S.W. and D.T.; formal analysis, S.W. and D.T.; investigation, S.W. and D.T.; resources, S.W. and D.T.; data curation, S.W. and D.T.; writing—original draft preparation, S.W. and D.T.; writing—review and editing, S.W.; visualization, S.W.; supervision, D.T.; project administration, S.W.; funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
The project is supported by the program of the Minister of Science and Higher Education under the name: ‘Regional Initiative of Excellence’ in 2019–2023 project number 025/RID/2018/19 financing amount PLN 12,000,000.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Węglarz, K.; Taler, D.; Taler, J. New non-iterative method for computation of tubular cross-flow heat exchangers. Energy 2022, 260, 124955. [Google Scholar] [CrossRef]
- Maleki, N.M.; Pourahmad, S.; Khoshkhoo, R.H.; Ameri, M. Performance improvement of a double tube heat exchanger using novel electromagnetic vibration (EMV) method in the presence of Al2O3-water and CuO-water nanofluid; An experimental study. Energy 2023, 281, 128193. [Google Scholar] [CrossRef]
- Desisa, T.R. Experimental and numerical investigation of heat transfer characteristics in solar flat plate collector using nanofluids. Int. J. Thermofluids 2023, 18, 100325. [Google Scholar] [CrossRef]
- Gupta, S.K.; Verma, H.; Yadav, N. A review on recent development of nanofluid utilization in shell & tube heat exchanger for saving of energy. Mater. Today Proc. 2022, 54 Pt 3, 579–589. [Google Scholar] [CrossRef]
- Mukherjee, S.; Wciślik, S.; Mishra, P.C.; Chaudhuri, P. Nanofluids: Critical issues, economics and sustainability perspectives. Particuology 2024, 87, 147–172. [Google Scholar] [CrossRef]
- Available online: https://www.sciencedirect.com/search?qs=nanofluids%2C%20plate%20heat%20exchanger&lastSelectedFacet=years (accessed on 5 September 2023).
- Heulings, S.M. Review of commercial pasteurization, Bulletin No. 147. Am. J. Public Health 1925, 15, 723–725. [Google Scholar] [CrossRef][Green Version]
- Mota, F.A.S.; Carvalho, E.P.; Ravagnani, M.A.S.S. Modeling and Design of Plate Heat Exchanger. In Heat Transfer Studies and Applications; InTech: London, UK, 2015. [Google Scholar] [CrossRef]
- Shah, R.K.; Sekulic, D.P. Fundamentals of Heat Exchanger Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003; p. 24. [Google Scholar]
- Iranmanesh, S.; Silakhori, M.; Naghavi, M.S.; Ang, B.C.; Ong, H.C.; Esmaeilzadeh, A. Using Graphene Nanoplatelets Nanofluid in a Closed-Loop Evacuated Tube Solar Collector—Energy and Exergy Analysis. J. Compos. Sci. 2021, 5, 277. [Google Scholar] [CrossRef]
- Lazarevikj, M.; Filkoski, R.V.; Markov, Z. CFD analysis of heat transfer and fluid flow in plate heat exchanger with nanofluid. In Proceedings of the 3rd South East European Conference on Sustainable Development of Energy, Water and Environment Systems—SDEWES SEE 2018, Novi Sad, Serbia, 30 June–4 July 2018. [Google Scholar]
- Wciślik, S. The Influence of Nusselt Correlation on Exergy Efficiency of a Plate Heat Exchanger Operating with TiO2:SiO2/EG:DI Hybrid Nanofluid. Inventions 2024, 9, 11. [Google Scholar] [CrossRef]
- Haghighi, E.B.; Saleemi, M.; Nikkam, N.; Khodabandeh, R.; Toprak, M.S.; Muhammed, M.; Palm, B. Accurate basis of comparison for convective heat transfer in nanofluids. Int. Commun. Heat Mass Transf. 2014, 52, 1–7. [Google Scholar] [CrossRef]
- Yashawantha, K.M.; Gurjar, G.; Vinod, A.V. Low Temperature Heat Transfer in Plate Heat Exchanger Using Ethylene Glycol–Water Based Al2O3 Nanofluid. Int. J. Thermophys. 2021, 42, 90. [Google Scholar] [CrossRef]
- Moghaieb, H.S.; Amendola, V.; Khalil, S.; Chakrabarti, S.; Maguire, P.; Mariotti, D. Nanofluids for Direct-Absorption Solar Collectors—DASCs: A Review on Recent Progress and Future Perspectives. Nanomaterials 2023, 13, 1232. [Google Scholar] [CrossRef] [PubMed]
- Nkurikiyimfura, I.; Wang, Y.; Safari, B.; Nshingabigwi, E. Electrical and thermal performances of photovoltaic/thermal systems with magnetic nanofluids: A review. Particuology 2021, 54, 181–200. [Google Scholar] [CrossRef]
- Choudhary, S.; Sachdeva, A.; Kumar, P. Investigation of the stability of MgO nanofluid and its effect on the thermal performance of flat plate solar collector. Renew. Energy 2020, 147, 1801–1814. [Google Scholar] [CrossRef]
- Ahmadlouydarab, M.; Ebadolahzadeh, M.; Ali, H.M. Effects of utilizing nanofluid as working fluid in a lab-scale designed FPSC to improve thermal absorption and efficiency. Phys. A Stat. Mech. Appl. 2020, 540, 123109. [Google Scholar] [CrossRef]
- Saffarian, M.R.; Moravej, M.; Doranehgard, M.H. Heat transfer enhancement in a flat plate solar collector with different flow path shapes using nanofluid. Renew. Energy 2020, 146, 2316–2329. [Google Scholar] [CrossRef]
- Mehdizadeh-Fard, M.; Pourfayaz, F.; Maleki, A. Exergy analysis of multiple heat exchanger networks: An approach based on the irreversibility distribution ratio. Energy Rep. 2021, 7, 174–193. [Google Scholar] [CrossRef]
- Tong, Y.; Lee, H.; Kang, W.; Cho, H. Energy and exergy comparison of a flat-plate solar collector using water, Al2O3 nanofluid, and CuO nanofluid. Appl. Therm. Eng. 2019, 159, 113959. [Google Scholar] [CrossRef]
- Ehyaei, M.A.; Ahmadi, A.; Assad, M.E.H.; Hachicha, A.A.; Said, Z. Energy, exergy and economic analyses for the selection of working fluid and metal oxide nanofluids in a parabolic trough collector. Sol. Energy 2019, 187, 175–184. [Google Scholar] [CrossRef]
- Mostafizur, R.M.; Rasul, M.G.; Nabi, M.N.; Haque, R.; Jahirul, M.I. Thermodynamic Analysis of a Flat Plate Solar Collector with Different Hybrid Nanofluids as Working Medium—A Thermal Modelling Approach. Nanomaterials 2023, 13, 1320. [Google Scholar] [CrossRef] [PubMed]
- Zhai, C.; Wu, W. Energetic, exergetic, economic, and environmental analysis of microchannel membrane-based absorption refrigeration system driven by various energy sources. Energy 2022, 239, 122193. [Google Scholar] [CrossRef]
- Orzechowski, T.; Stokowiec, K. Quasi-stationary phase change heat transfer on a fin. EPJ Web. Conf. 2016, 114, 02086. [Google Scholar] [CrossRef]
- De Oliveira, L.R.; Ribeiro, S.R.F.L.; Reis, M.H.M.; Cardoso, V.L.; Filho, E.P.B. Experimental study on the thermal conductivity and viscosity of ethylene glycol-based nanofluid containing diamond-silver hybrid material. Diam. Relat. Mater. 2019, 96, 216–230. [Google Scholar] [CrossRef]
- Akhgar, A.; Toghraie, D.; Sina, N.; Afrand, M. Developing dissimilar artificial neural networks (ANNs) to prediction the thermal conductivity of MWCNT-TiO2/Water-ethylene glycol hybrid nano fluid. Powder Technol. 2019, 355, 602–610. [Google Scholar] [CrossRef]
- Wohld, J.; Beck, J.; Inman, K.; Palmer, M.; Cummings, M.; Fulmer, R.; Vafaei, S. Hybrid Nanofluid Thermal Conductivity and Optimization: Original Approach and Background. Nanomaterials 2022, 12, 2847. [Google Scholar] [CrossRef] [PubMed]
- Hamid, K.A.; Azmi, W.H.; Nabil, M.F.; Mamat, R. Heat transfer augmentation of mixture ratio TiO2 to SiO2 in hybrid nanofluid. J. Mech. Eng. 2017, 4, 51–63. [Google Scholar]
- Javadi, F.S.; Sadeghipour, S.; Saidur, R.; BoroumandJazi, G.; Rahmati, B.; Elias, M.M.; Sohel, M.R. The effects of nanofluid on thermophysical properties and heat transfer characteristics of a plate heat exchanger. Int. Commun. Heat Mass Transf. 2013, 44, 58–63. [Google Scholar] [CrossRef]
- Okonkwo, E.C.; Wole-Osho, I.; Almanassra, I.W.; Abdullatif, Y.M.; Al-Ansari, T. An updated review of nanofluids in various heat transfer devices. J. Therm. Anal. Calorim. 2021, 145, 2817–2872. [Google Scholar] [CrossRef]
- Wciślik, S. A simple economic and heat transfer analysis of the nanoparticles use. Chem. Pap. 2017, 71, 2395–2401. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Wciślik, S.; Khadanga, V.; Mishra, P.C. Influence of nanofluids on the thermal performance and entropy generation of varied geometry microchannel heat sink. Case Stud. Therm. Eng. 2023, 49, 103241. [Google Scholar] [CrossRef]
- Wciślik, S. Efficient Stabilization of Mono and Hybrid Nanofluids. Energies 2020, 13, 3793. [Google Scholar] [CrossRef]
- Vladisavljević, G.T. Preparation of microparticles and nanoparticles using membrane-assisted dispersion, micromixing, and evaporation processes. Particuology 2024, 84, 30–44. [Google Scholar] [CrossRef]
- Dincer, I.; Rosen, M.A. Chapter 7—Exergy Analysis of Heat Pump Systems. In Exergy, 2nd ed.; Dincer, I., Rosen, M.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 101–113. ISBN 9780080970899. [Google Scholar] [CrossRef]
- Qing, S.H.; Rashmi, W.; Khalid, M.; Gupta, T.C.S.M.; Nabipoor, M.; Hajibeigy, M.T. Thermal conductivity and electrical properties of Hybrid SiO2-graphene naphthenic mineral oil nanofluid as potential transformer oil. Mater. Res. Express. 2017, 4, 015504. [Google Scholar] [CrossRef]
- Hamid, K.A.; Azmi, W.H.; Mamat, R.; Usri, N.A.; Najafi, G. Effect of Temperature on Heat Transfer Coefficient of Titanium Dioxide in Ethylene Glycol-based Nanofluid. J. Mech. Eng. Sci. 2015, 8, 1367–1375. [Google Scholar] [CrossRef]
- Teng, T.-P.; Hung, Y.-H. Estimation and experimental study of the density and specific heat for alumina nanofluid. J. Exp. Nanosci. 2014, 9, 707–718. [Google Scholar] [CrossRef]
- Raja, R.A.; Sunil, J.; Maheswaran, R. Estimation of thermo-physical properties of nanofluids using theoretical correlations. Int. J. Appl. Eng. Res. 2018, 13, 7950–7953. [Google Scholar]
- Ahammed, N.; Asirvatham, L.G.; Wongwises, S. Entropy generation analysis of graphene–alumina hybrid nanofluid in multiport minichannel heat exchanger coupled with thermoelectric cooler. Int. J. Heat Mass Transf. 2016, 103, 1084–1097. [Google Scholar] [CrossRef]
- Hormozi, F.; ZareNezhad, B.; Allahyar, H.R. An experimental investigation on the effects of surfactants on the thermal performance of hybrid nanofluids in helical coil heat exchangers. Int. Commun. Heat Mass Transf. 2016, 78, 271–276. [Google Scholar] [CrossRef]
- Sundar, L.S.; Sharma, K.V.; Singh, M.K.; Sousa AC, M. Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor—A review. Renew. Sustain. Energy Rev. 2017, 68, 185–198. [Google Scholar] [CrossRef]
- Zainon, S.N.M.; Azmi, W.H.; Hamisa, A.H. Thermo-physical Properties of TiO2-SiO2 Hybrid Nanofluids Dispersion with Water/Bio-glycol Mixture. J. Phys. Conf. Ser. 2021, 2000, 012003. [Google Scholar] [CrossRef]
- Apmann, K.; Fulmer, R.; Soto, A.; Vafaei, S. Thermal Conductivity and Viscosity: Review and Optimization of Effects of Nanoparticles. Materials 2021, 14, 1291. [Google Scholar] [CrossRef] [PubMed]
- Viessmann Technical Guide, VITOSOL Flat-Plate Collectors and Vacuum Tube Collectors Flat and Pitched Roof Installation, and Wall Mounting, 5822440 GB5, 2018. Available online: https://viessmanndirect.co.uk/files//faa19e98-f0eb-4b23-98a7-aa3201061e16/1805%20Vitosol%20Technical%20Guide%205822440VPA00013_1.PDF (accessed on 28 June 2023).
- Lavine, A.S.; Incropera, F.P. Fundamentals of Heat and Mass Transfer; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2020. [Google Scholar]
- Kakaç, S.; Liu, H. Heat Exchangers Selection, Rating, and Thermal Design, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Akturk, F.; Sezer-Uzol, N.; Aradag, S.; Kakac, S. Experimental investigation and performance analysis of gasketed-plate heat exchangers. J. Therm. Sci. Technol. 2015, 35, 43–52. [Google Scholar]
- Alklaibi, A.M.; Sundar, L.S.; Mouli, K.V.V.C. Experimental investigation on the performance of hybrid Fe3O4 coated MWCNT/Water nanofluid as a coolant of a Plate heat exchanger. Int. J. Therm. Sci. 2022, 171, 107249. [Google Scholar] [CrossRef]
- Sundar, L.S.; Bhramara, P.; Kumar, N.T.R.; Singh, M.K.; Sousa, A.C.M. Experimental heat transfer, friction factor and effectiveness analysis of Fe3O4 nanofluid flow in a horizontal plain tube with return bend and wire coil inserts. Int. J. Heat Mass Transf. 2017, 109, 440–453. [Google Scholar] [CrossRef]
- Sundar, L.S.; Singh, M.K.; Sousa, A.C.M. Heat transfer and friction factor of nanodiamond-nickel hybrid nanofluids flow in a tube with longitudinal strip inserts. Int. J. Heat Mass Transf. 2018, 121, 390–401. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics; Wiley Interscience: New York, NY, USA, 1988. [Google Scholar]
- Sundar, L.S.; Mesfin, S.; Ramana, E.V.; Said, Z.; Sousa, A.C.M. Experimental investigation of thermo-physical properties, heat transfer, pumping power, entropy generation, and exergy efficiency of nanodiamond + Fe3O4/60:40% water-ethylene glycol hybrid nanofluid flow in a tube. Therm. Sci. Eng. Prog. 2021, 21, 100799. [Google Scholar] [CrossRef]
- Kabeel, A.E.; El Maaty, T.A.; El Samadony, Y. The effect of using nano-particles on corrugated plate heat exchanger performance. Appl. Therm. Eng. 2013, 52, 221–229. [Google Scholar] [CrossRef]
- Teng, T.-P.; Hsiao, T.-C.; Chung, C.-C. Characteristics of carbon-based nanofluids and their application in a brazed plate heat exchanger under laminar flow. Appl. Therm. Eng. 2019, 146, 160–168. [Google Scholar] [CrossRef]
- Goodarzi, M.; Amiri, A.; Goodarzi, M.S.; Safaei, M.R.; Karimipour, A.; Languri, E.M.; Dahari, M. Investigation of heat transfer and pressure drop of a counter flow corrugated plate heat exchanger using MWCNT based nanofluids. Int. Commun. Heat Mass Transf. 2015, 66, 172–179. [Google Scholar] [CrossRef]
- Jiang, P.X.; Fan, M.H.; Si, G.S.; Ren, Z.P. Thermal–hydraulic performance of small scale micro-channel and porous-media heat-exchangers. Int. J. Heat Mass Transf. 2001, 44, 1039–1051. [Google Scholar] [CrossRef]
- Sheikh, R.; Fallahsohi, S.H.; Goodarzi, M.; Taheri, M.M.; Bagheri, M. Improving the efficiency of an exhaust thermoelectric generator based on changes in the baffle distribution of the heat exchanger. J. Therm. Anal. Calorim. 2021, 143, 523–533. [Google Scholar] [CrossRef]
- Ramirez-Tijerina, R.; Rivera-Solorio, C.I.; Singh, J.; Nigam, K.D.P. Numerical Study of Heat Transfer Enhancement for Laminar Nanofluids Flow. Appl. Sci. 2018, 8, 2661. [Google Scholar] [CrossRef]
- Alrashed, A.A.; Akbari, O.A.; Heydari, A.; Toghraie, D.; Zarringhalam, M.; Shabani, G.; Seifi, A.; Goodarzi, M. The numerical modeling of water/FMWCNT nanofluid flow and heat transfer in a backward-facing contracting channel. Phys. B Condens. Matter 2018, 537, 176–183. [Google Scholar] [CrossRef]
- Sundar, L.S.; Mesfin, S.; Raman, E.V.; Punnaiah, V.; Chamkha, A.J.; Sousa, A.C.M. Thermal entropy generation and exergy efficiency analyses of coiled wire inserted nanodiamond + Fe3O4/water hybrid nanofluid in a tube. J. Therm. Anal. Calorim. 2022, 147, 7917–7944. [Google Scholar] [CrossRef]
- Hsieh, S.S.; Liu, H.H.; Yeh, Y.F. Nanofluids spray heat transfer enhancement. Int. J. Heat Mass Transf. 2016, 94, 104–118. [Google Scholar] [CrossRef]
- Janaszek, A.; Nartowska, E.; Rozenvalde, A.; Zotovs, I. Comparison of the Use of Renewable Energy Sources (Res) by Poland and Latvia in the Perspective of the Environmental Objectives Set by the European Union. Civ. Environ. Eng. Rep. 2023, 33, 111–128. [Google Scholar] [CrossRef]
- Boujelbene, M.; Albouchi, F.; Ullah, Z.; Aldhabani, M.S.; Alsulami, S.H.; Hassan, A.M. Solar radiation and lower gravitational effects on wave oscillations in heat transfer along magnetic-driven porous cone in the presence of Joule heating. Case Stud. Therm. Eng. 2024, 53, 103782. [Google Scholar] [CrossRef]
- Boukholda, I.; Ullah, Z.; Mahrous, Y.M.; Alamer, A.; Amara, M.B.; Alsulami, M.D.; Faqihi, A.A.; Khedher, N.B. Analysis of thermal density and heat sink on dissipative nanofluid along magnetized sheet and applications in microelectronic cooling systems. Case Stud. Therm. Eng. 2024, 55, 104185. [Google Scholar] [CrossRef]
- Dąbek, L.; Kapjor, A.; Orman, Ł.J. Boiling heat transfer augmentation on surfaces covered with phosphor bronze meshes. MATEC Web. Conf. 2018, 168, 07001. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).