Water and Emerging Energy Markets Nexus: Fresh Evidence from Advanced Causality and Correlation Approaches

Abstract

This work provides an in-depth investigation of the dynamic interaction patterns between water stocks and renewable energy markets through the application of continuous wavelet analysis, dynamic correlation analysis, and time-varying Granger causality analysis. In addition, this study utilizes daily pricing indices, namely the S&P Global Water Index, Solactive Global Wind Energy Index, and Solactive Global Solar Energy Index, spanning from 18 May 2011 to 23 June 2022. The results show significant correlation patterns between the indices, ranging from moderate to high. Notably, robust correlations have been detected starting from 2015. The research also discovered a varied and inconsistent relationship between frequency and causation throughout different time periods. Moreover, the results reveal an asymmetry in the causal effects and a symmetry correlation at tail quantile ranges. Policymakers and market participants must consider these insights to make wise financial and strategic decisions.

1. Introduction

Climate change, sustainable development, and renewable energy (RWE) sources have been a matter of great research, especially over the last two decades [1,2,3,4,5,6,7,8,9]. Financial markets are a function of finance and are what drive the sustainability of the environment. Solar, water, and wind are prominent strategic resources. Its financing impacts returns and policymaking in the economy, as well as the financial system [10]. Investments in RWE not only promote sustainable development but also reduce investor risk [11,12]. Furthermore, the association between water stocks and RWE markets, specifically solar and wind energy, has served as the subject of considerable research in recent years [13]. The increasing demand for sustainable and clean energy (CE) sources has led to growing interest in understanding their potential effects on traditional energy sources, such as water stocks. The causality between solar and wind power and water stocks is gaining momentum after sensitivity towards sustainable development [14,15,16].

In a previous study by [17], solar and wind power had causal impacts on water stocks. These studies investigated the correlation between water stocks and RWE securities using traditional statistical methods, such as linear regression and correlation analyses. However, these methods may not adequately reflect the fluctuating and nonlinear nature of the interaction between these different industries. Recently, researchers have applied continuous wavelet analysis and dynamic correlation analysis to investigate the association between water stocks and RWE markets. A causal relationship exists between these markets, with water stocks having a causal effect on solar and wind power [18]. A further causality analysis of solar and wind power and water stocks was conducted using the wavelet transform and copula approach [12,19]. Wavelet coherence and copula to analyze the causality between solar and wind power and water stocks concluded that the causality is bidirectional between water stocks and solar and wind power [20,21]. Continuous wavelet analysis allows for the inspection of the dependence between these markets at multiple time scales, whereas dynamic correlation analysis enables the examination of the time-varying nature of the correlations among them.

In addition, researchers have begun to use the more advanced Granger causality analysis to analyze the predictability and spillover between water stocks and RWE markets. Water, solar, and wind energy firms’ risks are primarily internal to their respective sectors rather than being interrelated [22]. Using the DCC model, Ref. [23] has detected a weak spillover behavior between solar, wind, and CE and green bonds (GB) and cryptocurrency markets but in the short term. This indicates that investors can diversify their funds only in the short run because of their dynamic linkages, and no such benefits can be availed in the long run. Using the Diebold–Yilmaz connectedness index, this study has also revealed that the total spillover among the green bond markets, renewable energy markets and the cryptocurrency market is significant, suggesting connectedness among these markets. This confirms that during times of crisis or negative economic conditions, investors having securities from green bond markets, renewable energy markets and the cryptocurrency market are more likely to face simultaneous significant losses. Finally, the results of the time-frequency connectedness approach document that returns on renewable energy resources have the highest return spillover derived from other series during short-, medium- and long-term horizons, while returns on BITCOIN and green bonds have the least return spillovers. Ref. [13] has applied wavelet-based causality and correlation analyses to peruse the association between water stocks and RWE markets and found that there is strong causality between water stocks and RWE markets, with RWE markets having a significant impact on water stocks. Ref. [24] reported a pioneer work that used a time-varying Granger causality technique to examine the connection between water resources and RWE. The study discovered a substantial causal link from water resources to RWE.

With respect to these findings, it is clear that the link between water stocks and RWE markets is complex and dynamic. However, there is still much that is not understood regarding this relationship, and further research is needed to fully understand the potential impact of RWE markets on water stocks. The present study aims to add to the existing literature by applying continuous wavelet analysis, dynamic correlation analysis, and time-varying Granger causality analysis to investigate the relationship between water stocks and the solar and wind energy markets. By doing so, this study aims to provide a more comprehensive understanding of the dynamic and nonlinear nature of the link between these markets, as well as more evidence of their predictability.

Overall, this study is likely to contribute significantly to the literature by giving more in-depth knowledge of the link between water stocks and RWE markets, including spillover and predictability. These contributions appear critical to policymakers and market participants. Indeed, nations have a strong desire to safeguard the environment, and thus a study on the interaction between green energy and water is vital for creating environmental policy.

This study on the causal relationship between solar/wind energy and water markets is conducted using a wavelet-based analysis. The results show moderate to high correlation patterns between GWI and GSE/GWE, with strong correlations observed from 2015 onwards. The study also found a high strength of the causal effect between 2010 and 2011 on a 4~64 day frequency and between 2013 and 2017 on a 128–256 day frequency. Wavelet quantile correlation and in-phase and out-of-phase causal effects both supported the findings. The study emphasizes the importance of understanding the causal behavior of energy markets for effective policy and investment decisions. The outcome of this study may also have prominent implications for policymakers and investors in the RWE and water sectors.

This study has six sections following this order: Literature Review, Methodology, Data, and Results and Conclusions.

2. Literature Review

The integration of RWE sources into the energy market has gained significant attention owing to the need to reduce carbon emissions and address climate change. Water, solar, and wind are RWE sources that are often integrated into the energy market. The relationship between these RWE sources and the energy market is not straightforward, and understanding the causality between them is crucial for market forecasting, investing, hedging, diversification, and policy-making [25,26]. The focus of this literature review is on this field. Ref. [18] used wavelet analysis to investigate the causal links between water stocks and RWE markets. They proposed that linear causality is not supported at higher frequencies, but unidirectional and bidirectional linear causality are found in the short term. Non-linear causality is consistently found from RWE to oil prices at diverse frequencies, while causality from oil to RWE prices is mixed. Ref. [27] provided an overview of RWE companies on the stock exchange using a minimal spanning tree approach. The study showed that First Solar Inc., General Cable Corporation, and Trina Solar are crucial players in the RWE market based on their market capitalization. Ref. [28] explored the relationship between water and traditional asset classes. The study used cross-correlation and quantile regression methods and found that water assets can act as diversifiers, hedges, and safe havens for various financial assets. Ref. [29] analyzed the dynamic dependence and causality of the RWE stock markets on dirty energy prices. They conclude that RWE stocks have first- and second-order causal impacts on the oil and coal markets, but the gas market does not confirm any effect. Additionally, the results show that the CE index seems to have a higher time-series dependence than the others and is less exposed to oil prices than the NYSE [30]. Likewise, Ref. [31] used data from three cutting-edge businesses connected to green, clean, and sustainable investments to analyze the quantile time-frequency price connectivity. It was found that GB and CE sources respond to shocks at low and high time frame frequencies, but the global environment and sustainability index distributes shocks to other indices at low and high time frame frequencies. Moreover, the level of interconnectedness varies over time and depends on economic events [32].

As per a study, the DCCs of the Beijing CET market, the coal market, and the NEC’s stock market show time-varying correlations and persistence. Coal and new energy markets have high volatility. Granger causality shows bidirectional spillover between coal and the NEC’s stock market [33]. Ref. [34] explored the interlinkage between water stock prices and the global market. The outcomes suggest that the interdependence of world water stock market prices varies over time, with a quick response to shocks within 3 days. International diversification within the water sector is not useful, and cross-market contagion risk exists. Water authorities must consider events in other markets. Ref. [34] further studied the dynamics among Asian water stocks through the DCC-GARCH model and confirmed that volatility spillover exists among five water indices and diversification is possible due to their contrasting correlations. This has implications for academics, researchers, policymakers, and water investors worldwide. Ref. [13] examined the dynamic relationship among investor sentiments and dirty and RWE stock markets. The dirty energy sources, especially crude oil, have greater impacts on the RWE stock market than investor sentiment. This demonstrates how closely related the two markets are, with dynamic findings indicating that investor sentiment can partially explain the performance of RWE stocks over time. Just as energy price trends negatively affect them, agricultural price trends positively affect water companies’ stock returns, also showing that investor interest has a negative relationship with water companies’ stock returns [35].

CE stock (i.e., water, solar, and wind energy) has sparked debate about whether these sources are sensitive to spillover risk. Further, it becomes crucial in extreme situations. Variability and unpredictable outcomes of spillover behavior within these markets has been examined by many researchers in normal as well as extreme situations in the last few years. RWE markets exhibit stronger extreme risk spillover effects, particularly during market booms, with asymmetry. The water energy market plays a crucial role. Risk spillovers are high among RWE markets but low among non-renewable ones [24]. In a paper on the risk spillover between CE stocks and GB, Ref. [20] found a positive time-varying average and tail dependence between both markets, with mutually directed spillover effects. Risk spillover is asymmetric. In a study by [36], they showcased a significant connection between European emissions and CE prices, but not in the US, implying region-specific shocks. Diversification benefits were possible in European Union allowances and CE equities due to the low correlation with stock prices. In another study by [37], they provide an insight that CE dominates all markets and transmits shocks in the network. GB and Solactive Global Wind are major shock recipients. Bivariate and multivariate portfolios reduce risk, except for GB. The lower limit connectedness portfolio has the highest Sharpe ratio, especially during COVID-19.

RWE sources are not only important for investment, hedging, and diversification but also have crucial applications for economic growth. The use of total and fossil fuel energy leads to higher incomes. However, the effects of RWE consumption vary among different income groups. In the long term, energy does not significantly impact economic growth, suggesting conservative energy policies do not hinder growth [38]. Furthermore, Ref. [39] confirmed the long-term impact of stock market value on both types of RWE. The growth rate has a significant effect on hydropower, wind, solar, and nuclear energies in the short and long term. Another study by [40] checked the link between RWE consumption, financial development, and economic growth with the help of the Granger causality test. The results show that there is a unidirectional causality from financial development to RWE consumption in China and eastern China. Economic growth also causes unidirectional energy consumption in both the eastern and western regions of China. The growth average and symmetrical tail changes between the ranges of oil returns and global diverse and sectoral exchange energy indices indicate that significant and systemic risk contribute significantly to the downside and upside risk of oil price dynamics of segregated energy exchanges by approximately 30% [41]. While changes in agricultural and energy prices can affect water stock returns, a state space model to estimate dynamic beta coefficients reveals time-varying factor sensitivities, particularly during the 2008 economic and financial crisis [42].

Ref. [43] described that the current policy approach for dealing with CRFR relies on market-based solutions to address data gaps and pricing issues, despite CRFR’s unique characteristics. Instead, a precautionary financial policy option should be considered to better handle these long-term risks. Ref. [44] found strong evidence that green investments differ significantly from SRI investments in terms of financial performance and key firm characteristics. While green stocks outperformed SRI stocks between 2003 and 2007, they underperformed in both directions between 2008 and 2012, with an absolute multifactor alpha of more than 1 percent per month. Further, the paper by [45] originates that an increase in silver market volatility (VXSLV) has a negative impact on equity indexes, particularly on RWE firms. This effect remains significant even after controlling for oil price volatility (OVX), although OVX has a greater impact on alternative energy stocks. Ref. [46], using the DCC-GARCH connectedness framework, examined the connectedness of oil and RWE with stock markets. The results expose stronger total connectedness between stock markets and RWE, with increased connectedness during pandemics.

This literature review here highlights the importance of understanding the causality between water stocks and solar and wind energy markets. The integration of RWE sources into the energy market is complex, and the relationship between these variables is time-varying and nonlinear. Continuous wavelet analysis, dynamic correlation analysis, and time-varying Granger causality analysis ensure insights into the causal relationship between these variables and can be useful for market forecasting and policy-making. Further research is needed to understand the relationship between these variables across different regions and time periods.

3. Methodology

3.1. Granger Causality Test

In econometric analyses, in cases where the direction of the relationship between variables cannot be determined by economic theory, the existence and direction of the relationship between variables can be determined by the [47] test. In this test, variables are not separated as dependent and independent. In the Granger causality test, the interaction between variables can be analyzed simultaneously. The models to be used in this study for causality analysis are arranged as follows:

$${\mathrm{G}\mathrm{W}\mathrm{I}}_{\mathrm{t}}={\mathsf{\gamma }}_0+\sum _{\mathrm{i}=1}^{\mathrm{m}}{\mathsf{\gamma }}_{\mathrm{i}}{\mathrm{G}\mathrm{W}\mathrm{I}}_{\mathrm{t}-\mathrm{i}}+\sum _{\mathrm{i}=1}^{\mathrm{m}}{\mathsf{\theta }}_{\mathrm{i}}{\mathrm{R}\mathrm{W}\mathrm{I}}_{\mathrm{t}-\mathrm{i}}+{\mathsf{\vartheta }}_{\mathrm{t}}$$

$${RWI}_t={\phi }_0+\sum _{i=1}^m{\phi }_i{RWI}_{t-i}+\sum _{i=1}^m{\delta }_i{GWI}_{t-i}+{\epsilon }_i$$

where GWI and RWI denote the water and renewable energy indices, respectively. Here, the tested hypothesis is ${\sum }_{i=1}^m{\gamma }_i=0$, which means that ${GWI}_{t-1}$… … ${GWI}_{t-m}$ lagged variables have no place in the relationship and there is no causal relationship from GWI to RWI. However, the alternative hypothesis is ${\sum }_{i=1}^m{\gamma }_i\ne 0$, indicating that there is causality from GWI to RWI.

To find the sum of the error terms, ${\sum }_{i=1}^m{\gamma }_i{GWI}_{t-i}$ leaving out the term as follows:

$${GWI}_t={\gamma }_0+\sum _{i=1}^m{\gamma }_i{GWI}_{t-i}+{\vartheta }_t$$

The relationship is estimated and the sum of the coefficients of the error terms is found as ${\sum }_{i=1}^m{e}_t^2$.

In unconstrained relationships, the sum of the coefficients of the error terms is as follows:

$${GWI}_t={\alpha }_0+\sum _{i=1}^m{\alpha }_i{GWI}_{t-i}+\sum _{i=1}^m{\beta }_i{RWI}_{t-i}+u_t$$

The sum of squares of error terms is in the following form:

$${\sum }_{i=1}^m{u}_t^2$$

The F value calculation for calculating the test statistic is as follows:

$$F=\frac{{RSS}_R-{RSS}_{UR}/m}{{RSS}_{UR}/(n-k)}$$

Here ${RSS}_R$; ${RSS}_{UR}$ is the sum of squares of error terms in the unrestricted relationship. m is the number of lagged variables (constraints) excluded, n is the sample volume and k is the number of parameters.

In this case, if the calculated F value is less than the F value in the table, the hypothesis that there is no causal relationship from GWI to RWI is accepted. If it is large, the hypothesis is rejected and the hypothesis that there is a causal relationship from GWI to RWI is accepted.

3.2. Hong Causality Test

Because they could display time-varying results, the Hong causality tests we used—the rolling Hong test and the DCC-MGARCH Hong test—are superior to the conventional normal Granger causality test used in earlier research.

Let us denote the two relevant series by x_1,t and x_2,t and evaluate whether x_1,t causes x_2,t using a sample of observations T. According to [48], ARMA-GARCH models are based on the cross-field between the two-centered quadratic standardized innovation series obtained by converting it into two time series, and a test for variance causality is applied. We presume that the information we have made tends towards mean causality and therefore the x_1,t and x_2,t series are explicitly filtered by appropriate ARMA-GARCH models. In this scenario, we turn to the average cross-spread, which means that we evaluate without squaring them. The [48] test has the following statistical bases:

$$Q_H=\frac{T{\sum }_{j=1}^{T-1}{k}^2\left(\frac{j}{M}\right){\widehat{p}}_{\mathrm{2,1}}^2\left(j\right)-C_{1T}(k)}{\sqrt{2D_{1T}\left(k\right)}},$$

$$C_{1T}\left(k\right)=\sum _{j=1}^{T-1}\left(1-\frac{j}{T}\right)k^2\left(\frac{1}{M}\right), D_{1T}\left(k\right)=\sum _{j=1}^{T-1}\left(1-\frac{j}{T}\right) \left(1-\frac{j+1}{T}\right) k^4\left(\frac{1}{M}\right),$$

$$C_{1T}{\widehat{p}}_{\mathrm{2,1}}^2\left(j\right)=\frac{\sum _{t=j+1}^T{x}_{2,t}{x}_{1,t-j}}{\sqrt{{\sum }_{t=j+1}^T{x}_{1,t}^2\sqrt{{\sum }_{t=j+1}^T{x}_{2,t}^2}}}, k\left(z\right)=\left(1-\left|z\right|\right) I \left(\left|z\right|\right)<1),$$

J and M > 0. ${\widehat{p}}_{\mathrm{2,1}}^2\left(j\right)$ is the cross-correlation between $x_{1,t-j}$ and $x_{2,t}$, where the first term is lagged and we adopt the Bartlett kernel function $k\left(z\right)$. Finally, M is a lag cut off value that causes zero contribution for cross-correlations with lag j > M; that is, only cross-correlations up to lag M contribute to the assessment of causality.

3.3. Wavelet-Based Causality

Wavelet-based causality is a method using continuous wavelet transform (CWT). Ref. [49] proposed a measure of the correlation by the CWT given as follows:

$$p_{x_1{x}_2}\left(u,c\right)=\frac{R\left(V_{x_1{x}_2}\left(u,c\right)\right)}{\sqrt{{\left|V_{x_1}(u,c)\right|}^2{\left|V_{x_2}(u,c)\right|}^2}}$$

This correlation method simultaneously explains the joint movements of the series in both time and frequency.

The wavelet causality measure is denoted as follows:

$$C_{x_1\to x_2}\left(u,c\right)=\frac{R\left(V_{x_1{x}_2}\left(u,c\right)\right)I_{x_1\to x_2}\left(u,c\right)}{\sqrt{{\left|V_{x_1}\left(u,c\right)\right|}^2{\left|V_{x_2}\left(u,c\right)\right|}^2}}$$

For the phase difference between the variables, we propose an indicator function ($I_{x_1\to x_2}\left(u,c\right))$ that takes the value one if the variables are in phase and the value zero if not while based on the following:

$$I_{x_1\to x_2}\left(u,c\right)=\left\{\begin{array}{c} 1, if {\phi }_{xy}\left(u,c\right) ϵ (0,\frac{\pi }{2})\\ U (-\pi ,-\frac{\pi }{2})\\ 0, otherwise\end{array}\right.$$

This model gives useful information about the delay relationship (i.e., who starts first and causes who) and is coded in the phase difference (or even phase circle).

After applying a J level decomposition to $x_1$ and $x_2$ and obtaining the detail coefficients, we perform QC on the pair of wavelet details ${\mathrm{d}}_{\mathrm{j}}\left[{\mathrm{x}}_1\right]$ and ${\mathrm{d}}_{\mathrm{j}}\left[{\mathrm{x}}_2\right]$ for all J, resulting in WQC for each level J. We define the WQC for two time series $x_1$ and $x_2$ at a particular decomposition level J and quantile τ as follows:

$${WQC}_{\tau }\left(d_j\left[x_1\right],d_j\left[x_2\right]\right)=\frac{q{cov}_q(d_j\left[x_1\right],d_j\left[x_2\right])}{\sqrt{var\left({\varphi }_{\tau }\left(d_j\left[x_2\right]-Q_{\tau ,d_j\left[x_2\right]}\right)\right)var\left(d_j\left[x_1\right]\right)}}$$

We collect statistics at 4–8 day, 16–32 day, and 128–256 day intervals to broadly describe the behavior during one trade week, month, and year.

4. Data Specification

The study uses daily price indices obtained from Datastream running from 18 May 2011 to 23 June 2022. (It is important to note that using extended data cannot affect the results. In addition, we utilize data from 2011, as this year marks the start of significantly fluctuating market prices for renewable energy sources.) We use the S&P Global Water Index (GWI), Solactive Global Wind Energy Price Index (GWE), and Solactive Global Solar Energy Price Index (GSE). The S&P Global Water Index ensures liquid and tradable exposure to 50 companies operating in water-related businesses around the world. To create a diversified impact on the global water market, the 50 components are evenly distributed between two distinct water-related business groups: Water Services and Infrastructure, and Water Equipment and Supplies.

According to the statistics in

Table 1. Descriptive statistics.

	S&P‪ Global Water Index	Solactive‪ Global Solar Energy Index	Solactive‪ Global Wind Energy Index
	GWI	GSE	GWE
Mean	0.00024	−0.00037	−0.00007
Standard Deviation	0.00976	0.01189	0.01051
Kurtosis	13.82829	6.17866	5.74060
Skewness	−0.87313	−0.13766	−0.16617
Minimum	−0.11138	−0.06749	−0.06897
Maximum	0.07527	0.07984	0.06462
Obs	2896	2896	2896

, the selected indices had considerably varied means and standard deviations. GWI, to be more specific, has a strong positive return and a low variance, indicating a great investment opportunity. GSE and GWE, on the other hand, offer negative returns and great degree of vulnerability, making them less appealing to potential investors. Consequently, these statistics disclose that the performance of the selected markets differs.

Skewness reflects negative values for all the sample assets, suggesting a higher probability for a declining pattern of returns. Furthermore, the kurtosis measurements demonstrate that the data have a leptokurtic distribution, meaning that they have a fat tail and are not normally distributed. This supports the adoption of advanced analytic methods such as time-varying interdependence techniques for higher-order analysis.

In Figure 1, GWI exhibits significant volatility clustering at the start of 2019 as a result of the water crisis experienced by South Africa, certain regions of India, and various other parts of the world. In addition, this time period aligns with the occurrence of concerns over water investment following the publication of an article in CEOWORLD Magazine that specifically addresses future challenges associated with water scarcity (Read more at https://ceoworld.biz/2019/08/08/most-water-stressed-countries-in-the-world-for-2019/, accessed on 8 August 2019). Conversely, there was a notable occurrence of volatility clustering in the stocks of solar and wind energy businesses throughout the sample time from 2011 to 2015. The energy crisis suffered by many countries globally is a consequence of the European Debt Crisis and the Shale Oil Revolution. As a result, there has been a rise in the costs of conventional energy sources and a growing need for RWE sources.

5. Empirical Discussion of the Results

The empirical analysis section of this paper focuses on exploring the relationship between water stocks and solar and wind energy markets using different advanced methodologies (i.e., continuous wavelet analysis, dynamic correlation analysis, and time-varying Granger causality analysis). Initially, the investigation’s results for causality between these variables are presented in Table 2 (no tail causality for the DCC-MGARCH Hong tests), Figure 2 (rolling Hong tests), and Figure 3 (DCC-MGARCH Hong tests). Furthermore, causality in continuous wavelets and dynamic correlations are also discussed with the help of the results presented in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. It is essential to understand the dynamics between water, solar, and wind energy markets because they may provide useful information for policymakers, market participants, and researchers.

5.1. An In-Depth Investigation of Causality

We follow the same method as [50] to evaluate causality by selecting M = 10 for lag truncation, utilizing the Bartlett kernel, and using a rolling subsample size of S = 100 for the rolling Hong tests. However, we differ from [50] in that we do not consider contemporaneous causality. Ref. [50] defended this exclusion by mentioning differences in trading timing, but we do not agree with this reasoning since the indexes’ prices we are examining are from US-based exchanges and can be considered synchronous. Therefore, we exclude the contemporaneous causality of [47] for that reason.

Table 2. The rejection rate of the null hypothesis of no tail causality for the DCC-MGARCH Hong tests according to the normal critical value (first column) and the simulated critical value (second column).

	Normal	Simulated
Panel A: GWI vs. GSE
GSE ← GWI	100.00%	0.49%
GSE → GWI	8.24%	0.35%
GSE ↔ GWI	100.00%	0.76%
Panel B: GWI vs. GWE
GWE← GWI	82.89%	57.41%
GWE → GWI	11.86%	0.66%
GWE ↔ GWI	80.18%	48.75%

Notes: Each panel shows the unidirectional DCC-MGARCH Hong test from water stocks to solar and wind energy (first row), the unidirectional DCC-MGARCH Hong test from solar and wind to water stocks (second row), and the bidirectional DCC-MGARCH Hong test (third row). The period under consideration is from 18 May 2011 to 23 June 2022.

Table 2. The rejection rate of the null hypothesis of no tail causality for the DCC-MGARCH Hong tests according to the normal critical value (first column) and the simulated critical value (second column).

	Normal	Simulated
Panel A: GWI vs. GSE
GSE ← GWI	100.00%	0.49%
GSE → GWI	8.24%	0.35%
GSE ↔ GWI	100.00%	0.76%
Panel B: GWI vs. GWE
GWE← GWI	82.89%	57.41%
GWE → GWI	11.86%	0.66%
GWE ↔ GWI	80.18%	48.75%

Notes: Each panel shows the unidirectional DCC-MGARCH Hong test from water stocks to solar and wind energy (first row), the unidirectional DCC-MGARCH Hong test from solar and wind to water stocks (second row), and the bidirectional DCC-MGARCH Hong test (third row). The period under consideration is from 18 May 2011 to 23 June 2022.

Table 2 displays the rejection rates of the null hypothesis of no tail causality using the DCC-MGARCH Hong test with both normal and simulated critical values. The findings show that the rejection rate for the normal quantile critical value is substantially greater than that of the simulated quantile critical value. Even in this case, the rejection rate of the null hypothesis with the 99% normal quantile critical value is considerably higher than that of the simulated critical values for both GWI (Rows 1–3) and GWE (Rows 4–6). For instance, in the case of GWI → GSE (GWE), the rejection rate is 100% (82.89%) using the normal quantile critical value and only 0.49% (57.41%) using the simulated quantile. This discrepancy in the rejection rates leads to inconsistent conclusions regarding the rejection of the null hypothesis. Similarly, for GWI ← GSE (GWE) and GWI ↔ GSE (GWE), the rejection rates using the normal quantile critical values are 8.24% (11.86%) and 100.00% (80.18%), respectively, while those using the simulated quantile critical values are 0.35% (0.66%) and 0.76% (48.75%).

The simulated quantile critical value detects several statistically significant causality episodes that align with those obtained using the rolling Hong test, albeit with slightly different timings due to the selected rolling sub-sample size. Notably, the simulated quantile critical value identifies many additional significant causality episodes for GWI → GSE, GSE → GWI, and GSE ↔ GWI that were not detected in the rolling Hong test. These episodes are attributed to various factors, such as changes in government policies, technological advancements, and environmental concerns. It is important for investors to understand these causality episodes and the factors that influence them in order to make informed investment decisions in the solar energy and water markets.

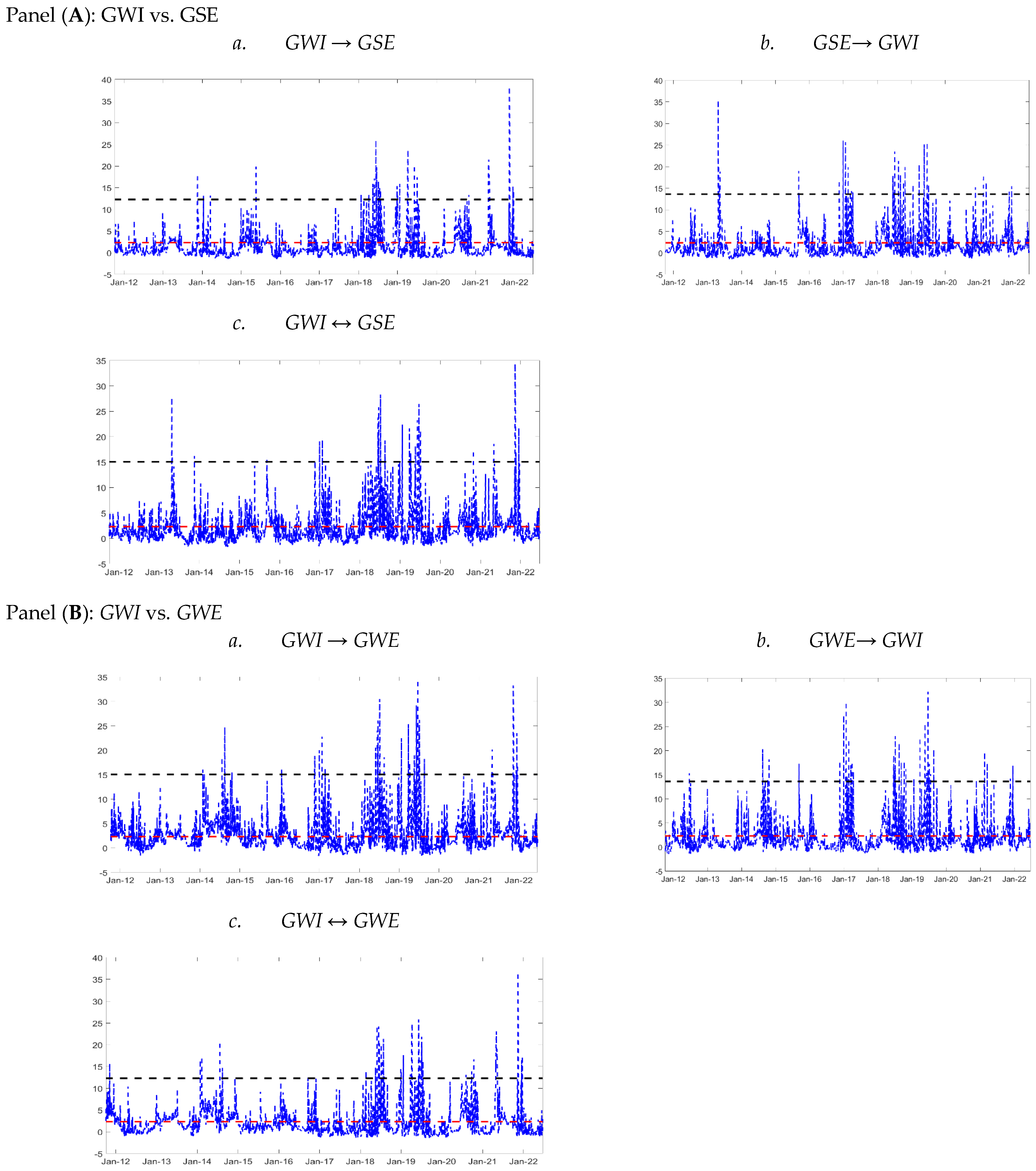
Furthermore, the findings of unidirectional and bidirectional rolling Hong tests are plotted in Figure 2. In panel A, the tests were performed from GWI to GSE (GSE ← GWI), from GSE to GWI (GSE → GWI), and bidirectional between GSE and GWI (GSE ↔ GWI). Panel B presents the rolling Hong test for GWI and GWE, aiming to identify tail predictability between the water and wind energy prices. The null hypothesis (no tail causality) was assessed using a 99% normal quantile critical value depicted by the dashed red line. Moreover, the black dashed line in the chart represents the simulated critical values at the 99% level, which were determined in the Methodology section. It is worth mentioning that the simulated critical value is considerably higher than the one calculated using the normal distribution, as shown by the black dashed line located well above the red dashed line.

The unidirectional GSE ← GWI test identified six significant causality episodes from GWI to GSE, namely in the beginning of 2014, April 2015, June 2018, first quarter of 2019, March 2021 and February 2022. Possible reasons for these causality episodes between solar energy and water from 2010 to 2022 include the increased use of solar energy for water pumping, solar thermal desalination, climate change, water conservation measures, climate change policy, the Paris Agreement, technological advancements, and environmental concerns for policy and regulatory changes. The causality episodes can be complex and multifaceted, and may be influenced by a range of factors.

Meanwhile, the unidirectional GSE → GWI test revealed seven significant causality episodes from solar energy to water. Additionally, the bidirectional GSE ↔ GWI test confirmed the significant causality episodes identified in the unidirectional tests. Ref. [17] has demonstrated these causal effects using classic statistical methods such as linear regression and correlation analyses. Our findings contribute to this by demonstrating that solar energy and water have a complex relationship, as seen in the span of 2011-2021. Water scarcity in California in 2014 led to an amplified request for solar energy. Solar power growth accelerated in 2013, and solar-powered desalination emerged in 2015. In 2017, concerns were raised about the water usage in solar panel manufacturing. Solar-powered irrigation initiatives were launched in 2018. Australia’s severe drought in 2019 increased the demand for solar energy. The pandemic in 2020 saw continued solar power growth, and in 2021, concerns arose about the environmental impact of water usage in concentrated solar power plants. The test statistic values were higher than those reported by [50] due to the inclusion of contemporaneous correlation in the rolling Hong tests. The study found that co-movements played a significant role, which is further explained in the DCC-MGARCH analysis.

Figure 2. Rolling Hong tests between water stocks and solar and wind energy. Notes: In each panel, the unidirectional rolling Hong test from water stocks to solar and wind energy (a), the unidirectional rolling Hong test from solar and wind energy to water stocks (b), and the bidirectional rolling Hong test are denoted (c). The dashed black (red) line indicates the 99% simulated (normal quantile) critical value. The rolling sample size is equal to 100.

Figure 2. Rolling Hong tests between water stocks and solar and wind energy. Notes: In each panel, the unidirectional rolling Hong test from water stocks to solar and wind energy (a), the unidirectional rolling Hong test from solar and wind energy to water stocks (b), and the bidirectional rolling Hong test are denoted (c). The dashed black (red) line indicates the 99% simulated (normal quantile) critical value. The rolling sample size is equal to 100.

At the same time, strong unidirectional causality is observed in panel B. Here, unidirectional causality from GWI to GWE (GWI → GWE), from GWE to GWI (GWE → GWI), and bidirectional between GWE and GWI (GSE ↔ GWI) experience many causality incidents. Highlighted is that causality was so pronounced from 2018 to 2020. Additionally, during 2022, high spikes of unidirectional causality from GWI to GWE and bidirectional causality between (GSE ↔ GWI) were observed. Refs. [18,21] all obtained similar results for the bidirectional causality or the causality effects of water on the RWE sources. However, when compared to their data, our analysis indicates that the link between wind energy and water stocks is complex and was influenced by several events and trends from 2014 to 2022. The European Union’s adoption of a RWE target in 2013, coupled with the rise of wind energy as the second-largest source of RWE in 2014, played significant roles in shaping the market. The extension of the Production Tax Credit (PTC) by the US government in 2014, along with the severe drought in California, boosted wind and water stocks, respectively. The Paris Climate Agreement in 2015 and the increasing global impetus towards RWE precipitated a shift towards wind stocks, while the prolonged drought in California drove water stocks. By 2018, wind energy had become the cheapest form of electricity, further boosting wind stocks, while competitive pressures continued to stimulate the industry in 2016. The proposed cuts to the PTC and the US withdrawal from the climate change agreement in 2017 had a negative impact on wind stocks, while hurricanes and floods in Texas and Florida adversely affected water stocks. The worldwide demand for RWE spurred wind stocks in 2018, while droughts and wildfires impacted water stocks. The global momentum towards decarbonization and RWE drove wind stocks in 2019, while water stocks were influenced by water scarcity and the California drought. The COVID-19 pandemic had also an impact on wind energy projects in 2020, while the US government set a target to achieve 30 GW of offshore wind capacity by 2030 in 2021. Correspondingly, the escalating global commitments to net-zero emissions drove wind stocks, while continuing droughts and wildfires in the western US affected water stocks. It is substantial to note that the causality between wind and water stocks in 2022 is subject to the influence of various factors, including government policies, market conditions, and global events (e.g., the 2022 Russian–Ukrainian War).

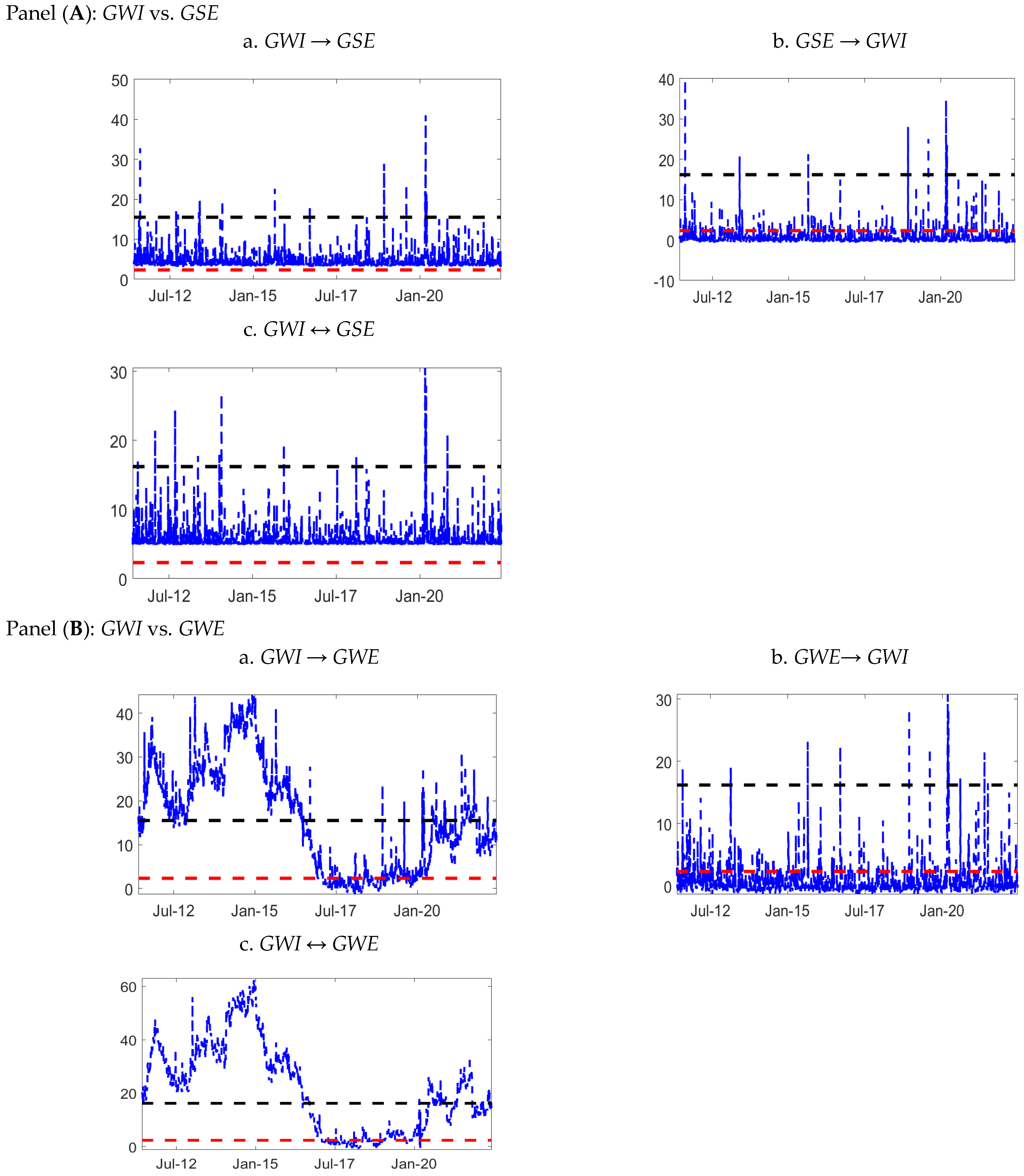
The preceding results in Figure 2 do not use all of the sample information because they focus just on tail quantiles. For this purpose, the DCC-MGARCH Hong tests are suggested. The outcomes of the Hong tests using DCC-MGARCH technique between GWI (water) and the solar/wind index are displayed in Figure 3. To do so, ARMA-GARCH models are utilized to generate standardized residuals from the returns, which are then used to construct rolling Hong tests. The findings acquired using the simulated critical value (black dashed line) are significantly distinct from those obtained using the normal quantile (red dashed line). Broadly, here again, we can discover many causality events but few causality movements are different from the rolling Hong test (refer to Figure 2). These events can be identified during 2011, 2012, and 2013. Between 2011 and 2013, wind and water stocks may have had a strong causality due to various factors. Favorable regulatory conditions for RWE, as well as prevailing market trends, could have influenced both types of stocks. Additionally, weather patterns and mergers and acquisitions in the RWE sector may have contributed to this trend. Similarly, during the same period, solar and water stocks have also been observed to have a high amount of causality due to several factors. Governments were focused on promoting RWE and water conservation, leading to an increase in demand for both types of stocks. Concerns about climate change also boosted the demand for RWE. Drought conditions in certain regions increased the demand for water stocks, especially in areas that relied heavily on agriculture and irrigation. Technological advancements in the solar and water sectors further contributed to the strong correlation between the two sectors. Lastly, socially responsible investors often favored both solar and water stocks due to their similar market characteristics, which also played a role in the correlation between the two sectors during this period.

Figure 3. DCC-MGARCH Hong tests between water stocks and solar and wind energy using [50] approach Notes: In each panel, the unidirectional rolling Hong test from water stocks to solar and wind energy (a), the unidirectional rolling Hong test from solar and wind energy to water stocks (b), and the bidirectional rolling Hong test are denoted (c). The dashed black (red) line indicates the 99% simulated (normal quantile) critical value.

Figure 3. DCC-MGARCH Hong tests between water stocks and solar and wind energy using [50] approach Notes: In each panel, the unidirectional rolling Hong test from water stocks to solar and wind energy (a), the unidirectional rolling Hong test from solar and wind energy to water stocks (b), and the bidirectional rolling Hong test are denoted (c). The dashed black (red) line indicates the 99% simulated (normal quantile) critical value.

In this part, we show rolling window wavelet correlation (RWWC) outcomes for each pair for the whole sample period. The results of CWT-based Granger causality technique applied to the daily returns of the GWI and GSE/GWE indexes are displayed in Figure 4 and Figure 5. Since contour charts contain three dimensions—frequency, time, and amplitude—they are used to show causal relationships. The frequency and time axes are located vertically and horizontally, respectively. Time encompasses the entire sample period, whereas frequency is shown in days and ranges from a maximum of 2 days (top of the plot) to a minimum of 1024 days (bottom of the plot). Time is represented as the total sample period. A color code that spans from dark blue (no causal effects) to dark yellow (high causal effects) indicates the intensity of the causal links between water and RWE daily returns. Red and white contours, respectively, reflect the statistically significant Granger causality correlations at the 10% and 5% levels. Based on 1000 Markov bootstrapped series, the significance levels are calculated. The region not impacted by edge effects is indicated by the green bold line, which represents the cone of influence.

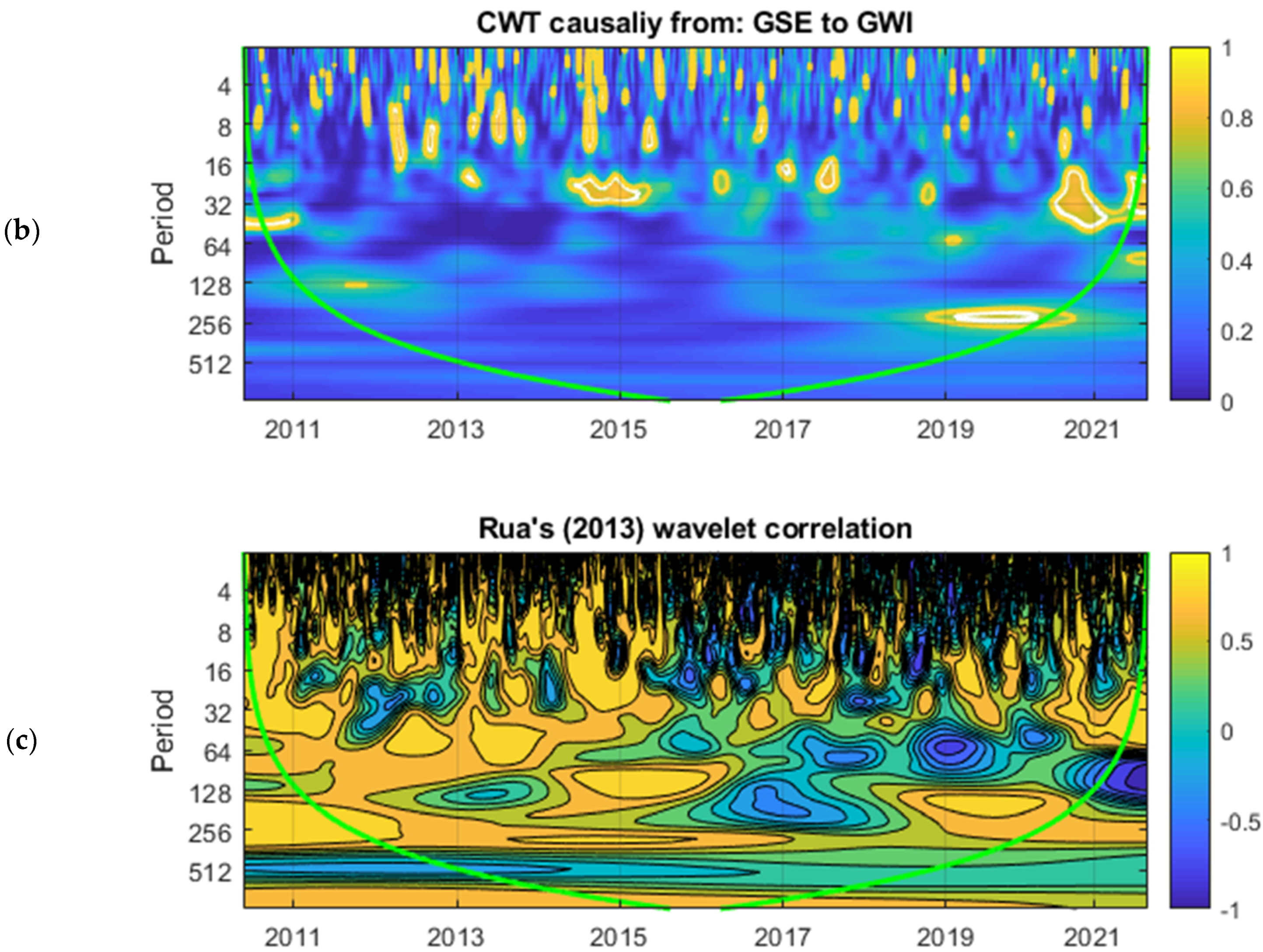
In Figure 4, there are three panels (a, b, and c); panels a and b represent the continuous wavelet transform causality from GWI to GSE and from GSE to GWI. Meanwhile, panel c represents the wavelet-based correlation of [49]. In the scalogram of panel a, we observe a high strength of the casual effect between 2010 and 2012 on the 128~256-day frequency, between 2012 and 2014 on the 32~64-day frequency, and during 2015–2016 on the frequency of 64~128 days. After 2016, we did not observe very strong causal effect from GWI to GSE. This is consistent with the findings of [24], who used a time-varying technique to discover significant causality between water resources and RWE markets, with water resources having a large impact on RWE markets. In the scalogram of panel b, we found no strong causal influence from GSE to GWI. This is not the case for [13], who conducted a wavelet-based causation and correlation analysis to inspect the link between water stocks and RWE markets and discovered that RWE markets had a considerable impact on water stocks. However, panel c displays that there is a strong negative correlation between the two variables throughout the sample time. More precisely, Figure 4, panel c depicts the degree of synchronization between GWI and GWE. Because there are three dimensions involved, the findings are shown as a contour map. The horizontal axis represents time, and the vertical axis represents frequency. The frequency is converted to time units (days) to facilitate comprehension. The color scale represents the wavelet-based metric and corresponds to the height in a surface plot. As a result, by analyzing the contour map, one may identify both frequency bands (in the vertical axis) and time intervals (in the horizontal axis) with higher synchronization and whether it has changed over time and between frequencies. The findings are consistent with those shown in panels a and b. The synchronizations occur at various frequencies and at different times, which reflects the time-varying correlations between GWI and GSE.

Figure 4. Continuous wavelet transform plot of causality between GWI and GSE. Notes: The white (red) contour indicates the 5% (10%) significance level. The significance levels are based on 3000 draws from Monte Carlo simulations estimated on an ARMA (1, 1) null of no statistical significance. The green line is the cone of influence (COI) earmarking the areas affected by the edge effects or phase. (a) CWT causality from GWI to GSE, (b) CWT causality from GSE to GWI, and (c) Rua’s wavelet correlation. (Color figure online).

Figure 4. Continuous wavelet transform plot of causality between GWI and GSE. Notes: The white (red) contour indicates the 5% (10%) significance level. The significance levels are based on 3000 draws from Monte Carlo simulations estimated on an ARMA (1, 1) null of no statistical significance. The green line is the cone of influence (COI) earmarking the areas affected by the edge effects or phase. (a) CWT causality from GWI to GSE, (b) CWT causality from GSE to GWI, and (c) Rua’s wavelet correlation. (Color figure online).

Figure 5. Continuous wavelet transform plot of causality between GWI and GWE. Notes: The white (red) contour indicates the 5% (10%) significance level. The significance levels are based on 3000 draws from Monte Carlo simulations estimated on an ARMA (1, 1) null of no statistical significance. The green line is the cone of influence (COI) earmarking the areas affected by the edge effects or phase. (a) CWT causality from GWI to GWE, (b) CWT causality from MSGLAE to GWE, and (c) Rua’s wavelet correlation. (Color figure online).

Figure 5. Continuous wavelet transform plot of causality between GWI and GWE. Notes: The white (red) contour indicates the 5% (10%) significance level. The significance levels are based on 3000 draws from Monte Carlo simulations estimated on an ARMA (1, 1) null of no statistical significance. The green line is the cone of influence (COI) earmarking the areas affected by the edge effects or phase. (a) CWT causality from GWI to GWE, (b) CWT causality from MSGLAE to GWE, and (c) Rua’s wavelet correlation. (Color figure online).

In Figure 5, again, the causality in the continuous wavelet transform (CWT) and Rua’s wavelet-based correlation between GWI and GWE are reported. Here, panels a and b represent the continuous wavelet transform causality from GWI to GWE and from GWE to GWI, while panel c describes Rua’s wavelet-based correlation. Panels identify a high strength of the causal effect between 2010 and 2011 on the 4~64 day frequency. Furthermore, the strength of the CWT causal effect has grown between 2013 and 2017 on the 128–256-day frequency. Other than a small causality during 2019 on the 128~256-day frequency, we did not observe very strong causal effect from GWI to GWE. At the same time, in scalogram 2, we observe only a high strength of the casual effect between 2010 and 2012 on the 128~256-day frequency and between 2013 and 2015 on the 32~128-day frequency. From 2015 to 2019, no strong causality is observed, but from 2019 onwards, a strong causal effect can be seen over a 256-day frequency from GSE to GWI. Furthermore, panel c suggests Rua’s wavelet-based correlation (2013), where a strong negative correlation can be observed between these two variables over time on the 128~256-day frequency, implying a long-term independence and diversification opportunities between both markets.

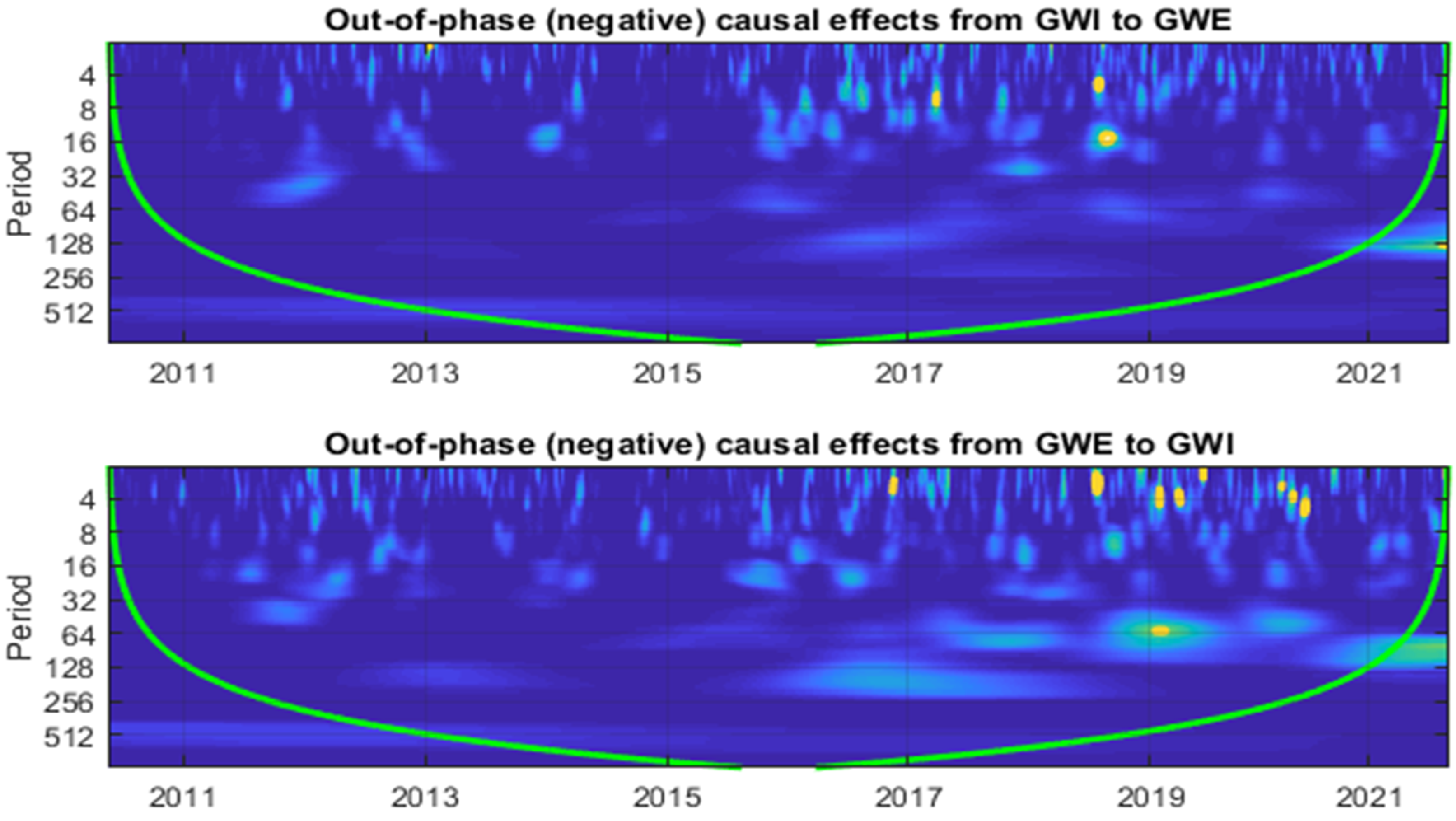
Figure 6. In-phase and out-of-phase plots of causality between GWI and GSE and GWE. Notes: The white (red) contour indicates the 5% (10%) significance level. Significance levels are based on 3000 plots from Monte Carlo simulations estimated over an ARMA (1, 1) null of no statistical significance. The green line is the cone of influence (COI) marking areas affected by edge effects or phase.

Figure 6. In-phase and out-of-phase plots of causality between GWI and GSE and GWE. Notes: The white (red) contour indicates the 5% (10%) significance level. Significance levels are based on 3000 plots from Monte Carlo simulations estimated over an ARMA (1, 1) null of no statistical significance. The green line is the cone of influence (COI) marking areas affected by edge effects or phase.

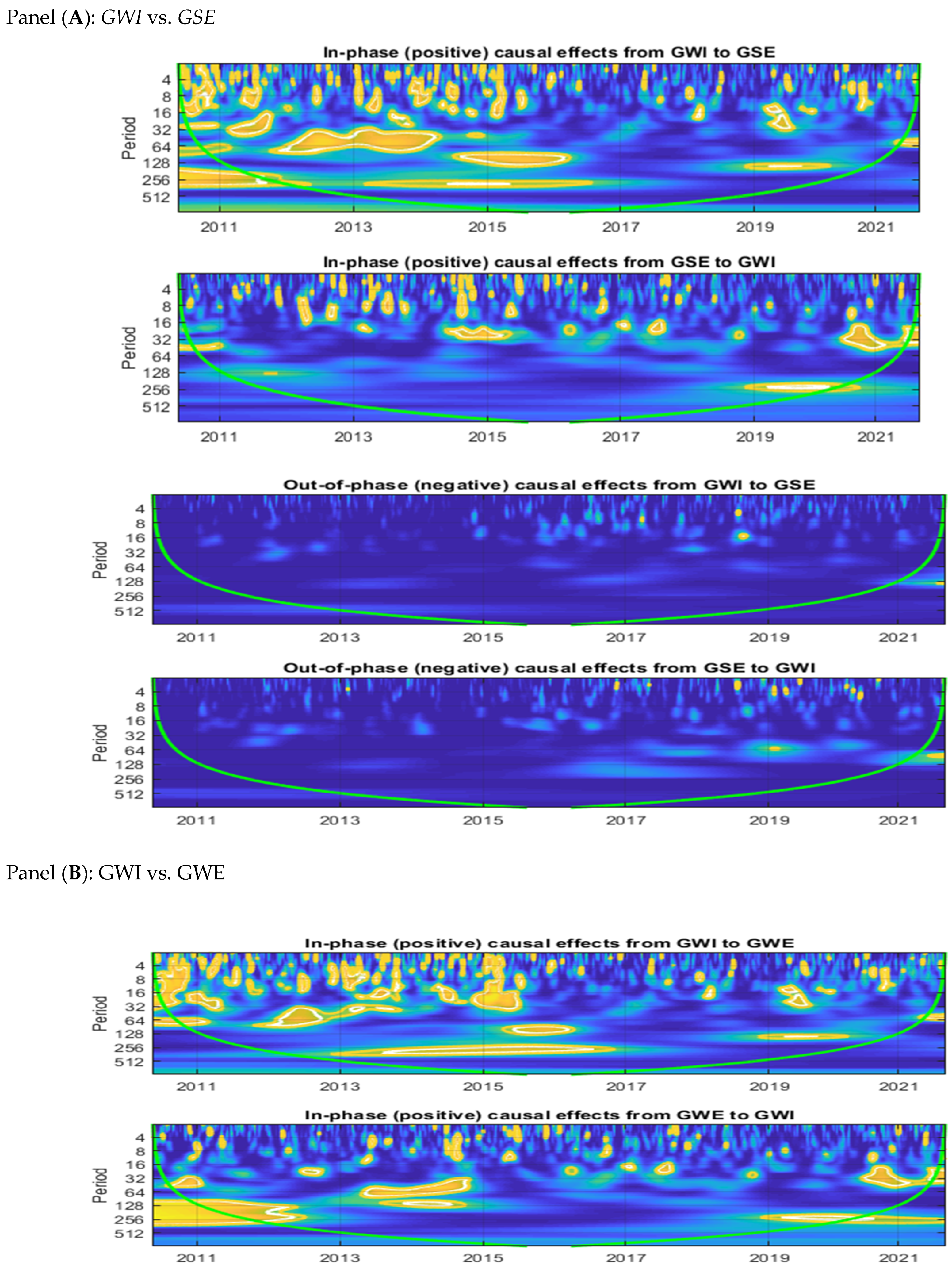
In Figure 6, further in-phase (positive), and out-of-phase (negative) causal effects are tested. The results are demonstrated in two panels, and both panels are indicating in-phase (positive) causal effects and out-of-phase (negative) causal effects between sample variables. In both panels, we have four scalograms that help us to understand the causal effects of the two variables in a robust manner. In panels a and b, we report the in-phase (positive) and out-of-phase (negative) causal effects between GWI and GSE/GWE. The white (red) contour denotes a level of significance of 5% (10%). The significance levels were calculated using 3000 Monte Carlo simulation draws with an ARMA (1, 1) null of no statistical significance. The green line represents the cone of influence, which denotes the areas influenced by edge effects or phase. From scalogram 1, we observed that there was a strong positive (in-phase) causal effect between 2010 and 2016 from GWI to GSE. Meanwhile, scalogram 2 suggests a weak causal effect from GSE to GWI. Next, in scalograms 3 and 4, out-of-phase causal effects are presented from GWI to GSE and from GSE to GWI, respectively. Very weak causal effects are seen amongst the variables. Furthermore, panel b also depicts in-phase (positive) and out-of-phase (negative) causal effects from GWI to GWE and vice versa. The first scalogram of panel b presents the in-phase (positive) causal effects from GWI to GWE, where a significant positive causal effect from GWI to GWE between 2010 and 2017 is prevalent. Specifically, from 2013 to 2016, a very strong positive causal effect from GWI to GWE can be seen. On the other hand, the second scalogram depicts in-phase (positive) causal effects from GWE to GWI, and here we found that the positive causal effects were very strong between 2010 to 2015, after that no significant positive causal effects were observed until 2019. Meanwhile, the third/fourth scalograms offer the out-of-phase(negative) causal effects from GWI/GWE to GWE/GWI. In these two scalograms, we do not observe any strong negative causal effects between sample variables, with the exception of a few tiny causal regions in the short term, namely, during the COVID-19 incident. These findings support our prior findings, which show the causative effects of GWI and GSE/GWE indexes.

5.2. An In-Depth Investigation of Correlation

A rolling window wavelet correlation (RWWC) was used to gain more insights into the behavior of the solar/wind and water relationships. Research outcomes are displayed in Figure 7 for each pair of energy markets. The strength of bilateral developments between each energy market pair is highlighted as the spectrum on the right side of its overall scalogram. This power spectrum ranges from low dispersion values (lower part of the scale) to high developmental changes (upper part of the scale) for each developmental scalogram. The strength of the color corresponding to the respective rolling window is shown across different color schemes, for example, blue (highly negative), green (medium to low negative), white (very low to zero), yellow (medium to low positive), and red (very high positive). Figure 7 consists three panels: panel a (GWI vs. GSE), panel b (GWI vs. GWE), and panel c (GSE vs. GWE). The rolling window wavelet results are based on different fragmentation levels from D1 to D5.

Figure 7. Rolling window wavelet correlations between water stocks and solar and wind energy markets (a 240 day window is used).

Figure 7. Rolling window wavelet correlations between water stocks and solar and wind energy markets (a 240 day window is used).

Panel a witnesses a moderate correlation pattern over the entire period at all decomposition levels, except the D5 decomposition level, where the highest to lowest variation in the correlation pattern can be detected. The correlation value varies from most negative (blue) to most positive (red). Panel b witnesses a high level of the correlation pattern until 2016 in all decomposition levels, except D5; in 2016, the correlation level decreased to moderate level. At decomposition level D5, we found a high level of the correlation pattern for the maximum time but during the times of 2012 to 2020, and this correlation behavior often declined and sometimes reached strongly negative. Panel c displays a totally different picture, where a moderate level of the correlation pattern is observed until 2016 at D1, and until 2014 at the D2, D3, and D4 decomposition levels. Here again, till 2015, the D5 level shows a variation in the correlation from high to moderate (negative). Interestingly, since 2015, a very high correlation is visible between solar and wind markets at all decomposition levels. These findings demonstrate once again that the complex linkages between the water and RWE markets make it impossible to combine them to establish a diversified portfolio.

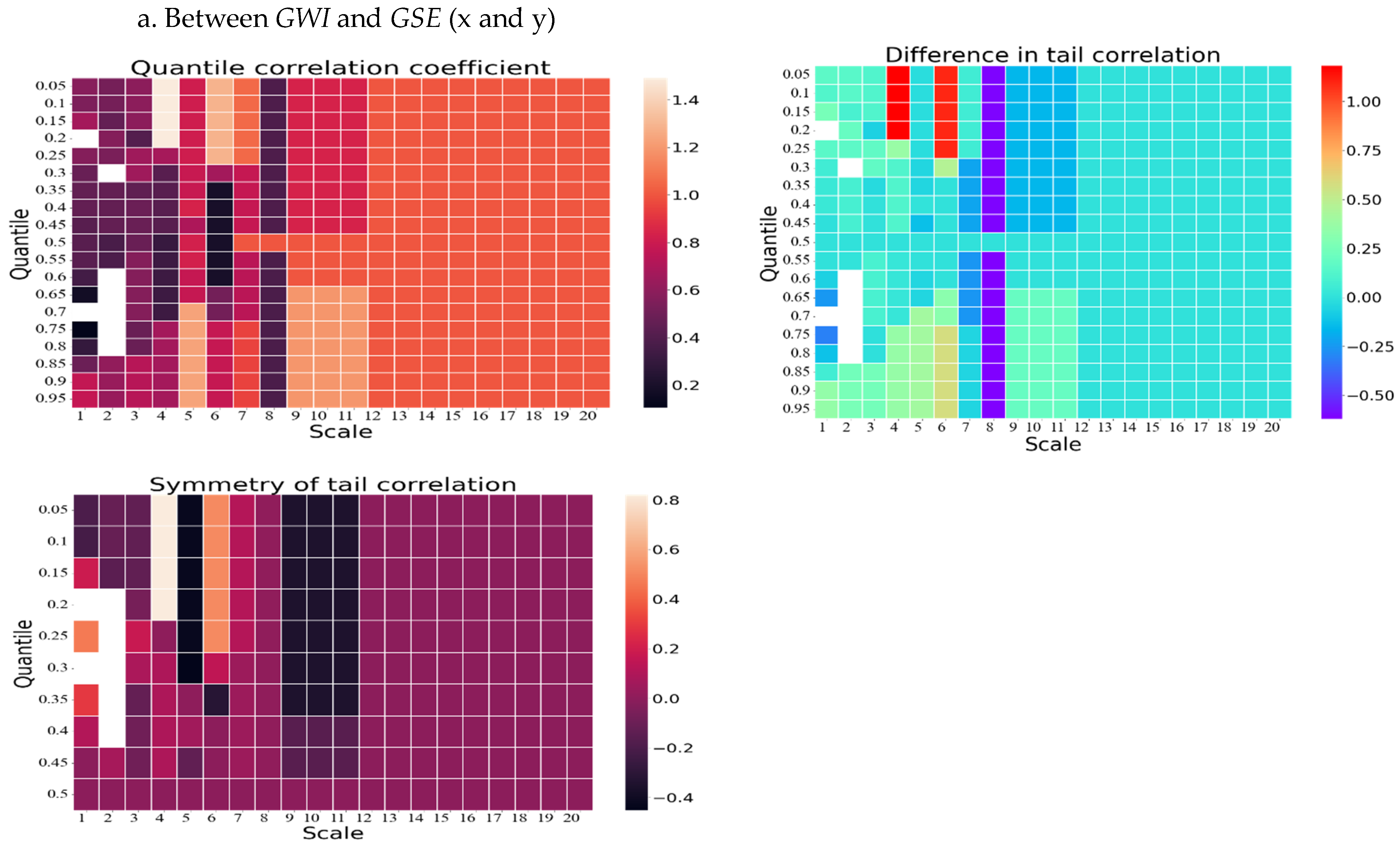
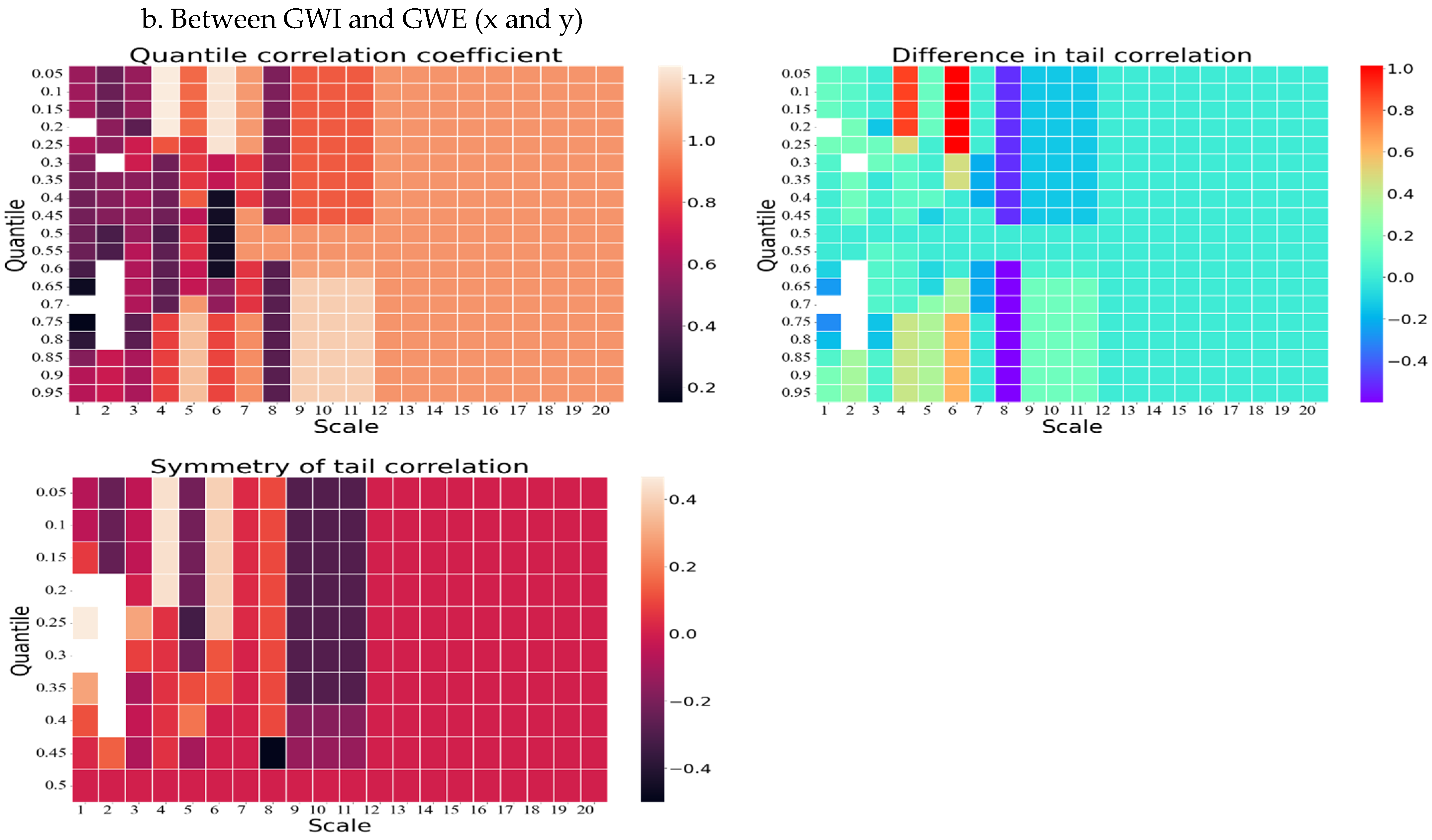
Instead of trying to approximate the conditional mean, we will instead investigate the relationship between these two markets at different quantiles. Figure 8 provides the information about the quantile correlation coefficient (QCC), difference in tail correlation (DTC), and symmetry of tail correlation (STC) of the GWI and GSE pair using the wavelet quantile correlation (WQC) approach. This figure also has two panels (panels a and b); panel a provides the information about the QCC, DTC, and STC of the GWI and GSE pair. Similarly, panel b consists of three scalogram (i.e., QCC, DTC, and STC) between GWI and GWE.

Initially, the QCC outcomes in panels a and b (GWI and GSE/GWE) reveal a weak to moderate correlation in comparison to all quantiles up to the eighth scale. However, the correlation steadily increases from moderate to high thereafter. Notably, the highest quantile correlation can be observed from the 0.60 quantile to the 0.95 quantile, from the ninth scale to the twelfth scale. Secondly, the DTC results of both panels present a similar scenario. With the exception of some initial quantiles for the fourth and sixth scales, where the highest correlations are observed, a low to moderate (positive and negative) correlation is evident throughout. Significantly, the eighth scale emphasizes a very low negative correlation. Thirdly, the tail correlation symmetry metric of GWI and GSE/GWE indicates the presence of asymmetry in the tail correlation. In the first four scales, the correlation level varies from negative low to highly positive. However, in the fifth scale, the correlation turns highly negative for the initial quantiles. Interestingly, at the sixth scale, this correlation reaches a moderately positive level. Lastly, except for the ninth to twelfth scales, where a moderately negative correlation is experienced, a low to zero correlation is prevalent throughout.

Figure 8. Results based on the wavelet quantile correlation between water stocks and solar and wind energy.

Figure 8. Results based on the wavelet quantile correlation between water stocks and solar and wind energy.

5.3. Discussion of the Results

Overall, our findings have significant consequences for both investors and governments. During tumultuous periods, there are strong spillovers between water, solar, and wind energy equities, indicating the lack of safe haven or hedging options amongst them. Furthermore, the correlation between water and RWE demonstrated that investors should utilize water to forecast RWE growth and vice versa, especially in the short and medium terms. This finding is consistent with prior studies, as the energy industry is the second-largest consumer of water, primarily for cooling at thermal power plants. Water demands by the energy industry will also increase. Indeed, fluctuations in energy prices and political considerations are driving the demand for alternative energy sources, such as hydroelectric energy, but also biofuels and shale gas, as well as energy-saving techniques.

The results of our analysis also show the significant relationship between solar energy and water between 2011 and 2021. Indeed, the water shortage that occurred in California in 2014 increased the demand for solar energy. The increase in the demand for solar energy as a result of water scarcity has led to the emergence of water desalination with solar energy. In 2018, irrigation with solar energy panels started in agriculture. It showed that the demand for solar energy was growing despite the pandemic in 2020. In 2021, concerns about the negative effects of solar power plants on environmental factors emerged. The test statistic values were larger than the test statistic values reported by [50].

Findings on the dependence between water and RWE can help governments develop an enabling policy environment that promotes industries and the private sector to manufacture and promote RWE consumption and water-efficient products. To that end, the government should find solutions to the chain reaction between RWE and water in order to stimulate investment in these sectors in order to replace fossil fuel energy with CE, improve water resource management, and reduce the effects of contaminated water on society and the environment as a whole.

6. Conclusions

In this paper, we tried to explain the causal relationship between water stocks and solar and wind energy markets using three different methods. The analyses we have made are continuous wavelet analysis, dynamic correlation analysis, and Granger causality analysis. We conducted this study because we thought that understanding the dynamics between water, solar, and wind energy would benefit investors, researchers, and policymakers. Ref. [50] used methods, but differently, in our study, we did not take simultaneous causality into account.

One of the main focal points of the study was to determine the causal relationships between water stocks and solar and wind energy markets. The analyses directed have shown that water stocks can influence energy markets during specific time intervals. This is crucial information for energy investors and policymakers when planning future trading strategies and environmental policies that will promote economic growth, respectively. Furthermore, continuous wavelet transforms and dynamic correlation analyses have exposed the time-varying relationships between water stocks and solar and wind energy markets. These dynamic analyses provide a valuable perspective for understanding how market conditions evolve over time.

The findings we obtained in our analysis generally show important results for both investors and policymakers. In risky periods, there are strong spillovers between water, solar, and wind energy equities, and in this case, it is observed that there are no hedging options. Moreover, the correlation between water and RWE has shown that investors should use water when forecasting RWE growth in the short and medium terms. Since the energy industry is the second-largest consumer of water, our analysis results are consistent with the results of previous studies. Water demand in the energy sector will gradually increase. Fluctuations in energy prices increase the demand for alternative energy sources such as biofuels and shale gas, as well as hydroelectric.

Consequently, the results arising from the relationship between water and RWE may help encourage the private sector to use RWE as a result of facilitating policies made by governments. By helping the development of this sector, governments must remove the negative impact of dirty water on the environment, ensure the efficient use of water resources, and ensure that more effective solutions are found between RWE and water in the relationship between society and the environment.

Findings from this study can be taken into consideration when designing energy policies and investment strategies. Understanding the relationships between water stocks and energy markets, particularly, can support sustainable energy policies for both energy companies and governments. In this context, proposed policy changes may include the more effective utilization of water resources; increased incentives for solar and wind energy projects; and the adoption of appropriate risk management strategies to cope with fluctuations in energy markets.

Last of all, this study represents a significant step toward comprehending the intricate relationships between water stocks and solar and wind energy markets. It is an important endeavor in developing effective policies for the sustainable energy sector.