Improving Photovoltaic Power Prediction: Insights through Computational Modeling and Feature Selection

Abstract

This work identifies the most effective machine learning techniques and supervised learning models to estimate power output from photovoltaic (PV) plants precisely. The performance of various regression models is analyzed by harnessing experimental data, including Random Forest regressor, Support Vector regression (SVR), Multi-layer Perceptron regressor (MLP), Linear regressor (LR), Gradient Boosting, k-Nearest Neighbors regressor (KNN), Ridge regressor (Rr), Lasso regressor (Lsr), Polynomial regressor (Plr) and XGBoost regressor (XGB). The methodology applied starts with meticulous data preprocessing steps to ensure dataset integrity. Following the preprocessing phase, which entails eliminating missing values and outliers using Isolation Feature selection based on a correlation threshold is performed to identify relevant parameters for accurate prediction in PV systems. Subsequently, Isolation Forest is employed for outlier detection, followed by model training and evaluation using key performance metrics such as Root-Mean-Squared Error (RMSE), Normalized Root-Mean-Squared Error (NRMSE), Mean Absolute Error (MAE), and R-squared (R²), Integral Absolute Error (IAE), and Standard Deviation of the Difference (SDD). Among the models evaluated, Random Forest emerges as the top performer, highlighting promising results with an RMSE of 19.413, NRMSE of 0.048%, and an R² score of 0.968. Furthermore, the Random Forest regressor (the best-performing model) is integrated into a MATLAB application for real-time predictions, enhancing its usability and accessibility for a wide range of applications in renewable energy.

1. Introduction

In the global pursuit of net-zero emissions, every country has committed to vigorously advancing clean energy initiatives. Among these efforts, PV energy production stands out as a crucial and rapidly developing sustainable energy source, playing a vital role in ensuring electrical systems’ safe, stable, and cost-effective operation. However, the inherently variable nature of PV energy production, influenced by seasonal fluctuations, meteorological conditions, diurnal changes, and solar radiation intensity, presents significant challenges to the reliable integration of large-scale PV grids into the electricity system [1,2,3,4]. Accurate predictions of PV electricity production capacity are therefore essential for developing power generation plans, optimizing power dispatching, and promoting the adoption of new energy sources, ultimately reducing operational costs and enhancing system stability.

There is a strong interest in predicting and forecasting energy production in multi-source systems, evaluating the power output of each component, and estimating energy generation under diverse climatic and operational conditions [5]. Various methodologies for predicting photovoltaic (PV) energy systems exist, with some studies employing neural networks for energy generation prediction [6,7,8]. Different prediction models have emerged, which can be classified based on criteria such as linearity or mathematical approach [9]. These classifications divide models into linear and nonlinear categories based on Artificial Intelligence techniques versus regressive models [10].

• Models Based on Past Values

These models rely solely on past values as inputs, which can either be the variable to be predicted or that variable supplemented with other influential variables. These influential variables might include those relevant to the specific time they occurred and locally measured meteorological variables from those past moments. These models can be broadly categorized as described in the following subsections.

1.1.

Persistence Models

When estimating the energy production of a photovoltaic system, one must use the power production recorded at the same time on a previously measured day of operation based only on historical records. The main application of this prediction method is performance benchmarking or comparisons with other modeling techniques [10].

1.2.

Statistical Approaches

These PV prediction methods use time series analysis to understand observed data series behavior or forecast future values. These methods are beneficial for short-term PV power production estimates. The following techniques are commonly used in statistical approaches:

Regression models: Here, PV power output is treated as a dependent variable explained by meteorological variables. These models usually require mathematical formulas and consider explanatory variables [11].

Auto-regressive models: Techniques such as ARMA (Auto-Regressive Moving Average) and ARIMA (Auto-Regressive Integrated Moving Average) are frequently used for PV prediction using time series. These techniques assume that past values of the series (the series’ history) influence future values through a combination of Auto-Regressive (AR) and Moving Average (MA) elements. In a pure Auto-Regressive process, future values of the series depend solely on past values. In Moving Average processes, future values depend on random variables independent of one another and are modeled as white noise [12].

1.3.

AI Techniques

These models are based on Artificial Intelligence approaches (machine learning and deep learning). Often, these methods require a large volume of data to estimate PV energy production accurately [13,14].

1.4.

Hybrid Models

These models integrate physical and statistical approaches to improve the accuracy of PV power estimation by leveraging the strengths of both methods. For instance, neuro-fuzzy systems combine the supervised learning ability of neural networks with the knowledge representation of fuzzy inference systems. A common term for such systems is Adaptive Neuro-Fuzzy Inference Systems (ANFIS), applied to PV power estimation [15]. Other examples of hybrid models include the use of neural networks optimized with genetic algorithms, ARMA models combined with neural networks, the integration of various types of neural networks, and the combination of atmospheric models like MM5 for radiation prediction with fuzzy logic or neural networks for power prediction [16].

2.

Physical Models use detailed physical principles and environmental conditions to estimate PV energy production

These models generally require input data such as solar radiation, temperature, and other climatic factors. Standard physical models include radiative transfer, thermal, geographical information systems (GIS), and engineering models [17].

Recent efforts in predicting and forecasting PV generation have focused on various modeling approaches, including physical models, statistical analysis models, Artificial Intelligence (AI) models, and hybrid models [17,18,19].

Physical models rely on geographic and meteorological data to compute PV power, considering solar radiation, humidity, and temperature factors. However, modeling complexities arise from the need for detailed geographic and meteorological data specific to PV plants to anticipate production accurately.

On the other hand, statistical models capture historical time series relationships, often utilizing autoregressive Moving Average models. These autoregressive integrated Moving Average models and similar techniques are known for their simplicity and computational efficiency. Yet, these models are best suited for stable time series data, whereas actual PV data exhibit high variability and significant errors [20].

The advent of smart metering technologies has provided abundant real-world data, opening new ways for machine learning and deep learning techniques to enhance data-driven algorithms for PV power generation forecasting. Moreover, integrating smart meters and data processing capabilities offers novel opportunities to improve the accuracy and reliability of PV production forecasts. By leveraging these advancements, researchers aim to develop more robust and effective prediction models capable of meeting the evolving needs of the renewable energy sector. Due to their potential for extracting representative features and data mining, AI-based models have proven to be more successful than physical and statistical ones [21].

In recent years, conventional machine learning algorithms have emerged as powerful tools for forecasting PV power generation. Demand response, proactive maintenance, energy production, and load predicting are just a few applications where machine learning models are the go-to toolkit for researchers [22]. These models can capture complex nonlinear relationships between various factors influencing power generation and accurately predicting future values [23]. The use of deep learning, nevertheless, can be useful when dealing with time series data.

Auto-Regressive Integrated Moving Averages (ARIMA) methods are adequate for the instantaneous forecasting of robust time series data. However, artificial neural networks (ANNs) are significantly more potent than ARIMA models and traditional quantitative approaches, especially for modeling complex interactions [24]. Due to their ability to handle nonlinear models, ANNs have increasingly become popular for forecasting time series data in recent years [25].

In this study, several machine learning regression models, including Linear regression (LR), Support Vector regressor (SVM), k-Nearest Neighbors regressor (KNN), Random Forest regressor (RF), Gradient Boosting regressor (GBR), and Multi-layer Perceptron regressor (MLP), Ridge regressor (Rr), Lasso regressor (Lsr), Polynomial regressor (Plr), and XGBoost regressor (XGB) were employed for PV power generation forecasting, yielding promising results. The effectiveness of the proposed regression model was compared with existing approaches.

This study contributes significantly to the field by advancing predictive modeling techniques for the renewable energy sector and providing valuable insights for optimizing PV systems and their management. Key contributions include using Pearson and Spearman correlation analyses to identify influential environmental variables and enhancing model interpretability and performance. Integration of Isolation Forest for outlier detection during data preprocessing ensures the removal of anomalies, thereby improving the model’s generalization ability and preventing overfitting. Furthermore, the adoption of Randomized Search CV streamlines hyperparameter tuning, with Random Forest emerging as the optimal model choice due to its ensemble nature and capability to capture nonlinear relationships, which are crucial for modeling the complex dynamics of PV system generation. Additionally, the integration of Python-trained (version 3.8.0) models into a MATLAB 2023 interface represents a significant advancement in accurately predicting key parameters such as PV generation, PDC, VDC, and IDC. Moreover, this interface extends beyond mere prediction by incorporating calculations for evaluating yield, losses, and performance ratios (PR), enabling a comprehensive assessment of system performance and health. This thorough analysis capability offers valuable insights for optimizing efficiency and addressing potential issues in PV systems.

The paper is structured as follows: Section 2 introduces the PV dataset used in this study, outlining the various environmental variables and parameters pertinent to PV systems. This section also describes data preprocessing techniques, detailing the strategies for refining sensor data and emphasizing the importance of cleaning and normalization for ensuring data accuracy and reliability. The use of Pearson and Spearman correlation analyses to identify significant environmental variables for predictive modeling is also detailed in this section. The approach to enhancing regression model performance through outlier detection using Isolation Forest during data preprocessing is also discussed. The methodology provides an overview of the regression models employed for predicting key parameters of PV systems while outlining our hyperparameter tuning process using Randomized Search CV, and the evaluation metrics utilized to optimize model performance are also analyzed in Section 2. The development of a MATLAB application for power prediction, highlighting the integration of Python-trained models and the interface’s capabilities for accurate prediction and system performance evaluation, is also presented in Section 2. Section 3 presents the results and their implications for the renewable energy sector and suggests potential avenues for future research. Finally, Section 4 focuses on the discussion of the main results obtained.

2. Materials and Methods

The data collected in this study are from a grid-connected, ground-mounted PV system in Ain El-Melh, located in the Algerian highlands and serving as the gateway to the vast desert. The site’s coordinates are 34°51″ N and 04°11″ E, with an elevation of 910 m above sea level.

This PV plant is integrated into Ain El-Melh’s medium voltage network and is part of a substantial 400 MW project overseen by the company SKTM, a subsidiary of Sonelgaz. Sonelgaz, mandated by the Algerian government for renewable energy development, has implemented 23 PV power plants across the highlands and central regions. The Ain El-Melh plant, boasting a total capacity of 20 MWp, spans 40 hectares. The key design specifications of this 20 MWp PV facility are detailed in

Table 1. Ain El-Melh PV power plant design parameters (20 MWp).

Parameter	Characteristics
Type of module	Poly-crystalline silicon
Efficiency of PV module	15%
Tilt and orientation	33° south
Type of installation	Fixed structure
PV rows distance	5 m
Inverter nominal power	500 KW
Characteristics of transformers	1250 kVA, 47–52 Hz, 315 V/31.5 kV

.

The PV modules are linked to 500 kW inverter cabinets via junction boxes, serving as the primary data source. Data gathering occurred from 1 January 2020, to 31 December 2021, with readings taken every fifteen minutes, resulting in 69,195 data points. This dataset encompasses parameters such as solar panel temperature, tilt radiation, total radiation, dispersion radiation, direct radiation, wind speed, humidity, pressure, voltage, current, and PV power.

Table 2. PV plant monitored data.

Feature	Description	Maximum	Minimum	Average
Tp	Module temperature (°C)	74.800	−2.5	27.987833
Gdin	Inclined irradiance(W/m2)	1651.200	0.0	310.162255
Gtotal	Total irradiance (W/m2)	1395.600	0.0	239.705539
Gdisp	Dispersion (W/m2)	686.400	0.0	76.567325
Gdirect	Direct irradiance (W/m2)	1365.600	0.0	232.813488
V_V	Wind speed (m/s)	22.200	0.0	3.760438
H	Humidity (%)	71.600	0.0	36.119596
P	Pressure (Pa)	927.000	0.0	912.473873
VDC	Voltage (V)	780.400	0.0	329.776418
IDC	Current (A)	985.400	0.0	183.593662
PDC	PV power (kW)	569.441	0.0	108.289535

shows an overview of the environmental and electrical parameters of the PV system.

Table 3. PV modules characteristics (Yingli Solar, YL2545-29b, Baoding, China).

PV Module	Specifications
STC power rating	250 Wp ± 5%
Number of cells	60
Vmp	29.8 V
Isc	8.92 A
Imp	8.39 A
Voc	37.6 V
Power temperature coefficient	−0.45%/K
NOCT (°C)	46 ± 2

provides the technical specifications of the PV modules utilized within this PV plant.

Data preprocessing is essential when working with the actual data collected from automatic sensors, as these data often contain errors and inconsistencies. Cleaning and organizing techniques are applied to prepare the data for use with machine learning models. The focus is correcting minor inconsistencies and removing erroneous or missing data from the monitoring dataset.

One challenge encountered is the presence of empty records, particularly during nighttime (between 9 p.m. and 4 a.m.) when no measurements are collected. While solar irradiation is naturally zero at night, air temperature data may still be missing. However, the absence of nighttime temperature data is irrelevant since there is no PV power production. Including nighttime data would only add redundant information, increasing the model complexity and calculation time without yielding meaningful results. To prevent the negative impact of empty records on learning models, rows containing null data are eliminated. The same procedure is applied to remove duplicated values or incomplete records.

After these preprocessing steps, the database ultimately contains 33,465 samples. The min-max normalization method optimizes the model’s performance and ensures data homogeneity. This process scales each data point to a range between 0 and 1. The equation for calculating the normalized value $x_{norm}$ for a given value x is

$$x_{norm }=\frac{x-\mathit{min}\left(x\right)}{\mathit{max}\left(x\right)-min\left(x\right)}$$

(1)

This normalization technique serves various purposes, including speeding up the optimization process, minimizing disparities between data values, removing dimensional influences, and reducing computational requirements.

The analysis examined correlation factors to ascertain the relationships among P_DC and individual weather factors. The correlation coefficient, denoted as r, indicates the degree of association between two variables, $x_i$ and $y_i$, and is expressed as follows [26,27,28]:

$$r=\frac{\sum _{i=1}^n(x_{i }-\overline{x_{i }})(y_{i }-\overline{y_{i }})}{\sqrt{\sum _{i=1}^n{(x_{i }-\overline{x_{i }})}^2\sum _{i=1}^n{(y_{i }-\overline{y_{i }})}^2}}$$

(2)

$$\overline{x_{i }}=\frac{1}{N}{\sum }_{i=1}^N{x}_i$$

(3)

$$\overline{y_{i }}=\frac{1}{N}{\sum }_{i=1}^N{y}_i$$

(4)

By applying Equations (3) and (4) to Equation (2), the following equation can be driven:

$$r=\frac{n\sum _{i=1}^n{x}_{i }{y}_{i }-\sum _{i=1}^n{x}_{i }\sum _{i=1}^n{y}_{i }}{\sqrt{n\sum _{i=1}^n{x_{i }}^2-(\sum _{i=1}^n{x_{i })}^2}\sqrt{n\sum _{i=1}^n{y_{i }}^2-(\sum _{i=1}^n{y_{i })}^2}}$$

(5)

where {$\overline{x_i}$, $\overline{y_i}$} and n are the mean and sample size, respectively, and {$x_i$, $y_i$} are the individual sample points indexed by i.

Two methods are used for estimating the correlation and correlation coefficients between two variables: Pearson and Spearman. The Pearson method assesses the linear relationship between variables, indicating a proportional change between them. Conversely, the Spearman method evaluates a simple (ordinal or rank) relationship, where variables tend to change together without necessarily being proportional.

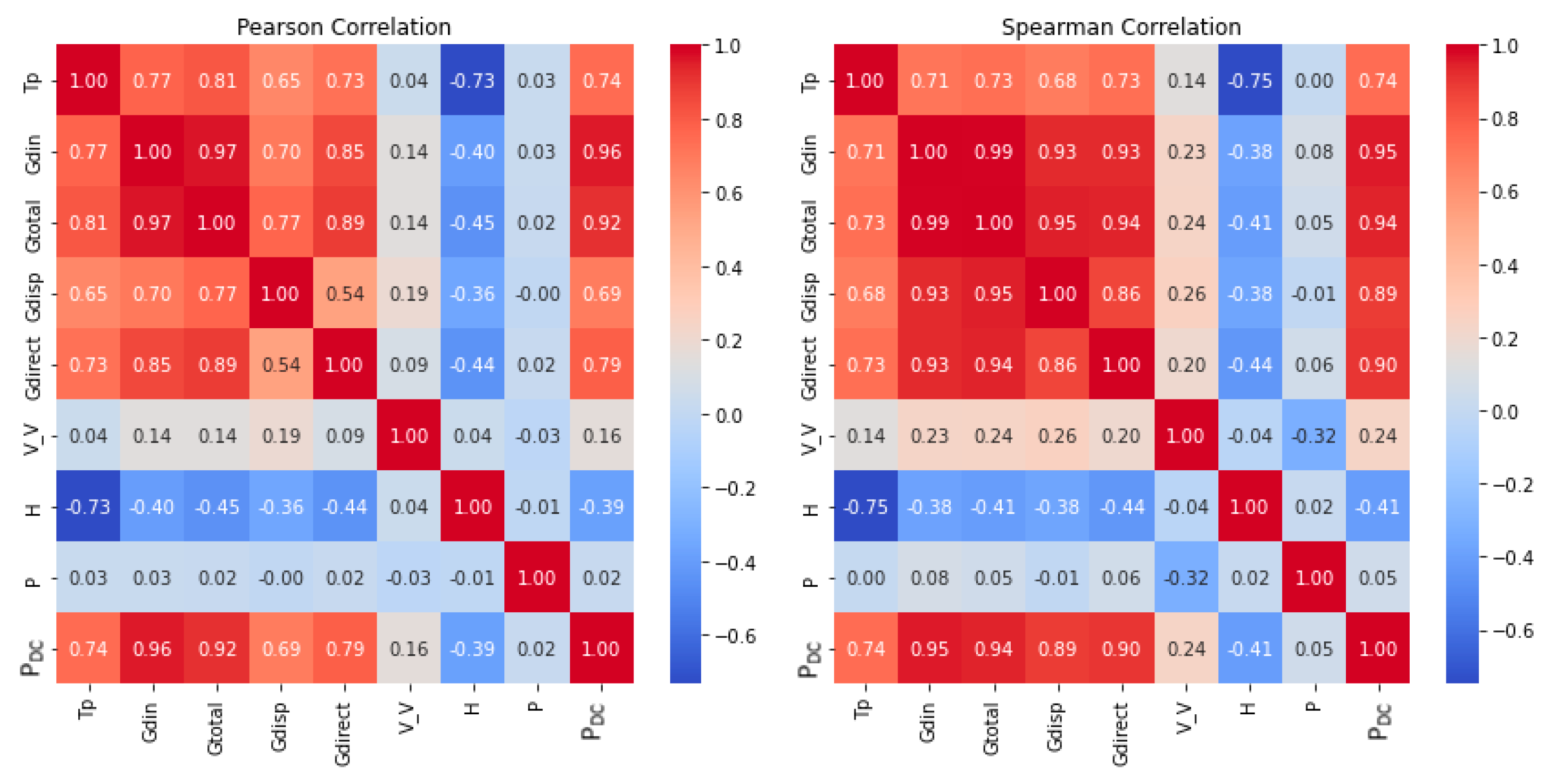
This study employed the Pearson correlation method to analyze the relationship between P_DC and environmental variables. Figure 1 illustrates the outcomes of this correlation analysis in the heatmap histograms in the diagonal plots demonstrating the frequency distributions of P_DC and environmental data.

The correlation matrix offers insights into the relationships between PV power generation, voltage, current, and environmental variables. Each cell in the matrix presents the correlation coefficient between two variables, ranging from −1 to 1. The sign of the coefficient indicates the direction of the relationship: “+” denotes a positive correlation, and “-” represents a negative correlation. A higher absolute correlation coefficient value signifies a stronger association between the variables [29,30].

Several noteworthy patterns were observed when analyzing the correlations. Variables such as tilt solar radiation, Gdin, total Irradiance, Gtotal, direct solar radiation, and Gdirect exhibit strong positive correlations with PV power generation P_DC, indicating that higher values of these environmental factors tend to coincide with increased PV power generation. Conversely, the variable H, representing humidity, demonstrates a notable negative correlation with PV power generation, suggesting that higher humidity levels may lead to decreased PV power output. Additionally, some variables—such as Tp, the temperature of the PV panel, and Gdisp, dispersed solar radiation—show moderate positive correlations with PV power generation. These correlations imply that temperature and dispersed solar radiation may also significantly influence PV power generation, albeit to a lesser extent than other factors like direct solar radiation Gdirect.

Moreover, variables such as V_V, wind speed, and P, pressure, exhibit weaker correlations with PV power generation, as indicated by their correlation coefficients close to zero. While these variables may still influence PV power generation, their impact appears to be relatively minor compared to other environmental factors.

Overall, this correlation analysis provides valuable insights into how various environmental variables relate to PV power generation. Understanding these relationships can inform decision-making processes for optimizing PV system performance, forecasting energy production, and designing more efficient renewable energy systems.

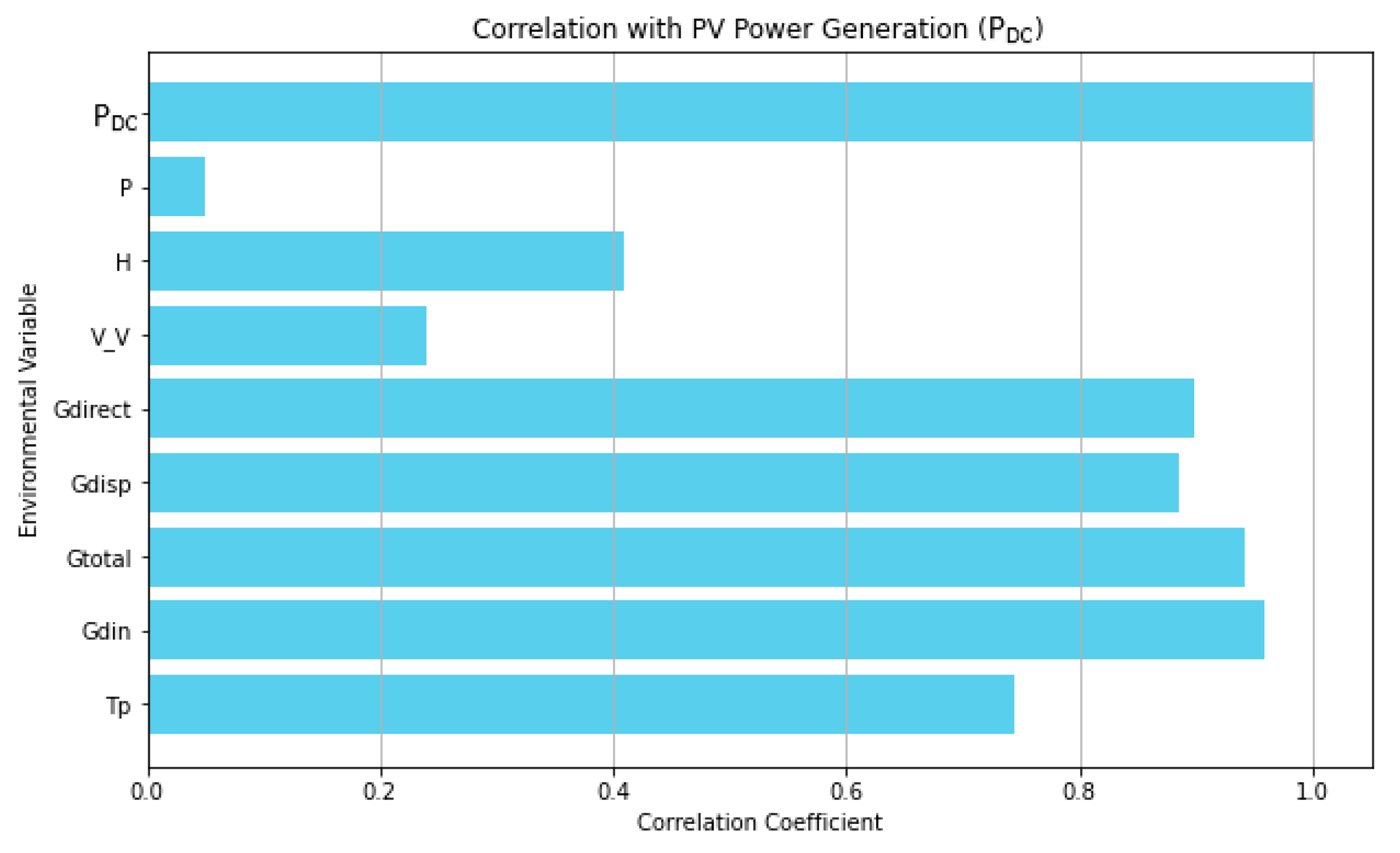
The target variable P_DC is defined after loading the dataset, removing any rows with missing values, and eliminating the outliers. Then, we compute Pearson and Spearman correlation coefficients separately with the target variable. The correlation coefficients from both methods were combined by selecting the maximum absolute value. After that, the features whose absolute correlation coefficients with the target variable are less than or equal to 0.1 were filtered. This process selects a subset of the original features that meet the correlation criterion. The number of input features remains the same; we do not remove any features from the dataset itself but identify which features are relevant based on the correlation threshold. This approach ensures that significant correlations are captured regardless of the method used. Figure 2 demonstrates feature selection based on the correlation threshold for P_DC data, identifying pertinent features crucial for accurate prediction and analysis in PV systems.

Isolation Forest is a popular algorithm used for outlier detection in machine learning. It isolates anomalies in the dataset rather than modeling the normal data points. This approach is particularly effective for high-dimensional datasets with complex structures. The main principle behind Isolation Forest is that anomalies are typically rare and have attributes that make them easy to isolate. The algorithm exploits this principle by randomly selecting a feature and then randomly selecting a split value between the maximum and minimum values of that feature. This process recursively occurs until all data points are isolated or a predefined maximum tree depth is reached. During the isolation process, anomalies are expected to be isolated with fewer splits than normal data points. Therefore, the path length to isolate an anomaly is typically shorter than that of a normal data point. By measuring the average path length across multiple isolation trees, Isolation Forest assigns anomaly scores to each data point. Data points with shorter average path lengths are considered more anomalous.

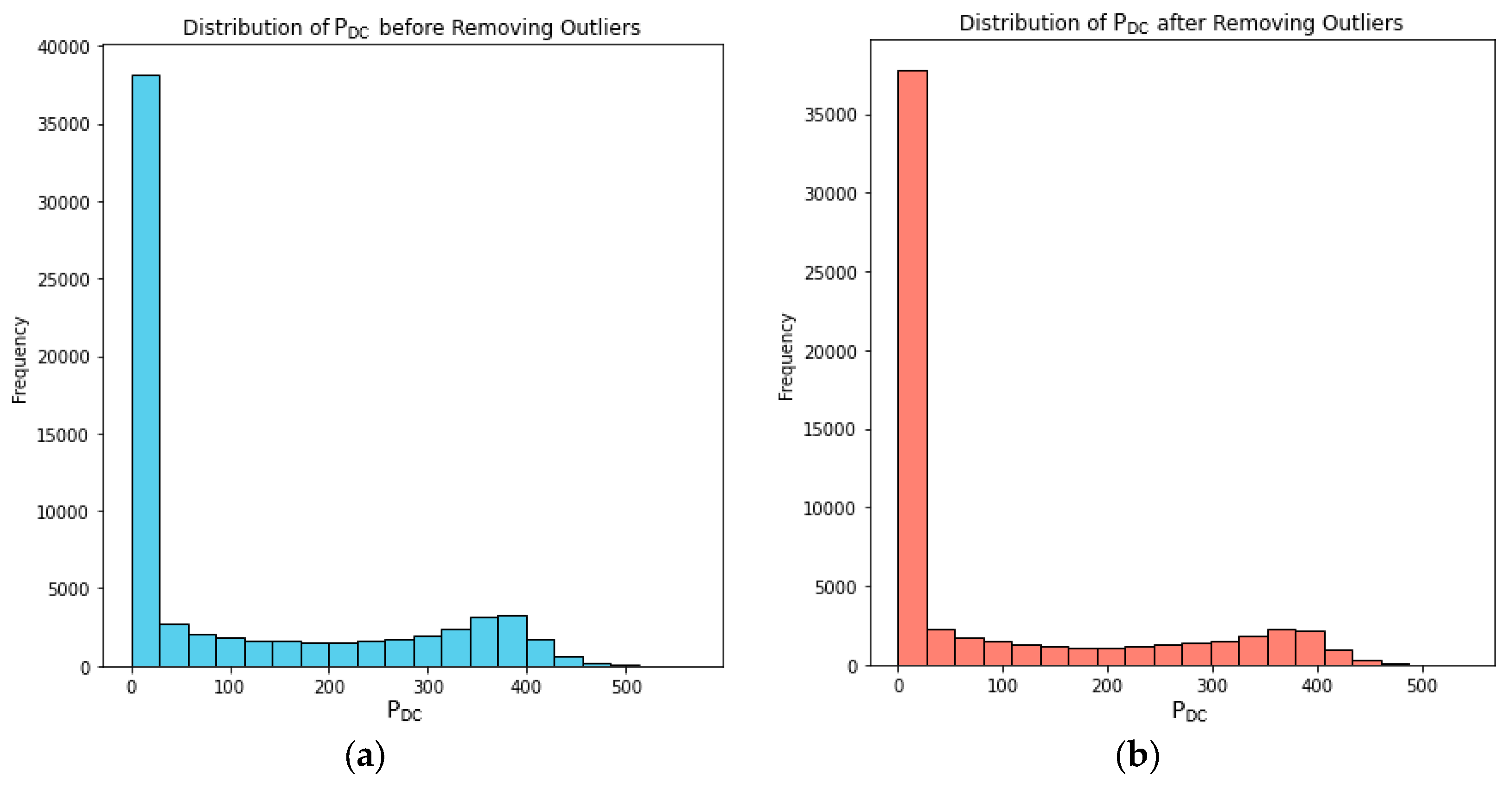
This work uses an Isolation Forest for outlier detection before training the regression models. Specifically, after loading and preprocessing the dataset, Isolation Forest is applied to detect and remove outliers using the Isolation Forest class from the sklearn library. After setting the contamination parameter, representing the expected proportion of outliers in the dataset, outlier predictions are then used to filter out the outliers from the original dataset, resulting in a cleaned dataset containing only the inlier data points. In Figure 3, we present the distributions of P_DC before and after removing outliers. The X-axis represents PV generation values, while the Y-axis represents the frequency of occurrence. By comparing the two distributions, we gain insights into how removing outliers affects the overall distribution of PV generation values.

Figure 3 allows us to compare the distribution of the target variables P_DC before and after removing outliers, providing insights into the impact of outlier removal on the data distribution. By identifying and removing outliers, Isolation Forest effectively isolates anomalous data points that may skew the distribution of the variables. By taking out many data points classified as outliers, Isolation Forest helps ensure that the resulting histograms accurately represent the distribution of normal data points within each bin. This enables a clearer understanding of how the data are distributed and how removing outliers affects the overall data distribution [31].

The methodology employed in this study began with thorough data preprocessing steps to ensure the integrity of the dataset. Missing values were addressed through either imputation or removal and through relevant features highly correlated with the target variable. Correlated features were identified using Pearson and Spearman correlation coefficients, and then, both sets of correlated features were merged. Additionally, outlier detection and removal were performed using Isolation Forest to enhance the robustness of the models. Subsequently, the data were split into training and testing sets for model evaluation. Following data preprocessing, ten regression models were selected for evaluation: k-Nearest Neighbors (KNN) [32], Support Vector regression (SVR) [33], Random Forest [34], Multi-layer Perceptron (MLP), Linear regressor (LR), Gradient Boosting [35], Ridge regressor(Rr) [36], Lasso regressor (Lsr) [37], Polynomial regressor (PLR) [38], and XGBoost regressor (XGB) [39]. Each model was subjected to hyperparameter tuning using Randomized Search CV, which involved optimizing various hyperparameters such as the number of estimators, maximum depth, learning rate, kernel type, activation function, and number of neighbors, etc.

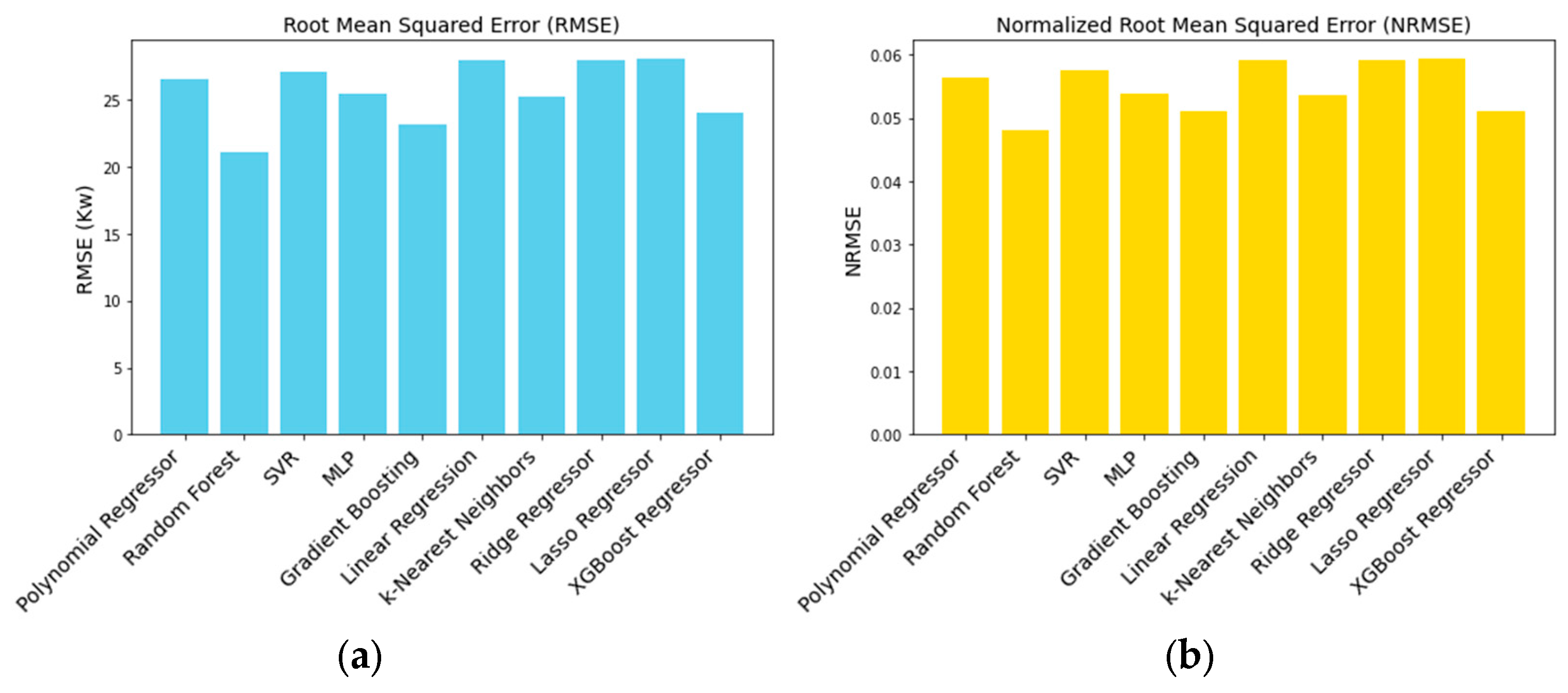
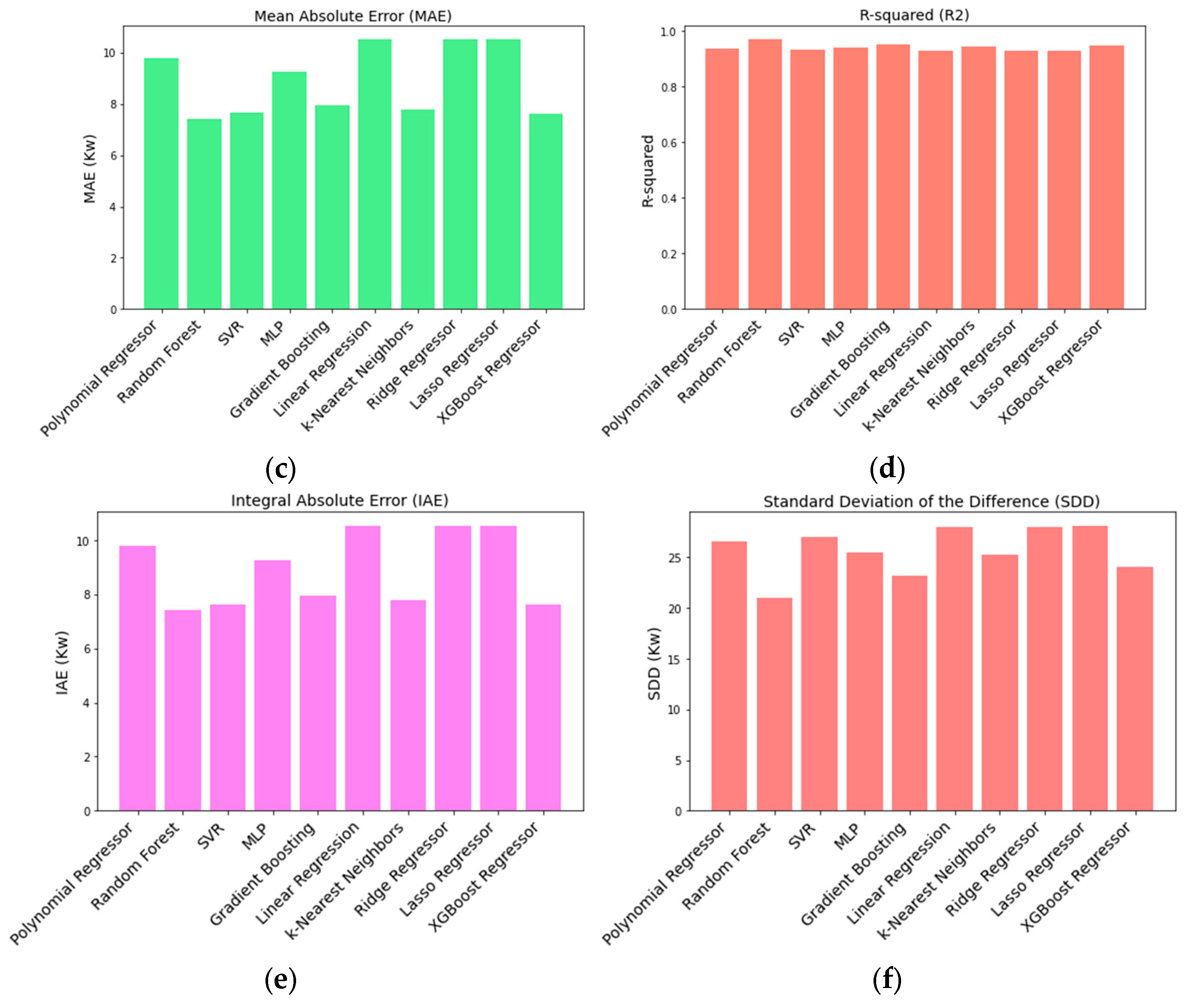
Once the hyperparameters were tuned, the performance of each model was evaluated using multiple metrics, including Root-Mean-Squared Error (RMSE), Normalized Root-Mean-Squared Error (NRMSE), Mean Absolute Error (MAE), R-squared (R²), Integral of Absolute Error (IAE), and Standard Deviation of Differences (SDD). These metrics, defined in Equations (6)–(11), provided insights into the models’ accuracy, precision, and goodness of fit [40,41,42].

$$MAE=\frac{1}{n}{\sum }_{i=0}^{n-1}\left|y_i-\widehat{y_i}\right|$$

(6)

$$RMSE=\sqrt{\frac{1}{n}{\sum }_{i=0}^{n-1}{\left(y_i-\widehat{y_i}\right)}^2}$$

(7)

$$R^2=1-\frac{{\sum }_{i=1}^{n-1}{\left(\widehat{y_i}-y_i\right)}^2}{{\sum }_{i=1}^{n-1}{\left(\overline{y_i}-y_i\right)}^2},\overline{y}={\sum }_{i=0}^{n-1}{y}_i$$

(8)

$$NRMSE=\frac{RMSE}{y_{max}-y_{min}}$$

(9)

$$SDD=\sqrt{\frac{{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{n}}$$

(10)

$$IAE={\int }_{to}^{tn}\left|y_i-\widehat{y_i}\right| dt$$

(11)

The model evaluation results were compared to identify the best-performing model for PV generation prediction. This analysis helped highlight the strengths and weaknesses of each model and facilitated the selection of the most suitable model.

The next step involves integrating this model into a MATLAB application after identifying and selecting the best prediction model based on its performance metrics (Random Forest in our work). This process typically entails exporting the model and any necessary preprocessing steps or feature engineering techniques, especially the normalization process, into a format compatible with MATLAB. Once integrated, the model can be deployed within the MATLAB application after being converted into a desktop application using MATLAB App Designer. This allows users to input relevant data and receive predictions or insights based on the model’s calculations. This seamless integration facilitates real-time or on-demand predictions within the MATLAB environment, enhancing the usability and accessibility of the predictive model for various applications and users.

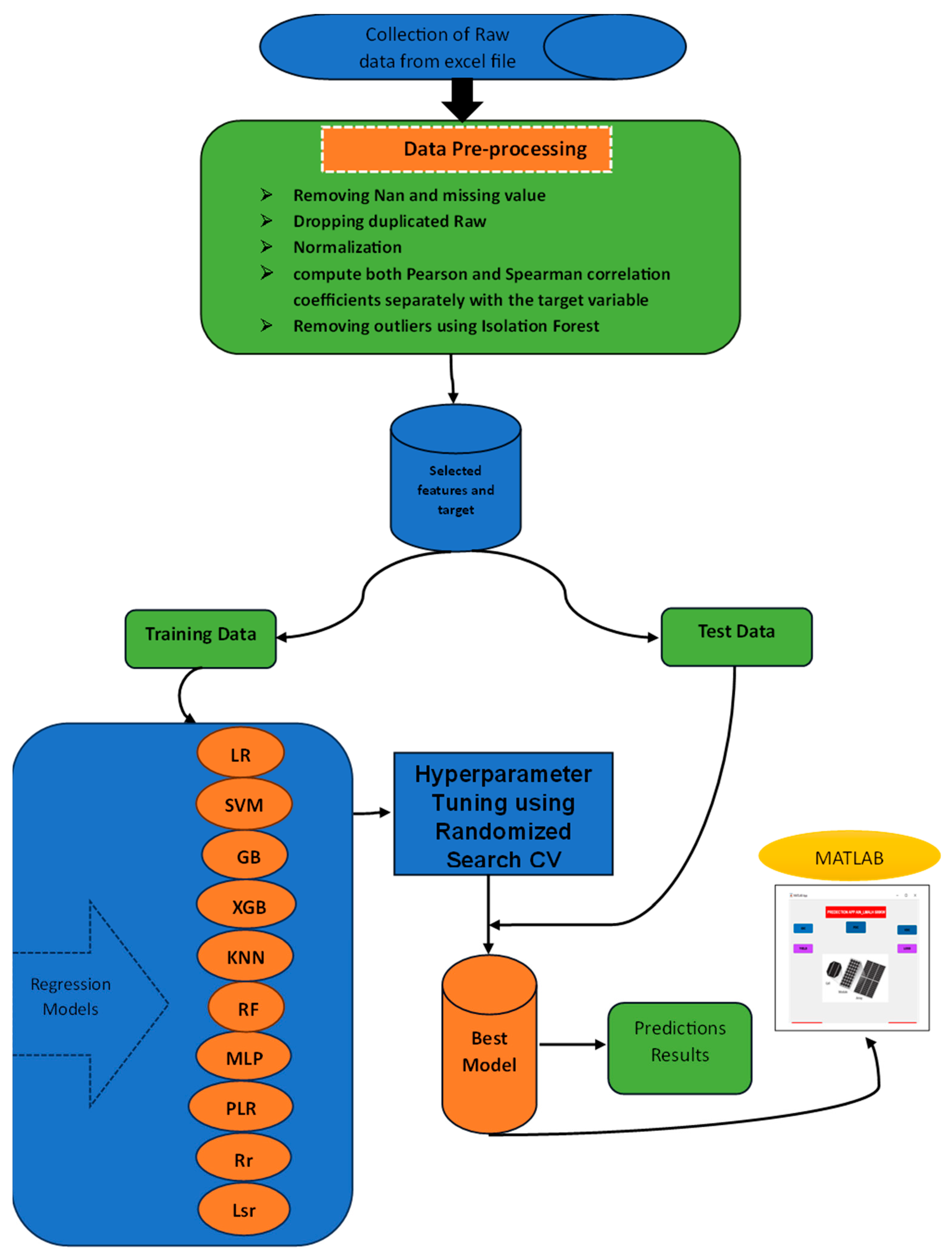
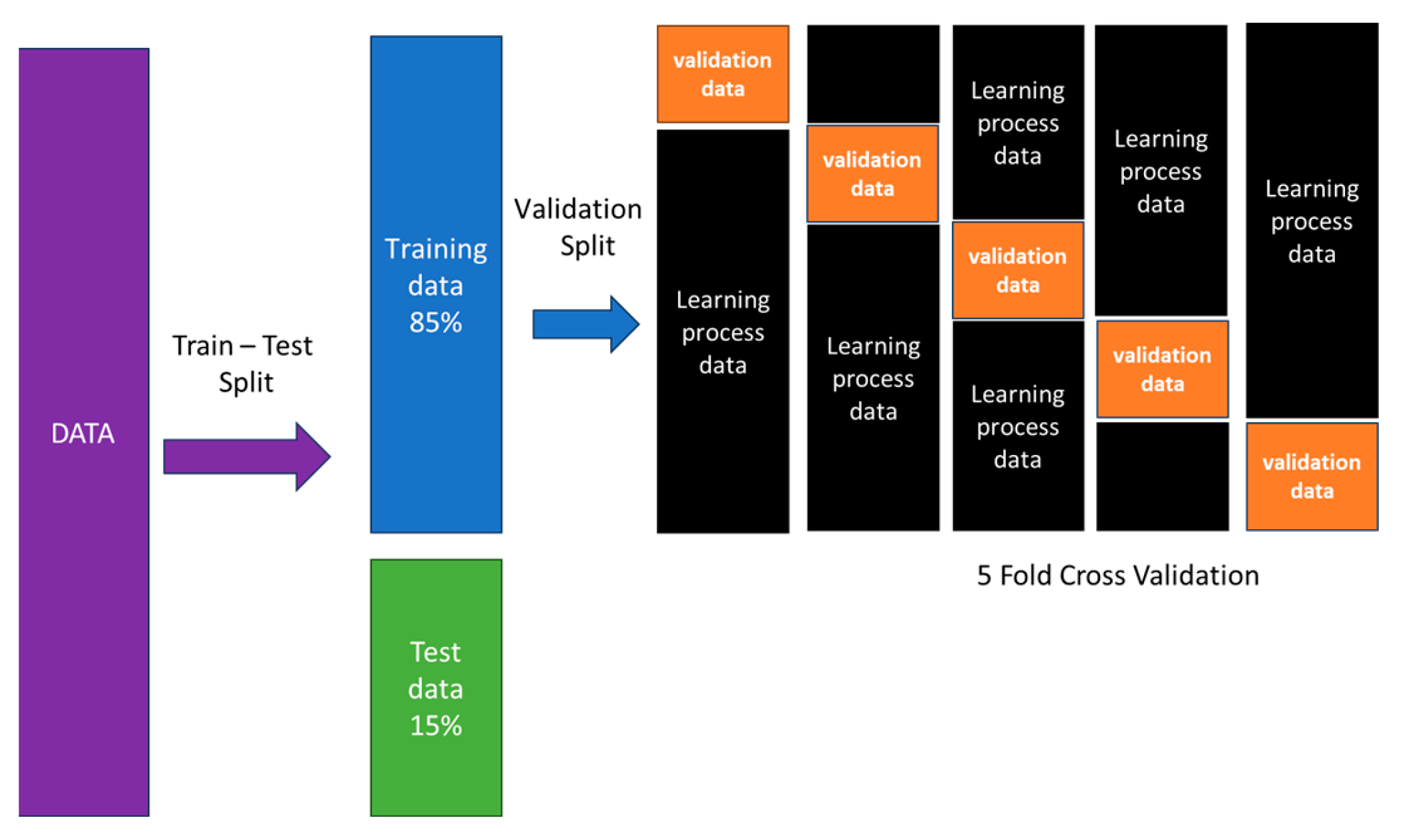
The methodology framework illustrated in Figure 4 guides the approach used. Data collection and preprocessing are initially set, including database exploration and normalization, followed by data segmentation into training and testing sets. In the modeling phase, the objective is to train the chosen algorithms using the training data until a satisfactory model is obtained. To achieve this goal, a Randomized Search algorithm is applied to identify the best hyperparameters for the best-performing model. Finally, the last stage entails evaluating the models using testing data and calculating estimation errors. Then, the best model, along with its scaler, is saved. Additionally, k-fold cross-validation is incorporated in the training process with a fold size of 5 to enhance the robustness of the evaluations.

Hyperparameters are parameters set before learning begins, influencing a model’s performance. Their adjustability directly impacts model effectiveness. Finding optimal hyperparameters involves trying various combinations. Over time, several approaches, like Grid Search and Random Search, have emerged for hyperparameter optimization. Grid Search, a traditional method, systematically explores a subset of the hyperparameter space through a complete search like the one used in previous work [43,44]. It is evaluated using various performance metrics, commonly employing cross-validation on the training data. The Random Search Algorithm, known as the Monte Carlo method or stochastic algorithm [45], operates by iteratively sampling parameter settings from a specified distribution [46], evaluating the model using cross-validation. In contrast to Grid Search, Random Search does not test all parameter values but samples several settings. Random Search performs more efficiently than Grid Search, as it avoids allocating excessive trials for less important dimensions to optimize the hyperparameters for all used models [47]. This research employs hyperparameter tuning through a Randomized Search algorithm. The Randomized Search CV function from the sci-kit-learn library is implemented for this purpose [48]. The Randomized Search CV function randomly selects hyperparameters and evaluates the results. Evaluation is conducted using cross-validation, where the data is divided into two subsets: the learning process data and the validation data. Thus, this study utilizes 5-fold cross-validation to obtain a robust model. The fundamental concept of cross-validation is to split data into two or more subsets, with one subset used to train the model and the other used for testing the model’s accuracy. K-fold cross-validation is the most typical kind of cross-validation. The data are randomly partitioned into k-equal subgroups, or folds, for k-fold cross-validation. The model is tested on the last fold after being tested on k-1 folds. This process is repeated k times so that each fold is used as a testing set once. The results from each fold are then averaged to produce an overall performance estimate. Figure 5 presents the process of using the cross-validation technique with 5-fold cross-validation.

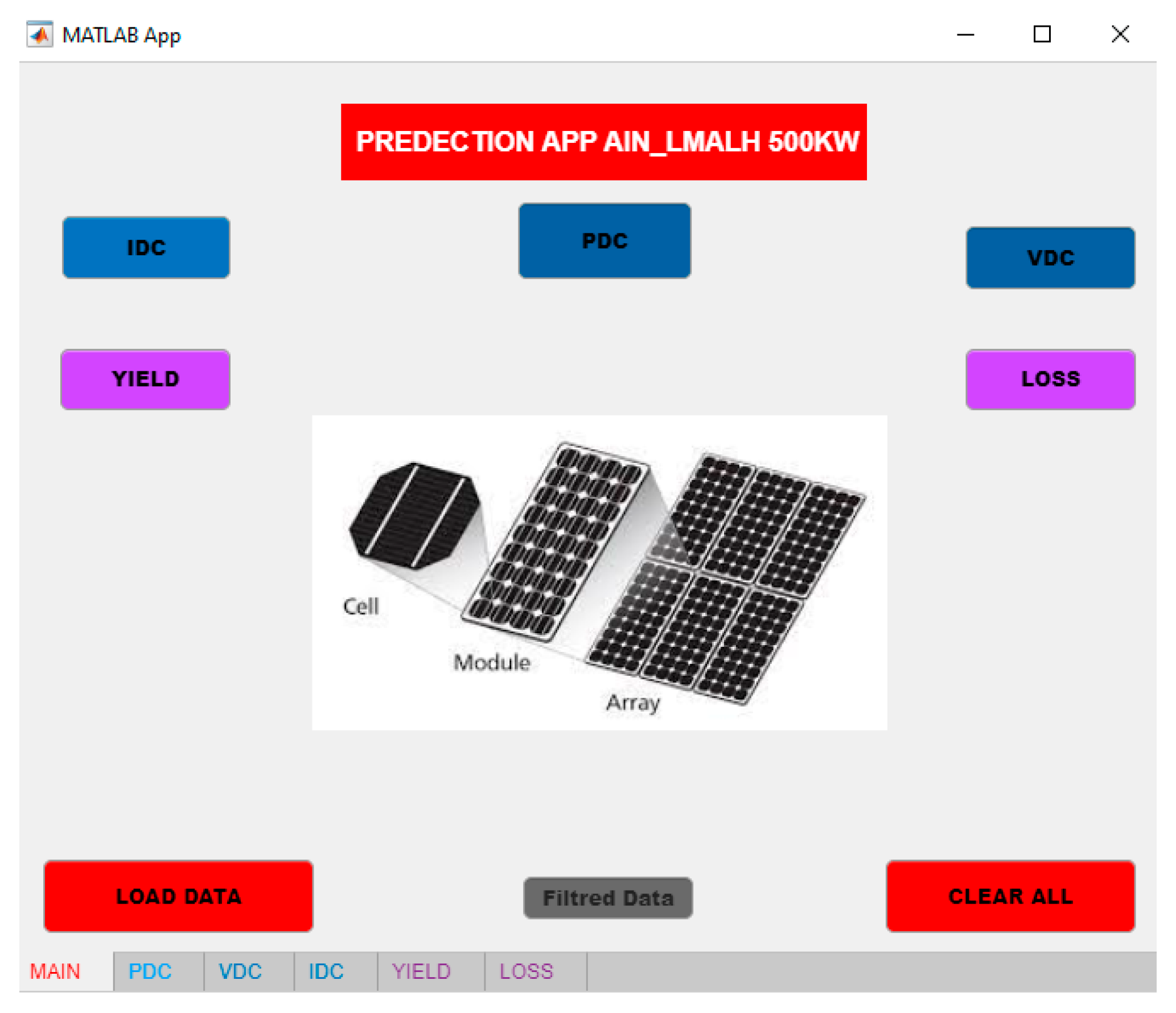
In predictive analytics for power systems, the fusion of Python-based machine learning models with MATLAB’s versatile application framework (App Designer) heralds a new era of efficiency and accuracy. The central focus of this work is the design and implementation of a user-friendly MATLAB application tailored for power prediction tasks. The application interface is created using MATLAB’s intuitive App Designer tool, allowing easy interaction and seamless integration with underlying algorithms. The application will enable users to input relevant data, select prediction parameters, and visualize measured and predicted results in real-time.

Key features of the developed application include the following:

Tab-Based Interface: The application is organized into tabs corresponding to different prediction tasks, such as predicting the power demand, voltage, and current.

Interactive Controls: Users can interact with various components such as buttons, state buttons, and toggle buttons to initiate prediction tasks and customize parameters.

Visualization Tools: Graphical representations, including UI Axes components, facilitate the visualization of measured and predicted data, aiding in the analysis and interpretation of results.

Export Functionality: The application allows users to export prediction results for further analysis or integration with external systems.

Streamlined Integration: Use the generated Excel file from the PV station directly for real-time prediction without any preprocessing required.

The designed MATLAB application offers a user-friendly interface with distinct tabs catering to various prediction types such as PV power generation (P_DC), PV voltage generation (VDC), PV current generation (IDC), yield, and loss calculations, as shown in Figure 6.

Each tab in the interface is meticulously crafted with intuitive functionality. It features clear visualization through UI Axes and streamlined operations with buttons for tasks like clearing data, triggering predictions, and exporting results.

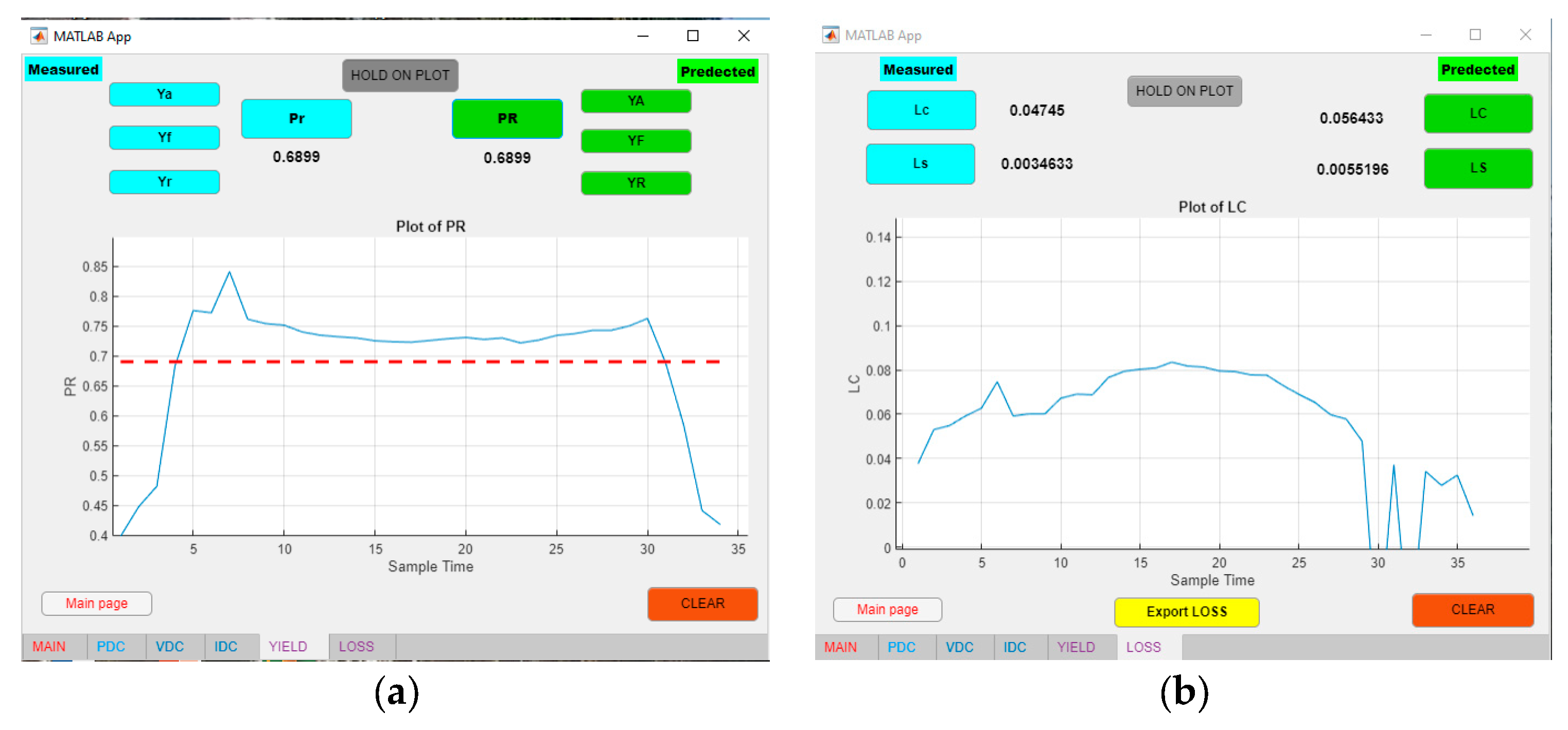
Additionally, in the yield tab and loss tab, the following calculations are performed:

Reference Yield: Yr for measured or actual, and YR for predicted.

This is when the sun must be shining with G0 = 1 kW/m² to radiate the energy Ht to the PV array of the PV module.

Reference Yield = Ht/G₀

(12)

Array Yield: Ya for measured or actual, and YA for predicted. It indicates when the PV system needs to work at the nominal power of the PV array P0 to produce the output DC energy E_DC.

Array Efficiency = E_DC/P₀

(13)

Final Yield: Yf for measured or actual, and YF for predicted. It is the time that the PV system needs to operate at the nominal power of the PV array P₀ to produce the output AC energy E_AC.

Final Yield = E_AC/P₀

(14)

System Losses: Ls for measured or actual, and LS for predicted.

System Losses = Array Efficiency − Final Yield

(15)

Array Capture Losses: Lc for measured or actual, and LC for predicted.

Array Capture Losses = Reference Yield − Array Efficiency

(16)

Performance Ratio: PR for measured or actual, and PR for predicted.

Performance Ratio = (Final Yield/Reference Yield) × 100

(17)

The performance ratio represents the ratio between the effective energy E_AC and those generated from an ideal, lossless PV installation assuming a 25 °C solar cell temperature with the same radiation level. Figure 7 shows the evaluation of the performance ratio and losses.

The “hold on plot” button enables users to maintain the UI Axes, allowing for the simultaneous plotting of two or more graphs for comparison purposes and enhancing accessibility.

Whether it involves predicting P_DC, I_DC current, analyzing V_DC voltages, or calculating losses, this MATLAB application allows users to integrate machine learning models seamlessly. This facilitates informed decision-making and optimizes performance in power system management.

3. Results

This section presents the results obtained along with the datasets used, showcasing the prediction outcomes of the PV system generation under various weather conditions. Furthermore, the results obtained from the MATLAB application are depicted in separate visualizations.

These results represent the performance metrics for different regression models across P_DC datasets. Figure 8 compares the measured and predicted PDC plots using Random Forest, MLP, and k-Nearest Neighbors, and Figure 9 compares the measured and predicted P_DC plots using RF.

Figure 10 and

Table 4. Comparative analysis of machine learning algorithms for predicting PV Power outputs.

Models	RMSE (Kw)	NRMSE	MAE (Kw)	R-Squared	IAE (Kw)	SDD (Kw)
Polynomial Regressor	26.5718	0.0563	9.7971	0.9347	9.7968	26.57
Random Forest	21.02	0.048	7.40	0.968	7.40	21.01
SVR	27.1202	0.0574	7.6380	0.9319	7.6377	26.91
MLP	25.4615	0.0539	9.2456	0.9400	9.2466	25.4533
Gradient Boosting	23.1536	0.0510	7.9418	0.9504	7.9434	23.1517
Linear Regression	27.9645	0.0592	10.5077	0.9276	10.5085	27.9614
k-Nearest Neighbors	25.2593	0.0535	7.7948	0.9409	7.7942	25.2444
Ridge Regressor	27.9648	0.0592	10.5085	0.9276	10.5093	27.9616
Lasso Regressor	28.0196	0.0593	10.4993	0.9273	10.4999	28.0167
XGBoost Regressor	24.0614	0.0510	7.6352	0.9464	7.6349	24.0536

show the comparative analysis of machine learning algorithms for predicting PV power outputs. As seen in the figure, Random Forest emerges as a top-performing model across all metrics, boasting an RMSE of 21.02 kW, an NRMSE of 0.048%, an MAE of 7.40 kW, an R-squared (R²) of 0.968, an IAE of 7.40 kW, and an SDD of 21.01 kW, indicating its superior predictive accuracy and robustness. Conversely, the Polynomial regressor exhibits higher errors across the board, with an RMSE of 26.5718 kW and an R-squared (R²) value of 0.9347. While SVR demonstrates competitive performance, it falls slightly behind Random Forest with an RMSE of 27.1202 kW and an R-squared (R²) value of 0.9319. MLP and k-Nearest Neighbors perform moderately well, but they are surpassed by Gradient Boosting, which achieves an RMSE of 23.1536 kW and an impressive R-squared (R²) value of 0.9504. Linear regression, Ridge regressor, and Lasso regressor display higher errors and lower R-squared (R²) values than the top-performing models. Finally, XGBoost regressor delivers strong results, with an RMSE of 24.0614 kW and an R-squared (R²) value of 0.9464, further highlighting the model’s predictive capability. These findings suggest that leveraging Random Forest or XGBoost regressor models would be most beneficial for accurate predictions of PV power outputs, offering superior predictive capabilities over alternative algorithms.

The same work and methodology used for the P_DC dataset are applied to I_DC and V_DC. Additionally, a filter to exclude all values where the PV generator was not working for better training performance is included for the VDC dataset.

Table 5. Optimization results and performance evaluation of machine learning models for power distribution predictions.

Dataset	Parameter	Value
PDC	Best Parameters	{‘max_depth’: 20, ‘min_samples_leaf’: 2, ‘min_samples_split’: 2, ‘n_estimators’: 200}
	Best RMSE	21.02 kW
	NRMSE	0.05%
	MAE	7.40 kW
	R-squared (R2)	0.968
	IAE	7.40 kW
	SDD	21.01 kW
IDC	Best Parameters	{‘max_depth’: 20, ‘min_samples_leaf’: 2, ‘min_samples_split’: 2, ‘n_estimators’: 200}
	Best RMSE	24.499 kW
	NRMSE	0.05%
	MAE	8.089 kW
	R-squared (R2)	0.957
	IAE	8.076 kW
	SDD	24.28 kW
VDC	Best Parameters	{‘max_depth’: 30, ‘min_samples_leaf’: 2, ‘min_samples_split’: 2, ‘n_estimators’: 150}
	Best RMSE	11.691 kW
	NRMSE	0.06%
	MAE	7.424 kW
	R-squared (R2)	0.953
	IAE	7.417 kW
	SDD	11.685 kW

shows the results obtained for P_DC, I_DC, and V_DC datasets, presenting various metrics and relevant parameters. The results presented in Figure 11 and Figure 12 pertain to the Random Forest, MLP, and k-Nearest Neighbors predictions across the test datasets for IDC and VDC, respectively.

Figure 13 compares the actual and predicted values for V_DC by using RF. The same information is presented in Figure 14 for I_DC.

The results obtained from the MATLAB app, utilizing the Random Forest regressor-trained models for prediction under different weather conditions for P_DC, I_DC, and VDC, respectively, are depicted in Figure 15, Figure 16 and Figure 17 for a clear day and in Figure 18, Figure 19 and Figure 20 for a cloudly day.

The results obtained from the MATLAB application utilize the trained Random Forest regressor models, demonstrating significant success in predicting PV system generation under various weather conditions.

4. Discussion

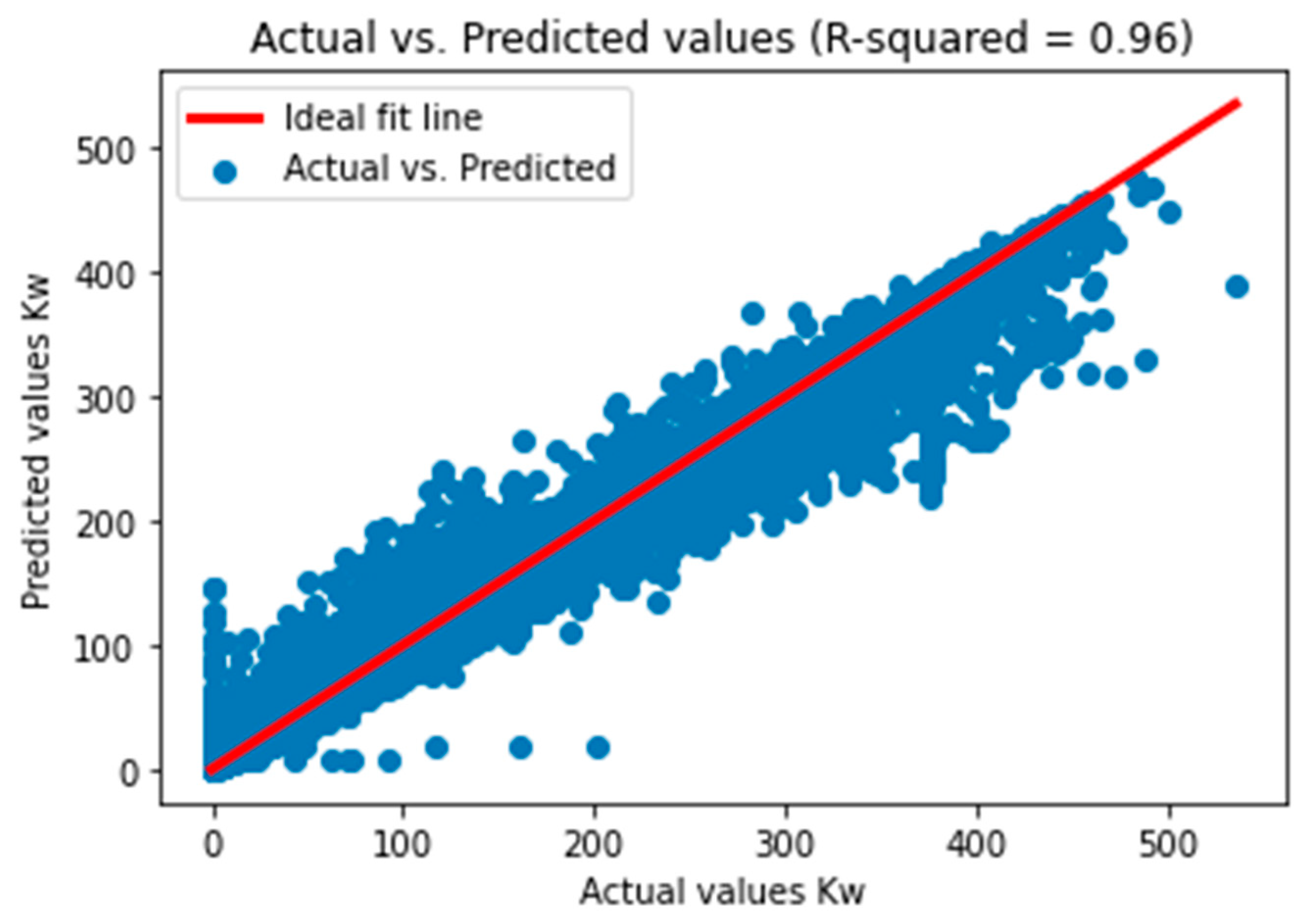
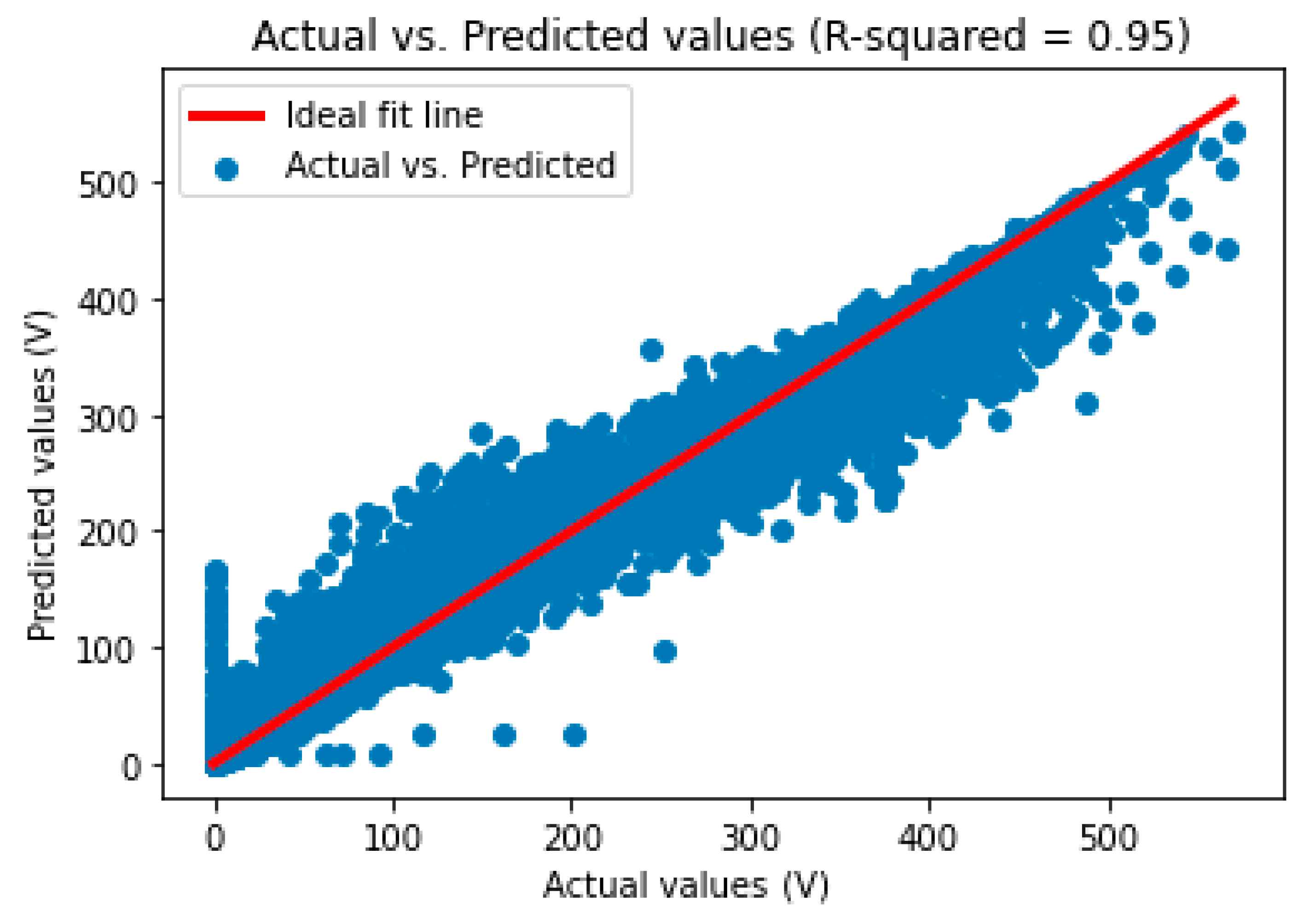
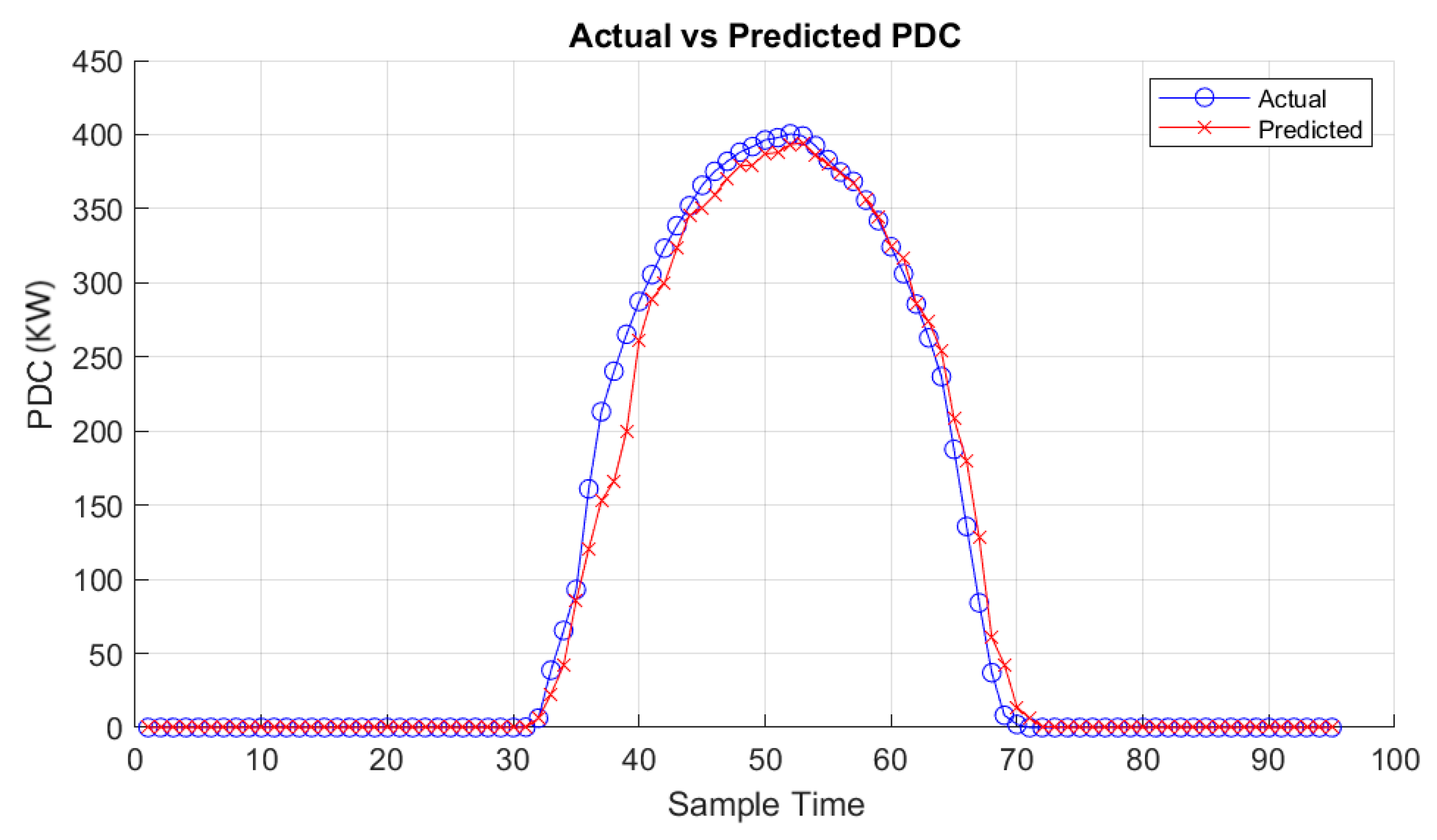
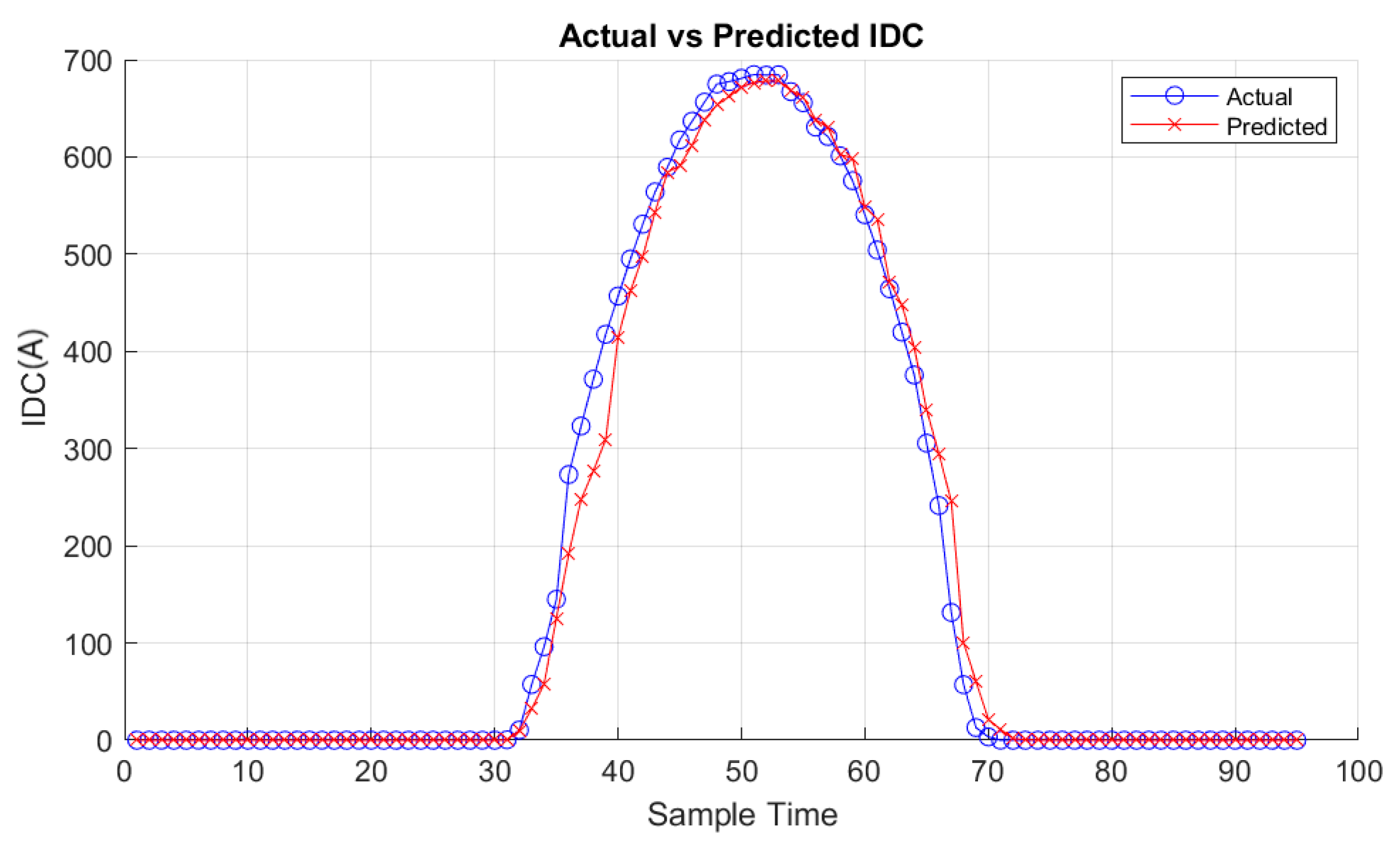
The analysis carried out showcases the effectiveness of the Random Forest regressor model in capturing the intricate relationships between environmental variables and PV system performance. For the PDC dataset, the Random Forest model achieved compelling performance with optimal parameters {‘max_depth’: 20, ‘min_samples_leaf’: 2, ‘min_samples_split’: 2, ‘n_estimators’: 200}, resulting in a best RMSE of 21.02 kW, NRMSE of 0.048%, MAE of 7.40 kW, and IAE of 7.4076 kW; an impressive R-squared value of 0.968; and an SDD of 21.01 kW. Similarly, for IDC prediction, the Random Forest model, using the same parameters, yielded promising results with a best RMSE of 24.499 kW, NRMSE of 0.0476%, MAE of 8.089 kW, R-squared (R²) of 0.957, IAE of 8.076 kW, and SDD of 24.28 kW, effectively capturing the complex nature of IDC despite fluctuations influenced by various factors. Additionally, for the VDC dataset, the Random Forest model, optimized with {‘max_depth’: 30, ‘min_samples_leaf’: 2, ‘min_samples_split’: 2, ‘n_estimators’: 150}, exhibited superior performance, achieving an RMSE of 11.691 kW, NRMSE of 0.060%, MAE of 7.424 kW, R-squared (R²) of 0.953, IAE of 7.417 kW, and SDD of 11.685 kW. The analysis revealed that each regression model exhibited varying degrees of performance. The Random Forest model demonstrated competitive performance, with low RMSE, NRMSE, MAE, IAE, and SDD and a high R² score. SVR and MLP showed moderate performance but may benefit from further optimization or feature engineering. MLP exhibited flexibility with different activation functions and hidden layer sizes but required careful tuning to avoid overfitting. Linear regression, Ridge regressor, and Lasso regressor showed less competitive performance. Conversely, k-Nearest Neighbors, Gradient Boosting, Polynomial regressor, and XGBoost regressor demonstrated moderate to strong predictive capability.

When considering the utilization of machine learning for PV power estimation, comparing results with those of previous studies in the literature is valuable. For instance, in [49], a season-customized artificial neural network (ANN) was proposed to forecast the PV power of a system in Italy, achieving an average Mean Absolute Error (MAE) of 17 W. Similarly, the work in [50] reported average MAE values of 33.63 W for Support Vector regression (SVR) and 50.69 W for ANN estimation of PV power output in Malaysia.

Furthermore, various methodologies have been employed to identify relevant features crucial for accurate prediction. One approach integrated correlation heatmaps with Bayesian optimization techniques, yielding an R-squared of 0.8917 when utilizing Long Short-Term Memory (LSTM) models with 41 diverse features [51]. Another study utilized wavelet transformation-based decomposition techniques with various regression models, including WT-LSTM, LSTM, Ridge regression, Lasso regression, and elastic-net regression, achieving a high R-squared of 0.9505 [52]. Moreover, tree-based feature importance and principal component analysis were employed in a separate study with ANN and Random Forest models [53]. This research emphasized the significance of temperature, humidity, day, and time in predicting PV output, resulting in an R-squared value of 0.9355. Additionally, traditional regression models such as Linear regression, SVR, K-Nearest Neighbors regression, Decision Tree regression, Random Forest regression, Multi-layer Perceptron, and Gradient Boosting regression were assessed using Pearson’s correlation and heatmap analyses, considering factors like hour, power, irradiance, wind speed, ambient temperature, and panel temperature. Among these models, Random Forest regression demonstrated the highest R-squared of 0.96, highlighting its effectiveness in predicting PV output power. These findings underscore the importance of feature selection methodologies in capturing pertinent features crucial for accurate prediction and analysis in PV systems [54].

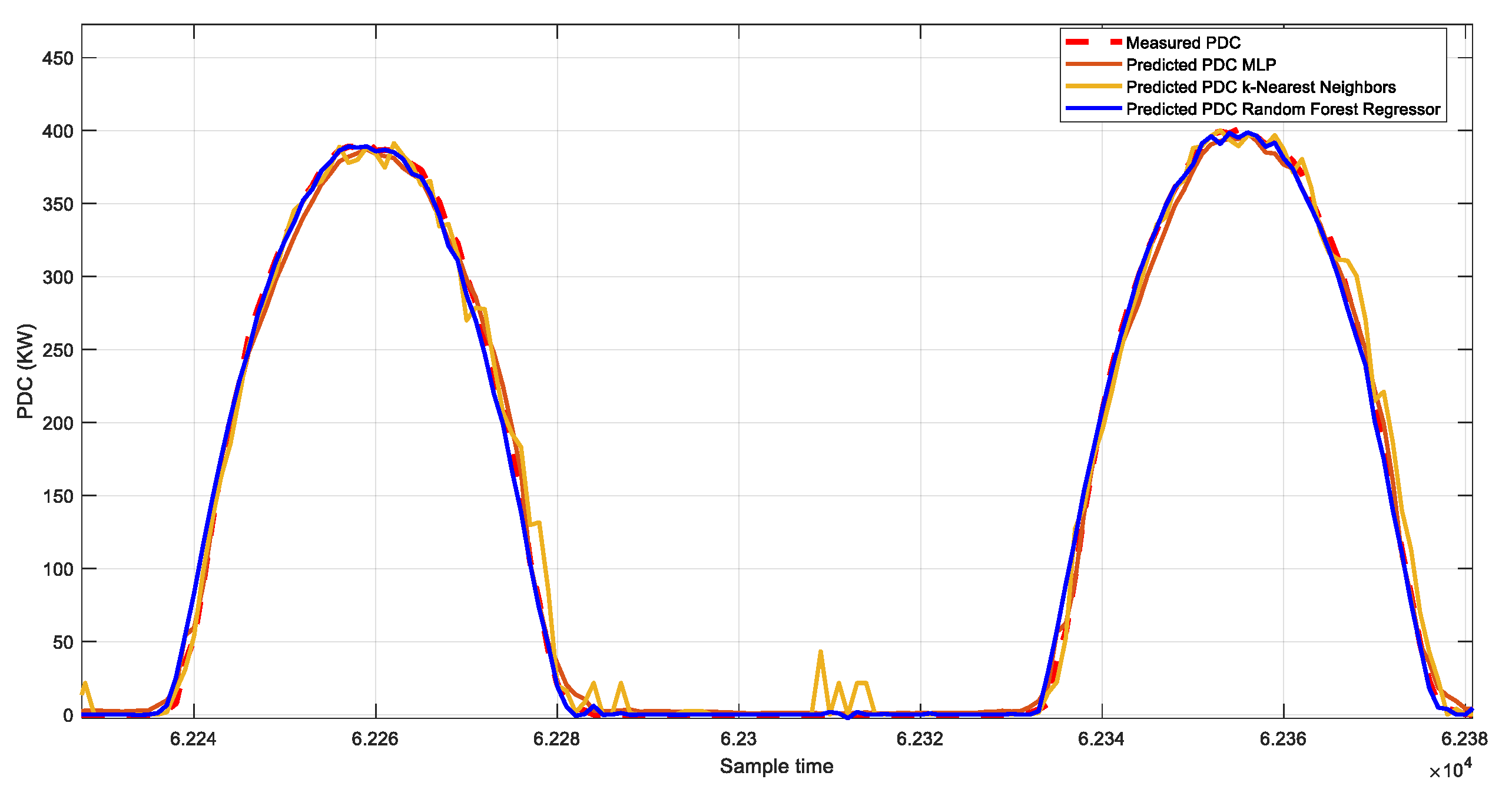
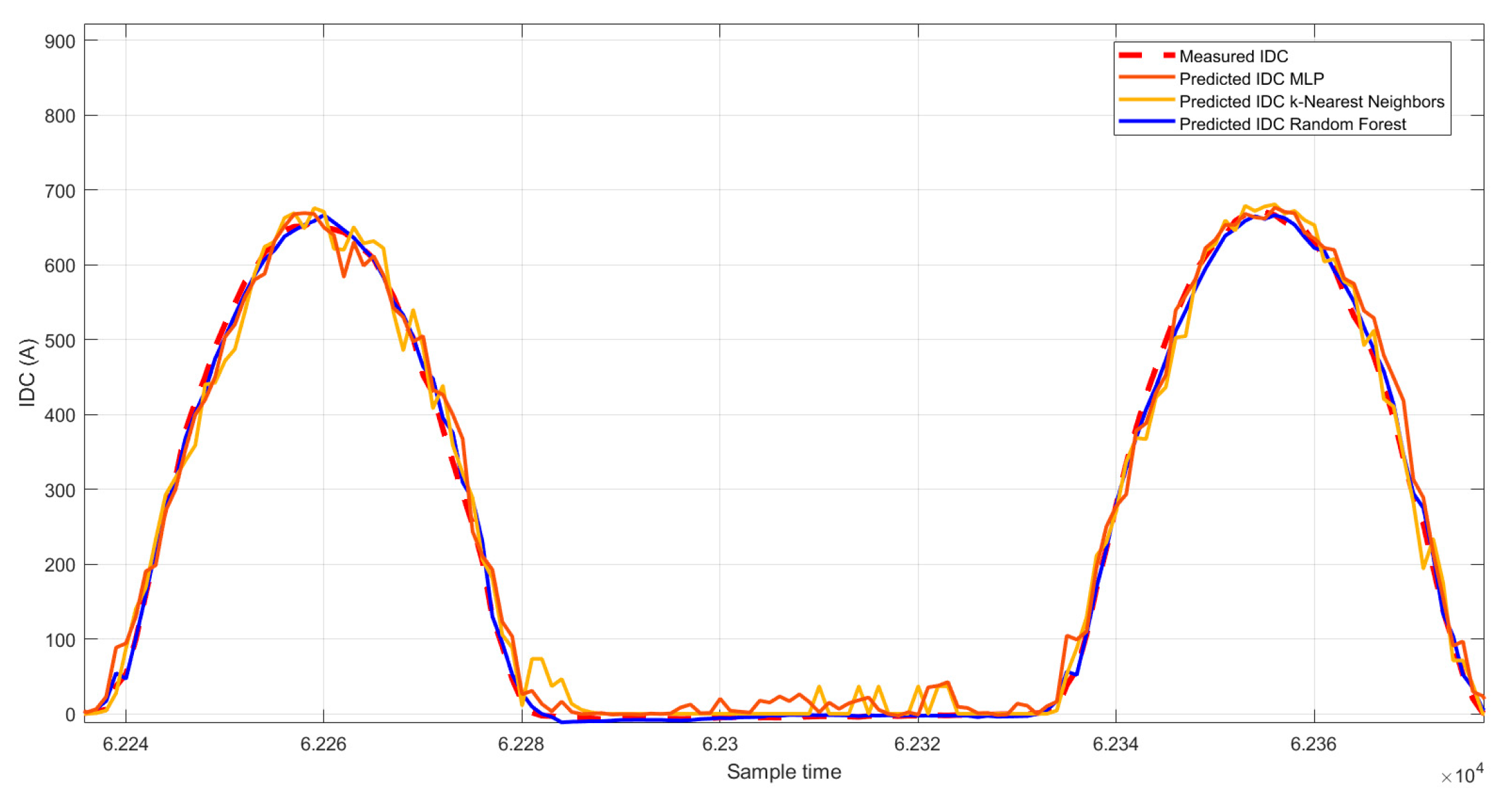
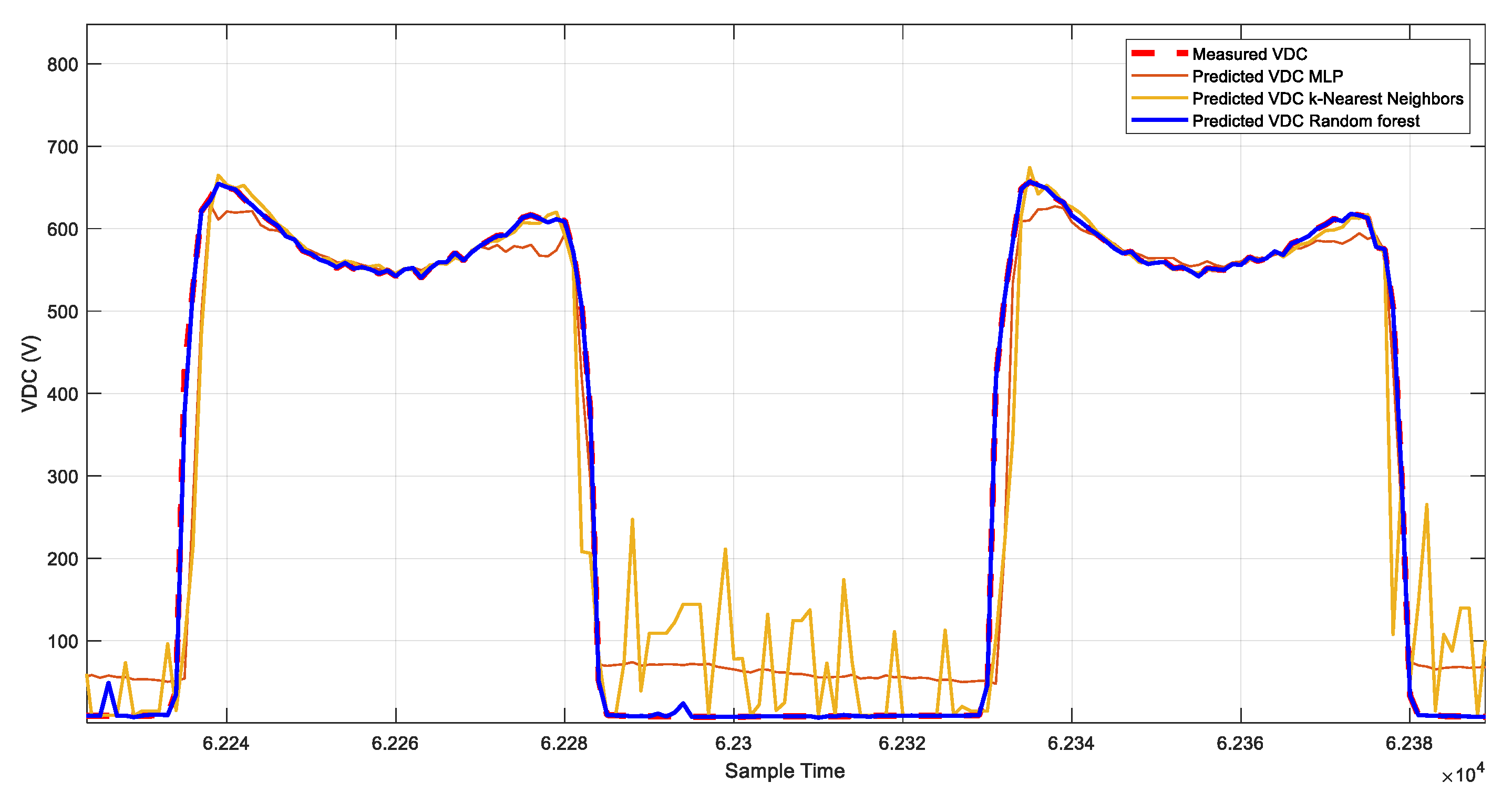
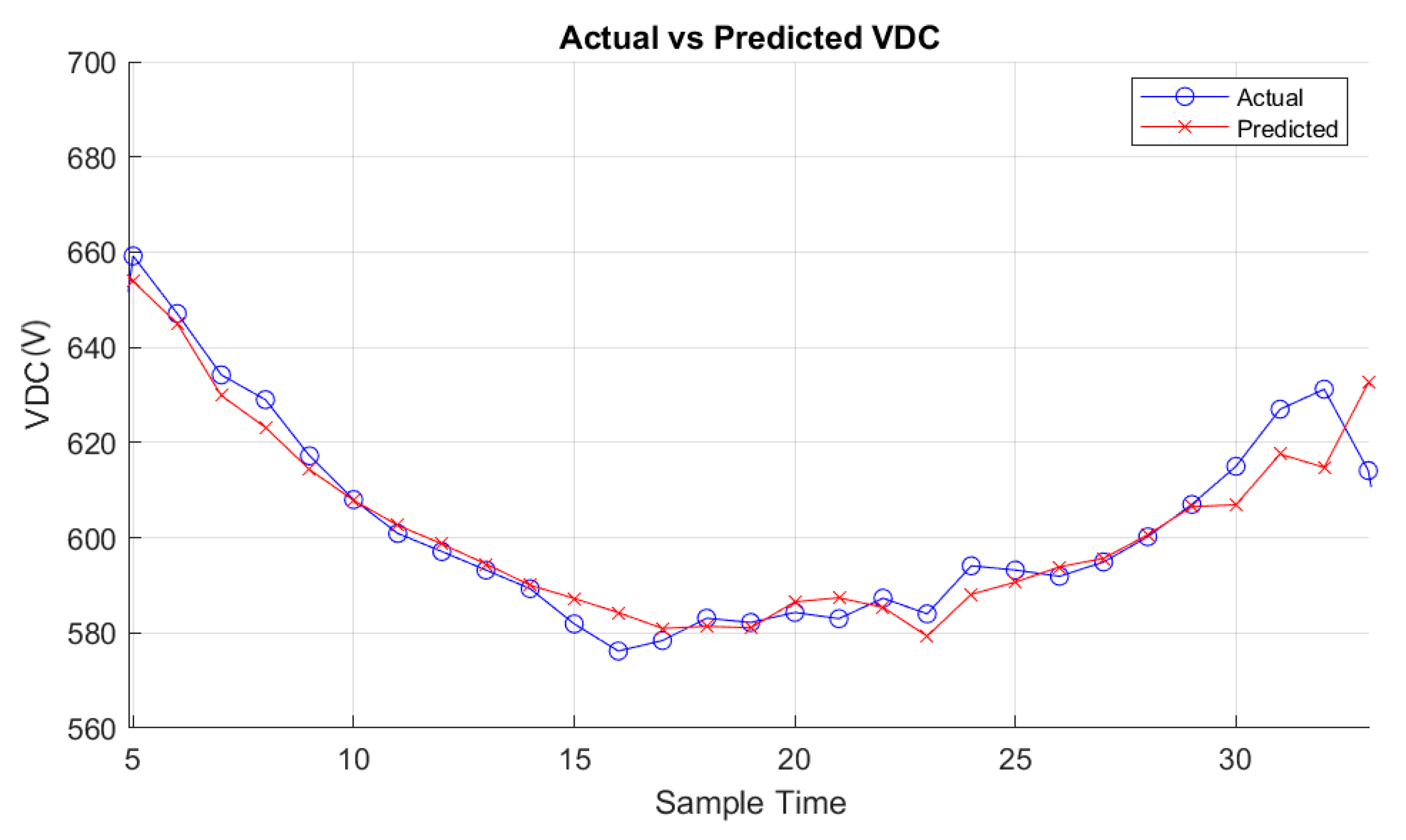
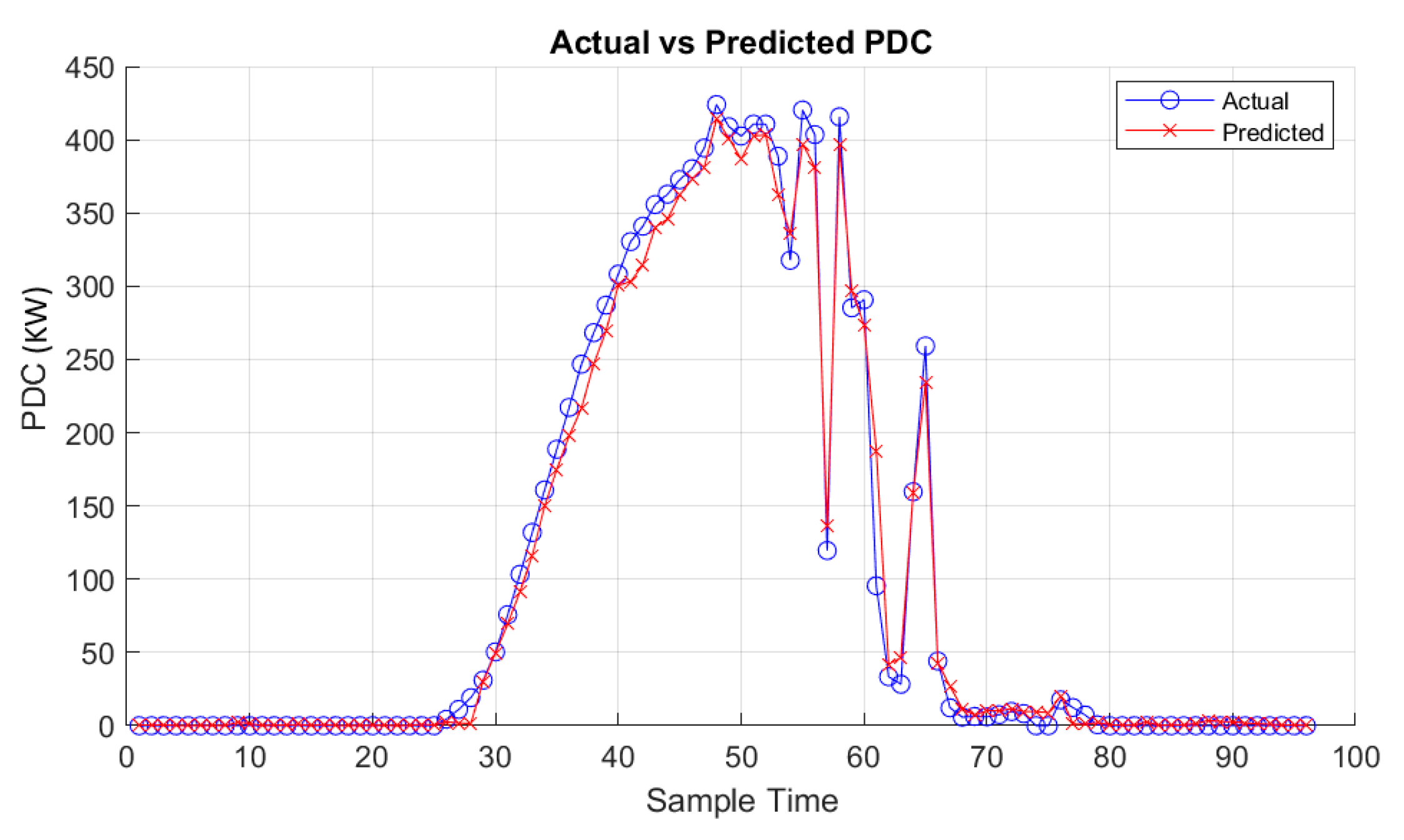
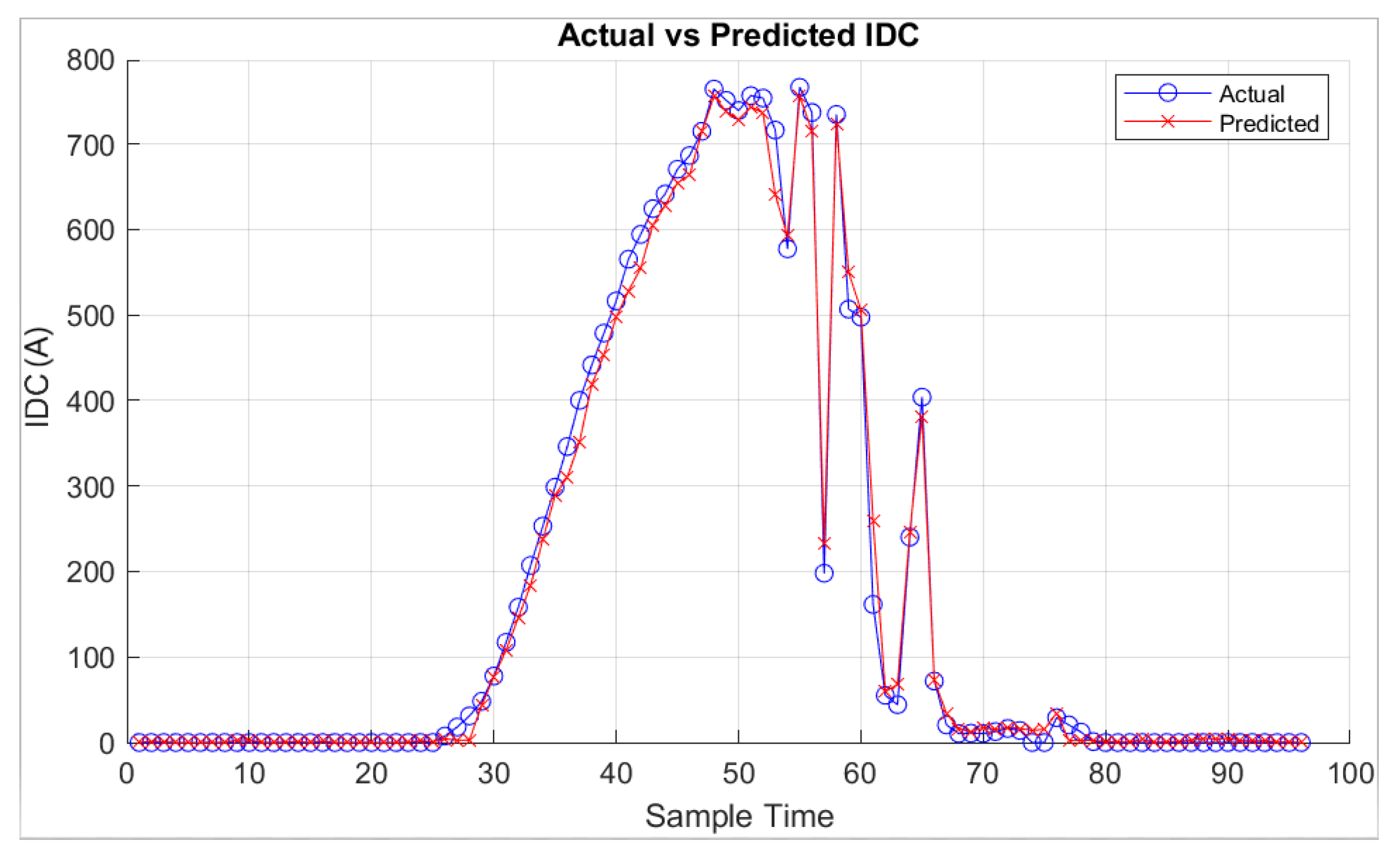
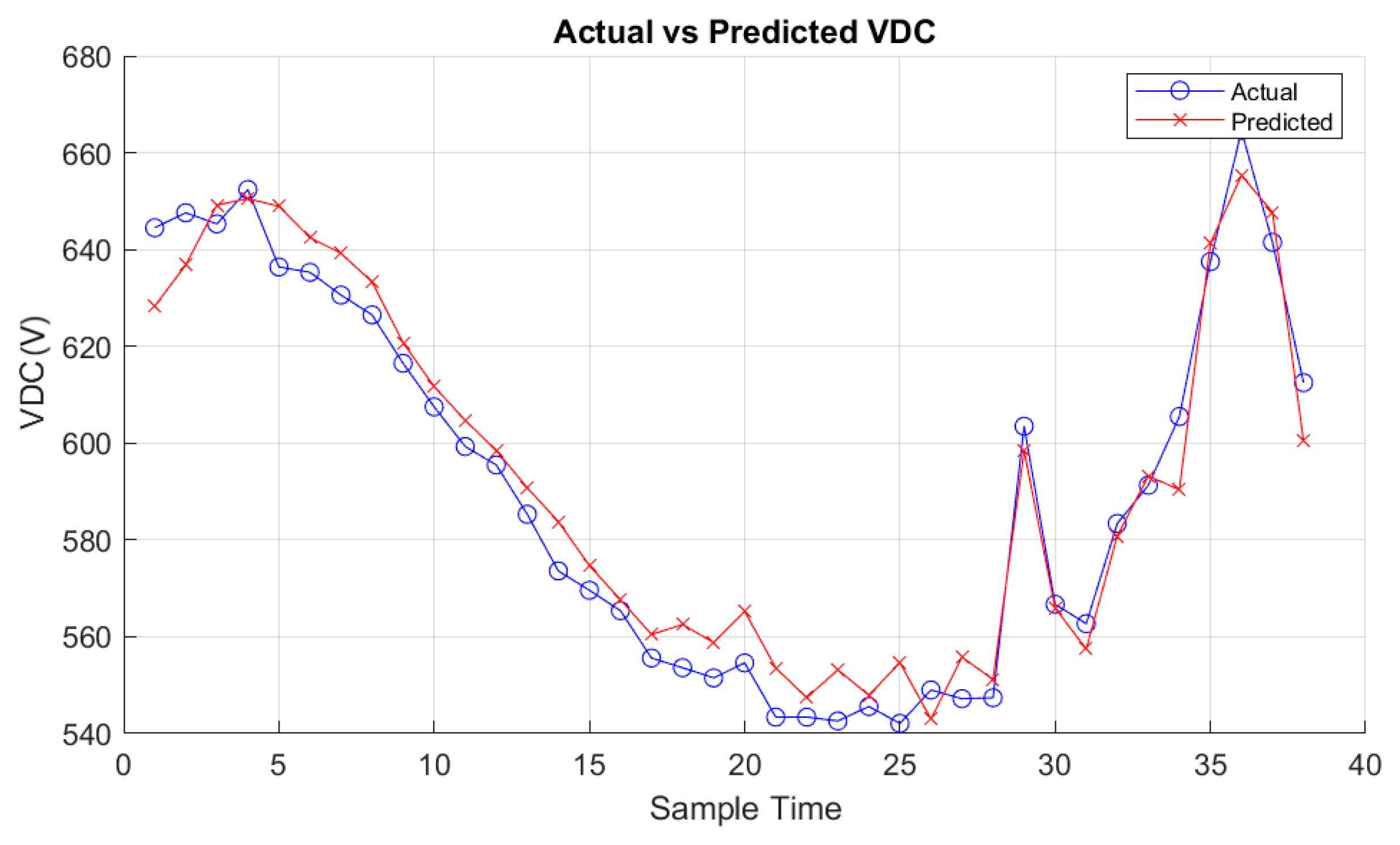
On the other hand, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20 vividly illustrate the predictive outcomes for two distinct days: one characterized by cloudy weather and the other by clear skies. One of the notable advantages of the approach lies in the meticulous selection of relevant features, achieved through Pearson and Spearman correlation analyses. The method ensures a comprehensive understanding of their relationships by computing both Pearson and Spearman correlation coefficients between each environmental variable and the target PV system generation. This approach enhances model interpretability and performance by incorporating linear and monotonic correlations, capturing various aspects of the data’s behavior. Additionally, the integration of Isolation Forest for outlier detection enables robust data preprocessing, effectively filtering out anomalies and improving model generalization. Moreover, implementing Randomized Search CV facilitates efficient hyperparameter tuning, with Random Forest emerging as the best-performing model. Random Forest’s ensemble nature and ability to handle nonlinear relationships make it particularly adept at capturing the complex dynamics of PV system generation. Its versatility, scalability, and resilience to overfitting further underscore its suitability for this application. Users can efficiently manage PV systems by seamlessly integrating the trained Random Forest model into the MATLAB application, leveraging accurate predictions to optimize resource allocation and decision-making.

5. Conclusions

This study has demonstrated the efficiency of employing machine learning techniques for accurately predicting PV power generation. Through meticulous data preprocessing, feature selection, and model evaluation, Random Forest is identified as the top-performing model for estimating power output from PV plants located in Algeria. Leveraging historical data and computational methods, our approach not only achieves impressive performance metrics such as a low RMSE of 19.413 and high R-squared value of 0.968 but also offers valuable insights into the significance of feature selection and outlier detection in enhancing prediction accuracy.

Furthermore, in addition to the models’ evaluation, integrating the best-performing model into a MATLAB application for real-time predictions is proposed. This step not only enhances the usability and accessibility of predictive modeling in renewable energy but also lays the groundwork for practical implementation in addressing energy demands and promoting sustainability.

One potential direction to further enhance prediction accuracy and robustness is the exploration of DEPP learning and hybrid techniques. Additionally, incorporating more weather data, such as cloud cover, could improve the predictive capabilities of the models, especially in regions with variable weather patterns like Algeria. Furthermore, extending this research to consider integrating energy storage systems, such as batteries, into the predictive models could facilitate better management of intermittent renewable energy sources like solar power. By forecasting both PV power generation and energy storage levels, operators can optimize energy dispatch strategies and improve grid stability.

As we move towards a future increasingly reliant on clean energy solutions, integrating advanced computational methods holds immense promise in revolutionizing the renewable energy sector.