Enhanced Thermal Modeling of Electric Vehicle Motors Using a Multihead Attention Mechanism

Abstract

The rapid advancement of electric vehicles (EVs) accentuates the criticality of efficient thermal management systems for electric motors, which are pivotal for performance, reliability, and longevity. Traditional thermal modeling techniques often struggle with the dynamic and complex nature of EV operations, leading to inaccuracies in temperature prediction and management. This study introduces a novel thermal modeling approach that utilizes a multihead attention mechanism, aiming to significantly enhance the prediction accuracy of motor temperature under varying operational conditions. Through meticulous feature engineering and the deployment of advanced data handling techniques, we developed a model that adeptly navigates the intricacies of temperature fluctuations, thereby contributing to the optimization of EV performance and reliability. Our evaluation using a comprehensive dataset encompassing temperature data from 100 electric vehicles illustrates our model’s superior predictive performance, notably improving temperature prediction accuracy.

1. Introduction

In recent years, the rapid development of electric vehicles has significantly enhanced the importance of motor temperature control and monitoring [1,2]. An efficient and reliable motor temperature management system not only extends the life of the motor but also ensures the safety and efficiency of electric vehicle operation [3]. However, the variability and complexity of driving conditions pose considerable challenges to the accuracy and reliability of motor temperature prediction [4].

In our study, we focus on estimating the temperature of a single component of the motor, specifically the stator temperature of the rear drive motor. The stator temperature is a critical parameter, as it directly impacts the motor’s performance and longevity. Monitoring this temperature allows for proactive cooling and ensures the motor operates within safe thermal limits. Measuring the stator temperature is a common practice in the industry due to its accessibility and the significant role it plays in motor health. In the prediction of the motor temperature, classical methods, such as lumped-parameter thermal networks [5,6], are capable of calculating the temperature of the internal elements of motors. However, these methods require expertise and may lack acceptable accuracy [7]. In [8], two deep neural networks were modeled using a conventional neural network and long short-term memory units to predict the temperature. The method achieves a 13% mean average performance improvement compared to existing state-of-the-art solutions, which shows the great potential of the deep neural network technique in motor prediction. In [9], a physical model-based machine learning method is proposed to predict the temperature of an electronic device in oil-gas exploration logging, which considers the impact of surrounding devices on the temperature of the electronic device. In [10], a deep learning method based on partition modeling is proposed to accurately reconstruct the temperature field of electronic equipment from limited observation. The partition modeling approach improves the reconstruction accuracy through shallow multilayer perceptron. However, the method is not self-adaptive and does not solve the temperature estimation of a region with large gradients well. In [11], a novel deep learning-based surrogate model, named parameters-to-temperature generative adversarial network, is proposed for generating high-quality temperature field images with various thermal parameters. This method shows high accuracy in generating temperature field images but may not generalize well to unseen thermal parameters or boundary conditions.

Inspired by the deep learning methodologies discussed in the literature review [12,13,14] and seeking to address the existing research gap in motor temperature prediction methods, this study introduces an innovative approach utilizing a multihead attention mechanism. The multihead attention mechanism introduces a novel neural network architecture that relies exclusively on an attention mechanism [15]. The proposed models employing this mechanism have demonstrated superior quality and increased parallelizability, significantly reducing training times. As a cornerstone of the transformer model architecture, this innovative mechanism has profoundly impacted numerous areas within natural language processing and beyond. Enabling the model to simultaneously process information from different representational subspaces at various positions has significantly enhanced the model’s interpretive capabilities [16]. The approach uses a multihead self-attention mechanism and a soft attention mechanism to heighten the focus on inherent feature information in the source text, enabling the precise identification of grammatical structures and semantic information. Reference [17] introduces a hybrid model, DNN-MHAT, combining a deep neural network with a multihead attention mechanism to tackle the challenges of high dimensionality. Tested on four review datasets and two Twitter datasets, the DNN-MHAT model achieves outstanding performance compared to state-of-the-art baseline methods. The integration of the multihead attention mechanism to more thoroughly learn sentiment information in texts is demonstrated in [18], where experiments on two Chinese short text datasets revealed that the MCNN-MA model achieves higher classification accuracy and a relatively low training time cost compared to other baseline models. Additionally, Ref. [19] proposes a novel multimodal sentiment analysis model based on the multihead attention mechanism, effectively enhancing performance on the Multimodal Opinion Utterances Dataset and the CMU Multimodal Opinion-level Sentiment Intensity corpus. By taking advantage of the multihead attention mechanism, this research introduces an innovative approach designed to enhance the predictive accuracy of motor temperature under diverse driving conditions and to improve the motor temperature prediction accuracy by analyzing the historical temperature data and the corresponding real temperature measurements, enhancing the reliability and safety of electric vehicle operation.

The structure of this article is organized as follows: Section 1 introduces the motor prediction methods and the multihead attention mechanism, drawing on a review of the relevant literature. Section 2 discusses the methodology, which encompasses feature engineering and model construction. Section 3 presents a case study that validates the proposed method. Finally, Section 4 concludes the article.

2. Methodology

In this section, we detail our method, from feature engineering to the construction of the model, highlighting our systematic approach to maximizing data utility. Starting with feature engineering, we meticulously identify key features from the data, laying the foundation for the model to accurately interpret patterns.

Moving to model construction, we apply a multihead attention model and techniques, emphasizing continuous refinement for precision, efficiency, and scalability. This iterative development, supported by feedback loops, enhances the model’s adaptability and accuracy.

2.1. Feature Engineering

The feature engineering can be divided into five parts:

• Feature selection;
• Driving segment division;
• Outlier data handling;
• Feature derivation;
• Data standardization.

Feature selection: Through rigorous expert analysis and a comprehensive literature review, we have delineated seven pivotal features that significantly influence motor temperature. The inlet water temperature and torque were meticulously chosen following expert insights, while the remaining quintet of features were extracted from scholarly research [20]. We have further distilled these features to capture the nuances of physical phenomena and to diminish the interference of data noise, encompassing amplitude, power, and cumulative indicators.

The table referenced as

Table 1. Key variables associated with the temperature of the motors.

Variable Name	Symbol
Motor speed	$v_{speed}$
Motor inlet water temperature	T
Actual current d-axis component	$i_d$
Actual current q-axis component	$i_q$
Actual voltage d-axis component	$u_d$
Actual voltage q-axis component	$u_q$
Load torque	m

succinctly outlines the key variables correlated with the temperature of the motors under investigation in this study. It is noteworthy that environmental temperature is excluded from our model. The task of securing precise and up-to-the-minute environmental temperature data is often fraught with challenges, especially amidst fluctuating and dynamic conditions. The vehicle’s sensors are predominantly engineered for the surveillance of internal systems rather than gauging external environmental conditions. However, the inlet water temperature serves as a surrogate for environmental temperature, offering a partial reflection of ambient conditions due to its susceptibility to the heat exchange dynamics between the motor and its surroundings. Our overarching ambition was to forge a model that is both straightforward and resilient, one that could yield accurate predictions utilizing data that are readily accessible from the vehicle’s systems. By concentrating on the variables that are most intimately connected to the motor’s thermal profile, we have endeavored to strike a harmonious balance between model complexity and the fidelity of its predictive capabilities. The selection of the remaining features was entrusted to a panel of experts with profound knowledge of electric motor operations and the sensor data gleaned from actual vehicle systems. Their expertise was instrumental in identifying features that are not only indicative of the motor’s thermal state but also pivotal to the predictive accuracy of our model. The discernment of these features was underpinned by a profound understanding of the influence each parameter wields over the thermal behavior of the motor. For instance, motor speed and current components are recognized for their direct bearing on heat generation, while voltage components shed light on energy conversion efficiency, which can have an indirect yet significant impact on temperature.

Driving segment division: This part is essential for focusing on relevant data; our methodology involves retaining data segments where the vehicle is operational. The model employs a multihead attention mechanism tailored for time-series data, where positioning information across different driving segments cannot be conflated. Therefore, retained signal segments indicate that the vehicle is powered on or in operation, including segments where the vehicle is stationary but powered up. Within each powered segment (typically featuring long intervals between them), segments are further divided based on whether the motor speed and torque are non-zero, ensuring continuity and fixed intervals between data points within each driving segment.

Outlier data handling: We employ robust methods to exclude data segments with potential sensor malfunctions or anomalies caused by external interference, enhancing the dataset’s quality. Given that the dataset originates from stored database records, sensor malfunctions or connectivity issues could lead to data loss, while electromagnetic interference or noise might introduce data anomalies. We exclude driving segments where any feature variable, excluding inlet water temperature, remains constant over 20 consecutive sampling points (approximately 1 min) or where the inlet water temperature is zero or constant over 200 points (approximately 10 min). In addition, we utilized the 3$\delta$ rule to eliminate outliers, calculated the mean $\mu$ and standard deviation $\delta$ of the data, and excluded driving segments where the data fell outside of the range of the mean plus or minus 3$\delta$.

Feature derivation: In order to enhance the accuracy of motor temperature predictions, this research emphasizes deriving new features with significant physical relevance or interpretability based on original characteristics. This includes creating features that represent the cumulative process of temperature changes and features aimed at reducing data noise. These derived features are crucial for capturing the physical processes affecting motor temperature, thereby facilitating more precise and interpretable temperature predictions. The derivation can be divided into five parts: (1) Current magnitude and voltage magnitude; (2) power-related characteristics; (3) interaction features; (4) smoothing features; (5) cumulative features.

• Current magnitude and voltage magnitude: The root sum square of the D-axis and Q-axis components for current and voltage are calculated as follows:

  $$i_s=\sqrt{i_d^2+i_q^2}$$

  (1)

  $$u_s=\sqrt{u_d^2+u_q^2}$$

  (2)
• Power-related features: These are used to represent the apparent power and effective power, respectively:

  $$S_{el}=1.5\times i_s\times u_s$$

  (3)

  $$P_{el}=i_d\times u_d+i_q\times u_q$$

  (4)

  $${\Delta }_p=S_{el}-P_{el}$$

  (5)
• Interaction features: The interaction between the current and motor speed is analyzed through the derived current magnitude feature, considering the vehicle’s speed as a modifying factor to assess the motor’s operational efficiency. Likewise, the interaction between power and motor speed is analyzed through the derived apparent power $S_{el}$:

  $$i_{sxw}=i_s\times v_{\mathrm{speed}}$$

  (6)

  $$S_{xw}=S_{el}\times v_{\mathrm{speed}}$$

  (7)
• Smoothing features: In order to reduce the influence of noise on each feature and highlight trend information, this study introduces the exponentially weighted moving average (EWMA) and standard deviation (EWMS). For each input parameter, X, these terms are computed at every timestep, t, and incorporated as derived features into the model (see Table 1):

  $${\mu }_t=\frac{{\sum }_{i=0}^t{\omega }_i{x}_{t-i}}{{\sum }_{i=0}^t{\omega }_i}$$

  (8)

  $${\sigma }_t=\frac{{\sum }_{i=0}^t{\omega }_i{(x_i-{\mu }_t)}^2}{{\sum }_{i=0}^t{\omega }_i}$$

  (9)

  where ${\omega }_i={(1-\alpha )}^i$ with $\alpha =2/(s+1)$, and s is the span that is to be chosen. In order to improve the efficiency of calculating EWMA and EWMS in the program, Equations (8) and (9) above are converted into a more common form:

  $${\mu }_t=\alpha {\mu }_{t-1}+(1-\alpha )x_t$$

  (10)

  $${\sigma }_t=\sqrt{\alpha {\sigma }_{t-1}^2+(1-\alpha ){(x_t-{\mu }_t)}^2}$$

  (11)
• Cumulative features: By integrating features such as current squared, voltage squared, and power-related features over time, a cumulative heat generation feature is derived. This feature aims to represent the total heat accumulation within the motor, offering insights into the long-term thermal stress and potential for overheating. This study replaced cumulative sums with cumulative averages to prevent numerical explosion as the same row segments continued:

  $${\rho }_t=\frac{{\sum }_{i=0}^t{\tau }_i}{n_t}$$

  (12)

  where ${\tau }_i$ is the feature to be cumulatively summed, and $n_t$ is the number of samples already accumulated.

The derivation of physical features plays a pivotal role in accurately predicting motor temperatures in electric vehicles. By incorporating both instantaneous and cumulative aspects of motor operation, such as power consumption and heat generation, this research offers a nuanced approach to understanding and managing the thermal dynamics of electric vehicle motors.

Data Standardization

In order to ensure the generalizability of our model across different operational conditions and to mitigate the impact of outliers, data standardization plays a crucial role in preprocessing. By standardizing the data, we aim to normalize the distribution of the features, making them more comparable and reducing the potential bias introduced by scale differences. The standardization process adjusts the values such that the mean of the observed data becomes 0 and the standard deviation becomes 1. This is achieved through the following transformation for each data point, x, in the dataset:

$$x^{\prime }=\frac{x-\mu }{\sigma }$$

(13)

where $x^{\prime }$ is the standardized value, $\mu$ is the mean of the dataset, and $\sigma$ is the standard deviation. This transformation ensures that each feature contributes equally to the analysis, thereby enhancing the reliability of the predictive model.

2.2. Model Construction

2.2.1. Multihead Attention Block

In our proposed methodology, the pivotal role of feature engineering is underscored by an advanced attention mechanism designed to elevate the model’s capacity to discern and prioritize relevant information amidst a vast dataset. At the heart of this approach is the innovative application of a multiheaded attention mechanism, which intricately dissects the data to identify and focus on the most significant features. This mechanism is particularly adept at handling complex datasets by dynamically adjusting the focus based on the data’s contextual relevance.

2.2.2. Multihead Attention Model

This section is divided into two parts to introduce the attention mechanism and the multihead attention mechanism.

Attention Mechanism

The attention mechanism is operationalized through the following equations, where the attention weights are computed to emphasize the importance of specific features over others. This is achieved by calculating the scaled dot-product attention as follows:

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

(14)

Here, Q, K, and V represent the Query, Key, and Value matrices, respectively, derived from the input data. The matrices Q and K are transposed and scaled by the square root of the dimensionality of the key vectors, $d_k$, ensuring a balanced attention mechanism. The SoftMax function then normalizes the attention weights, facilitating a selective emphasis on features that are deemed most relevant by the model. This selective focus allows for a nuanced interpretation of the input data, enhancing the model’s predictive accuracy and efficiency. The proposed approach not only enriches the model with a deeper understanding of the underlying structure of the data but also introduces a level of interpretability and focus that is critical for complex data analysis tasks.

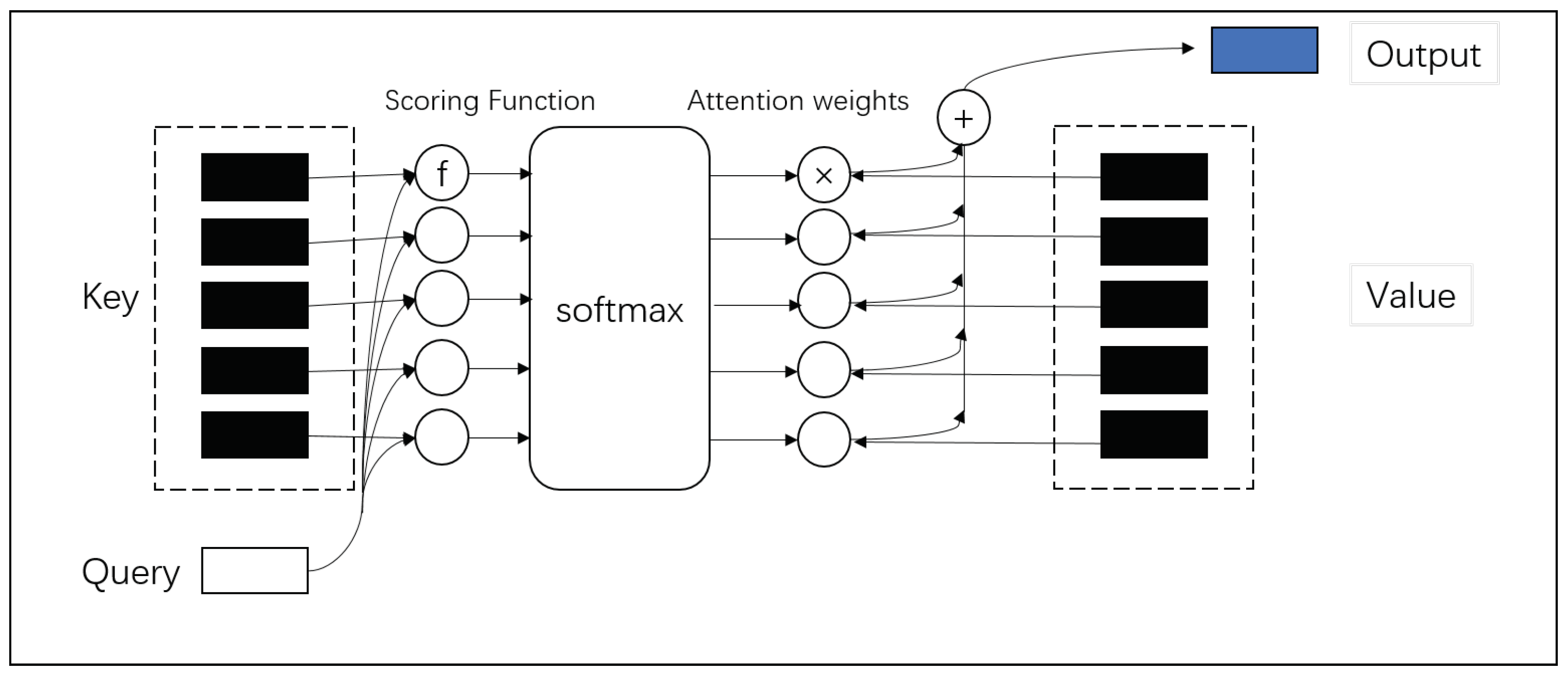
The architecture of the proposed attention mechanism is depicted in Figure 1, showcasing a comprehensive workflow from input features to the output layer.

At the core of this architecture lies the attention mechanism, structured around the interaction between three primary components: the Query, Key, and Value vectors, derived from the input data. The process initiates with the computation of attention scores via a scoring function, which assesses the relevance of each Key vector to the Query vector. This scoring function is critical for identifying the degree of attention that each Value vector should receive, ensuring that the most pertinent information is emphasized:

$$\mathrm{Attention}\mathrm{Scores}=\mathrm{Scoring}\mathrm{Function}(\mathrm{Query},\mathrm{Key})$$

(15)

Following the scoring process, a SoftMax layer is applied to the attention scores, normalizing them into a probability distribution and ensuring that the sum of attention weights across all Value vectors equals 1. This normalization step is essential for maintaining a balanced distribution of attention across the data:

$$\mathrm{Attention}\mathrm{Weights}=\mathrm{softmax}\left(\mathrm{Attention}\mathrm{Scores}\right)$$

(16)

The attention weights are then used to create a weighted sum of Value vectors, which represents the aggregated output of the attention mechanism. This output is a synthesis of the input data, filtered through the lens of the attention mechanism to highlight the most relevant information:

$$\mathrm{Output}=\sum (\mathrm{Attention}\mathrm{Weights}\times \mathrm{Value}\mathrm{Vectors})$$

(17)

This aggregated output is subsequently combined with the original input through a residual connection, fostering the integration of both direct and attention-processed information. This approach allows the model to benefit from the nuanced insights provided by the attention mechanism while retaining the foundational context of the original data. The resulting output encapsulates a refined understanding of the input features, optimized for further processing within the model or serving as the final output for prediction tasks. Through this innovative architecture, the model achieves an enhanced capacity for data interpretation, enabling more accurate and insightful analyses.

Multihead Attention Mechanism

In the architecture of the multihead attention mechanism, the computation of attention weights plays a central role, facilitating a nuanced analysis of the input data. Each input matrix is transformed into three distinct matrices: Queries (Q), Keys (K), and Values (V), which are essential components of the attention mechanism. The dimensions of these matrices are determined by the specific requirements of the application, with each matrix having dimensions of $R^{b\times n\times d}$, where b is the batch size, n is the sequence length, and d is the feature dimension. Unlike the attention mechanism, multihead attention divides each matrix uniformly along the third dimension into h matrices of the same size, called h heads. The dimension of each matrix, $q_i,k_i,v_i$, within each head is $R^{b\times n\times d_h}$. The attention mechanism is then applied as follows:

$$h_i=\mathrm{softmax}\left(\frac{q_i{k}_i^T}{\sqrt{d_h}}\right)v_i\in R^{b\times n\times d_h}$$

(18)

where $h_i$ represents the output of the attention mechanism for each head, $q_i$, $k_i$, and $v_i$ are the individual Query, key, and Value matrices for the i-th head, respectively, and $d_h$ is the feature dimension of the key matrix. Here, $d_h$ is equal to $\frac{d}{h}$. This equation underscores the importance of scaling the dot-product of $q_i$ and $k_i^T$ by the square root of $d_h$ to prevent the SoftMax function from entering regions where it has extremely small gradients, thereby ensuring a more stable and efficient learning process.

The output for each head is typically a matrix of size $b\times n\times d_h$. By concatenating the outputs along the third dimension (usually the feature dimension), a new matrix is formed with a size of $b\times n\times d$. This design allows each head to focus on different information, thereby enabling the exploration of more complex temporal relationships. By processing inputs in this manner, the multihead attention mechanism enhances the model’s ability to focus on different aspects of the input data, enabling more effective learning and representation of complex data relationships. The output of the multihead attention mechanism is consolidated through a transformation layer to ensure compatibility with subsequent layers of the network. This transformation is achieved by concatenating the outputs from each attention head, $[h_1,h_2,\dots ,h_n]$, and then applying a linear projection with a weight matrix $W_o\in R^{d\times d}$. The mathematical representation of this operation is given by

$$\mathrm{MultiHead}(Q,K,V)=[h_1,h_2,\dots ,h_n]W_o\in R^{b\times n\times d}$$

(19)

where Q, K, and V denote the Query, Key, and Value matrices, respectively; $h_i$ represents the output of the i-th attention head, and $W_o$ is the weight matrix used for the linear projection. This process ensures that the diverse perspectives captured by individual attention heads are effectively integrated, enhancing the model’s ability to interpret and process the input data comprehensively.

The architecture of the multihead attention mechanism is depicted in Figure 2.

2.2.3. Embedding Layer

The transformer model introduces a novel approach to incorporate the sequence order information through positional encoding. This encoding adds a unique signature to each token in the sequence, allowing the model to capture the order of the sequence without relying on recurrent or convolutional layers. Given a sequence of tokens $t_1,t_2,\dots ,t_n$ with dimensions of $R^{b\times n\times d}$, where b is the batch size, n is the sequence length, and d is the dimension of each token, the positional encoding, $PosE\in R^{b\times n\times d}$, is added directly to the tokens. This process ensures that the model can distinguish the positional relationship between tokens effectively. The positional encoding for each token is calculated as follows:

$$P_{i,2j}=sin\left(\frac{i}{{\mathrm{10,000}}^{2j/d}}\right)$$

(20)

$$P_{i,2j+1}=cos\left(\frac{i}{{\mathrm{10,000}}^{2j/d}}\right)$$

(21)

where i is the position of the token in the sequence, and j is the dimension. By using this method, each position in the sequence is encoded with a unique combination of sine and cosine functions, varying by wavelength across dimensions. This encoding not only facilitates the model’s understanding of the positional information but also enhances its capacity to learn sequence-dependent features without imposing a significant computational burden.

2.2.4. Residual Connection and Batch Normalization

In the advancement of neural network architectures, particularly in the development of transformer models, two critical innovations have been widely adopted: layer normalization and residual connections. The former technique, layer normalization, is applied across each feature vector independently within a batch, normalizing the data to have a mean of 0 and a variance of 1. This process is mathematically represented as

$$z_i^{\prime }=\frac{z_i-\mu }{\sqrt{{\sigma }^2+ϵ}}$$

(22)

where $z_i$ is the original activation, $\mu$ and ${\sigma }^2$ are the mean and variance computed across the feature dimensions, respectively, and $ϵ$ is a small constant added for numerical stability. Layer normalization facilitates stable and faster training by reducing the internal covariate shift.

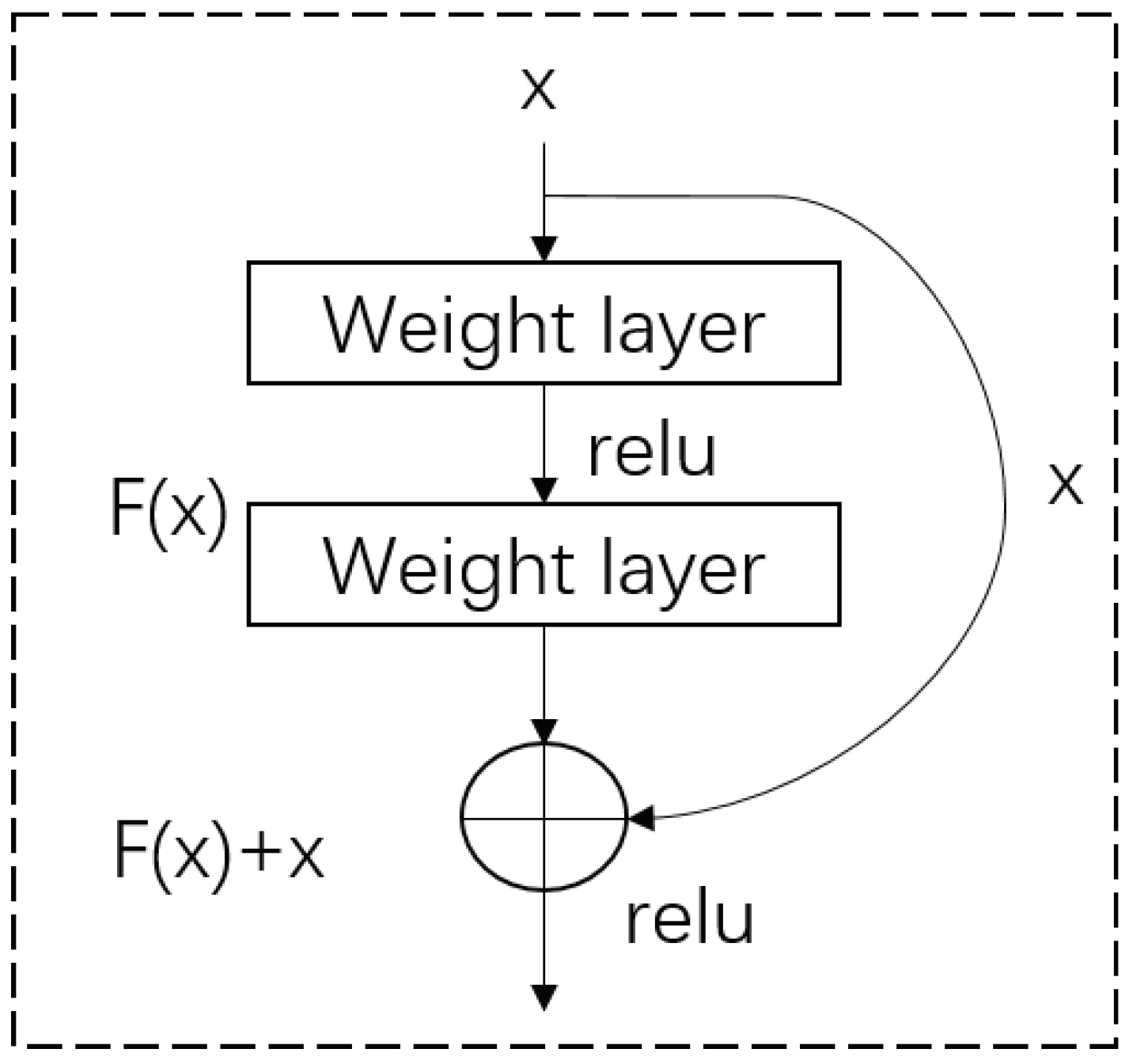
Moreover, residual connections, another cornerstone of modern architectures, allow layers to learn modifications to the identity mapping rather than complete transformations, significantly improving the flow of gradients during backpropagation and enabling the training of deeper networks. The residual connection is described by the following equation:

$$y=F\left(x\right)+x$$

(23)

where x is the input to the layer, and $F\left(x\right)$ represents the transformation applied by the layer. This simple yet powerful technique combats the vanishing gradient problem by providing an alternative path for gradient flow.

Together, layer normalization and residual connections have become indispensable in the design of deep neural networks, offering a pathway to enhancing model performance and training efficiency. Their integration into transformer models underscores the ongoing innovation in network design, aiming at achieving both depth and breadth in model architecture without compromising on training efficacy. The residual connection mechanism is depicted in Figure 3.

2.2.5. Feedforward Layer and Feature Aggregation Layer

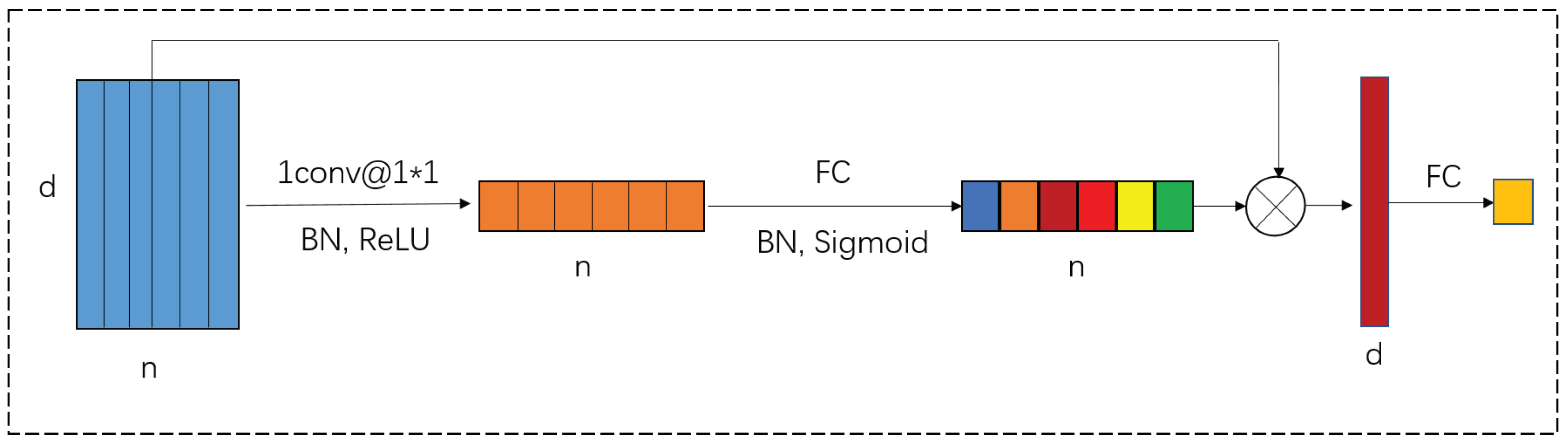
The proposed neural network architecture integrates a sophisticated feature transformation pipeline to enhance feature representation and model performance. Initially, the input features undergo a convolutional layer, denoted as $1\mathrm{conv}@1\times 1$, which applies a $1\times 1$ convolution to project the input features into a lower-dimensional space, facilitating direct input to the fully connected layer for prediction output, followed by batch normalization (BN) and rectified linear unit (ReLU) activation for normalization and nonlinear transformation. This process is represented as

$${\mathrm{Feature}}_{\mathrm{transformed}}=\mathrm{ReLU}\left(\mathrm{BN}(1\mathrm{conv}@1\times 1\left({\mathrm{Feature}}_{\mathrm{input}}\right))\right)$$

(24)

Subsequently, the transformed feature is passed through a fully connected (FC) layer for feature transformation and combined with another BN layer and a sigmoid activation function to refine the feature map further. The resultant feature map can then be regarded as an n-dimensional weight vector, and by weighted summing with the input features, a d-dimensional feature fusion vector can be obtained. Then, the feature fusion vector is passed through a second FC layer, projecting the aggregated features into the desired output dimension. The architecture ensures that each step contributes to a more discriminative and informative feature representation by incorporating both linear and nonlinear transformations, as well as normalization steps. This comprehensive approach to feature transformation and aggregation underscores the model’s capacity to learn complex patterns and relationships within the data, facilitating enhanced predictive accuracy and robustness.

The feature aggregation layer is depicted in Figure 4.

3. Case Study

In our experiments, we employed a dataset that included motor temperature data from 100 vehicles collected over a period of 20 days for the purposes of model training and evaluation. The driving data in our dataset genuinely originate from real-world scenarios, where the operating times for each vehicle are highly variable. Some vehicles may operate continuously throughout the day, such as those used in fleet operations, while others, such as personal commuter cars, may only be driven during specific periods, such as morning and evening rush hours. This variability in usage patterns ensures that our dataset encompasses a broad spectrum of driving conditions and times, including both sustained operation and sporadic usage. Such diversity is essential for developing a robust model capable of accurately predicting motor temperatures across a range of circumstances.

The segmentation of driving segments for each vehicle is especially crucial during the feature engineering phase. It enables us to capture the subtleties of motor temperature changes during various driving phases, such as acceleration, steady driving, and deceleration. Our model is designed to be adaptable to these fluctuations in driving times and conditions. By integrating features that reflect the vehicle’s operational status and recent driving history, the model can deliver more precise predictions irrespective of the specific usage pattern.

The dataset from these 100 vehicles was sourced from a particular model of Leapmotor, representing real driving data provided by the vehicle owners. This model does not distinguish between range-extended and pure electric versions; however, all its motors utilize the company’s proprietary oil-cooled electric drive technology. The dataset encompasses historical temperature data along with the corresponding true temperature labels. We divided the dataset into a training set and a test set, with the training set including motor temperature data from 90 vehicles to train the model and the test set comprising data from 10 vehicles to assess the model’s performance.

In this study, we implemented a sequence of 10 structurally identical multihead attention blocks, each characterized by distinct weights. This configuration allowed for the output of one block to serve as the input to the subsequent block. Specifically, the output from the first multihead attention block was forwarded to the second block, and this process continued sequentially. After the completion of this chain, the output from the 10th multihead attention block was then directed into a convolutional layer. This architecture was designed to enhance the model’s ability to process and learn from the input data in a stepwise, integrated manner, potentially increasing the depth and richness of the learned representations.

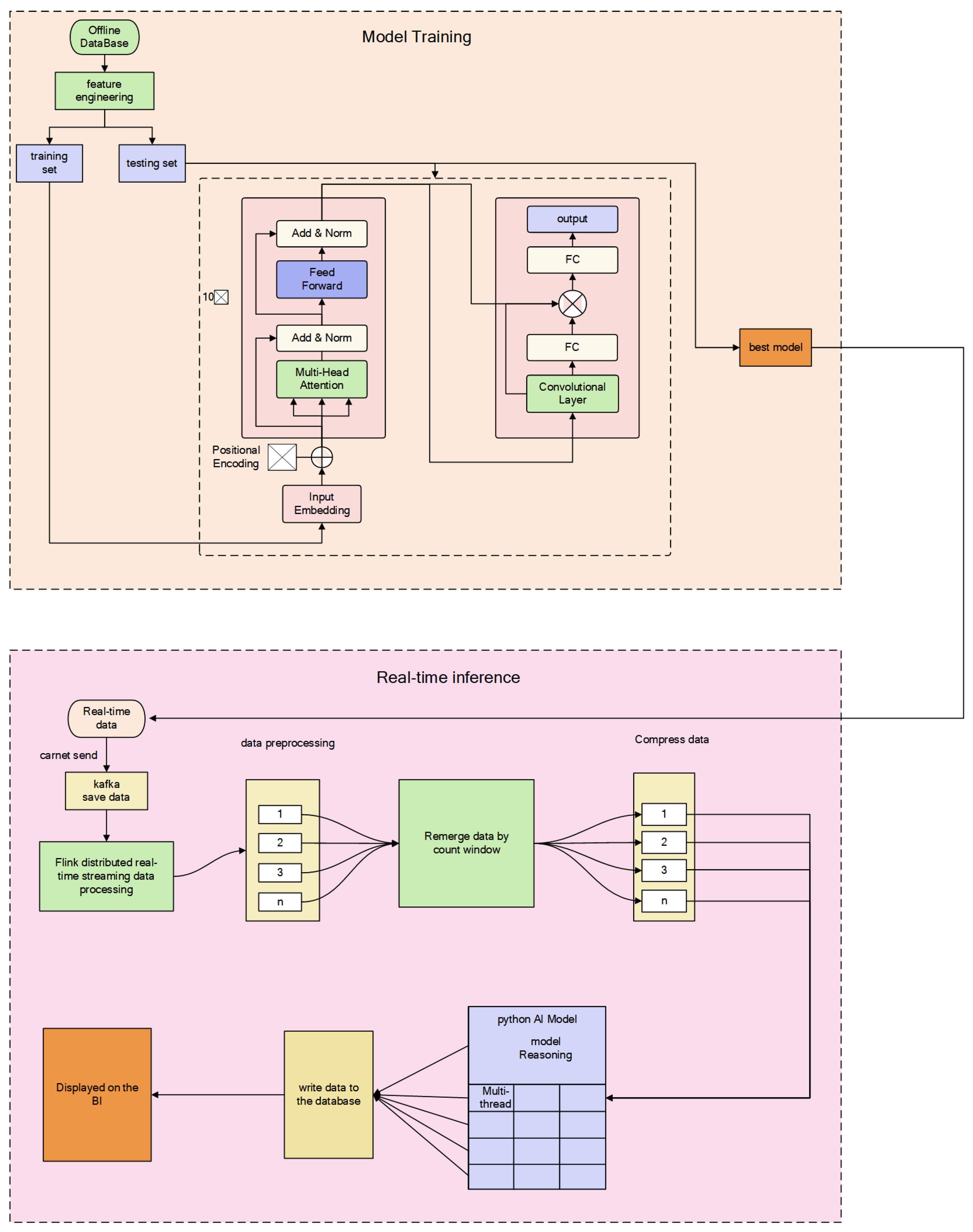
Our machine learning workflow in the case study is bifurcated into two primary processes: model training and real-time inference. During the model training phase, as depicted in Figure 5, we commence with an offline database, which undergoes feature engineering to prepare the training and testing sets. The model architecture includes an input embedding layer, followed by positional encoding. The core of the model comprises several blocks, each consisting of multihead attention and feedforward networks, integrated with add and norm layers for normalization. The output of the model is processed through a convolutional layer and subsequent fully connected (FC) layers to produce the final predictions. The best-performing model, as determined by our evaluation using the testing set, was then selected for deployment.

In the real-time inference stage, live data streams are processed through a Kafka-based system for data ingestion, followed by Flink for distributed real-time streaming data processing. Data preprocessing includes remerging via a count window to compress the data which are then fed into a Python AI model for reasoning. The inference results are written back to the database and can also be displayed on the BI dashboard, providing insights and actionable intelligence in real time.

In the performance evaluation of our model, we employed several widely recognized error metrics to assess its predictive accuracy. These metrics include the mean squared error (MSE), which measures the average of the squares of the errors; the root mean squared error (RMSE), providing the square root of MSE to maintain the error units consistency with the original data; and the mean absolute percentage error (MAPE), a measure of the average absolute percentage discrepancies between the predicted and observed values. The mathematical expressions for these metrics are defined as follows:

$$\mathrm{MSE}=\frac{1}{n}\sum _{i=1}^n{({\widehat{y}}_i-y_i)}^2$$

(25)

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{({\widehat{y}}_i-y_i)}^2}$$

(26)

$$\mathrm{MAPE}=\frac{1}{n}\sum _{i=1}^n\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|\times 100\%$$

(27)

where n is the number of observations, $y_i$ represents the actual values, and ${\widehat{y}}_i$ denotes the predicted values. These metrics collectively provide a comprehensive understanding of the model’s performance by not only highlighting the average error but also capturing the distribution and scale of the errors relative to the actual values.

The experimental results are shown in

Table 2. Experimental results.

CarID	TCN			LSTM			Transformer
	MSE	RMSE	MAPE	MSE	RMSE	MAPE	MSE	RMSE	MAPE
4	13.971	3.738	8.1%	9.122	3.020	4.6%	5.016	2.240	3.6%
14	20.521	4.530	10%	13.570	3.684	6.6%	3.391	1.841	3.4%
18	20.211	4.496	7.1%	10.002	3.163	5.0%	6.434	2.536	3.8%
23	20.9	4.572	10.0%	8.418	2.901	6.4%	8.619	2.936	6.1%
24	24.437	4.943	7.3%	15.827	3.978	5.6%	10.654	3.264	4.9%
29	10.091	3.177	4.1%	40.364	6.353	6.6%	8.961	2.994	3.7%
34	8.314	2.883	5.2%	8.053	2.838	5.1%	6.101	2.470	4.3%
38	7.521	2.742	5.1%	6.295	2.509	4.8%	3.061	1.750	3.3%
48	12.472	3.532	7.9%	12.128	3.483	7.9%	4.774	2.185	4.9%
49	13.568	3.684	6.6%	12.672	3.560	6.4%	5.438	2.332	4.5%

:

In Table 2, the “carID” in our dataset refers to a unique identifier assigned to each of the 100 vehicles in our study. This identifier ranges from 0 to 99, allowing for clear differentiation between individual cars.

From Table 2, it can be seen that the MAPE of all cars is below 7%. In addition, CarID 4 has the lowest MSE, suggesting its predictions were, on average, closer to the true values. CarIDs 23 and 18 have the lowest RMSE, indicating a tighter clustering of errors around the mean in the actual units. CarID 23 has the lowest MAPE, implying its predictions were closest (in percentage terms) to the actual values.

Through the analysis and comparison of the experimental results, we observed that the motor temperature prediction model based on multihead attention performs well in terms of prediction accuracy and stability. The model was able to keep the temperature prediction error within a range of ±3 °C for the 10 vehicles in the study after the outliers were removed. Compared to other traditional models, the multihead attention model more effectively captures the correlations and features within the sequential data.

In order to highlight the performance of the model established in this paper, we also constructed two commonly used time series forecasting models for comparison: the temporal convolutional network (TCN) and the long short-term memory network (LSTM). As can be seen from Table 2, with the exception of CarID23, the remaining nine vehicles in the test set demonstrated superior performance with our model, followed by LSTM. Specifically, our model achieved a root mean square error (RMSE) of less than 3 for almost all vehicles in the test set, whereas the other two models had an RMSE greater than 3 for most vehicles, indicating that our model is more accurate than traditional models.

In each picture of Figure 6, Figure 7 and Figure 8, two lines are plotted: the red line represents the actual temperature values (labeled as “True”), and the blue line represents the predicted temperatures (labeled as “Predict”). The x-axis represents time, while the y-axis shows the temperature values.

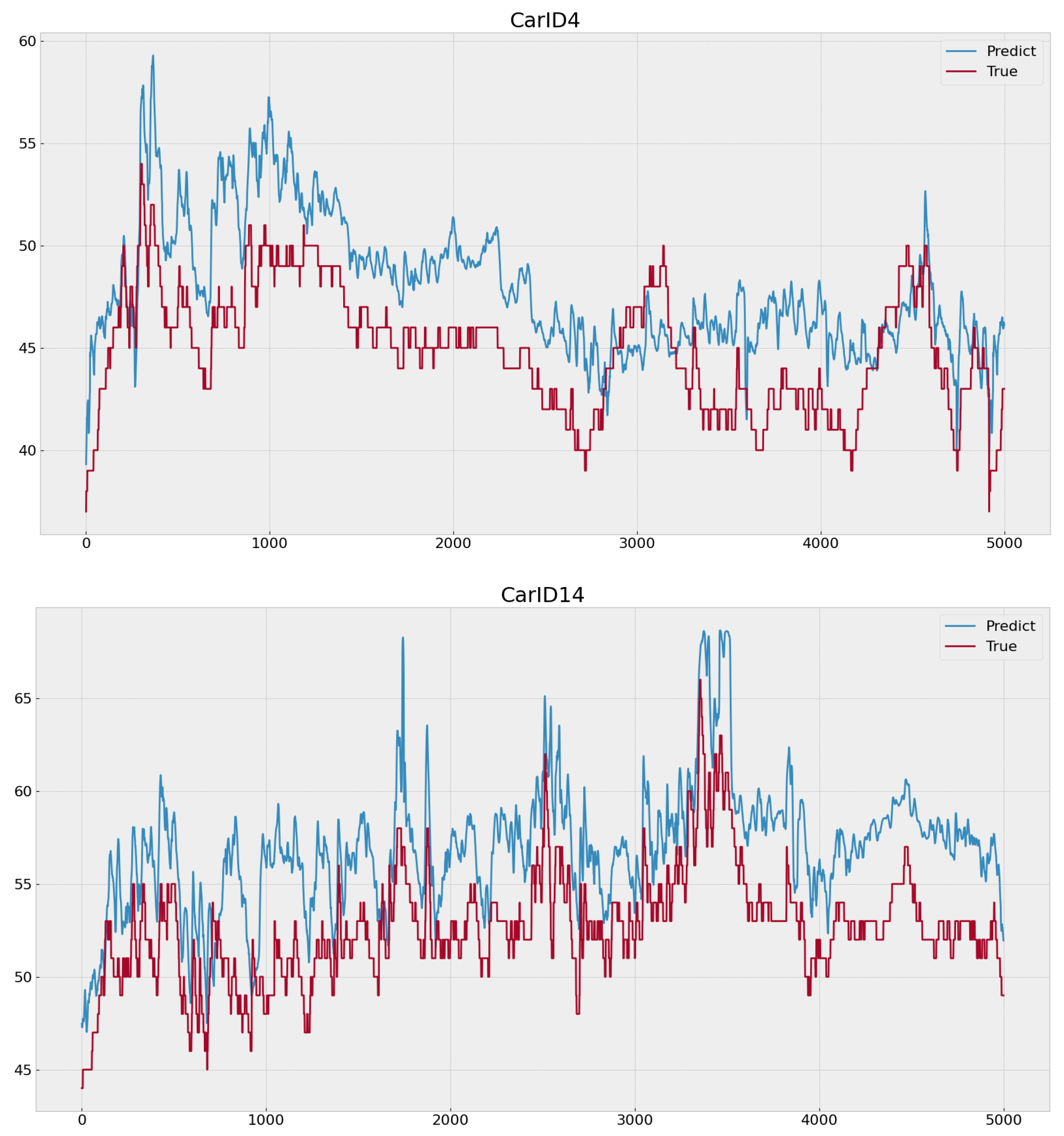
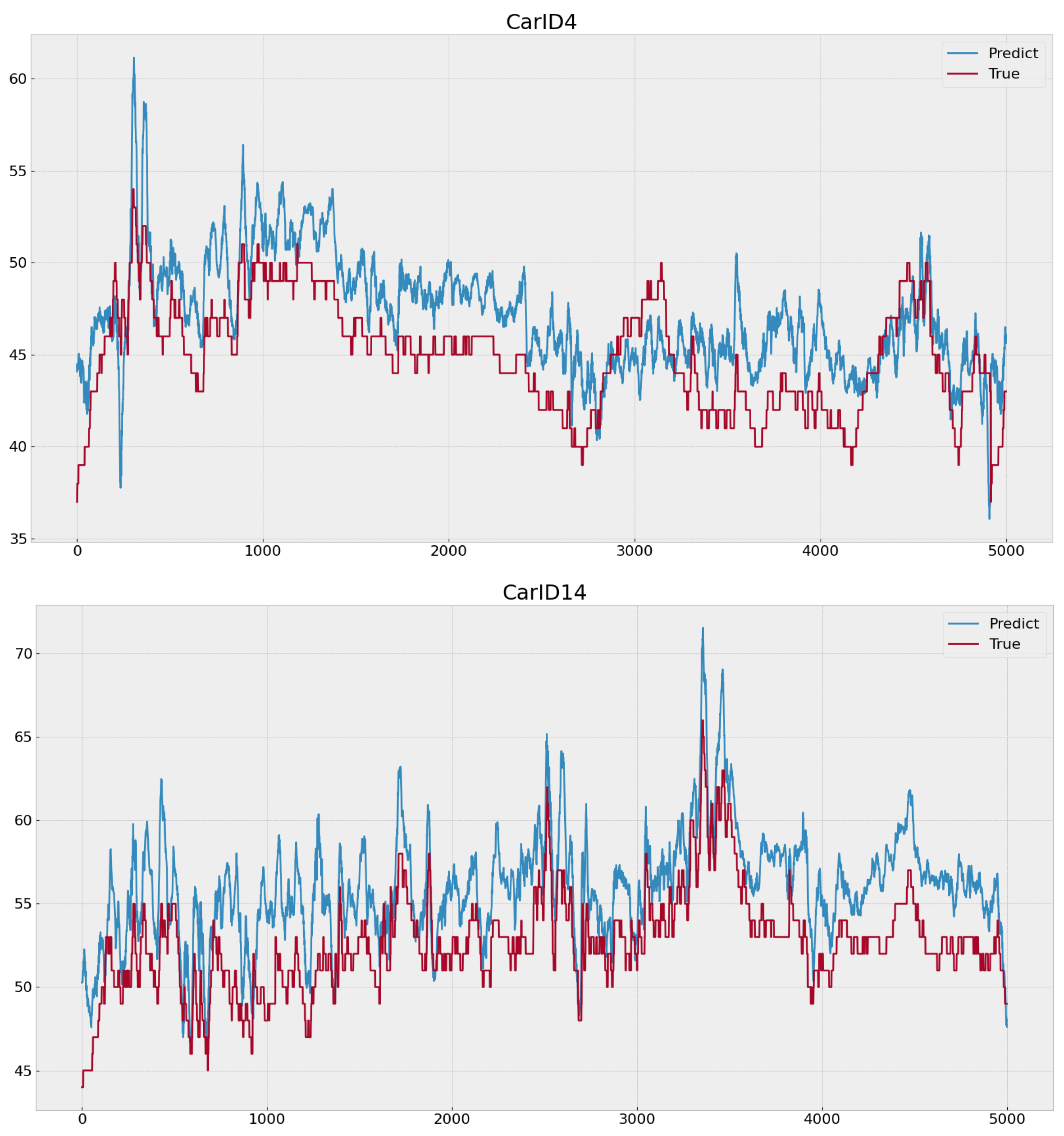
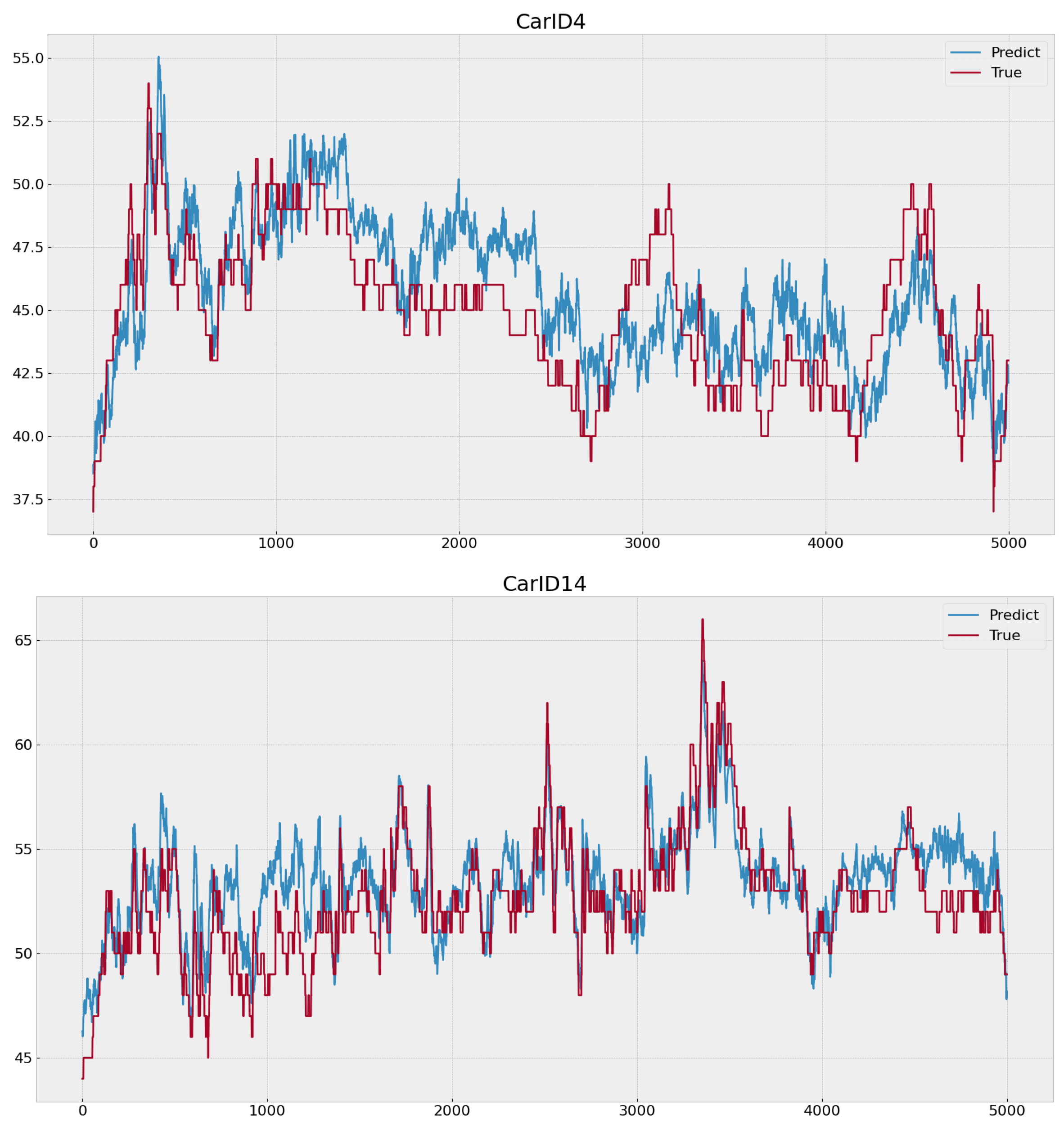
In order to more vividly illustrate the differences in model predictions, Figure 6, Figure 7 and Figure 8 depict the predictive performance of TCN, LSTM, and our model for CarID4 and CarID14, respectively. The horizontal axis represents time points, which are continuous time segments stitched together, with a 3 s interval between points. The vertical axis represents motor temperature values. It can be observed from the figures that our model provides noticeably more accurate predictions for these two vehicles, while LSTM outperforms TCN in predictions for CarID14.

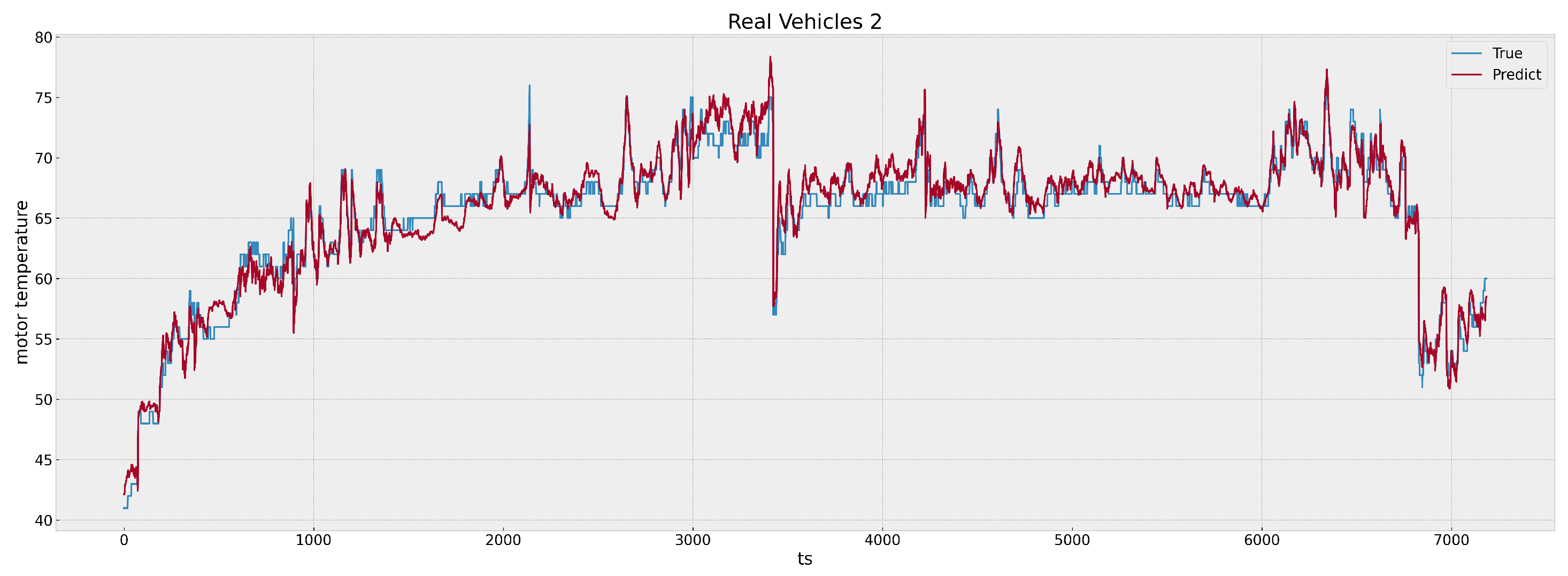
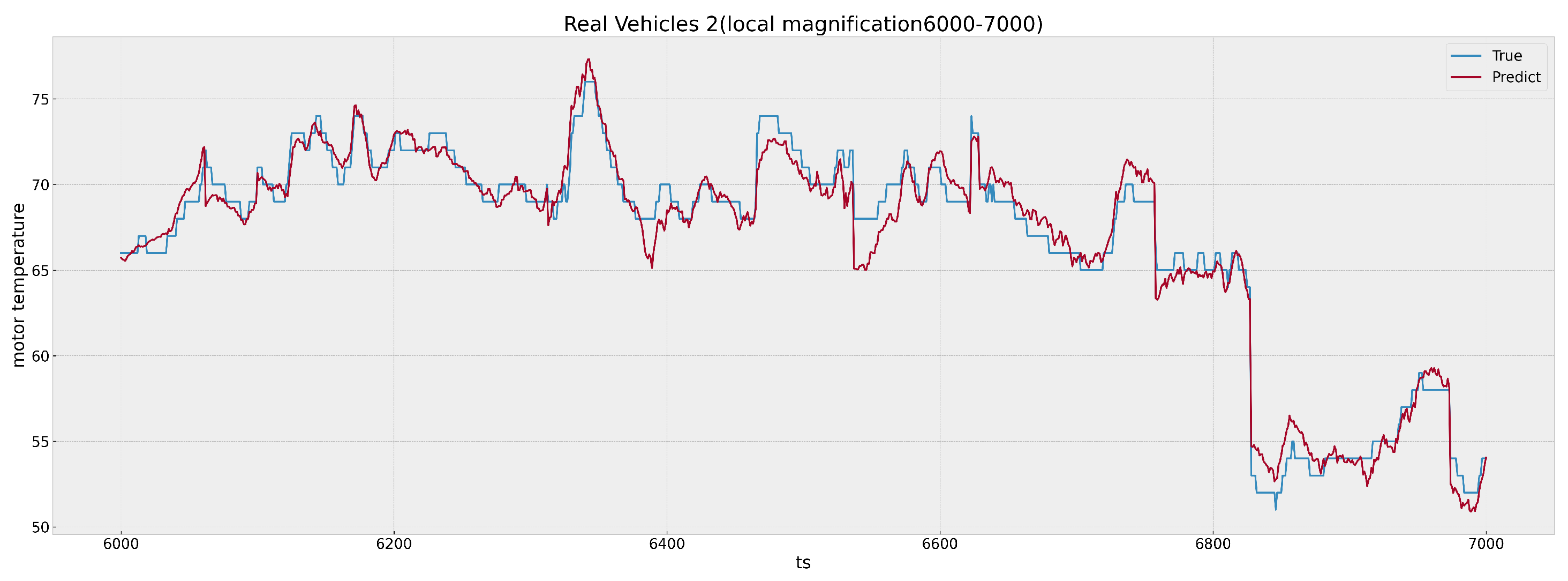
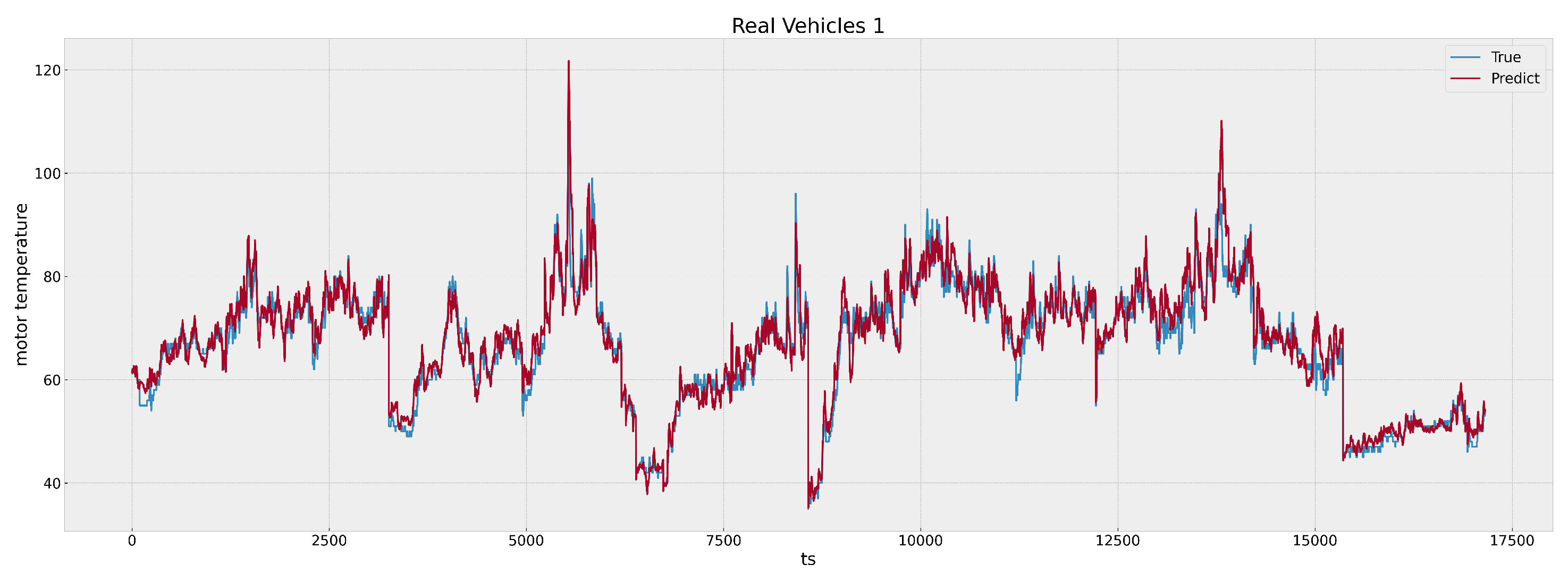
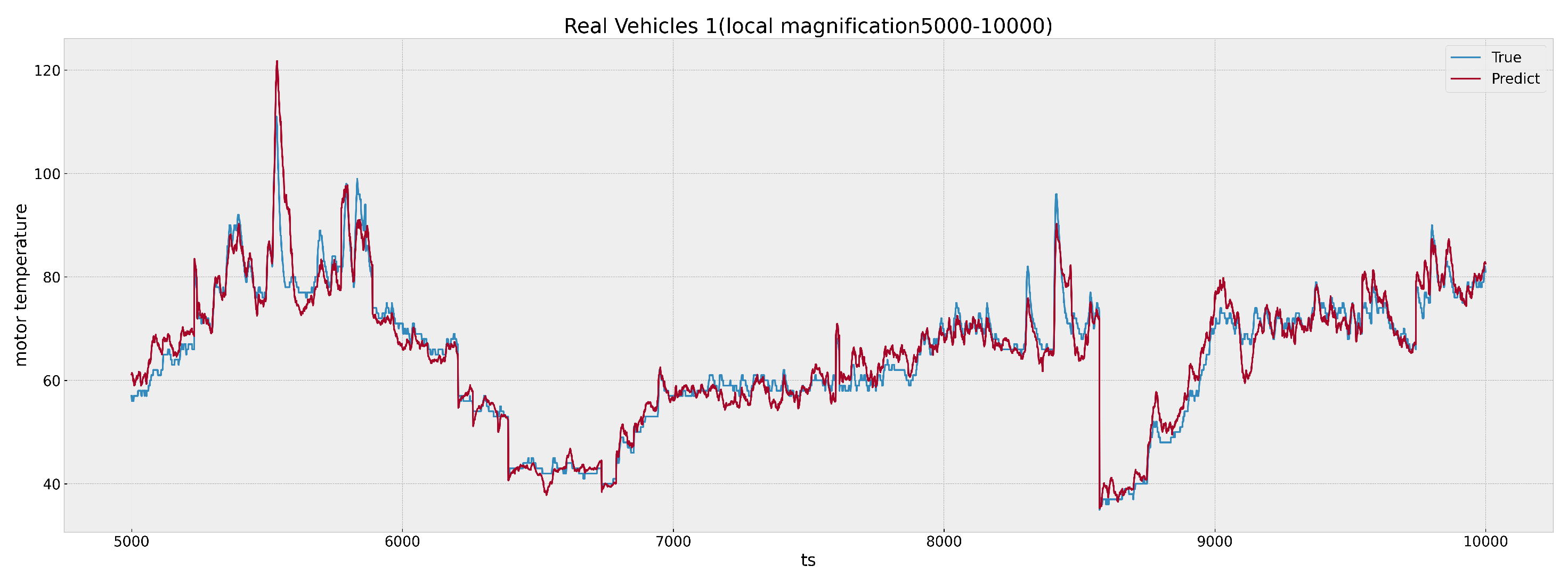
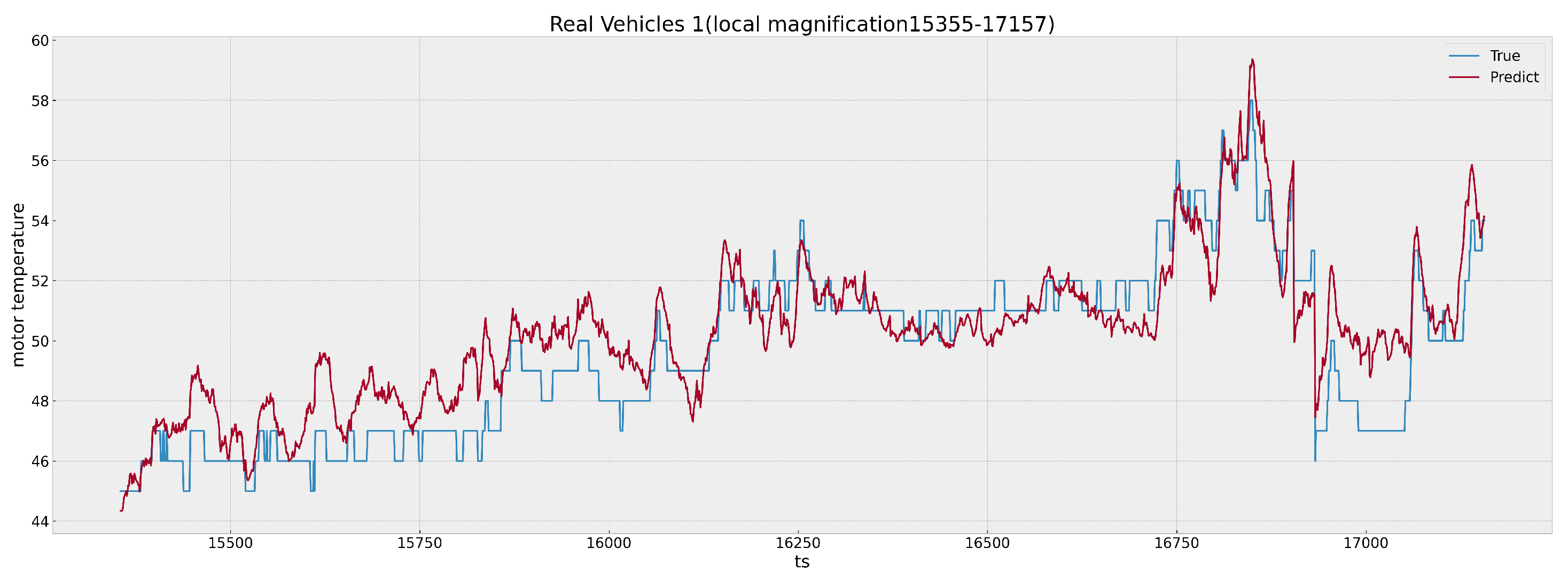
Figure 9, Figure 10, Figure 11 and Figure 12 illustrate the predictive performance of our model over a 24 h period in two randomly selected real cars, beginning on 29 September 2023 at 00:00 and ending at 23:59. Figure 10 and Figure 11 show the effect (after local magnification) of the time points from 5000 to 10,000 and from 15,355 to 17,157 in Figure 9; Figure 13 shows the effect (after local magnification) of the time points from 6000 to 7000 in Figure 12. The graph shows the plots of two lines representing the actual and predicted motor temperatures. The blue line signifies the real-time temperature readings (denoted as ‘True’), and the red line depicts the model’s predictions (denoted as ‘Predict’). The X-axis of the graph marks the time points when all the driving segments of the day are concatenated together, while the Y-axis denotes the temperature values. A visual inspection of the plot indicates a close correspondence between the predicted and actual temperature values, reflecting the model’s high degree of accuracy.

As depicted in Figure 9, Figure 10 and Figure 11, there is a noteworthy concordance between the predicted and actual data within the real vehicle tests. This close alignment underscores the superior performance of the proposed methodology.

4. Conclusions

This study presents a groundbreaking approach to thermal modeling for electric vehicle motors, leveraging the sophistication of the multihead attention mechanism. Our findings underscore the model’s exceptional ability to predict the temperature of the stator with heightened accuracy, surpassing conventional models. By incorporating advanced feature engineering and modeling techniques, we address the complex challenge of maintaining optimal motor temperatures under varied operational conditions, a critical aspect of the longevity and efficiency of electric vehicles.

The deployment of a multihead attention mechanism has proven to be a pivotal innovation, offering a nuanced understanding of temporal data relationships and enhancing the model’s predictive performance. The case study on a comprehensive dataset of 100 electric vehicles validates the model’s efficacy, demonstrating significant improvements in prediction accuracy and reliability. Such advancements are instrumental in devising more effective thermal management strategies, which are vital for optimizing electric vehicle performance and safety.