Disturbance-Observer-Based Second-Order Sliding-Mode Position Control for Permanent-Magnet Synchronous Motors: A Continuous Twisting Algorithm-Based Approach
Abstract
1. Introduction
- (1)
- A novel composite position controller, consisting of a CTA-PC and a modified STA-DO, is proposed for the field-oriented controlled PMSM servo system.
- (2)
- The performance of the proposed composite position controller is compared with that of the CTA-PC and the composite position controller, which combines a CTA-PC with a standard STA-DO.
2. Problem Formulation
2.1. Adopted FOC Strategy
2.2. Dynamic Model of the SMPMSM Servo System
3. Position Controller Design
3.1. Rotor Position Tracking Error Dynamics
3.2. Modified STA-DO Design
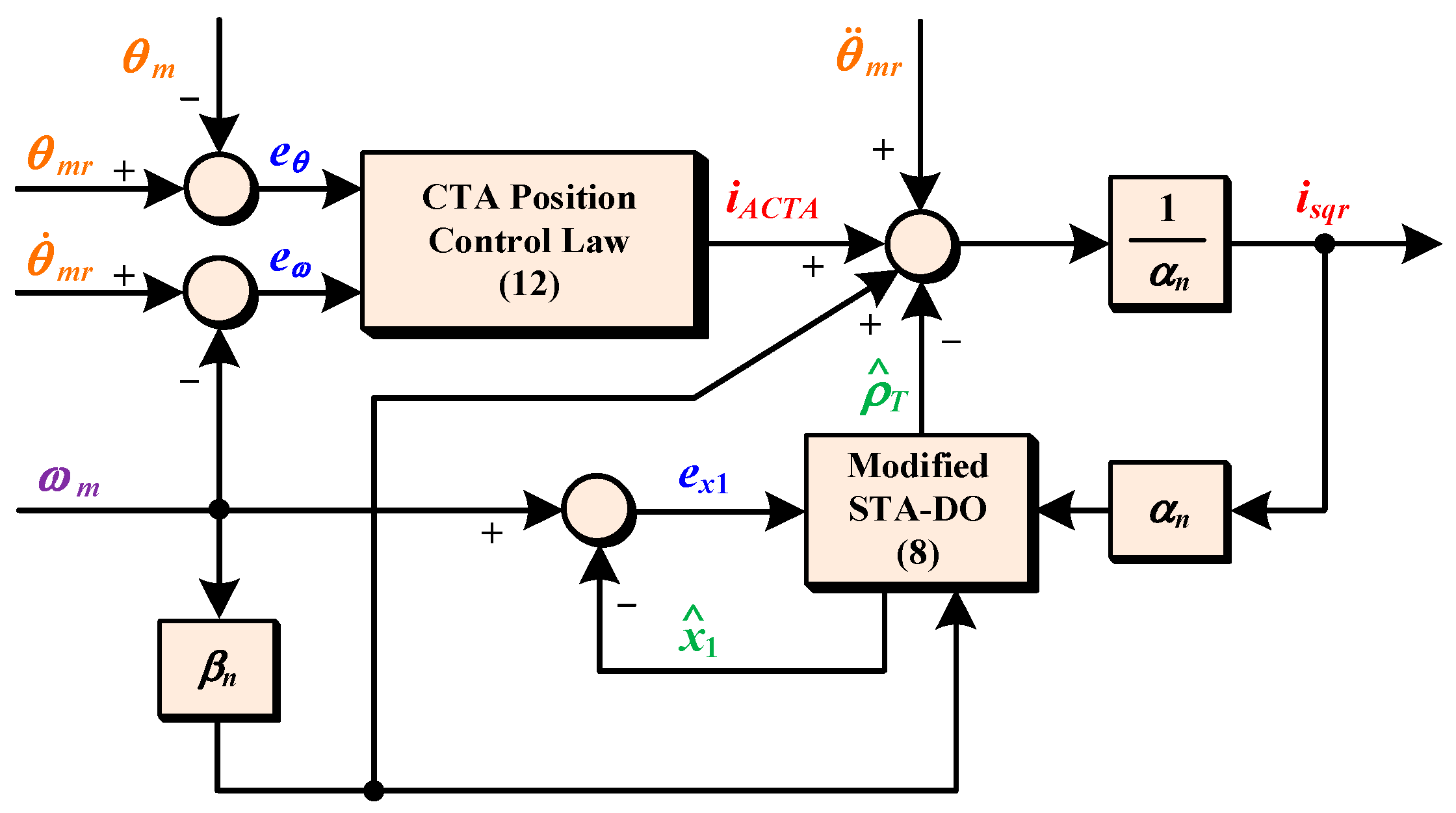
3.3. Proposed Composite Position Controller
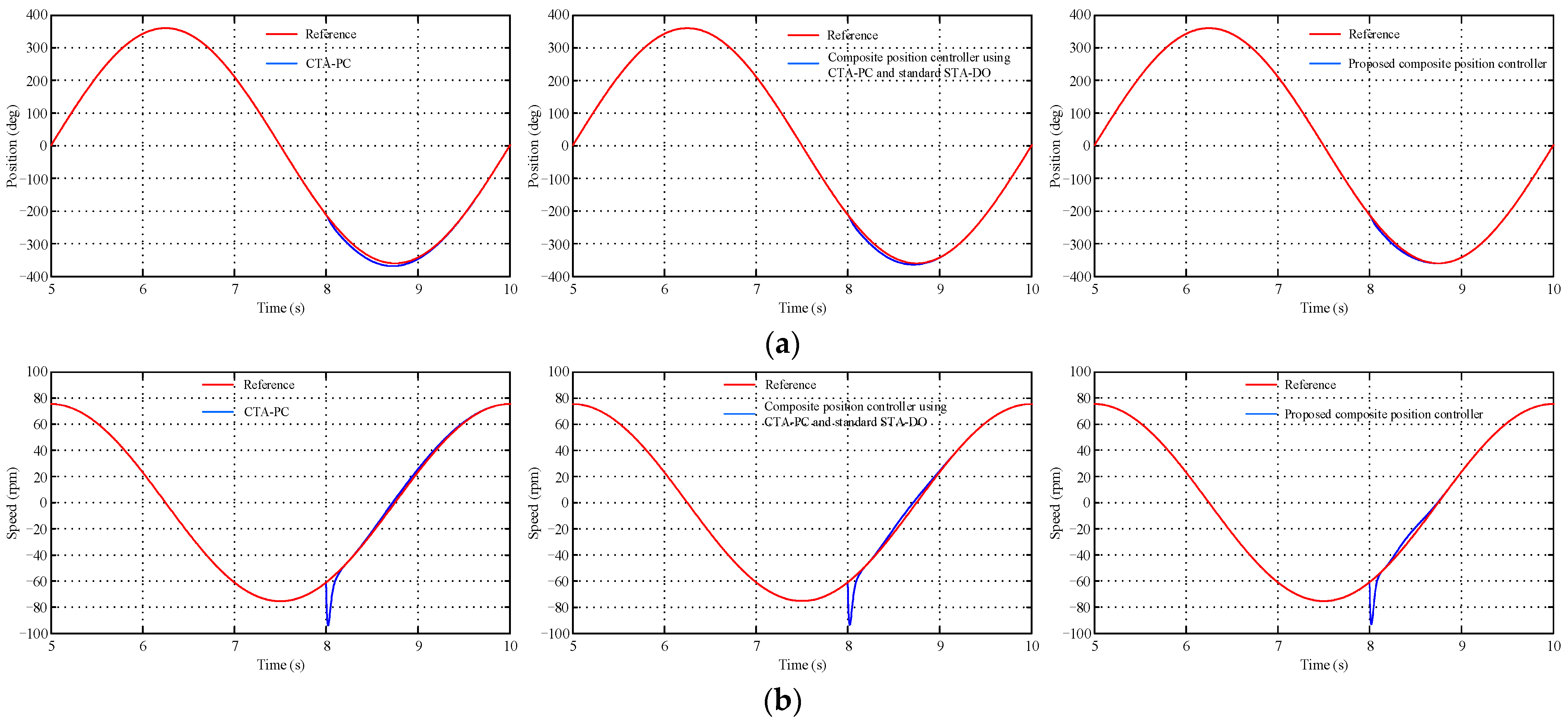
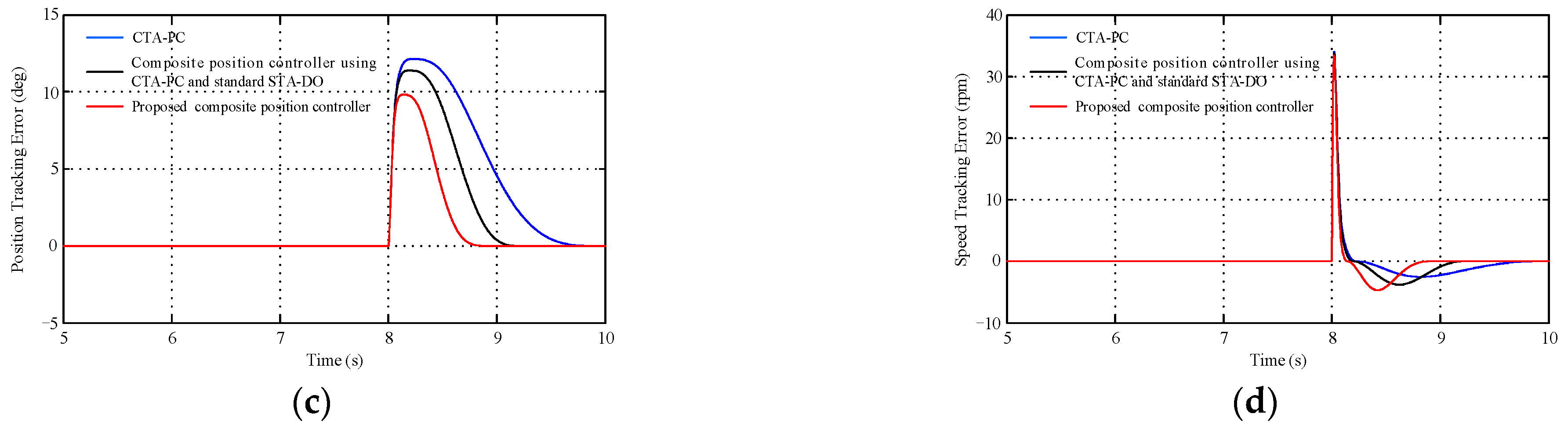
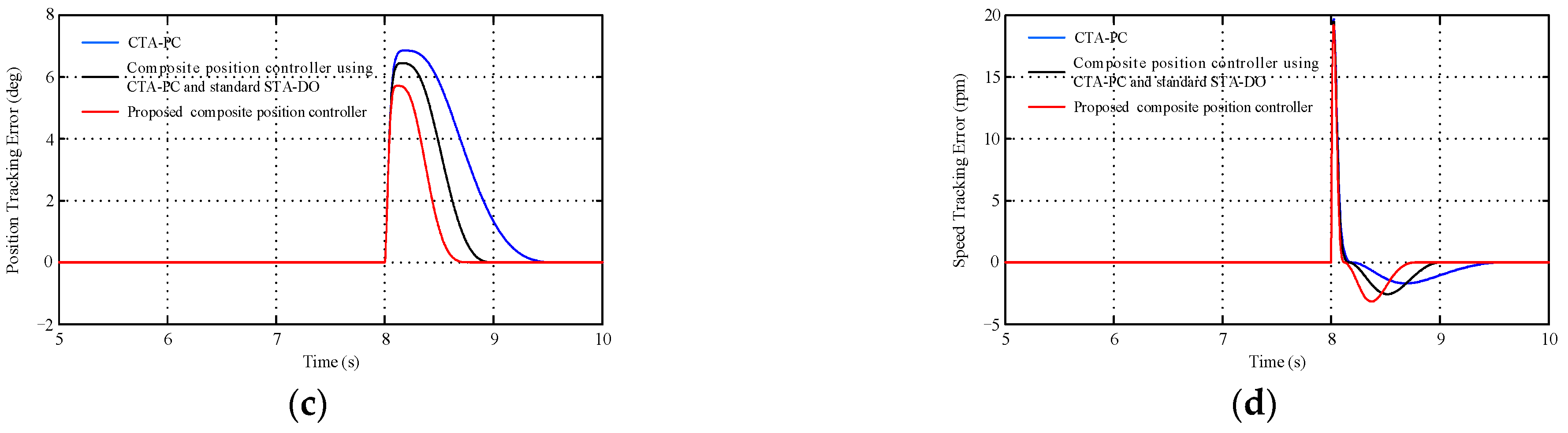
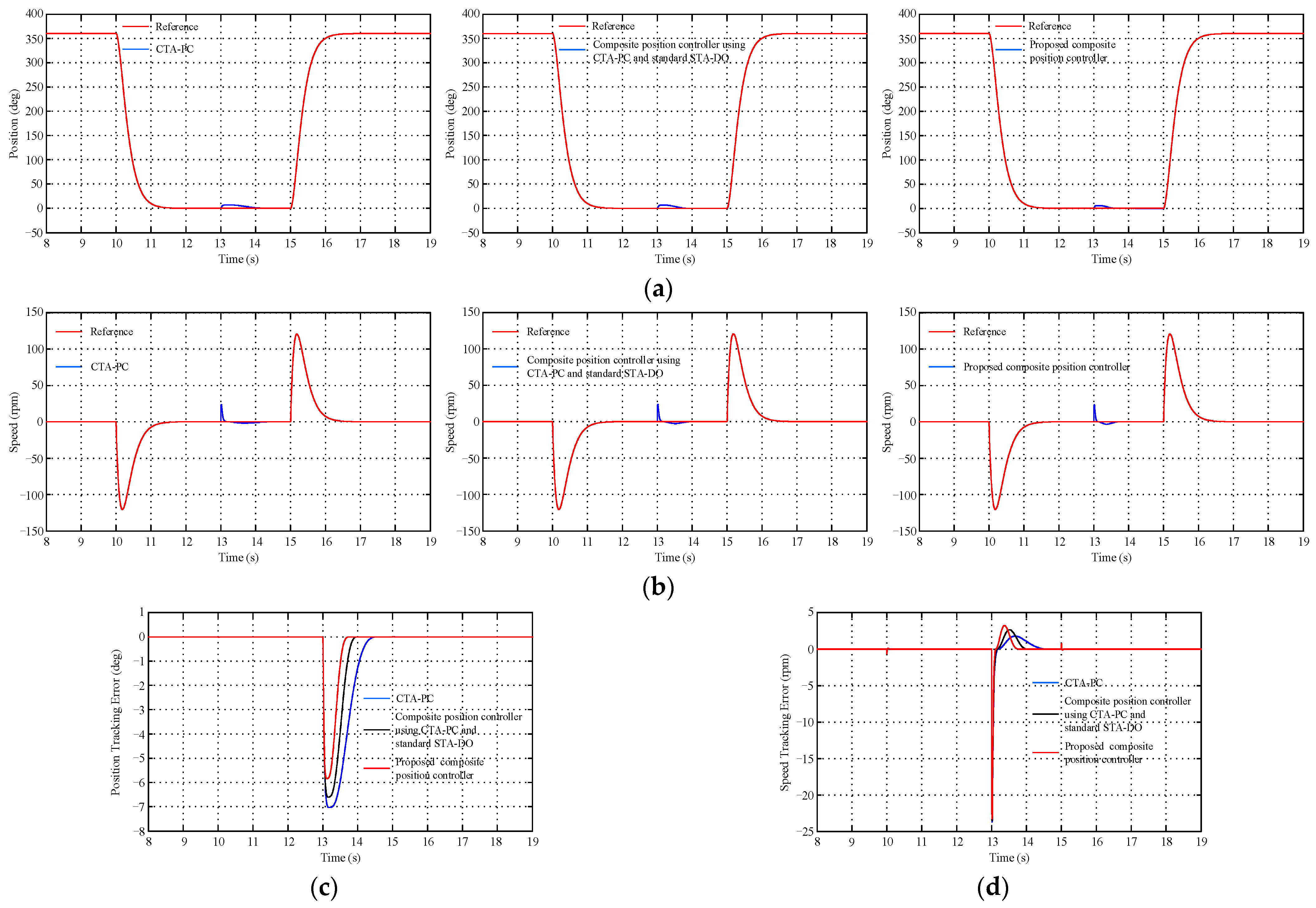
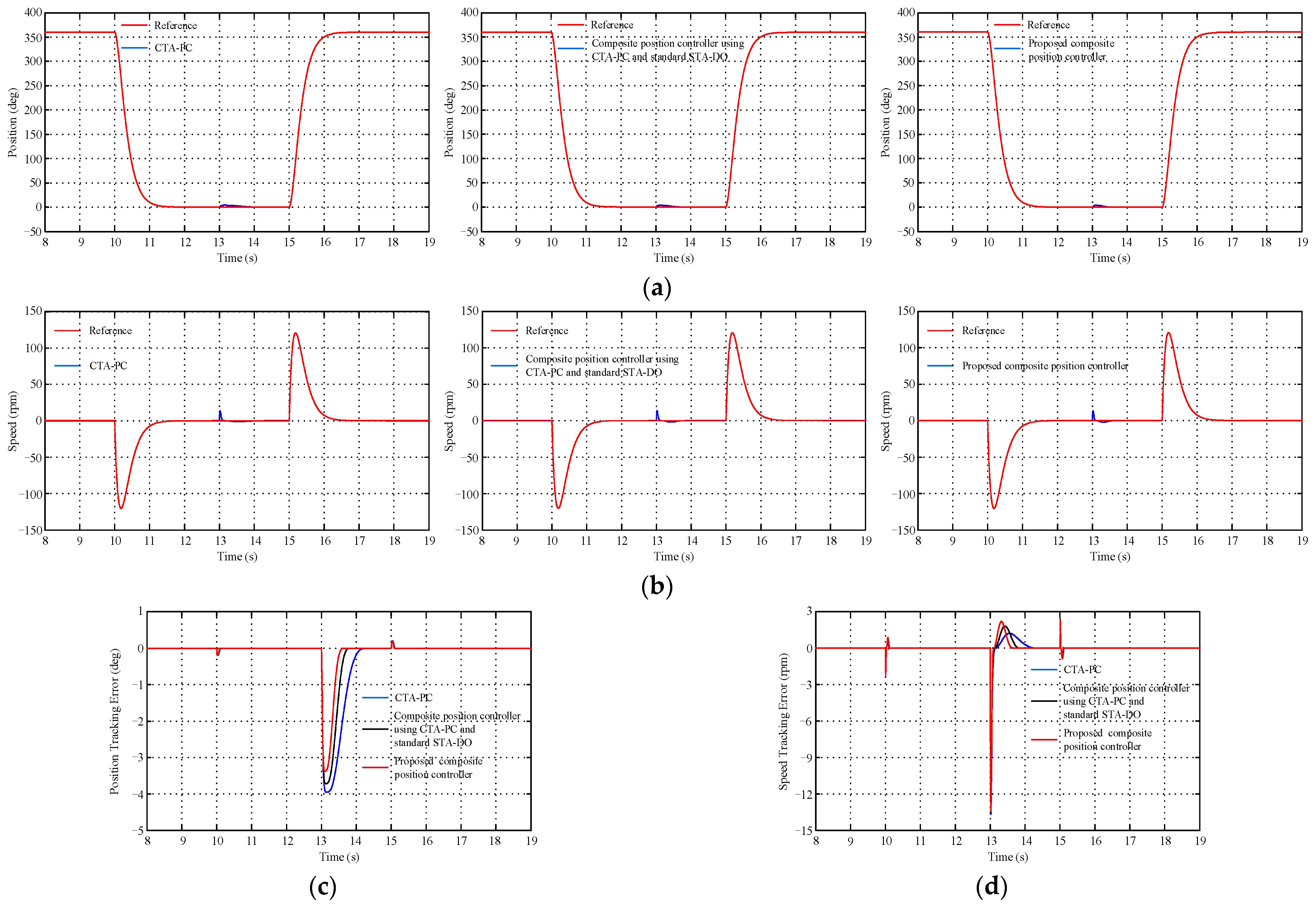
4. Simulation Results
5. Conclusions and Future Work
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Krishnan, R. Permanent Magnet Synchronous and Brushless DC Motor Drives; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Gieras, J.F. Permanent Magnet Motor Technology: Design and Applications, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Chau, K.T. Electric Vehicle Machines and Drives: Design, Analysis and Application; Wiley-IEEE Press: Singapore, 2015. [Google Scholar]
- Nguyen, P.H.; Hoang, E.; Gabsi, M. Performance synthesis of permanent-magnet synchronous machines during the driving cycle of a hybrid electric vehicle. IEEE Trans. Veh. Technol. 2011, 60, 1991–1998. [Google Scholar] [CrossRef]
- Liu, C.; Chau, K.T.; Lee, C.H.T.; Song, Z. A critical review of advanced electric machines and control strategies for electric vehicles. Proc. IEEE 2021, 109, 1004–1028. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2007. [Google Scholar]
- Yaramasu, V.; Wu, B.; Sen, P.C.; Kouro, S.; Narimani, M. High-power wind energy conversion systems: State-of-the-art and emerging technologies. Proc. IEEE 2015, 103, 740–788. [Google Scholar] [CrossRef]
- Le, X.C.; Duong, M.Q.; Le, K.H. Review of the modern maximum power tracking algorithms for permanent magnet synchronous generator of wind power conversion systems. Energies 2023, 16, 402. [Google Scholar] [CrossRef]
- Choi, J.H.; Jang, S.M.; Sung, S.Y.; Kim, J.M.; Park, Y.S.; Kim, Y.J.; Oh, D.H. Operating range evaluation of double-side permanent magnet synchronous motor/generator for flywheel energy storage system. IEEE Trans. Magn. 2013, 49, 4076–4079. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, C.; Wu, L.; Zheng, Y. Multi-objective optimal design of high-speed surface-mounted permanent magnet synchronous motor for magnetically levitated flywheel energy storage system. IEEE Trans. Magn. 2019, 55, 8202708. [Google Scholar] [CrossRef]
- Ji, W.; Ni, F.; Gao, D.; Luo, S.; Lv, Q.; Lv, D. Electromagnetic design of high-power and high-speed permanent magnet synchronous motor considering loss characteristics. Energies 2021, 14, 3622. [Google Scholar] [CrossRef]
- Hong, D.K.; Hwang, W.; Lee, J.Y.; Woo, B.C. Design, analysis, and experimental validation of a permanent magnet synchronous motor for articulated robot applications. IEEE Trans. Magn. 2018, 54, 8201304. [Google Scholar] [CrossRef]
- Luu, P.T.; Lee, J.Y.; Lee, J.H.; Park, J.W. Electromagnetic and thermal analysis of permanent-magnet synchronous motors for cooperative robot applications. IEEE Trans. Magn. 2020, 56, 7512804. [Google Scholar] [CrossRef]
- Zhen, S.; Li, Y.; Liu, X.; Wang, J.; Chen, F.; Chen, X. A Lyapunov-based robust control for permanent magnet synchronous motor in the modular joint of collaborative robot. Robotica 2023, 41, 1389–1406. [Google Scholar] [CrossRef]
- Ocak, O.; Onsal, M.; Aydin, M. Development of a 7.5 kW high speed interior permanent magnet synchronous spindle motor for CNC milling machine. In Proceedings of the 2018 XIII International Conference on Electrical Machines, Alexandroupoli, Greece, 3–6 September 2018. [Google Scholar]
- Wang, L.; Tang, Z.; Zhang, P.; Liu, X.; Wang, D.; Li, X. Double extended sliding mode observer-based synchronous estimation of total inertia and load torque for PMSM-driven spindle-tool systems. IEEE Trans. Ind. Inform. 2023, 19, 8496–8507. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, X.; Zhao, W. Influence of nonlinearity of servo system electrical characteristics on motion smoothness of precision CNC machine tools. Precis. Eng. 2023, 83, 82–101. [Google Scholar] [CrossRef]
- Huang, Z.; Huang, X.; Zhang, J.; Fang, Y.; Lu, Q. Design of an interior permanent magnet synchronous traction motor for high speed railway applications. In Proceedings of the 6th IET International Conference on Power Electronics, Machines and Drives, Bristol, UK, 27–29 March 2012. [Google Scholar]
- Yu, D.; Huang, X.Y.; Fang, Y.T.; Zhang, J. Design and comparison of interior permanent magnet synchronous traction motors for high speed railway applications. In Proceedings of the 2017 IEEE Workshop on Electrical Machines Design, Control and Diagnosis, Nottingham, UK, 20–21 April 2017. [Google Scholar]
- Torrent, M.; Perat, J.I.; Jiménez, J.A. Permanent magnet synchronous motor with different rotor structures for traction motor in high speed trains. Energies 2018, 11, 1549. [Google Scholar] [CrossRef]
- Lin, F.-J. Real-time IP position controller design with torque feedforward control for PM synchronous motor. IEEE Trans. Ind. Electron. 1997, 44, 398–407. [Google Scholar]
- Lin, F.-J.; Lin, Y.-S. A robust PM synchronous motor drive with adaptive uncertainty observer. IEEE Trans. Energy Convers. 1999, 14, 989–995. [Google Scholar]
- Sul, S.-K. Control of Electric Machine Drive Systems; Wiley-IEEE Press: Hoboken, NJ, USA, 2010. [Google Scholar]
- Li, S.; Yang, J.; Chen, W.-H.; Chen, X. Disturbance Observer-Based Control Methods and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Yang, J.; Chen, W.H.; Li, S.; Guo, L.; Yan, Y. Disturbance/uncertainty estimation and attenuation techniques in PMSM drives—A survey. IEEE Trans. Ind. Electron. 2017, 64, 3273–3285. [Google Scholar] [CrossRef]
- Liu, T.-H.; Pu, H.-T.; Lin, C.-K. Implementation of an adaptive position control system of a permanent-magnet synchronous motor and its application. IET Electr. Power Appl. 2010, 4, 121–130. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Yu, H.; Chen, B.; Lin, C. Approximation-based discrete-time adaptive position tracking control for interior permanent magnet synchronous motors. IEEE Trans. Cybern. 2015, 45, 1363–1371. [Google Scholar] [CrossRef]
- Peresada, S.; Nikonenko, Y.; Reshetnyk, V.; Rodkin, D. Adaptive position control and self-commissioning of the interior permanent magnet synchronous motors. In Proceedings of the 2019 IEEE International Conference on Modern Electrical and Energy Systems, Kremenchuk, Ukraine, 23–25 September 2019. [Google Scholar]
- Lin, F.J.; Lin, C.H. A permanent-magnet synchronous motor servo drive using self-constructing fuzzy neural network controller. IEEE Trans. Energy Convers. 2004, 19, 66–72. [Google Scholar] [CrossRef]
- Kumar, V.; Gaur, P.; Mittal, A.P. ANN based self tuned PID like adaptive controller design for high performance PMSM position control. Expert Syst. Appl. 2014, 41, 7995–8002. [Google Scholar] [CrossRef]
- Tian, Z.; Guo, H.; Ding, X.; He, X. A PID neural network control for position servo system with gear box at variable load. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference, Hangzhou, China, 17–20 October 2016. [Google Scholar]
- Uddin, M.N.; Lau, J. Adaptive-backstepping-based design of a nonlinear position controller for an IPMSM servo drive. Can. J. Elect. Comput. Eng. 2007, 32, 97–102. [Google Scholar] [CrossRef]
- Linares-Flores, J.; García-Rodríguez, C.; Sira-Ramirez, H.; Ramírez-Cárdenas, O.D. Robust backstepping tracking controller for low-speed PMSM positioning system: Design, analysis, and implementation. IEEE Trans. Ind. Inform. 2015, 11, 1130–1141. [Google Scholar] [CrossRef]
- El-Sousy, F.F.; El-Naggar, M.F.; Amin, M.; Abu-Siada, A.; Abuhasel, K.A. Robust adaptive neural-network backstepping control design for high-speed permanent-magnet synchronous motor drives: Theory and experiments. IEEE Access 2019, 7, 99327–99348. [Google Scholar] [CrossRef]
- Fuentes, E.; Kennel, R.M. A finite-set model predictive position controller for the permanent magnet synchronous motor. In Proceedings of the 2013 IEEE International Symposium on Sensorless Control for Electrical Drives and Predictive Control of Electrical Drives and Power Electronics, Munich, Germany, 17–19 October 2013. [Google Scholar]
- Mubarok, M.S.; Liu, T.H. Implementation of predictive controllers for matrix-converter-based interior permanent magnet synchronous motor position control systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 261–273. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X. Model predictive position control of permanent magnet synchronous motor servo system with sliding mode observer. Asian J. Control 2023, 25, 443–461. [Google Scholar] [CrossRef]
- Lin, C.K.; Liu, T.H.; Yang, S.H. Nonlinear position controller design with input–output linearisation technique for an interior permanent magnet synchronous motor control system. IET Power Electron. 2008, 1, 14–26. [Google Scholar] [CrossRef]
- Chen, Y.-T.; Yu, C.-S.; Chen, P.-N. Feedback linearization based robust control for linear permanent magnet synchronous motors. Energies 2020, 13, 5242. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, H.; Wang, S. Development of optimized cooperative control based on feedback linearization and error port-controlled Hamiltonian for permanent magnet synchronous motor. IEEE Access 2021, 9, 141036–141047. [Google Scholar] [CrossRef]
- Lin, F.-J.; Chiu, S.-L.; Shyu, K.-K. Novel sliding mode controller for synchronous motor drive. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 532–542. [Google Scholar]
- Lin, F.-J.; Shyu, K.-K.; Lin, Y.-S. Variable structure adaptive control for PM synchronous servo motor drive. IEEE Proc.-Electr. Power Appl. 1999, 146, 173–185. [Google Scholar] [CrossRef]
- Wei, R.-J. Total sliding-mode controller for PM synchronous servo motor drive using recurrent fuzzy neural network. IEEE Trans. Ind. Electron. 2001, 48, 926–944. [Google Scholar]
- El-Sousy, F.F. Robust tracking control based on intelligent sliding-mode model-following position controllers for PMSM servo drives. J. Power Electron. 2007, 7, 159–173. [Google Scholar]
- Utkin, V.I.; Guldner, J.; Shi, J.X. Sliding-Mode Control in Electro-Mechanical Systems, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Wang, S.; Tao, L.; Chen, Q.; Na, J.; Ren, X. USDE-based sliding mode control for servo mechanisms with unknown system dynamics. IEEE/ASME Trans. Mechatron. 2020, 25, 1056–1066. [Google Scholar] [CrossRef]
- Lu, H.; Yang, D.; Su, Z. Improved sliding mode control for permanent magnet synchronous motor servo system. IET Power Electron. 2023, 16, 169–179. [Google Scholar] [CrossRef]
- El-Sousy, F.F.; Amin, M.M.; Aziz, G.A.A.; Al-Durra, A.; Mohammed, O.A. Optimal super-twisting sliding-mode control using adaptive dynamic programming for uncertain linear-stage considering PMSM servo drive dynamics. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition, Detroit, MI, USA, 11–15 October 2020. [Google Scholar]
- Gil, J.; You, S.; Lee, Y.; Kim, W. Super twisting-based nonlinear gain sliding mode controller for position control of permanent-magnet synchronous motors. IEEE Access 2021, 9, 142060–142070. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.T.; Le, K.M.; Tran, H.N.; Jeon, J.W. An adaptive backstepping sliding-mode control for improving position tracking of a permanent-magnet synchronous motor with a nonlinear disturbance observer. IEEE Access 2023, 11, 19173–19185. [Google Scholar] [CrossRef]
- Liang, D.; Li, J.; Qu, R. Sensorless control of permanent magnet synchronous machine based on second-order sliding-mode observer with online resistance estimation. IEEE Trans. Ind. Appl. 2017, 53, 3672–3682. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; N’Diaye, A.; Cirrincione, M. Active-flux-based super-twisting sliding mode observer for sensorless vector control of synchronous reluctance motor drives. In Proceedings of the 2018 7th International Conference on Renewable Energy Research and Applications, Paris, France, 14–17 October 2018. [Google Scholar]
- Sadeghi, R.; Madani, S.M.; Ataei, M.; Kashkooli, M.A.; Ademi, S. Super-twisting sliding mode direct power control of a brushless doubly fed induction generator. IEEE Trans. Ind. Electron. 2018, 65, 9147–9156. [Google Scholar] [CrossRef]
- Wang, H.; Ge, X.; Liu, Y.-C. Second-order sliding-mode MRAS observer based sensorless vector control of linear induction motor drives for medium-low speed maglev applications. IEEE Trans. Ind. Electron. 2018, 65, 9938–9952. [Google Scholar] [CrossRef]
- Scalcon, F.P.; Fang, G.; Vieira, R.P.; Gründling, H.A.; Emadi, A. Discrete-time super-twisting sliding mode current controller with fixed switching frequency for switched reluctance motors. IEEE Trans. Power Electron. 2022, 37, 3321–3333. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Y.; Ge, X.; Zuo, Y.; Feng, X.; Chen, D.; Liu, Y.-C. Speed-sensorless control of induction motor drives with a STA-FLL speed estimation scheme. IEEE Trans. Ind. Electron. 2023, 70, 12168–12180. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Birkhäuser: New York, NY, USA, 2014. [Google Scholar]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Derafa, L.; Benallegue, A.; Fridman, L. Super twisting control algorithm for the attitude tracking of a four rotors. J. Frankl. Inst. 2012, 349, 685–699. [Google Scholar] [CrossRef]
- Vazquez, C.; Collado, J.; Fridman, L. Super twisting control of a parametrically excited overhead crane. J. Frankl. Inst. 2014, 351, 2283–2298. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; N’Diaye, A.; Cirrincione, M. Hermite neural network-based second-order sliding-mode control of synchronous reluctance motor drive systems. J. Frankl. Inst. 2021, 358, 400–427. [Google Scholar] [CrossRef]
- Chen, J.; Shuai, Z.; Zhang, H.; Zhao, W. Path following control of autonomous four-wheel-independent-drive electric vehicles via second-order sliding mode and nonlinear disturbance observer techniques. IEEE Trans. Ind. Electron. 2021, 68, 2460–2469. [Google Scholar] [CrossRef]
- Basbas, H.; Liu, Y.-C.; Laghrouche, S.; Hilairet, M.; Plestan, F. Review on floating offshore wind turbine models for nonlinear control design. Energies 2022, 15, 5477. [Google Scholar] [CrossRef]
- Torres-González, V.; Fridman, L.M.; Moreno, J.A. Continuous twisting algorithm. In Proceedings of the 54th IEEE Conference on Decision and Control, Osaka, Japan, 15–18 December 2015. [Google Scholar]
- Torres-González, V.; Sanchez, T.; Fridman, L.M.; Moreno, J.A. Design of continuous twisting algorithm. Automatica 2017, 80, 119–126. [Google Scholar] [CrossRef]
- Moreno, J.A.; Negrete, D.Y.; Torres-González, V.; Fridman, L. Adaptive continuous twisting algorithm. Int. J. Control 2016, 89, 1798–1806. [Google Scholar] [CrossRef]
- Pérez, U.; Capello, E.; Punta, E.; Perea, J.; Fridman, L. Fault detection and isolation for a 3-DOF helicopter with sliding mode strategies. In Proceedings of the 15th International Workshop on Variable Structure Systems, Graz, Austria, 9–11 July 2018. [Google Scholar]
- Pérez-Ventura, U.; Fridman, L.; Capello, E.; Punta, E. Fault tolerant control based on continuous twisting algorithms of a 3-DoF helicopter prototype. Control Eng. Pract. 2020, 101, 104486. [Google Scholar] [CrossRef]
- Ríos, H.; Falcón, R.; González, O.A.; Dzul, A. Continuous sliding-mode control strategies for quadrotor robust tracking: Real-time application. IEEE Trans. Ind. Electron. 2019, 66, 1264–1272. [Google Scholar] [CrossRef]
- Mechali, O.; Xu, L.; Senouci, A.; Xie, X.; Xin, C.; Mechali, A. Finite-time observer-based robust continuous twisting control for the attitude of an uncertain quadrotor UAV subjected to disturbances. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation, Beijing, China, 13–16 October 2020. [Google Scholar]
- Savitski, D.; Ivanov, V.; Augsburg, K.; Emmei, T.; Fuse, H.; Fujimoto, H.; Fridman, L.M. Wheel slip control for the electric vehicle with in-wheel motors: Variable structure and sliding mode methods. IEEE Trans. Ind. Electron. 2020, 67, 8535–8544. [Google Scholar] [CrossRef]
- Tiwari, P.M. Continuous twisting sliding mode control for spacecraft attitude maneuver. In Proceedings of the IEEE 12th International Conference on Communication Systems and Network Technologies, Bhopal, India, 8–9 April 2023. [Google Scholar]
- Gutiérrez-Oribio, D.; Tzortzopoulos, G.; Stefanou, I.; Plestan, F. Earthquake control: An emerging application for robust control. theory and experimental tests. IEEE Trans. Control Syst. Technol. 2023, 31, 1747–1761. [Google Scholar] [CrossRef]
- Kumar, V.; Mohanty, S.R. Resilient optimal gain control and continuous twisting observer for enhanced power system performance under uncertainties. IEEE Syst. J. 2023, 17, 2733–2744. [Google Scholar] [CrossRef]
- Moreno, J.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008. [Google Scholar]
- Moreno, J.A. On strict Lyapunov functions for some non-homogeneous super-twisting algorithms. J. Frankl. Inst. 2014, 351, 1902–1919. [Google Scholar] [CrossRef]
- Yin, Y.; Vazquez, S.; Marquez, A.; Liu, J.; Leon, J.I.; Wu, L.; Franquelo, L.G. Observer-based sliding-mode control for grid-connected power converters under unbalanced grid conditions. IEEE Trans. Ind. Electron. 2022, 69, 517–527. [Google Scholar] [CrossRef]
- Luo, W.; Vazquez, S.; Liu, J.; Gordillo, F.; Franquelo, L.G.; Wu, L. Control system design of a three-phase active front end using a sliding-mode observer. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 739–748. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; Djerdir, A.; Cirrincione, M. Disturbance-observer-based complementary sliding-mode speed control for PMSM drives: A super-twisting sliding-mode observer-based approach. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5416–5428. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; N’Diaye, A.; Djerdir, A.; Cirrincione, M. Super-twisting sliding-mode observer-based model reference adaptive speed control for PMSM drives. J. Frankl. Inst. 2023, 360, 985–1004. [Google Scholar] [CrossRef]
- Derafa, L.; El Hadri, A.; Fridman, L. External perturbation estimation based on super-twisting algorithm for attitude control of UAVs. IFAC Proc. Vol. 2012, 45, 746–752. [Google Scholar] [CrossRef]
- Shi, D.; Wu, Z.; Chou, W. Super-twisting extended state observer and sliding mode controller for quadrotor UAV attitude system in presence of wind gust and actuator faults. Electronics 2018, 7, 128. [Google Scholar] [CrossRef]
- Muñoz, F.; Bonilla, M.; González-Hernández, I.; Salazar, S.; Lozano, R. Super twisting vs modified super twisting algorithm for altitude control of an unmanned aircraft system. In Proceedings of the 12th International Conference on Electrical Engineering, Computing Science and Automatic Control, Mexico City, Mexico, 28–30 October 2015. [Google Scholar]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; N’Diaye, A.; Djerdir, A.; Cirrincione, M. Disturbance-observer-based speed control for SPMSM drives using modified super-twisting algorithm and extended state observer. Asian J. Control 2024, 26, 1089–1102. [Google Scholar] [CrossRef]
- Liu, J.; Luo, W.; Yang, X.; Wu, L. Robust model-based fault diagnosis for PEM fuel cell air-feed system. IEEE Trans. Ind. Electron. 2016, 63, 3261–3270. [Google Scholar] [CrossRef]
- Yang, Q.; Mao, K.; Zheng, S.; Zhou, C.; Zhong, Q. Position sensorless drive with online parameters estimation for magnetic suspension centrifugal compressor. IEEE Trans. Power Electron. 2023, 38, 9384–9394. [Google Scholar] [CrossRef]
- El-Sousy, F.F. Intelligent optimal recurrent wavelet Elman neural network control system for permanent-magnet synchronous motor servo drive. IEEE Trans. Ind. Inform. 2012, 9, 1986–2003. [Google Scholar] [CrossRef]
- El-Sousy, F.F. Adaptive hybrid control system using a recurrent RBFN-based self-evolving fuzzy-neural-network for PMSM servo drives. Appl. Soft Comput. 2014, 21, 509–532. [Google Scholar] [CrossRef]
- Lin, F.-J.; Huang, M.-S.; Chien, Y.-C.; Chen, S.-G. Intelligent backstepping control of permanent magnet-assisted synchronous reluctance motor position servo drive with recurrent wavelet fuzzy neural network. Energies 2023, 16, 5389. [Google Scholar] [CrossRef]
- Lin, F.-J.; Wang, P.-L.; Hsu, I.-M. Intelligent nonsingular terminal sliding mode controlled nonlinear time-varying system using RPPFNN-AMF. IEEE Trans. Fuzzy Syst. 2024, 32, 1036–1049. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2001. [Google Scholar]


| Set | |||||
|---|---|---|---|---|---|
| 1 | 25 | 15 | 2.3 | 1.1 | |
| 2 | 19 | 10 | 2.3 | 1.1 | |
| 3 | 13 | 7.5 | 2.3 | 1.1 | |
| 4 | 7 | 5 | 2.3 | 1.1 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Nominal power | 1 | Pole pairs | 2 |
| Nominal current | 4 | Nominal speed | 1800 |
| Stator resistance | 1.5 Ω | Nominal torque (N·m) | 3.6 |
| Stator inductance | 0.05 H | Nominal inertia (kg·m2) | 0.003 |
| Permanent-magnet flux linkage | 0.314 | Viscous friction coefficient | 0.0009 |
| Position Controller | Controller Parameters | Observer Parameters |
|---|---|---|
| CTA-PC | ,, , , | - |
| Composite Position Controller Using CTA-PC and Standard STA-DO | ,, , , | ,, , |
| Proposed Composite Poisition Controller | ,, , , | ,, , |
| Position Controller | Maximum Tracking Error (Deg) | Settling Time (s) |
|---|---|---|
| CTA-PC | 12.13 | 1.66 |
| Composite Position Controller Using CTA-PC and Standard STA-DO | 11.39 | 1.08 |
| Proposed Composite Position Controller | 9.81 | 0.78 |
| Position Controller | Maximum Tracking Error (Deg) | Settling Time (s) |
|---|---|---|
| CTA-PC | 6.85 | 1.35 |
| Composite Position Controller Using CTA-PC and Standard STA-DO | 6.44 | 0.88 |
| Proposed Composite Position Controller | 5.71 | 0.65 |
| Position Controller | Maximum Tracking Error (Deg) | Settling Time (s) |
|---|---|---|
| CTA-PC | 7.03 | 1.34 |
| Composite Position Controller Using CTA-PC and Standard STA-DO | 6.60 | 0.87 |
| Proposed Composite Position Controller | 5.83 | 0.65 |
| Position Controller | Maximum Tracking Error (Deg) | Settling Time (s) |
|---|---|---|
| CTA-PC | 3.96 | 1.06 |
| Composite Position Controller Using CTA-PC and Standard STA-DO | 3.72 | 0.69 |
| Proposed Composite Position Controller | 3.38 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.-C. Disturbance-Observer-Based Second-Order Sliding-Mode Position Control for Permanent-Magnet Synchronous Motors: A Continuous Twisting Algorithm-Based Approach. Energies 2024, 17, 2974. https://doi.org/10.3390/en17122974
Liu Y-C. Disturbance-Observer-Based Second-Order Sliding-Mode Position Control for Permanent-Magnet Synchronous Motors: A Continuous Twisting Algorithm-Based Approach. Energies. 2024; 17(12):2974. https://doi.org/10.3390/en17122974
Chicago/Turabian StyleLiu, Yong-Chao. 2024. "Disturbance-Observer-Based Second-Order Sliding-Mode Position Control for Permanent-Magnet Synchronous Motors: A Continuous Twisting Algorithm-Based Approach" Energies 17, no. 12: 2974. https://doi.org/10.3390/en17122974
APA StyleLiu, Y.-C. (2024). Disturbance-Observer-Based Second-Order Sliding-Mode Position Control for Permanent-Magnet Synchronous Motors: A Continuous Twisting Algorithm-Based Approach. Energies, 17(12), 2974. https://doi.org/10.3390/en17122974







