Optimization of Dropwise Condensation of Steam over Hybrid Hydrophobic–Hydrophilic Surfaces via Enhanced Statistically Based Heat Transfer Modelization
Abstract
1. Introduction
2. Physical Model
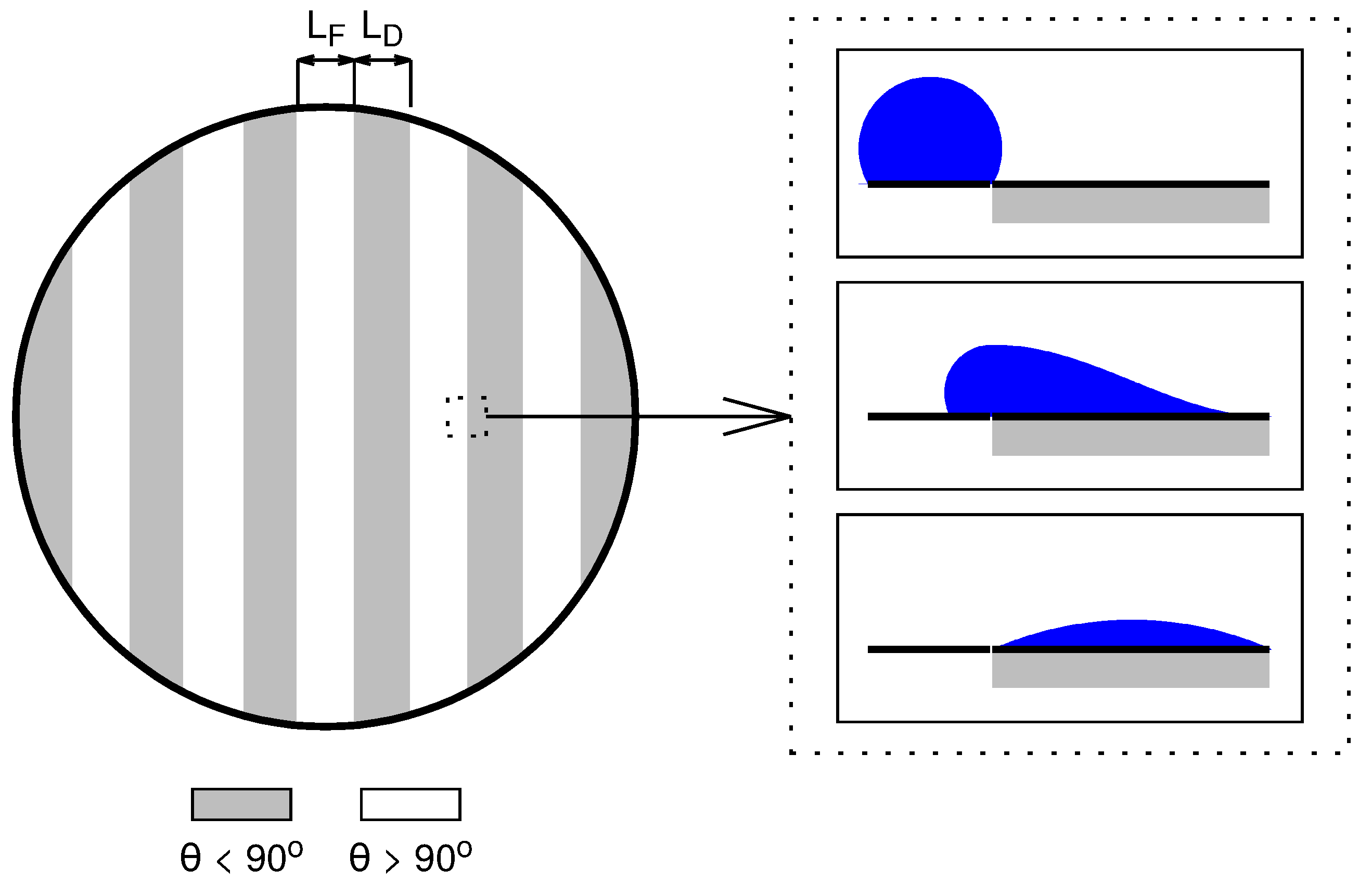
2.1. Problem Statement
2.2. Dropwise Condensation Model
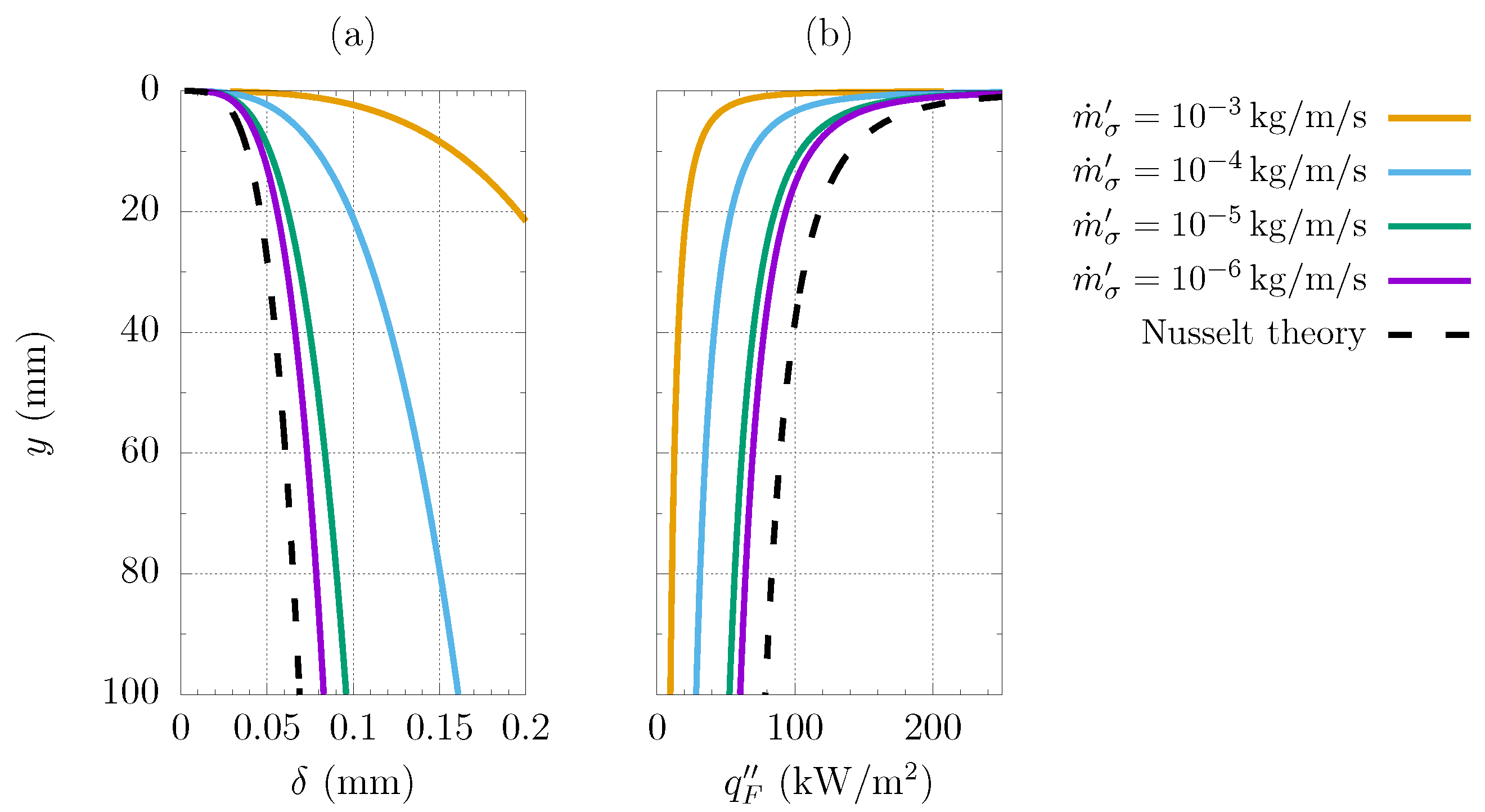
2.3. Filmwise Condensation Model
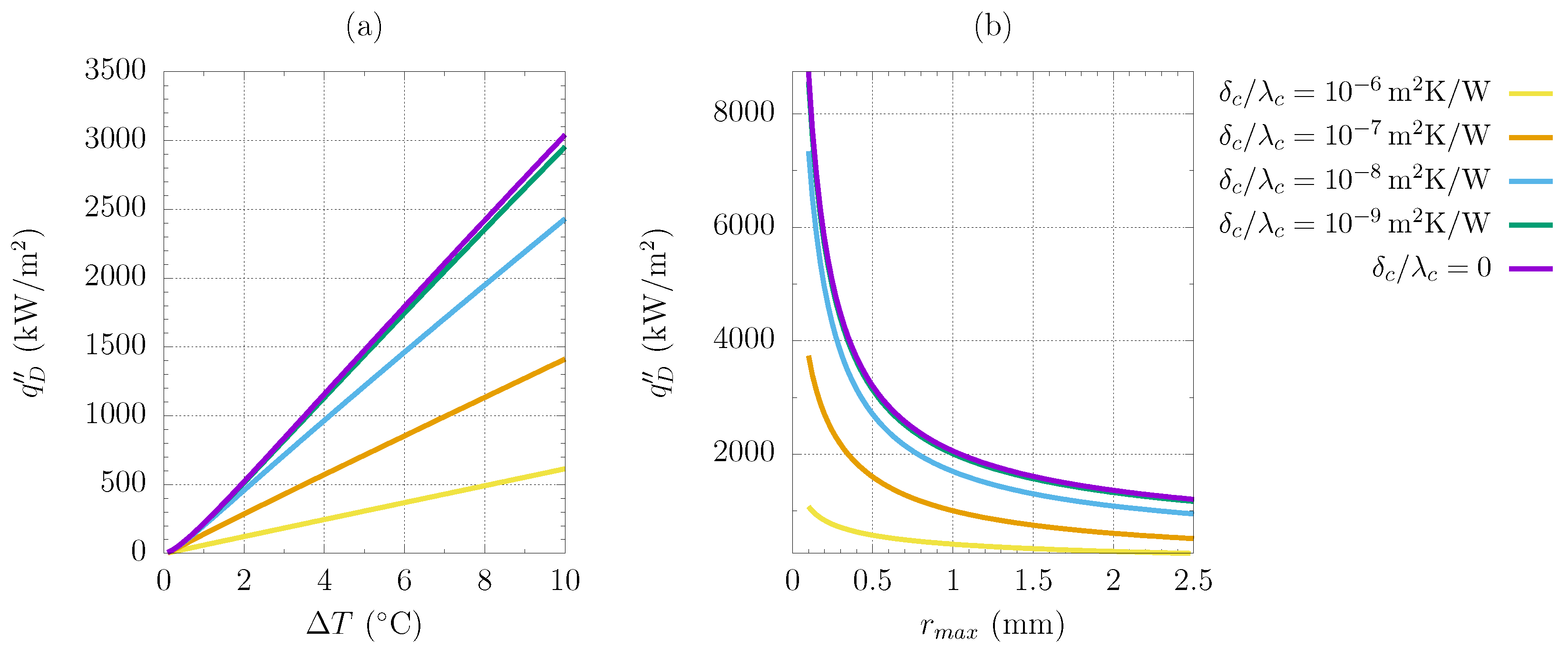
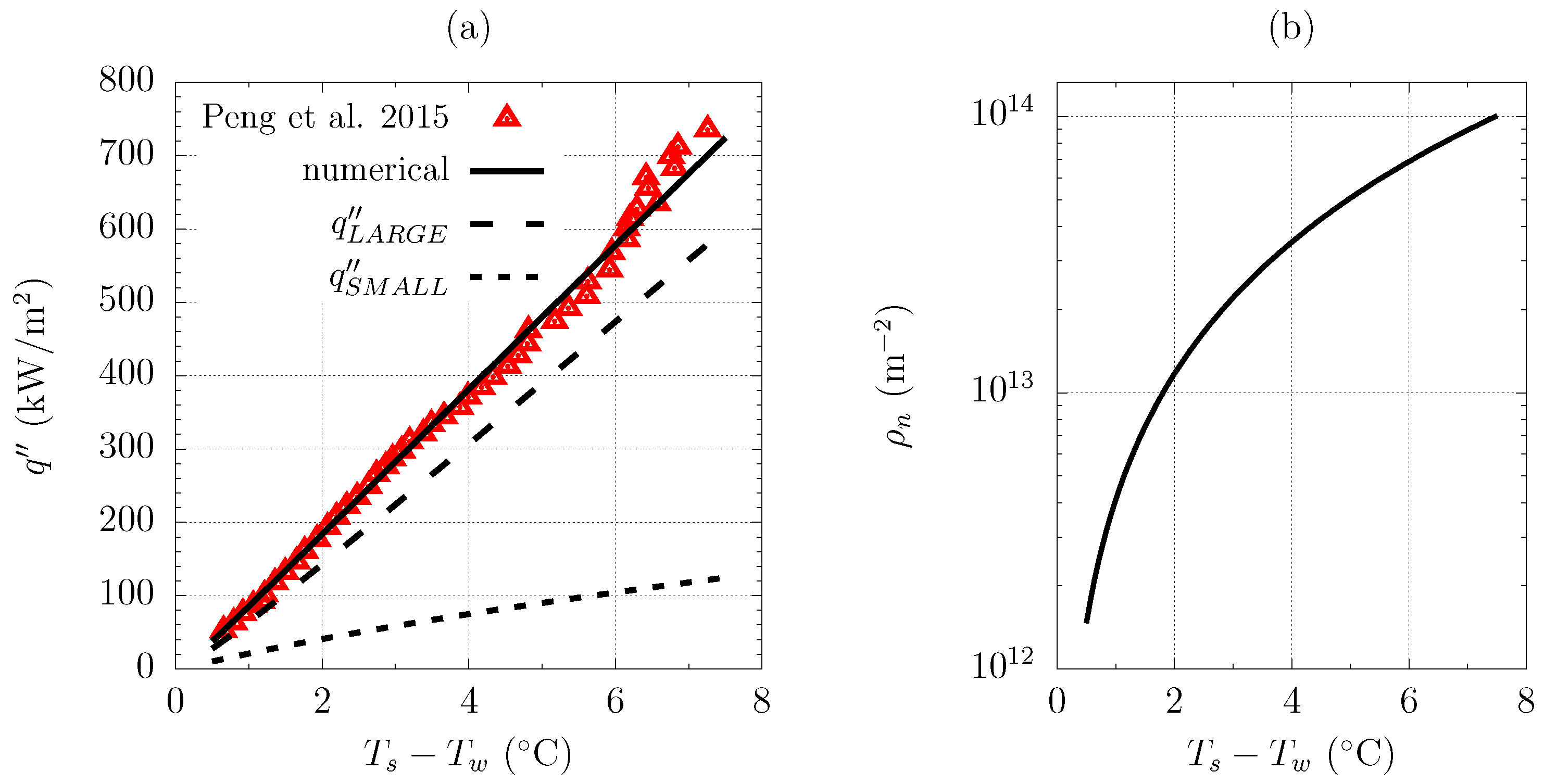
3. Results
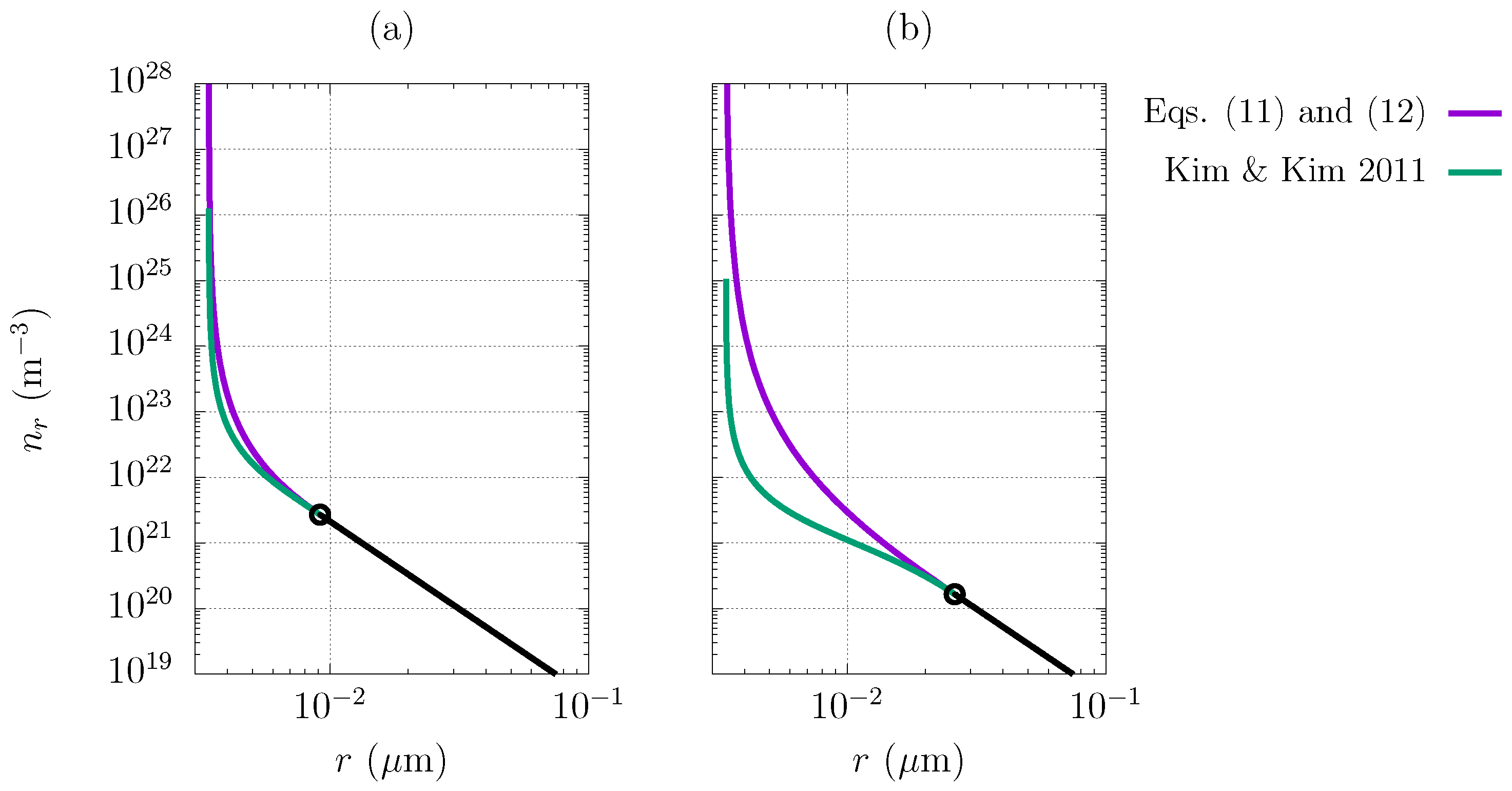
3.1. Model Validation
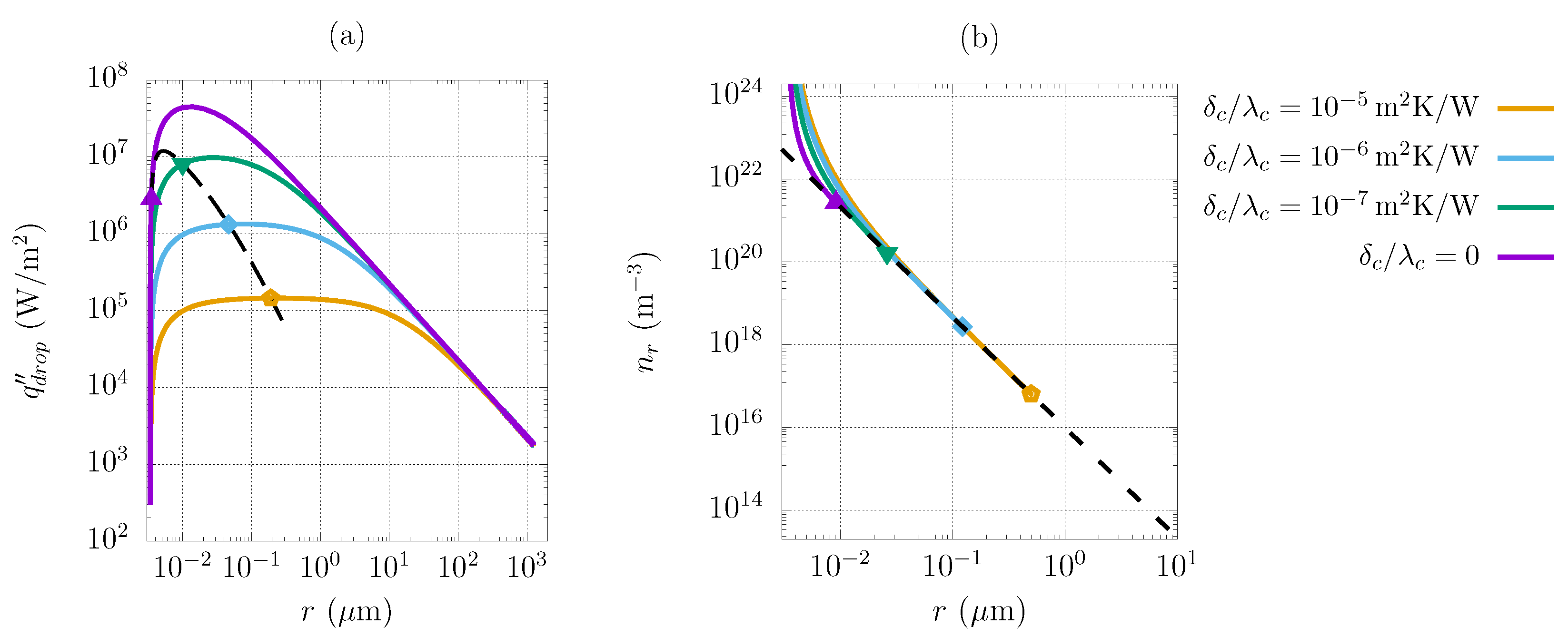
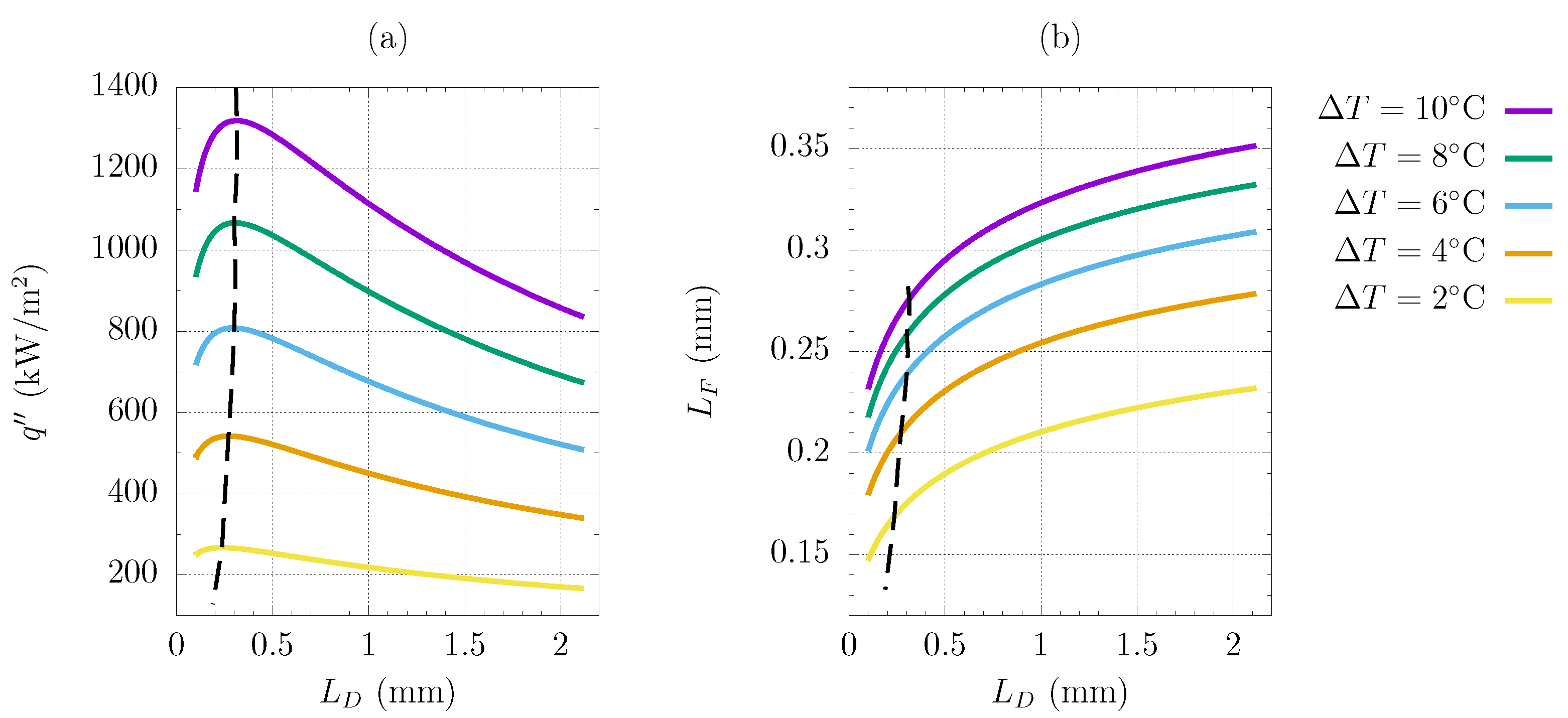
3.2. Hybrid Surface Optimization
- For a given substrate subcooling, the DWC specific heat flux was computed via Equation (5) as a function of the hydrophobic width ;
- The migrating flow rate per unit length was derived via Equation (26) as a function of and ;
- The critical hydrophilic width was computed as a function of , which in turn depends on the investigated value of ;
- Once had been traced as a function of , the FWC specific heat flux was computed via Equation (29) and combined with in order to estimate the global heat flux of the hybrid surface;
- The best configuration for a given substrate subcooling was identified as the one corresponding to the maximum global heat flux.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
| Abbreviations | |
| PBM | Probability-based model |
| IBM | Individual-based model |
| DWC | Dropwise condensation |
| FWC | Filmwise condensation |
| SAM | Self-assembled monolayer |
| Nomenclature | |
| Greek symbols | |
| rivulet thickness | |
| coating thickness | |
| availability | |
| static contact angle | |
| thermal conductivity | |
| dynamic viscosity | |
| density | |
| nucleation density | |
| surface tension | |
| sweeping time | |
| Other symbols | |
| g | gravity acceleration |
| G | droplet growth rate |
| latent heat of vaporization | |
| capillary length | |
| hydrophobic width | |
| hydrophilic width | |
| liquid mass flow rate | |
| small drop size distribution | |
| large drop size distribution | |
| q | heat flux |
| specific heat flux | |
| r | droplet radius |
| critical nucleation radius | |
| departure radius | |
| specific gas constant | |
| t | time |
| saturation temperature °C | |
| solid wall temperature °C | |
| y | downhill coordinate |
| Subscripts | |
| D | dropwise |
| e | coalescence |
| F | filmwise |
| n | nucleation |
| l | liquid |
| v | vapor |
References
- Parin, R.; Martucci, A.; Sturaro, M.; Bortolin, S.; Bersani, M.; Carraro, F.; Del Col, D. Nano-structured aluminum surfaces for dropwise condensation. Surf. Coatings Technol. 2018, 348, 1–12. [Google Scholar] [CrossRef]
- Alwazzan, M.; Egab, K.; Peng, B.; Khan, J.; Li, C. Condensation on hybrid-patterned copper tubes (I): Characterization of condensation heat transfer. Int. J. Heat Mass Transf. 2017, 112, 991–1004. [Google Scholar] [CrossRef]
- Zhang, B.J.; Kuok, C.; Kim, K.J.; Hwang, T.; Yoon, H. Dropwise steam condensation on various hydrophobic surfaces: Polyphenylene sulfide (PPS), polytetrafluoroethylene (PTFE), and self-assembled micro/nano silver (SAMS). Int. J. Heat Mass Transf. 2015, 89, 353–358. [Google Scholar] [CrossRef]
- Pang, G.; Dale, J.D.; Kwok, D.Y. An integrated study of dropwise condensation heat transfer on self-assembled organic surfaces through Fourier transform infra-red spectroscopy and ellipsometry. Int. J. Heat Mass Transf. 2005, 48, 307–316. [Google Scholar] [CrossRef]
- Peng, B.; Ma, X.; Lan, Z.; Xu, W.; Wen, R. Experimental investigation on steam condensation heat transfer enhancement with vertically patterned hydrophobic-hydrophilic hybrid surfaces. Int. J. Heat Mass Transf. 2015, 83, 27–38. [Google Scholar] [CrossRef]
- Stevens, K.A.; Crockett, J.; Maynes, D.; Iverson, B.D. Simulation of Drop-Size Distribution during Dropwise and Jumping Drop Condensation on a Vertical Surface: Implications for Heat Transfer Modeling. Langmuir 2019, 35, 12858–12875. [Google Scholar] [CrossRef]
- Subramanian, R.S.; Moumen, N.; Mc Laughlin, J.B. Motion of a drop on a solid surface due to a wettability gradient. Langmuir 2005, 21, 11844–11849. [Google Scholar] [CrossRef]
- Xie, J.; Xu, J.; Shang, W.; Zhang, K. Dropwise condensation on superhydrophobic nanostructure surface, part II: Mathematical model. Int. J. Heat Mass Transf. 2018, 127, 1170–1187. [Google Scholar] [CrossRef]
- Alwazzan, M.; Egab, K.; Peng, B.; Khan, J.; Li, C. Condensation on hybrid-patterned copper tubes (II): Visualization study of droplet dynamics. Int. J. Heat Mass Transf. 2017, 112, 950–958. [Google Scholar] [CrossRef]
- Yang, K.S.; Lin, K.H.; Tu, C.W.; He, Y.Z.; Wang, C.C. Experimental investigation of moist air condensation on hydrophilic, hydrophobic, superhydrophilic, and hybrid hydrophobic-hydrophilic surfaces. Int. J. Heat Mass Transf. 2017, 115, 1032–1041. [Google Scholar] [CrossRef]
- Croce, G.; Suzzi, N. Numerical simulation of dropwise condensation of steam over hybrid Surfaces via new non-dimensional heat transfer model. Fluids 2023, 8, 300. [Google Scholar] [CrossRef]
- Tancon, M.; Bortolin, S.; Del Col, D. Modeling of growth and dynamics of droplets during dropwise condensation of steam. Int. J. Heat Mass Transf. 2024, 222, 125109. [Google Scholar]
- Suzzi, N.; Croce, G. Numerical simulation of dropwise condensation over hydrophobic surfaces using vapor-diffusion model. Appl. Therm. Eng. 2022, 214, 118806. [Google Scholar] [CrossRef]
- Suzzi, N.; Croce, G.; D’Agaro, P. Numerical prediction of dropwise condensation performances over hybrid surfaces, under the action of gravity and vapor shear. In Proceedings of the ASME 18th International Conference on Nanochannels, Microchannels, and Minichannels, ICNMM, Online, 13–15 July 2020; p. ICNMM2020-1075. [Google Scholar]
- Croce, G.; D’Agaro, P.; Suzzi, N. Optimization of hybrid hydrophilic-hydrophobic surfaces for dropwise condensation enhancement. In Proceedings of the ASME 17th International Conference on Nanochannels, Microchannels, and Minichannels, ICNMM, St. John’s, NL, Canada, 23–26 June 2019; p. ICNMM2019-4291. [Google Scholar]
- Le Fevre, E.J.; Rose, J.W. A theory of heat transfer by dropwise condensation. In Proceedings of the 3rd International Heat Transfer Conference, Chicago, IL, USA, 7–12 August 1966; pp. 362–375. [Google Scholar]
- Kim, S.; Kim, K.J. Dropwise Condensation Modeling Suitable for Superhydrophobic Surfaces. ASME J. Heat Transf. 2011, 133, 081502. [Google Scholar] [CrossRef]
- Miljkovic, N.; Enright, R.; Wang, E.N. Modeling and Optimization of Superhydrophobic Condensation. ASME J. Heat Mass Transf. 2013, 135, 111004. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, P. Dropwise condensation theory revisited: Part I. Droplet nucleation radius. Int. J. Heat Mass Transf. 2015, 83, 833–841. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, P. Dropwise condensation theory revisited Part II. Droplet nucleation density and condensation heat flux. Int. J. Heat Mass Transf. 2015, 83, 842–849. [Google Scholar] [CrossRef]
- Lethuillier, J.; Lavieille, P.; Topin, F.; Miscevic, M. About Phenomenology and Modeling of Dropwise Condensation. In The Surface Wettability Effect on Phase Change; Springer: Cham, Switzerland, 2022; pp. 69–104. [Google Scholar]
- Suzzi, N.; Croce, G. Effect of hydrophobic coating on optimization of dropwise condensation of steam on hybrid surfaces. J. Phys. Conf. Ser. 2024; in press. [Google Scholar]
- Rose, J.W. Further aspects of dropwise condensation theory. Int. J. Heat Nad Mass Transf. 1976, 19, 1363–1370. [Google Scholar] [CrossRef]
- Peng, B.; Ma, X.; Lan, Z.; Xu, W.; Wen, R. Analysis of condensation heat transfer enhancement with dropwise-filmwise hybrid surface: Droplet sizes effect. Int. J. Heat Mass Transf. 2014, 77, 785–794. [Google Scholar] [CrossRef]
- Nusselt, W. Die Oberflachenkondensation des Wasserdampfes. Z. Ver. Dtsch. Ingenieure 1916, 60, 541–546, 569–575. [Google Scholar]
- Song, L.; Zhang, Y.; Yang, W.; Tan, J.; Cheng, L. Molecular Structure Effect of a Self-Assembled Monolayer on Thermal Resistance across an Interface. Polymers 2021, 13, 3732. [Google Scholar] [CrossRef]
- Mu, C.; Pang, J.; Lu, Q.; Liu, T. Effects of surface topography of material on nucleation site density of dropwise condensation. Chem. Eng. Sci. 2008, 63, 874–880. [Google Scholar] [CrossRef]
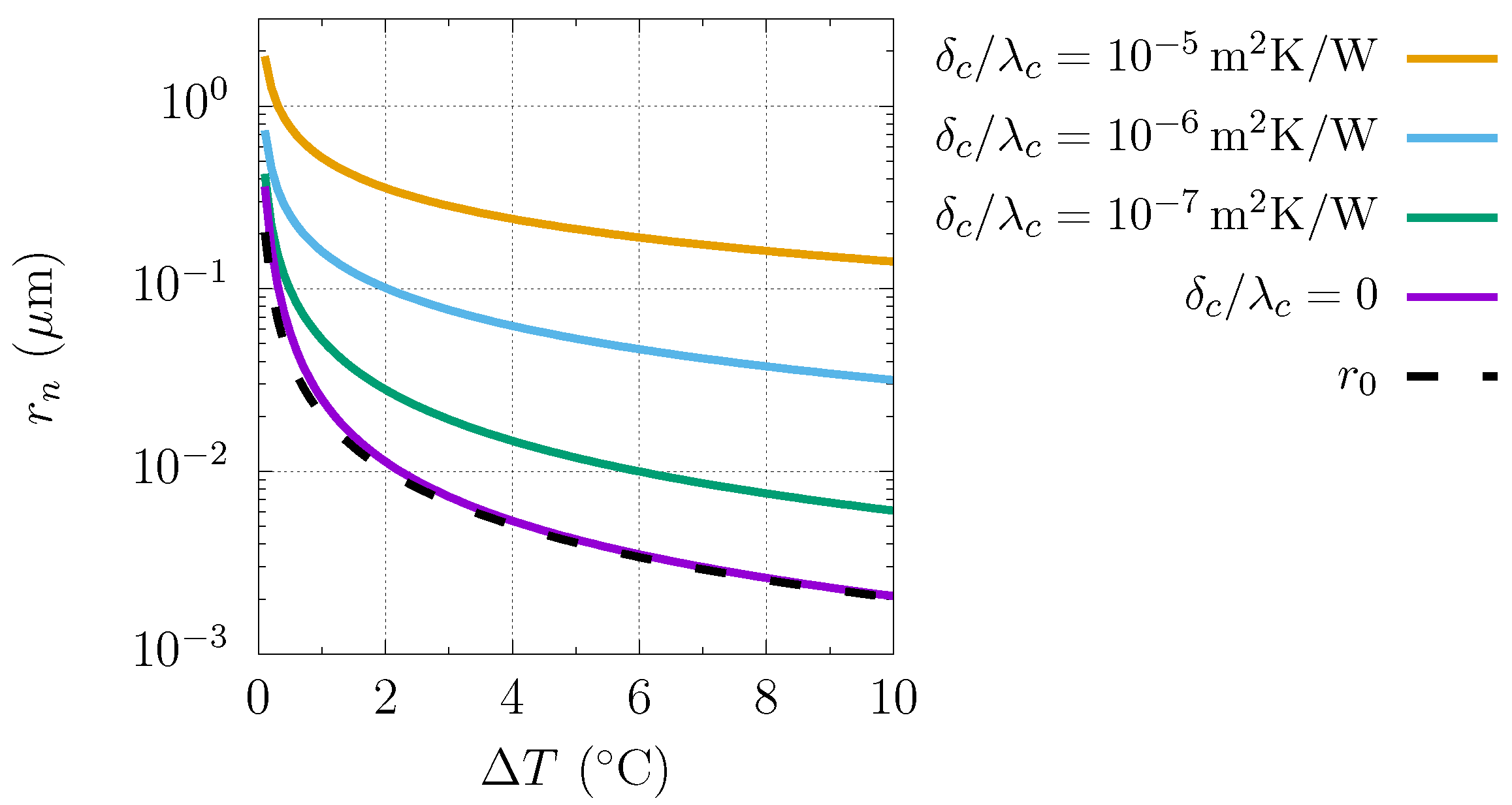
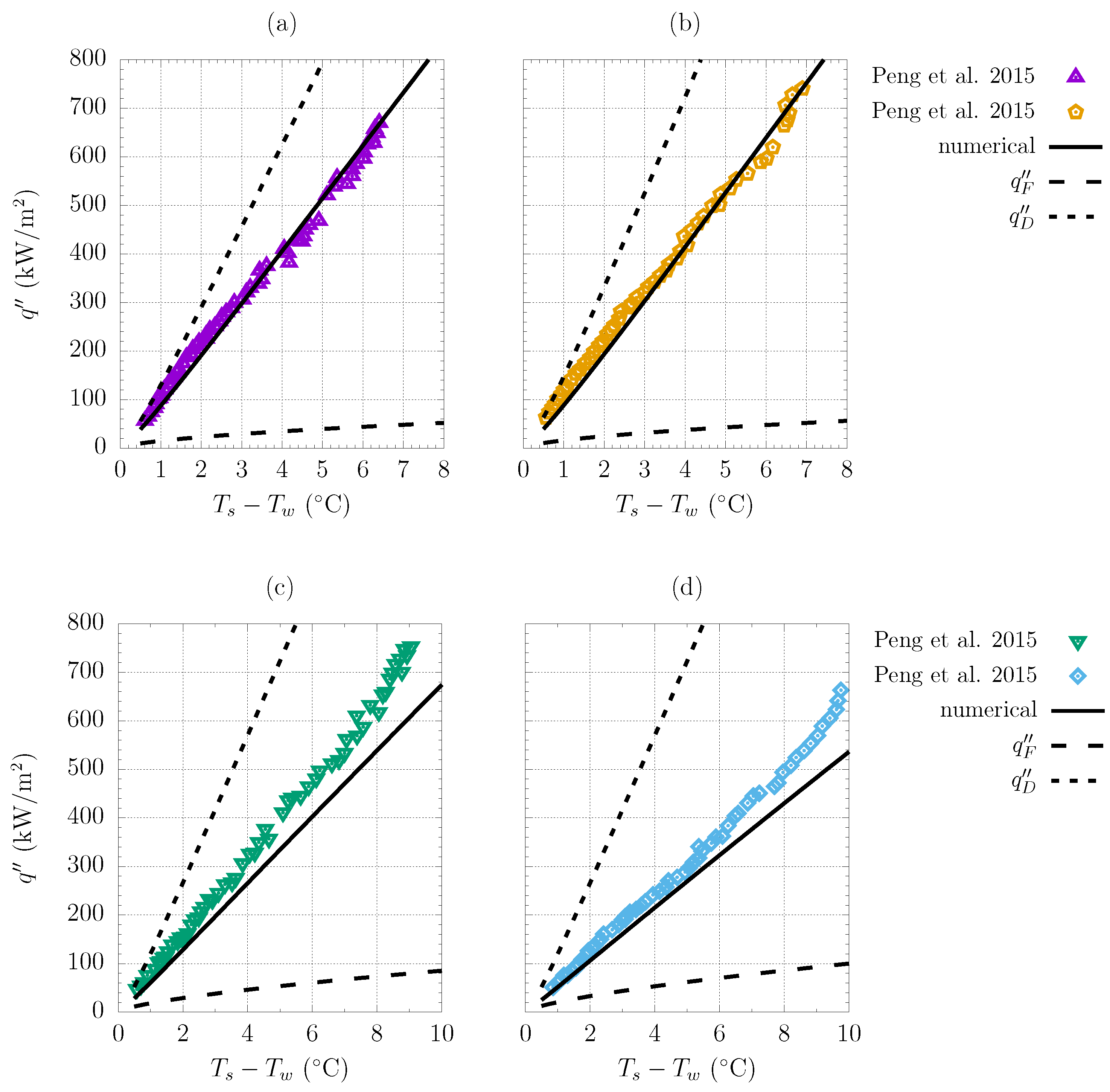

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Croce, G.; Suzzi, N. Optimization of Dropwise Condensation of Steam over Hybrid Hydrophobic–Hydrophilic Surfaces via Enhanced Statistically Based Heat Transfer Modelization. Energies 2024, 17, 2742. https://doi.org/10.3390/en17112742
Croce G, Suzzi N. Optimization of Dropwise Condensation of Steam over Hybrid Hydrophobic–Hydrophilic Surfaces via Enhanced Statistically Based Heat Transfer Modelization. Energies. 2024; 17(11):2742. https://doi.org/10.3390/en17112742
Chicago/Turabian StyleCroce, Giulio, and Nicola Suzzi. 2024. "Optimization of Dropwise Condensation of Steam over Hybrid Hydrophobic–Hydrophilic Surfaces via Enhanced Statistically Based Heat Transfer Modelization" Energies 17, no. 11: 2742. https://doi.org/10.3390/en17112742
APA StyleCroce, G., & Suzzi, N. (2024). Optimization of Dropwise Condensation of Steam over Hybrid Hydrophobic–Hydrophilic Surfaces via Enhanced Statistically Based Heat Transfer Modelization. Energies, 17(11), 2742. https://doi.org/10.3390/en17112742





