Network Reconfiguration for Loss Reduction Using Tabu Search and a Voltage Drop
Highlights
- A method for the systematic calculation of voltage differentials between component buses is introduced, providing a well-informed starting point crucial to the successful implementation of tabu search algorithms.
- A hybrid approach to generate neighborhoods which incorporates both voltage differences and randomness is adopted. This ensures consistently robust solutions at search speeds surpassing deterministic algorithms. The overall convergence is effective, yielding positive results in most cases.
- The main findings suggest a notable advancement in electrical network reconfiguration. Because it involves systematic voltage differential calculations and a hybrid neighborhood-generation approach, the proposed methodolgy promises enhanced efficiency. With an optimized initial solution and sustained robustness, the method is well-positioned to assist in the successful implementation of tabu search algorithms. Positive convergence results affirm the method's practical feasibility, offering improved solutions for minimizing losses in real-world electrical network reconfiguration.
Abstract
1. Introduction
- A method for calculating the voltage drop between the component buses of the meshes in order to generate an initial solution. This approach allows the tabu search algorithm to begin with a good solution, which is necessary for tabu search techniques to be implemented successfully;
- The hybrid neighborhood-generating method leverages the voltage drop information, which is a critical factor in energy systems, to guide the search process. By considering the voltage drop, the algorithm can focus on areas where improvements are most needed, ensuring that the generated solutions adhere to voltage stability requirements. This approach enhances the algorithm’s ability to explore promising regions of the solution space efficiently;
- The proposed method has demonstrated remarkable success in terms of achieving favorable conditions for initializing the initial solution and sustaining a productive neighborhood throughout the optimization process. This approach ensures that the algorithm starts from a promising point in the solution space, enhancing its chances of finding optimal solutions.
2. Theoretical Foundation
2.1. Distribution Network Reconfiguration Problem
2.1.1. Objective Function
2.1.2. Constraints
- Voltage Constraints:The voltage in the bus must satisfy the minimum and maximum limits, as follows:where is the minimum and is the maximum voltage value allowed for a given bus k. Commonly adopted values are 0.95 pu and 1.05 pu. This condition is valid for all buses in the system.
- Current Constraints:The current limit constraint on the branch is due to the technical characteristics of the branch used in the distribution system. The current passing through a line () cannot exceed the maximum current supported by that line (), as in:
- Radiality Constraints:The act of opening and closing switches in a distribution system must be performed in such a way that the system’s radiality is preserved. Radiality is defined as the lack of meshes in the system as well as the fulfillment of all related loads. The conditions for the imposition of radiality employed in this work are taken from Lavorato et al. [15] and are given below:
- Condition 1: the solution must have ; where A is the number of active branches, is the number of buses in the system, and is the number of substation buses in the system;
- Condition 2: The system must be connected. This implies that, in addition to the fact that the system must be connected to some substation, all loads must be attended to.
2.2. Classic Tabu Search Algorithm
- Initial solution: a feasible solution from the problem, namely, an initial solution, which is generally obtained by using the heuristic rule;
- Current solution: a possible solution to the problem;
- Movement: mechanism for generating a new solution by applying a perturbation in the current solution;
- Neighborhood: A feasible solution is derived from the original feasible solutions by searching with the movement strategy by determining which conforms to the problem constraints;
- Tabu List: list of last performed moves prohibited from being performed again by T iterations. In practice, the presence of the tabu list prevents cycling in the algorithm;
- Aspiration Criteria: list of criteria for a solution containing movements from the tabu list to be adopted as the current solution. If a generated neighbor is the best solution ever found but has moves in the tabu list, it can be accepted as the current solution.
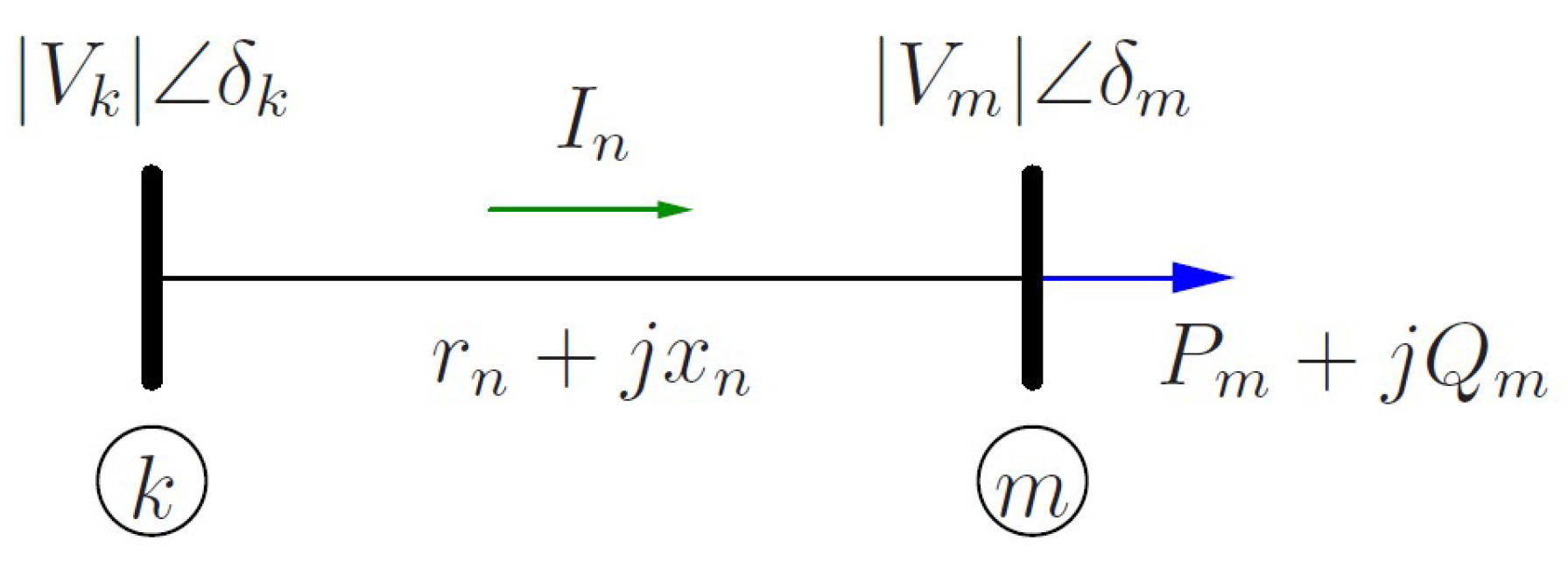
2.3. The Kirchhoff’s Circuit Laws and the Voltage Drop
- Kirchhoff’s law for current says that the algebraic sum of currents entering into the bus is zero [20], i.e.:where N is the number of branches connected to the bus and is the n-th current entering or leaving the bus.
- Kirchhoff’s law for voltage says that the algebraic sum of all voltages around a closed path (or loop, or mesh) is zero [20], i.e.:where M is the number of voltages in the loop (loads, sources, conductors, etc.) and is the m-th voltage.
3. The Modified Tabu Search Algorithm
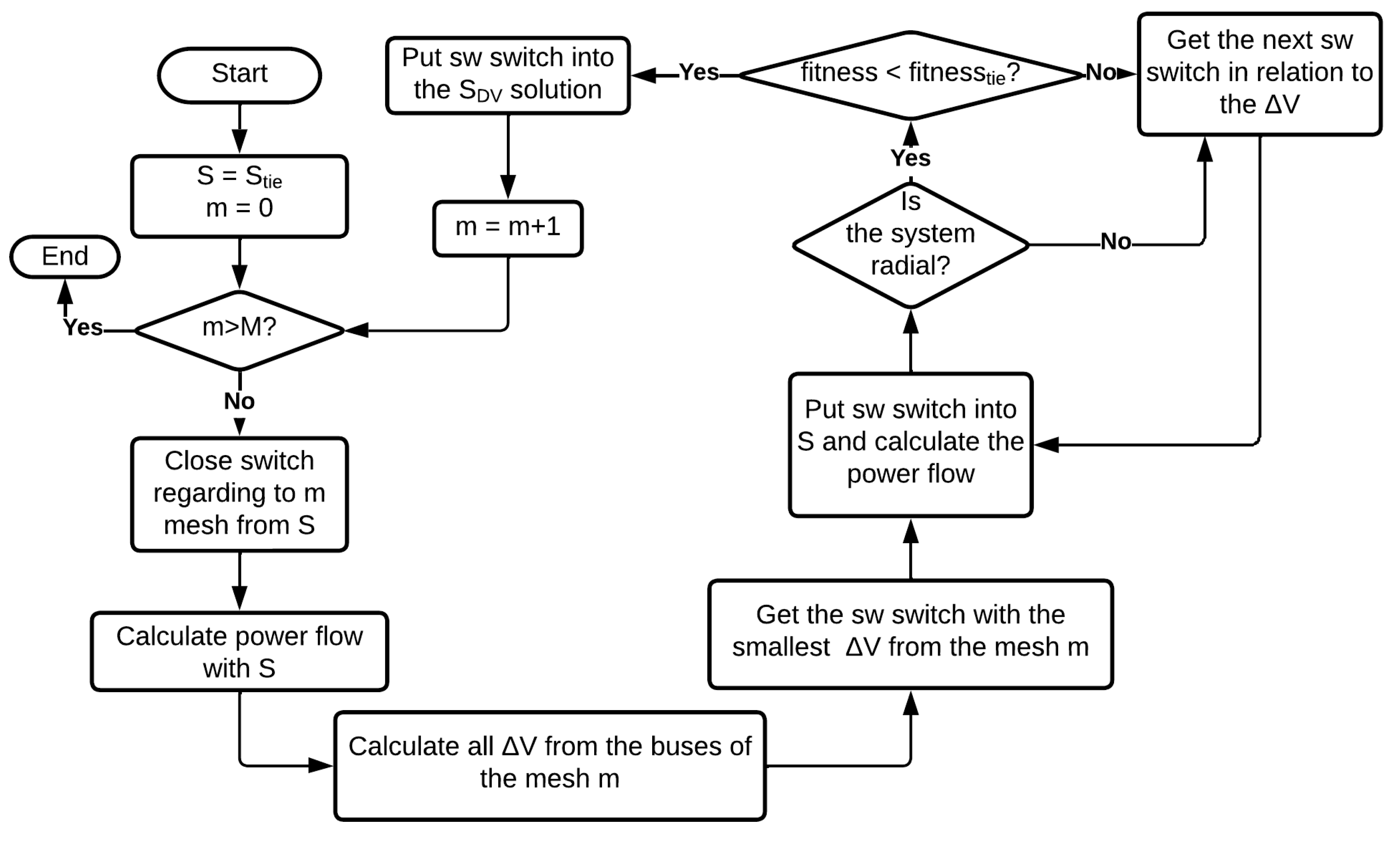
3.1. Initial Solution Using the Voltage Drop
3.2. The Hybrid Neighborhood Algorithm
- For a random algorithm: the algorithm randomly chooses whether the new switch will be immediately to the left or right of the currently opened switch and then chooses the new switch;
- For the algorithm: all the between the buses that have conductors connecting them within that mesh are calculated and then the chosen switch is the one with the smallest .
- For the algorithm with an emphasis on randomness: after generating the M neighbors that were generated by choosing the switch immediately lateral to the switch of S, it is possible to obtain neighbors going further, selecting not only those immediately to the left or immediately to right but also the second switch to the left or right and so on. To avoid this, the method is also limited to “walking” only to the number of switches that the smallest mesh has, to avoid having very distant neighbors;
- For the algorithm: after generating the M neighbors that were generated with the smallest of each mesh, it is possible to generate other M neighbors with the second smallest of each mesh and so on, up to the size of the smallest mesh of the system as was done for the case of randomness.
4. Application of the Modified Tabu Search
- In this step, the lines, switches, loads, and feeds are added, as well as the variables (number of iterations without improvement), T (size of the tabu list), (maximum number of iterations), and (number of neighbors to be generated at each iteration) are set;
- Get the initial solution using the method, as seen in Section 3.1;
- The iterative loop begins. . If is even, neighbors with an emphasis on randomness are generated. If is odd, the neighbors of the voltage differences are generated. Each neighbor already tracks its active loss value for that topology;
- The neighborhood is ordered according to the losses that each neighbor generates, in ascending order of losses, that is, the first neighbor will be the best, as it will have the lowest loss value. This neighbor is selected;
- If this neighbor is the best solution found during this iteration, the new S will be this neighbor (by the aspiration criterion); if not, the neighbor will be checked if any switch is on the tabu list. If not, it will be the new S solution. If it is in the tabu list, the algorithm will select the second best neighbor and perform the described test again until it finds a neighbor that has no switches on the tabu list. With the new S chosen, the tabu list is updated;
- If this new S solution is the best found, save it as (best solution ever found), save its losses as (best fitness ever found), and save the iteration number as ;
- Check the stopping criteria: if is greater than or if reaches the value of , the algorithm stops and goes to step 8. If none of the criteria are met, go to step 3;
- Show the results: the best solution found, the losses of the best solution, and the minimum and maximum voltages of this solution.
5. Simulations and Results
5.1. Initial Solution Method Results
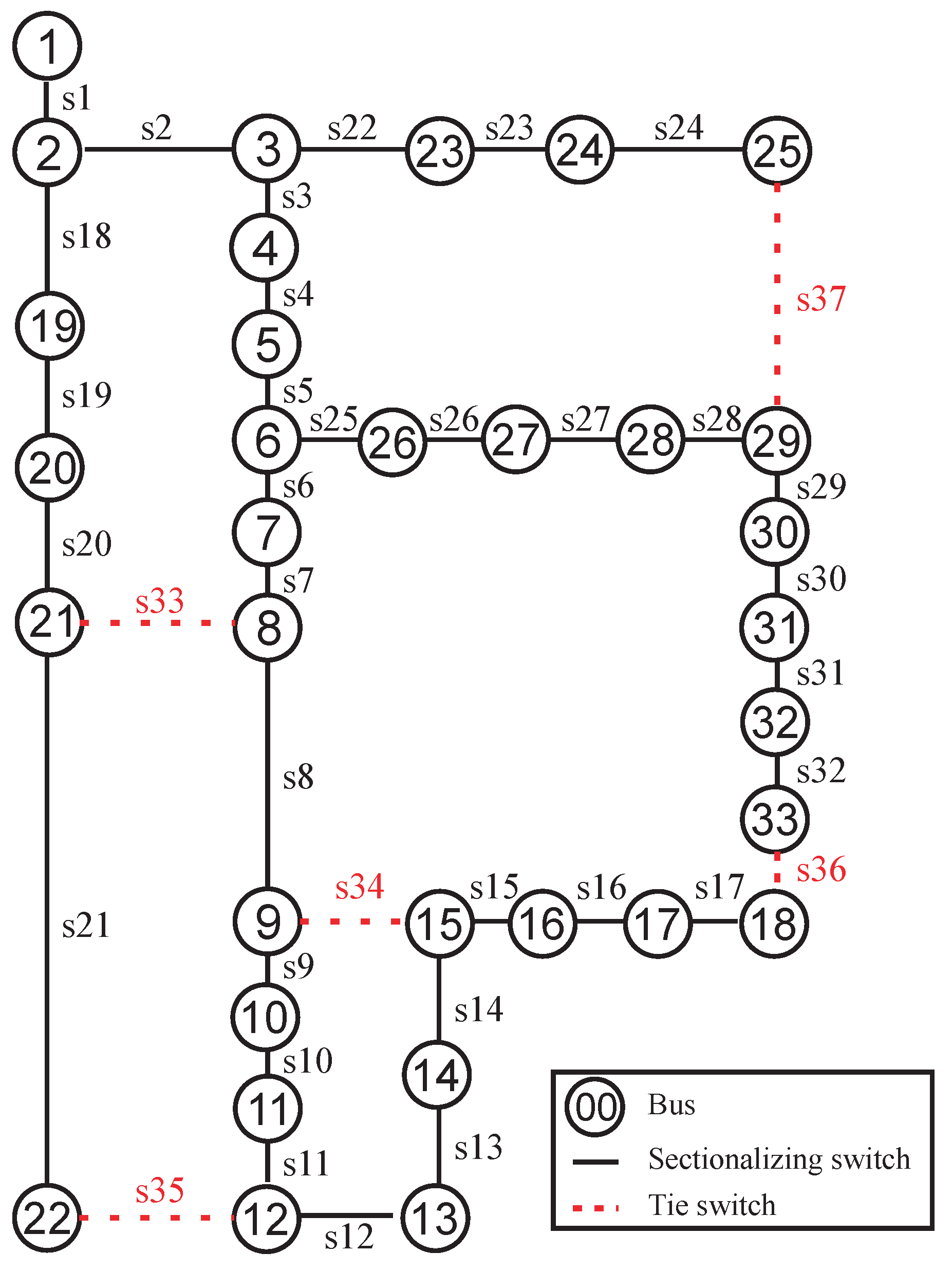
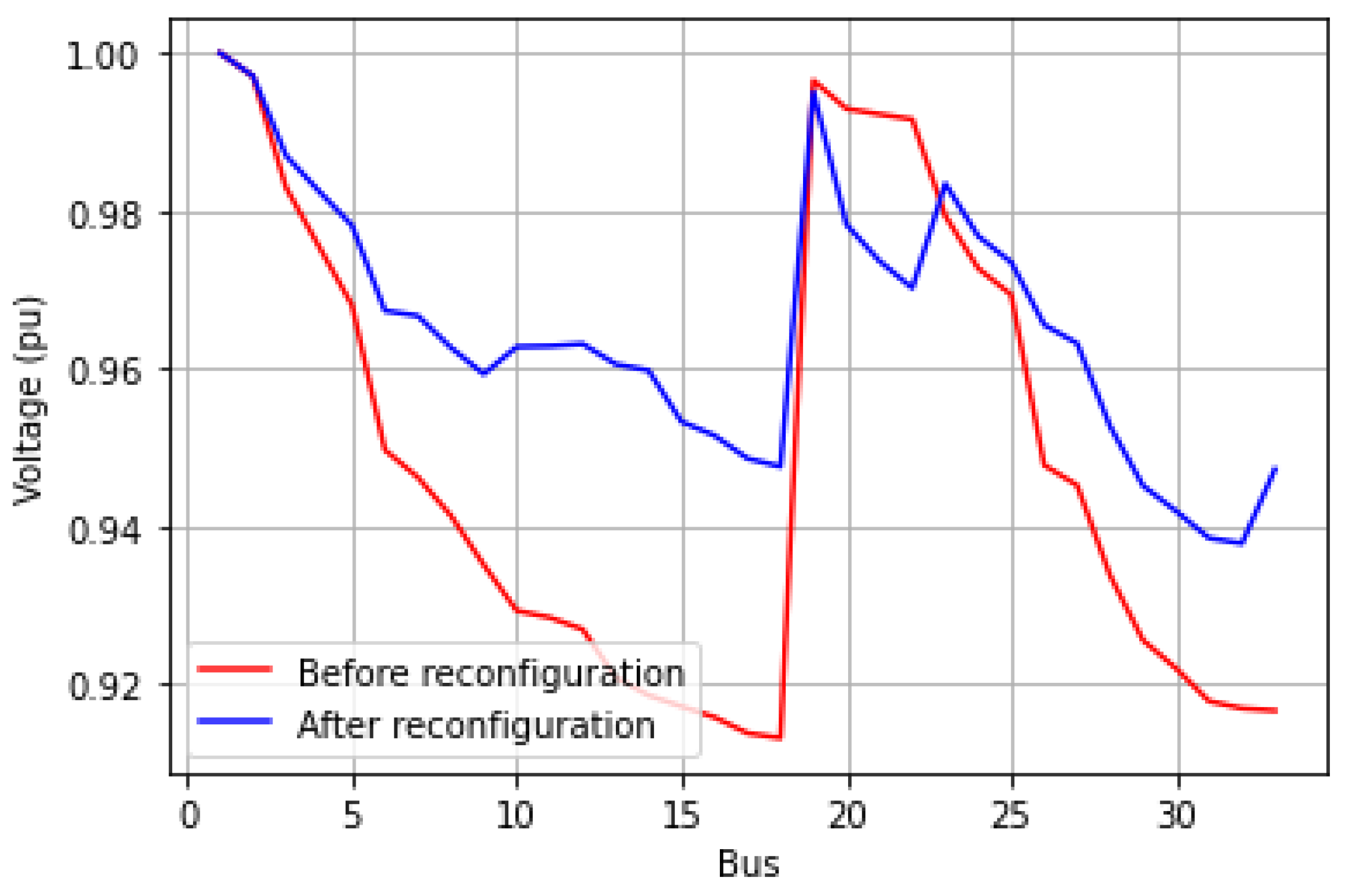
5.2. Case 1: 33-Bus System
5.3. Case 2: 69-Bus System
5.4. Case 3: 94-Bus System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pegado, R.; Ñaupari, Z.; Molina, Y.; Castillo, C. Radial distribution network reconfiguration for power losses reduction based on improved selective BPSO. Electr. Power Syst. Res. 2019, 169, 206–213. [Google Scholar] [CrossRef]
- Dias Santos, J.; Marques, F.; Garcés Negrete, L.P.; Andrêa Brigatto, G.A.; López-Lezama, J.M.; Muñoz-Galeano, N. A Novel Solution Method for the Distribution Network Reconfiguration Problem Based on a Search Mechanism Enhancement of the Improved Harmony Search Algorithm. Energies 2022, 15, 2083. [Google Scholar] [CrossRef]
- Gerez, C.; Coelho Marques Costa, E.; Sguarezi Filho, A.J. Distribution Network Reconfiguration Considering Voltage and Current Unbalance Indexes and Variable Demand Solved through a Selective Bio-Inspired Metaheuristic. Energies 2022, 15, 1686. [Google Scholar] [CrossRef]
- Merlin, A. Search for a minimal-loss operating spanning tree configuration for an urban power distribution system. In Proceedings of the 5th Power Systems Computation Conference, Cambridge, UK, 1–5 September 1975; Volume 1, pp. 1–18. [Google Scholar]
- Civanlar, S.; Grainger, J.; Yin, H.; Lee, S. Distribution feeder reconfiguration for loss reduction. IEEE Trans. Power Deliv. 1988, 3, 1217–1223. [Google Scholar] [CrossRef]
- Niknam, T.; Farsani, E.A. A hybrid self-adaptive particle swarm optimization and modified shuffled frog leaping algorithm for distribution feeder reconfiguration. Eng. Appl. Artif. Intell. 2010, 23, 1340–1349. [Google Scholar] [CrossRef]
- Glover, F. Tabu search: A tutorial. Interfaces 1990, 20, 74–94. [Google Scholar] [CrossRef]
- Jeon, Y.J.; Kim, J.C. Network reconfiguration in radial distribution system using simulated annealing and tabu search. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No. 00CH37077), Singapore, 23–27 January 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 4, pp. 2329–2333. [Google Scholar]
- Abdelaziz, A.Y.; Mohamed, F.; Mekhamer, S.; Badr, M. Distribution system reconfiguration using a modified Tabu Search algorithm. Electr. Power Syst. Res. 2010, 80, 943–953. [Google Scholar] [CrossRef]
- de Andrade, B.A.R.; Ferreira, N.R. Simulated annealing and tabu search applied on network reconfiguration in distribution systems. In Proceedings of the 2018 Simposio Brasileiro de Sistemas Eletricos (SBSE), Niteroi, Brazil, 12–16 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- García-Martínez, S.; Espinosa-Juárez, E.; Pérez-Rojas, C. Optimal Location of Voltage Sag Monitors Considering Electrical Network Reconfiguration in Presence of DG by Using Tabu Search. In Proceedings of the 2018 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 13–15 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 197–202. [Google Scholar]
- Bagheri, A.; Bagheri, M.; Lorestani, A. Optimal reconfiguration and DG integration in distribution networks considering switching actions costs using tabu search algorithm. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 7837–7856. [Google Scholar] [CrossRef]
- Mohamed, M.A.E.H.; Ali, Z.M.; Ahmed, M.; Al-Gahtani, S.F. Energy saving maximization of balanced and unbalanced distribution power systems via network reconfiguration and optimum capacitor allocation using a hybrid metaheuristic algorithm. Energies 2021, 14, 3205. [Google Scholar] [CrossRef]
- Sayed, M.M.; Mahdy, M.Y.; Abdel Aleem, S.H.; Youssef, H.K.; Boghdady, T.A. Simultaneous Distribution Network Reconfiguration and Optimal Allocation of Renewable-Based Distributed Generators and Shunt Capacitors under Uncertain Conditions. Energies 2022, 15, 2299. [Google Scholar] [CrossRef]
- Lavorato, M.; Franco, J.F.; Rider, M.J.; Romero, R. Imposing radiality constraints in distribution system optimization problems. IEEE Trans. Power Syst. 2011, 27, 172–180. [Google Scholar] [CrossRef]
- Lalla-Ruiz, E.; Melián-Batista, B.; Moreno-Vega, J.M. Artificial intelligence hybrid heuristic based on tabu search for the dynamic berth allocation problem. Eng. Appl. Artif. Intell. 2012, 25, 1132–1141. [Google Scholar] [CrossRef]
- Guimaraes, M.A.; Lorenzeti, J.F.; Castro, C.A. Reconfiguration of distribution systems for stability margin enhancement using tabu search. In Proceedings of the 2004 International Conference on Power System Technology, 2004, PowerCon 2004, Singapore, 21–24 November 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 2, pp. 1556–1561. [Google Scholar]
- Pan, N.H.; Hsaio, P.W.; Chen, K.Y. A study of project scheduling optimization using Tabu Search algorithm. Eng. Appl. Artif. Intell. 2008, 21, 1101–1112. [Google Scholar] [CrossRef]
- Al-Sultan, K.S. A tabu search approach to the clustering problem. Pattern Recognit. 1995, 28, 1443–1451. [Google Scholar] [CrossRef]
- Alexander, C.K.; Sadiku, M.N.; Sadiku, M. Fundamentals of Electric Circuits; McGraw-Hill Higher Education: Boston, MA, USA, 2007; pp. 34–39. [Google Scholar]
- Freitas, P.R.R.D. Impacto de Funções Inteligentes de Inversores de Sistemas Fotovoltaicos na Operação de Redes de Distribuição de Energia Elétrica. Ph.D. Thesis, Universidade de São Paulo, São Paulo, Brazil, 2020. [Google Scholar]
- Shirmohammadi, D.; Hong, H.W. Reconfiguration of electric distribution networks for resistive line losses reduction. IEEE Trans. Power Deliv. 1989, 4, 1492–1498. [Google Scholar] [CrossRef]
- Chiang, H.D.; Jean-Jumeau, R. Optimal network reconfigurations in distribution systems. II. Solution algorithms and numerical results. IEEE Trans. Power Deliv. 1990, 5, 1568–1574. [Google Scholar] [CrossRef]
- Goswami, S.K.; Basu, S.K. A new algorithm for the reconfiguration of distribution feeders for loss minimization. IEEE Trans. Power Deliv. 1992, 7, 1484–1491. [Google Scholar] [CrossRef]
- Baran, M.; Wu, F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Su, C.T.; Lee, C.S. Network reconfiguration of distribution systems using improved mixed-integer hybrid differential evolution. IEEE Trans. Power Deliv. 2003, 18, 1022–1027. [Google Scholar] [CrossRef]
- Savier, J.; Das, D. Impact of network reconfiguration on loss allocation of radial distribution systems. IEEE Trans. Power Deliv. 2007, 22, 2473–2480. [Google Scholar] [CrossRef]

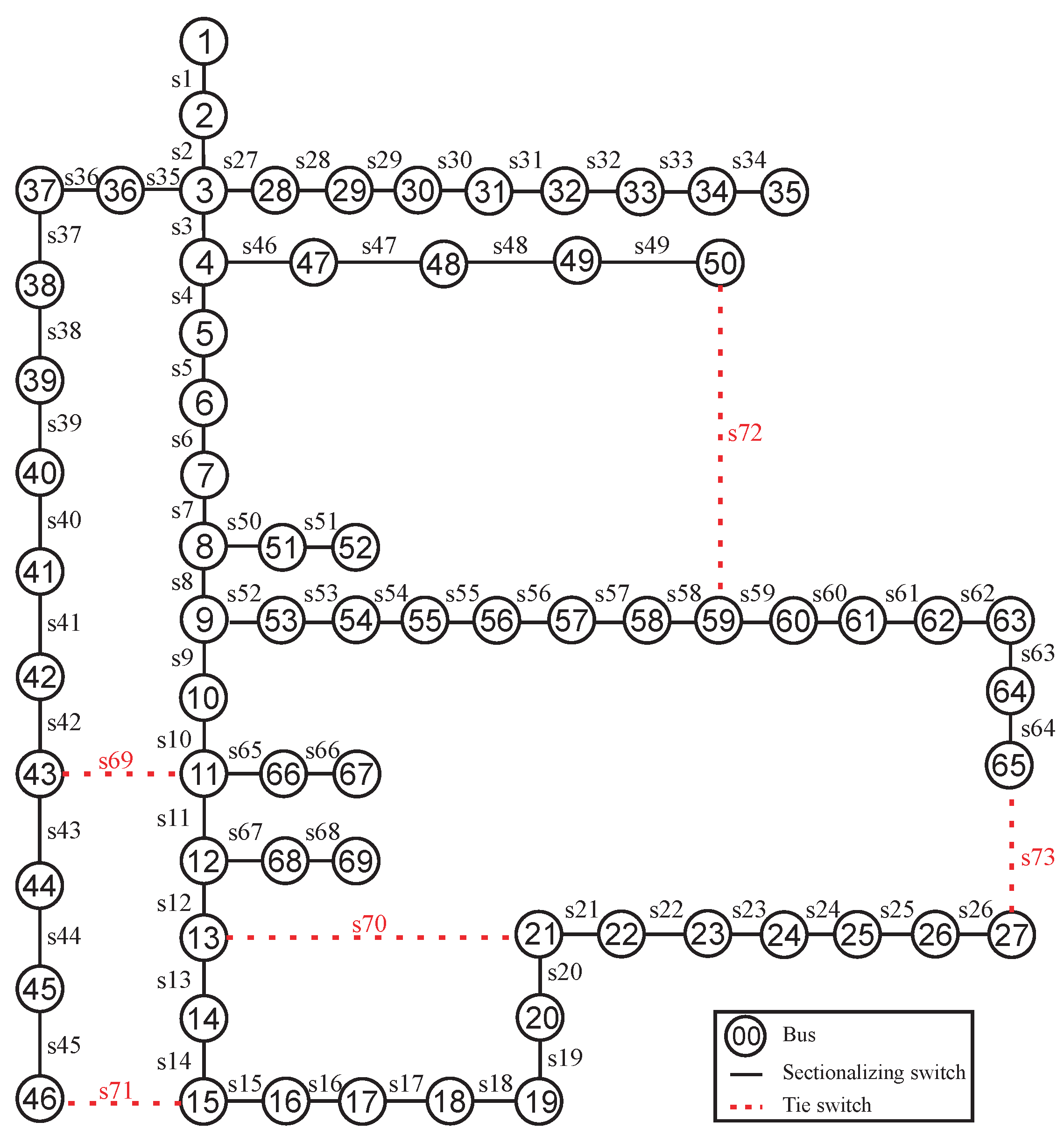
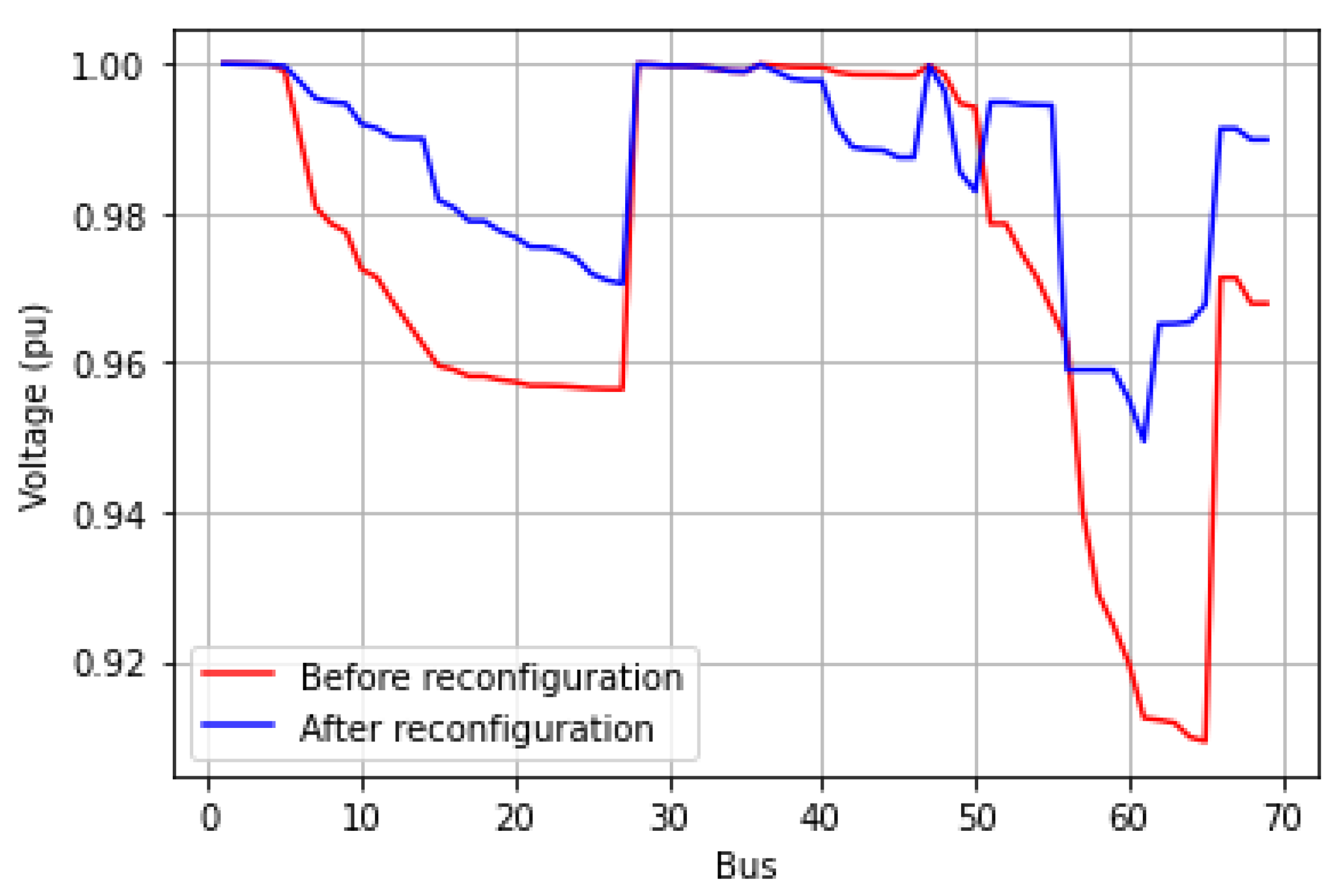
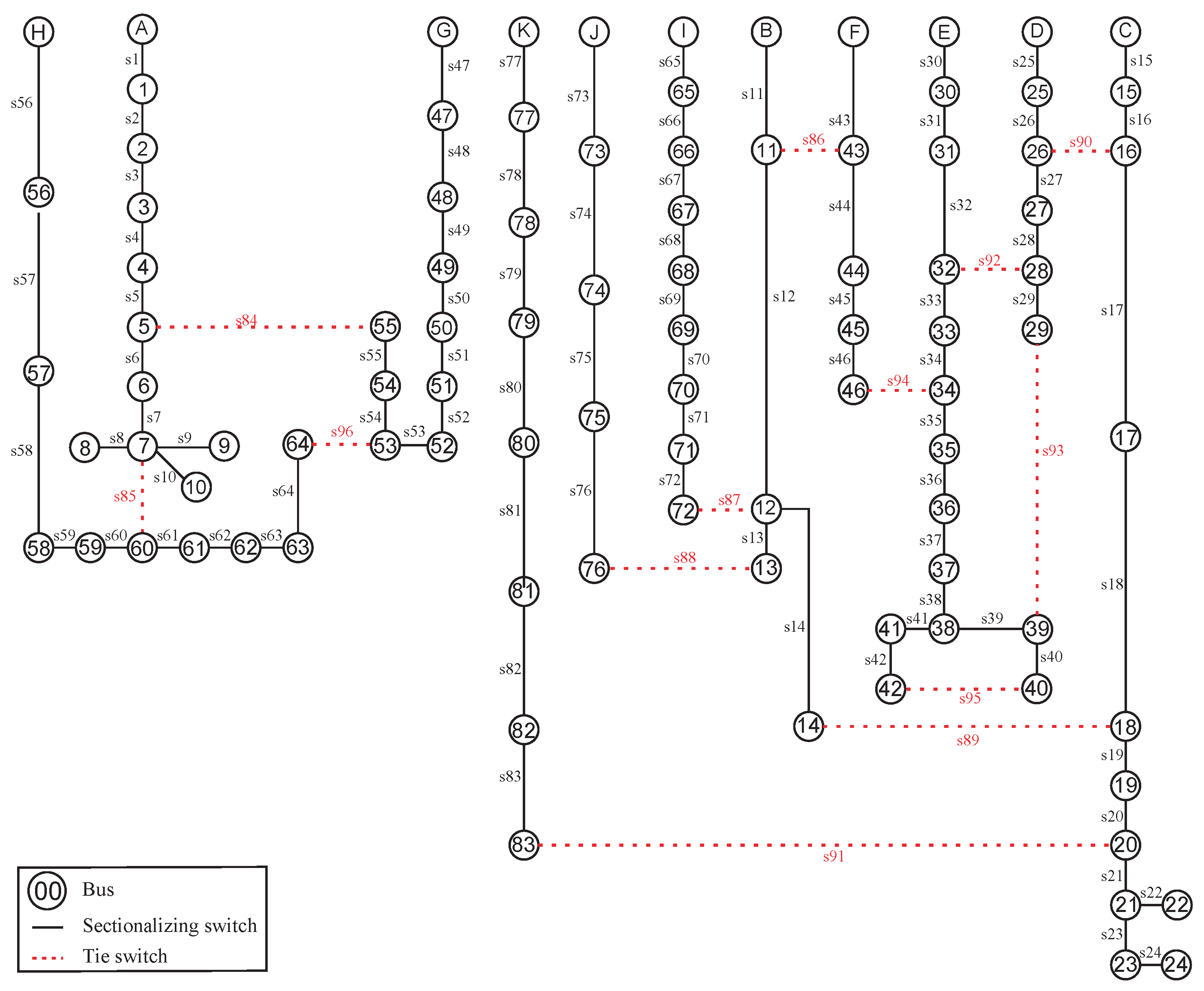
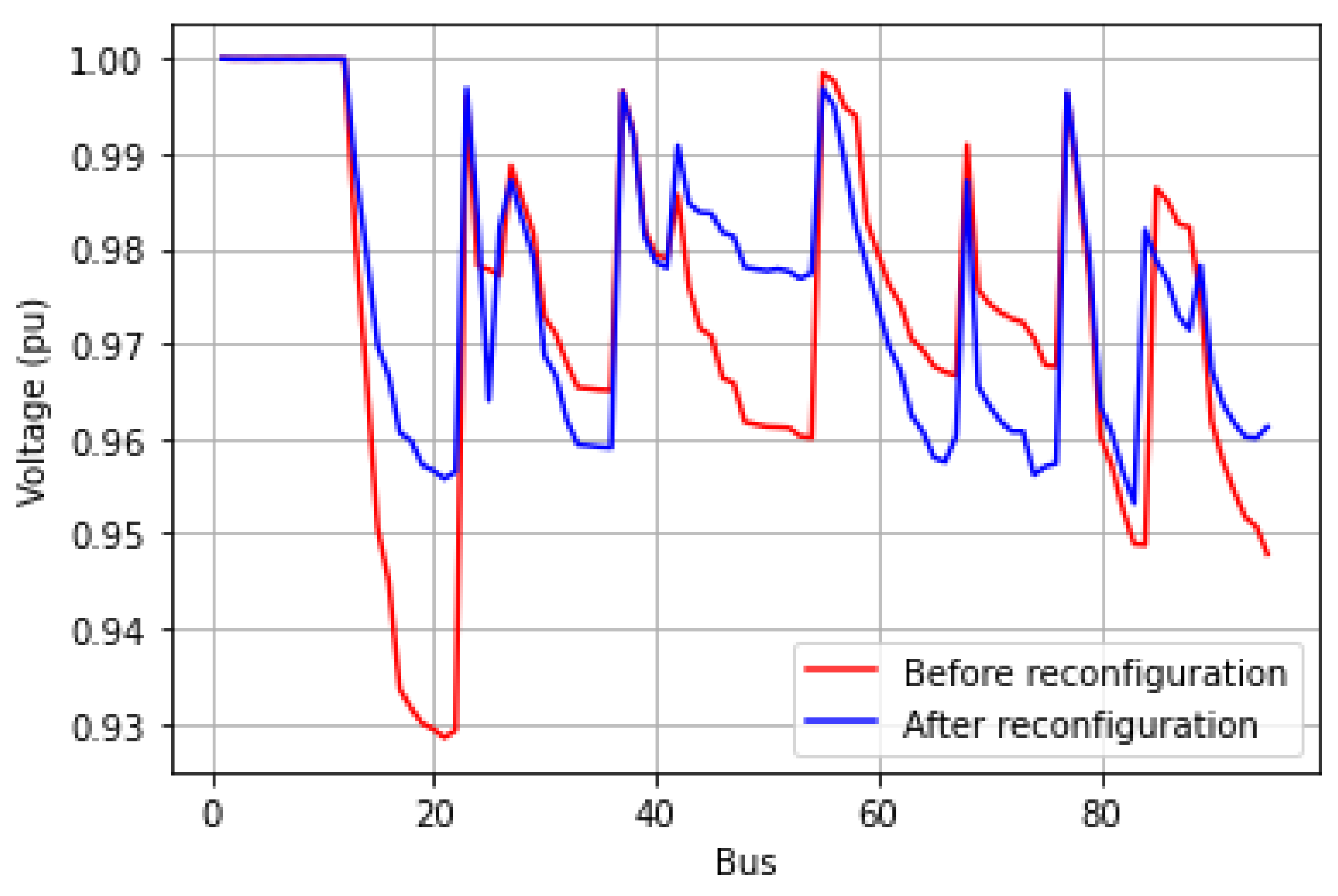
| System | Default Initial Solution | Initial Solution Using Method | Reduction |
|---|---|---|---|
| 33-Bus [25] | s33, s37, s35, s36, s34 202.27 kW | s6, s25, s11, s32, s14 163.22 kW | 19.31% |
| 94-Bus [26] | s96, s88, s91, s87, s89, s94, s95,s93, s92, s90, s84, s85, s86 532.8 kW | s96, s88, s82, s72, s89, s33, s42, s39, s92, s90, s84, s7, s86 485.41 kW | 8.89% |
| BTMax | T | NNb | Loss Average (kW) | Standard Deviation (kW) | Worst Solution | Losses (kW) | No. of Global Solutions |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 5 | 139.62 | 0.2419 | s7, s28, s10, s32, s14 | 140.72 | 91 |
| 10 | 2 | 10 | 139.57 | 0.1367 | s7, s28, s10, s32, s14 | 140.72 | 98 |
| 10 | 5 | 5 | 139.81 | 1.2575 | s7, s26, s10, s32, s14 | 147.98 | 90 |
| 10 | 5 | 10 | 139.58 | 0.1000 | s7, s37, s10, s32, s14 | 140.29 | 96 |
| 20 | 2 | 5 | 139.56 | 0 | - | - | 100 |
| 20 | 2 | 10 | 139.56 | 0 | - | - | 100 |
| 20 | 5 | 5 | 139.56 | 0 | - | - | 100 |
| 20 | 5 | 10 | 139.56 | 0 | - | - | 100 |
| Method | Loss Average (kW) | Standard Deviation | Worst Solution | No. of Global Solutions | Time (s) |
|---|---|---|---|---|---|
| Proposed method | 139.56 | 0 | - | 100 | 23.2 |
| Abdelaziz et al. [9] | 140.30 | 1.9496 | s33, s27, s11, s31, s34 148.71 kW | 68 | 33.8 |
| Andrade and Ferreira [10] | 139.75 | 0.9708 | s33, s28, s11, s32, s34 143.52 kW | 78 | 35.9 |
| Jeon and Kim [8] | 139.69 | 1.0410 | s33, s28, s9, s32, s34 144.38 kW | 85 | 44.2 |
| BTMax | T | NNb | Loss Average (kW) | Standard Deviation (kW) | Worst Solution | Losses (kW) | No. of Global Solutions |
|---|---|---|---|---|---|---|---|
| 20 | 5 | 5 | 101.15 | 4.41 | s55, s69, s12, s18, s26 | 122.76 | 36 |
| 20 | 5 | 15 | 98.47 | 0.047 | s58, s69, s12, s14, s61 | 98.94 | 79 |
| 20 | 15 | 5 | 100.25 | 3.06 | s55, s69, s13, s18, s63 | 115.75 | 38 |
| 20 | 15 | 15 | 98.47 | 0 | - | - | 100 |
| 30 | 5 | 5 | 99.96 | 1.663 | s57, s69, s13, s18, s63 | 105.58 | 41 |
| 30 | 5 | 15 | 98.47 | 0.01 | s55, s59, s13, s70, s61 | 98.57 | 89 |
| 30 | 15 | 5 | 100.33 | 2.65 | s55, s41, s13, s18, s63 | 115.75 | 39 |
| 30 | 15 | 15 | 98.47 | - | - | - | 100 |
| Method | Loss Average (kW) | Standard Deviation | Worst Solution | No. of Global Solutions | Time (s) |
|---|---|---|---|---|---|
| Proposed method | 98.47 | 0 | - | 100 | 148.45 |
| Abdelaziz et al. [9] | 98.5 | 0.14 | s55, s69, s14, s70, s63 99.49 kW | 96 | 353.83 |
| Andrade and Ferreira [10] | 98.56 | 0.58 | s55, s10, s14, s70, s61 104.12 kW | 92 | 177.78 |
| Jeon and Kim [8] | 98.5 | 0.14 | s55, s69, s14, s70, s63 99.49 kW | 97 | 200.55 |
| BTMax | T | NNb | Loss Average (kW) | Standard Deviation (kW) | Worst Solution | Losses (kW) | No. of Global Solutions |
|---|---|---|---|---|---|---|---|
| 1 | 5 | 13 | 470.67 | 0 | - | - | 100 |
| 1 | 5 | 26 | 470.67 | 0 | - | - | 100 |
| 1 | 10 | 13 | 470.67 | 0 | - | - | 100 |
| 1 | 10 | 26 | 470.67 | 0 | - | - | 100 |
| 10 | 5 | 13 | 470.67 | 0 | - | - | 100 |
| 10 | 5 | 26 | 470.67 | 0 | - | - | 100 |
| 10 | 10 | 13 | 470.67 | 0 | - | - | 100 |
| 10 | 10 | 26 | 470.67 | 0 | - | - | 100 |
| Method | Loss Average (kW) | Standard Deviation | Worst Solution | No. of Global Solutions |
|---|---|---|---|---|
| Proposed method | 470.67 | 0 | - | 100 |
| Abdelaziz et al. [9] | 471.55 | 4.6203 | s96, s13, s83, s72, s89, s34, s42, s39, s92, s90, s84, s85, s86 503.42 kW | 69 |
| Andrade and Ferreira [10] | 472.65 | 7.4419 | s96, s88, s82, s87, s89, s34, s42, s39, s92, s90, s84, s85, s86 508.21 kW | 52 |
| Jeon and Kim [8] | 471.78 | 5.5723 | s96, s13, s83, s72, s89, s34, s42, s39, s92, s90, s84, s85, s86 503.42 kW | 62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ñaupari Huatuco, D.Z.; Filho, L.O.P.; Pucuhuayla, F.J.S.; Rodriguez, Y.P.M. Network Reconfiguration for Loss Reduction Using Tabu Search and a Voltage Drop. Energies 2024, 17, 2744. https://doi.org/10.3390/en17112744
Ñaupari Huatuco DZ, Filho LOP, Pucuhuayla FJS, Rodriguez YPM. Network Reconfiguration for Loss Reduction Using Tabu Search and a Voltage Drop. Energies. 2024; 17(11):2744. https://doi.org/10.3390/en17112744
Chicago/Turabian StyleÑaupari Huatuco, Dionicio Zocimo, Luiz Otávio Pinheiro Filho, Franklin Jesus Simeon Pucuhuayla, and Yuri Percy Molina Rodriguez. 2024. "Network Reconfiguration for Loss Reduction Using Tabu Search and a Voltage Drop" Energies 17, no. 11: 2744. https://doi.org/10.3390/en17112744
APA StyleÑaupari Huatuco, D. Z., Filho, L. O. P., Pucuhuayla, F. J. S., & Rodriguez, Y. P. M. (2024). Network Reconfiguration for Loss Reduction Using Tabu Search and a Voltage Drop. Energies, 17(11), 2744. https://doi.org/10.3390/en17112744








