A Computational Analysis of Heat and Mass Transfer in an Indirect Evaporative Cooler Using the Spray Dryer Model

Abstract

Indirect evaporative coolers (IECs) for air conditioning rely on liquid water being sprayed into the exhaust stream of used air to induce evaporation and cool down the incoming stream of fresh air in an indirect heat exchanger. This paper describes a computational fluid dynamics analysis that makes use of the particle transport model to simulate the evaporation of the water droplets at the exhaust side of an IEC using a pre-implemented spray dryer model. Critical parameters include the average size of the droplets and the amount of water sprayed into the system. In addition to droplet evaporation, the evaporation of water from the wet wall on the exhaust side is accounted for. The results show the calculated temperature field in both air streams, the pressure distribution, the relative humidity distribution at the exhaust side and the particle tracks. The predicted wet bulb efficiency of around 30–35% is moderate but in agreement with the literature to date, and it can be attributed to the small heat exchanger size. A parametric study investigated the effect of the droplet size and mass flow rate. At an average size of 50 microns and below, the effect of the mass flow rate is quite strong, while at a higher droplet size the mass flow effect is small. Overall, the model can be used to shed fundamental understanding in order to increase the performance of the IEC while maintaining its compactness.

1. Introduction

The building sector accounts for an estimated 30–40% of the global electricity consumption, air conditioning and cooling for building applications, and it is one of the largest global consumers of electrical energy, accounting for an estimated 50% of the energy supplied [1]. With the further development in regions of hot and partly arid climate, combined with the effects of climate change, there is an increasing need to develop affordable and energy-efficient cooling technologies. Indirect evaporative coolers (IECs) are becoming increasingly popular as a simple and effective method to make incoming room air temperate by cooling it down in an indirect heat exchanger, where exhaust air from the building is passed on the other side and liquid water is sprayed in the stream to induce evaporative cooling. The wet side (exhaust side) of the heat exchanger is usually prepared in a way that the water is distributed evenly over the surface, often by treating the surface to produce a wicking effect. Alternatively, or in addition, water is sprayed in the form of small, micro-scale droplets into the working air on the exhaust side. In such case, the evaporation will occur around the droplets that have a larger surface area than the wetted wall. A general overview of the different technologies was given by Porumb et al. [2], while Pamionowski et al. [3] highlighted the Danish perspective.

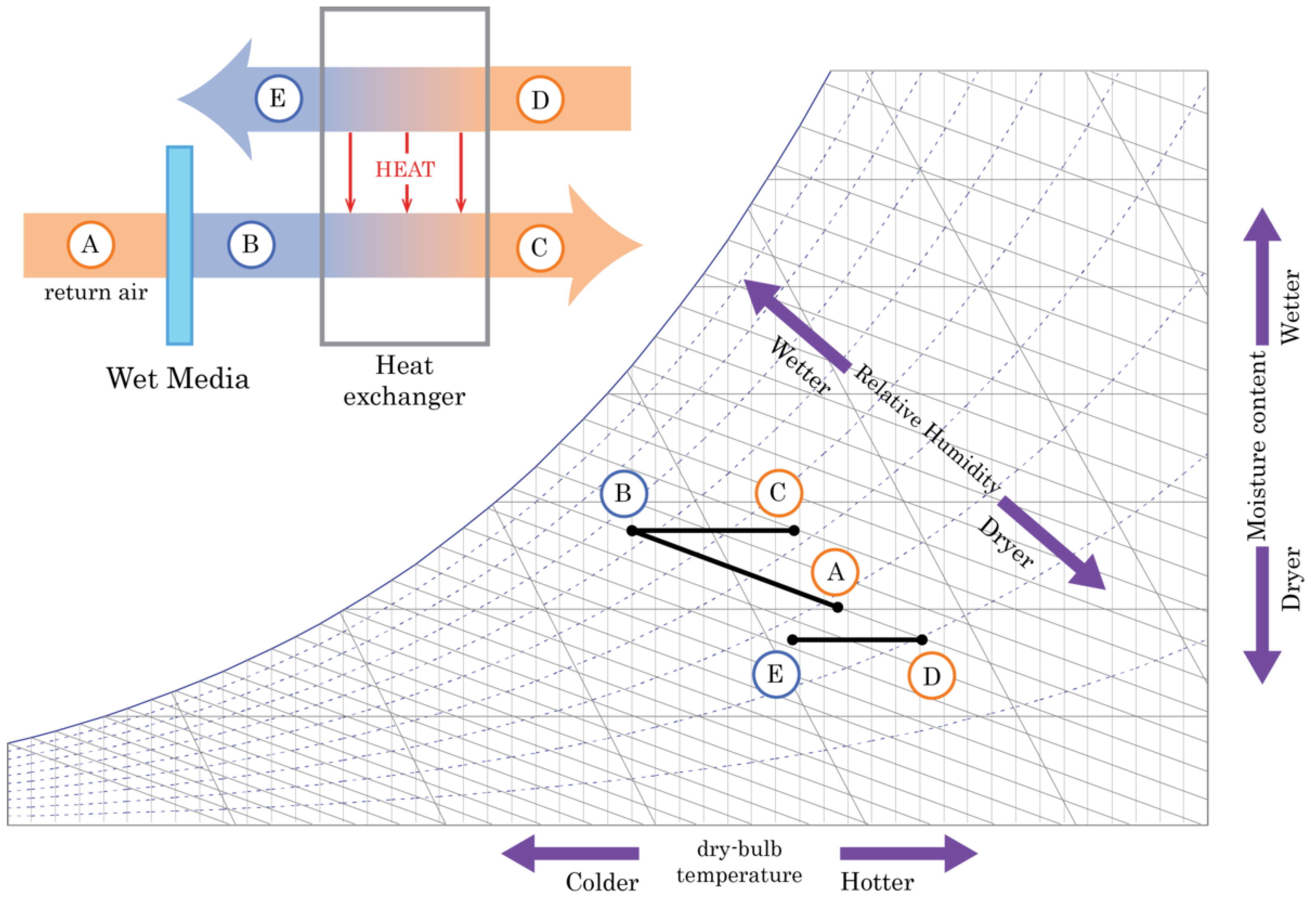
Figure 1 summarizes the processes in a thermodynamic diagram, where the state A denotes the air that is taken from the room (secondary air, working fluid), which is humidified by the addition of water to state B, a process which also leads to evaporative cooling as the secondary air has a relative humidity of maximum 60% for comfort purposes. In Figure 1, this cooled-down air is entering the heat exchanger and remains at a constant moisture level, and it is heated up again by the fresh (primary) air to state C, while in reality both processes are typically combined. The primary air in turn enters the heat exchanger from the outside at state D, and it is supposed to cool down to state E at a constant moisture level. This process is obviously the most effective in hot and dry climate zones, but it can also be applied in temperature regions such as Denmark [3].

It is understood that thermodynamic psychrometric charts as shown in Figure 1 are based on the assumption that thermodynamic equilibrium prevails, i.e., liquid water droplets cannot exist in an undersaturated stream of air. In this work, the heat and mass transfer of droplet evaporation is accounted for, which enables the verification of this assumption.

Generally, there are numerous design options for such an IEC. In the simplest, conventional design, both air streams are handled separately so that the secondary air is at a different inlet condition than the primary outlet air [5]. These authors list the shortcomings of the popular designs as (1) the limited heat exchanger area, (2) pure counter-flow heat exchangers cannot be obtained, and (3) uniform and even water distribution over the wet side of the heat exchanger is hard to obtain [5]. An important application for such a simple design is data centers, investigated by De Antonelli et al. [6]. This group found that the amount of water added to the system has an important effect on the system performance.

A vast improvement in the performance was obtained by redirecting part of the outlet primary air and using it as the secondary, working air (M-cycle). This cycle is based on patents filed in 1976 primarily by the Russian scientist Valeriy Maisotsenko and more recently in 2003 [7]. A detailed overview of the development of the M-cycle, also known as dew-point evaporative cooler, was recently given by Taler et al. [8]. A thermodynamic analysis of the M-cycle was conducted by Caliscan et al. [9]. Xu et al. [10] recently published an experimental study of this design with excellent results in terms of cooling performance. The overall length of the individual channels is often in the order of 1 m, which makes these systems bulky and expensive, and a size reduction is highly desirable.

In order to provide fundamental understanding of the heat and mass transfer phenomena that occur inside IECs, numerous modelling studies have previously been conducted. These models can be broadly divided into two categories: (i) mathematical models that are frequently based on a modified ɛ-NTU approach where differential heat and mass conservation equations are set up and integrated with the help of appropriate boundary conditions, while the heat and mass transfer at the boundaries are calculated via Nusselt and Sherwood numbers, or (ii) computational fluid dynamics (CFD) models that take advantage of established computational packages that can be easily extended to three dimensions and where even transient calculations pose no additional difficulties other than added computational cost.

Zhao et al. [11] conducted a numerical analysis of a counter-flow regenerative IEC by subdividing the heat exchanger geometry into control volumes and applying analytical heat and mass transfer equations.

Lee et al. [12] investigated the performance of different flow arrangements in the regenerative design with and without corrugated cells. This group employed the NTU method to calculate the performances of a flat plate, a corrugated plate and a finned type heat exchanger. They concluded that the finned type heat exchanger allowed for the most compact design.

Chen et al. [13,14] developed a different method by extending the transport theory that emerged out of the analogy between heat and mass transfer to account for the transport of moisture.

Woods and Kozubal [15] presented modelling and experimental results on a liquid desiccant air conditioner, which consists of two stages: a liquid desiccant dehumidifier and an indirect evaporative cooler. They presented fluid-thermal numerical models for each stage and experimental results of prototypes for each stage. Finally, they compared the modelled and experimental results and found very good agreement.

Anisimov et al. [16] developed a comprehensive network model to track heat and mass transfer in a dew-point evaporative cooler. Later on, this work was expanded by Pandelidis et al. [17,18] to study different design options.

Cui et al. [19] employed the methods of computational fluid dynamics by using the commercial software ANSYS Fluent 14.0 and apparently invoking the Euler–Lagrangian model for particle tracking. However, the details of the droplet sizes and numbers on the effect of the droplets were not given, and the problem was reduced to be one-dimensional. The model was then validated against experimental data with good agreement.

Xu et al. [20] applied computational fluid dynamics to study the optimum flow velocity in a dew-point indirect cooler. They carried out CFD simulation to determine the flow resistance factors of various elements within the dry and wet channels of the heat exchanger, while the finite-element-based Newton-iteration numerical simulation was undertaken to investigate its cooling capacity, cooling effectiveness and COP at various geometrical and operational conditions. They compared an irregular design with a flat plate design and found an improvement in performance of around 30%. The best ratio between working air and product air in their case was 0.3. Afterwards, Xu et al. [10] published the experimental results of a super-performance dew-point air cooler with a wet bulb effectiveness of 114% under certain operating conditions.

Wan et al. [21] used a two-dimensional computational fluid dynamics model to simulate the coupled heat and mass transfer processes. Then, a one-dimensional model was used to analyze the fluid stream side average Nusselt number and the cooling air side average Nusselt and Sherwood numbers based on the numerical results of the two-dimensional model. Later on, Wan et al. [22] developed a novel method to determine the heat transfer coefficients in an $NTU-Le-R$ model. Then, a two-dimensional computational fluid dynamics model was developed to simulate the evaporative cooling process within the cooler and compute the outlet data for the $NTU-Le-R$ model.

De Antonellis et al. [6] developed a phenomenological model for IECs in data centers where the indoor air temperature can greatly exceed the outdoor temperature. In their study, the air streams were considered separate. The wettability of the heat exchanger surface area was accounted for. However, the heat conduction inside the heat exchanger plates was neglected. The results showed an excellent agreement between experiments and the model. The same group has then simulated a cross-flow heat exchanger at different operating conditions and again obtained a very good agreement between their model and experiments [23]. Finally, they published experimental data of different heat exchanger arrangements of similar size as considered in this work [24]. Depending on the flow conditions, the measured wet bulb efficiencies were between 45% and 85%.

Lin et al. [25] first modelled a counter-flow heat exchanger using a mathematical model where they took into account longitudinal heat conduction and mass diffusion for two air streams, latent heat transfer between the working air and the water film, the temperature difference between the thin water film and the plate and various other mechanisms. This group then investigated a cycle where the supply air at the outlet was in part redirected and used as working air [26]. These authors also commented on the lack of fundamental understanding of local heat and mass transfer coefficients in IECs because of the fact that often Nusselt numbers and Sherwood numbers are taken based on the assumption of having a constant temperature boundary or a constant heat flux boundary which is known to be invalid in operating ICEs.

Oh et al. [27] developed a mathematical model to investigate different purge configurations. The results revealed that lower product air temperature and higher dew-point effectiveness were achieved with longer channel length and a purge ratio of around 35%.

Jafarian et al. [28] presented a modelling study using the CFD software Open FOAM 2.3.0. They considered the entrance region effect in the flow channels, i.e., the undeveloped flow region, and proposed a new boundary condition for the water flux in the secondary flow channel on the wet surface. Prior to that work, several authors had assumed either constant flux or constant temperature boundary condition or a hybrid version. They compared 2D and 3D results and found only minor differences. However, droplet evaporation was not considered. Instead, all the water was evaporated from the wet channel wall. The outlet air condition (temperature and relative humidity) of the supply channel was set equal to the inlet condition of the exhaust side, i.e., the M-cycle with one bypass at the end of the supply channel was assumed. This group conducted a detailed case study and had excellent agreement with experiments.

Min et al. [29] developed and validated a 2D model of a cross flow IEC considering condensation and optimized the channel geometry.

Finally, Liu et al. [30] first developed a two-dimensional numerical model of heat and mass transfer in a dew-point evaporative cooler that couples the momentum and mass transfer equations with the energy equation using various heat and mass transfer models. The numerical model was validated by experimental results from other studies and was then used to study the impacts of various operating conditions on the cooling in an improved dew-point evaporative cooler with a corrugated surface heat and mass exchanger. Liu et al. [31] then investigated the cooling performance of a high-efficiency dew-point evaporative cooler with optimized air and water flow arrangement using a combination of experiments and numerical simulation. The experimental results showed that the wet bulb efficiency of the dew-point evaporative cooler was increased by 29.3% and COP was increased by 34.6% compared to prior designs. The incoming temperature of the air was quite high and its relative humidity very low, and thus the efficiencies were above 90%.

In a very recent work, Zhu et al. [32] developed a three-dimensional model to simulate the air flow and moisture content transport of a regenerative dew-point evaporative cooler. This was one of the very few three-dimensional studies, as was also shown in the thorough literature review in that work.

All of the above modelling studies have in common that the cooling effect due to evaporation is only accounted for at the wet channel wall on the exhaust side, which holds true if the water is supplied by a wicking effect. In practice, however, it is common to supply the water in the form of droplets via nozzles, and there will be evaporation from the droplets as well. It is highly desirable to obtain an understanding about the expected magnitude of the droplet evaporation effect in comparison to the wall effect. A model that was based on the spray drying effect of droplets of various sizes was previously presented by our group [33]. However, in that work, only the droplet evaporation effect was accounted for, while the cooling effect on the wet wall was neglected, which led to very low predicted efficiencies. In practice, the amount of water splashed into the system is often by far exceeding the required amount according to psychrometric diagrams, and in this way, the wall on the exhaust side is usually perfectly wetted.

In the current work, we are investigating a design where supply air and exhaust air are separated, i.e., the exhaust air is taken from the room that is to be cooled. Liquid water is sprayed into this exhaust air to induce evaporative cooling, and in contrast to the previous work, the wall cooling effect is also accounted for. In the current study, we quantify the amount of water that is added to the secondary air from the plane wall, but then compare it to the amount of water that evaporates from the wall to induce cooling. The main question is whether it is important to account for the wall effect compared to the droplet evaporation rate and whether the water that is picked up from the wall can be in equilibrium with the amount of water provided by the droplets hitting the wall, assuming perfect wettability.

2. Model Description

The model applied in this study is based on the formerly commercial CFD solver CFX-4 (ANSYS Inc., Canonsburg, PA, USA). This software package has built-in physical models including flow in porous media, multiphase flow and multi-species flow. Moreover, it has leading capabilities in terms of customization via user subroutines that allowed for the manipulation of all important transport equations and parameters. The main disadvantage of CFX-4 is that it utilizes IJK-structured meshes, which makes the meshing procedure generally more complicated compared to unstructured meshes. On the other hand, it is widely known that hexahedral, structured meshes require less computational cells for the same modelling accuracy.

In the current work, the spray dryer model of CFX-4 was used to investigate the droplet evaporation on the exhaust side of the IEC. This model allowed for the specification of a number of discrete droplets into a background fluid, and the heat and mass transfer including the evaporation rate was automatically calculated based on the local Sherwood number. This Lagrangian type of modelling applies to flows with low volume fractions of the secondary fluid. The spray dryer model has also been implemented into various other commercial and open source CFD models. Details of the mathematical model are given below. The following assumptions are made:

• The problem is steady-state.
• The gases behave like ideal gases.
• The flow was considered to be laminar.
• The water droplets in the exhaust region are entering at random positions at the exhaust inlet.
• The droplets are prevented from bouncing off the walls by invoking an appropriate command. A droplet hitting the wall is taken out of consideration.
• At the surface of the exhaust side wall (“wet wall”), water is assumed to exist in an infinitely thin layer.

The last assumption holds true if the amount of water added to the system greatly exceeds the amount that is evaporated from the wall, which is the case here. Overall, the results from these calculations will give information as to how much water is evaporating from the droplets and how much water will evaporate from the wet surface.

2.1. Computational Domain and Numerical Grid

The computational domain consists of the supply side and the exhaust side, separated by an aluminium sheet. The computational domain and the numerical grid are shown in Figure 2. A total of 9 computational blocks have been specified, where Blocks 1–3 constitute the primary side and Blocks 7–9 the secondary side, while Blocks 4–6 represent the aluminium sheet. The heat exchanger is a counter-flow heat exchanger, and the air streams enter on the upper left and upper right side and leave via the lower right and lower left side, respectively. Due to symmetry conditions that are applied, only half of the channel heights had to be modelled, which is similar to the work by Jafarian et al. [28]. The length of the channels in this design is 300 mm. The overall quality of the grid is very good with very few skewed cells, which are located in the regions where less physical action happens. In the main flow region, the cells are nearly perfectly squared, which makes for numerical robustness and more accuracy. It was moreover verified that the main findings were not affected by the grid quality.

In the physical design of the IEC that was investigated here, the aluminium plates were corrugated, similar to the design investigated by Xu et al. [10]. In contrast, the modelling domain consisted of flat plates, but the pressure drop in the corrugated channels was matched by specifying the channel region as a porous medium, as will be described below.

2.2. Model Equations

For the gas phase, the laminar three-dimensional, steady-state Navier–Stokes equations are solved at both sides of the heat exchanger. In addition, one mass fraction equation for the water vapour is accounted for. For the general case of a porous medium, the detailed conservation equations are as follows [34]:

Continuity

$$\nabla ·\left(\rho ϵ\mathbf{U}\right)=S_{\mathrm{m}}$$

(1)

Momentum

$$\nabla ·(\rho ϵ\mathbf{U}\otimes \mathbf{U})=\mathbf{B}+\nabla \times \sigma$$

(2)

where $\sigma$ is the stress tensor:

$$\sigma =-p\delta +(\zeta -\frac{2}{3})\nabla ·ϵ\mathbf{U}\delta +\mu ϵ·(\nabla \mathbf{U}+{\left(\mathbf{U}\right)}^T)$$

(3)

Energy

$$\nabla ·\left(\rho ϵ\mathbf{U}H\right)-\nabla (\lambda ϵ\nabla \mathbf{T})=S_H$$

(4)

where U is the three-dimensional velocity vector, $ϵ$ is the volume porosity, $\rho$ is the density of the gas phase, $\mu$ is the molecular viscosity, $\zeta$ is the bulk viscosity, p the pressure, $\delta$ the Kronecker delta and $\lambda$ is the thermal conductivity. For the case of a non-porous region, the porosity simply becomes unity.

In the momentum equations, B is the body force [34]:

$$\mathbf{B}={\mathbf{B}}_{\mathbf{F}}-({\mathbf{R}}_{\mathbf{C}}+{\mathbf{R}}_{\mathbf{F}}|\mathbf{v}{|}^{\alpha })\mathbf{v}$$

(5)

In order to model the Hagen–Poiseuille equation in the channels of the heat exchanger (Blocks 2 and 8), ${\mathbf{B}}_{\mathbf{F}}$ and ${\mathbf{R}}_{\mathbf{F}}$ were set to zero and only the resistance constant ${\mathbf{R}}_{\mathbf{C}}$ was specified [33]:

$${\mathbf{R}}_{\mathbf{C}}=32\times \mu /d_h^2$$

(6)

where $d_h$ is the hydraulic diameter of the channels, here taken to be 4.24 mm. The porosity in the channel regions is set to $ϵ$ = 0.75, and this leads to an acceleration in the fluxes in the channel region compared to the inlet region.

In the energy equation, H is the total enthalpy that depends on the static enthalpy $h(T,p)$ according to [34]:

$$H=h+\frac{1}{2}{\mathbf{U}}^2$$

(7)

In the solid region, the energy equation simplifies to:

$$\nabla ·({\lambda }_s\nabla \mathbf{T})=0$$

(8)

The system of equations is closed by the ideal gas law:

$$\rho =\frac{pW}{RT}$$

(9)

where W is the molecular weight of air (28.84 g/mol) and R is the universal gas constant. In addition to these conservation equations, one species equation is solved for the water vapour in air:

$$\nabla ·\left(\rho \mathbf{U}{Y}_{H_{2}O}\right)-\nabla ·(\rho D_{H_{2}O-air}\nabla Y_{H_{2}O})=S_i$$

(10)

where $Y_{H_{2}O}$ is the mass fraction of water vapour and $D_{H_{2}O-air}$ is the binary diffusion coefficient of water vapour in air (see Equation (33)).

For the particle transport model in the Lagrangian reference frame, the partial differential equation is solved. The equation for the position of a particle is given as:

$$\frac{\xi }{dt}=\mathbf{C}$$

(11)

where $\xi$ is the computational position, t is time and $\mathbf{C}$ is computational velocity. The latter is obtained from the physical velocity of the particles $\mathbf{u}$ according to [34]:

$$\mathbf{C}={\left(\frac{dx}{d\xi }\right)}^{-1}\mathbf{u}$$

(12)

The momentum equations for the disperse phase result directly from Newton’s second law:

$$m\left(\frac{d\mathbf{u}}{dt}\right)=\mathbf{F}$$

(13)

where $\mathbf{F}$ is the force on the particle and m is its mass. The major component of the force term is the drag exerted on the particle by the continuous phase [34]:

$${\mathbf{F}}_{\mathbf{D}}=\frac{1}{8}\pi d^2\rho C_D\left|v_R\right|v_R$$

(14)

where the drag factor is given by the Schiller-Naumann model [34]:

$$C_D=\frac{24}{Re}(1+0.15R{e}^{0.687})$$

(15)

and the particle Reynolds number is defined as [34]:

$$Re=\frac{\rho |v_R|d}{\mu }$$

(16)

In addition to the drag force, the buoyancy force is accounted for [34]:

$${\mathbf{F}}_{\mathbf{B}}=\frac{1}{6}\pi d^3({\rho }_P-\rho )\mathbf{g}$$

(17)

In the CFX-4 spray dryer model that was employed in this work, the particle mass transfer depends on whether the particle is above or below the boiling point, which is described by Antoine’s equation:

$$P_{vap}=exp(A-\frac{B}{T+C})$$

(18)

If the saturation pressure is given in [Pa] and the temperature T in [K], then the coefficients for water are A = 23.296, B = 3816.44 and C = $-46.13$, respectively [34].

When the particle temperature is above the boiling point, the mass transfer is determined by the convective heat transfer:

$$\frac{dm}{dt}=-\frac{Q_c}{r_{evap}}$$

(19)

where $r_{evap}$ is the heat of vaporization ($2.44\times {10}^6\frac{\mathrm{J}}{\mathrm{kg}}$). The rate of convective heat transfer is given by:

$$Q_c=\pi d\lambda Nu(T_g-T)$$

(20)

where $\lambda$ is the thermal conductivity of the fluid, $T_g$ and T are the temperature of the fluid and the particle and $Nu$ is the Nusselt number given by [34]:

$$Nu=2+0.6\times R{e}^{0.5}{\left(\frac{\mu c_p}{\lambda }\right)}^{\frac{1}{3}}$$

(21)

where $c_p$ is the specific heat of the fluid (4186 J/kg). When the particle is below the boiling point, condensation occurs and the mass transfer is given by:

$$\frac{dm}{dt}=\pi d\rho D_{H_{2}O-air}Sh\left(\frac{W_C}{W_G}\right)log\left(\frac{1-X}{1-X_G}\right)$$

(22)

Here, $W_C$ and $W_G$ are the molecular weights of the vapour and the mixture in the continuous phase, while X and $X_G$ are the molar fractions in the drop and in the gas phase. Finally, the Sherwood number $Sh$ for a droplet with the diameter d is given by:

$$Sh=2+0.6\times R{e}^{0.5}{\left(\frac{\mu }{\rho D_{H_{2}O-air}}\right)}^{\frac{1}{3}}$$

(23)

In CFX-4, these equations are easily invoked by applying the spray dryer model and specifying the secondary phase as liquid water. The average droplet diameter and the overall mass flow rate has to be specified at the secondary inlet. Then, a random distribution of droplets is applied over the inlet area to match the mass and energy flux at the inlet. A Rossin–Ramler size distribution is assumed, and four different droplet sizes are modelled. A total of 50 different positions are specified, to the effect that overall 200 droplets are tracked.

2.3. Boundary Conditions

2.3.1. Comparison with Experimental Conditions

The cases investigated in the current study correspond to boundary conditions, as shown in Figure 3. For an adiabatic cooler, these conditions correspond to a worst-case scenario where the outside air is the same as the indoor air, 26 °C. For indoor comfort, this is the maximum temperature along with a relative humidity of 60% of both outside air and inside air.

The definition of the wet bulb efficiency ${\eta }_{wb}$ of an IEC is:

$${\eta }_{wb}=\frac{T_{db,in}-T_{db,out}}{T_{db,in}-T_{wb,in}}$$

(24)

where all temperatures refer to the primary, supply air stream and the subscript $db$ refers to dry bulb temperature, while $wb$ refers to the wet bulb temperature, respectively.

In the case where the primary air stream is cooled down to 21 °C, as shown in Figure 3, the wet bulb efficiency would be 87.4%. However, depending on the test scenarios, initial tests of the hardware resulted in efficiencies of only 30–40%, while later tests yielded a dry bulb efficiency of around 90%, which left room for interpretation. It is noted that Figure 3 shows the desired outlet conditions which are not necessarily in agreement with experiments.

The mass flow rate of 0.4 kg/s is the flow of air through the former HCP-P 1200 heat exchanger. This mass flow rate corresponds to a volumetric flow rate of

$$\dot{V}=\dot{m}/{\rho }_g\approx 1200{\mathrm{m}}^3/\mathrm{h}$$

(25)

However, the new unit in question is an HCP-P 1600 system, designed to provide cooling air for a classroom with an area of around 80 m² and a height of around 3 m, yielding a total classroom volume of around 240 m³. Depending on the heating load in the classroom, this air needs to be replaced 3–7 times per hour [3]. Thus, the full load of the current HCP-P 1600 system is 1600 $\frac{{\mathrm{m}}^3}{\mathrm{h}}$, or 0.52 $\frac{\mathrm{kg}}{\mathrm{s}}$, which translates into 2.4 $\frac{\mathrm{g}}{\mathrm{s}}$ per single cell.

Consulting a psychrometric diagram, it can be seen that both incoming air streams have a water content of 12.6 g water/kg dry air. For the desired outlet point of the secondary air stream according to Figure 3, the moisture content is 14.1 g water/kg dry air. Thus, we are adding 1.5 g water/kg dry air. Taking the air stream per cell as 2.4 g/s, this means we have to add 3.6 × 10⁻³ $\frac{\mathrm{g}}{\mathrm{s}}$ of water per unit cell. If all this water would evaporate, the cooling power supplied by each plate would be:

$$P_{evap}=3.6\times {10}^{-6}\mathrm{kg}/\mathrm{s}\times 2.44\times {10}^6\mathrm{J}/\mathrm{kg}=8.78W$$

(26)

amounting to 1.9 kW of theoretical cooling power of the HCP-P 1600 system. This theoretical coolant rate, however, is divided into the desired cooling of the supply air stream and the necessary cooling of the secondary air stream. The design of the heat exchanger will play an important role in the division of this coolant rate.

In practice, the total mass flow of water into the system was around 70 L/h, or 90 × 10⁻³ g/s per plate, which means that the moisture level was far higher than in the psychrometric charts. This is owing to the fact that it is difficult to accurately control the water flux. Moreover, the droplet size in these experiments was quite large, and this means that not all the water could be evaporated. Thus, an oversupply of water was provided to ensure a high efficiency, and this means that the real conditions of the secondary, working air leaving the system can be quite different from the states in Figure 3. The excess water was recirculated.

2.3.2. Discussion of Droplet Size

In an IEC, the size of the droplets sprayed into the secondary air stream is expected to be of great importance. In the current system, the nozzles yield a droplet diameter of around 100 microns (shown below) in conjunction with a large oversupply of water. It would be desirable to optimize the droplet size and flow rate such that no water would have to be recirculated. To this end, however, it must be ensured that all water that is supplied is also evaporated, and this requires a fundamental understanding of the droplet size and evaporation rate such as that which is offered by the spray dryer model.

The droplet size is typically characterized by the Sauter mean diameter (SMD), also denoted D₃₂. A general equation to calculate the SMD is [35]:

$$D_{32}=Const.\times {\sigma }^a\times {\nu }^b\times {\dot{m}}^c\times \Delta P^d$$

(27)

where $\sigma$ is the surface tension between the liquid and the gas, $\nu$ is the kinematic viscosity of the liquid, $\dot{m}$ is the mass flow rate of the liquid and $\Delta P$ is the pressure drop of the liquid over the nozzle, while the coefficients $a,b,c$ and d are experimentally determined parameters. Radcliffe suggested the following equation [36]:

$$D_{32}=7.3\times {\sigma }^{0.60}\times {\nu }^{0.20}\times {\dot{m}}^{0.25}\times \Delta P^{-0.40}$$

(28)

which matched experimental data well. Subsequently, a different expression that yielded similar results was suggested by Jasuja [37]:

$$D_{32}=4.4\times {\sigma }^{0.60}\times {\nu }^{0.16}\times {\dot{m}}^{0.22}\times \Delta P^{-0.43}$$

(29)

Both of the former expressions have the disadvantage that the units are inconsistent. Lefebvre suggests an expression that has consistent units [35]:

$$D_{32}=2.25\times {\sigma }^{0.25}\times {\nu }^{0.25}\times {({\rho }_l/{\rho }_g)}^{0.25}\times {\dot{m}}^{0.25}\times \Delta P^{-0.5}$$

(30)

Note that in the last equation, the density of the air ${\rho }_g$ is introduced, while in the other equations, all properties are based on liquid water. All these equations suggest that the mean droplet diameter increases with increasing mass flow rate, but it decreases with increasing pressure drop across the nozzle. Finally, the minimum attainable droplet size was determined from fundamental considerations by Lee and Robinson to be [38]:

$$D_{32,min}=12\times \sigma /{\rho }_l\times u_{inj}^2$$

(31)

which highlights the importance of the injection velocity $u_{inj}$ for the droplet diameter.

The current experimental set-up of the hardware showing the placements of the nozzles is shown in Figure 4.

The total number of nozzles for the HCP-P 1600 is 18. Thus, using a liquid water flow rate of around 70 L/h, we obtain a water mass flow rate of 1.0 g/s per nozzle. The absolute water pressure is 4.8 bar, i.e., the pressure drop across the nozzle is 3.8 × 10⁵ Pa. Taking the surface tension to be 0.072 N/m and the kinematic viscosity to be 8.72 × 10⁻⁷ m²/s, this yields an SDM in the order of 100 microns according to Equations (28) and (29). This value will be used as a rough order of magnitude in the current study. However, in our previous study, we found that the performance of an IEC can be drastically improved by reducing the droplet size [33]. Therefore, in this study, we have modelled a droplet size in the range from 25 microns to 100 microns.

All the input conditions for the base case are summarized in

Table 1. Summary of inlet boundary conditions for base case.

Property	Value	Unit
Supply temperature	26	°C
Exhaust temperature	26	°C
Droplet temperature	26	°C
Supply relative humidity	60	%
Exhaust relative humidity	60	%
Droplet moisture content	100	%
Supply velocity	2.44	m/s
Exhaust velocity	2.44	m/s
Droplet velocity	0.0	m/s

. The fact that the droplet inlet temperature was set to 26 °C ensured that the whole cooling effect is ascribed to phase change. The droplet inlet velocity of 0 m/s was specified out of convenience. This meant that all droplet acceleration was due to viscous drag. The droplets were small enough that this did not affect the results. The moisture content of 100% means that the droplets consist of pure water.

2.3.3. Wall Treatment

In most other modelling articles, the evaporation of water and therefore the cooling effect is accounted for on the wall surface of the secondary air stream. By contrast, in this model, the evaporation of water from the droplets and thereby the cooling effect in the free stream is accounted for as well. However, in initial calculations, it was found that this droplet evaporation effect alone does not lead to satisfactory results [33], and therefore the cooling effect on the wet wall was added to the model.

For the heat and mass transfer directly at the boundary where the no-slip condition is invoked, heat transfer is governed by pure conduction and mass transfer by pure diffusion because the velocity approaches zero. Mathematically, this is expressed as [39]:

$$j_{H_{2}O}=\frac{{\dot{m}}_{H_{2}O}}{A_s}=-\rho \times D_{H_{2}O-air}\frac{\partial w_{H_{2}O}}{\partial y}{|}_{y=0}=h_{mass}\times (w_{H_{2}O,s}-w_{H_{2}O,\infty })$$

(32)

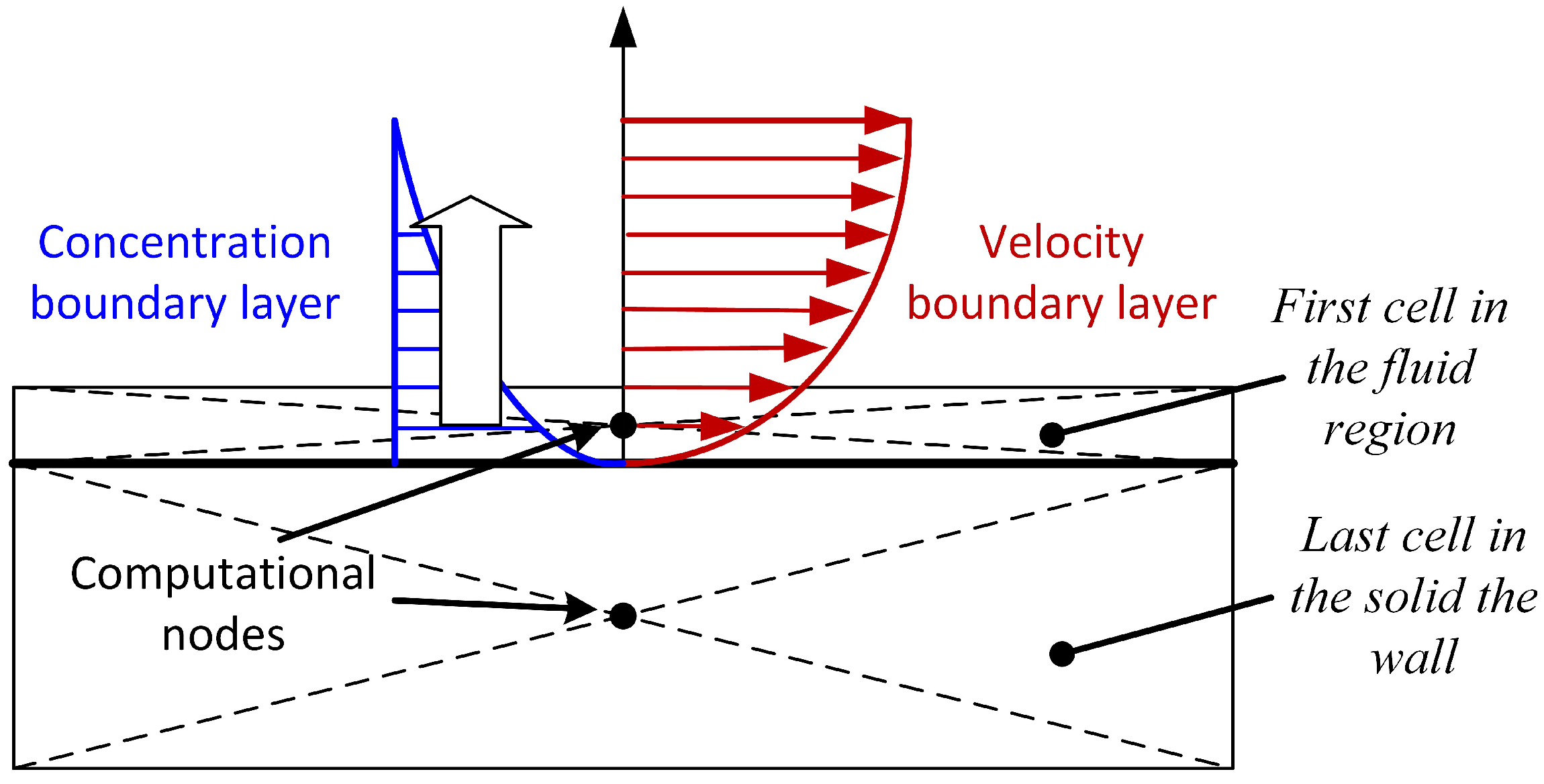
Because both the convective mass transfer coefficient $h_{mass}$ and the water vapour mass fraction in the free stream $w_{H_{2}O,\infty }$ are unknown, it is more convenient to implement the first expression which includes the diffusion coefficient near the wall. To this end, the first cell layer of the computational mesh near the wall should be very thin as the expression becomes accurate for an infinitive thin cell, as shown in Figure 5.

In the current model, it is assumed that the wet wall at the exhaust side is completely covered by a thin film of water, and therefore water vapour is at its saturation concentration directly on the wet wall. Inside the first cell layer, the water vapour concentration is calculated by the CFD code, and with this knowledge the amount of water that is diffusing into the fluid domain can be calculated. The diffusion coefficient $D_{H_{2}O-air}$ for water vapour in air is given by [40]:

$$D_{H_{2}O-air}=1.87\times {10}^{-10}\times T^{2.072}/P$$

(33)

where P is the total pressure in atm and T is the temperature in K. This water vapour flow must then be the amount of water that evaporates from the wall, leading to a cooling term in the energy equation:

$$S_H={\dot{m}}_{H_{2}O}\times r_{evap}$$

(34)

where $r_{evap}$ is the heat of evaporation (2440 × 10³ J/kg). This boundary condition is in fact very close to the one used by Jafaria et al. [28]. However, in our code, only the sink term due to evaporation is implemented; the heat conduction terms used by that group are automatically accounted for by CFX-4. As mentioned above, the model by Jafaria et al. [28] was based on OpenFOAM, and the equality of heat balances was a convergence criterion in that work.

Thus, there are two separate cooling mechanisms implemented in the secondary air stream, cooling from droplet evaporation and cooling from wall evaporation. These two terms act in competition: if there is a large amount of water evaporating from the wall, this leads to a larger relative humidity in the free gas stream, which results in a reduced droplet evaporation, and vice versa. In the discussion of the results, a focus is put on distinguishing between these two effects.

2.3.4. Solution Procedure

As is shown above, the particle transport equations are a set of ordinary differential equations. In CFX-4, the partial differential equations are solved for the flow calculation and then the ordinary differential equations are solved for the particle transport model. So, the particle transport model forms an extra loop in the solution procedure outside the flow calculation. The number of iterations for each of these outer loops should be in the order of 10, and then the inner iterations to solve the particle differential of the flow should be in the order of a few hundreds, depending on the complexity of the flow [34]. Overall, the model proved surprisingly robust, and in the parametric study, it took around 1 h to obtain a converged solution from an initial guess of a prior calculation on a laptop computer with a 2.60 GHz CPU.

3. Results

The Results section consists of two subsections: a detailed analysis of the base case results and a parametric study where the effects of the droplet size and the mass flow rate of liquid water on the predicted efficiency are summarized.

The overall inlet conditions for the air streams are summarized in Table 1. In addition to this, the mass flow rate of the water droplets and their average size must be specified. The size of the droplets was specified by an average droplet size and an exponent for the Rossin–Rammler distribution which was set to 3 [34]. A total of 200 droplets followed, and they emerged from 50 random positions along the inlet of the secondary air stream. When the mass flow rate of the droplets is changed, the amount of droplets, size distribution and random position stay the same, but the rate of droplet per time changes, and thus the potential cooling power of the droplets changes.

3.1. Base Case Results

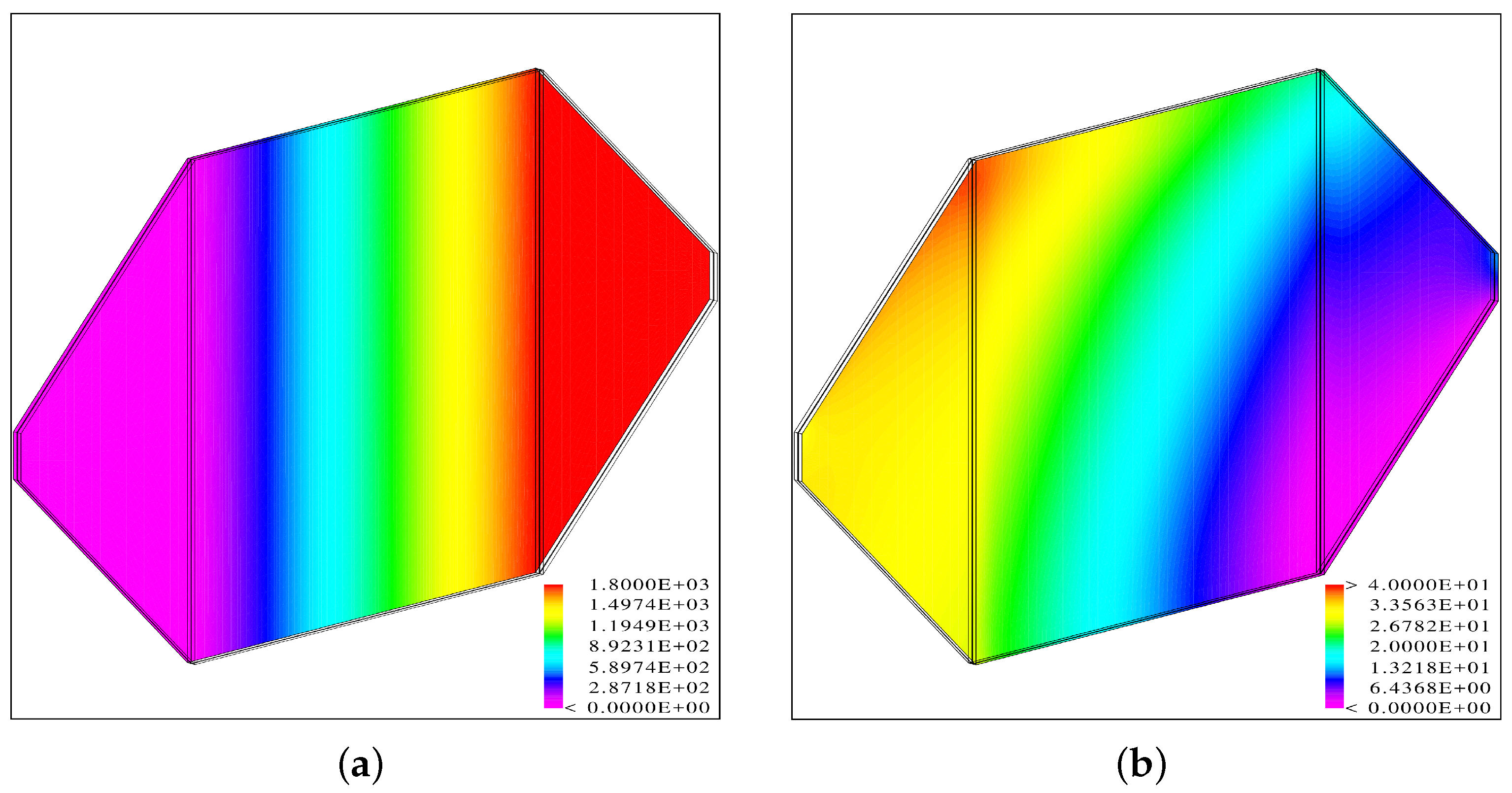
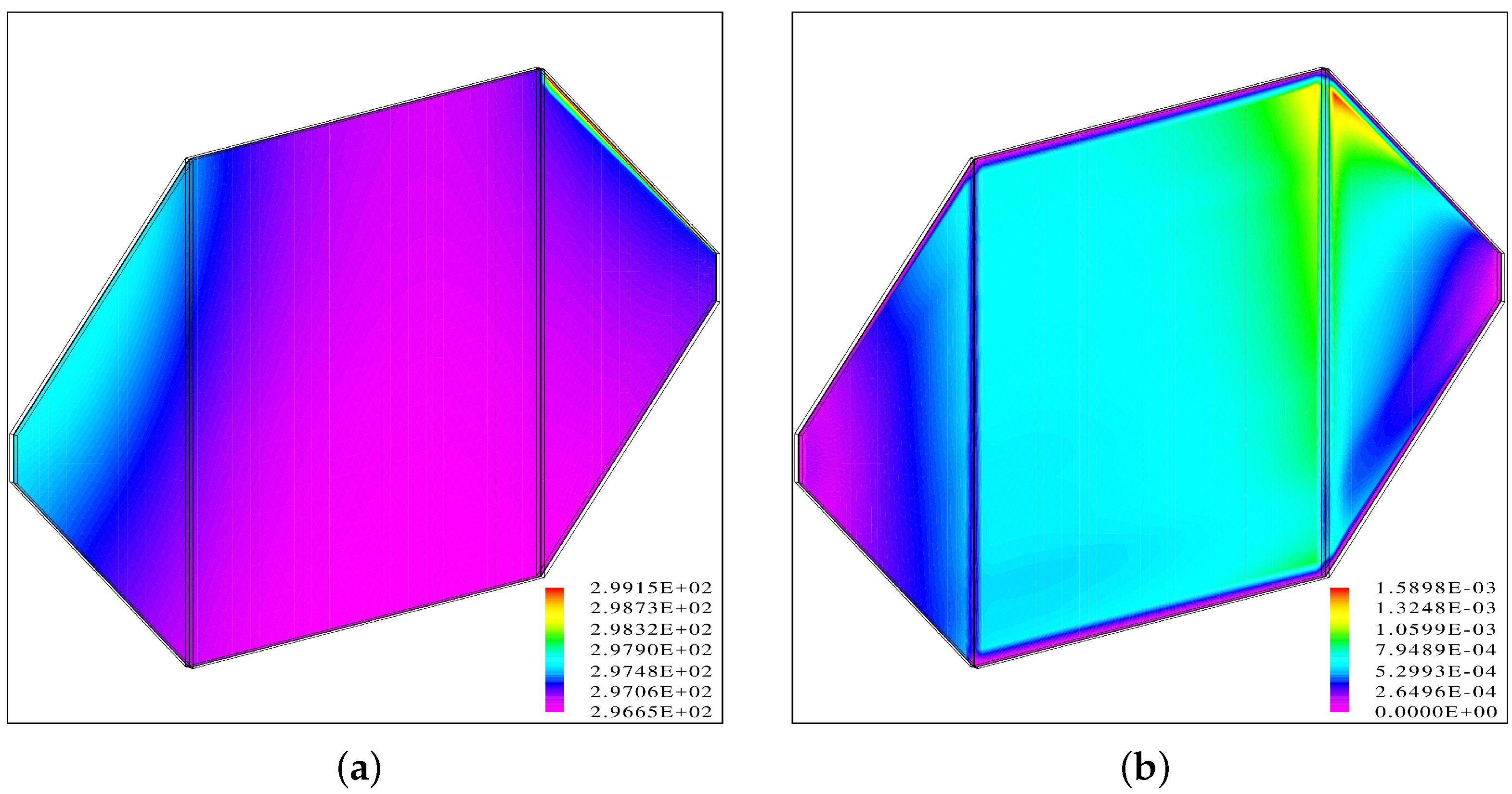
In the base case, the average droplet size was specified as 50 microns, and the total mass flow rate of liquid water was 10 mg/s. The detailed distribution of the temperature in the secondary and primary air stream is shown in Figure 6. As CFX-4 is based on SI units, the temperature is given in degrees K. Naturally, most of the physical effects occur inside the secondary air stream, while in the primary air stream, only the temperature is of interest. Clearly, it is the supply stream temperature drop that is the parameter that should be maximized, as the wet bulb efficiency is based on this.

The calculated temperature drop in the center of the secondary flow stream is slight, below 2 °C. This is substantially below the targeted temperature drop of around 5 °C, and the calculated efficiency is accordingly lower. It will be shown below that the cooling rate depends strongly on the average droplet size, and a smaller droplet size leads to a higher efficiency.

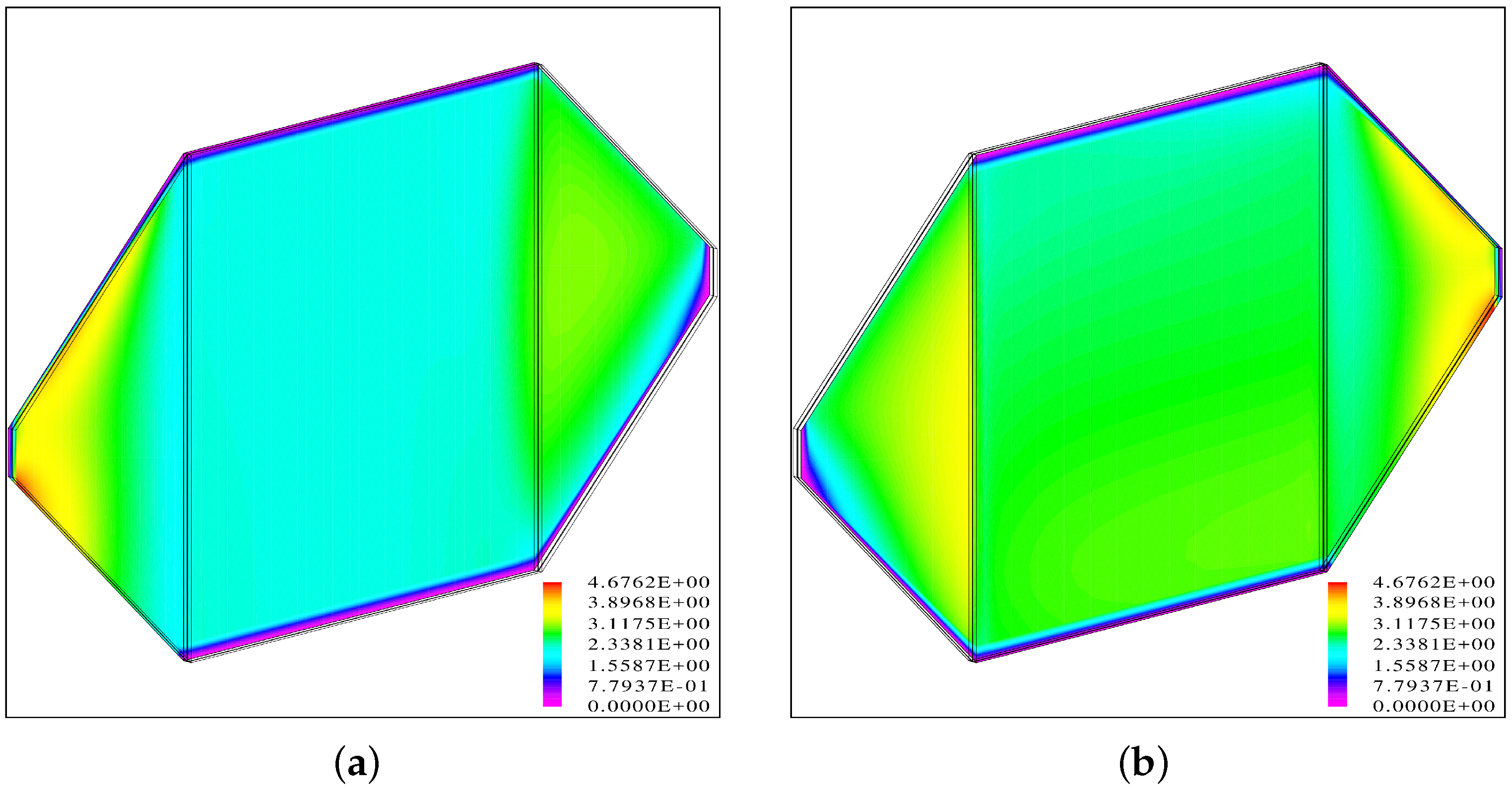
The calculated distribution of the relative pressure is shown in Figure 7. At both outlets, the relative pressure is set to zero, and the inlet pressure and the overall pressure drop result from the calculation. It is interesting that the exhaust side pressure drop is substantially higher than the supply side, where no phase change or multiphase flow occurs. At both sides, the resistances and the dry flow rates were equal, and therefore the higher pressure drop must be a result of the interphase drag and the evaporation.

The speed is the absolute velocity, shown in Figure 8. The results indicate a fairly even distribution of the flow across all channels.

The relative humidity at the exhaust side, shown in Figure 9, indicates that the air at the exhaust side is far from its thermodynamic equilibrium state, which would not permit the gas phase to be below saturation in the presence of liquid water. Therefore, the underlying assumption of thermodynamic equilibrium when employing psychrometric charts as in Figure 1 is not fulfilled. Of all the water sprayed into the exhaust stream, only a small amount evaporates. Near the wet wall, however, the local relative humidity is around 90%. This high value results from two effects: the addition of water vapour to the gas phase due to evaporation and the mere drop in temperature which will lead to an increased local relative humidity.

Overall, there is a lot of cooling occurring on the wet wall, and the lowest local temperatures can be found here, as can be seen in Figure 10. Moreover, the calculated cooling power on the wet wall is shown in Figure 10. These values are calculated from the local amount of mass transfer on the wall, Equation (34), multiplied with the latent heat of evaporation.

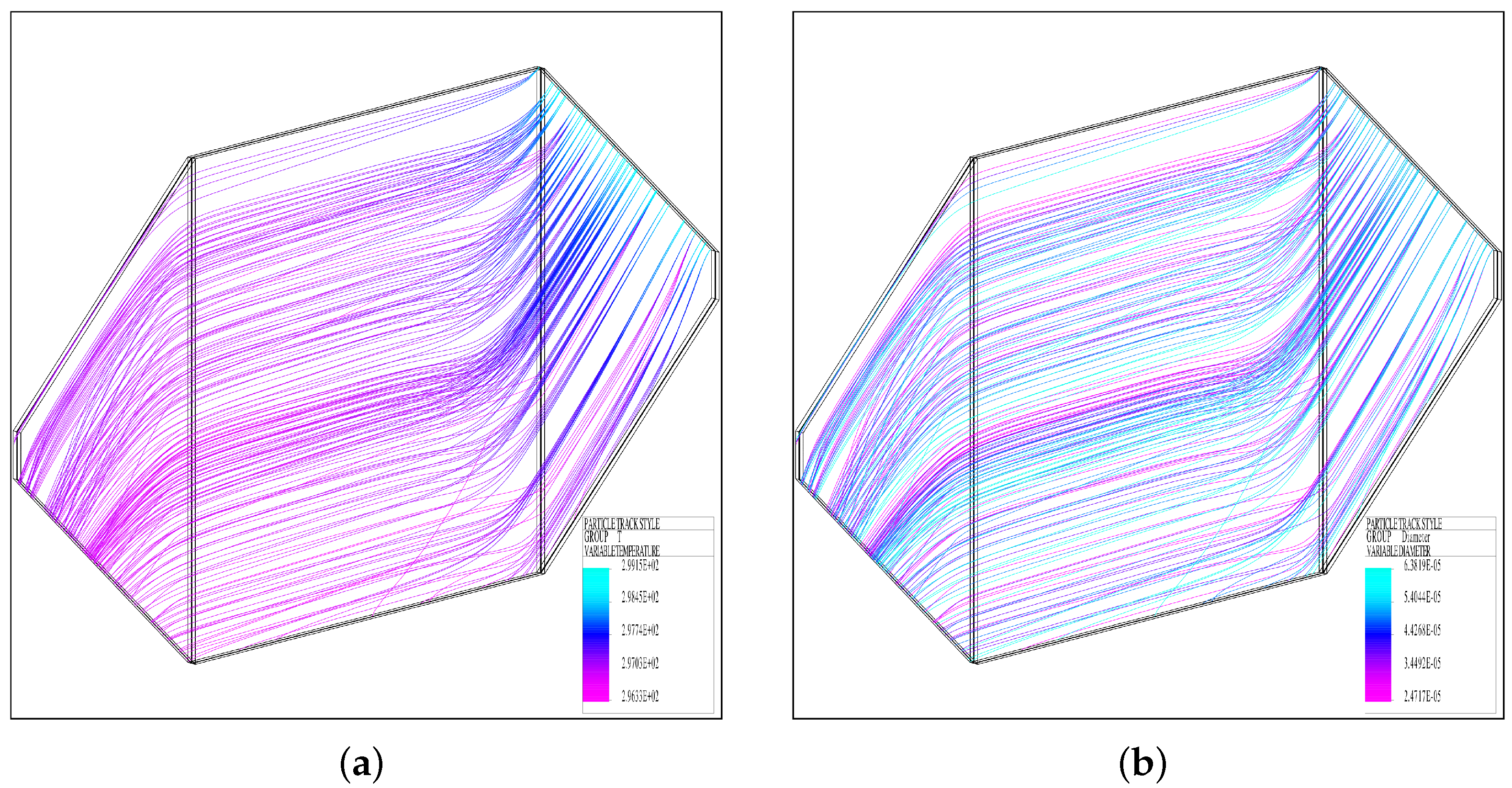
Finally, the particle tracks are shown in Figure 11. The spray dryer model naturally calculates the temperature and mass of the droplets. The overall amount of water that is undergoing phase change is also reported in the output file.

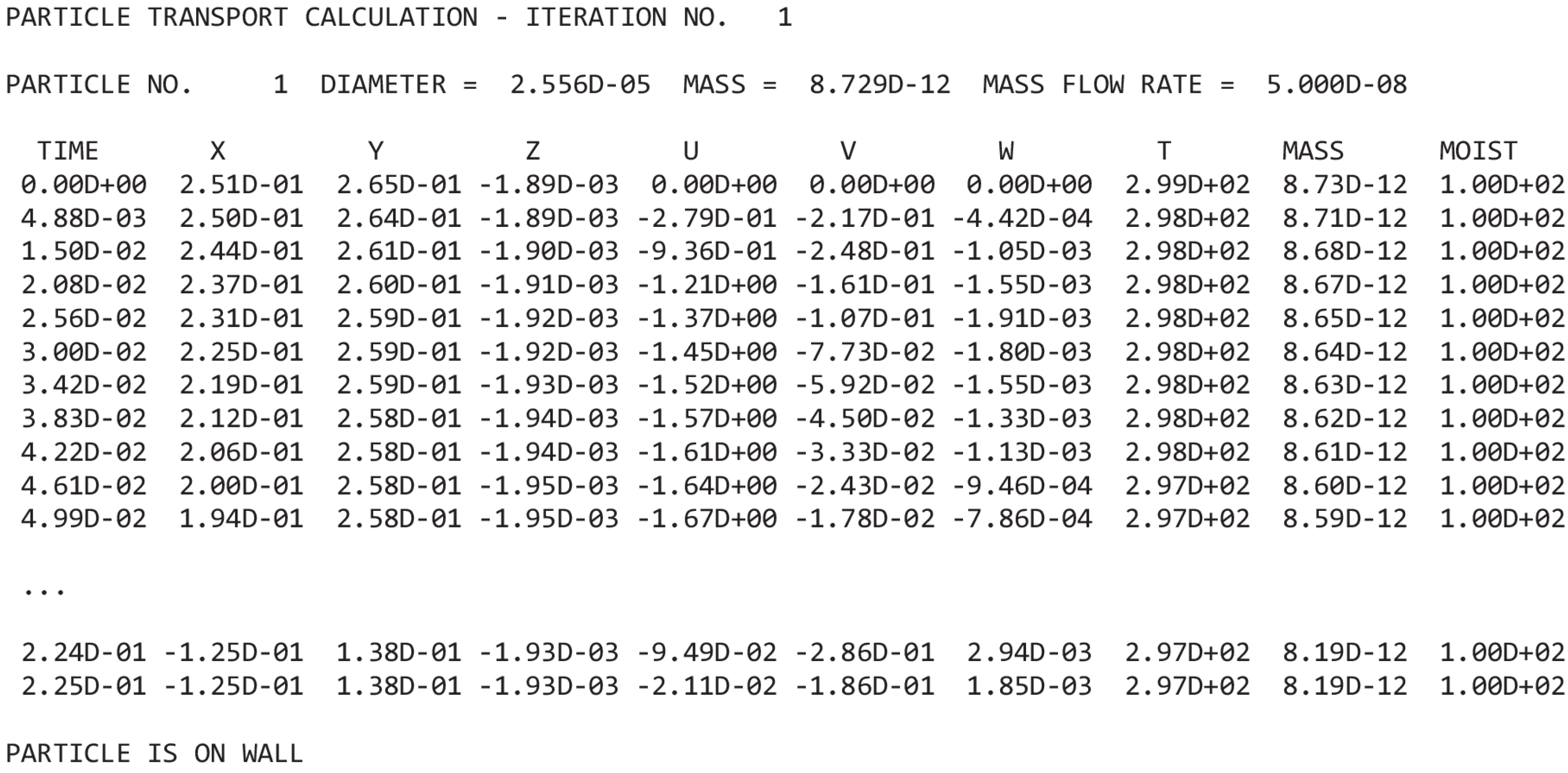
The particle tracks in the Lagrangian framework are also reported in detail. Figure 12 exemplarily shows a snippet from the output file of the history of particle No. 1, which remains inside the computational domain for 0.225 s before it hits a wall. Once a particle hits a wall, it is taken out of consideration. It can also be seen how the mass is reduced to evaporation. The total mass flow rate shown in Figure 12 indicates how many of this particle class are entering the domain for every given time.

The predicted performance of the cooler in this case is calculated to be

$${\eta }_{wb}=\frac{T_{db,in}-T_{db,out}}{T_{db,in}-T_{wb,in}}=\frac{26.0-24.29}{26.0-20.28}=30\%$$

(35)

which is far below the targeted performance of 84%. Prior experiments resulted in a varying efficiency between 35% and 90%, strongly depending on the operating and test conditions. However, in experiments, the inlet water temperature was below the one used here, and, as mentioned above, the water supply was higher than the one used in this case. Note that an efficiency of just 30% is close to the values obtained by Jafarian et al. [28] when the channel length is below 500 mm, as is the case here. Besides the work by Jafarian et al. [28], higher efficiencies were also calculated by Xu et al. [20], who used a channel length in the order of 1 m and investigated different climate regions. The limited area of the heat exchanger was already listed by Duan et al. [5] as one of the performance-reducing factors.

It is the goal of this work to shed light into fundamental underlying phenomena in order to better understand the factors that are important for the performance. It was shown above that in the current model, the aluminium plate that is separating the supply side and exhaust side is planar, while in practice it is corrugated, offering a higher volumetric surface area. Besides the short channel length employed here, this can be one reason why the model might be underpredicting the performance. Keeping that in mind, a parametric study was conducted in order to find out whether, for the given conditions, a better performance can be obtained by adjusting the liquid water flow rate and the droplet size.

3.2. Parametric Study

In the first parametric study, the effects of the droplet size distribution and of the liquid mass flow rate were evaluated, where the average droplet size was varied between 25 microns, 50 microns (base case), 75 microns and 100 microns, respectively, and the mass flow rate was varied between 5 mg/s, 10 mg/s (base case), 20 mg/s, 30 mg/s, 40 m/s and 50 mg/s, respectively.

Table 2. Key results for an average droplet size of 25 microns.

${\dot{\mathit{m}}}_{\mathit{l}}$ [mg/s]	${\mathit{P}}_{\mathit{drop}}$ [W]	${\mathit{P}}_{\mathit{wall}}$ [W]	${\mathit{P}}_{\mathit{sup}}$ [W]	$\mathbf{\Delta }{\mathit{T}}_{\mathit{exh}}$ [K]	$\mathbf{\Delta }{\mathit{T}}_{\mathit{sup}}$ [K]	${\mathit{\eta }}_{\mathit{wb}}$ [%]
5	1.835	4.727	4.048	−1.028	−1.639	31.52
10	3.333	4.463	4.202	−1.336	−1.701	32.72
20	5.710	4.031	4.452	−1.836	−1.803	34.66
30	7.583	3.694	4.636	−2.156	−1.877	36.10
40	9.116	3.431	4.770	−2.356	−1.931	37.14
50	10.345	3.204	4.884	−2.529	−1.977	38.03

,

Table 3. Key results for an average droplet size of 50 microns.

${\dot{\mathit{m}}}_{\mathit{l}}$ [mg/s]	${\mathit{P}}_{\mathit{drop}}$ [W]	${\mathit{P}}_{\mathit{wall}}$ [W]	${\mathit{P}}_{\mathit{sup}}$ [W]	$\mathbf{\Delta }{\mathit{T}}_{\mathit{exh}}$ [K]	$\mathbf{\Delta }{\mathit{T}}_{\mathit{sup}}$ [K]	${\mathit{\eta }}_{\mathit{wb}}$ [%]
5	0.646	5.539	4.172	−0.745	−1.689	32.48
10	1.235	5.431	4.222	−0.842	−1.709	32.87
20	3.367	5.226	4.318	−1.037	−1.748	33.62
30	3.409	5.046	4.404	−1.198	−1.783	34.29
40	4.377	4.875	4.478	−1.336	−1.813	34.87
50	5.275	4.719	4.542	−1.466	−1.839	35.37

,

Table 4. Key results for an average droplet size of 75 microns.

${\dot{\mathit{m}}}_{\mathit{l}}$ [mg/s]	${\mathit{P}}_{\mathit{drop}}$ [W]	${\mathit{P}}_{\mathit{wall}}$ [W]	${\mathit{P}}_{\mathit{sup}}$ [W]	$\mathbf{\Delta }{\mathit{T}}_{\mathit{exh}}$ [K]	$\mathbf{\Delta }{\mathit{T}}_{\mathit{sup}}$ [K]	${\mathit{\eta }}_{\mathit{wb}}$ [%]
5	0.288	4.997	3.876	−0.664	−1.569	30.18
10	0.571	4.953	3.890	−0.704	−1.575	30.29
20	1.127	4.870	3.914	−0.777	−1.585	30.48
30	1.667	4.792	3.936	−0.850	−1.594	30.65
40	2.190	4.714	3.956	−0.915	−1.602	30.80
50	2.699	4.651	3.976	−0.972	−1.610	30.96

and

Table 5. Key results for an average droplet size of 100 microns.

${\dot{\mathit{m}}}_{\mathit{l}}$ [mg/s]	${\mathit{P}}_{\mathit{drop}}$ [W]	${\mathit{P}}_{\mathit{wall}}$ [W]	${\mathit{P}}_{\mathit{sup}}$ [W]	$\mathbf{\Delta }{\mathit{T}}_{\mathit{exh}}$ [K]	$\mathbf{\Delta }{\mathit{T}}_{\mathit{sup}}$ [K]	${\mathit{\eta }}_{\mathit{wb}}$ [%]
5	0.190	5.017	3.866	−0.640	−1.565	30.10
10	0.381	4.992	3.870	−0.664	−1.567	30.13
20	0.756	4.943	3.878	−0.704	−1.570	30.20
30	1.122	4.895	3.884	−0.737	−1.573	30.24
40	1.488	4.851	3.890	−0.777	−1.575	30.29
50	1.845	4.807	3.896	−0.810	−1.577	30.34

summarize the key results. The first column lists the mass flow rate of water into the secondary air stream; the second column, $P_{drop}$, is the cooling power of the droplets, calculated from the reported mass transfer of water from the droplets multiplied with the heat of evaporation. The cooling at the wet wall, $P_{wall}$, is the calculated amount of water undergoing phase change, also multiplied with the heat of evaporation. Noting that the overall cooling is split between the supply side and the exhaust side, the supply side cooling power $P_{sup}$ was extracted from the enthalpy fluxes reported in the output file.

The changes in the temperatures at both the supply and exhaust sides were then calculated from the respective enthalpy balances and reported mass flow rates, and finally, the wet bulb efficiencies were determined from the supply side temperature drop.

4. Discussion

The focus of this work was put on distinguishing two different evaporation phenomena: droplet evaporation and wall evaporation, both of which lead to a cooling effect. For an internal evaporative cooling unit, the main property of importance is the degree of cooling of the supply air, also expressed in terms of the wet bulb efficiency. The general trends are an increase in $\eta$ with increasing water supply, which, however, is less pronounced for larger droplet sizes. In the current design, a realistic drop size is around 50–100 microns. Overall, the predicted performances are below expectation.

However, by comparing these predicted performances with literature data, e.g., as published by Javarian et al. [28] or Xu et al. [20], we note that the predicted performances were higher mostly due to the longer channel lengths investigated. Therefore, the reported efficiencies here are not necessarily unrealistic. In particular, the important role of the channel length and the size of the IEC were shown in the first reference above.

Looking at the results calculated here, the main option for increasing the efficiency appears to be to reduce the droplet size as much as possible. This could be accomplished by adjusting the nozzles and the mass flow rates or adjusting the water pressure according to Equation (30). It is important to recall that the current design is not operating according to psychrometric diagrams; the gas phase and liquid phase are not in thermodynamic equilibrium. Longer flow channels, a higher area for heat exchange and smaller droplets will likely bring this design closer to its anticipated operating point, as is shown in Figure 3. Our preliminary work has shown that, under the conditions investigated, the droplets start to fully evaporate for a size in the range of 10 microns [33]. Table 2 also shows that for a low droplet size, it is beneficial to increase the flow rate, while the other tables show that for larger droplet sizes, the beneficial effect of splashing a high amount of water is small, always assuming there is enough water to keep the supply side wall wetted.

As mentioned above, another reason why the calculated performance is low is that the water temperature was set equal to the temperature of the air streams, which was performed in order to distinguish the effect of evaporation from convective cooling. We can thus expect a better performance when using colder water for the spraying.

It is also instructive to investigate the effect of a bypass, i.e., reducing the amount of exhaust air passing through the heat exchanger, as was investigated by Riangvilaikul and Kumar [41] and Jafarian et al. [28]. Later on, the role of the channel length and other geometrical adjustments can also be studied, but the focus in near-future work will be on increasing the performance of the current design while maintaining its compactness.

5. Conclusions

In this work, a first attempt was made to develop a computational fluid dynamics model of an indirect evaporative cooler by combining the Eulerian model for air flow with a Lagrangian model for droplet evaporation. To this end, the spray dryer model as was priorly implemented in a commercial software tool has been employed. The design investigated was a compact IEC with a channel length in the order of 300 mm. The model was used to study the effect of the water droplet size and mass flow rate on the performance for a given set of inlet air conditions, both at the supply side and exhaust side. The outcome of the modelling study can be summarized as follows:

• Under the conditions investigated, thermodynamic equilibrium at the exhaust side was not established, i.e., the relative humidity of the exhaust air at the exit was around 80–85% while liquid water was entrained.
• For a realistic droplet size in the order of 100 microns, the predicted wet bulb efficiency was around 30%. This value only improved substantially when the droplet size was reduced to 50 microns and below.
• For a realistic droplet size in the order of 100 microns, there is almost no beneficial effect predicted by increasing the mass flow of the water provided that the exhaust side wall is wetted.
• From comparing with the literature results, it can be concluded that the main reason for the predicted poor performance is the short channels of around 300 mm.
• A further reason for the calculated low efficiency is the fact that the water temperature was set equal to the air stream temperatures of 26 °C. A colder water temperature is more realistic and will lead to a better predicted performance.
• The effect of a bypass such that the amount of exhaust air is lower than the required amount of supply air can be easily investigated with the current model and is subject to future work.