Numerical Study of Heat Transfer and Fluid Flow Characteristics of a Hydrogen Pulsating Heat Pipe with Medium Filling Ratio
Abstract
1. Introduction
2. Numerical Model
2.1. Mathematical Model and Governing Equations
2.2. Solution Approach
3. Experimental Parameters and Geometry Model
3.1. Experimental Conditions
3.2. 2D Model for Simulation
3.3. Grid-Independence and Initial Distribution
4. Results and Discussion
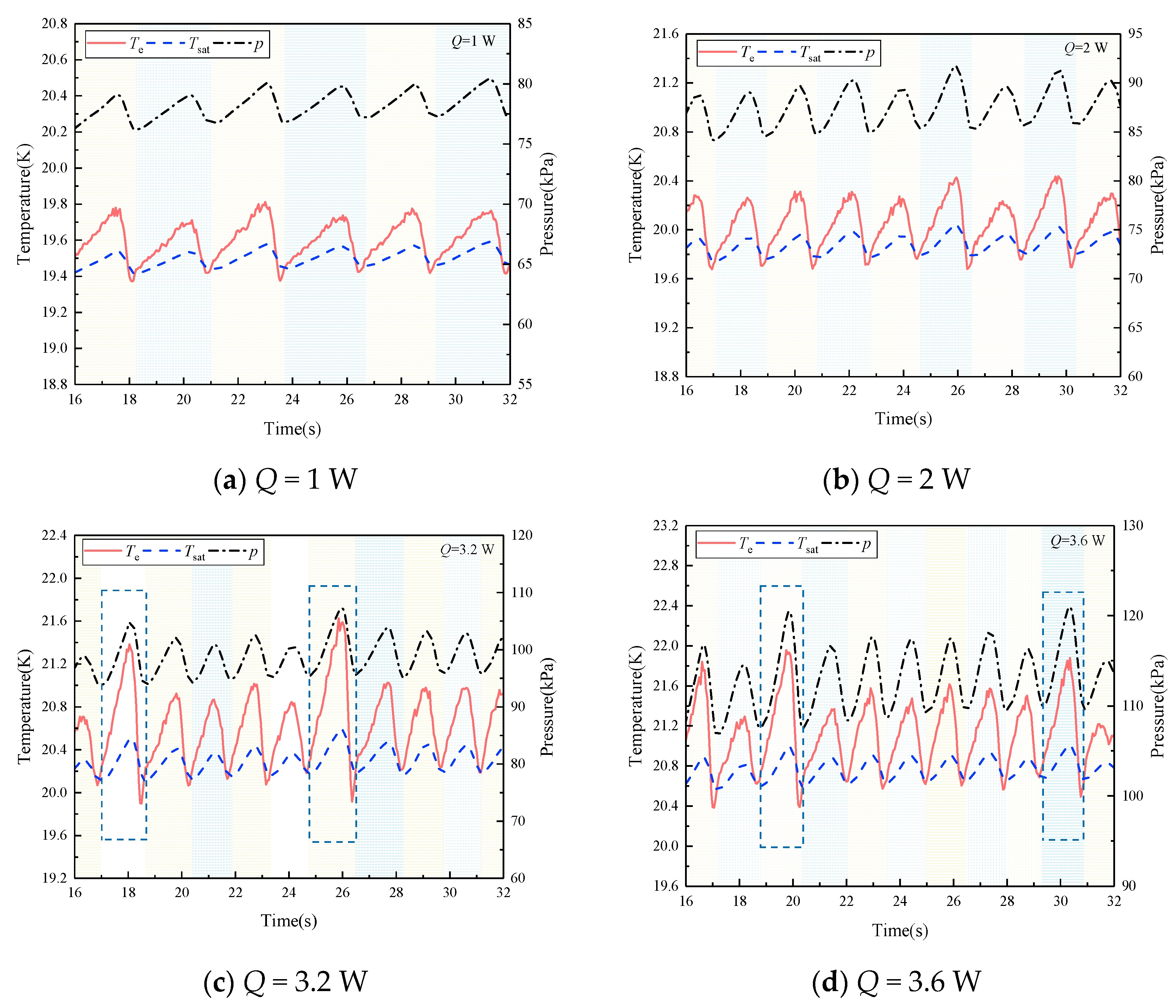
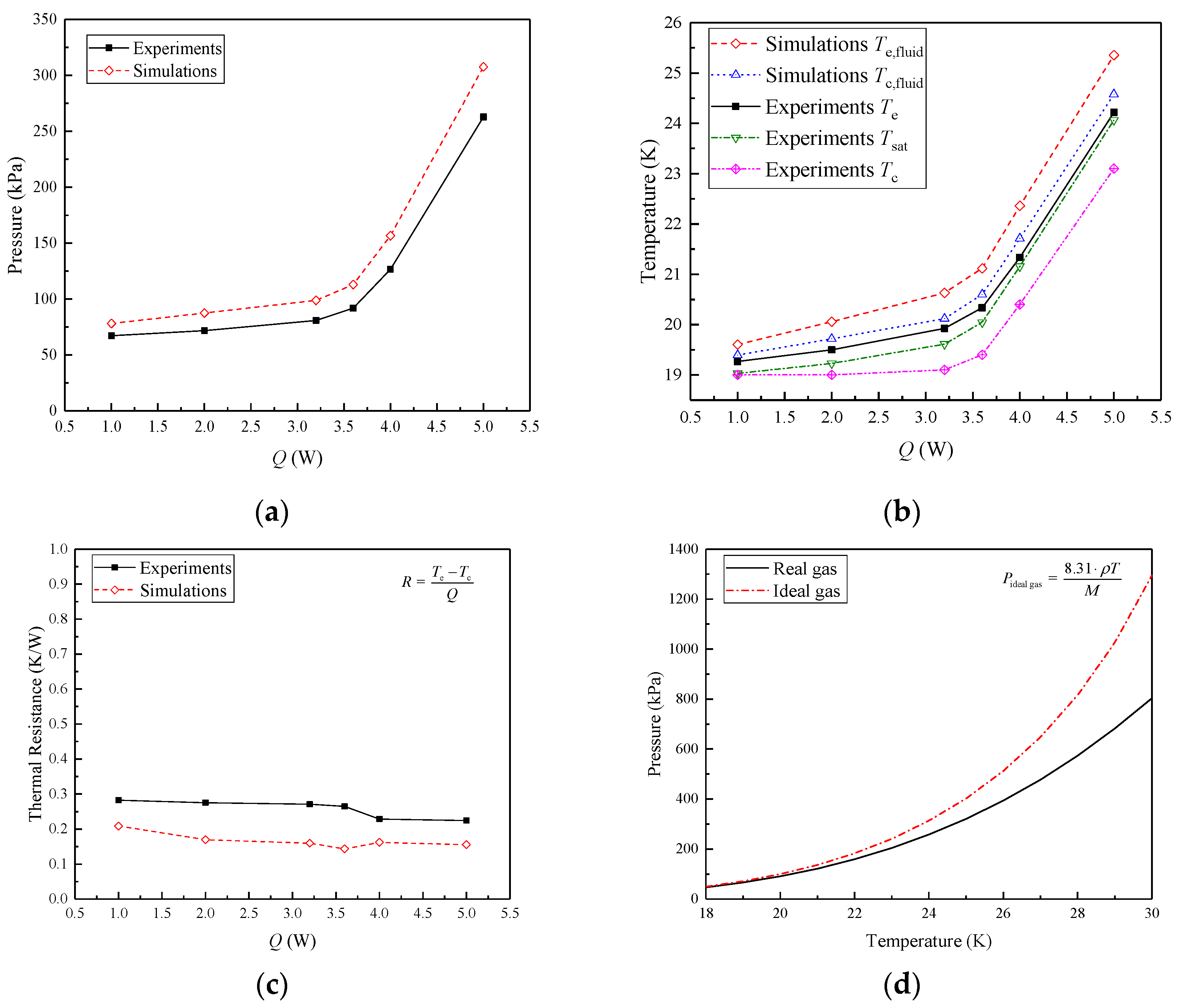
4.1. Comparison between Simulation and Experiment
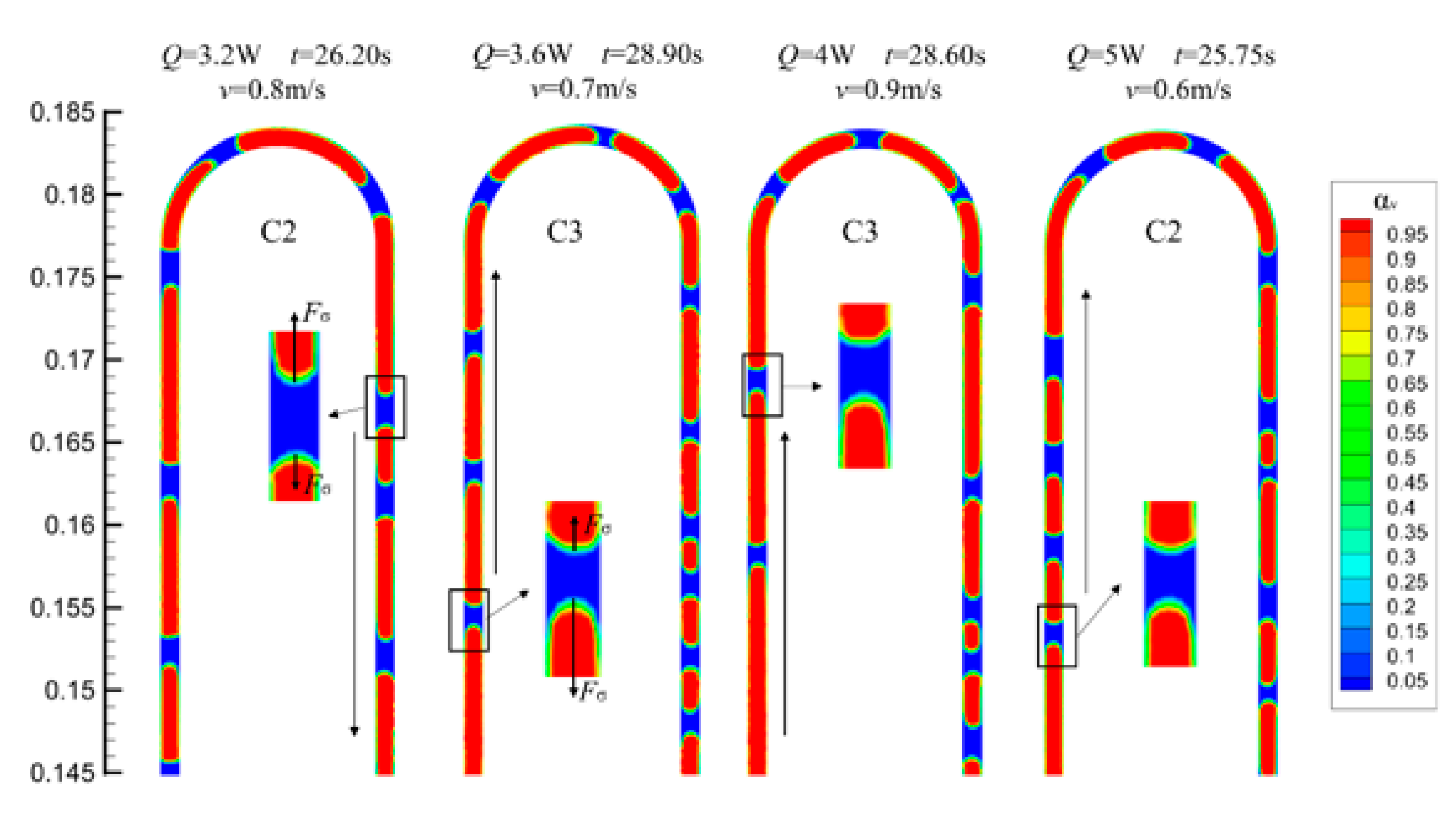
4.2. The Evaporation and Condensation Inside the PHP
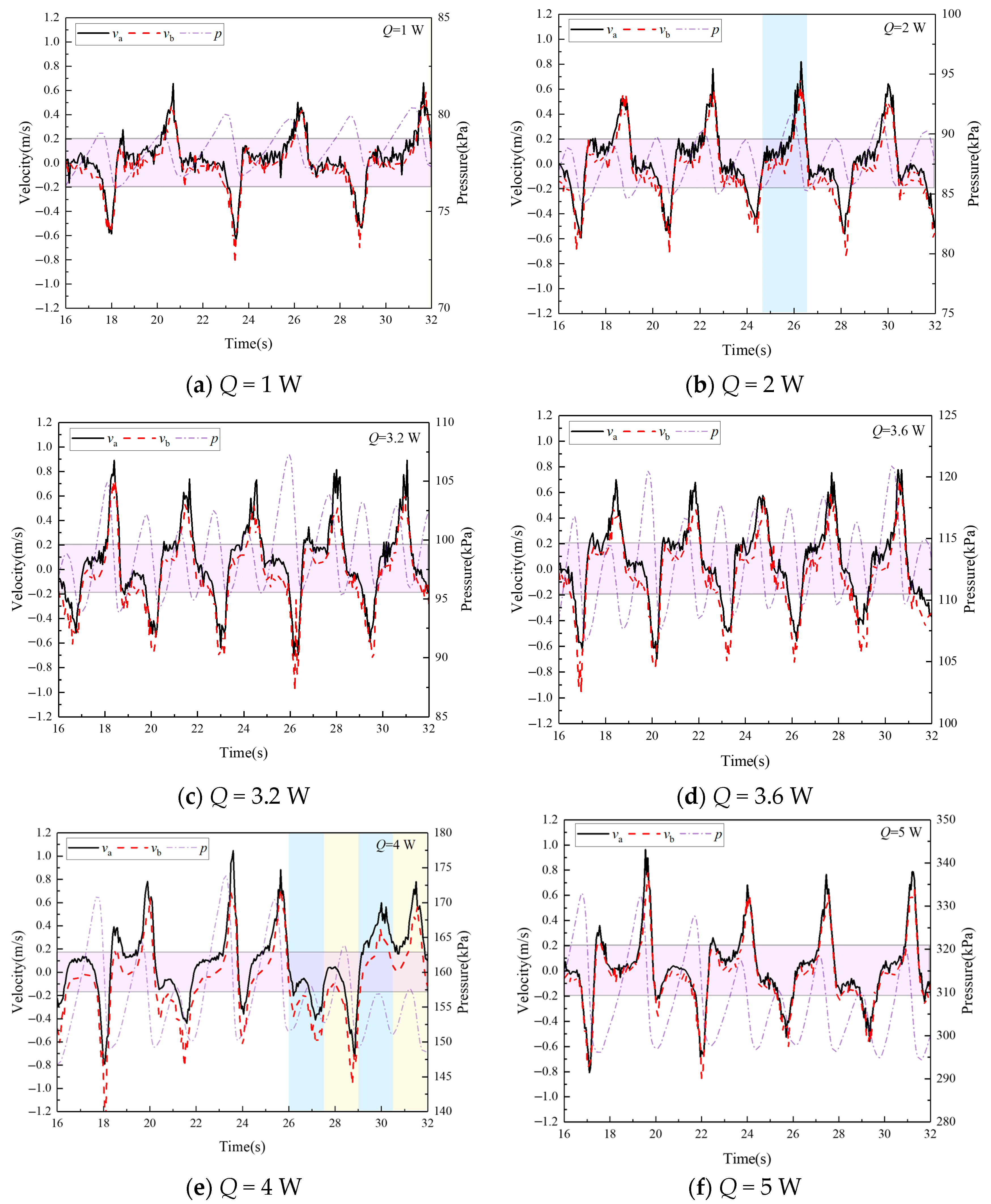
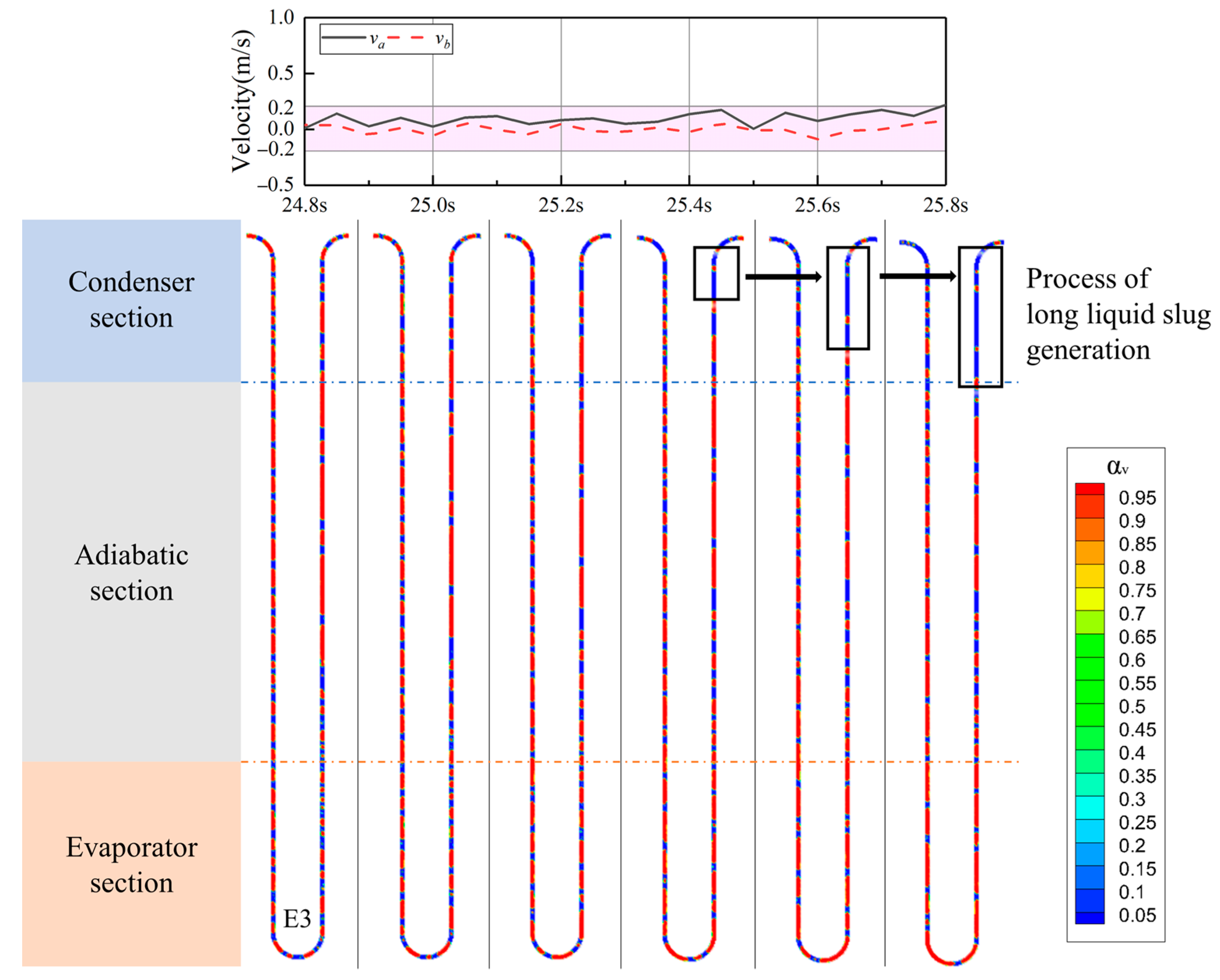
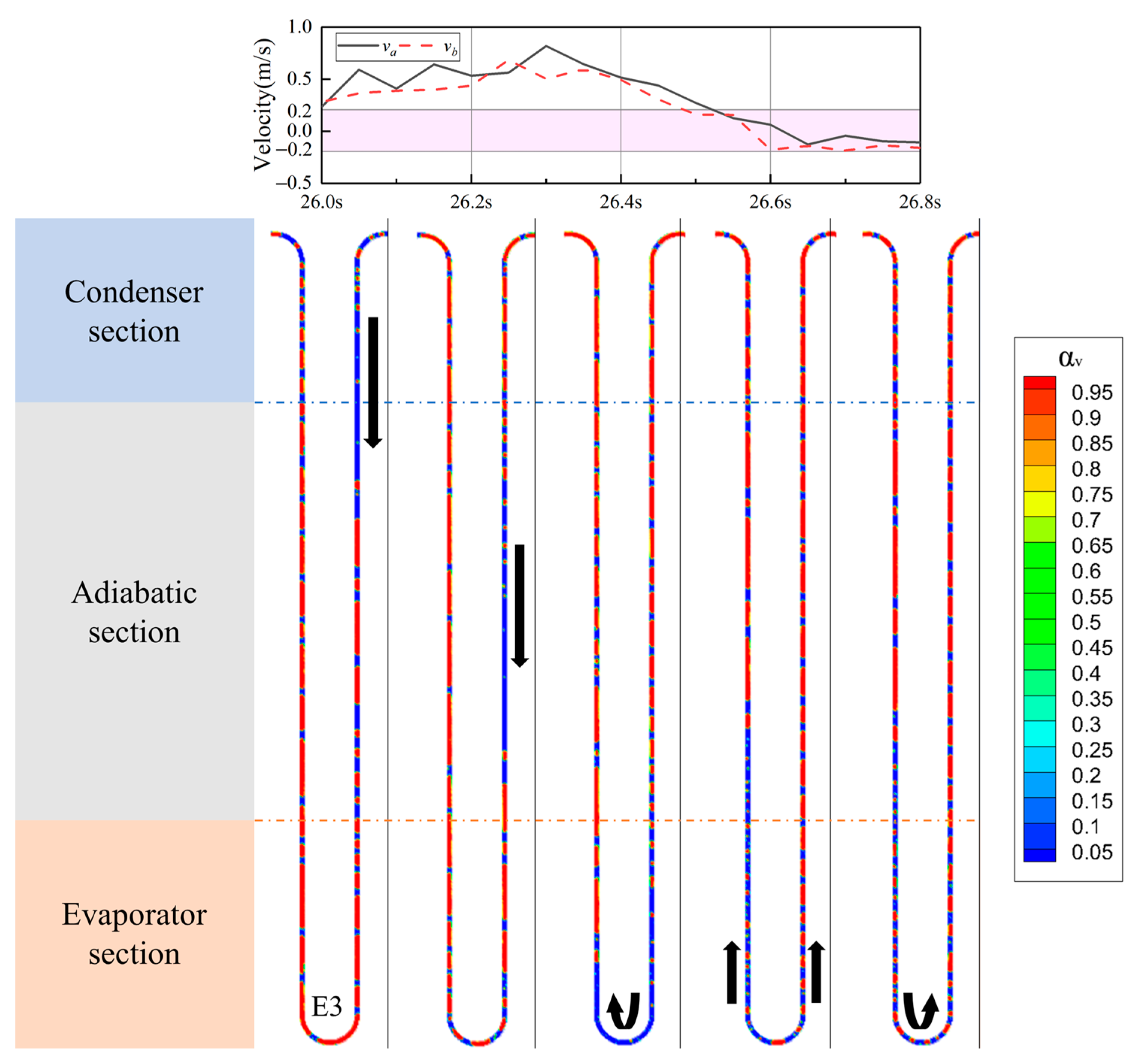
4.3. The Velocity Characteristics in the Stable Operation
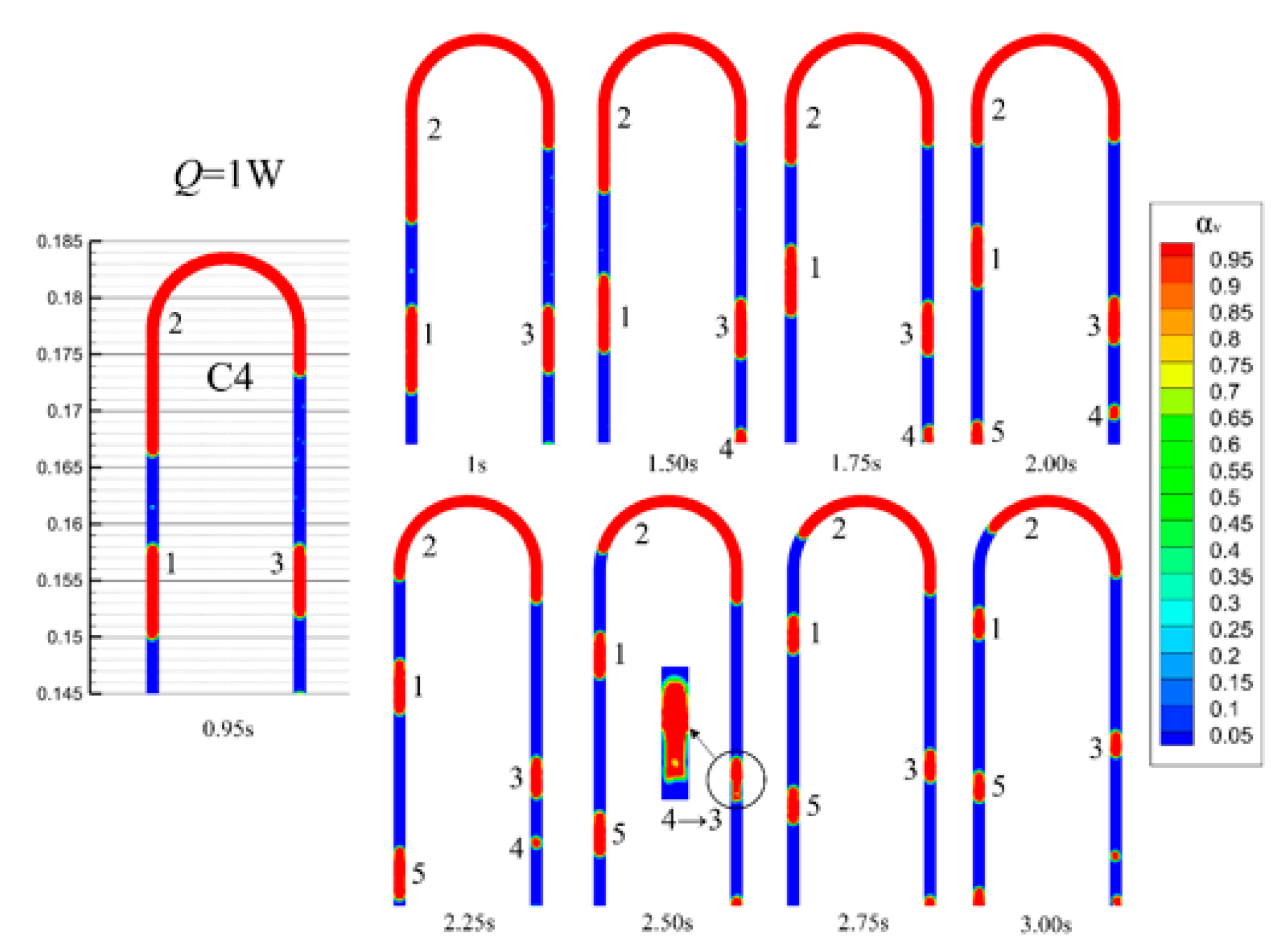
4.4. The Vapor–Liquid Distribution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | |
| d | inner diameter, mm |
| E | energy, J/kg |
| F | force, N |
| FR | filling ratio, % |
| g | acceleration of gravity, m/s2 |
| hfg | latent heat, J/kg |
| k | thermal conductivity, W/(m·K) |
| L | length, mm |
| N | number of turns |
| p | pressure, kPa |
| Q | heat load, W |
| R | thermal resistance, K/W |
| Sh | energy source, J/(m3·s) |
| Sm | mass source, kg/(m3·s) |
| Svol | volume force source, kg/(m2·s2) |
| T | temperature, K |
| v | velocity, m/s |
| Greek symbols | |
| α | void fraction |
| β | empirical coefficient, s−1 |
| θ | inclination angle, ° |
| κ | surface curvature |
| μ | dynamic viscosity, Pa·s |
| ρ | density, kg/m3 |
| σ | surface tension coefficient, N/m |
| Subscripts | |
| a | adiabatic |
| c | condensation |
| e | evaporation |
| l | liquid |
| v | vapor |
| sat | saturation |
References
- Andersson, J.; Grönkvist, S. Large-scale storage of hydrogen. Int. J. Hydrog. Energy 2019, 44, 11901–11919. [Google Scholar] [CrossRef]
- Al Ghafri, S.Z.; Munro, S.; Cardella, U.; Funke, T.; Notardonato, W.; Trusler, J.M.; Leachman, J.; Span, R.; Kamiya, S.; Pearce, G. Hydrogen liquefaction: A review of the fundamental physics, engineering practice and future opportunities. Energy Environ. Sci. 2022, 15, 2690–2731. [Google Scholar] [CrossRef]
- Notardonato, W.; Baik, J.; McIntosh, G. Operational Testing of Densified Hydrogen Using G-M Refrigeration. AIP Conf. Proceeding 2004, 170, 664–674. [Google Scholar]
- Notardonato, W.; Swanger, A.; Fesmire, J.; Jumper, K.; Johnson, W.; Tomsik, T. Zero boil-off methods for large-scale liquid hydrogen tanks using integrated refrigeration and storage. IOP Conf. Ser. Mater. Sci. Eng. 2017, 278, 012012. [Google Scholar] [CrossRef]
- Hastings, L.J.; Plachta, D.; Salerno, L.; Kittel, P. An overview of NASA efforts on zero boiloff storage of cryogenic propellants. Cryogenics 2001, 41, 833–839. [Google Scholar] [CrossRef]
- Plachta, D.; Stephens, J.; Johnson, W.; Zagarola, M. NASA cryocooler technology developments and goals to achieve zero boil-off and to liquefy cryogenic propellants for space exploration. Cryogenics 2018, 94, 95–102. [Google Scholar] [CrossRef]
- Wan, C.; Zhu, S.; Shi, C.; Bao, S.; Zhi, X.; Qiu, L.; Wang, K. Numerical simulation on pressure evolution process of liquid hydrogen storage tank with active cryogenic cooling. Int. J. Refrig. 2023, 150, 47–58. [Google Scholar] [CrossRef]
- Faraji, H.; Yıldız, Ç.; Arshad, A.; Arıcı, M.; Choukairy, K.; El Alami, M. Passive thermal management strategy for cooling multiple portable electronic components: Hybrid nanoparticles enhanced phase change materials as an innovative solution. J. Energy Storage 2023, 70, 108087. [Google Scholar] [CrossRef]
- Winkler, M.; Vergez, M.; Mahlke, A.; Gebauer, M.; Müller, P.; Reising, C.; Bartholomé, K.; Schäfer-Welsen, O. Flat-Plate PHP with Gravity-Independent Performance and High Maximum Thermal Load. Energies 2023, 16, 7463. [Google Scholar] [CrossRef]
- Sun, Q.; Qu, J.; Li, X.; Yuan, J. Experimental investigation of thermo-hydrodynamic behavior in a closed loop oscillating heat pipe. Exp. Therm. Fluid Sci. 2017, 82, 450–458. [Google Scholar] [CrossRef]
- Ayel, V.; Slobodeniuk, M.; Bertossi, R.; Romestant, C.; Bertin, Y. Flat plate pulsating heat pipes: A review on the thermohydraulic principles, thermal performances and open issues. Appl. Therm. Eng. 2021, 197, 117200. [Google Scholar] [CrossRef]
- Mameli, M.; Besagni, G.; Bansal, P.K.; Markides, C.N. Innovations in pulsating heat pipes: From origins to future perspectives. Appl. Therm. Eng. 2022, 203, 117921. [Google Scholar] [CrossRef]
- Mushan, S.G.; Deshmukh, V.N. A review of pulsating heat pipes encompassing their dominant factors, flexible structure, and potential applications. Int. J. Green Energy 2024, 1–38. [Google Scholar] [CrossRef]
- Pfotenhauer, J.M.; Sun, X.; Berryhill, A.; Shoemaker, C.B. The influence of aspect ratio on the thermal performance of a cryogenic pulsating heat pipe. Appl. Therm. Eng. 2021, 196, 117322. [Google Scholar] [CrossRef]
- Li, M.N.; Li, L.F.; Xu, D. Effect of filling ratio and orientation on the performance of a multiple turns helium pulsating heat pipe. Cryogenics 2019, 100, 62–68. [Google Scholar] [CrossRef]
- Liang, Q.; Fang, C.; Li, Y.; Liu, J.; Zhao, W.; Ai, L. Cooldown characteristics of a neon cryogenic pulsating heat pipe. J. Low Temp. Phys. 2022, 207, 278–294. [Google Scholar] [CrossRef]
- Dixit, T.; Authelet, G.; Mailleret, C.; Gouit, F.; Stepanov, V.; Baudouy, B. High performance and working stability of an 18 W class neon pulsating heat pipe in vertical/horizontal orientation. Cryogenics 2023, 132, 103670. [Google Scholar] [CrossRef]
- Mueller, B.; Pfotenhauer, J.; Miller, F. Performance of nitrogen pulsating heat pipes as passive thermal switches in a redundant cryocooler application. Appl. Therm. Eng. 2021, 196, 117213. [Google Scholar] [CrossRef]
- Li, S.Z.; Bu, Z.C.; Fang, T.G.; Wang, Y.; Shen, Y.; Tao, X.; Jiao, B.; Gan, Z. Experimental study on the thermo-hydrodynamic characteristics of a nitrogen pulsating heat pipe. Int. Commun. Heat Mass Transf. 2023, 146, 106920. [Google Scholar] [CrossRef]
- Sun, X.; Li, S.; Jiao, B.; Gan, Z.; Pfotenhauer, J.; Wang, B.; Zhao, Q.; Liu, D. Experimental study on hydrogen pulsating heat pipes under different number of turns. Cryogenics 2020, 111, 103174. [Google Scholar] [CrossRef]
- Chandratilleke, R.; Hatakeyama, H.; Nakagome, H. Development of cryogenic loop heat pipes. Cryogenics 1998, 38, 263–269. [Google Scholar] [CrossRef]
- Natsume, K.; Mito, T.; Yanagi, N.; Tamura, H.; Tamada, T.; Shikimachi, K.; Hirano, N.; Nagaya, S. Heat transfer performance of cryogenic oscillating heat pipes for effective cooling of superconducting magnets. Cryogenics 2011, 51, 309–314. [Google Scholar] [CrossRef]
- Mito, T.; Natsume, K.; Yanagi, N.; Tamura, H.; Terazaki, Y. Enhancement of thermal properties of HTS magnets using built-in cryogenic oscillating heat pipes. IEEE Trans. Appl. Supercond. 2013, 23, 4602905. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Shafii, M.B.; Faghri, A.; Zhang, Y.W. Thermal modeling of unlooped and looped pulsating heat pipes. J. Heat Transf. -Trans. ASME 2001, 123, 1159–1172. [Google Scholar] [CrossRef]
- Nikolayev, V.S. Physical principles and state-of-the-art of modeling of the pulsating heat pipe: A review. Appl. Therm. Eng. 2021, 195, 117111. [Google Scholar] [CrossRef]
- Mucci, A.; Kholi, F.K.; Chetwynd-Chatwin, J.; Ha, M.Y.; Min, J.K. Numerical investigation of flow instability and heat transfer characteristics inside pulsating heat pipes with different numbers of turns. Int. J. Heat Mass Transf. 2021, 169, 120934. [Google Scholar] [CrossRef]
- Dreiling, R.; Dubois, V.; Zimmermann, S.; Nguyen-Xuan, T.; Schreivogel, P.; di Mare, F. Numerical investigation of slug flow in pulsating heat pipes using an interface capturing approach. Int J Heat Mass Transf. 2022, 199, 123459. [Google Scholar] [CrossRef]
- Liu, Y.; Dan, D.; Wei, M.; Zheng, S.; Sun, J. Numerical investigation on the start-up and heat transfer performance of dual-diameter pulsating heat pipes. Appl. Therm. Eng. 2024, 236, 121709. [Google Scholar] [CrossRef]
- Sun, X.; Li, S.Z.; Wang, B.; Jiao, B.; Pfotenhauer, J.; Miller, F.; Gan, Z. Numerical study of the thermal performance of a hydrogen pulsating heat pipe. Int. J. Therm. Sci. 2022, 172, 107302. [Google Scholar] [CrossRef]
- Gan, Z.H.; Sun, X.; Jiao, B.; Han, D.; Deng, H.; Wang, S.; Pfotenhauer, J.M. Experimental Study on a Hydrogen Closed Loop Pulsating Heat Pipe with Different Adiabatic Lengths. Heat Transf. Eng. 2019, 40, 205–214. [Google Scholar] [CrossRef]
- Pagliarini, L.; Cattani, L.; Bozzoli, F.; Mameli, M.; Filippeschi, S.; Rainieri, S.; Marengo, M. Thermal characterization of a multi-turn pulsating heat pipe in microgravity conditions: Statistical approach to the local wall-to-fluid heat flux. Int. J. Heat Mass Transf. 2021, 169, 120930. [Google Scholar] [CrossRef]
- Iwata, N.; Bozzoli, F.; Pagliarini, L.; Cattani, L.; Vocale, P.; Malavasi, M.; Rainieri, S. Characterization of thermal behavior of a micro pulsating heat pipe by local heat transfer investigation. Int. J. Heat Mass Transf. 2022, 196, 14. [Google Scholar] [CrossRef]
- Blasiak, P.; Opalski, M.; Parmar, P.; Czajkowski, C.; Pietrowicz, S. The Thermal-Flow Processes and Flow Pattern in a Pulsating Heat Pipe-Numerical Modelling and Experimental Validation. Energies 2021, 14, 5952. [Google Scholar] [CrossRef]







| Researchers (Year) | Tube Material | L (m) | d (mm) | N (-) | FR (%) | θ (°) | Q (W) | λ (W/m·K) | |
|---|---|---|---|---|---|---|---|---|---|
| Chandratilleke et al. [21] (1998) | -- | 0.46 | 3 | 4 | -- | 10 | 2.5~7.5 | 15,650~18,925 | |
| Mito and Natsume et al. | [22] (2011) | Stainless steel | 0.16 | 0.78 | 5 | 31~80 | 90 | 0~1.2 | 500~3000 |
| [23] (2013) | 0.225 | 1.5 | 11 | 23~60 | 90 | 0~2 | Max: 850 | ||
| Gan et al. | [20] (2020) | Copper and Stainless steel | 0.6 | 2.3 | 2, 5 | 28, 34, 50 | 90 | 0~5.5 | 10,000~70,000 |
| Pfotenhauer et al. [14] (2021) | Stainless steel | 1.2226 | 0.5 | 4 | 50, 70 | 0, 90 | 0.1~1.8 | 10,000~220,000 | |
| Working Fluid | Tcrit (K) | Operating Range (K) | ρl (kg/m3) | ρv (kg/m3) |
| Hydrogen | 33.15 | 14~30 | 54.54~76.97 | 0.13~10.45 |
| Water | 647.1 | 275~400 | 937.49~999.89 | 5.51 × 10−3~1.37 |
| Working Fluid | µl (Pa × s) | σ (mN/m) | hfg (kJ/kg) | (dp/dT)sat (kPa/K) |
| Hydrogen | 6.5 × 10−6~2.55 × 10−5 | 0.44~2.99 | 453.85~300.89 | 4.31~129.57 |
| Water | 2.19 × 10−4~1.68 × 10−3 | 53.58~75.39 | 2182.8~2496.5 | 0.05~7.48 |
| Initial Sets | Boundary Conditions | |||||||
|---|---|---|---|---|---|---|---|---|
| Fluid domain temperature: 19 K Liquid Volume Fraction: 0.51 Pressure: 66,294 Pa | Time | 0~0.95 s | 0.95~32 s | |||||
| Evaporator | 19 K | 1 W | 2 W | 3.2 W | 3.6 W | 4 W | 5 W | |
| Condenser | 19 K | 19 K | 19 K | 19.1 K | 19.4 K | 20.4 K | 23.1 K | |
| Q (W) | Error of P (%) | Error of Te (%) |
|---|---|---|
| 1 | 16.26 | 1.75 |
| 2 | 21.96 | 2.85 |
| 3.2 | 22.12 | 3.54 |
| 3.6 | 22.92 | 3.84 |
| 4 | 23.69 | 4.81 |
| 5 | 23.71 | 4.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Bu, Z.; Jiao, B.; Wang, B.; Gan, Z. Numerical Study of Heat Transfer and Fluid Flow Characteristics of a Hydrogen Pulsating Heat Pipe with Medium Filling Ratio. Energies 2024, 17, 2697. https://doi.org/10.3390/en17112697
Yang D, Bu Z, Jiao B, Wang B, Gan Z. Numerical Study of Heat Transfer and Fluid Flow Characteristics of a Hydrogen Pulsating Heat Pipe with Medium Filling Ratio. Energies. 2024; 17(11):2697. https://doi.org/10.3390/en17112697
Chicago/Turabian StyleYang, Dongyu, Zhicheng Bu, Bo Jiao, Bo Wang, and Zhihua Gan. 2024. "Numerical Study of Heat Transfer and Fluid Flow Characteristics of a Hydrogen Pulsating Heat Pipe with Medium Filling Ratio" Energies 17, no. 11: 2697. https://doi.org/10.3390/en17112697
APA StyleYang, D., Bu, Z., Jiao, B., Wang, B., & Gan, Z. (2024). Numerical Study of Heat Transfer and Fluid Flow Characteristics of a Hydrogen Pulsating Heat Pipe with Medium Filling Ratio. Energies, 17(11), 2697. https://doi.org/10.3390/en17112697





