Modeling of Heat and Mass Transfer in Cement-Based Materials during Cement Hydration—A Review

Abstract

Cement-based materials encompass a broad spectrum of construction materials that utilize cement as the primary binding agent. Among these materials, concrete stands out as the most commonly employed. The cement, which is the principal constituent of these materials, undergoes a hydration reaction with water, playing a crucial role in the formation of the hardened composite. However, the exothermic nature of this reaction leads to significant temperature rise within the concrete elements, particularly during the early stages of hardening and in structures of substantial thickness. This temperature rise underscores the critical importance of predictive modeling in this domain. This paper presents a review of modeling approaches designed to predict temperature and accompanying moisture fields during concrete hardening, examining different levels of modeling accuracy and essential input parameters. While modern commercial finite element method (FEM) software programs are available for simulating thermal and moisture fields in concrete, they are accompanied by inherent limitations that engineers must know. The authors further evaluate effective commercial software tools tailored for predicting these effects, intending to provide construction engineers and stakeholders with guidance on managing temperature and moisture impacts in early-age concrete.

1. Introduction

Cement-based materials (CBMs) encompass a wide range of construction materials that utilize cement as a primary binding agent. The versatility of cement-based materials lies in their adaptability to various construction needs through adjustments in composition, curing methods, and additives. Therefore, cement-based materials are essential in modern construction, offering a balance of strength and easy production, which is crucial for building resilient and sustainable infrastructure. Among these materials, concrete as a cement-based material is the most commonly used. Comprising a mixture of cement, aggregates, and water, concrete forms a solid and robust material that can be shaped into various forms and sizes to meet construction requirements. Despite its ancient origins, concrete remains immensely popular due to its strength, durability, and versatility, making it a solid and durable option for civil engineering projects. Concrete is pivotal in a wide array of construction projects, ranging from buildings and bridges to roads and dams. Its ability to form solid and robust structural components makes it ideal for foundations, columns, beams, slabs, and walls. In bridge construction, concrete is preferred for its capacity to withstand heavy loads and its durability. For road construction, concrete provides a durable and long-lasting surface capable of handling high traffic volumes with minimal maintenance. Further, in tunneling and underground construction, concrete is favored for its structural integrity and fire resistance. Shotcrete, a type of sprayed concrete, is commonly used to reinforce tunnel linings, stabilizing excavated surfaces and preventing collapses. Concrete is also crucial in the construction of dams, reservoirs, and other water-retaining structures due to its impermeability and high compressive strength. Concrete is increasingly utilized in sustainable construction practices. Innovations such as recycled concrete aggregates, low-carbon cement, and permeable concrete contribute to environmentally friendly building solutions. Additionally, concrete’s thermal mass properties improve energy efficiency in buildings by reducing heating and cooling demands, especially when combined with phase change materials [1,2]. Finally, concrete’s adaptability and reliability make it indispensable in civil engineering. Its diverse applications span nearly every aspect of infrastructure development, contributing to the construction of safe, durable, and efficient structures that meet modern society’s needs. Advances in concrete technology continue to enhance its performance, sustainability, and application scope, solidifying its role as a widely used material in the field of civil engineering.

The multi-phase structure of concrete, comprising the cement paste, aggregates, and the interfacial transition zone (ITZ), creates a complex and interdependent system. Each phase contributes distinct properties that, when combined, determine the overall behavior of concrete in various applications. Therefore, advances in understanding its multi-phase structure are still desired to improve concrete performance and make it more durable, sustainable, and suitable for modern civil engineering challenges [3,4,5]. Nevertheless, accurately describing the multi-phase nature of concrete, including its microstructure and the properties and interactions of its components, remains a challenging task. Nevertheless, the main component of concrete is cement, which plays a main role in its formation and performance. When water is added to cement, it reacts with the calcium silicates to form calcium silicate hydrates (C-S-Hs) and calcium hydroxide, resulting in a strong and durable matrix that binds the aggregates together, creating hardened concrete. The hydration reaction is crucial for achieving hardened concrete. However, this exothermic reaction can cause issues, particularly during the early hardening period, leading to significant temperature increases inside concrete structures.

Early thermal effects on concrete emerged as a significant problem in the 19th and 20th centuries with the construction of large dams, highlighting issues related to the heat of hydration [6]. Notable examples of early concrete dams include the Hoover Dam (completed in 1936) and the Grand Coulee Dam (completed in 1942) in the United States. Today, issues related to temperature increases due to the hydration process are also observed in large foundations, bridge abutment walls, tank walls, and massive retaining walls. These structures, where the dimensions of the cross-section are substantial enough for the heat of hydration to cause detrimental effects, are generally referred to as mass concrete structures or just mass concrete [6]. The temperature rise in such elements, which can reach up to 100 °C, poses two primary concerns. The first is the need to limit the maximum temperature to the range of 65–70 °C to prevent delayed ettringite formation (DEF), which can damage the concrete [7]. The second concern is the thermal gradients that develop across the cross-section of the element due to surface heat exchange and gradual cooling to ambient temperature. In mass concrete, the interior can heat up significantly more than the exterior, creating thermal gradients. As the inner concrete expands and the outer concrete contracts, this differential movement can cause thermal cracking. Additionally, the expansion during the heating phase and subsequent contraction during the cooling phase can also lead to significant internal stresses, resulting in cracks that compromise the structural integrity and watertightness of the element as this nature of thermal changes mainly affects wall structures, and therefore also tanks requiring the tightness. Specifications typically limit the maximum temperature difference between the inner part and the surfaces of a concrete structure to 15–20 °C as well as the difference between maximum temperature and final stable temperature to the range of 15–20 °C, as it is believed that concrete can withstand strains caused by such temperature differences [8,9]. Thus, it is necessary to control the temperature and changes in the structure and appropriate technology of concreting, curing conditions and fresh concrete mix proportions must be ensured to fulfil these temperature limits. It should be mentioned that the issue is even more complex, because, in this early period, when temperatures caused by the exothermic hydration reaction are generated, moisture loss through diffusion and thermal effects also occur, including internal water consumption during cement hydration. Because early-age cracking due to the described thermal and moisture effects caused by the hydration is a durability concern, as it can initiate reinforcement corrosion, predicting and estimating temperature and moisture effects during concrete hardening is crucial for construction engineers to mitigate these issues. This is evidenced by numerous scientific articles and reported engineering problems [10,11,12,13,14].

This paper reviews modeling approaches for predicting temperature and moisture fields during concrete hardening, discussing various levels of accuracy in modeling and important input parameters. Nowadays, commercial finite element method (FEM) software programs are available for simulating thermal and humidity fields in concrete, but they come with limitations that engineers need to understand. The authors review effective commercial software tools for predicting these effects, aiming to provide guidance to construction engineers and stakeholders in managing temperature and moisture effects in early-age concrete.

2. Theory and Existing Models

2.1. General Model for Heat and Mass Transfer

Typically, the equations governing the transport of mass and heat stem from the general balance equation. Considering a general quantity, A, the balance equation (Equation (1)) can be expressed as follows:

$$\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{o}\mathrm{f} A=\left(\mathrm{i}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{x} \mathrm{o}\mathrm{f} A\right)-(\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{x} \mathrm{o}\mathrm{f} A)+(\mathrm{G}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}/\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{m}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{o}\mathrm{f} A).$$

(1)

Equation (1) applies to any system, but often needs to be formulated as differential equations, especially when quantity A varies across the body under consideration or changes over time. Therefore, we focus on a fixed spatial volume, V, bounded by a surface, S, where we establish a balance between the changes in mass and heat within this volume and the net fluxes of mass or energy across the surface, S. Various types of fluxes must be taken into account: diffusive, convective, and radiative. Additionally, changes in the mass of a specific chemical species within volume V can result from chemical reactions. By following this approach, heat and mass transport can be described by Equation (2) that still maintain a general form, but are tailored to specific scenarios of heat and mass transfer in concrete during its curing process:

$$\left(\genfrac{}{}{0pt}{}{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{c}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}}{\mathrm{i}\mathrm{n} \mathrm{h}\mathrm{e}\mathrm{a}\mathrm{t} \mathrm{o}\mathrm{r} \mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}}\right)=\left(\genfrac{}{}{0pt}{}{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{f}\mathrm{l}\mathrm{u}\mathrm{x}}{\mathrm{o}\mathrm{f} \mathrm{h}\mathrm{e}\mathrm{a}\mathrm{t} \mathrm{o}\mathrm{r} \mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}}\right)+\left(\genfrac{}{}{0pt}{}{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{f}\mathrm{l}\mathrm{u}\mathrm{x}}{\mathrm{o}\mathrm{f} \mathrm{h}\mathrm{e}\mathrm{a}\mathrm{t} \mathrm{o}\mathrm{r} \mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}}\right)+\left(\genfrac{}{}{0pt}{}{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{f}\mathrm{l}\mathrm{u}\mathrm{x}}{\mathrm{o}\mathrm{f} \mathrm{h}\mathrm{e}\mathrm{a}\mathrm{t} \mathrm{o}\mathrm{r} \mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}}\right)+\left(\genfrac{}{}{0pt}{}{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}{\mathrm{o}\mathrm{f} \mathrm{h}\mathrm{e}\mathrm{a}\mathrm{t} \mathrm{o}\mathrm{r} \mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}}\right).$$

(2)

However, applying Equation (2) to describe thermal and humidity fields in early-age cement-based materials, particularly in the concrete, presents significant complexity. It is important to acknowledge that concrete is a porous body consisting of three phases: liquid, gaseous, and solid matrix. Moreover, coupled heat and moisture transfer in curing concrete involves chemical (due to the hydration process) and structural (due to the developing body properties) changes. While the challenge in modeling thermal fields caused by the heat of the hydration process is the nonlinearity and non-stationarity of this process and the necessity to consider internal heat sources along with the appropriate thermal properties of concrete, a challenge in modeling moisture fields arises from the diverse water transport mechanisms in the concrete, where water exists in various forms depending on the void types it occupies. Water in concrete can be categorized as capillary water, water vapor, adsorbed water, interlayer water, and water chemically combined during hydration. Each form of water undergoes different transport mechanisms influenced by the evolving microstructure of early-age concrete during hydration. Consequently, equations describing moisture transport should be tailored independently for each water form. However, due to the high complexity and near impossibility of modeling all intricacies, simplified descriptions are often employed. Therefore, models are developed as a compromise between physical accuracy and practical feasibility.

Nowadays, extensive research has focused on modeling heat and mass transfer in concrete and numerous works in the last 3 years emphasize the continuing relevance of this topic (

Table 1. Recent literature on modeling heat and mass transfer in concrete *.

Year	Chosen Studies Related to the Subject of Heat and Mass Transfer in Cement-Based Materials	General Scope of the Article
2024	Chen B. et al. [34]	thermal analysis/thermal property prediction model based on the experiments, hydration kinetics, and composite material equivalence theory
	Mirković U. et al. [35]	thermal analysis/FEM/Lusas Academic software (Available online: https://www.lusas.com (accessed on 1 March 2022))/validation
	Zhang J. et al. [12]	fully coupled hygro-thermo-mechanical model/FEM/validation
	Sumarno A. et al. [36]	thermal analysis/2D model
	Zhang S. et al. [37]	thermal fields/numerical simulation/ABAQUS 2021/validation
	Yu H. et al. [38]	thermal fields/numerical simulation/validation
2023	Mansour D. et al. [13]	thermal analysis/3D-finite difference model/MS Excel
	Van Tran M. et al. [39]	thermal analysis/numerical simulation/Ansys Fluent software/validation
	Cai Y. et al. [40]	thermal field/3D-FEM simulation/ABAQUS/validation
	Lajimi N. et al. [41]	hygro-thermal analysis/numerical simulation/DIGITAL Visual FORTRAN 95
	Ebid A. M. et al. [14]	State of the art on heat and mass transfer in self-compacting concrete and geopolymer concrete
	Wasik M. et al. [42]	the prototype of the experimental stand for heat and moisture transfer investigation in building materials
	Zhu J. et al. [43]	temperature field analysis/mesoscale simulation
	Prskalo S. et al. [44]	multi-field model/finite element code PANDAS
	Yin H. et al. [45]	multi-field model/3D flow lattice model (FLM)
	Rossat D. et al. [46]	thermo-hydro-mechanical model/FE simulation/validation
	Lyu C. et al. [47]	thermo-hydro-force coupling model/FE simulation/COMSOL Multiphysics/validation
	Li X. et al. [48]	thermal analysis/FEM/Midas FEA software/validation
	Meghwar S. L. et al. [49]	moisture diffusion/FE simulation/validation
2022	Yikici A. et al. [50]	thermal analysis/3D numerical model/finite volume method (FVM)/MATLAB/validation
	Cheng P. et al. [51]	coupled thermo-hydro-mechanical–phase field/2D numerical simulation/Fortran/The Intel® oneAPI Math Kernel Library PARDISO
	Bondareva et al. [52]	mathematical model of the unsteady coupled heat and mass transfer in concrete containing PCM/validation
	Mostafavi S.A. et al. [53]	thermal model/MATLAB
	Zhang Z. et al. [54]	moisture transport/2D computational fluid dynamics (CFDs) model
	Smolana A. et al. [55]	thermo-mechanical analysis/FEM simulation/DIANA FEA 10.2/validation
	Kuryłowicz-Cudowska A. et al. [56]	1D finite difference (FD) method/MATLAB/2D-FEM/GiD software/validation
2021	Chiniforush A.A. et al. [57]	coupled 3D thermal–mechanical numerical analysis/MATLAB/COMSOL ABAQUS 6.14 Multiphysics numerical platform/validation
	You W. et al. [58]	multi-field coupling model/3D-FEM simulation
	Azenha M. et al. [59]	recommendations/state of the art regarding modeling the thermo-chemo-mechanical behavior of massive concrete structures
	Pohl C. et al. [60]	three-phase transport model/X-ray computer tomography/validation
	Zhang Z. et al. [61]	thermo-mechanical analysis/3D-FEM simulation/ABAQUS/validation
	Kanavaris F. et al. [62]	thermo-chemo-hygro-mechanical (TCHM) simulation/MATLAB/DIANA FEA

* According to Scopus database.

). Early mathematical models for heat and moisture transfer in porous materials were proposed by Luikov [15,16], Harmathy [17], and De Vries [18]. Today, a variety of mathematical and numerical models exist in the literature, differing in complexity. Notably, more advanced models designed for concrete consider its porous and multi-phase nature, as well as chemical and physical phenomena [19,20,21,22,23,24]. In the realm of engineering applications, especially early-age massive concrete structures, commonly used equations often neglect thermodiffusion cross-effects [25,26,27,28,29]. Although coupled thermodiffusion equations derived from irreversible thermodynamics laws are available [30,31], they are rarely applied due to the perception that thermodiffusion cross-effects minimally influence thermal and moisture fields in early-age mass concrete, alongside technical challenges in their practical application to engineering tasks. Sophisticated models are computationally intensive and impractical for large concrete structures. In some cases, moisture diffusion is neglected, and only thermal fields are analyzed for massive structures [32,33]. The details of the applied models are provided in the next sections.

2.2. Modeling Heat and Mass Transfer in Concrete

The transfer of heat and moisture in cement-based materials, such as concrete, adheres to the fundamental principles outlined by Fourier’s law for heat transfer and Fick’s second law for moisture diffusion. However, a notable challenge emerges during the early stages of maturation. Initially, concrete comprises a mixture of liquids and solids with diverse diameters and shapes. As cement hydration progresses, the composition undergoes structural transformations, transitioning the concrete from a fluid mixture to a solid material.

In considering the evolving structure of concrete during its hardening process, two approaches for modeling early-age concrete emerge, summarized schematically in Figure 1 and comparatively discussed in the accompanying

Table 2. Methodologies for modeling heat and mass transfer in concrete.

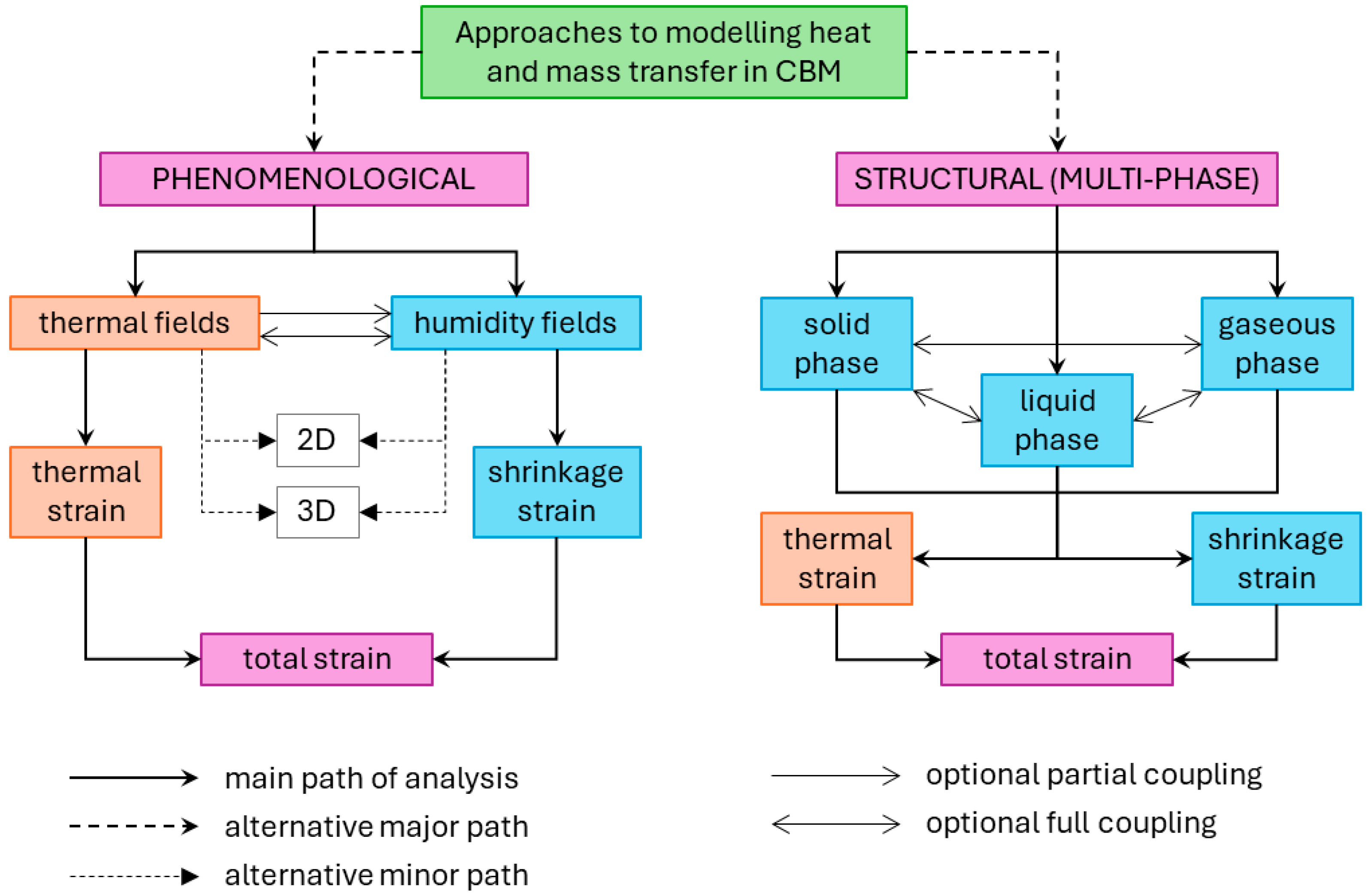
Possible Modeling Strategies	Advantages and Scope of Use	Disadvantages and Limitations
I. Multi-phase models	Enables accounting for heat and moisture transport intricacies in concrete—a porous medium. Suitable for fundamental research and modeling of laboratory-scale experiments.	Analysis is typically confined to 1-dimensional analysis due to model complexity and numerous associated parameters, necessitating auxiliary testing for determining relevant coefficient values.
II. Phenomenological models	Simplifying concrete as a homogeneous solid material facilitates its application in modeling heat and mass transfer for large-scale elements and structures. This approach enables 2- and 3-dimensional analyses with a balanced trade-off between computational effort and result accuracy.	Fails to consider all phenomena associated with the porous nature of concrete, particularly concerning the multidimensionality of the moisture diffusion process.
II.1 Thermal analysis only	Suitable for analyzing massive concrete structures where thermal strains induced by hydration heat are predominant, with drying effects being negligible.	Does not accommodate moisture analysis.
II.2 Moisture analysis only	Suitable for analyzing thin-walled or small-section elements where drying effects are predominant and hydration heat effects are negligible.	Does not facilitate thermal analysis, including variations in ambient temperature.
II.3a Uncoupled thermal and moisture analysis	Suitable for the general-purpose analysis of semi-massive concrete structures, accounting for significant variations in both temperature and moisture.	Does not consider the mutual influence of temperature on moisture diffusion or humidity on temperature transfer in the analyzed element.
II.3b Partially coupled thermal and moisture analysis	Typically, the impact of temperature on moisture diffusion is accounted for, enabling a more realistic modeling of moisture transfer within the analyzed element.	The modeling complexity increases due to both the higher number of model parameters and the numerical solution of coupled equations.
II.3c Fully coupled thermal and moisture analysis	Enables realistic modeling of both heat and mass transfer in concrete elements.	Among all phenomenological approaches, this method poses the greatest computational challenge due to the multitude of parameters and the numerical solution of interdependent heat and mass transfer equations.

. The first approach involves multi-phase models, which conduct a comprehensive analysis of physical phenomena and assess the influence of the material’s internal structure on these phenomena. This method entails defining appropriate constitutive equations for the solid, liquid, and gaseous phases within the medium, which are then averaged for a multi-phase environment. Several studies have developed multi-phase models for early-age concrete, notable among them are the works of Gawin et al. [31,63] and Di Luzio and Cusatis [27,28], alongside numerous other references, including recent contributions [44,45,58,64].

However, the multi-phase approach faces a significant challenge due to the multitude of parameters relevant to describing concrete behavior and the resulting complexity in modeling. Additionally, the intricate equations and extensive computational demands involved often lead to reliance on 1D approximations. Consequently, such analyses tend to overlook a thorough examination of the temperature and humidity distribution throughout the entire volume of the structural member. Despite employing an advanced multi-phase model, the actual prediction of thermal–humidity fields simplifies to one dimension (1D), which may not fully capture spatial complexities. This limitation becomes particularly evident in structural elements, like bridge abutments or massive pillars, which possess shapes differing from simple foundation slabs or blocks.

In contrast, the phenomenological approach is more commonly employed for modeling heat and mass transfer in concrete. This method treats concrete as a continuous medium, employing a macroscopic description of thermal and moisture phenomena. Numerous examples of applications of phenomenological models can be found in the literature, including references such as [46,65,66,67,68,69,70,71,72,73]. Therefore, this review focuses on the phenomenological approach to modeling heat and mass transfer in hardening cement-based materials. The upcoming sections delve into the detailed phenomenological approaches concerning heat and mass transfer in concrete, providing comprehensive insights. Additionally,

Table 3. Historical summary of the works marking milestones in the advancement of modeling heat and mass transfer in concrete.

Publication [Author, Year]	Major Development/Milestone
Fourier, 1822 [74]	Formulation of the law for heat transfer.
Fick, 1855 [75]	Formulation of the second law of moisture diffusion.
De Vries, 1958 [18] Luikov, 1964 [15] Harmathy, 1970 [17]	Formulation of equations for heat and mass transfer in porous materials.
Hirschfeld, 1948 [76] De Vries, 1958 [18] Luikov, 1964 [15] Harmathy, 1970 [17]	Formulation of heat equation with source function from hydration heat for hardening concrete.
De Vries, 1958 [18] Luikov, 1964 [15] Harmathy, 1970 [17]	Formulation of the equation for moisture diffusion with sink function due to bounding of water during hydration.
Bažant and Thounguthai, 1978 [19]	Partial coupling of heat and moisture diffusion—definition of the moisture diffusion coefficient as dependent on temperature.
Andreasik, 1982 [77]	Partial coupling of heat and moisture diffusion—definition of the thermal diffusion coefficient as dependent on humidity.
Černy and Rovnanikova, 2002 [78] Klemczak, 2011 [79]	Full coupling of thermal and moisture diffusion equations.
Neville, 1963 [80]	Definition of the thermal diffusion coefficient of hardening concrete as dependent on the degree of hydration, moisture content, and temperature.
Van Breugel, 1980 [81]	Definition of thermal conductivity of concrete as independent of the temperature for typical temperature ranges during operation.
Gawin et al., 2006 [31]	Definition of thermal conductivity of concrete as dependent on the moisture content.
Tatro, 2006 [82]	Definition of the specific heat of concrete as dependent on the temperature.
Hancox, 1966 [83] Bažant and Najjar, 1972 [84]	Definition of the moisture diffusion coefficient as dependent on the moisture content.
Gawin, 1993 [30]	Definition of the coefficient for partial coupling of thermal diffusion with moisture content.
Wyrwał and Szczęsny, 1989 [85]	Definition of the coefficient for partial coupling of moisture diffusion with temperature.
Faria et al., 2006 [66]	Definition of the combined convection–radiation coefficient of heat exchange.
Rastrup, 1954 [86] Hansen and Pedersen, 1977 [87]	Formulation of the equivalent age concept for hardening concrete and Arrhenius-based equation of the equivalent age dependent on the activation energy.
Bogue, 1955 [88]	Definition of the formula for calculation of the cumulative hydration heat of Portland cement-based concrete.
Schindler and Folliard, 2005 [89]	Definition of the formula for calculation of the cumulative hydration heat of mixed-binder concrete.
Ulm and Coussy, 1998 [90]	Definition of the Arrhenius-based affinity law for hardening concrete.
Cervera et al., 1999 [91]	Proposals for the normalized affinity function.

summarizes the significant works that mark milestones in the advancement of these modeling approaches.

2.2.1. Heat Diffusion

Heat diffusion in concrete is governed by the heat equation derived from Fourier’s law, where the heat flux vector is directly proportional to the temperature gradient and is combined with the energy conservation law. The generation of heat within the material resulting from hydration is accounted for by introducing the rate of hydration heat generation, $\dot{Q}\left(t,T\right)$, as a source function:

$$\dot{T}=\mathrm{d}\mathrm{i}\mathrm{v}\left(K_{TT} \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\left(T\right)\right)+\frac{C·\dot{Q}\left(t,T\right)}{c_b·\rho },$$

(3)

where:

• $T$—temperature, K;
• $K_{TT}$—thermal diffusion coefficient, m²/s;
• $c_b$—specific hear of concrete, kJ/(kg·K);
• $\rho$—density of concrete, kg/m³;
• $C$—amount of cement, kg/m³.

2.2.2. Moisture Diffusion

To incorporate moisture transport resulting from both self-desiccation and surface drying, it is advantageous to employ Fick’s second law of diffusion to describe moisture diffusion. According to this law, the moisture flux vector is proportional to the gradient of moisture concentration. Given that moisture diffusion in hardening concrete is also influenced by cement hydration (self-desiccation), a mass sink function has been introduced. This function is dependent on the rate of hydration heat generation, $\dot{Q}\left(t,T\right)$:

$$\dot{c}=\mathrm{d}\mathrm{i}\mathrm{v}\left(D_{WW} \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\left(c\right)\right)-K_H·\dot{Q}\left(t,T\right),$$

(4)

where:

• $c$—moisture concentration by mass, kg/kg, which is in the following relation with the moisture content by volume W, m³/m³:

  $$c·\rho =W·{\rho }_w,$$

  (5)

  where $\rho$ and ${\rho }_w$ are the density of concrete and volume density of water in concrete, kg/m³, respectively;
  $D_{TT}$—moisture diffusion coefficient, m²/s;
• $K_H$—coefficient to reflect the effect of hydration on the moisture content, m³/J.

Throughout the hydration process, the moisture content decreases due to internal drying and the binding of water by cement. Consequently, the quantity of moisture is intricately tied to the advancement of hydration and is quantified by the coefficient of water–cement proportionality, denoted as $K_H$. This coefficient establishes the relationship between the amount of bound water and the rate of heat generation. Given the reduction in the overall water content, this coefficient consistently holds a positive value. The component $\left(K_H·\dot{Q}\left(t,T\right)\right)$ in the equation can be interpreted as the autogenous shrinkage of concrete.

2.2.3. Coupling

Partial coupling is commonly employed, where the impact of temperature on the rate of moisture diffusion is considered. Following the work of Bažant and Thonguthai [19], the moisture diffusion coefficient is expressed not only as a function of relative pore humidity but also temperature. This formulation remains the state-of-the-art definition when accounting for the temperature effect on moisture diffusion, as evidenced by subsequent studies [49,69,92].

While thermal and moisture phenomena operate on different time scales [93], some previous studies have advocated for considering the influence of moisture on thermal diffusion. For instance, Andreasik [77] defined the thermal diffusion coefficient as a function of humidity. However, contemporary research typically neglects this effect.

Klemczak [79] introduced an alternative approach to coupling thermal and moisture fields. Rather than adjusting the thermal diffusion coefficient, this method maintains it constant while incorporating the mutual influence of temperature and moisture gradients, and consequently their migration. This is achieved through the introduction of additional coupling coefficients: $K_{TW}$ to signify the impact of moisture transport on heat transfer, and coefficient $D_{WT}$ to represent the influence of heat transfer on moisture transport. The coupled equations take the following form:

$$\dot{T}=\mathrm{d}\mathrm{i}\mathrm{v}\left(K_{TT} \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\left(T\right)+K_{TW} \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\left(c\right)\right)+\frac{C·\dot{Q}\left(t,T\right)}{c_b·\rho },$$

(6a)

$$\dot{c}=\mathrm{d}\mathrm{i}\mathrm{v}\left(D_{WW} \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\left(c\right)+D_{WT} \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\left(T\right)\right)-K_H·\dot{Q}\left(t,T\right).$$

(6b)

2.2.4. Boundary Conditions

Heat transfer through the surface of the element occurs in five forms [94]: solar radiation, convection, thermal radiation, evaporation, and condensation. The last two have a negligible influence and are usually not considered in heat transfer analysis. The boundary conditions are commonly defined with the Newton’s cooling law, see, e.g., [10,95]. Analogical boundary conditions are defined for moisture transfer, see, e.g., [54,92]. The heat and moisture flux are expressed as follows:

$$\tilde{q}=\frac{h}{c_b·\rho }\left(T_{\mathrm{s}\mathrm{u}\mathrm{r}}-T_a\right),$$

(7a)

$$\tilde{\eta }=\beta \left(c_{\mathrm{s}\mathrm{u}\mathrm{r}}-c_a\right),$$

(7b)

where:

• $h$—coefficient of heat exchange, W/(m²K);
• $\beta$—coefficient of moisture exchange, m/s;
• $T_{\mathrm{s}\mathrm{u}\mathrm{r}}$, $T_a$—surface and ambient temperature, respectively, K;
• $c_{\mathrm{s}\mathrm{u}\mathrm{r}}$, $c_a$—surface and ambient humidity, respectively, kg/kg.

2.3. Model Parameters

2.3.1. Coefficients in Thermal Analysis

The thermal diffusion coefficient is defined as a function of thermal conductivity, specific heat, and density:

$$K_{TT}=\frac{\lambda }{c_b·\rho },$$

(8)

with the first two parameters being dependent on the degree of hydration, moisture content, and temperature [80]. Several years ago, studies [81,96] demonstrated that the effect of temperature on thermal conductivity can be disregarded within typical temperature ranges observed during concrete hardening. However, in the case of specific heat, its value notably increases with the temperature [82]. While Gawin et al. [31] proposed defining thermal conductivity as a function of moisture content, this approach has not been widely adopted in phenomenological models. Research has shown that the specific heat and thermal diffusivity of concrete decrease over time as hydration progresses [97,98,99]. Nonetheless, it is generally accepted that assuming constant average values of thermal diffusivity when modeling hardening concrete yields accurate predictions. Briffaut et al. [100] demonstrated that assuming constant values of thermal parameters for concrete produces conservative results, with expected temperatures tending to be overestimated.

The averaged values of specific heat and thermal conductivity are suggested to be computed based on the composition of the concrete mix. This involves calculating a weighted average, considering the specific heat and thermal conductivity of its individual constituents, with weights assigned according to their mass [33,101]:

$$\lambda =\sum p_i·{\lambda }_i,$$

(9a)

$$c_b=\sum p_i·c_{b,i},$$

(9b)

While this formulation holds true for specific heat (following the rule of mixtures [102]), in the case of thermal conductivity, it serves merely as an approximation. Expressing a material property as a weighted average of its constituent properties implies that the constituents are interconnected in parallel. However, this assumption does not accurately represent the arrangement of constituents in concrete, as they are randomly positioned relative to each other. Therefore, a more sophisticated definition of thermal conductivity was introduced by Bohm and Nogales [103], employing the Mori–Tanaka scheme:

$$\lambda ={\lambda }_{\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{e}}+\frac{3·f_{\mathrm{a}\mathrm{g}\mathrm{g}}·{\lambda }_{\mathrm{a}\mathrm{g}\mathrm{g}}·\left({\lambda }_{\mathrm{a}\mathrm{g}\mathrm{g}}-{\lambda }_{\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{e}}\right)}{3·{\lambda }_{\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{e}}+f_{\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{e}}·\left({\lambda }_{\mathrm{a}\mathrm{g}\mathrm{g}}-{\lambda }_{\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{e}}\right)},$$

(10)

where $f_i$ are volume fractions of mix constituents. Indeed, it is evident that the thermal properties of concrete are predominantly influenced by the thermal properties of the aggregate (agg) used, which typically accounts for 60–80% of the total mass of a concrete mix.

The specific heat of ordinary concrete typically falls within the range of 0.84 to 1.17 J/(gK) [45], with a commonly utilized value of 1 J/(gK). On the other hand, thermal conductivity is reported to vary from 2.0 to 4.0 W/(mK) and beyond, depending on the aggregate used. Notably, crushed aggregates, such as basalt and granite, tend to exhibit lower thermal conductivity, around 3.0 W/(mK), while sandstone and limestone hover around this value. Quartzite and dolomite are known for having the highest thermal conductivity [45,56].

Little is known about the coefficients for coupling of thermal–moisture equations, $K_{TW}$ and $D_{WT}$. Gawin [18] proposed the coefficient $K_{TW}=0.9375·{10}^{-4}$ (m²K)/s. Wyrwał and Szczęsny [85] proposed the coefficient $D_{WT}=2·{10}^{-11}$ m²/(Ks). These values have been successfully used by Klemczak [79].

The heat exchange coefficient (refer to Equation (7a)) in concrete models predominantly considers free and forced convection, along with the combined influence of convection and radiation. Faria et al. [66] proposed calculating the total convection–radiation heat exchange coefficient as:

$$h=h_p+h_r,$$

(11)

Through the linearization of the radiation heat exchange rate formula derived from the equilibrium of radiation energy for two black bodies as proposed by Branco et al. [104]. The coefficient of heat exchange by radiation was suggested to be calculated as a function of the emissivity of concrete e as:

$$h_r=e\left[4.8+0.075·\left(T_a-5\right)\right].$$

(12)

The coefficient of heat exchange by free convection is recommended as $h_p=6.0$ W/(m²K) [104]. However, it is important to note that this heat exchange coefficient varies with wind speed [100,105]. Several researchers have proposed definitions of heat exchange by forced convection as functions of wind speed [100,104,106]. Typically, the coefficient of heat exchange by convection can reach values as high as 25 W/(m²K) in very windy conditions [59].

The effect of the materials covering the surface of the element, such as formwork or insulation, can be addressed using the following formula, derived from the assumption that the layers of the covering material are interconnected in series [66,107]:

$$h_{p,\mathrm{e}\mathrm{q}}=\frac{1}{\frac{1}{h_p}+\sum \frac{d_i}{{\lambda }_i}},$$

(13)

where $d_i$ is the thickness and ${\lambda }_i$ is the thermal conductivity of the i-th layer.

When the analyzed element is in contact with soil or an adjacent element, such as foundation or neighboring segment or lift, it is advisable to explicitly model the adjacent body to accurately capture the heat exchange between them. Modeling guidelines considering geometric aspects have been outlined by the RILEM TC 287-CCS in [59]. Further analyses and recommendations regarding subsoil considerations can be found in [55,108,109].

2.3.2. Coefficients in Moisture Analysis

The moisture diffusion coefficient depends on the humidity of concrete. Several authors have put forth functions to describe this dependency. Hancox [83], for instance, introduced a quadratic function to delineate the diffusion coefficient as a function of the volumetric moisture content, $W$, m³/m³:

$$D_{WW}=a_2·{W_1}^2+a_1·W_1+a_0,$$

(14)

where:

• $W_1=6W+0.7$;
• $a_0$, $a_1$, $a_2$—calibration coefficients.

Andreasik [77] proposed to simplify $W_1=W$ and $a_2=2·{10}^{-7}$, $a_1=0.2$, $a_0=0$.

Ayano and Wittmann [110] proposed an exponential function for the moisture diffusion coefficient expressed as a function of the relative humidity of concrete $c$, kg/kg:

$$D_{WW}=a·\mathrm{e}\mathrm{x}\mathrm{p}\left[b·\left(1-c\right)\right],$$

(15)

where $a$ and $b$ are experimentally determined calibration coefficients. A similar, though more elaborate, formulation was proposed by Mensi et al. [111].

The formulation currently widely employed for defining the moisture diffusion coefficient, as seen in references such as [47] and also implemented in the Model Code 2010 standard [112], was introduced by Bažant and Najjar [84] and further refined by Abbasnia et al. [113]:

$$D_{WW}=D_{WW,1}·\left[{\overline{D}}_{WW,0}+\frac{1-{\overline{D}}_{WW,0}}{1+{\left[\frac{1-c}{1-c_{0.5}}\right]}^n}\right],$$

(16)

where:

• $D_{WW,1}$—diffusion coefficient in saturated concrete (for $c=1.0$), which can be estimated according to Model Code 2010 as:

  $$D_{WW,1}=\frac{{10}^{-8} \left[\frac{{\mathrm{m}}^2}{\mathrm{s}}\right]}{f_{cm}-8 \left[\mathrm{M}\mathrm{P}\mathrm{a}\right]},$$

  (17)

  and according to Abbasnia et al. [113] as a linear function of the water-to-cement ratio:

  $$D_{WW,1}=\left[1.157+9.92·\left(w/c-0.45\right)\right]·{10}^{-10},$$

  (18)
• ${\overline{D}}_{WW,0}$—ratio $\frac{D_{WW,0}}{D_{WW,1}}$; ${\overline{\alpha }}_{WW,0}=0.05$ can be assumed;
• $D_{WW,0}$—minimum $D_{WW}$ at $c=0.0$;
• $c_{0.5}$—relative humidity at $D_{WW}=0.5D_{WW,1}$; $c_{0.5}=0.8$ [84] or $c_{0.5}=0.75$ [113];
• $n$—exponent; Model Code [112] suggests constant value $n=15$, while Abbasnia et al. [113] note that the value of the exponent increases with an increasing w/c.

Another proposal for the moisture diffusion coefficient was provided by Xi et al. [114]:

$$D_{WW}={\alpha }_h+{\beta }_h·\left[1-2^{-10·{\gamma }_h·\left(c-1\right)}\right],$$

(19)

where:

• ${\alpha }_h$—coefficient representing the lower bound of diffusivity approached at a low humidity level;
• ${\beta }_h$—diffusivity increment from a low humidity level to a saturation state;
• ${\gamma }_h$—coefficient characterizing the humidity level at which the diffusivity begins to increase.

The humidity exchange coefficient, $\beta$ (see Equation (7b)), is suggested to remain constant. The value may vary considerably among different authors; the experimentally determined value $\beta =2.78·{10}^{-8}$ m/s is frequently cited. Kwak et al. [26] defined the humidity exchange coefficient as dependent on the water-to-cement ratio:

$$\beta =\left(6.028·w/c-2.378\right)·{10}^{-7},$$

(20)

for which the value $\beta =2.78·{10}^{-8}$ m/s is obtained for a w/c ratio of 0.44, which is a typical value for ordinary concrete.

In the presence of the covering material, Andreasik [77] suggested to modify the $\beta$ coefficient:

$${\beta }_{\mathrm{e}\mathrm{q}}=\beta ·\frac{{\alpha }_{WW,i}}{{\alpha }_{WW,i}+d_i·{\beta }_i},$$

(21)

• ${\alpha }_{WW,i}$—moisture diffusion coefficient of the covering material, m²/s;
• $d_i$—thickness of the covering material layer, m;
• ${\beta }_i$—humidity exchange coefficient of the covering layer, m/s.

2.3.3. Heat of hydration

The source/sink functions in Equations (1), (2), (6a) and (6b) are linked to the rate of hydration heat development, $\dot{Q}\left(t\right)=\mathrm{d}Q/\mathrm{d}t$. Therefore, various authors have proposed functions for hydration heat development over time. When devising these functions, it is essential for them to be differentiable. Furthermore, it is important to note that the hydration process is temperature-dependent, particularly when the assumed time development of $Q$ is derived from the results of isothermal calorimetry measurements. Consequently, two approaches have been suggested to represent this dependence: methods based on the equivalent time and methods based on affinity.

The first group of methods utilizes the equivalent time instead of the real time. The concept of the equivalent time as a measure of progressing maturity was introduced by Rastrup [86], who defined the equivalent time as the time during which the concrete would need to be cured at a constant reference temperature to attain the same level of maturity as concrete undergoing its actual curing process. The formulation currently in use for the equivalent time, as implemented in the latest version of the EN 1992-1-1 standard [115], was derived by Hansen and Pedersen [87] from the Arrhenius law:

$$t_{\mathrm{e}\mathrm{q}}\left(t,T\right)=\underset{0}{\overset{t}{\int }}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{E_a}{R}·\left(\frac{1}{T}-\frac{1}{T_{\mathrm{r}\mathrm{e}\mathrm{f}}}\right)\right]\mathrm{d}t,$$

(22)

where:

• $T_{\mathrm{r}\mathrm{e}\mathrm{f}}$—reference temperature, K;
• $E_a$—apparent activation energy, J/mol,
• $R$—universal gas constant, 8.314 J/(mol K).

The activation energy serves as a pivotal factor, representing the binder’s sensitivity to temperature. Its value can be determined experimentally or calculated using one of the proposed methodologies found in the literature, as detailed in references such as [116] and [117].

Functions describing hydration heat development using equivalent time have been proposed, typically taking the form of rational functions of time. For instance, references such as [65,66] have suggested formulations akin to:

$$Q\left(t,T\right)=Q_{\infty }·\frac{a·t_{\mathrm{e}\mathrm{q}}}{1+a·t_{\mathrm{e}\mathrm{q}}},$$

(23)

or—more often—exponential functions of time, e.g., [118,119,120,121], of the form resembling:

$$Q\left(t,T\right)=Q_{\infty }·\mathrm{e}\mathrm{x}\mathrm{p}\left[-a·t_{\mathrm{e}\mathrm{q}}\right].$$

(24)

All these formulations are empirically derived by calibration against experimental results. In Equations (20) and (21), $Q_{\infty }$ represents the cumulative heat at the end of hydration. The most widely used method to calculate the cumulative hydration heat of mixed binders is the one proposed by Schindler and Folliard [89] following Bogue’s proposal developed for Portland cement [88].

In the affinity approach, the degree of hydration (reaction) is employed instead of the equivalent time, also following the Arrhenius law, as defined by Ulm and Coussy [90]:

$$\dot{\alpha }={\tilde{A}}_{T_{\mathrm{r}\mathrm{e}\mathrm{f}}}\left(\alpha \right)·\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{E_a}{R}·\left(\frac{1}{T}-\frac{1}{T_{\mathrm{r}\mathrm{e}\mathrm{f}}}\right)\right].$$

(25)

Here, the degree of hydration is defined as a ratio between the hydration heat generated up to the analyzed time and the cumulative heat at the end of hydration:

$$\alpha =\frac{Q\left(t\right)}{Q_{\infty }}.$$

(26)

Given the practical difficulty in experimentally determining the value of $Q_{\infty }$, the definition of the degree of hydration remains theoretical. However, the formula proposed by Schindler and Folliard [89] for $Q_{\infty }$ may still be applied. Alternatively, de Schutter and Taerwe [99] proposed using the degree of reaction as a convenient measure of maturity progress, where the theoretical cumulative heat, $Q_{\infty }$, is substituted with the cumulative heat measured at the end of the hydration test, denoted as $Q_{\mathrm{m}\mathrm{a}\mathrm{x}}$.

Analogous to the functions of hydration heat development based on equivalent time, analytical formulations for affinity have also been proposed. Notably, the proposal of Cervera et al. [91], refined by Gawin et al. [63], and further developed by Leal da Silva and Šmilauer [122] stands out. They suggested empirical laws for determining the model coefficients $B_1$, $B_2$, and $\overline{\eta }$ instead of relying solely on experimental fitting:

$${\tilde{A}}_{T_{\mathrm{r}\mathrm{e}\mathrm{f}}}\left(\alpha \right)=B_1·\left(\frac{B_2}{{\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}}+\alpha \right)·\left({\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}-\alpha \right)·\mathrm{e}\mathrm{x}\mathrm{p}\left(-\overline{\eta }·\frac{\alpha }{{\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right).$$

(27)

Other proposals for the normalized affinity function can be found in references such as [123,124,125].

3. Numerical Applications

Various numerical methods are available for solving the equations of heat and mass transfer, each with its strengths and suitable applications. The lattice Boltzmann method (LBM) [126,127] and discrete element method (DEM) [128,129] offer distinct advantages for specific types of problems, particularly those involving complex boundaries, particle interactions, and microscopic scale levels. In contrast, traditional methods like the finite element method (FEM) [130] and finite volume method (FVM) [131] provide robust and versatile tools for a wide range of engineering and scientific applications. Selecting the appropriate method depends on the specific requirements of the problem, including geometry, material properties, and computational resources.

However, the FEM has become the most popular method for solving the discussed equations describing the transport of heat and moisture in concrete. To solve equations of heat and mass transfer (Equations (3) and (4), or (6a) and (6b)) using the finite element method (FEM), the initial step involves discretizing the analysis domain into a finite number of smaller subdomains known as finite elements (FEs). Within each element, the solution is approximated using a set of basis functions defined over that element. The spatial discretization proceeds by dividing the analyzed member into a mesh of 1-, 2-, or 3-dimensional finite elements, such as triangles, quadrilaterals, tetrahedrons, or others. Within each element, the solution is represented using interpolation functions which are also known as shape functions. The system of equations is typically formulated using the Galerkin method, which is a specific form of the weighted residual method. In the Galerkin method, the shape functions serve as weighting functions, and it is assumed that the unknown functions are approximated as a linear combination of these shape functions. Subsequently, the global system of equations is assembled by combining the elemental equations while incorporating boundary and initial conditions. Time derivatives appearing in heat and mass transfer equations can be replaced by difference approximations suitable for numerical integration. The resulting system of equations is then solved numerically to determine the nodal values of temperature and moisture concentration. It is important to note that the considered problem and the resulting FE formulation are highly nonlinear in the analyzed case. The nonlinearity arises from dependencies within the components (such as hydration heat, thermal, and moisture coefficients) of the matrices in the FE formulation, which are functions of the current values of temperature and moisture. Therefore, iterative techniques must be employed at each considered time step to converge to the solution. Further details on the transformation of heat and mass transport equations into their equivalent form as finite element matrix equations can be found in various works, including references [56,79,130,132], among others.

Therefore, the finite element method is a valuable tool for solving heat and mass transfer problems and is consequently widely utilized in various available tools. These available tools, based on the mathematical models described in Section 2, allow for the recognition of the thermal and moisture phenomena throughout the entire time of concrete curing. Some of the tools are commercially available professional FE software, but simultaneously, some researchers [69,79,133] created original programs and procedures dedicated to solving problems in early-age mass concrete. Commercial software tools typically focus on determining thermal fields and are commonly used for this purpose. Examples of such tools include DIANA FEA, MIDAS, ABAQUS, and ANSYS. However, these tools relatively rarely incorporate coupled equations for heat and mass transfer, and moisture analysis is often omitted as well.

The following sections provide a brief overview of the prevailing commercial programs frequently employed in the analysis of thermal and moisture effects on concrete structures, with references to the pertinent literature. It is crucial to acknowledge that the commercial software packages discussed here utilize their own distinctive notations within the integrated equations, which may occasionally differ from those outlined in Section 2. To facilitate the reader’s future utilization of these discussed software programs, the original notations, along with explanations of their corresponding values, are retained when referencing these programs.

3.1. DIANA FEA

DIANA FEA [96] allows the computation of the transient temperature fields in concrete through the implementation of the heat balance equation (see Equation (3)) in an FE code, where the rate of internal heat generation is defined using the affinity approach as a function of the degree of hydration, $\alpha$:

$$\dot{Q}\left(t,T\right)=Af(\alpha )e^{-\frac{E_a}{RT}}$$

(28)

with:

• $f\left(\alpha \right)$—normalized heat generation rate;
• $A$—rate constant.

The convective heat transfer between the concrete and the environment may be assumed by the coefficient $h$ (Equation (11)), considering both convection and radiation. This simplifies the FEA simulation of concrete boundaries. In heat flow analysis, it is possible to specify the heat of hydration, conductivity, and heat capacity of the material. Parameters may be constant or dependent on temperature, T, or the degree of reaction. In the case of properties that are dependent on the degree of reaction, it is necessary to provide a set of degrees of reaction and a corresponding set of values for each property in the form of a diagram. During the analysis, DIANA will determine the current value for the material properties through linear interpolation.

There is no possibility to calculate moisture fields in DIANA software. However, shrinkage strains may be input as discrete functions [93,134]. Shrinkage strains can be estimated using commonly known analytical shrinkage strain functions [112,115,135]. However, considering the significant dimensions of cross-sections, especially in massive concrete members, this approach appears overly simplistic. A more effective method was proposed by Azenha et al. [136], where changes in humidity across the thickness of the analyzed element are first determined using Equation (29), and these changes are then used to calculate shrinkage strains. The procedure for determining the parameters for the moisture model, involving an implementation of the 1D moisture balance equation is based on the equation, proposed in Model Code 2010 [112]:

$$\frac{\partial H}{\partial t}={\left(\frac{\partial W}{\partial H}\right)}^{-1}\mathrm{d}\mathrm{i}\mathrm{v}\left(D_H \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\left(H\right)\right)+\frac{\partial H_s}{\partial t}$$

(29)

where:

• ${\left(\frac{\partial W}{\partial H}\right)}^{-1}$—moisture capacity;
• $W$—total water concentration, kg/m²s;
• $t$—time, s;
• $D_H$—moisture diffusivity, m²/s.

This equation enables the macroscale modeling of the relative humidity field $\left(H\right)$ inside the concrete pores, taking into account the simulation of moisture transport through a diffusion-type equation, which considers the internal $H$ as a driving potential. The term $\frac{\partial H_s}{\partial t}$, corresponding to the internal variation in $H$ caused by self-desiccation, might be disregarded due to its negligible influence on the pore humidity and the constant moisture capacity of cementitious materials under typical environmental relative humidity. The boundary conditions align with those discussed in the previous section (Equation (7b)).

Commonly, the model is created by constructing an FE mesh based on a defined geometry. The geometry can either be imported as an externally defined model or created within the DIANA preprocessor. Specific characteristics, such as materials, loadings, connections, and physical properties, are assigned to specific geometry definitions or element sets, while the FE mesh is automatically generated. The assigned properties encompass various aspects, including element class (such as two-dimensional body elements, three-dimensional bodies or solid plates and shells, trusses and cables, beams, interfaces, springs and mass elements, reinforcements, etc.), material (specific material models for concrete and soil), geometry (parameters defining thickness, cross-section shape, and local axis for the geometry shapes), and data (advanced parameters, like integration schemes and methods different from the default, definition of shape factors, consideration of correction terms in mass elements, etc.).

The evaluation of the degree of hydration concept within the DIANA 6.1 environment was conducted by De Schutter [137,138]. The modeling of the early-age thermal behavior of concrete using DIANA was performed by Lawrence [139]. Furthermore, a discussion on the available DIANA software options can be found in [140]. Examples of applications of mass concrete slabs are provided in [55,108].

3.2. MIDAS

The heat of hydration analysis in MIDAS is largely classified into several sub-analyses [141]. MIDAS/Gen allows for the calculation of the changes in nodal temperatures with time due to conduction, convection, and heat source in the process of cement hydration. The rate of heat transfer through conduction is determined using the Fourier’s law-based equation (Equation (3)), and the heat of hydration is calculated based on an adiabatic temperature rise equation:

$$T=K\left(1-{\mathrm{e}}^{-v_{r}t}\right)$$

(30)

where:

• $T$—adiabatic temperature rise, °C;
• $K$—maximum adiabatic temperature rise, °C;
• $v_r$—response speed, 1/day;
• $t$—time, days.

Similarly to the previous software, the total convection–radiation heat transfer coefficient can be specified, which may be determined using methods outlined in Section 2.3.1. or by employing any empirical formula.

Changes in material properties resulting from the process of maturing concrete can be expressed in terms of temperature and time. A more comprehensive understanding of the process for analyzing the heat of hydration can be obtained from [142].

Similar to the DIANA FEA software, the determination of moisture fields is not possible with MIDAS. The state of the art shows that the application of MIDAS is usually limited to determining the temperature field in the concrete caused by the hydration heat, particularly in bridge components [48,143,144].

3.3. ABAQUS

ABAQUS has the capability to address various types of heat transfer problems, including uncoupled heat transfer analysis, fully coupled thermal stress analysis, and adiabatic analysis [145]. Uncoupled heat transfer analysis encompasses conduction, forced convection, and boundary radiation. The thermal analysis in ABAQUS is based on the law of energy conservation and Fourier’s law [146,147]. It allows for the application of initial conditions and boundary conditions of Dirichlet and Newton types, which consider convection heat loss and radiation emission heat loss.

Compared to the already mentioned MIDAS FEA, which is a software commonly used for the early crack resistance analysis of mass concrete providing the built-in parameters and formulas in the analysis, ABAQUS is found to be a more versatile finite element software that offers greater flexibility in parameter adjustments. When combined with detailed engineering data, ABAQUS allows for simulation results that closely approximate the real situation [148]. In the XFEM-based simulation conducted by Sheng et al. [148], the temperature field of the massive structure was determined using the subroutine HETVAL in ABAQUS. Since the software does not allow for the calculation of the humidity field, the shrinkage strain was proposed to be calculated using the following equation:

$$\epsilon ={\epsilon }_s+{\epsilon }_w=1-\sqrt[3]{1-k_1·E^{k_2}·\left(V_{cs}-V_o\right)}+\frac{v_{p}S\rho RT}{3M}\left(\frac{1}{K_s}-\frac{1}{K}\right)\ln \left(RH\right)$$

(31)

where:

• ${\epsilon }_s$—concrete shrinkage strain during the humidity saturation period;
• ${\epsilon }_w$—concrete shrinkage strain during the humidity decline period;
• $E$—elastic modulus of concrete;
• $V_o$—chemical shrinkage at the starting moment;
• $V_{cs}$—chemical shrinkage at any moment;
• $S$—saturation fraction;
• $R$—universal gas constant;
• $M$—molar weight of water;
• $T$—absolute temperature;
• $K$—bulk modulus of the concrete;
• $K_s$—bulk modulus of the aggregate;

and then simulated using the subroutine UEXPAN. The graphical illustration of the simulation process is presented in Figure 2.

As can be seen, FE analysis software ABAQUS was applied to simulate the transient temperature field of the early hydration heat of the 50 m precast box girder in [40]. The simulation employed a DC3D8 element (an eight-node linear heat transfer hexahedron element) in a subroutine called UMATHT. The simulation was based on the adiabatic temperature rise equation and other thermal parameters, considering the development of the hydration degree, thermal conductivity, and specific heat with equivalent age.

3.4. ANSYS

Another commercially available software for solving thermal problems in mass concrete is ANSYS [149]. Similarly to the previously described software, the program enables the determination of the temperature field in a medium resulting from the internal heat source and the conditions imposed on its borders. Heat flow by conduction at any point in the medium or on the surface may be determined using Fourier’s law (Equation (3)). The general heat transfer equation is evaluated by the heat flow passing through that body. In order to solve Fourier’s equation, the consideration of the heat of hydration, $Q$, for the case of the concrete is required. A comprehensive description of the methodology for predicting the early-age thermal behavior of concrete using a modified USERMATTH subroutine for ANSYS can be found in [150], which is presented in the form of a flow chart in Figure 3.

Examples of the application of ANSYS for the determination of thermal fields in concrete structures can be referred to, e.g., [151]. Recently, thermal properties and temperature rise in geopolymer concrete structures were analyzed in [152]. Simpler, 2D models for predicting hydration heat in a concrete mass floor and the cross-section of a concrete dam, respectively, were presented in [153,154]. It is important to note that, as an alternative to the basic ANSYS structural module that enables a simplified thermal analysis of concrete structures, a more advanced module called ANSYS Fluent can be chosen. This is demonstrated, for example, in [155]. The module uses computational fluid dynamics (CFDs) as an alternative to the finite element method to solve the differential equations governing heat flow.

Worth mentioning is a comparative study of the heat transfer analysis of RC walls modeled using ABAQUS and ANSYS [156]. It demonstrated that the temperatures could be predicted with nearly the same accuracy for both FE software packages, assuming the same mesh size and time stepping size.

3.5. B4Cast

B4Cast software specializes in conducting FEM simulations of temperature and stress in 3D concrete structures during the hardening process [157]. This software calculates the evolution of temperatures and stresses based on maturity, utilizing either the Arrhenius or Nurse-Saul functions. It assumes the parabolic variation in temperature, maturity, and stress within each element.

In a separate study, B4Cast software was employed to determine the temperature distribution and temperature history at different sections of the concrete, considering various pouring conditions [158]. Additionally, a thermal analysis of the raft foundation was carried out using B4Cast, and the findings were presented in [159].

3.6. ATENA

While the material behavior of concrete undoubtedly depends on temperature and moisture conditions, the mentioned software packages only consider the first component. In contrast, ATENA software, developed by Cervenka et al. [160,161] for the simulation of cracks in early-age concrete with the consideration of heat development and cracking due to thermal and shrinkage strains, enables the calculation of both moisture and temperature histories. ATENA offers two constitutive models for transport analysis: CCModelBaXi94 and CCTransportMaterial. CCModelBaXi94 includes a simple constant linear model for heat transport and a nonlinear model (based on [114]) for moisture transport. However, the model was originally designed only for mortar, so it can only predict the moisture movement in pores filled by water–cement paste as it does not account for aggregate. CCMaterialTransport material allows users to input laboratory-measured moisture and heat characteristics. The heat and moisture flow governing equations can be written in the following general form, which also accounts for full coupling:

$$\frac{\partial Q}{\partial t}=C_{Th}\frac{\partial h}{\partial t}+C_{TT}\frac{\partial T}{\partial t}+C_{Tw}\frac{\partial w}{\partial t}+C_{Tt}=-\frac{\partial }{\partial x}\left(K_{Th}grad\left(h\right)+K_{TT}grad\left(T\right)+K_{Tw}grad\left(w\right)+K_{Tgrav}\right)$$

(32a)

$$\frac{\partial w}{\partial t}=C_{wh}\frac{\partial h}{\partial t}+C_{wT}\frac{\partial T}{\partial t}+C_{ww}\frac{\partial w}{\partial t}+C_{wt}=-\frac{\partial }{\partial x}\left(D_{wh}grad\left(h\right)+D_{wT}grad\left(T\right)+D_{ww}grad\left(w\right)+D_{wgrav}\right)$$

(32b)

where $w$ represents the water concentration by mass, kg/kg, and $h$ represents the internal relative humidity. Further details regarding the model coefficients can be found in [132].

The expanded version of the CCMaterialTransport material is CCTransport materialLevel7. This version automatically calculates the moisture and temperature capacity, as well as conductivity/diffusivity, including the rate of hydration heat and moisture consumption during concrete hydration. All parameters and characteristics from CCMaterialTransport can still be used as input. A comprehensive explanation of the theory employed in ATENA software can be found in [132].

3.7. JCMAC

The JCI Committee on Promotion and Development of Computer Code for Crack Control in Massive Concrete released JCMAC series, which is a software for the thermal stress analysis of mass concrete. The committee has now released five software packages, but particularly interesting is JCMAC3 and the latest JCMAC3-U version of the software, which enables both temperature and humidity transfer analyses.

In addition to the determination of temperature fields by solving classical Fourier’s equation (see Equation (3)), JMAC3 offers the moisture transfer module, in which the vapor pressure inside the concrete is regarded as an unknown potential value, and the governing equation presented below, analogical to Equation (4), is discretized and solved:

$${\left(\frac{dq}{dP}\right)}_P\frac{\partial P}{\partial t}=\mathrm{d}\mathrm{i}\mathrm{v}\left(D_P \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\left(P\right)\right)-{\dot{q}}_h$$

(33)

where:

• $P$—vapor pressure within the concrete;
• $q$—moisture density;
• ${\left(\frac{dq}{dP}\right)}_P$—moisture capacity;
• $D_P$—diffusion coefficient;
• $q_h$—moisture density loss by hydration.

4. Conclusions

This paper provides a comprehensive review of modeling approaches for predicting temperature and moisture distributions during the hardening of concrete. It discusses varying levels of modeling accuracy and the critical input parameters involved. Additionally, the review covers an assessment of commercial finite element method (FEM) software programs, outlining their fundamental features.

The fundamental theory of modeling heat and mass transfer, particularly in early-age concrete applications focusing on thermal–humidity fields associated with cement hydration, is examined. This includes discussions on the essential material data reflected in model coefficients. A brief overview of available commercial software underscores the necessity of not only using specialized software (due to the complexity of equations describing heat and mass transport phenomena), but also possessing a comprehensive understanding of concrete’s thermal properties, which are influenced not only by its composition but also by time and temperature changes.

To accurately predict temperature and humidity variations, it is imperative to hold both advanced software tools and a detailed understanding of the discussed phenomena and concrete’s evolving thermal characteristics over time and under varying thermal conditions.