Research on Virtual Energy Storage Scheduling Strategy for Air Conditioning Based on Adaptive Thermal Comfort Model
Abstract
1. Introduction
- This paper proposes an air conditioning regulation scheme based on user adaptive thermal comfort, taking into account different seasons and different regions that can accurately assess the user’s regulation choices;
- This paper sets up a demand response compensation mechanism that takes into account the adjustable capacity and response power of air conditioning users, which can fully incentivize users to actively participate in the capacity reserve and power response of the grid.
2. Air-Conditioned Building Virtual Energy Storage Model
2.1. Human Comfort Range
- (1)
- Users who do not accept centralized temperature regulation, i.e., choose the temperature to be maintained at an optimal body temperature. This category of air conditioning users basically does not have the ability to respond to demand.
- (2)
- Users who can accept temperature regulation in a small range, i.e., the range of regulation temperature corresponds to the temperature range that achieves 90% satisfaction. This category of air conditioning users has a partial demand response capability.
- (3)
- Users who can accept temperature regulation in a wide range, i.e., the range of regulation temperature corresponds to the temperature range that achieves 80% satisfaction. This category of air conditioning users has the highest demand response capability.
2.2. Virtual Energy Storage Model for Air Conditioning Building Systems
2.3. Virtual Energy Storage Indicator
3. Optimization Scheduling Strategy Considering Air Conditioning Building Virtual Energy Storage
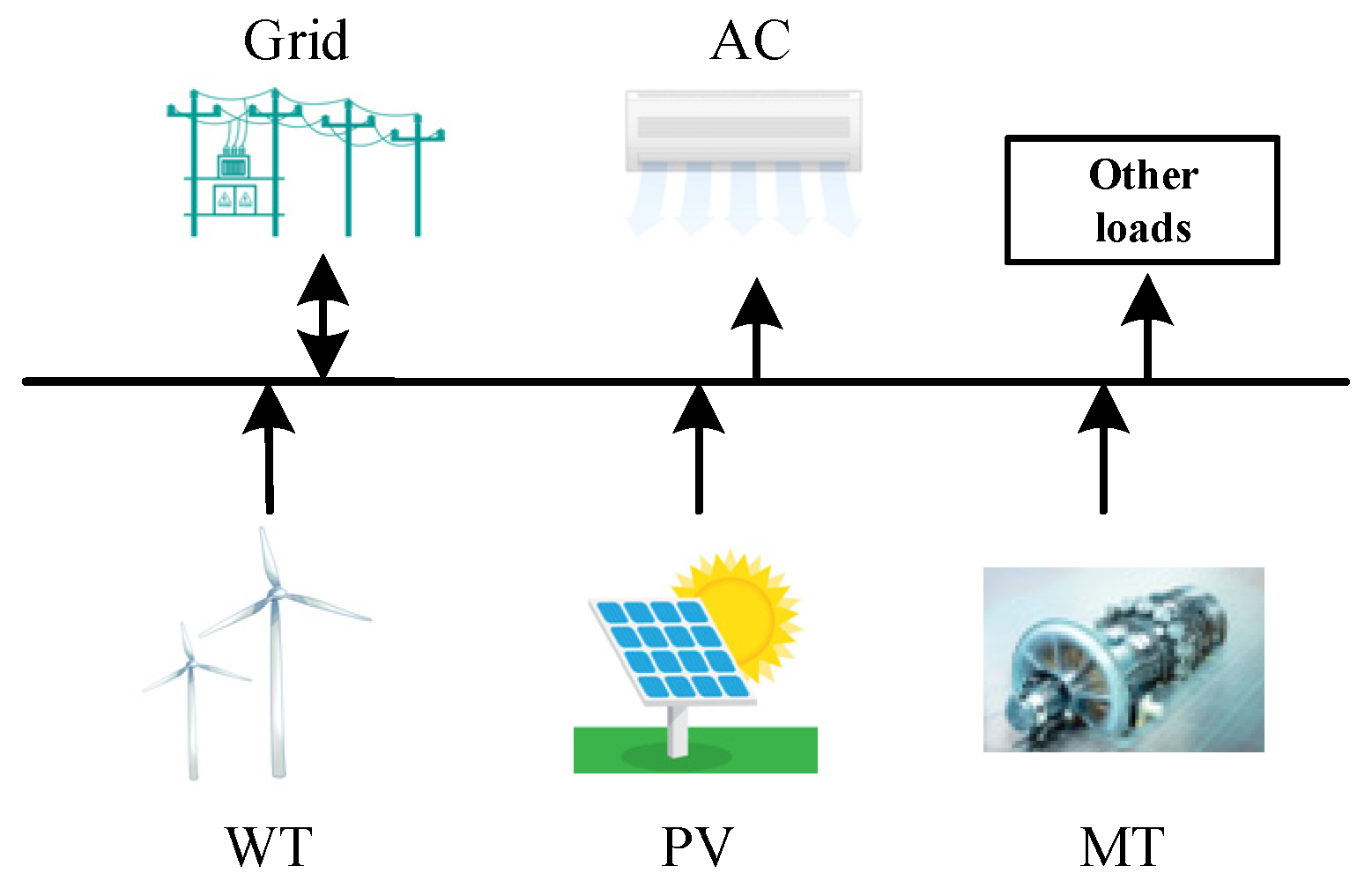
3.1. Microgrid Structure
3.2. Optimization Scheduling Model for Microgrids Considering Virtual Energy Storage
3.2.1. Objective Function
- Microgrid revenue:
- 2.
- Carbon emissions:
- 3.
- User satisfaction:
3.2.2. Constraint Condition
- Energy balance constraint:
- 2.
- Power constraint:
- 3.
- Temperature regulation constraint:
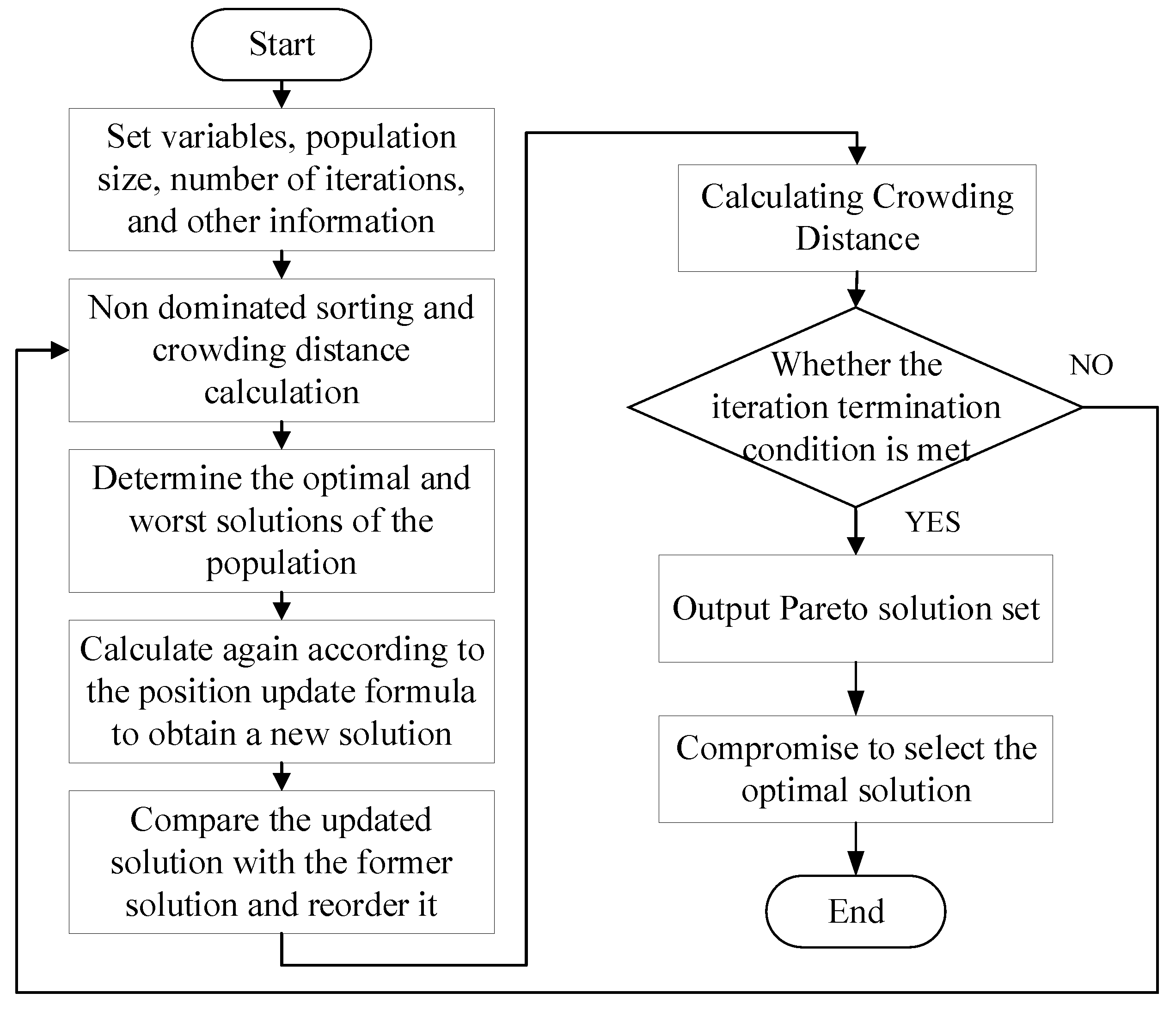
4. Multi Objective JAYA Algorithm
4.1. MO-JAYA Algorithm
4.2. MO-JAYA Algorithm Process
5. Analysis of Examples
- (1)
- Case 1: Users do not accept temperature control, meaning that the air conditioning temperature will always be maintained at the highest satisfactory temperature.
- (2)
- Case 2: Considering that 90% of the users are satisfied with a temperature adjustment range of 21.9 °C to 27.3 °C or 22 °C to 23.6 °C, it is assumed that 90% of the users are willing to participate in the demand response by accepting that the temperature can be regulated within that range when the air conditioning is working, while 10% of the users only accept the most comfortable temperature and do not participate in the demand response.
- (3)
- Case 3: Considering that 80% of the users are satisfied with a temperature regulation range of 20.4–28.9 or 18–28.9, it is assumed that 80% of the users are willing to participate in the demand response by accepting that the temperature can be regulated within that range when the air conditioning is operating. The remaining 10% of users are only satisfied with a temperature regulation range of 22–23.6, and 10% of users only accept the most comfortable temperature and do not participate in demand response.
- Summer Case 1
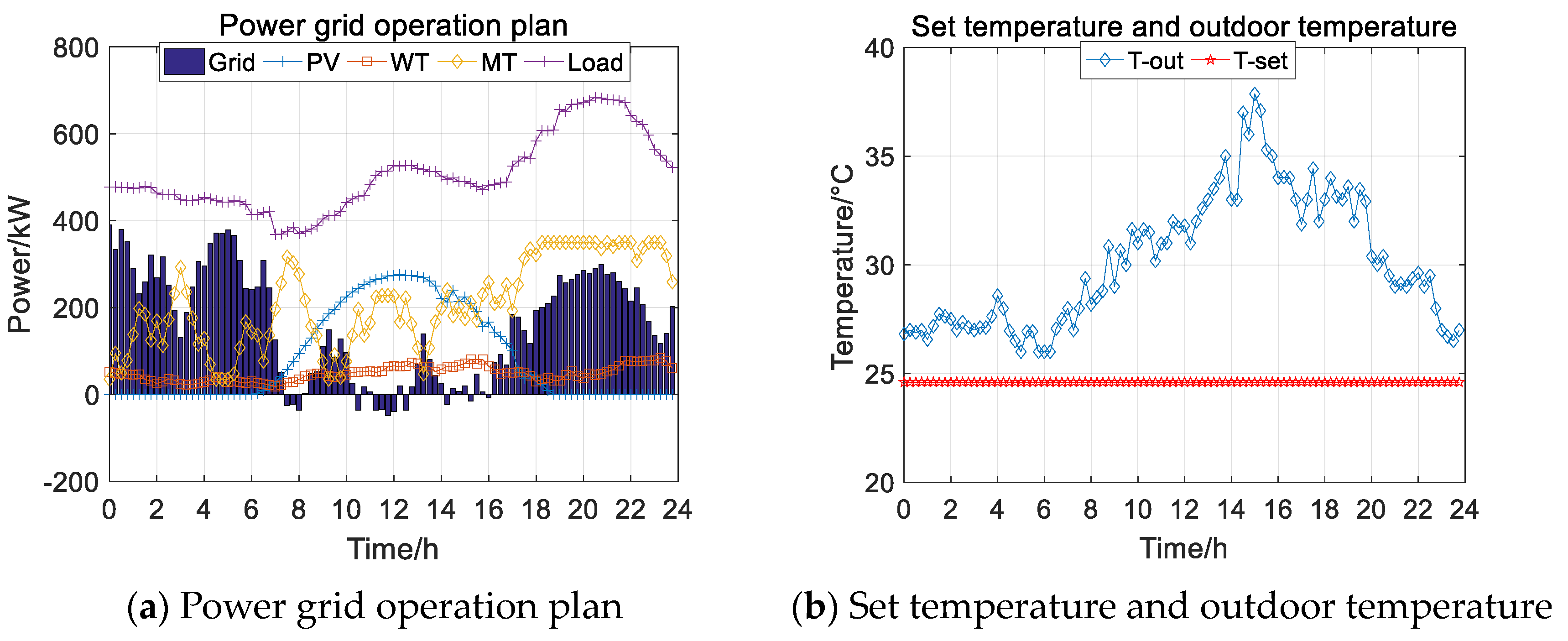
- 2.
- Summer Case 2
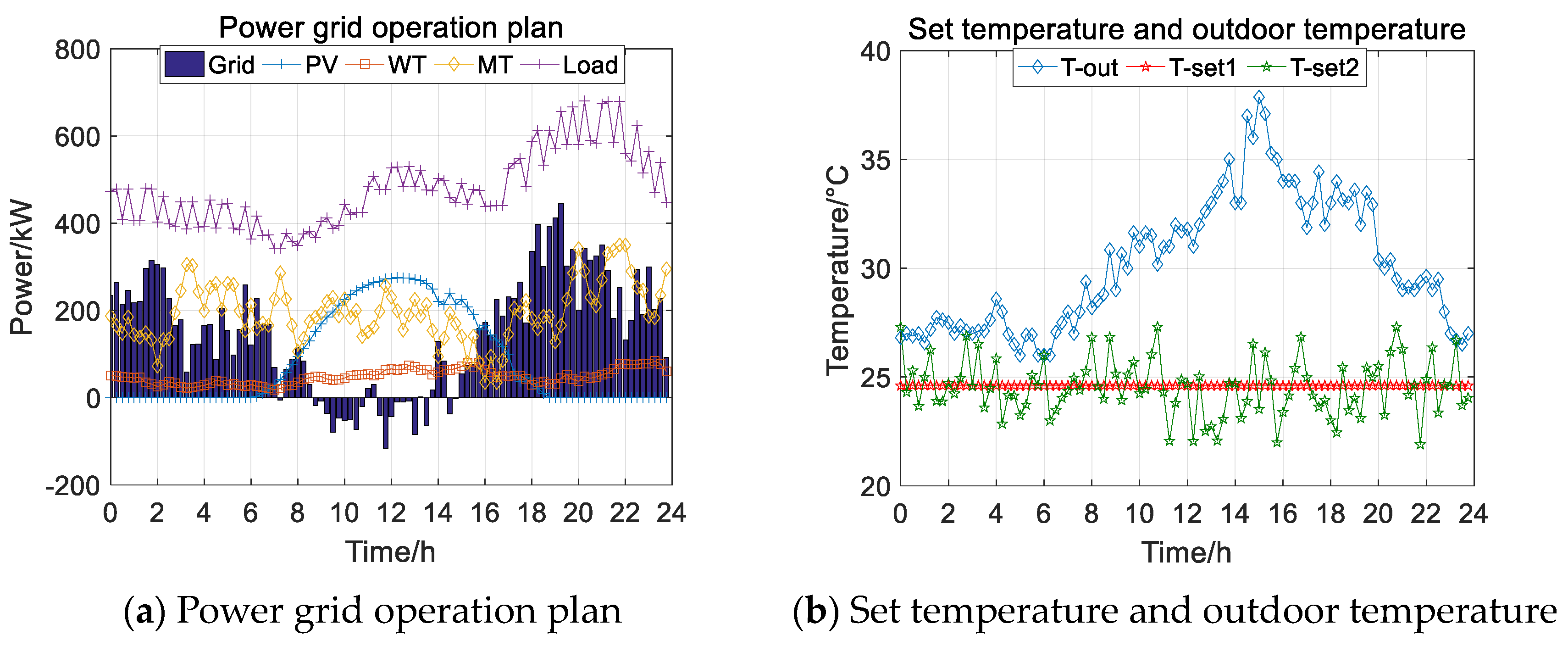
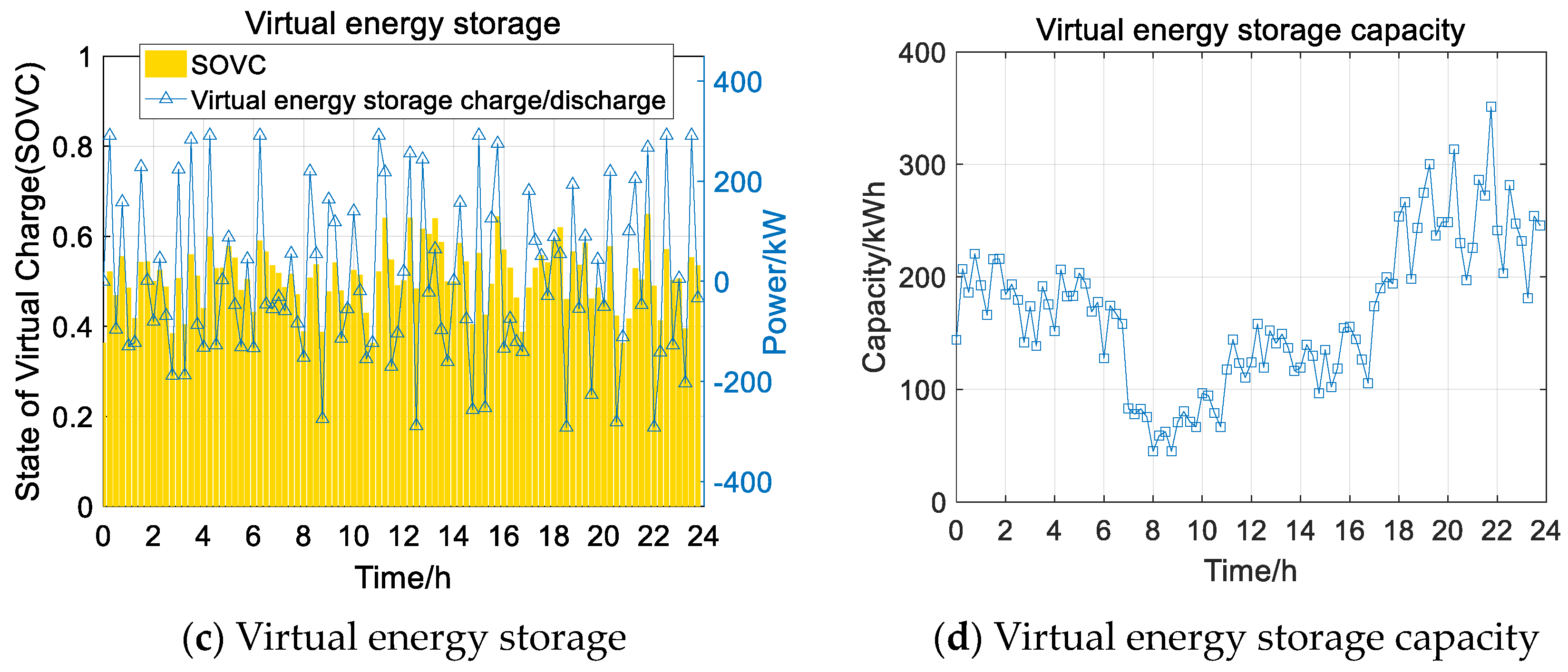
- 3.
- Summer Case 3
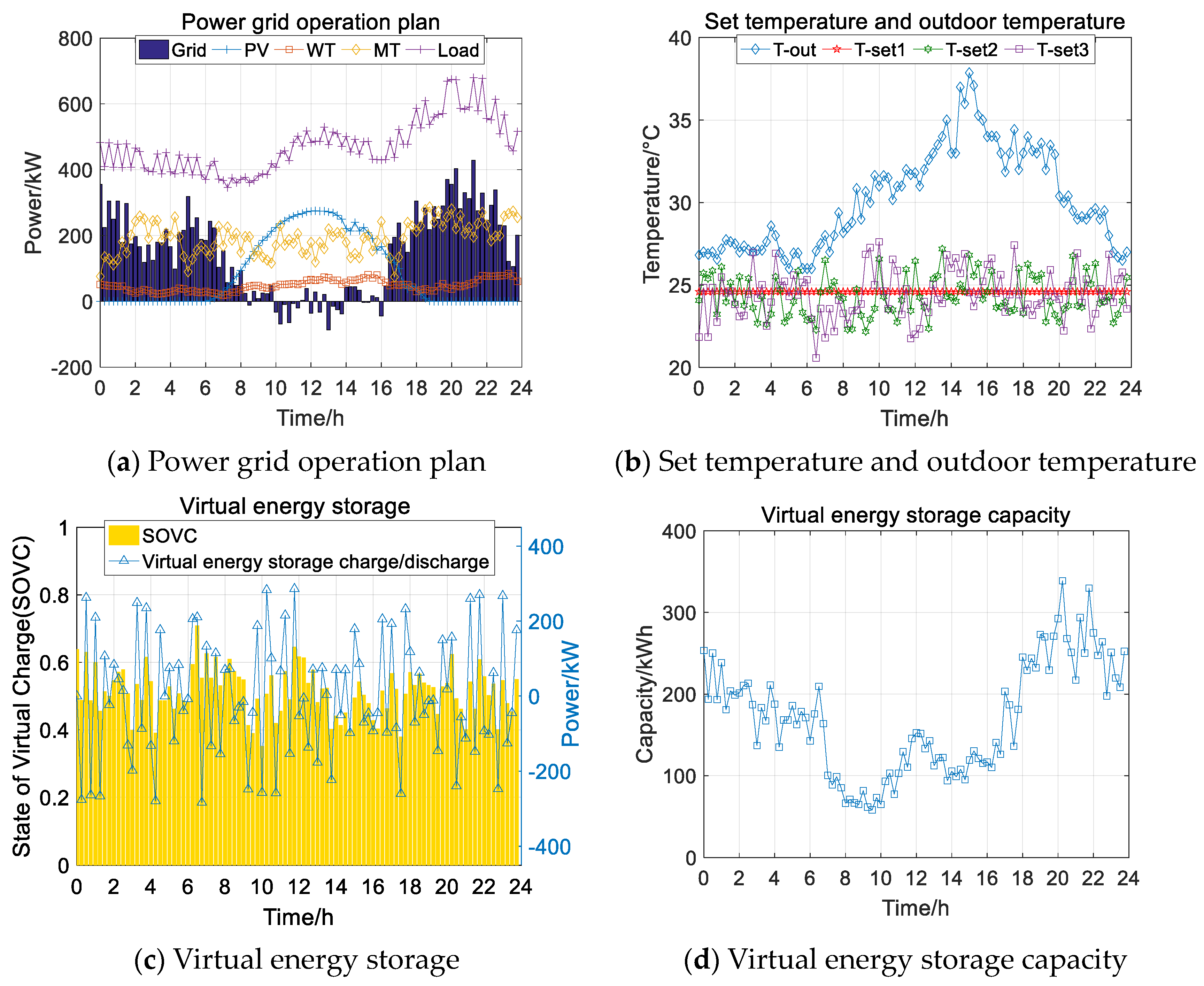
- 4.
- Winer Case 1

- 5.
- Winer Case 2


- 6.
- Winer Case 3
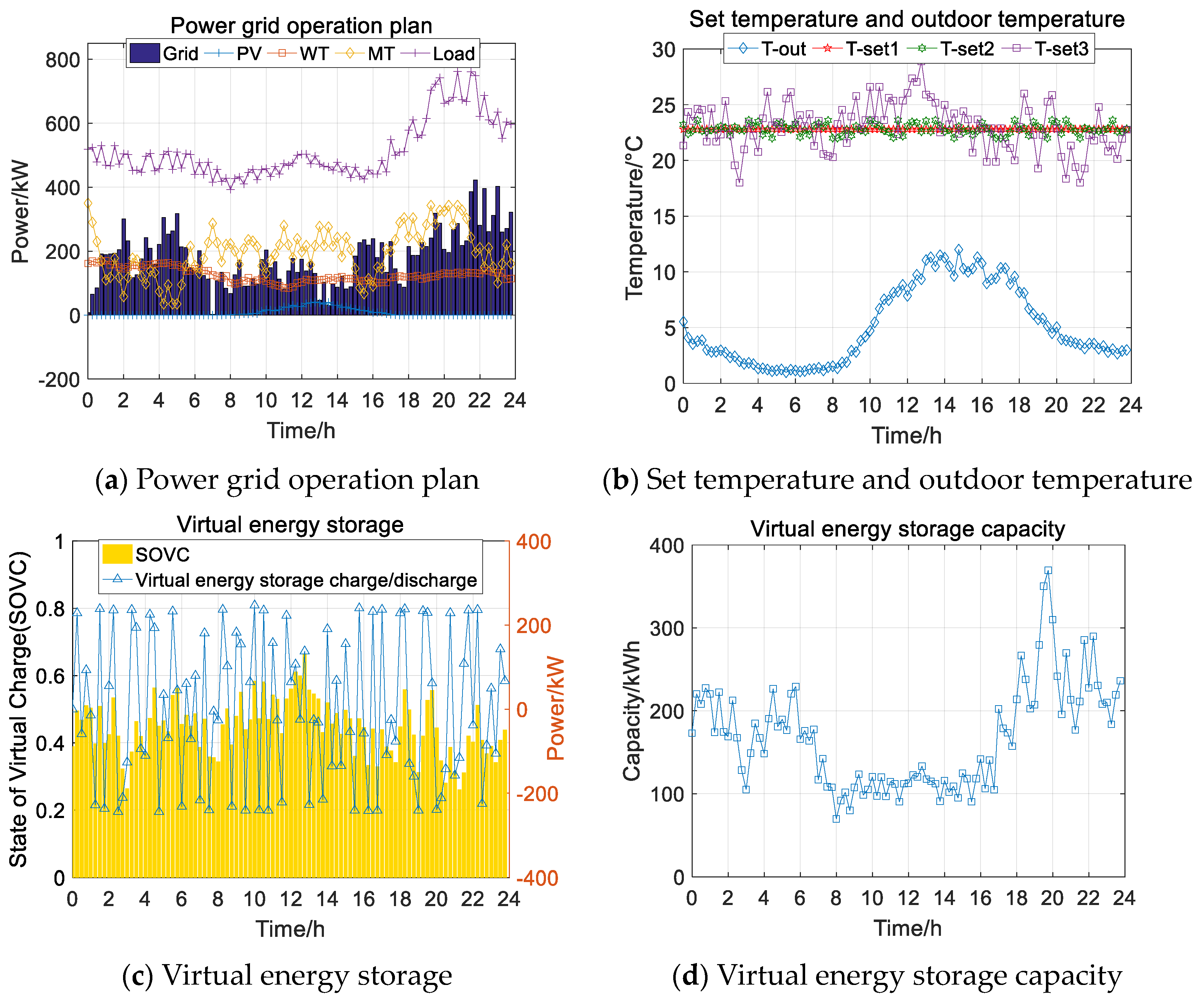
6. Conclusions
- In this paper, by differentially considering thermal comfort models under different climatic geographies and personalized comfort grading based on user satisfaction, not only can we maximize the potential of air-conditioned buildings’ virtual energy storage, but also maximize the flexibility to satisfy different user wishes. The specific regulation grouping of users can also be further subdivided according to actual needs.
- The regulation strategy constructed in this paper can be combined with a digital regulation platform of a power grid. For example, a virtual power plant has the ability of mass data information processing, which can be used as an interface for air conditioning loads to participate in demand-side response and provide data support and a control platform for differentiated consideration of thermal comfort, which can not only ensure the comfort of users through more data surveys, but also improve the economy and environmental protection of power grid operations.
- The strategy constructed in this paper can effectively reduce part of the load peak and take into account the thermal comfort of users at the same time, but it only considers the virtual energy storage characteristics of air conditioning loads, and when combined with other types of virtual energy storage at the same time, it can further explore the potential of user-demand-side regulation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, R.; Liu, Z.; Jin, X.; Shi, Y. Inspiration of the UK ESO power supply sustainability measures under European energy crisis to China power system operator. Electr. Power 2023, 56, 177–184. [Google Scholar]
- Tushar, W.; Wang, T.; Lan, L.; Xu, Y.J.; Withanage, C.; Yuen, C.; Wood, K.L. Policy design for controlling set-point temperature of ACs in shared spaces of buildings. Energy Build. 2017, 134, 105–114. [Google Scholar] [CrossRef]
- Speake, A.; Wilson, E.J.H.; Zhou, Y.Y.; Horowitz, S. Component-level analysis of heating and cooling loads in the US residential building stock. Energy Build. 2023, 299, 113559. [Google Scholar] [CrossRef]
- Pachano, J.E.; Iglesias, M.F.V.; Saiz, J.C.; Bandera, C.F. Two-stage multi-step energy model calibration of the cooling systems of a large-space commercial building. Appl. Therm. Eng. 2023, 230, 120638. [Google Scholar] [CrossRef]
- Xie, K.; Hui, H.; Ding, Y. Review of modeling and control strategy of thermostatically controlled loads for virtual energy storage system. Prot. Contr. Mod. Power Syst. 2019, 423, 1–13. [Google Scholar] [CrossRef]
- Wang, Y.; Tong, Y.; Huang, M.; Yang, L.; Zhao, H. Research on virtual energy storage model of air conditioning loads based on demand response. Power Syst. Technol. 2017, 41, 394–401. [Google Scholar]
- Zhang, P.; Wang, M. Variation Characteristics Analysis and Short-Term Forecasting of Load Based on CEEMDAN. In Proceedings of the 2021 International Symposium on Electrical, Electronics and Information Engineering, Virtual Online, 19–21 February 2021. [Google Scholar]
- Song, M.; Gao, C.; Su, W.H. Modeling and controlling of air-conditioning load for demand response applications. Autom. Electr. Power Syst. 2016, 40, 158–167. [Google Scholar]
- Zhang, Y.; Li, N.; Ding, H.; Lu, M.; Yang, D.; Wang, Q. Air-conditioning load aggregation scheduling strategy based on user differentiated thermal comfort. Electr. Power Eng. Technol. 2023, 42, 133–140. [Google Scholar]
- Lv, G.; Ji, Y.; Zhang, Y.; Wang, W.; Zhang, J.; Chen, J.; Nie, Y. Optimization of building microgrid energy system based on virtual energy storage. Front. Energy. 2023, 10, 1053498. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, N.; Zhao, H. Optimal strategy for domestic electric water heaters based on virtual energy storage characteristics. Desalin. Water Treat. 2019, 168, 357–365. [Google Scholar] [CrossRef]
- Pan, E.; Li, H.; Wang, Z.; Peng, D.; Zhao, L.; Fan, L.; Wang, Y.; Huang, F.; Ma, Y.; Liu, L. Operation optimization of integrated energy systems based on heat storage characteristics of heating network. Energy Sci. Eng. 2021, 9, 223–238. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, L.; Huang, H.; Shi, S.; Xiao, X. Optimization method of HVAC load group distribution network for integrated buildings taking into account occupancy effects. Power Syst. Technol. 2023; in press. [Google Scholar]
- Zhu, L.; Hong, J.; Yang, S.; Hu, Z.; Shao, Y.; Wu, C.; He, G. Online modeling of virtual energy storage for inverter air conditioning clusters in CDL-based demand response. Energy Rep. 2023, 9, 2024–2034. [Google Scholar] [CrossRef]
- Zhao, J.; Jin, Y.; Li, H.; Wang, J.; Li, W. Design and optimization of building intergated renewable energy system based on virtual energy storage. Acta Energiae Solaris Sinica. 2021, 42, 91–97. [Google Scholar]
- Cao, B. Research on the Impacts of Climate and Built Environment on Human Thermal. Ph.D. Thesis, Tsinghua University, Beijing, China, 2012. [Google Scholar]
- Zhu, C.; Chen, H.; Yin, J.; Zhang, X.; Zhou, L. Economic dispatching strategy for building CCHP coupling system based on virtual energy storage model. Power Demand Side Manag. 2021, 23, 52–57+100. [Google Scholar]
- Dai, R.; Zhao, B.; Zhang, X.; Yu, J.; Fan, B.; Liu, B. Joint virtual energy storage modeling with electric vehicle participation in energy local area smart grid. Complexity 2020, 2020, 3102729. [Google Scholar] [CrossRef]
- Dai, Q.; Yang, L.; Lin, Z.; Lan, Z.; Wang, Y.; Liu, Z. Multi-storage planning of integrated energy system considering functional area difference and virtual storage. Electr. Power Autom. Equip. 2021, 41, 182–190. [Google Scholar]
- Ge, S.; Liu, J.; Liu, H.; Wang, Y.; Zhao, C.; Sun, W. Economic Dispatch of Energy Station with Building Virtual Energy Storage in Demand Response Mechanism. Autom. Electr. Power Syst. 2020, 44, 35–43. [Google Scholar]
- Xue, S.; Che, Y.; He, W.; Zhao, Y.; Zhang, R. Control strategy of electric heating loads for reducing power shortage in power grid. Processes 2019, 7, 273. [Google Scholar] [CrossRef]
- Gabriele, F.; Marco, B.; Dimosthenis, T.; Vasiliki, K.; Georgios, G.; Antonis, P. Demand flexibility enabled by virtual energy storage to Improve renewable energy penetration. Energies 2020, 13, 5128. [Google Scholar] [CrossRef]
- Guo, X.; Gao, C.; Wang, C.; Li, L.; Liu, W. Peak adjustment strategy based on central air conditioning virtual energy storage model. Power Demand Side Manag. 2022, 24, 42–46. [Google Scholar]
- Lian, Z.; Cao, B.; Du, H.; Mou, D.; Lai, D.; Zhai, Y. Determination method of comfortable zone for indoor thermal environment. Build. Sci. 2022, 38, 9–15. [Google Scholar]
- ANSI/ASHRAE, ANSI/ASHRAE Standard 55-2023—Thermal Environmental Conditions for Human Occupancy, USA. 2023. Available online: https://www.ashrae.org/technical-resources/bookstore/standard-55-thermal-environmental-conditions-for-human-occupancy (accessed on 1 January 2024).
- Wang, J.J.; Wu, H.B.; Yang, S.H.; Bi, R.; Lu, J.H. Analysis of decision-making for air conditioning users based on the discrete choice model. Int. J. Electr. Power Energy Syst. 2021, 131, 106963. [Google Scholar] [CrossRef]
- Qi, N.; Cheng, L.; Xu, H.L.; Wang, Z.H.; Zhou, X.Y. Practical demand response potential evaluation of air-conditioning loads for aggregated customers. Energy Rep. 2020, 6, 71–78. [Google Scholar] [CrossRef]
- Yang, Y.; Song, L.T. Day ahead and real Time aggregate regulation of air conditioning load on demand response. J. Glob. Energy Interconnect. 2023, 6, 529–537. [Google Scholar]
- Berrouk, F.; Bouchekara, R.E.H.H.; Chaib, A.E.; Abido, M. A new multi-objective Jaya algorithm for solving the optimal power flow problem. J. Electr. Syst. 2018, 14, 165–181. [Google Scholar]
- Wang, J.; Bian, Y.; Xu, Q.; Kong, X. Distributionally robust optimal dispatching of microgrid considering risk and carbon trading mechanism. High Volt. Eng. 2023; in press. [Google Scholar]
- Wang, Y.; Hu, C.; Wu, B.; Zhang, J.; Zi, Z.; Kang, L. Matching Characteristic Research of Building Renewable Energy System Based on Virtual Energy Storage of Air Conditioning Load. Energies 2020, 13, 1269. [Google Scholar] [CrossRef]
- Lei, X.; Tang, W.Z.; Li, Z.Y.; He, J.Y.; Liu, Q.Y. Distribution Network Expansion Planning Considering Optimal Operation of Regional Integrated Energy System. Power Syst. Technol. 2018, 42, 3459–3468. [Google Scholar]
- Sun, K.; Chen, W.; Chen, J.; Yin, W. A resilience enhancement strategy for multi-microgrid in extreme scenarios based on electric vehicles. Power Syst. Prot. Control 2023, 51, 53–65. [Google Scholar]
- Zeng, B.; Zhang, J.H.; Yang, X.; Wang, J.H.; Dong, J.; Zhang, Y.Y. Integrated planning for transition to low-carbon distribution system with renewable energy generation and demand response. IEEE Trans. Power Syst. 2014, 29, 1153–1165. [Google Scholar] [CrossRef]
- Li, Z.K.; Li, Y.M.; Luo, X.; Wang, W.; Wei, Y.J. Optimal operation of microgrid in the park considering carbon trading and the proportion of green electricity. Electr. Meas. Instrum. 2022; in press. [Google Scholar]
- Fan, S.C.; Huang, X.M.; Zhang, Y.J.; Huang, G.Q.; Yang, J.X.; Li, Q.H. Modeling of expansion planning for distribution transformer considering orderly charging. Autom. Electr. Power Syst. 2021, 45, 62–70. [Google Scholar]
- Jin, G.; Pan, D.; Chen, Q.; Shi, C.; Li, G. Fuzzy Random Day-Ahead Optimal Dispatch of DC Distribution Network Considering the Uncertainty of Source-Load. Trans. China Electrotech. Soc. 2021, 36, 4517–4528. [Google Scholar]
- Chen, Y. Thermal Comfort Characteristics and Energy-Saving Operation Modes of Residential Buildings in Hangzhou Based on Personal Comfort Systems. Master’s Thesis, Chongqing University, Chongqing, China, 2021. [Google Scholar]
- Chen, Z. Study on Energy Consumption and Load Characteristics of Residential Buildings in Typical Cities in Hot Summer and Cold Winter Areas. Master’s Thesis, Zhejiang University, Hangzhou, China, 2022. [Google Scholar]
- Du, H.; Lian, Z.; Lai, D.Y.; Liu, W.; Lin, D.; Zhai, Y.; Cao, B.; Zhang, Y.; Zhou, X.; Wang, Z.; et al. Method of determining acceptable air temperature thresholds in Chinese HVAC buildings based on a data-driven model. Energy Build. 2021, 241, 110920. [Google Scholar] [CrossRef]
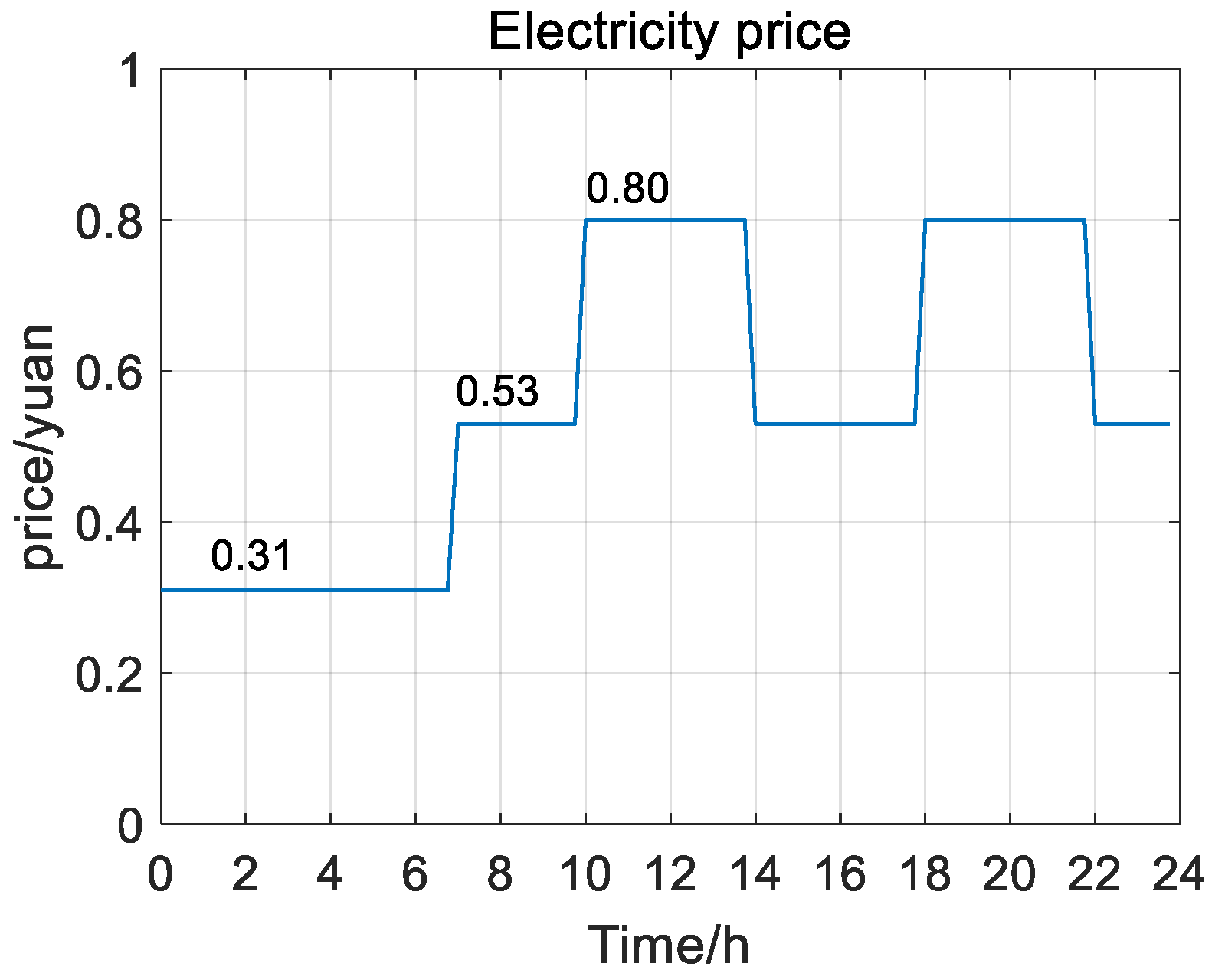
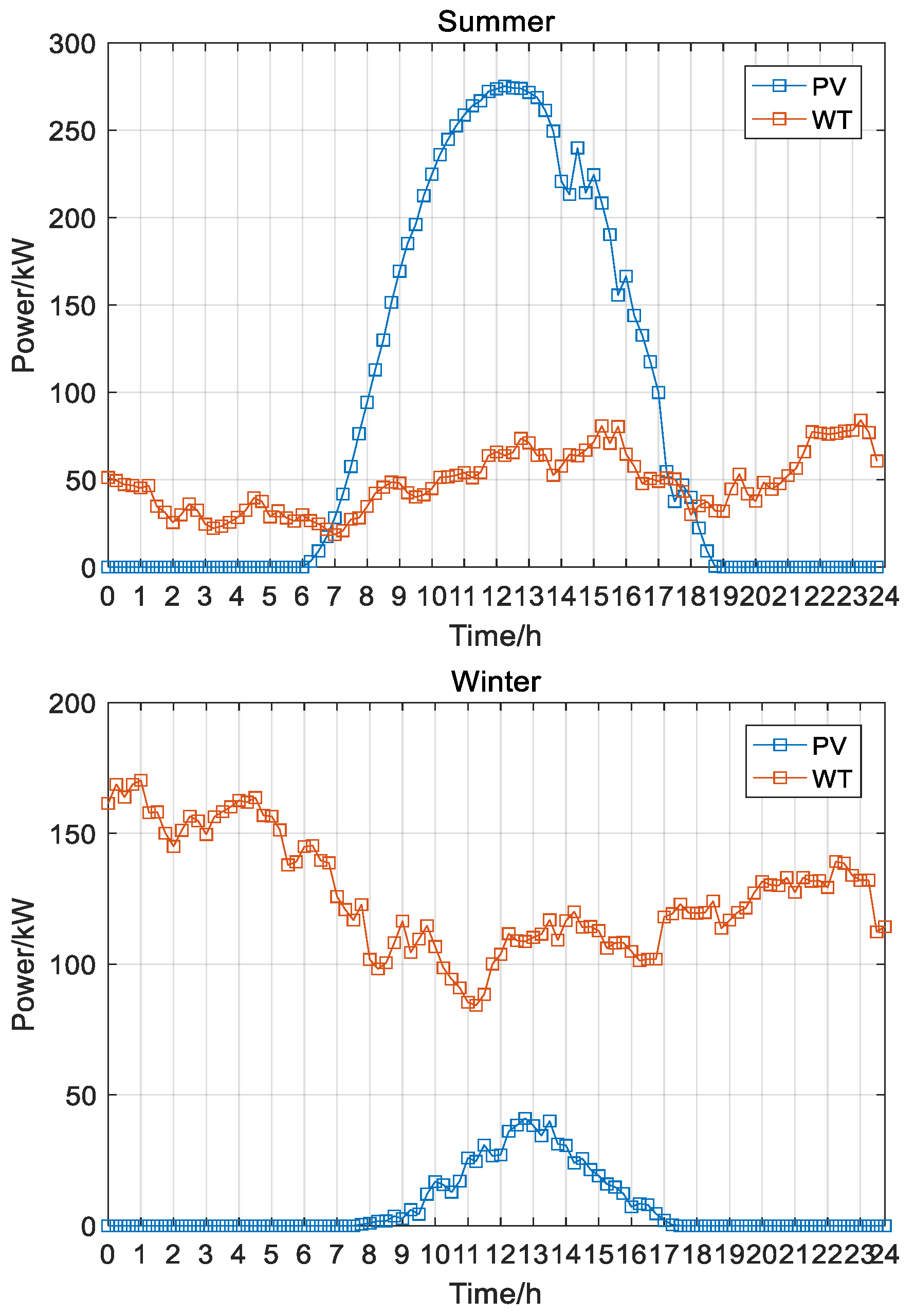
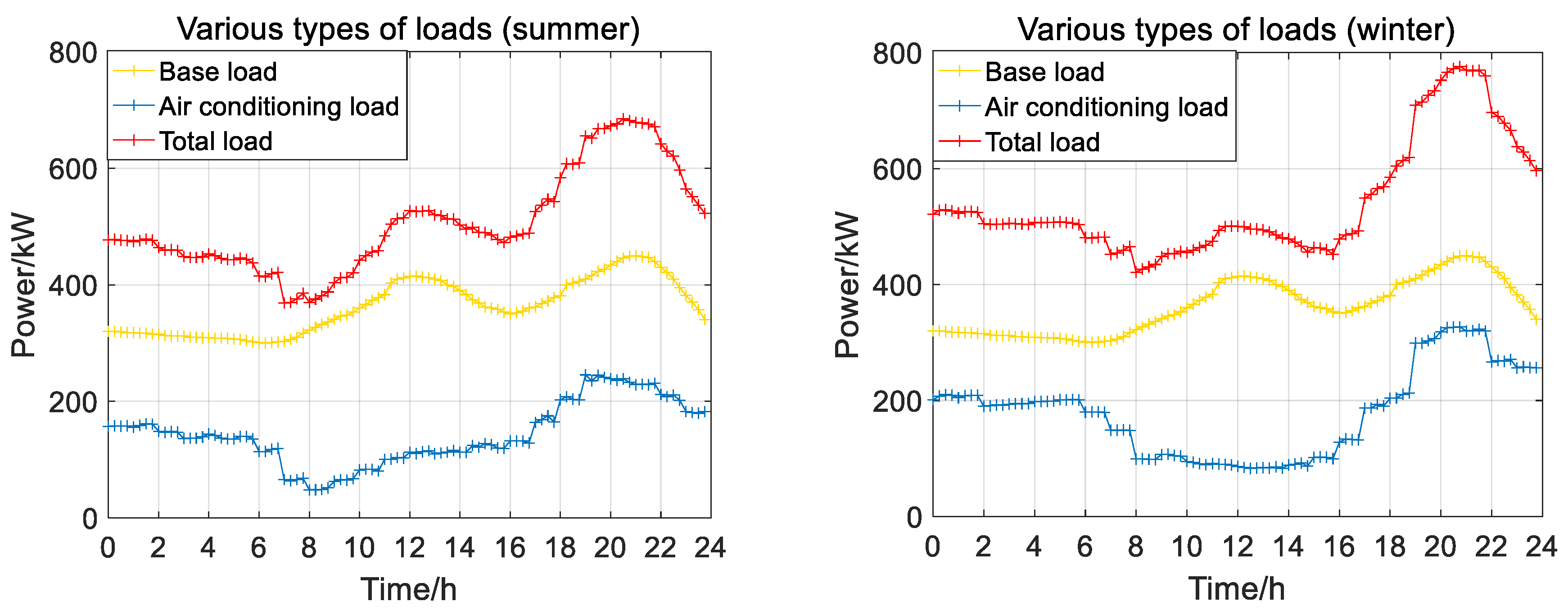
| Type of Energy Source | Operation Costs (Yuan/kWh) |
|---|---|
| wind power | 0.056 |
| photovoltaic power | 0.08 |
| micro gas turbines | 0.7 |
| Type | Carbon Emission Coefficient (kg/kWh) |
|---|---|
| 0.458 | |
| 0.92 |
| Type of Energy Source | Installed Capacity (kW) |
|---|---|
| micro gas turbines | 350 |
| wind power | 192 |
| photovoltaic power | 390 |
| Season | Building Type | Thermal Comfort Satisfaction |
|---|---|---|
| Summer | Office | |
| Summer | Residence | |
| Winter | Office | |
| Winter | Residence |
| Season | Satisfaction | Temperature Range |
|---|---|---|
| Summer | Maximum satisfaction | 24.6 |
| Summer | 90% | 21.9–27.3 |
| Summer | 80% | 20.4–28.9 |
| Winter | Maximum satisfaction | 22.8 |
| Winter | 90% | 22–23.6 |
| Winter | 80% | 18–28.9 |
| Season | Microgrid Revenue (Yuan) | Carbon Emissions (kg) | User’s Electricity Purchase Cost (Yuan) |
|---|---|---|---|
| Summer Case 1 | 1321.3 | 5967.3 | 6970.3 |
| Summer Case 2 | 1550.7 | 5593.7 | 6561.3 |
| Summer Case 3 | 1621.7 | 5484.6 | 6479.8 |
| Winter Case 1 | 1062.7 | 6395.3 | 7386.8 |
| Winter Case 2 | 1306.8 | 6225.1 | 6983.4 |
| Winter Case 3 | 1401.7 | 6224.9 | 6976.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, R.; Wu, E.; Lan, L.; Fu, C.; Guo, M.; Chen, F.; Wang, M.; Zou, J. Research on Virtual Energy Storage Scheduling Strategy for Air Conditioning Based on Adaptive Thermal Comfort Model. Energies 2024, 17, 2670. https://doi.org/10.3390/en17112670
Lv R, Wu E, Lan L, Fu C, Guo M, Chen F, Wang M, Zou J. Research on Virtual Energy Storage Scheduling Strategy for Air Conditioning Based on Adaptive Thermal Comfort Model. Energies. 2024; 17(11):2670. https://doi.org/10.3390/en17112670
Chicago/Turabian StyleLv, Ran, Enqi Wu, Li Lan, Chen Fu, Mingxing Guo, Feier Chen, Min Wang, and Jie Zou. 2024. "Research on Virtual Energy Storage Scheduling Strategy for Air Conditioning Based on Adaptive Thermal Comfort Model" Energies 17, no. 11: 2670. https://doi.org/10.3390/en17112670
APA StyleLv, R., Wu, E., Lan, L., Fu, C., Guo, M., Chen, F., Wang, M., & Zou, J. (2024). Research on Virtual Energy Storage Scheduling Strategy for Air Conditioning Based on Adaptive Thermal Comfort Model. Energies, 17(11), 2670. https://doi.org/10.3390/en17112670







