Elements of Transition-State Theory in Relation to the Thermal Dissociation of Selected Solid Compounds
Abstract
1. Introduction and Aim of the Work
2. Relation between Arrhenius Law and TST
3. The Concept Based on the Equilibrium Constant According to Equation (1)
4. Examples of Analysis Using Equation (1)
4.1. Formal Assumptions
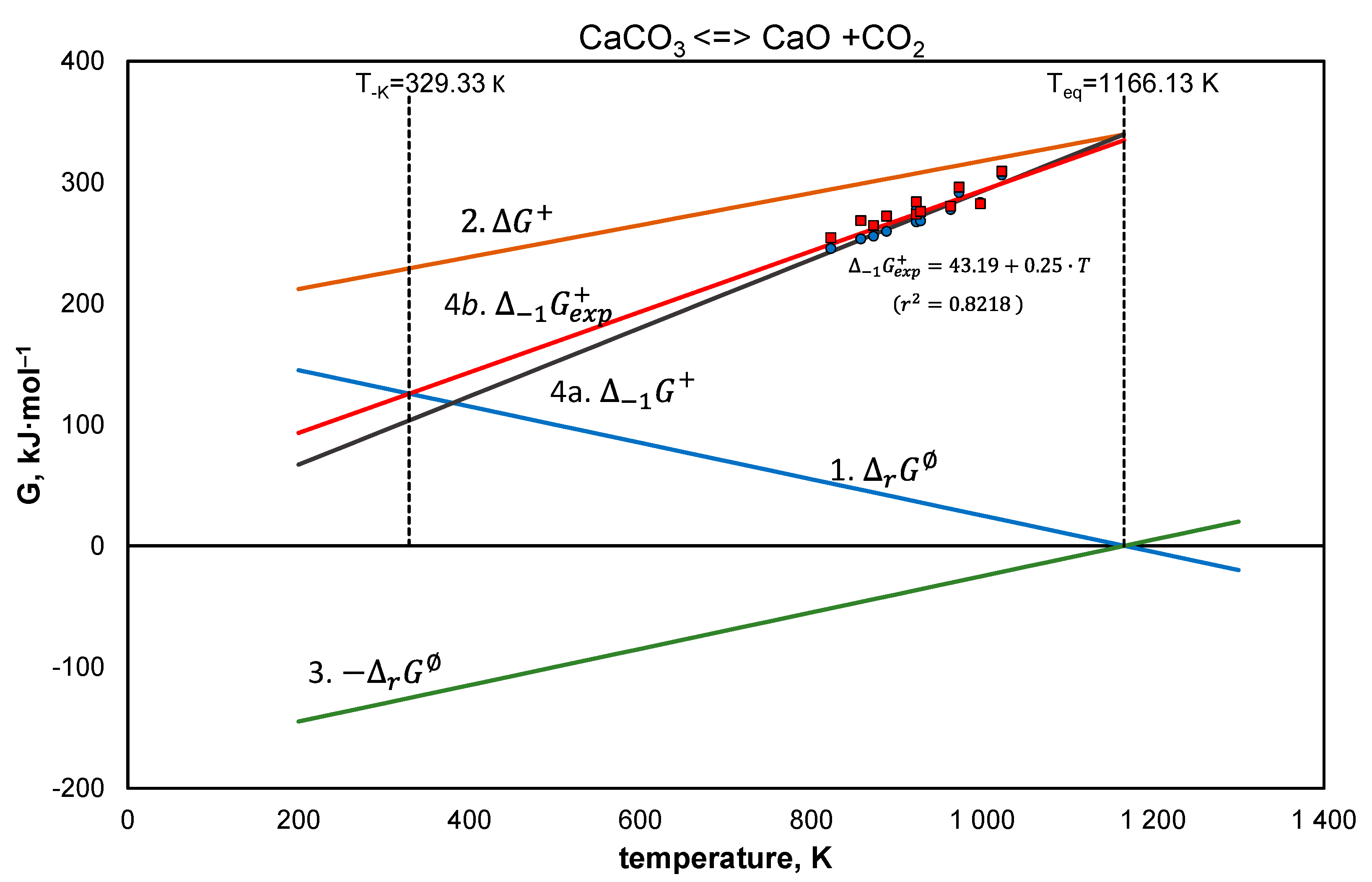
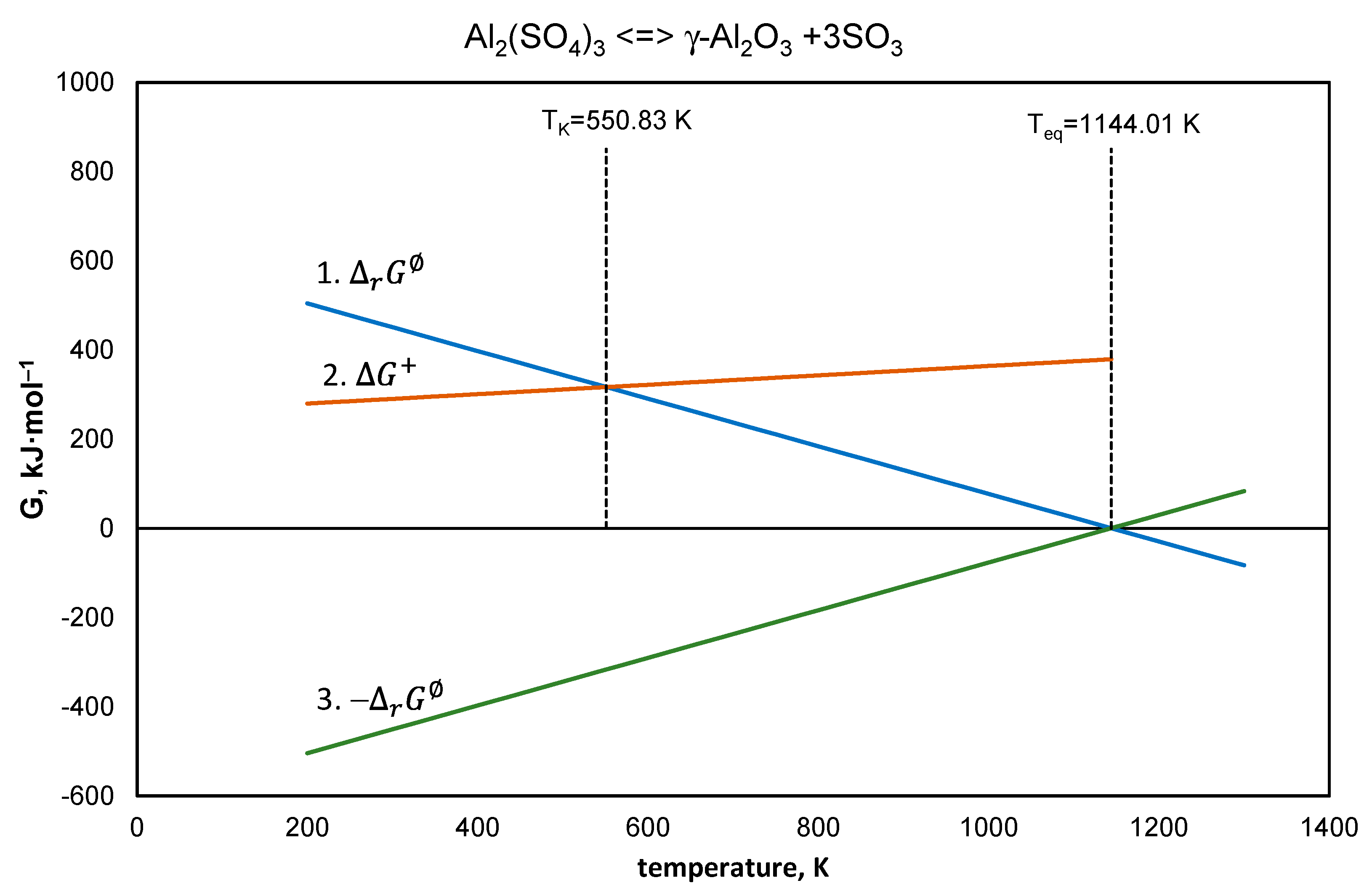
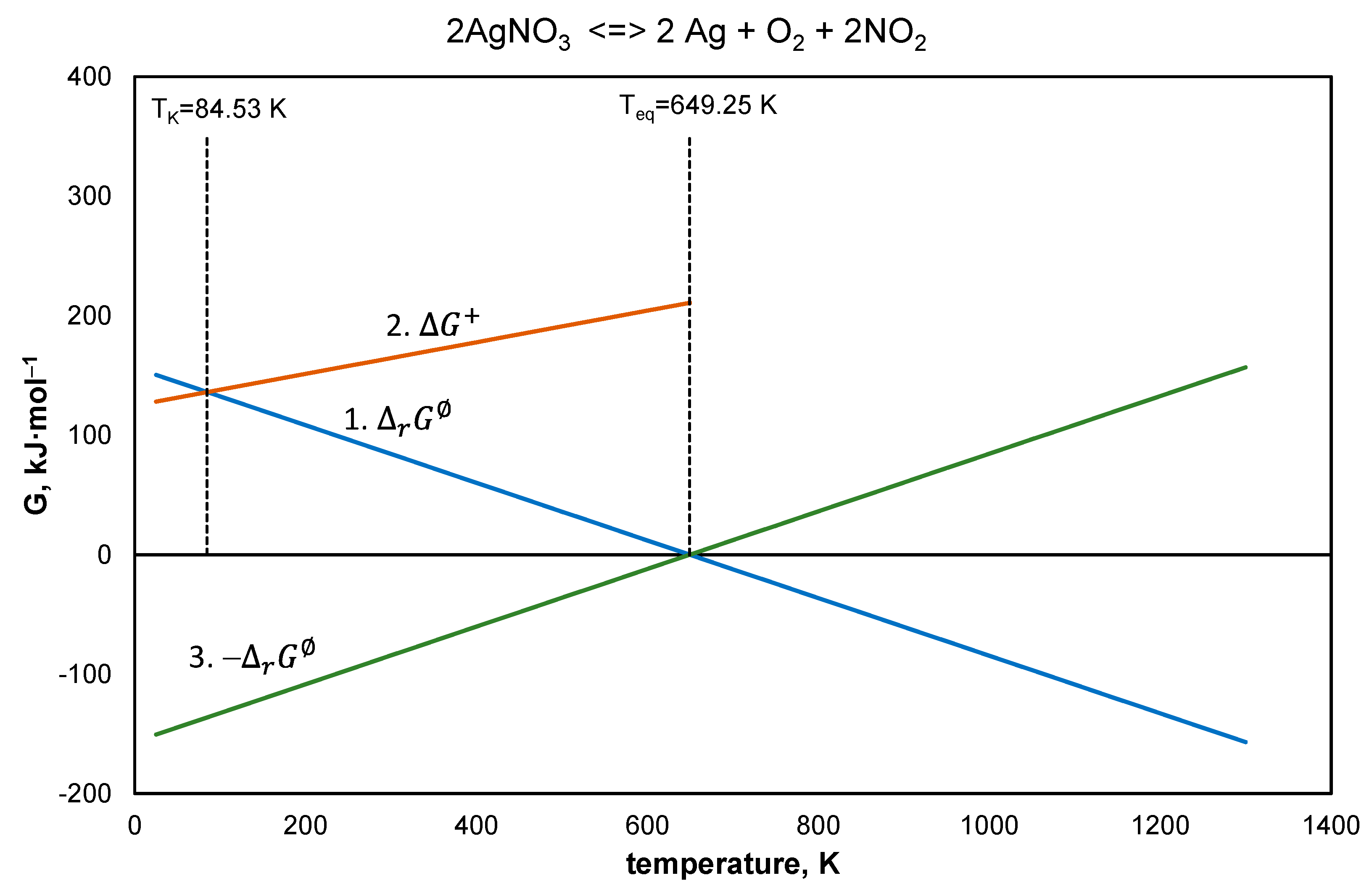
- Equation (26), —line 1,
- Equation (27), —line 2,
- Equation (26) after reversal of the signs —line 3,
- Equation (12) for experimental data of the activation state of a reversible reaction, (line 4a), represented by the results of experimental studies, (line 4b),
- other, explained for the specific example—line 5.
4.2. Calcite
4.3. Iron(III) Sulphate (Ferric Sulphate)

4.4. Aluminum Sulfate
4.5. Silver Nitrate
4.6. Ammonium Perchlorate

5. Entropy of Activation at Isokinetic Temperature
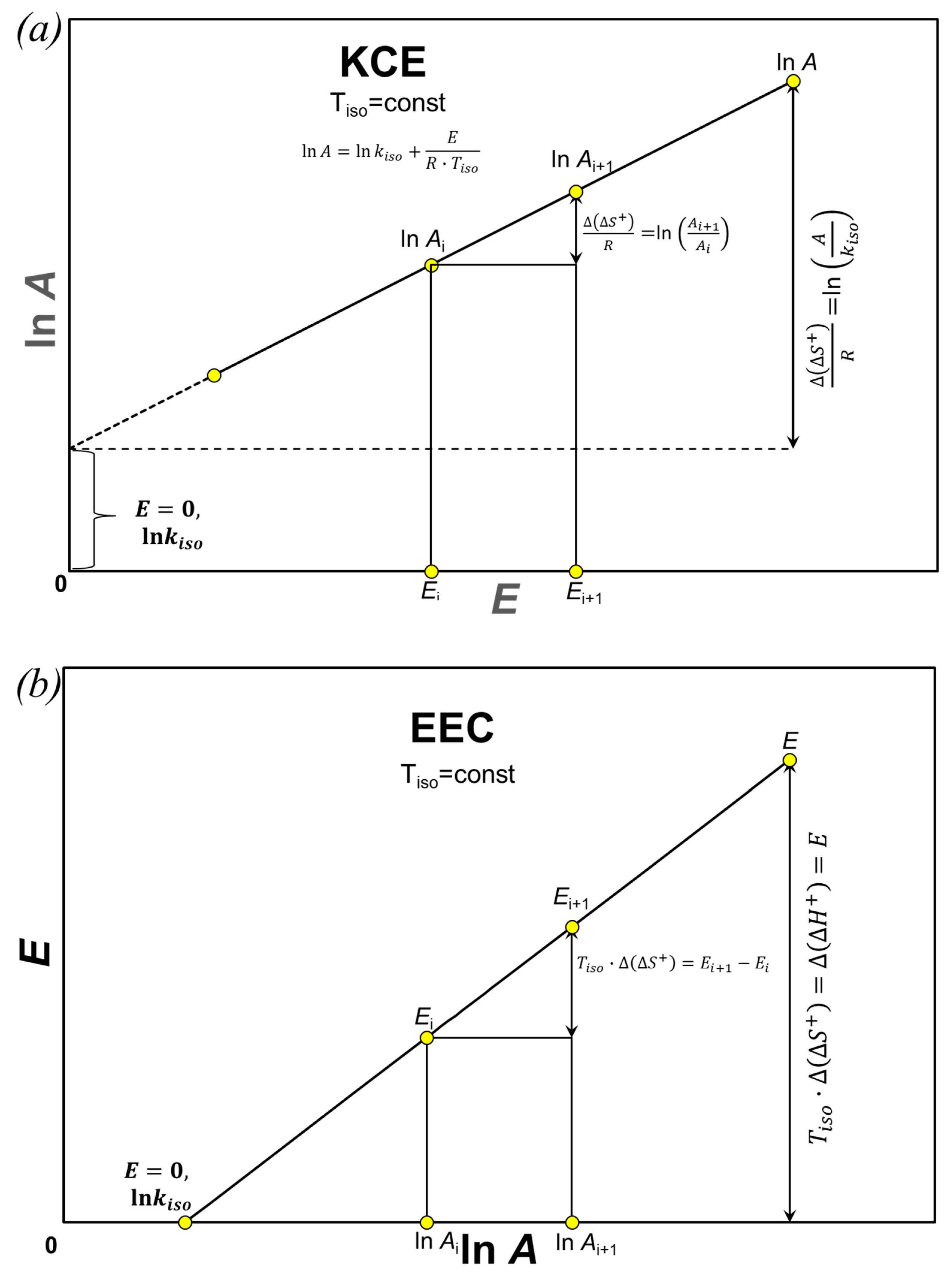
6. Discussion
7. Final Remarks
8. Proof of Concept
9. Conclusions
- The reference to the thermodynamic equilibrium constant in terms of the kinetic dissociation reaction/process of solids to its reversibility (Equation (1)) creates the possibility of identifying the thermodynamics of activation processes according to TST. The possibility of analyzing ‘forwards to backwards’ relations for these issues is therefore extended, which is made possible by the relational Equation (18).
- This temperature is common to the activation process of thermal dissociation and reversible synthesis. The isoequilibrium temperature () is of great importance and is determined by the intersection of the Gibbs free energy (lines 1 and 2), i.e., according to the thermodynamic approach and determined by the kinetic parameters of this distribution for the reversible reaction.
- The crux of the matter leads to the equality of the equilibrium constants for the decomposition reaction and those experimentally determined for the reversible reaction.
- Therefore, it is extremely important to correctly determine Arrhenius kinetic parameters. KCE is based on isentropic equilibration of these parameters at isoconversion temperature Tiso close to equilibrium temperature Teq.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| coefficients of strictly thermodynamic significance | |
| pre-exponential factor, s−1 | |
| 2.08364· K−1·s−1 ratio of Boltzmann to Planck’s constant | |
| const in Equation (28), J·mol−1 | |
| activation energy, J·mol−1 | |
| and | thermodynamic functions; respectively: free enthalpy, enthalpy, and entropy |
| temperature profile of a reversible reaction, J·mol−1 | |
| activation entropy in isokinetic temperature (Multi-Excitation Entropy) Equations (53) and (54), J·mol−1·K−1 | |
| 6.62607· J·s, Planck constant | |
| rate constant, s−1 | |
| 1.38065· J·K−1, Boltzmann constant, | |
| equilibrium constant | |
| 0, 1, or 2, coefficients | |
| pressure, MPa | |
| 8.314 J·mol−1·K−1, universal gas constant | |
| coefficients of linear determination | |
| heating rate, K·s−1 | |
| time, s | |
| absolute temperature, K | |
| conversion degree, 0 < α ≤ 1 | |
| transmission coefficient | |
| frequency (decomposition frequency of transition state [25]) s−1 | |
| Subscripts | |
| 0 | initial |
| 1,2 | forward |
| −1 | backward |
| c | compensation |
| eq | equilibrium |
| exp | experiment |
| f | final |
| i | ith value |
| iso | isokinetic value |
| K | isoequilibrium for forward |
| (−K) | isoequilibrium for backward |
| m | maximum of rate reaction/process |
| r | reaction |
| TST | Transition-State Theory |
| Superscripts | |
| + | activation functions |
| ∅ | standard condition |
| gas, solid | |
| Abbreviations | |
| FWO | Flynn–Wall–Ozawa Equation, |
| KAS | Kissinger–Akahira–Sunose Equation, |
| EEC | Entalphy–Entropy Compensation, |
| KCE | Kinetic Compensation Effect (IE or Constable plot, also IKR), |
| RPM | Random Pore Models [58], |
| RRKM | Rice–Ramsperger–Kassel–Marcus Theory [51], |
| TST | Transition-State Theory. |
Appendix A
Appendix A.1. General form of Equations (22) and (23)
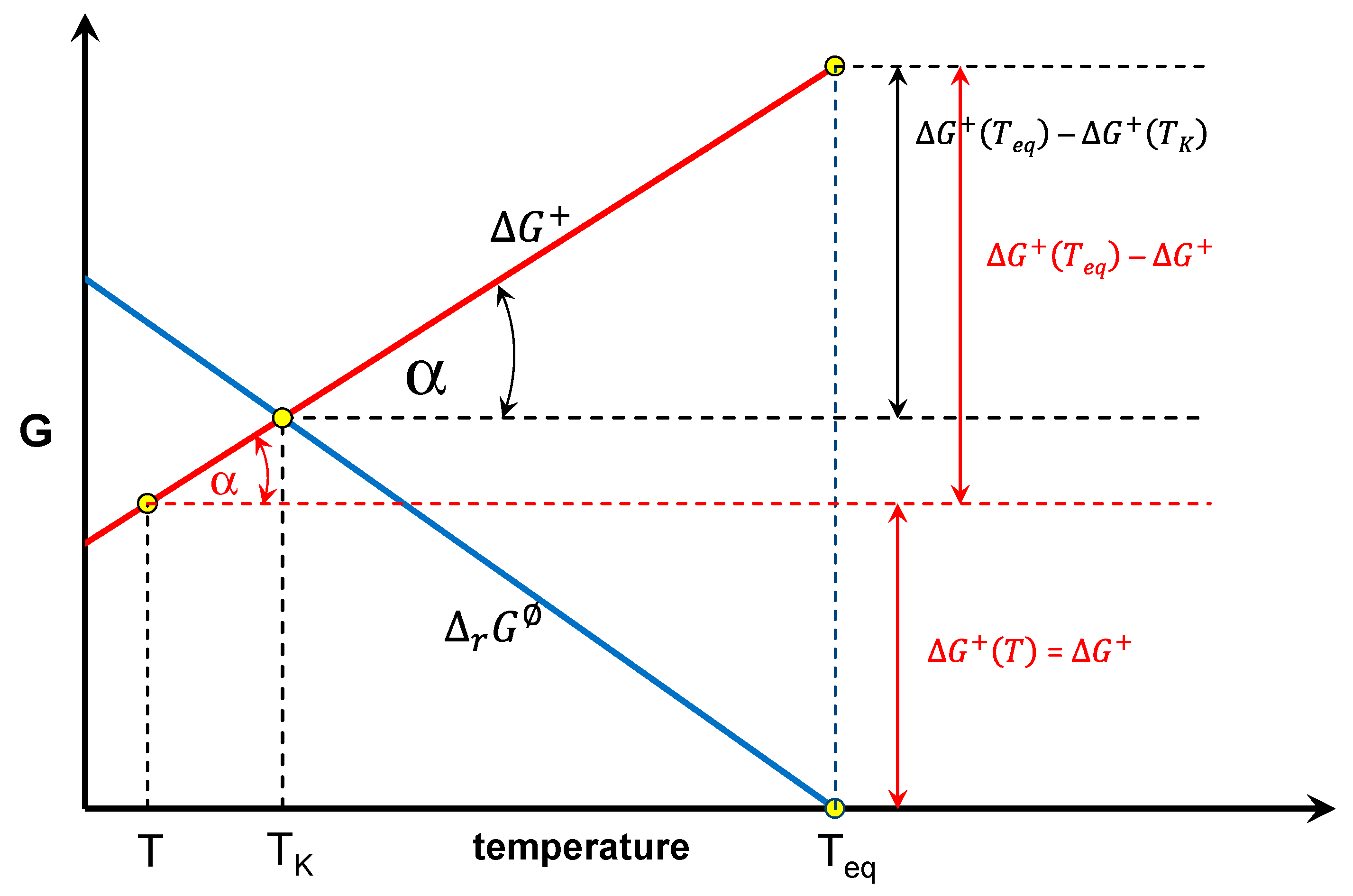
Appendix A.2. Importance of Equation (14) in Relation to KCE Expressed by Equations (55) and (56)
- For (Figure A2a, points 1 → 2):
- 2
- For const, var (Figure A2a, points 3 → 4, from Equation (A5)):
- 3
- For var, const (Figure A2b):

References
- Eyring, H. The Activated Complex in Chemical Reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Garrett, B.C.; Klippenstein, S.J. Current Status of Transition-State Theory. J. Phys. Chem. 1996, 100, 12771–12800. [Google Scholar] [CrossRef]
- Evans, M.G.; Polanyi, M. On the introduction of thermodynamic variables into reaction kinetics. Trans. Faraday Soc. 1937, 33, 448–452. [Google Scholar] [CrossRef]
- Shannon, R.D. Activated complex theory applied to the thermal decomposition of solids. Trans. Faraday Soc. 1964, 60, 1902–1913. [Google Scholar] [CrossRef]
- Garrett, B.C. Perspective on “The transition state method”. Theor. Chem. Acc. 2000, 103, 200–204. [Google Scholar] [CrossRef] [PubMed]
- Atanassov, A.; Genieva, S.; Vlaev, L. Study on the Thermooxidative Degradation Kinetics of Tetrafluoroethylene-Ethylene Copolymer Filled with Rice Husks Ash. Polym. Technol. Eng. 2010, 49, 541–554. [Google Scholar] [CrossRef]
- Kim, Y.S.; Kim, Y.S.; Kim, S.H. Investigation of Thermodynamic Parameters in the Thermal Decomposition of Plastic Waste−Waste Lube Oil Compounds. Environ. Sci. Technol. 2010, 44, 5313–5317. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Chen, B. Investigation of thermodynamic parameters in the pyrolysis conversion of biomass and manure to biochars using thermogravimetric analysis. Bioresour. Technol. 2013, 146, 485–493. [Google Scholar] [CrossRef]
- Rony, A.H.; Kong, L.; Lu, W.; Dejam, M.; Adidharma, H.; Gasem, K.A.; Zheng, Y.; Norton, U.; Fan, M. Kinetics, thermodynamics, and physical characterization of corn stover (Zea mays) for solar biomass pyrolysis potential analysis. Bioresour. Technol. 2019, 284, 466–473. [Google Scholar] [CrossRef]
- Sahoo, A.; Kumar, S.; Mohanty, K. A comprehensive characterization of non-edible lignocellulosic biomass to elucidate their biofuel production potential. Biomass Convers. Biorefinery 2020, 12, 5087–5103. [Google Scholar] [CrossRef]
- Pinzi, S.; Buratti, C.; Bartocci, P.; Marseglia, G.; Fantozzi, F.; Barbanera, M. A simplified method for kinetic modeling of coffee silver skin pyrolysis by coupling pseudo-components peaks deconvolution analysis and model free-isoconversional methods. Fuel 2020, 278, 118260. [Google Scholar] [CrossRef]
- Genieva, S.; Gonsalvesh, L.; Georgieva, V.; Tavlieva, M.; Vlaev, L. Kinetic analysis and pyrolysis mechanism of raw and impregnated almond shells. Thermochim. Acta 2021, 698, 178877. [Google Scholar] [CrossRef]
- Banerjee, A.; Vithusha, T.; Krishna, B.B.; Kumar, J.; Bhaskar, T.; Ghosh, D. Pyrolysis of de-oiled yeast biomass of Rhodotorula mucilaginosa IIPL32: Kinetics and thermodynamic parameters using thermogravimetric analysis. Bioresour. Technol. 2021, 340, 125534. [Google Scholar] [CrossRef]
- Patidar, K.; Singathia, A.; Vashishtha, M.; Sangal, V.K.; Upadhyaya, S. Investigation of kinetic and thermodynamic parameters approaches to non-isothermal pyrolysis of mustard stalk using model-free and master plots methods. Mater. Sci. Energy Technol. 2022, 5, 6–14. [Google Scholar] [CrossRef]
- Tasar, S. Thermal conversion behavior of cellulose and hemicellulose fractions isolated from tea leaf brewing waste: Kinetic and thermodynamic evaluation. Biomass Convers. Biorefinery 2022, 12, 2935–2947. [Google Scholar] [CrossRef]
- Sun, C.; Tan, H.; Zhang, Y. Simulating the pyrolysis interactions among hemicellulose, cellulose and lignin in wood waste under real conditions to find the proper way to prepare bio-oil. Renew. Energy 2023, 205, 851–863. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction Kinetics in Differential Thermal Analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Conner, W. A general explanation for the compensation effect: The relationship between and activation energy. J. Catal. 1982, 78, 238–246. [Google Scholar] [CrossRef]
- Laidler, K.J.; King, M.C. The Development of transition-state theory. J. Phys. Chem. 1983, 87, 2657–2664. [Google Scholar] [CrossRef]
- Hanggi, P.; Talkner, P.; Borkovec, M. Reaction-Rate Theory: Fifty Years After Kramers. Rev. Mod. Phys. 1990, 62, 251–341. [Google Scholar] [CrossRef]
- Topaler, M.; Makri, N. Quantum rates for a double well coupled to a dissipative bath: Accurate path integral results and comparison with approximate theories. J. Chem. Phys. 1994, 101, 7500–7519. [Google Scholar] [CrossRef]
- Rooney, J.J. Isokinetic temperature and the compensation effect in catalysis. J. Mol. Catal. A Chem. 1998, 133, 303–305. [Google Scholar] [CrossRef]
- McBane, G.C.; de Levie, R.; Yan, Z.; Chang, Y.; Mayo, D.; Maslak, V.; Xia, S.; Badjić, J.D.; Williams, C.K.; Galley, W.C.; et al. Chemistry from Telephone Numbers: The False Isokinetic Relationship. J. Chem. Educ. 1998, 75, 919–922. [Google Scholar] [CrossRef]
- Liu, L.; Guo, Q.-X. Isokinetic Relationship, Isoequilibrium Relationship, and Enthalpy−Entropy Compensation. Chem. Rev. 2001, 101, 673–696. [Google Scholar] [CrossRef]
- Yelon, A.; Movaghar, B.; Crandall, R.S. Multi-excitation entropy: Its role in thermodynamics and kinetics. Rep. Prog. Phys. 2006, 69, 1145–1194. [Google Scholar] [CrossRef]
- Principles of Chemical Kinetics-2nd Edition. Available online: https://www.elsevier.com/books/principles-of-chemical-kinetics/house/978-0-12-356787-1 (accessed on 14 March 2023).
- Yelon, A.; Sacher, E.; Linert, W. Multi-Excitation Entropy, Entropy–Enthalpy Relations, and their Impact on Catalysis. Catal. Lett. 2011, 141, 954–957. [Google Scholar] [CrossRef]
- Revell, L.E.; Williamson, B.E. Why Are Some Reactions Slower at Higher Temperatures? J. Chem. Educ. 2013, 90, 1024–1027. [Google Scholar] [CrossRef]
- Yin, C.; Du, J. The power-law reaction rate coefficient for an elementary bimolecular reaction. Phys. A Stat. Mech. Appl. 2014, 395, 416–424. [Google Scholar] [CrossRef]
- Carvalho-Silva, V.H.; Aquilanti, V.; de Oliveira, H.C.B.; Mundim, K.C. Deformed transition-state theory: Deviation from Arrhenius behavior and application to bimolecular hydrogen transfer reaction rates in the tunneling regime. J. Comput. Chem. 2016, 38, 178–188. [Google Scholar] [CrossRef]
- Sanjeev, R.; Padmavathi, D.A.; Jagannadham, V. The ‘Yard Stick’ to Interpret the Entropy of Activation in Chemical Kinetics: A Physical-Organic Chemistry Exercise. World J. Chem. Educ. 2018, 6, 78–81. [Google Scholar] [CrossRef]
- Khrapunov, S. The Enthalpy-entropy Compensation Phenomenon. Limitations for the Use of Some Basic Thermodynamic Equations. Curr. Protein Pept. Sci. 2018, 19, 1088–1091. [Google Scholar] [CrossRef]
- Braun, A.; Chen, Q.; Yelon, A. Hole and Protonic Polarons in Perovskites. Chimia 2019, 73, 936–942. [Google Scholar] [CrossRef]
- Sapunov, V.N.; Saveljev, E.A.; Voronov, M.S.; Valtiner, M.; Linert, W. The Basic Theorem of Temperature-Dependent Processes. Thermo 2021, 1, 45–60. [Google Scholar] [CrossRef]
- Vyazovkin, S. Determining Preexponential Factor in Model-Free Kinetic Methods: How and Why? Molecules 2021, 26, 3077. [Google Scholar] [CrossRef]
- Linert, W. The isokinetic relationship. X. Experimental examples to the relationship between isokinetic temperatures and active heat bath frequencies. Chem. Phys. 1989, 129, 381–393. [Google Scholar] [CrossRef]
- Rooney, J. An explanation of isokinetic temperature in heterogeneous catalysis. Catal. Lett. 1998, 50, 15. [Google Scholar] [CrossRef]
- Larsson, R. Catalysis as a resonance effect, V. Factors that determine the isokinetic temperature in catalytic reactions. React. Kinet. Catal. Lett. 1999, 68, 115–124. [Google Scholar] [CrossRef]
- Armstrong, A.A.; Amzel, L.M. Role of Entropy in Increased Rates of Intramolecular Reactions. J. Am. Chem. Soc. 2003, 125, 14596–14602. [Google Scholar] [CrossRef]
- Craig, I.R.; Thoss, M.; Wang, H. Proton transfer reactions in model condensed-phase environments: Accurate quantum dynamics using the multilayer multiconfiguration time-dependent Hartree approach. J. Chem. Phys. 2007, 127, 144503. [Google Scholar] [CrossRef]
- Piskulich, Z.A.; Mesele, O.O.; Thompson, W.H. Activation Energies and Beyond. J. Phys. Chem. A 2019, 123, 7185–7194. [Google Scholar] [CrossRef]
- Ivanova, Y.; Pukhovskaya, S.; Mamardashvili, N.; Koifman, O.; Kruk, M. Rate-acidity hysteresis and enthalpy-entropy compensation upon metalloporphyrin formation: Implication for the metal ion coordination mechanism. J. Mol. Liq. 2018, 275, 491–498. [Google Scholar] [CrossRef]
- Odai, K.; Umesaki, K. Kinetic Study of Transition Mutations from G–C to A–T Base Pairs in Watson–Crick DNA Base Pairs: Double Proton Transfers. J. Phys. Chem. A 2021, 125, 8196–8204. [Google Scholar] [CrossRef]
- Nakamura, S.; Sakai, H.; Fuki, M.; Kobori, Y.; Tkachenko, N.V.; Hasobe, T. Enthalpy–Entropy Compensation Effect for Triplet Pair Dissociation of Intramolecular Singlet Fission in Phenylene Spacer-Bridged Hexacene Dimers. J. Phys. Chem. Lett. 2021, 12, 6457–6463. [Google Scholar] [CrossRef]
- Shpanko, I.V.; Sadovaya, I.V. Enthalpy–Entropy Compensation in Reactions of Oxirane Ring Opening. Russ. J. Phys. Chem. A 2022, 96, 2307–2317. [Google Scholar] [CrossRef]
- Slocombe, L.; Winokan, M.; Al-Khalili, J.; Sacchi, M. Quantum Tunnelling Effects in the Guanine-Thymine Wobble Misincorporation via Tautomerism. J. Phys. Chem. Lett. 2022, 14, 9–15. [Google Scholar] [CrossRef]
- Maciejewski, M.; Oswald, H.-R.; Reller, A. Thermal transformations of vaterite and calcite. Thermochim. Acta 1994, 234, 315–328. [Google Scholar] [CrossRef]
- Mianowski, A.; Baraniec, I. Three-parametric equation in evaluation of thermal dissociation of reference compound. J. Therm. Anal. Calorim. 2009, 96, 179–187. [Google Scholar] [CrossRef]
- Vyazovkin, S. When can the effect of thermal inertia be considered negligible? Int. J. Chem. Kinet. 2021, 53, 1058–1060. [Google Scholar] [CrossRef]
- Galukhin, A.V.; Nikolaev, I.; Nosov, R.V.; Islamov, D.; Vyazovkin, S. Solvent-induced changes in the reactivity of tricyanate esters undergoing thermal polymerization. Polym. Chem. 2021, 12, 6179–6187. [Google Scholar] [CrossRef]
- Bŀażejowski, J.; Rak, J.; Gutowski, M. On the possibilities of theoretical analysis of kinetics of the thermal decomposition of solids. J. Therm. Anal. Calorim. 1995, 43, 45–55. [Google Scholar] [CrossRef]
- Barin, I. Thermochemical Data of Pure Substances; VCH: Weinheim, Germany, 1997. [Google Scholar]
- Brown, M.; Maciejewski, M.; Vyazovkin, S.; Nomen, R.; Sempere, J.; Burnham, A.; Opfermann, J.; Strey, R.; Anderson, H.; Kemmler, A.; et al. Computational aspects of kinetic analysis: Part A: The ICTAC kinetics project-data, methods and results. Thermochim. Acta 2000, 355, 125–143. [Google Scholar] [CrossRef]
- Tagawa, H. Thermal decomposition temperatures of metal sulfates. Thermochim. Acta 1984, 80, 23–33. [Google Scholar] [CrossRef]
- Warner, N.A.; Ingraham, T.R. Kinetic studies of the thermal decomposition of ferric sulphate and aluminum sulphate. Can. J. Chem. Eng. 1962, 40, 263–267. [Google Scholar] [CrossRef]
- Coombs, P.G.; Munir, Z.A. The decomposition of iron(III) sulfate in air. J. Therm. Anal. 1989, 35, 967–976. [Google Scholar] [CrossRef]
- Janković, B.; Stopić, S.; Bogović, J.; Friedrich, B. Kinetic and thermodynamic investigations of non-isothermal decomposition process of a commercial silver nitrate in an argon atmosphere used as the precursors for ultrasonic spray pyrolysis (USP): The mechanistic approach. Chem. Eng. Process. Process. Intensif. 2014, 82, 71–87. [Google Scholar] [CrossRef]
- Bhatia, S.K.; Perlmutter, D.D. Effect of the product layer on the kinetics of the CO2-lime reaction. AIChE J. 1983, 29, 79–86. [Google Scholar] [CrossRef]
- Gupta, H.; Fan, L.-S. Carbonation−Calcination Cycle Using High Reactivity Calcium Oxide for Carbon Dioxide Separation from Flue Gas. Ind. Eng. Chem. Res. 2002, 41, 4035–4042. [Google Scholar] [CrossRef]
- Fedunik-Hofman, L.; Bayon, A.; Donne, S.W. Comparative Kinetic Analysis of CaCO3/CaO Reaction System for Energy Storage and Carbon Capture. Appl. Sci. 2019, 9, 4601. [Google Scholar] [CrossRef]
- Brittain, R.D.; Hildenbrand, D.L. Catalytic decomposition of gaseous sulfur trioxide. J. Phys. Chem. 1983, 87, 3713–3717. [Google Scholar] [CrossRef]
- Karasawa, H.; Sasahira, A.; Hoshino, K. Thermal decomposition of SO3. Int. J. Nucl. Hydrogen Prod. Appl. 2006, 1, 134. [Google Scholar] [CrossRef]
- Ishikawa, H.; Ishii, E.; Uehara, I.; Nakane, M. Catalyzed thermal decompositon of H2SO4 and production of HBr by the reaction of SO2 with Br2 and H2O. Int. J. Hydrogen Energy 1982, 7, 237–246. [Google Scholar] [CrossRef]
- GESTIS-Stoffdatenbank. Available online: https://gestis.dguv.de/data?name=003720&lang=en%20%20%202012-09-03 (accessed on 19 March 2023).
- Ismael, S.; Deif, A.; Maraden, A.; Yehia, M.; Elbasuney, S. Ammonium perchlorate catalyzed with novel porous Mn-doped Co3O4 microspheres: Superior catalytic activity, advanced decomposition kinetics and mechanisms. J. Therm. Anal. Calorim. 2023, 148, 11811–11824. [Google Scholar] [CrossRef]
- Krug, R.R. Detection of the Compensation Effect(θ Rule). Ind. Eng. Chem. Fundam. 1980, 19, 50–59. [Google Scholar] [CrossRef]
- Mianowski, A.; Radko, T.; Bigda, R. Isokinetic and Compensation Temperature in the Analysis of Thermal Dissociation of the Solid Phase under Dynamic Conditions. Energies 2023, 16, 5692. [Google Scholar] [CrossRef]
- Griessen, R.; Boelsma, C.; Schreuders, H.; Broedersz, C.P.; Gremaud, R.; Dam, B. Single Quality Factor for Enthalpy-Entropy Compensation, Isoequilibrium and Isokinetic Relationships. Chemphyschem 2020, 21, 1632–1643. [Google Scholar] [CrossRef] [PubMed]
- Griessen, R.; Dam, B. Simple Accurate Verification of Enthalpy-Entropy Compensation and Isoequilibrium Relationship. Chemphyschem 2021, 22, 1774–1784. [Google Scholar] [CrossRef] [PubMed]
- Janković, B.; Manić, N.; Perović, I.; Vujković, M.; Zdolšek, N. Thermal decomposition kinetics of deep eutectic solvent (DES) based on choline chloride and magnesium chloride hexahydrate: New details on the reaction mechanism and enthalpy–entropy compensation (EEC). J. Mol. Liq. 2023, 374, 121274. [Google Scholar] [CrossRef]
- Schmitz, G.; Lente, G. Fundamental concepts in chemical kinetics. ChemTexts 2019, 6, 1. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Linert, W. Thermally induced reactions of solids: Isokinetic relationships of non-isothermal systems. Int. Rev. Phys. Chem. 1995, 14, 355–369. [Google Scholar] [CrossRef]
- Mianowski, A.; Radko, T.; Siudyga, T. Kinetic compensation effect of isoconversional methods. React. Kinet. Mech. Catal. 2021, 132, 37–58. [Google Scholar] [CrossRef]
- Langmuir, I. The Evaporation, Condensation and Reflection of Molecules and the Mechanism of Adsorption. Phys. Rev. B 1916, 8, 149–176. [Google Scholar] [CrossRef]
- Britton, H.T.S.; Gregg, S.J.; Winsor, G.W. The calcination of dolomite. Part I.—The kinetics of the thermal decomposition of calcite and of magnesite. Trans. Faraday Soc. 1952, 48, 63–69. [Google Scholar] [CrossRef]
- Šesták, J. Where did you come from and where are you heading to, thermal analysis of heating effects? J. Therm. Anal. Calorim. 2023, 148, 13141–13156. [Google Scholar] [CrossRef]
- Lyon, R.E. A Physical Basis for Kinetic Compensation. J. Phys. Chem. A 2023, 127, 2399–2406. [Google Scholar] [CrossRef] [PubMed]
- Šimon, P.; Dubaj, T.; Cibulková, Z. Frequent flaws encountered in the manuscripts of kinetic papers. J. Therm. Anal. Calorim. 2022, 147, 10083–10088. [Google Scholar] [CrossRef] [PubMed]
- Vyazovkin, S. Isoconversional Kinetics of Thermally Stimulated Processes; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Sestak, J. Thermal Analysis and Thermodynamic Properties of Solids; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Silva, V.H.; Aquilanti, V.; de Oliveira, H.C.; Mundim, K.C. Uniform description of non-Arrhenius temperature dependence of reaction rates, and a heuristic criterion for quantum tunneling vs classical non-extensive distribution. Chem. Phys. Lett. 2013, 590, 201–207. [Google Scholar] [CrossRef]
- Starikov, E. Valid entropy–enthalpy compensation: Fine mechanisms at microscopic level. Chem. Phys. Lett. 2013, 564, 88–92. [Google Scholar] [CrossRef]
- Chakraborty, H.; Tarafdar, P.K.; Bruno, M.J.; Sengupta, T.; Lentz, B.R. Activation Thermodynamics of Poly(Ethylene Glycol)-Mediated Model Membrane Fusion Support Mechanistic Models of Stalk and Pore Formation. Biophys. J. 2012, 102, 2751–2760. [Google Scholar] [CrossRef]
- Sronsri, C.; Noisong, P.; Danvirutai, C. Isoconversional kinetic, mechanism and thermodynamic studies of the thermal decomposition of NH4Co0.8Zn0.1Mn0.1PO4·H2O. J. Therm. Anal. Calorim. 2015, 120, 1689–1701. [Google Scholar] [CrossRef]
- Sronsri, C.; Danvirutai, C.; Noisong, P. Double function method for the confirmation of the reaction mechanism of LiCoPO4 nanoparticle formation, reliable activation energy, and related thermodynamic functions. React. Kinet. Catal. Lett. 2017, 121, 555–577. [Google Scholar] [CrossRef]
- Sronsri, C.; Boonchom, B. Thermal kinetic analysis of a complex process from a solid-state reaction by deconvolution procedure from a new calculation method and related thermodynamic functions of Mn0.90Co0.05Mg0.05HPO4·3H2O. Trans. Nonferrous Met. Soc. China 2018, 28, 1887–1902. [Google Scholar] [CrossRef]
| Reaction/Temperature Range P = 0.1 MPa | kJ∙mol−1 | kJ∙mol−1 | kJ∙mol−1 | in s−1 | [52] kJ∙mol−1 | [52] J∙mol−1∙K−1 | ||
|---|---|---|---|---|---|---|---|---|
| CaCO3(s) = CaO(s) + CO2(g) calcite, T = 298–1200 K | 174.92 [52] | 0.150 [52] | 185.55 | 0.132 | 191.0 [53] | 15.40 [53] | 178.3 | 158.9 |
| Fe2(SO4)3(s) = Fe2O3(s) + 3SO3(g) hematite, T = 298–1200 K | 566.41 [52] | 0.538 [52] | - | - | - | - | 571.4 | 550.2 |
| 582.39 [54] | 0.557 [54] | 209.73 | 0.048 | 218.4 | 25.84 | |||
| 823–923 K [56] | ||||||||
| 526.51 [55] | 0.501 [55] | 74.40 | 0.253 | 83.3 | 1.33 | |||
| 973–1123 K [55] | ||||||||
| Al2(SO4)3(s) = γ-Al2O3(s) + 3SO3(g) T = 900–1250 K | 610.90 [54] | 0.534 [54] | 258.92 | 0.105 | 267.8 | 19.06 | 596.6 | 583.3 |
| 923–1223 K [55] | ||||||||
| 2AgNO3(s) = 2Ag(s) + O2(g) + 2NO2(g) T = 298–600 K | 156.47 [52] | 0.241 [52] | 124.94 | 0.132 | 129.2 [57] | 15.20 [57] | 157.5 | 244.7 |
| 4NH4ClO4(s) = 4HCl(g) + 2N2(g) + 5O2(g) + 6H2O(g) T = 298–500 K | −159.98 [52] | 0.636 [52] | 96.83 | 0.048 | 100.0 [53] | 25.0 [53] | −159.3 | 638.4 |
| 2NH4ClO4(s) = Cl2(g) + N2(g) + 2O2(g) + 4H2O(g) T = 298–500 K | −188.78 [52] | 0.603 [52] | −187.9 | 606.3 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mianowski, A.; Radko, T.; Bigda, R. Elements of Transition-State Theory in Relation to the Thermal Dissociation of Selected Solid Compounds. Energies 2024, 17, 2669. https://doi.org/10.3390/en17112669
Mianowski A, Radko T, Bigda R. Elements of Transition-State Theory in Relation to the Thermal Dissociation of Selected Solid Compounds. Energies. 2024; 17(11):2669. https://doi.org/10.3390/en17112669
Chicago/Turabian StyleMianowski, Andrzej, Tomasz Radko, and Rafał Bigda. 2024. "Elements of Transition-State Theory in Relation to the Thermal Dissociation of Selected Solid Compounds" Energies 17, no. 11: 2669. https://doi.org/10.3390/en17112669
APA StyleMianowski, A., Radko, T., & Bigda, R. (2024). Elements of Transition-State Theory in Relation to the Thermal Dissociation of Selected Solid Compounds. Energies, 17(11), 2669. https://doi.org/10.3390/en17112669






