Abstract
In recent years, integration of solar photovoltaic (PV) systems into distribution networks has been increasing rapidly, as it has become the most promising renewable energy source (RES) in the transition of power generation from centralised to decentralised systems. With the power electronic (PE) interfaces that use high-frequency internal switching, all renewable energy sources are considered to be harmonic emitters, especially near switching frequencies, i.e., above 2 kHz. This paper evaluates the behaviour of high-frequency harmonics in the 2–20 kHz range due to the parallel operation of multiple solar PV inverters connected to a low-voltage (LV) network. The circulation current component that flows within the installation due to the low impedance paths at higher frequencies is analysed. Summation of high-frequency harmonic currents is observed with phase diversity analysis. The circulating current component can become 14 times higher than the grid current component at higher frequencies.
1. Introduction
Harmonic studies on voltage and current distortion have primarily been concentrated at frequencies below 2 kHz, with these frequencies referred to as low-frequency harmonics. An extensive amount of knowledge is presented in the literature in this regard. Waveform distortion due to high frequencies (above 2 kHz), also referred to as supraharmonic emissions, has only been considered in the recent past, as the existence of power electronic (PE) interfaces in every renewable energy source (RES) presents a source of high-frequency harmonics [1].
The connection of RES to the electricity network generally comprises a PE interface, which is considered to be a supraharmonic source, especially for switching frequencies, which often lie below 20 kHz. Presently, supraharmonic impact associated with integration of RES has become a major concern for network operators, consumers, and equipment manufacturers, as increasing RES has led to increasing power quality issues, including interference with communication and control systems, overheating of power equipment, increased losses in power lines, and resonance and voltage distortion [2]. Generally, the switching frequencies for smaller single-phase inverters often lie in the 15–20 kHz range, while switching frequencies for large three-phase inverters handling high power, e.g., with a nominal rating of 1 MW or more, are commonly below 5 kHz [3].
Even though the voltage and current waveform variations have been studied extensively, complete understanding of PV inverter switching frequency behaviour has not been achieved [4]. This behaviour is influenced by several external and internal factors, such as the inverter power output, voltage variation of the DC bus of the inverter, inverter topology, switching frequency, number of inverters in operation at a location, conductor capacitance, other loads connected to the system, and system impedance variation. The authors of [5] suggest that low-frequency RES models can be extended up to the 100th order (5 kHz for the 50 Hz system), where its accuracy over the 2 kHz frequency has to be verified with an understanding of high-frequency emission characteristics.
High-frequency measuring equipment along with the necessary current measuring devices, i.e., high-frequency current clamps and Rogowski coils, enable the investigation of harmonic distortion above 2 kHz [6]. The lack of a normative supraharmonic emission measurement method has become another challenge in characterising supraharmonic emissions. There are three methods specified by international regulations: IEC 61000-4-7 (informative) [7], IEC 61000-4-30 (informative) [8], and CISPR 16-1-1 [9]. All three measurement methods rely on discrete Fourier transformation (DFT) to characterise emissions. The two methods in IEC regulations are informative, while the only normative method covers laboratory emissions in the 9–150 kHz range. Each method has various advantages and disadvantages [10].
Low-pass filtering and damping circuits are included in the inverter to smooth the output current waveform of the inverter. For cost effectiveness, manufacturers try to minimise the size of external reactors and increase the size of the output capacitor, which impacts the current source behaviour of the inverter and creates the possibility of resonance with the network reactance [11]. This resonance can occur at higher frequencies depending upon the front-end filter design criterion. In [12,13], the resonance introduced due to the front-end filter of inverters is investigated, and a proposed control scheme-based solution to mitigate the resonance impact is presented.
Contribution and Paper Organization
This paper investigates the impact of high-frequency harmonics of a grid-tied rooftop solar PV system. The high-frequency emission bands have been identified based on the field measurements taken by varying the number of inverters in operation at a time. Two high-frequency emission bands are identified. Understanding the characteristics of harmonics in the range of 2–20 kHz in terms of the circulation–current component within inverters and the grid–current component is addressed. The understanding of PV inverters can be used to develop mathematical models, numerical simulations, and measurement-based models that are essential for future electricity networks.
The remainder of the paper is organised as follows. The measurement setup used to capture the time-domain current waveforms and the supraharmonic emission measurement method used to identify emissions associated with solar PV system are presented in Section 2. In Section 3, mathematical equations are derived for two current components, identified as the circulation current component and the grid current component, based on measurements that can be applied to emissions at any frequency of interest. Section 4 identifies the two high-frequency emission bands, i.e., broadband emissions in the 2–5 kHz range and narrowband emissions in the 15–17 kHz range. The derived mathematical expressions are applied to emissions in these two bands to identify the magnitude of circulation that occurs between the inverters. In Section 5, the dominant current components at two frequency bands are identified compared to the phase diversity characteristics of the current emissions. Section 6 details the conclusions of the study.
2. Measurement Framework
The study primarily investigates the emissions based on field measurements. Understanding of high-frequency emission characteristics where background emissions exist is pivotal to identifying emission bands with practical on-site operating scenarios.
The measurements were taken from a rooftop solar PV system that consists of six identical inverters each rated at 20 kW. Each inverter has been given an alphabetical identifier ranging from A through to F. The total power generated by all six inverters is fed to the utility network via two circuits. A Hioki MR8847A Memory HiCorder was used to record the individual inverter waveforms and aggregated currents of combined inverters. Hioki 9661 high-frequency current clamps were used to capture current waveforms. The data logger was configured to measure four current signals, i.e., the same phase of inverter A, B, and C, as well as half of the aggregation circuit. The measurement setup is illustrated in Figure 1.
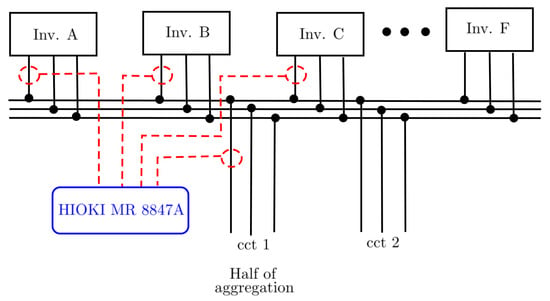
Figure 1.
Measurement setup of solar PV system.
The captured time-domain waveforms were then converted to the frequency-domain through the DFT using the MATLAB R2022b software package. As per the Nyquist criterion, the maximum frequency of the frequency-domain shall be half of the sampling frequency used to measure the time-domain waveform [14]. The sampling rate was set to 100 kHz; thus, harmonics in the range of 0–50 kHz can be identified using DFT.
This study utilises the supraharmonic measurement method detailed in Annex B (informative) of IEC 61000-4-7, which specifies the use of a frequency analysis technique with a 5 Hz frequency resolution with 200 ms of signal. The frequency spectrum is then grouped into 200 Hz bands, and an amplitude at the middle of each frequency band is derived using the root sum squared (RSS) method as given in (1), where and are the amplitude of the spectrum at frequency f and the RSS value of band b, respectively.
The method in IEC 61000-4-7 is provided for high-frequency emission measurements in the 2–9 kHz range. For continuity of analysis, the same method is extended to assess emissions above 9 kHz in this study.
Measurements were taken while varying the number of inverters in operation at a time. Maintaining an approximately equal power output by each inverter in each operating scenario has enabled consideration of the harmonic impact against the number of inverters in operation. The summary of measurements indicating which inverters are operating at any given time is provided in Table 1.

Table 1.
Summary of the studies.
The magnitude of high-frequency emissions may change with the power output of the PV inverter. This study aims to assess the emission characteristics against the number of inverters only. Thus, the power output of each inverter was maintained at approximately 16 kW or 80% of its rated value during all measurements taken for this study.
3. Parallel Inverter Operation
Generally, a solar PV inverter consists of an in-built LCL filter to suppress the harmonic content of the current flowing to the grid. This section analyses a grid-tied system of n parallel solar PV inverters to better understand the behaviour of inverter current components. A similar study for AC voltage sources connected to a load is presented in [15], while similar information for wind farm operation is presented in [16]. Mathematical equations are derived to allow for understanding of inverter current components. The analytical understanding of these emissions is important for characterising them with reasonable accuracy.
Suppose n inverters are connected to the grid as shown in Figure 2. All inverters have the same output impedance (Z). The inverter output currents before and after LCL filters are represented as and , respectively. The output voltages of the inverters are given by . The grid is represented by the equivalent Thevenin voltage with impedance and magnitude .
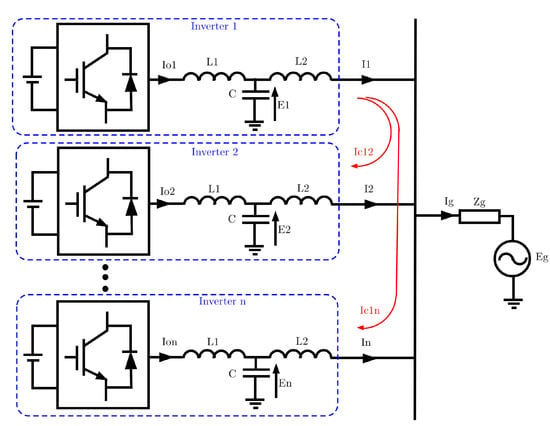
Figure 2.
Diagram of n inverters with LCL filters connected in parallel.
Each inverter current is divided into two components: the grid current component supplied to the grid and a circulating current component that is being circulated between the inverter units [17]. This is demonstrated in Figure 3, where is the inverter output current, is the circulating current from inverter 1 to inverter 2, is the grid current component from inverter 1, and is the total grid current formed by individual inverter grid current components. Each inverter current is given by (2) as follows:
where is the grid current component from unit i, and is the circulating current between units i and j. The resultant circulating current component of unit i can be represented by a single term ; hence, (2) can be rewritten as follows:
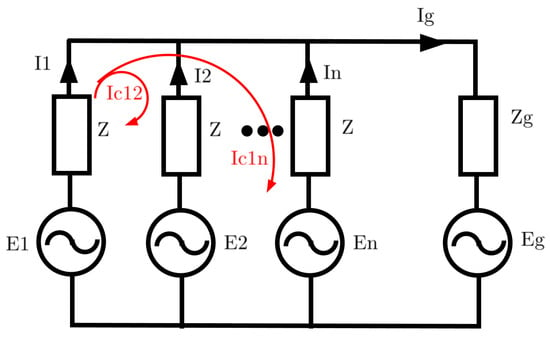
Figure 3.
Equivalent circuit of n inverters with LCL filters connected in parallel.
Similarly, the grid current () is the summation of grid current components of each inverter unit as given by (4):
Applying Kirchhoff’s voltage law to the circuit in Figure 3:
The inverter 1 output current () can then be obtained using the superposition theorem as shown in (6):
By evaluating (6), the inverter 1 current can be rewritten as follows:
From (7), two components of the inverter i current can be written as follows:
- 1.
- Grid current component ():
- 2.
- Circulating current component ():
From (9), it is evident that the circulating current component depends on the individual output voltages of parallel inverters. If all the inverters produce the same voltage, no circulating current component occurs, which is the ideal case. The circulating current component is proportional to the term , which is useful for understanding the high-frequency harmonic current behaviour. At higher frequencies, the grid impedance appears higher compared to the capacitive path of the LCL filter circuit. The circulating current thus becomes higher and tends to circulate between the inverter units rather flowing towards the grid.
The impact of is considered to be insignificant for high-frequency analysis [18]; thus, the term becomes negligible. As such, the ratio between the circulating current component and the grid current component can be derived using (3) and (4) as follows:
Assuming and , (10) can be rewritten as follows:
From (11), current measurements from inverter terminals and the aggregation cable can be used to calculate the ratio between the resultant circulating current component and the grid current component for an inverter. The known ratio and the total grid current formed by multiple inverters can be used to calculate the circulation current component.
4. Data Analysis
Time-domain current waveforms were measured at the locations shown in Figure 1 with an analysis interval of 200 ms and with a sampling rate of 100 kHz. This measurement arrangement allows the frequency spectrum up to 50 kHz to be obtained. The frequency spectrum, with a spectral component resolution of 5 Hz for each of the measured current waveforms for each study detailed in Table 1, is depicted in Figure 4.
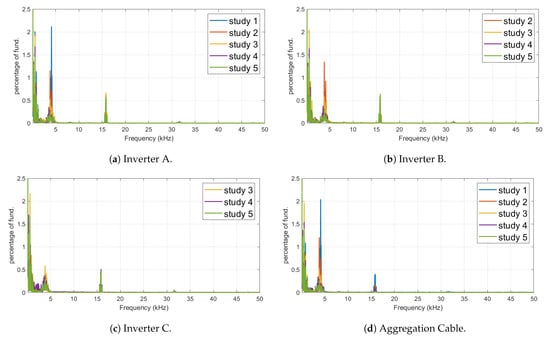
Figure 4.
Current harmonic spectrum with 5 Hz spectral resolution up to 50 kHz.
It can be seen that individual inverters show similar frequency spectrum characteristics, which can be categorised in to three frequency bands based on the magnitudes of the frequency spectrum, i.e., low-frequency harmonics (0–2 kHz range), broadband spectrum in the 2–5 kHz range, and narrowband spectrum at approximately 16 kHz. The spectral components present near 16 kHz are due to the switching frequency of the inverter, which is 15.8 kHz.
With respect to Figure 2, measurements were taken to record inverter output terminal current, i.e., , , , and summated grid current . Harmonic spectra of currents , , , and correspond to Figure 4a–d, respectively.
4.1. Broadband Harmonics between 2–5 kHz
Irrespective of the number of inverters in operation, each energised inverter and the aggregation cable show similar characteristics for a particular study. Figure 5 shows the frequency spectrum variation within the 2–5 kHz range for three of the inverters plus the aggregation cable. Frequency spectra with 200 Hz bands were obtained according to (1). For study 2 (plotted in red), inverter A and B and the aggregation cable have approximately equal harmonic current emission characteristics. Similarly, for study 3 (plotted in orange), all four measurements show a similar pattern of magnitude characteristics.
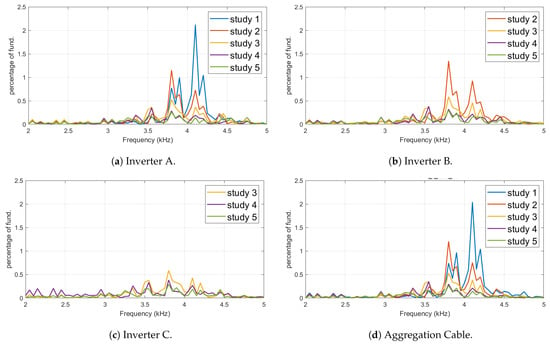
Figure 5.
Current harmonic spectrum between 2–5 kHz range according to the IEC 61000-4-7 measurement method.
During study 1, since no other inverters are switched on, all of the harmonics generated by inverter A propagate to the supply grid. As expected, both inverter A and the aggregation cable have similar characteristics for single inverter operation, where the maximum individual harmonic component occurs at 4.1 kHz. However, when the second inverter is switched on, the maximum individual harmonic component occurs at 3.8 kHz, and emission magnitudes tend to decrease significantly. This phenomenon is identified as the resonance introduced by front-end filters, where increasing the number of inverters in operation affects the impedance characteristics seen by an individual inverter.
The ratio between the circulating current component and grid current component for significant harmonics in the 2–5 kHz range is calculated according to (11) and listed in Table 2. The grid current component of parallel connected inverters, which can be measured in the aggregation cable, is approximately equal to that which can be summated in individual inverters in the 2–5 kHz frequency range. The circulation current component is one-tenth of the grid current component at 4.2 kHz under study 5, which is the highest value obtained for the ratio. At all the other instances, the ratio is less than that. It is evident that the grid current component of the inverter current outweighs the circulating current component for emissions up to 5 kHz.

Table 2.
The ratio for harmonics under 5 kHz.
4.2. Narrowband Harmonics at Switching Frequency (15.8 kHz)
Figure 6 shows the current frequency spectrum variation within the 15–17 kHz range for three inverters plus the aggregation cable. Frequency spectra with 200 Hz bands were obtained according to (1), as specified in IEC 61000-4-7. It is evident that the frequency spectrum close to the switching frequency remains approximately constant in magnitude irrespective of the number of inverters in operation. Similar to harmonics in the 2–5 kHz range, in the single inverter operation, all the harmonic currents propagate to the grid, as there are no circulation current paths.
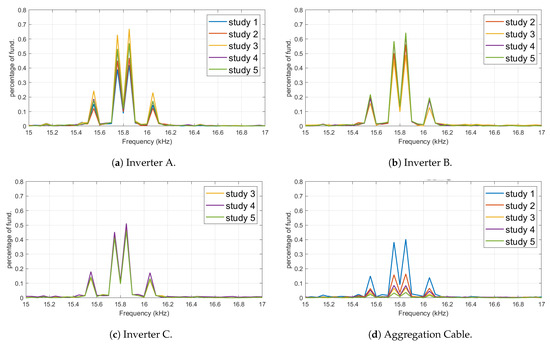
Figure 6.
Current harmonic spectrum in the 15–17 kHz range according to the IEC 61000-4-7 measurement method.
Similar to the case for lower frequency emissions, the ratio between the circulating current component and the grid current component for significant harmonics in the 15–17 kHz range has been calculated according to (11) and is listed in Table 3. With an increasing number of inverters in operation, the aggregation cable current magnitude decreases. It is evident that the circulating current component increases as the number of inverters in operation increases, as it creates circulation paths for harmonic currents to flow.

Table 3.
The ratio for harmonics at 15–17 kHz.
For the single inverter operation, values indicate that the grid current component dominates, as no circulation paths exist. With the next inverter switched on, harmonic currents tend to circulate within inverters, resulting in reduced harmonic currents flowing into the supply grid. The circulation current component can go as high as 14 times the grid current component, as seen at 15.75 kHz in study 5, which is the highest value obtained for the ratio. The circulating current component is dominant in 15–17 kHz range.
4.3. Phase Diversity
The high-frequency emission characteristics can be understood with phase diversity analysis of the measured current waveforms. Individual harmonic orders were plotted in the phasor plane to identify the characteristics of circulating and grid current components.
The percentage of fundamental current components at 3.8 kHz, 4.1 kHz, and 15.75 kHz are shown in Figure 7, Figure 8 and Figure 9 for 1-inverter, 2-inverter, and 3-inverter operation, respectively. For 1-inverter operation, all high-frequency harmonics seen at inverter 1 terminals are seen in the grid current. Individual harmonics in the two measurements are in phase, as depicted in Figure 7, irrespective of the frequency of interest. For multiple inverter operation, it is observed that harmonics at 3.8 kHz and 4.1 kHz are in phase, as depicted in Figure 8a,b and Figure 9a,b. However, harmonics at 15.75 kHz are dispersed in multiple quadrants of the phasor plane, as depicted in Figure 8c and Figure 9.
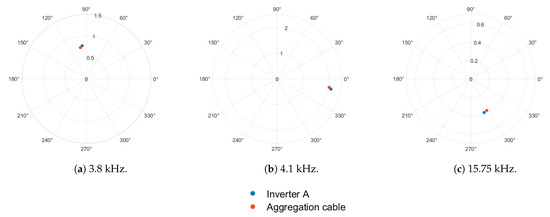
Figure 7.
Phasor plot of harmonics during single-inverter operation.
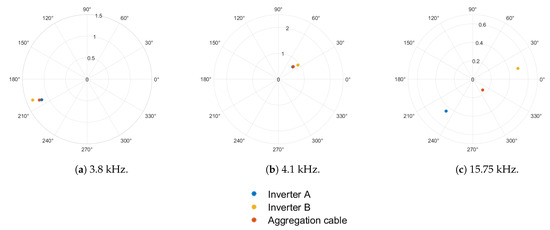
Figure 8.
Phasor plot of harmonics during two-inverter operation.
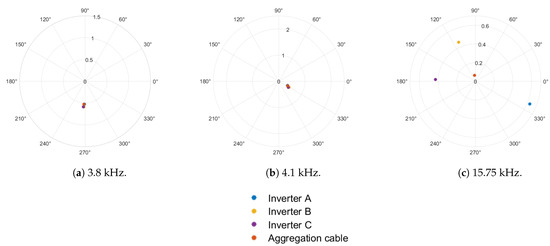
Figure 9.
Phasor plot of harmonics during three-inverter operation.
5. Discussion
This study only focused on field measurements of a rooftop solar PV system in order identify high-frequency emissions and their characteristics in terms of phase diverseness.
5.1. Analysis of Measured Results
As shown in Section 4, for the analysed system, the grid current component is the dominant component of the total harmonic current when compared to the circulation current component, up to 5 kHz. The majority of the current output of each individual inverter is fed to the grid rather than circulating within the installation in this frequency range. According to Figure 5, which plots the percentage harmonic components with respect to the fundamental component, it is clearly visible that the aggregation cable harmonics show the similarity of each individual inverter’s harmonic content.
Based on the measurements analysed in this study, when the frequency increases, the circulation current component becomes more dominant compared to the grid current component, as seen in Figure 6. Thus, arithmetic addition of harmonics is not valid for this installation close to the switching frequency range.
In terms of summation of individual harmonic emissions, vector addition is always true. The phase diversity analysis illustrates the placement of individual harmonics, which helps to understand the harmonic summation calculations. Especially for high-frequency emissions, concerns exist whether these emissions propagate to the electricity supply network or circulate within the installation. This study proves that not all the high-frequency emissions stay within the installation. The resonance emissions (emissions in 2–5 kHz range) follow arithmetic addition, as identical inverters have done in phase emissions; however, the magnitude of the resonance emissions is inversely proportional to the number of inverters in operation. Switching frequency emissions does not follow arithmetic addition, as cancellation happens due to the dispersed characteristics.
5.2. Future Work
High-frequency emissions of grid-tied RES systems occur due to both primary and secondary emissions. The work reported in this paper does not address the contribution of other equipment connected to the same LV network. It is understood that the high-frequency harmonics in the 2–5 kHz range can occur due to the resonance effects caused by the LCL filter inside the PV inverter and neighbouring equipment with PE interfaces. Identifying interaction characteristics of different harmonic sources in the high-frequency range is another concern to be assessed. Resonance phenomena are unavoidable for a system consisting of inductors and capacitors, where investigation into possible control-based solutions should be studied further.
Incorporating modelling results or numerical simulations may be required to validate mathematical expressions derived for the two phenomena identified by the measurements. The complete understanding of these emissions is required prior to introducing potential harmonic mitigating strategies. Investigation of different RESs, such as wind turbines and energy storage systems, should be considered for a better understanding of voltage regulation and electromagnetic interference.
6. Conclusions
This paper uses field measurements to characterise harmonic behaviour of a grid-tied rooftop solar PV system consisting of six identical three-phase inverters, each rated at 20 kW. Analysis of measurement data indicates that there are three harmonic current emission bands present within the frequency spectrum up to 20 kHz as follows:
- Low-frequency band in the 0–2 kHz range;
- Broadband high-frequency band in the 2–5 kHz range due to the resonance introduced by the front-end filter of the inverter;
- Narrowband high-frequency band near 16 kHz due to the switching frequency of the inverters.
The emissions in the broadband high-frequency range have been investigated in order to characterise how emissions from individual inverters may combine and to evaluate propagation behaviour. General mathematical expressions for harmonic currents have been derived for a system consisting of multiple inverters connected in parallel. It has been identified that the inverter current comprises two components called the circulation current component and the grid current component. It was observed that the grid current component is dominant up to approximately 5 kHz, whereas the circulating current component dominates at switching frequencies. Since arithmetic addition of emissions appears to be valid up to resonance frequency, it is concluded that low-frequency harmonic models can be extended up to the resonance frequency.
When the number of inverters increases, the magnitude of the harmonic current emission of each inverter in the 2–5 kHz frequency range tends to decrease. However, the total harmonic emission in this range propagates to the aggregation cable. The magnitude of the switching frequency harmonic currents of each inverter do not vary significantly as the number of inverters in operation increases. However, it is noted that these harmonic currents largely circulate between inverters. Phase diversity analysis proves that harmonic currents of individual inverters and the aggregation cable have converged at phase angle properties up to 5 kHz. At switching frequencies, the inverter harmonic currents are dispersed in multiple quadrants.
This work was mainly aimed at enhancing understanding of high-frequency harmonic propagation into a supply network from rooftop solar PV systems with multiple inverters. This analysis can be used to develop high-frequency models for solar PV inverters. To fully understand the harmonic content in the 2–5 kHz range, further mathematical modelling of PV inverters is required.
Author Contributions
Conceptualization, K.P.; methodology, K.P., S.E. and J.D.; original draft preparation, K.P.; review and editing, S.E., J.D. and D.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received external funding from the Australian government via the Global Innovations Linkage (GIL) program, grant number: GIL73697.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| AC | Alternating Current |
| CISPR | Comité International Spécial des Perturbations Radioélectriques (English: International Special Committee on Radio Interference) |
| DC | Direct Current |
| DFT | Discrete Fourier Transform |
| GIL | Global Innovations Linkage |
| IEC | International Electrotechnical Commission |
| LCL | Inductor–Capacitor–Inductor |
| LV | Low-Voltage |
| PE | Power Electronic |
| PV | Photovoltaic |
| RES | Renewable Energy Source |
| RSS | Root Sum Squared |
References
- Alfalahi, S.T.Y.; Alkahtani, A.A.; Al-Shetwi, A.Q.; Al-Ogaili, A.S.; Abbood, A.A.; Mansor, M.B.; Fazea, Y. Supraharmonics in Power Grid: Identification, Standards, and Measurement Techniques. IEEE Access 2021, 9, 103677–103690. [Google Scholar] [CrossRef]
- Darmawardana, D.; Perera, S.; Robinson, D.; Ciufo, P.; Meyer, J.; Klatt, M.; Jayatunga, U. Investigation of high frequency emissions (supraharmonics) from small, grid-tied, photovoltaic inverters of different topologies. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–6. [Google Scholar]
- Moreno-Munoz, A.; Gil-de-Castro, A.; Romero-Cavadal, E.; Rönnberg, S.; Bollen, M. Supraharmonics (2 to 150 kHz) and multi-level converters. In Proceedings of the 2015 IEEE 5th International Conference on Power Engineering, Energy and Electrical Drives (POWERENG), Riga, Latvia, 11–13 May 2015; pp. 37–41. [Google Scholar]
- Bollen, M.; Meyer, J.; Amaris, H.; Blanco, A.M.; Castro, A.G.D.; Desmet, J.; Klatt, M.; Kocewiak, Ł.; Rönnberg, S.; Yang, K. Future work on harmonics—Some expert opinions Part I—Wind and solar power. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 904–908. [Google Scholar]
- Val Escudero, M.; Lietz, G.; Emin, Z.; Jensen, C.; Kocewiak, Ł. CIGRE TB 766: JWG C4/B4.38 Network Modelling for Harmonic Studies; CIGRE: Paris, France, 2019; ISBN 978-2-85873-468-9. [Google Scholar]
- Meyer, J.; Bollen, M.; Amaris, H.; Blanco, A.M.; Castro, A.G.D.; Desmet, J.; Klatt, M.; Kocewiak, Ł.; Rönnberg, S.; Yang, K. Future work on harmonics—Some expert opinions Part II—Supraharmonics, standards and measurements. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 909–913. [Google Scholar]
- IEC Standard 61000-4-7; General Guide on Harmonics and Interharmonics Measurements, for Power Supply Systems and Equipment Connected Thereto. IEC: Geneva, Switzerland, 2002.
- IEC Standard 61000-4-30; Testing and Measurement Techniques-Power Quality Measurement Methods. IEC: Geneva, Switzerland, 2015.
- CISPR 16-1-1; Specification for Radio Disturbance and Immunity Measuring Apparatus and Methods—Part 1-1: Radio Disturbance and Immunity Measuring Apparatus—Measuring Apparatus. IEC: Geneva, Switzerland, 2019.
- Gallarreta, A.; Fernández, I.; Ritzmann, D.; Lodetti, S.; Khokhlov, V.; Wright, P.; Meyer, J.; de la Vega, D. A Light Measurement Method for 9–150 kHz Disturbances in Power Grids Comparable to CISPR Quasi-Peak. IEEE Trans. Instrum. Meas. 2022, 71, 9005410. [Google Scholar] [CrossRef]
- Enslin, J.H.; Hulshorst, W.T.; Atmadji, A.M.; Heskes, P.J.; Kotsopoulos, A.; Cobben, J.F.G.; Van der Sluijs, P. Harmonic interaction between large numbers of photovoltaic inverters and the distribution network. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003. [Google Scholar] [CrossRef]
- Lu, M.; Wang, X.; Loh, P.C.; Blaabjerg, F. Resonance Interaction of Multiparallel Grid-Connected Inverters with LCL Filter. IEEE Trans. Power Electron. 2017, 32, 894–899. [Google Scholar] [CrossRef]
- Saleem, M.; Ko, B.-S.; Kim, S.-H.; Kim, S.; Chowdhry, B.S.; Kim, R.-Y. Active Disturbance Rejection Control Scheme for Reducing Mutual Current and Harmonics in Multi-Parallel Grid-Connected Inverters. Energies 2019, 12, 4363. [Google Scholar] [CrossRef]
- Mendes, T.M.; Duque, C.A.; da Silva, L.R.M.; Ferreira, D.D.; Meyer, J.; Ribeiro, P.F. Comparative analysis of the measurement methods for the supraharmonic range. Int. J. Electr. Power Energy Syst. 2020, 118, 105801. [Google Scholar] [CrossRef]
- Shamseh, M.B.; Kawamura, A.; Yoshino, T. A novel autonomous control scheme for parallel, LCL-based UPS systems. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–8. [Google Scholar]
- Schwanz, D.; Bollen, M. Harmonics and Wind Power, Report 2018:469. Available online: https://energiforsk.se/en/programmes/wind-power-industry-network/reports/harmonics-and-wind-power/ (accessed on 14 June 2023).
- Augustine, S.; Mishra, M.K.; Lakshminarasamma, N. Circulating current minimization and current sharing control of parallel boost converters based on Droop Index. In Proceedings of the CIRED 2021—The 26th International Conference and Exhibition on Electricity Distribution, Online, 20–23 September 2021; pp. 454–460. [Google Scholar]
- Wang, Y.; Luo, D.; Xiao, X. Evaluation of supraharmonic emission levels of multiple grid-connected VSCs. IET Gener. Transm. Distrib. 2019, 13, 5597–5604. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).