A Model-Free Deep Reinforcement Learning-Based Approach for Assessment of Real-Time PV Hosting Capacity
Abstract
1. Introduction
- Development of a DNN-based surrogate model to perform voltage calculations using smart meter data, integrating the model-free aspects in the proposed methodology.
- Evaluation of the real-time HC using the SAC algorithm. The proposed approach only requires real-time customer voltages and solar irradiation data to provide a fast and accurate estimate of real-time HC at each customer connection point.
- A comparative analysis is presented between the model-based and model-free HC assessments, highlighting advantages and disadvantages of both approaches.
2. Problem Formulation
2.1. System Model and Constraints
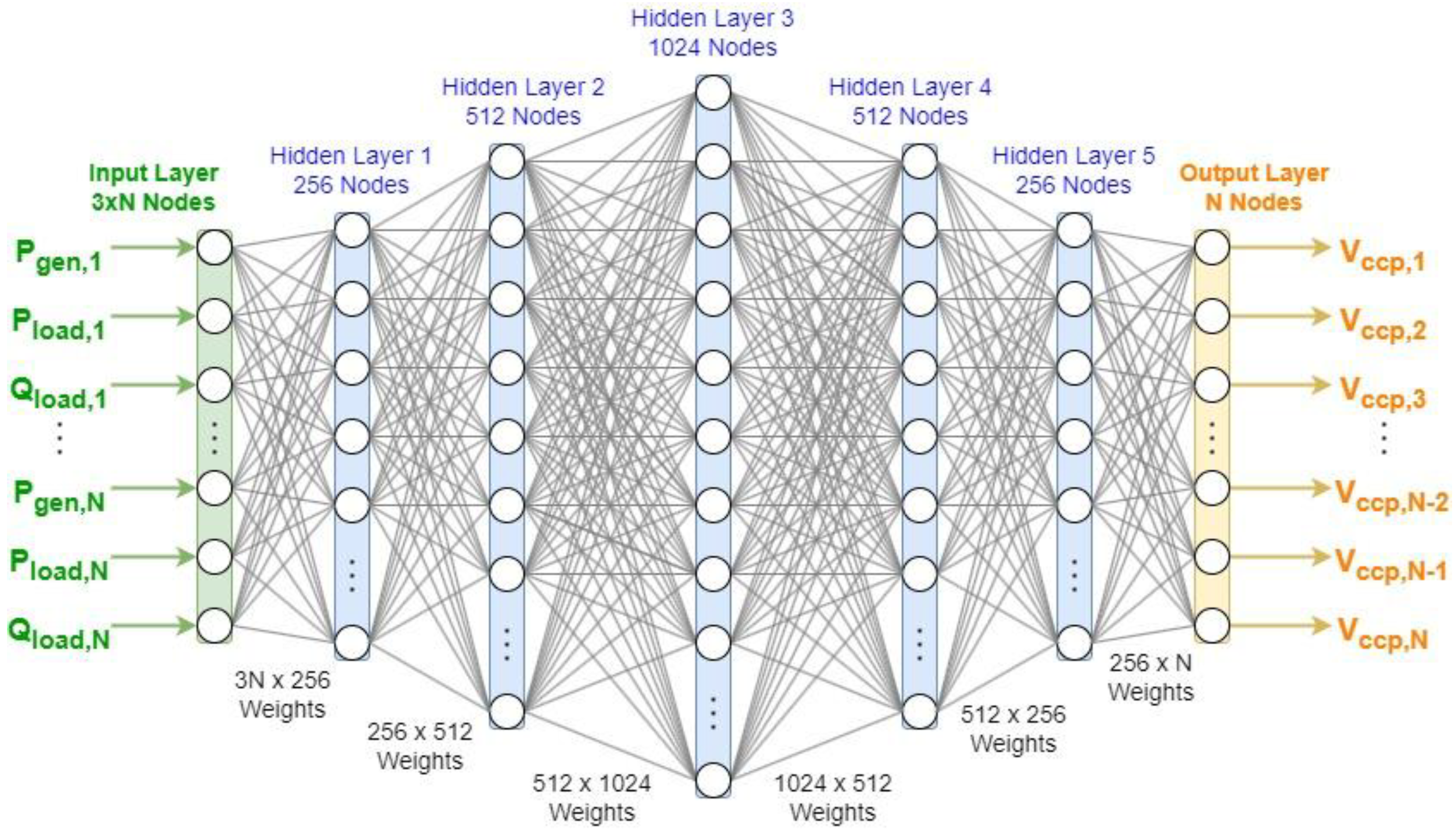
2.2. Surrogate Model of the Network
3. Hosting Capacity Assessment Framework
3.1. Formulation of Markov Decision Process
- Environment: the environment that the agent interacts with is the actual LV distribution network.
- Agent: the agent is the controller that estimates the rated capacity of the customer PV inverters.
- State: the state of the environment at time consists of two observations , where is the global horizontal irradiation at customer .
- Action: the action that an agent takes is the estimated real-time HC of each customer , denoted by the rated capacity . To reduce the search space and prevent the estimates of the SAC algorithm reaching unrealistically high values during periods of low solar irradiation, action is clipped between 0 and , , where is the upper limit for PV capacity that is unlikely to be achieved during periods of high solar irradiation.
- Reward Function: the immediate reward that an agent receives for taking an action at state while satisfying voltage constraints is given in (6).
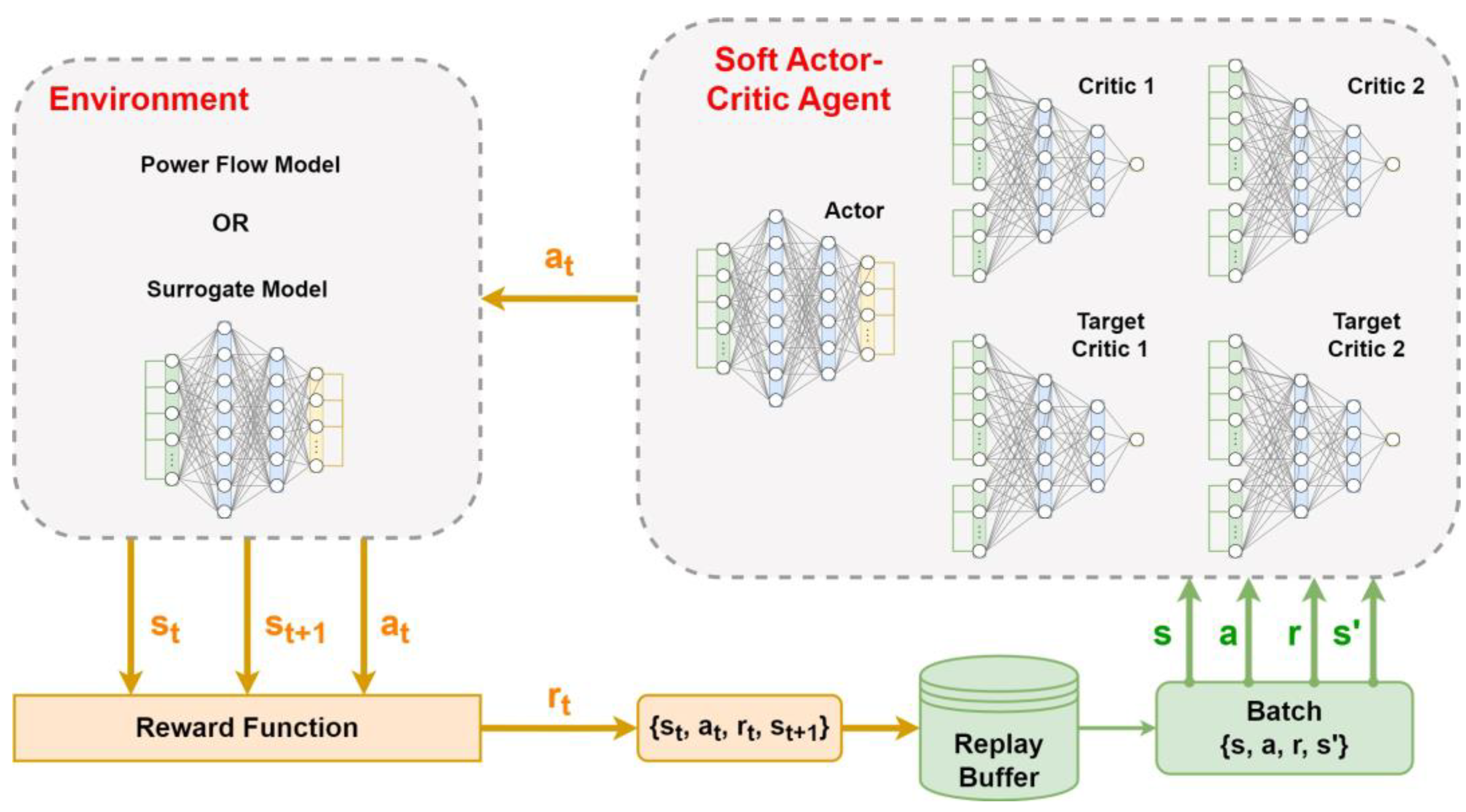
3.2. Soft Actor–Critic Algorithm
| Algorithm 1: Soft Actor–Critic | |
| 1: | Initialize critics , and actor with random parameters , , and respectively. |
| 2: | Initialize target critics and with main network parameters and |
| 3: | Initialize the empty replay buffer , |
| 4: | for to do: |
| 5: | Observe state of the environment and take action |
| 6: | Execute action . Then observe next state and attain reward |
| 7: | Register experience tuple in the replay buffer |
| 8: | if |
| 9: | Randomly sample a batch of transitions from |
| 10: | Sample next action from the actor network |
| 11: | Compute the target for the critic network updates |
| 12: | Update critics and by gradient decent using: for |
| 13: | Update the policy by gradient accent using: |
| 14: | Update target networks with : for |
| 15: | end if |
| 16: | end for |
4. Numerical Study
4.1. Experimental Setup
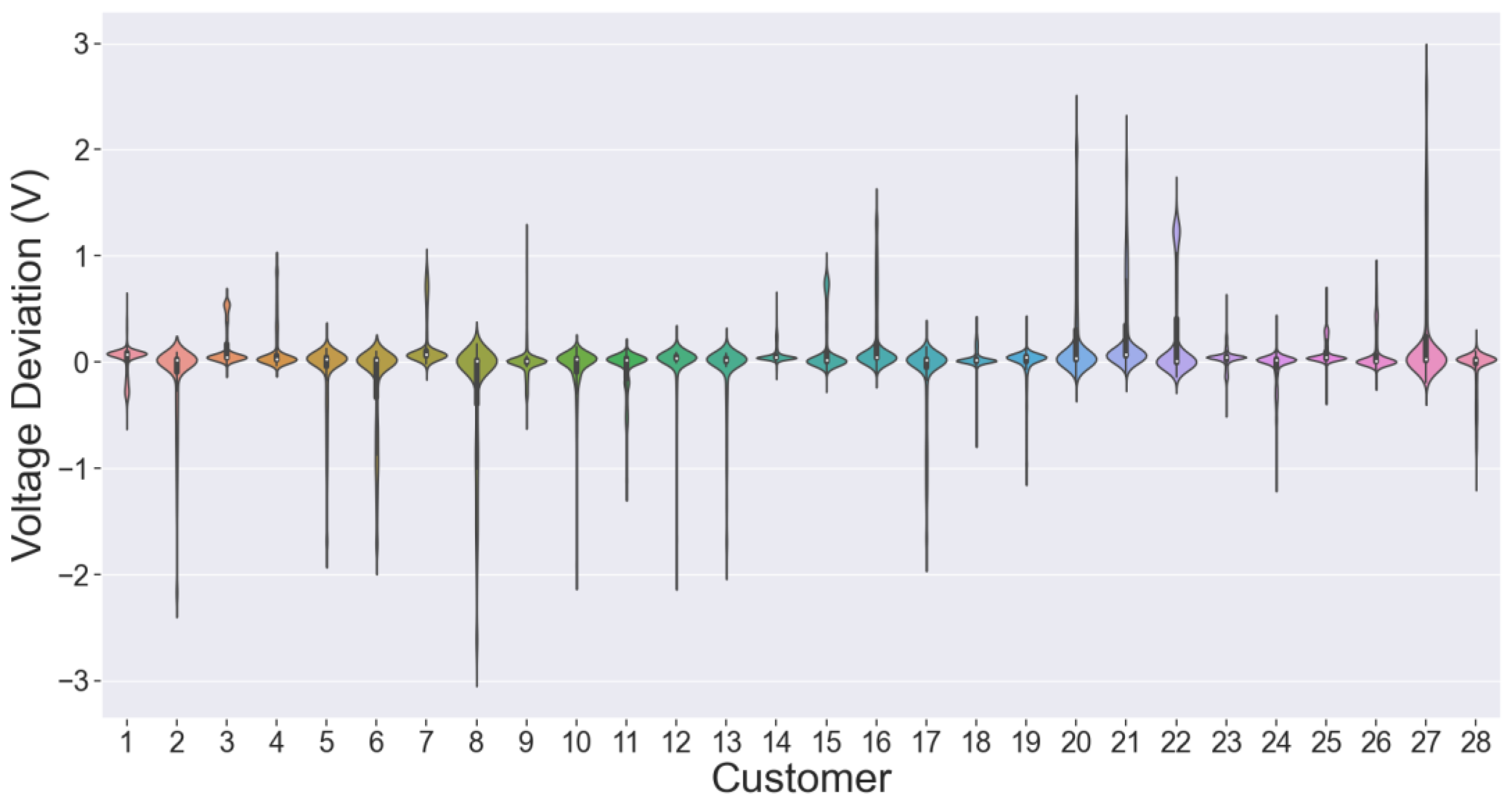
4.2. Surrogate Model Performance Evaluation
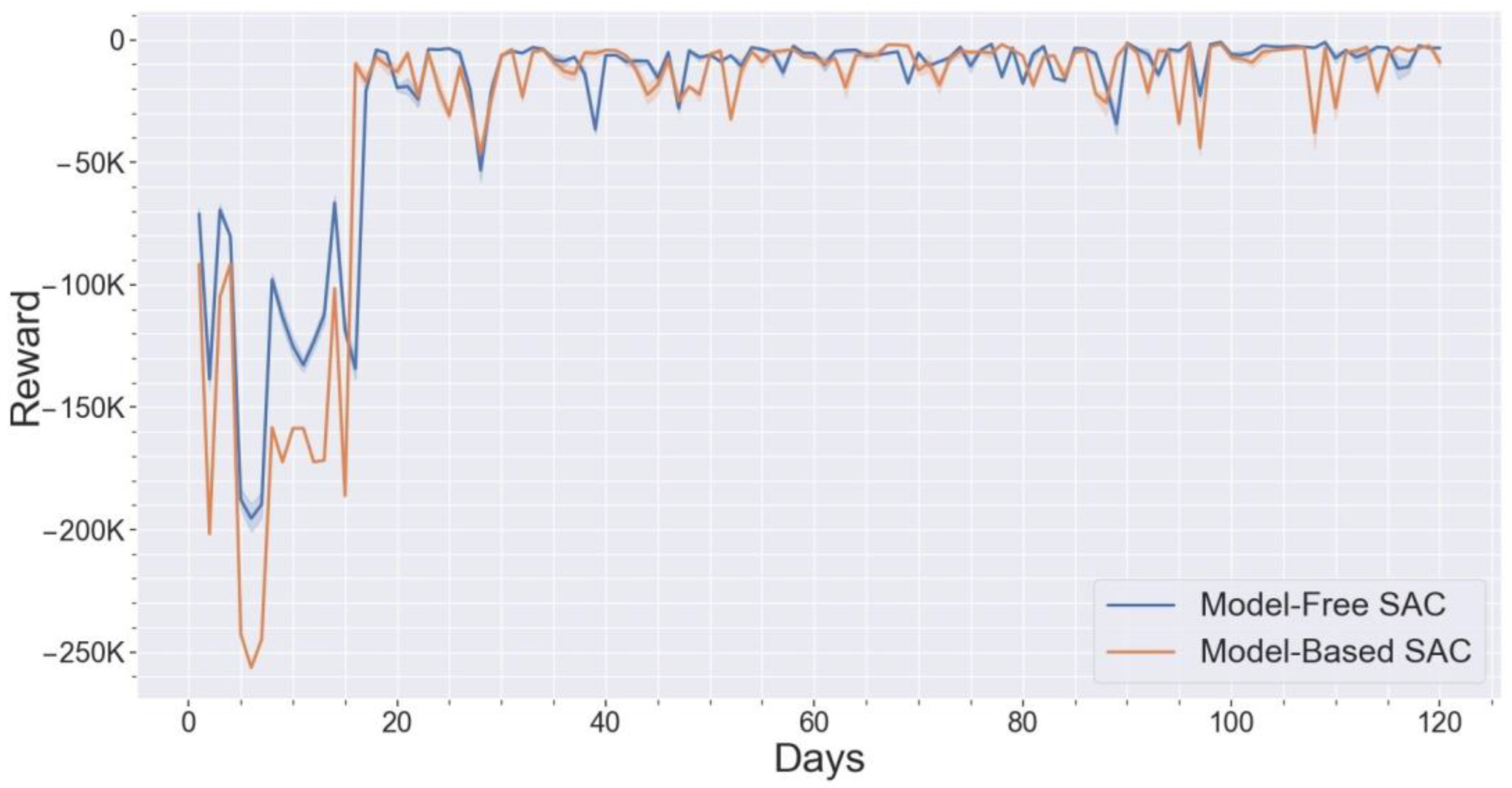
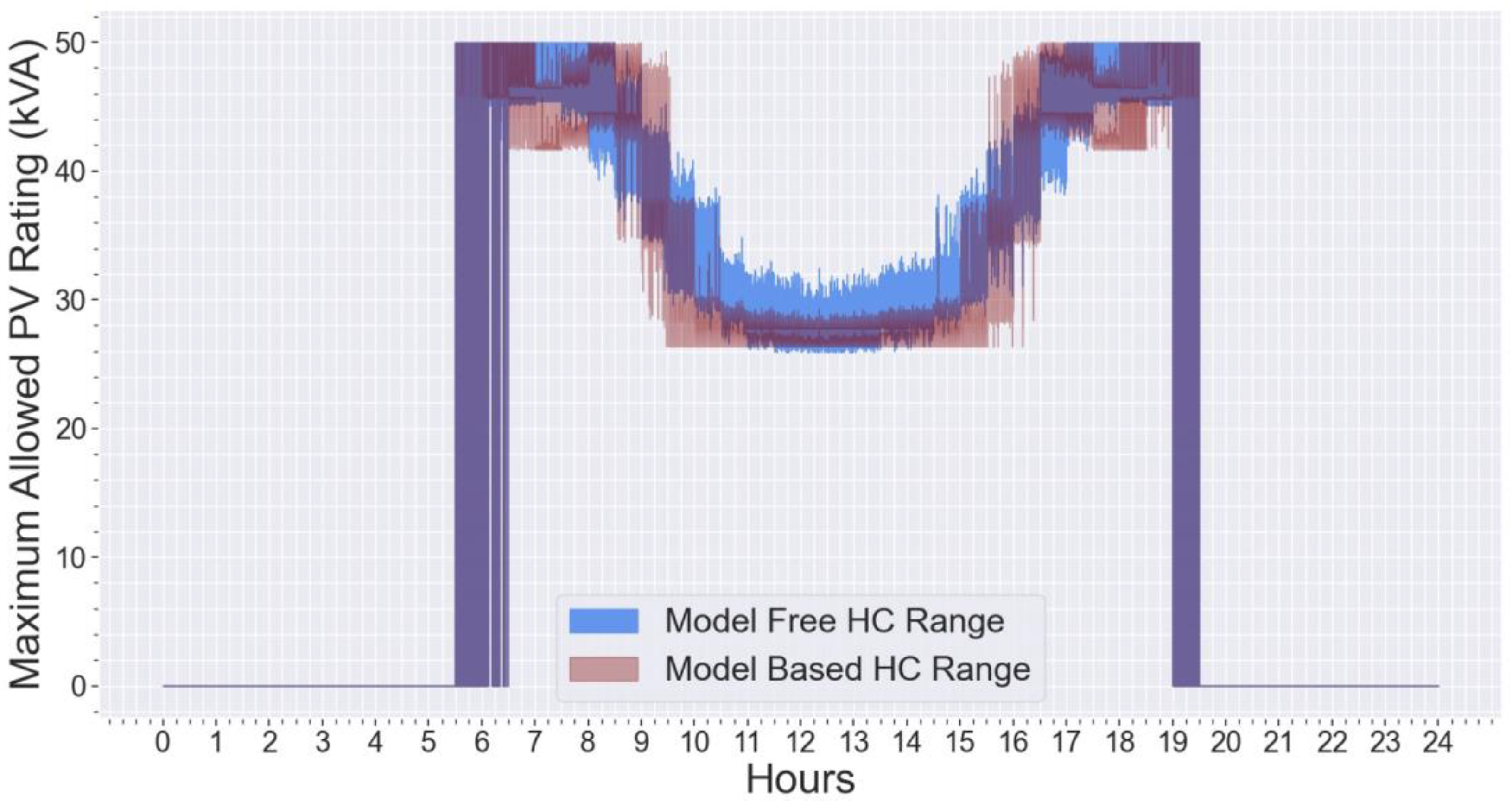
4.3. Hosting Capacity Assessment Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rajabi, A.; Elphick, S.; David, J.; Pors, A.; Robinson, D. Innovative approaches for assessing and enhancing the hosting capacity of PV-rich distribution networks: An Australian perspective. Renew. Sustain. Energy Rev. 2022, 161, 112365. [Google Scholar] [CrossRef]
- Mulenga, E.; Bollen, M.H.J.; Etherden, N. A review of hosting capacity quantification methods for photovoltaics in low-voltage distribution grids. Int. J. Electr. Power Energy Syst. 2020, 115, 105445. [Google Scholar] [CrossRef]
- Ebe, F.; Idlbi, B.; Morris, J.; Heilscher, G.; Meier, F. Evaluation of PV hosting capacities of distribution grids with utilisation of solar roof potential analyses. CIRED Open Access Proc. J. 2017, 2017, 2265–2269. [Google Scholar] [CrossRef]
- Kabir, M.N.; Mishra, Y.; Bansal, R.C. Probabilistic load flow for distribution systems with uncertain PV generation. Appl. Energy 2016, 163, 343–351. [Google Scholar] [CrossRef]
- Deboever, J.; Grijalva, S.; Reno, M.J.; Broderick, R.J. Fast Quasi-Static Time-Series (QSTS) for yearlong PV impact studies using vector quantization. Sol. Energy 2018, 159, 538–547. [Google Scholar] [CrossRef]
- Torquato, R.; Salles, D.; Pereira, C.O.; Meira, P.C.M.; Freitas, W. A Comprehensive Assessment of PV Hosting Capacity on Low-Voltage Distribution Systems. IEEE Trans. Power Deliv. 2018, 33, 1002–1012. [Google Scholar] [CrossRef]
- Bassi, V.; Ochoa, L.F.; Alpcan, T.; Leckie, C. Electrical Model-Free Voltage Calculations Using Neural Networks and Smart Meter Data. IEEE Trans. Smart Grid 2022, 14, 3271–3282. [Google Scholar] [CrossRef]
- Wu, J.T.; Yuan, J.; Weng, Y.; Ayyanar, R. Spatial-Temporal Deep Learning for Hosting Capacity Analysis in Distribution Grids. IEEE Trans. Smart Grid 2022, 14, 354–364. [Google Scholar] [CrossRef]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the 31st International Conference on International Conference on Machine Learning, Beijing, China, 21–26 June 2014; Volume 1, pp. 605–619. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft Actor-Critic Algorithms and Applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. arXiv 2018, arXiv:1801.01290. [Google Scholar]
- Chen, X.; Qu, G.; Tang, Y.; Low, S.; Li, N. Reinforcement Learning for Selective Key Applications in Power Systems: Recent Advances and Future Challenges. IEEE Trans. Smart Grid 2022, 13, 2935–2958. [Google Scholar] [CrossRef]
- Cao, D.; Zhao, J.; Hu, W.; Ding, F.; Yu, N.; Huang, Q.; Chen, Z. Model-free voltage control of active distribution system with PVs using surrogate model-based deep reinforcement learning. Appl. Energy 2022, 306, 117982. [Google Scholar] [CrossRef]
- Kou, P.; Liang, D.; Wang, C.; Wu, Z.; Gao, L. Safe deep reinforcement learning-based constrained optimal control scheme for active distribution networks. Appl. Energy 2020, 264, 114772. [Google Scholar] [CrossRef]
- AS/NZS 4777.2:2020; Grid Connection of Energy Systems via Inverters, Part 2: Inverter Requirements. Australian/New Zealand Standards: Sydney, Australia, 2020.
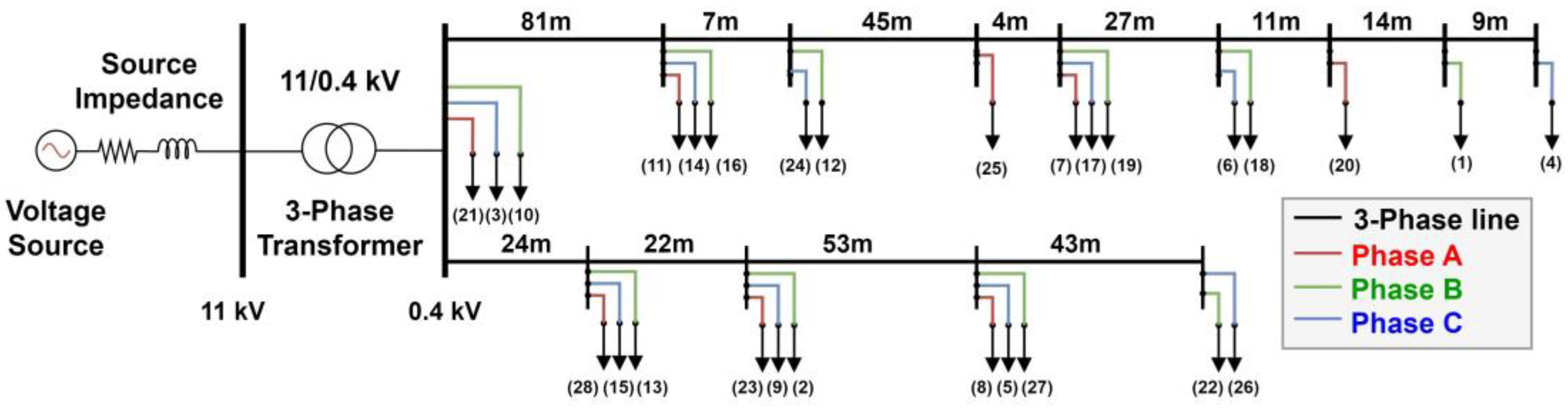
| R1 Ohm/km | X1 Ohm/km | R0 Ohm/km | X0 Ohm/km | |
|---|---|---|---|---|
| Main Feeder | 0.298557 | 0.259633 | 1.132508 | 0.945961 |
| Service Feeder | 1.480003 | 0.088 | - | - |
| Network Constraints | ||||
| Nominal voltage = 230 V | Maximum voltage limit = 258 V | Minimum voltage limit = 218 V | Transformer rating = 1 MVA | |
| Data Set | Days | Time Step Resolution | Time Steps | Simulation |
|---|---|---|---|---|
| 1 | 120 | 30 min | 5760 | Training of the surrogate model and the SAC agents |
| 2 | 120 | 30 min | 5760 | Surrogate model evaluation |
| 3 | 1 | 5 s | 17,280 | HC assessment |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suchithra, J.; Robinson, D.A.; Rajabi, A. A Model-Free Deep Reinforcement Learning-Based Approach for Assessment of Real-Time PV Hosting Capacity. Energies 2024, 17, 2075. https://doi.org/10.3390/en17092075
Suchithra J, Robinson DA, Rajabi A. A Model-Free Deep Reinforcement Learning-Based Approach for Assessment of Real-Time PV Hosting Capacity. Energies. 2024; 17(9):2075. https://doi.org/10.3390/en17092075
Chicago/Turabian StyleSuchithra, Jude, Duane A. Robinson, and Amin Rajabi. 2024. "A Model-Free Deep Reinforcement Learning-Based Approach for Assessment of Real-Time PV Hosting Capacity" Energies 17, no. 9: 2075. https://doi.org/10.3390/en17092075
APA StyleSuchithra, J., Robinson, D. A., & Rajabi, A. (2024). A Model-Free Deep Reinforcement Learning-Based Approach for Assessment of Real-Time PV Hosting Capacity. Energies, 17(9), 2075. https://doi.org/10.3390/en17092075







