Optimizing Insulated-Gate Bipolar Transistors’ Lifetime Estimation: A Critical Evaluation of Lifetime Model Adjustments Based on Power Cycling Tests
Abstract
1. Introduction
2. Power Cycling Test Methods
- Direct Current (DC) Cycling: The majority of power cycling assessments have utilized the direct current (DC) cycling method, in which a stable DC current source is applied to the device under test (DUT) as a load pulse [28]. In this approach, the primary cause of temperature increase in the switching device is conduction loss. Since the device remains continuously active, there are no switching losses. Benefits of the DC testing setup include its relative simplicity and the ability to effortlessly conduct “real-time” measurements of electrical and thermal parameters without interrupting the power cycling process. However, this method does not accurately simulate real-world electrical stimulation of devices, as there is no switching or high voltage involved [13].
- Pulse-Width Modulation (PWM) Cycling: The PWM cycling testing technique more closely replicates the actual operating conditions that devices face in practical applications. During PWM cycling, the switching device’s temperature rises as a result of both conduction and switching losses. This assessment demonstrates the real-time measurement of junction temperature during operation, specifically under power cycling conditions produced by PWM modulation [29].
- Temperature Fluctuations (Passive Thermal Cycles): During temperature fluctuations, the switching apparatus’s heat primarily rises due to ambient air, with no electrical energy usage contributing to losses in IGBT components. The duration of temperature fluctuation cycles is extended compared to power cycling, but they offer a similar range of temperature shifts.
- 4.
- Constant pulse duration (ton and toff): Throughout the test, the initial operating factors, such as load current, gate voltage, and load pulse duration, remain unchanged. This approach is the most rigorous, as it does not account for any deterioration, resulting in the shortest lifetime.
- 5.
- Constant thermal fluctuation (ΔTc): The duration of the load pulse, ton, and the cooling period, toff, were regulated by a thermocouple placed in a hole within the heat sink, situated beneath the chip’s center. Choosing suitable temperature control boundaries for the thermocouple ensured uniform starting conditions for temperature fluctuation and load pulse length across all tests. This approach helps mitigate the effects of changes in coolant temperature or pressure, which was essential during the early stages of power cycling when multiple test benches shared a single cooling system. Additionally, this method counteracts any degradation in the thermal connection between the module and the heat sink, leading to an increased number of cycles before failure. Contemporary testing systems now feature separate cooling mechanisms, rendering this technique outdated.
- 6.
- Steady power loss (Ploss): By controlling the gate voltage, a consistent level of power loss can be sustained during the on-state. Without proper control, an elevated junction temperature leads to increased losses due to the positive temperature coefficient of the on-state voltage. As the junction temperature rises from accumulated thermal damage during power cycling evaluations, the subsequent increase in power losses further expedites the degradation through a self-reinforcing cycle. By adjusting the gate voltage, this impact can be counterbalanced, producing stable power loss pulses with unvarying amplitude throughout the examination. This approach extends the lifespan of the tested parameters by over double in comparison to the first strategy.
- 7.
- Constant thermal fluctuation (ΔTj): In the fourth approach, the thermal variation ΔTj and the average temperature Tjm remain unchanged during the entire experiment. This can be accomplished by controlling the current or gate voltage or by modifying the pulse duration (ton) and pulse pause (toff). The control algorithm’s quality also influences the number of cycles until failure. In this particular experiment, a threefold enhancement in lifetime was successfully attained.
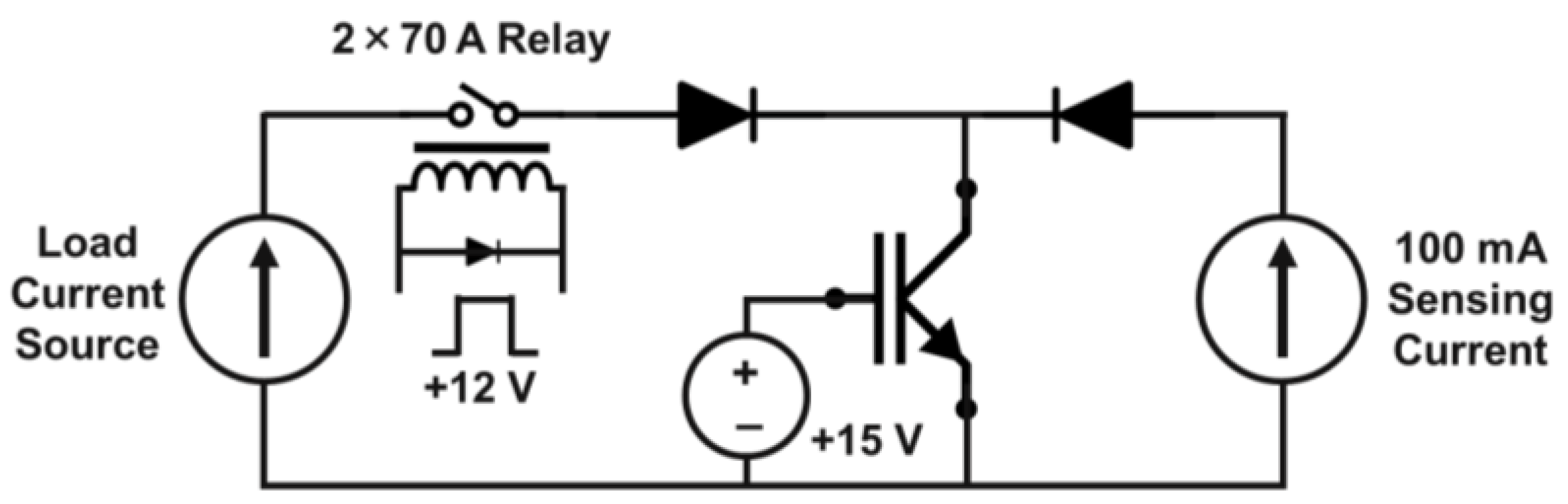
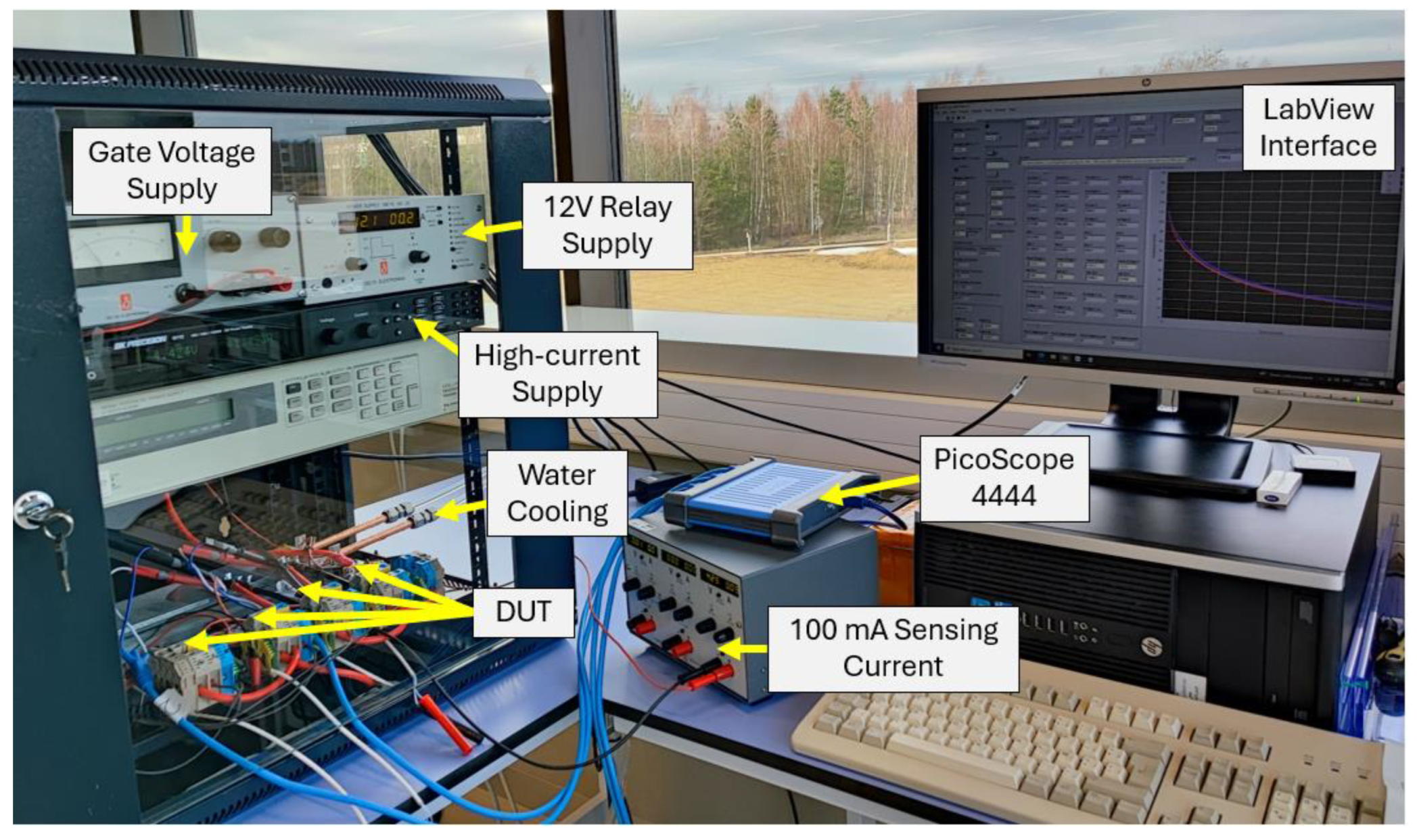
3. Power Cycling Test Setup
- 8.
- Current: The IGBT undergoes constant thermal fluctuations at elevated currents. Typically, the current is adjusted to match the device’s specified capacity [12]. To accelerate testing, currents higher than the rated levels are occasionally used [48,49]. Nonetheless, employing values beyond the recommended range is discouraged, as accelerated conditions can lead to entirely distinct failure modes.
- 9.
- Temperature: Operating temperature is a crucial factor in determining the duration of power cycling tests. Achieving substantial temperature fluctuations is essential for accelerating device degradation and failure while staying within the device’s specifications. Greater temperature swings have a more pronounced impact than the highest temperature [50]. The highest temperature (Tjmax) typically ranges from 100 to 150 °C [13]. The testing process employs an adjustable water-cooling mechanism for heat dissipation. Utilizing a water-cooling system allows the system’s temperature to be set lower than the surrounding environment. However, in humid conditions, condensation may form on the heatsink plate due to the cooler temperature of the heatsink lowering the air temperature nearby, consequently reducing its moisture-carrying capacity. When the air becomes oversaturated with moisture, further cooling may lead to condensation on the heatsink plate’s surface. Condensation on the heatsink plate can pose several problems, such as the potential for short circuits or damage to electronic components. To avoid these issues, the temperature of the water-cooling system should not drop below 15 °C.
- 10.
- Cycling time: The temperature fluctuation at the junction is determined by testing a combination of the heating power, heating duration, and the thermal resistance of the device [51]. Various studies have demonstrated that distinct dominant failure mechanisms are activated within the structure depending on the length of the heating period [52,53]. From a traditional perspective, shorter cycle tests primarily affect the lifetime of bond wires, whereas longer cycles predominantly lead to failures in the solder layers [54]. The boundary between short and long cycles remains somewhat ambiguous. Some sources classify short cycles as those with heating durations under 20 s, while others consider any test with a cycle time of less than 1 min to be short. In real applications, short cycle tests typically last only a few seconds, while long cycle tests extend beyond one minute. To achieve the cooling system’s reference temperature at the end of each power cycle, the power-OFF interval (toff) is twice the length of the power-ON period (ton) [55]. Consequently, initial adjustments for power cycle tests involve setting Tjmin and Tjmax by modifying Iload, ton, toff, and the cooling to suitable levels [56]. During the test, Tjmin, Tjmax, and the resulting VCE are not further regulated, causing any increase in VCE to shift the junction temperatures. Nevertheless, VCE variability is advantageous as it mirrors actual/practical applications.
- 11.
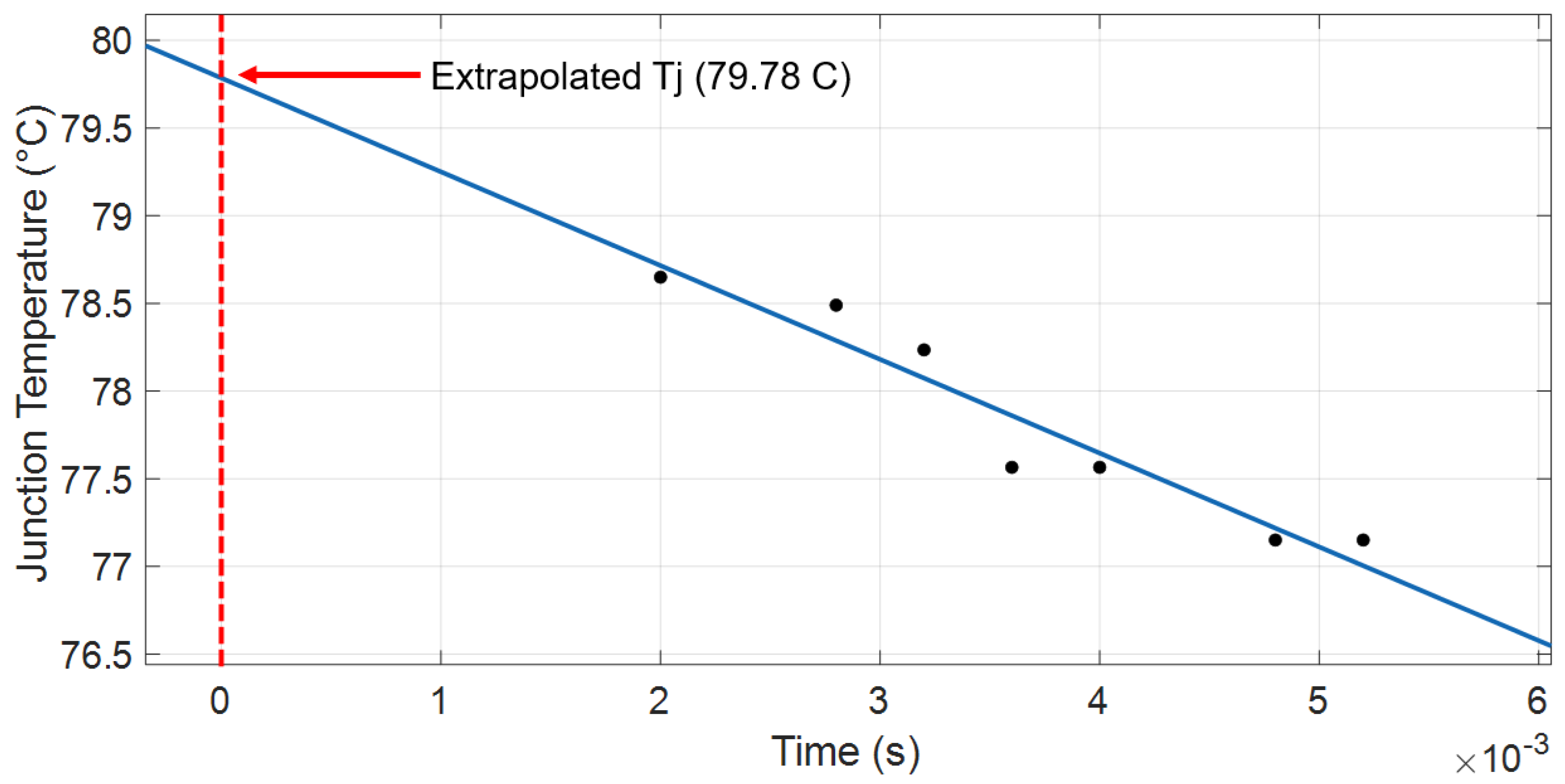
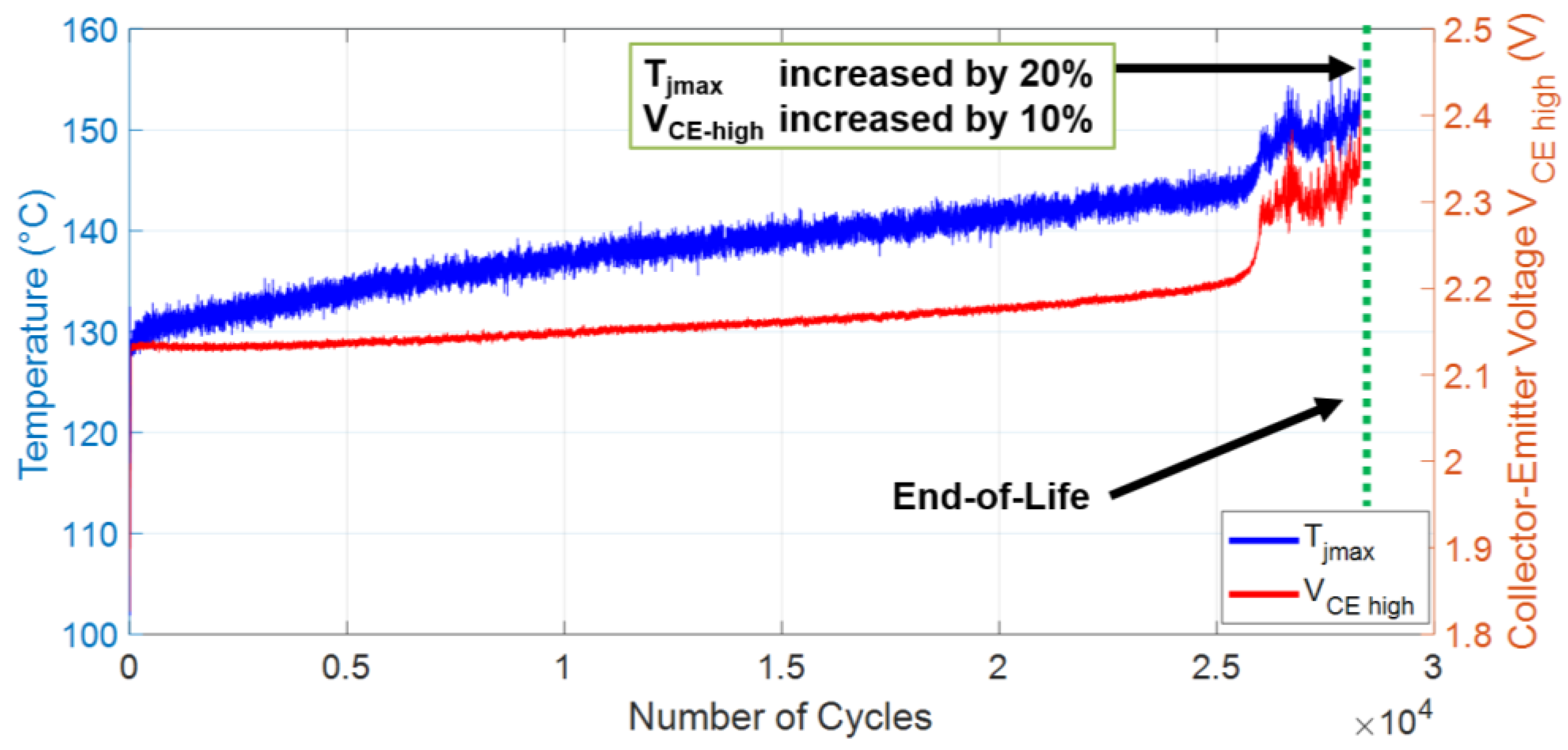
- End-of-Life (EOL) benchmarks: In the majority of testing configurations, temperature and electrical data are observed throughout each cycle. If these values experience a change exceeding a predetermined threshold (for example, 20%), the EOL criteria are considered to have been met [57]. Studies have shown that a 20% increase in Rth signifies solder-fatigue failure [58]. Thermal resistance is characterized as the temperature difference between two adjacent isothermal surfaces divided by the total heat flow between them. In a power semiconductor, the junction Tj and case TC serve as the two isothermal surfaces, with Ploss representing the total heat flow between them (voltage multiplied by total current = load current + sensing current). As such, the thermal resistance can be mathematically represented as follows [28]:
4. IGBT’s Lifetime Models
- β1 = −3.483.
- β2 = 1917.
- β3 = −0.438.
- β4 = −0.717.
- β5 = −0.751.
- β6 = −0.564.
5. Results and Discussion
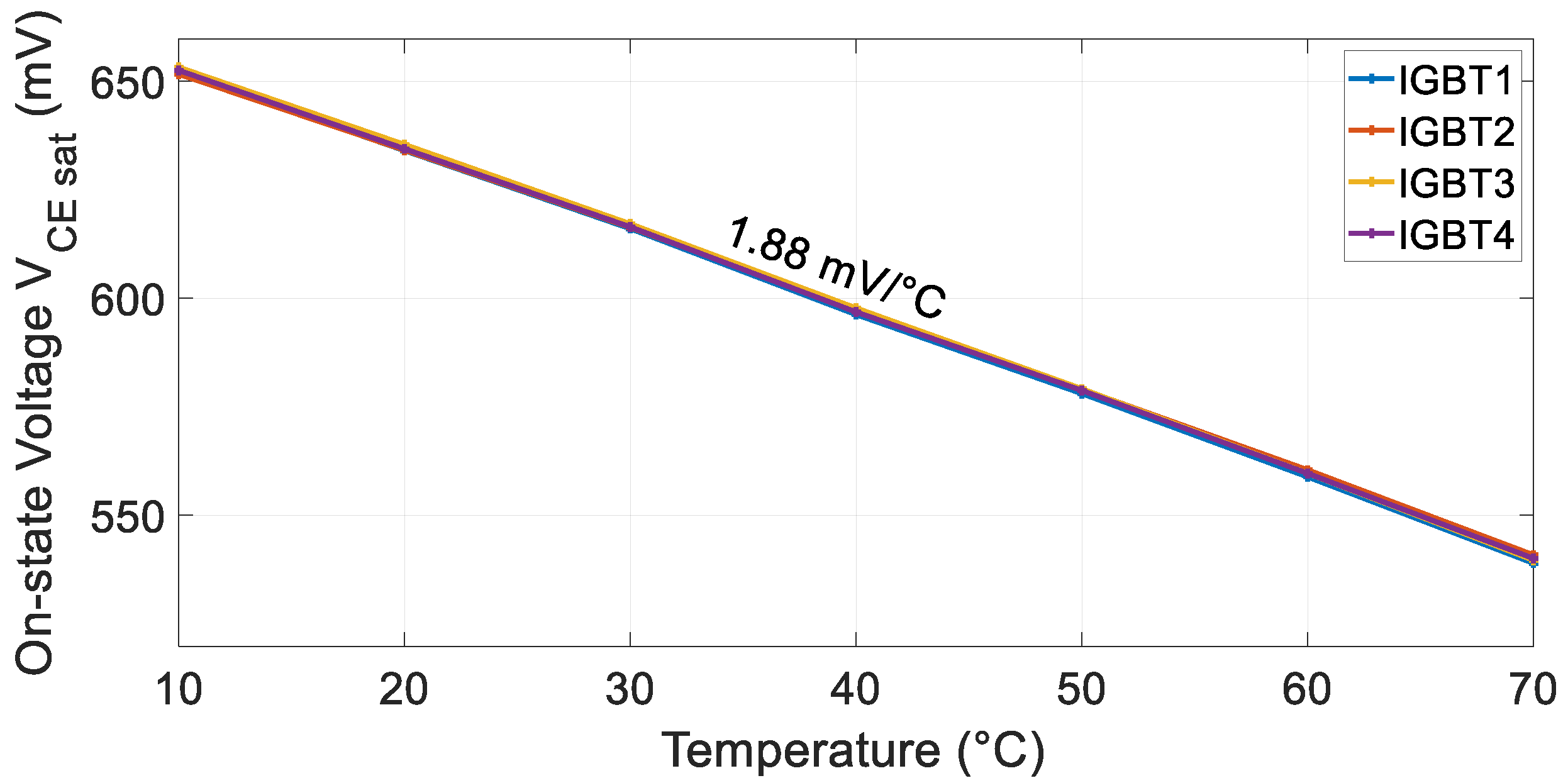
5.1. Power Cycling Results
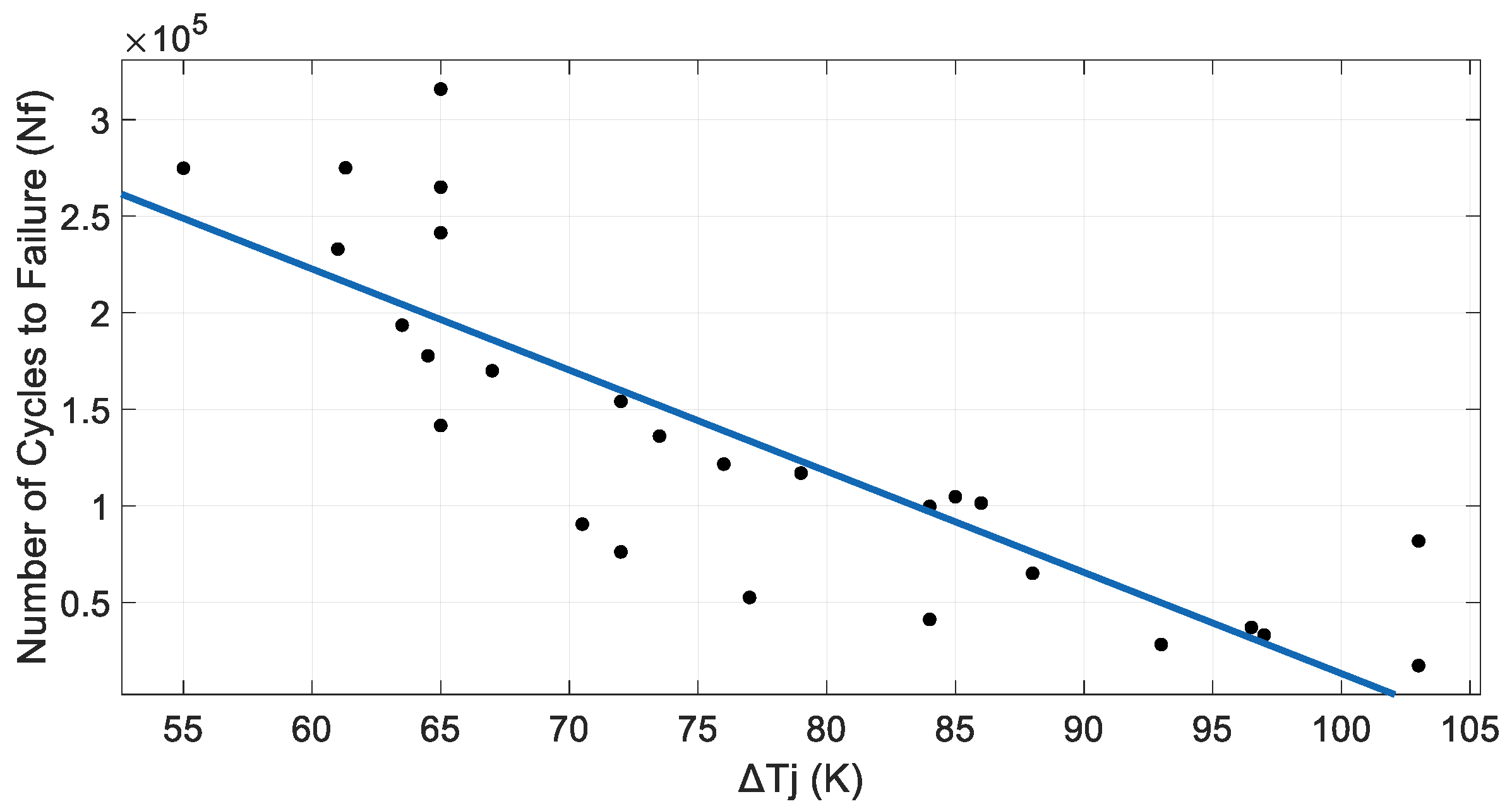
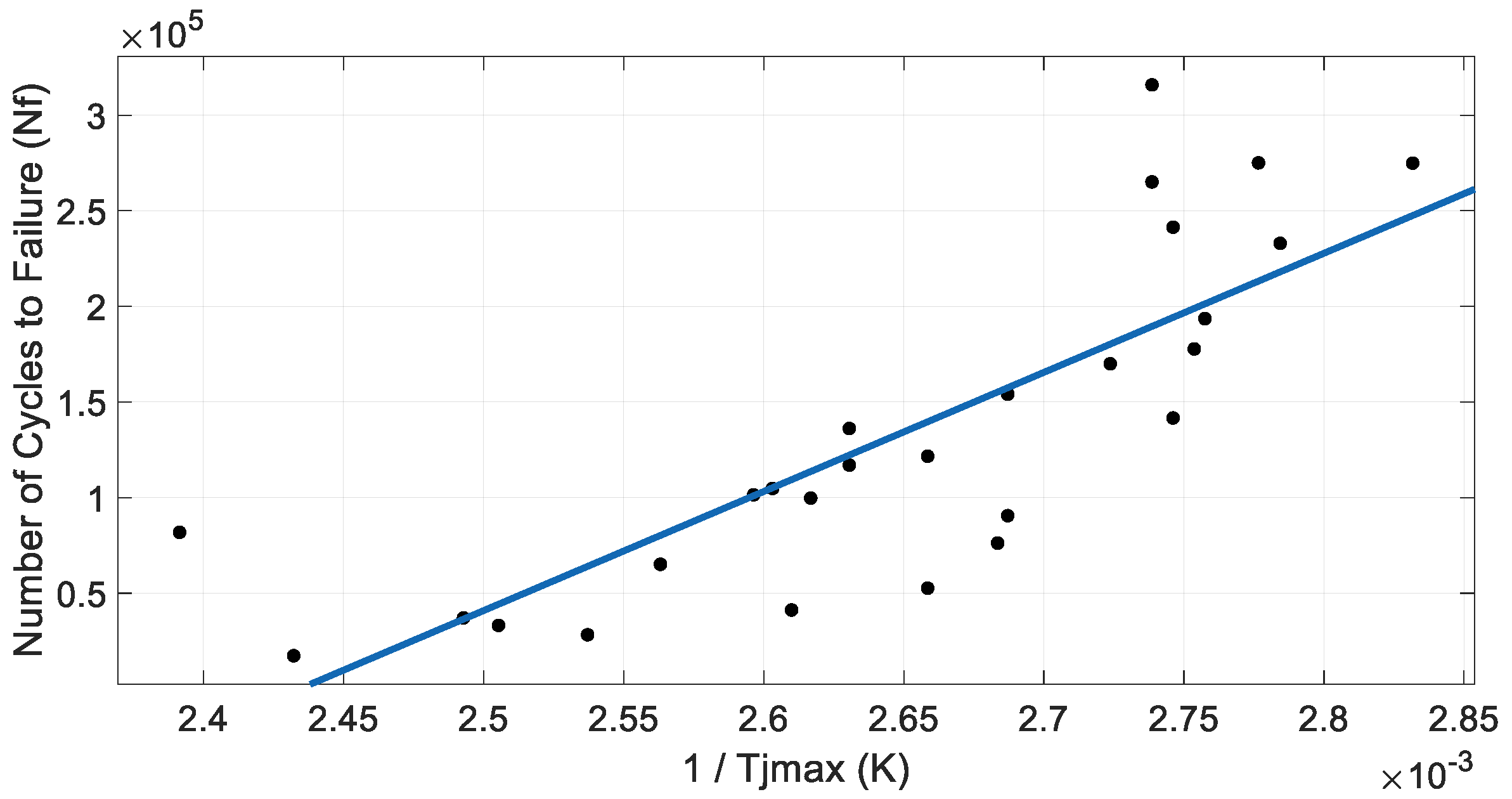
5.2. IGBT’s Modified Lifetime Models
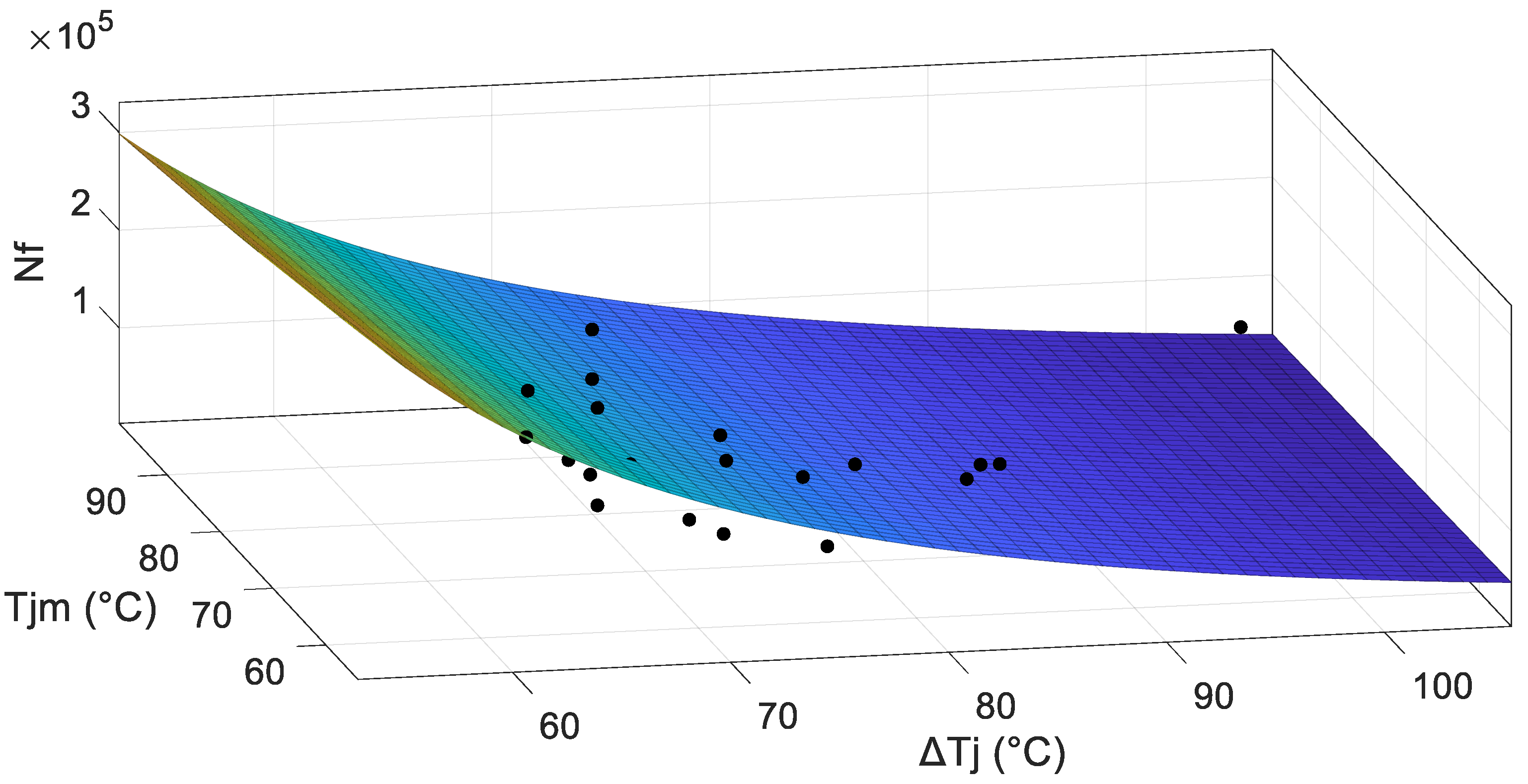
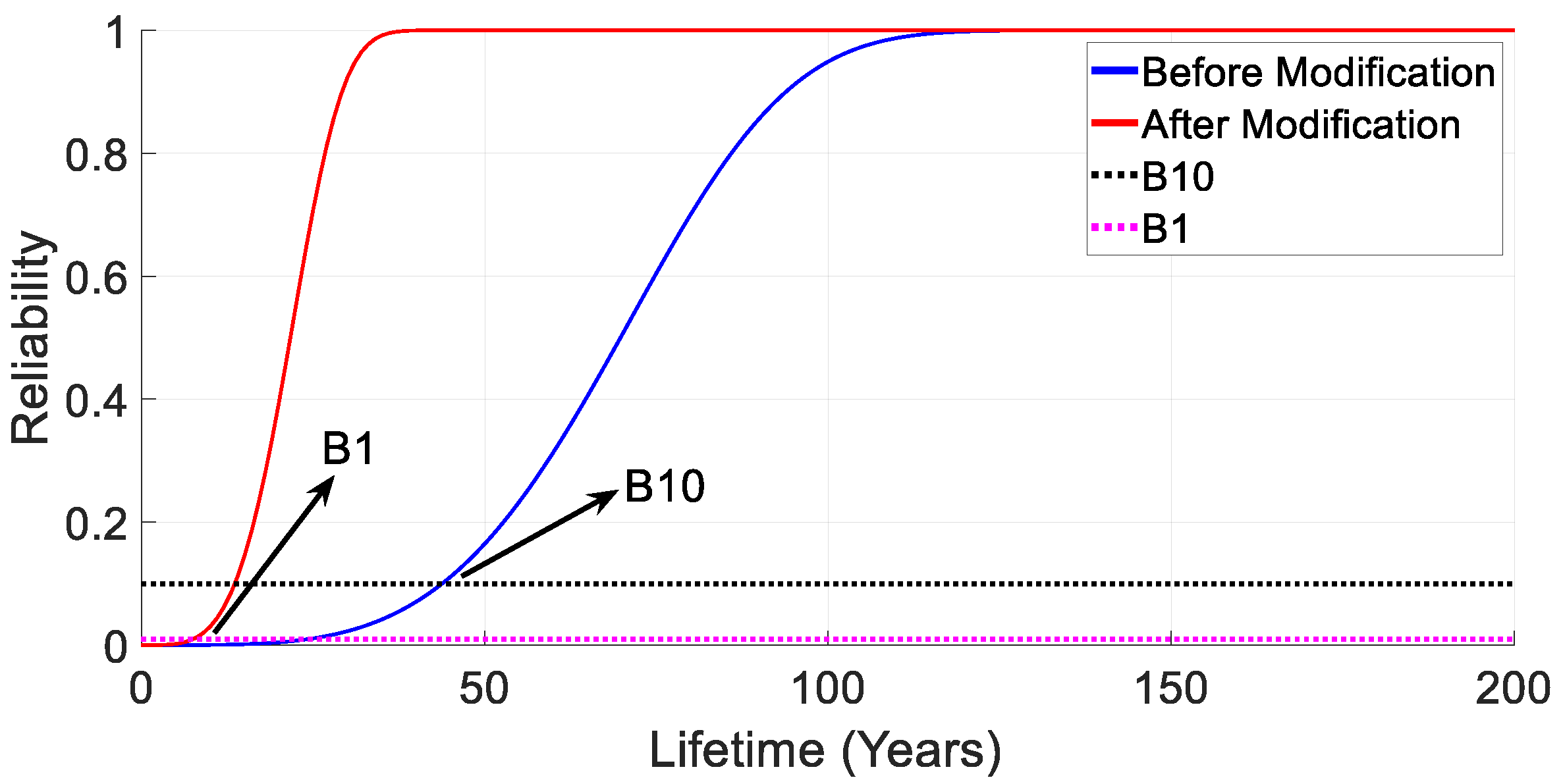
5.3. Example of the Modified Lifetime Models
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Li, Y.S.; Liu, J.X.; Shao, H.Q.; yuan Chen, Z.; Li, J.Y. Research on performance parameter degradation of high voltage and high power IGBT module in power cycling test. J. Phys. Conf. Ser. 2022, 2290, 012041. [Google Scholar] [CrossRef]
- Tounsi, M.; Oukaour, A.; Tala-Ighil, B.; Gualous, H.; Boudart, B.; Aissani, D. Characterization of high-voltage IGBT module degradations under PWM power cycling test at high ambient temperature. Microelectron. Reliab. 2010, 50, 1810–1814. [Google Scholar] [CrossRef]
- Ali, S.H.; Ugur, E.; Akin, B. Analysis of Vth variations in IGBTs under thermal stress for improved condition monitoring in automotive power conversion systems. IEEE Trans. Veh. Technol. 2018, 68, 193–202. [Google Scholar] [CrossRef]
- Anderson, J.M.; Cox, R.W. On-line condition monitoring for MOSFET and IGBT switches in digitally controlled drives. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 3920–3927. [Google Scholar]
- Moeini, R.; Tricoli, P.; Hemida, H.; Baniotopoulos, C. Increasing the reliability of wind turbines using condition monitoring of semiconductor devices: A review. IET Renew. Power Gener. 2018, 12, 182–189. [Google Scholar] [CrossRef]
- Halick, M.S.M.; Kandasamy, K.; Jet, T.K.; Sundarajan, P. Online computation of IGBT on-state resistance for off-shelf three-phase two-level power converter systems. Microelectron. Reliab. 2016, 64, 379–386. [Google Scholar] [CrossRef]
- Frank, Ø.B. Power Cycle Testing of Press-Pack IGBT Chips. Master’s Thesis, NTNU, Trondheim, Norway, 2014. [Google Scholar]
- Patil, N.; Das, D.; Goebel, K.; Pecht, M. Identification of failure precursor parameters for insulated gate bipolar transistors (IGBTs). In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–5. [Google Scholar]
- Wang, B.; Cai, J.; Du, X.; Zhou, L. Review of power semiconductor device reliability for power converters. CPSS Trans. Power Electron. Appl. 2017, 2, 101–117. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Li, C.; Li, J. Analysis of fault precursor parameters under accelerated aging tests for IGBT modules. In Proceedings of the 2020 17th China International Forum on Solid State Lighting & 2020 International Forum on Wide Bandgap Semiconductors China (SSLChina: IFWS), Shenzhen, China, 23–25 November 2020; pp. 238–241. [Google Scholar]
- Hu, Z.; Ge, X.; Xie, D.; Zhang, Y.; Yao, B.; Dai, J.; Yang, F. An aging-degree evaluation method for IGBT bond wire with online multivariate monitoring. Energies 2019, 12, 3962. [Google Scholar] [CrossRef]
- GopiReddy, L.R.; Tolbert, L.M.; Ozpineci, B. Power cycle testing of power switches: A literature survey. IEEE Trans. Power Electron. 2014, 30, 2465–2473. [Google Scholar]
- Smet, V.; Forest, F.; Huselstein, J.-J.; Richardeau, F.; Khatir, Z.; Lefebvre, S.; Berkani, M. Ageing and failure modes of IGBT modules in high-temperature power cycling. IEEE Trans. Ind. Electron. 2011, 58, 4931–4941. [Google Scholar] [CrossRef]
- Gao, B.; Yang, F.; Chen, M.; Chen, Y.; Lai, W.; Liu, C. Thermal lifetime estimation method of IGBT module considering solder fatigue damage feedback loop. Microelectron. Reliab. 2018, 82, 51–61. [Google Scholar] [CrossRef]
- Wang, F.; Yang, Y.; Huang, T.; Xu, Y. Lifetime prediction of electronic devices based on the P-stacking machine learning model. Microelectron. Reliab. 2023, 146, 115027. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Wang, Z.; Yang, Y.; Blaabjerg, F. Impact of lifetime model selections on the reliability prediction of IGBT modules in modular multilevel converters. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 4202–4207. [Google Scholar]
- Huang, H.; Mawby, P.A. A lifetime estimation technique for voltage source inverters. IEEE Trans. Power Electron. 2012, 28, 4113–4119. [Google Scholar] [CrossRef]
- Choi, U.-M.; Ma, K.; Blaabjerg, F. Validation of lifetime prediction of IGBT modules based on linear damage accumulation by means of superimposed power cycling tests. IEEE Trans. Ind. Electron. 2017, 65, 3520–3529. [Google Scholar] [CrossRef]
- Ali, S.H.; Heydarzadeh, M.; Dusmez, S.; Li, X.; Kamath, A.S.; Akin, B. Lifetime estimation of discrete IGBT devices based on Gaussian process. IEEE Trans. Ind. Appl. 2017, 54, 395–403. [Google Scholar] [CrossRef]
- Ismail, A.; Saidi, L.; Sayadi, M.; Benbouzid, M. Remaining useful lifetime prediction of thermally aged power insulated gate bipolar transistor based on Gaussian process regression. Trans. Inst. Meas. Control 2020, 42, 2507–2518. [Google Scholar] [CrossRef]
- Moniruzzaman, M.; Okilly, A.H.; Choi, S.; Baek, J.; Mannan, T.I.; Islam, Z. A Comprehensive Study of Machine Learning Algorithms for GPU based Real-time Monitoring and Lifetime Prediction of IGBTs. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024; pp. 2678–2684. [Google Scholar]
- Qin, F.; Bie, X.; An, T.; Dai, J.; Dai, Y.; Chen, P. A lifetime prediction method for IGBT modules considering the self-accelerating effect of bond wire damage. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 2271–2284. [Google Scholar] [CrossRef]
- Li, L.-L.; Liu, Z.-F.; Tseng, M.-L.; Zhou, L.; Qi, F.-D. Prediction of IGBT power module remaining lifetime using the aging state approach. Microelectron. Reliab. 2019, 102, 113476. [Google Scholar] [CrossRef]
- Li, W.; Wang, B.; Liu, J.; Zhang, G.; Wang, J. IGBT aging monitoring and remaining lifetime prediction based on long short-term memory (LSTM) networks. Microelectron. Reliab. 2020, 114, 113902. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, J.; You, H.; Jia, R.; Wang, X.; Zhang, X. A remaining useful life prediction method of IGBT based on online status data. Microelectron. Reliab. 2021, 121, 114124. [Google Scholar] [CrossRef]
- Li, L.; He, Y.; Wang, L.; Wang, C.; Liu, X. IGBT lifetime model considering composite failure modes. Mater. Sci. Semicond. Process. 2022, 143, 106529. [Google Scholar] [CrossRef]
- Bayerer, R.; Herrmann, T.; Licht, T.; Lutz, J.; Feller, M. Model for power cycling lifetime of IGBT modules-various factors influencing lifetime. In Proceedings of the 5th International Conference on Integrated Power Electronics Systems, Nuremberg, Germany, 11–13 March 2008; pp. 1–6. [Google Scholar]
- Sathik, M.H.M.; Sundararajan, P.; Sasongko, F.; Pou, J.; Natarajan, S. Comparative analysis of IGBT parameters variation under different accelerated aging tests. IEEE Trans. Electron Devices 2020, 67, 1098–1105. [Google Scholar] [CrossRef]
- Rashed, A.; Forest, F.; Huselstein, J.-J.; Martire, T.; Enrici, P. On-line [TJ, Vce] monitoring of IGBTs stressed by fast power cycling tests. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–9. [Google Scholar]
- Scheuermann, U.; Junghaenel, M. Limitation of power module lifetime derived from active power cycling tests. In Proceedings of the CIPS 2018: 10th International Conference on Integrated Power Electronics Systems, Stuttgart, Germany, 20–22 March 2018; pp. 1–10. [Google Scholar]
- Ghimire, P.; Pedersen, K.B.; Rannestad, B.; Munk-Nielsen, S. Ageing monitoring in IGBT module under sinusoidal loading. Microelectron. Reliab. 2015, 55, 1945–1949. [Google Scholar] [CrossRef]
- Choi, U.; Blaabjerg, F.; Iannuzzo, F. Advanced power cycler with intelligent monitoring strategy of IGBT module under test. Microelectron. Reliab. 2017, 76, 522–526. [Google Scholar] [CrossRef]
- Jia, Y.; Huang, Y.; Xiao, F.; Deng, H.; Duan, Y.; Iannuzzo, F. Impact of solder degradation on V CE of IGBT module: Experiments and modeling. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 10, 4536–4545. [Google Scholar] [CrossRef]
- Saha, S.; Celaya, J.R.; Vashchenko, V.; Mahiuddin, S.; Goebel, K.F. Accelerated aging with electrical overstress and prognostics for power MOSFETs. In Proceedings of the IEEE 2011 EnergyTech, Cleveland, OH, USA, 25–26 May 2011; pp. 1–6. [Google Scholar]
- Marrakh, R.; Bouhdada, A. Modeling of interface defect distribution for an n-mosfets under hot-carrier stressing. Act. Passiv. Electron. Compon. 2000, 23, 137–144. [Google Scholar] [CrossRef]
- Zeng, G.; Cao, H.; Chen, W.; Lutz, J. Difference in device temperature determination using pn-junction forward voltage and gate threshold voltage. IEEE Trans. Power Electron. 2018, 34, 2781–2793. [Google Scholar] [CrossRef]
- Blackburn, D.L. Temperature measurements of semiconductor devices—A review. In Proceedings of the Twentieth Annual IEEE Semiconductor Thermal Measurement and Management Symposium (IEEE Cat. No. 04CH37545), San Jose, CA, USA, 11–12 March 2004; pp. 70–80. [Google Scholar]
- Eleffendi, M.A.; Johnson, C.M. Evaluation of on-state voltage V CE (ON) and threshold voltage Vth for real-time health monitoring of IGBT power modules. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar]
- Avenas, Y.; Dupont, L.; Khatir, Z. Temperature measurement of power semiconductor devices by thermo-sensitive electrical parameters—A review. IEEE Trans. Power Electron. 2011, 27, 3081–3092. [Google Scholar] [CrossRef]
- Zhu, Y.; Xiao, M.; Su, X.; Lu, K.; Wu, Z.; Yang, G. IGBT junction temperature measurement under active-short-circuit and locked-rotor modes in new energy vehicles. IEEE Access 2020, 8, 114401–114412. [Google Scholar] [CrossRef]
- Baker, N.; Munk-Nielsen, S.; Iannuzzo, F.; Liserre, M. IGBT junction temperature measurement via peak gate current. IEEE Trans. Power Electron. 2015, 31, 3784–3793. [Google Scholar] [CrossRef]
- Arya, A.; Chanekar, A.; Deshmukh, P.; Verma, A.; Anand, S. Accurate online junction temperature estimation of IGBT using inflection point based updated I–V characteristics. IEEE Trans. Power Electron. 2021, 36, 9826–9836. [Google Scholar] [CrossRef]
- Qiu, X.; Zhang, G.; Chen, W.; Yu, T.; Hou, X.; Zhang, Q.; Xu, G. Review of igbt junction temperature extraction and estimation methods. IOP Conf. Ser. Mater. Sci. Eng. 2020, 774, 012091. [Google Scholar] [CrossRef]
- Zhu, Y.; Ma, K.; Cai, X. Thermal characterization method of power semiconductors based on H-bridge testing circuit. IEEE Trans. Power Electron. 2019, 34, 8268–8273. [Google Scholar] [CrossRef]
- Baker, N.; Dupont, L.; Munk-Nielsen, S.; Iannuzzo, F.; Liserre, M. IR camera validation of IGBT junction temperature measurement via peak gate current. IEEE Trans. Power Electron. 2016, 32, 3099–3111. [Google Scholar] [CrossRef]
- Amoiridis, A.; Anurag, A.; Ghimire, P.; Munk-Nielsen, S.; Baker, N. Vce-based chip temperature estimation methods for high power IGBT modules during power cycling—A comparison. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–9. [Google Scholar]
- Sleszynski, W.; Nieznanski, J.; Cichowski, A.; Luszcz, J.; Wojewodka, A. Evaluation of selected diagnostic variables for the purpose of assessing the ageing effects in high-power IGBTs. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; pp. 821–825. [Google Scholar]
- Wei, L.; Kerkman, R.J.; Lukaszewski, R.A. Evaluation of power semiconductors power cycling capabilities for adjustable speed drive. In Proceedings of the 2008 IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 5–9 October 2008; pp. 1–10. [Google Scholar]
- Wei, L.; Lukaszewski, R.A.; Lipo, T.A. Analysis of power cycling capability of IGBT modules in a conventional matrix converter. In Proceedings of the 2008 IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 5–9 October 2008; pp. 1–8. [Google Scholar]
- Sankaran, V.; Chen, C.; Avant, C.; Xu, X. Power cycling reliability of IGBT power modules. In Proceedings of the IAS’97. Conference Record of the 1997 IEEE Industry Applications Conference Thirty-Second IAS Annual Meeting, New Orleans, LA, USA, 5–9 October 1997; pp. 1222–1227. [Google Scholar]
- Sarkany, Z.; Vass-Varnai, A.; Rencz, M. Effect of power cycling parameters on predicted IGBT lifetime. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–9. [Google Scholar]
- Amro, R.; Lutz, J.; Rudzki, J.; Thoben, M.; Lindemann, A. Double-sided low-temperature joining technique for power cycling capability at high temperature. In Proceedings of the 2005 European Conference on Power Electronics and Applications, Dresden, Germany, 11–14 September 2005; p. 10-pp. [Google Scholar]
- Herrmann, T.; Feller, M.; Lutz, J.; Bayerer, R.; Licht, T. Power cycling induced failure mechanisms in solder layers. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–7. [Google Scholar]
- Wu, W.; Held, M.; Jacob, P.; Scacco, P.; Birolini, A. Investigation on the long term reliability of power IGBT modules. In Proceedings of the International Symposium on Power Semiconductor Devices and IC’s: ISPSD’95, Yokohama, Japan, 23–25 May 1995; pp. 443–448. [Google Scholar]
- Tran, S.-H.; Khatir, Z.; Lallemand, R.; Ibrahim, A.; Ousten, J.-P.; Ewanchuk, J.; Mollov, S.V. Constant Δtj power cycling strategy in DC mode for top-metal and bond-wire contacts degradation investigations. IEEE Trans. Power Electron. 2018, 34, 2171–2180. [Google Scholar] [CrossRef]
- Held, M.; Jacob, P.; Nicoletti, G.; Scacco, P.; Poech, M.-H. Fast power cycling test of IGBT modules in traction application. In Proceedings of the Second International Conference on Power Electronics and Drive Systems, Singapore, 26–29 May 1997; pp. 425–430. [Google Scholar]
- Hutzler, A.; Zeyss, F.; Vater, S.; Tokarski, A.; Schletz, A.; März, M. Power Cycling Community 1995–2014. Bodo’s Power Syst. 2014, 2014, 78–80. [Google Scholar]
- Scheuermann, U.; Hecht, U. Power cycling lifetime of advanced power modules for different temperature swings. PCIM Nuremberg 2002, 5964, 2201–2207. [Google Scholar]
- Wintrich, A. Power Cycle Model for IGBT Product Lines; SEMIKRON Application Note AN 21-001; SEMIKRON: Nuremberg, Germany, 2021. [Google Scholar]
- Choi, U.; Jørgensen, S.; Iannuzzo, F.; Blaabjerg, F. Power cycling test of transfer molded IGBT modules by advanced power cycler under different junction temperature swings. Microelectron. Reliab. 2018, 88, 788–794. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, R.; Iannuzzo, F.; Wang, H. Aging investigation of the latest standard dual power modules using improved interconnect technologies by power cycling test. Microelectron. Reliab. 2022, 138, 114740. [Google Scholar] [CrossRef]
- Abuelnaga, A.; Narimani, M.; Bahman, A.S. A review on IGBT module failure modes and lifetime testing. IEEE Access 2021, 9, 9643–9663. [Google Scholar] [CrossRef]
- Tian, B.; Qiao, W.; Wang, Z.; Gachovska, T.; Hudgins, J.L. Monitoring IGBT’s health condition via junction temperature variations. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition-APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 2550–2555. [Google Scholar]
- Riedel, G.; Schmidt, R.; Liu, C.; Beyer, H.; Alaperae, I. Reliability of large area solder joints within IGBT modules: Numerical modeling and experimental results. In Proceedings of the 2012 7th International Conference on Integrated Power Electronics Systems (CIPS), Nuremberg, Germany, 6–8 March 2012; pp. 1–6. [Google Scholar]
- Ciappa, M. Selected failure mechanisms of modern power modules. Microelectron. Reliab. 2002, 42, 653–667. [Google Scholar] [CrossRef]
- Busca, C.; Teodorescu, R.; Blaabjerg, F.; Munk-Nielsen, S.; Helle, L.; Abeyasekera, T.; Rodríguez, P. An overview of the reliability prediction related aspects of high power IGBTs in wind power applications. Microelectron. Reliab. 2011, 51, 1903–1907. [Google Scholar] [CrossRef]
- Alhmoud, L. Reliability improvement for a high-power IGBT in wind energy applications. IEEE Trans. Ind. Electron. 2018, 65, 7129–7137. [Google Scholar] [CrossRef]
- Kovačević, I.; Drofenik, U.; Kolar, J.W. New physical model for lifetime estimation of power modules. In Proceedings of the 2010 International Power Electronics Conference-ECCE ASIA, Sapporo, Japan, 21–24 June 2010; pp. 2106–2114. [Google Scholar]
- Lutz, J. Packaging and reliability of power modules. In Proceedings of the CIPS 2014: 8th International Conference on Integrated Power Electronics Systems, Nuremberg, Germany, 25–27 February 2014; pp. 1–8. [Google Scholar]
- Böttcher, M.; Paulsen, M.; Fuchs, F.W. Laboratory setup for power cycling of igbt modules with monitoring of on-state voltage and thermal resistance for state of aging detection. In Proceedings of the Conference Records PCIM 2012, Nuremberg, Germany, 8–10 May 2012. [Google Scholar]
- Schmidt, R.; Zeyss, F.; Scheuermann, U. Impact of absolute junction temperature on power cycling lifetime. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Hoffmann, F.; Kaminski, N. Power cycling capability and lifetime estimation of discrete silicon carbide power devices. Mater. Sci. Forum 2020, 1004, 977–984. [Google Scholar] [CrossRef]
- Scheuermann, U.; Schmidt, R. Impact of load pulse duration on power cycling lifetime of Al wire bonds. Microelectron. Reliab. 2013, 53, 1687–1691. [Google Scholar] [CrossRef]
- Deng, E.; Zhang, J.; Zhao, Z.; Chen, J.; Li, J.; Huang, Y. Influence of the clamping force on the power cycling lifetime reliability of press pack IGBT sub-module. J. Eng. 2019, 2019, 2435–2439. [Google Scholar] [CrossRef]
- Feller, L.; Hartmann, S.; Schneider, D. Lifetime analysis of solder joints in high power IGBT modules for increasing the reliability for operation at 150 C. Microelectron. Reliab. 2008, 48, 1161–1166. [Google Scholar] [CrossRef]
- Choi, U.; Vernica, I.; Zhou, D.; Blaabjerg, F. Comparative evaluation of reliability assessment methods of power modules in motor drive inverter. Microelectron. Reliab. 2020, 114, 113730. [Google Scholar] [CrossRef]
- Dusmez, S.; Ali, S.H.; Heydarzadeh, M.; Kamath, A.S.; Duran, H.; Akin, B. Aging precursor identification and lifetime estimation for thermally aged discrete package silicon power switches. IEEE Trans. Ind. Appl. 2016, 53, 251–260. [Google Scholar] [CrossRef]
- Patil, N.; Celaya, J.; Das, D.; Goebel, K.; Pecht, M. Precursor parameter identification for insulated gate bipolar transistor (IGBT) prognostics. IEEE Trans. Reliab. 2009, 58, 271–276. [Google Scholar] [CrossRef]
- Yangjie, B.; Jiang, Q. Summary of Life Prediction and Failure Analysis of IGBT Modules Based on Accelerated Aging Test. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Chamund, D.; Newcombe, D. IGBT Module Reliability; Application Note AN5945-6; Dynex Semiconductor: Lincoln, UK, 2015. [Google Scholar]
- Zeng, G.; Borucki, L.; Wenzel, O.; Schilling, O.; Lutz, J. First results of development of a lifetime model for transfer molded discrete power devices. In Proceedings of the PCIM Europe 2018: International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 5–7 June 2018; pp. 1–8. [Google Scholar]
- Obreja, V.V.; Obreja, A.C. Activation energy values from the temperature dependence of silicon pn junction reverse current and its origin. Phys. Status Solidi (A) 2010, 207, 1252–1256. [Google Scholar] [CrossRef]
- Ramminger, S.; Seliger, N.; Wachutka, G. Reliability model for Al wire bonds subjected to heel crack failures. Microelectron. Reliab. 2000, 40, 1521–1525. [Google Scholar] [CrossRef]
- Scheuermann, U.; Schmidt, R. Impact of solder fatigue on module lifetime in power cycling tests. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August 2011; pp. 1–10. [Google Scholar]





| Modified | Confidence Bounds (±) | Conventional | |
|---|---|---|---|
| A | 5.47 × 106 | 1.063 × 10−6 | 3.43 × 1014 |
| α | −5.528 × 10−8 | 5.392 | −4.923 |
| ar | 0.177 | - | 0.290 |
| β1 [1/K] | −0.000878 | 0.044826 | −0.009012 |
| β0 | 10.746 | 10.079 | 1.942 |
| C | 1.434 | - | 1.434 |
| γ | −1.208 | - | −1.208 |
| Derived Value | Confidence Bounds (±) | |
|---|---|---|
| kb | 4.278 × 1010 | 1.527 × 10−9 |
| β1 | −2.910 | 3.501 |
| β2 | 1083.714 | 6098.460 |
| β3 | −4.521 | 4.510 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alavi, O.; De Ceuninck, W.; Daenen, M. Optimizing Insulated-Gate Bipolar Transistors’ Lifetime Estimation: A Critical Evaluation of Lifetime Model Adjustments Based on Power Cycling Tests. Energies 2024, 17, 2616. https://doi.org/10.3390/en17112616
Alavi O, De Ceuninck W, Daenen M. Optimizing Insulated-Gate Bipolar Transistors’ Lifetime Estimation: A Critical Evaluation of Lifetime Model Adjustments Based on Power Cycling Tests. Energies. 2024; 17(11):2616. https://doi.org/10.3390/en17112616
Chicago/Turabian StyleAlavi, Omid, Ward De Ceuninck, and Michaël Daenen. 2024. "Optimizing Insulated-Gate Bipolar Transistors’ Lifetime Estimation: A Critical Evaluation of Lifetime Model Adjustments Based on Power Cycling Tests" Energies 17, no. 11: 2616. https://doi.org/10.3390/en17112616
APA StyleAlavi, O., De Ceuninck, W., & Daenen, M. (2024). Optimizing Insulated-Gate Bipolar Transistors’ Lifetime Estimation: A Critical Evaluation of Lifetime Model Adjustments Based on Power Cycling Tests. Energies, 17(11), 2616. https://doi.org/10.3390/en17112616






