An Improved Single-Phase Multiple DC Source Inverter Topology for Distributed Energy System Applications
Abstract
1. Introduction
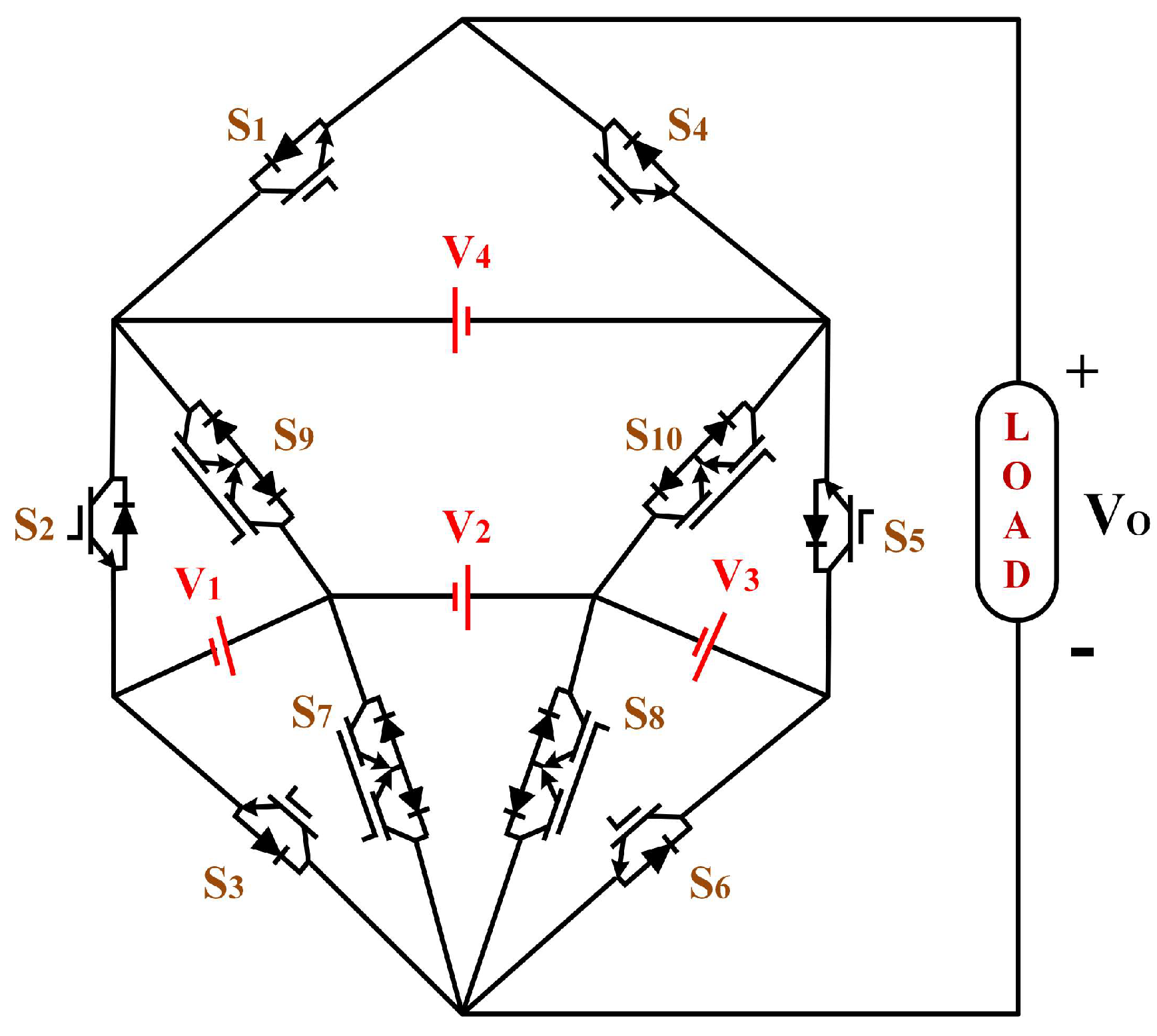
2. Description of the Proposed Topology
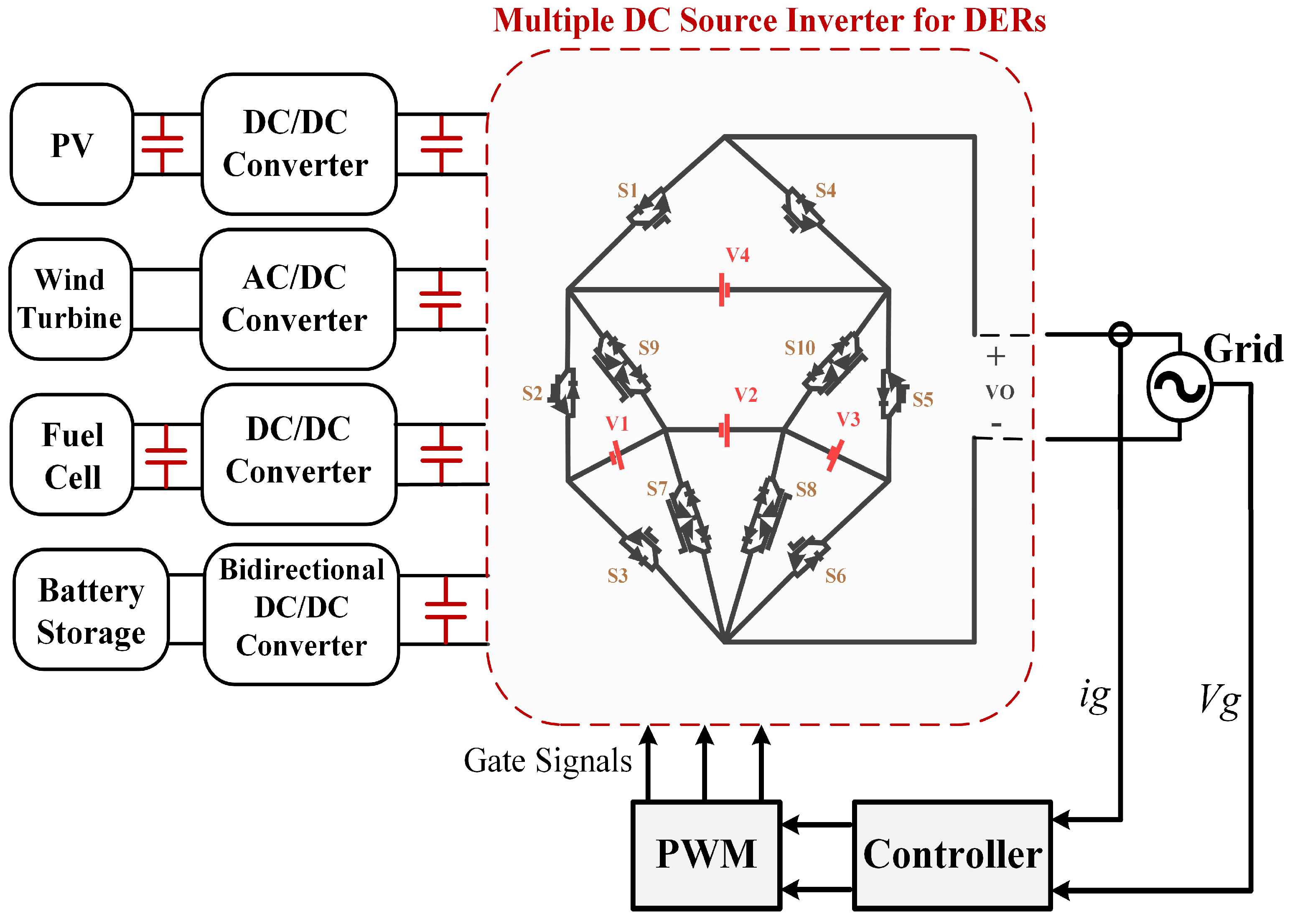
2.1. Circuit Configuration
2.2. Proposed DC Source Selection Algorithm
2.3. Operation of the Proposed Topology
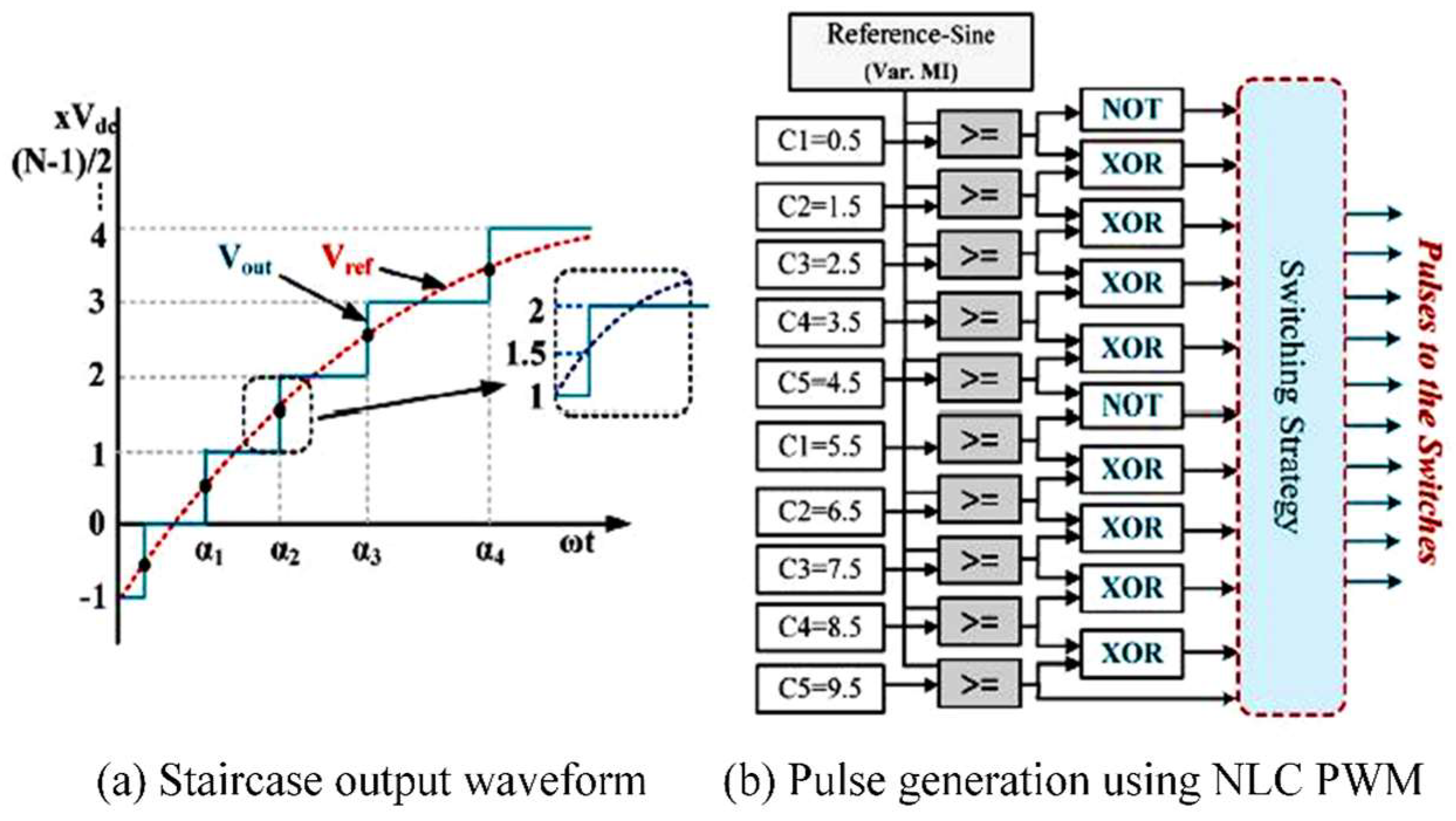
2.4. Switching Technique
2.5. Total Standing Voltage (TSV)
2.6. Cost Analysis
3. Results and Discussion
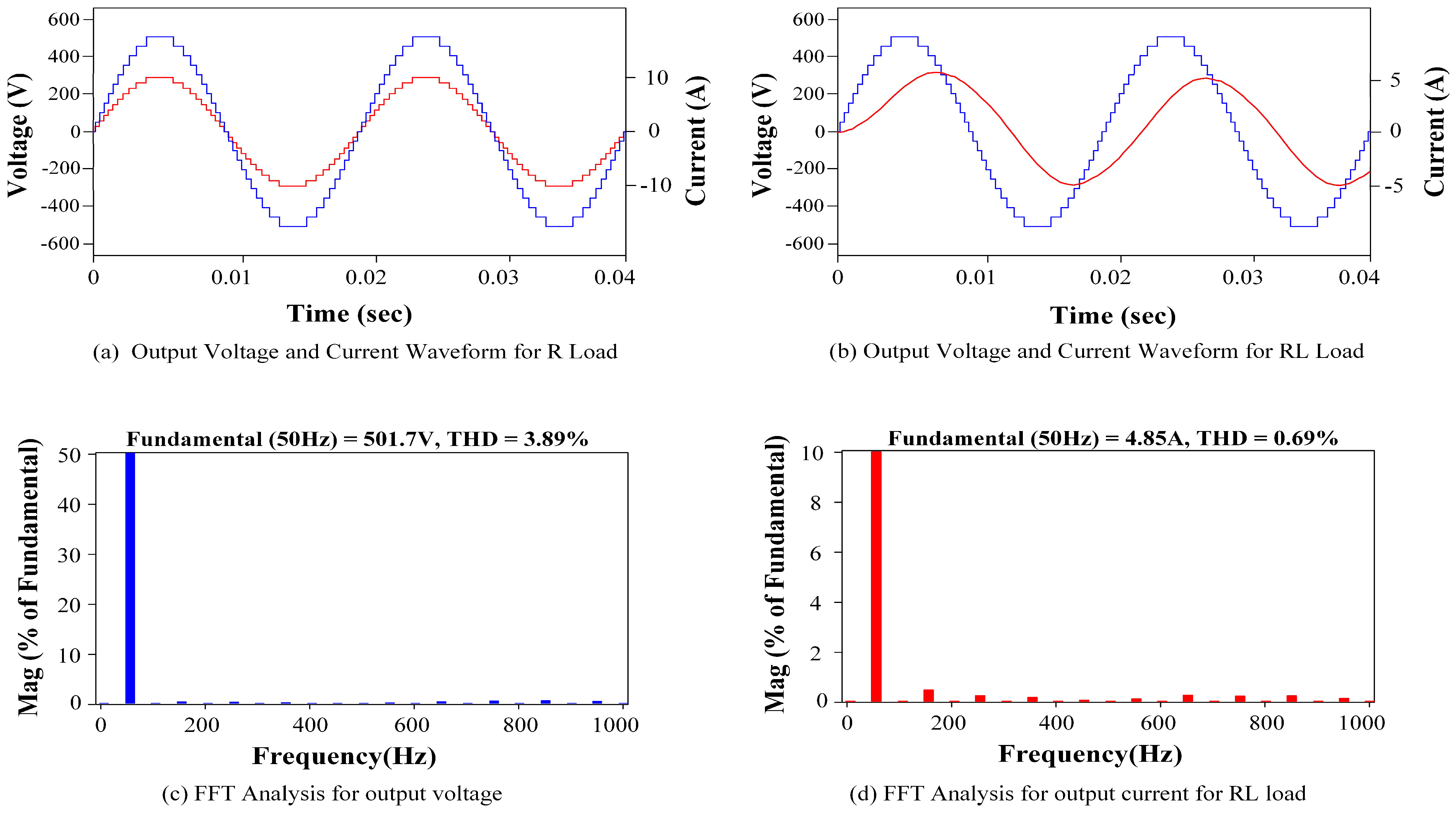
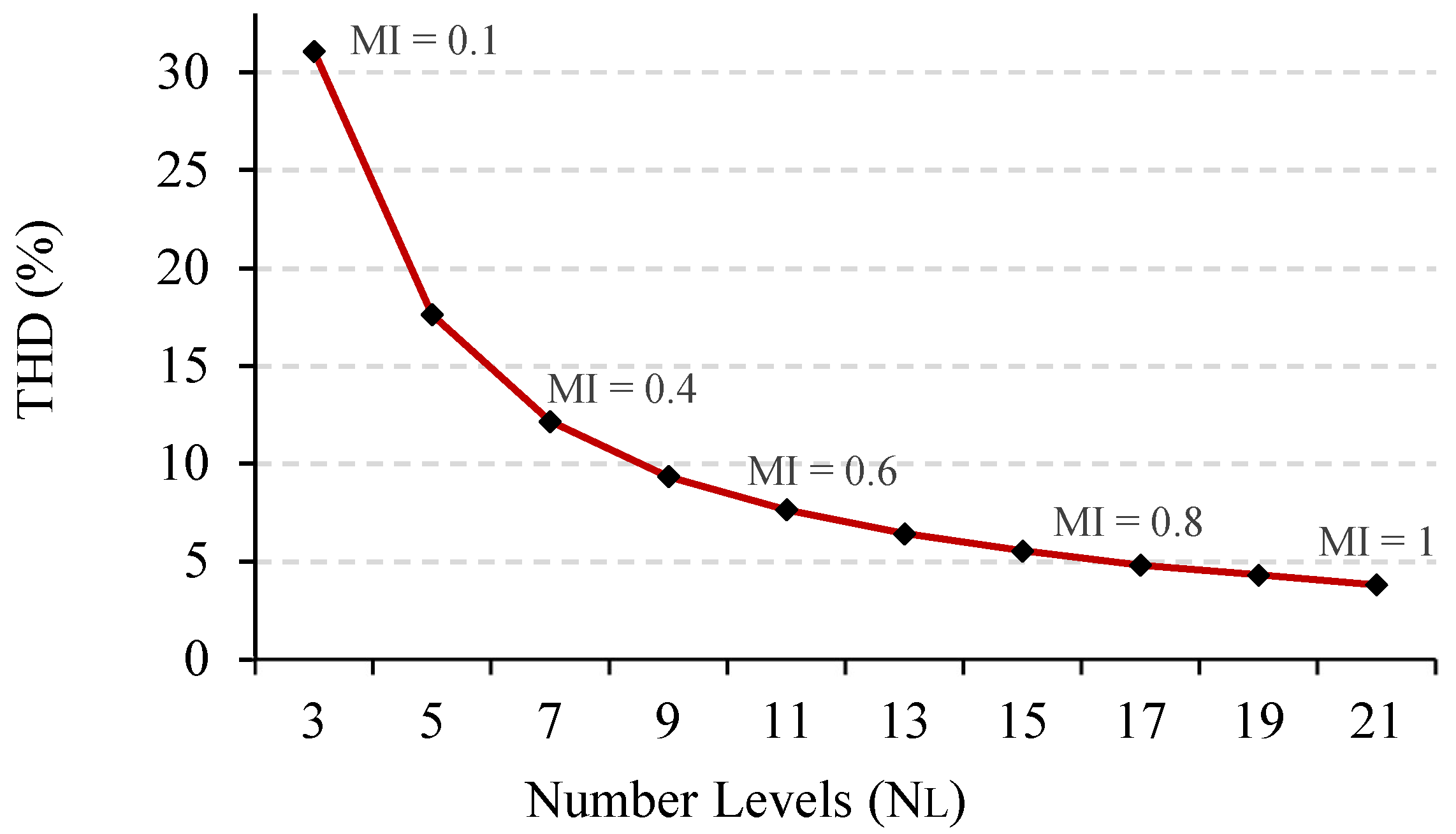
3.1. Simulation Results
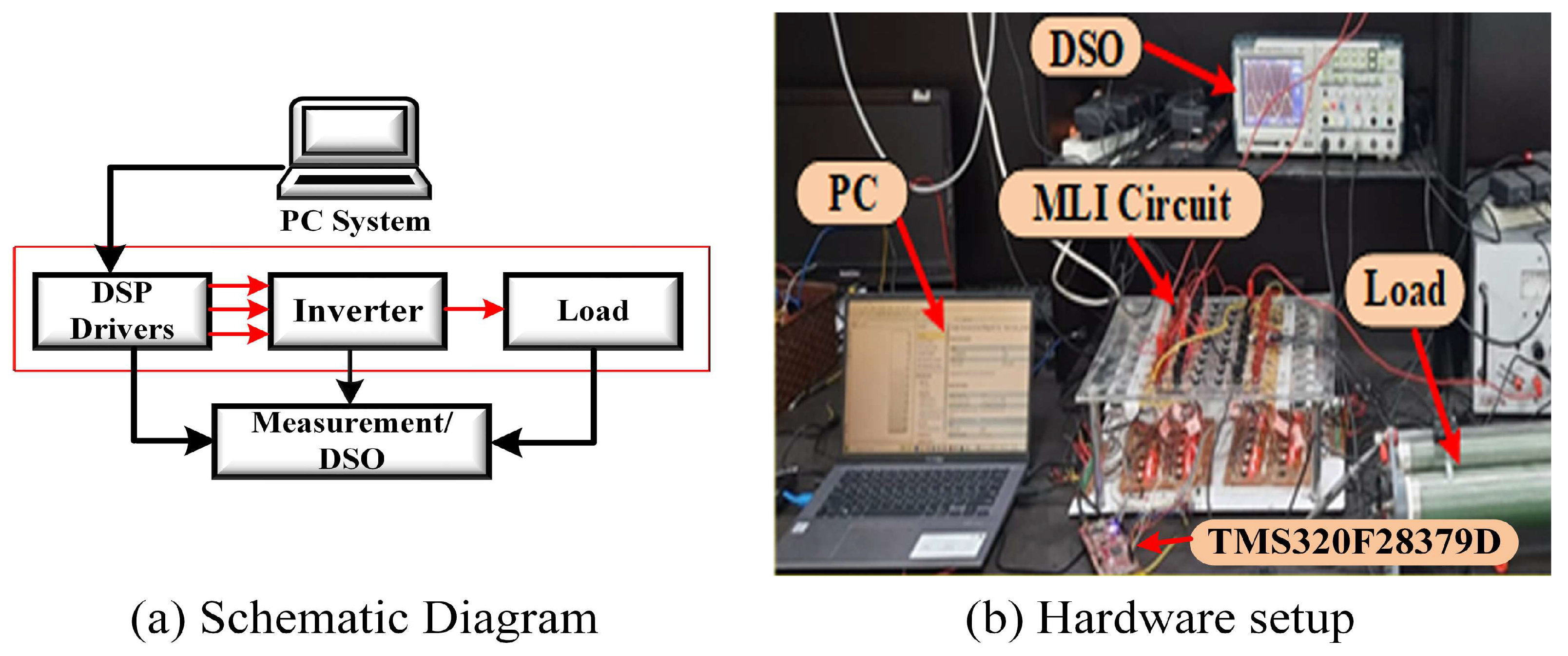
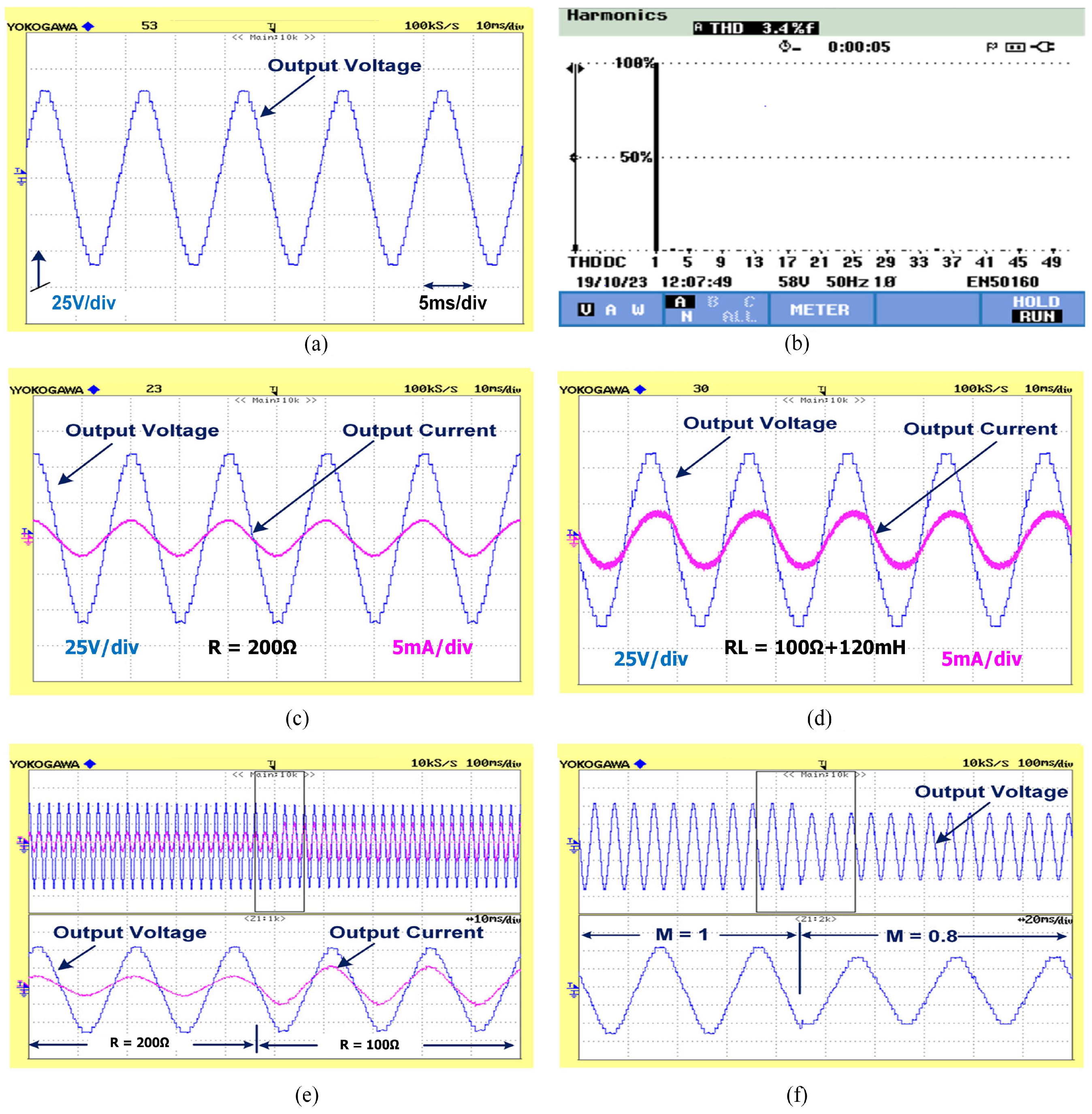
3.2. Experimental Results
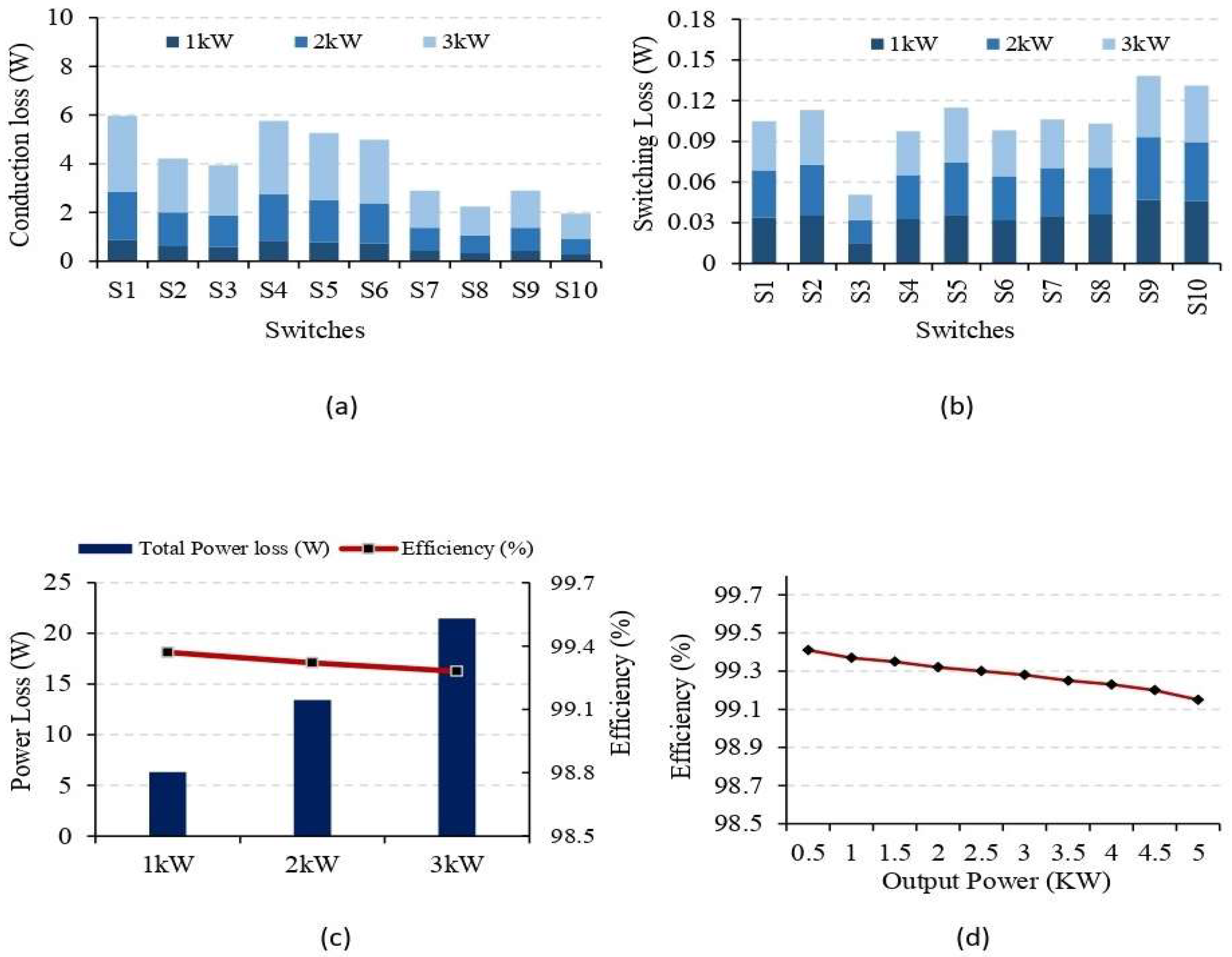
4. Power Loss Analysis
5. Comparative Analysis
6. Application of the Proposed Topology
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Memon, A.J.; Mahar, M.A.; Larik, A.S.; Shaikh, M.M. A Comprehensive Review of Reduced Device Count Multilevel Inverters for PV Systems. Energies 2023, 16, 5638. [Google Scholar] [CrossRef]
- Paul, S.; Jana, K.C.; Majumdar, S.; Pal, P.K.; Mahato, B. Performance analysis of a multimodule staircase (MM-STC)-type multilevel inverter with reduced component count and improved efficiency. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 6619–6633. [Google Scholar] [CrossRef]
- IEEE 519; IEEE Standards of Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2022.
- Huang, Z.; Zhou, D.; Wang, L.; Shen, Z.; Li, Y. A Review of Single-Stage Multiport Inverters for Multisource Applications. IEEE Trans. Power Electron. 2023, 38, 6566–6584. [Google Scholar] [CrossRef]
- Barzegarkhoo, R.; Forouzesh, M.; Lee, S.S.; Blaabjerg, F.; Siwakoti, Y. Switched-capacitor multilevel inverters: A comprehensive review. IEEE Trans. Power Electron. 2022, 37, 11209–11243. [Google Scholar] [CrossRef]
- Salem, A.; Van Khang, H.; Robbersmyr, K.G.; Norambuena, M.; Rodriguez, J. Voltage source multilevel inverters with reduced device count: Topological review and novel comparative factors. IEEE Trans. Power Electron. 2020, 36, 2720–2747. [Google Scholar] [CrossRef]
- Venkataramanaiah, J.; Suresh, Y.; Panda, A.K. A review on symmetric, asymmetric, hybrid and single DC sources based multilevel inverter topologies. Renew. Sustain. Energy Rev. 2017, 76, 788–812. [Google Scholar] [CrossRef]
- Omer, P.; Kumar, J.; Surjan, B.S. A review on reduced switch count multilevel inverter topologies. IEEE Access 2020, 8, 22281–22302. [Google Scholar] [CrossRef]
- Avanaki, H.N.; Barzegarkhoo, R.; Zamiri, E.; Yang, Y.; Blaabjerg, F. Reduced switch-count structure for symmetric multilevel inverters with a novel switched-DC-source submodule. IET Power Electron. 2018, 12, 311–321. [Google Scholar] [CrossRef]
- Vijeh, M.; Rezanejad, M.; Samadaei, E.; Bertilsson, K. A general review of multilevel inverters based on main submodules: Structural point of view. IEEE Trans. Power Electron. 2019, 34, 9479–9502. [Google Scholar] [CrossRef]
- Yousofi-Darmian, S.; Barakati, S.M. A new asymmetric multilevel inverter with a reduced number of components. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 4333–4342. [Google Scholar] [CrossRef]
- Yang, K.; Lan, X.; Zhang, Q.; Tang, X. Unified selective harmonic elimination for cascaded h-bridge asymmetric multilevel inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 2138–2146. [Google Scholar] [CrossRef]
- Taghvaie, A.; Adabi, J.; Rezanejad, M. A multilevel inverter structure based on a combination of switched-capacitors and DC sources. IEEE Trans. Ind. Inform. 2017, 13, 2162–2171. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.A.; Sarebanzadeh, M.; Rivera, M.; Babaei, E.; Wheeler, P. A Reduced Single-Phase Switched-Diode Cascaded Multilevel Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 3556–3569. [Google Scholar] [CrossRef]
- Kakar, S.; Ayob, S.B.M.; Iqbal, A.; Nordin, N.M.; Arif, M.S.B.; Gore, S. New Asymmetrical Modular Multilevel Inverter Topology With Reduced Number of Switches. IEEE Access 2021, 9, 27627–27637. [Google Scholar] [CrossRef]
- Dhanamjayulu, C.; Kaliannan, P.; Padmanaban, S.; Maroti, P.K.; Holm-Nielsen, J.B. A new three-phase multilevel asymmetrical inverter with optimum hardware components. IEEE Access 2020, 8, 212515–212528. [Google Scholar] [CrossRef]
- Shalchi Alishah, R.; Bertilsson, K.; Hosseini, S.H.; Babaei, E.; Aalami, M.; Ali, J.S.M.; Gharehpetian, G.B. A new generalized cascade multilevel converter topology and its improved modulation technique. Int. J. Circuit Theory Appl. 2021, 49, 1103–1120. [Google Scholar] [CrossRef]
- Majumdar, S.; Mahato, B.; Jana, K.C. Optimum structure-based multilevel inverter with doubling circuit configuration. J. Circ. Syst. Comput. 2019, 28, 1950194. [Google Scholar] [CrossRef]
- Rawa, M.; Mohamed Ali, J.S.; Siddique, M.D.; Mekhilef, S.; Wahyudie, A.; Seyedmahmoudian, M.; Stojcevski, A. A new multilevel inverter topology with reduced dc sources. Energies 2021, 14, 4709. [Google Scholar] [CrossRef]
- Mahato, B.; Majumdar, S.; Jana, K.C. Reduction in controlled power switches for a single-phase novel multilevel inverter. Int. J. Electron. 2019, 106, 1200–1215. [Google Scholar] [CrossRef]
- Mahato, B.; Majumdar, S.; Jana, K.C. A new and generalized MLI with overall lesser power electronic devices. J. Circ. Syst. Comput. 2020, 29, 2050058. [Google Scholar] [CrossRef]
- Akbari, A.; Ebrahimi, J.; Jafarian, Y.; Bakhshai, A. A Multilevel Inverter Topology with an Improved Reliability and a Reduced Number of Components. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 553–563. [Google Scholar] [CrossRef]
- Maamar, A.E.T.; Kermadi, M.; Helaimi, M.; Taleb, R.; Mekhilef, S. An Improved Single-Phase Asymmetrical Multilevel Inverter Structure with Reduced Number of Switches and Higher Power Quality. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2092–2096. [Google Scholar] [CrossRef]
- Oskuee, M.R.J.; Karimi, M.; Naderi, Y.; Ravadanegh, S.N.; Hosseini, S.H. A new multilevel voltage source inverter configuration with minimum number of circuit elements. J. Cent. South. Univ. 2017, 24, 912–920. [Google Scholar] [CrossRef]
- Deliri, S.; Varesi, K.; Padmanaban, S. An extendable single-input reduced-switch 11-level switched-capacitor inverter with quintuple boosting factor. IET Gener. Transm. Distrib. 2023, 17, 621–631. [Google Scholar] [CrossRef]
- Karakılıç, M.; Hata¸s, H.; Nuri Almalı, M. Design of a 21-level multilevel inverter with minimum number of devices count. Int. J. Circ. Theor. Appl. 2023, 51, 5705–5723. [Google Scholar] [CrossRef]
- Arif, M.S.B.; Mustafa, U.; Ahmad, S.; Ayob, S.B.; Ashique, R.H.; Tayyab, M. Asymmetrical 21-level inverter topology with minimum variety of dc sources and reduced component counts. Int. J. Circ. Theor. Appl. 2023, 51, 1697–1718. [Google Scholar] [CrossRef]
- Karimi, M.; Kargar, P.; Varesi, K. An extendable asymmetric boost multilevel inverter with self-balanced capacitors. Int. J. Circ. Theor. Appl. 2022, 50, 1297–1316. [Google Scholar] [CrossRef]
- Deliri Saeid Varesi, K.; Siwakoti, Y.P.; Blaabjerg, F. Generalized diamond-type single DC-source switched-capacitor based multilevel inverter with step-up and natural voltage balancing capabilities. IET Power Electron. 2021, 14, 1208–1218. [Google Scholar] [CrossRef]
- Arif, M.S.B.; Sarwer, Z.; Siddique, M.D.; Ayob, S.; Iqbal, A.; Mekhilef, S. Asymmetrical multilevel inverter topology with low total standing voltage and reduced switches count. Int. J. Circuit Theory Appl. 2021, 49, 1757–1775. [Google Scholar] [CrossRef]
- Fahad, M.; Siddique, M.D.; Iqbal, A.; Sarwar, A.; Mekhilef, S. Implementation and analysis of a 15-level inverter topology with reduced switch count. IEEE Access 2021, 9, 40623–40634. [Google Scholar] [CrossRef]
- Dhanamjayulu, C.; Prasad, D.; Padmanaban, S.; Maroti, P.K.; Holm-Nielsen, J.B.; Blaabjerg, F. Design and implementation of seventeen level inverter with reduced components. IEEE Access 2021, 9, 16746–16760. [Google Scholar] [CrossRef]
- Samadaei, E.; Sheikholeslami, A.; Gholamian, S.A.; Adabi, J. A square T-type (ST-type) module for asymmetrical multilevel inverters. IEEE Trans. Power Electron. 2017, 33, 987–996. [Google Scholar] [CrossRef]
- Hassan, A.; Yang, X.; Chen, W. A novel 19L hybrid multilevel inverter system synthesizes reduced number of switches for hybrid renewable energy applications. Int. Trans. Electr. Energy Syst. 2021, 31, e12856. [Google Scholar] [CrossRef]
- Meraj, S.T.; Yahaya, N.Z.; Hasan, K.; Masaoud, A. Single phase 21 level hybrid multilevel inverter with reduced power components employing low-frequency modulation technique. Int. J. Power Electron. Drive Syst. 2020, 11, 810–822. [Google Scholar] [CrossRef]
- Agrawal, R.; Jain, S. Multilevel inverter for interfacing renewable energy sources with low/medium-and high-voltage grids. IET Renew. Power Gen. 2017, 11, 1822–1831. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, J.; Shahidehpour, M.; Bai, L.; Xiao, Y.; Li, H. Cooperative Operation of Distributed Energy Resources and Thermal Power Plant with a Carbon-Capture-Utilization-and-Storage System. IEEE Trans. Power Syst. 2024, 39, 1850–1866. [Google Scholar] [CrossRef]
- Shirkhani, M.; Tavoosi, J.; Danyali, S.; Sarvenoee, A.K.; Abdali, A.; Mohammadzadeh, A.; Zhang, C. A review on microgrid decentralized energy/voltage control structures and methods. Energy Rep. 2023, 10, 368–380. [Google Scholar] [CrossRef]
- Duan, Y.; Zhao, Y.; Hu, J. An initialization-free distributed algorithm for dynamic economic dispatch problems in microgrid: Modeling, optimization and analysis. Sustain. Energy Grids Netw. 2023, 34, 101004. [Google Scholar] [CrossRef]
- Lin, X.; Wen, Y.; Yu, R.; Yu, J.; Wen, H. Improved Weak Grids Synchronization Unit for Passivity Enhancement of Grid-Connected Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 7084–7097. [Google Scholar] [CrossRef]
- Shao, B.; Xiao, Q.; Xiong, L.; Wang, L.; Yang, Y.; Chen, Z.; Blaabjerg, F.; Guerrero, J.M. Power coupling analysis and improved decoupling control for the VSC connected to a weak AC grid. Int. J. Electr. Power Energy Syst. 2023, 145, 108645. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, D.; Liang, W.; Zhang, X. Current Reconstruction of Three-Phase Voltage Source Inverters Considering Current Ripple. IEEE Trans. Transp. Electrif. 2023, 9, 1416–1427. [Google Scholar] [CrossRef]
- Hu, J.; Zou, Y.; Soltanov, N. A multilevel optimization approach for daily scheduling of combined heat and power units with integrated electrical and thermal storage. Expert Syst. Appl. 2024, 250, 123729. [Google Scholar] [CrossRef]
- Hou, M.; Zhao, Y.; Ge, X. Optimal scheduling of the plug-in electric vehicles aggregator energy and regulation services based on grid to vehicle. Int. Trans. Electr. Energy Syst. 2017, 27, e2364. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Z.; Yuan, X.; Wang, Y.; Shen, X. L2-Gain Adaptive Robust Control for Hybrid Energy Storage System in Electric Vehicles. IEEE Trans. Power Electron. 2021, 36, 7319–7332. [Google Scholar] [CrossRef]
- Fang, Z.; Liang, J.; Tan, C.; Tian, Q.; Pi, D.; Yin, G. Enhancing Robust Driver Assistance Control in Distributed Drive Electric Vehicles through Integrated AFS and DYC Technology. IEEE Trans. Intell. Veh. 2024, 1–14. [Google Scholar] [CrossRef]



| Algorithm | Magnitude of DC Voltage Source | Output Voltage Levels, (NL) |
|---|---|---|
| I | 9 | |
| II | 11 | |
| III | 13 | |
| IV | 15 | |
| V | 17 | |
| VI | 19 | |
| VII | 21 |
| Vo | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | Vin | Positive Levels |
| 1 V | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | V1 | |
| 2 V | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | V3 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | V4 − V3 | ||
| 3 V | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | V2 | |
| 4 V | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | V4 | |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | V1 + V2 | ||
| 5 V | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | V2 + V3 | |
| 6 V | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | V1 + V2 + V3 | |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | V3 + V4 | ||
| 7 V | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | V2 + V4 | |
| 8 V | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | V1 + V2 + V4 | |
| 9 V | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | V2 + V3 + V4 | |
| 10 V | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | V1 + V2 + V3 + V4 | |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | Zero Level |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | – | ||
| −1 V | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | −V1 | Negative Levels |
| −2 V | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | −V3 | |
| −3 V | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | −V2 | |
| −4 V | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | −V4 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | −V1 − V2 | ||
| −5 V | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | −V2 − V3 | |
| −6 V | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | −V1 − V2 − V3 | |
| −7 V | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | −V2 − V4 | |
| −8 V | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | −V1 − V2 − V3 | |
| −9 V | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | −V2 − V3 − V4 | |
| −10 V | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | −V1 − V2 − V3 − V4 |
| Parameter/Device | Value |
|---|---|
| DC Sources | V1 = 50 V, V2 = 150 V, V3 = 100 V, V4 = 200 V |
| Switches | IGBT |
| Load Resistance | 100 Ω, 50 Ω |
| Load Inductance | 80 mH, 40 mH |
| Modulation Index | 1, 0.6, 0.4 |
| Parameter/Device | Value/Type/Rating |
|---|---|
| DC Sources | V1 = 6 V, V2 = 18 V, V3 = 12 V, V4 = 24 V |
| Switches | IGBT, FGA25N120, 1200 V/25 A |
| Microcontroller | TMS320F28379D, 200 MHz |
| Driver IC | TLP 250 |
| Digital Signal Oscilloscope | Yokogawa DL1640 |
| Power Quality Analyzer | Fluke 435-II |
| Load Resistance | 100 Ω, 200 Ω |
| Load Inductance | 90 mH, 120 mH |
| Modulation Index | 1, 0.8 |
| Topology | NL | NDC | NSW | NIGBT | NGD | NCap | Nd | NSW/NL | CF/Level |
|---|---|---|---|---|---|---|---|---|---|
| [30] | 15 | 4 | 8 | 10 | 8 | 0 | 0 | 0.53 | 1.78 |
| [31] | 15 | 4 | 11 | 12 | 11 | 0 | 0 | 0.73 | 2.14 |
| [32] | 17 | 4 | 14 | 16 | 14 | 2 | 0 | 0.82 | 1.97 |
| [33] | 17 | 4 | 9 | 12 | 9 | 0 | 0 | 0.53 | 1.76 |
| [16] | 19 | 3 | 13 | 13 | 13 | 0 | 0 | 0.68 | 1.69 |
| [34] | 19 | 4 | 10 | 11 | 10 | 3 | 2 | 0.53 | 1.79 |
| [35] | 21 | 6 | 10 | 10 | 10 | 3 | 0 | 0.48 | 1.57 |
| [36] | 21 | 4 | 12 | 16 | 12 | 4 | 0 | 0.67 | 1.88 |
| [27] | 21 | 4 | 12 | 12 | 12 | 0 | 2 | 0.48 | 1.53 |
| Proposed | 21 | 4 | 10 | 14 | 10 | 0 | 0 | 0.48 | 1.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, M.F.; Bin Arif, M.S.; Mustafa, U.; Abdelrahem, M.; Rodriguez, J.; Ayob, S.M. An Improved Single-Phase Multiple DC Source Inverter Topology for Distributed Energy System Applications. Energies 2024, 17, 2146. https://doi.org/10.3390/en17092146
Ahmad MF, Bin Arif MS, Mustafa U, Abdelrahem M, Rodriguez J, Ayob SM. An Improved Single-Phase Multiple DC Source Inverter Topology for Distributed Energy System Applications. Energies. 2024; 17(9):2146. https://doi.org/10.3390/en17092146
Chicago/Turabian StyleAhmad, Mohd Faraz, M. Saad Bin Arif, Uvais Mustafa, Mohamed Abdelrahem, Jose Rodriguez, and Shahrin Md. Ayob. 2024. "An Improved Single-Phase Multiple DC Source Inverter Topology for Distributed Energy System Applications" Energies 17, no. 9: 2146. https://doi.org/10.3390/en17092146
APA StyleAhmad, M. F., Bin Arif, M. S., Mustafa, U., Abdelrahem, M., Rodriguez, J., & Ayob, S. M. (2024). An Improved Single-Phase Multiple DC Source Inverter Topology for Distributed Energy System Applications. Energies, 17(9), 2146. https://doi.org/10.3390/en17092146










