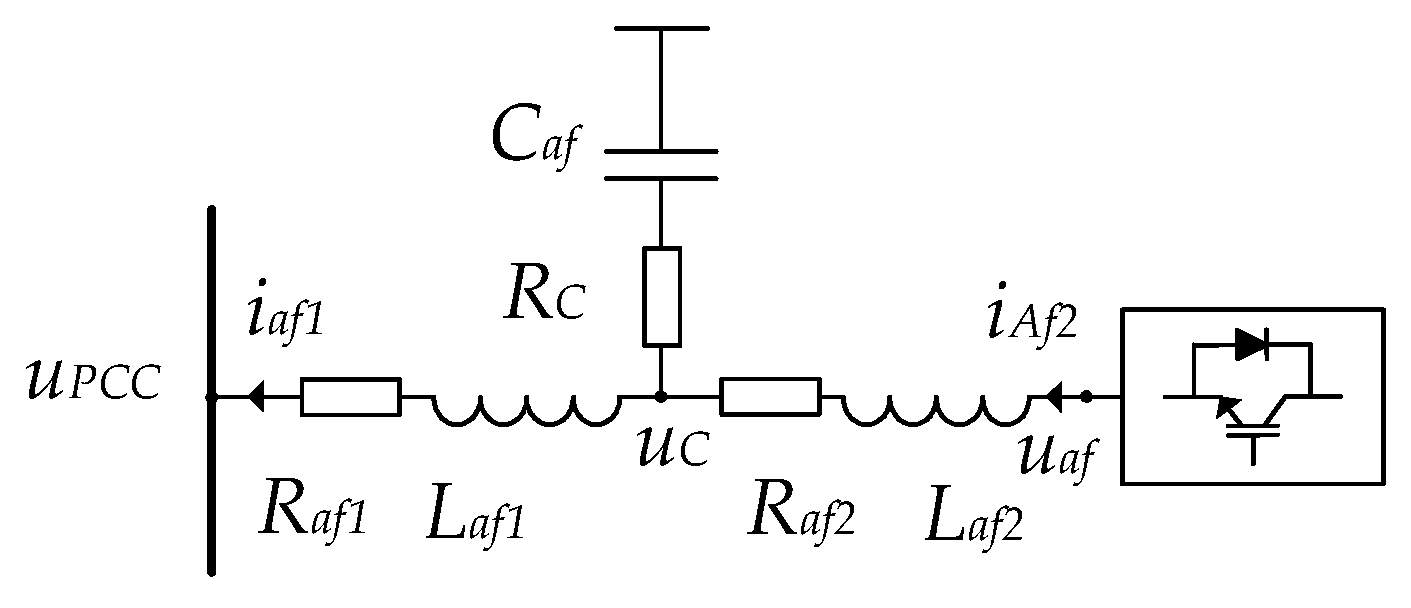1. Introduction
The electrical power system (EPS) is currently facing significant changes, largely driven by the massive integration of distributed energy resources (DER), heat pumps (HP), and an anticipated large-scale transition of the transportation sector to electric vehicles (EVs). This increase in the number of modern loads, many of which connect to the EPS through power electronic converters, presents substantial challenges not only in terms of planning and operating the EPS efficiently but also in maintaining adequate power quality (PQ) parameters. Power quality issues, particularly harmonic distortion, converter-driven instability, and harmonic instability, have become more pronounced with the widespread adoption of power electronic-interfaced equipment. As industrial processes and everyday technologies become more sophisticated, ensuring a high power quality is no longer just a preference but a critical necessity [
1,
2,
3,
4,
5].
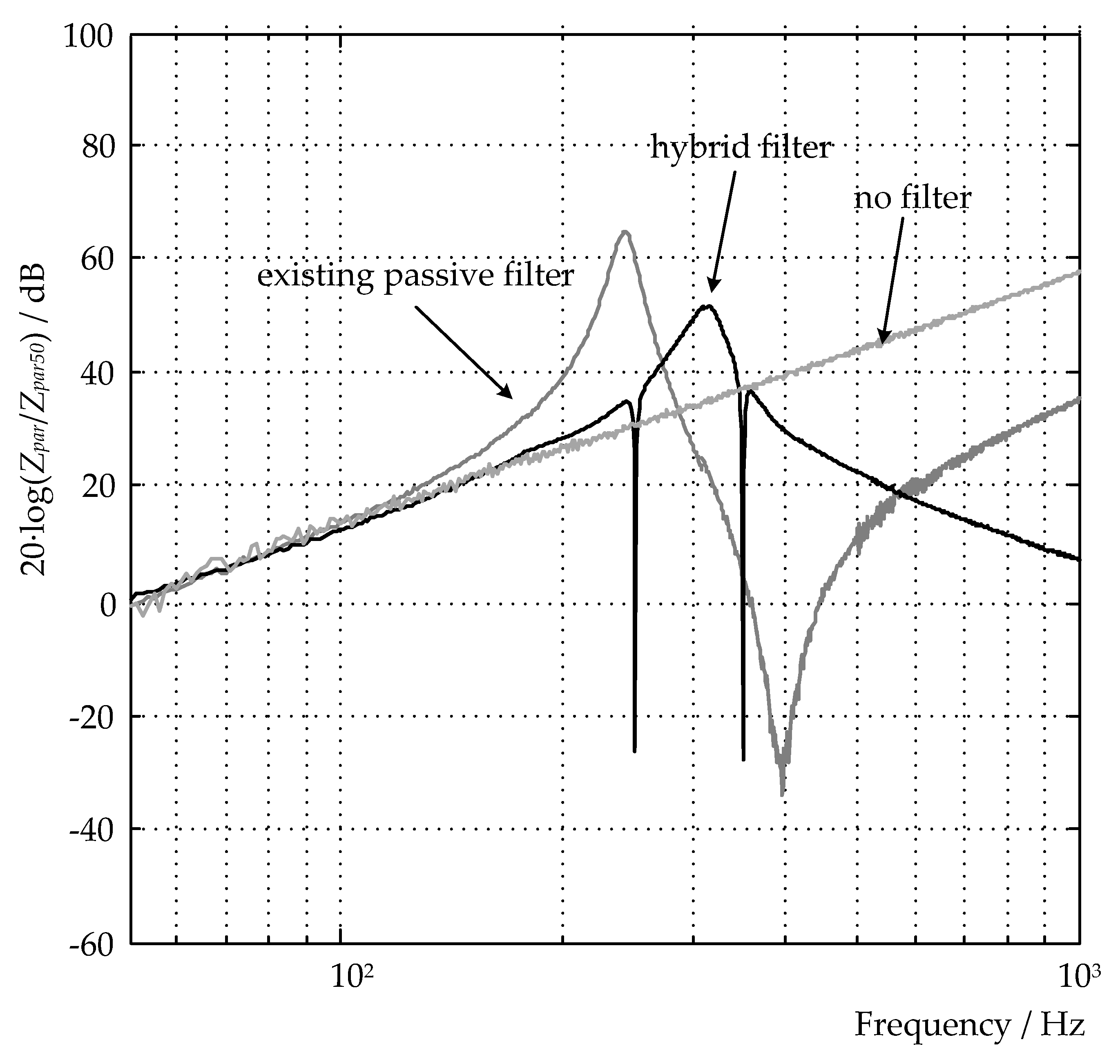
Traditionally, maintaining appropriate levels of harmonic distortions in power systems has relied heavily on passive filters. These conventional solutions are known for their simplicity and cost-effectiveness in filtering out harmonics. However, passive filters have several disadvantages; they are typically designed for specific operating conditions and lack the flexibility to adapt to dynamic changes in the network. This can lead to issues such as resonance and over- or under-compensation, potentially worsening power quality issues instead of improving them [
6,
7,
8]. On the other hand, active (converter-based) power devices offer more precise control over a wide range of frequencies and can adapt to changing conditions but come at a higher cost and complexity [
9,
10].
In this context, hybrid filters have emerged as a promising solution, combining the advantages of both passive and active filters while mitigating their respective limitations. The synergy between the passive components’ cost-effectiveness and the active components’ flexibility allows for more effective and efficient harmonic mitigation and reactive power compensation across varying conditions [
11,
12,
13,
14,
15,
16,
17,
18]. For example, the authors in [
11,
12] proposed hybrid filter topologies combining passive and active elements, demonstrating improved performance in harmonic filtering and resonance damping. However, these solutions require high ratings for the active components, which increases the costs and complexity.
There is an extensive literature on the potential of hybrid filters, highlighting various configurations and control strategies which exploit the benefits of integrated solutions. In [
12,
13], the authors proposed a series connection of the active inverter with the passive filter. They reported good filtering performance of the proposed topology; however, with the series connection of both active and passive parts, the inverter’s required current rating remains high, as the full fundamental frequency current flows through the inverter. In other cases, such as in papers [
14,
19], authors propose parallel combinations of both parts, which require the full voltage ratings of the inverter. Other authors also report some disadvantages of hybrid filters. Paper [
20] presents a hybrid system aiming to reduce point-of-common-coupling (PCC) voltage total harmonic distortion (THD); however, a significant limitation noted was the complexity of the control system needed to effectively manage the hybrid filter. In [
21], the authors addressed damping harmonic resonance with hybrid filters in industrial settings, noting that customization for specific industrial applications can add complexity to the integration process. In recent studies, for example [
22], authors discuss a new topology of hybrid active power filters that integrates passive
LC single-tuned circuits to reduce the overall system ratings. Their paper focuses on parameter design and might lack testing data to validate the theoretical improvements in stability and ratings’ reduction. In [
23], the negative impact of DC-side voltage fluctuations on the system and their effect on experimental results are discussed. The above paper highlights that controlling the DC-side voltage is crucial to enhancing the performance of hybrid filters. Our paper addresses this issue by proposing a robust control strategy for the DC-side voltage, ensuring stability, and enhancing harmonic elimination. Through simulations, we demonstrate that our approach effectively manages DC-side voltage fluctuations.
The primary goal of this paper is to introduce an improved topology that combines the advantages of passive and active components to achieve effective harmonic filtering, resonance damping, and reactive power compensation at a significantly lower cost than that of fully active systems or other hybrid filter configurations. The proposed hybrid filter involves a parallel connection of a three-phase two-level voltage-source converter (VSC) with the circuit of a double-tuned passive filter (DTPF). The analytical and simulation results show that the power rating of the active part of the hybrid filter is only around 2% of the load rating. This substantially reduces the size and (operational) cost compared to traditional setups, with dimensions up to four times smaller than those required in a series hybrid filter configuration and at least forty times smaller than a standalone active filter [
24]. A brief analysis of the hybrid filter’s dimensions is presented in this paper, with a more detailed analysis available in [
25].
The second contribution of this paper is the development of a state-feedback controller, designed to enhance the performance of the proposed hybrid filter, especially in systems with complex impedance conditions, such as those in industrial environments with harmonic resonances. The control strategies for hybrid filters traditionally use wideband approaches, with proportional control being the most common approach [
26,
27,
28,
29,
30,
31]. However, the high proportional constants needed for effective filtering tend to compromise transient performance with the proposed topology [
25]. Additionally, the poor dynamic behavior of this topology under fluctuating loads has been documented in [
32], where a proportional–integral (PI) regulator implemented in the harmonic reference frame (HRF) was used to control the active part of the hybrid filter. Other authors have analyzed various control techniques such as sliding-mode control [
28] and fuzzy neural network control [
29], which enable the precise tracking of reference signals. However, these techniques increase the system’s order and complexity, making the application of such advanced control methods more challenging. Therefore, in this paper, a state-feedback controller in HRF is proposed, tailored for each harmonic frequency, offering an effective and stable control approach. The use of a state-feedback controller offers several advantages over conventional PI or proportional–resonant (PR) controllers. Firstly, since it is based on the system model, it provides accurate control and makes real-time adjustments based on system states (voltages and currents), ensuring a good dynamic response to system changes. Secondly, the state-feedback approach utilizes all available information about the system’s current state, not just error signals. Furthermore, state-feedback controllers are highly customizable and can be tuned to address specific system characteristics, such as resonance frequencies, when used with hybrid filters.
Through detailed analyses and simulations on a real industrial network model, this paper validates the theoretical benefits of the proposed hybrid filter. The results are expected to aid in the development of a more robust cost-effective solution for reactive power compensation, harmonic mitigation, and resonance damping, thereby supporting the sustainable development of modern power systems.
The novel contributions of this paper are the following:
- −
Hybrid filter topology: We developed a novel hybrid filter topology that integrates double-tuned passive filters with a three-phase two-level voltage-source converter in a parallel connection. This design significantly reduces the power rating required for the active components, lowering the operational costs and physical dimensions compared to traditional hybrid and standalone filters. Unlike previous designs, our approach offers a cost-effective solution with enhanced harmonic attenuation.
- −
Enhanced filtering performance: The double-tuned passive filter provides superior harmonic attenuation across a wider range of frequencies, making it more effective than previous designs.
- −
State-feedback controller: A state-feedback controller tailored for each harmonic frequency is introduced, ensuring accurate control and real-time adjustments based on the system’s state. This approach improves the stability and filtering performance compared to conventional wideband control strategies like the PI or PR controllers used in existing hybrid filters.
- −
Robustness to parameter variations: Our analysis demonstrates the design’s robustness against variations in passive component parameters, highlighting the reliability and practicality of the hybrid filter in real-world applications, a critical aspect often overlooked in previous research.
The structure of this paper is as follows.
Section 2 introduces the proposed topology of the hybrid filter, explaining the configuration and benefits.
Section 3 details the design of the state-feedback controller, including its mathematical model and implementation.
Section 4 analyzes the filtering characteristics through mathematical models and simulation results.
Section 5 assesses the hybrid filter’s performance under various conditions, including steady-state and transient responses, and explores the impact of passive filter parameter variations on the performance of the system. Finally,
Section 6 concludes with a summary of the findings, the implications for filter design and operation, and future research directions.
2. Hybrid Filter Parallel Topology
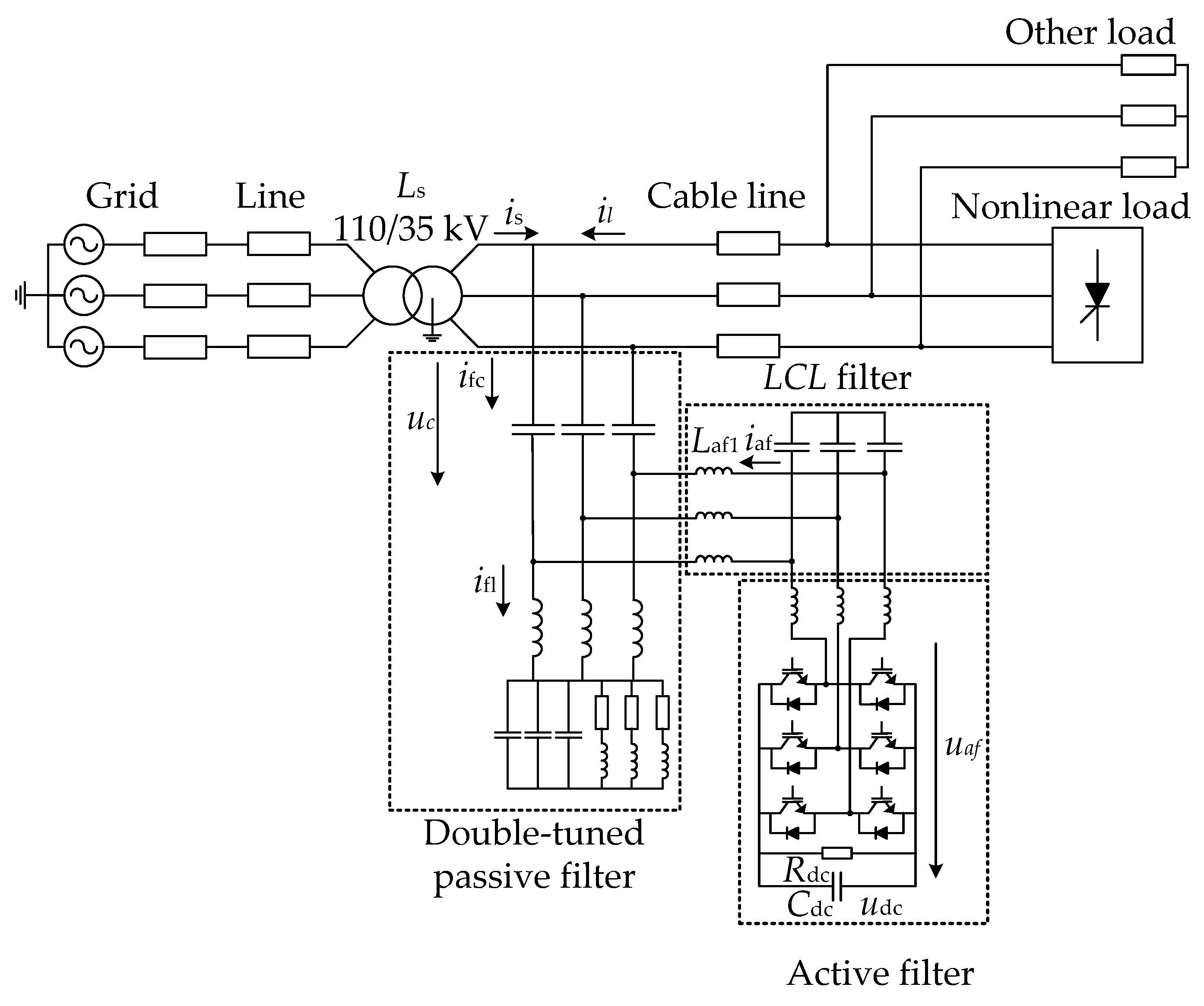
Figure 1 shows the proposed topology of the hybrid filter along with a nonlinear load, a supply transformer, and a network represented with an equivalent model. The hybrid filter comprises a three-phase two-level voltage converter, connected in parallel to the circuit of the double-tuned passive part. The system voltage is denoted by
us, with
Rs and
Ls representing the system impedance. The nonlinear load, which generates harmonic currents (
ilh), is connected to the network and depicted on the right side of the diagram.
The double-tuned passive filter is designed to mitigate specific harmonic frequencies more effectively than single-tuned filters. It includes primary tuning components such as the capacitor (Cpf), the inductor (Lpf), and the resistor (Rpf). Additionally, secondary tuning components (Cpf2 and Lpf2) enable the filter to target multiple harmonics, thereby providing better attenuation across a wider range of harmonic frequencies. The double-tuned topology has been chosen because it offers enhanced performance in filtering out harmonics, particularly those at the fifth and seventh orders, which are common in power systems with nonlinear loads.
Parallel to the passive filter is the active filter, which is configured using a two-level inverter. The choice of a two-level inverter is due to its simplicity, cost-effectiveness, and ease of control compared to multi-level inverters.
The active filter includes an LCL filter at its output, consisting of coupling inductors (Laf1 and Laf2), and a coupling capacitor (Caf). The LCL filter is used because it provides a superior filtering performance and better attenuation of the high-frequency switching harmonics generated by the inverter. The LCL filter also helps in reducing the overall ratings and power losses.
The DC side of the inverter is modeled with a DC-link capacitor (Cdc) and a resistor (Rdc) that represents the DC-side losses. The DC-link capacitor is crucial as it maintains a stable DC voltage level, which is necessary for the proper operation of the inverter.
The main advantage of this topology is that, due to the voltage drop across the capacitor Cpf of the passive filter, the voltage on the converter is relatively small (in the order of a few percent of the nominal supply voltage). Additionally, the fundamental component of the current through the converter is small due to the parallel circuit. This results in a reduced size and power rating for the active filter. Subsequently, the dimensions of the active part of the filter of the proposed topology will be analyzed. As it will be evident, the dimensions of the proposed topology are in the order of a few percent of the power of the compensated load.
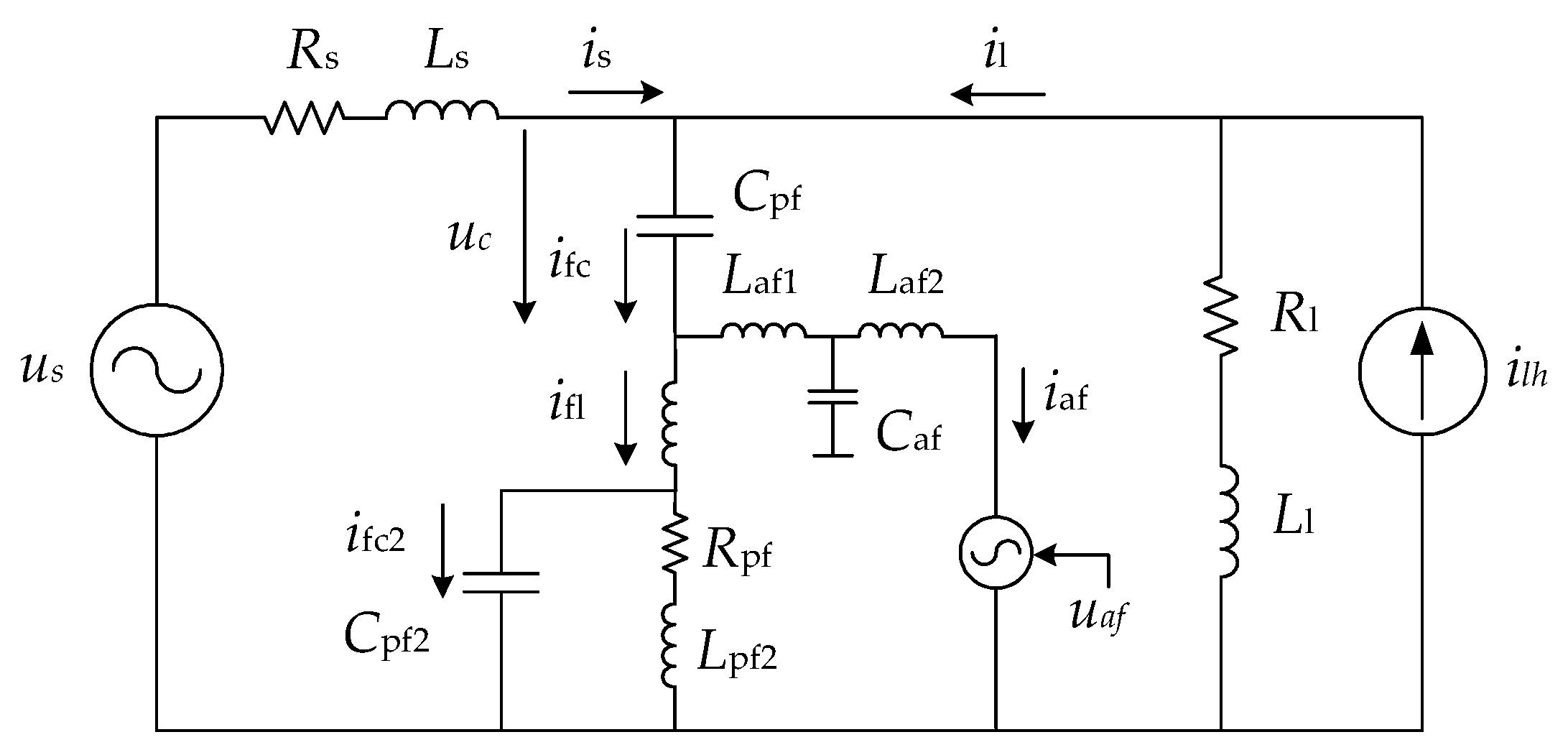
Figure 2 shows a single-line circuit of the proposed topology. It provides a simplified representation of the three-phase system, depicting all three phases with a single conductor line. This illustration facilitates the clear and straightforward visualization of the component connections and interactions within the hybrid filter without the complexity of a full three-phase layout. The symbols used are as follows: system voltage is denoted by
us, and
Rs and
Ls constitute the system impedance. The harmonic current of the nonlinear load is represented by
ilh. The load impedance is characterized by
Rl and
Ll.
Cpf,
Lpf,
Rpf,
Cpf2, and
Lpf2 are the elements of the double-tuned passive filter.
Laf1,
Laf2, and
Caf are the coupling impedances of the active filter (
LCL filter). The converter output voltage is represented by an ideal voltage source,
uaf.
Required Ratings of the Active Part
The analysis of the voltage and current dimensions of the proposed filter topology for the use of a single-tuned passive filter was presented in [
25]. Below, we summarize the key equations of the rating analysis when using the topology proposed in this paper. Some of these equations will be needed later for deriving the controller for the active part.
The active filter must provide a small component of base voltage at the point of common coupling (PCC) to divert the base active current to flow in the parallel circuit. This voltage is equal to the voltage drop on the parallel circuit for a pure double-tuned passive filter, and it depends on the tuning frequencies of the passive part. It can be expressed as follows:
Here, f1 is the fundamental frequency (i.e., 50 Hz), and ft1 and ft1 are the tuned frequencies of the passive filter.
The harmonic voltage across the active part of the hybrid filter is equal to
where the subscript
h denotes the harmonic order,
uafh represents the voltage across the active part of the hybrid filter at harmonic order
h,
ush is the source voltage at harmonic order
h,
ilh is the load current at harmonic order
h,
XCh is the reactance of the passive filter capacitor at harmonic order
h, and
i represents the imaginary unit.
The current flowing in the active part is given by the following:
where
fh is the frequency of the corresponding harmonic, and
iafh is the active filter current at harmonic order
h.
The power ratings are given by (4).
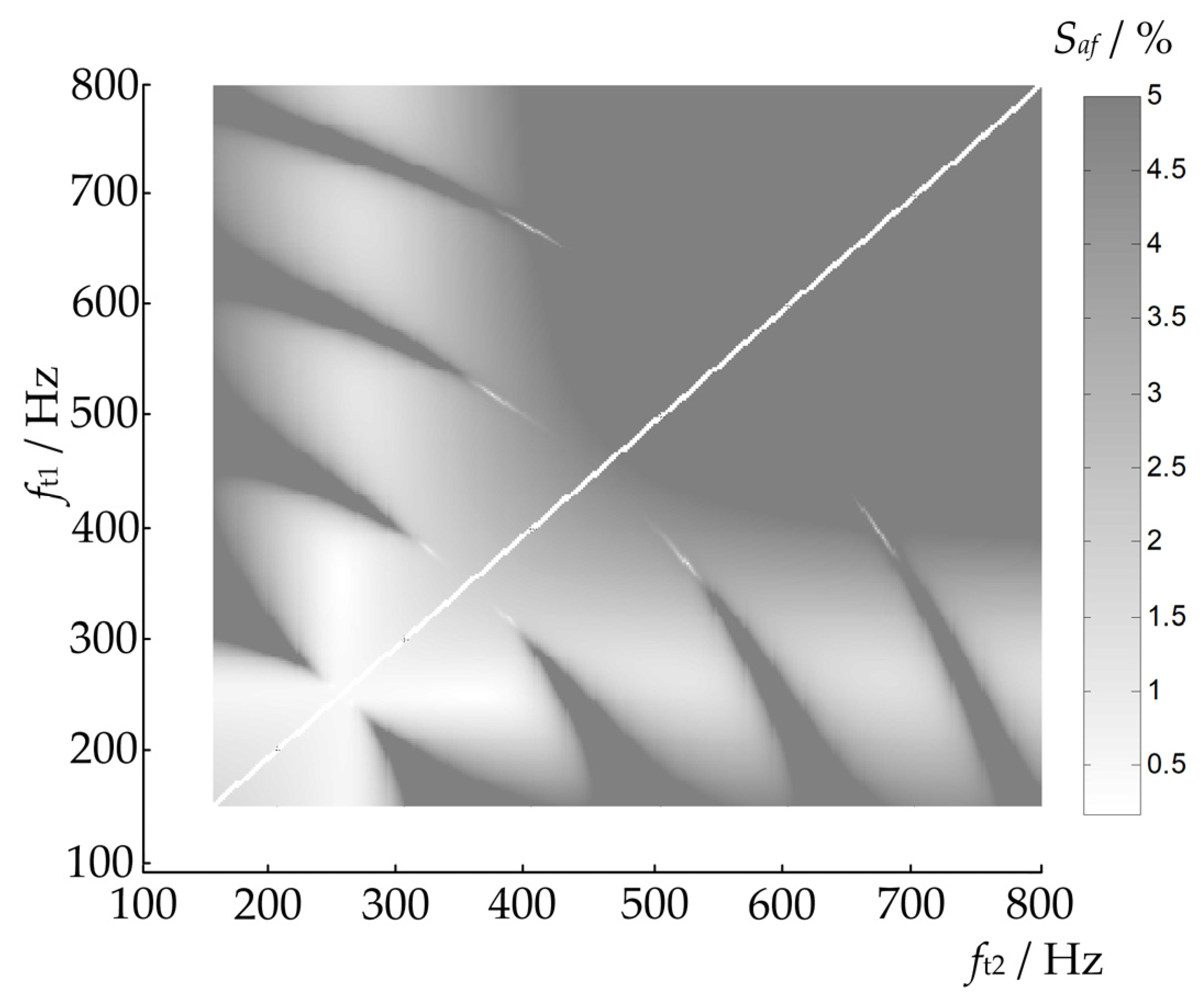
Figure 3 shows the required dimensions of the active part of the hybrid filter for various tuning frequencies of the passive part. As it can be seen from the figure, the dimensions of the active part are strongly dependent on the tuning frequency of the passive part or the combinations of tunings and have the lowest values (around 0.5%) when both stages of the passive part of the filter are tuned close to the harmonics present in the network (in this case, the fifth and seventh harmonics).
The figure above presents a heatmap where the x-axis represents the tuning frequency ft2 of the second stage of the passive filter, and the y-axis represents the tuning frequency ft1 of the first stage. The color gradient indicates the required power rating of the active filter Saf as a percentage of the total system power. The white diagonal line indicates points where ft1 = ft2, which are not practical since the filter stages should be tuned to different frequencies to target different harmonics effectively.
When the passive filter stages are tuned close to the prominent harmonic frequencies in the network, such as the fifth (250 Hz) and seventh (350 Hz) harmonics, the active filter’s power rating is minimized. This is because the passive filter stages effectively attenuate these harmonics, reducing the burden on the active filter. Consequently, the active filter mainly compensates for any residual harmonics, allowing it to operate with smaller dimensions and lower power ratings.
As the tuning frequencies of the passive filter deviate from these optimal points, the passive filter’s effectiveness in harmonic attenuation is lower. This increases the harmonic content that the active filter must compensate for, thereby increasing its required dimensions and power rating. The heatmap shows that the active filter’s power rating increases significantly as the tuning frequencies move away from the optimal points, illustrating the importance of the proper tuning of the passive stages.
It can also be observed that the theoretically lowest dimensions are even below 0.5%, which was the smallest dimension for a singly tuned filter as previously noted in [
25]. Namely, as established in [
25], in the case of a single-tuned passive filter, the dimensions of the necessary active part are largely conditioned by the tuning of the passive part and increase significantly as they deviate from the optimal tuning. By using a double-tuned filter, this problem is largely mitigated. There are several suitable tuning combinations where the dimensions of the active part of the filter remain low (e.g., <2%).
3. Control Algorithm Design
To improve the filtering characteristics of the proposed filter and ensure a stable operation, the linear–quadratic (LQ) regulator in state space is presented, which will be derived in the
dq0-coordinate system based on the mathematical models from
Section 3.1 and
Section 3.2. The LQ regulator will be derived for symmetric voltage and current conditions. In addition to the basic current regulation loop which allows the tracking of reference values, the regulation of the DC voltage will also be presented in more detail, and the control branch of the regulator will be described, which will function to limit the current through the voltage converter. The controller will be designed to control the hybrid filter shown in
Figure 1. The algorithm has never been used in the literature for controlling the presented topology of the hybrid filter.
The regulator in the state space will be implemented based on a general mathematical model, which will be presented in
Section 3.1. The state variables in the model of the regulator are the network current
is and the voltage across the capacitor of the passive filter
uc. The number of state variables usually (but not always) corresponds to the number of reactive elements in the circuit—the number of inductors and capacitors. For the capacitors, the state variable is typically voltage, and, for the inductors, it is the current. To significantly simplify the mathematical modeling of the hybrid filter, we considered the following simplifications. If the coupling impedance of the active part (
LCL filter) or, more correctly, the voltage drop across the impedance is small, then the current through the impedance does not significantly affect other state variables (
is or
uc). This allows one to omit the current of the impedance in the mathematical model of the device.
3.1. Mathematical Model of the Hybrid Filter in State Space
To derive the regulator in the state space, a state-space mathematical model for the specific topology presented in
Section 2 is required first. The mathematical model will be derived in the rotating
dq-coordinate system.
In electrical engineering, the dq0 transformation, or the “direct-quadrature-zero” transformation, is used to simplify the analysis of three-phase electrical circuits. It is a mathematical transformation that has the property of converting a three-phase system into two components (dq) under symmetrical conditions—the zero component is zero in symmetry—and alternating quantities become direct quantities if the transformation is synchronized with the fundamental frequency (i.e., 50 Hz). This greatly simplifies the calculations, which can then be performed on direct quantities before using the inverse transformation to convert the dq quantities back into a three-phase system. This transformation is widely used in the analysis of three-phase synchronous machines or to simplify control algorithms for power converters. The dq0 transformation is very similar to the transformation first proposed by Robert H. Park in 1929, although there are some minor differences.
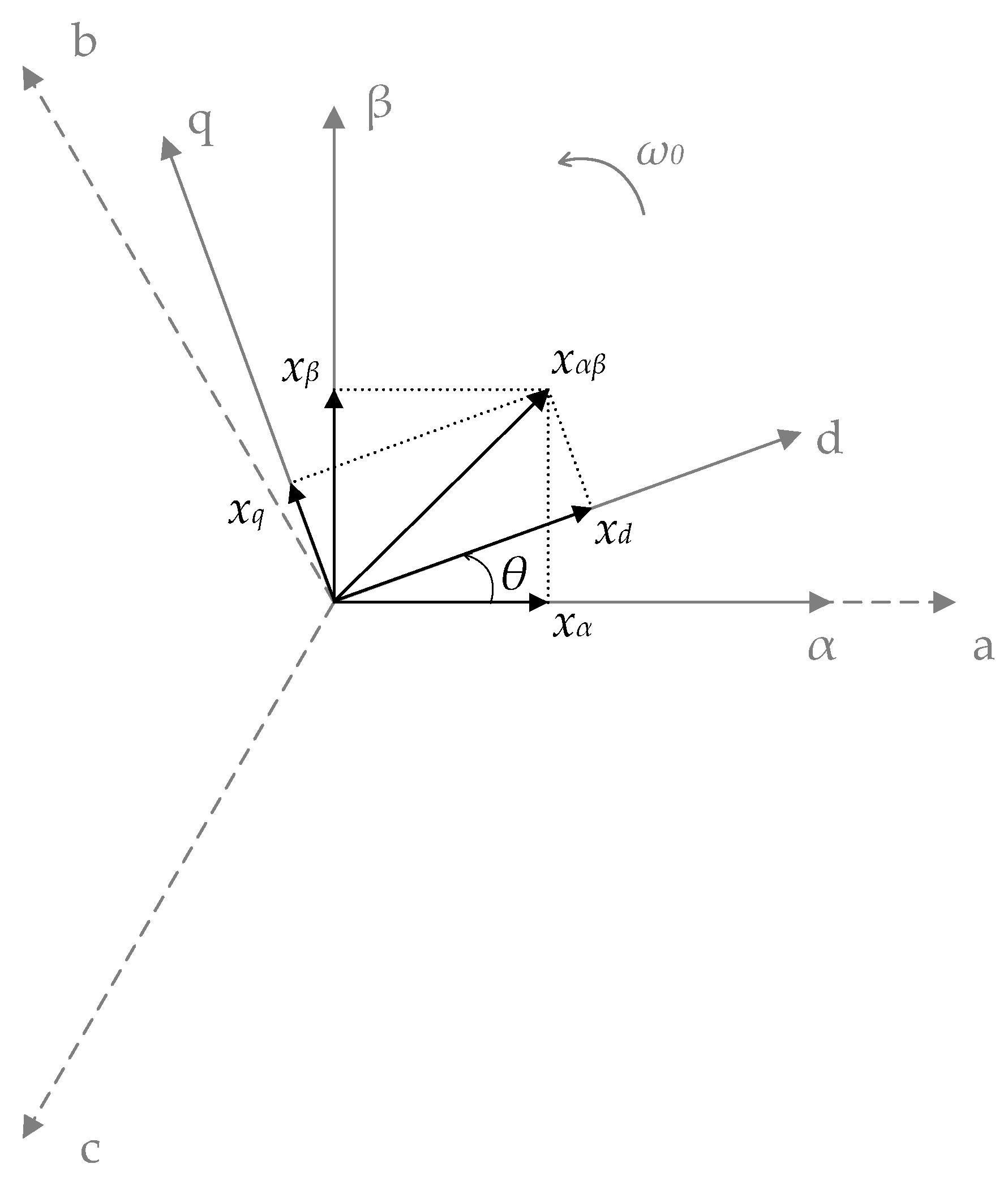
Three-phase quantities, whose sum equals zero, can be represented by a single vector in the complex plane.
Figure 4 illustrates the relationships between the stationary (αβ) coordinate system and the rotating (dq) coordinate system, which rotates at synchronous speed θ = ω
1t. The orthogonal projections of the vector
xαβ onto the axes of the three-phase system provide the instantaneous values of the three-phase quantities. If the projection is performed onto the stationary orthogonal axes αβ instead of the phase axes, we obtain the Clarke or diagonal components.
To write the equations in the state space, we first define the state variables
xi, which form the state vector
x. For the given topology shown in
Figure 1, with the equivalent circuit shown in
Figure 2, the voltage on the capacitor
uc and the current of the system inductance
is are chosen as the state variables. The coupling impedance of the active part of the filter is omitted, and the load impedance is considered as an infinite value, which represents the worst case (ideal harmonic current source). Other assumptions are that the converter voltage
uaf influences the dynamics of the system inductance current
is but does not directly control the capacitor voltages
uc, and that disturbances from the source voltage and the load current impact the dynamics of the inductor current and the capacitor
Cpf voltage.
The state-space mathematical model describes a linear system with n first-order differential equations, where n indicates the order of the system. The equations are written in a three-phase system, for one phase. The variables are given in vectors, and the algebraic and differential equations are in matrix form.
According to Kirchhoff’s laws for the given topology (
Figure 2) and after a transformation to the
dq-coordinate system, we obtain the following:
Next, the state vector, the input vector, and the vector of external variables for the system shown in
Figure 1 are defined:
where
- −
T is the operator for matrix transposition,
- −
isd,q are the d- and q-components of the system current,
- −
ucd,q are the d- and q-components of the capacitor voltage,
- −
uafd,q are the d- and q-components of the voltage of the active filter (reference value),
- −
usd,q are the d- and q-components of the supply voltage,
- −
ild,q are the d- and q-components of the load current.
A linear system of
n first-order differential equations is written as
and
The matrices in (9) and (10) are given as follows:
We assume that the parameters
Rs,
Ls, and
Cpf in (11) and (12) are constant. The mathematical model provides the state of the network shown in
Figure 1 at any time. The system is linear and time-invariant in the
dq-coordinate system. Due to Park’s transformation, the equations are coupled via the coupling term related to the fundamental frequency of the system or the angular velocity of the rotating coordinate system. By adjusting the angular velocity
ω, System (9) can be used for different harmonic frequencies. In the next subsection, the mathematical model will be used to derive the state-space controller.
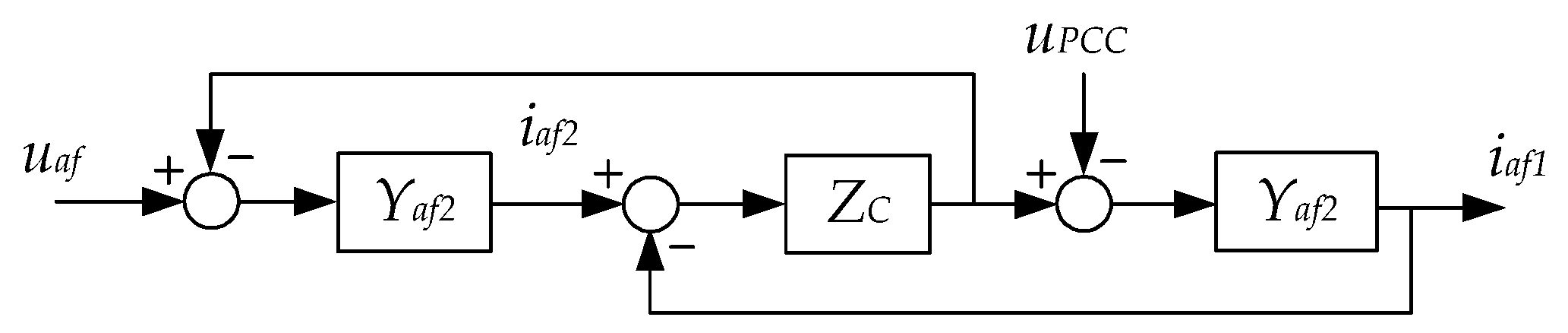
In
Figure 5, the mathematical model is represented graphically.
3.2. Design of the Control Algorithm in State Space
If the measurements of all the state variables are available, the control law can be expressed as follows:
where
K is the control matrix.
The purpose of the control is to keep the difference r − x as close to 0 as possible, where r is the vector of the reference values. The above control law does not allow this because there are external variables d (“disturbances”) present that cannot be influenced (e.g., harmonically distorted supply voltage and distorted load current).
This problem is addressed by adding an integral term. The system of equations in the state space is upgraded with a new state variable:
We obtain the following control equation (without feedback):
Given that System (9) is controllable, the linear–quadratic regulator (LQR) can be written as follows:
xI is the output from the integrator, defined as follows:
Inserting (18) into (9) results in the matrix equation of the regulator in
dq-coordinates without a feedback loop:
The matrix equation of the regulator in
dq-coordinates with a feedback loop is, thus, the following:
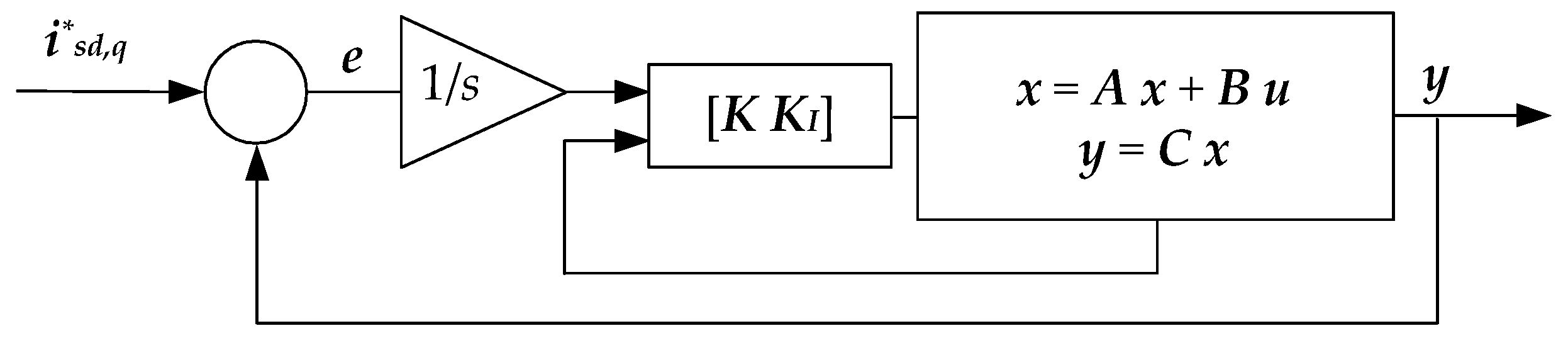
The diagram of the main current loop of the regulator in state space is shown in
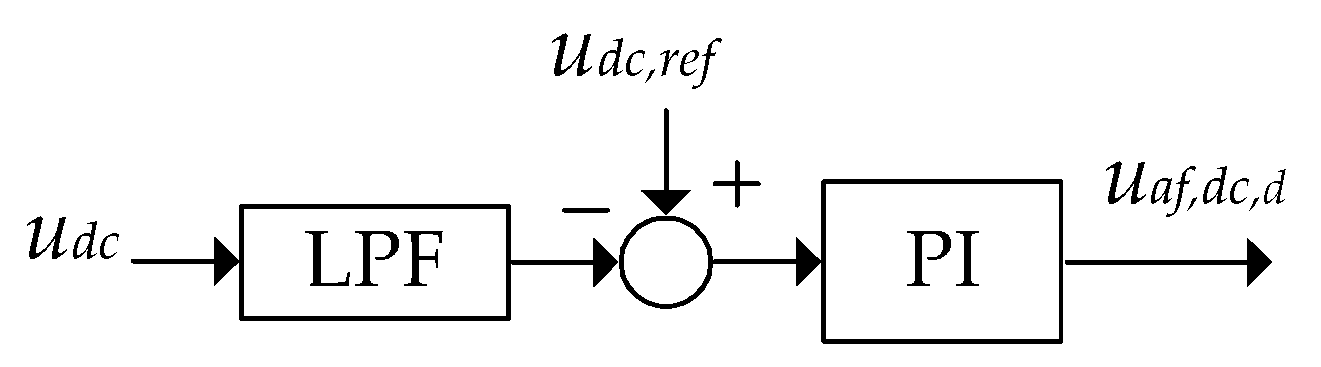
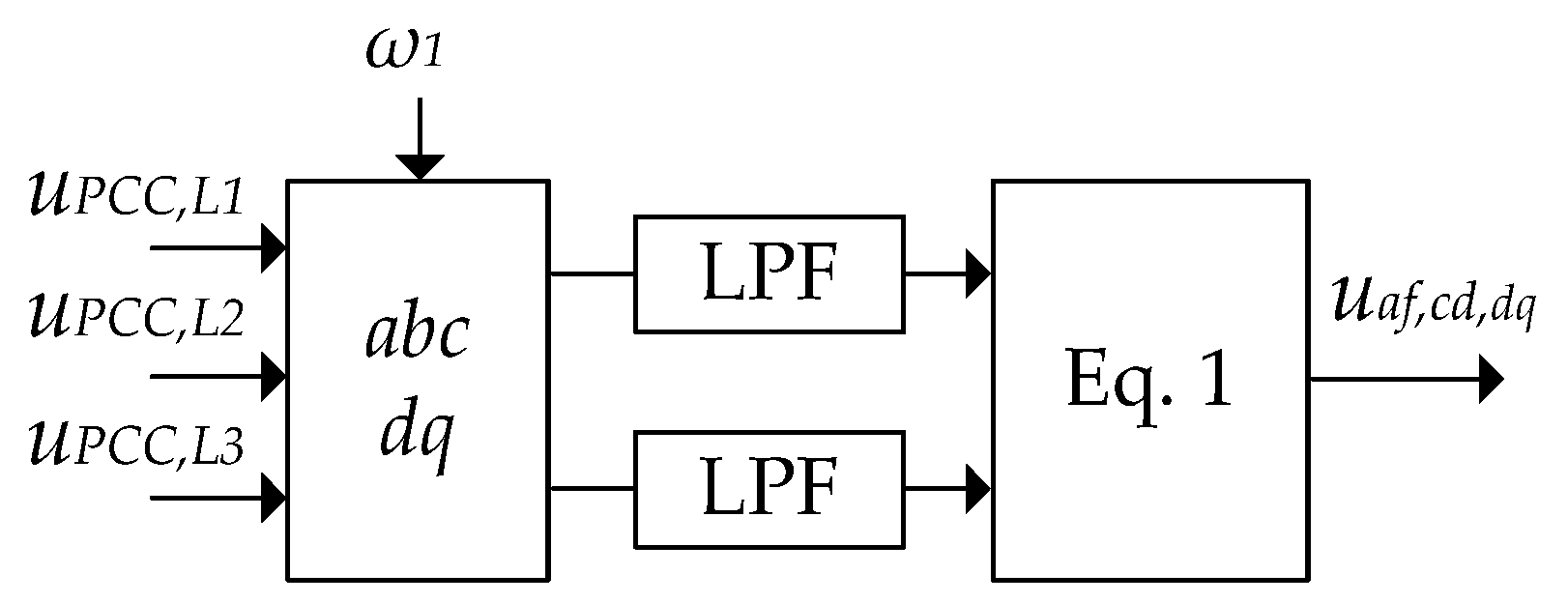
Figure 6. The DC voltage controller and the control branch for current redirection are shown in
Figure 7 and
Figure 8. The outputs of all the control branches of the controller are ultimately summed into a combined output variable,
uaf, which represents the input to the modulator.
The next important step in designing the state-space regulator is determining the constants K and KI. To determine the constants, we need the values of the network elements, which will be presented in the next section.
3.3. DC Voltage Regulation
The proper regulation of the voltage on the DC side of the converter is essential for the efficient operation of the device. The principle of DC voltage regulation is based on active power, where charging the capacitor with active power raises the DC-side voltage, and discharging the capacitor lowers it. According to pq-theory, the DC component in the dq-coordinate system represents the active power component; hence, regulation is performed in the synchronous-rotating coordinate system.
As shown in
Figure 7, the difference between the measured and filtered actual DC voltage and the reference voltage value serves as the input for the PI component, whose output corresponds to the
d-component (the reference value of the
q-component is zero). Using a low-pass filter with a tuning frequency of 20 Hz, we remove harmonic currents and other distortions from the measured voltage. The output of the regulator is added to the reference voltage value.
3.4. Redirection of the Fundamental Current Component
To achieve the lowest current ratings in the active part of the filter, the fundamental frequency filter current must be redirected to the parallel circuit of the double-tuned filter. For this purpose, a control branch is added to the main current loop of the regulator, which is shown in
Figure 8. In the control branch, the voltage drop across the parallel circuit is calculated as it would be without the influence of the active part of the filter, according to Equation (1). Consequently, a very small component of the fundamental frequency current flows through the active part of the filter, which is necessary for charging the DC capacitor.
3.5. General Guidelines for Designing Hybrid Filters
In this section, a concise presentation of the general design guidelines for the hybrid filter described in this paper is provided. These guidelines are intended to assist engineers and researchers in effectively designing, implementing, and optimizing hybrid filters for improved harmonic filtering and resonance damping in electrical power systems.
Presented parallel topology: Utilize a parallel connection of a three-phase two-level voltage-source converter with a double-tuned passive filter. This configuration reduces the power ratings and costs.
Component selection: Select and parameterize double-tuned passive filters based on the dominant harmonic frequencies in the network. Ensure that the passive components (capacitors and inductors) are tuned close to the present harmonics to improve harmonic attenuation and minimize the physical size of the active components.
Calculate necessary ratings: Use detailed equations from this paper to determine the minimal active-part ratings required for effective performance, considering the tuning frequencies and expected harmonic levels.
- 2.
Control Algorithm Design
Develop a state-space control strategy: Design a state-feedback controller tailored to each harmonic frequency. This controller should be based on a state-space mathematical model of the hybrid filter system.
Implement LQ regulator: Utilize a linear–quadratic regulator derived in the dq0-coordinate system.
Parameter optimization: Use mathematical modeling to derive the necessary control parameters. Ensure that the regulator can track reference values effectively while managing the dynamic behavior of the hybrid filter under varying load conditions.
- 3.
Simulation and Validation:
Modeling and simulation: Simulate the hybrid filter using EMT software like PSCAD to evaluate performance under different scenarios, such as steady-state and transient conditions.
Performance assessment: Analyze the filter’s effectiveness in real-time simulations to ensure that it meets the desired filtering characteristics, focusing on the reduction inharmonic distortions and maintaining system stability.
- 4.
Measurement Methods for Passive Components
For designing a reliable hybrid filter, accurately characterizing the passive components, such as capacitors and inductors, is crucial. State-of-the-art measurement methods are essential to ensure proper characterization, directly impacting the filter’s performance:
Impedance analyzers: Advanced impedance analyzers offer comprehensive impedance measurements across various frequencies. These devices help in understanding the frequency-dependent behavior of inductors and capacitors, which is vital to designing filters which operate effectively across a range of harmonic frequencies.
Network analyzers: Vector network analyzers (VNAs) can measure the complex impedance of passive components with high precision. VNAs are particularly useful for characterizing the parasitic elements of inductors and capacitors, which can significantly impact the performance of hybrid filters. For example, the authors in [
26] discuss using VNAs to overcome the effect of test fixtures on the measurement of parasitic in capacitors and inductors. They highlight the importance of compensating for parasitic effects to ensure accurate impedance measurements.
Quality factor (Q) measurement: The quality factor, or Q, of inductors and capacitors is a critical parameter that affects filter performance. High-Q components result in lower energy losses and better filtering characteristics. Instruments like Q meters or impedance analyzers can accurately measure the Q factor. The authors in [
27] describe using VNA-based fixture adapters for wideband accurate impedance extraction of single-phase EMI-filtering chokes, emphasizing the need for systematic parasitic de-embedding to achieve precise measurements up to 120 MHz.
6. Conclusions
The main objective of this paper was to propose and validate an improved parallel hybrid filter configuration that incorporated both passive and active filter components, enhancing harmonic filtering and resonance damping in electrical power systems. The proposed topology utilized a double-tuned passive filter in parallel with a three-phase two-level voltage-source converter, which allowed for a considerable reduction in power rating and operational costs. As demonstrated, the double-tuned design of the passive filter significantly reduced the dimensions of the active part because the ratings were highly dependent on the tuning frequency of the passive components. Our findings indicated that the smallest dimensions (theoretically below 0.5%) were achieved when the passive part was tuned close to the harmonic components present in the network. Tuning the filter at 245 Hz and 395 Hz resulted in reducing the dimensions of the active part to 135 kVA, which was approximately 2.5% of the size of the passive part of the device.
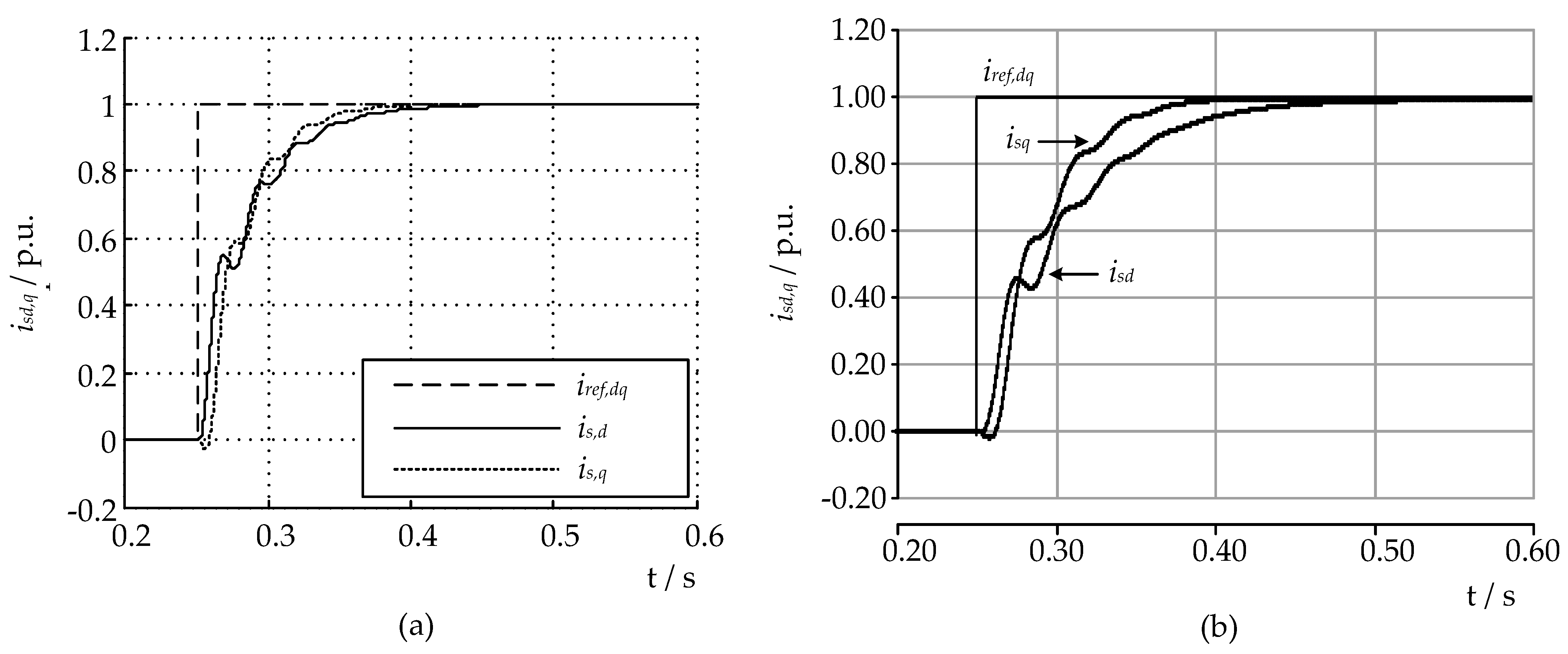
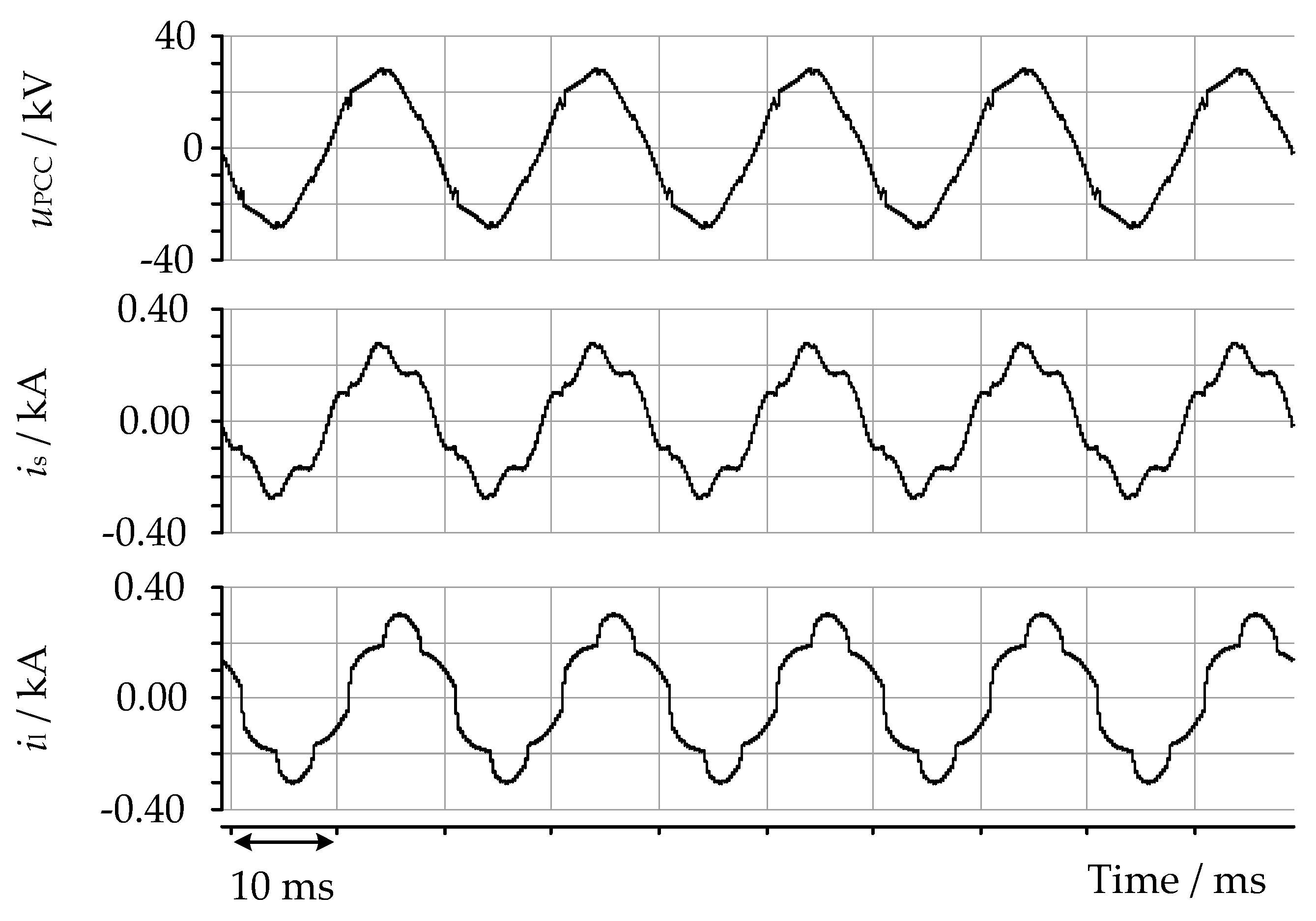
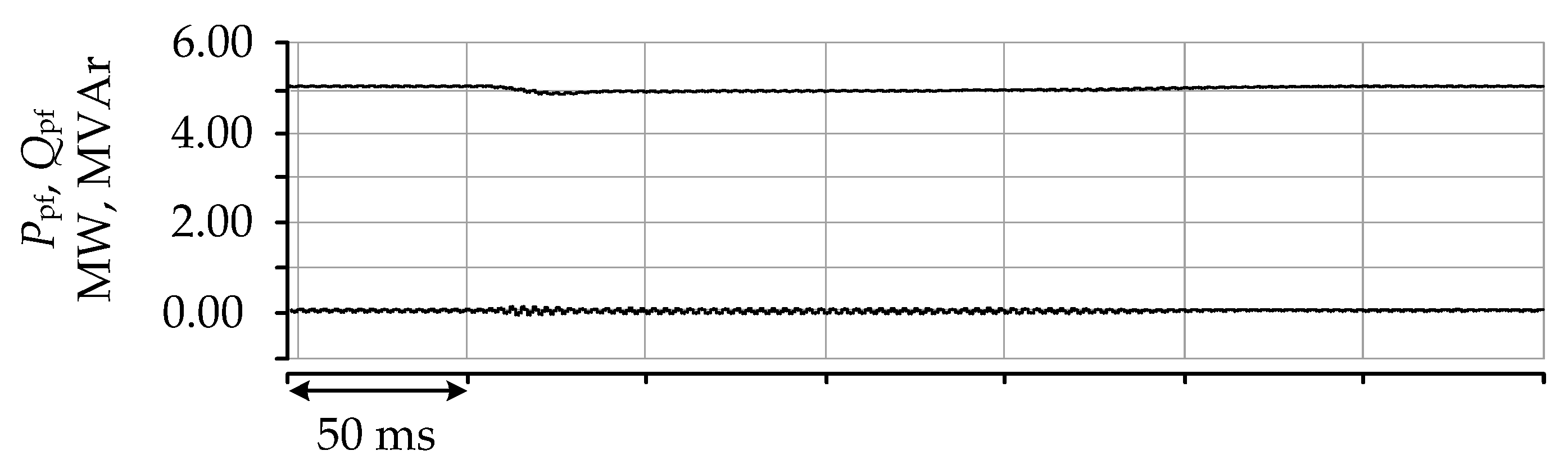
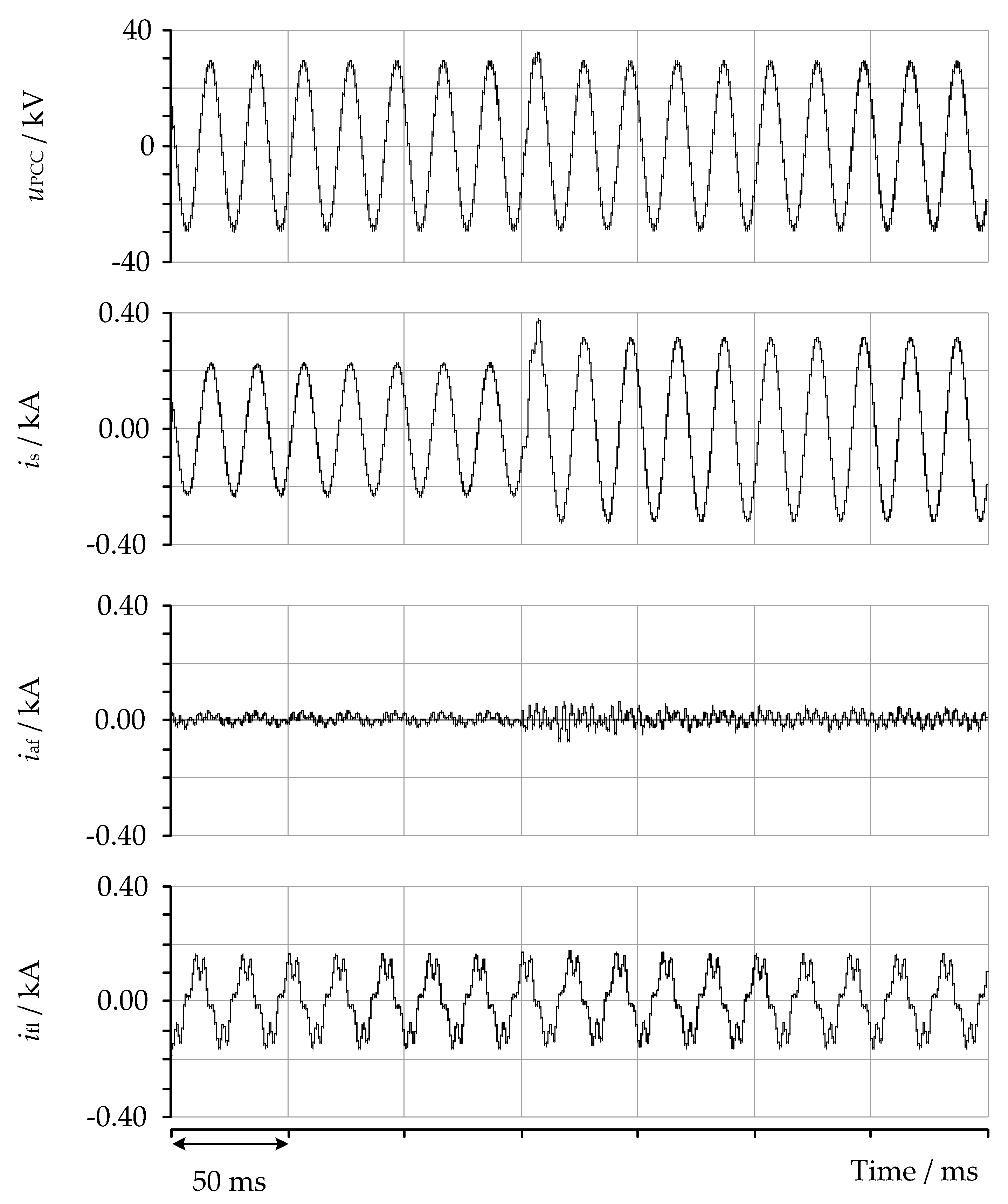
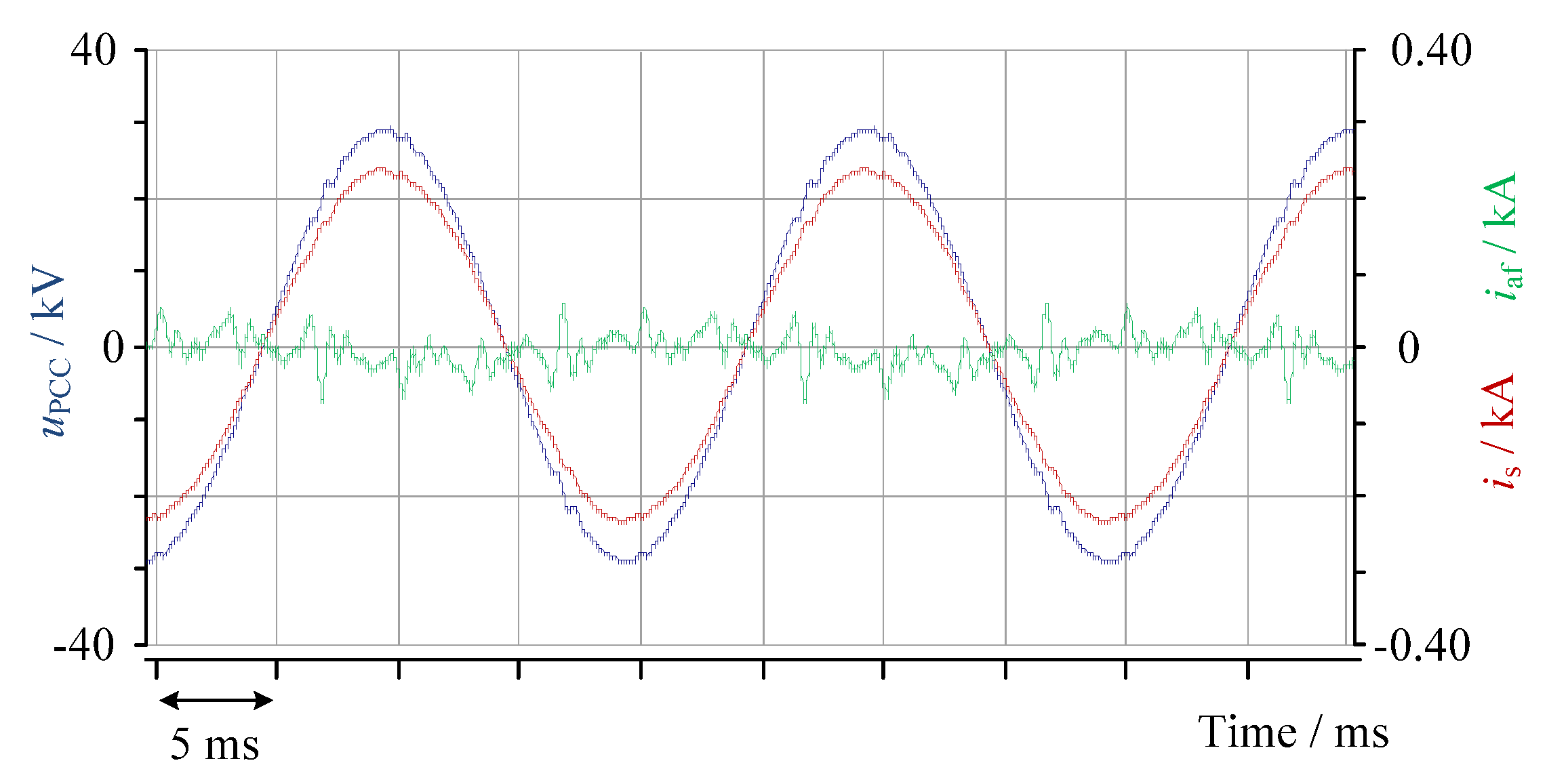
In the second part of the paper, a state-feedback controller was presented, and a mathematical model was developed for designing the controller. The effectiveness of the proposed hybrid filter was demonstrated through computer simulations using a real industrial network model. The results showed that the hybrid filter offered an effective solution for reactive power compensation and harmonic filtering. The filter operated stably during changes in load current and the startup of the device, quickly reached a new steady state, and did not cause any other undesirable effects.
The proposed hybrid filter topology and control methodology provide a robust solution for enhancing power quality in industrial electrical systems. The reduction in active filter dimensions leads to lower costs and increased efficiency, making the solution feasible for widespread (industrial) application. Additionally, the approach is adaptable to other topological structures, offering flexibility in different contexts.
However, this study has some limitations. The impact of variations in the passive component parameters was analyzed, showing the design’s robustness against potential deviations expected over the operational lifespan. As it has been shown, these deviations can affect the filtering performance and, in some more extreme cases, could lead to unstable operation. This topic needs further research. Future work will also focus on a more detailed harmonic analysis, including potential supply-side distortions, and will investigate the coupling of dq-components on the stability of the control algorithms. Active damping techniques for the LCL filter and the implementation of the proposed solutions on a laboratory prototype are also planned, which will provide practical insights and validation.
Overall, this research contributes to the advancement of hybrid filtering techniques, promoting improved harmonic mitigation and power quality in industrial applications. The findings have significant implications for designing cost-effective and efficient harmonic filters.