Online EVs Vehicle-to-Grid Scheduling Coordinated with Multi-Energy Microgrids: A Deep Reinforcement Learning-Based Approach
Abstract
1. Introduction
- (1)
- Integration of V2G and multi-energy DR: Unlike existing literature, which often focuses solely on V2G scheduling or multi-energy DR in isolation, our framework integrates both aspects into a unified scheduling model. This integration allows for coordinated management of V2G and multi-energy flexible loads, maximizing the overall profitability of MMOs while adhering to operational constraints.
- (2)
- DRL-based online scheduling framework with novel SAC algorithm: A novel online scheduling framework is proposed that leverages DRL to optimize the utilization of EV batteries within multi-energy microgrids. By formulating the scheduling problem as an MDP and employing a SAC algorithm, our framework dynamically schedules V2G activities in response to real-time grid conditions and energy demand patterns.
2. Formulation of V2G Scheduling Coordinated with Multi-Energy Microgrids
2.1. The Overall Framework
2.2. The Upper-Level Problem
2.3. The Formulation of Lower-Level Problem
3. MDP Formulation for MMOs Online V2G Scheduling in Multi-Energy Microgrids
3.1. States
3.2. Actions
3.3. Reward
3.4. Transition Function
4. SAC Algorithm for Solving MDP Formulation
4.1. Preliminaries
4.2. Training Process
| Algorithm 1 The Proposed DRL-based Online V2G in Multi-energy Microgrids with SAC | |
| 1: | Initialize replay buffer |
| 2: | Initialize actor , critic , and target network |
| 3: | for each epoch do |
| 4: | for each state transition step do |
| 5: | Given , take actions based on (32) |
| 6: | Observe the multi-energy demands (19) with as V2G scheduling and multi-energy prices |
| 7: | Solve the scheduling model and obtain operation costs |
| 8: | Receive and record them in buffer |
| 9: | end for |
| 10: | for each gradient step do |
| 11: | |
| 12: | |
| 13: | |
| 14: | |
| 15: | end for |
| 16: | end for |
5. Case Studies and Discussion
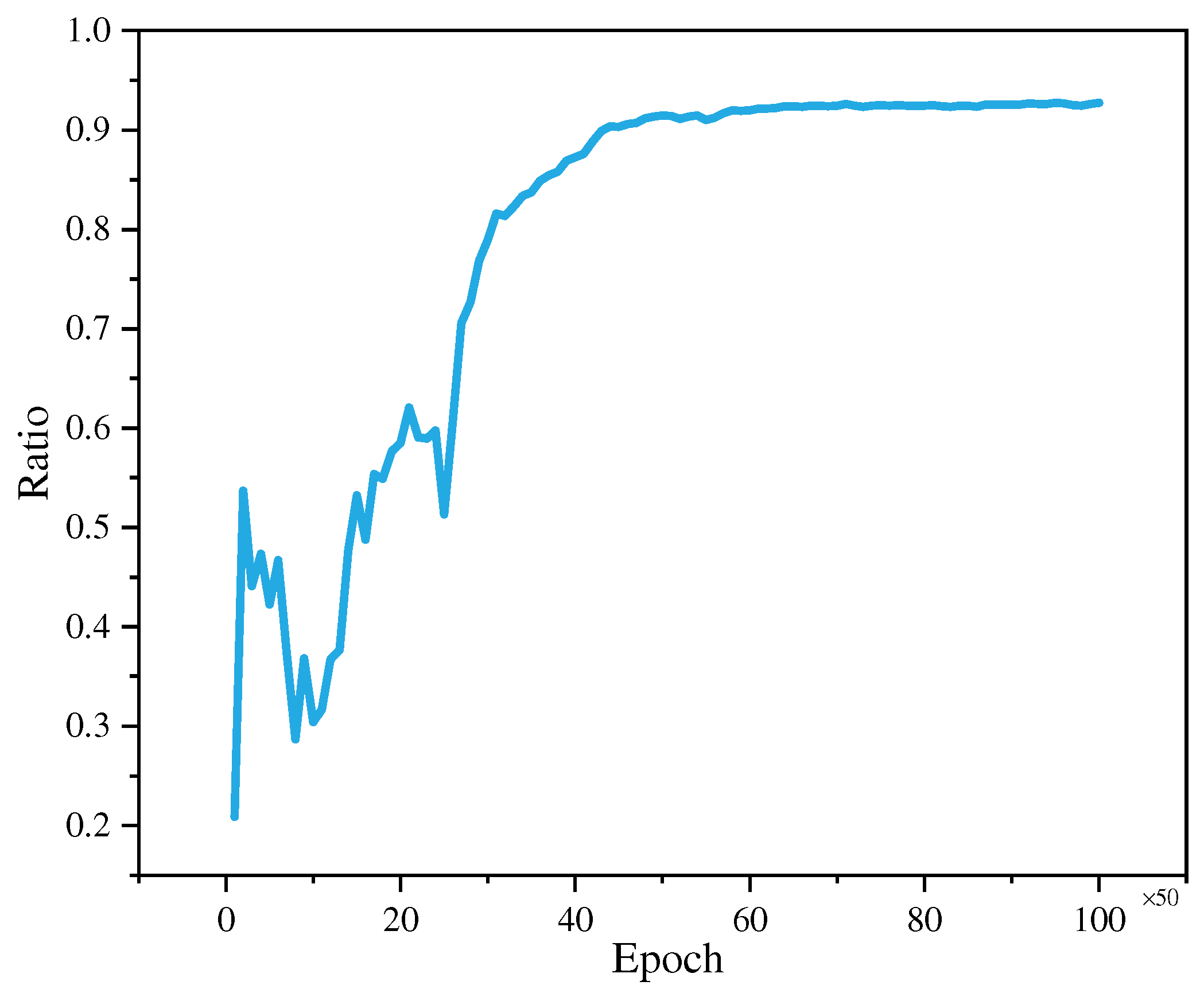
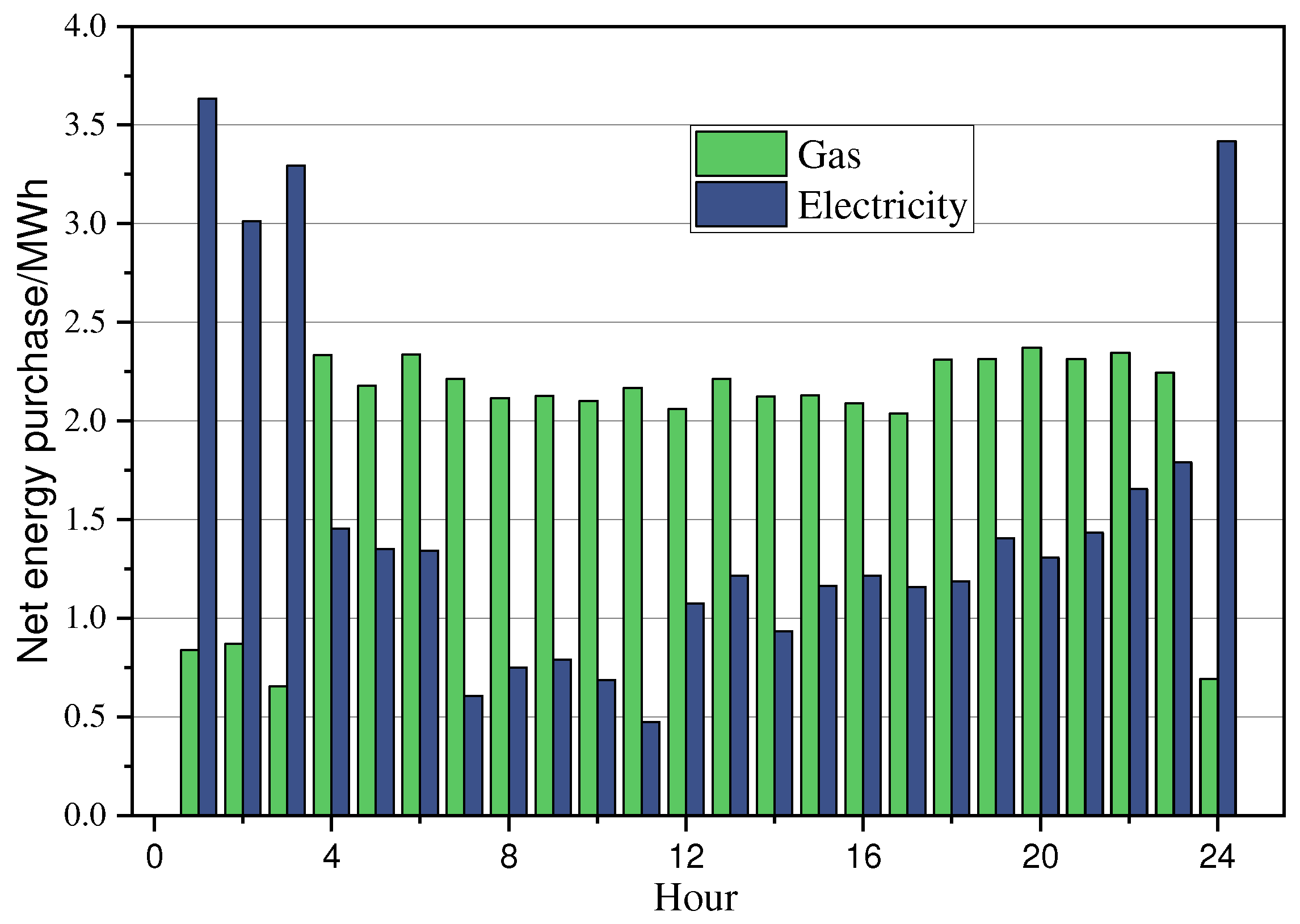
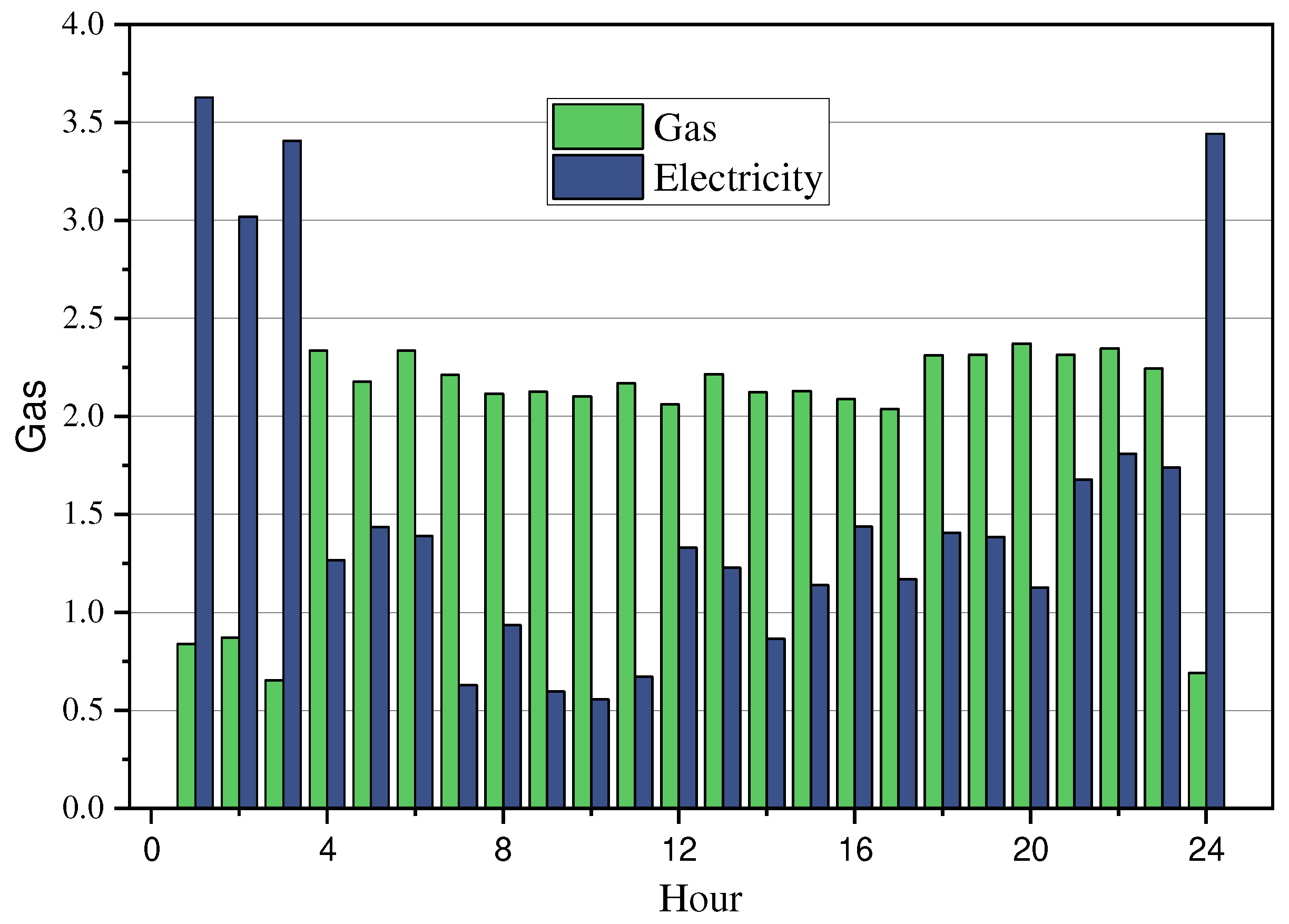
5.1. Training Process and Results of Case I
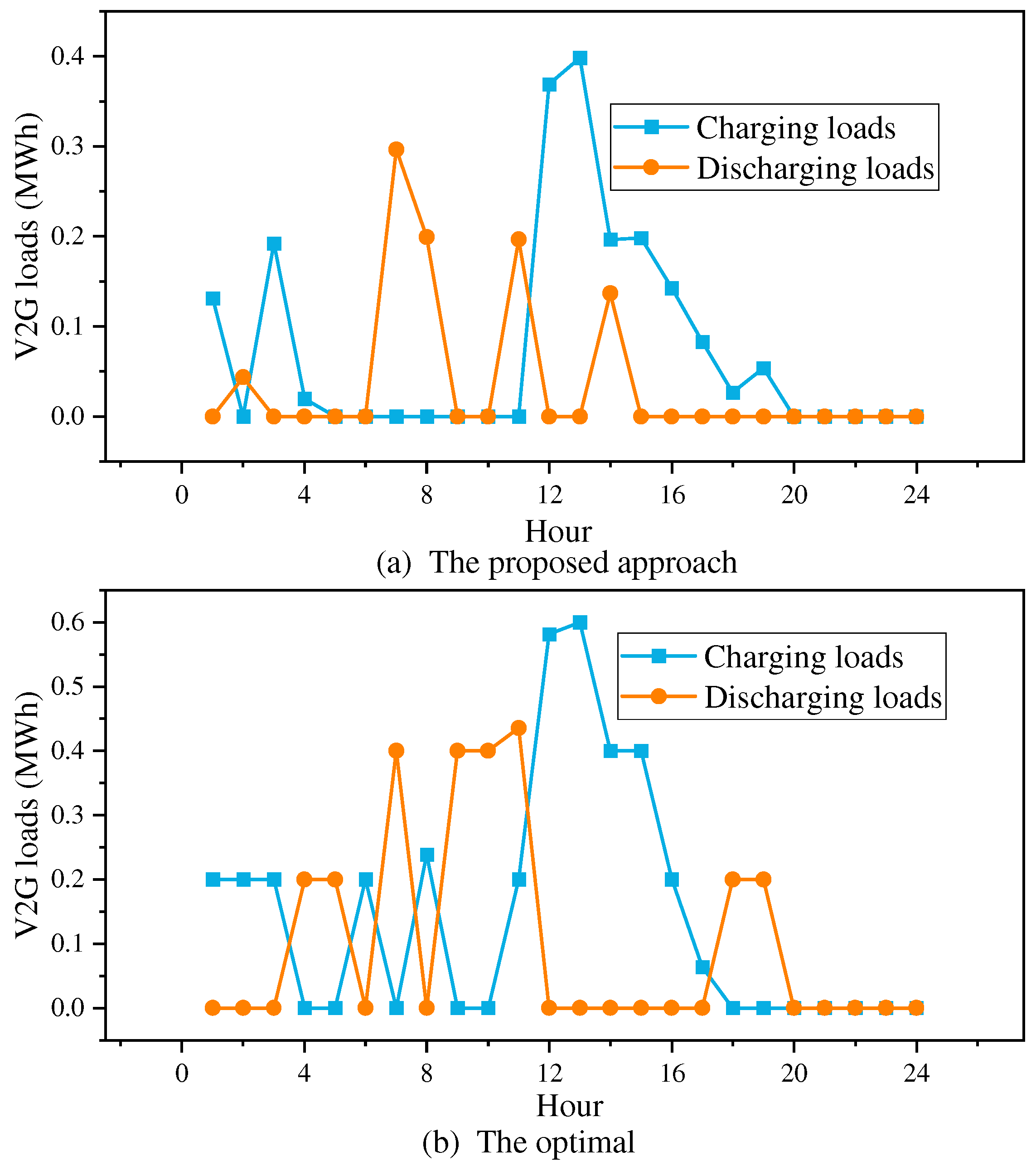
5.2. Training Process and Results of Case II
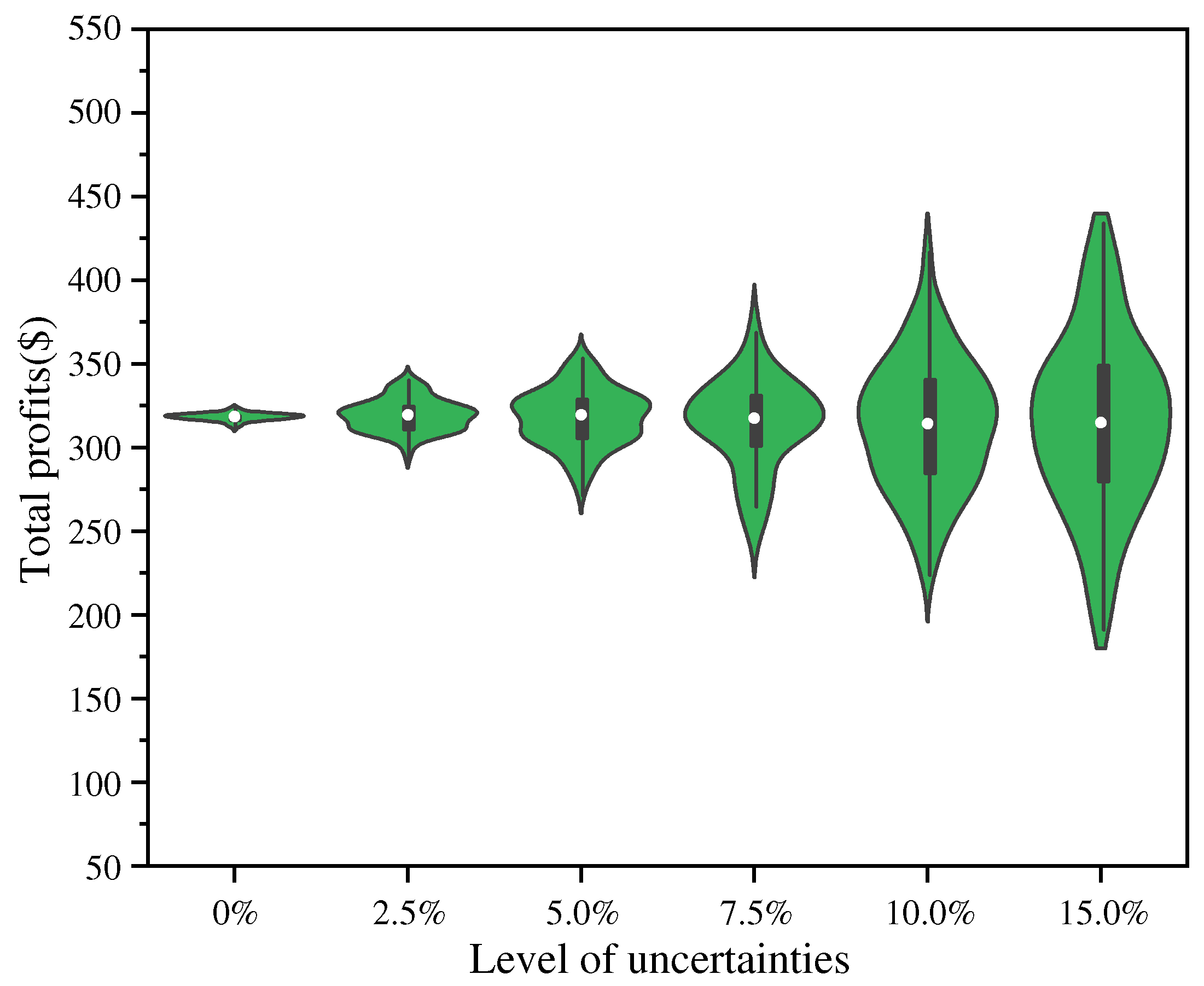
5.3. Tests on the Robustness and Efficiency of the SAC Algorithm
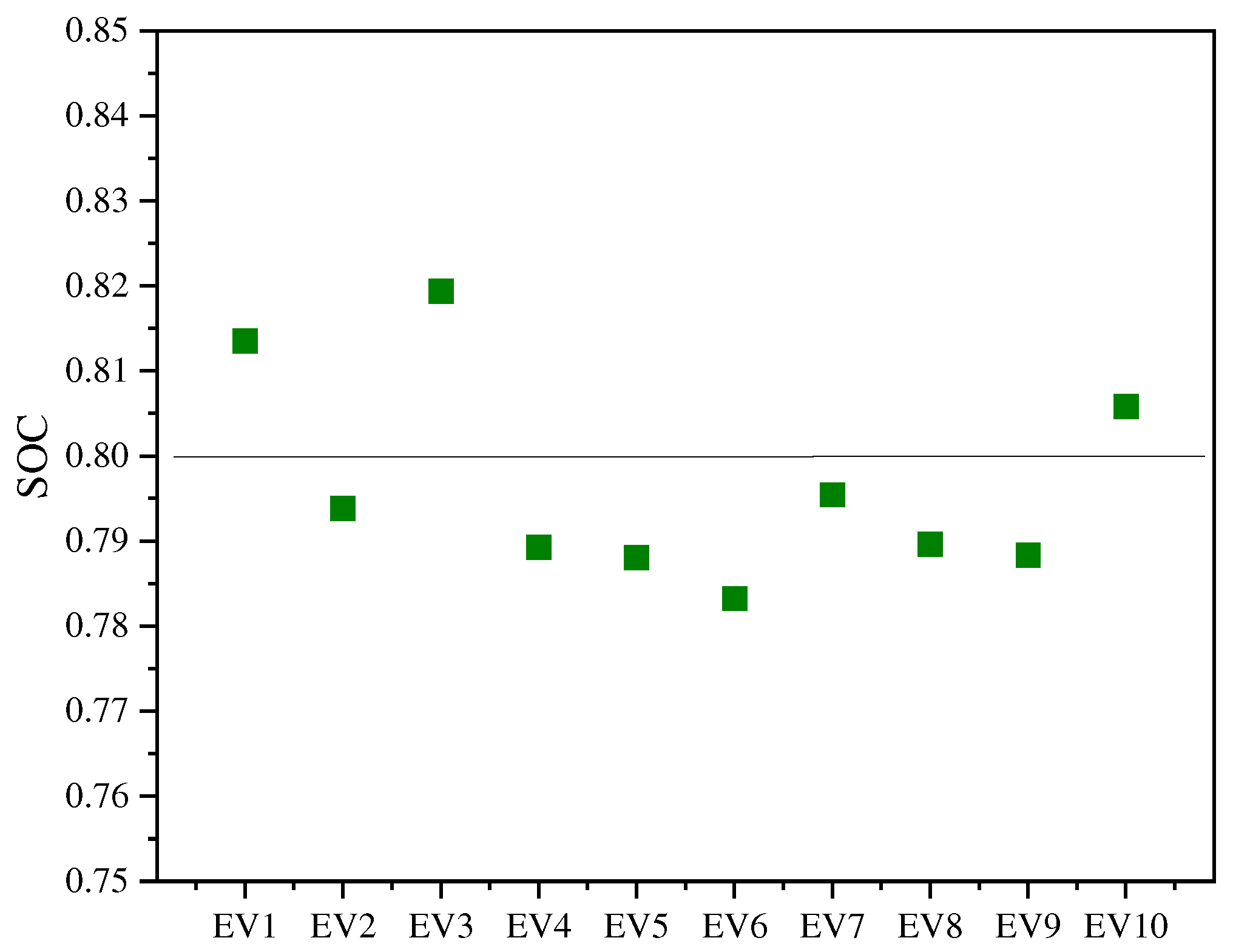
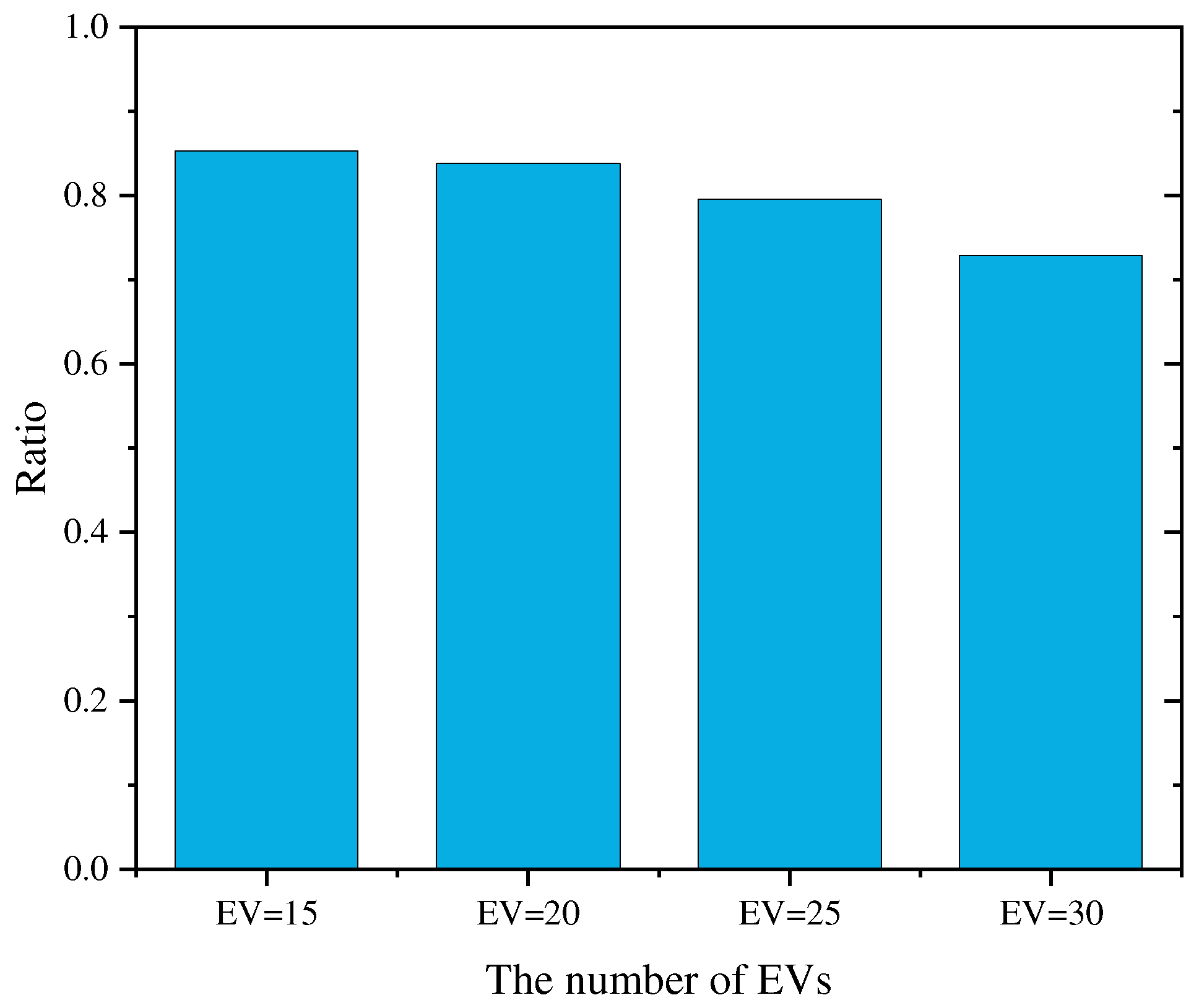
5.4. Tests on the Scenarios with Different Numbers of EVs
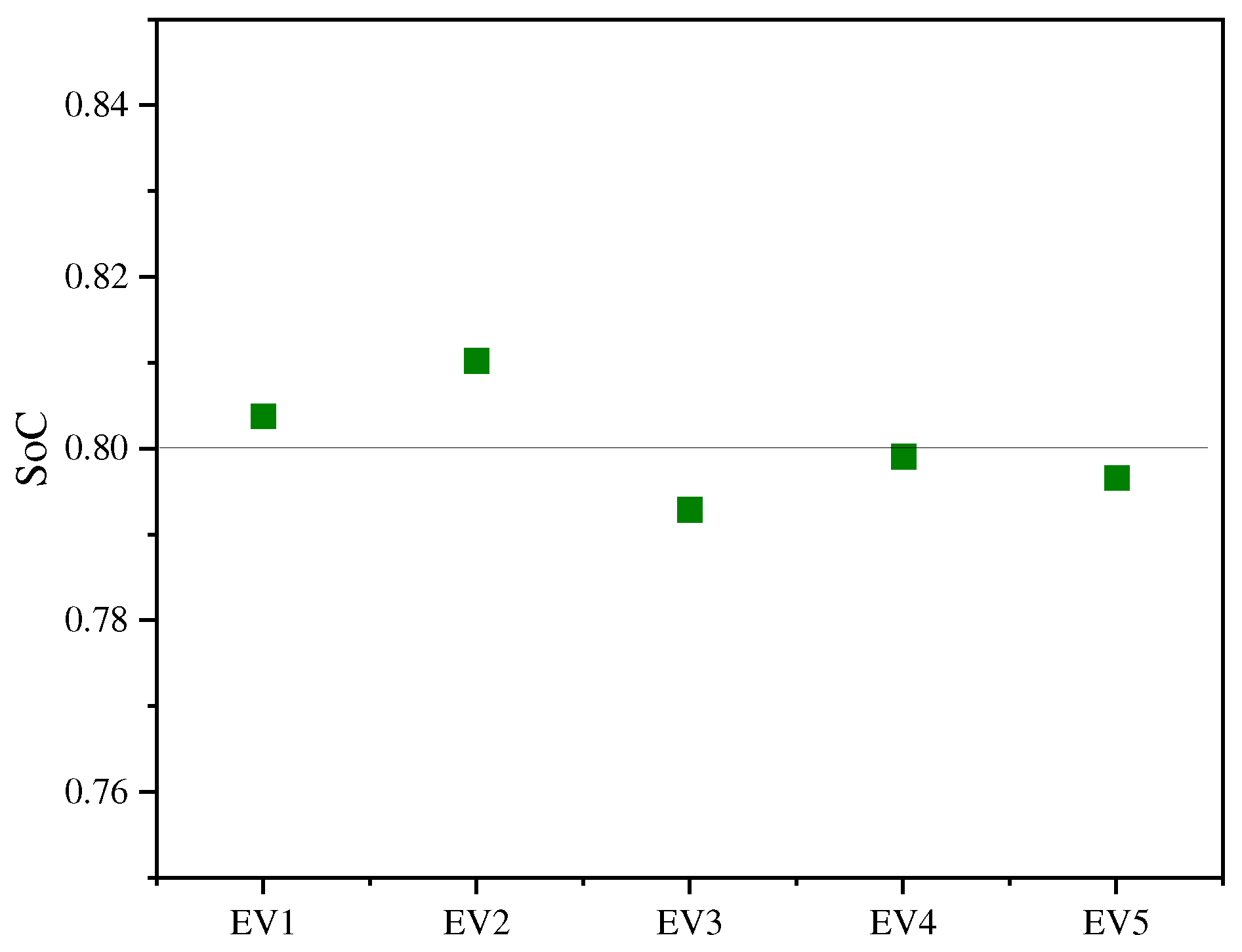
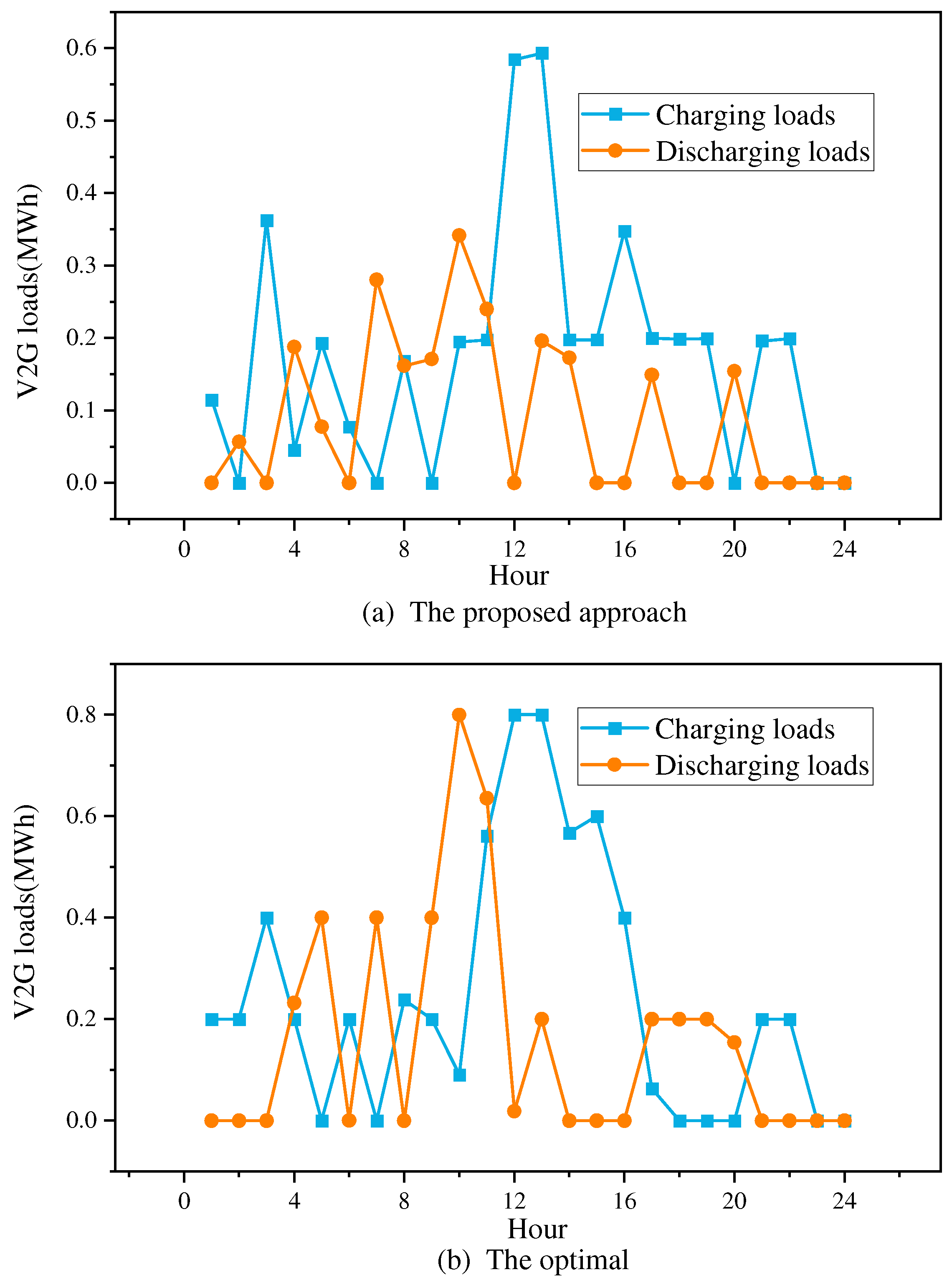
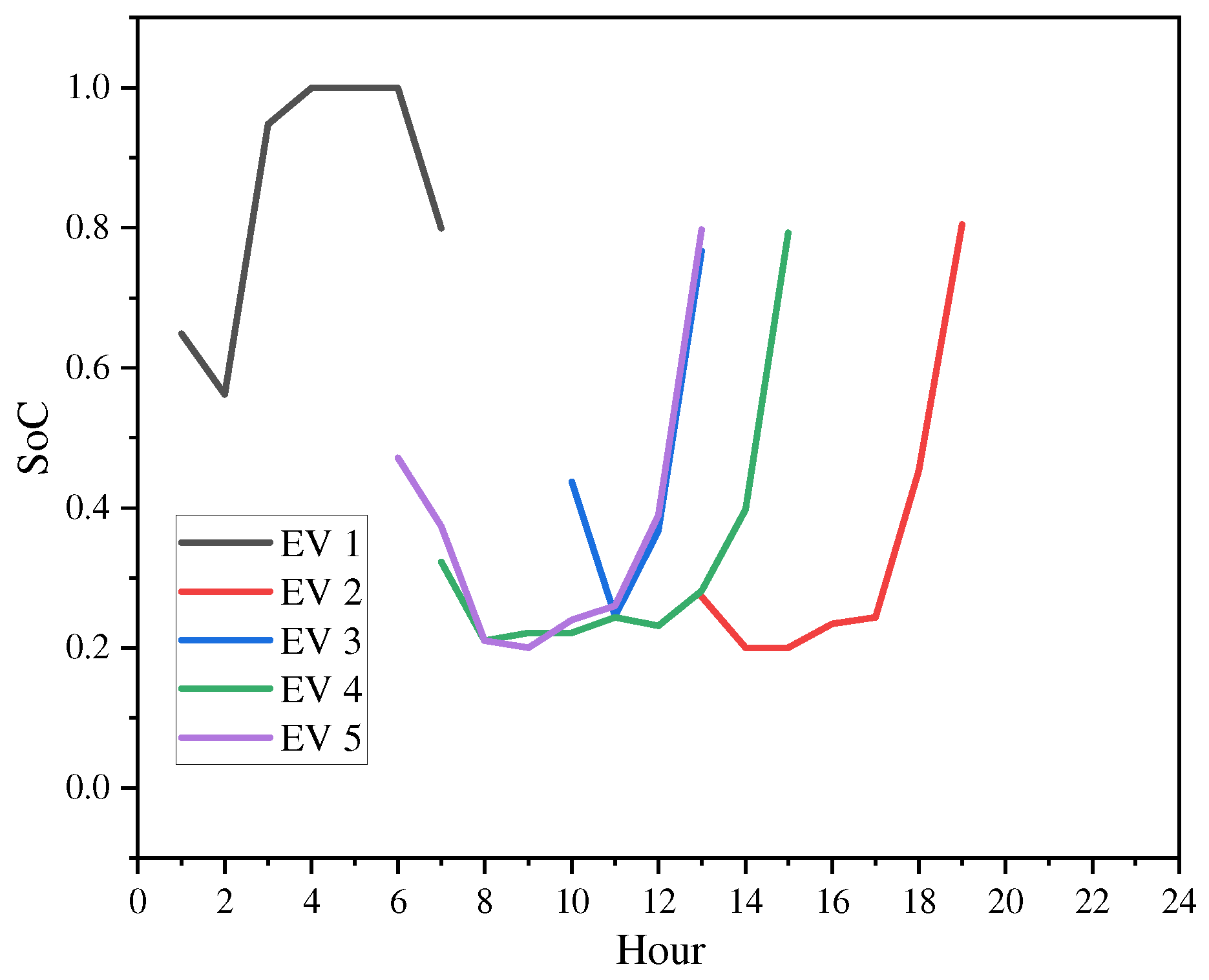
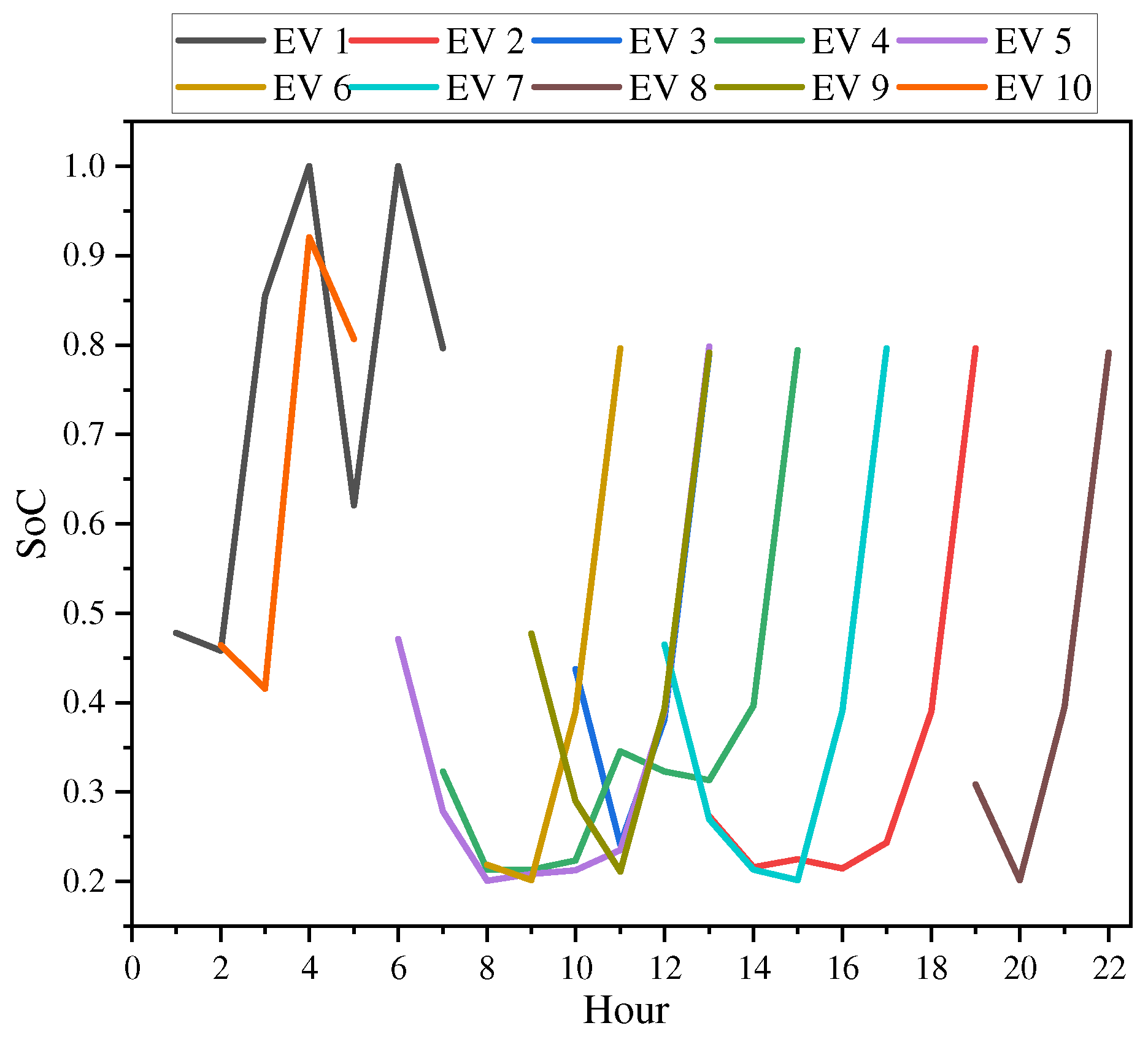
5.5. The Daily Battery Profiles of EVs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, K.; Shao, C.; Zhang, H.; Wang, X. Strategic Pricing of Electric Vehicle Charging Service Providers in Coupled Power-Transportation Networks. IEEE Trans. Smart Grid 2023, 14, 2189–2201. [Google Scholar] [CrossRef]
- Shao, C.; Li, K.; Qian, T.; Shahidehpour, M.; Wang, X. Generalized User Equilibrium for Coordination of Coupled Power-Transportation Network. IEEE Trans. Smart Grid 2023, 14, 2140–2151. [Google Scholar] [CrossRef]
- Martin, X.A.; Escoto, M.; Guerrero, A.; Juan, A.A. Battery Management in Electric Vehicle Routing Problems: A Review. Energies 2024, 17, 1141. [Google Scholar] [CrossRef]
- Armenta-Déu, C.; Demas, L. Optimization of Grid Energy Balance Using Vehicle-to-Grid Network System. Energies 2024, 17, 1008. [Google Scholar] [CrossRef]
- Belany, P.; Hrabovsky, P.; Florkova, Z. Probability Calculation for Utilization of Photovoltaic Energy in Electric Vehicle Charging Stations. Energies 2024, 17, 1073. [Google Scholar] [CrossRef]
- Qian, T.; Shao, C.; Wang, X.; Shahidehpour, M. Deep Reinforcement Learning for EV Charging Navigation by Coordinating Smart Grid and Intelligent Transportation System. IEEE Trans. Smart Grid 2020, 11, 1714–1723. [Google Scholar] [CrossRef]
- Qian, T.; Shao, C.; Wang, X.; Zhou, Q.; Shahidehpour, M. Shadow-Price DRL: A Framework for Online Scheduling of Shared Autonomous EVs Fleets. IEEE Trans. Smart Grid 2022, 13, 3106–3117. [Google Scholar] [CrossRef]
- Panchanathan, S.; Vishnuram, P.; Rajamanickam, N.; Bajaj, M.; Blazek, V.; Prokop, L.; Misak, S. A Comprehensive Review of the Bidirectional Converter Topologies for the Vehicle-to-Grid System. Energies 2023, 16, 2503. [Google Scholar] [CrossRef]
- Chai, Y.T.; Che, H.S.; Tan, C.; Tan, W.-N.; Yip, S.-C.; Gan, M.-T. A Two-Stage Optimization Method for Vehicle to Grid Coordination Considering Building and Electric Vehicle User Expectations. Int. J. Electr. Power Energy Syst. 2023, 148, 108984. [Google Scholar] [CrossRef]
- Rahman, M.M.; Gemechu, E.; Oni, A.O.; Kumar, A. The Development of a Techno-Economic Model for Assessment of Cost of Energy Storage for Vehicle-to-Grid Applications in a Cold Climate. Energy 2023, 262, 125398. [Google Scholar] [CrossRef]
- Hou, L.; Dong, J.; Herrera, O.E.; Mérida, W. Energy Management for Solar-Hydrogen Microgrids with Vehicle-to-Grid and Power-to-Gas Transactions. Int. J. Hydrogen Energy 2023, 48, 2013–2029. [Google Scholar] [CrossRef]
- Elkholy, M.H.; Said, T.; Elymany, M.; Senjyu, T.; Gamil, M.M.; Song, D.; Ueda, S.; Lotfy, M.E. Techno-Economic Configuration of a Hybrid Backup System within a Microgrid Considering Vehicle-to-Grid Technology: A Case Study of a Remote Area. Energy Convers. Manag. 2024, 301, 118032. [Google Scholar] [CrossRef]
- Wan, M.; Yu, H.; Huo, Y.; Yu, K.; Jiang, Q.; Geng, G. Feasibility and Challenges for Vehicle-to-Grid in Electricity Market: A Review. Energies 2024, 17, 679. [Google Scholar] [CrossRef]
- Jia, H.; Ma, Q.; Li, Y.; Liu, M.; Liu, D. Integrating Electric Vehicles to Power Grids: A Review on Modeling, Regulation, and Market Operation. Energies 2023, 16, 6151. [Google Scholar] [CrossRef]
- Wang, W.; Chen, J.; Pan, Y.; Yang, Y.; Hu, J. A Two-Stage Scheduling Strategy for Electric Vehicles Based on Model Predictive Control. Energies 2023, 16, 7737. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, H.; Xie, T.; Li, H.; Zhang, K.; Wang, R. Research on the Dispatching of Electric Vehicles Participating in Vehicle-to-Grid Interaction: Considering Grid Stability and User Benefits. Energies 2024, 17, 812. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Smart Decentralized Electric Vehicle Aggregators for Optimal Dispatch Technologies. Energies 2023, 16, 8112. [Google Scholar] [CrossRef]
- Ahsan, S.M.; Khan, H.A.; Sohaib, S.; Hashmi, A.M. Optimized Power Dispatch for Smart Building and Electric Vehicles with V2V, V2B and V2G Operations. Energies 2023, 16, 4884. [Google Scholar] [CrossRef]
- Xu, C.; Huang, Y. Integrated Demand Response in Multi-Energy Microgrids: A Deep Reinforcement Learning-Based Approach. Energies 2023, 16, 4769. [Google Scholar] [CrossRef]
- Chen, T.; Bu, S.; Liu, X.; Kang, J.; Yu, F.R.; Han, Z. Peer-to-Peer Energy Trading and Energy Conversion in Interconnected Multi-Energy Microgrids Using Multi-Agent Deep Reinforcement Learning. IEEE Trans. Smart Grid 2022, 13, 715–727. [Google Scholar] [CrossRef]
- Good, N.; Mancarella, P. Flexibility in Multi-Energy Communities With Electrical and Thermal Storage: A Stochastic, Robust Approach for Multi-Service Demand Response. IEEE Trans. Smart Grid 2019, 10, 503–513. [Google Scholar] [CrossRef]
- Bahrami, S.; Chen, Y.C.; Wong, V.W.S. Deep Reinforcement Learning for Demand Response in Distribution Networks. IEEE Trans. Smart Grid 2021, 12, 1496–1506. [Google Scholar] [CrossRef]
- Agostinelli, F.; McAleer, S.; Shmakov, A.; Baldi, P. Solving the Rubik’s Cube with Deep Reinforcement Learning and Search. Nat. Mach. Intell. 2019, 1, 356–363. [Google Scholar] [CrossRef]
- Duan, J.; Shi, D.; Diao, R.; Li, H.; Wang, Z.; Zhang, B.; Bian, D.; Yi, Z. Deep-Reinforcement-Learning-Based Autonomous Voltage Control for Power Grid Operations. IEEE Trans. Power Syst. 2020, 35, 814–817. [Google Scholar] [CrossRef]
- Huang, Y.; Li, G.; Chen, C.; Bian, Y.; Qian, T.; Bie, Z. Resilient Distribution Networks by Microgrid Formation Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2022, 13, 4918–4930. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Z.; Lee, W.-J. Soft Actor–Critic Algorithm Featured Residential Demand Response Strategic Bidding for Load Aggregators. IEEE Trans. Ind. Appl. 2022, 58, 4298–4308. [Google Scholar] [CrossRef]
- Kuang, Y.; Wang, X.; Zhao, H.; Qian, T.; Li, N.; Wang, J.; Wang, X. Model-Free Demand Response Scheduling Strategy for Virtual Power Plants Considering Risk Attitude of Consumers. CSEE J. Power Energy Syst. 2023, 9, 516–528. [Google Scholar] [CrossRef]
- Li, H.; Wan, Z.; He, H. Constrained EV Charging Scheduling Based on Safe Deep Reinforcement Learning. IEEE Trans. Smart Grid 2020, 11, 2427–2439. [Google Scholar] [CrossRef]
- Wan, Z.; Li, H.; He, H.; Prokhorov, D. Model-Free Real-Time EV Charging Scheduling Based on Deep Reinforcement Learning. IEEE Trans. Smart Grid 2019, 10, 5246–5257. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Wu, F.; Tang, B.; Fan, W. Effective Charging Planning Based on Deep Reinforcement Learning for Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 542–554. [Google Scholar] [CrossRef]
- Liu, R.; Xie, M.; Liu, A.; Song, H. Joint Optimization Risk Factor and Energy Consumption in IoT Networks with TinyML-Enabled Internet of UAVs. IEEE Internet Things J. 2024. [Google Scholar] [CrossRef]
- Liu, R.; Qu, Z.; Huang, G.; Dong, M.; Wang, T.; Zhang, S.; Liu, A. DRL-UTPS: DRL-Based Trajectory Planning for Unmanned Aerial Vehicles for Data Collection in Dynamic IoT Network. IEEE Trans. Intell. Veh. 2022, 8, 1204–1218. [Google Scholar] [CrossRef]
- Qian, T.; Shao, C.; Li, X.; Wang, X.; Chen, Z.; Shahidehpour, M. Multi-Agent Deep Reinforcement Learning Method for EV Charging Station Game. IEEE Trans. Power Syst. 2022, 37, 1682–1694. [Google Scholar] [CrossRef]
- Qian, T.; Shao, C.; Li, X.; Wang, X.; Shahidehpour, M. Enhanced Coordinated Operations of Electric Power and Transportation Networks via EV Charging Services. IEEE Trans. Smart Grid 2020, 11, 3019–3030. [Google Scholar] [CrossRef]



| Hour | Probability of Arrival |
|---|---|
| 1 | 0.070 |
| 2 | 0.070 |
| 3 | 0.062 |
| 4 | 0.060 |
| 5 | 0.023 |
| 6 | 0.033 |
| 7 | 0.050 |
| 8 | 0.060 |
| 9 | 0.060 |
| 10 | 0.050 |
| 11 | 0.040 |
| 12 | 0.030 |
| 13 | 0.030 |
| 14 | 0.040 |
| 15 | 0.040 |
| 16 | 0.060 |
| 17 | 0.040 |
| 18 | 0.060 |
| 19 | 0.040 |
| 20 | 0.040 |
| 21 | 0.030 |
| 22 | 0.005 |
| 23 | 0.005 |
| 24 | 0.002 |
| Lasting Hours | Probability |
|---|---|
| 1 | 0.00 |
| 2 | 0.10 |
| 3 | 0.15 |
| 4 | 0.20 |
| 5 | 0.15 |
| 6 | 0.15 |
| 7 | 0.13 |
| 8 | 0.05 |
| 9 | 0.05 |
| 10 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, W.; Yu, X.; Guo, Z.; Qian, T.; Li, Y. Online EVs Vehicle-to-Grid Scheduling Coordinated with Multi-Energy Microgrids: A Deep Reinforcement Learning-Based Approach. Energies 2024, 17, 2491. https://doi.org/10.3390/en17112491
Pan W, Yu X, Guo Z, Qian T, Li Y. Online EVs Vehicle-to-Grid Scheduling Coordinated with Multi-Energy Microgrids: A Deep Reinforcement Learning-Based Approach. Energies. 2024; 17(11):2491. https://doi.org/10.3390/en17112491
Chicago/Turabian StylePan, Weiqi, Xiaorong Yu, Zishan Guo, Tao Qian, and Yang Li. 2024. "Online EVs Vehicle-to-Grid Scheduling Coordinated with Multi-Energy Microgrids: A Deep Reinforcement Learning-Based Approach" Energies 17, no. 11: 2491. https://doi.org/10.3390/en17112491
APA StylePan, W., Yu, X., Guo, Z., Qian, T., & Li, Y. (2024). Online EVs Vehicle-to-Grid Scheduling Coordinated with Multi-Energy Microgrids: A Deep Reinforcement Learning-Based Approach. Energies, 17(11), 2491. https://doi.org/10.3390/en17112491






