Novel Hybrid Mexican Axolotl Optimization with Fuzzy Logic for Maximum Power Point Tracker of Partially Shaded Photovoltaic Systems
Abstract
1. Introduction
1.1. The Literature Survey
1.2. Motivation and Innovation
1.3. Paper Outlines
2. PV System Description
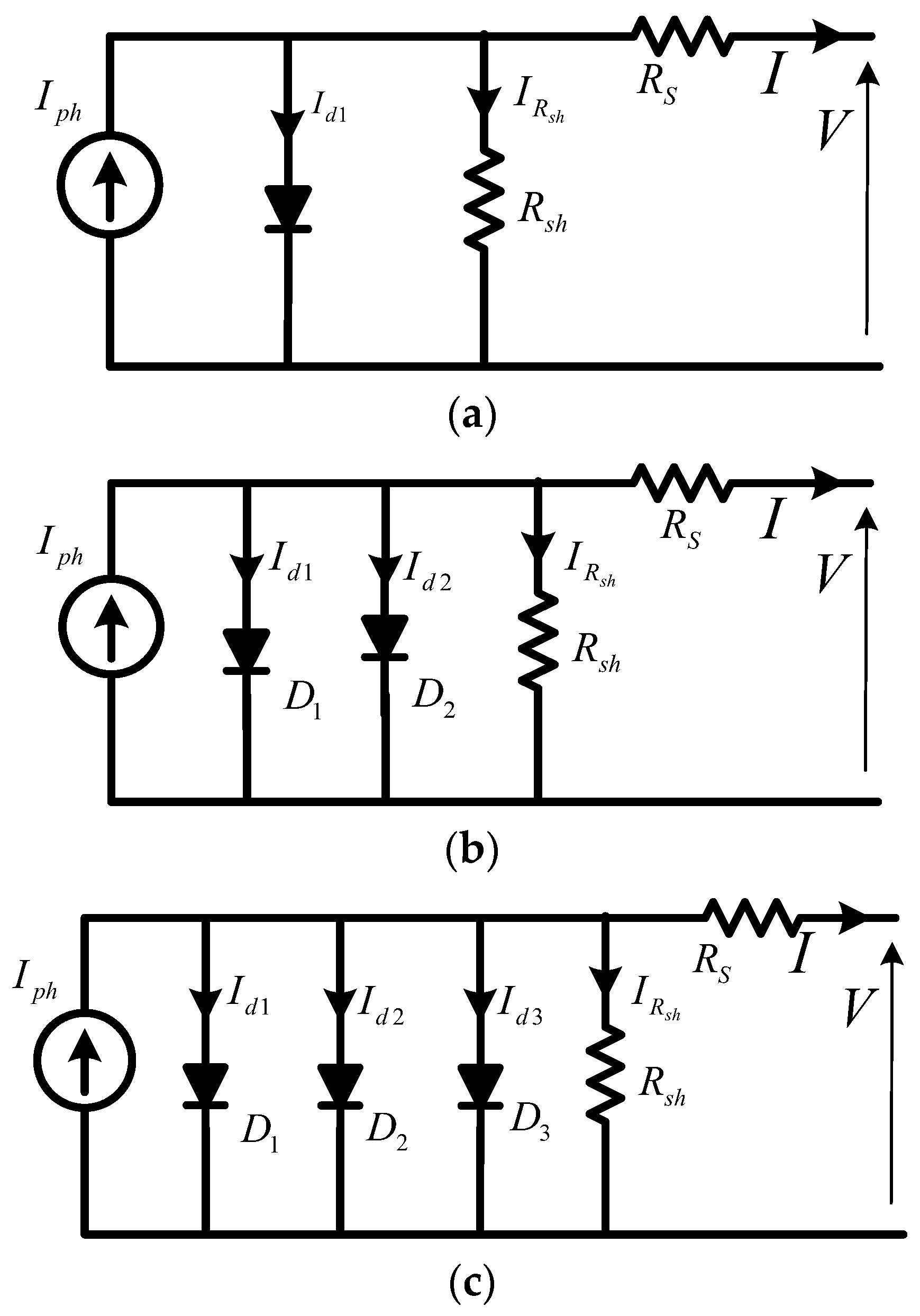
2.1. PV Cell Modelling
2.2. DC–DC Converter
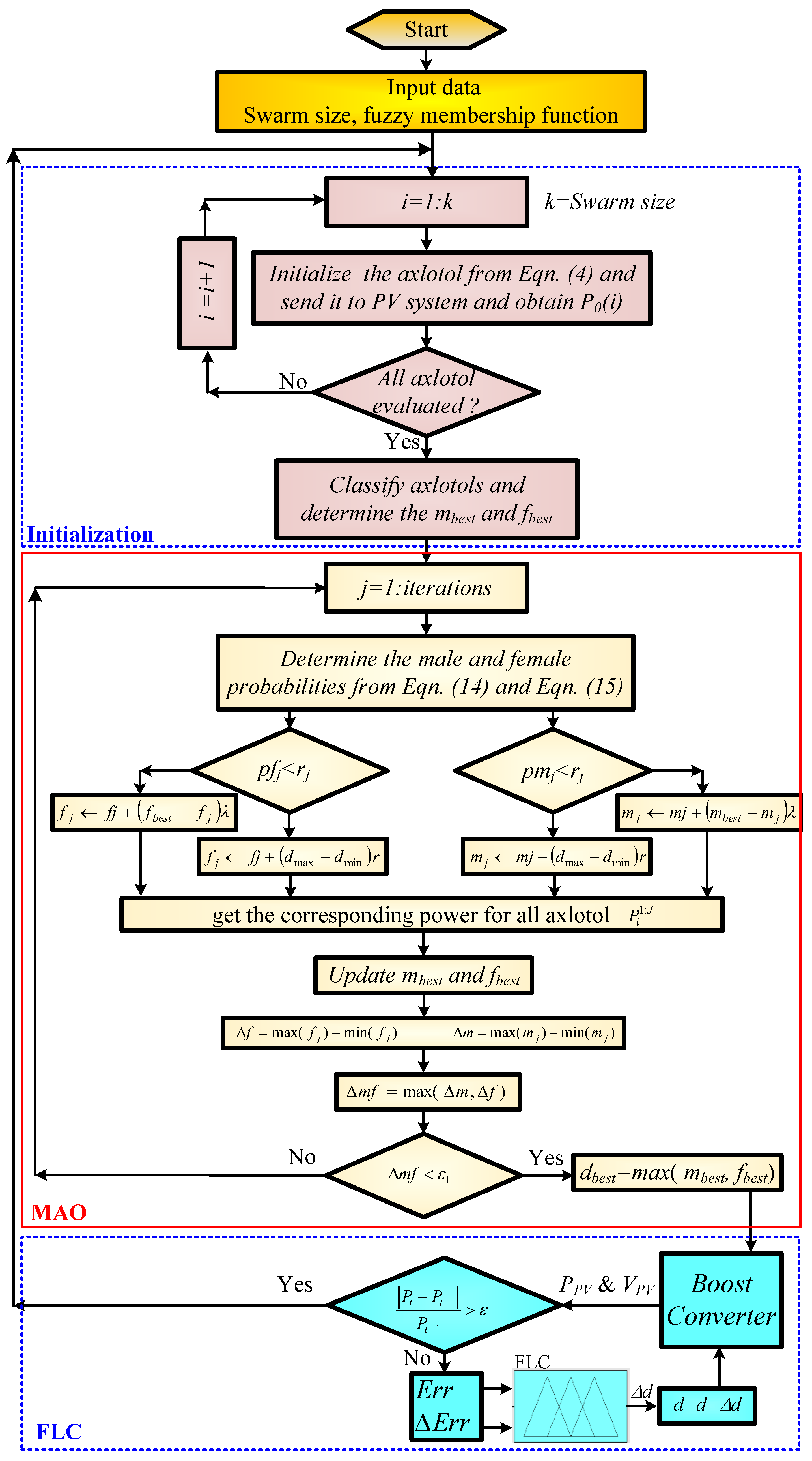
3. The Mexican Axolotl Optimization Algorithm
- Initialize the female and male search agents by providing each duty ratio between the minimum and maximum boost converter duty ratio. In normal operation of the MAO, the position of these search agents is selected randomly but as discussed before the random initialization causes longer CT in PV MPPT, and for this reason, the initialization of search agents will be according the anticipated peaks positions obtained from Equation (13).where k is the axolotl order, and dmin, and dmax are the range of the boost converter duty ratio.
- 2.
- Ascertain the produced power, or fitness value, for every search agent position (boost converter duty ratio).
- 3.
- Classify the male and female populations [45] based on random selection.
- 4.
- Based on the fitness values, select the top male and female candidates.
- 5.
- Use the new position to obtain the new PV power from the PV model and update the mbest and fbest.
- 6.
- If max(mj) − min(mj) and max(fj) − min(fj) is less than ε1, where ε1 is a predefined tolerance (ε1 = 0.01), then transfer the control to the FLC as will be described in the following section; otherwise, go to step 4.
4. The Fuzzy Logic Controller
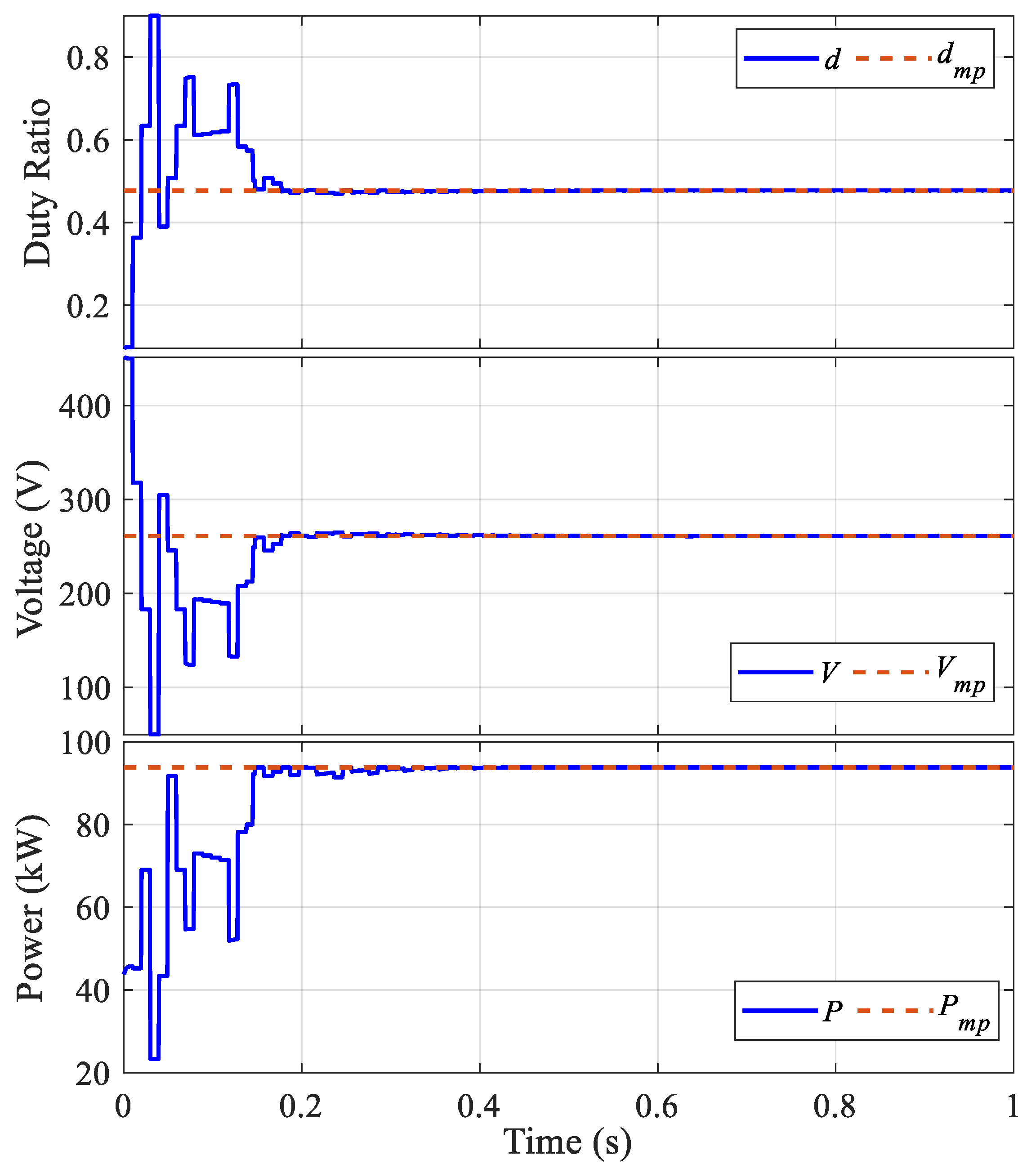
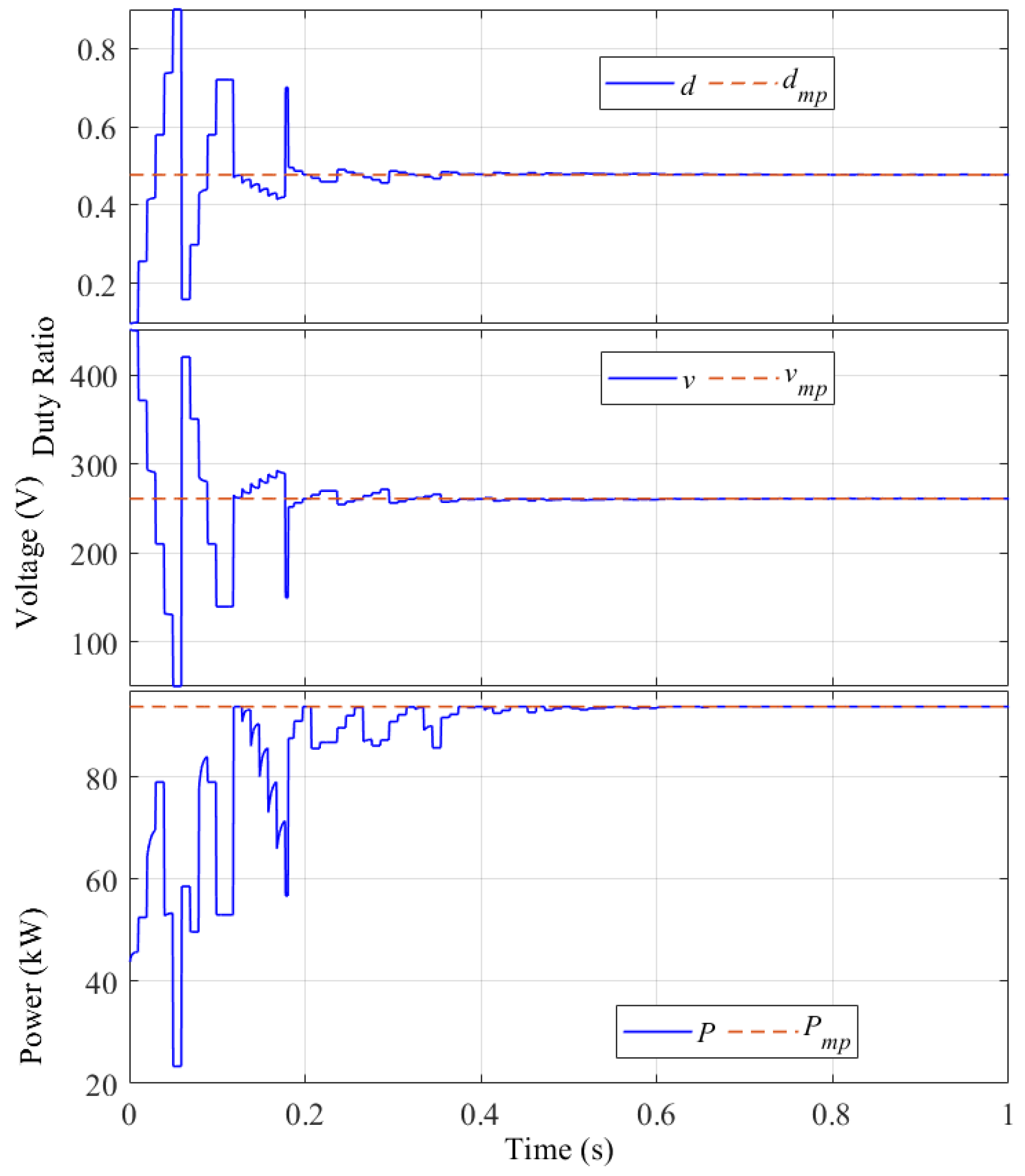
5. Simulation Results
5.1. Input Data
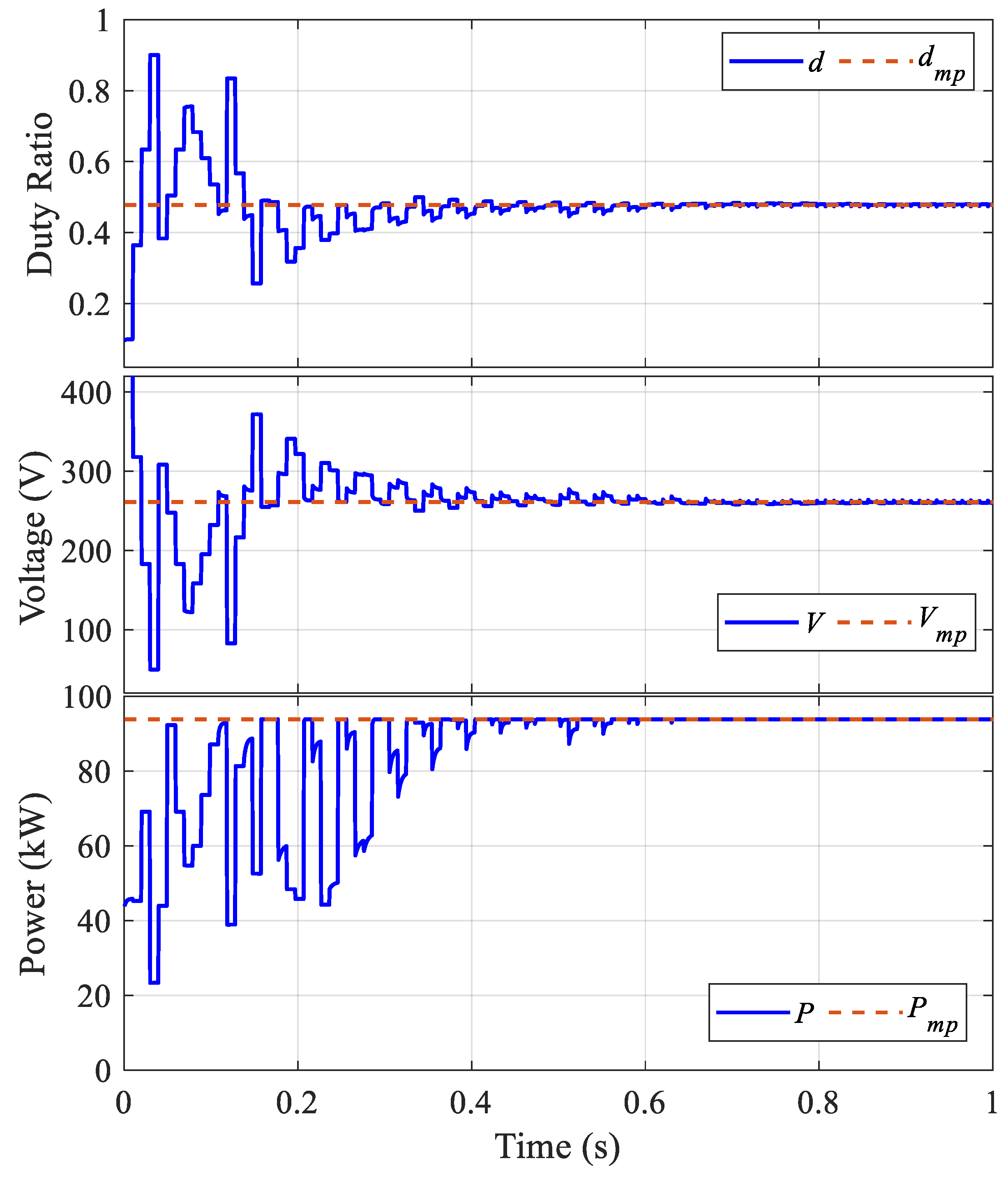
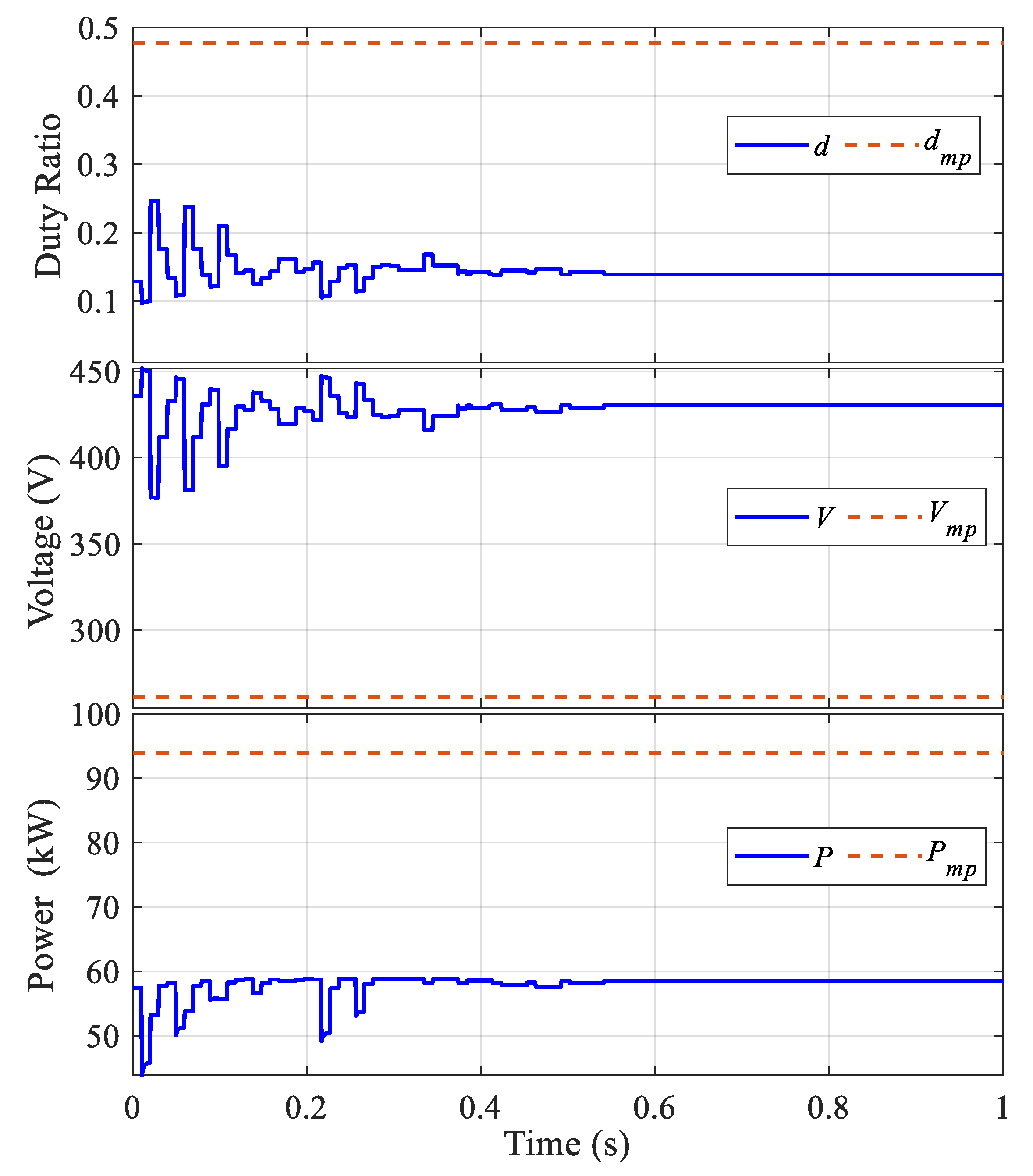
5.2. The Comparison between MAO and Other Optimization Algorithms
5.3. The Effect of Swarm-Size and Shading Pattern Change
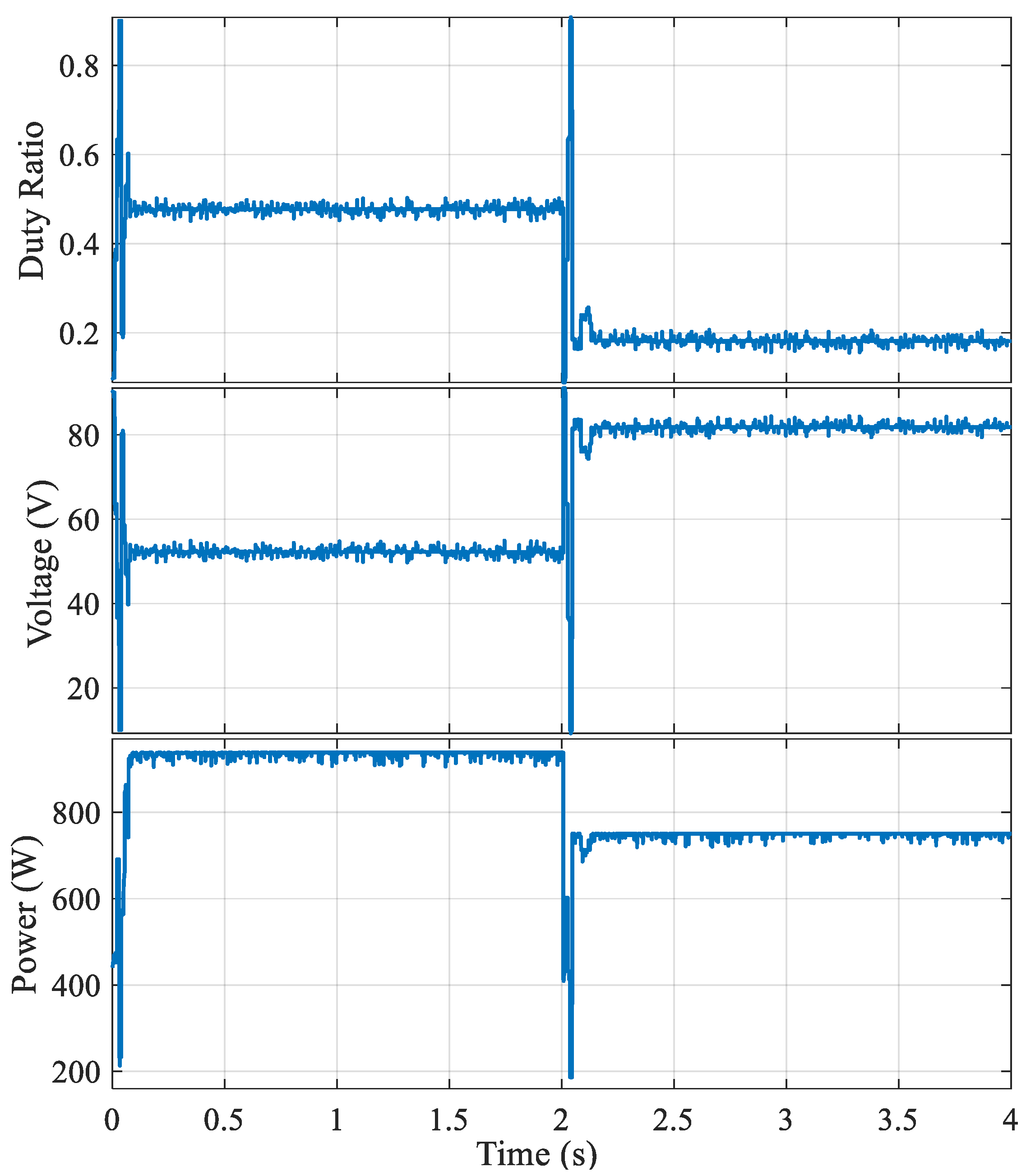
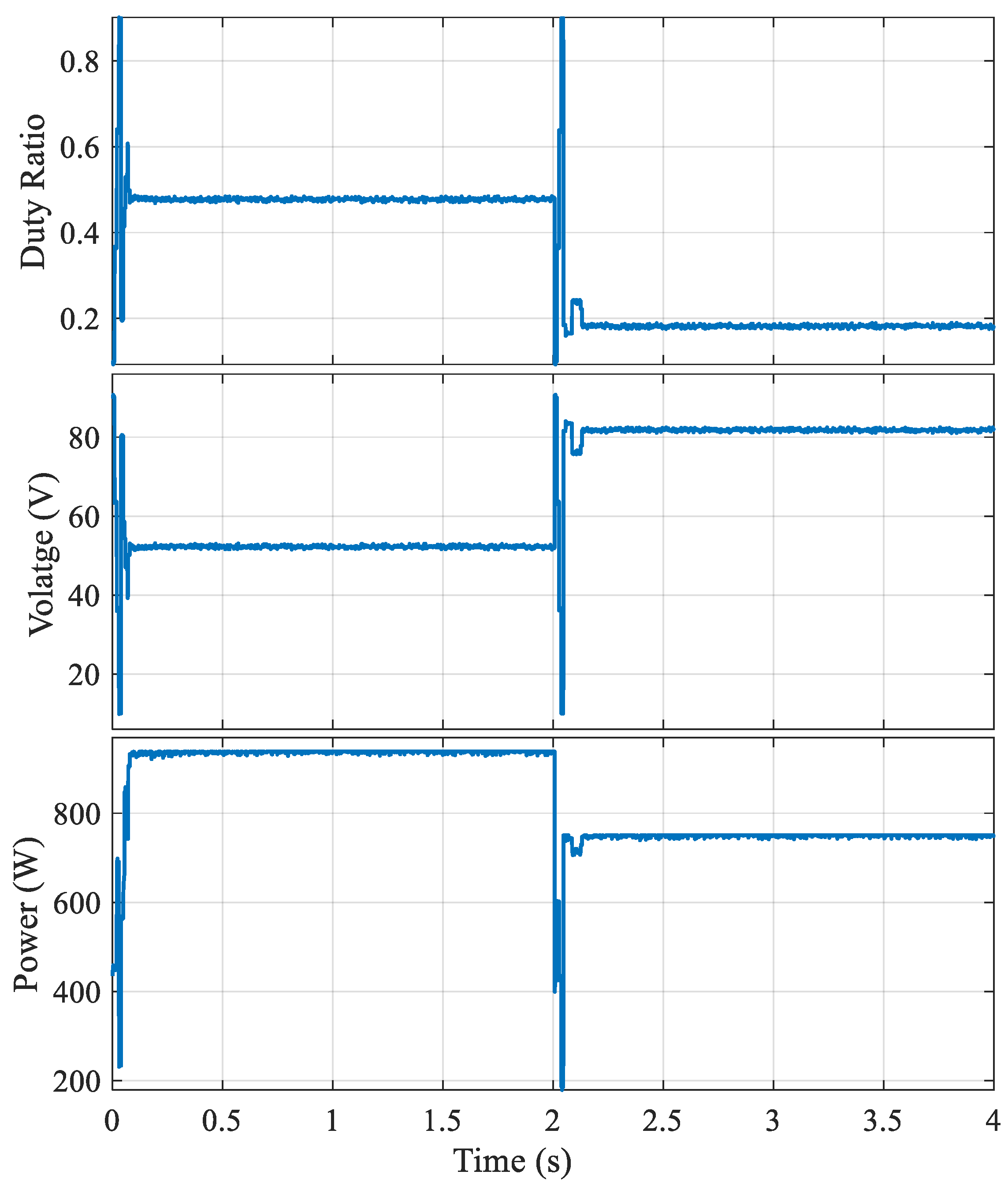
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PV | Photovoltaic | |
| FLC | Fuzzy logic controller | |
| P–V | Power–voltage characteristic | |
| MOAs | Metaheuristic optimization algorithms | |
| CT | Convergence time | |
| MAO | Mexican axolotl optimization | |
| MPPT | Maximum power point tracker | |
| IEA | International energy agency | |
| PSO | Particle swarm optimization | |
| GWO | Grey wolf optimizer | |
| MCA | Musical chairs algorithm | |
| SFLA | Shuffled frog leaping algorithm | |
| Rs | Series resistance | |
| Rsh | Shunt resistance | |
| n1, n2 | Ideality factors | |
| Id | Diode saturation current | |
| Iph | Photon generated current | |
| T | Module temperature in Ko | |
| K | Boltsman’s constant | |
| VDC | DC-link voltage | |
| V | PV terminal voltage | |
| d | Duty ratio | |
| VD | Conduction diode voltage | |
| RPV | Internal PV resistance | |
| Req | Boost converter resistance | |
| RD | Diode forward resistance | |
| Rsw | Switching-ON resistance | |
| RL | Load resistance | |
| Cin | Input capacitance | |
| F | Switching frequency | |
| Input voltage ripple | ||
| Cout | Output capacitance | |
| PSC | Partial shading condition | |
| MPP | Maximum power point | |
| HC | Hill climbing | |
| P&O | Perturb and observe | |
| GHG | Greenhouse gas | |
| EV | Electric vehicle | |
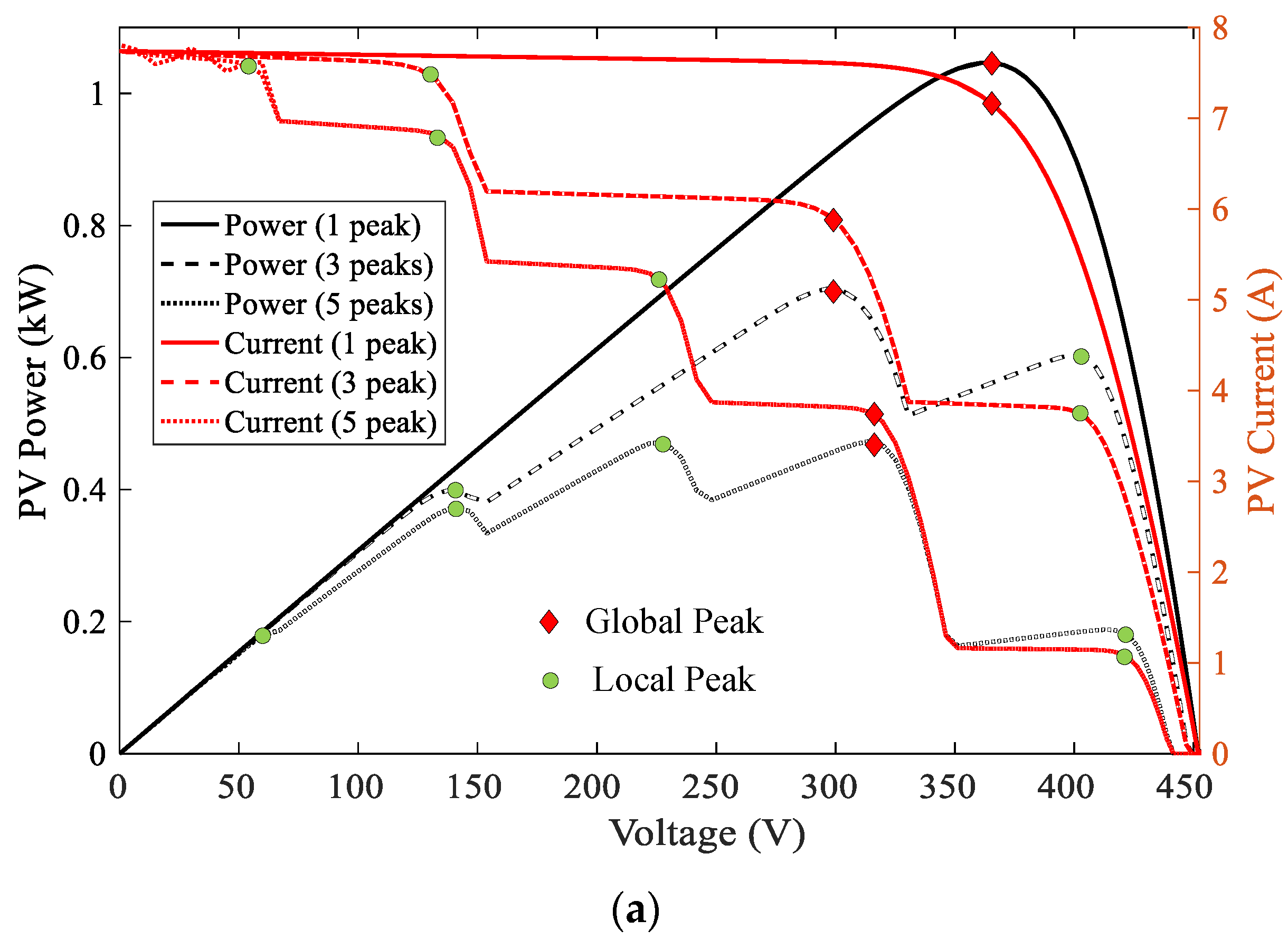
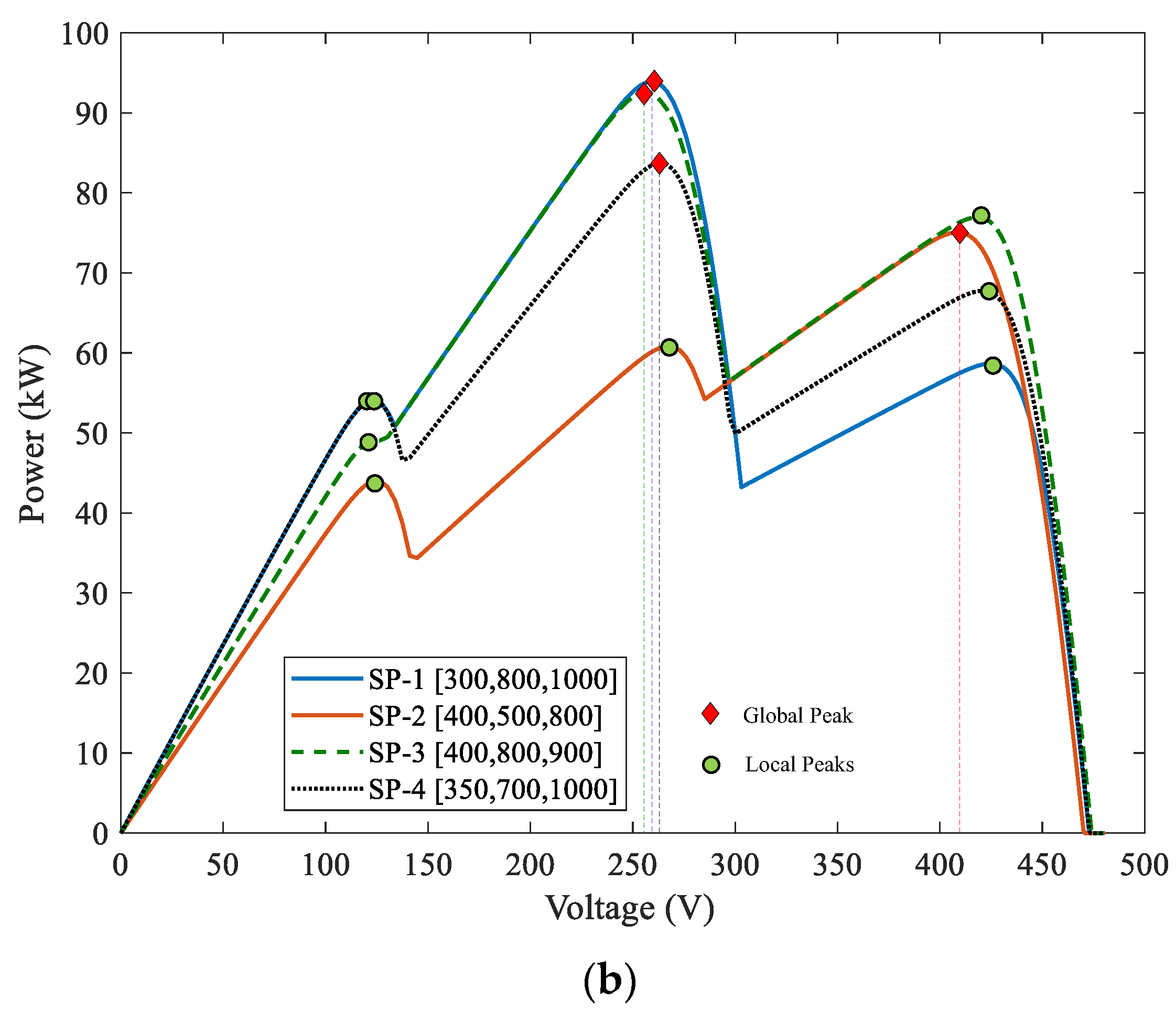
| GP | Global peak | |
| LPs | Local peaks | |
| CS | Cuckoo search | |
| SDM | Single diode model | |
| DDM | Double-diode model | |
| TDM | Triple-diode model | |
| rj | Random number [0, 1] | |
| pmj | inverse probability of axolotl male | |
| pfj | Axolotl female inverse probability | |
| ε1 | Predefined tolerance | |
| mj & fj | Axolotl male and female positions | |
| mbest | The best axolotl male position | |
| fbest | The best axolotl female position | |
| OMj | The axolotl male value | |
| OFj | The axolotl female value | |
| dmax | Maximum duty ratio | |
| dmin | Minimum duty ratio | |
| λ | Random number [0, 1] | |
| E | Change in power to voltage | |
| Voc | Open-circuit PV voltage | |
| L | Inductance of boost converter | |
| Vmp | Voltage at MPP | |
| dmp | Duty ratio at MPP | |
| Imp | Current at MPP | |
| Isc | Short circuit PV current | |
| k | Axolotl order | |
References
- IEA’s World Energy Outlook 2022. Available online: https://www.iea.org/reports/world-energy-outlook-2022 (accessed on 1 June 2023).
- Jately, V.; Azzopardi, B.; Joshi, J.; Sharma, A.; Arora, S. Experimental Analysis of hill-climbing MPPT algorithms under low irradiance levels. Renew. Sustain. Energy Rev. 2021, 150, 111467. [Google Scholar] [CrossRef]
- Mamatha, G. Perturb and observe MPPT algorithm implementation for PV applications. Int. J. Comput. Sci. Inf. Technol. 2015, 6, 1884–1887. [Google Scholar]
- Eltamaly, A. Modeling of fuzzy logic controller for photovoltaic maximum power point tracker. In Proceedings of the Solar Future Conference, Istanbul, Turkey, 11–12 February 2010. [Google Scholar]
- Robles Algarín, C.; Taborda Giraldo, J.; Rodriguez Álvarez, O. Fuzzy Logic Based MPPT Controller for a PV System. Energies 2017, 10, 2036. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Alolah, A.I.; Abdulghany, M.Y. Digital implementation of general purpose fuzzy logic controller for photovoltaic maximum power point tracker. In Proceedings of the SPEEDAM 2010, Pisa, Italy, 14–16 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 622–627. [Google Scholar]
- Abbassi, R.; Abbassi, A.; Heidari, A.A.; Mirjalili, S. An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 2019, 179, 362–372. [Google Scholar] [CrossRef]
- Awadallah, M.A. Variations of the bacterial foraging algorithm for the extraction of PV module parameters from nameplate data. Energy Convers. Manag. 2016, 113, 312–320. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Deotti, L.M.P.; Pereira, J.L.R.; da Silva Júnior, I.C. Parameter extraction of photovoltaic models using an enhanced Lévy flight bat algorithm. Energy Convers. Manag. 2020, 221, 113114. [Google Scholar] [CrossRef]
- Rajalakshmi, M.; Chandramohan, S.; Kannadasan, R.; Alsharif, M.H.; Kim, M.-K.; Nebhen, J. Design and Validation of BAT Algorithm-Based Photovoltaic System Using Simplified High Gain Quasi Boost Inverter. Energies 2021, 14, 1086. [Google Scholar] [CrossRef]
- Baatiah, A.O.; Eltamaly, A.M.; Alotaibi, M.A. Improving Photovoltaic MPPT Performance through PSO Dynamic Swarm Size Reduction. Energies 2023, 16, 6433. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Al-Saud, M.; Abokhalil, A.G. A novel scanning bat algorithm strategy for maximum power point tracker of partially shaded photovoltaic energy systems. Ain Shams Eng. J. 2020, 11, 1093–1103. [Google Scholar] [CrossRef]
- Koh, J.S.; Tan, R.H.G.; Lim, W.H.; Tan, N.M.L. A Modified Particle Swarm Optimization for Efficient Maximum Power Point Tracking under Partial Shading Condition. IEEE Trans. Sustain. Energy 2023, 14, 1822–1834. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel particle swarm optimization optimal control parameter determination strategy for maximum power point trackers of partially shaded photovoltaic systems. Eng. Optim. 2022, 54, 634–650. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A Novel Strategy for Optimal PSO Control Parameters Determination for PV Energy Systems. Sustainability 2021, 13, 1008. [Google Scholar] [CrossRef]
- Jordehi, A.R. Enhanced leader particle swarm optimisation (ELPSO): An efficient algorithm for parameter estimation of photovoltaic (PV) cells and modules. Sol. Energy 2018, 159, 78–87. [Google Scholar] [CrossRef]
- Hashim, N.; Salam, Z. Critical evaluation of soft computing methods for maximum power point tracking algorithms of photovoltaic systems. Int. J. Power Electron. Drive Syst. 2019, 10, 548. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Optimal control parameters for bat algorithm in maximum power point tracker of photovoltaic energy systems. Int. Trans. Electr. Energy Syst. 2021, 31, e12839. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Liu, Y.-H.; Huang, S.-C.; Huang, J.-W.; Liang, W.-C. A Particle Swarm Optimization-Based Maximum Power Point Tracking Algorithm for PV Systems Operating under Partially Shaded Conditions. IEEE Trans. Energy Convers. 2012, 27, 1027–1035. [Google Scholar] [CrossRef]
- Ratnaweera, A.; Halgamuge, S.; Watson, H. Self-Organizing Hierarchical Particle Swarm Optimizer with Time-Varying Acceleration Coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Alireza, A. PSO with adaptive mutation and inertia weight and its application in parameter estimation of dynamic systems. Acta Autom. Sin. 2011, 37, 541–549. [Google Scholar]
- Merchaoui, M.; Hamouda, M.; Sakly, A.; Mimouni, M.F. Fuzzy logic adaptive particle swarm optimisation based MPPT controller for photovoltaic systems. IET Renew. Power Gener. 2020, 14, 2933–2945. [Google Scholar] [CrossRef]
- Dziri, S.; Alhato, M.M.; Bouallègue, S.; Siarry, P. Improved Particle Swarm Optimizer-Based MPPT Control of PV Systems under Dynamic Partial Shading. In Proceedings of the 2022 19th International Multi-Conference on Systems, Signals & Devices (SSD), Sétif, Algeria, 6–10 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1603–1608. [Google Scholar]
- Eltamaly, A.M.; Al-Saud, M.; Abokhalil, A.G.; Farh, H.M. Simulation and experimental validation of fast adaptive particle swarm optimization strategy for photovoltaic global peak tracker under dynamic partial shading. Renew. Sustain. Energy Rev. 2020, 124, 109719. [Google Scholar] [CrossRef]
- Tambouratzis, G. Investigating the Effect of Hyperparameter Values and Size on Swarm Optimization Effectiveness. In Proceedings of the 2022 IEEE Symposium Series on Computational Intelligence (SSCI), Singapore, 4–7 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1636–1643. [Google Scholar]
- Eltamaly, A.M. An Improved Cuckoo Search Algorithm for Maximum Power Point Tracking of Photovoltaic Systems under Partial Shading Conditions. Energies 2021, 14, 953. [Google Scholar] [CrossRef]
- Rabie, A.H.; Eltamaly, A.M. A new NEST-IGWO strategy for determining optimal IGWO control parameters. Neural Comput. Appl. 2023, 35, 15143–15165. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel benchmark shading pattern for PV maximum power point trackers evaluation. Sol. Energy 2023, 263, 111897. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Optimal Dispatch Strategy for Electric Vehicles in V2G Applications. Smart Cities 2023, 6, 3161–3191. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Performance of smart maximum power point tracker under partial shading conditions of photovoltaic systems. J. Renew. Sustain. Energy 2015, 7, 043141. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Al-Saud, M.S.; Abo-Khalil, A.G. Performance improvement of PV systems’ maximum power point tracker based on a scanning PSO particle strategy. Sustainability 2020, 12, 1185. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Farh, H.M.H.; Abokhalil, A.G. A novel PSO strategy for improving dynamic change partial shading photovoltaic maximum power point tracker. Energy Sources Part A Recover. Util. Environ. Eff. 2020, 1–15. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A critical evaluation on maximum power point tracking methods for partial shading in PV systems. Renew. Sustain. Energy Rev. 2015, 47, 933–953. [Google Scholar] [CrossRef]
- Ben Regaya, C.; Farhani, F.; Hamdi, H.; Zaafouri, A.; Chaari, A. A new MPPT controller based on a modified multiswarm PSO algorithm using an adaptive factor selection strategy for partially shaded PV systems. Trans. Inst. Meas. Control 2024. [Google Scholar] [CrossRef]
- Harrison, A.; Alombah, N.H.; Ndongmo, J.d.D.N. Solar irradiance estimation and optimum power region localization in PV energy systems under partial shaded condition. Heliyon 2023, 9, e18434. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Farh, H.M. Dynamic global maximum power point tracking of the PV systems under variant partial shading using hybrid GWO-FLC. Sol. Energy 2019, 177, 306–316. [Google Scholar] [CrossRef]
- Garud, K.S.; Jayaraj, S.; Lee, M.-Y. A review on modeling of solar photovoltaic systems using artificial neural networks, fuzzy logic, genetic algorithm and hybrid models. Energy Rep. 2020, 45, 6–35. [Google Scholar] [CrossRef]
- Salim, J.A.; Albaker, B.M.; Alwan, M.S.; Hasanuzzaman, M. Hybrid MPPT approach using Cuckoo Search and Grey Wolf Optimizer for PV systems under variant operating conditions. Glob. Energy Interconnect. 2022, 5, 627–644. [Google Scholar] [CrossRef]
- Koad, R.B.A.; Zobaa, A.F.; El-Shahat, A. A Novel MPPT Algorithm Based on Particle Swarm Optimization for Photovoltaic Systems. IEEE Trans. Sustain. Energy 2016, 8, 468–476. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A Grey Wolf-Assisted Perturb & Observe MPPT Algorithm for a PV System. IEEE Trans. Energy Convers. 2017, 32, 340–347. [Google Scholar] [CrossRef]
- Farh, H.M.H.; Eltamaly, A.M.; Othman, M.F. Hybrid PSO-FLC for dynamic global peak extraction of the partially shaded photovoltaic system. PLoS ONE 2018, 13, e0206171. [Google Scholar] [CrossRef]
- Mao, M.; Zhou, L.; Yang, Z.; Zhang, Q.; Zheng, C.; Xie, B.; Wan, Y. A hybrid intelligent GMPPT algorithm for partial shading PV system. Control Eng. Pract. 2019, 83, 108–115. [Google Scholar] [CrossRef]
- Rao, C.S.V.P.; Pandian, A.; Reddy, C.R.; Aymen, F.; Alqarni, M.; Alharthi, M.M. Location Determination of Electric Vehicles Parking Lot with Distribution System by Mexican AXOLOTL Optimization and Wild Horse Optimizer. IEEE Access 2022, 10, 55408–55427. [Google Scholar] [CrossRef]
- Villuendas-Rey, Y.; Velázquez-Rodríguez, J.L.; Alanis-Tamez, M.D.; Moreno-Ibarra, M.-A.; Yáñez-Márquez, C. Mexican Axolotl Optimization: A Novel Bioinspired Heuristic. Mathematics 2021, 9, 781. [Google Scholar] [CrossRef]
- Al-Shabi, M.; Ghenai, C.; Bettayeb, M.; Ahmad, F.F.; Assad, M.E.H. Estimating PV models using multi-group salp swarm algorithm. IAES Int. J. Artif. Intell. 2021, 10, 398. [Google Scholar] [CrossRef]
- Alam, D.; Yousri, D.; Eteiba, M. Flower Pollination Algorithm based solar PV parameter estimation. Energy Convers. Manag. 2015, 101, 410–422. [Google Scholar] [CrossRef]
- Batzelis, E.I.; Papathanassiou, S.A. A Method for the Analytical Extraction of the Single-Diode PV Model Parameters. IEEE Trans. Sustain. Energy 2016, 7, 504–512. [Google Scholar] [CrossRef]
- Belgacem, C.; El-Amine, A. Parameters Extraction of the Au/SnO2-Si(n)/Al pn Junction Solar Cell Using Lambert W Function. Silicon 2015, 7, 279–282. [Google Scholar] [CrossRef]
- Brano, V.L.; Ciulla, G. An efficient analytical approach for obtaining a five parameters model of photovoltaic modules using only reference data. Appl. Energy 2013, 111, 894–903. [Google Scholar] [CrossRef]
- Cannizzaro, S.; Di Piazza, M.; Luna, M.; Vitale, G. Generalized classification of PV modules by simplified single-diode models. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2266–2273. [Google Scholar]
- Cotfas, D.; Cotfas, P.; Kaplanis, S. Methods to determine the dc parameters of solar cells: A critical review. Renew. Sustain. Energy Rev. 2013, 28, 588–596. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Musical chairs algorithm for parameters estimation of PV cells. Sol. Energy 2022, 241, 601–620. [Google Scholar] [CrossRef]
- Hasanien, H.M. Shuffled Frog Leaping Algorithm for Photovoltaic Model Identification. IEEE Trans. Sustain. Energy 2015, 6, 509–515. [Google Scholar] [CrossRef]
- Shongwe, S.; Hanif, M. Comparative Analysis of Different Single-Diode PV Modeling Methods. IEEE J. Photovolt. 2015, 5, 938–946. [Google Scholar] [CrossRef]
- Ranaivoson, S.S.A.; Saincy, N.; Sambatra, E.J.R.; Andrianajaina, T.; Razafinjaka, N.J. Experimentation of MPPT Control Driving a Buck Converter with PV Module Disturbances and Variable Load in a Nanogrid. Int. J. Recent Technol. Eng. (IJRTE) 2023, 12, 95–101. [Google Scholar] [CrossRef]
- Varatharaju, V.; Senthilkumar, B.; Manivannan, R.; Mahalakshmi, S.; Geetha, C.; Gomathi, S. MPPT Control using Modified Sepic Converter in PV Modules Connected DC Micro Grid Systems. In Proceedings of the 2023 7th International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 11–13 April 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 181–186. [Google Scholar]
- Farh, H.M.; Eltamaly, A.M.; Al-Saud, M.S. Interleaved boost converter for global maximum power extraction from the photovoltaic system under partial shading. IET Renew. Power Gener. 2019, 13, 1232–1238. [Google Scholar] [CrossRef]
- Nasiri, M.; Chandra, S.; Taherkhani, M.; McCormack, S.J. Impact of Input Capacitors in Boost Converters on Stability and Maximum Power Point Tracking in PV systems. In Proceedings of the 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), Fort Lauderdale, FL, USA, 20–25 June 2021; pp. 1004–1008. [Google Scholar]
- Hayat, A.; Sibtain, D.; Murtaza, A.F.; Shahzad, S.; Jajja, M.S.; Kilic, H. Design and Analysis of Input Capacitor in DC–DC Boost Converter for Photovoltaic-Based Systems. Sustainability 2023, 15, 6321. [Google Scholar] [CrossRef]
- Obukhov, S.; Ibrahim, A.; Diab, A.A.Z.; Al-Sumaiti, A.S.; Aboelsaud, R. Optimal Performance of Dynamic Particle Swarm Optimization Based Maximum Power Trackers for Stand-Alone PV System under Partial Shading Conditions. IEEE Access 2020, 8, 20770–20785. [Google Scholar] [CrossRef]
- Rashmi, K.; Patil, R. Energy Aware cross Layer Based Clustering and Congestion Control Using Mexican Axolotl Algorithm in VANET. Int. J. Comput. Netw. Appl. (IJCNA) 2022, 9, 701–711. [Google Scholar]
- Łukasiewicz, J. On three-valued logic. Ruch Filoz. 1920, 5, 170–171. [Google Scholar]
- Zadeh, L.A. Fuzzy Sets and Systems. System Theory; Polytechnic Press: New York, NY, USA, 1965; pp. 29–39. [Google Scholar]

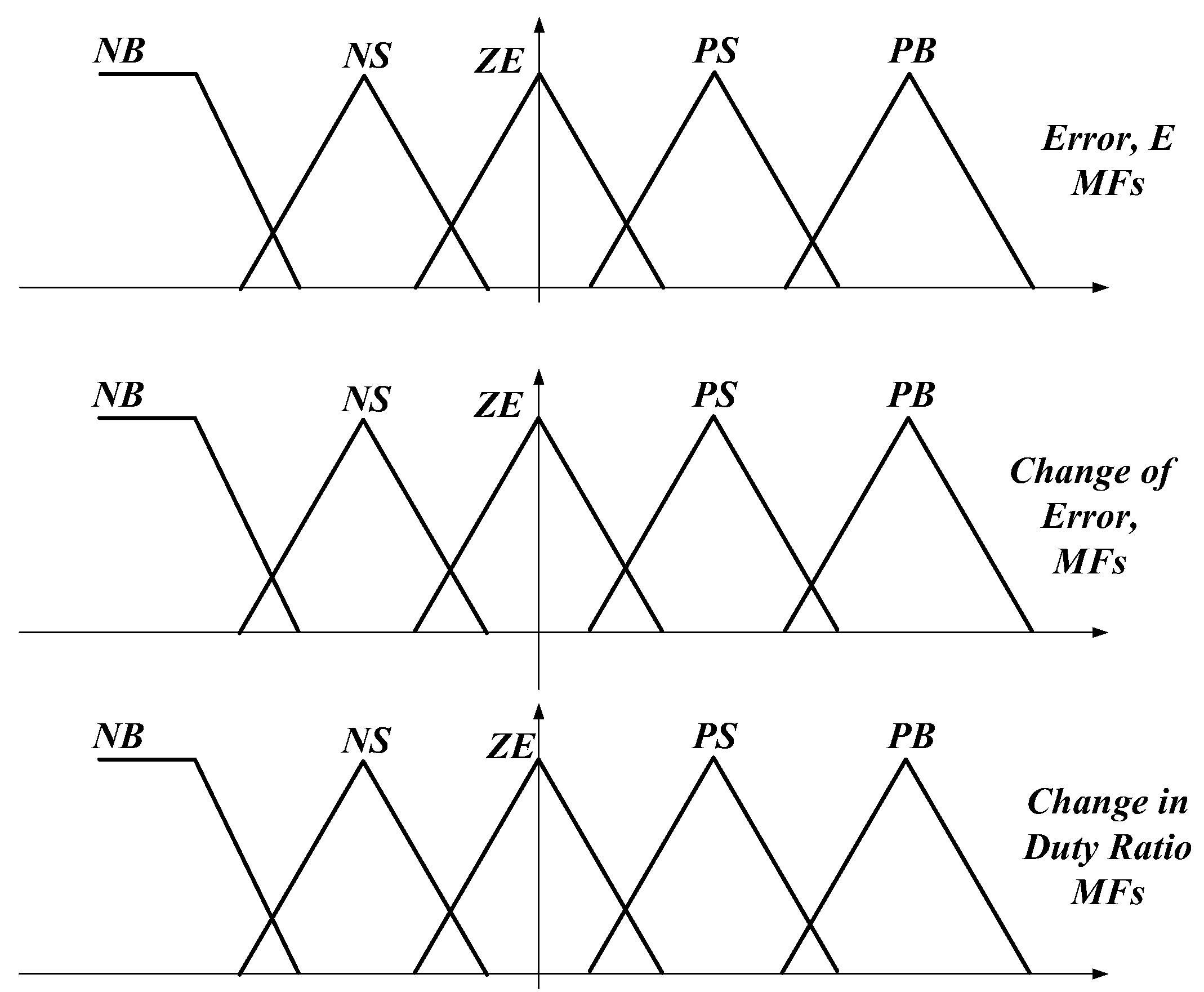
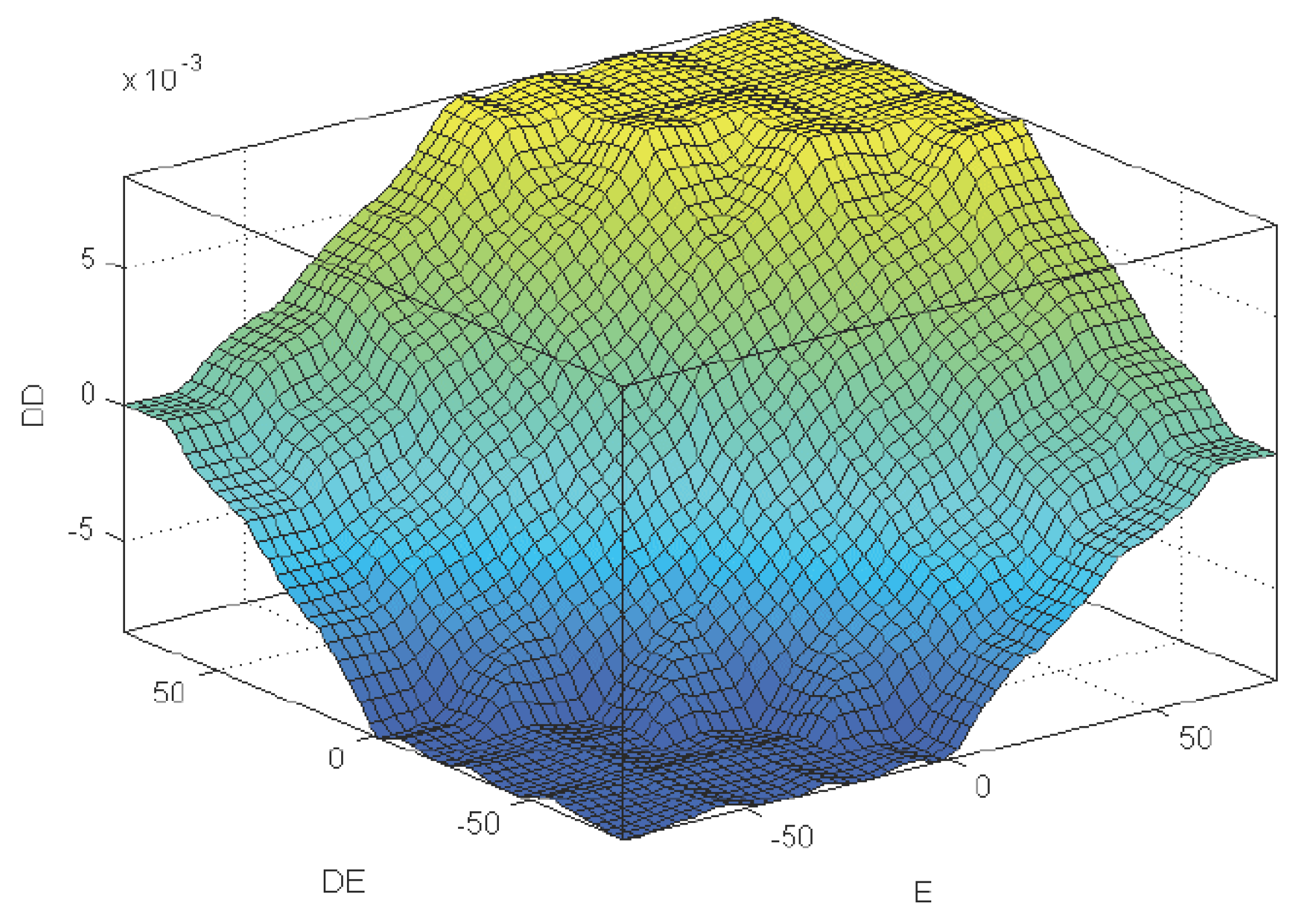



| E | NB | NS | ZE | PS | PB | |
|---|---|---|---|---|---|---|
| E | ||||||
| NB | NB | NB | NB | NM | ZE | |
| NS | NB | NM | NS | ZE | PM | |
| ZE | NB | NS | ZE | PS | PB | |
| PS | NM | ZE | PS | PM | PB | |
| PB | ZE | PM | PB | PB | PB | |
| Item | Specification | Item | Specification |
|---|---|---|---|
| Name | Sunperfect Solar CRM185S156P-54 | IL (A) | 7.9281 |
| Rated power | 185 W | I0 (A) | 1.9997 × 10−10 |
| Cells per module | 54 | n1 | 0.95194 |
| Voc (V) | 32.2 | Rsh (Ω) | 185.00028 |
| Isc (A) | 7.89 | Rs (Ω) | 0.43433 |
| Vmp (V) | 25.2 | Imp (A) | 7.35 |
| Item | Specification | Item | Specification |
|---|---|---|---|
| Cin | 25 μF | F | 20 kHz |
| Cout | 75 μF | Sampling period | 0.01 s |
| L | 80 μH | Current sensor | LTS 25-NP |
| MOSFET | IXFP72N20X3 | Voltage sensor | LV 25-P |
| MOSFET current | 72 | MOSFET driver | 74HC14 |
| MOSFET voltage | 200 | Sampling rate | 0.01 s |
| Items | MAO | FLC | PSO | MAO-FLC |
|---|---|---|---|---|
| PV Power (kW) | 93.88 | 54.21 | 93.89 | 93.89 |
| CT (s) | 0.38 | 0.53 | 0.62 | 0.29 |
| Ripples (%) | 1.3 | 0.01 | 0.57 | 0.01 |
| Swarm Size | CT (s) |
|---|---|
| 4 | 0.29 |
| 6 | 0.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eltamaly, A.M.; Alotaibi, M.A. Novel Hybrid Mexican Axolotl Optimization with Fuzzy Logic for Maximum Power Point Tracker of Partially Shaded Photovoltaic Systems. Energies 2024, 17, 2445. https://doi.org/10.3390/en17112445
Eltamaly AM, Alotaibi MA. Novel Hybrid Mexican Axolotl Optimization with Fuzzy Logic for Maximum Power Point Tracker of Partially Shaded Photovoltaic Systems. Energies. 2024; 17(11):2445. https://doi.org/10.3390/en17112445
Chicago/Turabian StyleEltamaly, Ali M., and Majed A. Alotaibi. 2024. "Novel Hybrid Mexican Axolotl Optimization with Fuzzy Logic for Maximum Power Point Tracker of Partially Shaded Photovoltaic Systems" Energies 17, no. 11: 2445. https://doi.org/10.3390/en17112445
APA StyleEltamaly, A. M., & Alotaibi, M. A. (2024). Novel Hybrid Mexican Axolotl Optimization with Fuzzy Logic for Maximum Power Point Tracker of Partially Shaded Photovoltaic Systems. Energies, 17(11), 2445. https://doi.org/10.3390/en17112445








