A Comprehensive Examination of Vector-Controlled Induction Motor Drive Techniques
Abstract
1. Introduction
- To be able to study and evaluate a drive system, it is necessary for the drive structure to be transformed into a mathematical model.
- The imposed response of the drive system when external disturbances are presented is obtained via an optimal regulator.
- Direct measurements of motor signals (mostly rotor speed) that are compared with reference signals via closed loops;
- Estimation of motor signals with motor parameter estimation in sensorless control systems (without rotor speed measurement), through the following methodologies of implementation:
- Speed assessment with state equation;
- Slip frequency computation method;
- Flux guessing and flux VC;
- Sensorless control for observer-based speed;
- Model reference adaptive systems (MRASs);
- Kalman filter-based algorithms (KFs);
- Sensorless through parameter estimation;
- Sensorless established using a neural network (NN);
- Sensorless based on fuzzy logic (FL).
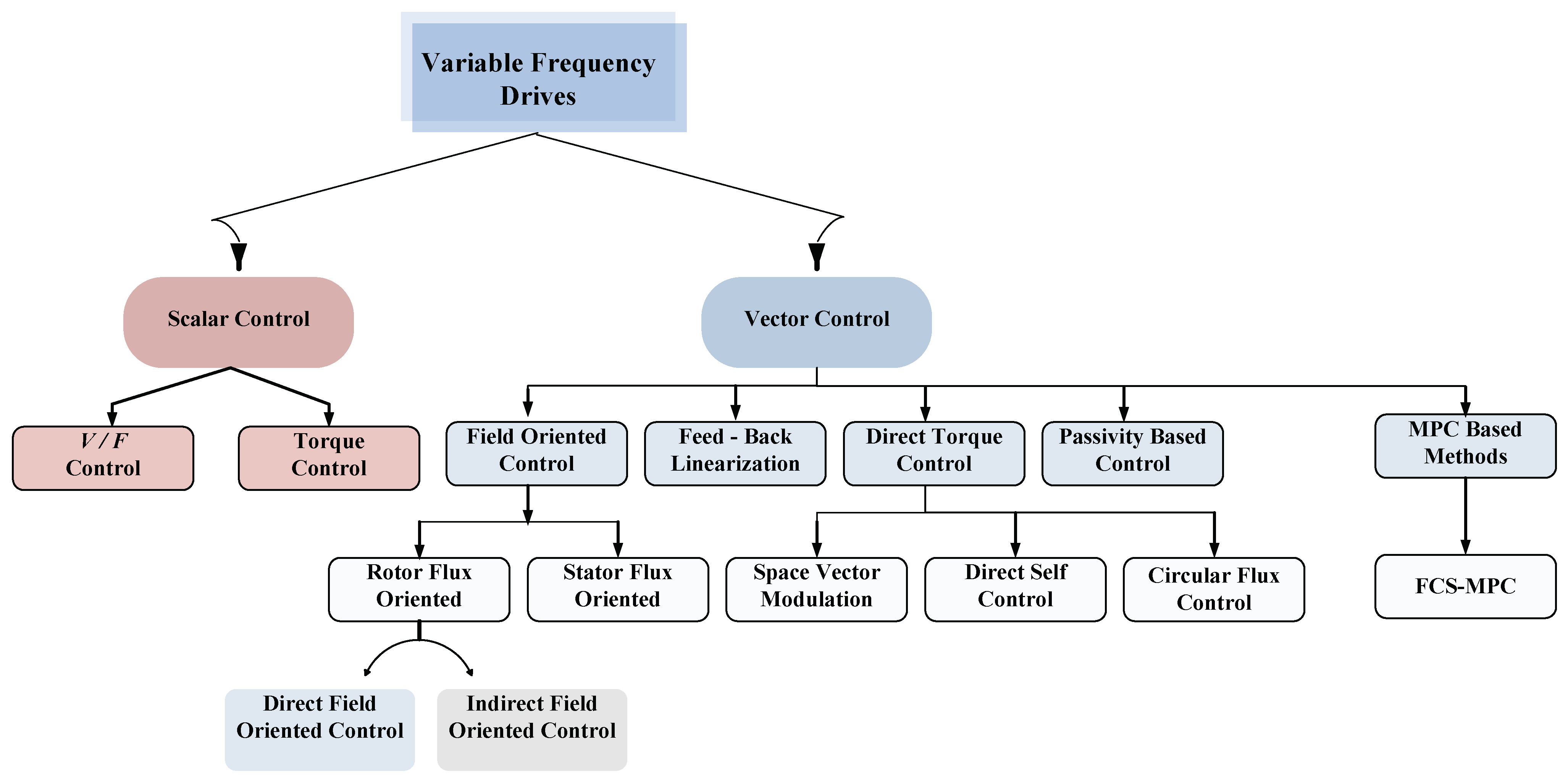
- Scalar control (SCC):
- A.1.
- Methods based on the constant ratio of voltage frequency ();
- A.2.
- Methods based on stator current and slip frequency, which have been mostly executed through machine parameter direct measurement.
- Vector control (VC):
- B.1.
- Field orientation control (FOC):
- B.1.1.
- Direct field orientation (DFOC);
- B.1.2.
- Indirect field orientation (IFOC).
- Direct torque (DTC) and stator flux vector control (SFVC).
- Model predictive control (MPC) and finite control set model predictive control (FCS-MPC).
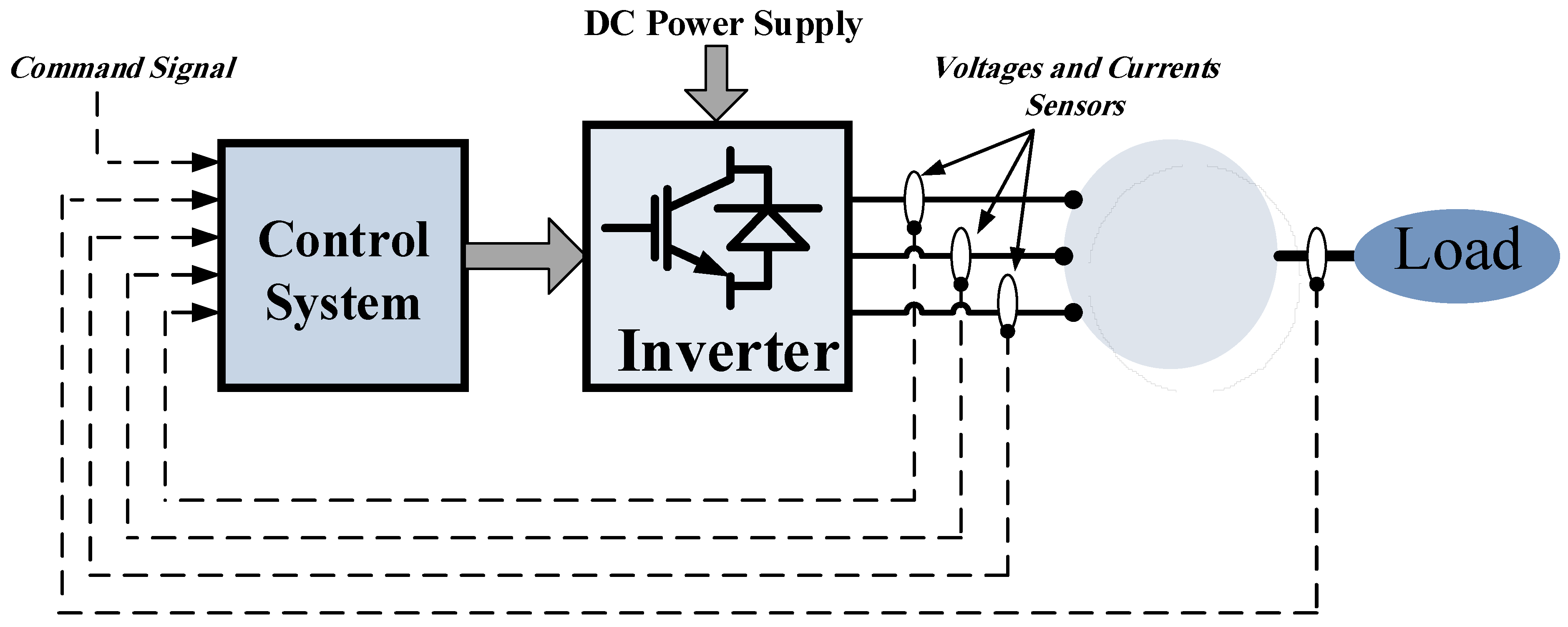
2. Variable Frequency Drives (VFDs)
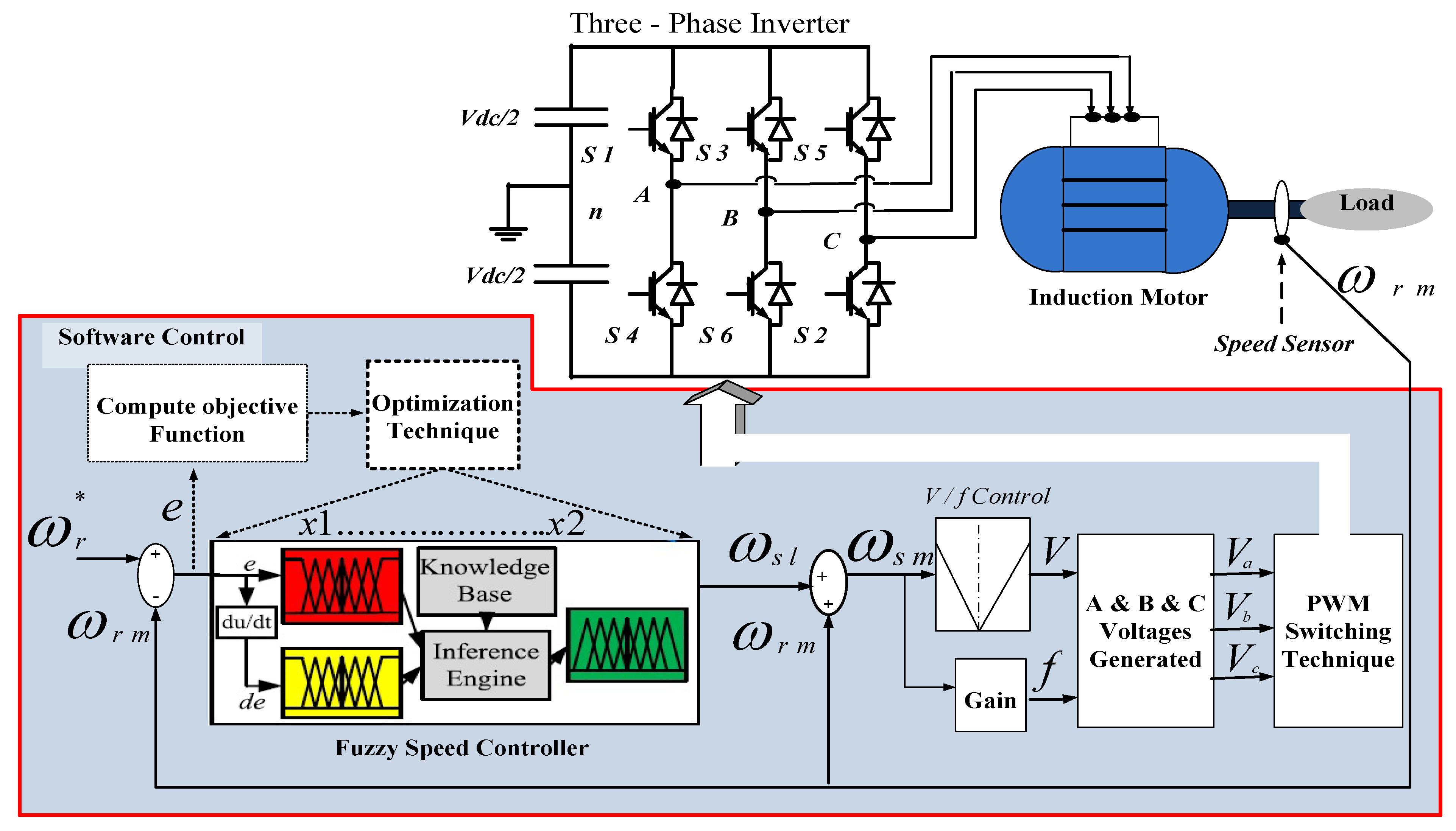
2.1. Scalar Control
2.2. Vector Control
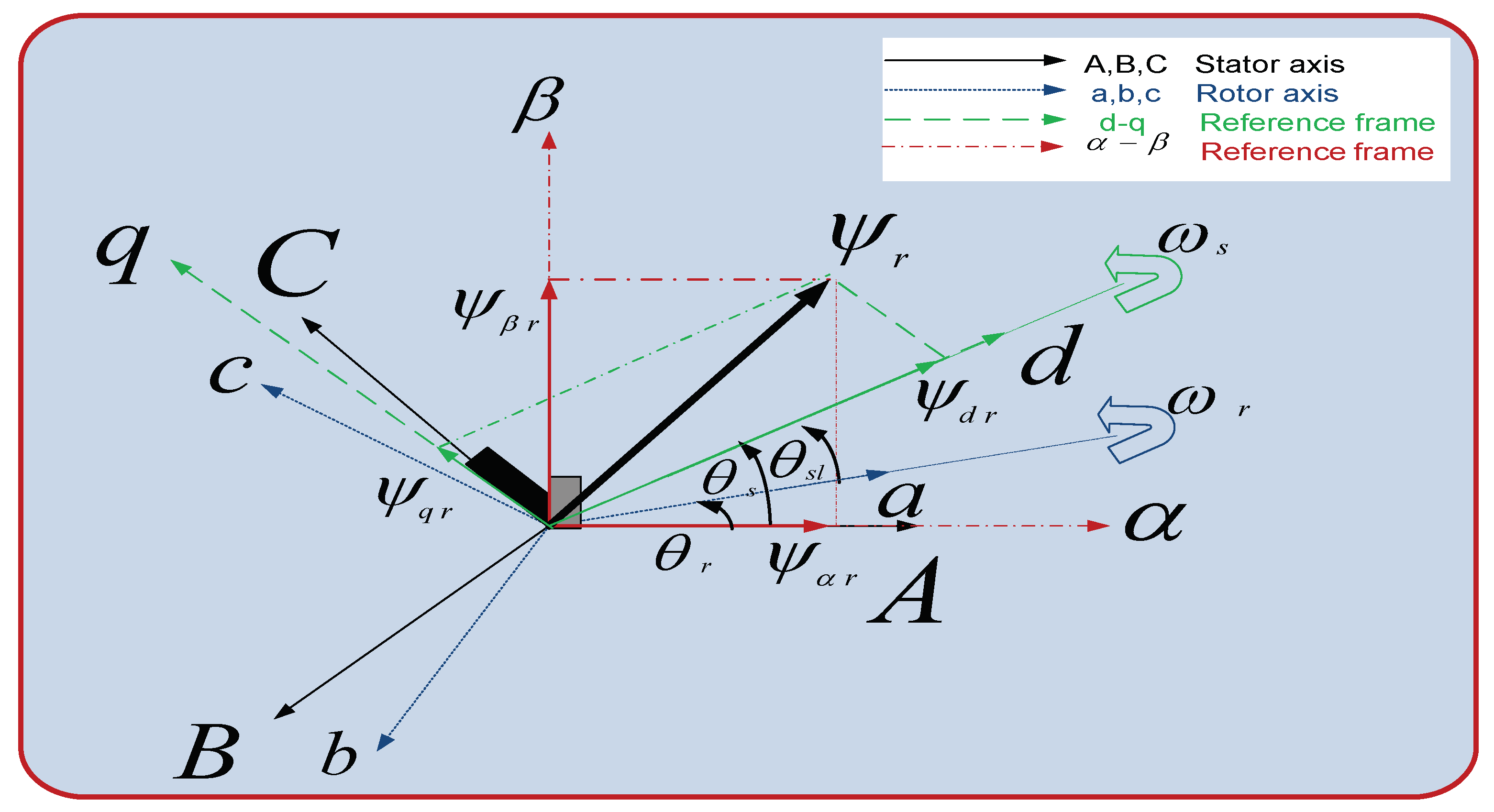
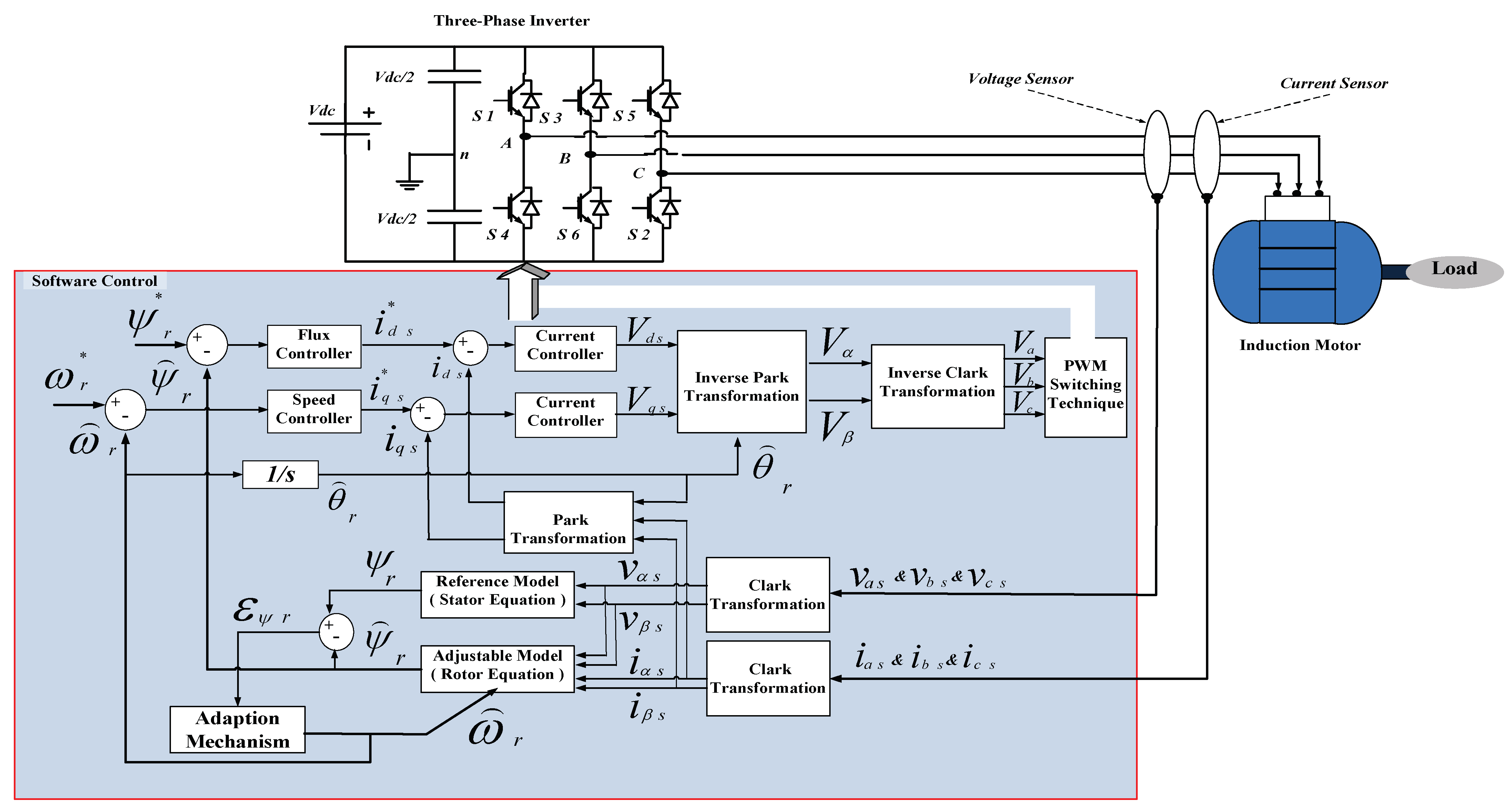
2.2.1. Basic Concept of Vector Control
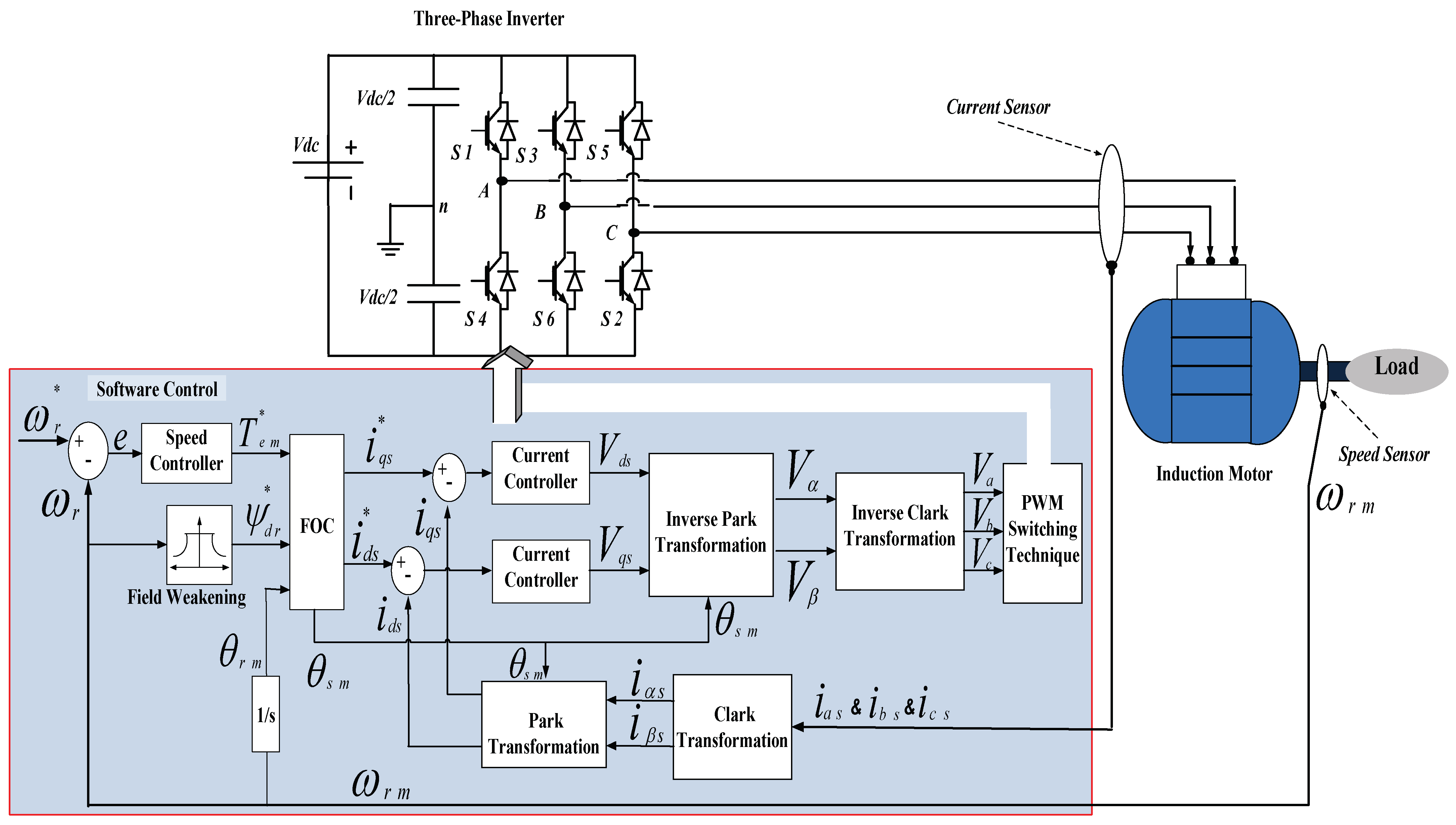
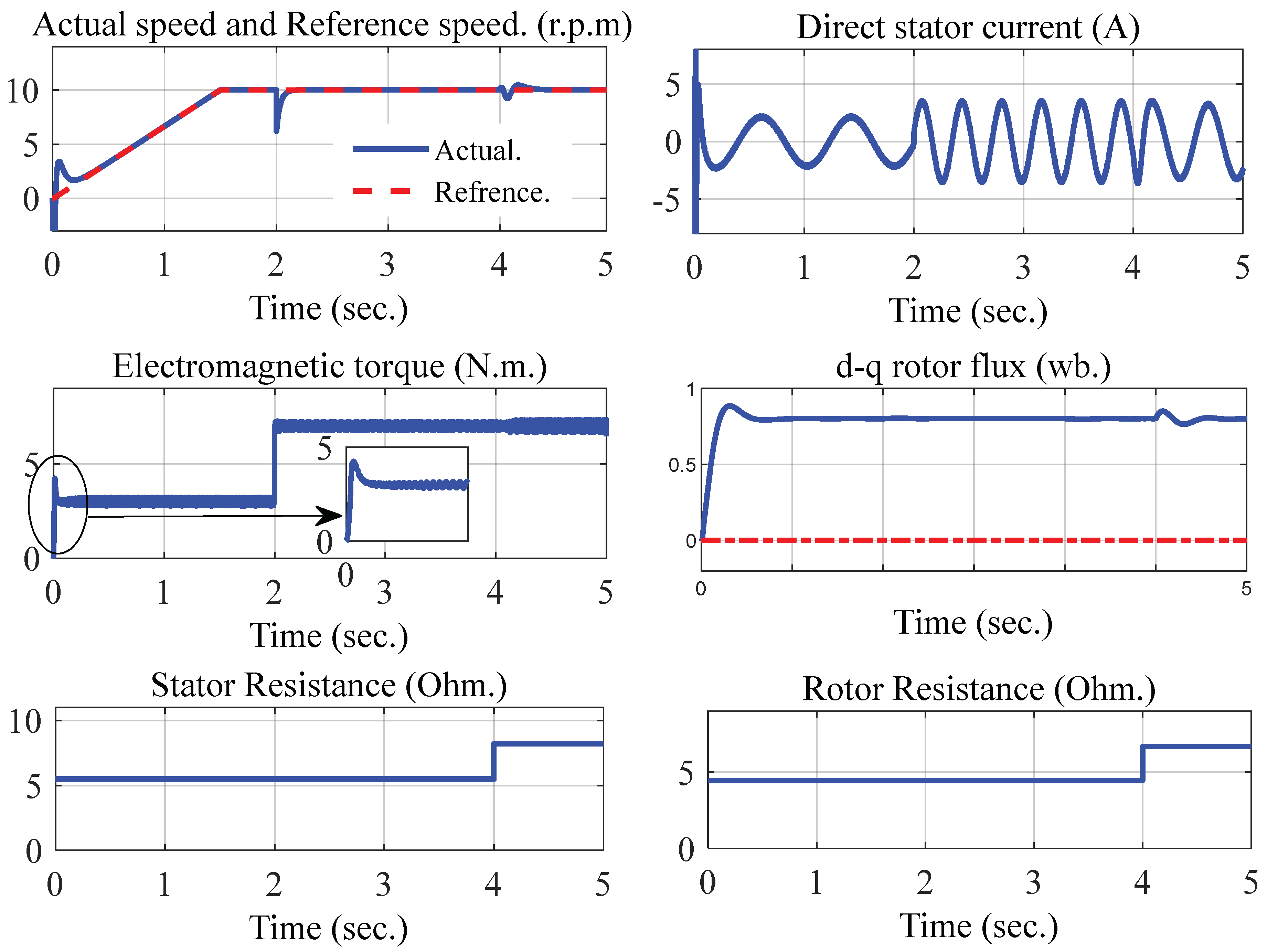
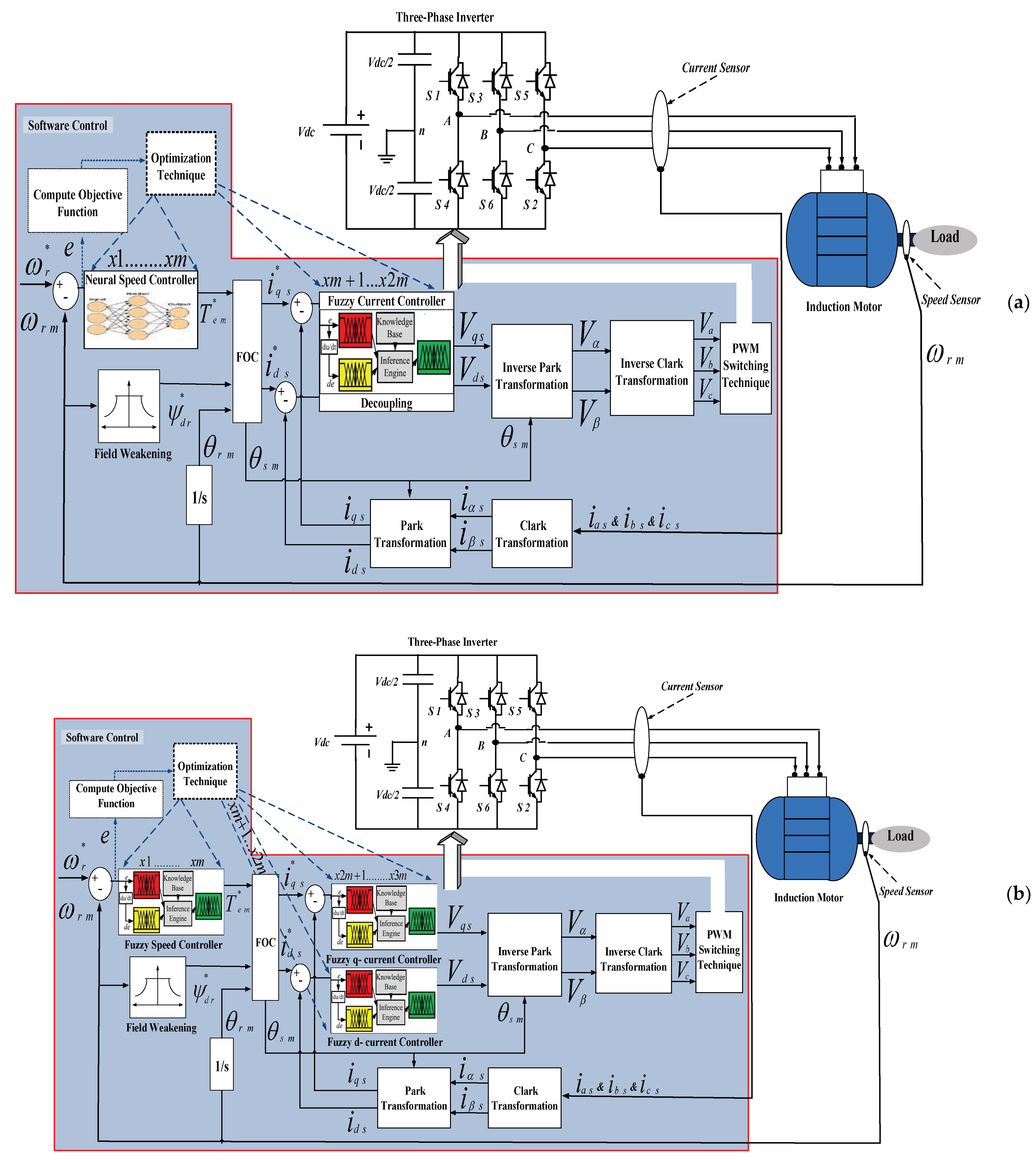
2.2.2. Direct Field-Oriented Control
2.2.3. Indirect Field-Oriented Control
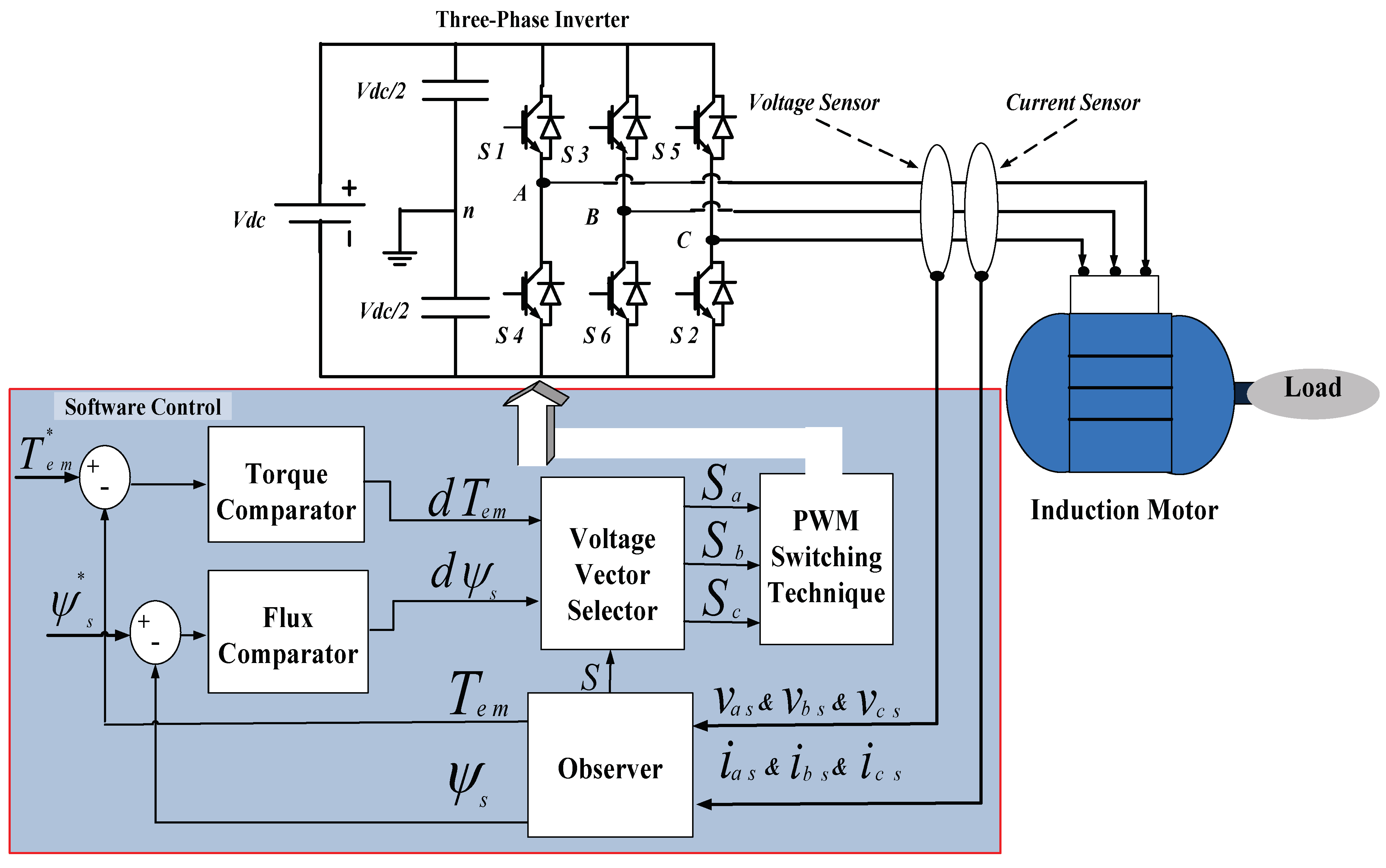
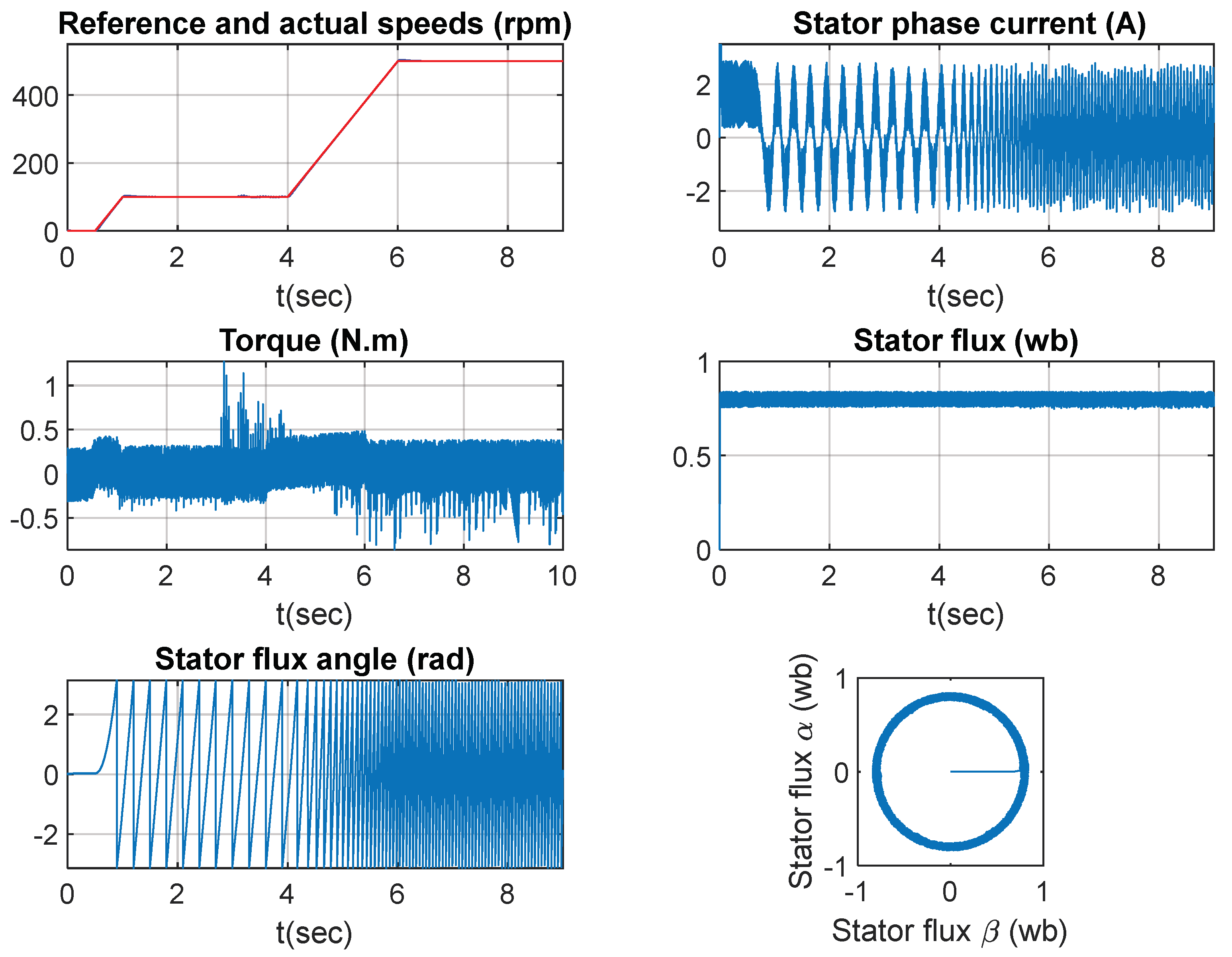
2.2.4. Direct Torque Control
3. Control Techniques
3.1. Microprocessor/Digital Control
3.2. Observers
- i.
- MRAS observer.
- ii.
- Luenberger observer.
- iii.
- Sliding mode observer.
- iv.
- Kalman observer.
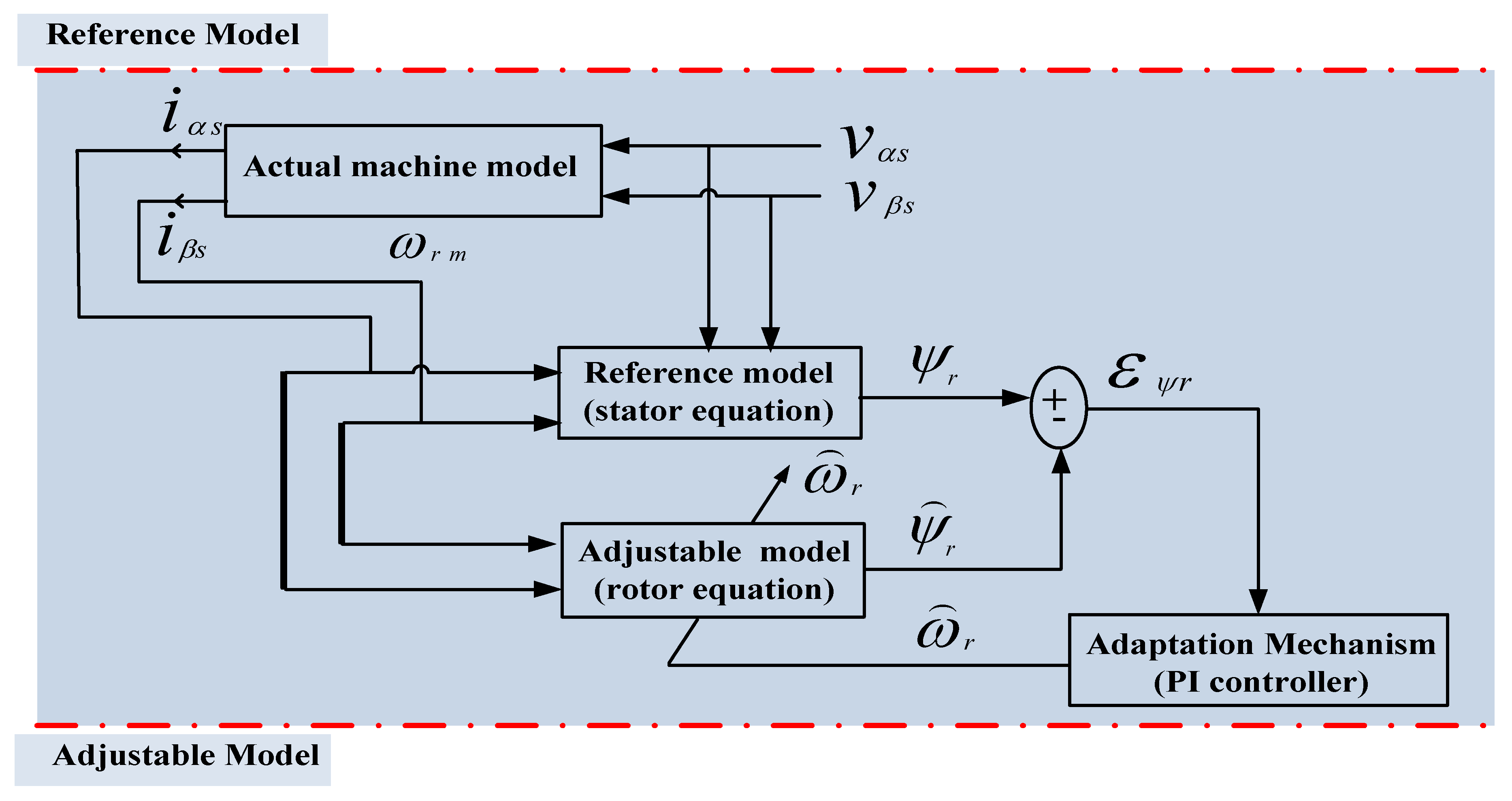
3.2.1. Model Reference Adaptive System Observer
3.2.2. Luenberger Observer
- Motor:
- Observer:
3.2.3. Sliding Mode Observer
3.2.4. Kalman Observer
3.3. Model Reference Adaptive System Based Control for IMs
- Torque current components—MRAS;
- Rotor flux—MRAS;
- Adaptive nonlinear flux observer.
3.4. Intelligent Control
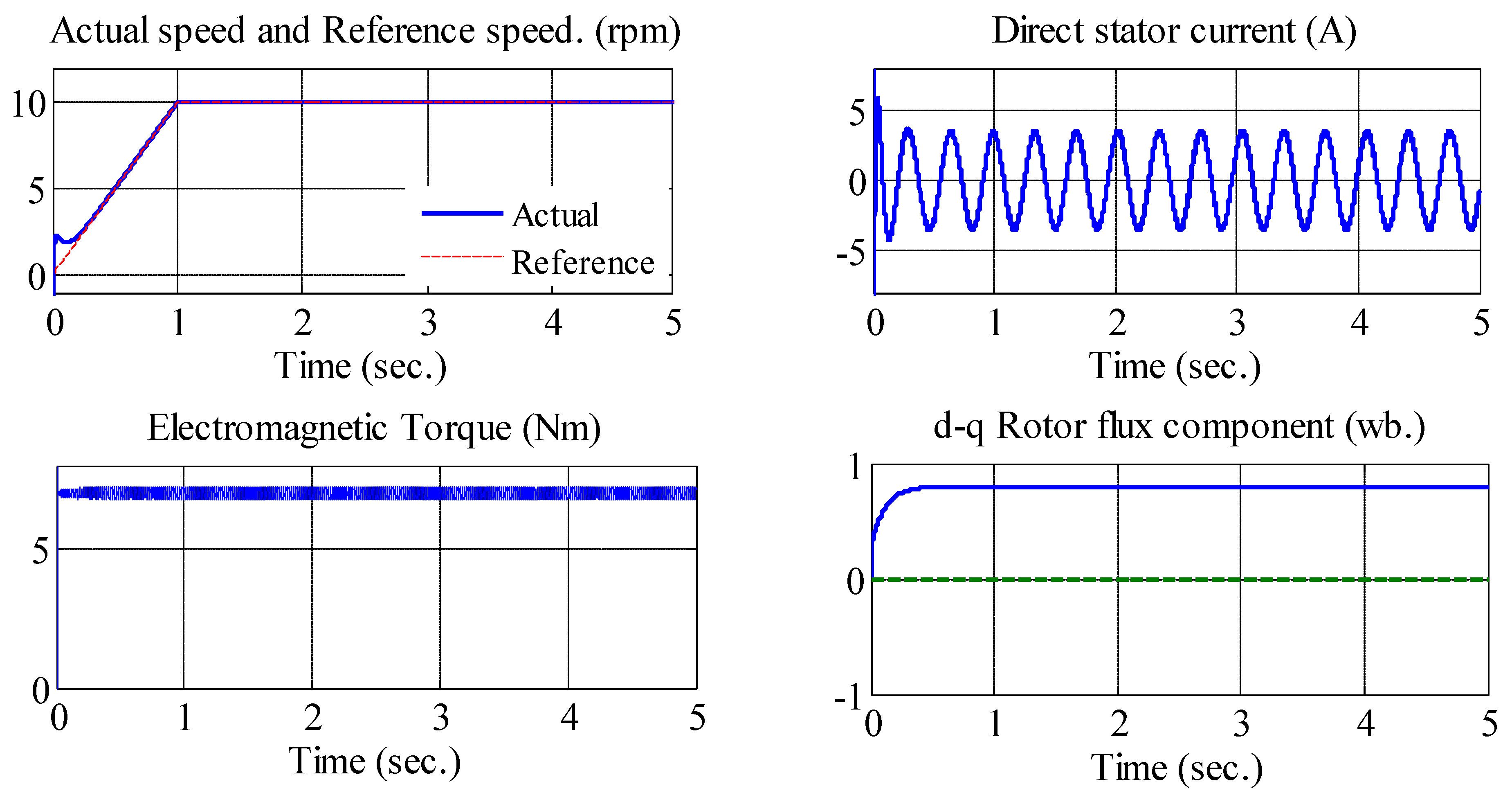
4. Motor Parameter Estimation
5. Low-Speed and Field-Weakening Operation
5.1. Low-Speed Operation
5.2. Field-Weakening Operation
6. Magnetic Saturation and Core Loss Impact
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, B.; Narimani, M. High-Power Converters and AC Drives, 2nd ed.; John Wiley& Sons: New York, NY, USA, 2017; pp. 101–105. [Google Scholar] [CrossRef]
- Holtz, J. Sensorless position control of induction motors. In An emerging technology, Proceedings of the AMC’98—Coimbra. 1998 5th International Workshop on Advanced Motion Control, Coimbra, Portugal, 29 June–1 July 1998; IEEE: Piscataway, NJ, USA, 1998; pp. 1–14. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Al-Sayed, A.-H.M.; Mohammed, H.H.A.; Mohammed, Y.S. Literature Review of Induction Motor Drives. In Development of Adaptive Speed Observers for Induction Machine System Stabilization; Springer: Singapore, 2020; pp. 7–18. [Google Scholar] [CrossRef]
- Murata, T.; Tsuchiya, T.; Takeda, I. Vector control for induction machine on the application of optimal control theory. IEEE Trans. Ind. Electron. 1990, 37, 283–290. [Google Scholar] [CrossRef]
- Koga, K.; Ueda, R.; Sonoda, T. Constitution of V/f control for reducing the steady-state speed error to zero in induction motor drive system. IEEE Trans. Ind. Appl. 1992, 28, 463–471. [Google Scholar] [CrossRef]
- Costa, C.A.; Nied, A.; Nogueira, F.G.; Turqueti, M.D.A.; Rossa, A.J.; Dezuo, T.J.M.; Barra, W. Robust Linear Parameter Varying Scalar Control Applied in High Performance Induction Motor Drives. IEEE Trans. Ind. Electron. 2020, 68, 10558–10568. [Google Scholar] [CrossRef]
- Otkun, Ö. Newton–Raphson based scalar speed control and optimization of IM. Automatika 2021, 62, 55–64. [Google Scholar] [CrossRef]
- Yussif, N.; Sabry, O.H.; Abdel-Khalik, A.S.; Ahmed, S.; Mohamed, A.M. Enhanced Quadratic V/f-Based Induction Motor Control of Solar Water Pumping System. Energies 2020, 14, 104. [Google Scholar] [CrossRef]
- Ustun, S.V.; Demirtas, M. Optimal tuning of PI coefficients by using fuzzy-genetic for V/f controlled induction motor. Expert Syst. Appl. 2008, 34, 2714–2720. [Google Scholar] [CrossRef]
- Siddavatam, R.P.R.; Loganathan, U. Slip Gain Estimation Scheme for Transient Vector Estimator-Based High-Performance Control of Induction Motor Drives. Trans. Indian Natl. Acad. Eng. 2021, 6, 311–321. [Google Scholar] [CrossRef]
- Suetake, M.; da Silva, I.N.; Goedtel, A. Embedded DSP-Based Compact Fuzzy System and Its Application for Induction-Motor $V/f$ Speed Control. IEEE Trans. Ind. Electron. 2010, 58, 750–760. [Google Scholar] [CrossRef]
- Almani, M.N.; Hussain, G.A.; Zaher, A.A. An Improved Technique for Energy-Efficient Starting and Operating Control of Single Phase Induction Motors. IEEE Access 2021, 9, 12446–12462. [Google Scholar] [CrossRef]
- Ahmad, S.; Mishra, A. Mathematical Modelling, Simulation and Control of Five-Phase Induction Motor Drives. In Proceedings of the International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET), Patna, India, 10–11 July 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Iftikhar, M.H.; Park, B.-G.; Kim, J.-W. Design and Analysis of a Five-Phase Permanent-Magnet Synchronous Motor for Fault-Tolerant Drive. Energies 2021, 14, 514. [Google Scholar] [CrossRef]
- Akroum, H.; Kidouche, M.; Aibeche, A. A dSPACE DSP Control Platform for V/F Controlled Induction Motor Drive and Parameters Identification. In Advances in Computer, Communication, Control and Automation; Springer: Berlin/Heidelberg, Germany, 2011; Volume 121, pp. 305–312. [Google Scholar] [CrossRef]
- Munoz-Garcia, A.; Lipo, T.; Novotny, D. A new induction motor V/f control method capable of high-performance regulation at low speeds. IEEE Trans. Ind. Appl. 1998, 34, 813–821. [Google Scholar] [CrossRef]
- Dybkowski, M.; Klimkowski, K. Artificial Neural Network Application for Current Sensors Fault Detection in the Vector Controlled Induction Motor Drive. Sensors 2019, 19, 571. [Google Scholar] [CrossRef] [PubMed]
- Sathishkumar, H.; Parthasarathy, S. A novel neural network intelligent controller for vector controlled induction motor drive. Energy Procedia 2017, 138, 692–697. [Google Scholar] [CrossRef]
- Yin, S.; Xia, J.; Zhao, Z.; Zhao, L.; Liu, W.; Diao, L.; Jatskevich, J. Fast Restarting of Free-Running Induction Motors Under Speed-Sensorless Vector Control. IEEE Trans. Ind. Electron. 2019, 67, 6124–6134. [Google Scholar] [CrossRef]
- Srivastava, S.P.; Pathak, M.K. Modified Reference Model for Rotor Flux-Based MRAS Speed Observer Using Neural Network Controller. IETE J. Res. 2018, 65, 80–95. [Google Scholar] [CrossRef]
- Perdukova, D.; Palacky, P.; Fedor, P.; Bober, P.; Fedak, V. Dynamic Identification of Rotor Magnetic Flux, Torque and Rotor Resistance of Induction Motor. IEEE Access 2020, 8, 142003–142015. [Google Scholar] [CrossRef]
- Reza, C.; Islam, D.; Mekhilef, S. A review of reliable and energy efficient direct torque controlled induction motor drives. Renew. Sustain. Energy Rev. 2014, 37, 919–932. [Google Scholar] [CrossRef]
- Maes, J.; Melkebeek, J. Speed-sensorless direct torque control of induction motors using an adaptive flux observer. IEEE Trans. Ind. Appl. 2000, 36, 778–785. [Google Scholar] [CrossRef]
- Tabasian, R.; Ghanbari, M.; Esmaeli, A.; Jannati, M. Direct field-oriented control strategy for fault-tolerant control of induction machine drives based on EKF. IET Electr. Power Appl. 2020, 36, 778–785. [Google Scholar] [CrossRef]
- Blaschke, F. The principle of field orientation as applied to the new TRANSVECTOR closed loop control system for rotating field machines. Siemens Rev. 1972, 34, 217–220. [Google Scholar]
- Hasse, K. Zum dynamischen Verhalten der Asynchron maschine bei Betrieb mit variabler Standerfreqenz und Standerspannung. ETZ-A 1968, 89, 77–81. [Google Scholar]
- Farah, N.; Talib, M.H.N.; Shah, N.S.M.; Abdullah, Q.; Ibrahim, Z.; Lazi, J.B.M.; Jidin, A. A Novel Self-Tuning Fuzzy Logic Controller Based Induction Motor Drive System: An Experimental Approach. IEEE Access 2019, 7, 68172–68184. [Google Scholar] [CrossRef]
- Hannan, M.A.; Ali, J.A.; Mohamed, A.; Amirulddin, U.A.U.; Tan, N.M.L.; Uddin, M.N. Quantum-Behaved Lightning Search Algorithm to Improve Indirect Field-Oriented Fuzzy-PI Control for IM Drive. IEEE Trans. Ind. Appl. 2018, 54, 3793–3805. [Google Scholar] [CrossRef]
- Devanshu, A.; Singh, M.; Kumar, N. An Improved Nonlinear Flux Observer Based Sensorless FOC IM Drive with Adaptive Predictive Current Control. IEEE Trans. Power Electron. 2019, 35, 652–666. [Google Scholar] [CrossRef]
- Basic, M.; Vukadinovic, D.; Grgic, I.; Bubalo, M. Speed-Sensorless Vector Control of an Induction Generator Including Stray Load and Iron Losses and Online Parameter Tuning. IEEE Trans. Energy Convers. 2019, 35, 724–732. [Google Scholar] [CrossRef]
- Zeb, K.; Ali, Z.; Saleem, K.; Uddin, W.; Javed, M.A.; Christofides, N. Indirect field-oriented control of induction motor drive based on adaptive fuzzy logic controller. Electr. Eng. 2016, 99, 803–815. [Google Scholar] [CrossRef]
- Savarapu, S.; Narri, Y. High performance of brain emotional intelligent controller for DTC-SVM based sensorless induction motor drive. J. Supercomput. 2021, 77, 1–22. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Mei, X.; Rodríguez, J.; Kennel, R. Advanced Control Strategies of Induction Machine: Field Oriented Control, Direct Torque Control and Model Predictive Control. Energies 2018, 11, 120. [Google Scholar] [CrossRef]
- Devanshu, A.; Singh, M.; Kumar, N. Nonlinear flux observer-based feedback linearisation control of IM drives with ANN speed and flux controller. Int. J. Electron. 2020, 108, 139–161. [Google Scholar] [CrossRef]
- Aktas, M.; Awaili, K.; Ehsani, M.; Arisoy, A. Direct torque control versus indirect field-oriented control of induction motors for electric vehicle applications. Eng. Sci. Technol. Int. J. 2020, 23, 1134–1143. [Google Scholar] [CrossRef]
- Hannan, M.A.; Jamal, A.A.; Mohamed, A.; Hussain, A. Optimization techniques to enhance the performance of induction motor drives: A review. Renew. Sustain. Energy Rev. 2018, 81, 1611–1626. [Google Scholar] [CrossRef]
- Bennett, S. Nicholas Minorsky and the automatic steering of ships. IEEE Control Syst. Mag. 1984, 4, 10–15. [Google Scholar] [CrossRef]
- Borja, P.; Ortega, R.; Scherpen, J.M.A. New Results on Stabilization of Port-Hamiltonian Systems via PID Passivity-Based Control. IEEE Trans. Autom. Control 2020, 66, 625–636. [Google Scholar] [CrossRef]
- Ulusoy, S.; Nigdeli, S.M.; Bekdaş, G. Novel metaheuristic-based tuning of PID controllers for seismic structures and verification of robustness. J. Build. Eng. 2020, 33, 101647. [Google Scholar] [CrossRef]
- Kim, B.S.; Kim, T.Y.; Park, T.C.; Yeo, Y.K. A model predictive functional control based on proportional-integral-derivative (PID) and proportional-integral-proportional-derivative (PIPD) using extended non-minimal state space: Application to a molten carbonate fuel cell process. Korean J. Chem. Eng. 2018, 35, 1601–1610. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi A. Zadeh; World Scientific: Singapore, 1996; pp. 394–432. [Google Scholar]
- Benlaloui, I.; Chrifi-Alaoui, L.; Ouriagli, M.; Khemis, A.; Khamari, D.; Drid, S. Improvement of the induction motor sensorless control based on the type-2 fuzzy logic. Electr. Eng. 2021, 103, 1473–1482. [Google Scholar] [CrossRef]
- Lamamra, K.; Batat, F.; Mokhtari, F. A new technique with improved control quality of nonlinear systems using an optimized fuzzy logic controller. Expert Syst. Appl. 2019, 145, 113148. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, J.; Meng, B.; Chen, X. Further results on fuzzy sampled-data stabilization of chaotic nonlinear systems. Appl. Math. Comput. 2020, 379, 125225. [Google Scholar] [CrossRef]
- De Barros, O., Jr.; Amorim, T.S.; Carletti, D.; Neto, A.F.; Encarnação, L.F. Design of an Enhanced FLC-Based Controller for Selective Harmonic Compensation in Active Power Filters. Electronics 2020, 9, 2052. [Google Scholar] [CrossRef]
- Begum, M.; Eskandari, M.; Abuhilaleh, M.; Li, L.; Zhu, J. Fuzzy-Based Distributed Cooperative Secondary Control with Stability Analysis for Microgrids. Electronics 2021, 10, 399. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Durairaj, S.; Padmavathi, S. A Performance Improvement of the Fuzzy Controller-Based Multi-Level Inverter-Fed Three-Phase Induction Motor with Enhanced Time and Speed of Response. J. Electr. Eng. Technol. 2021, 16, 1131–1141. [Google Scholar] [CrossRef]
- Bensalem, Y.; Abbassi, R.; Jerbi, H. Fuzzy Logic Based-Active Fault Tolerant Control of Speed Sensor Failure for Five-Phase PMSM. J. Electr. Eng. Technol. 2020, 16, 287–299. [Google Scholar] [CrossRef]
- Steczek, M.; Chudzik, P.; Lewandowski, M.; Szelag, A. PSO-Based Optimization of DC-Link Current Harmonics in Traction VSI for an Electric Vehicle. IEEE Trans. Ind. Electron. 2019, 67, 8197–8208. [Google Scholar] [CrossRef]
- Acikgoz, H.; Yildiz, C.; Coteli, R.; Dandil, B. DC-link voltage control of three-phase PWM rectifier by using artificial bee colony based type-2 fuzzy neural network. Microprocess. Microsyst. 2020, 78, 103250. [Google Scholar] [CrossRef]
- Ganthia, B.P.; Pradhan, R.; Sahu, R.; Pati, A.K. Artificial Ant Colony Optimized Direct Torque Control of Mathematically Modeled Induction Motor Drive Using PI and Sliding Mode Controller. In Recent Advances in Power Electronics and Drives; Kumar, J., Jena, P., Eds.; Springer: Singapore, 2020; pp. 389–408. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Back, T. Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Duan, F.; Zivanovic, R.; Al-Sarawi, S.; Mba, D. Induction Motor Parameter Estimation Using Sparse Grid Optimization Algorithm. IEEE Trans. Ind. Inform. 2016, 12, 1453–1461. [Google Scholar] [CrossRef]
- Sakthivel, V.; Bhuvaneswari, R.; Subramanian, S. Multi-objective parameter estimation of induction motor using particle swarm optimization. Eng. Appl. Artif. Intell. 2010, 23, 302–312. [Google Scholar] [CrossRef]
- Ali, J.A.; Hannan, M.A.; Mohamed, A.; Abdolrasol, M.G. Fuzzy logic speed controller optimization approach for induction motor drive using backtracking search algorithm. Measurement 2016, 78, 49–62. [Google Scholar] [CrossRef]
- Hu, Z.; Hameyer, K. A Method of Constraint Handling for Speed-Controlled Induction Machines. IEEE Trans. Ind. Electron. 2016, 63, 4061–4072. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Anosov, V.N. Implementation of full order observer for speed sensorless vector control of induction motor drive. In Proceedings of the 2014 15th International Conference of Young Specialists on Micro/Nanotechnologies and Electron Devices (EDM), Novosibirsk, Russia, 30 June–4 July 2014; pp. 347–352. [Google Scholar] [CrossRef]
- Boukhalfa, G.; Belkacem, S.; Chikhi, A.; Benaggoune, S. Genetic algorithm and particle swarm optimization tuned fuzzy PID controller on direct torque control of dual star induction motor. J. Central South Univ. 2019, 26, 1886–1896. [Google Scholar] [CrossRef]
- Chiang, C.-L.; Su, C.-T. Tracking control of induction motor using fuzzy phase plane controller with improved genetic algorithm. Electr. Power Syst. Res. 2004, 73, 239–247. [Google Scholar] [CrossRef]
- Kim, D.H. GA–PSO based vector control of indirect three phase induction motor. Appl. Soft Comput. 2007, 7, 601–611. [Google Scholar] [CrossRef]
- Rojas, C.A.; Rodriguez, J.R.; Kouro, S.; Villarroel, F. Multiobjective Fuzzy-Decision-Making Predictive Torque Control for an Induction Motor Drive. IEEE Trans. Power Electron. 2016, 32, 6245–6260. [Google Scholar] [CrossRef]
- Mousavi, M.S.; Davari, S.A.; Nekoukar, V.; Garcia, C.; Rodriguez, J. A Robust Torque and Flux Prediction Model by a Modified Disturbance Rejection Method for Finite-Set Model-Predictive Control of Induction Motor. IEEE Trans. Power Electron. 2021, 36, 9322–9333. [Google Scholar] [CrossRef]
- Zhao, Q.; Yang, Z.; Sun, X.; Ding, Q. Speed-sensorless control system of a bearingless induction motor based on iterative central difference Kalman filter. Int. J. Electron. 2020, 107, 1524–1542. [Google Scholar] [CrossRef]
- Aziz, A.; Rez, H.; Diab, A. Robust Sensorless Model-Predictive Torque Flux Control for High-Performance Induction Motor Drives. Mathematics 2021, 9, 403. [Google Scholar] [CrossRef]
- Santiseban, J.; Stephan, R. Vector control methods for induction machines: An overview. IEEE Trans. Educ. 2001, 44, 170–175. [Google Scholar] [CrossRef]
- Saidur, R.; Mekhilef, S.; Ali, M.; Safari, A.; Mohammed, H.A. Applications of variable speed drive (VSD) in electrical motors energy savings. Renew. Sustain. Energy Rev. 2012, 16, 543–550. [Google Scholar] [CrossRef]
- Gopal, B.T.V.; Shivakumar, E.G.; Ramesh, H.R. Design of Deep Learning Controller for Vector Controlled Induction Motor Drive. In Data Engineering and Communication Technology; Raju, K.S., Senkerik, R., Lanka, S.P., Rajagopal, V., Eds.; Springer: Singapore, 2020; pp. 639–647. [Google Scholar]
- Gandhi, K.; Saxena, S.; Ali, M. Vector Control of 3-Phase Induction Motor. MIT Int. J. Electr. Instrum. Eng. 2013, 3, 85–88. [Google Scholar]
- Amezquita-Brooks, L.; Liceaga-Castro, J.; Liceaga-Castro, E. Speed and Position Controllers Using Indirect Field-Oriented Control: A Classical Control Approach. IEEE Trans. Ind. Electron. 2013, 61, 1928–1943. [Google Scholar] [CrossRef]
- Jemli, M.; Ben Azza, H.; Gossa, M. Real-time implementation of IRFOC for Single-Phase Induction Motor drive using dSpace DS 1104 control board. Simul. Model. Prac. Theory 2009, 17, 1071–1080. [Google Scholar] [CrossRef]
- Dominic, D.A.; Chelliah, T.R. Analysis of field-oriented controlled induction motor drives under sensor faults and an overview of sensorless schemes. ISA Trans. 2014, 53, 1680–1694. [Google Scholar] [CrossRef]
- Shukla, S.; Singh, B. Reduced Current Sensor Based Solar PV Fed Motion Sensorless Induction Motor Drive for Water Pumping. IEEE Trans. Ind. Inform. 2018, 15, 3973–3986. [Google Scholar] [CrossRef]
- Takahashi, I.; Noguchi, T. A New Quick-Response and High-Efficiency Control Strategy of an Induction Motor. IEEE Trans. Ind. Appl. 1986, 22, 820–827. [Google Scholar] [CrossRef]
- Yen-Shin, L.; Jian-Ho, C. A new approach to direct torque control of induction motor drives for constant inverter switching frequency and torque ripple reduction. IEEE Trans. Energy Convers. 2001, 16, 220–227. [Google Scholar] [CrossRef]
- Sekhar, O.C.; Lakhimsetty, S.; Bhat, A.H. A comparative experimental analysis of fractional order PI controller based direct torque control scheme for induction motor drive. Int. Trans. Electr. Energy Syst. 2020, 31, e12705. [Google Scholar] [CrossRef]
- Vasudevan, M.; Arumugam, R.; Paramasivam, S. Real time implementation of viable torque and flux controllers and torque ripple minimization algorithm for induction motor drive. Energy Convers. Manag. 2006, 47, 1359–1371. [Google Scholar] [CrossRef]
- Kumar, D.D.; Kumar, N.P. Dynamic torque response improvement of direct torque controlled induction motor. J. Physics Conf. Ser. 2020, 1706, 012100. [Google Scholar] [CrossRef]
- Kumar, K.V.P.; Kumar, T.V. Enhanced direct torque control and predictive torque control strategies of an open-End winding induction motor drive to eliminate common-mode voltage and weighting factors. IET Power Electron. 2019, 12, 1986–1997. [Google Scholar] [CrossRef]
- Yan, L.; Wang, F. Observer-Predictor-Based Predictive Torque Control of Induction Machine for Robustness Improvement. IEEE Trans. Power Electron. 2021, 36, 9477–9486. [Google Scholar] [CrossRef]
- Lin, A.K.; Koepsel, W.W. A Microprocessor Speed Control System. IEEE Trans. Ind. Electron. Control. Instrum. 1977, 24, 241–247. [Google Scholar] [CrossRef]
- Gabriel, R.; Leonhard, W.; Nordby, C.J. Field-Oriented Control of a Standard AC Motor Using Microprocessors. IEEE Trans. Ind. Appl. 1980, 16, 186–192. [Google Scholar] [CrossRef]
- Sen, P.C.; Trezise, J.C.; Sack, M. Microprocessor Control of an Induction Motor with Flux Regulation. IEEE Trans. Ind. Electron. Control. Instrum. 1981, 28, 17–21. [Google Scholar] [CrossRef]
- Koyama, M.; Yano, M.; Kamiyama, I.; Yano, S. Microprocessor-Based Vector Control System for Induction Motor Drives with Rotor Time Constant Identification Function. IEEE Trans. Ind. Appl. 1986, 22, 453–459. [Google Scholar] [CrossRef]
- Kadyrov, I.; Karaeva, N.; Andarbekov, Z.; Kadyrkulova, K. Features of Designing a Variable-Frequency Electric Drive Control System with a Microprocessor-Based Sinusoidal Signal Generator. In High-Performance Computing Systems and Technologies in Scientific Research, Automation of Control and Production; Jordan, V., Filimonov, N., Tarasov, I., Faerman, V., Eds.; Springer: Cham, Switzerland, 2020; pp. 201–217. [Google Scholar]
- Pham, M.T.; Kim, J.-M.; Kim, C.H. Deep Learning-Based Bearing Fault Diagnosis Method for Embedded Systems. Sensors 2020, 20, 6886. [Google Scholar] [CrossRef]
- Heath, S. Embedded Systems Design; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Sidek, A.; Som, M.M. A Review of FPGA-based Implementation related to Electrical Engineering and Contribution to MPPT, Converter and Motor Drive Control. Multidiscip. Appl. Res. Innov. 2021, 2, 357–365. [Google Scholar]
- Landau, Y.D. Adaptive control: The model reference approach. IEEE Trans. Syst. Man, Cybern. 1984, 14, 169–170. [Google Scholar] [CrossRef]
- Zeitz, M. The extended Luenberger observer for nonlinear systems. Syst. Control Lett. 1987, 9, 149–156. [Google Scholar] [CrossRef]
- Utkin, V. Variable structure systems with sliding modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Chen, Y.; Bu, W.; Qiao, Y. Research on the Speed Sliding Mode Observation Method of a Bearingless Induction Motor. Energies 2021, 14, 864. [Google Scholar] [CrossRef]
- Krim, S.; Krim, Y.; Mimouni, M.F. Sensorless direct torque control based on nonlinear integral sliding mode controllers for an induction motor drive: Experimental verification. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 235, 249–268. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Madhukar, P.S.; Prasad, L. State Estimation using Extended Kalman Filter and Unscented Kalman Filter. In Proceedings of the International Conference on Emerging Trends in Communication, Control and Computing (ICONC3), Lakshmangarh, India, 21–22 February 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Gaikwad, K.A.; Bhanuse, V. State of Charge Estimation Using Extended Kalman Filter. In Advances in Signal and Data Processing; Merchant, S.N., Warhade, K., Adhikari, D., Eds.; Springer: Singapore, 2021; pp. 101–110. [Google Scholar]
- Aziz, A.G.M.A.; Diab, A.A.Z.; El Sattar, M.A. Speed Sensorless Vector Controlled Induction Motor Drive Based Stator and Rotor Resistances Estimation Taking Core Losses into Account. In 2017 Nineteenth International Middle East Power Systems Conference (MEPCON); IEEE: Piscataway, NJ, USA; pp. 1059–1068.
- Kubota, H.; Matsuse, K.; Nakano, T. DSP-based speed adaptive flux observer of induction motor. IEEE Trans. Ind. Appl. 1993, 29, 344–348. [Google Scholar] [CrossRef]
- Ammar, A. Second-order sliding mode-direct torque control and load torque estimation for sensorless model reference adaptive system–based induction machine. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 235, 15–29. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Li, S.; Yang, G.; Deng, R.; Hussain, H. Multiplane Rotor Resistance Online Estimation Strategy for Multiphase Induction Machine under Non-Sinusoidal Power Supply. IEEE Trans. Power Electron. 2021, 36, 9487–9500. [Google Scholar] [CrossRef]
- Misra, P.; Kumar, B. Rotor Resistance Estimation for Improved Performance of MRAS-Based Sensorless Speed Estimation of Induction Motor Drives; Springer: Singapore, 2020; pp. 177–187. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Korzonek, M.; Tarchala, G. Performance Analysis of Speed-Sensorless Induction Motor Drive Using Discrete Current-Error Based MRAS Estimators. Energies 2020, 13, 2595. [Google Scholar] [CrossRef]
- Lascu, C.; Boldea, I.; Blaabjerg, F. Comparative study of adaptive and inherently sensorless observers for variable-speed induction-motor drives. IEEE Trans. Ind. Electron. 2006, 53, 57–65. [Google Scholar] [CrossRef]
- Ohyama, K.; Asher, G.; Sumner, M. Comparative analysis of experimental performance and stability of sensorless induction motor drives. IEEE Trans. Ind. Electron. 2006, 53, 178–186. [Google Scholar] [CrossRef]
- Marvin, M.; Seymour, A.P. Perceptrons; MIT Press: Cambridge, MA, USA, 1969. [Google Scholar]
- McClelland, J.L.; Rumelhart, D.E.; PDP Group. Parallel Distributed Processing; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals, Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Lima, F.; Kaiser, W.; da Silva, I.N.; de Oliveira, A.A.A. Open-loop neuro-fuzzy speed estimator applied to vector and scalar induction motor drives. Appl. Soft Comput. 2014, 21, 469–480. [Google Scholar] [CrossRef]
- Jeen-Shing, W.; Lee, C.S.G. Efficient neuro-fuzzy control systems for autonomous underwater vehicle control. In Proceedings of the 2001 ICRA IEEE International Conference on Robotics and Automation, Seoul, Republic of Korea, 21–26 May 2001; Volume 3, pp. 2986–2991. [Google Scholar]
- Nauck, D.; Klawonn, F.; Kruse, R. Foundations of Neuro-fuzzy Systems; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Jang, J.-S. Neuro-fuzzy Modeling: Architectures, Analyses, and Applications; University of California: Berkeley, CA, USA, 1992. [Google Scholar]
- Jang, J.-S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Hanumanthakari, S. Comparative Analysis of Different Types of Membership Functions for Fuzzy Logic Controller in Direct Torque Control of Induction Motor. In Intelligent Computing in Control and Communication; Springer: Singapore, 2021; pp. 405–416. [Google Scholar] [CrossRef]
- Sada, S.; Ikpeseni, S. Evaluation of ANN and ANFIS modeling ability in the prediction of AISI 1050 steel machining performance. Heliyon 2021, 7, e06136. [Google Scholar] [CrossRef] [PubMed]
- Zeb, K.; Uddin, W.; Haider, A.; Belal, S.; Mehmood, C.A.; Khan, M.A.; Kim, H.J. Robust speed regulation of indirect vector control induction motor using fuzzy logic controllers based on optimization algorithms. Electr. Eng. 2017, 100, 787–802. [Google Scholar] [CrossRef]
- Yang, S.; Ding, D.; Li, X.; Xie, Z.; Zhang, X.; Chang, L. A Novel Online Parameter Estimation Method for Indirect Field Oriented Induction Motor Drives. IEEE Trans. Energy Convers. 2017, 32, 1562–1573. [Google Scholar] [CrossRef]
- Zerdali, E. A Comparative Study on Adaptive EKF Observers for State and Parameter Estimation of Induction Motor. IEEE Trans. Energy Convers. 2020, 35, 1443–1452. [Google Scholar] [CrossRef]
- Zhao, H.; Eldeeb, H.H.; Wang, J.; Zhan, Y.; Xu, G.; Mohammed, O.A. Online Estimation of Rotor Temperature in Induction Motors Based on Parameter Identification. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 1629–1634. [Google Scholar] [CrossRef]
- Cao, P.; Zhang, X.; Yang, S.; Xie, Z.; Zhang, Y. Reactive-Power-Based MRAS for Online Rotor Time Constant Estimation in Induction Motor Drives. IEEE Trans. Power Electron. 2018, 33, 10835–10845. [Google Scholar] [CrossRef]
- Mahsahirun, S.N.; Yusof, Z.M.; Idris, N.R.N. Offline Artificial Neural Network Rotor Flux Estimator for Induction Motor. In Proceedings of the IEEE 2nd International Conference on Artificial Intelligence in Engineering and Technology (IICAIET), Kota Kinabalu, Malaysia, 26–27 September 2020; pp. 1–6. [Google Scholar]
- Fang-Zheng, P.; Fukao, T. Robust speed identification for speed-sensorless vector control of induction motors. IEEE Trans. Ind. Appl. 1994, 30, 1234–1240. [Google Scholar] [CrossRef]
- Holtz, J.; Juntao, Q. Sensorless vector control of induction motors at very low speed using a nonlinear inverter model and parameter identification. IEEE Trans. Ind. Appl. 2002, 38, 1087–1095. [Google Scholar] [CrossRef]
- Talla, J.; Leu, V.Q.; Smidl, V.; Peroutka, Z. Adaptive Speed Control of Induction Motor Drive with Inaccurate Model. IEEE Trans. Ind. Electron. 2018, 65, 8532–8542. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Korzonek, M.; Tarchala, G. Stability Improvement Methods of the Adaptive Full-Order Observer for Sensorless Induction Motor Drive—Comparative Study. IEEE Trans. Ind. Inform. 2019, 15, 6114–6126. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Lascu, C.; Fadali, M.S. Square Root Unscented Kalman Filters for State Estimation of Induction Motor Drives. IEEE Trans. Ind. Appl. 2013, 49, 92–99. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; El-Sayed, A.-H.M.; Abbas, H.H.; Sattar, M.A. Robust Speed Controller Design Using H_infinity Theory for High-Performance Sensorless Induction Motor Drives. Energies 2019, 12, 961. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.; Yu, Y.; Zhang, X.; Xu, D.G. Unified Complex Vector Field-Weakening Control for Induction Motor High-Speed Drives. IEEE Trans. Power Electron. 2020, 36, 7000–7011. [Google Scholar] [CrossRef]
- Accetta, A.; Cirrincione, M.; Pucci, M.; Sferlazza, A. State Space-Vector Model of Linear Induction Motors Including End-Effects and Iron Losses Part I: Theoretical Analysis. IEEE Trans. Ind. Appl. 2019, 56, 235–244. [Google Scholar] [CrossRef]
- Lin, P.; Lai, Y. Novel Voltage Trajectory Control for Field-Weakening Operation of Induction Motor Drives. IEEE Trans. Ind. Appl. 2011, 47, 122–127. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, B.; Yu, Y.; Zhang, J.; Dong, J.; Xu, D.G. Analysis and Optimization of Current Dynamic Control in Induction Motor Field-Weakening Region. IEEE Trans. Power Electron. 2020, 35, 8860–8866. [Google Scholar] [CrossRef]
- Zhang, X.; Foo, G.H.B.; Rahman, M.F. A Robust Field-Weakening Approach for Direct Torque and Flux Controlled Reluctance Synchronous Motors with Extended Constant Power Speed Region. IEEE Trans. Ind. Electron. 2019, 67, 1813–1823. [Google Scholar] [CrossRef]
- Tarvirdilu-Asl, R.; Nalakath, S.; Xia, Z.; Sun, Y.; Wiseman, J.; Emadi, A. Improved Online Optimization-Based Optimal Tracking Control Method for Induction Motor Drives. IEEE Trans. Power Electron. 2020, 35, 10654–10672. [Google Scholar] [CrossRef]
- Accetta, A.; Alonge, F.; Cirrincione, M.; D’Ippolito, F.; Pucci, M.; Rabbeni, R.; Sferlazza, A. Robust Control for High Performance Induction Motor Drives Based on Partial State-Feedback Linearization. IEEE Trans. Ind. Appl. 2019, 55, 490–503. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, A.; Zarri, L. A Robust Method for Field Weakening Operation of Induction Motor Drives with Maximum Torque Capability. In Proceedings of the Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, USA, 8–12 October 2006; Volume 1, pp. 111–117. [Google Scholar] [CrossRef]
- Nasir, B.A. An Accurate Iron Core Loss Model in Equivalent Circuit of Induction Machines. J. Energy 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Mthombeni, T.L.; Pillay, P. Physical Basis for the Variation of Lamination Core Loss Coefficients as a Function of Frequency and Flux Density. In Proceedings of the IECON 2006 - 32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006; pp. 1381–1387. [Google Scholar] [CrossRef]
- Kowal, D.; Sergeant, P.; Dupré, L.; Vandenbossche, L. Comparison of Iron Loss Models for Electrical Machines with Different Frequency Domain and Time Domain Methods for Excess Loss Prediction. IEEE Trans. Magn. 2015, 51, 1–10. [Google Scholar] [CrossRef]
- Grotstollen, H.; Wiesing, J. Torque capability and control of a saturated induction motor over a wide range of flux weakening. IEEE Trans. Ind. Electron. 1995, 42, 374–381. [Google Scholar] [CrossRef]
- Liu, L.; Du, X.; Shen, S. Indirect field-oriented torque control of induction motor considering magnetic saturation effect: Error analysis. IET Electr. Power Appl. 2017, 11, 1105–1113. [Google Scholar] [CrossRef]
- Lipcak, O.; Bauer, J. Offline method for experimental identification of load-dependent saturation of induction motor taking into account variation of inverse rotor time constant. IET Power Electron. 2020, 13, 1828–1836. [Google Scholar] [CrossRef]
- Hughes, A.; Drury, B. Electric Motors and Drives: Fundamentals, Types and Applications; Newnes: London, UK, 2019. [Google Scholar]
- Levi, E.; Mingyu, W. A speed estimator for high performance sensorless control of induction motors in the field weakening region. IEEE Trans. Power Electron. 2002, 17, 365–378. [Google Scholar] [CrossRef]
- Denkena, B.; Bergmann, B.; Klemme, H. Cooling of motor spindles—A review. Int. J. Adv. Manuf. Technol. 2020, 110, 1–22. [Google Scholar] [CrossRef]







| Symbol | Parameters | Values |
|---|---|---|
| Rated voltage | ||
| No. pole pairs | ||
| Rated frequency | ||
| Stator resistance | ||
| Rotor resistance | ||
| Stator self-inductance | ||
| Rotor self-inductance | ||
| Magnetizing inductance | ||
| Moment of inertia | ||
| Nominal stator flux | ||
| Nominal torque | ||
| Core resistance | ||
| Sampling time |
| Sector Number () | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 0 | 0 | |||||||
| 0 | 0 | 0 | 0 |
| Scalar Control | Vector Control | |
|---|---|---|
| Prototype implementation | Easy design-in prototype implementation | Problematic design in a prototype implementation |
| Cost | Low cost | High cost |
| Structure | Simple structure | Complex structure |
| Parameter dependency | Without the requirement for IM parameter identification | Necessitates and is sensible to IM parameters |
| Low-speed operation | Poor performance when operating at low velocities | High rendering in FOC and low performance of DTC in low-velocity responses |
| Sensors needed | Only velocity sensor | Many sensors are required: six sensors in DFOC, four sensors in IFOC, and six sensors in DTC |
| Coordinate transformations | Without requirement for coordinate transformations | Especially in FOC, it must be transformed in coordinates |
| Ripples | Minimizes the ripple of current | High-current/torque ripple in DTC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aziz, A.G.M.A.; Abdelaziz, A.Y.; Ali, Z.M.; Diab, A.A.Z. A Comprehensive Examination of Vector-Controlled Induction Motor Drive Techniques. Energies 2023, 16, 2854. https://doi.org/10.3390/en16062854
Aziz AGMA, Abdelaziz AY, Ali ZM, Diab AAZ. A Comprehensive Examination of Vector-Controlled Induction Motor Drive Techniques. Energies. 2023; 16(6):2854. https://doi.org/10.3390/en16062854
Chicago/Turabian StyleAziz, Ahmed G. Mahmoud A., Almoataz Y. Abdelaziz, Ziad M. Ali, and Ahmed A. Zaki Diab. 2023. "A Comprehensive Examination of Vector-Controlled Induction Motor Drive Techniques" Energies 16, no. 6: 2854. https://doi.org/10.3390/en16062854
APA StyleAziz, A. G. M. A., Abdelaziz, A. Y., Ali, Z. M., & Diab, A. A. Z. (2023). A Comprehensive Examination of Vector-Controlled Induction Motor Drive Techniques. Energies, 16(6), 2854. https://doi.org/10.3390/en16062854









