Analysis and Evaluation of Photovoltaic Cell Defects and Their Impact on Electricity Generation
Abstract
:1. Introduction
2. Photovoltaic Cell
3. Photovoltaic Cell Parameters
3.1. Open-Circuit Voltage UOC
3.2. Short Circuit Current ISC
3.3. Maximum Power PMPP
- –
- Perturbation and Observation
- –
- Incremental Conductance
3.4. Perturbation and Observation P&O
3.5. Incremental Conductance
3.6. Effectiveness η
3.7. Series Resistance RS
3.8. Parallel Resistance Rp
4. Mathematical Model of a Photovoltaic Cell
5. Photovoltaic Cell Analysis and Experiments
- –
- Temperature conditions of the photovoltaic panel;
- –
- Connecting photovoltaic panels—in series, in parallel;
- –
- Various faults on the photovoltaic panels in the string.
- (A)
- Case study I–Effect of temperature on photovoltaic panel power
- (B)
- Case study II—Effect of serial resistance on photovoltaic panel power
- (C)
- Case study III–Effect of solar radiation on the photovoltaic panel power
- (D)
- Case study IV—Operation of photovoltaic panels for different connections
- (E)
- Case study V—MPP point Finding
6. Conclusions and Discussion
- (a)
- Replacing a damaged photovoltaic panel—which is sometimes problematic in practice, since it is necessary to replace a panel with similar parameters;
- (b)
- Use of bypass diodes—depending on the extent of panel damage.
Author Contributions
Funding
Conflicts of Interest
References
- Pavlík, M. Obnoviteľné Zdroje Energie vo Všeobecnosti, 1st ed.; Technická Univerzita v Košiciach: Košice, Slovakia, 2019; p. 75. ISBN 978-80-553-3317-5. [Google Scholar]
- Kolcun, M.; Mešter, M.; Džmura, J.; Pavlík, M. Elektrárne, 1st ed.; Technická Univerzita v Košiciach: Košice, Slovakia, 2017; p. 202. ISBN 978-80-553-3119-5. [Google Scholar]
- Pavlík, M. Obnoviteľné Zdroje a iné Netradičné Zdroje Energie, 1st ed.; Technická Univerzita v Košiciach: Košice, Slovakia, 2019; p. 82. ISBN 978-80-553-3341-0. [Google Scholar]
- Kalogirou, S.A. Solar Energy Engineering—Processes and Systems, 2nd ed.; Elsevier Science & Technology: Amsterdam, The Netherlands, 2014; pp. 257–321. ISBN 978-0-12-397270-5. [Google Scholar]
- Kolcun, M.; Medveď, D.; Petráš, J.; Stolárik, R.; Vaško, Š. Výskum Charakteristík Fotovoltaických Komponentov pre Efektívne Projektovanie Solárnych Systémov, 1st ed.; Technická Univerzita v Košiciach: Košice, Slovakia, 2014; p. 120. ISBN 978-80-553-1961-2. [Google Scholar]
- Said, S.; Massoud, A.; Benammar, M.; Ahmed, S. A Matlab/Simulink-Based Photovoltaic Array Model Employing SimPower System Toolbox. J. Energy Power Eng. 2012, 6, 1965–1975. [Google Scholar]
- Zielinska, A.; Skowron, M.; Bien, A. Modelling of photovoltaic cells in variable conditions of temperature and intensity of solar insolation as a method of mapping the operation of the installation in real conditions. In Proceedings of the 2018 International Interdisciplinary PhD Workshop (IIPhDW), Świnouście, Poland, 9–12 May 2018; pp. 200–204. [Google Scholar] [CrossRef]
- Hasani, A.H.; Abdullah, S.F.; Zuhdi, A.W.M.; Bahrudin, M.S.; Za’Abar, F.; Harif, M.N. Modelling and Simulation of Photovoltaic Solar Cell using Silvaco TCAD and Matlab Software. In Proceedings of the 2018 IEEE International Conference on Semiconductor Electronics (ICSE), Kuala Lumpur, Malaysia, 15–17 August 2018; pp. 214–217. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Ding, K.; Feng, L.; Hamelmann, F.U.; Chen, X. Model Parameter Analysis of Cracked Photovoltaic Module under Outdoor Conditions. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), Calgary, AB, Canada, 15 June–21 August 2020; pp. 2509–2512. [Google Scholar] [CrossRef]
- Yan, C.; Wen, Y.; Jinzhao, L.; Jingjing, B. PROTEUS-based simulation platform to study the photovoltaic cell model under partially shaded conditions. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011; pp. 3446–3449. [Google Scholar] [CrossRef]
- Ma, R.; Yan, C.; Yu, J.; Liu, T.; Liu, H.; Li, Y.; Chen, J.; Luo, Z.; Tang, B.; Lu, X.; et al. High-Efficiency Ternary Organic Solar Cells with a Good Figure-of-Merit Enabled by Two Low-Cost Donor Polymers. ACS Energy Lett. 2022, 7, 2547–2556. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, M.; Xu, J.; Li, C.; Yan, J.; Zhou, G.; Zhong, W.; Hao, T.; Song, J.; Xue, X.; et al. Single-junction organic solar cells with over 19% efficiency enabled by a refined double-fibril network morphology. Nat. Mater. 2022, 21, 656–663. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, E.M.G.; Godina, R.; Pouresmaeil, E.; Catalao, J.P.S. Simulation study of a photovoltaic cell with increasing levels of model complexity. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Das, N.; Al Ghadeer, A.; Islam, S. Modelling and analysis of multi-junction solar cells to improve the conversion efficiency of photovoltaic systems. In Proceedings of the 2014 Australasian Universities Power Engineering Conference (AUPEC), Perth, WA, Australia, 28 September–1 October 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Chtita, S.; Chaibi, Y.; Derouich, A.; Belkadid, J. Modeling and Simulation of a Photovoltaic Panel Based on a Triple Junction Cells for a Nanosatellite. In Proceedings of the 2018 International Symposium on Advanced Electrical and Communication Technologies (ISAECT), Rabat, Morocco, 21–23 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Maniak, T. Modelovanie Parametrov Fotovoltickýchh Článkov. Bachelor’s Thesis, Technická Univerzita v Košiciach, Košice, Slovakia, 2021; p. 77. [Google Scholar]
- Dzúr, D. Sledovanie Parametrov Fotovoltických Článkov. Bachelor’s Thesis, Technická Univerzita v Košiciach, Košice, Slovakia, 2021; p. 67. [Google Scholar]
- Pavlík, M. Determination of effect of photovoltaic cells defect on electricity produce by use mathematical model. Prz. Elektrotechniczny 2022, 1, 200–203. [Google Scholar] [CrossRef]
- Pavlík, M.; Dzúr, D. Sledovanie Parametrov Fotovoltaických Článkov. In Electrical Engineering and Informatics 13: Proceedings of the Faculty of Electrical Engineering and Informatics of the Technical University of Košice; Technická Univerzita v Košiciach: Košice, Slovensko, 2022; pp. 362–368. ISBN 978-80-553-4120-0. [Google Scholar]
- Shi, S.; Hou, Y.; Yang, T.; Huang, C.; Yao, S.; Zhao, C.; Liu, Y.; Zhang, Z.; Liu, T.; Zou, B. Simple Solvent Treatment Enabled Improved PEDOT:PSS Performance toward Highly Efficient Binary Organic Solar Cells. ACS Omega 2022, 7, 41789–41795. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.; Warner, M.; Bhattacharya, I. Adaptive Step Size Incremental Conductance Based Maximum Power Point Tracking (MPPT). In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), Calgary, AB, Canada, 15 June–21 August 2020; pp. 2335–2339. [Google Scholar] [CrossRef]
- Fu, Q.; Tong, N. A New PSO Algorithm Based on Adaptive Grouping for Photovoltaic MPP Prediction. In Proceedings of the 2010 2nd International Workshop on Intelligent Systems and Applications, Wuhan, China, 22–23 May 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Saripalli, B.P.; Singh, G.; Singh, S. Cell Modelling and Analysis of Five-Parameter Three Diode model of Photovoltaic Module. In Proceedings of the 2021 IEEE 4th International Conference on Computing, Power and Communication Technologies (GUCON), Kuala Lumpur, Malaysia, 24–26 September 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Garcia, A.S.; Kristensen, S.T.; Strandberg, R. Analytical Modeling of the Temperature Sensitivity of the Maximum Power Point of Solar Cells. IEEE J. Photovoltaics 2022, 12, 1237–1242. [Google Scholar] [CrossRef]
- Mo, S.; Ye, Q.; Jiang, K.; Mo, X.; Shen, G. An improved MPPT method for photovoltaic systems based on mayfly optimization algorithm. Energy Rep. 2022, 8 (Suppl. S5), 141–150. [Google Scholar] [CrossRef]
- Dadkhah, J.; Niroomand, M. Optimization Methods of MPPT Parameters for PV Systems: Review, Classification, and Comparison. J. Mod. Power Syst. Clean Energy 2021, 9, 225–236. [Google Scholar] [CrossRef]
- Alanazi, A.; Alanazi, M.; Arabi, S.; Sarker, S. A New Maximum Power Point Tracking Framework for Photovoltaic Energy Systems Based on Remora Optimization Algorithm in Partial Shading Conditions. Appl. Sci. 2022, 12, 3828. [Google Scholar] [CrossRef]
- Cherukuri, S.K.; Rayapudi, S.R. A novel global MPP tracking of photovoltaic system based on whale optimization algorithm. Int. J. Renew. Energy Dev. 2016, 5, 225–232. [Google Scholar] [CrossRef]
- Belan, A. Model fotovoltického článku. Posterus 2013, 6. Available online: https://www.posterus.sk/?p=16396&output=pdf (accessed on 2 March 2023).
- Gupta, D.; Kumari, N.; Samadhiya, A. Photovoltaic Modeling using Single Diode Model in MATLAB. In Proceedings of the 2020 IEEE International Conference on Computing, Power and Communication Technologies (GUCON), Greater Noida, India, 2–4 October 2020; pp. 734–739. [Google Scholar] [CrossRef]
- Swain, S.C.; Dash, R.; Ali, S.M.; Mohanta, A.K. Performance evaluation of photovoltaic system based on solar cell modelling. In Proceedings of the 2015 International Conference on Circuits, Power and Computing Technologies [ICCPCT-2015], Nagercoil, India, 19–20 March 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Mazur, D.; Gołębiowski, L.; Smoleń, A.; Gołębiowski, M.; Szczerba, Z. Modeling and Analysis of the AFPM Generator in a Small Wind Farm System. In International Workshop on Modeling Social Media; Springer: Cham, Switzerland, 2019; Volume 548, pp. 202–210. [Google Scholar] [CrossRef]
- Aljoaba, S.Z.; Cramer, A.M.; Walcott, B.L. Thermo-electrical modeling of light wavelength effects on photovoltaic cell performance. In Proceedings of the 2011 37th IEEE Photovoltaic Specialists Conference, Seattle, WA, USA, 19–24 June 2011; p. 000192. [Google Scholar] [CrossRef]
- Hayder, W.; Abid, A.; Ben Hamed, M. Modeling of a photovoltaic cell based on recurrent neural networks. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Murtinger, K.; Beranovský, J.; Tomeš, M. Fotovoltaika: Elektrická Energie ze Slunce, 1st ed.; EkoWATT: Praha, Czech Republic, 2009; p. 93. ISBN 978-80-87333-01-3. [Google Scholar]
- Dec, G.; Drałus, G.; Mazur, D.; Kwiatkowski, B. Forecasting Models of Daily Energy Generation by PV Panels Using Fuzzy Logic. Energies 2021, 14, 1676. [Google Scholar] [CrossRef]
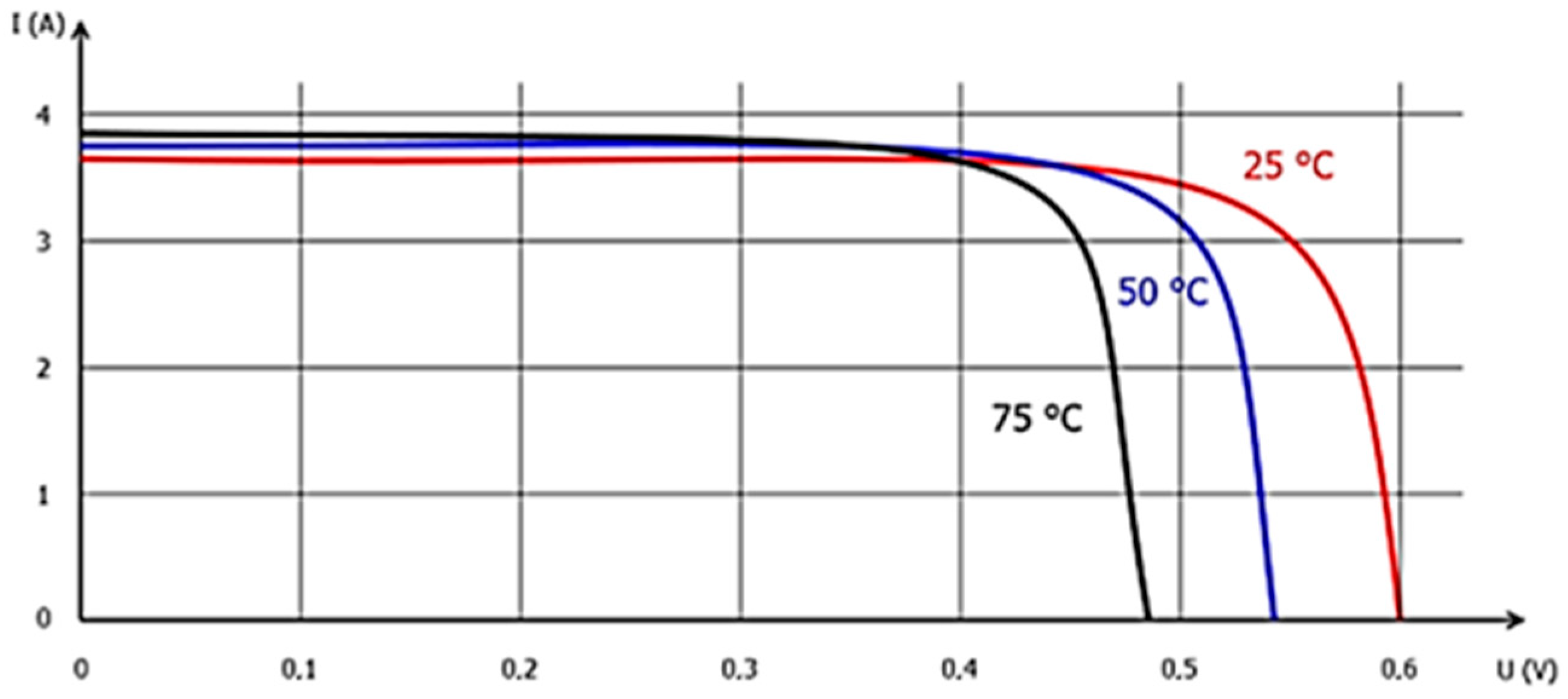


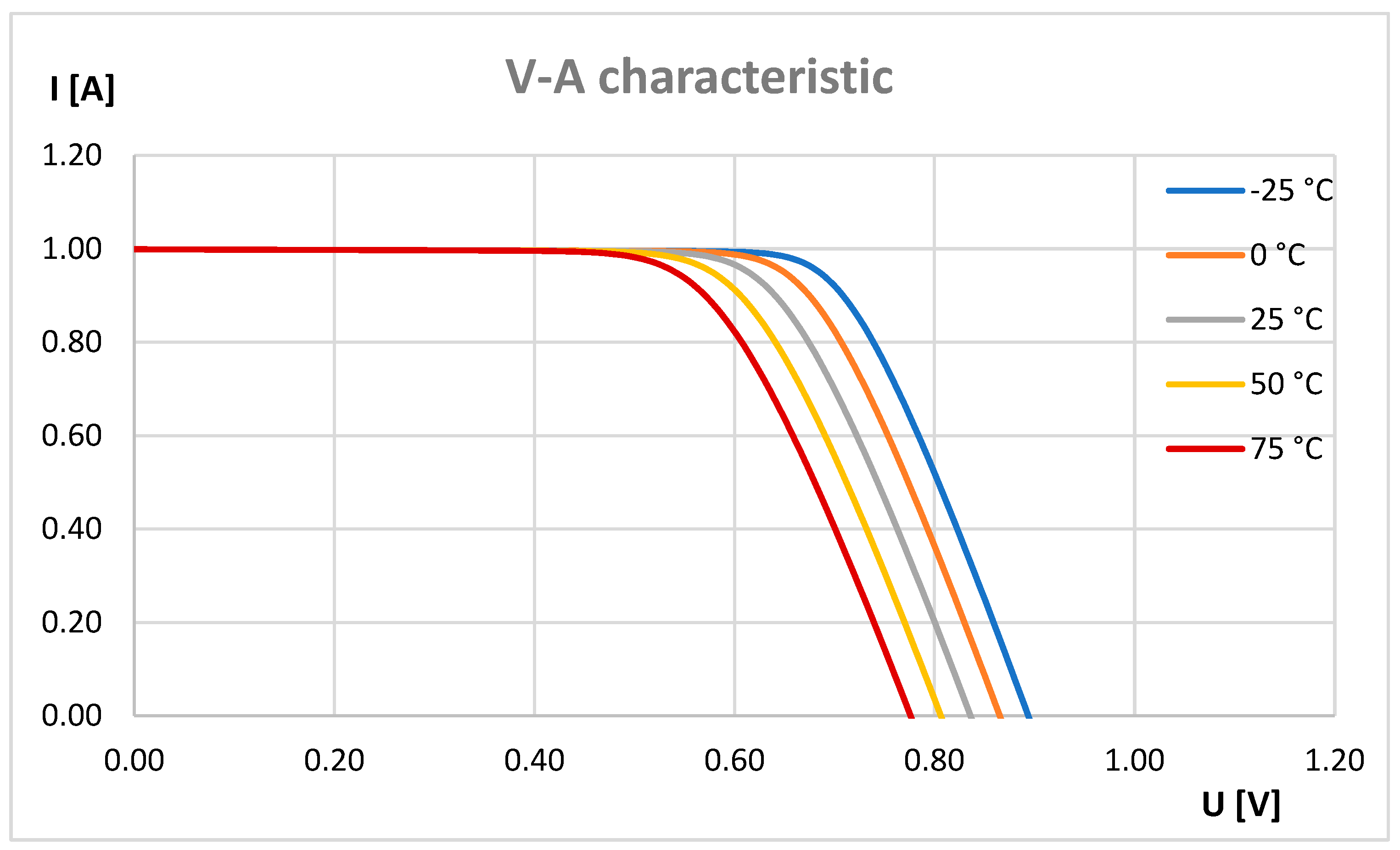






| Datasheet | Parameters |
|---|---|
| Total power, | |
| Voltage in , | |
| Current in , | |
| Short current | |
| Open circuit voltage | |
| Termal coeficient for open circuit voltage , | |
| Termal coeficient for short current , | |
| Cell number | |
| Svetlom generovaný prúd |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlík, M.; Beňa, L.; Medved’, D.; Čonka, Z.; Kolcun, M. Analysis and Evaluation of Photovoltaic Cell Defects and Their Impact on Electricity Generation. Energies 2023, 16, 2576. https://doi.org/10.3390/en16062576
Pavlík M, Beňa L, Medved’ D, Čonka Z, Kolcun M. Analysis and Evaluation of Photovoltaic Cell Defects and Their Impact on Electricity Generation. Energies. 2023; 16(6):2576. https://doi.org/10.3390/en16062576
Chicago/Turabian StylePavlík, Marek, L’ubomír Beňa, Dušan Medved’, Zsolt Čonka, and Michal Kolcun. 2023. "Analysis and Evaluation of Photovoltaic Cell Defects and Their Impact on Electricity Generation" Energies 16, no. 6: 2576. https://doi.org/10.3390/en16062576
APA StylePavlík, M., Beňa, L., Medved’, D., Čonka, Z., & Kolcun, M. (2023). Analysis and Evaluation of Photovoltaic Cell Defects and Their Impact on Electricity Generation. Energies, 16(6), 2576. https://doi.org/10.3390/en16062576






