Distribution System State Estimation and False Data Injection Attack Detection with a Multi-Output Deep Neural Network
Abstract
1. Introduction
- Unlike transmission networks, which have a mesh structure, DNs generally have radial or weakly meshed configuration.
- DNs generally consist of many buses compared to transmission networks, making installation of measurement devices at all buses in DNs economically impractical.
- DNs normally have large resistance to reactance ratios (, compared to transmission lines.
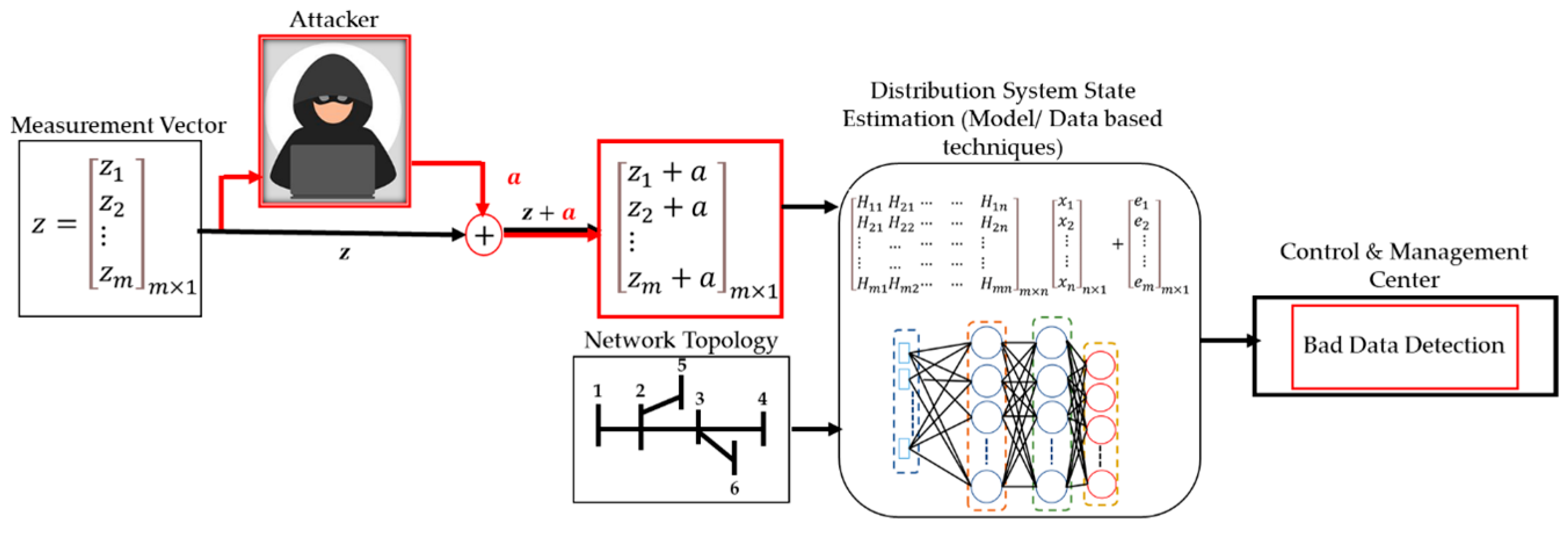
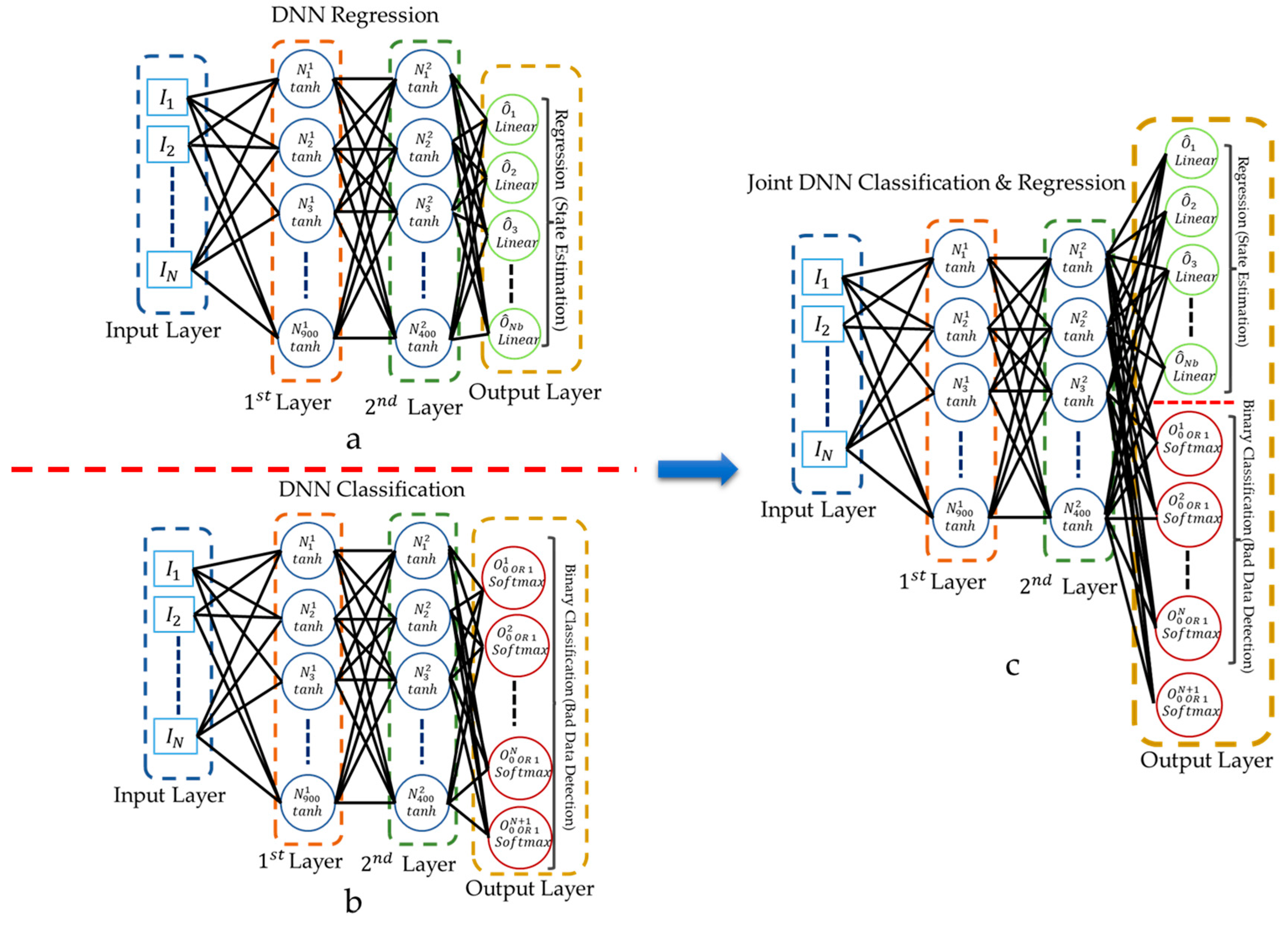
- We design a single DNN model to simultaneously perform DSSE calculation and FDIA detection based on PMU measurement inputs. The results are compared to when DSSE calculation and FDIAs are performed separately using two independent DNN models.
- Having classification nodes, where N is the number of PMU measurements, allows the DNN to identify which PMU measurement, if any, was affected by FDIA, or if none of the measurements were affected.
- The performance of the proposed method is investigated for FDIA detection on PMU measurements with different attack scenarios.
- To make a comparison between data-based and model-based approaches, DSSE calculation is performed using the WLS as a model-based approach.
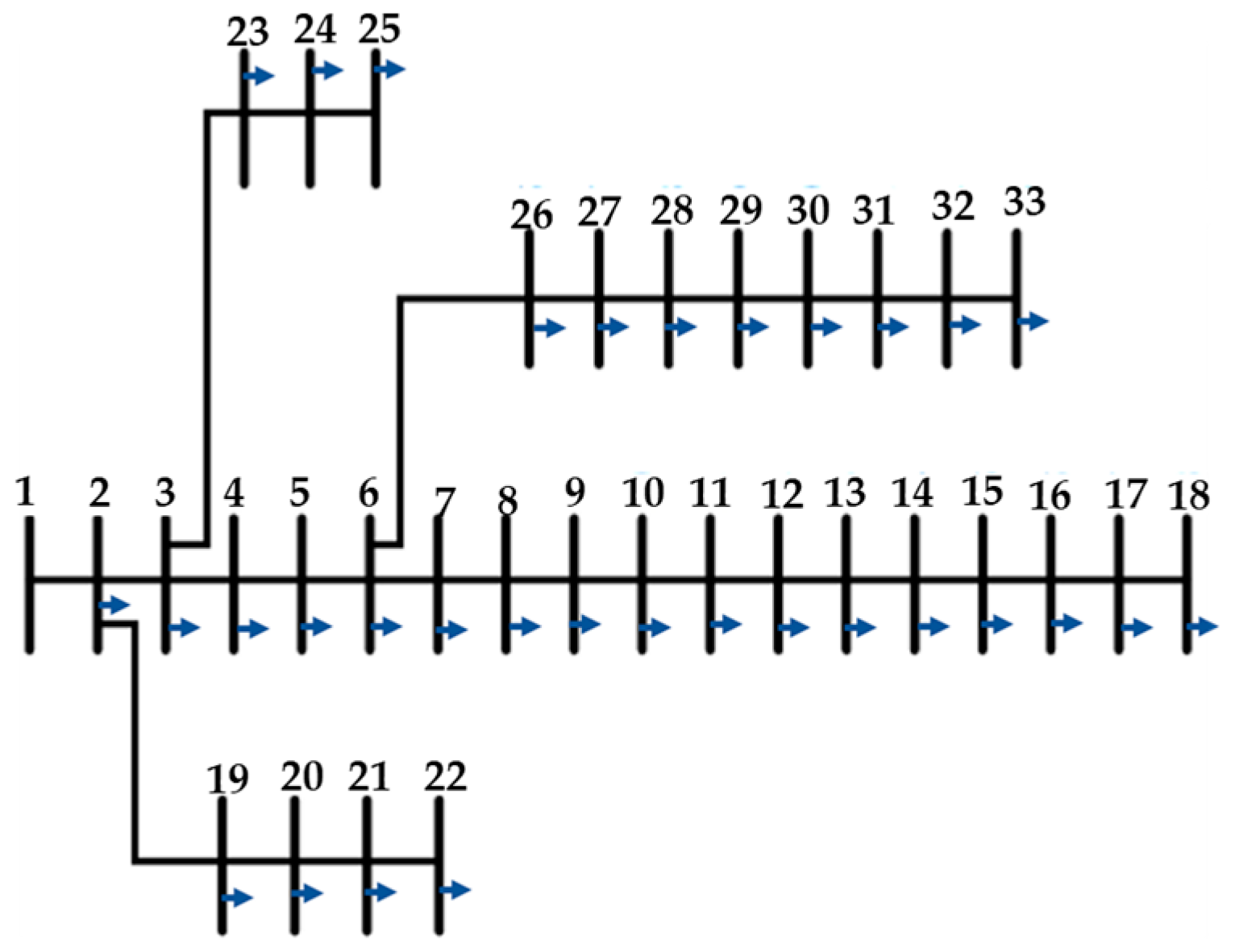
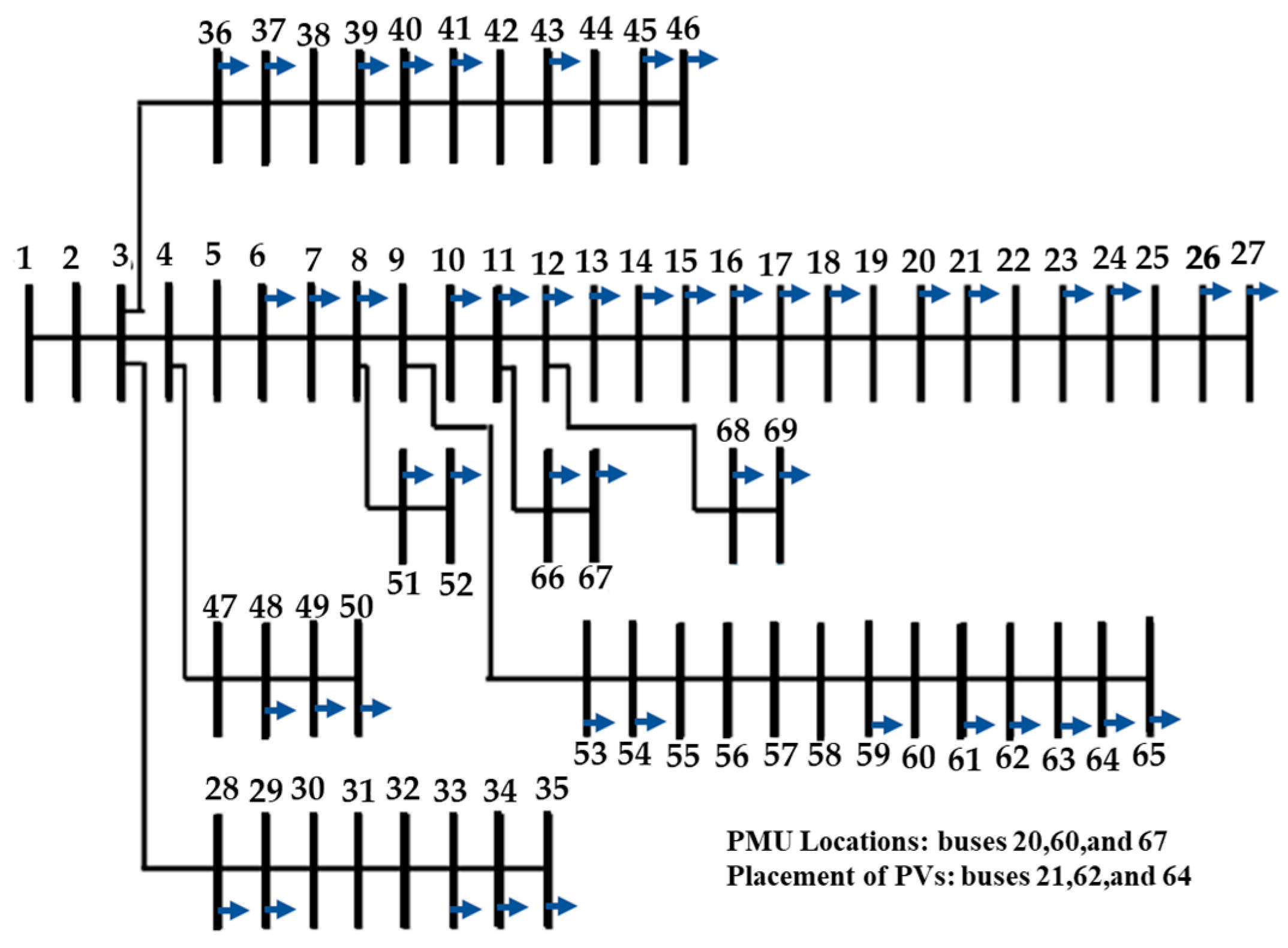
- The effectiveness of the proposed method is tested for passive and active distribution networks: the 33 and 69 IEEE distribution networks, respectively.
- We show that the proposed method accurately calculates state estimation variables, even in the presence of erroneous measurements.
- The execution time comparison between the proposed method, the disjoint DNN model for DSSE calculation and FDIA detection, and the model-based approach is calculated. The results indicate that performing FDIA detection and DSSE calculation simultaneously lead to a significant decrease in execution time.
2. Power System State Estimation
WLS Formulation for State Estimation
3. False Data Injection Attacks (FDIAs)
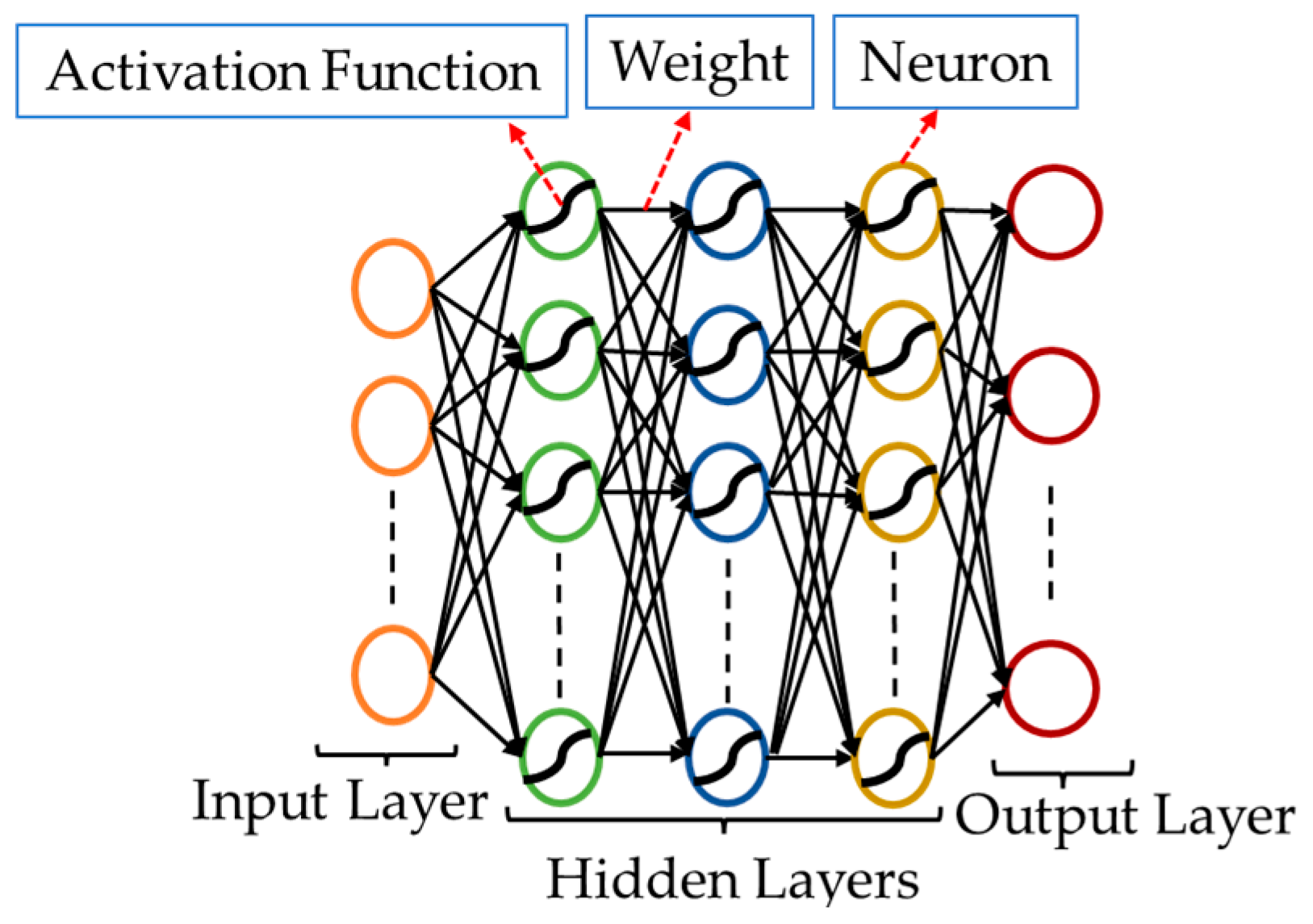
Machine Learning Approach to Detect FDIAs
4. Methodology
5. Results
5.1. Case Study I
- The number of Monte Carlo trials is chosen as 12,000;
- A Gaussian distribution, with of the nominal value, is considered for power injection on the buses.
- Three PMUs are assumed as the available measurement devices in the network which are located at buses 9, 16, and 31 [63]. Voltage and branch current magnitudes from each PMU are used for FDIA detection and for performing DSSE using the proposed method. For each PMU, 12,000 samples are given according to the number of Monte Carlo trials.
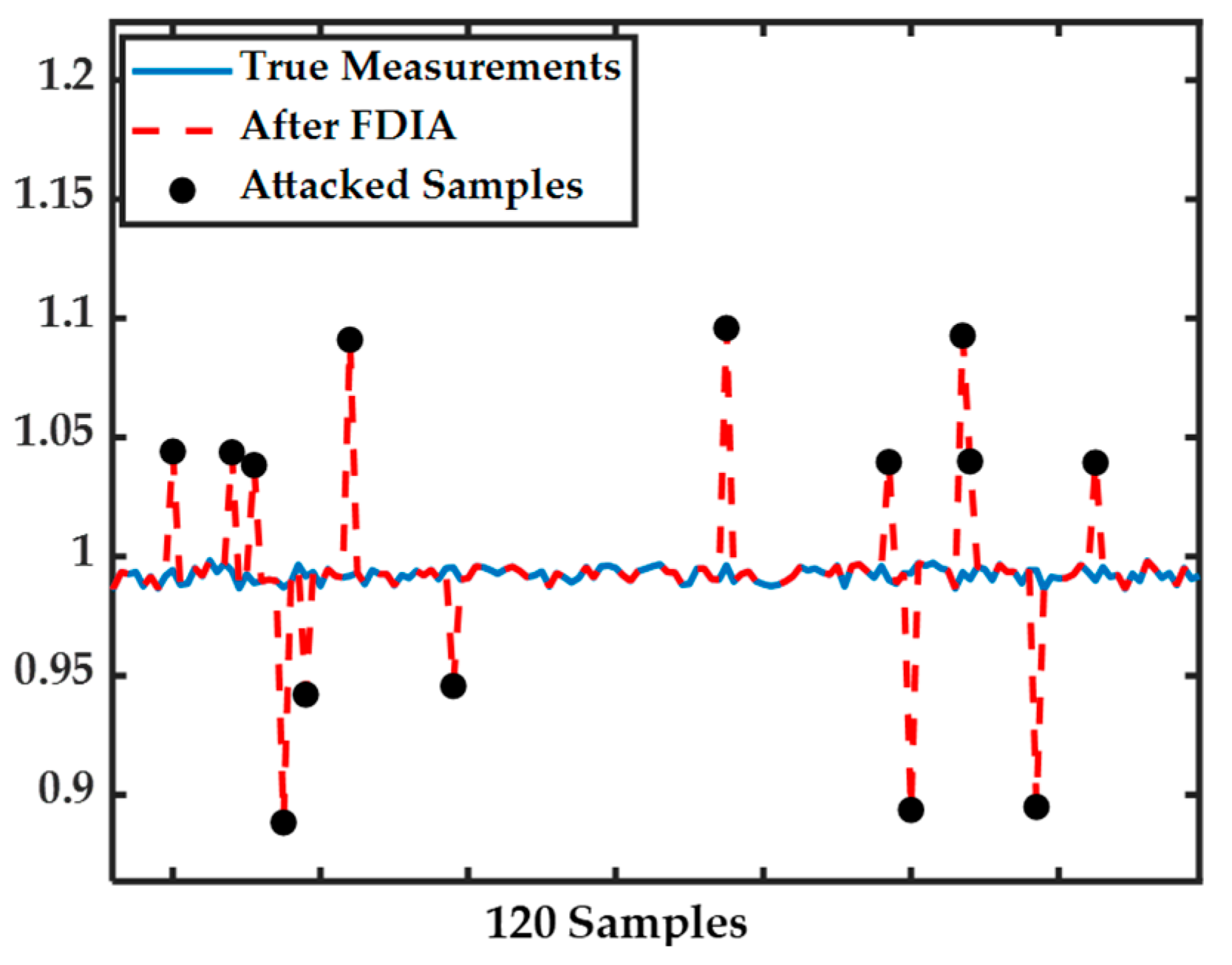
- Two types of attack vectors are injected into available measurements:
- (1)
- , as in [40].
- (2)
- , where and are the average and standard deviation of each measurement vector, respectively. In this case, we assume that the attacker knows the distribution of each measurement and wants to falsify measurements based on the true measurement distribution.
- For training and test sets, and of of the data were used, respectively.
- The pseudo-measurements of active and reactive power injections and flows are generated to make the system observable and to perform WLS calculations with the inclusion of the PMU measurements.
- Voltage magnitudes and phase angles for all the buses are considered as a state variable: , where , are the voltage phase angle and magnitude, respectively, and is the number of buses. It is assumed that there are no measurement devices installed in the slack bus and and .
- The standard deviation is considered as 50% of the nominal value for pseudo-measurements and 3% of the actual value of active and reactive power flow measurements. A Gaussian error, with , is added to PMU measurements (voltage and branch current magnitudes) to model uncertainty. To model the zero injection buses, the error of virtual measurements is considered to be .
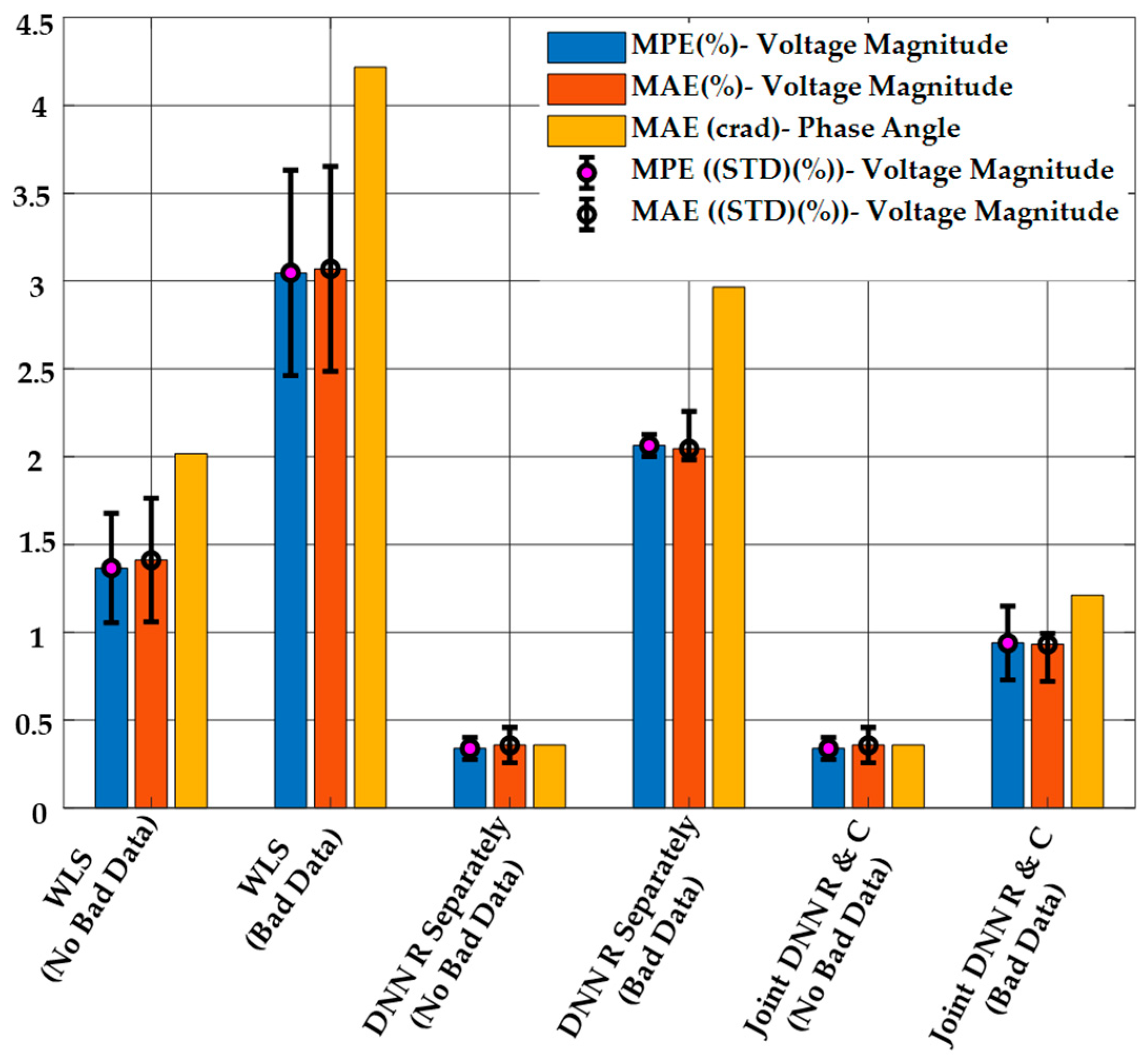
5.1.1. False Data Injection Attacks on Measurements with
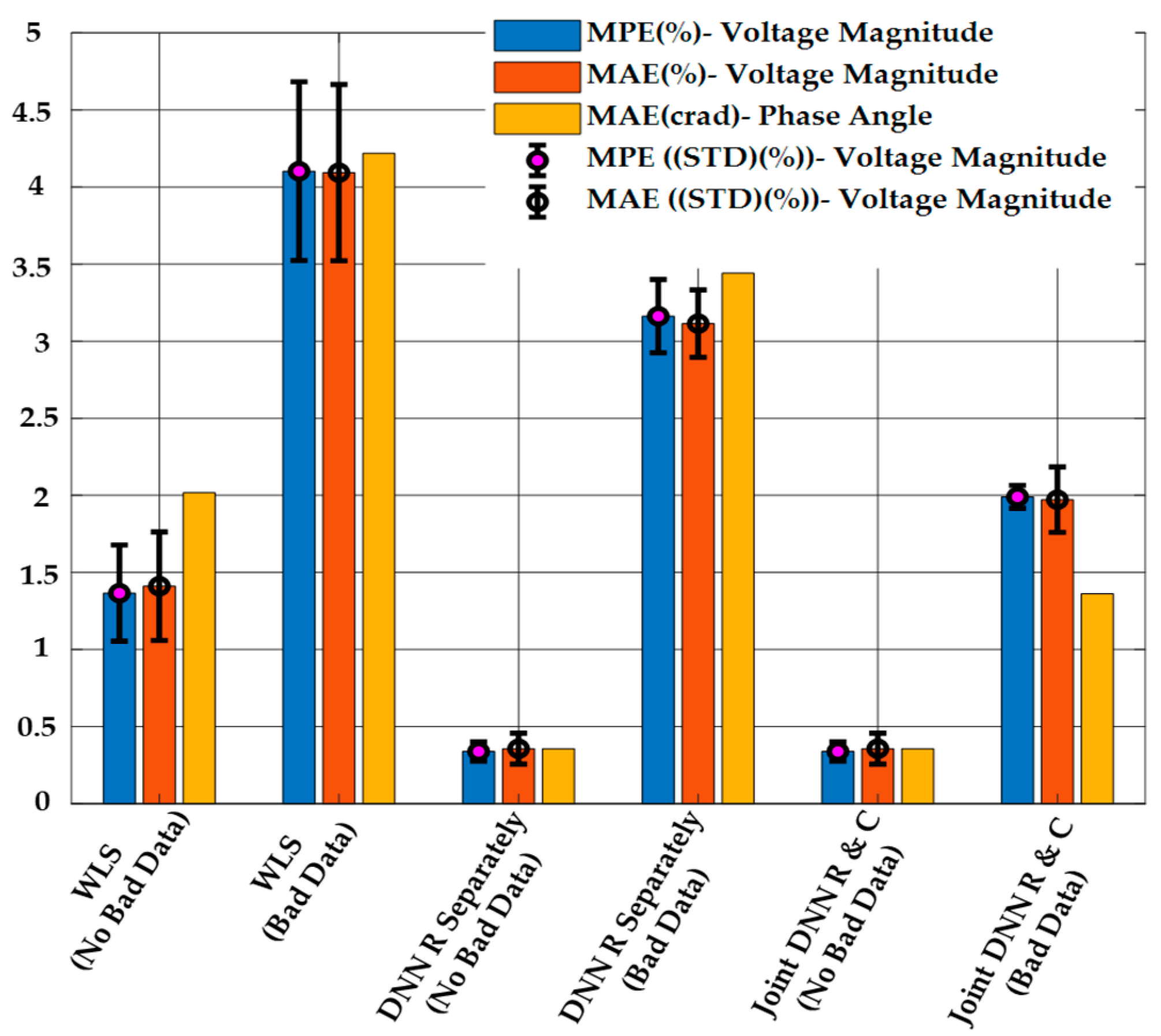
5.1.2. False Data Injection Attacks on Measurements with
5.2. Case Study II
- Three PMUs—located at buses 20, 60, and 67 [63]—are assumed as the available measurement devices in the network. The bus voltage and branch current magnitudes from each PMU are used for detection of FDIAs and for performing DSSE using the proposed method. We have 8760 samples with a temporal resolution of one sample per hour for each PMU, resulting in data for one year.
- Two types of attack vector are injected into available measurements:
- (1)
- [40].
- (2)
- , where and are the average and standard deviation of each measurement vector, respectively. In this case, we assume that the attacker knows the distribution of each measurement and wants to falsify measurements based on the true measurement distribution.
- All the data are then split into train and test sets with a ratio of and .
- The pseudo-measurements of active and reactive power injections and flows are generated to make the system observable and to perform WLS calculations with the inclusion of PMU measurements.
- Voltage magnitudes and phase angles for all buses are considered as state variable: , where , are voltage phase and magnitude, respectively, and is the number of buses. It is assumed that there are no measurement devices installed in the slack bus and that and .
- The standard deviation is considered as 50% of the nominal value for pseudo-measurements and 3% of the actual value of active and reactive power flow measurements. A Gaussian error, with , is added to the PMU measurements (i.e., the voltage and branch current magnitudes) to model the uncertainty. To model zero injection buses, the error in virtual measurements is considered to be .
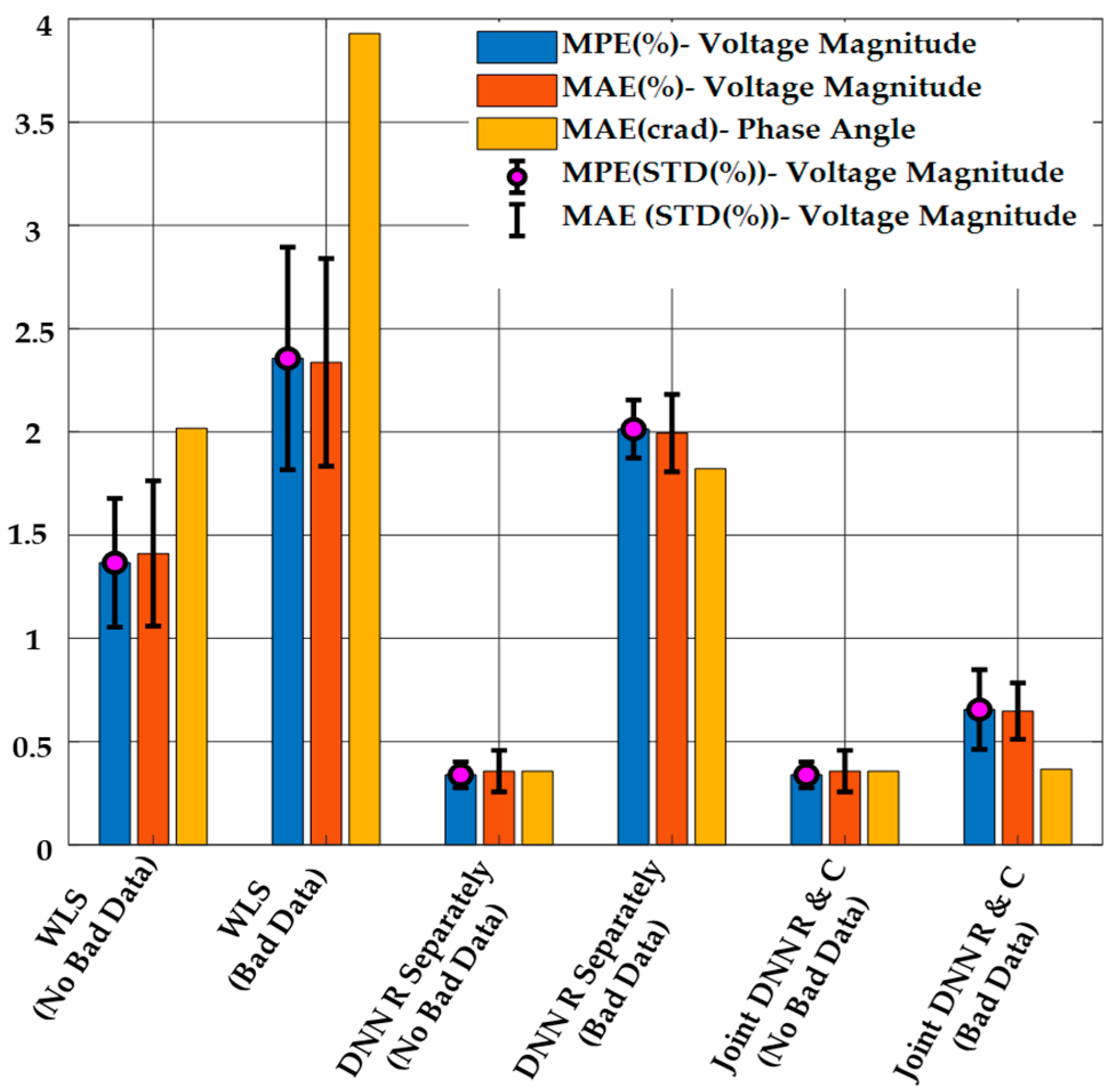
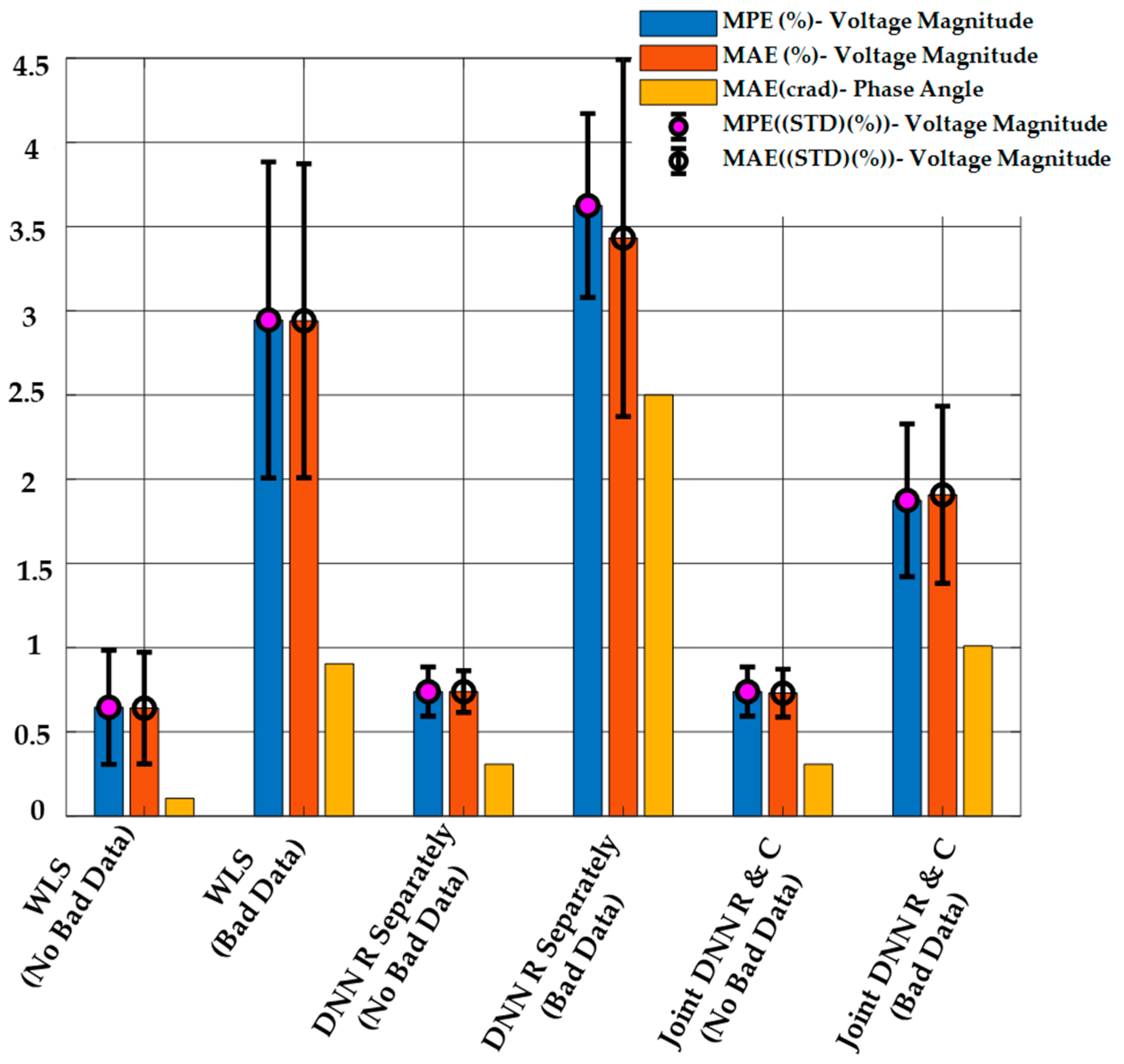
5.2.1. False Data Injection Attacks on Measurements with
5.2.2. False Data Injection Attacks on Measurements with
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Ning, P.; Reiter, M.K. False data injection attacks against state estimation in electric power grids. ACM Trans. Inf. Syst. Secur. 2011, 14, 21–32. [Google Scholar] [CrossRef]
- Singh, S.K.; Khanna, K.; Bose, R.; Panigrahi, B.K.; Joshi, A. Joint-Transformation-Based Detection of False Data Injection Attacks in Smart Grid. IEEE Trans. Ind. Inform. 2018, 14, 89–97. [Google Scholar] [CrossRef]
- Deng, R.; Xiao, G.; Lu, R.; Member, S. Defending Against False Data Injection Attacks on Power System State Estimation. IEEE Trans. Ind. Inform. 2017, 13, 198–207. [Google Scholar] [CrossRef]
- Saldaña-González, A.E.; Sumper, A.; Aragüés-Peñalba, M.; Smolnikar, M. Advanced distribution measurement technologies and data applications for smart grids: A review. Energies 2020, 13, 3730. [Google Scholar] [CrossRef]
- Chakhchoukh, Y.; Ishii, H. Coordinated Cyber-Attacks on the Measurement Function in Hybrid State Estimation. IEEE Trans. Power Syst. 2015, 30, 2487–2497. [Google Scholar] [CrossRef]
- Zhuang, P.; Member, S.; Deng, R.; Liang, H. Estimation in Multiphase and Unbalanced Smart Distribution Systems. IEEE Trans. Smart Grid 2019, 10, 6000–6013. [Google Scholar] [CrossRef]
- Xie, L.; Mo, Y.; Sinopoli, B. False Data Injection Attacks in Electricity Markets. In Proceedings of the 2010 First IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; pp. 226–231. [Google Scholar] [CrossRef]
- Jia, L.; Thomas, R.J.; Tong, L. Impacts of malicious data on real-time price of electricity market operations. In Proceedings of the 2012 45th Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2012; pp. 1907–1914. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Nematbakhsh, E.; Jordehi, A.R.; Tostado-Veliz, M.; Jurado, F.; Leonowicz, Z. A Risk-Based Bi-Level Bidding System to Manage Day-Ahead Electricity Market and Scheduling of Interconnected Microgrids in the presence of Smart Homes. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I & CPS Europe), Prague, Czech Republic, 28 June–1 July 2022. [Google Scholar] [CrossRef]
- Chen, J.; Liang, G.; Cai, Z.; Hu, C.; Xu, Y.; Luo, F.; Zhao, J. Impact analysis of false data injection attacks on power system static security assessment. J. Mod. Power Syst. Clean Energy 2016, 4, 496–505. [Google Scholar] [CrossRef]
- Monticelli, A.; Garcia, A. Reliable Bad Data Processing for Real-Time State Estimation. IEEE Power Eng. Rev. 1983, 3, 31–32. [Google Scholar] [CrossRef]
- Hug, G.; Giampapa, J.A. Vulnerability assessment of AC state estimation with respect to false data injection cyber-attacks. IEEE Trans. Smart Grid 2012, 3, 1362–1370. [Google Scholar] [CrossRef]
- Deng, R.; Xiao, G.; Lu, R.; Liang, H.; Vasilakos, A.V. False data injection on state estimation in power systems-attacks, impacts, and defense: A survey. IEEE Trans. Ind. Inform. 2017, 13, 411–423. [Google Scholar] [CrossRef]
- Liu, X.; Li, Z.; Liu, X.; Li, Z. Masking Transmission Line Outages via False Data Injection Attacks. IEEE Trans. Inf. Forensics Secur. 2016, 11, 1592–1602. [Google Scholar] [CrossRef]
- Ghiasi, M.; Niknam, T.; Wang, Z.; Mehrandezh, M.; Dehghani, M.; Ghadimi, N. A comprehensive review of cyber-attacks and defense mechanisms for improving security in smart grid energy systems: Past, present and future. Electr. Power Syst. Res. 2023, 215, 108975. [Google Scholar] [CrossRef]
- Chowdhury, S.; Chowdhury, S.; Crossley, P. Microgrids and Active Distribution Networks; Iet Renewable Energy Series 6; The Institution of Engineering and Technology: Stevenage, UK, 2009; ISBN 9781849190145. [Google Scholar]
- Mobtahej, M.; Esapour, K.; Tajalli, S.Z.; Mohammadi, M. Effective demand response and GANs for optimal constraint unit commitment in solar-tidal based microgrids. IET Renew. Power Gener. 2022, 16, 3485–3495. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, B.; Mobtahej, M.; Baziar, A.; Khan, B. Advanced Reactive Power Compensation of Wind Power Plant Using PMU Data. IEEE Access 2021, 9, 67006–67014. [Google Scholar] [CrossRef]
- Zhao, J.; Gómez-Expósito, A.; Netto, M.; Mili, L.; Abur, A.; Terzija, V.; Kamwa, I.; Pal, B.; Singh, A.K.; Qi, J.; et al. Power System Dynamic State Estimation: Motivations, Definitions, Methodologies, and Future Work. IEEE Trans. Power Syst. 2019, 34, 3188–3198. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, J.; Yu, W.; An, D.; Zhang, N.; Zhao, W. On false data-injection attacks against power system state estimation: Modeling and countermeasures. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 717–729. [Google Scholar] [CrossRef]
- Abdelmalak, M.; Venkataramanan, V.; MacWan, R. A Survey of Cyber-Physical Power System Modeling Methods for Future Energy Systems. IEEE Access 2022, 10, 99875–99896. [Google Scholar] [CrossRef]
- Barja-Martinez, S.; Aragüés-Peñalba, M.; Munné-Collado, Í.; Lloret-Gallego, P.; Bullich-Massagué, E.; Villafafila-Robles, R. Artificial intelligence techniques for enabling Big Data services in distribution networks: A review. Renew. Sustain. Energy Rev. 2021, 150, 111459. [Google Scholar] [CrossRef]
- Zamzam, A.S.; Fu, X.; Sidiropoulos, N.D. Data-driven learning-based optimization for distribution system state estimation. arXiv 2018, 34, 4796–4805. [Google Scholar] [CrossRef]
- Rudin, C.; Waltz, D.; Anderson, R.; Boulanger, A.; Salleb-Aouissi, A.; Chow, M.; Dutta, H.; Gross, P.; Huang, B.; Ierome, S.; et al. Machine learning for the New York City power grid. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 328–345. [Google Scholar] [CrossRef]
- Abdelmalak, M.; Member, S.; Hooshyar, H.; Member, S. Real-Time EMT-Phasor Co-Simulation Modeling for Large-Scale Power Grids: Challenges and Solutions. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar]
- Anderson, B.R.N.; Ieee, M.; Boulanger, A.; Powell, W.B.; Scott, W. Adaptive Stochastic Control for the Smart Grid. Proc. IEEE 2011, 99, 14–21. [Google Scholar] [CrossRef]
- Ozay, M.; Esnaola, I.; Yarman Vural, F.T.; Kulkarni, S.R.; Poor, H.V. Machine Learning Methods for Attack Detection in the Smart Grid. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1773–1786. [Google Scholar] [CrossRef] [PubMed]
- Sayghe, A.; Hu, Y.; Zografopoulos, I.; Liu, X.R.; Dutta, R.G.; Jin, Y.; Konstantinou, C. Survey of machine learning methods for detecting false data injection attacks in power systems. IET Smart Grid 2020, 3, 581–595. [Google Scholar] [CrossRef]
- Musleh, A.S.; Chen, G.; Dong, Z.Y. A Survey on the Detection Algorithms for False Data Injection Attacks in Smart Grids. IEEE Trans. Smart Grid 2020, 11, 2218–2234. [Google Scholar] [CrossRef]
- Esmalifalak, M.; Member, S.; Liu, L.; Member, S. Detecting Stealthy False Data Injection Using Machine Learning in Smart Grid. IEEE Syst. J. 2014, 11, 1–9. [Google Scholar]
- Yan, J.; Tang, B.; He, H. Detection of false data attacks in smart grid with supervised learning. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1395–1402. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Rezaee Jordehi, A.; Marzband, M.; Tostado-Véliz, M.; Jurado, F.; Aguado, J.A. An IoT-enabled hierarchical decentralized framework for multi-energy microgrids market management in the presence of smart prosumers using a deep learning-based forecaster. Appl. Energy 2023, 333, 120560. [Google Scholar] [CrossRef]
- Foroutan, S.A.; Salmasi, F.R. Detection of false data injection attacks against state estimation in smart grids based on a mixture Gaussian distribution learning method. IET Cyber-Phys. Syst. Theory Appl. 2017, 2, 161–171. [Google Scholar] [CrossRef]
- Joachims, T. Making Large-Scale Support Vector Machine Learning Practical. In Advances in Kernel Methods; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar] [CrossRef]
- Mohammadpourfard, M.; Sami, A.; Seifi, A. A statistical unsupervised method against false data injection attacks: A visualization-based approach. Expert Syst. Appl. 2017, 84, 242–261. [Google Scholar] [CrossRef]
- Mohammadpourfard, M.; Sami, A.; Weng, Y. Identification of False Data Injection Attacks With Considering the Impact of Wind Generation and Topology Reconfigurations. IEEE Trans. Sustain. Energy 2018, 9, 1349–1364. [Google Scholar] [CrossRef]
- Sivasangari, A.; Jyotsna, J.; Pravalika, K. SQL Injection Attack Detection using Machine Learning Algorithm. In Proceedings of the 2021 5th International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 3–5 June 2021; pp. 1166–1169. [Google Scholar] [CrossRef]
- Nur, S.; Najwa, F.; Mustaffa, B. Detection of False Data Injection Attack using Machine Learning approach. Mesop. J. Cyber Secur. 2022, 2022, 38–46. [Google Scholar] [CrossRef]
- Ramirez, I.S.; Pedro, F.; García, M. False alarm detection in wind turbine by classification models. Adv. Eng. Softw. 2023, 177, 103409. [Google Scholar] [CrossRef]
- Mohammadpourfard, M.; Weng, Y.; Tajdinian, M. Benchmark of machine learning algorithms on capturing future distribution network anomalies. IET Gener. Transm. Distrib. 2019, 13, 1441–1455. [Google Scholar] [CrossRef]
- Santos, R.Z.S.; Orillaza, J.R.C. Distribution system state estimator using SCADA and μ PMU measurements: An FDI attack vulnerability analysis. In Proceedings of the 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Kota Kinabalu, Malaysia, 7–10 October 2018; pp. 469–474. [Google Scholar] [CrossRef]
- Ozay, M.; Esnaola, I.; Yarman Vural, F.T.; Kulkarni, S.R.; Vincent Poor, H. Distributed models for sparse attack construction and state vector estimation in the smart grid. In Proceedings of the 2012 IEEE Third International Conference on Smart Grid Communications (SmartGridComm), Tainan, Taiwan, 5–8 November 2012; pp. 306–311. [Google Scholar] [CrossRef]
- Wang, Y.; Xing, A.; Qu, Z.; Han, X.; Dong, H.; Georgievitch, P.M. False data injection attack detection based on interval affine state estimation. Electr. Power Syst. Res. 2022, 210, 108100. [Google Scholar] [CrossRef]
- Ganjkhani, M.; Gilanifar, M.; Giraldo, J.; Parvania, M. Integrated Cyber and Physical Anomaly Location and Classification in Power Distribution Systems. IEEE Trans. Ind. Inform. 2021, 17, 7040–7049. [Google Scholar] [CrossRef]
- Kamal, M.; Farajollahi, M.; Nazaripouya, H.; Mohsenian-Rad, H. Cyberattacks against Event-Based Analysis in Micro-PMUs: Attack Models and Counter Measures. IEEE Trans. Smart Grid 2021, 12, 1577–1588. [Google Scholar] [CrossRef]
- Azimian, B.; Biswas, R.S.; Moshtagh, S.; Pal, A.; Tong, L.; Dasarathy, G. State and Topology Estimation for Unobservable Distribution Systems Using Deep Neural Networks. IEEE Trans. Instrum. Meas. 2022, 71, 9003514. [Google Scholar] [CrossRef]
- Abur, A.; Expósito, A.G. Power System State Estimation: Theory and Implementation; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Dehghanpour, K.; Wang, Z.; Wang, J.; Yuan, Y.; Bu, F. A survey on state estimation techniques and challenges in smart distribution systems. arXiv 2018, 10, 2312–2322. [Google Scholar] [CrossRef]
- Ahmad, F.; Rasool, A.; Ozsoy, E.; Sekar, R.; Sabanovic, A.; Elitaş, M. Distribution system state estimation-A step towards smart grid. Renew. Sustain. Energy Rev. 2018, 81, 2659–2671. [Google Scholar] [CrossRef]
- Liao, H.; Milanović, J.V. Pathway to cost-efficient state estimation of future distribution networks. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016. [Google Scholar] [CrossRef]
- Džafić, I.; Gilles, M.; Jabr, R.A.; Pal, B.C.; Henselmeyer, S. Real time estimation of loads in radial and unsymmetrical three-phase distribution networks. IEEE Trans. Power Syst. 2013, 28, 4839–4848. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, N. State estimation for unbalanced electric power distribution systems using AMI data. In Proceedings of the 2017 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 23–26 April 2017. [Google Scholar] [CrossRef]
- Muscas, C.; Sulis, S.; Angioni, A.; Ponci, F.; Monti, A. Impact of different uncertainty sources on a three-phase state estimator for distribution networks. IEEE Trans. Instrum. Meas. 2014, 63, 2200–2209. [Google Scholar] [CrossRef]
- Majumdar, A.; Pal, B.C. A three-phase state estimation in unbalanced distribution networks with switch modelling. In Proceedings of the 2016 IEEE First International Conference on Control, Measurement and Instrumentation (CMI), Kolkata, India, 8–10 January 2016; pp. 474–478. [Google Scholar] [CrossRef]
- Kong, X.; Chen, Y.; Yong, C.; Ma, X.; Kong, J. Stepwise robust distribution system state estimation considering PMU measurement. J. Renew. Sustain. Energy 2019, 11, 025506. [Google Scholar] [CrossRef]
- Huang, Y.F.; Werner, S.; Huang, J.; Kashyap, N.; Gupta, V. State estimation in electric power grids: Meeting new challenges presented by the requirements of the future grid. IEEE Signal Process. Mag. 2012, 29, 33–43. [Google Scholar] [CrossRef]
- Simeone, O. An Introduction to Quantum Machine Learning for Engineers. Found. Trends Signal Process. 2022, 16, 1–223. [Google Scholar] [CrossRef]
- Neranjan Thilakarathne, N.; Mohan, K.K.; Surekha, L.; Hussain, A. Smart Grid: A Survey of Architectural Elements, Machine Learning and Deep Learning Applications and Future Directions. J. Intell. Syst. Internet Things 2021, 3, 32–42. [Google Scholar] [CrossRef]
- Zhang, D.; Han, X.; Deng, C. Review on the research and practice of deep learning and reinforcement learning in smart grids. CSEE J. Power Energy Syst. 2018, 4, 362–370. [Google Scholar] [CrossRef]
- B, P.; Pham, Q.-V.; Liyanage, M.; Deepa, N.; VVSS, M.; Reddy, S.; Maddikunta, P.K.R.; Khare, N.; Gadekallu, T.R.; Hwang, W.-J. Deep Learning for Intelligent Demand Response and Smart Grids: A Comprehensive Survey. arXiv 2021, 1–25. [Google Scholar]
- Moradzadeh, A.; Mohammadpourfard, M.; Konstantinou, C.; Genc, I.; Kim, T.; Mohammadi-Ivatloo, B. Electric Load Forecasting under False Data Injection Attacks using Deep Learning. Energy Rep. 2022, 8, 9933–9945. [Google Scholar] [CrossRef]
- Radhoush, S.; Vannoy, T.; Whitaker, B.M.; Nehrir, H. Simultaneous State Estimation and Bad Data Detection on PMU Measurements in Active Distribution Power Networks. In Proceedings of the 2022 North American Power Symposium (NAPS), Salt Lake City, UT, USA, 9–11 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Lee, K.Y.; Park, J.S.; Kim, Y.S. Optimal placement of pmu to enhance supervised learning-based pseudo-measurement modelling accuracy in distribution network. Energies 2021, 14, 7767. [Google Scholar] [CrossRef]
- Office of Energy Efficiency & Renewable Energy (EERE). Commercial and Residential Hourly Load Profiles. Available online: https://openei.org/datasets/files/961/pub/ (accessed on 23 February 2023).
- Sedighizadeh, M.; Jahangir, M.; Gandomkar, M.; Esfandeh, S. Distributed generation location and capacity effect on voltage stability of distribution network. Int. Conf. Math. Methods Comput. Tech. Electr. Eng. Proc. 2010, 25, 89–94. [Google Scholar]
- Joseph, A. Shaw ORSL Weather Station; The Montana State University Weather Station: Bozeman, MT, USA; Available online: https://www.montana.edu/orsl/weather.html (accessed on 23 February 2023).
- NREL. PVWatts Version 5 Manual. Available online: https://pvwatts.nrel.gov/ (accessed on 23 February 2023).



| Joint DNN Regression and Classification | DNN Classification Separately | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual Values | FDIA | 421 | 3 | 0 | 0 | 0 | 0 | 0 | 245 | 0 | 0 | 0 | 0 | 179 | 0 | |
| 110 | 260 | 0 | 0 | 0 | 0 | 0 | 0 | 248 | 0 | 0 | 0 | 122 | 0 | |||
| 71 | 0 | 229 | 3 | 7 | 4 | 0 | 0 | 0 | 228 | 3 | 3 | 80 | 0 | |||
| 40 | 0 | 0 | 266 | 2 | 2 | 0 | 0 | 0 | 0 | 268 | 0 | 42 | 0 | |||
| 36 | 0 | 0 | 0 | 201 | 0 | 0 | 0 | 0 | 0 | 0 | 199 | 38 | 0 | |||
| 1 | 0 | 0 | 0 | 0 | 228 | 0 | 0 | 0 | 0 | 0 | 0 | 229 | 0 | |||
| No FDIA | 0 | 0 | 0 | 0 | 0 | 0 | 2076 | 0 | 0 | 0 | 0 | 0 | 0 | 2076 | ||
| No FDIA | No FDIA | |||||||||||||||
| Predicted Values | Predicted Values | |||||||||||||||
| Accuracy = -Score = 0.8885 | -Score = 0.8142 | |||||||||||||||
| Joint DNN Regression and Classification | DNN Classification Separately | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual Values | FDIA | 74 | 8 | 1 | 1 | 2 | 1 | 7 | 45 | 0 | 1 | 0 | 0 | 0 | 48 | |
| 6 | 74 | 0 | 0 | 0 | 0 | 3 | 5 | 44 | 0 | 0 | 0 | 0 | 34 | |||
| 0 | 1 | 57 | 0 | 0 | 0 | 18 | 7 | 0 | 29 | 0 | 0 | 0 | 40 | |||
| 2 | 0 | 0 | 16 | 2 | 0 | 57 | 0 | 0 | 0 | 1 | 0 | 0 | 76 | |||
| 0 | 0 | 1 | 1 | 1 | 1 | 71 | 0 | 0 | 0 | 0 | 0 | 0 | 75 | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 73 | 0 | 0 | 0 | 0 | 0 | 0 | 74 | |||
| No FDIA | 0 | 0 | 4 | 13 | 7 | 20 | 3437 | 0 | 0 | 0 | 0 | 0 | 0 | 3481 | ||
| No FDIA | No FDIA | |||||||||||||||
| Predicted Values | Predicted Values | |||||||||||||||
| Accuracy = -Score = 0.5556 | Accuracy = -Score = 0.4028 | |||||||||||||||
| Joint DNN Regression and Classification | DNN Classification Separately | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual Values | FDIA | 271 | 25 | 39 | 22 | 10 | 28 | 5 | 91 | 4 | 3 | 0 | 0 | 0 | 68 | |
| 0 | 312 | 11 | 5 | 5 | 3 | 3 | 13 | 73 | 1 | 0 | 0 | 0 | 60 | |||
| 2 | 1 | 283 | 8 | 1 | 15 | 4 | 13 | 0 | 65 | 0 | 0 | 0 | 71 | |||
| 0 | 0 | 0 | 244 | 31 | 22 | 0 | 4 | 0 | 0 | 2 | 0 | 0 | 143 | |||
| 0 | 0 | 0 | 0 | 235 | 22 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 116 | |||
| 3 | 0 | 0 | 0 | 0 | 222 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 140 | |||
| No FDIA | 81 | 0 | 0 | 0 | 13 | 0 | 2024 | 0 | 0 | 0 | 0 | 0 | 0 | 3093 | ||
| No FDIA | No FDIA | |||||||||||||||
| Predicted Values | Predicted Values | |||||||||||||||
| Accuracy = -Score = 0.8557 | Accuracy = -Score = 0.4028 | |||||||||||||||
| Joint DNN Regression and Classification | DNN Regression Separately | WLS | ||||
|---|---|---|---|---|---|---|
| FDIA | ||||||
| 0.62 (s) | 0.42 (s) | 1.35 (s) | 0.78 (s) | 30.91 (s) | ||
| 0.40 (s) | 0.47 (s) | 0.35 (s) | 0.58 (s) | 23.49 (s) | ||
| 0.63 (s) | 0.56 (s) | 1.02 (s) | 0.75 (s) | 27.55 (s) | ||
| Joint DNN Regression and Classification | DNN Classification Separately | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual Values | FDIA | 36 | 2 | 1 | 1 | 0 | 2 | 1 | 34 | 0 | 1 | 5 | 1 | 1 | 1 | |
| 1 | 31 | 3 | 0 | 0 | 0 | 2 | 1 | 31 | 1 | 0 | 1 | 1 | 1 | |||
| 2 | 0 | 27 | 0 | 0 | 0 | 1 | 4 | 0 | 25 | 0 | 0 | 1 | 0 | |||
| 0 | 0 | 0 | 1 | 0 | 0 | 31 | 4 | 0 | 0 | 3 | 0 | 0 | 29 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 33 | 0 | 0 | 0 | 1 | 0 | 0 | 132 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 42 | 0 | 0 | 0 | 2 | 0 | 0 | 40 | |||
| No FDIA | 0 | 0 | 0 | 3 | 3 | 3 | 2666 | 0 | 0 | 0 | 108 | 10 | 0 | 2557 | ||
| No FDIA | No FDIA | |||||||||||||||
| Predicted Values | Predicted Values | |||||||||||||||
-Score = 0.5334 | -Score = 0.5231 | |||||||||||||||
| Joint DNN Regression and Classification | DNN Classification Separately | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual Values | FDIA | 22 | 2 | 2 | 2 | 0 | 0 | 4 | 22 | 3 | 1 | 2 | 0 | 0 | 4 | |
| 0 | 18 | 0 | 1 | 6 | 1 | 3 | 0 | 17 | 0 | 2 | 4 | 1 | 5 | |||
| 0 | 0 | 25 | 1 | 0 | 4 | 7 | 1 | 0 | 24 | 1 | 0 | 2 | 9 | |||
| 0 | 0 | 1 | 21 | 0 | 0 | 9 | 0 | 2 | 1 | 18 | 0 | 0 | 10 | |||
| 0 | 2 | 0 | 0 | 18 | 1 | 10 | 0 | 2 | 0 | 0 | 17 | 2 | 10 | |||
| 0 | 0 | 0 | 0 | 1 | 8 | 22 | 0 | 1 | 0 | 0 | 0 | 9 | 21 | |||
| No FDIA | 0 | 0 | 0 | 0 | 0 | 1 | 2699 | 0 | 0 | 0 | 0 | 0 | 1 | 2699 | ||
| No FDIA | No FDIA | |||||||||||||||
| Predicted Values | Predicted Values | |||||||||||||||
-Score = 0.7224 | -Score = 0.7021 | |||||||||||||||
| Joint DNN Regression and Classification | DNN Classification Separately | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual Values | FDIA | 64 | 1 | 1 | 2 | 1 | 0 | 4 | 64 | 0 | 2 | 1 | 1 | 0 | 5 | |
| 0 | 47 | 1 | 0 | 9 | 0 | 4 | 0 | 45 | 2 | 0 | 9 | 1 | 4 | |||
| 0 | 3 | 53 | 4 | 3 | 0 | 1 | 0 | 5 | 52 | 2 | 4 | 0 | 1 | |||
| 1 | 1 | 1 | 52 | 0 | 0 | 4 | 1 | 2 | 0 | 52 | 0 | 0 | 4 | |||
| 0 | 10 | 0 | 0 | 47 | 1 | 13 | 0 | 14 | 0 | 0 | 41 | 3 | 13 | |||
| 0 | 0 | 0 | 0 | 0 | 13 | 41 | 0 | 0 | 0 | 0 | 0 | 13 | 41 | |||
| No FDIA | 0 | 0 | 0 | 0 | 0 | 4 | 2505 | 0 | 0 | 0 | 0 | 0 | 8 | 2501 | ||
| No FDIA | No FDIA | |||||||||||||||
| Predicted Values | Predicted Values | |||||||||||||||
| Accuracy = -Score = 0.7921 | Accuracy = -Score = 0.7709 | |||||||||||||||
| Joint DNN Regression and Classification | DNN Regression Separately | WLS | ||||
|---|---|---|---|---|---|---|
| FDIA | ||||||
| 0.41 (s) | 0.63 (s) | 0.24 (s) | 0.15(s) | 43 (s) | ||
| 0.24 (s) | 0.23 (s) | 0.15 (s) | 0.15 (s) | 51 (s) | ||
| 0.17 (s) | 0.15 (s) | 0.18(s) | 0.23 (s) | 59 (s) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radhoush, S.; Vannoy, T.; Liyanage, K.; Whitaker, B.M.; Nehrir, H. Distribution System State Estimation and False Data Injection Attack Detection with a Multi-Output Deep Neural Network. Energies 2023, 16, 2288. https://doi.org/10.3390/en16052288
Radhoush S, Vannoy T, Liyanage K, Whitaker BM, Nehrir H. Distribution System State Estimation and False Data Injection Attack Detection with a Multi-Output Deep Neural Network. Energies. 2023; 16(5):2288. https://doi.org/10.3390/en16052288
Chicago/Turabian StyleRadhoush, Sepideh, Trevor Vannoy, Kaveen Liyanage, Bradley M. Whitaker, and Hashem Nehrir. 2023. "Distribution System State Estimation and False Data Injection Attack Detection with a Multi-Output Deep Neural Network" Energies 16, no. 5: 2288. https://doi.org/10.3390/en16052288
APA StyleRadhoush, S., Vannoy, T., Liyanage, K., Whitaker, B. M., & Nehrir, H. (2023). Distribution System State Estimation and False Data Injection Attack Detection with a Multi-Output Deep Neural Network. Energies, 16(5), 2288. https://doi.org/10.3390/en16052288







