Optimum Parallel Processing Schemes to Improve the Computation Speed for Renewable Energy Allocation and Sizing Problems
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Contribution
- A parallel computation approach based on the master/slave method is applied to the optimal allocation and sizing of DG units in a DN, considering minimizing energy losses and DG costs.
- The impacts of the number of parallel processors on the optimal control parameters, objective functions, and dependability of the method are determined.
- The range of the optimal number of parallel processors providing better speedup and efficiency is determined.
- Optimum solutions for the different number of processors are discussed with respect to three multi-objective optimization performance criteria.
2. Problem Formulation
2.1. Objectives
2.1.1. Active Energy Losses
2.1.2. Annual DG Costs
2.2. Problem Constraints
2.2.1. Equality Constraints (Power Balance Equations)
2.2.2. Limits of Main Grid Supply
2.2.3. Limits of WT and PV Generation
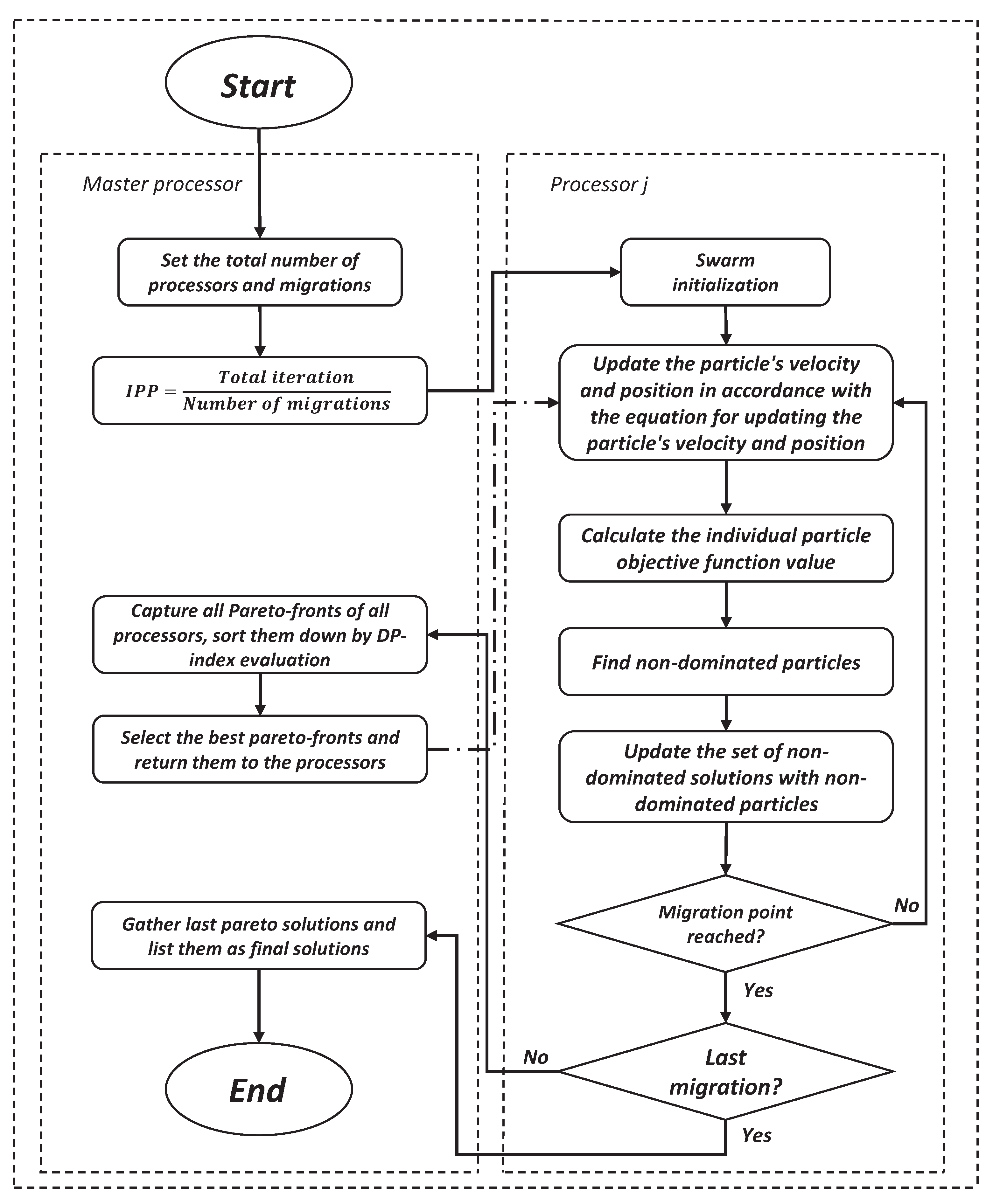
3. Implementation of Particle Swarm Optimization Algorithm and Parallel Processing
3.1. Particle Swarm Optimization Algorithm
3.2. Overview of Multi-Objective Optimization Process
3.3. Parallel Processing of Multi-Objective PSO Algorithm
- The new particle is not added to the archive set if at least one non-dominated particle dominates it.
- An additional particle is added to the set if it dominates any non-dominated particle, and the corresponding particle is thus removed.
- This new solution is added to the set if the new particle does not dominate any non-dominated particles in the set.
- In the case that the set of non-dominated particles reaches its capacity when a new particle needs to be added, the grid mechanism is used to reorganize the objective domain, and the most-crowded segment removes a particle from the set. Please refer to [40] for more details.
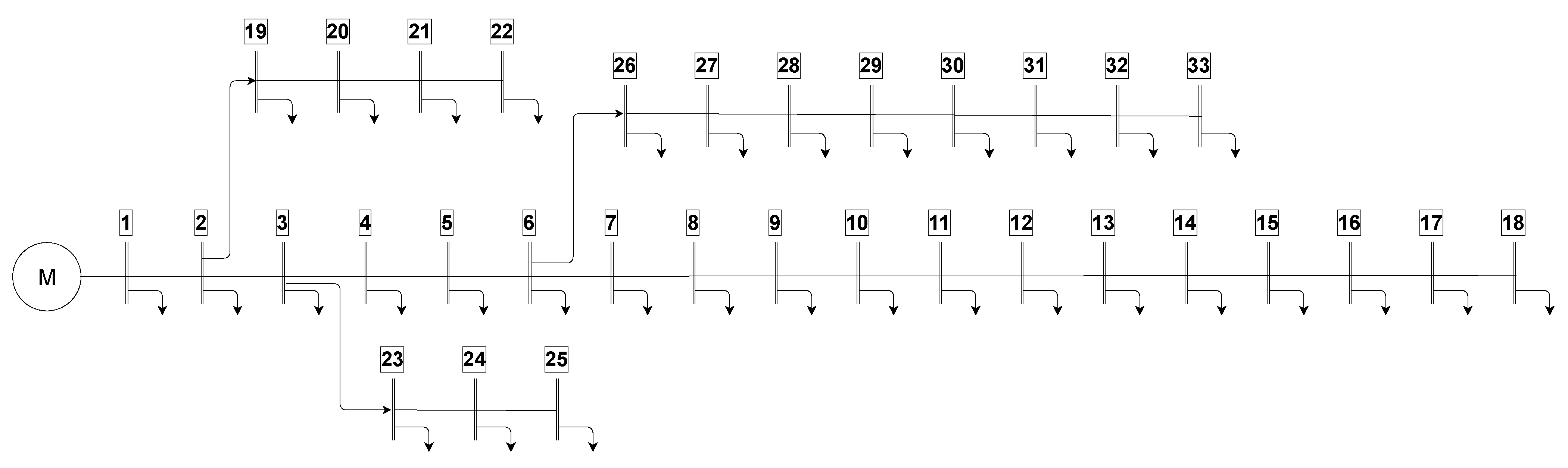
4. Test Systems
5. Results and Discussion
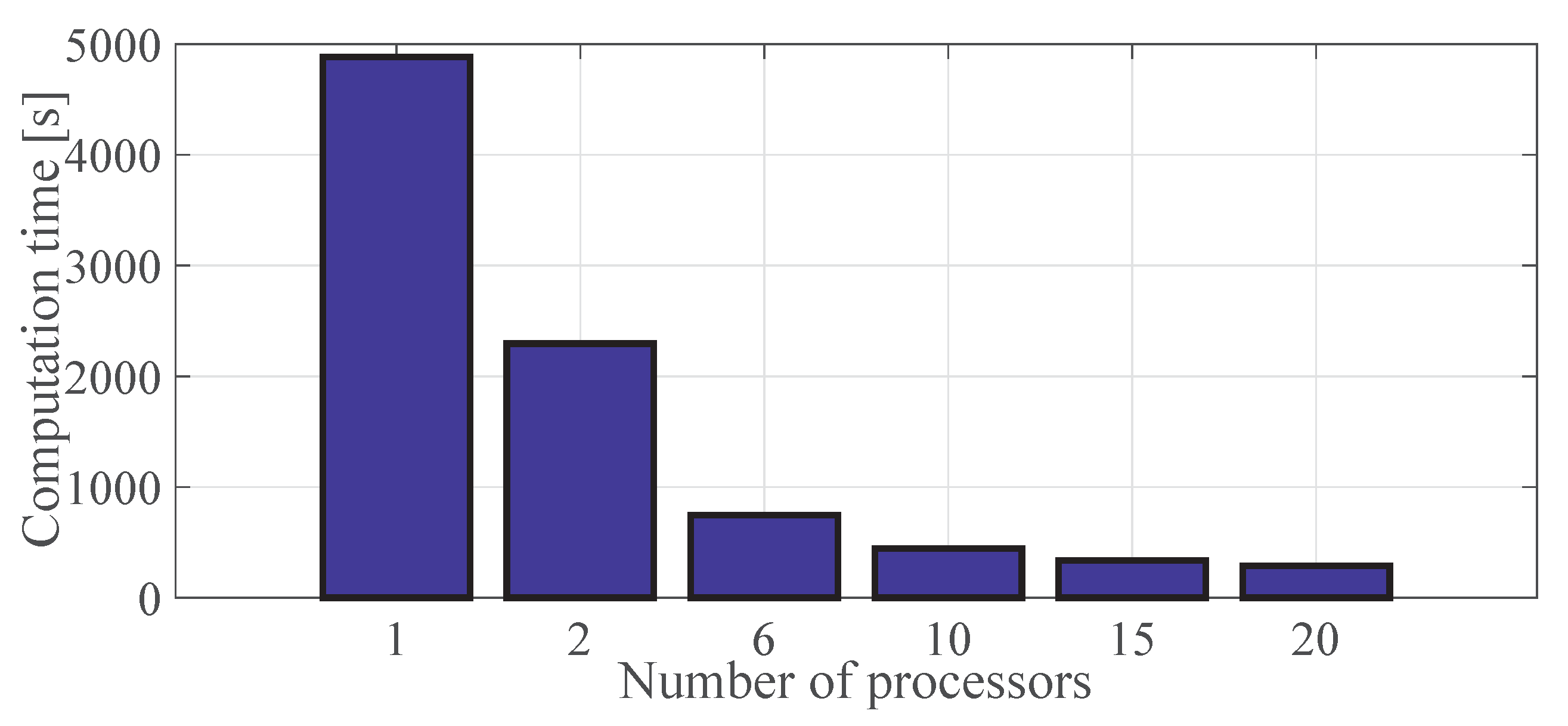
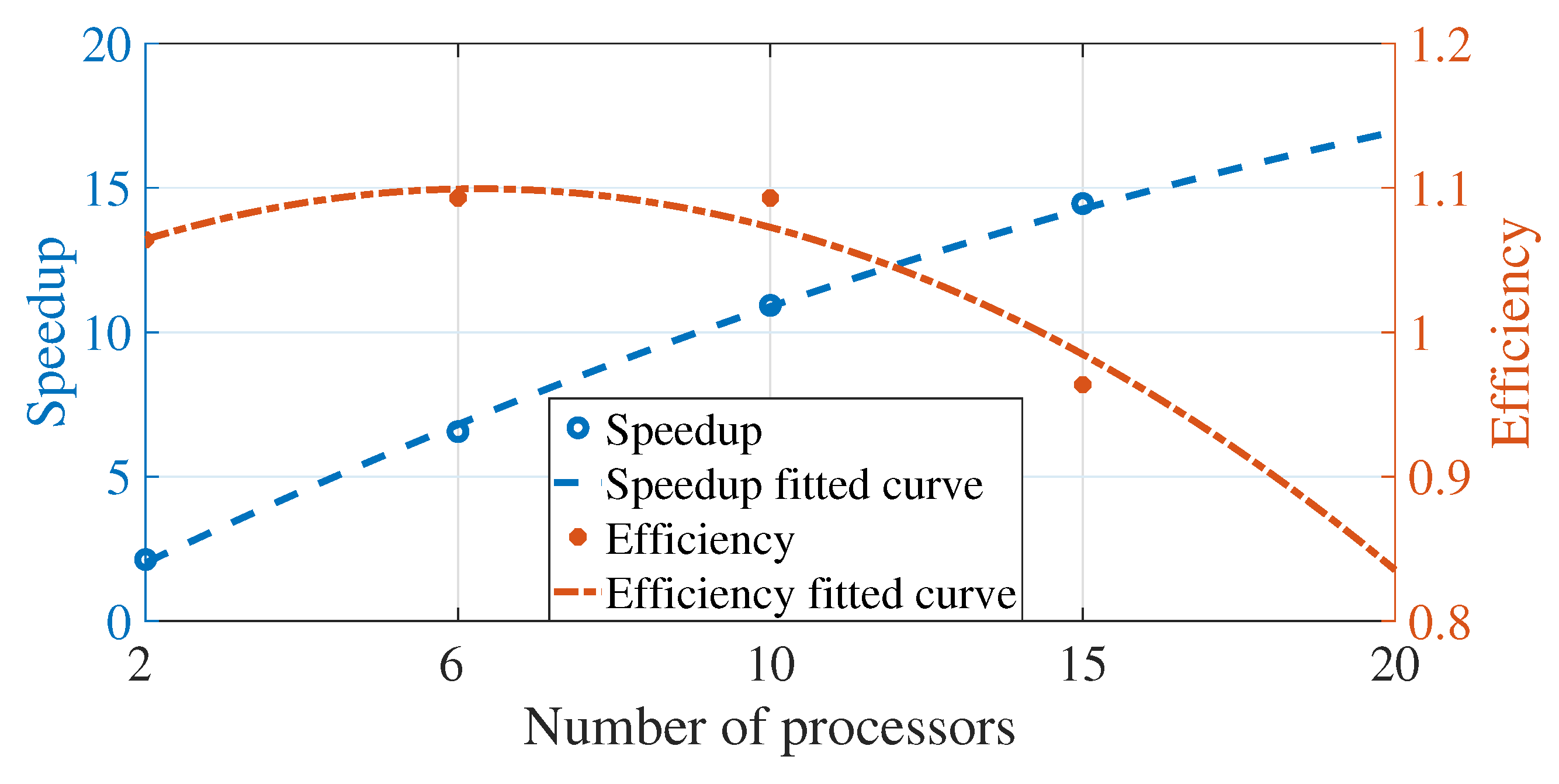
5.1. Speedup and Efficiency
5.2. Pareto Solutions
5.2.1. Domination Percentage
5.2.2. Spacing Metric
5.2.3. Hypervolume Index
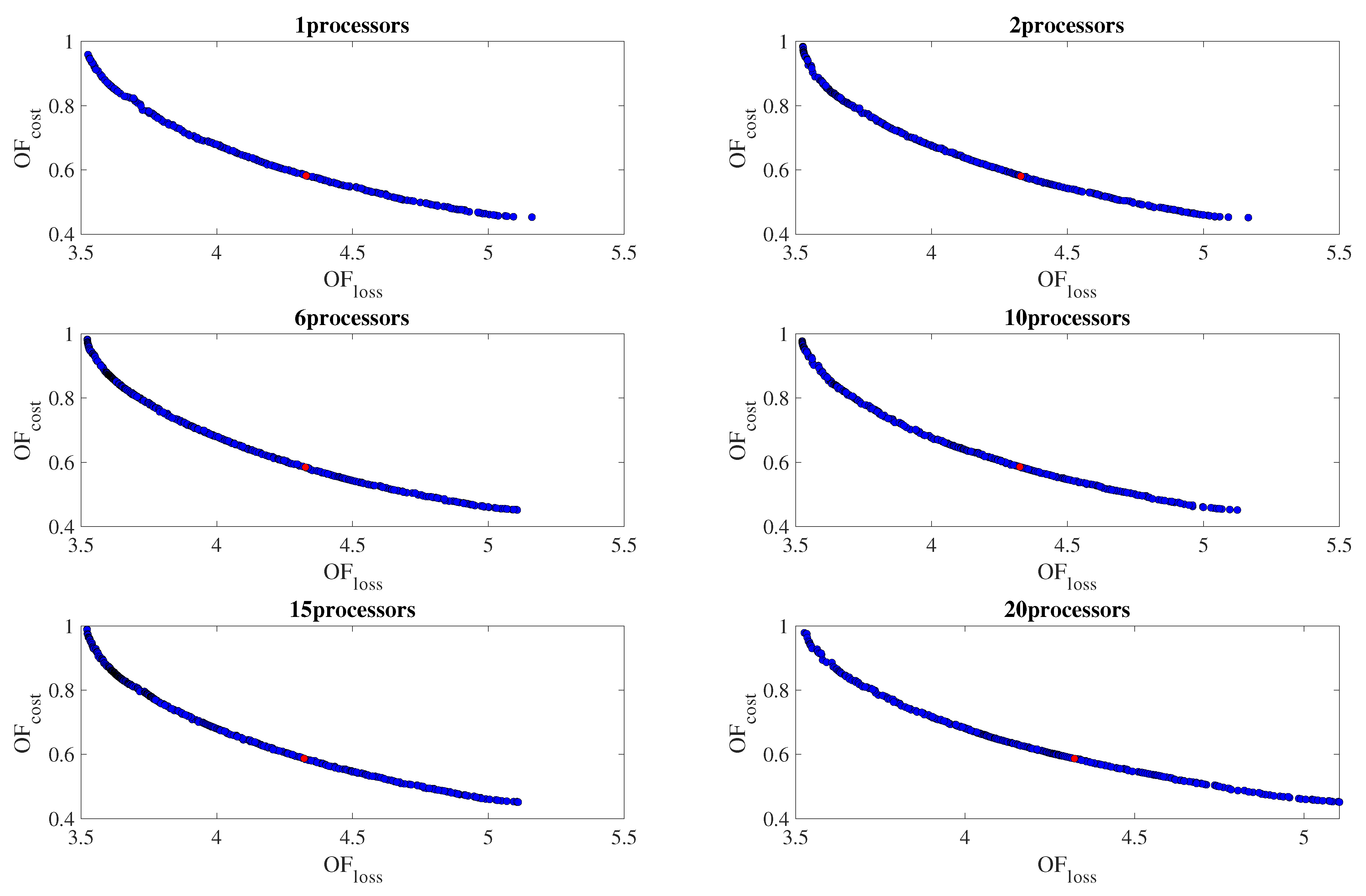
5.2.4. Pareto Solution Candidate and Corresponding Values
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aghaei, J.; Muttaqi, K.M.; Azizivahed, A.; Gitizadeh, M. Distribution expansion planning considering reliability and security of energy using modified PSO (Particle Swarm Optimization) algorithm. Energy 2014, 65, 398–411. [Google Scholar] [CrossRef]
- Kumawat, M.; Gupta, N.; Jain, N.; Bansal, R.C. Swarm-intelligence-based optimal planning of distributed generators in distribution network for minimizing energy loss. Electr. Power Compon. Syst. 2017, 45, 589–600. [Google Scholar] [CrossRef]
- Tan, W.S.; Hassan, M.Y.; Rahman, H.A.; Abdullah, M.P.; Hussin, F. Multi-distributed generation planning using hybrid particle swarm optimisation-gravitational search algorithm including voltage rise issue. IET Gener. Transm. Distrib. 2013, 7, 929–942. [Google Scholar] [CrossRef]
- Yammani, C.; Maheswarapu, S.; Matam, S.K. A Multi-objective Shuffled Bat algorithm for optimal placement and sizing of multi distributed generations with different load models. Int. J. Electr. Power Energy Syst. 2016, 79, 120–131. [Google Scholar] [CrossRef]
- Abu-Mouti, F.S.; El-Hawary, M.E. Optimal Distributed Generation Allocation and Sizing in Distribution Systems via Artificial Bee Colony Algorithm. IEEE Trans. Power Deliv. 2011, 26, 2090–2101. [Google Scholar] [CrossRef]
- Lalitha, M.P.; Reddy, V.V.; Usha, V. Optimal DG Placement for Minimum Real Power Loss in Radial Distribution Systems Using PSO. J. Theor. Appl. Inf. Technol. 2010, 13, 108. [Google Scholar]
- Borges, C.L.T.; Falcao, D.M. Impact of distributed generation allocation and sizing on reliability, losses and voltage profile. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 2, p. 5. [Google Scholar]
- Javed, H.; Muqeet, H.A.; Shehzad, M.; Jamil, M.; Khan, A.A.; Guerrero, J.M. Optimal energy management of a campus microgrid considering financial and economic analysis with demand response strategies. Energies 2021, 14, 8501. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ceylan, O.; Ozdemir, A. Distributed energy resource allocation using multi-objective grasshopper optimization algorithm. Electr. Power Syst. Res. 2021, 201, 107564. [Google Scholar] [CrossRef]
- Nusair, K.; Alhmoud, L. Application of equilibrium optimizer algorithm for optimal power flow with high penetration of renewable energy. Energies 2020, 13, 6066. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ceylan, O.; Ozdemir, A. Grey wolf optimizer for allocation and sizing of distributed renewable generation. In Proceedings of the 2019 54th International Universities Power Engineering Conference (UPEC), Bucharest, Romania, 3–6 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Chiang, M.Y.; Huang, S.C.; Hsiao, T.C.; Zhan, T.S.; Hou, J.C. Optimal Sizing and Location of Photovoltaic Generation and Energy Storage Systems in an Unbalanced Distribution System. Energies 2022, 15, 6682. [Google Scholar] [CrossRef]
- Dharavat, N.; Sudabattula, S.K.; Velamuri, S.; Mishra, S.; Sharma, N.K.; Bajaj, M.; Elgamli, E.; Shouran, M.; Kamel, S. Optimal Allocation of Renewable Distributed Generators and Electric Vehicles in a Distribution System Using the Political Optimization Algorithm. Energies 2022, 15, 6698. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, Q.; Liu, S.; Zhao, L. Distribution Strategy Optimization of Standalone Hybrid WT/PV System Based on Different Solar and Wind Resources for Rural Applications. Energies 2022, 15, 5307. [Google Scholar] [CrossRef]
- Schultz, H.S.; Carvalho, M. Design, Greenhouse Emissions, and Environmental Payback of a Photovoltaic Solar Energy System. Energies 2022, 15, 6098. [Google Scholar] [CrossRef]
- Li, X.; Jones, G. Optimal Sizing, Location, and Assignment of Photovoltaic Distributed Generators with an Energy Storage System for Islanded Microgrids. Energies 2022, 15, 6630. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.; Wang, Y.; Li, F.; Zhang, Y.; Tian, C. Operation optimization in a smart micro-grid in the presence of distributed generation and demand response. Sustainability 2018, 10, 847. [Google Scholar] [CrossRef]
- Majidi, M.; Ozdemir, A.; Ceylan, O. Optimal DG allocation and sizing in radial distribution networks by Cuckoo search algorithm. In Proceedings of the 2017 19th International Conference on Intelligent System Application to Power Systems (ISAP), San Antonio, TX, USA, 17–20 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Sultana, U.; Khairuddin, A.B.; Mokhtar, A.; Zareen, N.; Sultana, B. Grey wolf optimizer based placement and sizing of multiple distributed generation in the distribution system. Energy 2016, 111, 525–536. [Google Scholar] [CrossRef]
- Ayalew, M.; Khan, B.; Giday, I.; Mahela, O.P.; Khosravy, M.; Gupta, N.; Senjyu, T. Integration of Renewable Based Distributed Generation for Distribution Network Expansion Planning. Energies 2022, 15, 1378. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ceylan, O.; Ozdemir, A. Impacts of Load and Generation Volatilities on the Voltage Profiles Improved by Distributed Energy Resources. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Turin, Italy, 1–4 September 2020; pp. 1–6. [Google Scholar]
- Nekooei, K.; Farsangi, M.M.; Nezamabadi-Pour, H.; Lee, K.Y. An improved multi-objective harmony search for optimal placement of DGs in distribution systems. IEEE Trans. Smart Grid 2013, 4, 557–567. [Google Scholar] [CrossRef]
- Dias Santos, J.; Marques, F.; Garcés Negrete, L.P.; Andrêa Brigatto, G.A.; López-Lezama, J.M.; Muñoz-Galeano, N. A Novel Solution Method for the Distribution Network Reconfiguration Problem Based on a Search Mechanism Enhancement of the Improved Harmony Search Algorithm. Energies 2022, 15, 2083. [Google Scholar] [CrossRef]
- Hadidian-Moghaddam, M.J.; Arabi-Nowdeh, S.; Bigdeli, M.; Azizian, D. A multi-objective optimal sizing and siting of distributed generation using ant lion optimization technique. Ain Shams Eng. J. 2018, 9, 2101–2109. [Google Scholar] [CrossRef]
- Abul’Wafa, A.R. Ant-lion optimizer-based multi-objective optimal simultaneous allocation of distributed generations and synchronous condensers in distribution networks. Int. Trans. Electr. Energy Syst. 2019, 29, e2755. [Google Scholar] [CrossRef]
- VC, V.R. Ant Lion optimization algorithm for optimal sizing of renewable energy resources for loss reduction in distribution systems. J. Electr. Syst. Inf. Technol. 2018, 5, 663–680. [Google Scholar]
- Hinneck, A.; Pozo, D. Optimal Transmission Switching: Improving Exact Algorithms by Parallel Incumbent Solution Generation. IEEE Trans. Power Syst. 2022, 1–14. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, W.; Dai, C.; Cai, W. Dynamic multi-group self-adaptive differential evolution algorithm for reactive power optimization. Int. J. Electr. Power Energy Syst. 2010, 32, 351–357. [Google Scholar] [CrossRef]
- Angulo, A.; Rodríguez, D.; Garzón, W.; Gómez, D.F.; Al Sumaiti, A.; Rivera, S. Algorithms for bidding strategies in local energy markets: Exhaustive search through parallel computing and metaheuristic optimization. Algorithms 2021, 14, 269. [Google Scholar] [CrossRef]
- Rodríguez-García, J.; Ribó-Pérez, D.; Álvarez Bel, C.; Peñalvo-López, E. Maximizing the Profit for Industrial Customers of Providing Operation Services in Electric Power Systems via a Parallel Particle Swarm Optimization Algorithm. IEEE Access 2020, 8, 24721–24733. [Google Scholar] [CrossRef]
- Tsai, C.-F.; Dao, T.-K.; Pan, T.-S.; Nguyen, T.-T.; Chang, J.-F. Parallel bat algorithm applied to the economic load dispatch problem. J. Internet Technol. 2016, 17, 761–769. [Google Scholar]
- Ceylan, O.; Liu, G.; Tomsovic, K. Parallel harmony search based distributed energy resource optimization. In Proceedings of the 2015 18th International Conference on Intelligent System Application to Power Systems (ISAP), Porto, Portugal, 11–16 September 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Alba, E. Parallel Evolutionary Computations; Springer: Berlin/Heidelberg, Germany, 2006; Volume 22. [Google Scholar]
- Shigeto, Y.; Sakai, M. Parallel computing of discrete element method on multi-core processors. Particuology 2011, 9, 398–405. [Google Scholar] [CrossRef]
- Fox, G.C.; Williams, R.D.; Messina, G.C. Parallel Computing Works! Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Schmidberger, M.; Morgan, M.; Eddelbuettel, D.; Yu, H.; Tierney, L.; Mansmann, U. State-of-the-art in Parallel Computing with R. J. Stat. Softw. 2009. [Google Scholar] [CrossRef]
- Salleh, S.; Zomaya, A.Y. Scheduling in Parallel Computing Systems: Fuzzy and Annealing Techniques; Springer Science & Business Media: New York, NY, USA, 2012; Volume 510. [Google Scholar]
- Scarcello, L.; Giordano, A.; Mastroianni, C. Edge Computing Parallel Approach for Efficient Energy Sharing in a Prosumer Community. Energies 2022, 15, 4543. [Google Scholar] [CrossRef]
- Eager, D.L.; Zahorjan, J.; Lazowska, E.D. Speedup versus efficiency in parallel systems. IEEE Trans. Comput. 1989, 38, 408–423. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ceylan, O.; Ozdemir, A.; Fotuhi-Firuzabad, M. A multi-objective framework for distributed energy resources planning and storage management. Appl. Energy 2022, 314, 118887. [Google Scholar] [CrossRef]
- Rana, A.; Darji, J.; Pandya, M. Backward/forward sweep load flow algorithm for radial distribution system. Int. J. Sci. Res. Dev. 2014, 2, 398–400. [Google Scholar]
- Nebro, A.J.; Durillo, J.J.; Garcia-Nieto, J.; Coello Coello, C.A.; Luna, F.; Alba, E. SMPSO: A new PSO-based metaheuristic for multi-objective optimization. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making(MCDM), Nashville, TN, USA, 30 March–2 April 2009; pp. 66–73. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Censor, Y. Pareto optimality in multiobjective problems. Appl. Math. Optim. 1977, 4, 41–59. [Google Scholar] [CrossRef]
- Younesi, S.; Ahmadi, B.; Ceylan, O.; Ozdemir, A. Allocation of Distributed Generators Using Parallel Grey Wolf Optimization. Mod. Power Syst. 2021, 22, 387–408. [Google Scholar]
- Baran, M.; Wu, F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 9, 101–102. [Google Scholar]
- EPIAS. EPIAS Transparency Platform. Available online: https://seffaflik.epias.com.tr/transparency/index.xhtml (accessed on 3 June 2022).
- Intel. Intel Xeon Processor. Available online: https://ark.intel.com/content/www/us/en/ark/products/91754/intel-xeon-processor-e5-2680-v4-35m-cache-2-40-ghz.html (accessed on 3 June 2022).
- Sharma, G.; Martin, J. MATLAB®: A language for parallel computing. Int. J. Parallel Program. 2009, 37, 3–36. [Google Scholar] [CrossRef]
- Amdahl, G.M. Validity of the Single Processor Approach to Achieving Large Scale Computing Capabilities, Reprinted from the AFIPS Conference Proceedings, Vol. 30 (Atlantic City, N.J., Apr. 18–20), AFIPS Press, Reston, Va., 1967, pp. 483–485, when Dr. Amdahl was at International Business Machines Corporation, Sunnyvale, California. IEEE Solid-State Circuits Soc. Newsl. 2007, 12, 19–20. [Google Scholar] [CrossRef]
- Alba, E. Parallel evolutionary algorithms can achieve super-linear performance. Inf. Process. Lett. 2002, 82, 7–13. [Google Scholar] [CrossRef]





| Max DG number | 8 | (USD/kW) | 1830 |
| DG types | 2 | (USD/kW) | 1600 |
| (year) | 30 | (USD/kW-yr) | 18 |
| (year) | 25 | (USD/kW-yr) | 25 |
| # Processor | Average | STD | Min | Max |
|---|---|---|---|---|
| 1 | 4886 | 414 | 4405 | 6115 |
| 2 | 2297 | 372 | 1741 | 3122 |
| 6 | 745 | 120 | 590 | 1100 |
| 10 | 448 | 67 | 378 | 651 |
| 15 | 338 | 70 | 275 | 610 |
| 20 | 290 | 66 | 227 | 557 |
| x | DP(x,1) | DP(x,2) | DP(x,6) | DP(x,10) | DP(x,15) | DP(x,20) |
|---|---|---|---|---|---|---|
| 1 | 65 | 39 | 26 | 21 | 17 | |
| 2 | 22 | 18 | 13 | 9 | 6 | |
| 6 | 53 | 80 | 25 | 35 | 11 | |
| 10 | 61 | 81 | 68 | 39 | 22 | |
| 15 | 65 | 90 | 60 | 52 | 29 | |
| 20 | 73 | 89 | 74 | 61 | 47 |
| # Processor | Average | STD | Min | Max |
|---|---|---|---|---|
| 1 | 0.0088 | 0.0036 | 0.0030 | 0.0195 |
| 2 | 0.0063 | 0.0022 | 0.0038 | 0.0158 |
| 6 | 0.0082 | 0.0041 | 0.0032 | 0.0281 |
| 10 | 0.0100 | 0.0048 | 0.0034 | 0.0261 |
| 15 | 0.0105 | 0.0053 | 0.0030 | 0.0283 |
| 20 | 0.0111 | 0.0049 | 0.0028 | 0.0299 |
| # Processor | Average | STD | Min | Max |
|---|---|---|---|---|
| 1 | 0.1688 | 0.0048 | 0.1533 | 0.1759 |
| 2 | 0.1882 | 0.0040 | 0.1777 | 0.1953 |
| 6 | 0.1805 | 0.0048 | 0.1664 | 0.1890 |
| 10 | 0.1839 | 0.0042 | 0.1752 | 0.1916 |
| 15 | 0.1735 | 0.0045 | 0.1607 | 0.1828 |
| 20 | 0.1850 | 0.0042 | 0.1756 | 0.1931 |
| PSC-1 | PSC-2 | PSC-6 | ||||||
|---|---|---|---|---|---|---|---|---|
| Type | Location | Size (kW) | Type | Location | Size (kW) | Type | Location | Size (kW) |
| WT | 8 | 500 | WT | 10 | 530 | WT | 8 | 500 |
| WT | 13 | 830 | WT | 14 | 650 | WT | 13 | 810 |
| WT | 18 | 490 | WT | 17 | 530 | WT | 18 | 500 |
| WT | 25 | 460 | WT | 25 | 480 | WT | 25 | 410 |
| WT | 30 | 920 | WT | 30 | 1000 | WT | 30 | 1000 |
| WT | 32 | 1000 | WT | 32 | 1000 | WT | 32 | 1000 |
| Total unit size (kW) | 4200 | 4190 | 4220 | |||||
| Total losses (kWh) | 4329 | 4329 | 4326 | |||||
| PSC-10 | PSC-15 | PSC-20 | ||||||
| Type | Location | Size (kW) | Type | Location | Size (kW) | Type | Location | Size (kW) |
| WT | 10 | 700 | WT | 12 | 500 | PV | 8 | 150 |
| WT | 16 | 1000 | WT | 14 | 490 | WT | 13 | 1000 |
| WT | 25 | 590 | WT | 18 | 590 | WT | 17 | 590 |
| WT | 30 | 940 | WT | 25 | 680 | WT | 25 | 500 |
| WT | 32 | 1000 | WT | 30 | 1000 | WT | 30 | 1000 |
| WT | 33 | 980 | WT | 32 | 1000 | |||
| Total unit size (kW) | 4230 | 4240 | 4240 | |||||
| Total losses (kWh) | 4324 | 4321 | 4322 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Younesi, S.; Ahmadi, B.; Ceylan, O.; Ozdemir, A. Optimum Parallel Processing Schemes to Improve the Computation Speed for Renewable Energy Allocation and Sizing Problems. Energies 2022, 15, 9301. https://doi.org/10.3390/en15249301
Younesi S, Ahmadi B, Ceylan O, Ozdemir A. Optimum Parallel Processing Schemes to Improve the Computation Speed for Renewable Energy Allocation and Sizing Problems. Energies. 2022; 15(24):9301. https://doi.org/10.3390/en15249301
Chicago/Turabian StyleYounesi, Soheil, Bahman Ahmadi, Oguzhan Ceylan, and Aydogan Ozdemir. 2022. "Optimum Parallel Processing Schemes to Improve the Computation Speed for Renewable Energy Allocation and Sizing Problems" Energies 15, no. 24: 9301. https://doi.org/10.3390/en15249301
APA StyleYounesi, S., Ahmadi, B., Ceylan, O., & Ozdemir, A. (2022). Optimum Parallel Processing Schemes to Improve the Computation Speed for Renewable Energy Allocation and Sizing Problems. Energies, 15(24), 9301. https://doi.org/10.3390/en15249301









