An Effective Power Dispatch of Photovoltaic Generators in DC Networks via the Antlion Optimizer
Abstract
1. Introduction
1.1. General Context
1.2. Motivation
1.3. State of the Art
1.4. Scope and Main Contributions
- The implementation of a mathematical formulation that observes all technical and operating constraints that constitute the operation of DC grids under a scenario of PV distributed generation.
- A new master–slave methodology to solve the optimal power dispatch in DC grids which employs the ALO and a matrix hourly power flow method and yields the best results with regard to solution quality (best solution and standard deviation).
- The implementation of two DC grids (GCN and SN) that represent the average PV power generation and demand reported in Colombia.
- A methodology that allows identifying the optimization method that optimally balances solution quality and processing times for solving the problem of optimal power dispatch in DC grids.
- The identification of the current economic needs associated with operating GCN and SN in Colombia.
1.5. Paper Structure
2. Mathematical Formulation
2.1. Objective Functions
2.2. Set of Constraints
2.3. Fitness Function
3. Codification and Optimization Methodology
3.1. Antlion Optimizer
3.1.1. Generating the Initial Population
3.1.2. Evaluating the Fitness Function and Selecting the Incumbent
3.1.3. Algorithm Advancement Method
| Algorithm 1: Iterative process proposed for the ALO. |
 |
3.2. Matrix Hourly Power Flow
| Algorithm 2: Iterative process for matrix hourly power flow based on successive approximations. |
 |
4. Test Systems, Generation and Demand Curves, and Additional Considerations
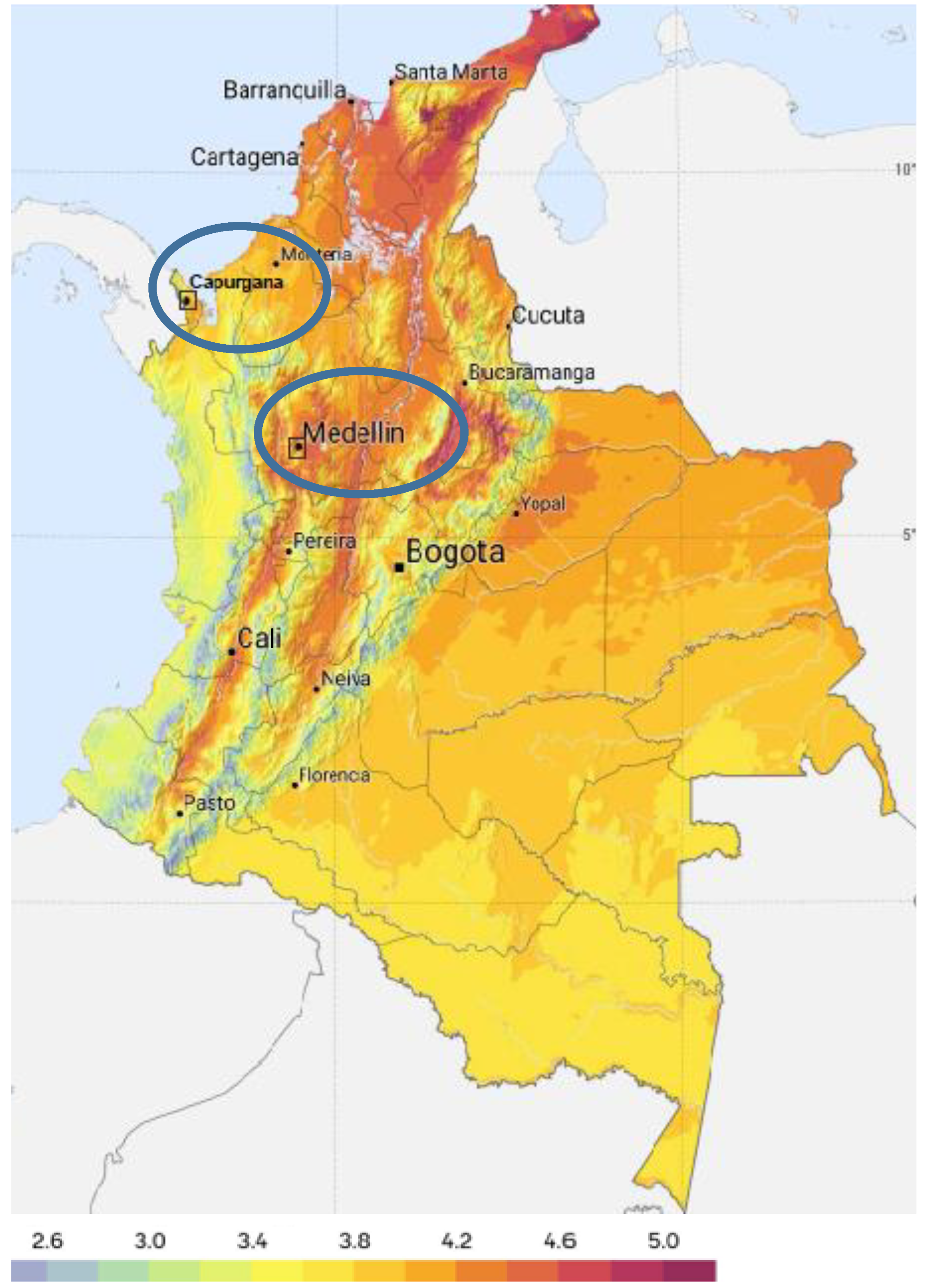
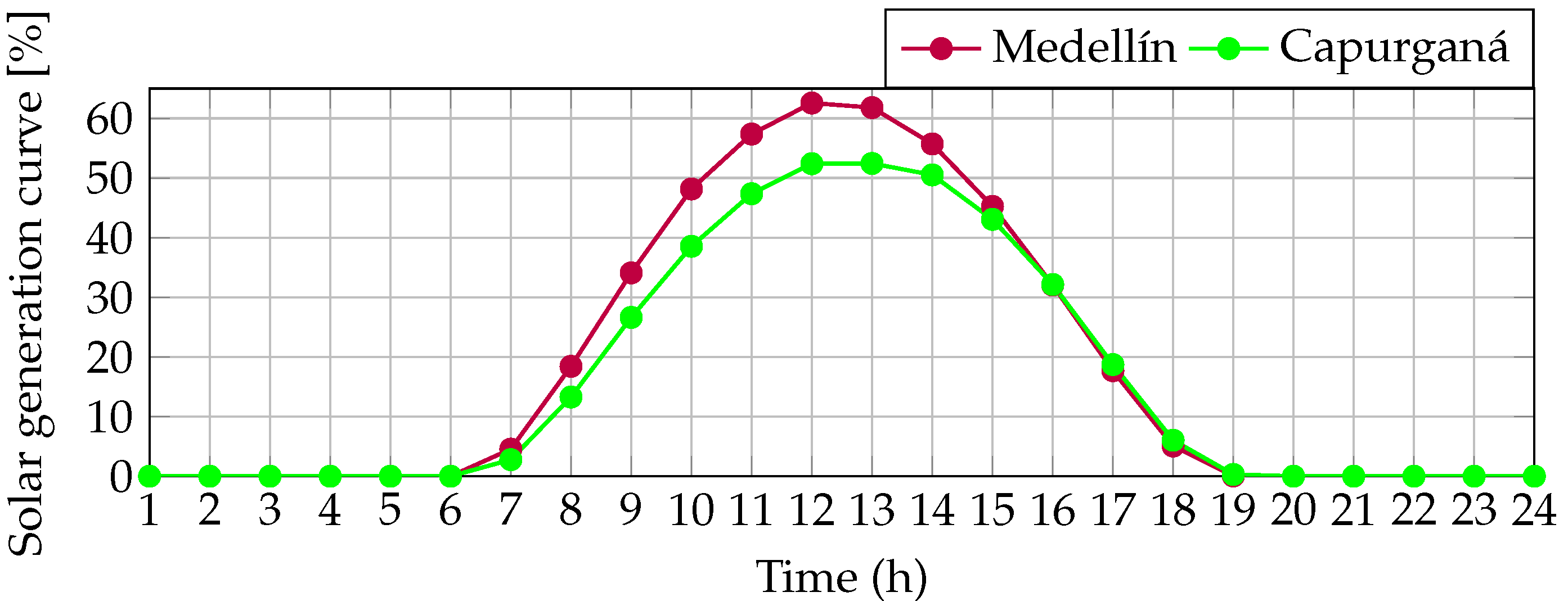
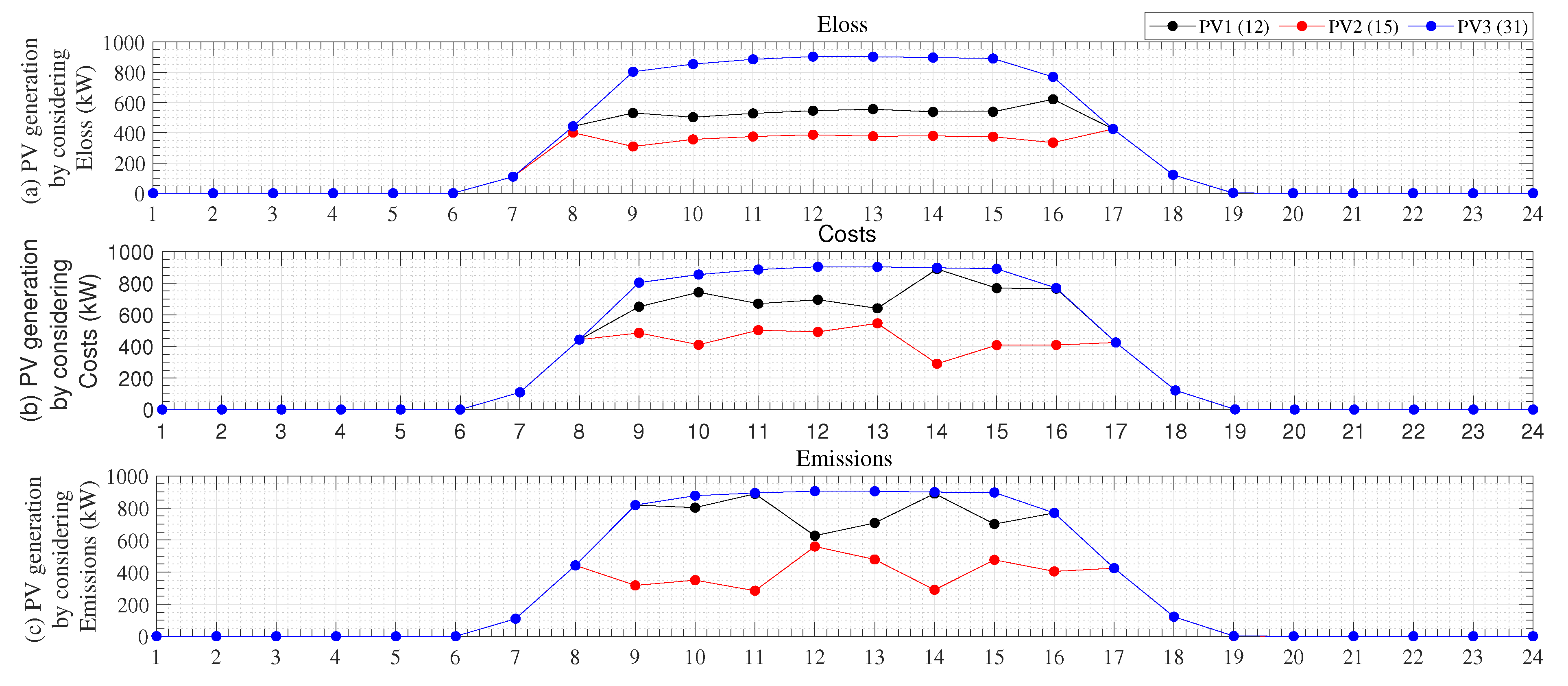
4.1. PV Generation Curves
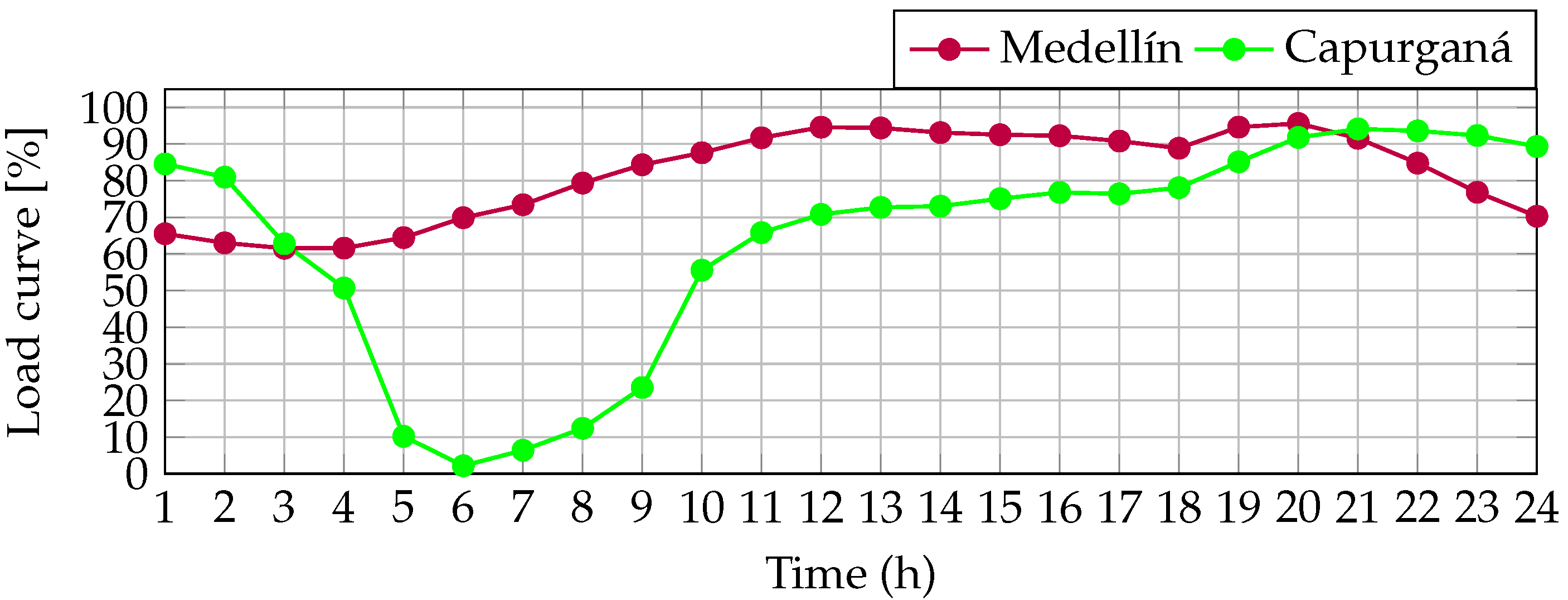
4.2. Power Demand Curves
4.3. Test Systems
4.4. Grid-Connected Test Feeder
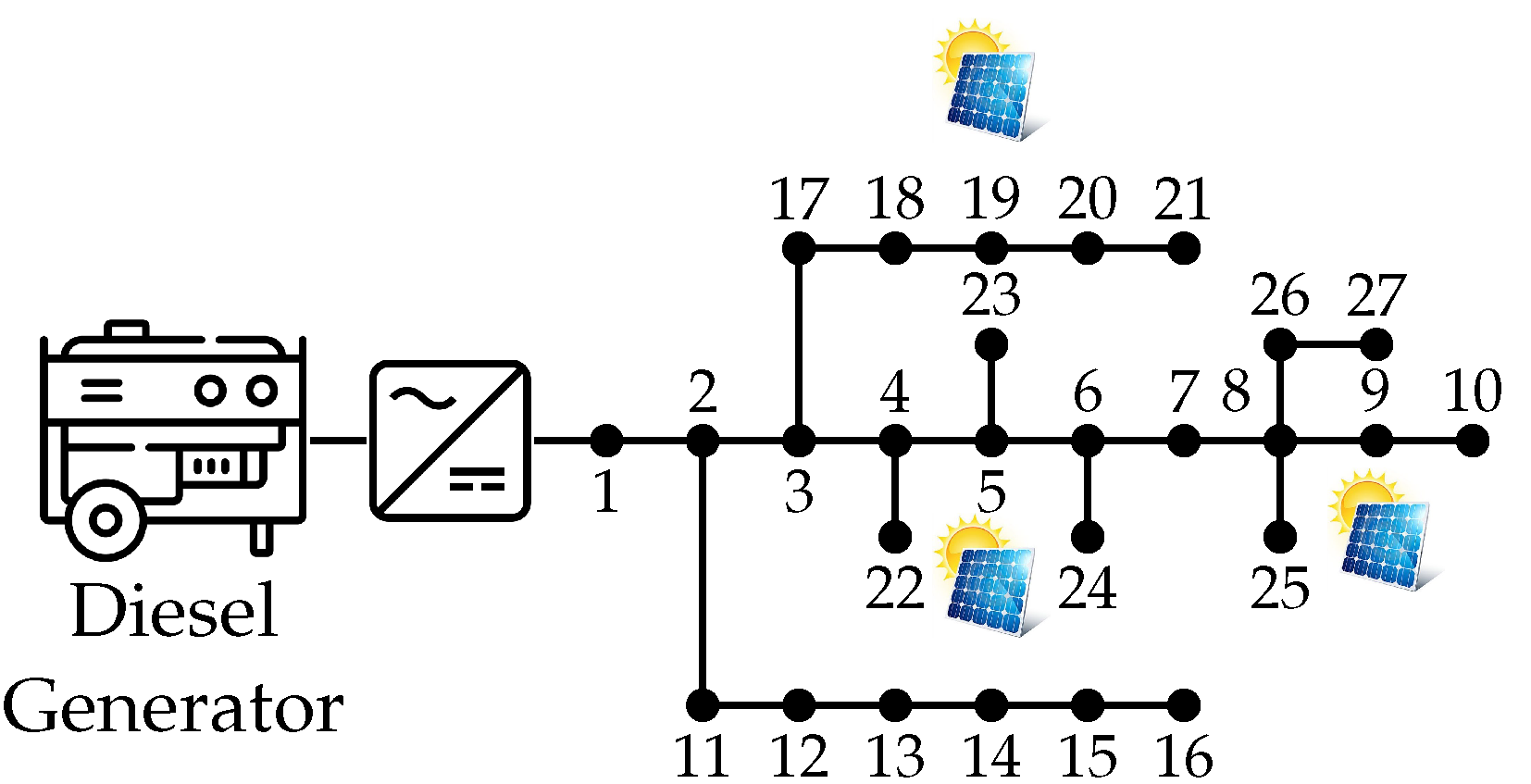
4.5. Standalone Test Feeder
4.6. Comparison Methods
5. Simulation Results and Discussions
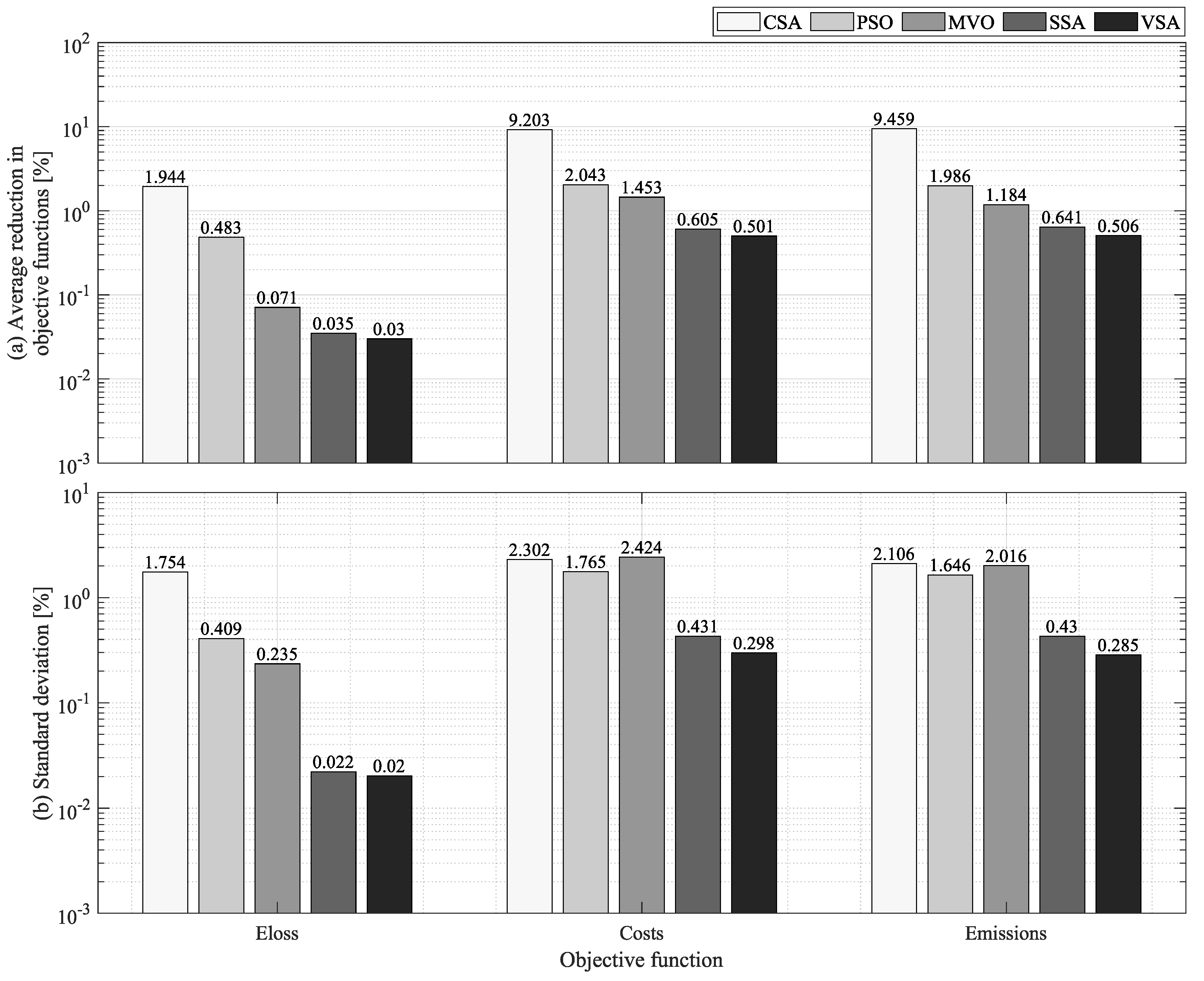
5.1. Standalone Test Feeder
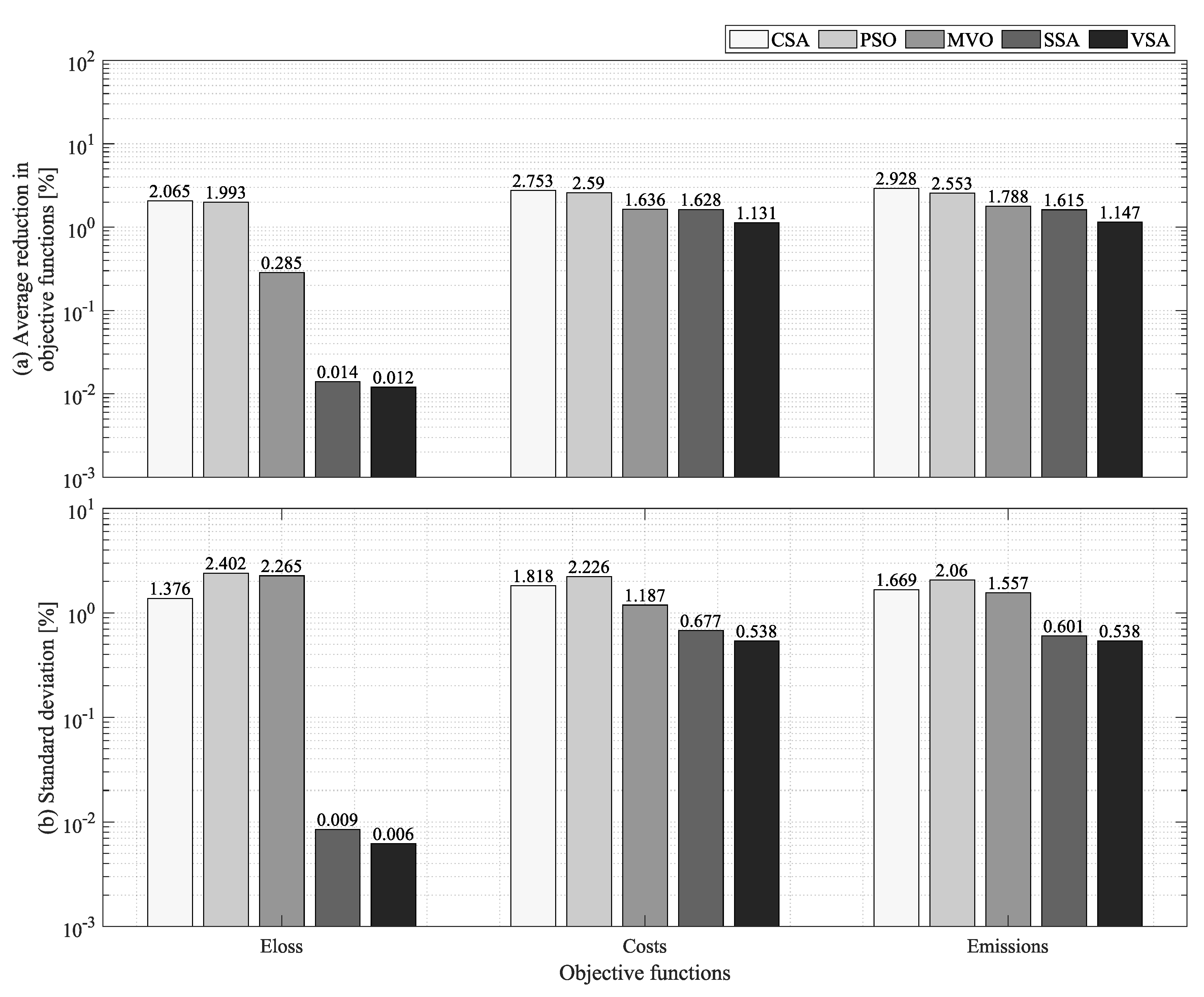
5.2. Grid-Connected Test Feeder
5.3. Average Processing Times
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hernandez, J.; Velasco, D.; Trujillo, C. Analysis of the effect of the implementation of photovoltaic systems like option of distributed generation in Colombia. Renew. Sustain. Energy Rev. 2011, 15, 2290–2298. [Google Scholar] [CrossRef]
- Dong, J.; Feng, T.T.; Sun, H.X.; Cai, H.X.; Li, R.; Yang, Y. Clean distributed generation in China: Policy options and international experience. Renew. Sustain. Energy Rev. 2016, 57, 753–764. [Google Scholar] [CrossRef]
- Boumaiza, A.; Sanfilippo, A.; Mohandes, N. Modeling multi-criteria decision analysis in residential PV adoption. Energy Strategy Rev. 2022, 39, 100789. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Zhang, S.Y.; Hubbard, B.; Yao, X. The emergence of the solar photovoltaic power industry in China. Renew. Sustain. Energy Rev. 2013, 21, 229–236. [Google Scholar] [CrossRef]
- Chang, G.W.; Chinh, N.C. Coyote optimization algorithm-based approach for strategic planning of photovoltaic distributed generation. IEEE Access 2020, 8, 36180–36190. [Google Scholar] [CrossRef]
- Singh, G.K. Solar power generation by PV (photovoltaic) technology: A review. Energy 2013, 53, 1–13. [Google Scholar] [CrossRef]
- Solargis Solar Resource Maps of Colombia. Available online: https://solargis.com/maps-and-gis-data/download/colombia (accessed on 22 November 2022).
- Rakhshani, E.; Rouzbehi, K.J.; Sánchez, A.; Tobar, A.C.; Pouresmaeil, E. Integration of large scale PV-based generation into power systems: A survey. Energies 2019, 12, 1425. [Google Scholar] [CrossRef]
- Díaz González, J.J. Viabilidad Regulatoria para Implementar Sistemas de Micro Redes Con Fuentes No Convencionales de Energía Renovable–FNCER–por Intercolombia SAESP. 2018. Available online: http://bibliotecavirtualoducal.uc.cl/vufind/Record/oai:localhost:10185-28863 (accessed on 24 January 2023).
- Moreno, C.; Milanes, C.B.; Arguello, W.; Fontalvo, A.; Alvarez, R.N. Challenges and perspectives of the use of photovoltaic solar energy in Colombia. Int. J. Electr. Comput. Eng. 2022, 12, 4521–4528. [Google Scholar] [CrossRef]
- De Brito, M.A.G.; Galotto, L.; Sampaio, L.P.; e Melo, G.d.A.; Canesin, C.A. Evaluation of the main MPPT techniques for photovoltaic applications. IEEE Trans. Ind. Electron. 2012, 60, 1156–1167. [Google Scholar] [CrossRef]
- Mishra, V.L.; Chauhan, Y.K.; Verma, K. A critical review on advanced reconfigured models and metaheuristics-based MPPT to address complex shadings of solar array. Energy Convers. Manag. 2022, 269, 116099. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Montoya, O.D.; Ramos-Paja, C.A. An energy management system for optimal operation of BSS in DC distributed generation environments based on a parallel PSO algorithm. J. Energy Storage 2020, 29, 101488. [Google Scholar] [CrossRef]
- Li, C.; De Bosio, F.; Chen, F.; Chaudhary, S.K.; Vasquez, J.C.; Guerrero, J.M. Economic dispatch for operating cost minimization under real-time pricing in droop-controlled DC microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 5, 587–595. [Google Scholar] [CrossRef]
- Younes, Z.; Alhamrouni, I.; Mekhilef, S.; Reyasudin, M. A memory-based gravitational search algorithm for solving economic dispatch problem in micro-grid. Ain Shams Eng. J. 2021, 12, 1985–1994. [Google Scholar] [CrossRef]
- Tan, Q.; Ding, Y.; Ye, Q.; Mei, S.; Zhang, Y.; Wei, Y. Optimization and evaluation of a dispatch model for an integrated wind-photovoltaic-thermal power system based on dynamic carbon emissions trading. Appl. Energy 2019, 253, 113598. [Google Scholar] [CrossRef]
- Gao, S.; Jia, H.; Marnay, C. Techno-economic evaluation of mixed AC and DC power distribution network for integrating large-scale photovoltaic power generation. IEEE Access 2019, 7, 105019–105029. [Google Scholar] [CrossRef]
- Lin, J.C.W.; Liu, Q.; Fournier-Viger, P.; Hong, T.P.; Voznak, M.; Zhan, J. A sanitization approach for hiding sensitive itemsets based on particle swarm optimization. Eng. Appl. Artif. Intell. 2016, 53, 1–18. [Google Scholar] [CrossRef]
- Lin, J.C.W.; Yang, L.; Fournier-Viger, P.; Wu, J.M.T.; Hong, T.P.; Wang, L.S.L.; Zhan, J. Mining high-utility itemsets based on particle swarm optimization. Eng. Appl. Artif. Intell. 2016, 55, 320–330. [Google Scholar] [CrossRef]
- Spea, S.R. Combined economic emission dispatch solution of an isolated renewable integrated micro-grid using crow search algorithm. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 47–52. [Google Scholar]
- Rosales-Muñoz, A.A.; Grisales-Noreña, L.F.; Montano, J.; Montoya, O.D.; Perea-Moreno, A.J. Application of the multiverse optimization method to solve the optimal power flow problem in direct current electrical networks. Sustainability 2021, 13, 8703. [Google Scholar] [CrossRef]
- Velasquez, O.S.; Montoya Giraldo, O.D.; Garrido Arevalo, V.M.; Grisales Norena, L.F. Optimal power flow in direct-current power grids via black hole optimization. Adv. Electr. Electron. Eng. 2019, 17, 24–32. [Google Scholar] [CrossRef]
- Rosales Muñoz, A.A.; Grisales-Noreña, L.F.; Montano, J.; Montoya, O.D.; Giral-Ramírez, D.A. Optimal Power Dispatch of Distributed Generators in Direct Current Networks Using a Master–Slave Methodology That Combines the Salp Swarm Algorithm and the Successive Approximation Method. Electronics 2021, 10, 2837. [Google Scholar] [CrossRef]
- Garzon-Rivera, O.; Ocampo, J.; Grisales-Noreña, L.; Montoya, O.; Rojas-Montano, J. Optimal power flow in Direct Current Networks using the antlion optimizer. Stat. Optim. Inf. Comput. 2020, 8, 846–857. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Ocampo-Toro, J.A.; Rosales-Muñoz, A.A.; Cortes-Caicedo, B.; Montoya, O.D. An Energy Management System for PV Sources in Standalone and Connected DC Networks Considering Economic, Technical, and Environmental Indices. Sustainability 2022, 14, 16429. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Ramos-Paja, C.A.; Gonzalez-Montoya, D.; Alcalá, G.; Hernandez-Escobedo, Q. Energy management in PV based microgrids designed for the Universidad Nacional de Colombia. Sustainability 2020, 12, 1219. [Google Scholar] [CrossRef]
- Gbadamosi, S.L.; Nwulu, N.I. Optimal power dispatch and reliability analysis of hybrid CHP-PV-wind systems in farming applications. Sustainability 2020, 12, 8199. [Google Scholar] [CrossRef]
- Luna, A.C.; Diaz, N.L.; Andrade, F.; Graells, M.; Guerrero, J.M.; Vasquez, J.C. Economic power dispatch of distributed generators in a grid-connected microgrid. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea, 1–5 June 2015; pp. 1161–1168. [Google Scholar]
- Gil-González, W.; Montoya, O.D.; Holguín, E.; Garces, A.; Grisales-Noreña, L.F. Economic dispatch of energy storage systems in dc microgrids employing a semidefinite programming model. J. Energy Storage 2019, 21, 1–8. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Rosales-Muñoz, A.A.; Cortés-Caicedo, B.; Montoya, O.D.; Andrade, F. Optimal Operation of PV Sources in DC Grids for Improving Technical, Economical, and Environmental Conditions by Using Vortex Search Algorithm and a Matrix Hourly Power Flow. Mathematics 2023, 11, 93. [Google Scholar] [CrossRef]
- Lin, C.W.; Hong, T.P.; Yang, K.T.; Wang, S.L. The GA-based algorithms for optimizing hiding sensitive itemsets through transaction deletion. Appl. Intell. 2015, 42, 210–230. [Google Scholar] [CrossRef]
- Lin, J.C.W.; Zhang, Y.; Zhang, B.; Fournier-Viger, P.; Djenouri, Y. Hiding sensitive itemsets with multiple objective optimization. Soft Comput. 2019, 23, 12779–12797. [Google Scholar] [CrossRef]
- NASA. NASA Prediction of Worldwide Energy Resources, Washington, DC, United States. Available online: https://power.larc.nasa.gov/ (accessed on 21 September 2022).
- XM SA ESP. Sinergox Database, Colombia. Available online: https://sinergox.xm.com.co/Paginas/Home.aspx (accessed on 21 September 2022).
- Instituto de Planificación y Promoción de Soluciones Energéticas para Zonas No Interconectadas. Informes Mensuales de Telimetría, Colombia. Available online: https://ipse.gov.co/cnm/informe-mensuales-telemetria/ (accessed on 21 September 2022).
- Zolghadr-Asli, B.; Bozorg-Haddad, O.; Chu, X. Crow search algorithm (CSA). In Advanced Optimization by Nature-Inspired Algorithms; Springer: Berlin/Heidelberg, Germany, 2018; pp. 143–149. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. A new metaheuristic for numerical function optimization: Vortex Search algorithm. Inf. Sci. 2015, 293, 125–145. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jangir, P.; Saremi, S. Multi-objective ant lion optimizer: A multi-objective optimization algorithm for solving engineering problems. Appl. Intell. 2017, 46, 79–95. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Beckington, UK, 2010. [Google Scholar]
- Falaghi, H.; Ramezani, M.; Haghifam, M.R.; Milani, K.R. Optimal selection of conductors in radial distribution systems with time varying load. In Proceedings of the CIRED 2005-18th International Conference and Exhibition on Electricity Distribution, Turin, Italy, 6–9 June 2005; pp. 1–4. [Google Scholar]
- Grisales-Noreña, L.; Montoya-Giraldo, O.; Gil-González, W. Optimal Integration of Distributed Generators into DC Microgrids Using a Hybrid Methodology: Genetic and Vortex Search Algorithms. Arab. J. Sci. Eng. 2022, 47, 14657–14672. [Google Scholar] [CrossRef]
- Abou El Ela, A.; El-Sehiemy, R.A.; Shaheen, A.; Shalaby, A. Application of the crow search algorithm for economic environmental dispatch. In Proceedings of the 2017 nineteenth international Middle East power systems conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 78–83. [Google Scholar]
- Verma, S.; Shiva, C.K. A novel salp swarm algorithm for expansion planning with security constraints. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 1335–1344. [Google Scholar] [CrossRef]



| Method | Year | Objective Function | Considered | Not Considered | Reference |
|---|---|---|---|---|---|
| Genetic algorithm | 2016 | Minimization of operating costs | Variable power demand and generation Costs associated with renewable and conventional generators voltage profile limits Average solution analysis | Average processing time analysis Standard deviation analysis Comparison methods Maximum current line | [14] |
| Non-dominant sorting genetic algorithm-II | 2019 | Minimization of operating costs and energy losses | Best solution analysis Comparison methods | Average solution analysis Average processing time analysis Standard deviation analysis Maximum current line | [17] |
| Crow search algorithm | 2019 | Minimization of operating costs and emissions | Best solution analysis Comparison methods | Average solution analysis Average processing time analysis Standard deviation analysis Maximum current line | [20] |
| Black hole optimization | 2019 | Minimization of power losses | Best solution analysis Comparison methods | Average solution analysis Average processing time analysis Standard deviation analysis Maximum current line | [22] |
| Parallel particle swarm optimizer | 2020 | Minimization of the energy purchasing costs | Best solution analysis Average processing time analysis Average solution analysis Standard deviation analysis Comparison methods voltage profile limits Maximum current line | [13] | |
| Antlion optimizer | 2020 | Minimization of power losses | Best solution analysis Average processing time analysis Comparison methods | Average solution analysis Standard deviation analysis Maximum current line | [24] |
| Salp swarm algorithm | 2021 | Minimization of power losses | Best solution anylisis Average processing time analysis Average solution analysis Standard deviation analysis Comparison methods Maximum current line | variable power generation and demand | [23] |
| Memory-based gravitational search algorithm | 2021 | Minimization of operating costs | Best solution analysis Comparison methods | Average processing time analysis Average solution analysis Standard deviation analysis Maximum current line | [15] |
| Multiverse optimizer | 2021 | Minimization of power losses | Best solution analysis Average solution analysis Standard deviation analysis Comparison methods | Average processing time analysis Maximum current line | [21] |
| Salp swarm algorithm | 2022 | Minimization of energy losses, operating costs, and emissions | Average solution analysis Average processing time analysis Standard deviation analysis Comparison methods Maximum current line | [30] |
| Line l | Node i | Node j | (kW) | (A) | |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 0.0922 | 100 | 320 |
| 2 | 2 | 3 | 0.4930 | 90 | 280 |
| 3 | 3 | 4 | 0.3660 | 120 | 195 |
| 4 | 4 | 5 | 0.3811 | 60 | 195 |
| 5 | 5 | 6 | 0.8190 | 60 | 195 |
| 6 | 6 | 7 | 0.1872 | 200 | 95 |
| 7 | 7 | 8 | 1.7114 | 200 | 85 |
| 8 | 8 | 9 | 1.0300 | 60 | 70 |
| 9 | 9 | 10 | 1.0400 | 60 | 55 |
| 10 | 10 | 11 | 0.1966 | 45 | 55 |
| 11 | 11 | 12 | 0.3744 | 60 | 55 |
| 12 | 12 | 13 | 1.4680 | 60 | 40 |
| 13 | 13 | 14 | 0.5416 | 120 | 40 |
| 14 | 14 | 15 | 0.5910 | 60 | 25 |
| 15 | 15 | 16 | 0.7463 | 60 | 20 |
| 16 | 16 | 17 | 1.2890 | 60 | 20 |
| 17 | 17 | 18 | 0.7320 | 90 | 20 |
| 18 | 2 | 19 | 0.1640 | 90 | 30 |
| 19 | 19 | 20 | 1.5042 | 90 | 25 |
| 20 | 20 | 21 | 0.4095 | 90 | 20 |
| 21 | 21 | 22 | 0.7089 | 90 | 20 |
| 22 | 3 | 23 | 0.4512 | 90 | 85 |
| 23 | 23 | 24 | 0.8980 | 420 | 70 |
| 24 | 24 | 25 | 0.8900 | 420 | 40 |
| 25 | 6 | 26 | 0.2030 | 60 | 85 |
| 26 | 26 | 27 | 0.2842 | 60 | 85 |
| 27 | 27 | 28 | 1.0590 | 60 | 70 |
| 28 | 28 | 29 | 0.8042 | 120 | 70 |
| 29 | 29 | 30 | 0.5075 | 200 | 55 |
| 30 | 30 | 31 | 0.9744 | 150 | 40 |
| 31 | 31 | 32 | 0.3105 | 210 | 25 |
| 32 | 32 | 33 | 0.3410 | 60 | 20 |
| Line l | Node i | Node j | (kW) | (A) | |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 0.0140 | 0 | 195 |
| 2 | 2 | 3 | 0.7463 | 0 | 145 |
| 3 | 3 | 4 | 0.4052 | 297.5 | 85 |
| 4 | 4 | 5 | 1.1524 | 0 | 70 |
| 5 | 5 | 6 | 0.5261 | 255 | 70 |
| 6 | 6 | 7 | 0.7127 | 0 | 55 |
| 7 | 7 | 8 | 1.6628 | 212.5 | 55 |
| 8 | 8 | 9 | 5.3434 | 0 | 20 |
| 9 | 9 | 10 | 2.1522 | 266.05 | 20 |
| 10 | 2 | 11 | 0.4052 | 85 | 70 |
| 11 | 11 | 12 | 1.1524 | 340 | 55 |
| 12 | 12 | 13 | 0.5261 | 297.5 | 40 |
| 13 | 13 | 14 | 1.2358 | 19125 | 25 |
| 14 | 14 | 15 | 2.8835 | 106.25 | 20 |
| 15 | 15 | 16 | 5.3434 | 255 | 20 |
| 16 | 3 | 17 | 1.2942 | 255 | 55 |
| 17 | 17 | 18 | 0.7027 | 127.5 | 40 |
| 18 | 18 | 19 | 3.3234 | 297.5 | 40 |
| 19 | 19 | 20 | 1.5172 | 340 | 20 |
| 20 | 20 | 21 | 0.7127 | 85 | 20 |
| 21 | 4 | 22 | 8.2528 | 106.25 | 20 |
| 22 | 5 | 23 | 9.1961 | 55.25 | 20 |
| 23 | 6 | 24 | 0.7463 | 69.7 | 20 |
| 24 | 8 | 25 | 2.0112 | 255 | 20 |
| 25 | 8 | 26 | 3.3234 | 63.75 | 20 |
| 26 | 26 | 27 | 0.5261 | 170 | 20 |
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| 0.1302 | USD/kWh | 0.1644 | kg/kWh | ||
| 0.2913 | USD/kWh | 0.2671 | kg/kWh | ||
| 0.0019 | USD/kWh | ±10 | % |
| Method | Optimization Parameter | Value |
|---|---|---|
| ALO | Number of particles | 95 |
| Maximum iterations | 972 | |
| Non-improving iterations | 292 | |
| CSA | Number of particles | 177 |
| Maximum iterations | 471 | |
| Non-improving iterations | 295 | |
| Awareness probability () | 0.65826 | |
| Flight length () | 3.25058 | |
| PSO | Number of particles | 159 |
| Maximum iterations | 492 | |
| Non-improving iterations | 229 | |
| Maximum inertia () | 0.99456 | |
| Minimum inertia () | 0.32458 | |
| Cognitive component () | 0.061368 | |
| Social component () | 1.5456 | |
| MVO | Number of particles | 41 |
| Maximum iterations | 1326 | |
| Non-improving iterations | 188 | |
| Wep-min | 0.68125 | |
| Wep-max | 0.51768 | |
| P parameter | 3 | |
| SSA | Number of particles | 141 |
| Maximum iterations | 1577 | |
| Non-improving iterations | 547 | |
| VSA | Number of particles | 163 |
| Maximum iterations | 762 | |
| Non-improving iterations | 762 | |
| x parameter | 0.08 |
| Standalone Test Feeder | |||
|---|---|---|---|
| Objective function | (kWh) | (USD) | |
| Whitout PV-DGs | 489.3042 | 18,485.0507 | 16,951.2974 |
| Average solution | |||
| Objective function/ Method | (kWh) | (USD) | |
| ALO | 359.6843 | 11,962.6688 | 10,930.9273 |
| CSA | 369.1944 | 13,663.8328 | 12,534.4183 |
| PSO | 362.0496 | 12,340.2908 | 11,267.5734 |
| MVO | 360.0291 | 12,231.1691 | 11,131.5617 |
| SSA | 359.8537 | 12,074.5543 | 11,039.5781 |
| VSA | 359.8317 | 12,055.3410 | 11,016.6177 |
| Percent average reduction (%) | |||
| Objective function/ Method | |||
| ALO | 26.4907 | 35.2846 | 35.5157 |
| CSA | 24.5471 | 26.0817 | 26.0563 |
| PSO | 26.0073 | 33.2418 | 33.5297 |
| MVO | 26.4202 | 33.8321 | 34.3321 |
| SSA | 26.4560 | 34.6794 | 34.8747 |
| VSA | 26.4605 | 34.7833 | 35.0102 |
| Standard deviation (%) | |||
| Objective function/ Method | |||
| ALO | 0.0010 | 0.0059 | 0.0032 |
| CSA | 1.7548 | 2.3077 | 2.1093 |
| PSO | 0.4095 | 1.7711 | 1.6491 |
| MVO | 0.2356 | 2.4301 | 2.0192 |
| SSA | 0.0230 | 0.4363 | 0.4329 |
| VSA | 0.0212 | 0.3042 | 0.2886 |
| Average processing time (s) | |||
| Objective function/ Method | |||
| ALO | 56.51 | 56.87 | 56.96 |
| CSA | 6.54 | 6.76 | 6.74 |
| PSO | 4.21 | 4.43 | 4.44 |
| MVO | 2.02 | 1.80 | 1.90 |
| SSA | 12.59 | 12.90 | 13.12 |
| VSA | 7.69 | 7.84 | 7.78 |
| Grid-Connected Test Feeder | |||
|---|---|---|---|
| Objective function | (kWh) | (USD) | |
| Whitout PV-DGs | 2186.2803 | 9776.3892 | 12345.1497 |
| Average solution | |||
| Objective function/ Method | (kWh) | (USD) | |
| ALO | 1225.0193 | 7138.8122 | 8967.2586 |
| CSA | 1270.1562 | 7407.9046 | 9328.7685 |
| PSO | 1268.5973 | 7392.0432 | 9282.4081 |
| MVO | 1231.2531 | 7298.7157 | 9187.9682 |
| SSA | 1225.3323 | 7297.9712 | 9166.6746 |
| VSA | 1225.2909 | 7249.3825 | 9108.9096 |
| Percent average reduction (%) | |||
| Objective function/ Method | |||
| ALO | 43.9679 | 26.9791 | 27.3621 |
| CSA | 41.9033 | 24.2266 | 24.4337 |
| PSO | 41.9746 | 24.3888 | 24.8093 |
| MVO | 43.6827 | 25.3434 | 25.5743 |
| SSA | 43.9536 | 25.3511 | 25.7468 |
| VSA | 43.9555 | 25.8481 | 26.2147 |
| Standard deviation (%) | |||
| Objective function/ Method | |||
| ALO | 0.0046 | 0.0319 | 0.0296 |
| CSA | 1.3806 | 1.8500 | 1.6987 |
| PSO | 2.4065 | 2.2579 | 2.0891 |
| MVO | 2.2694 | 1.2190 | 1.5868 |
| SSA | 0.0131 | 0.7089 | 0.6306 |
| VSA | 0.0108 | 0.5697 | 0.5676 |
| Average processing time (s) | |||
| Objective function/ Method | |||
| ALO | 60.67 | 61.11 | 59.65 |
| CSA | 36.37 | 36.45 | 36.87 |
| PSO | 5.96 | 6.47 | 6.60 |
| MVO | 2.45 | 2.47 | 2.48 |
| SSA | 20.85 | 21.47 | 21.29 |
| VSA | 9.93 | 10.37 | 10.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grisales-Noreña, L.F.; Rosales-Muñoz, A.A.; Montoya, O.D. An Effective Power Dispatch of Photovoltaic Generators in DC Networks via the Antlion Optimizer. Energies 2023, 16, 1350. https://doi.org/10.3390/en16031350
Grisales-Noreña LF, Rosales-Muñoz AA, Montoya OD. An Effective Power Dispatch of Photovoltaic Generators in DC Networks via the Antlion Optimizer. Energies. 2023; 16(3):1350. https://doi.org/10.3390/en16031350
Chicago/Turabian StyleGrisales-Noreña, Luis Fernando, Andrés Alfonso Rosales-Muñoz, and Oscar Danilo Montoya. 2023. "An Effective Power Dispatch of Photovoltaic Generators in DC Networks via the Antlion Optimizer" Energies 16, no. 3: 1350. https://doi.org/10.3390/en16031350
APA StyleGrisales-Noreña, L. F., Rosales-Muñoz, A. A., & Montoya, O. D. (2023). An Effective Power Dispatch of Photovoltaic Generators in DC Networks via the Antlion Optimizer. Energies, 16(3), 1350. https://doi.org/10.3390/en16031350








