Abstract
With the increasing penetration of converter-based power sources into the power system, the performance of the converter has become a key factor for enhancing grid reliability, especially during asymmetrical faults. To meet the low voltage ride-through requirements, the converter should feed the reactive power to the grid for voltage support while ensuring the maximum current limitation for the converter’s safety. For such injections, the grid codes are defined. This paper presents a novel and simplified reference current generation scheme to fulfill the requirement of recent grid codes, ensure the current limit of the converter and confirm better utilization of the converter’s current capacity during asymmetrical faults. Moreover, it also discusses the new sequence extraction scheme based on the delay sample method in the stationary reference frame and the control modifications for the negative sequence current injection. The proposed scheme was tested for different priority injection schemes. Its performance was also compared with other control schemes. Detailed simulation studies, in MATLAB/Simulink, were presented to confirm the performance of the proposed scheme under different faulty conditions. The results confirmed the supremacy of the proposed scheme over the available schemes for better utilization of the converter’s current capacity during asymmetrical faults. It also ensured the peak current limitation of the converter while fulfilling the recent grid code requirements. Moreover, the results showed that the new scheme has 10% more current capacity compared to the other schemes due to better incorporation of the angle between the positive and negative phase sequences of the voltage.
1. Introduction
Due to increased global warming, depleting conventional energy sources, and increased greenhouse gases, most countries are switching to renewable energy sources (mostly wind and solar). Under #mission2030, Austria plans to achieve a completely renewable electricity generation for national balance by 2030, and to achieve this milestone, 22–27 TWh of more energy generation is expected across all renewable technologies. Additionally, the Austrian government is also committed to installing one million solar systems (roof-mounted) by 2030 [1]. In [2], the global renewable energy trend is discussed; this shows a steady increase in renewable energy sources worldwide. Solar and wind power has increased to 10% of the total world’s electricity generation and this trend is increasing. However, there are some challenges concerning integrating renewable energy sources with conventional power systems.
The introduction is subdivided into three subsections: Motivation and Incitement, Literature Review, and Contribution and Paper Organization.
1.1. Motivation and Incitement
Most renewable energy resources are intermittent in nature and need a converter for their connection with the power system. Due to the increasing share of converter-based power sources, certain actions are required from the converters, particularly in faulty situations. Among these actions, the low voltage ride-through (LVRT) is gaining more attention in faulty situations. The LVRT was initially required to ensure the converter connection during voltage dips/sags [3]. It also avoids the loss of power generation. Most of the new converters have reactive power control capability, which makes them suitable for supporting the grid voltage in faulty conditions and providing fault current contribution for selective grid protection.
For modern power systems, the system operators demand voltage support from the converters to avoid the possibility of voltage collapse. The converter’s response in faulty conditions is defined by the grid codes. The conventional control schemes for the grid-side converter (GSC) do not address the grid’s requirements under unsymmetrical faults. Most of the grid faults are asymmetrical [4] but, due to the conventional control schemes, the GSC provides equal voltage support to all the phases irrespective of the fault type. This may cause overvoltage in the healthy phases and the voltage difference among the phases will also increase during unbalanced faults [5].
In order to provide more voltage support to the faulty phase(s), the negative sequence current is injected, which fulfills the requirements of recent grid codes under unbalanced faults. Moreover, in order to get better voltage support, the full current capacity of the converter is utilized [6]. The conventional control scheme needs to be modified to comply with the recent grid code requirements. During asymmetrical faults, a different amount of current is injected in each phase and needs to be flexibly controlled to ensure the peak current limitation of the converter. Figure 1 presents the positive and negative sequence current injection requirements mentioned in German grid codes (VDEAR-N 4100 and VDEAR-N 4110) [7]. The motivation of this work was to provide the different voltage support of each phase during unbalanced faults and to use the maximum converter’s current capacity for this purpose.
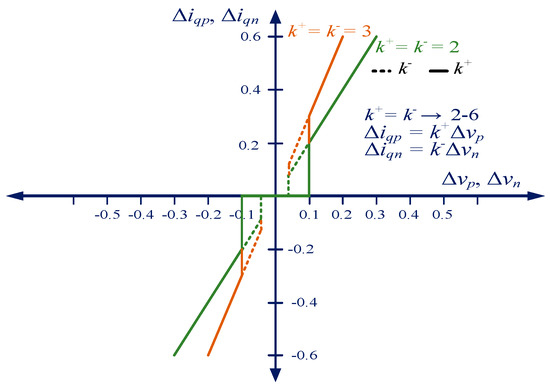
Figure 1.
Current injection requirements of recent grid codes (VDEAR−N 4110).
1.2. Literature Review
One approach for the implementation of the recent grid codes is to split the voltage phasor into positive and negative sequence components. The negative sequence current injection can be used for different purposes, e.g., minimizing the dc link voltage ripples, and improving the injected power quality and voltage support in asymmetrical faults, etc. [5]. Broadly, the negative sequence control is achieved by changing the power references for the negative sequence, which inherently induces different currents in each phase. This is normally known as power control. The other method is to identify the reference current components directly [6]. In this manuscript, the direct reference current calculation methodology was used.
The authors previously presented another simplified reference current generation scheme for the GSC in case of asymmetrical faults in [5]. This scheme, however, required a hard limit for the angle of the reference current’s positive sequence and did not ensure better utilization of the converter’s current capacity during asymmetrical faults. In [6], the authors presented a reference power generation strategy during unbalanced faults. It ensured the peak current limitation. However, the proposed scheme needed to calculate the reactive power in each phase, and then the minimum of these three was used as a reference reactive power in LVRT conditions. Moreover, the calculation for reference reactive power also required the true value of the angular difference between the positive and negative sequences, which is highly dependent on the sequence extraction method and the filters’ time constants. This angular difference is also hard to estimate correctly in the case of transients. In [7], the authors presented the effect of negative sequence current injection in the case of unbalanced faults. However, to ensure the safe operation of the converter, the angle between voltage sequence phasors was used to calculate the maximum current in each phase.
In [8], the authors proposed a current limiting scheme for the offshore wind power plant. The proposed strategy ensured the maximum current limitation during unbalanced faults. However, for maximum current limitation, this scheme considered the positive and negative sequence current phasors to be in-phase, which did not ensure the maximum utilization of the converter’s current capacity. Moreover, it injected the maximum real power during different faults and did not comply with recent grid codes. In [9], the reference current generation scheme was discussed for asymmetrical faults. This scheme calculated the reference real and reactive power for the LVRT conditions. However, this scheme needed a separate phase-locked loop (PLL) for the positive and negative sequences; it also needed the angle difference between the voltage sequence phasors.
In [10], the authors presented the impact of negative sequence current injection over the voltage unbalance in the case of a microgrid, but the maximum current limitation strategy was not discussed. In [11], the authors discussed the control of the grid following the converter in the case of unbalanced conditions. It did not discuss the maximum current limit of the converter. In [12], the authors presented a control scheme to address the LVRT in unbalanced conditions. However, this scheme considered the angle difference between positive and negative voltage sequences, which is highly dependent on the sequence extraction scheme.
In [13], a negative sequence current injection scheme was presented with different values for the proportional constant for the negative sequence (k−). However, this scheme also needed angle information to confirm the safe operation of the converter and it did not confirm better utilization of the converter’s current capacity. In [14], the authors proposed a control scheme for the static synchronous compensator (STATCOM) under unbalanced conditions. This scheme also involved the true angle difference between the voltage sequence phasors. It computed the current for each phase and identified that the maximum of these should be less than or equal to the current limit of the converter.
The publications cited in this section confirm that either the true angle difference between the positive and negative voltage sequences is required to completely utilize the current limit for the converter, or the numeric addition of positive and negative sequence current phasors needs to be kept lower than the maximum allowed current limit of the converter. The first approach depends on the sequence extraction scheme and the filters’ time constant, whereas the second scheme is unable to confirm the maximum utilization of the converter’s current capacity in unbalanced faults.
1.3. Contribution and Paper Organization
This manuscript aimed to develop a new current injection scheme for GSC during unsymmetrical faults. The proposed scheme incorporated the requirements of the recent grid codes for faulty conditions. It ensured the peak current limitation of the converter, and it did not require angle information about the positive and negative sequence voltage phasors. The proposed scheme also ensured the better utilization of the converter’s current capacity during asymmetrical faults. It used one inner current controller for both positive and negative sequence current injection. The major contributions of this manuscript are:
- Simplified and accurate current limiting scheme for unbalanced faults, which fulfills the requirements of recent grid codes while ensuring the maximum current limit of the converter.
- Ensuring better utilization of the converter’s capacity during unbalanced faults.
- A robust control scheme for the negative sequence current injection without a dedicated PLL.
- Sequence extraction scheme in αβ-domain based on the delay sampling method.
- Comparison of the priority injection schemes for different types of faults.
The phase angle between positive and negative sequence voltage phasors is dependent on the sequence extraction scheme and in different scenarios, it may not be computed accurately. Thus, the proposed scheme did not use it to ensure the maximum current limit of the converter.
The rest of the paper is organized as follows: The layout of the test network is discussed in Section 2. In Section 3, the conventional and proposed control schemes for GSC are presented. The priority selection schemes, along with the maximum current limit strategy, are also discussed in Section 3. Section 4 discusses the results for different priority schemes under different fault scenarios. Finally, the paper is concluded in Section 5.
2. Layout of Test Network
The general layout of the test network is given in Figure 2.
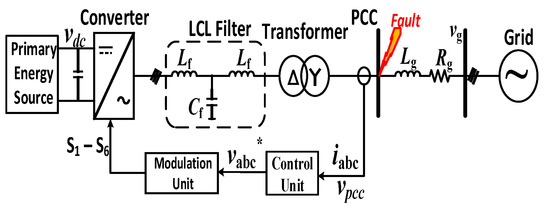
Figure 2.
Schematic diagram of the network under consideration.
A primary energy source was connected to the grid with the help of a 2-level three-phase converter, an LCL filter, and a step-up Y-∆ transformer. The measurements were taken at the point of common coupling (PCC). An unbalanced fault was applied at PCC. The control unit required the current and voltage information at PCC, and it represented both the proposed control scheme and the conventional one. The output of the control unit was the reference three-phase voltage which was passed to the modulation unit. By using the pulse width modulation (PWM) technique, the modulation unit generated the six pulses for the converter’s switches. The control scheme compensated for the voltage drop across the filter and the transformer. The parameters, related to Figure 2, are given in Table 1. For per unit (p.u.) calculations, 100 kVA and 400 V were used as base power and base voltage line to line (L-L) respectively.

Table 1.
Network Parameters.
3. Control Schemes
The conventional control scheme provides equal voltage support to each phase irrespective of the type of fault. The proposed control scheme, along with different priority injection schemes, provides more voltage support to the faulty phase(s) compared to the healthy phase(s). Both the conventional and proposed control schemes are discussed in this section.
3.1. Conventional Control Scheme
The conventional control scheme is developed in the synchronous rotating reference (dq) frame. The layout of the conventional control scheme is given in Figure 3. The inputs for the control scheme are the measured three-phase voltages and currents at the PCC. The reference real and reactive powers are also the input to the control scheme.
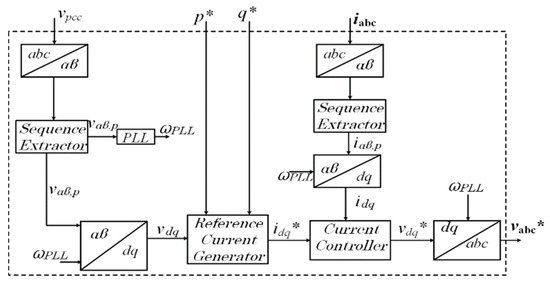
Figure 3.
Conventional control scheme.
In the conventional control scheme, only the positive sequence injection is performed; the expression given in this section is applied to the positive sequence component. The three-phase measured voltages and currents are transformed into the synchronous rotating reference frame. The mathematical expressions for these transformations are discussed in [15]. The mathematical expressions, considering only the fundamental frequency, are given in (1):
where the subscripts abc are used for each phase, αβ is used for the stationary reference frame components, and dq is used for the rotating reference frame components. ω and θ are the angular frequency and initial phase angle of the voltage phasor, respectively. Such expressions can also be derived for the current. The three-phase active and reactive power expressions in the dq-frame are given in (2):
where p and q are the three-phase real and reactive powers, respectively. Considering the ideal performance of the synchronous reference frame PLL (SRF-PLL), the q-component of voltage (vq) is zero. Thus:
for the generation of reference active and reactive current components in normal conditions, the expressions in (3) are used. The reference currents in normal conditions are given in (4):
where the superscript * is used to define the reference quantities. Moreover, the real power injection has priority in normal conditions. In faulty conditions, the grid operators demand voltage support from the converters. Thus, the reactive current injection is given priority and its value is dependent on the voltage dip. The expressions for the generation of reference currents in faulty conditions are given in (5) where the proportional constant for positive sequence (k+) ranges from 2 to 6. The range of the proportional constant is defined in German grid code (VDE-AR-N 4110). A summary of this code can be found in [16]:
where the subscript prefault stands for “steady state value before fault” and ∆ is used to define the difference between nominal value and actual value for a particular quantity. The current limits in normal and faulty situations are given in (6) and (7), respectively. The limit for the id is less than imaxNC (maximum allowed current in normal conditions). This is to have some margin for the reactive power support in normal conditions:
where the superscript lim and max stand for the limit of the particular quantity and maximum converter’s current respectively. In this manuscript, the parameter with superscription of ** was the actual value of a particular component after applying its limit to its reference value, e.g.:
The current controller mentioned in Figure 3 was the PI controller. The calculations for the control gains of the inner PI current controller and for SRF-PLL are discussed in [17]. This scheme is defined as “balanced current injection” (BCI) scheme throughout this manuscript.
3.2. Proposed Control Scheme
The BCI was derived for the balanced conditions. However, most of the faults are unbalanced faults and the grid operators require different voltage support for each phase. This can be achieved by controlling the positive and negative sequence injection. The purpose is to inject the reactive current in positive and negative sequences in faulty conditions while the maximum current limit of the converter is ensured. Different priority injection schemes are possible. The layout of the proposed control scheme is given in Figure 4.
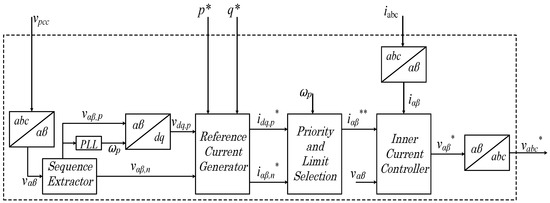
Figure 4.
Proposed control scheme.
To fulfill the recent grid codes, only the positive and negative sequence extraction is important. Thus, the zero sequence is not discussed in this section. The voltage and current phasors can be transformed into positive, negative, and zero sequence components [18]. The mathematical expressions are given below [19].
In this manuscript, the subscript p and the superscript “+” were used for the positive sequence variables. Similarly, the subscript n and the superscript “−“ were used for the negative sequence. From (9), it is clear that the angular frequency of the positive and negative sequences is the same, but the direction of rotation is opposite to each other. Figure 5 represents the phasor addition of the positive and negative sequence components [20].
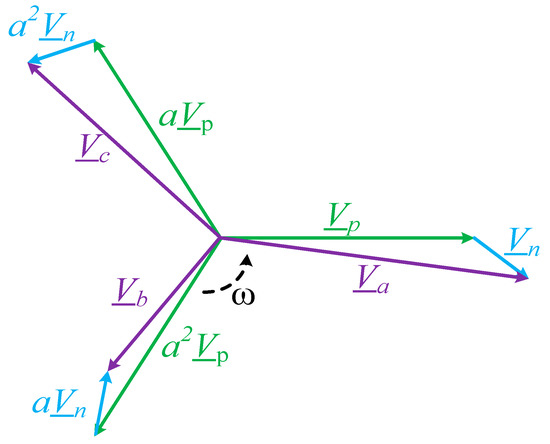
Figure 5.
Phasor diagram of the resultant voltage from its sequence components.
The Clark transformation was applied to (9) and the expressions are given in (10).
3.2.1. Sequence Extraction Scheme
For real-time sequence extraction, there are different techniques available in the literature [21,22,23,24,25]. The most common scheme is to take the orthogonal signals of the αβ components of the resultant voltage. The expressions for the positive and negative sequences, in terms of the resultant signal and its orthogonal signals, are given below. The expression given in (11) can be easily derived by shifting the original αβ components by 90°:
where the signal with superscript T represents the orthogonal of that signal. The important task is to acquire the orthogonal of a signal in real time. For this purpose, the first-order generalized integrator (FOGI), or the second-order generalized integrator (SOGI) can be used. The layout of the FOGI is given in Figure 6.
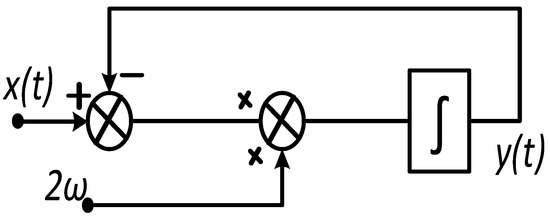
Figure 6.
Control layout of FOGI.
The transfer function (Laplace) and the output (in time domain) for the FOGI are given in (12).
By using FOGI, the orthogonal of a signal can be achieved with just one integrator. It is important to mention here that due to the distortion in the input signals, a low-pass filter was used to remove the high-frequency distortions. The filter also affected the magnitude of the signal, and it also changed the phase angle, which can cause inaccuracy while calculating the limits for different current components. The other method is to use SOGI. The layout for the SOGI is given in Figure 7.
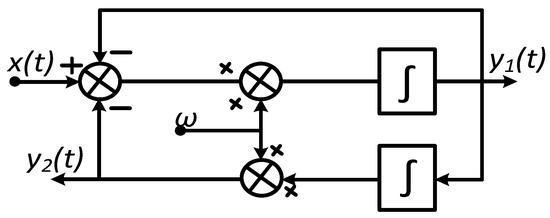
Figure 7.
Control layout of SOGI.
The SOGI uses two integrators, and it gives two outputs, one is the same as the input and the other is orthogonal to the input. The expressions for SOGI are given in (13).
The advantage of SOGI is that it also acts as active filter. It is also important to mention here that the FOGI and SOGI methods work well if the signal frequency is exactly equal to the reference angular frequency “ω” (used in the layouts of FOGI and SOGI).
Another method is the delay sampling method. This method is discussed in [22] with the synchronous rotating frame of reference for the positive sequence. The newly developed extraction method is based on the delay sampling method in the stationary frame of reference. The unit sample delay is introduced in (10) and the new expressions are given in (14).
After doing some mathematical steps, the final expressions are given in (15).
In order to introduce the sample delays in the discrete domain, the signal was delayed by double the sampling time and the Z−2Ts operator was introduced. The output of the delayed operator was used as the delayed signal in (15). The layout diagram is given in Figure 8 and the expressions for the discrete domain are given in (16).
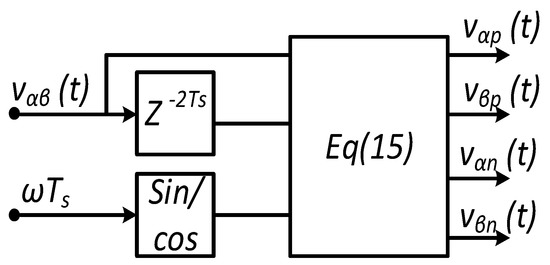
Figure 8.
Sequence extraction method based on delay sample period in αβ domain.
As is clear from the above expressions, in this scheme, there is no need to acquire the orthogonal of a signal in real time. However, the active filter is required to get the fundamental component of the signal. The active filter is normally of higher order and can be replaced with the first-order low pass filter if the unit step delay (Ts) is at least five times the controller step time; but, in this case, more harmonic injections are expected.
3.2.2. Reference Current Generation Scheme
The proposed scheme is designed in such a way that the positive sequence reference current calculation is the same as the BCI scheme for the normal conditions. Thus, for the positive sequence current generation (active and reactive current components), the expressions given in (4) are valid. However, the priority and current limits are different and are discussed later in this section. The reference currents in faulty conditions are given below.
For the negative sequence current injection, the αβ-frame of reference is used instead of the dq-frame of reference. The major drawback with αβ-frame design is that the constant limit clips the signal. Thus, applying a constant limit in αβ-domain can cause harmonic injection. In order to address this problem, the expressions of the αβ-components were derived with respect to a dc amplitude. For unbalanced faults, the negative sequence current injection should be proportional to the change in voltage magnitude in the negative sequence. Moreover, the current injection needs to be the reactive current, and its value should be equal to k-∆vn. For this purpose, the expression given below in (18) was derived.
If the magnitude of iαβ,n* is calculated from (18), it comes to be iqn* = k−∆vn, which is according to the grid codes. To verify that the injected current in the negative sequence corresponds to the reactive power, the following expressions were derived.
In (19), the first expression confirms that the real power component in the negative sequence is zero. Hence, the transfer of reactive power is ensured. Moreover, the second expression in the same equation confirms that the phase angle between voltage and current of the negative sequence is 90°, which confirms the voltage support in the negative sequence. Hence, by using (18), the negative sequence reactive current injection is confirmed without a dedicated PLL for the negative sequence. Moreover, the constant current limit is also applicable with this approach, which changes the amplitude of the αβ components accordingly.
3.2.3. Priority and Limit Selection
For unbalanced faults, the resultant current is the phasor summation of the positive and negative sequence currents. Unlike the circular trajectory of the positive and negative sequence current phasors, the resultant current’s trajectory is elliptical. The authors of this paper have discussed this in detail in another publication [5]. Figure 9 illustrates the trajectory of the resultant current and its sequence components.
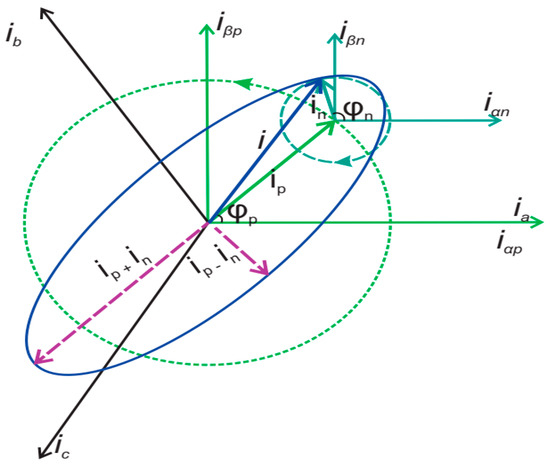
Figure 9.
Phasor diagram for the resultant current and its sequence components [5].
The reason for the elliptical trajectory is the opposite rotation of the positive and negative sequence components. As the converter is designed in the grid following methodology, the positive sequence current phasor is rotated with the angle of the positive sequence voltage and the same is true for the negative sequence. The maximum amplitude of the resultant current is achieved when the phase angle of the positive and negative phase sequences is the same (numeric addition of both the positive and negative sequences). Similarly, the minimum of the resultant current is equal to the numeric subtraction of the positive and negative sequence phasors’ magnitude.
In this section, a new current limiting scheme is introduced, which does not need the information of the true angle between the positive and negative sequence voltage phasors. At the same time, the proposed scheme also ensures better utilization of the converter’s current capacity compared to the scheme presented in [5]. The mathematical expression for the resultant current is given in (20):
where φ is the initial phase angle of the corresponding current phasor. The expressions for the idp, iqp, idn and iqn are the horizontal and vertical projections of the positive and negative current phasors in the synchronous rotating frame of reference.
If all three phasors are rotated with the e−j(ωt+θp) and applying the definition of (21) to (20), then the new expression is as given in (22).
After performing the mathematical steps in (22), the mathematical formula for the magnitude of the resultant current is given in (23). It is important to mention here that the magnitude of the resultant current will not be changed due to the above mathematical steps.
Equation (23) can be further simplified because, in the negative sequence, only the reactive current injection is required. Thus, putting idn = 0 in (23) leads to a simpler expression that is given in (24).
By examining the expression in (24), it is clear that it is dependent on the time and initial angle of the positive and negative phase sequences, which is in accordance with previous literature. It is important to mention here that in balanced situations, (24) converges to the expressions given in (6) and (7). The further simplification of (24) is discussed within the priority scheme, where the limits for the different components of the current are calculated.
Normally, in faulty situations, the reactive current injection is given priority over the real component of the current. Two priority schemes are discussed here. In the first scheme, the reactive current injection in the negative sequence has the highest priority, after this, the reactive current injection in the positive sequence is given priority, and lastly, the limit for the active current component in the positive sequence is computed. In this manuscript, this scheme is termed as the “NQP” priority scheme. In the other scheme, the positive sequence reactive current’s limit is computed first, then the negative sequence reactive current is given priority, and lastly, the limit for the active component of the positive sequence current is computed. This scheme is termed as the “QNP” priority scheme.
As discussed earlier for the NQP, first the full current capacity of the converter is used for the negative sequence reactive current injection. If the actual current computed from the grid codes is less than the current capacity of the converter, then the remaining capacity is used to decide the current limit for the reactive current injection of the positive sequence. For this purpose, the expression given in (24) is used but it can be simplified. While deciding the limit for the iqp, idp can be put to zero and the cos term can be defined as equal to one (maximum limit).
Similarly, while computing the current limit for the idp, the term involving idp is taken as maximum (sin(δ) to 1). The term iqpcos(δ) is a critical one, which decides the better use of the converter’s current capacity. If the numeric addition of positive and negative sequence current phasors is limited to the maximum current capacity, then cos(δ) should be taken as one; however, this scenario does not give the better utilization of the converter’s current capacity. On the other hand, if the cos(δ) is taken as zero then the maximum utilization of the converter’s current capacity is ensured but, in this case, the maximum current in the faulty phase may go up to 5% higher than the maximum converter’s current limit. In order to get better performance, this value is selected as ¼ (cos(δ) to 1/4) in these calculations. These values are selected to simplify the expression for the idp and also to get the accurate current limit. Keeping in view the above discussion, the current limits for NQP are given in (25) and for the QNP are given in (26).
By carefully examining the expression given in (25) and (26), it is clear that the iqn is considered to be in phase with the iqp while computing the limits for iqp and, for idp the major projection of iqn is projected on the idp. In this way, simpler expressions can be computed for the current limits in unbalanced conditions. This scheme works well irrespective of the type of fault, the severity of the fault, and the reference real and reactive powers. Moreover, it is not affected by the low-pass filters and the performance limitations of the PLL.
It is also important to mention here that only one inner current controller can be used both for the positive and negative sequence current injection. For this scheme, the quasi-proportional resonant controller (QPR) was used as the inner current controller. The calculation for the control gains of QPR is discussed in [26].
4. Results and Discussions
The response of the proposed scheme with different priority schemes was compared with the response of the conventional scheme and with the response of the in-phase sequence phasor scheme discussed in detail in [5]. In this paper, the scheme presented in [5] is denoted by “PNSIa”.
A numerical example, illustrating the performance of this scheme with different priority injection schemes is given below. This also includes the calculations for the BCI and PNSIa control schemes.
4.1. Numerical Example
Assuming that an asymmetrical fault occurs on the network shown in Figure 2, all the quantities stated below are in per unit (p.u).
For vp = 0.6 and vn = 0.29, the reference real power (p*) is 0.95 and q* = 0, k± = 2. The pre-fault reactive current will be zero in this case. The maximum current limit (imax) is 1.2 p.u. To calculate the reference reactive current, use the expression given in (17).
idp* = 1.58; iqp* = −0.8; iqn* = −0.58
4.1.1. BCI Scheme
To calculate the limit and actual reference value of the particular quantities, the expressions given in (7) and (8) can be used when iqnlim is zero.
iqnlim = 0; iqn** = 0; iqplim = imax = ±1.2; iqp** = −0.8;
idplim = ±0.895; idp** = 0.895;
ip = 1.2; in = 0; i = ip + in = 1.2
4.1.2. QNP Priority with Proposed Scheme
To calculate the limit and actual reference value of the particular quantities, the expressions given in (8) and (26) are used.
iqplim = imax = ±1.2; iqp** = −0.8; iqnlim = ±0.4; iqn** = −0.4;
idplim = ±0.4; idp** = 0.4;
ip = 0.8944; in = 0.4; i = ip + in = 1.295
4.1.3. NQP Priority with Proposed Scheme
To calculate the limit and actual reference value of the particular quantities, the expressions given in (8) and (25) are used.
iqnlim = ±1.2; iqn** = −0.58; iqplim = ±0.62; iqp** = −0.62;
idplim = ±0.36; idp** = 0.36;
ip = 0.715; in = 0.58; i = ip + in = 1.295
4.1.4. NQP Priority with PNSIa Scheme
To calculate the limit and actual reference value of the particular quantities, use the expressions given in [5].
iqnlim = ±1.2; iqn** = −0.58; iqplim = ±0.62; iqp** = −0.62;
idplim = 0.0; idp** = 0.0;
ip = 0.62; in = 0.58; i = ip + in = 1.2
This example confirms better utilization of the current capacity of the converter with the proposed scheme. Moreover, it also confirms that the NQP priority injection is better when compared to the QNP, as it prioritizes the negative sequence current injection.
4.2. Simulation Results
These control schemes were tested consecutively on the network shown in Figure 2. Different types of faults were applied at PCC and the response of each control scheme was observed. The fault duration for each fault was 0.2 s. The first fault was applied at 0.05 s, and it was repeated every 0.4 s. In the 0.2 s interval between the faults, the system settled and reached a steady state pre-fault condition. For the first fault occurrence, the BCI control was activated. In the next fault occurrence, the control shifted to the proposed scheme with the QNP priority injection scheme. Similarly, for the third fault duration, the NQP priority injection control was activated and for the fourth fault occurrence, the PNSIa scheme was activated. It is also important to mention that the PNSIa also had the NQP priority scheme in this study. Moreover, for the simulation results, the reference real power was 0.95 p.u and the reference reactive power was zero.
With such a fault occurrence scheme, the transient response of each scheme was also tested. Moreover, the active current injection in the positive sequence was rate limited and it did not allow a sudden increase in the real current component of the positive sequence. In faulty conditions, the maximum current limit is 1.2 p.u and the k± was chosen as 2 for these simulations.
4.2.1. Single Line to Ground Fault (SLG)
The response of the single line to ground fault (b-G) is given in Figure 10. The subplot Figure 10a shows the three-phase voltages at PCC. This graph confirms that the maximum healthy phase(s) voltage was more in the BCI control (1.085 p.u) compared to the rest of the control schemes. The three-phase converter’s current injection is shown in subplot Figure 10b. This graph shows that the BCI scheme injected the same amount of current in each phase regardless of the type of fault, but all the other schemes were able to provide more voltage support to the faulty phase(s), which is the requirement of the recent grid codes.
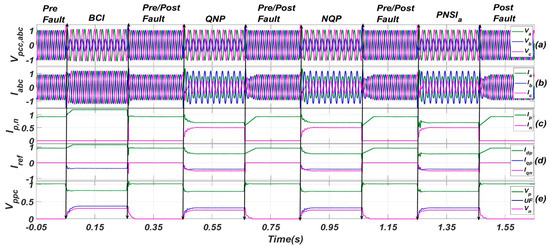
Figure 10.
Performance comparison of different schemes for SLG Fault. (a) instantaneous three phase voltages (phase to neutral) at PCC, (b) instantaneous three phase converter’s currents, (c) magnitude of positive and negative sequence current phasor, (d) reference current components for positive and negative sequences, (e) magnitude of positive and negative sequence voltage phasor along with unbalanced factor.
Moreover, as far as the maximum current in any phase is concerned, all the control schemes gave better results for the SLG faults. The positive and negative sequence current phasors are presented in subplot Figure 10c. This graph also confirms that there was no negative sequence current injection in the BCI control but for all the other schemes, its value was dependent upon the recent grid codes requirement and the capacity of the converter. In this case, the magnitude of the positive and negative current phasors was almost identical. The negative sequence current injection was purely the reactive one, but the positive sequence current injection was the vector sum of its active and reactive components. This can be confirmed from the subplot Figure 10d, which shows the magnitude of each component of the current.
The subplot Figure 10e shows the magnitude of the positive and negative sequence voltages, and the unbalanced factor (UF), which is defined as the ratio of magnitudes of the negative sequence voltage phasor to the positive sequence voltage phasor (vn/vp). Less UF means more uniform voltage among the phases. According to subplot Figure 10e, the proposed scheme results in less UF factor compared to the BCI scheme. It is also important to mention here that in case of high impedance faults, the different priority schemes give the same result. This is due to the lower reactive current requirement arising from lower ∆vp and ∆vn. However, with the increasing severity of the fault, the priority schemes have different responses, which will be discussed for the line-to-line fault and double line-to-ground faults.
4.2.2. Line-to-Line Fault (LL)
A line-to-line fault was applied between phase “a” and “b”. The response of the different control schemes is given in Figure 11. From subplot Figure 11a, it is clear that the healthy phase had more overvoltage in the BCI, followed by the QNP, NQP, and PNSIa schemes, respectively. The maximum amplitudes are given in Table 2. Moreover, subplot Figure 11b shows that almost every control scheme was able to confirm the safe operation of the converter. As far as the comparison for the PNSIa scheme is concerned, it is clear from the subplot Figure 11b, that the PNSIa scheme injected more current in the healthy phase and less current in one of the faulty phases compared to the NQP priority scheme with the proposed control. Similarly, from subplot Figure 11c, it is clear that the PNSIa scheme injected a lower total current compared to the proposed scheme. This is because the PNSIa scheme confirmed the converter’s safe operation by limiting the maximum point of the elliptical trajectory to the maximum current and considering the numeric addition of sequence phasors; however, the proposed scheme did not consider both the phasors exactly in phase. This is the reason why the numeric addition of the positive and negative sequence current phasors was more than the maximum current limit of the converter for the QNP and NQP, although the maximum phase current was still within the converter’s current limit. This means that the PNSIa scheme did not use the full capacity of the converter, but the newly proposed scheme was able to use it efficiently.
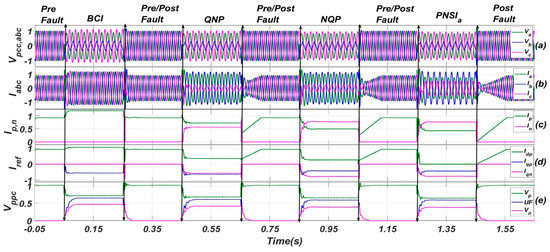
Figure 11.
Performance comparison of different schemes for LL Fault. (a) instantaneous three phase voltages (phase to neutral) at PCC, (b) instantaneous three phase converter’s currents, (c) magnitude of positive and negative sequence current phasor, (d) reference current components for positive and negative sequences, (e) magnitude of positive and negative sequence voltage phasor along with unbalanced factor.

Table 2.
Comparison of Control Schemes.
As far as the comparison of the QNP and NQP priority schemes is concerned, subplot Figure 11d shows that the share of the active current increased in the QNP compared to the NQP. Moreover, from subplot Figure 11e, it is clear that the UF was almost equal for the NQP and PNSIa schemes, followed by the QNP and BCI schemes, respectively. Hence, based on the UF and better utilization of the converter, it can be concluded that the proposed control scheme with NQP priority injection is more suitable compared to the rest of the schemes.
4.2.3. Double Line to Ground Fault (DLG)
To apply DLG fault, phase “b” and “c” are grounded. The control schemes were also compared for this type of fault. Figure 12 shows the response of these control schemes in the case of a DLG fault. As far as the overvoltage in the healthy phase is concerned, the response of the control schemes was similar to their response in the case of an LL fault, i.e., NQP and PNSIa schemes gave better results, followed by the QNP and BCI schemes, respectively.
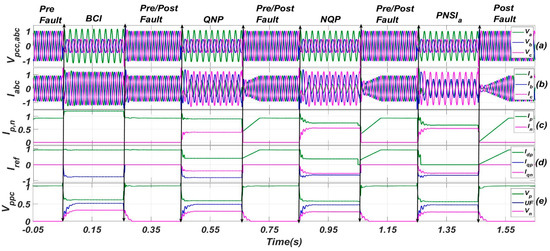
Figure 12.
Performance comparison of different schemes for DLG Fault. (a) instantaneous three phase voltages (phase to neutral) at PCC, (b) instantaneous three phase converter’s currents, (c) magnitude of positive and negative sequence current phasor, (d) reference current components for positive and negative sequences, (e) magnitude of positive and negative sequence voltage phasor along with unbalanced factor.
Subplot Figure 12b shows that the NQP scheme not only confirmed the converter’s safe operation, but it also injected more current in the faulty phases and less current in the healthy phase compared to any other scheme fulfilling the recent grid codes. From subplot Figure 12c, it is clear that, even though the QNP scheme worked at the same current capacity and incorporated the angular difference between the positive and negative sequence voltage phasors, the UF was less for the NQP schemes compared to the QNP scheme. Moreover, subplot Figure 12e shows that the NQP and PNSIa schemes had less UF compared to the QNP and BCI. Overall, the performance of the control schemes for the DLG fault was similar to their performance for the LL fault.
Table 2 summarizes the comparison of the proposed scheme with different priority injections, the BCI scheme, and the PNSIa scheme. The key parameters were the healthy phase overvoltage, voltage unbalance factor, maximum current injection in the healthy and faulty phase(s), the converter’s current limitation, and the maximum utilization of the converter. Different color bars are used in order to define the performance of the schemes for a particular parameter. Green is for the best performance followed by light green, orange, and red, respectively.
From Table 2, it is clear that the performance of all the schemes, except the BCI scheme, was almost identical for the SLG fault. The reason is that due to less severity of the fault, there was less deviation of the positive and negative sequence voltages from its nominal values, and the calculated reference current was less than its limit for all these three schemes.
For the LL fault, the response of the proposed scheme with NQP priority was better when compared to the responses of the PNSIa and BCI schemes. The proposed scheme results in better utilization of the converter’s current capacity, which is clear from the last row of the LL fault section in Table 2. The numeric sum of the positive and negative sequence currents was more than the maximum allowed limit for the current, but no phase current was more than its maximum value, which shows better incorporation of the angular phasor difference between the positive and negative sequence voltage phasors by the proposed schemes. As far as the comparison of the different priority injection schemes is concerned, the NQP provided less UF when compared to the QNP. The same was also true for the DLG fault. The last three columns in Table 2 present the percentage reduction in the parameters, obtained by using a particular control scheme. This reduction was calculated with respect to the BCI scheme (conventional control). The important parameters were the reduction in UF, healthy phase overvoltage, and the reduction in current for the healthy phase. The better performance of the NQP was evident for all these parameters.
As the proposed scheme and the PNSIa fulfill the recent grid codes, the difference between the two schemes is in the current limitation calculation. From these results, it can be confirmed that the PNSIa limits the current based on the numeric addition of the positive and negative sequence current phasors, due to which, it is unable to use the converter’s current capacity effectively in case of asymmetrical faults; however, the proposed scheme is able to use the converter’s current capacity effectively. Hence, better utilization of the converter is ensured by the proposed current limiting scheme. Moreover, unlike the PNSIa scheme, the newly proposed scheme does not need to consider the angle of the positive sequence current phasor. From a grid perspective, the NQP priority scheme is better than the QNP priority scheme. Like the PNSIa scheme, the results presented in [6,7,8,9] show that the numeric sum of the positive and negative sequence current phasors is equal to the maximum current capacity of the converter, which means that the presented schemes are unable to use the maximum current capacity of the converter effectively. The proposed scheme provides better utilization of the converter’s current capacity, and it also does not need the true angular difference between the positive and negative sequences.
5. Conclusions
In this paper, a new control scheme is presented that ensures the safe operation of the converter in unbalanced faults while fulfilling the requirements of recent grid codes. It also ensures better utilization of the converter’s current capacity during asymmetrical faults. This scheme does not need the angle difference between voltage sequence phasors, so its performance is not affected by the error caused by sequence extraction and PLL performance in such conditions. It also does not need to compute the reference current for each phase. Moreover, the new scheme also simplifies the negative sequence reactive current injection control and does not need a separate PLL for it. Additionally, a sequence extraction scheme based on the delay sample period was developed in the αβ-domain. The simulation results confirm the better utilization of the converter with the proposed control scheme. Its performance was also compared with the conventional control scheme, the PNSIa scheme, and other schemes presented in the literature. The results show its advantage over these schemes. Moreover, the two priority schemes were also compared; it was found that the NQP priority scheme gives better performance compared to the QNP scheme under different faulty conditions.
As the proposed scheme allows better utilization of the converter’s current capacity compared to the already available schemes in the literature, it provides better voltage support in LVRT conditions; hence, it improves the voltage stability of the power system having high penetration of the converter-based power sources. Even though the proposed scheme provides better utilization of the converter’s current capacity during unbalanced faults without using the true angle difference between the positive and negative voltage phase sequences, this utilization can be further improved by achieving the true angle difference between the two sequences. This work can be extended in the future to incorporate the zero sequence. The impact of different values of the proportional constant for positive and negative sequence injection (k-factor) can also be investigated with this scheme. The optimal negative sequence injection can also be performed to achieve a better unbalanced factor.
Author Contributions
Conceptualization, M.A. and H.R.; Methodology, M.A.; Software, M.A.; Validation, M.A., H.R., and R.S.; Formal Analysis, M.A.; Investigation, M.A.; Resources, R.S.; Data Curation, M.A.; Writing—Original Draft Preparation, M.A.; Writing—Review and Editing, M.A. and H.R.; Visualization, M.A.; Supervision, H.R.; Project Administration, H.R. and R.S.; Funding Acquisition, H.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “Higher Education Commission, Pakistan” and “Agency for Education, and Internationalization (OeAD), Austria” under the program “OSS-III/HEC Overseas Scholarships for PhD in Selected Fields, Phase III, Batch 1”.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Supported by TU Graz Open Access Publishing Fund.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbol | Description |
| k+- | Proportional constant for positive and negative sequence injection |
| ∆vp | Change in magnitude of the positive sequence voltage phasor |
| ∆vn | Change in magnitude of the negative sequence voltage phasor |
| ∆iqp | Change in reactive current injection for positive sequence |
| ∆iqn | Change in reactive current injection for negative sequence |
| vg | Grid’s voltage |
| Rg | Grid’s resistance |
| Lg | Grid’s inductance |
| Lf | Filter’s inductance |
| Cf | Filter’s capacitance |
| vdc | DC link voltage |
| vabc* | Converter’s reference voltage |
| vpcc | Three-phase voltage at Point of Common Coupling (PCC) |
| iabc | Three-phase feed in current by the converter |
| f | Fundamental frequency |
| ω | Angular frequency (2пf) |
| ωPLL | Angular frequency for phase-locked loop |
| p* | Reference real power of the converter |
| q* | Reference reactive power of the converter |
| vαβ | Alpha-Beta (αβ) components of measured voltage |
| vdq | dq-components of measured voltage phasor |
| idq | dq-components of measured current phasor |
| idq* | dq-components of the reference current |
| vdq* | dq-components of the reference voltage |
| θ | Initial phase angle of the voltage phasor |
| θp | Initial phase angle of the positive sequence voltage phasor |
| ωp | Angular frequency of positive sequence voltage phasor |
| θn | Initial phase angle of the negative sequence voltage phasor |
| vp | Magnitude of the positive sequence voltage phasor |
| vn | Magnitude of the negative sequence voltage phasor |
| vαβ,p | αβ-components of the positive sequence voltage |
| vαβ,n | αβ-components of the negative sequence voltage |
| vdq,p | dq-components of the positive sequence voltage |
| idq,p* | dq-components of the reference current for the positive sequence |
| iαβ,n* | αβ-components of the reference current for the negative sequence |
| iαβ | αβ-components of the measured current |
| iαβ** | αβ-components of the reference current after applying the priority and current limit scheme |
| Vp | Positive sequence voltage phasor |
| Vn | Negative sequence voltage phasor |
| a | Unity phasor with an angle of 120° |
| Ts | Unit sample time |
| imax | Magnitude of maximum current |
| ixlim | Limit value for the current of type “x” |
| ip | Positive sequence current phasor’s magnitude |
| in | Negative sequence current phasor’s magnitude |
| i | Phasor of measured current |
| φp,n | Initial angle of the corresponding current phasor |
References
- Austria, “Energy Policy Review, IEA, Paris. Available online: https://www.iea.org/reports/austria-2020 (accessed on 27 December 2022).
- Renewables 2022 Global Status Report, REN21 Secretariat, Paris. Available online: https://www.ren21.net/wp-content/uploads/2019/05/GSR2022_Full_Report.pdf (accessed on 27 December 2022).
- Martín-Martínez, S.; Gómez-Lázaro, E.; Molina-Garcia, A.; Vigueras-Rodriguez, A.; Milligan, M.; Muljadi, E. Participation of wind power plants in the Spanish power system during events. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Bollen, M.H.J. IEEE Industry Applications Society, IEEE Power Electronics Society, and IEEE Power Engineering Society. Understanding Power Quality Problems: Voltage Sags and Interruptions; IEEE Press: New York, NY, USA, 2000. [Google Scholar]
- Abubakar, M.; Akbari, H.; Renner, H. Development of Reference Current Calculation Scheme for Grid-Side Converter during Unbalanced Faults. In Proceedings of the 2022 Second International Conference on Sustainable Mobility Applications, Renewables and Technology (SMART), Cassino, Italy, 23–25 November 2022; pp. 1–9. [Google Scholar]
- Camacho, A.; Castilla, M.; Miret, J.; Borrell, A.; Vicuña, L.G. Active and Reactive Power Strategies With Peak Current Limitation for Distributed Generation Inverters During Unbalanced Grid Faults. IEEE Trans. Ind. Electron. 2015, 62, 1515–1525. [Google Scholar] [CrossRef]
- Shamseh, M.B.; Inzunza, R.; Fukasawa, I.; Tanaka, T.; Ambo, T. Grid Support During Asymmetrical Faults using Negative Sequence Current Injection. In Proceedings of the 2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 24–28 November 2019; pp. 1–6. [Google Scholar]
- Moawwad, A.; Moursi, M.E.; Weidong, X. A novel transient control strategy for VSC-HVDC connecting offshore wind power plant. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; p. 1. [Google Scholar]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Current Reference Generation Based on Next-Generation Grid Code Requirements of Grid-Tied Converters During Asymmetrical Faults. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3784–3797. [Google Scholar] [CrossRef]
- Azevedo, G.; Delgado, J.R.; Cavalcanti, M.; Neves, F.; Rodriguez, P. A Negative-sequence Current Injection Method To Mitigate Voltage Imbalances In Microgrids. Eletrônica Potência 2011, 16, 296–303. [Google Scholar] [CrossRef]
- Zarei, S.F.; Mokhtari, H.; Ghasemi, M.A.; Peyghami, S.; Davari, P.; Blaabjerg, F. Control of Grid-Following Inverters Under Unbalanced Grid Conditions. IEEE Trans. Energy Convers. 2020, 35, 184–192. [Google Scholar] [CrossRef]
- Shabestary, M.M.; Mohamed, Y.A.R.I. Asymmetrical Ride-Through and Grid Support in Converter-Interfaced DG Units Under Unbalanced Conditions. IEEE Trans. Ind. Electron. 2019, 66, 1130–1141. [Google Scholar] [CrossRef]
- Almeida, V.A.F.; Taranto, G.N.; Marinho, J.M.T. Phasor-domain Dynamic Model of Asymmetric Current Injection Controller for Converter-interfaced Generator. J. Mod. Power Syst. Clean Energy 2021, 9, 1269–1278. [Google Scholar] [CrossRef]
- Camacho, A.; Castilla, M.; Miret, J.; Velasco, M.; Guzman, R. Positive-Sequence Voltage Control, Full Negative-Sequence Cancellation, and Current Limitation for Static Compensators. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6613–6623. [Google Scholar] [CrossRef]
- Paap, G.C. Symmetrical components in the time domain and their application to power network calculations. IEEE Trans. Power Syst. 2000, 15, 522–528. [Google Scholar] [CrossRef]
- Technical Connection Rules for Medium-Voltage (VDE-AR-N 4110). Available online: https://www.vde.com/en/fnn/topics/technical-connection-rules/tcr-for-medium-voltage (accessed on 9 January 2023).
- Li, X.; Lin, H. A Design Method of Phase-Locked Loop for Grid-Connected Converters Considering the Influence of Current Loops in Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2420–2429. [Google Scholar] [CrossRef]
- Boemer, J.C.; Rawn, B.G.; Gibescu, M.; Coster, E.; Meijden, M.A.M.M.; Kling, W.L. Contribution of negative-sequence controlled distributed generation to power system stability under unbalanced faults: A discussion paper. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–8. [Google Scholar]
- Pal, S.; Mishra, M.; Verma, A.; Kasari, P.R.; Das, B.; Chakraborti, A. Control of Grid Connected Converters Under Unbalanced Grid Faults. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–6. [Google Scholar]
- Wijnhoven, T.; Deconinck, G.; Neumann, T.; Erlich, I. Control aspects of the dynamic negative sequence current injection of type 4 wind turbines. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–37 July 2014; pp. 1–5. [Google Scholar]
- Meligy, A.; Qoria, T.; Colak, I. Assessment of Sequence Extraction MethodsApplied to MMC-SDBC STATCOM Under Distorted Grid Conditions. IEEE Trans. Power Delivvery 2022, 37, 4923–4932. [Google Scholar] [CrossRef]
- Du, L.; Xiong, L.; Li, M.; Tang, Z.; Xiu, L.; Ma, X. Fast positive sequence component detection schemes based on delay operational period filter. CSEE J. Power Energy Syst. 2020, 1–8. [Google Scholar]
- Hamed, H.A.; Abdou, A.F.; Bayoumi, E.; El-Kholy, E.E. Effective design and implementation of GSS-PLL under voltage dip and phase interruption. IET Power Electron. 2018, 11, 1018–1028. [Google Scholar] [CrossRef]
- Pinto, J.; Carvalho, A.; Rocha, A.; Araújo, A. Comparison of DSOGI-Based PLL for Phase Estimation in Three-Phase Weak Grids. Electricity 2021, 2, 244–270. [Google Scholar] [CrossRef]
- Svensson, J.; Bongiorno, M.; Sannino, A. Practical Implementation of Delayed Signal Cancellation Method for Phase-Sequence Separation. IEEE Trans. Power Deliv. 2007, 22, 18–26. [Google Scholar] [CrossRef]
- Nowak, M.; Binkowski, T.; Piróg, S. Proportional-Resonant Controller Structure with Finite Gain for Three-Phase Grid-Tied Converters. Energies 2021, 14, 6726. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).