Application of an Analytical Model of a Belt Feeder for Assessing the Load and Stability of Its Structure

Abstract

Belt conveyors, owing to their simple construction, high reliability and relatively low energy consumption, are the basic means of transporting loose and granular materials. Currently, thanks to continuous development, belt conveyors can reach a length of up to several kilometres, and their belt width can be more than two meters. Such possibilities are achieved thanks to increasingly better belts and drives. However, the most common are short belt conveyors with a length of up to 40 m and belt widths of up to 1 m, frequently referred to as belt feeders. Apart from the mining industry, they are widely used in power engineering, metallurgy and other industries (chemical plants, trans-shipment ports, storage yards, etc.). The design of machines, including belt feeders, is based on calculations. Modern design in technology is based on advanced computational methods and the possibilities of computer technology. Multi-variant simulation calculations are necessary, especially in the case of belt feeders, where none of the devices—despite the use of typical elements and subassemblies—are a repeatable solution. Only this procedure guarantees the selection of rational solutions already at the early stages of design. Therefore, in this article, an analytical model of a typical belt feeder was developed and its stability and forces in the supports were determined. This allowed the development of an application for testing the stability of the belt feeder at the design stage or when introducing structural changes.

1. Introduction

Belt conveyors are devices transporting various types of materials with granulation adapted to width b_t. The belt is an element that moves the material at a certain speed [1,2]. The efficiency of the conveyor results from the active cross-sectional area of the material on the belt F_p (trough) and its speed v_t. The characteristic parameters of the belt conveyor are therefore its length b_t and speed v_t [3,4,5]. These parameters, together with the type of transported material and the inclination of the conveyor α_p, determine the size of installed power N_p [6,7]. A typical belt conveyor with an upper conveyor belt consists of a return pulley, a supporting structure, usually in the form of a grid with idlers, and a drive with an electric motor or, less frequently, a hydraulic motor and a mechanical transmission. The movement of the belt, powered by the drive, at a certain speed v_t on idlers built on supports (trestles) from the return pulley to the drive, and causing the material to be transferred with the required efficiency, is a working movement. In contrast, the movement of the belt from the drive to the return pulley is a return (idle) movement; in this case, the belt also moves on idlers, but only single ones. As mentioned before, belt conveyors are devices that transport various types of materials in a continuous way. Therefore, they are mostly applied wherever constant feeding of material with a certain efficiency is required [3,4].

The above information applies to all belt conveyors with lengths ranging from several metres to even several kilometres, and belt widths from several centimetres to more than two meters [8,9]. This group of conveyors includes short belt conveyors with a length of up to 40 m and a belt width reaching up to 1 m, often referred to as belt feeders [10,11].

Due to their broad scope of work, belt feeders are eagerly chosen by investors in various industries. They are commonly used in reloading and transporting works, warehouses, landfills, construction sites, plants processing and exploiting materials and mineral resources (Figure 1), and for transporting excavated material and overlayers in the mining industry. These devices guarantee the stable and safe transport of materials. The entire process is convenient and quick, which brings significant benefits (saving time and money). Users are sure that the investment in high-class feeders will pay off quickly, and the profits will be felt for years. The use of belt feeders means easy assembly, disassembly, and transport because the structures are modular—assembled from ready-made elements. It allows the modernisation of production or distribution and adapting it to current standards. A large selection of parts and accessories allows users to modify the structure as needed. Additionally, the operation of belt feeders is quite quiet.

For the mineral resources industry, belt feeders are, among others, used in opencast rock mining for transporting the crushed mineral. They are usually included in the process line, moving the mineral from one loading point (feeder, tank, screen, or crusher) to another discharge point (other means of transport, warehouse, or heap). Typically, the above-mentioned feeders consist of a drive (Figure 2), a return pulley (Figure 3) and a route (Figure 4) with idlers and a belt. Such a feeder moves the material lying on the belt at angle α_tp, usually upwards. The maximum value of this angle results from the frictional coupling between the transported material and the belt μ_tu (α_tp + Δα_tp ≤ arctgμ_tu). It can work horizontally (Δα_tp = 0°) and on a downward negative slope (Δα_tp ˂ 0°) or on an upward positive slope (Δα_tp > 0°) [3]. Additional equipment utilised with such feeders are a charging hopper (Figure 5) and a discharge hopper, external and internal scrapers, platforms (Figure 6), as well as various types of protection related mainly to health and safety regulations and control (Figure 7) [12,13].

A characteristic feature of these feeders is their installation in the workplace, on stationary or mobile supports. Straight stationary supports (SSSs) are built on previously made foundations (Figure 8), and their number is dependent on the length of the feeder. The V-type stationary supports (VSSs), equipped with slides (skids), hold the feeder structure at the required angle α_tp, resting on the ground (Figure 9). If wheels are installed in place of skids, V-type mobile supports (VMS) are used (Figure 10). Belt feeders with V-type stationary supports are the most common [1,2,3], which poses a big challenge due to the stability of the structure, both during operation and at standstill. This issue requires the testing of the feeder’s stability [14] at the design stage and subsequent operational tests.

The available literature is rich in issues related to various aspects of belt conveyors. There are a few articles related to belt feeders; among others, Maton [15] and Bates [16] tested and calculated the load on such feeders. However, as yet, there is no description of the problem related to the stability of the belt feeder structure and its load. Therefore, an analytical model of a typical belt feeder with V-type supports was developed, and its stability and the forces in the supports were determined. It is worth emphasising that all the parameter values adopted for the calculations were obtained from belt feeder manufacturers and users. These are the actual values with which these feeders work. As a result, an application was developed using computer technology to test the feeder’s stability at the design stage or while making changes.

2. Analytical Model of the Belt Feeder

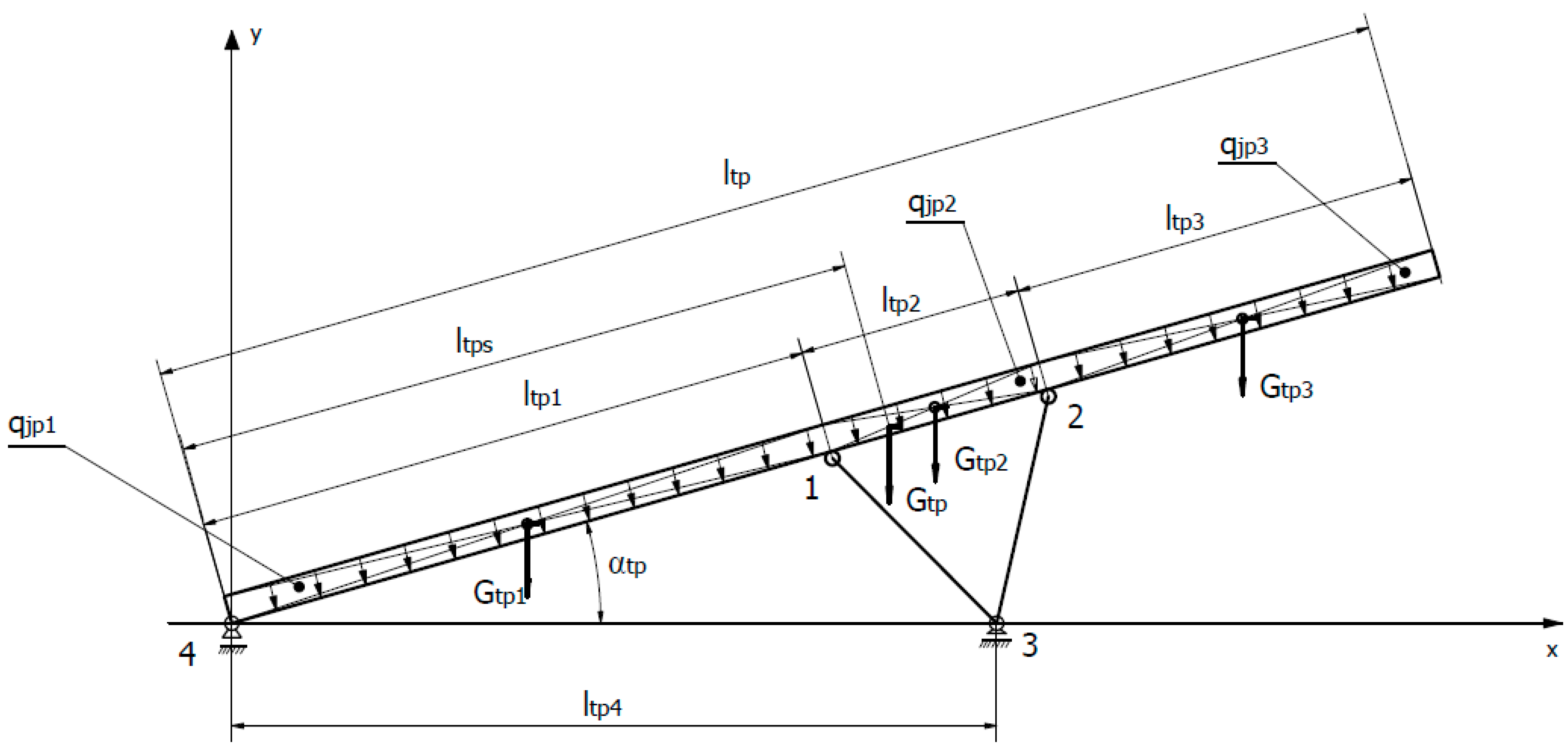
The starting point for developing an analytical model of the VSS and VMS belt feeder in order to assess its stability is the reduction of masses [17]. This allows the determination of the coordinates of the centre of mass of the feeder’s supporting structure (Figure 11). The continuous linear load q_jpi,, different for the three parts of the belt feeder (1), was assumed as rectangles with known coordinates of the centre of mass. The first part of the feeder’s supporting structure is the section stretching from the hopper (return pulley) to the first support, the second part is the section between the supports, and the third one stretches from the second support to the discharge (drive). This model does not take into account the weights of the feeding hopper G_z (drum, belt tension, hopper, and covers) or the discharge G_w (drum, counterweight drive, and platform). These will be taken into account when determining the forces and moments for the entire feeder.

$$G_{\mathrm{t}\mathrm{p}}={\sum }_{i=1}^n{q}_{\mathrm{t}\mathrm{p}i}·l_{\mathrm{t}\mathrm{p}i}$$

(1)

where:

• q_tpi—linear continuous load for the i-th section of the feeder;
• l_tpi—length of the i-th section of the feeder;
• n—number of feeder sections under consideration.

Concentrated weights for the three sections of the belt feeder can be determined from dependencies (2), (3), and (4). The total weight of the supporting structure of the belt feeder G_tp is the sum of three individual weights G_tp1, G_tp2, and G_tp3 (5). Similarly, the total length of the belt feeder l_tp is the sum of its three sections l_tp1, l_tp2, and l_tp3 (6). For the conditions of equilibrium relative to the y-axis, it is possible to determine the resultant moment M_Gtp as well as single moments for the three masses M_Gtp1, M_Gtp2, and M_Gtp3, which balance each other (7). The structural dimensions of the feeder’s route and the locations of the concentrated weights G_tp1, G_tp2, and G_tp3 (8), (9), (10), and the resultant mass (11) allow the determination of the coordinate of the centre of mass l_tps of the resultant mass M_Gtp for different (13) or identical continuous linear loads q_tpi (14).

$$G_{\mathrm{t}\mathrm{p}1}=q_{\mathrm{t}\mathrm{p}1}·l_{\mathrm{t}\mathrm{p}1}$$

(2)

$$G_{\mathrm{t}\mathrm{p}2}=q_{\mathrm{t}\mathrm{p}2}·l_{\mathrm{t}\mathrm{p}2}$$

(3)

$$G_{\mathrm{t}\mathrm{p}3}=q_{\mathrm{t}\mathrm{p}3}·l_{\mathrm{t}\mathrm{p}3}$$

(4)

$$G_{\mathrm{t}\mathrm{p}}=G_{\mathrm{t}\mathrm{p}1}+G_{\mathrm{t}\mathrm{p}2}+G_{\mathrm{t}\mathrm{p}3}$$

(5)

$$l_{\mathrm{t}\mathrm{p}}=l_{\mathrm{t}\mathrm{p}1}+l_{\mathrm{t}\mathrm{p}2}+l_{\mathrm{t}\mathrm{p}3}$$

(6)

$$M_{\mathrm{G}\mathrm{t}\mathrm{p}}=M_{\mathrm{G}\mathrm{t}\mathrm{p}1}+M_{\mathrm{G}\mathrm{t}\mathrm{p}2}+M_{\mathrm{G}\mathrm{t}\mathrm{p}3}$$

(7)

$$M_{\mathrm{G}\mathrm{t}\mathrm{p}1}=G_{\mathrm{t}\mathrm{p}1}·0.5{·l}_{\mathrm{t}\mathrm{p}1}·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(8)

$$M_{\mathrm{G}\mathrm{t}\mathrm{p}2}=G_{\mathrm{t}\mathrm{p}2}·\left(l_{\mathrm{t}\mathrm{p}1}+0.5·l_{\mathrm{t}\mathrm{p}2}\right)·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(9)

$$M_{\mathrm{G}\mathrm{t}\mathrm{p}3}=G_{\mathrm{t}\mathrm{p}3}·\left(l_{\mathrm{t}\mathrm{p}1}+l_{\mathrm{t}\mathrm{p}2}+0.5{·l}_{\mathrm{t}\mathrm{p}3}\right)·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(10)

$$M_{\mathrm{G}\mathrm{t}\mathrm{p}}=G_{\mathrm{t}\mathrm{p}}·l_{\mathrm{t}\mathrm{p}\mathrm{s}}·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(11)

On the basis of Formula (7) as well as (8), (9), and (10), the M_Gtp dependence can be expressed (12) as follows:

$$M_{\mathrm{G}\mathrm{t}\mathrm{p}}=\left[G_{\mathrm{t}\mathrm{p}1}·0.5·l_{\mathrm{t}\mathrm{p}1}+G_{\mathrm{t}\mathrm{p}2}·\left(l_{\mathrm{t}\mathrm{p}1}+0.5{·l}_{\mathrm{t}\mathrm{p}2}\right)+G_{\mathrm{t}\mathrm{p}3}·\left(l_{\mathrm{t}\mathrm{p}1}+l_{\mathrm{t}\mathrm{p}2}+0.5·l_{\mathrm{t}\mathrm{p}3}\right)\right]·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(12)

Based on Formula (11) and Formulas (2)–(5), the coordinate of the centre of mass l_ps describes dependence (13) or (14) if (6) is taken into consideration.

$$l_{\mathrm{t}\mathrm{p}\mathrm{s}}=\frac{M_{\mathrm{G}\mathrm{t}\mathrm{p}}}{G_{\mathrm{t}\mathrm{p}}·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}\right)}==\frac{0.5·G_{tp1}·l_{\mathrm{t}\mathrm{p}1}+G_{\mathrm{t}\mathrm{p}2}·\left(l_{\mathrm{t}\mathrm{p}1}+0.5·l_{\mathrm{t}\mathrm{p}2}\right)+G_{\mathrm{t}\mathrm{p}3}·\left(l_{\mathrm{t}\mathrm{p}1}+l_{\mathrm{t}\mathrm{p}2}+0.5·l_{\mathrm{t}\mathrm{p}3}\right)}{G_{\mathrm{t}\mathrm{p}}}$$

(13)

$$l_{\mathrm{t}\mathrm{p}\mathrm{s}}=\frac{0.5·l_{\mathrm{t}\mathrm{p}1}^2+l_{\mathrm{t}\mathrm{p}2}·\left(l_{\mathrm{t}\mathrm{p}1}+0.5·l_{\mathrm{t}\mathrm{p}2}\right)+l_{\mathrm{t}\mathrm{p}3}·\left(l_{\mathrm{t}\mathrm{p}1}+l_{\mathrm{t}\mathrm{p}2}+0.5·l_{\mathrm{t}\mathrm{p}3}\right)}{l_{\mathrm{t}\mathrm{p}1}+l_{\mathrm{t}\mathrm{p}2}+l_{\mathrm{t}\mathrm{p}3}}$$

(14)

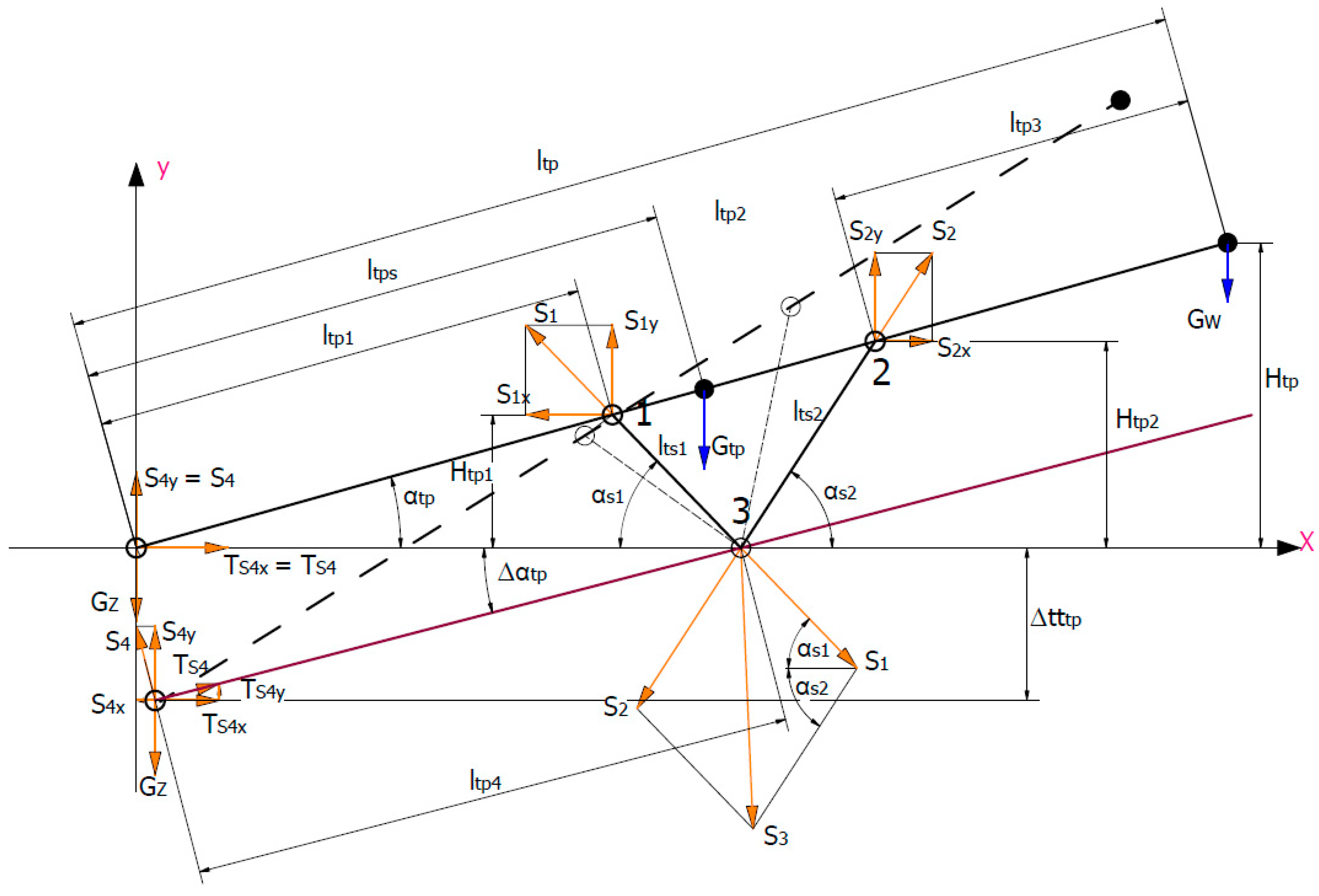
The above dependencies allowed the development of an analytical model of the VSS or VMS belt feeder (Figure 12), located in a horizontal excavation (Δα_tp = 0°), inclined upwards (Δα_tp > 0°) and inclined downwards (Δα_tp ˂ 0°). The belt feeder, with the load-bearing structure weight G_tp, the weight of the discharge (drive) G_w, and the feeding hopper (return pulley) G_z, is supported at points 3 and 4. The feeder’s return pulley (point 4) exerts pressure on the ground with the force of reaction S₄, whereas reaction S₃ at point 3 comes from two forces S₁ and S₂ in the supports having lengths l_st1 and l_st2. At point 3, friction force T_s4 will occur. Attaching the supports in points 1 and 2 should ensure the stability of the feeder (permanent equilibrium); i.e., in this case, reaction S₄ must always be positive. This is possible when the moment about pole (point) 3 is zero or positive. By projecting the forces onto the x- and y-axes and determining the moments of these forces relative to point 3, dependencies describing reaction forces S₁, S₂, S₃, and S₄ can be obtained. However, prior to this, it is necessary to establish the relationships between the construction parameters of the feeder, especially with α_tp, Δα_tp, and l_tp. Height H_tp, to which the feeder can transport the material, is described by dependence (15), whereas heights H_tp1 and H_tp2 can be determined from dependencies (16) and (17). The angles of inclination of support 1 α_s1 having length l_tp1 and of support 2 α_s2 with length l_tp2 are described by dependencies (18) and (19). The required support length 1 l_ts1 results from the value of angle α_s1 and height H_tp1 (20). The same is true for support 2, where its length l_tp2 also results from the value of angle α_s1 and height H_tp2 (21).

$$H_{\mathrm{t}\mathrm{p}}=l_{\mathrm{t}\mathrm{p}}·\sin \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}4}·\sin \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(15)

$$H_{\mathrm{t}\mathrm{p}1}=l_{\mathrm{t}\mathrm{p}1}·\sin \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}4}·\sin \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(16)

$$H_{\mathrm{t}\mathrm{p}2}=\left(l_{\mathrm{t}\mathrm{p}1}+l_{\mathrm{t}\mathrm{p}2}\right)·\sin \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}4}·\sin \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(17)

$${\alpha }_{\mathrm{s}1}=\arctan \left(\frac{H_{\mathrm{t}\mathrm{p}1}}{l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}1}·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)}\right)$$

(18)

$${\alpha }_{\mathrm{s}2}=\arctan \left(\frac{H_{\mathrm{t}\mathrm{p}2}}{\left(l_{\mathrm{t}\mathrm{p}1}+l_{\mathrm{t}\mathrm{p}2}\right)·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)}\right)$$

(19)

$$l_{\mathrm{s}\mathrm{t}1}=\frac{H_{\mathrm{t}\mathrm{p}1}}{\sin \left({\alpha }_{\mathrm{s}1}\right)}$$

(20)

$$l_{\mathrm{s}\mathrm{t}2}=\frac{H_{\mathrm{t}\mathrm{p}2}}{\sin \left({\alpha }_{\mathrm{s}2}\right)}$$

(21)

When the above analytical relationships between the design parameters of the belt feeder are known, it is possible, using the force balance equations (x- and y-axis) and moments (point 3), to obtain the dependencies describing the searched reaction forces S₁, S₂, S₃, and S₄ and to test the stability of the structure. The sum of the projections of forces on the x-axis should be zero (22).

$${\sum }_i{P}_{i\mathrm{x}}=T_{\mathrm{s}4\mathrm{x}}-S_{4\mathrm{x}}-S_{1\mathrm{x}}+S_{2\mathrm{x}}=0$$

(22)

$$T_{\mathrm{s}4\mathrm{x}}=S_{4\mathrm{y}}·{\mu }_{\mathrm{x}}={\mu }_{\mathrm{x}}{·S}_4·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(23)

$$S_{4\mathrm{x}}=S_4·\sin \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(24)

$$S_{1\mathrm{x}}=S_1·\cos \left({\alpha }_{\mathrm{s}1}\right)$$

(25)

$$S_{2\mathrm{x}}=S_2·\cos \left({\alpha }_{\mathrm{s}2}\right)$$

(26)

$$A_{\mathrm{s}4\mathrm{x}}{·S}_4-S_1·\cos \left({\alpha }_{\mathrm{s}1}\right)+S_2·\cos \left({\alpha }_{\mathrm{s}2}\right)=0$$

(27)

$$A_{\mathrm{s}4\mathrm{x}}={\mu }_{\mathrm{x}}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-\sin \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(28)

Similarly, when these forces are projected onto the y-axis, their sum should also be zero (29).

$${\sum }_i{P}_{i\mathrm{y}}{-G}_{\mathrm{z}}+S_{4\mathrm{y}}+T_{\mathrm{s}4\mathrm{y}}+S_{1\mathrm{y}}{-G}_{\mathrm{t}\mathrm{p}}+S_{2\mathrm{y}}{-G}_{\mathrm{w}}=0$$

(29)

$$S_{4\mathrm{y}}=S_4·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(30)

$$S_{1\mathrm{y}}=S_1·\sin \left({\alpha }_{\mathrm{s}1}\right)$$

(31)

$$S_{2\mathrm{y}}=S_2·\sin \left({\alpha }_{\mathrm{s}2}\right)$$

(32)

$$T_{\mathrm{s}4\mathrm{y}}=S_{4\mathrm{x}}·{\mu }_{\mathrm{y}}={\mu }_{\mathrm{y}}{·S}_4·\sin \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(33)

$$G_{\mathrm{z}}+G_{\mathrm{t}\mathrm{p}}+G_{\mathrm{w}}=G_{\mathrm{z}\mathrm{p}\mathrm{w}}$$

(34)

$$A_{\mathrm{s}4\mathrm{y}}{·S}_4+S_1·\sin \left({\alpha }_{\mathrm{s}1}\right)+S_2·\sin \left({\alpha }_{\mathrm{s}2}\right)-G_{\mathrm{z}\mathrm{p}\mathrm{w}}=0$$

(35)

$$A_{\mathrm{s}4\mathrm{y}}={\mu }_{\mathrm{y}}·\sin \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(36)

For the structure to remain in equilibrium, the sum of the moments relative to point 3 should also be zero (37). As a result of transforming Equation (37) and introducing additional notations (38), (39), (40), (41), (42), and (43), the dependence describing force S₄ (44) was obtained.

$$\begin{array}{ll}{\displaystyle \sum _i}{M}_{i03}& =G_{\mathrm{z}}·l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)+T_{\mathrm{s}4\mathrm{x}}·l_{\mathrm{t}\mathrm{p}4}·\sin \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-S_{4\mathrm{x}}·l_{\mathrm{t}\mathrm{p}4}·\sin \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-T_{\mathrm{s}4\mathrm{y}}·l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-S_{4\mathrm{y}}\\ & ·l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)+S_{1\mathrm{x}}·H_{\mathrm{t}\mathrm{p}1}-S_{1\mathrm{y}}\left[l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}1}·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)\right]\\ & +G_{\mathrm{t}\mathrm{p}}\left[l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}s}·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)\right]\\ & +S_{2\mathrm{y}}\left[\left(l_{\mathrm{t}\mathrm{p}1}+l_{\mathrm{t}\mathrm{p}2}\right)·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)\right]-S_{2\mathrm{x}}·H_{\mathrm{t}\mathrm{p}2}\\ & -G_{\mathrm{w}}\left[l_{\mathrm{t}\mathrm{p}}·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)\right]=0\end{array}$$

(37)

$$A_{\mathrm{s}1\mathrm{y}}=l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}1}·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(38)

$$A_{\mathrm{s}2\mathrm{y}}=\left(l_{\mathrm{t}\mathrm{p}1}+l_{\mathrm{t}\mathrm{p}2}\right)·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)$$

(39)

$$A_{\mathrm{z}\mathrm{p}\mathrm{w}}=G_{\mathrm{z}}·l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)+G_{\mathrm{t}\mathrm{p}}\left[l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}s}·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)\right]$$

$$-G_{\mathrm{w}}\left[l_{\mathrm{t}\mathrm{p}}·\cos \left({\alpha }_{\mathrm{t}\mathrm{p}}+{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}4}·\cos \left({∆\alpha }_{\mathrm{t}\mathrm{p}}\right)\right]$$

(40)

$$A_{\mathrm{s}4}=0.5\left({\mu }_{\mathrm{x}}-{\mu }_{\mathrm{y}}\right)l_{\mathrm{t}\mathrm{p}4}·\sin \left(2{∆\alpha }_{\mathrm{t}\mathrm{p}}\right)-l_{\mathrm{t}\mathrm{p}4}$$

(41)

$$A_{\mathrm{s}1}=H_{\mathrm{t}\mathrm{p}1}·\cos \left({\alpha }_{\mathrm{s}1}\right)-A_{\mathrm{s}1\mathrm{y}}·\sin \left({\alpha }_{\mathrm{s}1}\right)$$

(42)

$$A_{\mathrm{s}2}=A_{\mathrm{s}2\mathrm{y}}·\sin \left({\alpha }_{\mathrm{s}2}\right)-H_{\mathrm{t}\mathrm{p}2}·\cos \left({\alpha }_{\mathrm{s}2}\right)$$

(43)

$$S_4=-\frac{A_{\mathrm{s}1}·S_1+A_{\mathrm{s}2}·S_2+A_{\mathrm{z}\mathrm{p}\mathrm{w}}}{A_{\mathrm{s}4}}$$

(44)

By transforming Equation (22) and introducing additional notations (45), (46), and (47), the force S₁ dependence (48) was obtained.

$$-\frac{A_{\mathrm{s}4\mathrm{x}}}{A_{\mathrm{s}4}}\left(A_{\mathrm{s}1}·S_1+A_{\mathrm{s}2}·S_2+A_{\mathrm{z}\mathrm{p}\mathrm{w}}\right)-S_1·\cos \left({\alpha }_{\mathrm{s}1}\right)+S_2·\cos \left({\alpha }_{\mathrm{s}2}\right)=0$$

(45)

$$B_{\mathrm{s}2\mathrm{x}}=\cos \left({\alpha }_{\mathrm{s}2}\right)-\frac{A_{\mathrm{s}4\mathrm{x}}·A_{\mathrm{s}2}}{A_{\mathrm{s}4}}$$

(46)

$$B_{\mathrm{s}1\mathrm{x}}=\cos \left({\alpha }_{\mathrm{s}1}\right)+\frac{A_{\mathrm{s}4\mathrm{x}}·A_{\mathrm{s}1}}{A_{\mathrm{s}4}}$$

(47)

$$S_1=\frac{B_{\mathrm{s}2\mathrm{x}}·S_2·A_{\mathrm{s}4}-A_{\mathrm{s}4\mathrm{x}}·A_{\mathrm{z}\mathrm{p}\mathrm{w}}}{B_{\mathrm{s}1\mathrm{x}}·A_{\mathrm{s}4}}$$

(48)

By transforming Equation (29) and introducing additional notations (49), (50), and (51), the force S₂ (52) dependence (52) was obtained.

$$S_1\left(\sin \left({\alpha }_{\mathrm{s}1}\right)-\frac{A_{\mathrm{s}4\mathrm{y}}·A_{\mathrm{s}1}}{A_{\mathrm{s}4}}\right)+S_2\left(\sin \left({\alpha }_{\mathrm{s}2}\right)-\frac{A_{\mathrm{s}4\mathrm{y}}·A_{\mathrm{s}2}}{A_{\mathrm{s}4}}\right)-\frac{A_{\mathrm{s}4\mathrm{y}}·A_{\mathrm{z}\mathrm{p}\mathrm{w}}}{A_{\mathrm{s}4}}-G_{\mathrm{z}\mathrm{p}\mathrm{w}}=0$$

(49)

$$B_{\mathrm{s}2\mathrm{y}}=\sin \left({\alpha }_{\mathrm{s}2}\right)-\frac{A_{\mathrm{s}4\mathrm{y}}·A_{\mathrm{s}2}}{A_{\mathrm{s}4}}$$

(50)

$$B_{\mathrm{s}1\mathrm{y}}=\sin \left({\alpha }_{\mathrm{s}1}\right)-\frac{A_{\mathrm{s}4\mathrm{y}}·A_{\mathrm{s}1}}{A_{\mathrm{s}4}}$$

(51)

$$S_2=\frac{\left(A_{\mathrm{s}4\mathrm{y}}·A_{\mathrm{z}\mathrm{p}\mathrm{w}}+G_{\mathrm{z}\mathrm{p}\mathrm{w}}·A_{\mathrm{s}4}\right)B_{\mathrm{s}1\mathrm{x}}+A_{\mathrm{s}4\mathrm{x}}·A_{\mathrm{z}\mathrm{p}\mathrm{w}}·B_{\mathrm{s}1\mathrm{y}}}{A_{\mathrm{s}4}\left(B_{\mathrm{s}2\mathrm{y}}·B_{\mathrm{s}1\mathrm{x}}+B_{\mathrm{s}2\mathrm{x}}·B_{\mathrm{s}1\mathrm{y}}\right)}$$

(52)

Reaction S₃ at point 3 is the geometric sum of forces S₁ and S₂ (53).

$$S_3=\sqrt{S_1^2+S_2^2-2S_1·S_2·\cos \left({\alpha }_{\mathrm{s}1}+{\alpha }_{\mathrm{s}2}\right)}$$

(53)

The obtained analytical dependencies resulting from the adopted model of the belt feeder make it possible to determine the forces that are important for its structure load and stability. This is, of course, particularly important at the stage of creating the model, and designing and preparing documentation, but also when making changes to the feeder structure (modernising). As mentioned in the introduction, one should also remember the adhesion of the excavated material to the belt, expressed by the coefficient of friction μ_tu, which corresponds to friction angle ρ_tw. Then, the total angle of feeder inclination (α_tp + Δα_tp) cannot exceed the value of angle ρ_tw (54). Of course, changing the angle of the feeder’s inclination also requires checking its stability.

$${\alpha }_{\mathrm{t}\mathrm{p}}+{\mathsf{\Delta }\alpha }_{\mathrm{t}\mathrm{p}}\le {\arctan \mu }_{\mathrm{t}\mathrm{u}}$$

(54)

The above-mentioned comments and requirements resulted in the development of an algorithm and a computer application that enable the load of the feeder structure and its stability to be calculated, without the need to use CAD programs.

3. Application for Designing and Analysing the Construction of a Belt Feeder

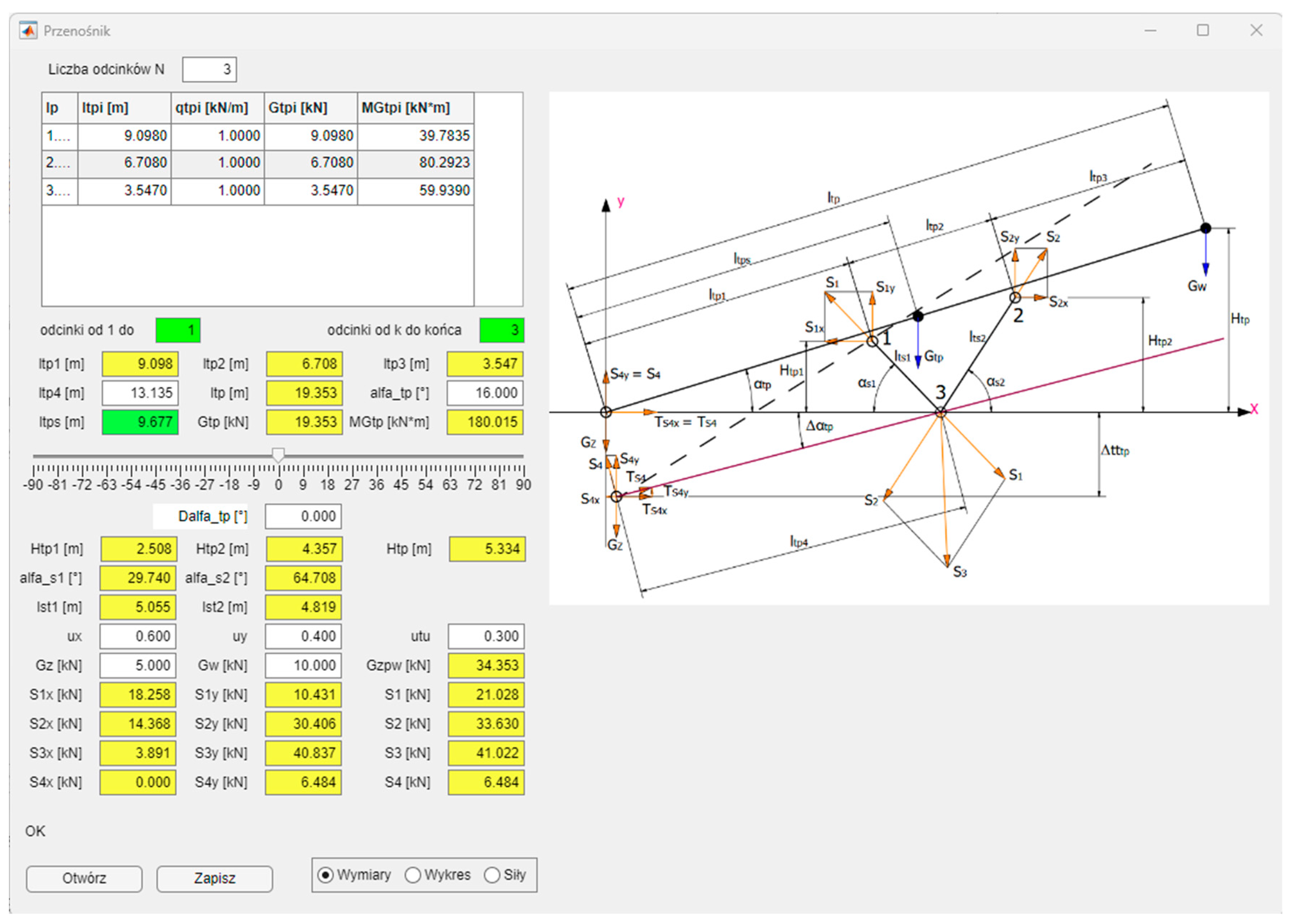
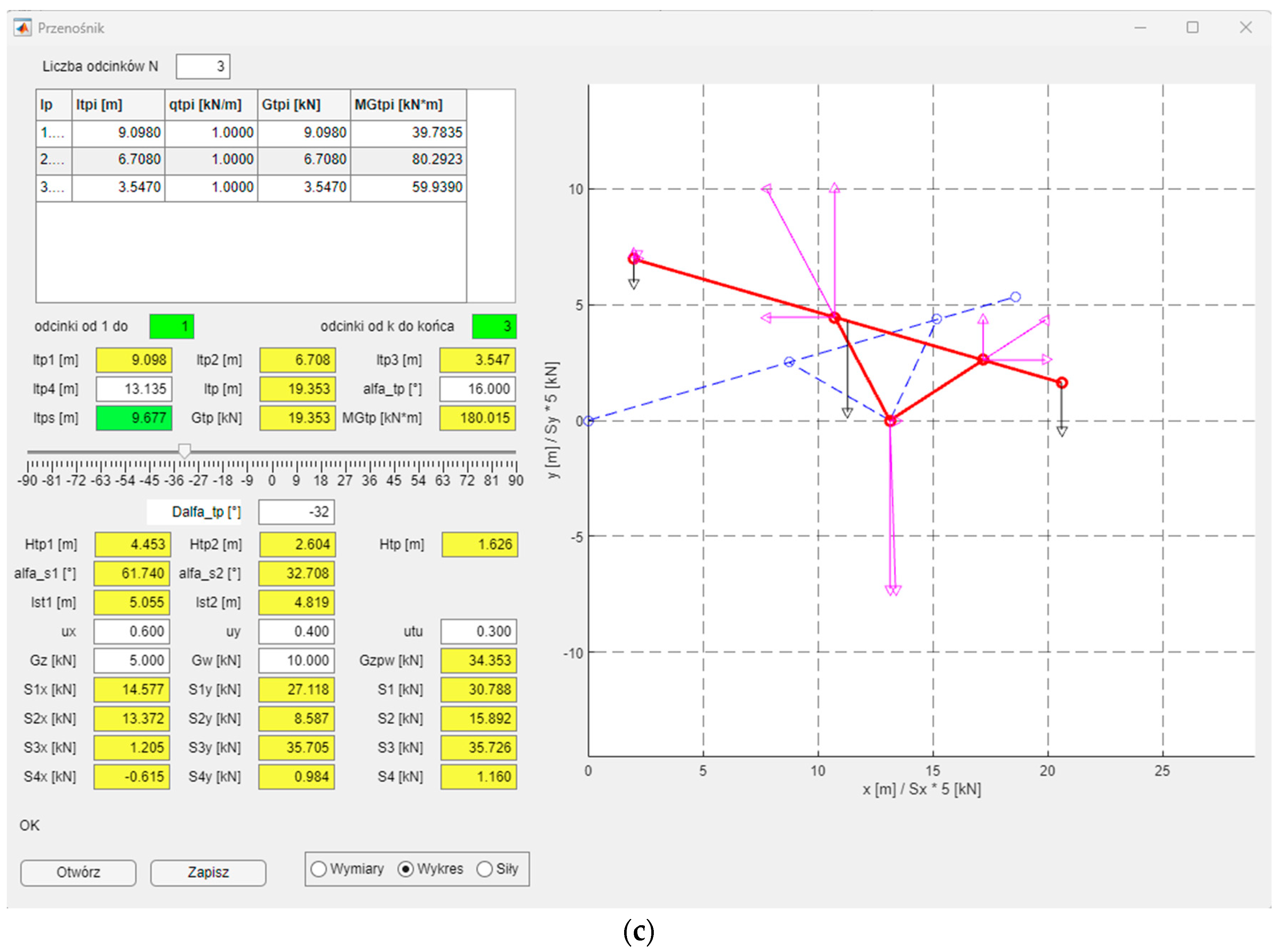
In order to support the design and analysis of the feeder load, an application in the Matlab environment has been developed. After compilation, it will be an independent application. Figure 13 shows the main application window.

In the left part of the application window, one can see the data entered by the user and the results of calculations based on the relationships presented in the previous section. The input data are the lengths and weights of the feeder elements (top right corner of the application), the distance l_tp4, the angle of the feeder inclination α_tp, the angle of the feeder’s deviation from the base plane (lowering or elevating the starting point of the feeder), orthogonal components of the friction coefficients μ_x and μ_y, as well as the forces (of weights) G_z and G_w. All these quantities are entered in the white edit boxes. Yellow and green edit boxes are reserved for calculation results. Each change in the input quantity causes recalculation of all the dependencies. The input data entered in the feeder calculations can be saved in a text file with the “Save” button to enable quick loading of the data with the “Open” button without re-entering the data manually. An important element of the application is the ability to change the value of angle Δα_tp, i.e., rotate the feeder around support point 3.

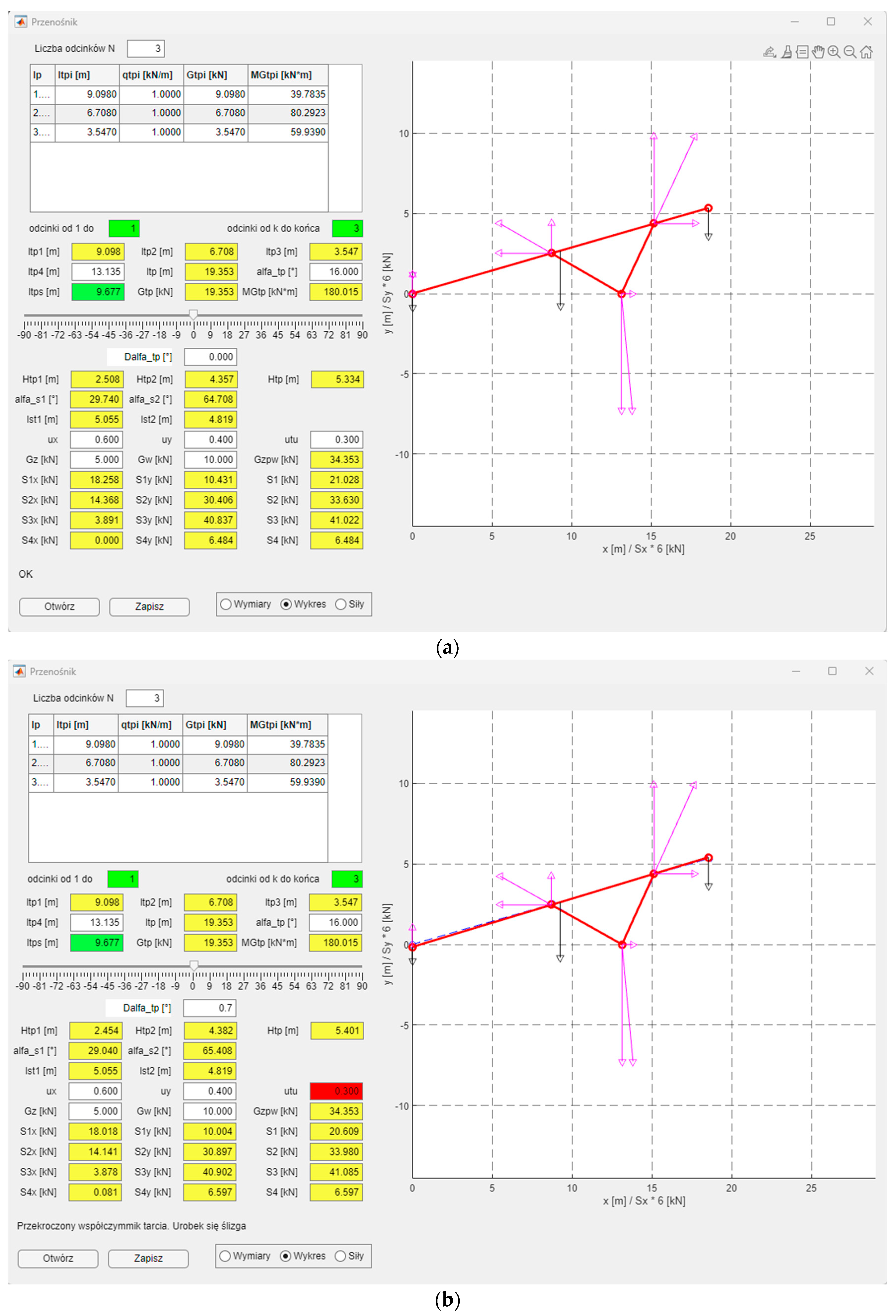
In the lower right part of the application, there is a three-position switch for selecting the drawings located on the right side of the application. Initially, a diagram of the feeder with its marked dimensions (parameters) and the forces acting on it is drawn. This considerably facilitates entering the input data and interpreting the obtained results, as they can be quickly located. The second option “Graph” is a visualisation of the feeder based on the entered and calculated data (Figure 14). In this option, the designed feeder is drawn in the neutral position (Δα_tp = 0°) with a blue dashed line, and in the position taking into account the set angle Δα_tp. In the case of the second option, the acting forces (weights) G_z, G_w, G_zpw (black), as well as forces S₁, S₂, S₃, and S₄ with their orthogonal components are drawn. 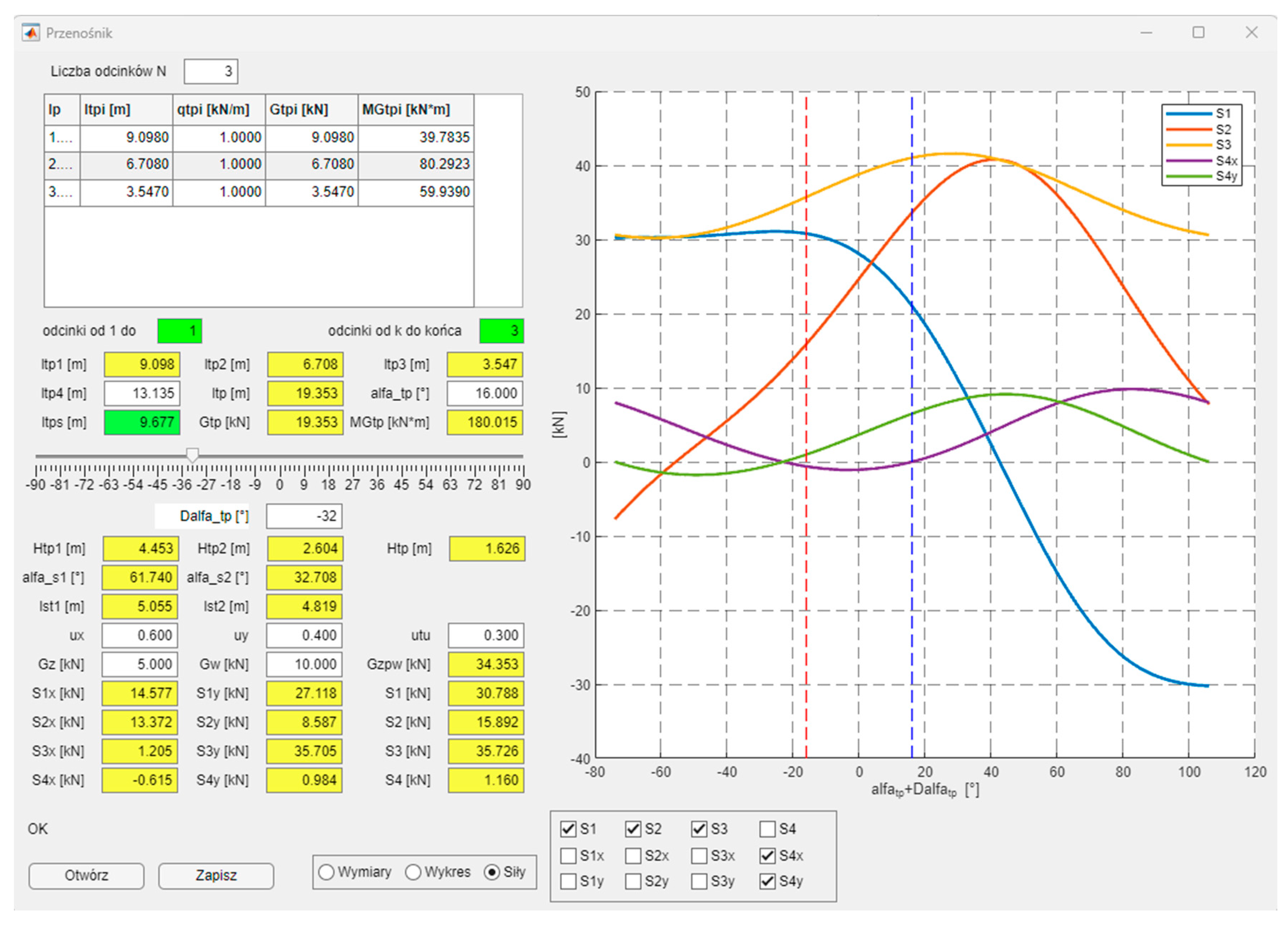A change in angle Δα_tp by means of a slider updates the calculations and the schematic drawing of the feeder. The third drawing option includes graphs of S_i forces with their orthogonal components as a function of the sum of angles α_tp and Δα_tp (Figure 15).

The values of the forces acting on the feeder depend on its positioning. Graphs of these functions can be helpful in the process of designing the feeder. Twelve “checkboxes” have been placed under the graphs so that the designer can choose which forces they want to depict, also taking into account their orthogonal components. Two vertical dashed lines are also drawn on the graph. The blue line represents the feeder in the neutral position (Δα_tp = 0°), whereas the red one defines the feeder’s position after taking into account the rotation of the feeder relative to support point 3. Every change in the feeder parameters is updated in the calculations and in the diagrams. 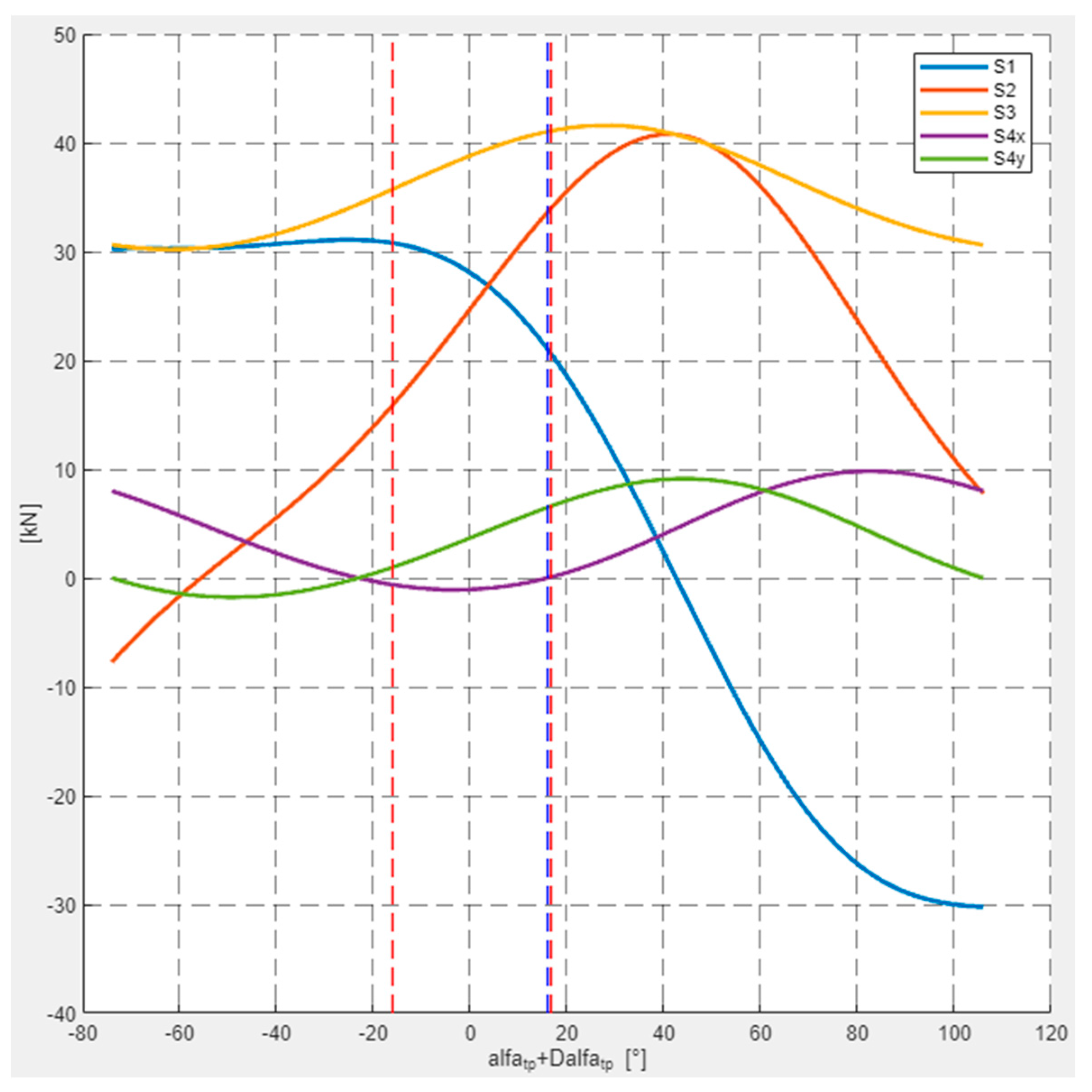Figure 16 shows the same graphs as in the application (Figure 15) with an additional red vertical line marked for Δα_tp = 0.7°.

4. Usage of the Application

The results of the calculations (yellow and green edit boxes on Figure 13) together with Figure 14, Figure 15 and Figure 16 were obtained with the use of the application in question and the data of a real feeder with a length of 20 m, inclination α_tp = 6°, and a belt width of 1000, placed on V-type stationary supports. (Figure 10). This feeder is mainly designed to work on inclination α_tp = 16°, in which case Δα_tp = 0°. This is due to the coupling of the transported material with the belt, where angle ρ_tu = 16.7° (54) for μ_tu = 0.3, in which case Δα_tp = 0.7°. Increasing the upward inclination for this type of feeder (Δα_tp > 0°) is practically impossible in the case of a smooth belt. In the event that the feeder works downwards (Δα_tp < 0°), its total inclination can reach −32°. The value and sense of force S_4y lead to the conclusion that the feeder’s stability can also be maintained (Figure 16, green). It can be easily seen that the course of force S_4y is decreasing in the examined range. Conversely, force S_4x increases in value. For Δα_tp = 0°, force S_4x has a zero value, which is consistent with reality. In the range of permissible belt inclination angles (−32° ˂ α_tp ˂ 0.7°), force S₂ has a positive and increasing value. The opposite is true for force S₁, as its value is also positive but decreasing, whereas the resultant value of these forces, i.e., force S₃ for angle α_tp = 16°, reaches its maximum. 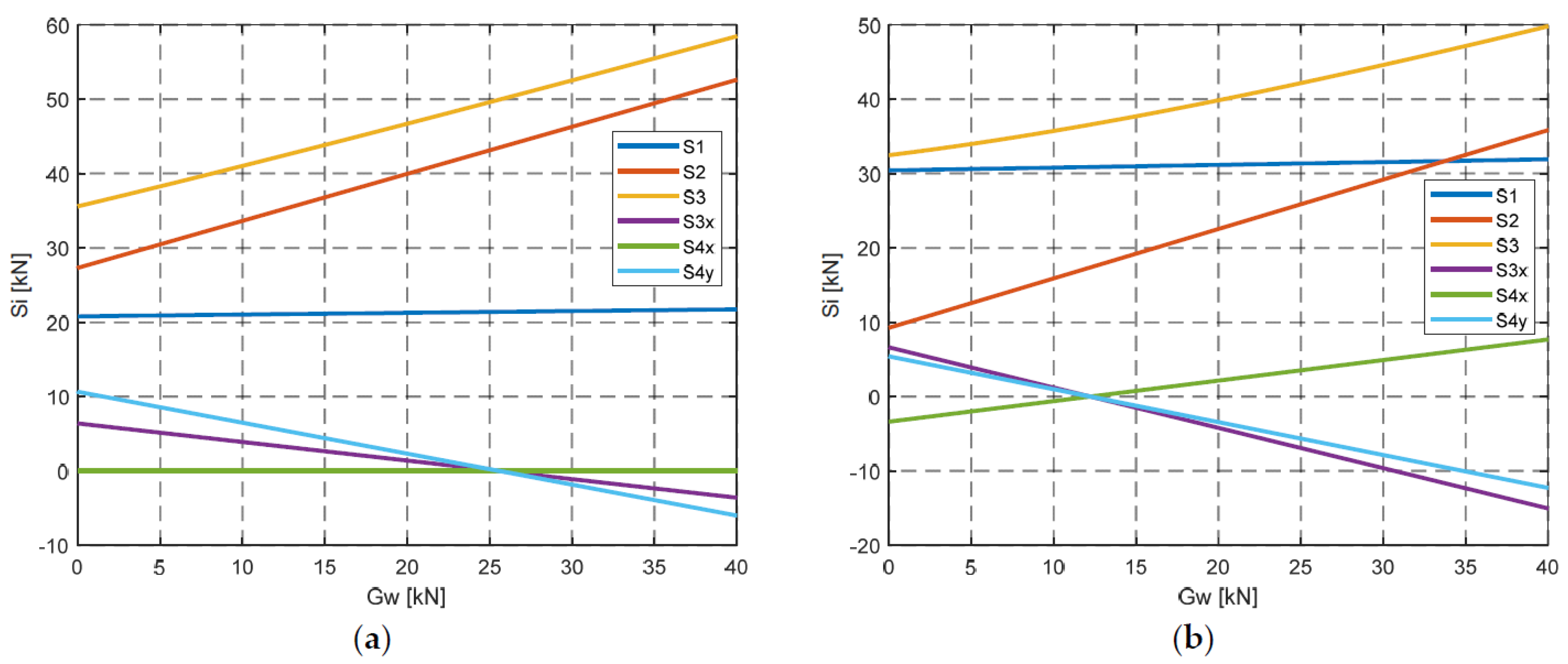It should be noted that force S_4y also has a positive value in this range, which leads to the conclusion that the feeder has the required stability. It may change when the weight of the discharge G_w increases. In such a case, force S_4y has a negative value above weight G_w = 25.5768 kN, which indicates the loss of stability of the feeder when it is working on an upward slope (Δα_tp > 0°), Figure 17a. However, in the case of a feeder working on a downward slope with weight G_w > 12.2258 kN, force S_4y also has a negative value (Δα_tp < 0°), which causes loss of stability (Figure 17b). Of course, the application allows other cases related to the design parameters of the feeder to be considered.

5. Conclusions

The previously described construction of belt feeders as well as their physical and mathematical models allowed the development of an algorithm and a computer application. The main goal of this project was to create a tool that would enable the structure of the designed and constructed feeder to be tested without the need for additional documentation. This is particularly useful at the stage of starting up a specific feeder in its place of work, where small changes in its construction and installation are often required. To sum up, it can be said that:

• The model of a belt feeder, based on currently produced and used feeders of this type, enables analytical testing of their stability and structure load.
• The developed algorithm and computer application enable and expedite computational processes with the possibility of their visualisation, especially when making structural and functional changes to existing objects.
• The discussed application is used in practice by companies producing and installing this type of feeder. Users of these feeders also employ it, as it responds to their needs.