Abstract
This paper presents an application of the Simulink stvmgain S-function for the thermal modelling of a building zone based on the resistance–capacitance scheme of EN ISO 13790. That model in the form of the state-space matrix with time-varying elements was used in simulations of a building with hourly and, suggested in that standard, daily averaged ventilation airflow in five European cities. The following two ventilation schedules were used: occupancy-based; and wind-dependent. Comparative simulations were conducted in EnergyPlus. In general, the results obtained for the annual heating and cooling demand were better for hourly than daily averaged ventilation with an error below 10%. However, in several cases of cooling, the error was above 30%. When considering hourly indoor air temperatures, the proposed method provided very good results with MAE of up to 0.52 °C and 0.46 °C, RMSE < 0.69 °C and 0.62 °C, and CV(RMSE) < 3.09% and 2.75% for the daily averaged and hourly ventilation flow, respectively. For wind-driven ventilation, the temperatures were as follows: MAE < 0.49 °C and 0.48 °C; RMSE < 0.69 °C and 0.68 °C; and CV(RMSE) < 3.01% and 2.97%.
1. Introduction
Thermal network models, also known as resistance–capacitance (RC) networks, introduced by Beuken [1] and then rapidly developed in combination with the lumped capacitance method by other researchers, are widely used in a transient heat flow analysis at relatively low computational costs [2]. They are frequently employed in the thermal modelling of different physical objects of various complexities, such as the hard disk drive [3], the two-phase closed thermosyphon [4], the high-power LED light [5], the combustion chamber of the diesel engine [6], or the passive-cooled battery pack [7]. In addition to these problems, thermal networks are commonly used in building-related simulations. Here, the range of applications is very wide and includes issues such as passive solar systems [8], flat plate solar collectors [9,10], and air zone models [11].
Recently, thermal networks have been more and more frequently used for load estimation of buildings [12] and dynamic modelling of buildings [13,14]. The growing importance of the energy assessment of buildings has made thermal network models more frequently used in the prediction of indoor conditions [15] or thermal loads [16]. These two fields of application resulted in the development of many schemes of various complexities [17,18,19,20,21].
One such circuit was introduced by EN ISO 13790 [22] in the form of the 5R1C (five resistors and one capacitor) network model of a building zone. The hourly calculation procedure described in that standard can be applied to popular spreadsheets for typical cases [23,24,25]. It uses hourly weather data and introduces hourly schedules for internal gains and building occupation. However, it recommends (in Section 9.3 and Appendix J of the standard) calculations based on daily averaged values of the ventilation flow.
Common simulation practice, especially in energy auditing of buildings [26,27,28], is to use a constant ventilation airflow for the whole year [19,29,30,31,32]. On the other hand, detailed simulation tools enable the introduction of hourly and sub-hourly schedules [33,34,35]. Hence, these two approaches are present in the literature. However, no deeper analysis of their use on the simulated thermal performance of a building has been performed so far. Thus, an investigation in this direction should be conducted. For this purpose, an application of the Matlab/Simulink package is proposed in this paper. This tool offers a wide range of possibilities to build appropriate simulation models that can be used for different purposes related to the dynamic analysis of buildings and their systems [36,37,38].
Recently, the network model of EN ISO 13790 has been implemented in the Matlab/Simulink environment. Zadeiks et al. [39] used the modified 6R1C version of the 5R1C generic model with additional thermal conductance to separate the infiltration airflow. Under assumed constant ventilation, the simulation of the heating energy demand of a single room in November resulted in a 1.37% deviation in comparison to the IDA-ICE tool. Measurement in a real educational building resulted in a 10.68% difference in heating consumption in December.
The same tool was used in [40]. The authors modified the 5R1C model to the 6R2C scheme with separated ventilation and infiltration flows and an additional internal air capacitance combined with an air handling unit (AHU). Then, daily heating and cooling energy consumption in an educational building were analysed. The average root mean square error (RMSE) between simulation and measurement of daily and monthly cooling was 47.9% and 1.98%, respectively. For the heating mode, these indices were from 18.6% to 51.1% and from 1.55% to 7.39%, respectively. The authors recommended further analysis of the building at the level of zones, each with its ventilation unit.
Buonomano et al. [41] modified the 5R1C circuit, adding two new thermal conductances to model a building façade integrated with a solar thermal collector. Then, that scheme was implemented in Matlab. The authors performed these experiments in a multi-floor building with a 23.8 m2 south-facing wall with a 4 m2 window and six flat-plate solar collectors. Ventilation airflows were estimated based on the working schedules. The maximum difference between measured and simulated absorbing plate and glass cover temperatures was up to 1.3°C and 0.9°C, respectively.
Cirrincione et al. [42] measured monthly energy for space heating and cooling of a historic city hall building. Constant ventilation was adopted. In reference to EnergyPlus, in Matlab, the simulation of the EN ISO 13790 and EN ISO 52016 [43] models revealed significant differences in cooling, but the authors did not present a detailed analysis.
Vivian et al. [44] simulated the heating and cooling peak loads and thermal demand of an apartment in four thermal capacity versions, each in four locations. In Matlab, they implemented the 5R1C model of EN ISO 13790 and the 7R2C model of the German VDI 6007-1 standard [45] and then compared the results with the dynamic tool TRNSYS. The authors assumed a constant ventilation airflow rate in all cases. Performed simulations revealed that, depending on the building’s insulation and structure, the analysed models tended to overestimate the peak heat load by up to 8.1% and 4.0%, while the cooling peak load differed by up to −14.5% and +4.1% for 5R1C and 7R2C models, respectively. Annual needs for space heating differed by up to 33% and 16%, respectively. Smaller differences of −5.1% and +4.7% were noticed for space cooling.
Based on the state-space description, Michalak [46] implemented the 5R1C model in Simulink. Two ventilation schedules, each in a single-family building, in 20 European locations were considered. Annual heating and cooling demands, compared to the detailed simulations in EnergyPlus, showed differences of up to 10.75% and 17.20%, respectively. Indoor air temperature showed good agreement with the reference data.
In [47,48], authors implemented the 5R1C model in Mathcad and simulated the monthly heating energy consumption of a single room in a thermally heavy building with constant ventilation flow. Differences between that model and detailed calculations in EnergyPlus were up to 7%.
The presented review shows that simulations of buildings with the use of the 5R1C model were performed mainly with constant airflow rates. When considering varying conditions, the authors focused on the accuracy of the indoor air temperature and thermal demand prediction by the model.
The importance of these two elements from the point of view of the building users is obvious. On the other hand, the operative temperature is used for a proper assessment of the thermal comfort of the space. The thermal model of standard EN ISO 13790 makes it possible to calculate this, so it is advisable to evaluate it from this point of view.
The impact of daily averaged ventilation airflow suggested by EN ISO 13790 on the accuracy of the simulations was not analysed, and this is the research gap that requires a more detailed study. Therefore, this paper aims to determine the impact of hourly and daily averaged ventilation schedules on the accuracy of the annual heating and cooling needs calculated via the simple hourly method and the 5R1C thermal network model of a building from EN ISO 13790. The thermal model of a building zone was described in state space and then implemented in the Matlab/Simulink R2017b environment using the time-varying matrix gain S-functions. Then, the simulation results were compared with the detailed simulation in EnergyPlus. Finally, concluding remarks were given.
2. Materials and Methods
2.1. Linear Time-Varying State-Space Thermal Model of a Building Zone
2.1.1. Theoretical Background
The degree of difficulty of the analysis and modelling of the behaviour of the physical systems over time depends mainly on the complexity of their mathematical description. Slightly simplifying, one can assume that under this criterion, systems can be classified as time-invariant or time-varying [49]. Time-invariant models are simpler and, therefore, are more likely to be used. But the time scale of the model is not always small when compared to the life span of the modelled process. Then, the time invariance cannot be assumed, and the time-varying systems analysis should be applied [50]. Such models are called linear time-variant or linear time-varying (LTV) models. The theoretical background of this class of systems is given in the literature [49,50,51].
Mathematical models of the physical systems may assume different forms. Linear dynamic systems can be described by the ordinary differential equations (ODEs), input/output model (black-box model), transfer functions, or state-space notation. The compact form of the latter form ensures that even a large system can be represented by the set of two equations. They have the same form, regardless of the order of the system, making the development of the solution techniques very easy. Finally, the matrix/vector modelling is very efficient from a computational standpoint for computer implementation. Thanks to these features, state-space form is widely used in building simulation [52,53,54].
The LTV system is represented in state space by the set of the two equations:
for
where u, x, and y signals are called the input, state, and output of the system, respectively; A is the system matrix (with dimensions of n × n); B is the input matrix (n × p); C is the output matrix (r × n), and D is the feed-forward matrix (r × p). The first-order differential Equation (1) is called the state equation, and Equation (2) is called the output equation [49]. This system of equations describes an input–output relationship between the input (u) and output (y) signals. For the known input u, the state Equation (1) should be solved to determine the state x. Then, the known state x can be substituted into the output Equation (2) to obtain the output y.
x′ = A(t) x(t) + B(t) u(t)
y = C(t) x(t) + D(t) u(t)
Ordinary differential equations describing a considered system can be directly implemented in Matlab with the use of available solvers or using the S-Functions in Simulink [55]. The second solution also allows for user-friendly graphical modelling, where different mathematical operations are performed in block diagrams [56].
2.1.2. Time-Varying Matrix in Matlab/Simulink
One of the potential ways of implementing a time-varying state-space thermal model of a building is to write a specially designed function. Matlab gives the possibility to call its own subroutines (written in C, C++, or Fortran) from the command line. These programs are called binary MEX files and are loaded and executed by the Matlab interpreter. Each MEX file may contain only one function or subroutine, and it has the same name as the MEX file. For the users’ convenience, the Matlab/Simulink package contains exemplary C MEX S-functions [57]. One of them is function stvmgain saved in the stvmgain.c file. It is the source for the continuous time-varying matrix gain S-function block. Because the application of this function is rarely met—only two papers with its application were found [46,58]—it requires an additional explanation.
The stvmgain S-function has two parameters, i.e., the “gain” (K) and the “sample time”, defined in the initial part of the stvmgain.c file as follows:
/* first parameter: gain */ #define K_IDX 0 #define K_PARAM(S) ssGetSFcnParam(S,K_IDX) /* second parameter: sample time */ #define SAMPLE_TIME_IDX 1 #define SAMPLE_TIME_PARAM(S)ssGetSFcnParam(S,SAMPLE_TIME_IDX) #define NPARAMS 2
These variables are user-defined and can be adjusted in the box “S-function parameters” in the window “Function Block Parameters: S-Function”. For example, if the box “S-function parameters” is filled with [2 2; 2 2], 1, it means that input gain K has two columns and two rows, and all their values are equal to two. The sample time is set to 1. These values are used only at the initial step of the simulation.
According to the information included in the stvmgain.c file, this block has two inputs. The first is the input signal, and the second is the input gain. The gain K defines the number of columns and rows of the input gain as follows:
#define NOUTPUTS mxGetM(K_PARAM(S)) /* rows of K */ #define NINPUTS mxGetN(K_PARAM(S)) /* columns of K */
The following S-function methods are used to validate entered parameters to verify that they are okay. Also, one sample time is set to use. The information about sizes is used by Simulink to determine the S-function block’s characteristics (number of inputs, outputs, states, etc.). Among others, the number of columns of U must match the number of columns in K. It means that the width of the input signal is columns of U (NINPUTS) + number of the elements of K (matrix_size):
numInputs = NINPUTS + matrix_size;and the S-function has a single input port whose width is set by the following numInputs:
if (!ssSetNumInputPorts(S, 1)) return; ssSetInputPortWidth(S, 0, numInputs);
The same concerns the output port whose width is NOUTPUTS:
if (!ssSetNumOutputPorts(S, 1)) return; ssSetOutputPortWidth(S, 0, NOUTPUTS);
The mdlOutputs method computes the signals that this block emits. It is invoked by Simulink at each simulation time step. It computes the S-function’s outputs at the current time step and stores the results in the S-function’s output signal arrays.
To perform the matrix multiplication and to create an output, the matrix memory storage is needed because the results from one calculation step are used in the next one. For such a case, work vectors for data storage should be used. The ssGetRWork(S) macro was used to obtain the real-valued (real_T) work vector. It returns a pointer (*kPtr) to the allocated work vector. This is a very important part of this function as it determines how the input signal and input gain multiplication procedure is carried out. It is defined as follows [57]:
staticvoidmdlOutputs(SimStruct*S, int_Ttid) { real_T*y= ssGetOutputPortRealSignal(S,0); InputRealPtrsTypeuPtrs = ssGetInputPortRealSignalPtrs(S,0); real_T*kPtr = ssGetRWork(S); size_ti,j; real_Taccum; UNUSED_ARG(tid); /* Matrix Multiply: y = K * u */ for (i = 0; i< NOUTPUTS; i++) { accum = 0.0; /* K * u */ for (j = 0; j < NINPUTS; j++) { accum += kPtr[i + NOUTPUTS*j] * U(j); } y[i] = accum; } }
The temporary variable accum is used to store the calculated value of the k-th element of the output matrix, where k = {0, 1, …, (i·j) − 1}. The multiplication procedure of the input gain K and input signal u starts from k = 0, when i = 0 and j = 0, to k = i·j − 1 for i < NOUTPUTS and j < NINPUTS. The pointer kPtr[i + NOUTPUTS * j] indicates the position in the vector containing elements of the input gain (K).
Because the first input parameter for the stvmgain function is the input signal (u, x, or y) and the second is the input gain (A, B, C, or D), the system of Equations (1) and (2) should be converted into the following form:
x′(t) = x(t) A(t) + u(t) B(t)
y(t) = x(t) C(t) + u(t) D(t)
Solutions of pairs of Equations (1)–(4) should be the same. However, in matrix multiplication, the order of factors has an impact on the product.
The input data to the stvmgain block are in the form of a row vector. The operation of the multiplication of row and column vectors is commutative. However, a problem can occur when the number of columns or rows is higher than one.
To properly perform the multiplication procedure using the stvmgain function, let us examine the process of the B and u multiplications in detail using the exemplary second-order 4R2C model presented in [59]. As two capacitors (2C) are present in this system, it has two state variables (n = 2). It has five inputs (m = 5), namely, the internal and solar gain, supply air, ambient air, and water supply temperature. Finally, two outputs (r = 2) can be defined: concrete core; and zone temperatures. Hence, matrix A has the dimensions of [2 × 2], B = [2 × 5], C = [2 × 2] and D = [2 × 5]. Vector u = [5 × 1] and v = [2 × 1].
In this model, the variable NOUTPUTS = 2 (rows of B) and NINPUTS = 5 (columns of B). The input signal for the stvmgain function is the column vector u. It should be written in the form of a row vector as u11, u21, u31, u41, u51. Its elements are indexed by the U(j) variable from j = 0 (U(j) = u11) to j = 5 (U(j) = u51). The same form should have the second input parameter—the time-varying matrix B: b11; b12; b13; b14; b15; b21; b22; b23; b24; b25. The elements of matrix B are indexed by the pointer kPtrin the same way as for the u vector.
The multiplication procedure in the stvmgain S-function is presented in Table 1. For the successive steps, the values of all internal variables can be seen. The calculation loop starts from the index i = 0 and j = 0 and ends for i and j, determined according to the number of inputs and outputs of the system, respectively.

Table 1.
The multiplication procedure of the stvmgain function.
If the set of real numbers is R, the multiplication of two matrices, A and B, is defined only if the number of columns in A is equal to the number of rows in B. If A Rm×n and B Rn×p, then C = AB Rm×p, and the ij-th element cij of the matrix C is:
Continuing, in the case of B = [2 × 5] and u = [5 × 1], we obtain the resulting matrix of 2 × 1 with the elements b11·u11 + b12·u21 + b13·u31 + b14·u41 + b15·u51 in the first row and b21·u11 + b22·u21 + b23·u31 + b24·u41 + b25·u51 in the second one. So, by looking at Table 1, it is obvious that there are some differences between the resulting summations for these two methods. Knowing that, the input matrix B can be modified in the way that output vectors in both cases will be the same.
2.2. Thermal Network Model of EN ISO 13790
The EN ISO 13790 standard [22] describes the simple hourly method for the calculation of building energy demand for space heating and cooling. This method is based on an equivalent thermal–electric network model of a building zone, which consists of five resistances and one capacitance (5R1C), as presented in Figure 1. It has been described in detail recently [60,61,62,63].
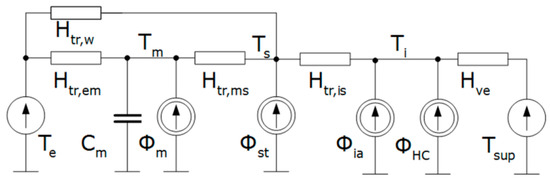
Figure 1.
The thermal network model of the building zone from EN ISO 13790.
Internal and solar gains are split into three parts, Φia, Φst, and Φm, connected to the indoor air (Ti), the central node (Ts), and the thermal mass (Tm) temperature nodes, respectively. The central node, Ts, is a mix of the indoor air temperature and mean radiant temperature. ΦHC is heating or cooling power supplied to or extracted from a zone. The heat transfer by ventilation (Hve) connects the supply air temperature (Tsup) with the internal environment. Htr,w is the thermal transmission coefficient of doors, windows, curtain walls, and glazed walls and is connected with the temperature of external air (Te). The thermal transmission coefficient of opaque building elements is split into the external (Htr,em) and the internal (Htr,ms) parts, connected to the single thermal capacity (Cm) representing the thermal mass of a zone. Coupling conductance Htr,is connects Ti and Ts. Values of all elements of this model can be determined according to the calculation procedure described in that standard.
At each time step, heat fluxes Φia, Φst, and Φm are obtained from heat fluxes due to internal sources (Φint) and solar irradiance (Φsol), using the following equations given in that standard:
Then, heat transfer by ventilation is computed from the relationship:
where
ρa—air density, kg/m3;
ca—specific heat of air at constant pressure, J/(kg·K);
qv—ventilation airflow rate, m3/s.
As presented in Figure 1, heat transfer by ventilation (Hve) is connected directly to the indoor air node. Hence, it directly affects thermal conditions within a considered zone. This connection, within the calculation procedure, forms the thermal–airflow coupling in the considered 5R1C model.
The dynamic solution of this network is based on the Crank–Nicholson scheme. The resulting nodal temperatures Ti and Ts are the averages for the considered one hour. The thermal mass temperatures Tm,t and Tm,t−1 are the instantaneous values at time t and t − 1, respectively. Tm,t is obtained via
The total heat flow rate to the mass node is given by
with the equivalent thermal conductances Htr,1, Htr,2, and Htr,3, as follows:
Then, the average values of nodal temperatures are computed as follows:
and
Based on them, the operative temperature can be computed:
One can notice that the ventilation airflow is calculated first, and then, the heating or cooling power is required to maintain the setpoint indoor temperature, and the resulting air temperatures are obtained. Then, in the next time step, the ventilation airflow rate (and Hve) is calculated once again from the ventilation schedule, and the whole procedure is repeated. Heat transfer by ventilation is not corrected due to actual thermal conditions, but it is computed once at each time step. This kind of thermal–airflow coupling is called sequential coupling [64,65,66]. Its schematic workflow is presented in Figure 2.
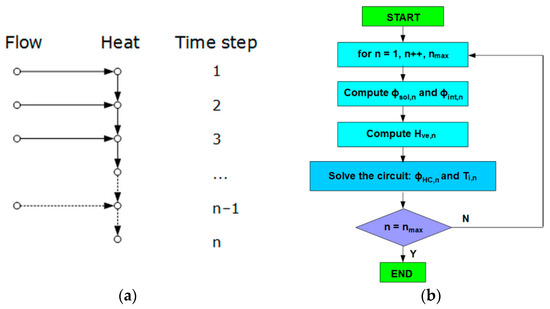
Figure 2.
Sequential airflow thermal coupling: (a) General form; (b) Calculation algorithm of EN ISO 13790.
There are also several simplifications in that model that should be remembered when comparing its results with other tools. At first, all partitions are lumped in a single thermal capacity (Cm). Next, solar gains are distributed to the “s” and “m” nodes at constant shares, independent of the position of the sun.
Heat transfer by ventilation air (Hve) is calculated under the assumption of the constant value of volumetric heat capacity of air ρaca = 1200 J/m3K, independent of outdoor thermal conditions.
Also, the numerical algorithm (Crank–Nicolson method) applied to solve the differential equation of the 5R1C model may differ from those used in other tools, which may be the next source of discrepancies.
2.3. The 5R1C Network in Matlab/Simulink
This circuit can be easily solved by the node potential method and represented in the state-space notation, which is commonly used when describing thermal models of buildings [15,20,52]. The details of this derivation can be found in [46,67].
As there is a single capacitor (Cm), there can be one dynamic equation with Tm. Input vector u is given by input variables Te, Tsup, Φm, Φst, Φia, and ΦHC. The output vector is formed from Ti and Ts. In such a case, the matrix A has the dimensions of [1 × 1], B = [1 × 6], C = [1 × 2], and D = [2 × 6]. Vector u = [6 × 1] and v = [2 × 1]. The output vector consists of Ti and Ts. Hence, we obtain
and
Then,
and:
with:
Based on this solution, the time-varying state-space model of the building given by the set of Equations (1) and (2) was built in the form of four “stvmgain” function blocks (Figure 3). The input and time-varying values of elements of the A, B, C, and D matrices at each time step are applied to the corresponding inputs.
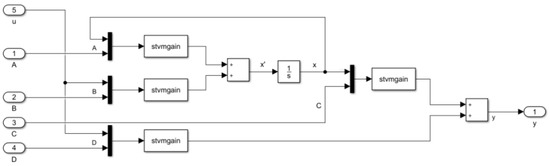
Figure 3.
The schematic diagram of the time-varying state-space block in Simulink.
This sub-system can be easily connected with the control system to maintain the required indoor air or operative temperature. The elements of the matrices A, B, C, and D given by Equations (23)–(27) and input vector (u) by Equation (21) can be calculated at each time step of the simulation. If hourly values of weather data and building occupation schedules are known, they can be generated in Matlab by the S-function written in MAT-file and then saved in data-file values of the elements of all matrices and input vector for the whole year (8760 time steps). The data are saved in the form of a row vector as a sequence of samples consisting of the time stamps (consecutive hours of the year) and the corresponding elements of the given matrix. The diagram of the whole model is presented in Figure 4.
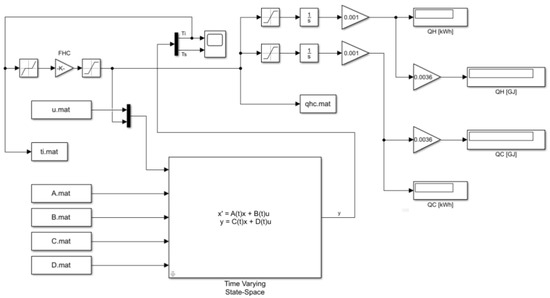
Figure 4.
The schematic diagram of the simulation model in Simulink.
The initial temperature of the thermal mass of the building was set to 20 °C in the“1/s” (integrator) block. Indoor temperature control is based on the air temperature (Ti). In the “Dead zone” block, the “Start of dead zone” and the “End of dead zone” parameters were set to 20 and 26 as the set point temperatures for heating and cooling, respectively. The temperature error gain in the FHC block was set to −5000 to obtain the negative control feedback. Then, the saturation block was used to set the maximum available thermal power ΦHC.
2.4. Validation of the Model
Validation and verification (V&V) of the results provided by various building energy performance simulation tools have recently been widely analysed [68,69,70,71].
For validation purposes, there are traditionally selected three kinds of comparative tests: analytical solutions; detailed simulation tools; or experimental data [69]. Due to a lack of appropriate measurements, the validation of the model was performed by comparison with the detailed simulations in EnergyPlus software (Version 8.1) [72]. This tool was treated as a reference numerical experiment to which the analysed 5R1C model created in the Matlab/Simulink environment was compared.
When comparing simulation results from different tools, their constraints should also be taken into account. The main features of the 5R1C model are given in Section 2.1. EnergyPlus is a much more sophisticated tool, and more advanced algorithms have been implemented for the solution of coupled thermal–airflow problems. As given in Engineering Reference [73], it is an integrated simulation tool whose major parts (building, system, and plant) must be solved simultaneously.
According to [74], in EnergyPlus, the room air models are coupled with the heat balance routines within the framework presented by Griffith and Chen [75], assuming that at each time step, the air model provides conditions to compute air temperature, which passes to load and energy routine. Then, the latter passes the values for the indoor temperature to the air model. As a result, thermal and airflow models iterate within the same time step until convergence criteria (error) are satisfied. This kind of thermal–airflow coupling is called onion coupling [76].
The simulations were performed for five cities (Table 2) in different climatic zones of Europe. These zones were defined in [77] based on the number of heating (HDD) and cooling (CDD) degree days. In all simulations, the weather data from the EnergyPlus website [72] were used.

Table 2.
Test locations. The base temperature: 18.3 °C (65 °F).
In each location, the same model of the two-storey house on the rectangular plan of 9.7 m × 8.1 m, 5.4 m high, and with a flat roof, inhabited by a family of five, was used. The longer wall of the building was oriented in the east–west direction. It had a total conditioned floor area of Af = 148.6 m2, with the total area of all surfaces facing the building zone Atot = 559.4 m2 and an internal volume of 367.45 m3.
The thermophysical properties of the used materials are given in Table 3. They were taken from [78] and the manufacturers’ data. The layers of the external partitions were given from the external to the internal side. In the case of the ceiling—from the upper to the lower storey.

Table 3.
The thermophysical properties of the opaque components.
To obtain comparable results in both tools, the same geometric dimensions of the test building were used, the weather data and simulation time step [79]. Also, the internal setpoint temperatures in all cases were set to 20 °C and 26 °C for heating and cooling, respectively. The ground temperature was calculated following EN ISO 13370 [80] and in addition, the fictitious layer of the virtual ground was applied in EnergyPlus. For windows modelling in EnergyPlus, a “Simple Glazing System” with U = 1.5 W/m2K and SHGC = 0.77 was used. The internal ceiling was described by the “InternalMass” option, not as a separate wall. Following EN 6946 [81],convection heat transfer coefficients were also assumed: 20 W/m2·K for all outside surfaces; 2.5 W/m2·K for the inside surfaces of the vertical partitions; and 0.7 W/m2·K for the inside surfaces of the roof and the ground floor. Solar absorptance of all wall surfaces and of the roof was αsr = 0.6 and αsr = 0.9, respectively. Internal gains were applied according to Table 4.

Table 4.
The schedule of internal gains in the test building.
The values of the internal gains were obtained from [82,83]. The values of the ventilation rate were taken from EN 16798-1 [84]. In the first case, mechanical ventilation was assumed. As such buildings are thermally “tight”, there was omitted impact of infiltration in this case for simplification of calculations. In the second case, natural ventilation (including infiltration) was assumed.
Hourly values of ventilation airflow in Simulink were calculated using the program written in a MAT file using ventilation schedules presented in Table 4. They were saved by this program, together with the outdoor temperature and internal and solar gains, in the data file assigned “u.mat” in Figure 4. The same ventilation schedule was used in EnergyPlus in the “ZoneVentilation” group.
Two ventilation schedules were studied, each with hourly and daily patterns. In the first case, the hourly ventilation airflow rate was taken from Table 4. In the second case, an impact of wind velocity on ventilation flow was also included, and it was assumed that hourly ventilation airflow from Table 4 was influenced by wind speed.
Ventilation airflow rate may be computed in EnergyPlus using several relationships. They are described in Engineering Reference to EnergyPlus [73]. One of them has the following form:
where
- qve—current hourly ventilation airflow rate, m3/s;
- qve,des—design ventilation airflow rate, m3/s;
- Fschedule—user-defined schedule value (dimensionless);
- vvind—wind velocity, m/s;
- a, b, c, d—user-defined coefficients (dimensionless).
This equation is based on the work by Coblenz and Achenbach [85] and has been developed for low-rise buildings [86], which means that it is applicable to the case building studied in the presented manuscript.
As stated in [73], this model was also used in DOE-2 (EnergyPlus predecessor). Adjusting the generic model to SI units, the default values of 0, 0, 0.224 (wind speed), and 0 were obtained for the above equation. At a wind speed of 4.47 m/s (10 mph), this relationship gives a factor of 1.0, and for the typical summer and winter conditions, it has the values of 0.75 and 1.34, respectively. Hence, by multiplication the design ventilation airflow rate by the hourly wind speed, the hourly ventilation airflow rate is obtained following the relationship
where vwind is the hourly wind speed (in m/s) in the considered location.
qve = qve,des· 0.224 · vwind
Daily ventilation airflow rate was calculated from hourly values using the following relationship:
Inserting the relevant values from Table 4 to Equation (30), we obtain 175.04 m3/h and 255.0 m3/h for weekdays and weekends, respectively.
The base ventilation schedule was used at first. In the next step, it was modified by the introduction of the wind-dependent factor. All tests were performed in two ways. In the first one, according to EN ISO 13790 recommendations, daily averaged airflows were assumed. In the second one, the hourly values of the ventilation airflows were applied.
2.5. Evaluation of the Model
The presented model was evaluated in two ways: by the assessment of annual energy demand for space heating and cooling; and hourly indoor air temperature.
Obtained results of the annual heating (QH) and cooling (QC) demand were used for the calculation of absolute errors, according to EN 15265 [87]:
where Qtot,ref is the total reference annual heating and cooling demand.
rQH = |QH − QH,ref|/Qtot,ref,
rQC = |QC − QC,ref|/Qtot,ref.
EN 15265 defines three levels of accuracy. The best one is level A, with rQH ≤ 0.05 and rQC ≤ 0.05; level B is with rQH ≤ 0.10 and rQC ≤ 0.10, and the worst, C, is with rQH ≤ 0.15 and rQC ≤ 0.15.
However, these errors may provide results that are too optimistic in some cases. For example, when cooling demand dominates, even significant differences in heating, when divided by total demand, may result in a low value of error for heating. Hence, it seems appropriate to use the following relative errors:
δQH = (QH,ref−QH)/QH,ref,
δQC = (QC,ref− QC)/QC,ref.
In the second step, the statistical analysis of indoor air temperature and the operative temperature was performed using the mean absolute error (MAE), the root mean square error (RMSE),the mean square error (MSE), and the coefficient of variance in the root mean square error (CV(RMSE)) [88,89,90,91,92].
Assuming that xi is the actual (reference) value of temperature taken from EnergyPlus simulations, is the value predicted by the proposed model; is the average reference value of temperature, and n is the total number of samples; then, the aforementioned metrics are given by the following relationships:
3. Results and Discussion
3.1. Energy Use for Space Heating and Cooling
As was mentioned in the previous section, the reference simulations in EnergyPlus were performed in five different cities. The same simulation scheme was applied in each city. The Simulink model was simulated similarly, but the proposed ventilation pattern was applied in two ways: for the daily averaged and hourly ventilation airflows.
The reference values of energy for space heating and cooling are given in Table 5. It can be noticed that they differ between locations both in absolute values and in shares of heating and cooling energy in the total annual demand

Table 5.
The reference annual heating and cooling demand from EnergyPlus (base case).
Results in Figure 5 indicate whether the tested model underestimates.
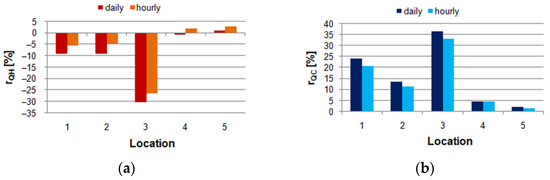
Figure 5.
Errors of the simulated annual heating and cooling demand (basic variant) in relation to total reference heating and cooling demand (following EN 15265): (a) Heating; (b) Cooling.
Hourly patterns of ventilation flow introduced in the 5R1C model resulted in better prediction of the annual heating energy consumption in three cases (1, 2, and 3). In two locations (4 and 5), daily ventilation patterns gave slightly better results.
These results are noteworthy because of the climatic conditions and the resulting heating and cooling needs of the building. According to the data in Table 2 and [77], location 1 lay in the cooling-dominated zone (about 78% of the total annual needs), while locations 4 and 5 were dominated by heating with a share of 77% and 95%, respectively. In contrast, in the other two zones, heating and cooling of the building required comparable amounts of energy. In these cases, the share of heating was in the second and third locations of 47% and 37%, respectively.
Following the EN 15265 indications, it can be stated that the analysed method provided results at the A and C levels in two (4, 5) and one (2) locations, respectively. In two places (1 and 3), the results were worse than for the C level.
However, when computing the heating errors with respect to their reference values, the situation changed significantly, showing larger deviations. In four cases, the calculated annual heating demand could be assumed to be accurate enough. But in the case of cooling, the discrepancies were more significant (Figure 6), which indicates the need to investigate the reasons for these errors. Once again, hourly patterns of ventilation resulted in better accuracy. Only for heating in locations 4 and 5,the trend was the opposite, but errors were still below 3%.
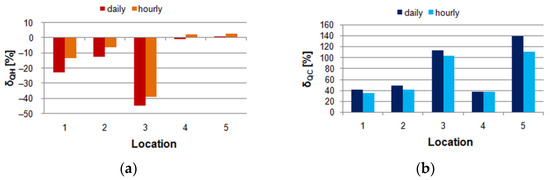
Figure 6.
Errors of the simulated annual heating and cooling demand (basic variant) in relation to their reference values: (a) Heating; (b) Cooling.
When applying wind dependency of ventilation airflow, the situation changed, as presented in Table 6. In all cases, due to the impact of wind, values of QH,ref and QC,ref changed with a larger share of cooling energy. Values of errors are given in Figure 7.

Table 6.
The reference annual heating and cooling demand from EnergyPlus (wind impact).
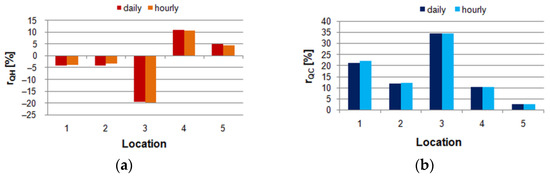
Figure 7.
Errors of the simulated annual heating and cooling demand in relation to the total reference heating and cooling demand (following EN 15265) in wind-induced ventilation: (a) Heating; (b) Cooling.
One result for heating (location 3) was worse, with a value of −19.8% in comparison to −19.6% for the daily schedule. Different outcomes were noticed for cooling, where in all locations, the errors for hourly values were slightly higher, but these differences were almost unnoticeable (Figure 7). Summing up, the model with daily averaged ventilation flow passed the B level in one location (5), the C level in two locations (2 and 4), and in the remaining two (1 and 3), it was out of the range. For hourly schedules, results were better, and in A and C levels, there were one (5) and two (2 and 4) locations, respectively.
When considering relative errors (Figure 8), the situation was similar. In the case of heating, in one case, the hourly schedule resulted in worse results for annual heating needs. For cooling, in all cases, daily patterns produced slightly better results. However, these differences were almost unnoticeable. Assuming the value of 15% as the maximum acceptable level, the heating demand was calculated properly in three cases (1, 2, and 5).
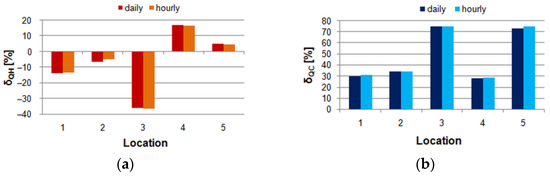
Figure 8.
Relative errors of the simulated annual heating and cooling demand in comparison to total reference heating and cooling demand in wind-induced ventilation: (a) Heating; (b) Cooling.
The differences between daily and hourly errors presented in Figure 7 and Figure 8 are almost unnoticeable when compared to those in Figure 5 and Figure 6. It can be surprising but can be explained by a short analysis of wind velocities in all locations. The daily values were computed using hourly weather data. Then, the degree of agreement between the hourly and daily values was assessed using statistical indicators given in Section 2.5. The obtained values of MSE and RMSE errors were from 0.6 m/s to 1.5 m/s and from 1.0 m/s to 2.0 m/s, respectively. According to works on wind velocity prediction [93,94,95], the values of this order mean low differences between these two datasets.
To obtain a wider view of these values, a short comparison with other studies devoted to simulations of the thermal performance of residential buildings using the simple hourly method of EN ISO 13790 is needed. The summary of these works is given in Table 7. If more than one test case was investigated, then the maximum values were given (the worst case).

Table 7.
Maximum errors of heating and cooling demand of residential buildings calculated using the 5R1C model.
Different ways of the 5R1C model’s implementation were used. MS Excel, Matlab 2010 and 2017, and Python programming were dominant. In three cases, the authors did not give information on the simulation method and tool. As the reference, EnergyPlus was used (in four cases), and in one case, IDA ICE, TRNSYS 17, and PHPP were used.
Values of errors for heating varied from −44.3% to 33.0%. In the case of cooling, the discrepancies from −29.6% to 53.0% were reported. For total heating and cooling, demand differences were from −12.0% to 10.6%. However, in selected cases, the discrepancies were larger.
Atmaca et al. [97] studied a residential building located in Istanbul (Turkey), with a floor area of 65.3 m2. Various construction materials for the external walls were considered: steel; brick; aerated concrete; concrete; and stone with varying insulation thickness. The results showed that the simple hourly method, in comparison to the reference simulations in EnergyPlus, usually overestimated cooling needs (by 24.7% to 32.7%). However, two significant exceptions, of −272% and −268%, in the case of cooling, were noticed for brick walls with 3.75 cm of insulation and 77 cm of concrete walls, respectively. But as no further details on these discrepancies were provided, there was no certainty that these values were not the result of an editorial error rather than a calculation error. Heating needs were underestimated from −11.8% to −30.1%, but in the case of a steel wall, overestimation from 19.2% to 21.6% was obtained.
3.2. Indoor Air Temperature
Simulations showed the positive impact of hourly ventilation patterns on the accuracy of indoor temperature prediction by the 5R1C model (Table 8) for the base case.

Table 8.
Statistical measures for indoor air temperature simulations at the base case.
In all studied locations, the statistical measures of hourly indoor air temperature were better for hourly (H) than for daily averaged (D) ventilation schedules. A more detailed analysis of the statistical metrics [102,103,104] provides information on the quality of the studied solution.
The MAE error, interpreted as the average absolute difference between the reference and modelled temperature, was below 0.52 °C in all cases. Its value was lower for hourly patterns from 0.03 °C (4-rd location) to 0.07 °C (the first and second locations).
RMSE measures the average distance between the predicted and reference values. In the considered case, it varied from 0.47 °C (4-rd location) to 0.67 °C (the first and second locations). RMSE takes into account the higher-weight large errors, being more sensitive when they are undesirable. Its low values mean that there were no significant deviations between the reference and modelled indoor air temperature.
The mean squared error (MSE) provides information about the distance between the regression line and the considered set of points. In all analysed cases, it did not exceed 0.48 °C2 and 0.22 °C2 for daily and hourly patterns, respectively.
The coefficient of variation in the RMSE (CV RMSE) is the RMSE divided by the mean value of the reference variable. It measures the variability in the errors between the reference and modelled temperature. Following ASHRAE recommendations, for the well-performing model, CV RMSE should not exceed 15% [63,105]. Hence, in all cases, the model performed with satisfactory accuracy.
Taking into account wind as a time-varying factor, driving ventilation did not negatively affect the accuracy of the results (Table 9).

Table 9.
Statistical measures for indoor air temperature simulations for doubled ventilation.
As previously mentioned, hourly ventilation patterns provided more accurate results in all locations. MAE was below 0.49 °C, and it was larger in all locations for daily than for hourly ventilation schedules by up to 0.05 °C in the second location. RMSE did not exceed the values of 0.69 °C and 0.68 °C. Satisfactory results were also obtained for MSE and CV(RMSE) measures.
Several authors also reported the results of indoor air temperature measurements and simulations with the application of the 5R1C network. Some of them presented only graphs with no detailed values [106,107]. However, there are also wider studies.
Prada et al. [108] simulated, using the simple hourly method and TRNSYS, and measured indoor air temperature. They chose a room with a floor area of 109.17 m2 in a university building. Ventilation was turned on during the building’s opening hours with a constant air change rate of 1 per hour. They reported that the range of variation between the values predicted by EN ISO 13790 and measured reached ±13%.
Tudor et al. [109] conducted a 33-day monitoring campaign of a sports hall with heating and cooling based on thermo-active building systems supplied by a ground source absorption heat pump. Hourly simulations at a constant airflow rate of 3000 m3/h resulted in mean bias error (MBE) and RMSE of indoor air temperature of 0.09 °C and 1.37 °C, respectively.
Panão et al. [110] modified the 5R1C model for the simulation of thermal conditions in a test cell with a double skin façade under various conditions. MAE of indoor air temperature in a cell compared to measurements did not exceed 1.5 °C. They also showed a review of experiments in buildings and test cells in free-running conditions, showing that the mean and maximum errors of internal air temperature simulated with the use of more advanced tools (EnergyPlus, ESP-r, TRNSYS, or artificial networks) were from 0.3 °C to 2.9 °C and from 1.8 °C to 21.9 °C, respectively.
Yang et al. [111] simulated and experimentally evaluated the performance of a henhouse. The temperature was measured at 14 various points in different areas in the front, middle, and back of the hen house for 90 days of the experiment. Comparison with the simulations revealed that the maximum error between the predicted and measured indoor temperatures was 6.85%.
Michalak [112] measured thermal conditions in a single room of a multi-story building with mechanical ventilation. During the experiments, the radiator in the room was turned off, and ventilation air was assumed to be the only heat source. Constant ventilation airflow was assumed during the whole experiment. Comparison of simulations with measurements resulted in MAE and RMSE of indoor air of 2.37 °C and 2.45 °C, respectively. When the author additionally included heat flux from the bottom story through the floor, MAE = 1.28 °C and RMSE = 1.38 °C were obtained. In addition, MSE dropped from 5.98 °C2 to 1.91 °C2.
The presented values confirm that the prediction of indoor air temperature with the 5R1C model of EN ISO 13790 in comparison to the detailed simulation tool is very accurate despite significant variation in ventilation airflow rate in all considered cases.
3.3. Operative Temperature
Simulated hourly operative temperature showed accuracy comparable to that in the case of the indoor air temperature in both ventilation patterns (Table 10 and Table 11).

Table 10.
Statistical measures for operative temperature simulations for the base case.

Table 11.
Statistical measures for operative temperature simulations for doubled ventilation.
In the base case, MAE varied from 0.35 °C (location 2) to 0.40 °C (1) and from 0.34 °C (4) to 0.42 °C (2) for the daily and hourly flow rates, respectively. In the second pattern, MAE was from 0.35 °C (location 2) to 0.40 °C (1) and from 0.35 °C (2) to 0.39 °C (3) in the same order, as previously discussed. CV(RMSE) did not exceed 1.77% and 2.38% in the base case and in doubled flows, respectively.
In indoor thermal comfort assessment in modern, especially low-energy and passive, buildings, operative temperature is of special significance. Despite that, few authors considered operative temperature prediction by the 5R1C model predictions.
Kalmár [113] measured the operative temperature in an educational building with a high percentage of glazing during summer and then compared it with values obtained from the model of EN ISO 13790. The authors noticed large differences of up to 10 °C in one day with high direct solar radiation. However, as the authors stated, these discrepancies could be reduced when changing the location of measurements to one that is less influenced by solar radiation.
Csáky [61] measured the internal air and mean radiant temperature in two, east- and west-oriented, offices for four days in August. These data were used as inputs for the 5R1C model to obtain cooling loads for different variants of glazing area and orientation. No comparisons between simulations and measurements were given.
This short comparison confirms that the aspects of indoor comfort during simulations of buildings should also be taken into account. In [114,115], the authors analysed various building energy performance simulation tools in terms of indoor thermal comfort indicators, especially the mean radiant temperature and operative temperature. The obtained results showed that good knowledge of implemented algorithms and mathematical models was necessary to perform reliable simulations, often being the basis for further design. However, the EN ISO 13790 model was not considered.
4. Conclusions
This paper presents the simulation of the thermal performance of a building with varying ventilation airflow. Using the stvmgain S-function, a state-space model with time-varying parameters was built. The 5R1C network was implemented in the Matlab/Simulink environment. Based on a model of a single-family building, the comparative simulations in EnergyPlus were also performed.
The results obtained for the annual energy use for space heating and cooling were more accurate in the case of hourly than daily averaged ventilation airflow rates. In comparison to the reference values from EnergyPlus, the errors were below 10%. However, in several cases of cooling, their values exceeded 30%, which was unacceptable. Other researchers reported even worse values but without a deeper analysis of the sources of these discrepancies. Only Capizzi et al. [116] noted that during their experiments, they measured total energy consumption, including sensible and latent, while the 5R1C model was intended to provide only sensible energy.
Errors for cooling were larger than for heating, which is in line with findings presented by Vivian et al. [44]. They suggested that the 5R1C model was less capable of properly predicting cooling than heating power. As that model is still widely used in scientific and engineering practice, these findings require further analysis to explain the reasons for such large differences.
The second part of this study was devoted to the analysis of the indoor air temperature simulation. The obtained results were very good with mean absolute error MAE < 0.49 °C, root mean square error RMSE < 0.69 °C, mean square error MSE < 0.47 °C2, and Coefficient of Variation in the RMSE: CV RMSE < 3.09%. For operative temperature, the CV(RMSE) was below 2.38%. Regardless of location, the results were better for hourly ventilation schedules.
So far, there has not been a study devoted to this problem. Therefore, this paper confirms that daily averaging of ventilation airflow, suggested by EN ISO 13790, should not be applied when using the simple hourly method. This is made all the easier by the fact that this method allows for the use of hourly building use patterns and ambient climate parameters.
Funding
Research project supported/partly supported by the program “Excellence initiative—research university” for the AGH University of Science and Technology.
Data Availability Statement
Data are available on request.
Conflicts of Interest
The author declares no conflict of interest.
References
- Both, W. Measurement of the thermal impedance of laser diodes via thermal transients. J. Therm. Anal. 1988, 34, 1311–1320. [Google Scholar] [CrossRef]
- Lauster, M.; Teichmann, J.; Fuchs, M.; Streblow, R.; Mueller, D. Low order thermal network models for dynamic simulations of buildings on city district scale. Build. Environ. 2014, 73, 223–231. [Google Scholar] [CrossRef]
- Low, Y.L.; See, B.L.I.; Tan, C.P.H.; Mou, J.Q.; Ong, E.H. Thermal network model for temperature prediction in hard disk drive. Microsyst. Technol. 2009, 15, 1653–1656. [Google Scholar] [CrossRef]
- Ziapour, B.M.; Shaker, H. Heat transfer characteristics of a two-phase closed thermosyphon using different working fluids. Heat Mass Transf. 2010, 46, 307–314. [Google Scholar] [CrossRef]
- Ma, L.; Yang, Y.; Liu, J. Cooling of high power LEDs through ventilating ambient air to front surface of chip. Heat Mass Transf. 2013, 49, 85–94. [Google Scholar] [CrossRef]
- Ghorbani, M.; Akbarpour, S. The multi-zone model of the low heat rejection engine for DI diesel injection engines. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 365–375. [Google Scholar] [CrossRef]
- Jung, S.; Park, S.H.; Choi, B.C. Power control strategy for preventing thermal failure of passively cooled automotive battery packs. Int. J. Automot. Technol. 2017, 18, 117–124. [Google Scholar] [CrossRef]
- Sameti, M.; Kasaeian, A. Numerical simulation of combined solar passive heating and radiative cooling for a building. Build. Simul. 2015, 8, 239–253. [Google Scholar] [CrossRef]
- Deng, J.; Yang, X.; Xu, Y.; Yang, M. Entransy analysis on the thermal performance of flat plate solar air collectors. Build. Simul. 2017, 10, 193–202. [Google Scholar] [CrossRef]
- Buonomano, A.; Forzano, C.; Kalogirou, S.A.; Kyriakou, C.; Palombo, A. Building façade integrated solar thermal collectors for water heating: Simulation model and case studies. In Proceedings of the First International Conference on Building Integrated Renewable Energy Systems, Dublin, Ireland, 6–9 March 2017. [Google Scholar]
- Chen, H.; Wang, X. A modified zone model for estimating equivalent room thermal capacity. Front. Energy 2013, 3, 351–357. [Google Scholar] [CrossRef]
- Dong, B.; Gorbounov, M.; Yuan, S.; Wu, T.; Srivastav, A.; Bailey, T.; O’Neill, Z. Integrated energy performance modeling for a retail store building. Build. Simul. 2013, 6, 283–295. [Google Scholar] [CrossRef]
- Mara, T.A.; Tarantola, S. Application of Global Sensitivity Analysis of Model Output to Building Thermal Simulations. Build. Simul. 2008, 1, 290–302. [Google Scholar] [CrossRef]
- Bertagnolio, S.; Andre, P.; Lemort, V. Simulation of a building and its HVAC system with an equation solver: Application to audit. Build. Simul. 2010, 3, 139–152. [Google Scholar] [CrossRef]
- Belić, F.; Slišković, D.; Hocenski, Ž. Detailed Thermodynamic Modeling of Multi-Zone Buildings with Resistive-Capacitive Method. Energies 2021, 14, 7051. [Google Scholar] [CrossRef]
- Ahn, J. Thermal Control Processes by Deterministic and Network-Based Models for Energy Use and Control Accuracy in a Building Space. Processes 2021, 9, 385. [Google Scholar] [CrossRef]
- Freier, J.; Ceccolini, C.; Arnold, M.; Hesselbach, J. A Lumped-Capacitance Model for the Assessment of Energy Flexibility in different Building Typologies. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Turin, Italy, 1–4 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Underwood, C.P. An improved lumped parameter method for building thermal modelling. Energy Build. 2014, 79, 191–201. [Google Scholar] [CrossRef]
- Tindale, A. Third-order lumped-parameter simulation method. Build. Serv. Eng. Res. Technol. 1993, 14, 87–97. [Google Scholar] [CrossRef]
- Lombard, C.; Mathews, E. A two-port envelope model for building heat transfer. Build. Environ. 1998, 34, 19–30. [Google Scholar] [CrossRef]
- Gouda, M.; Danaher, S.; Underwood, C. Low-order model for the simulation of a building and its heating system. Build. Serv. Eng. Res. Technol. 2000, 21, 199–208. [Google Scholar] [CrossRef]
- EN ISO 13790; Energy Performance of Buildings—Calculation of Energy Use for Space Heating and Cooling. International Organization for Standardization: Geneva, Switzerland, 2009.
- Mijakowski, M.; Narowski, P.; Sowa, J. Integrated calculations of thermal behaviour of buildings and processes in AHU—The tool for assessment of energy performance of complex buildings. In Proceedings of the Eleventh International IBPSA Conference, Glasgow, Scotland, 27–30 July 2009; pp. 875–882. Available online: http://www.ibpsa.org/proceedings/bs2009/bs09_0875_882.pdf (accessed on 14 September 2023).
- Zangheri, P.; Armani, R.; Pietrobon, M.; Pagliano, L.; Boneta, M.F.; Müller, A. Heating and Cooling Energy Demand and Loads for Building Types in Different Countries of the EU; Report in the Frame of the EU Project ENTRANZE; Politecnico di Milano: Milan, Italy, 2014; Available online: https://www.entranze.eu/files/downloads/D2_3/Heating_and_cooling_energy_demand_and_loads_for_building_types_in_different_countries_of_the_EU.pdf (accessed on 22 August 2023).
- Tagliabue, L.C.; Buzzetti, M.; Marenzi, G. Energy performance of greenhouse for energy saving in buildings. Energy Procedia 2012, 30, 1233–1242. [Google Scholar] [CrossRef][Green Version]
- Barwińska Małajowicz, A.; Knapková, M.; Szczotka, K.; Martinkovičová, M.; Pyrek, R. Energy Efficiency Policies in Poland and Slovakia in the Context of Individual Well-Being. Energies 2023, 16, 116. [Google Scholar] [CrossRef]
- Barwińska-Małajowicz, A.; Pyrek, R.; Szczotka, K.; Szymiczek, J.; Piecuch, T. Improving the Energy Efficiency of Public Utility Buildings in Poland through Thermomodernization and Renewable Energy Sources—A Case Study. Energies 2023, 16, 4021. [Google Scholar] [CrossRef]
- Szczotka, K.; Barwińska-Małajowicz, A.; Szymiczek, J.; Pyrek, R. Thermomodernization as a Mechanism for Improving Energy Efficiency and Reducing Emissions of Pollutants into the Atmosphere in a Public Utility Building. Energies 2023, 16, 5026. [Google Scholar] [CrossRef]
- Hesaraki, A.; Myhren, J.A.; Holmberg, S. Multi-zone Demand-controlled Ventilation in Residential Buildings: An experimental case study. In Proceedings of the 35th AIVC Conference, 4th TightVent Conference and 2nd Venticool Conference, Poznań, Poland, 24–25 September 2014. [Google Scholar]
- Ben-David, T.; Rackes, A.; Lo, L.J.; Wen, J.; Waring, M.S. Optimizing ventilation: Theoretical study on increasing rates in offices to maximize occupant productivity with constrained additional energy use. Build. Environ. 2019, 166, 106314. [Google Scholar] [CrossRef]
- Witkowska, A.; Krawczyk, D.A.; Rodero, A. Investment Costs of Heating in Poland and Spain—A Case Study. Proceedings 2019, 16, 40. [Google Scholar] [CrossRef]
- Mokhtari, F.; Semmar, D.; Chikhi, M.; Merzouk, N.K.; Oukaci, S. Investigation of the improvement building envelope impact on energy consumption using energy audit. MATEC Web Conf. 2020, 307, 01031. [Google Scholar] [CrossRef][Green Version]
- Franco, A.; Schito, E. Definition of Optimal Ventilation Rates for Balancing Comfort and Energy Use in Indoor Spaces Using CO2 Concentration Data. Buildings 2020, 10, 135. [Google Scholar] [CrossRef]
- Rucińska, J.; Trząski, A. Measurements and Simulation Study of Daylight Availability and Its Impact on the Heating, Cooling and Lighting Energy Demand in an Educational Building. Energies 2020, 13, 2555. [Google Scholar] [CrossRef]
- Bonomolo, M.; Di Lisi, S.; Leone, G. Building Information Modelling and Energy Simulation for Architecture Design. Appl. Sci. 2021, 11, 2252. [Google Scholar] [CrossRef]
- Campana, J.P.; Morini, G.L. BESTEST and EN ISO 52016 Benchmarking of ALMABuild, a New Open-Source Simulink Tool for Dynamic Energy Modelling of Buildings. Energies 2019, 12, 2938. [Google Scholar] [CrossRef]
- Corbin, C.D.; Henze, G.P.; May-Ostendorp, P. A model predictive control optimization environment for real-time commercial building application. J. Build. Perform. Simul. 2013, 6, 159–174. [Google Scholar] [CrossRef]
- Marenzi, G. Building Simulation Models in Control Systems for Energy Efficiency. Ph.D. Thesis, Polytechnic University of Milan, Milan, Italy, 2017. Available online: https://www.politesi.polimi.it/handle/10589/132577?mode=full (accessed on 1 December 2023).
- Zadeiks, K.; Senfelds, A.; Avotins, A.; Dzenis, M. Development of Dynamic Simulation Model for Building Energy Management Systems. In Proceedings of the ERDEV 2018, Jelgava, Latvia, 23–25 May 2018; Available online: https://www.tf.lbtu.lv/conference/proceedings2018/Papers/N374.pdf (accessed on 10 July 2023).
- Dzelzitis, E.; Zadeiks, K.; Avotins, A.; Senfelds, A. Selection of Key Parameters for Energy Management of Building Heating Systems. In Proceedings of the 2019 Nordic Workshop on Power and Industrial Electronics (NORPIE), Narvik, Norway, 25–27 September 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Buonomano, A.; Forzano, C.; Kalogirou, S.A.; Palombo, A. Building-façade integrated solar thermal collectors: Energy-economic performance and indoor comfort simulation model of a water based prototype for heating, cooling, and DHW production. Renew. Energy 2019, 137, 20–36. [Google Scholar] [CrossRef]
- Cirrincione, L.; Marvuglia, A.; Peri, G.; Rizzo, G.; Scaccianoce, G. The European standards for energy efficiency in buildings: An analysis of the evolution with reference to a case study. AIP Conf. Proc. 2019, 2191, 020049. [Google Scholar] [CrossRef]
- EN ISO 52016-1; Energy Performance of Buildings—Energy Needs for Heating and Cooling, Internal Temperatures and Sensible and Latent Heat Loads—Part 1: Calculation Procedures. European Committee for Standardization: Brussels, Belgium, 2017.
- Vivian, J.; Zarrella, A.; Emmi, G.; De Carli, M. Analysis of simplified lumped-capacitance models to simulate thermal behaviour of buildings. In Proceedings of the 3rd Building Simulation Applications Conference BSA 2017, Bozen-Bolzano, Italy, 8–10 February 2017; pp. 265–272. Available online: http://www.ibpsa.org/proceedings/BSA2017/9788860461360_33.pdf (accessed on 14 September 2023).
- VDI 6007 Part 1 1:2015-06; Calculation of Transient Thermal Response of Rooms and Buildings: Modelling of Rooms. Beuth Verlag GmbH: Berlin, Germany, 2015.
- Michalak, P. The development and validation of the linear time varying Simulink-based model for the dynamic simulation of the thermal performance of buildings. Energy Build. 2017, 141, 333–340. [Google Scholar] [CrossRef]
- Deshko, V.; Sukhodub, I.; Bilous, I. Mathematical models for determination of energy need for heating. J. New Technol. Environ. Sci. 2017, 1, 45–51. [Google Scholar]
- Bilous, I.Y.; Deshko, V.I.; Sukhodub, I.O. Mathematical models for determination of specific energy need for heating used in Ukraine. J. New Technol. Environ. Sci. 2018, 2, 13–25. [Google Scholar]
- Hespanha, J.P. Linear Systems Theory; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Sandberg, H. Linear Time Varying Systems: Modelling and Reduction; Department of Automatic Control, Lund Institute of Technology: Lund, Sweden, 2002. [Google Scholar]
- Williams, R.L.; Lawrence, D.A. Linear State-Space Control Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Fateh, A.; Borelli, D.; Spoladore, A.; Devia, F. A State-Space Analysis of a Single Zone Building Considering Solar Radiation, Internal Radiation, and PCM Effects. Appl. Sci. 2019, 9, 832. [Google Scholar] [CrossRef]
- Harish, V.S.K.V.; Kumar, A.; Alam, T.; Blecich, P. Assessment of State-Space Building Energy System Models in Terms of Stability and Controllability. Sustainability 2021, 13, 11938. [Google Scholar] [CrossRef]
- Ma, L.; Huang, Y.; Zhang, J.; Zhao, T. A Model Predictive Control for Heat Supply at Building Thermal Inlet Based on Data-Driven Model. Buildings 2022, 12, 1879. [Google Scholar] [CrossRef]
- (Jos) van Schijndel, A.W.M. A review of the application of SimuLink S-functions to multi domain modelling and building simulation. J. Build. Perform. Simul. 2014, 7, 165–178. [Google Scholar] [CrossRef]
- Kalagasidis, S.A. A multi-level modelling and evaluation of thermal performance of phase change materials in buildings. J. Build. Perform. Simul. 2013, 7, 289–308. [Google Scholar] [CrossRef]
- Simulink®. Developing S-Functions, R2015a. 2015. MathWorks®. Available online: http://www.mathworks.com/help/pdf_doc/simulink/sfunctions.pdf (accessed on 14 September 2023).
- Kajiwara, H.; Apkarian, P.; Gahinet, P. Wide-Range Stabilization of an Arm-Driven Inverted Pendulum Using Linear Parameter-Varying Techniques. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Boston, MA, USA, 10–12 August 1998; pp. 1853–1865. Available online: http://pierre.apkarian.free.fr/papers/AIAA98.pdf (accessed on 14 September 2023).
- Sourbron, M.; Verhelst, C.; Helsen, L. Building models for model predictive control of office buildings with concrete core activation. J. Build. Perform. Simul. 2013, 6, 175–198. [Google Scholar] [CrossRef]
- Mutani, G.; Todeschi, V.; Beltramino, S. Energy Consumption Models at Urban Scale to Measure Energy Resilience. Sustainability 2020, 12, 5678. [Google Scholar] [CrossRef]
- Csáky, I. Analysis of Daily Energy Demand for Cooling in Buildings with Different Comfort Categories—Case Study. Energies 2021, 14, 4694. [Google Scholar] [CrossRef]
- Pfafferott, J.; Rißmann, S.; Halbig, G.; Schröder, F.; Saad, S. Towards a Generic Residential Building Model for Heat–Health Warning Systems. Int. J. Environ. Res. Public Health 2021, 18, 13050. [Google Scholar] [CrossRef]
- Cui, Y.; Zhu, Z.; Zhao, X.; Li, Z.; Qin, P. Bayesian Calibration for Office-Building Heating and Cooling Energy Prediction Model. Buildings 2022, 12, 1052. [Google Scholar] [CrossRef]
- Jreijiry, D.; Husaunndee, A.; Inard, C.; Villenave, J.G. Control of ventilation in buildings using SIMBAD building and HVAC toolbox. In Proceedings of the Building Simulation 2003, Eighth International IBPSA Conference, Eindhoven, The Netherlands, 11–14 August 2003; pp. 591–598. Available online: http://www.ibpsa.org/proceedings/bs2003/bs03_0591_598.pdf (accessed on 16 October 2023).
- Brohus, H.; Frier, C.; Heiselberg, P.; Haghighat, F. Quantification of uncertainty in predicting building energy consumption: A stochastic approach. Energy Build. 2012, 55, 127–140. [Google Scholar] [CrossRef]
- Ramponi, R. Computational Modeling of Urban Wind Flow and Natural Ventilation Potential of Buildings; Technische Universiteit Eindhoven: Eindhoven, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Michalak, P. The simple hourly method of EN ISO 13790 standard in Matlab/Simulink: A comparative study for the climatic conditions of Poland. Energy 2014, 75, 568–578. [Google Scholar] [CrossRef]
- Neymark, J.; Judkoff, R.; Knabe, G.; Le, H.T.; Dürig, M.; Glass, A.; Zweifel, G. Applying the building energy simulation test (BESTEST) diagnostic method to verification of space conditioning equipment models used in whole-building energy simulation programs. Energy Build. 2002, 34, 917–931. [Google Scholar] [CrossRef]
- Im, P.; New, R.J.; Joe, J. Empirical Validation of Building Energy Modeling using Flexible Research Platform. In Proceedings of the 16th IBPSA International Conference, Rome, Italy, 2–4 September 2019; Available online: https://www.osti.gov/servlets/purl/1607030 (accessed on 1 December 2023).
- Palladino, D.; Nardi, I. Approaching the validation of building energy models: Billing vs indoor environmental data. E3S Web Conf. 2020, 197, 02001. [Google Scholar] [CrossRef]
- Del Ama Gonzalo, F.; Moreno Santamaría, B.; Montero Burgos, M.J. Assessment of Building Energy Simulation Tools to Predict Heating and Cooling Energy Consumption at Early Design Stages. Sustainability 2023, 15, 1920. [Google Scholar] [CrossRef]
- EnergyPlus. Available online: https://energyplus.net (accessed on 1 December 2023).
- U.S. Department of Energy. EnergyPlus™ Version 22.1.0 Documentation: Engineering Reference; U.S. Department of Energy: Washington, DC, USA, 2022. Available online: https://energyplus.net/assets/nrel_custom/pdfs/pdfs_v22.1.0/EngineeringReference.pdf (accessed on 1 December 2023).
- Pan, Y.; Li, H.; Huang, Z. Study on energy modeling methods of atrium buildings. In Proceedings of the Eleventh International IBPSA Conference “Building Simulation 2009”, Glasgow, Scotland, 27–30 July 2009; pp. 250–257. Available online: http://www.ibpsa.org/proceedings/BS2009/BS09_0250_257.pdf (accessed on 1 December 2023).
- Griffith, B.; Chen, Q.Y. Framework for Coupling Room Air Models to Heat Balance Model Load and Energy Calculations (RP-1222). HVAC&R Res. 2004, 10, 91–111. [Google Scholar] [CrossRef]
- Oropeza-Perez, I.; Østergaard, P.A.; Remmen, A. Ventilated buildings optimization by using a coupled thermal-airflow simulation program. In Proceedings of the Building Simulation 2011, 12th Conference of International Building Performance Simulation Association, Sydney, Austrilia, 14–16 November 2011; pp. 2666–2671. Available online: https://vbn.aau.dk/ws/files/148212063/VENTILATED_BUILDINGS_OPTIMISATION_BY_USING_A_COUPLED_THERMALAIRFLOW.pdf (accessed on 1 December 2023).
- Tsikaloudaki, K.; Laskos, K.; Bikas, D. On the Establishment of Climatic Zones in Europe with Regard to the Energy Performance of Buildings. Energies 2012, 5, 32–44. [Google Scholar] [CrossRef]
- EN ISO 10456; Building Materials and Products—Hygrothermal Properties—Tabulated Design Values and Procedures for Determining Declared and Design Thermal Values. International Organization for Standardization: Geneva, Switzerland, 2007.
- Kim, Y.-J.; Yoon, S.-H.; Park, C.-S. Stochastic comparison between simplified energy calculation and dynamic simulation. Energy Build. 2013, 64, 332–342. [Google Scholar] [CrossRef]
- ISO 13370:2017; Thermal Performance of Buildings—Heat Transfer via the Ground—Calculation Methods. International Organization for Standardization: Geneva, Switzerland, 2017.
- ISO 6946:2017; Building Components and Building Elements-Thermal Resistance and Thermal Transmittance-Calculation Methods. International Organization for Standardization: Geneva, Switzerland, 2017.
- EnergyPlus™ Version 9.6.0 Documentation. Input Output Reference. U.S. Department of Energy, 23 September 2021. Available online: https://energyplus.net/assets/nrel_custom/pdfs/pdfs_v9.6.0/InputOutputReference.pdf (accessed on 1 December 2023).
- Ahmed, K.; Kurnitski, J.; Olesen, B.W. Data for Occupancy Internal Heat Gain Calculation in Main Building Categories. Data Brief 2017, 15, 1030–1034. [Google Scholar] [CrossRef] [PubMed]
- EN 16798-5-1; Energy Performance of Buildings—Ventilation for Buildings—Part 1: Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings Addressing Indoor Air Quality, Thermal Environment, Lighting and Acoustics—Module M1–6. The European Committee for Standardization: Brussels, Belgium, 2017.
- Achenbach, P.R.; Coblenz, C. Field measurements of air infiltration in ten electrically heated houses. Ashrae Trans. 1963, 69, 358–365. [Google Scholar]
- Ng, L.C.; Persily, A.K.; Emmerich, S.J. Improving infiltration modeling in commercial building energy models. Energy Build. 2015, 88, 316–323. [Google Scholar] [CrossRef]
- EN 15265; Energy Performance of Buildings—Calculation of Energy Needs for Space Heating and Cooling Using Dynamic Methods—General Criteria and Validation Procedures. European Committee for Standardization: Brussels, Belgium, 2007.
- Pham, H. A New Criterion for Model Selection. Mathematics 2019, 7, 1215. [Google Scholar] [CrossRef]
- Kadad, I.M.; Ramadan, A.A.; Kandil, K.M.; Ghoneim, A.A. Relationship between Ultraviolet-B Radiation and Broadband Solar Radiation under All Sky Conditions in Kuwait Hot Climate. Energies 2022, 15, 3130. [Google Scholar] [CrossRef]
- Piotrowski, P.; Rutyna, I.; Baczyński, D.; Kopyt, M. Evaluation Metrics for Wind Power Forecasts: A Comprehensive Review and Statistical Analysis of Errors. Energies 2022, 15, 9657. [Google Scholar] [CrossRef]
- Salah, S.; Alsamamra, H.R.; Shoqeir, J.H. Exploring Wind Speed for Energy Considerations in Eastern Jerusalem-Palestine Using Machine-Learning Algorithms. Energies 2022, 15, 2602. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, L.; Qian, J. Application of Combined Models Based on Empirical Mode Decomposition, Deep Learning, and Autoregressive Integrated Moving Average Model for Short-Term Heating Load Predictions. Sustainability 2022, 14, 7349. [Google Scholar] [CrossRef]
- Abdel-Aal, R.E.; Elhadidy, M.A.; Shaahid, S.M. Modeling and forecasting the mean hourly wind speed time series using GMDH-based abductive networks. Renew. Energy 2009, 34, 1686–1699. [Google Scholar] [CrossRef]
- Tahir, Z.U.R.; Asim, M.; Jamil, S.; Shad, R.; Hayat, N.; Moaz, A.; Akram, M.T.; Safyan, M. Comparison of Reanalysis, Analysis and Forecast datasets with measured wind data for a Wind Power Project in Jhimpir, Pakistan. J. Phys. Conf. Ser. 2018, 1102, 012004. [Google Scholar] [CrossRef]
- Christoforou, E.; Emiris, I.Z.; Florakis, A.; Rizou, D.; Zaharia, S. Spatio-Temporal Deep Learning for Day-Ahead Wind Speed Forecasting Relying on WRF Predictions. Energy Syst. 2021, 14, 473–493. [Google Scholar] [CrossRef]
- Vujnović, N.; Vidak, D.; Jakšić, F.; Kedmenec, Ž.; Dović, D.; Horvat, I. Differences in calculations of annual heating and cooling energy need carried out by modified simple hourly method and dynamic simulations. Trans. Famena 2021, XLV, 35–48. [Google Scholar] [CrossRef]
- Atmaca, M.; Kalaycioglu, E.; Yilmaz, Z. Evaluation of the Heating & Cooling Energy Demand of a Case Residential Building by Comparing the National Calculation Methodology of Turkey and EnergyPlus through Thermal Capacity Calculations; Technical Report; Energy Systems Laboratory, Texas A&M University: College Station, TX, USA, 2011. [Google Scholar]
- Fantin Do Amaral Silva, G.; Bergel Gómez, R. Energy Performance Modelling Introducing the Building Early-Stage Design Optimization Tool (BeDOT). Master’s Thesis, Structural Engineering and Building Technology, Chalmers University of Technology, Gothenburg, Sweden, 2018. Available online: https://odr.chalmers.se/items/6cb65337-b57e-431d-aee5-0ee0c1e72e5a (accessed on 1 December 2023).
- Bergel, R.; Fantin do Amaral Silva, G.; Tillberg, M.; Sasic Kalagasidis, A. Energy Performance Modelling: Introducing the Building Early-stage Design Optimization Tool (BeDOT). In Proceedings of the 16th IBPSA Conference, Rome, Italy, 2–4 September 2019; pp. 278–285. [Google Scholar] [CrossRef]
- Bilous, I.Y.; Deshko, V.I.; Sukhodub, I.O. Building energy modeling using hourly infiltration rate. Mag. Civ. Eng. 2020, 96, 27–41. [Google Scholar] [CrossRef]
- Džiugaitė-Tumėnienė, R.; Jankauskas, V.; Motuzienė, V. Energy balance of a low energy house. J. Civ. Eng. Manag. 2012, 18, 369–377. [Google Scholar] [CrossRef]
- Jierula, A.; Wang, S.; OH, T.-M.; Wang, P. Study on Accuracy Metrics for Evaluating the Predictions of Damage Locations in Deep Piles Using Artificial Neural Networks with Acoustic Emission Data. Appl. Sci. 2021, 11, 2314. [Google Scholar] [CrossRef]
- Lee, S.-H. Performance Evaluation of Machine Learning and Deep Learning-Based Models for Predicting Remaining Capacity of Lithium-Ion Batteries. Appl. Sci. 2023, 13, 9127. [Google Scholar] [CrossRef]
- Yan, Q.; Yang, C.; Wan, Z. A Comparative Regression Analysis between Principal Component and Partial Least Squares Methods for Flight Load Calculation. Appl. Sci. 2023, 13, 8428. [Google Scholar] [CrossRef]
- Piotrowska-Woroniak, J.; Szul, T. Application of a Model Based on Rough Set Theory (RST) to Estimate the Energy Efficiency of Public Buildings. Energies 2022, 15, 8793. [Google Scholar] [CrossRef]
- Arcuri, N.; Bruno, R.; Pizzuti, G. A simplified hourly calculation code to evaluate the buildings heating load: A case study for Italian climatic conditions. In Proceedings of the Summer Computer Simulation Conference (SummerSim 2016), Montreal, QC, Canada, 24–27 July 2016; pp. 1–7. Available online: https://dl.acm.org/citation.cfm?id=3015599 (accessed on 1 December 2023).
- Bruno, R.; Pizzuti, G.; Arcuri, N. The Prediction of Thermal Loads in Building by Means of the en ISO 13790 Dynamic Model: A Comparison with TRNSYS. Energy Procedia 2016, 101, 192–199. [Google Scholar] [CrossRef]
- Prada, A.; Baratieri, M.; Baggio, P.; Gasparella, A. Dynamic simulation of buildings: Comparison between different approaches. Fiz. Budowli W Teor. I Prakt. 2010, 5, 41–46. [Google Scholar]
- Tudor, A.; Pfafferott, J.; Maier, N. Optimizing the operation of earth-to-air heat exchangers in high-performance ventilation systems for low-energy buildings—A case study. In Proceedings of the 34th AIVC, 3rd TightVent, 2nd Cool Roofs’, 1st Venticool Conference, Athens, Greece, 25–26 September 2013; Available online: https://www.aivc.org/resource/optimizing-operation-earth-air-heat-exchangers-high-performance-ventilation-systems-low?volume=34784 (accessed on 1 December 2023).
- Panão, M.J.O.; Santos, C.A.; Mateus, N.M.; Da Graça, G.C. Validation of a lumped RC model for thermal simulation of a double skin natural and mechanical ventilated test cell. Energy Build. 2016, 121, 92–103. [Google Scholar] [CrossRef]
- Yang, L.; Du, L.; Yang, C.; Hu, C.; Yu, C.; Du, H.; Li, Q. Construction and verification of an environment and energy prediction model for Controlled Environment Housing. E3S Web Conf. 2021, 245, 01008. [Google Scholar] [CrossRef]
- Michalak, P. Simulation and Experimental Study on the Use of Ventilation Air for Space Heating of a Room in a Low-Energy Building. Energies 2023, 16, 3456. [Google Scholar] [CrossRef]
- Kalmár, F. Summer operative temperatures in free running existing buildings with high glazed ratio of the facades. J. Build. Eng. 2016, 6, 236–242. [Google Scholar] [CrossRef]
- D’Ambrosio Alfano, F.R.; Olesen, B.W.; Pepe, D.; Palella, B.I. Working with Different Building Energy Performance Tools: From Input Data to Energy and Indoor Temperature Predictions. Energies 2023, 16, 743. [Google Scholar] [CrossRef]
- D’Ambrosio Alfano, F.R.; Pepe, D.; Riccio, G.; Vio, M.; Palella, B.I. On the effects of the mean radiant temperature evaluation in the assessment of thermal comfort by dynamic energy simulation tools. Build. Environ. 2023, 236, 110254. [Google Scholar] [CrossRef]
- Capizzi, G.; Sciuto, G.L.; Cammarata, G.; Cammarata, M. Thermal transients simulations of a building by a dynamic model based on thermal-electrical analogy: Evaluation and implementation issue. Appl. Energy 2017, 199, 323–334. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).