RETRACTED: A Kalman Filter-Based Distributed Cyber-Attack Mitigation Strategy for Distributed Generator Units in Meshed DC Microgrids

Abstract

To ensure fast dynamics and the stability of multiple distributed generator units (DGUs) in DC microgrids, communication links among the controllers of DGUs are generally adopted. However, those communication channels are vulnerable to cyber-attacks. To alleviate this hassle, a Kalman Filter (KF)-based distributed cyber-attack mitigation strategy, which is highly involved in both primary and secondary control, is proposed in this paper. The KF, as a robust state estimator, is utilized to accurately estimate the authentic terminal voltages and currents of the DGUs. Based on the discrepancies between the estimated and measured parameters of the systems under cyber-attacks, the proposed control can adaptively compensate the attack signals via an adaptive proportional integral (API) controller and a fractional API (FAPI) controller in cyber-attack-mitigation layers. The main advantage of using the proposed control scheme compared to conventional schemes is the fast dynamic response. The simulation results verify this merit by comparing the adopted KF and comparing it with conventional artificial neural networks (ANN), while the experimental results validate that effectiveness of the proposed control and showcase the superiority of the FAPI control in terms of its perfect compensation for different types of cyber-attacks.

1. Introduction

With the high penetration of renewable energy sources (RESs), microgrids have been gaining increasing attention over the last two decades. Compared to their AC counterparts, DC microgrids have better efficiency due to their having fewer conversion stages for dominant DC loads, such as data centers, power supplies and healthcare equipment. Research activities regarding DC microgrids have been extensively conducted in recent years, particularly hierarchical control schemes for multiple grid-connected power electronics, which are widely adopted in renewable energies, energy storage systems, and most loads.

Hierarchical control schemes can generally be categorized into centralized control schemes, decentralized control schemes, and distributed control schemes [1]. For centralized control schemes, all the measurements of DGUs are sent to the control center, which provides control signals to regulate the DGUs in an integrated manner. Due to its single point of failure and communication delays, this scheme suffers from high costs and vulnerability to cyber-attacks. For decentralized control schemes, no communication is needed between the DGUs. The local controllers of DGUs undertake all the control responsibilities. The costs of decentralized control schemes are low, and they are robust against cyber-attacks. Nevertheless, these control schemes are not reliable. Changes in the operating conditions will cause steady-state offsets. For distributed control schemes, the information of DGUs is disseminated throughout the DC microgrid, with limited communication links [2]. Being different from the centralized control schemes with central-to-node communication, the distributed control schemes only require communication between the two neighboring DGUs. As a result, the communication costs may be lower. Furthermore, due to this distributed communication, the anti-cyber-attack abilities of the distributed control schemes are better than those of the centralized control schemes [3]. With the communication links, the reliability of the distributed control schemes should be better than that of the decentralized control schemes. Therefore, distributed control schemes are the most popular control schemes for DGUs in DC microgrids. The proposed control scheme is established based on the conventional distributed control schemes by incorporating Kalman Filters (KFs) to enhance the anti-cyber-attack abilities.

Cyber-attacks are becoming one of the most critical issues, causing instabilities in microgrids or even traditional power grids. Attackers can access the measurements being used in state estimators or control loops. A manipulated attack signal can result in oscillations or even blackouts [4]. Typical cyber-attacks include (1) Denial of Service (DoS) attacks [5], (2) replay attacks [6], and (3) false data injection attacks (FDIAs) [7]. For the DoS attack, the attacker prevents either the measurements or control variables from reaching the predetermined values, which results in a deterioration in dynamic performance and stability. Since DoS attacks can cause data to become unavailable, they can easily be detected [8]. For the replay attacks, the attacker records the measurements of the system during healthy conditions and replays the measurements to deceive the power system operator while performing an attack on the system. These attacks can be detected using the watermarking schemes presented in [6]. FDIAs are generally considered to be the most dangerous attacks due to their covert and undetectable properties [9]. The serious consequences of importing FDIAs to the DC microgrids are reported in [10].

Several conventional methods have been proposed to detect FDIAs. A multi-objective complex optimization problem was formulated based on the parity method to detect FDIAs in [11]. One issue regarding this approach is the computational burden. In [12], FDIAs are detected by the candidate invariants. Any change in the candidate invariants means the presence of cyber-attacks. However, how to mitigate these cyber-attacks is not considered. The grey wolf optimization technique and deep machine learning were employed in [13]. The main drawback of this method is the training of the deep neural network, which is difficult and the real-time compensation of cyber-attacks, which is impossible. One method to recognize FDIAs on the bus voltages of DC microgrids is presented in [14]. However, this approach is valid only if the droop control is adopted in the primary loop. Cyber-attacks are usually considered faults in many case studies. To distinguish their differences, a framework for risk assessment is presented in [15]. The method proposed in [15] was designed based on a discordant element, which enables the detection of attack locations. Nevertheless, this method was only established based on the current measurements, while cyber-attacks on voltages are not detectable. A recurrent neural network (RNN) strategy is reported to detect FDIAs on DUGs in DC microgrids under a very wide range of operating conditions [16]. A nonlinear autoregressive exogenous model (NARX) is used to train the RNN online to estimate DC voltages and currents. Based on the estimated output, DC voltages and currents of DGUs, the estimated errors are derived to identify cyber-attacks. However, this method also cannot compensate for or mitigate the cyber-attacks. To detect as well as compensate for the FDIAs, extra mitigation layers are proposed in [17,18,19] for the existing hierarchical control strategies. These mitigation layers were designed based on neutral networks as the state estimators. The main issue with these methods is that the training of neural networks is tedious and time-consuming. In addition, training occurs offline, where the system may be subjected to different disturbances. An alternative model predictive control (MPC) method is proposed in [20], although this method suffers from the same issue.

Apparently, existing FDIA detection and mitigation control strategies, estimated based on conventional hierarchical control, contain several research gaps and cannot achieve complete cybersecurity in DC microgrids. First, most existing schemes are proposed to address the DGUs in parallel DC microgrids rather than meshed DC microgrids. Second, many effective solutions are only proposed to detect the attack signals, whileecorresponding mitigating strategies are not proposed. Third, partial attack positions (either current attack or voltage attack) are considered. Holistic attack signal detection and mitigation strategies are rarely presented.

To bridge the aforementioned research gaps, a Kalman Filter (KF)-based distributed hierarchical control scheme is proposed in this paper. Compared to the artificial neural networks (ANNs), the KF adopted in this paper, being inherited from the traditional KF, is more intuitive and can be easily implemented in inexpensive digital controllers with much simpler algorithms. Consequently, the dynamic response of the proposed control with KF is superior to the conventional hierarchical control with ANN. Furthermore, the KF is robust enough to ensure the adaptability of the proposed control schemes for multiple DUGs in meshed DC microgrids under various operating conditions. A fractional adaptive proportional integral (FAPI) control, when integrated in the hierarchical control scheme, can further enhance the adaptability as compared to the conventional API and PI control. The major contribution of the paper can be summarized as follows:

(1)

This might be the first paper to present a holistic control algorithm to mitigate both the voltage and current FDIAs of DGUs in meshed DC microgrids.

(2)

This might be the first paper to use KF as the state estimator to authenticate the voltage and current measurements being used for the hierarchical control loops. This heavily reduces the computational burden as compared to the conventional counterparts with ANN.

(3)

A mitigation layer is proposed with FAPI controllers that update their gains automatically with the variations in system parameters.

(4)

Both simulation and experimental verificatications are presented of the superior dynamic responses of the proposed distributed control compared to conventional control schemes.

The rest of the paper is divided as follows: Section 2 exhibits the meshed DC microgrid system and the distributed control strategy, Section 3 explains the proposed cyber-attack detection and mitigation strategy, Section 4 discusses the simulation results, Section 5 presents an experimental study to verify the effectiveness of the proposed strategy by, and finally, Section 6 concludes the paper.

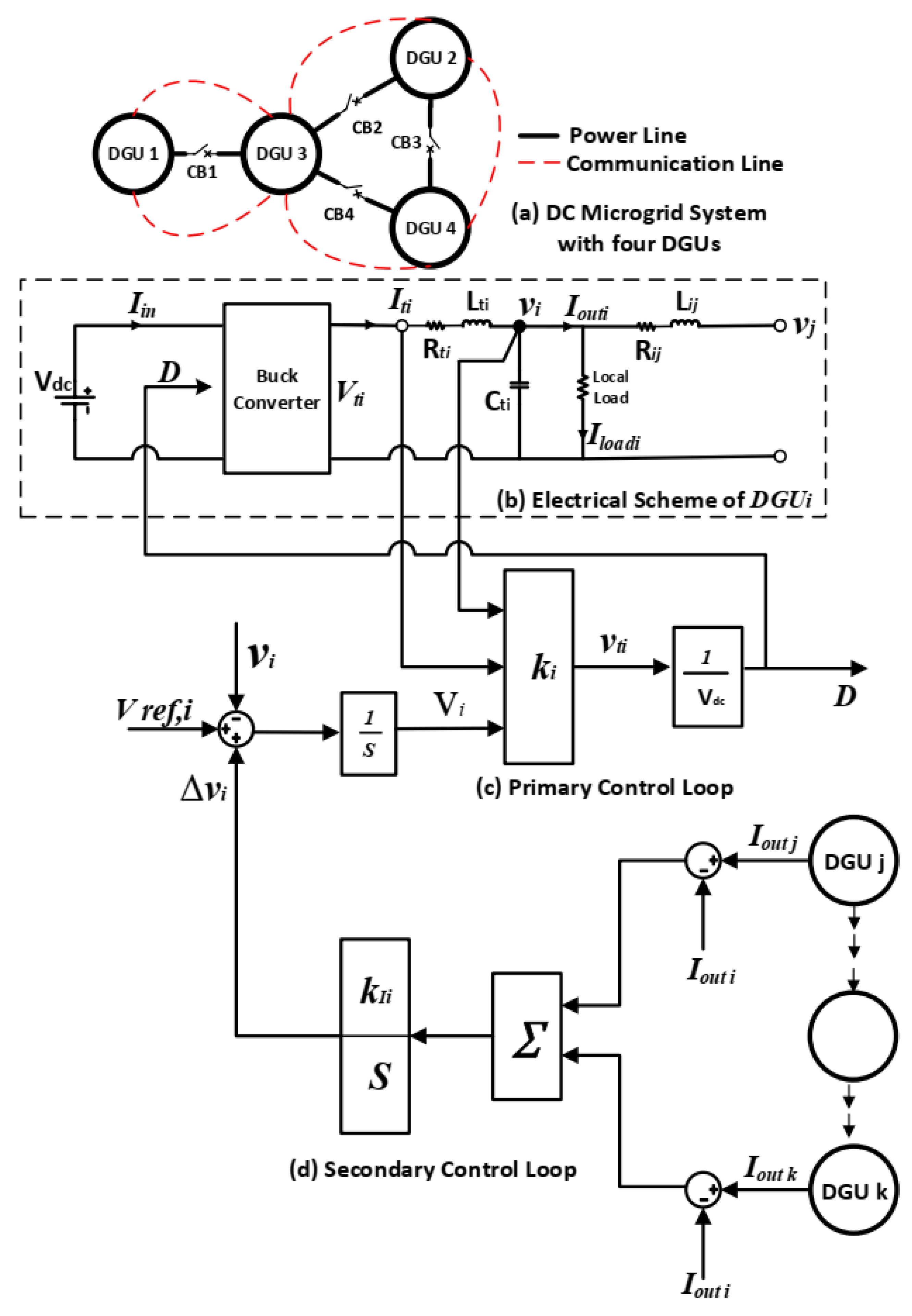
2. System Model and Distributed Control Strategy

A meshed DC microgrid presented in Figure 1a was used to evaluate the effectiveness of the proposed detection and mitigation layers. The microgrid consists of four DGUs, where DGU3 represents the coupling node between the right and left parts of the microgrid. Each DGU is represented by a DC source V_dc, which is interfaced with the microgrid through a buck converter. The output terminal voltage of the converter V_ti is filtered to supply the local load that is connected at the Point of Common Coupling (PCC) of each unit. In Figure 1b, v_i is the PCC voltage of DGU_i. I_ti is the inductor current. I_loadi is local load current. R_ti, L_ti, and C_ti are the filter resistance, inductance and capacitance, respectively. R_ij and L_ij refer to the resistance and the inductance of the transmission line between DGU_i and DGU_j. By exploiting the Quasi-Stationary Line (QSL) model presented in [21], L_ij can be neglected from the state-space model.

The system can be represented by the following state space model [21]:

$${\dot{X}}_i\left(t\right)=A_i{X}_i\left(t\right)+B_i{U}_i\left(t\right)+M_i{E}_i\left(t\right)+{\xi }_i\left(t\right)$$

(1)

$$Y_i\left(t\right)=C_i{X}_i\left(t\right)$$

(2)

$$Z_i\left(t\right)=H_i{Y}_i\left(t\right)$$

(3)

$${\xi }_i(t)={\sum }_{j\in \mathbb{N}i}{A}_{ij}{X}_j$$

(4)

where X_i(t) is the state vector. U_i(t) is the input vector. E_i(t) represents the external input which is the local load current I_loadi. Y_i(t) is the system measurement. Z_i(t) is the controlled variable v_i. ξ_i(t) provides the effects of the neighboring DGUs. N_i is the set of neighbors of DGU_i [21]. The state-space matrices of A_i, B_i, C_i, H_i, and M_i are provided in the Appendix A. The electrical and communications topographies of the microgrid are shown in Figure 1a, where the power and communication lines are indicated. The communication links between neighboring DGUs allow for the sharing of their states.

2.1. The Primary Controller

The primary control loop is based on a state feedback controller, shown in Figure 1c, to regulate the DGU voltage [21]. The controller action vti is obtained from (5):

$$v_{ti}=U_i\left(t\right)=k_i{X}_i=D_i{V}_{\mathrm{d}\mathrm{c}}$$

(5)

where k_i is a gain vector R^1×3. X_i = [v_i, I_ti, V_i]^T is the state vector and D_i is the duty cycle of the converter. The term V_i is added to the states [v_i, I_ti]^T to represent the integral action needed to eliminate the steady-state error of the PCC voltage v_i, error(t). This integral action is given by Equation (6), where Z_ref,i(t) is the reference value of the controlled variable v_i, H_i, and C_i are provided in the Appendix A.

$${\dot{V}}_i\left(t\right)=\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}\left(t\right)=Z_{ref,i}\left(t\right)-Z_i\left(t\right)=Z_{ref,i}\left(t\right)-H_i{C}_i{X}_i$$

(6)

Finally, the controller action is divided by V_dc to obtain the duty cycle for the converter. It is worth noting that the average model 1/V_dc is accurate enough to describe the buck converters used for DGUs in a system-level microgrid, since the parameters of inductors and loads are generally designed to ensure the buck converter operates at continuous conduction modes (CCMs). In many system-level investigations, such simple but accurate linear models have been adopted [21].

2.2. The Secondary Controller

A secondary controller, shown in Figure 1d, is utilized to guarantee equal current-sharing between all the DGUs under all operating conditions [22,23]. The errors in current-sharing between the neighboring DGUs are summed together and processed by an integrator with a gain k_Ii, as follows:

$$∆{\dot{v}}_i=k_{Ii}{\sum }_{j=1,j\ne i}^{Ni}(I_{outj}-I_{outi})$$

(7)

where $J\in Ni$ is the set of neighbors of DGU_i, ∆v_i is the correction term added to the voltage reference, and I_outi is the output current of DGU_i.

The stability of the microgrid system is discussed in [21], where the gain vector of the primary controller k_li is derived from a semi-definite programming problem to ensure the stability of the DC microgrid.

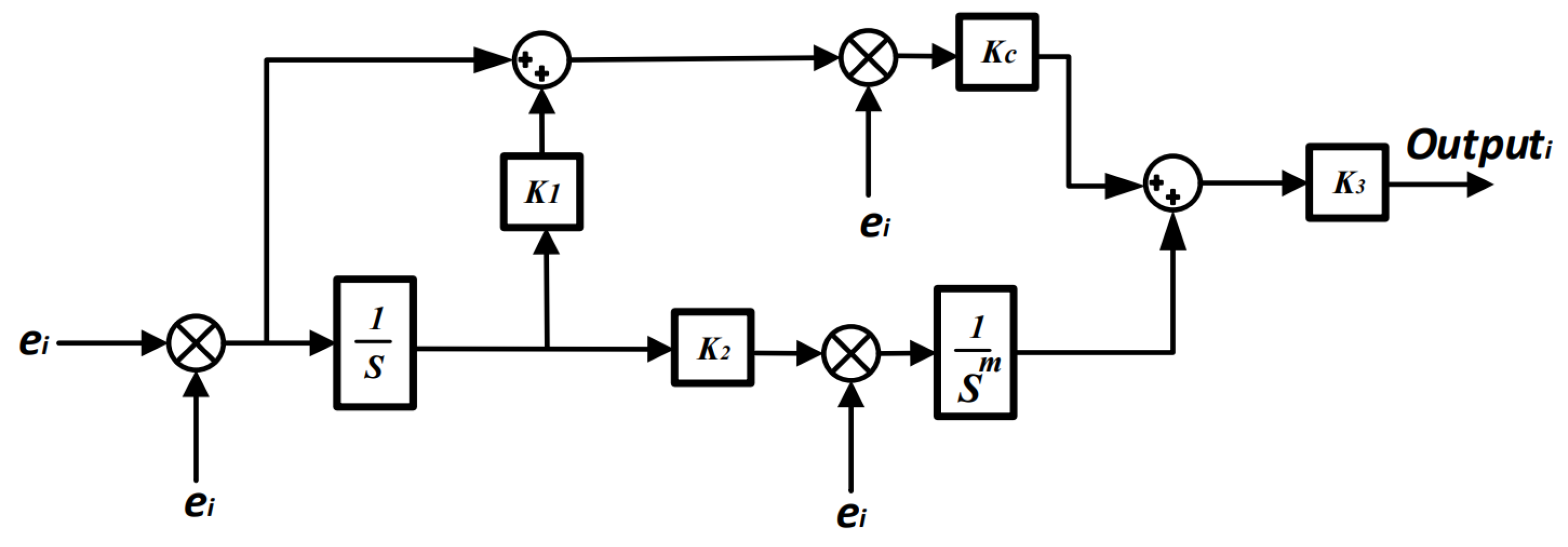
3. Proposed Cyber-Attack-Mitigation Layers

The proposed current and voltage cyber-attack-mitigation layers are based on state estimation utilizing the Kalman Filter (KF). The mitigation layers set corrective actions for false data injected into the PCC voltage and the shared current of each DGU_i to secure the measured signals needed for the primary and secondary controllers to achieve adequate PCC voltage regulation and current-sharing, respectively.

3.1. Kalman Filter

The KF is considered as a state observer for stochastic systems [24,25]. The KF algorithm uses the available measurements to predict unmeasurable states, which represent the attacked measurements in this application. The KF predicts the optimal posteriori state estimate ${\hat{x}}_k$ from the previous priori predicted state ${\hat{x}}_{k-1}$ , as given by:

$${\hat{x}}_k=\underset{{\hat{x}}_k}{\underbrace{A{\hat{x}}_{k-1}+B{u}_k}}+K_k({\gamma }_k-C_{\nu i/ii}\left(\underset{{\hat{x}}_k}{\underbrace{A{\hat{x}}_{k-1}+B{u}_k}}\right))$$

(8)

where y_k is the measurement vector, u_k is the input vector, K_k is the KF gain, and A, B, and C_vi/ii are the DGU_i state-space model matrices. With the aid of the state-space model of DGU_i, two KFs are utilized to estimate the terminal voltage ${\overline{v}}_i$ and output current ${\tilde{I}}_{outi}$ of each DGU_i in the microgrid. To utilize the KF to estimate DGU_i states, the state-space model given by (1)–(4) needs to be manipulated to fit (8). For example, the state-space model of DGU1 is presented below, with the neighboring unit of DGU3:

$$\left.{\dot{x}}_1\left(t\right)=\left[\begin{array}{ccc}\frac{-1}{R_{13}{c}_{t1}}& \frac{1}{c_{t1}}& 0\\ \frac{-1}{L_{t1}}& -\frac{R_{t1}}{L_{t1}}& 0\\ -1& 0& 0\end{array}\right.\right]\left[\begin{array}{c}{\nu }_1\\ l_{t1}\\ V_1\end{array}\right]+\left[\begin{array}{c}0\\ \frac{1}{L_{t1}}\\ 0\end{array}\right]v_{t1}+\begin{array}{c}\\ \left[\begin{array}{c}\frac{-1}{c_{t1}}\\ 0\\ 0\end{array}\right]I_{load1}+\left[\begin{array}{ccc}\frac{1}{R_{13}{c}_{t1}}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}{v}_3\\ l_{t3}\\ V_3\end{array}\right]\end{array}$$

(9)

Simplifying (9) can be achieved as follows:

$${\dot{x}}_1\left(t\right)=\underset{A}{\underbrace{\left[\begin{array}{ccc}\frac{-1}{R_{13}{c}_{t1}}& \frac{1}{c_{t1}}& 0\\ \frac{-1}{L_{t1}}& -\frac{R_{t1}}{L_{t1}}& 0\\ -1& 0& 0\end{array}\right]}}\left[\begin{array}{c}{v}_1\\ l_{t1}\\ V_1\end{array}\right]+\underset{B^m}{\underbrace{\left[\begin{array}{ccc}0& \frac{-1}{c_{t1}}& \frac{1}{R_{13}{c}_{t1}}\\ \frac{1}{L_{t1}}& 0& 0\\ 0& 0& 0\end{array}\right]}}\underset{u^m}{\underbrace{\left[\begin{array}{c}{v}_{t1}\\ l_{load1}\\ v_3\end{array}\right]}}$$

(10)

where B^m and u^m are the modified system matrices used by the KF state estimator, expressed by (8), in place of B and u. According to the control action of (5), v_t1 can be represented by the duty cycle D₁. In addition, I_L1 which refers to the local load current, is assumed to be known. Moreover, v₃ is considered tightly regulated at the nominal value. Therefore, the only input to the KF-based estimator is the duty cycle D₁. Finally, the measurement vectors C_vi and C_ii, used for the KF to estimate the PCC voltage $\overline{v_i}$ and the inductor current ${\tilde{I}}_{outi}$, respectively, are given as follows:

$$C_{vi}=[0 1 0]$$

(11)

$$C_{ii}=[1 0 0]$$

(12)

Once the inductor current is estimated, the output current ${\tilde{I}}_{outi}$ can be calculated. The same concept can be applied to the other DGUs. The estimated states ${\overline{v}}_i$ and ${\tilde{I}}_{outi}$ are compared with the measurements to detect any cyber-attack on terminal voltage and/or output current, respectively. Afterwards, voltage and current cyber-attack-mitigation layers set proper corrective actions to guarantee that the primary and the secondary control loops are using authenticated data to regulate the controlled variables. The implementation steps of the KF are given as the following:

(1)

Initialization Step

Assume zero initial values for the state vector ${\hat{x}}_{k-1}$ and randomly initialize the error covariance matrix P_k−1.

(2)

Prediction Step

In this step, a priori estimate of the state vector is predicted using (13). In addition, the uncertainty of the estimated state vector is represented by the priori estimate error covariance $P_k^{-}$ as in (14), where Q is the process noise.

$${\hat{x}}_k^{-}=A{\hat{x}}_{k-1}+B{u}_k$$

(13)

$$P_k^{-}=A{P}_{k-1}{A}^T+Q$$

(14)

(3)

Update Step

The priori estimates are used to find the Kalman gain K_k, posteriori estimates of the states ${\hat{x}}_k$, and error covariance P_k according to (15)–(18), respectively, such that the error covariance is minimized:

$$K_k=\frac{P_k^{-}{C}_{vi/ii}^T}{C_{vi/ii}{P}_k^{-}{C}_{vi/ii}^T+R}$$

(15)

$${\hat{x}}_k={\hat{x}}_k^{-}+K_k(y_k-C_{vi/ii}{\hat{x}}_k^{-})$$

(16)

$$P_k=(I-K_k{C}_{vi/ii})P_k^{-2}$$

(17)

where R is the measurement noise. The Kalman gain decides how the measurement y_k and the priori state estimate ${\hat{x}}_k^{-}$ manipulate the update of ${\hat{x}}_k$. If the measurement noise is negligible, the measurement y_k contributes to the calculation of ${\hat{x}}_k$ more than ${\hat{x}}_k^{-}$. On the other hand, if the error in the priori estimate is negligible, the update of ${\hat{x}}_k$ mostly depends on its priori estimate. The KF recursively performs these steps to estimate the states continuously [26].

3.2. Stability of Kalman Filter

The stability of the KF is mainly based on the state prediction error ε between the estimated states $\hat{x}$ and the actual states x [27]. The filter is stable if the error ε converges to zero. The estimation error and its dynamics $\stackrel{·}{\epsilon }$ are given by:

$$\epsilon =x-\hat{x}$$

(18)

$$\dot{\epsilon }=\dot{x}-\dot{\hat{x}}$$

(19)

Using (8), (19) can be rewritten as:

$$\dot{\epsilon }=\underset{\dot{x}}{\underbrace{Ax+Bu}}-\left(\underset{\dot{\hat{x}}}{\underbrace{A\hat{x}+Bu+K(Cx-C\hat{x})}}\right)$$

(20)

The estimation error dynamics can be simplified as:

$$\dot{\epsilon }=(A-KC)\epsilon$$

(21)

If the term (A − KC) is a Hurwitz matrix, the estimation error ε will decrease with time, and $\hat{x}$ will continue to converge to actual states. To prove that (A − KC) is a Hurwitz matrix, let us assume a new variable ξ with a new dynamic, given as follows:

$$\dot{\xi }=(A-KC{)}^T\xi$$

(22)

Knowing that transposing does not affect the eigenvalues of a matrix, the stability of $\stackrel{·}{\epsilon }$ is the same as $\stackrel{·}{\xi }$. Using a Lyapunov energy function V(ξ), given in (23), the stability can be proven, where P is a symmetric positive definite matrix obtained by solving the algebraic Riccati Equation (24) when t→∞ [28]. The derivative of the Lyapunov function is given by (25) which can be simplified to (26), as follows:

$$V\left(\xi \right)={\xi }^{T}P\xi$$

(23)

$$AP+P{A}^T-KCP+B^{T}QB=0$$

(24)

$$\dot{V}(\xi )={\xi }^{T}P\dot{\xi }+{\dot{\xi }}^{T}P\xi$$

(25)

$$\dot{V}\left(\xi \right)={\xi }^T(AP+P{A}^T-2\mathrm{K}\mathrm{C}\mathrm{P})\xi$$

(26)

To ensure stability, $\dot{V}\left(\xi \right)$ should be a negative definite (i.e., $\dot{V}\left(\xi \right)$ < 0), and this can be confirmed if (AP + PA^T − 2 KCP) is a negative definite using (24):

$$AP+P{A}^T-2KCP=-B^{T}QB-KCP$$

(27)

Since the sum of B^TQB and KCP is a positive definite matrix, the left-hand side of (27) is a negative definite matrix. This ensures that the derivative of the Lyapunov energy function V(ξ) is decreasing. Hence, matrix (A − KC) is Hurwitz, and the stability of the filter is ensured.

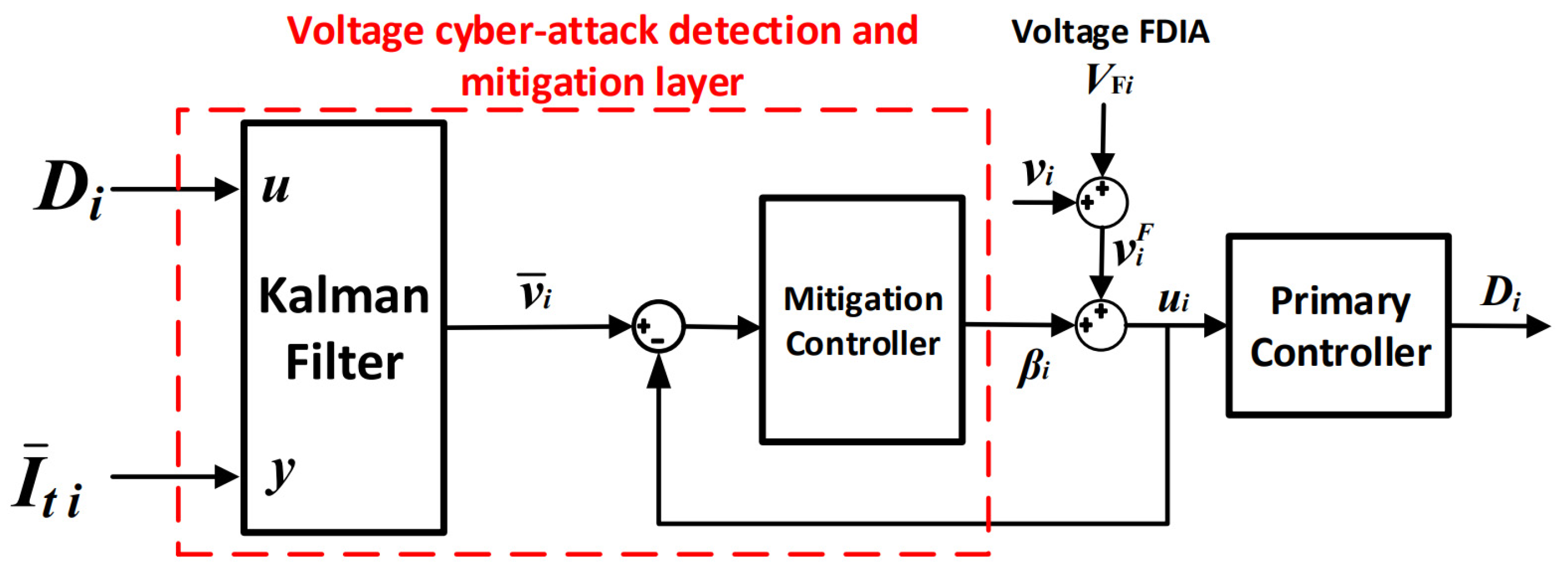
3.3. Voltage Cyber-Attack-Mitigation Layer

The PCC voltage of a DGUi under cyber-attack can be represented as follows:

$$v_i^F=v_i+V_{Fi}$$

(28)

where V_Fi is the magnitude of FDIA regarding the PCC voltage v_i. The proposed mitigation layer for voltage cyber-attack, illustrated in Figure 2, is based on the KF algorithm to estimate the DGU_i voltage $\overline{v}i$ from the duty cycle D_i and the estimated inductor current $\overline{I}$_ti, which is obtained from the second KF used for current cyber-attack detection, as shown in Figure 3. Using $\overline{I}$_ti rather than actual measurements ensures healthy data are input to the KF, and hence ensures an accurate estimation of the state, ${\overline{v}}_i$. Consequently, the estimated voltage is compared with the measurement being sent to the primary controller, u_i, which is influenced by FDIA. The error is processed by the mitigation controller to set the mitigation signal β_i, which is used to correct the measurement by canceling out the false injected data V_Fi. This action guarantees that the primary controller receives the actual authenticated voltage measurement v_i.

The mitigation controller needs to have a fast dynamic response to be able to cancel out the FDIA once it is initiated, u_i = ${\overline{v}}_i$ = v_i. The rising and settling times should be minimized to achieve the required corrective action given by:

$${\beta }_i=\overline{v_i}-v_i^F\cong v_i-v_i^F=-V_{Fi}$$

(29)

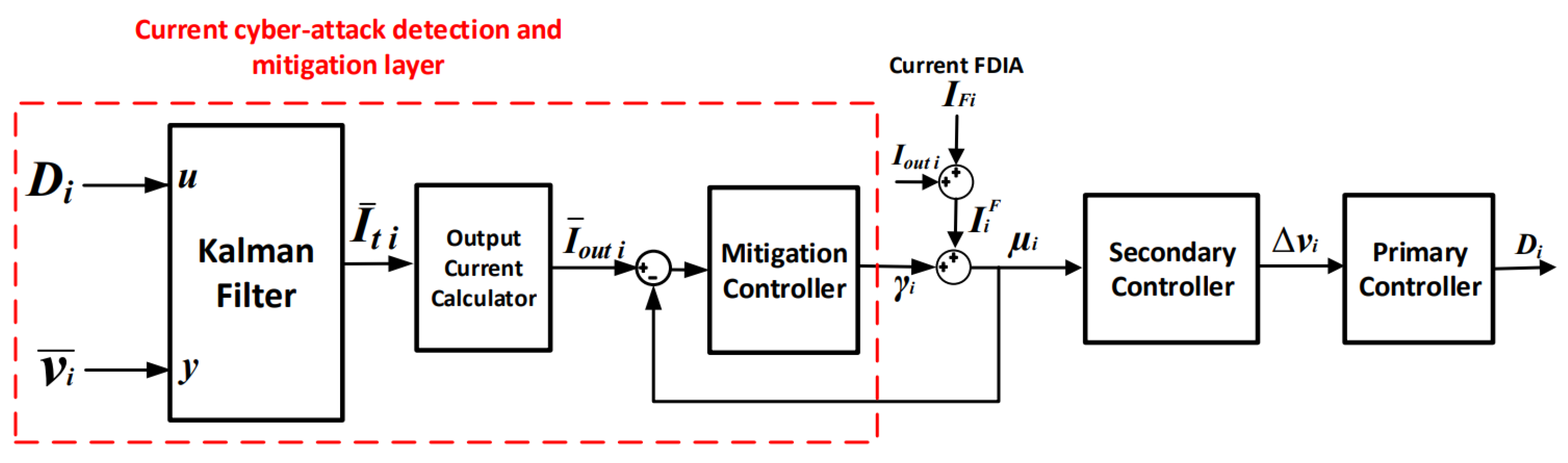
3.4. Current Cyber-Attack-Mitigation Layer

Figure 3 illustrates the proposed detection and mitigation layer for cyber-attacks on the output current of DGU_i. A KF is employed to estimate the output current $\overline{I}$_ti using D_i and the estimated voltage ${\overline{v}}_i$, which is secured from the KF used to detect voltage cyber-attacks, as shown in Figure 2. This action ensures an authentic estimation of $\overline{I}$_ti, Consequently, $\overline{I}$_outi is calculated based on the known filter capacitance. The output current measurement under FDIA (i.e., $I_i^F$), which is used by the secondary controller for current sharing, can be represented as:

$$I_i^F=I_{outi}+I_{Fi}$$

(30)

where I_Fi is the FDIA on the output current of DGU_i. To ensure proper current-sharing between DGUs, the term I_Fi should be cancelled out from the current measurement. The different between the output current measurement and the estimated version is diminished by the mitigation controller, which determines the correction term γ_i. Assuming perfect estimation from the KF and the fast dynamic response of the controller, the corrective action can be expressed as follows:

$${\gamma }_i={\overline{I}}_{outi}-I_i^F\cong I_{outi}-I_i^F=-I_{Fi}$$

(31)

Obviously, the control strategies of either grid-forming converters or grid-following converters will not affect the cyber-attack detection and mitigation layers if they are incorporated into the holistic control loop. The proposed controllers used in the voltage and the current-mitigation layers are introduced in the next subsection.

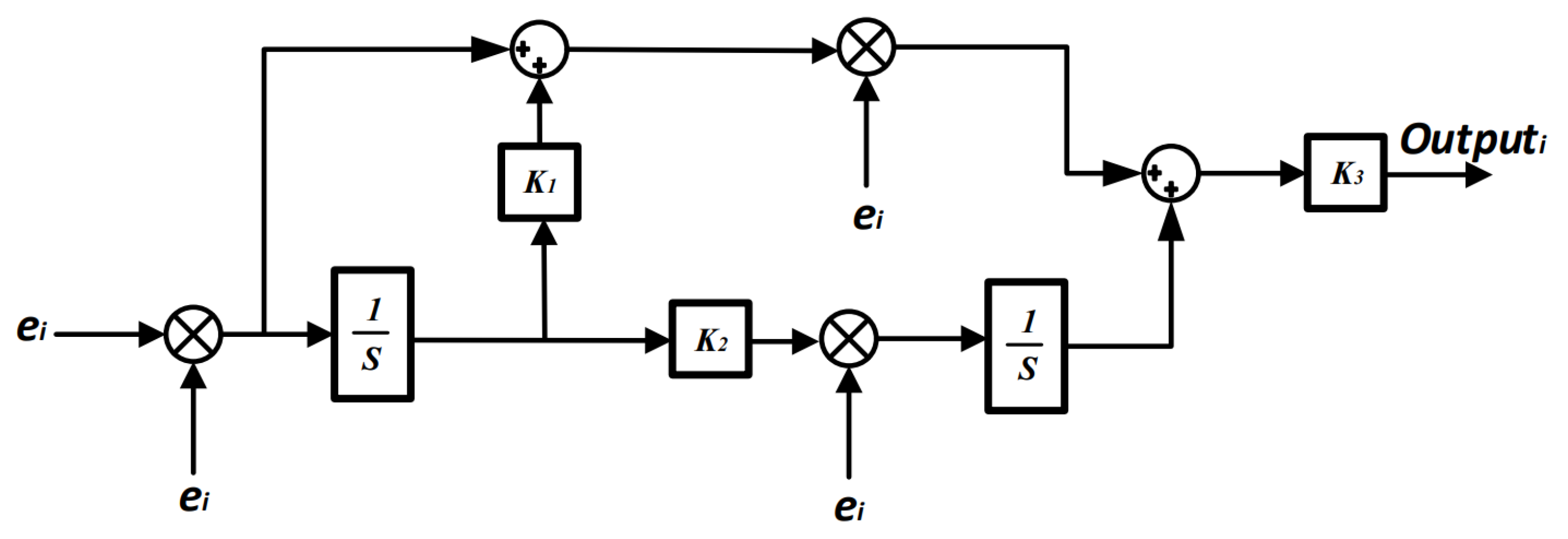
3.5. Fractional Adaptive Controllers for Mitigation Layers

Adaptive controllers are used in microgrids to overcome the sudden changes and disturbances that the system may encounter [29,30]. Figure 4 illustrates the block diagram of the adaptive PI controller used to enhance the dynamic performance of the proposed cyber-attack-mitigation layers. Adaptive PI controllers can withstand sudden changes in the system as they utilize the error signal e_i to update the proportional gain K_p and the integral gain K_i online and overcome the disturbances that the system may encounter [31].

The fractional-order adaptive PI (FAPI) controller takes advantage of the fractional-order calculus [32] by introducing the fractional integrator in Figure 5 to better fit complex systems and improve the dynamic performance. It introduces less overshoots, achieves a better settling time and lowers the rise times. The FAPI controller has one more degree of freedom compared to conventional PI controllers because of the addition of the fractional term. This extra degree of freedom allows for further adjustment of the controller’s performance [33].

The output of the FAPI controller is described by the following:

$$Outpu{t}_i=K_3\left((K_c\ast K_p\ast e_i)+(\frac{1}{S^m}\ast K_i\ast e_i)\right)$$

(32)

where m is the fractional term of the integrator; K_p and K_i represent the adaptive proportional gain and integral gain of the FAPI and are adapted as follows:

$$K_p=e_i^2+(K_1\ast \frac{1}{s}\ast e_i^2)$$

(33)

$$K_i=(K_2\ast \frac{1}{s}\ast e_i^2)$$

(34)

where K₁, K₂, K₃, and K_c are constants that are chosen arbitrarily to initially adjust the controller performance. These two adaptive controllers are employed for the secondary layer and the proposed mitigation layers for voltage and current cyber-attacks. Comparisons between the dynamic performance of the adaptive controllers and a tuned PI controller are conducted in the next section.

4. Simulation Results

The distributed control strategy with the proposed cyber-attack-mitigation layers based on the KF, as shown in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, was simulated using the MATLAB/Simulink software package [34]. Scenarios where the microgrid is subjected to different cyberattacks were considered to verify the effectiveness of the proposed detection and mitigation layers. The secondary controller was turned on simultaneously when closing the tieline breakers at t = 1.5 s to form a meshed DC microgrid. In addition, for all DGUs, V_ref,i = 48 V.

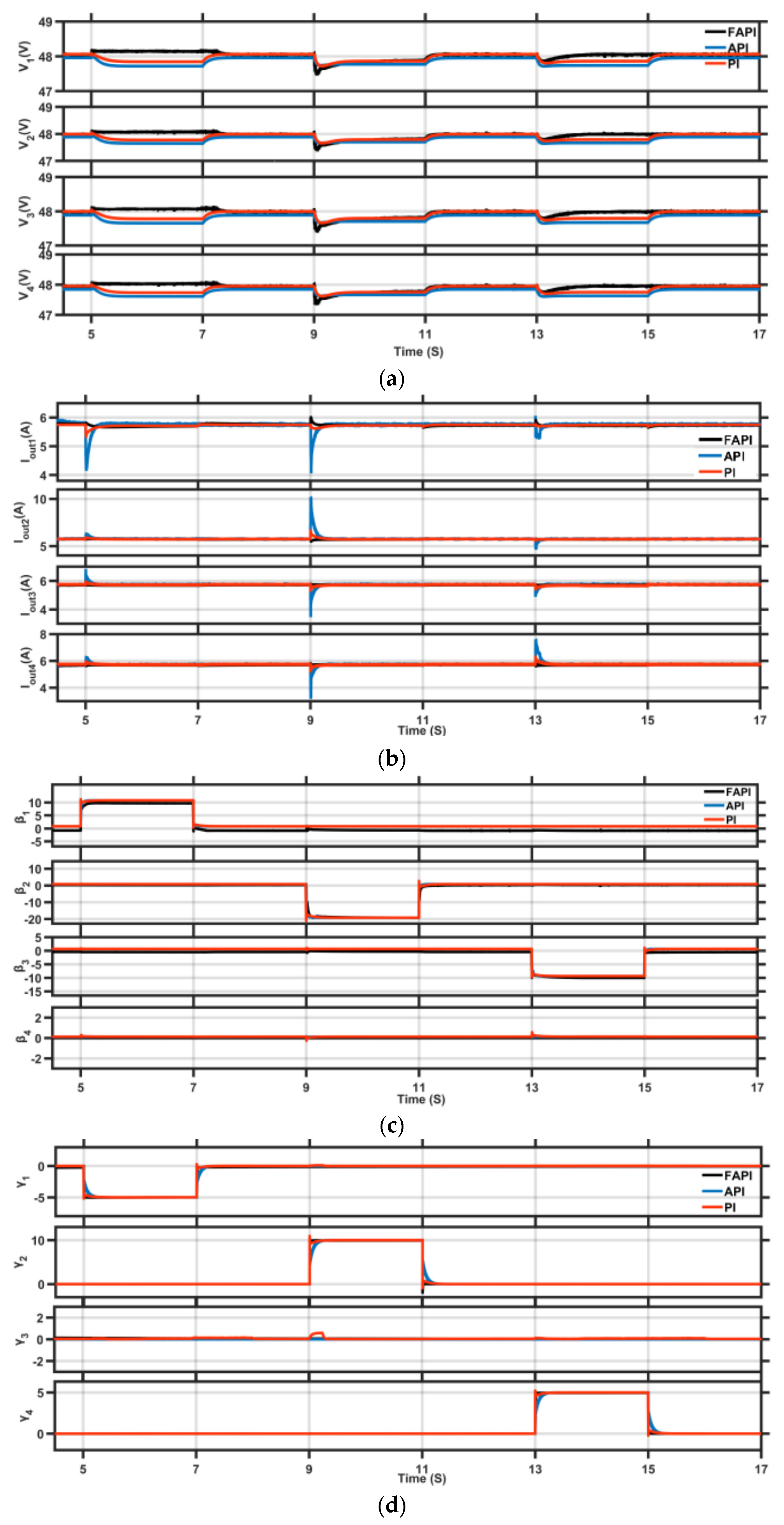
4.1. Case Study 1: Mixed Attacks

Mixed FDIAs on voltage and current measurements of DGUs are assumed as follows: DGU₁ is firstly cyber-attacked by V_F1 = −10 V and I_F1 = 5 A from t = 5 s to t = 7 s. Afterwards, DGU₂ is subjected to more aggressive cyber-attacks of V_F2 = 20 V and I_F2 = −10 A from t = 9 s to t = 11 s, simultaneously. Finally, DGU₃ and DGU₄ face cyber-attacks of V_F3 = 10 V and I_F4 = −5 A during the interval from t = 13 s to t = 15 s.

Figure 6a shows that, at the instant of each cyber-attack, a negligible voltage deviation occurs, which does not have any major effect on the voltage stability of the system. In addition, Figure 6b indicates that the secondary controller succeeds in achieving perfect current-sharing regardless of cyber-attacks. The mitigation signals for voltages and current cyber-attacks are displayed in Figure 6c,d, respectively, when PI, API, and FAPI controllers are utilized. It can be observed that the corrective actions of the mitigation layers are exactly opposite of those of the cyber-attack values, as expressed by (29) and (31). This action reveals the success of the proposed KF in accurately estimating DGU states. Moreover, this result demonstrates that the FAPI controller offers the best dynamic performance compared to the other controllers in terms of tight tracking without over/undershoots and a fast response. On the other hand, the slightly slower response of API and PI controllers leads to over/undershoots when different voltage and current cyber-attacks are initiated, as depicted in Figure 6.

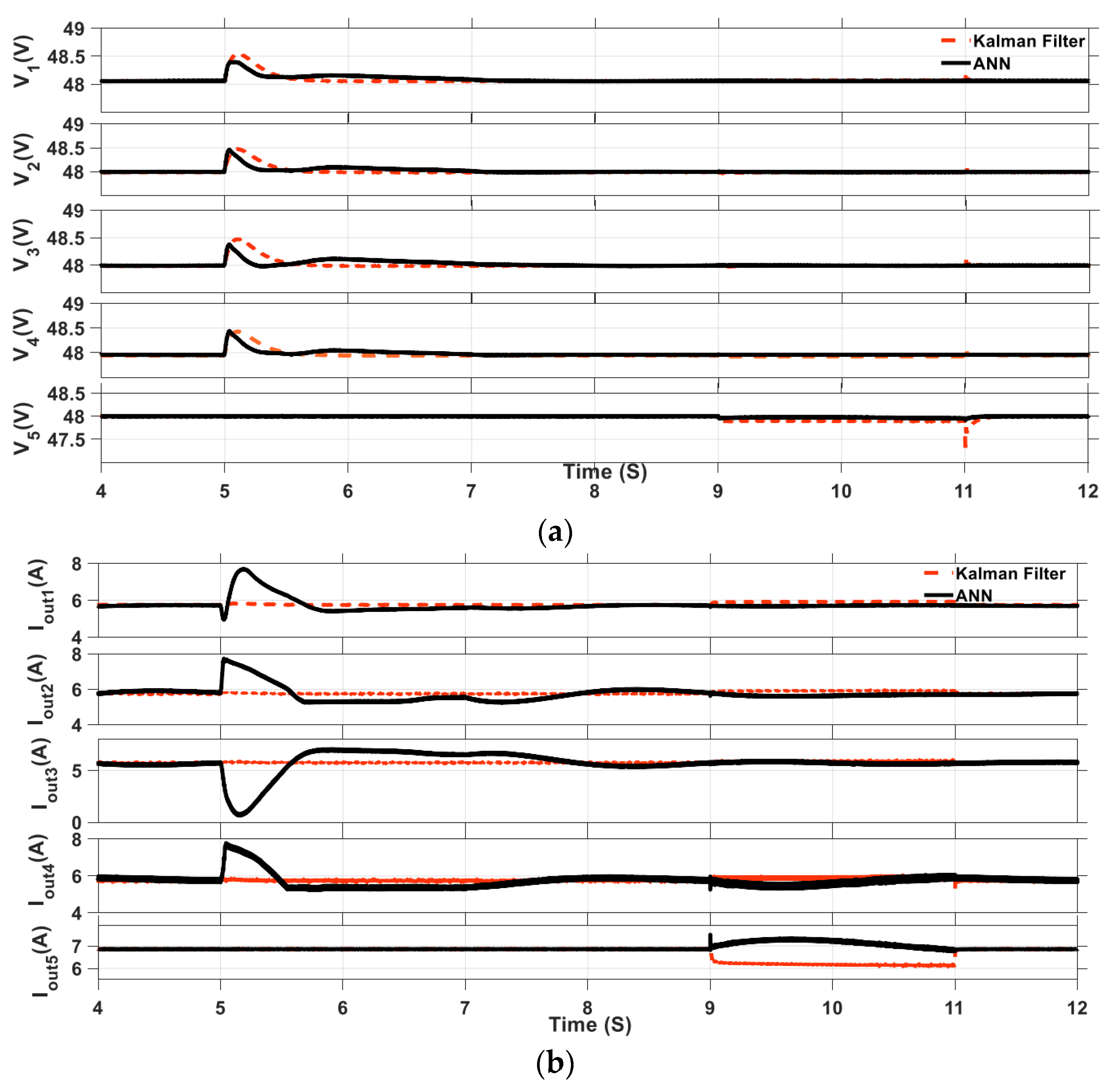
4.2. Case Study 2: Comparison between KF and ANNs

This subsection is dedicated to presenting a comparison between the dynamic performance of the proposed cyber-attack mitigation technique based on KF and a recent scheme based on ANNs [17,18,19,20]. FDIAs of the voltage measurements of DGUs 1, 2, and 4 were applied during the interval [5 s–7 s] with a magnitude of V_F = −20 V. The voltage of each DGU is given by Figure 7a, which shows that there is a steady-state error when ANNs are used in the mitigation layers. On the other hand, the steady-state error while using KF is almost zero. Figure 7b demonstrates that using ANNs results in an overshoot of the output current from each DGU. This overshoot is due to the interaction between the ANN used for the voltage mitigation layer of the third DGU, even though it is not attacked, as indicated in Figure 7c. Therefore, the KF is more accurate in estimating authentic healthy measurements than trained ANN. Moreover, the performance of ANN depends mainly on the training process, which needs healthy measurements under different operating conditions, which is a time-consuming process.

The plug and play ability of the proposed system is tested when DGU5 is connected to DGU4 during the interval [9 s–11 s]. Before connecting DGU5, the four DGUs shared their loads evenly at 5.7 A each, while DGU5 supplied its local load alone at 6.85 A. Once DGU5 is plugged into the DC microgrid, the four DGUs, together with the DGU5, contribute to the supply of their local loads. Consequently, an equal current-sharing between the five DGUs is achieved, where each DGU supplies approximately 6 A, as illustrated in Figure 7b. Moreover, Figure 7 shows that the KF with the FAPI provides a faster dynamic performance when DGU5 is turned off, as equal current-sharing occurs instantaneously.

Figure 7 justifies the superiority of the proposed cyber-attack mitigation scheme based on KF compared to the ANN-based strategy. Moreover, the results show that DGU5 is connected and disconnected smoothly. In addition, the proposed FAPI-based secondary controller achieves instantaneous current-sharing between the five DGUs. On the other hand, using the secondary controller presented in [19], there is a delay in achieving current-sharing.

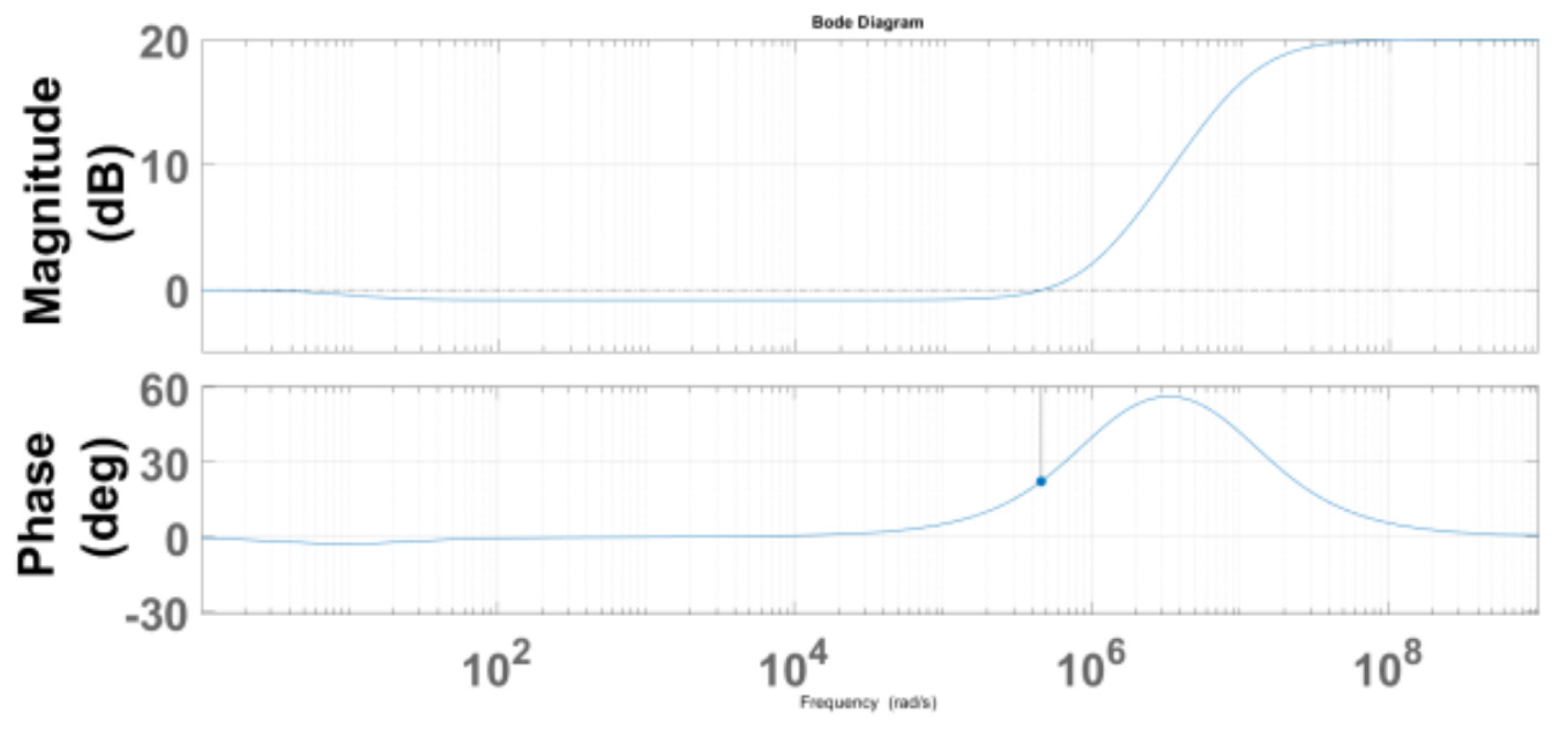
4.3. Case Study 3: Mitigation Layer Stability

The closed-loop stability of the proposed mitigation layer based on the KF is proved by the bode plot of Figure 8. The stability margins indicate the stable performance of the proposed system.

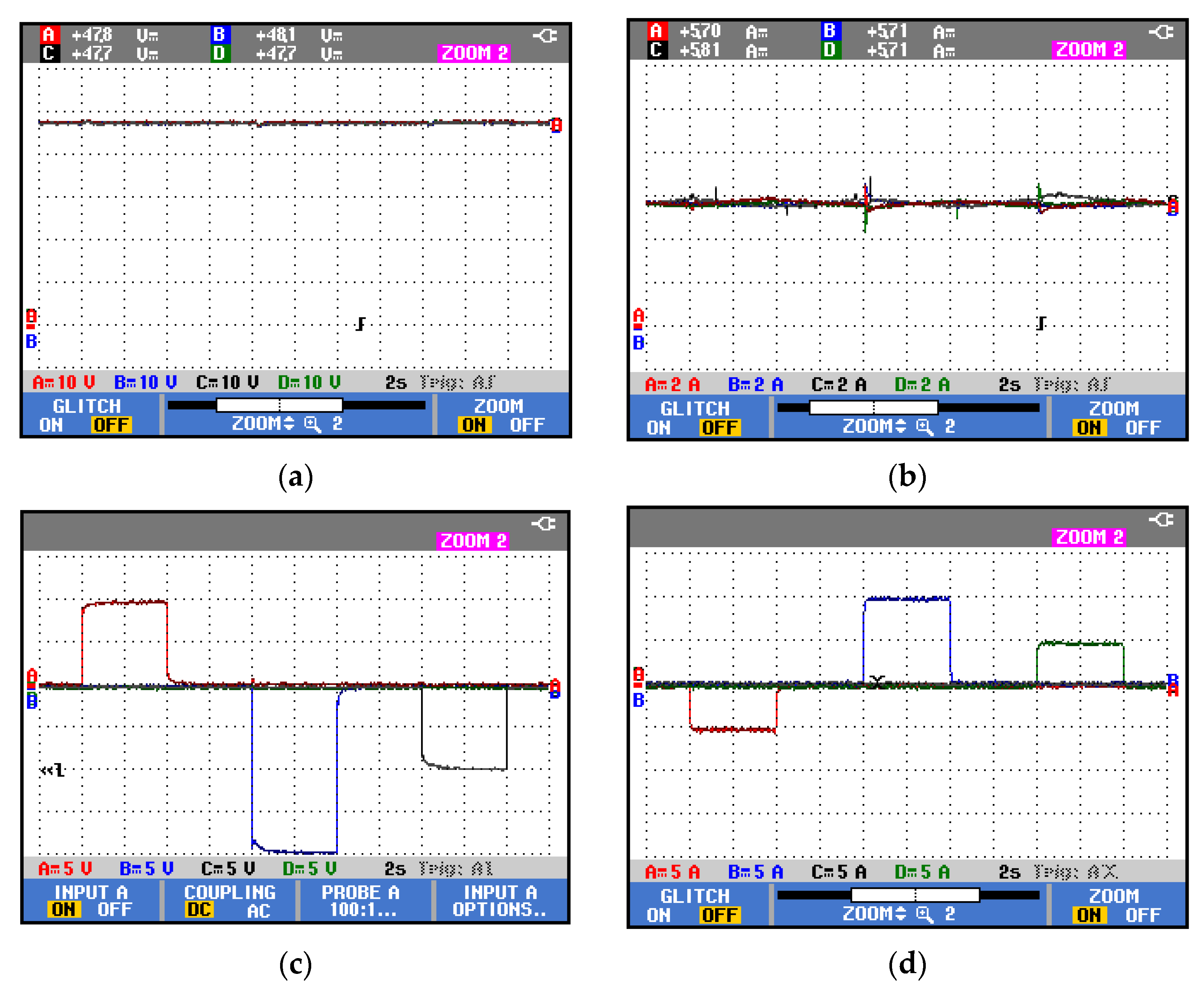
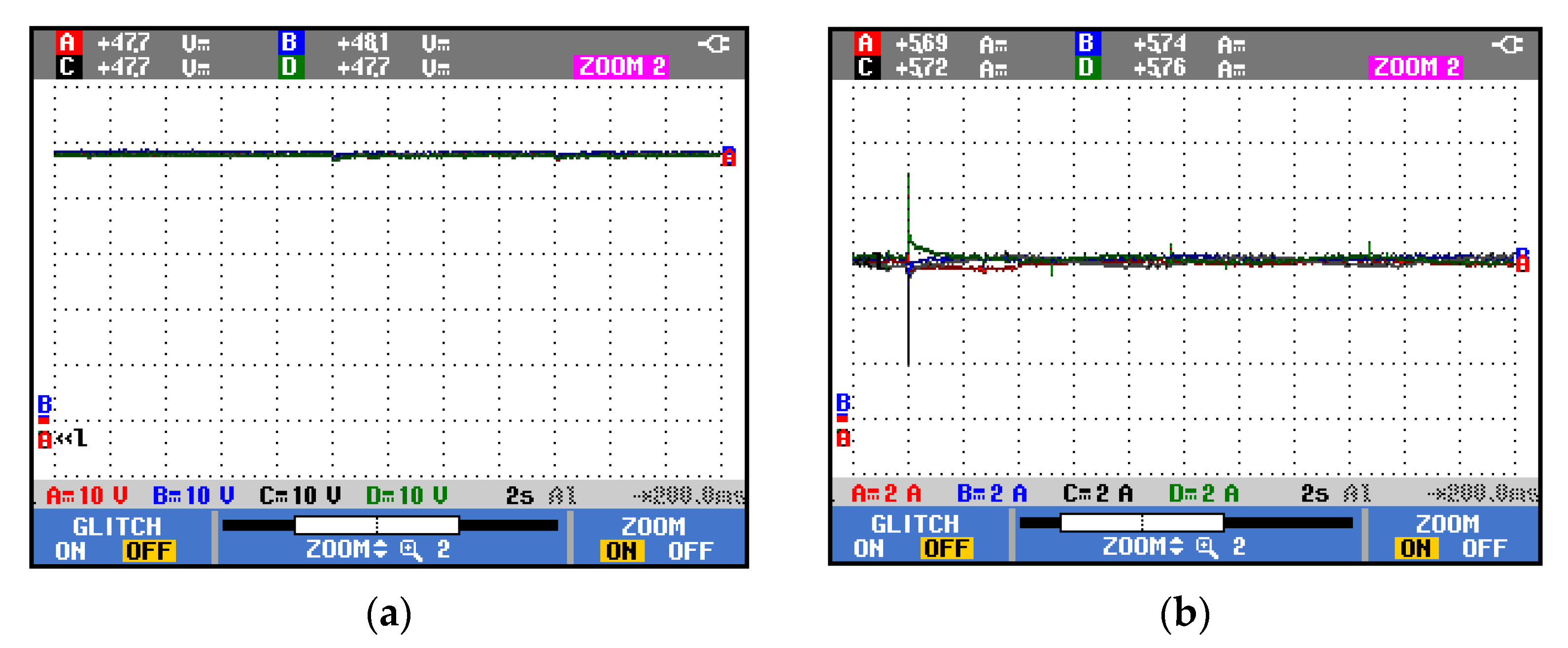
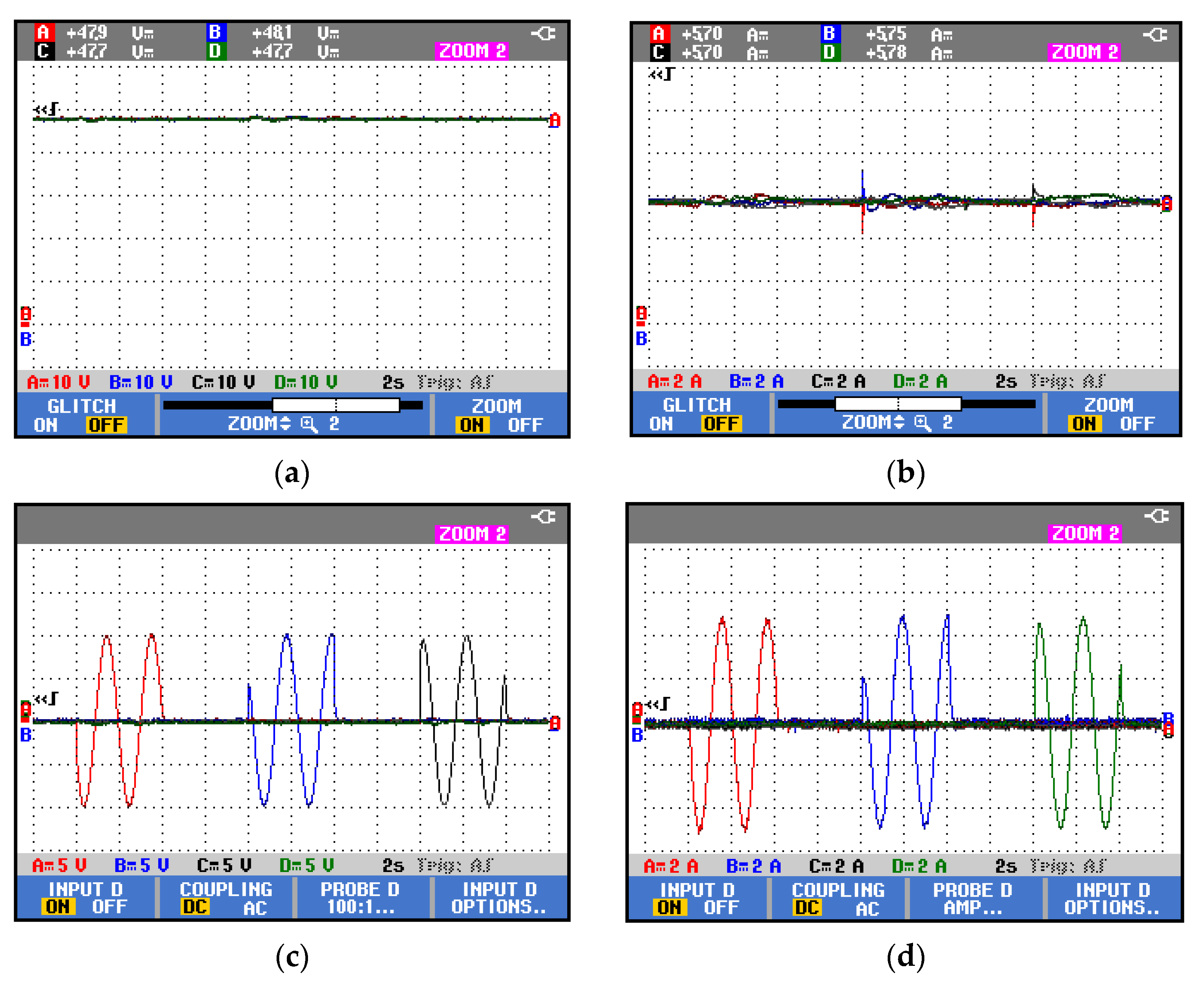
5. Experimental Results

Experimental work was conducted to verify the effectiveness of the proposed voltage and current cyber-attack-mitigation layers. The microgrid system with different control loops was implemented using Hardware in the Loop Typhoon HIL-402 [35] and dSPACE Mircolab box RTI-1202 [36]. Different controllers were used for the secondary and the proposed mitigation layers to validate the superiority of the FAPI controller. Moreover, the dynamic performance of the proposed system under time-varying FDIAs is investigated.

5.1. API Controller

The cyber-attacks scenario used in the simulation was considered in this case study. All cyber-attacks have a time interval of four seconds. Figure 9a shows that the terminal voltage of each DGU is subjected to small deviations during the initiation of any cyber-attack. As a result, the output currents are subjected to overshoots once an attack is initiated, as illustrated in Figure 9b. The corrective actions taken by the voltage and current cyber-attack-mitigation layers of each DGU are shown in Figure 9c,d. As in the simulation case study, these results demonstrate that each layer takes an action that opposes the attack on the corresponding layer; however, the API controller has a slow dynamic performance. The quite large increase in time is the main reason for the voltage deviations and current overshoots at the time of these attacks. Therefore, the API controllers were replaced with other controllers in the following case studies.

5.2. Tuned PI Controller

In this section, the API controllers were replaced with tuned PI controllers in the secondary layers and mitigation layers. The same cyber-attacks scenario was considered. The experimental results show that, using PI controllers, the voltages of all DGUs follow their reference, Figure 10a, with lower voltage deviations than the case using API controllers. In addition, the DGUs maintained an equal current-sharing with less overshoot at the instant of cyber-attacks, as shown in Figure 10b. The action of the voltage and current cyber-attack-mitigation layers is illustrated in Figure 10c,d, respectively. The corrective action of each mitigation layer opposes the applied cyberattack, with a faster response than the API controller. The tuned PI controller is superior to the API controller. As the API controller gains are chosen arbitrarily, the API mitigation controller has a slower dynamic performance, as shown by Figure 9c,d. On the other hand, the tuned PI controller gains are tuned online by dSPACE. Hence, the tuned PI will provide a fast response for mitigation layers, as indicated by Figure 10c,d. However, the disadvantage of PI controllers is the need for proper tuning to mitigate cyberattacks with a fast dynamic performance. Moreover, the current-sharing is disturbed at the initiation of any attack.

5.3. FAPI Controller

Finally, the FAPI controller is utilized to enhance the system capability of cyber-attack mitigation and improve the dynamic performance. The experimental results show that the terminal voltage of each DGU is regulated, as in Figure 11a, at the reference value 48 V. The current-sharing is properly maintained between all units, as in Figure 11b, regardless of the values of cyber-attacks with the minimum overshoot during the attacks. Since the settling time of the FAPI is smaller than that of API and PI, the proposed cyber-attack mitigation strategy based on the KF algorithm can accurately and instantly set the corrective actions without shoots, as demonstrated in Figure 11c,d. Moreover, there is no cross-coupling or interaction between the corrective actions set by the different mitigation layers. Another advantage of the FAPI controller is that it does not require time-consuming tuning because of its adaptive nature.

Comparing the controllers used in the above case studies, the following deductions were made. While the API controller continuously changed its gains based on the error, the tuned PI controller gains were adjusted online manually by the dSPACE when observing the response of the system in real-time (HIL). On the other hand, the FAPI has an extra tunable parameter m that provides an extra degree of freedom, which results in an enhanced dynamic performance.

Table 1. Controller comparisons.

Controller	Settling Time (s)	Current MPOS%
API	2	+145%
Tuned PI	1	+22.8%
FAPI	0.25	−65%

shows a comparison between the dynamic performance of the three controllers based on the Maximum Peak Overshoot (MPOS) of the current and the settling time. The settling time is a critical specification for the mitigation process, as a lower settling time indicates faster mitigation of the FDIA. Moreover, higher positive current overshoots are critical as they may cause the tripping of circuit-breakers in the DC microgrid. Therefore, a lower settling time and lower current overshoots indicate a better dynamic performance. Compared to the conventional API and tuned PI, the settling time of the proposed FAPI can be reduced by about 87.5% and 75%, respectively. The MPOS can be mitigated by about 210% and 87.8%, respectively. Apparently, the dynamic performance of the DGUs in meshed DC microgrids can be significantly improved by adopting the proposed FAPI control.

5.4. Time-Varying Cyber-Attack Using FAPI Controller

The robustness of the FAPI controller was further evaluated by considering time-varying voltage and current cyber-attacks. The voltage and current cyber-attacks on DGU_1,2,3 are presented in (34), and the current cyber-attack on DGU_1,2,4 is shown by (35). The time interval of each attack was four seconds.

$$V_{F\mathrm{1,2},3}\left(t\right)=10\sin \left(\pi t\right)$$

(35)

$$I_{F\mathrm{1,2},4}\left(t\right)=5\sin \left(\pi t\right)$$

(36)

Figure 12a verifies the robustness of the FAPI controller with the KF for the voltage cyber-attack-mitigation layer. The voltages of all DGUs were tightly regulated at the reference value 48 V. Additionally, Figure 12b validates the effectiveness of the FAPI controller-based current cyber-attack-mitigation layer, since it maintained proper current-sharing between DGUs despite the aggressive cyber-attacks on current measurements of DGU1,2,4. The mitigation signals for the voltage and current cyber-attacks are shown in Figure 12c,d, respectively. With the aid of the proposed strategy, each layer set appropriate corrective actions for DGUs to lessen the effect of cyber-attacks on the measurements necessary for proper voltage regulation and current-sharing in a microgrid. Furthermore, the results validate the effectiveness of the proposed control strategies in detecting and mitigating different spectrums of DFIAs.

6. Conclusions

This paper presents a novel distributed control for distributed generator units (DGUs) in meshed DC microgrids. The new control scheme comprises two cyber-attack and mitigation layers that aim to cancel out the effects of false data injection attacks (DFIAs). A Kalman Filter (KF) is utilized in each mitigation layer to accurately estimate the terminal voltage and current of each DGU. The data monitored by KF were compared to the measured data. The differences between the two data were used to adaptively forge the compensation signals to mitigate the DFIAs. Both the simulation and experimental results demonstrate the effectiveness of the proposed anti-cyber-attack control scheme in mitigating the attack signals, while maintaining the terminal voltages to track the references. To exhibit a superior dynamic performance and zero offsets under operation condition variations during cyber-attacks, the proposed strategy, based on the fractional adaptive proportional integral (FAPI) control, was fairly compared to the conventional PI control and the intermediate API control. Furthermore, the KF of the proposed control was also compared to the artificial neural networks (ANN) of the counterpart during simulation. The KF exhibits a better dynamic tracking performance. The practical results show that the proposed control strategy can reduce settling time by at least 75% settling time and mitigated overshoot by 85% as compared to the conventional control strategies. In the future work, more types of cyber-attacks will be considered for the proposed control for DGUs in various structures of DC microgrids, or even AC microgrids.