DelayNet: Enhancing Temporal Feature Extraction for Electronic Consumption Forecasting with Delayed Dilated Convolution

Abstract

In the face of increasing irregular temperature patterns and climate shifts, the need for accurate power consumption prediction is becoming increasingly important to ensure a steady supply of electricity. Existing deep learning models have sought to improve prediction accuracy but commonly require greater computational demands. In this research, on the other hand, we introduce DelayNet, a lightweight deep learning model that maintains model efficiency while accommodating extended time sequences. Our DelayNet is designed based on the observation that electronic series data exhibit recurring irregular patterns over time. Furthermore, we present two substantial datasets of electricity consumption records from South Korean buildings spanning nearly two years. Empirical findings demonstrate the model’s performance, achieving 21.23%, 43.60%, 17.05% and 21.71% improvement compared to recurrent neural networks, gated-recurrent units, temporal convolutional neural networks and ARIMA models, as well as greatly reducing model complexity and computational requirements. These findings indicate the potential for micro-level power consumption planning, as lightweight models can be implemented on edge devices.

1. Introduction

According to recent observations, the frequency and intensity of extreme weather events are increasing globally and becoming more severe [1,2]. Due to abnormal temperatures and climate changes, there is an increasing volatility in power consumption [3]. Since electrical energy must be produced and consumed simultaneously due to its physical characteristics [4], accurate prediction of power demand is crucial when planning power generation at the national and power plant levels. For instance, failing to predict power demand accurately may result in not only budget overspending on excessive power generation facilities but also wasted electrical energy. On the other hand, if there is a shortage of electrical energy, power outages can occur. In fact, in South Korea, a power outage occurred in September 2011 due to a shortage of electricity [5].

The most effective application of electricity demand forecasting pertains to predicting the power consumption of individual buildings. The consumption of energy in buildings is anticipated to witness a surge of over 40% in the forthcoming two decades, accounting for 30–45% of the total global energy consumption. Systems such as the Home Energy Management System (HEMS) and Building Energy Management Systems (BEMS) are structured in diverse forms, contingent upon the type and size of the building. These systems are under research not only for collecting and monitoring building-level electricity consumption [6,7] data, but also for enabling the forecasting of electricity consumption. In buildings of larger scale, extensive cloud servers and server rooms exist, equipped with substantial computing power for BEMS. However, medium and smaller-scale buildings typically possess only small-scale server rooms or MCUs at the level of edge computing. Consequently, the availability of computing power resources emerges as a critical element in the research of electricity forecasting.

Research on electricity demand forecasting has seen substantial progress encompassing a variety of methodologies from machine learning to deep learning techniques. In earlier studies, there were efforts aimed at forecasting household electricity consumption by categorizing patterns of electricity usage data, which were accumulated through home systems [8]. Investigations were initiated where the characteristics of electricity utilization data were grouped and examined, and uniquely normalized data was employed to educate machine learning models for forecasting purposes [9]. Additionally, studies were conducted on systems with the capability to predict long-term electricity demand, utilizing machine learning models trained with time-series-analyzed monthly electricity consumption data [10].

In more recent advancements, deep learning techniques have been integrated, utilizing multilayer perceptron (MLP), recurrent neural network (RNN), and long-short-term memory (LSTM) for training models on household electricity consumption data for predictive purposes [11]. There has been a noteworthy study that proposed a hybrid convolutional long-short-term-memory (CNN-LSTM) model specifically aiming to predict residential energy consumption [12]. Additionally, innovative approaches have been adopted where electricity consumption data was manipulated to conform with the characteristics inherent to sequential data, employing Transformer models for the purpose of electricity demand prediction [13]. This convergence of methodologies highlights the evolving landscape of machine learning research in addressing the challenges of electricity demand forecasting.

Typically, power consumption prediction models employ temporal convolutional neural networks (TCNs), effectively capturing the local features, a strength of CNN, but they fall short of adequately incorporating time-series characteristics. To counter this, advanced approaches have been developed, combining CNN and RNN and introducing models in the Transformer family that apply attention mechanisms. This evolution in methodologies has led to a notable improvement in the accuracy of electricity demand forecasting models, which are trained using electricity usage data. However, this advancement in accuracy has consequently demanded a parallel increase in both the model’s capacity and the computing power required.

In this paper, we aim to propose DelayNet, a lightweight building power consumption prediction model for BEMS that can be applied to medium- and small-sized buildings. The proposed DelayNet interprets the Dilated Convolution of TCN [14] in a new way and applies Dilated Delay Convolution, thus well reflecting both local features and time-series characteristics while using fewer parameters and fewer computational operations. The main contributions of this paper are as follows:

• We publish our in-house power consumption dataset, a reliable dataset collected from residences over a period of two years.
• We propose DelayNet, a stable yet lightweight deep learning model for predicting the power consumption of buildings. The DelayNet can retain the local feature of TCN while reflecting long sequence characteristics. Compared to previous works, the Delay Block maintains the same number of filters while increasing the interval between sequences, significantly reducing the number of parameters and computational operations while exhibiting high performance.

The structure of the remainder of this paper is as follows: Section 2 will explore studies related to predicting power consumption. Section 3 will give a detailed explanation of the common deep learning models used for such predictions and discuss the background and approach of the proposed DelayNet. In Section 4, we will share the actual data on power consumption that we collected and the results of our experiments. Finally, Section 5 will conclude the paper.

2. Related Works

Research efforts have been dedicated to extracting features from energy consumption data and predicting power demand to ensure a stable power supply. These efforts can be divided into three main categories: statistical-based approaches, machine learning-based approaches, and deep learning-based approaches.

Statistical-based methods have been utilized for predicting power demand. These approaches involved conducting simple and multiple linear regression analyses as well as quadratic regression analyses using building data collected on an hourly and daily basis [15]. It was noted that as the time intervals increased, the quality of the models [16] improved. In the context of forecasting daily power consumption in commercial buildings, research was conducted on both multiple regression and genetic programming models. While the genetic programming model displayed a slight performance advantage over the multiple regression model, it did have the drawback of longer training times. Additionally, a study presented a method for predicting next-day electricity prices in the Spanish and Californian power markets based on the autoregressive integrated moving average (ARIMA) methodology [17]. Customized ARIMA models were developed for each dataset. Furthermore, research focused on building load forecasting using a hybrid model that combined clustering techniques with ARIMA models [18]. It was observed that the hybrid model yielded improved predictive performance compared to using a standalone ARIMA model. However, these traditional statistical models often encounter difficulties when handling complex datasets that are non-linear and noisy, leading to potential reductions in prediction accuracy.

In the context of machine-learning-based approaches, research endeavors have focused on the application of the Random Forest ensemble learning method to predict the maximum energy consumption [19]. Random Forest was chosen for its ability to optimize and mitigate overfitting, and attempts were made to improve performance by including not only basic current loads but also data from GSM network call records. Furthermore, a study investigated the utilization of the Support Vector Regression (SVR) model to forecast demand response criteria in office buildings [20]. Enhancements in performance were sought by introducing foundational electrical loads and ambient temperature into the model. It is important to note that these machine learning-based methods may face challenges as the volume of data increases.

In the domain of deep learning-based techniques, research has delved into the development of models for short-term load prediction. This includes a study that combines CNN (Convolutional Neural Network) with K-means clustering [21]. Additionally, there has been investigation into LSTM (Long-Short-Term-Memory) models for short-term load forecasting [22]. Building upon these findings, hybrid models integrating CNN and LSTM networks have been explored for short-term load prediction [23]. Furthermore, research has been conducted on S2S (Sequence to Sequence) models, such as LSTM-based S2S structures [24] and GRU-based S2S structures [25]. In these cases, crucial autocorrelation coefficients in time series data were used for data analysis. Moreover, research has examined the integration of Attention mechanisms into S2S structures [26]. For time series prediction, there has been exploration of TCN (Temporal Convolutional Network) models, which adapt CNN filters for time series data [27].

Inspired by the Transformer model’s exceptional performance in Natural Language Processing (NLP) [28], research has also extended to power demand prediction models based on the Transformer architecture [13]. The basic Transformer structure has been customized to optimize it for power demand prediction in this context. More recently, models like Informer have emerged, which are Transformer-based models fine-tuned specifically for time series data prediction [29]. Additionally, there are models like Autoformer, which employ autocorrelation coefficients for time series prediction within a Transformer framework [30], and Fedformer, which optimizes computation by using frequency domain operations in a Transformer architecture [31].

These deep learning-based methods have demonstrated impressive performance not only in short-term and long-term power demand forecasting but also in various other time series prediction tasks. However, it is essential to acknowledge that the pursuit of higher performance often results in significantly larger model sizes and computational requirements. For example, the computational complexity of Transformers is $O\left(L^2\right),$ meaning computational demands increase quadratically with the length of the input sequence.

As previously mentioned, research in power demand prediction has explored a variety of methods, including those based on statistics, machine learning, and deep learning. However, most of these studies aimed to improve the accuracy of power demand prediction models by incorporating additional variables and leveraging big data alongside the provided power data. Nevertheless, our research reveals that using highly complicated models does not always lead to better outcomes. When dealing with specific tasks and limited data, it is often better to create a custom model that suits the task well and learns effectively, instead of using complex models that need a lot of data to work correctly.

3. DelayNet

This section outlines our contribution, the Delay Dilated Convolutional Grouping Network (DelayNet), designed for time series forecasting. Our proposed architecture draws inspiration from TCN models and shares a close relationship with the Stride-TCN design. To provide context, we will briefly demonstrate developments in time series forecasting before introducing our model.

3.1. Preliminaries

Time series forecasting (TSF) finds numerous applications and can be categorized into two tasks: Single Step Prediction and Multi-Step Prediction. Concerning time series datasets, they can be categorized into Multivariable and Univariable Datasets. In this research, our primary focus is on the task of Multi-Step Prediction within the context of Univariable time series data.

The task of power demand forecasting shares commonalities with the broader field of time series prediction, which finds applications across diverse domains. Specifically, predicting power demand from power consumption data can be likened to the challenge of univariate time series forecasting [32].

$${\widehat{y}}_{t+1}=f_s\left({\mathit{y}}_{t-k:t},{\mathit{x}}_{t-k:t}\right)$$

(1)

Equation (1) presents a mathematical model for time series prediction tasks. In this context, $\widehat{y}$ represents the predicted value, while $\mathit{x}$ and $\mathit{y}$ denote input values. Time is denoted by $t$, and $k$ is the window size, while $s$ represents static metadata values that remain constant over time. For univariate time series prediction, we can define it as the forecasted value derived by applying input values and static metadata from time step $t-k$ to $t$ to a function $f$. This framework allows us to construct 2 subcomponents, as in Equations (2) and (3).

$${\mathit{z}}_t=g_{encoder}\left({\mathit{x}}_{t-k:t}\right)$$

(2)

$${\widehat{y}}_{t+1}=g_{decoder}\left({\mathit{z}}_t,{\mathit{y}}_{t-k:t}\right)$$

(3)

In this framework, $z_t$ represents a latent vector. The process involves transforming input values into latent values using an encoder, and these resultant latent values are subsequently employed for generating final predictions through a decoder. Within $g_{encoder}$, a variety of deep learning models can be applied, offering flexibility, while $g_{decoder}$ can encompass a range of models, spanning from basic linear functions to more complex ones like Sequence-to-Sequence (S2S) models. In the context of univariate time series prediction, non-linear functions are primarily employed within $g_{encoder}$. Next, we will introduce some common deep learning-based models for TSF.

Deep Learning Model Based TSF

Deep learning models for time series forecasting can be categorized into four primary types, each distinguished by how the encoder and decoder functions are constructed.

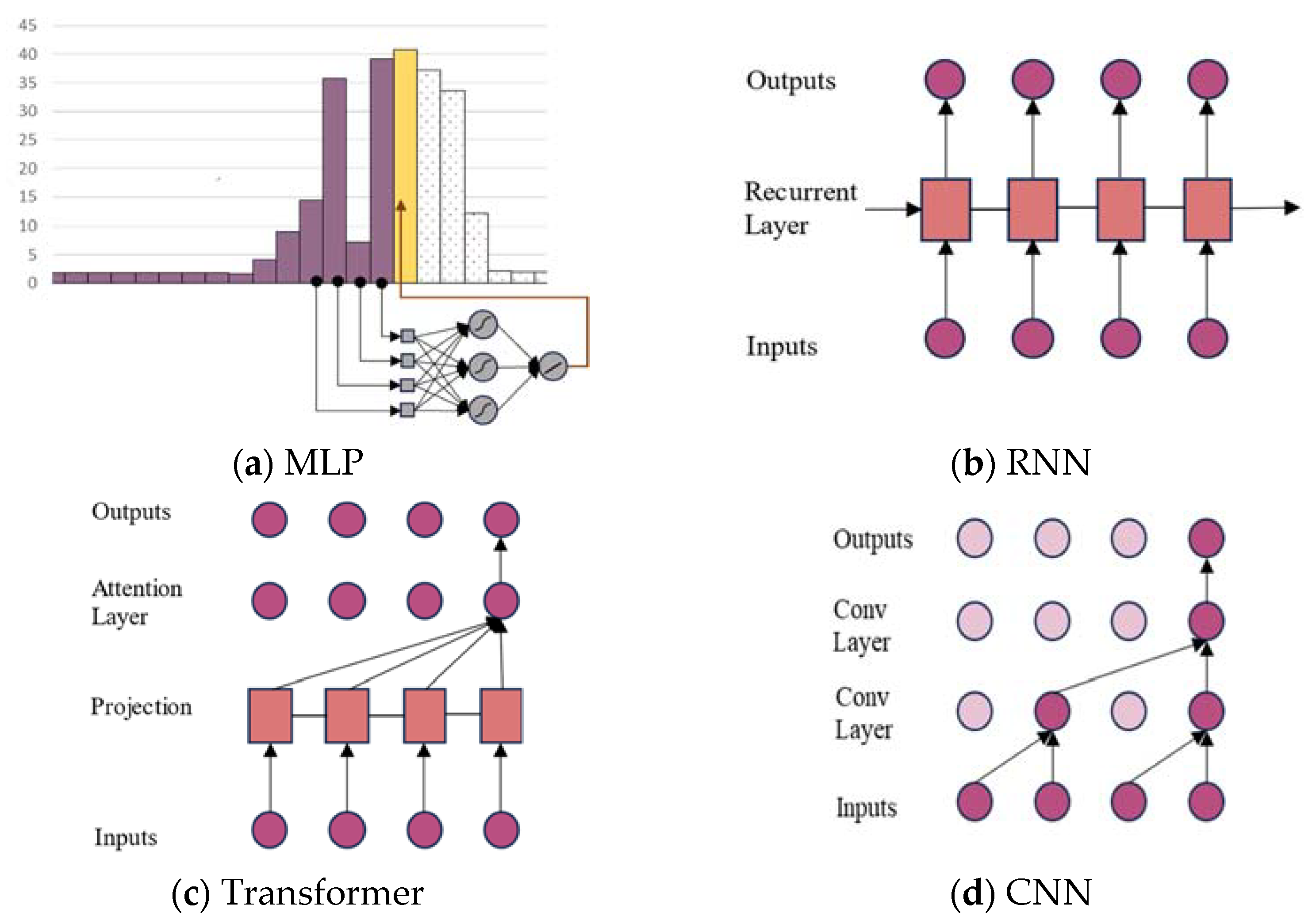
Firstly, the MLP-based TSF, depicted in Figure 1a, employs perceptrons as fundamental components, Equation (4). These perceptrons take inputs ${\mathit{x}}_{t-k:t}$, apply weights $\mathit{W}$, add biases $b$, and utilize activation functions $f$ to compute predictions. While effective for simple and short-term data, MLP models struggle with large datasets due to their substantial computational requirements.

$${\widehat{y}}_{t+1}=g_{decoder}=f\left(\mathit{W}{\mathit{x}}_{t-k:t}+b\right)$$

(4)

On the other hand, RNN-based TSF, represented in Figure 1b, utilizes recurrent neural networks (RNNs) that incorporate information from previous hidden layers into current computations, Equations (5) and (6). This allows them to capture long-range dependencies in sequential data. However, RNNs have limitations, such as fixed window sizes and challenges related to gradient issues and long-distance prediction.

$${\mathit{z}}_t=g_{endoder}=f\left(\left[{\mathit{U}}_e{\mathit{x}}_t,{\mathit{V}}_e{\mathit{z}}_{t-1}\right]+b_e\right)$$

(5)

$${\widehat{y}}_{t+1}=g_{encoder}=f\left(\left[U_d{y}_t,{\mathit{V}}_d{\mathit{z}}_t,{\mathit{W}}_d{\mathit{h}}_{t-1}\right]+b_d\right)$$

(6)

The third type is Transformer-based TSF, as seen in Figure 1c, leverages attention mechanisms to consider relationships between tokens in input sequences, Equation (7). Transformers are capable of incorporating important information from past time steps directly into predictions. However, they are characterized by complex models, high computational costs for attention calculations $O\left(n^2\right)$, and suboptimal performance on smaller datasets.

$${\mathit{z}}_t=g_{encoder}=f\left({\displaystyle \sum }_{i=t-k}^{t-1}\alpha \left({\mathit{K}}_t,{\mathit{Q}}_i\right){\mathit{v}}_t\right)$$

(7)

$${\widehat{y}}_{t+1}=g_{decoder}=f\left(\mathit{W}\left[{\mathit{z}}_{t-k:t}\right]+b\right)$$

(8)

Lastly, to adapt CNNs for time series, causal convolution is essential to ensure that the model only considers past data. In this context, hidden states $z_t$ and filter weights $W_t$ play crucial roles. To increase the receptive field while minimizing computational demands, Dilated convolution is employed, as shown in Figure 1d, allowing the model to capture $d$ long-term dependencies, Equation (9). CNN-based time series forecasting excels in capturing local correlations and addressing long-range dependencies [33], making it a valuable tool for time series data analysis.

$${\mathit{z}}_t=g_{encoder}=f\left({\displaystyle \sum }_{i=0}^{\lfloor \frac{k}{d_l}\rfloor }{\mathit{W}}_t{\mathit{x}}_{t-di}\right)$$

(9)

$${\widehat{y}}_{t+1}=g_{decoder}=f\left(\mathit{W}\left[{\mathit{z}}_{t-k:t}\right]+b\right)$$

(10)

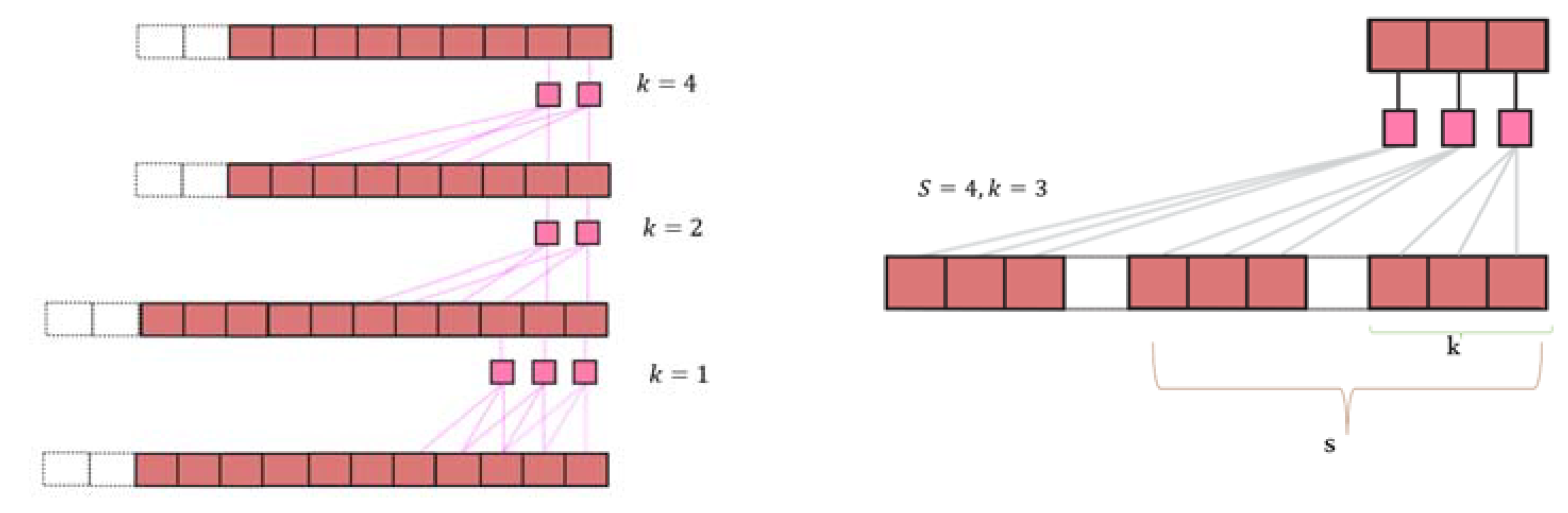
3.2. Rethinking TCN

Conventional TCNs [34] using 1D causal convolution and made use of dilated convolutions, as seen in Figure 2a, to enhance their capacity for information capture. However, to extend the receptive field for examining longer-term patterns in time series data, it is necessary to stack multiple dilated convolutions. This led to an increase in both model size and computational complexity. Nonetheless, TCNs offer an advantage by maintaining solid performance with a more compact model and lower computational demands when compared to other types of models for univariate time series prediction. To address this efficiency concern, Anh et al. introduced Stride-Dilated TCN (Stride-TCN), as depicted in Figure 2b [14]. Stride-TCN introduced a stride parameter into dilated convolutions, resulting in a significant enlargement of the receptive field using a single dilated convolution.

While TCN exhibits relatively dense connections for convolution calculations, resulting in an inflated model size that does not effectively harness sequence repetitiveness, Stride-TCN was introduced to mitigate this issue. However, Stride-TCN’s optimal performance requires an intricate and computationally expensive hyperparameter search using Bayesian Optimization [14], leading to prolonged training times. Moreover, it came to our attention that TCN and Stride-TCN inadequately capture sequence information, as they rely on a single connection between repeating intervals (dilated). This limitation is particularly significant when dealing with energy data, where individual values carry limited informational value.

Our model draws inspiration from the architectural foundations of TCN and Stride-TCN, underpinned by a crucial observation regarding the repetitive nature of data sequences, particularly in the context of electronic consumption data. Within DelayNet, we propose a fresh adaptation of the TCN model by incorporating Delay Dilated convolutions. This approach enables us to fully capture the nuances of time series data while keeping the model’s parameter and computational demands relatively low. The primary objective is to substantially increase the receptive field, addressing the constraints observed in previous TCN models.

DelayNet exhibits a structure akin to the original TCN and stride-TCN, comprising two fundamental components: dilated and causal 1D convolutional layers. However, the novel aspect of Delay Dilated Convolution lies in its distinct approach. As depicted in Figure 3, each layer denoted as $l$ is directly computed based on the preceding layer, $l-1$. The nodes within layer $l$, represented as $x_i^l$, are determined by a convolution size $K$, which encompasses a delay gap extending upwards from layer $l-1$. Likewise, the calculation of node $x_{i+1}^l$ in layer $l$ follows the same methodology as $x_i^l$. This computation facilitates the aggregation of information from the delayed data, as previously mentioned, within the confines of a single causal 1D convolution filter size.

$$z_t=g_{encoder}=DelayBlock\left({\mathit{x}}_{t-k:t}\right)$$

(11)

$${\widehat{y}}_{t+1}=g_{decoder}=ML{P}_W\left(z_{t-k:t}\right)$$

(12)

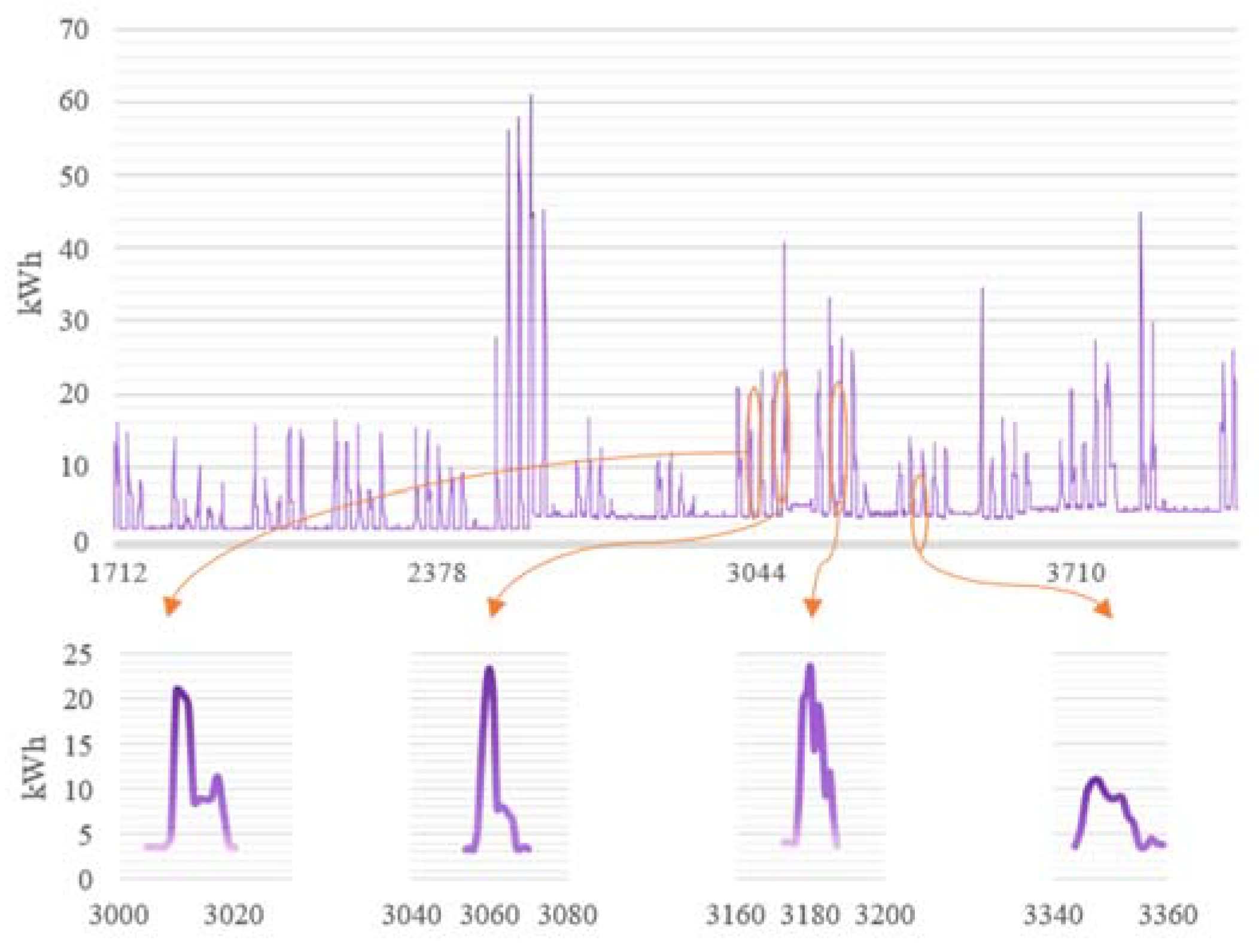
In essence, this signifies that delayed dilated convolution can place a more significant emphasis on capturing the seasonal and cyclical characteristics inherent in time series data, while maintaining an equal number of convolution operations. Especially when dealing with datasets employed for predicting power demand, as visualized in Figure 4, the seasonal and cyclical patterns influenced by climate conditions and building-specific attributes often outweigh the trend component. Hence, delayed dilated convolutional filters can yield substantial benefits in such scenarios. Furthermore, by employing fewer convolutional filters with a delayed gap, it becomes feasible to acquire a considerable receptive field while simultaneously reducing both parameter quantities and computational intricacies. Consequently, this approach allows for crafting models suitable for forecasting power demand in small to medium-sized building systems, making them adaptable to environments with constrained server resources or embedded systems, while also maintaining cost-effectiveness.

4. Experiments

In our experiment, we explore three scenarios to assess the performance and efficiency of DelayNet in comparison to other established models across various configurations.

Scenario 1 (Model Comparison): In the first scenario, we evaluate the performance of DelayNet with a small model size, emphasizing high accuracy. We compare it against a range of well-established models, including LSTM, MLP, GRU, TCN with two layers, ARIMA, and StrideTCN-2. This comparison aims to discern how DelayNet’s compact architecture fares in accuracy against more complex counterparts, shedding light on its suitability for resource-efficient forecasting.

Scenario 2 (Model Depth Analysis): In the second scenario, we delve into the impact of model depth on forecasting capabilities. We analyze Deeper-DelayNet with stacking five and seven layers. By exploring how these architectures handle increased depth, we aim to identify the optimal trade-off between model complexity and forecasting accuracy.

Scenario 3 (Lightweight Models Comparison): In the third scenario, we investigate Light-DelayNet versus Light-TCN, emphasizing efficiency and computational simplicity. This comparison seeks to elucidate how these lightweight variants of DelayNet and TCN perform.

4.1. Dataset

In our empirical studies, we conducted experiments using two publicly available datasets and two privately acquired datasets. All these datasets are accessible online, the size comparison is shown in Figure 5. It is worth noting that our research specifically centers on univariate time-series forecasting, which means we concentrated on time series data with a single dimension for each of the mentioned datasets. The key statistics of the dataset corpus are summarized in

Table 1. Summary of Dataset.

Dataset	Length	No. Variables	Attributions
France	34,589	7	Global active power, Global reactive power, Voltage, Global intensity, Submetering 1, Submetering 2, Submetering 3
Spain	8760	2	Energy consumption, Outside temperature
CNU	11,209	2	Energy consumption, Outside temperature
Gyeonggi	17,001	1	Energy consumption

.

• Individual Household Electric Power Consumption (France): This dataset is accessible online [35] and offers minute-by-minute electric power consumption data from a single household in France. The data spans 47 months, covering the period from December 2006 to November 2010. It comprises multivariable sequences, including total active power consumption, total reactive power consumption, average current intensity, active energy for the kitchen, active energy for the laundry, and active energy for climate control systems [36]. The dataset contains a total of 2,075,259 multivariable sequences. For our research, we specifically utilized 34,589 univariable sequences, focusing on the hourly global active power data. Our analysis centers on the total electricity consumption of a specific ID: 20.
• Energy Consumption from Spain (Spain): Dataset is available online [37], provides hourly energy consumption data, outside temperatures for the region, and metadata for 499 customers in Spain. This dataset covers approximately one year, from 1 January to 31 December 2019, totaling 8760 data points. Our primary interest in this research is the total electricity consumption of a particular ID.
• CNU Energy Consumption (CNU): This dataset features a real-world collection of energy consumption data from 90 distinct locations within CNU (Chonnam National University), available online [38]. The data was meticulously gathered at an hourly frequency over a span of 1.3 years, starting from 1 January 2021 and completing on 14 January 2022. Each location contributes valuable insights through a total of 11,232 data points. A notable enhancement in this upgraded CNU energy consumption dataset is the inclusion of additional dependable multivariate data, such as temperature, humidity, wind speed, and more. These supplementary variables were sourced from records maintained by the South Korean Meteorological Administration during the same period. Our experiment focuses on the total electricity consumption of a particular location, namely, “Gongdae 7th Building, HV_02”.
• Gyeonggi-do Building Power Usage (Gyeonggi): This is a real-world dataset collected directly from household electricity consumption, also accessible online [39]. It encompasses hourly records of building power consumption spanning approximately 1.9 years, ranging from 1 January 2021 to 14 January 2022. The dataset covers around 17,001 specific commercial buildings situated in Gyeonggi Province, South Korea. We have chosen to concentrate on two specific buildings within this dataset, namely, ID 9654 and 6499. These buildings were selected based on our data analysis, as they exhibit minimal missing data, making them ideal candidates for our experiments.

Before the training process, it is crucial to perform preprocessing steps. This is necessitated by the relatively high-power values present in the datasets. For instance, in the case of CNU dataset, the power values exhibit a mean of approximately $130.48$ and a standard deviation of around $46.97$. To circumvent potential challenges such as numerical errors and distortion of the dataset, we employ min-max normalization. This normalization method transforms the features to a standardized range of $\left[0,1\right]$, ensuring uniformity and optimal training performance. The min-max normalization is calculated in Equation (13).

$$z_i=\frac{x_i-\min \left(\mathit{x}\right)}{\max \left(\mathit{x}\right)-\min \left(\mathit{x}\right)}$$

(13)

In this experiment, we conducted time-series forecasting tasks using each of four datasets. To provide further details, most models employed an input window of 168 h and generated forecasts with output windows ranging from 1 to 144 h. For each dataset, we followed a chronological split, dividing it into three distinct subsets: $80\%$ for the training set, $10\%$ for the validation set, and $10\%$ for the testing set.

4.2. Configurations

We utilized two evaluation metrics for univariate forecasting, namely the Mean Absolute Error (MAE, $k=1$) and Mean Squared Error (MSE, $k=2$), which are defined as follows:

$$\mathrm{Error}=\frac{1}{n}{\displaystyle \sum }_{i=1}\Vert Y_i-\widehat{Y_i}{\Vert }_k^k$$

(14)

In our study, we employ input sequences of a fixed length, precisely 168 data points, as the foundation for our forecasting endeavors. Our forecasting horizon extends from short-term predictions of $1$ to $24$ time steps ahead, with a keen focus on assessing the model’s performance in long-term forecasting, spanning $36$, $48$, $60$, $72$, $84$, $96$, $108$, $120$, $132$ and $3$ steps into the future. To ensure consistency and comparability, we normalize our input sequences. During training, we utilize two loss functions, Huber and Mean Squared Error (MSE), each serving specific aspects of our predictive goals. Additionally, we employ a ReduceLROnPlateau callback on Adam optimizer to dynamically adjust the learning rate during training of ten epochs. This setup aims to explore the model’s capabilities across various forecasting horizons. All the models were trained/tested on a single Nvidia A100 40GB GPU. The source code is available at github.com/andrewlee1807/DelayNet (accessed on 23 September 2023).

4.3. Model Comparision

Table 2. Performance on CNU dataset.

Methods	Delay-Net2		LSTM		MLP		GRU		TCN-2 Layers		ARIMA		Stride-TCN 2 Layers
Metric	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
1	0.0018	0.0284	0.0021	0.0306	0.0026	0.0346	0.0022	0.0311	0.0020	0.0306	0.0025	0.0337	0.0145	0.0819
5	0.0058	0.0510	0.0073	0.0559	0.0061	0.0532	0.0065	0.0529	0.0067	0.0539	0.0135	0.0781	0.0154	0.0866
10	0.0085	0.0630	0.0108	0.0683	0.0082	0.0631	0.0096	0.0637	0.0094	0.0627	0.0261	0.1166	0.0153	0.0866
15	0.0099	0.0686	0.0111	0.0728	0.0088	0.0652	0.0109	0.0685	0.0109	0.0700	0.0326	0.1347	0.0148	0.0864
20	0.0110	0.0737	0.0128	0.0776	0.0101	0.0718	0.0119	0.0717	0.0119	0.0742	0.0339	0.1377	0.0150	0.0867
24	0.0108	0.0718	0.0105	0.0715	0.0098	0.0697	0.0124	0.0734	0.0117	0.0736	0.0319	0.1314	0.0153	0.0868
36	0.0096	0.0727	0.0125	0.0786	0.0103	0.0719	0.0122	0.0738	0.0136	0.0800	0.0335	0.1348	0.0155	0.0871
48	0.0110	0.0771	0.0129	0.0806	0.0115	0.0760	0.0111	0.0706	0.0144	0.0819	0.0351	0.1377	0.0148	0.0861
60	0.0109	0.0771	0.0137	0.0817	0.0117	0.0771	0.0121	0.0758	0.0153	0.0861	0.0361	0.1399	0.0191	0.0982
72	0.0102	0.0755	0.0135	0.0805	0.0128	0.0805	0.0126	0.0768	0.0144	0.0839	0.0363	0.1403	0.0157	0.0881
84	0.0101	0.0752	0.0135	0.0796	0.0122	0.0786	0.0128	0.0796	0.0146	0.0844	0.0363	0.1404	0.0150	0.0869
96	0.0098	0.0756	0.0154	0.0885	0.0118	0.0775	0.0134	0.0807	0.0144	0.0844	0.0364	0.1406	0.0180	0.0951
108	0.0099	0.0759	0.0148	0.0861	0.0122	0.0782	0.0131	0.0803	0.0145	0.0849	0.0365	0.1410	0.0141	0.0839
120	0.0099	0.0756	0.0139	0.0797	0.0122	0.0780	0.0135	0.0815	0.0140	0.0840	0.0368	0.1415	0.0133	0.0829
132	0.0096	0.0744	0.0137	0.0794	0.0120	0.0780	0.0137	0.0820	0.0138	0.0830	0.0369	0.1418	0.0133	0.0820
144	0.0103	0.0765	0.0138	0.0806	0.0129	0.0788	0.0133	0.0807	0.0137	0.0828	0.0370	0.1420	0.0132	0.0816
Better (in average)			21.23	6.64	9.42	67.18	43.60	2.21	17.05	2.74	21.71	7.03	38.04	19.82

,

Table 3. Performance on Gyeonggi dataset.

Methods	DelayNet		LSTM		MLP		GRU		TCN-2 Layers		ARIMA		StrideTCN-2 Layers
Metric	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
1	0.0018	0.0172	0.0021	0.0199	0.0026	0.0243	0.0020	0.0195	0.0019	0.0199	0.0023	0.0161	0.0058	0.0351
5	0.0045	0.0280	0.0050	0.0311	0.0049	0.0334	0.0051	0.0321	0.0049	0.0314	0.0078	0.0337	0.0071	0.0435
10	0.0050	0.0308	0.0060	0.0351	0.0056	0.0348	0.0062	0.0362	0.0055	0.0344	0.0119	0.0465	0.0069	0.0397
15	0.0050	0.0308	0.0073	0.0401	0.0059	0.0363	0.0067	0.0379	0.0058	0.0362	0.0137	0.0523	0.0063	0.0373
20	0.0056	0.0329	0.0071	0.0403	0.0060	0.0365	0.0068	0.0380	0.0062	0.0381	0.0141	0.0534	0.0074	0.0422
24	0.0055	0.0362	0.0063	0.0377	0.0061	0.0372	0.0071	0.0387	0.0064	0.0387	0.0136	0.0516	0.0066	0.0390
36	0.0058	0.0385	0.0076	0.0433	0.0062	0.0392	0.0073	0.0414	0.0063	0.0399	0.0140	0.0531	0.0076	0.0434
48	0.0068	0.0386	0.0062	0.0391	0.0063	0.0396	0.0074	0.0424	0.0063	0.0406	0.0143	0.0543	0.0074	0.0456
60	0.0061	0.0392	0.0065	0.0408	0.0062	0.0397	0.0064	0.0422	0.0065	0.0416	0.0147	0.0556	0.0081	0.0459
84	0.0059	0.0393	0.0063	0.0396	0.0063	0.0417	0.0069	0.0435	0.0064	0.0408	0.0149	0.0569	0.0077	0.0487
96	0.0064	0.0410	0.0060	0.0375	0.0064	0.0437	0.0068	0.0448	0.0065	0.0424	0.0151	0.0575	0.0067	0.0424
132	0.0064	0.0417	0.0066	0.0399	0.0065	0.0442	0.0067	0.0424	0.0064	0.0426	0.0156	0.0591	0.0065	0.0399
144	0.0063	0.0418	0.0066	0.0403	0.0064	0.0428	0.0070	0.0433	0.0063	0.0421	0.0156	0.0593	0.0080	0.0459
Better (in average)			10.28	6.22	7.00	8.47	13.45	9.57	5.81	7.22	54.73	27.51	23.22	17.23

,

Table 4. Performance on France dataset.

Methods	Delay-Net		LSTM		MLP		GRU		TCN-2 Layers		ARIMA		Stride-TCN 2 Layers
Metric	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
1	0.0052	0.0485	0.0054	0.0501	0.0054	0.0511	0.0054	0.0494	0.0053	0.0493	0.0076	0.0561	0.0098	0.0786
5	0.0074	0.0621	0.0075	0.0611	0.0076	0.0634	0.0072	0.0599	0.0075	0.0611	0.0165	0.0870	0.0097	0.0715
10	0.0078	0.0641	0.0078	0.0630	0.0080	0.0651	0.0079	0.0638	0.0082	0.0652	0.0193	0.0965	0.0098	0.0754
15	0.0080	0.0648	0.0080	0.0641	0.0082	0.0656	0.0084	0.0662	0.0084	0.0667	0.0192	0.0963	0.0089	0.0721
20	0.0082	0.0653	0.0082	0.0649	0.0083	0.0657	0.0083	0.0654	0.0089	0.0688	0.0202	0.0994	0.0092	0.0721
24	0.0083	0.0664	0.0083	0.0654	0.0084	0.0664	0.0082	0.0652	0.0086	0.0679	0.0195	0.0968	0.0095	0.0736
36	0.0085	0.0688	0.0087	0.0685	0.0086	0.0673	0.0085	0.0662	0.0090	0.0706	0.0198	0.0980	0.0113	0.0847
48	0.0086	0.0682	0.0093	0.0702	0.0087	0.0692	0.0087	0.0686	0.0089	0.0700	0.0200	0.0986	0.0099	0.0789
60	0.0087	0.0692	0.0088	0.0683	0.0088	0.0695	0.0087	0.0688	0.0091	0.0718	0.0202	0.0994	0.0094	0.0737
72	0.0088	0.0704	0.0088	0.0689	0.0088	0.0696	0.0087	0.0688	0.0091	0.0714	0.0203	0.1000	0.0099	0.0788
84	0.0089	0.0702	0.0095	0.0727	0.0089	0.0704	0.0087	0.0692	0.0092	0.0725	0.0204	0.1006	0.0117	0.0875
96	0.0089	0.0707	0.0092	0.0722	0.0089	0.0706	0.0087	0.0695	0.0092	0.0731	0.0204	0.1010	0.0095	0.0765
120	0.0089	0.0710	0.0098	0.0738	0.0091	0.0714	0.0088	0.0698	0.0094	0.0734	0.0204	0.1016	0.0119	0.0893
144	0.0091	0.0725	0.0095	0.0737	0.0092	0.0723	0.0089	0.0710	0.0094	0.0741	0.0204	0.1022	0.0117	0.0878
Better (in average)			2.78	0.46	1.46	0.67	−0.07	−1.08	3.99	2.42	55.26	29.58	18.49	15.01

and

Table 5. Performance on Spain dataset.

Methods	Delay-Net2		LSTM		MLP		GRU		TCN-2 Layers		ARIMA		Stride-TCN 2 Layers
Metric	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
1	0.0075	0.0642	0.0127	0.0842	0.0086	0.0679	0.0095	0.0726	0.0083	0.0692	0.0093	0.0729	0.0177	0.1002
5	0.0124	0.0820	0.0156	0.0942	0.0123	0.0810	0.0137	0.0872	0.0132	0.0841	0.0286	0.1278	0.0227	0.1157
10	0.0139	0.0867	0.0163	0.0979	0.0151	0.0914	0.0147	0.0903	0.0153	0.0912	0.0465	0.1687	0.0214	0.1101
15	0.0146	0.0893	0.0162	0.0974	0.0147	0.0902	0.0168	0.0955	0.0163	0.0948	0.0544	0.1869	0.0210	0.1084
20	0.0152	0.0912	0.0158	0.0955	0.0146	0.0896	0.0154	0.0924	0.0164	0.0950	0.0550	0.1884	0.0215	0.1088
24	0.0153	0.0914	0.0157	0.0947	0.0154	0.0922	0.0165	0.0950	0.0174	0.0981	0.0506	0.1783	0.0213	0.1080
36	0.0161	0.0941	0.0165	0.0973	0.0169	0.0971	0.0160	0.0942	0.0176	0.0989	0.0530	0.1836	0.0208	0.1079
48	0.0164	0.0953	0.0167	0.0973	0.0163	0.0956	0.0160	0.0944	0.0187	0.1017	0.0533	0.1843	0.0305	0.1343
72	0.0169	0.0971	0.0180	0.1014	0.0172	0.0989	0.0167	0.0966	0.0201	0.1056	0.0552	0.1880	0.0354	0.1438
84	0.0166	0.0958	0.0178	0.1011	0.0188	0.1029	0.0169	0.0974	0.0202	0.1071	0.0557	0.1891	0.0216	0.1096
96	0.0172	0.0978	0.0183	0.1030	0.0189	0.1031	0.0168	0.0974	0.0203	0.1067	0.0563	0.1904	0.0221	0.1106
108	0.0172	0.0979	0.0182	0.1015	0.0185	0.1018	0.0170	0.0984	0.0204	0.1064	0.0568	0.1913	0.0216	0.1094
132	0.0170	0.0981	0.0186	0.1023	0.0171	0.0985	0.0173	0.0991	0.0201	0.1049	0.0580	0.1933	0.0211	0.1075
144	0.0176	0.0992	0.0186	0.1033	0.0190	0.1031	0.0178	0.1003	0.0194	0.1040	0.0582	0.1936	0.0207	0.1073
Better (in average)			9.64	6.85	4.19	2.48	3.89	2.54	11.78	6.32	65.67	45.65	31.94	18.62

present a comprehensive analysis of DelayNet’s performance in comparison to other baseline models across the CNU, Gyeonggi, France, and Spain datasets, respectively. In these experiments, DelayNet is configured to the settings of followings, the kernel size is set to $3$, the gap of $6$, the delay factor of $7$, the number of filters is $16$ while the number of stacks is $3$. The results reveal that DelayNet is better than other models, including LSTM, MLP, GRU, 2layers-TCN, ARIMA, and 2layers-Stride-TCN, with an average in (MSE, MAE) across horizon decrease (21.23%, 6.64%), (9.42%, 2.21%), (17.05%, 2.74%), (21.71%, 7.03%), (67.18%, 43.60%) and (38.4%, 19.82%), respectively on CNU dataset. Similarly, on Gyeonggi dataset, DelayNet better than other models with the margin of (10.28%, 6.22%), (7.0%, 8.47%), (13.45%, 9.57%), (5.81%, 7.22%), (54.37%, 27.51%), and (23.22%, 17.23%). On Spain dataset, DelayNet is also better than other models with the margin of (9.46%, 6.85%), (4.19%, 2.48%), (3.89%, 2.54%), (11.78%, 6.32%), (65.67%, 45.65%) and (31.94%, 18.62%). This demonstrates the robust predictive capabilities of Delay-Net, making it a compelling choice for time series forecasting tasks. We compare model’s parameters in Figure 6.

The proposed model demonstrates better performance not only in short-term predictions but also in longer-term forecasting scenarios. For instance, when examining the CNU (Table 2) and Gyeonggi (Table 3) datasets, DelayNet surpasses all other methods in terms of MSE for prediction horizons ranging from 72- to 144-time steps. Moreover, even on larger datasets like France, DelayNet delivers great performance, securing the second-best results with only a slight margin (0.07% in MSE and 1.08% in MAE) behind the leading GRU-based methods (Table 4). These outcomes underscore the model’s proficiency in capturing both short and long-term patterns within time series data.

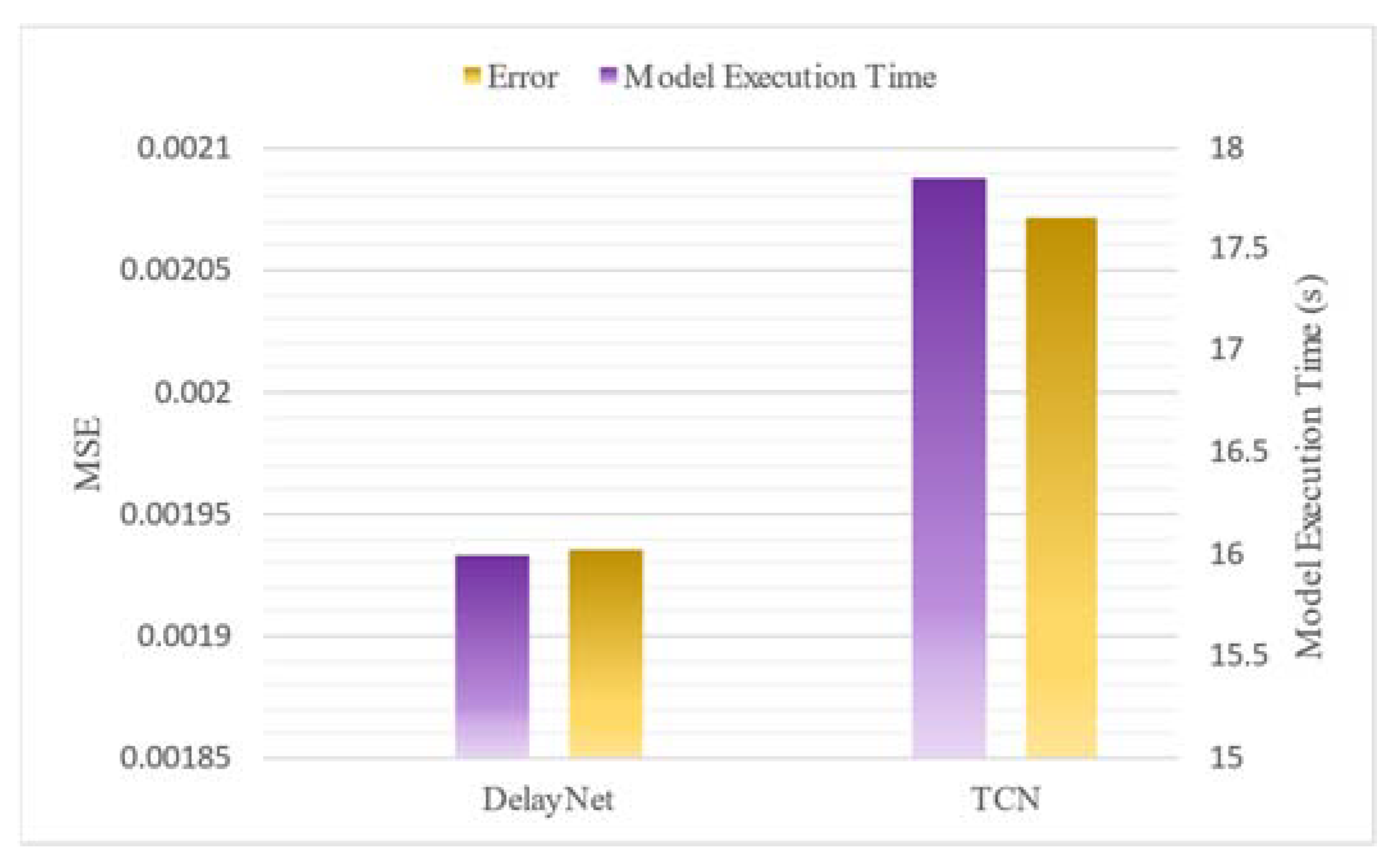
For more emphasize the robustness of our method, we measure the runtime of DelayNet and TCN when forecasting range is 1 h, Figure 7. The results indicate that DelayNet exhibits inferior performance compared to TCN, with a discernable gap of approximately 1% and 1.5 s in metrics, respectively.

4.4. Depth Analysis

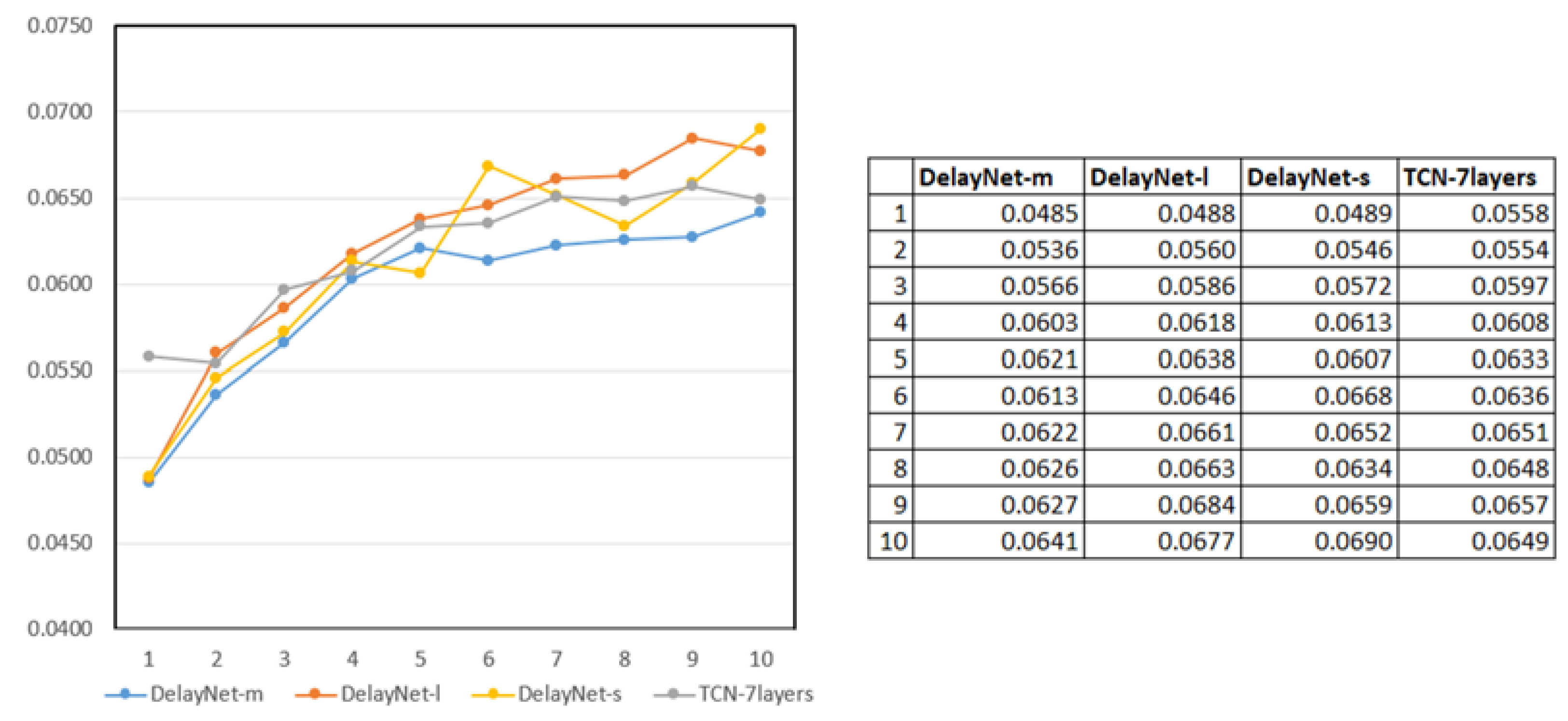
Figure 8 provides an insightful comparison of DelayNet models of varying sizes against a seven-layer TCN model. DelayNet models are characterized by different sizes in terms of the number of parameters (small: $62\mathrm{K}$, medium: $148 \mathrm{K}$, large: $649 \mathrm{K}$), while the TCN model comprises 640 K parameters. The analysis reveals that DelayNet consistently delivers competitive forecasting accuracy across different sizes, despite variations in parameter count. Remarkably, the medium-sized DelayNet (DelayNet-m) and the TCN exhibits similar MAE values, underscoring their robust predictive capabilities. Intriguingly, the small-sized DelayNet (DelayNet-s), despite its reduced parameter size, also performs exceptionally well, achieving MAE values that are on par with its larger counterparts. This underscores DelayNet’s ability to strike a harmonious balance between model complexity and predictive accuracy, rendering it an appealing choice for a wide range of forecasting tasks. Nonetheless, as the model depth increases with DelayNet-l, we observe an escalation in errors compared to other models. While this phenomenon may suggest overfitting, it is useful to note that there are instances in which DelayNet-l outperforms TCN within certain timeframes. On average, DelayNet-s, DelayNet-m and DelayNet-l demonstrates approximately a $13.44\%,$ $12.24\%$ and $12.99\%$ improvement in forecasting accuracy over TCN-7layers across the $10$ forecasting horizons.

4.5. Light-Weight Model Comparision

The baseline DelayNet architecture relies on a kernel size of 3 and maintains a gap of 5, ensuring that the gap size exceeds the kernel size. It references data from the past, specifically 2-time steps back, within each kernel mask and employs 16 filters within each kernel mask. Furthermore, it consists of a single block within the model, with a minimum requirement of at least one block. In contrast, the Light-DelayNet architecture adopts a larger kernel size of 12 and features a substantial gap of 24, which provides a more extensive distance between connections within a kernel mask, surpassing the kernel size. Additionally, Light-DelayNet incorporates three connections into each kernel mask from the past and retains 16 filters within each kernel mask. To enhance model performance, Light-DelayNet introduces increased depth by employing two blocks, offering greater potential for capturing complex temporal patterns and improving forecasting accuracy.

In the architectural comparison between Light-TCN and Light-DelayNet, both models employ a kernel size of $12$, $16$ filters, and process input sequences of width $168$, indicating a foundational structural similarity. However, Light-TCN utilizes a list of dilation values $\left[1, 2\right]$ to capture diverse temporal patterns, enabling the model to attend to different time scales within the data. In contrast, Light-DelayNet opts for a more straightforward design with a single stack, potentially reflecting a streamlined approach. Both Light-TCN and Light-DelayNet models possess an equivalent number of parameters, totaling 9521. These highlight the trade-off between complexity and adaptability in time series forecasting models, offering researchers flexibility in choosing the most suitable model.

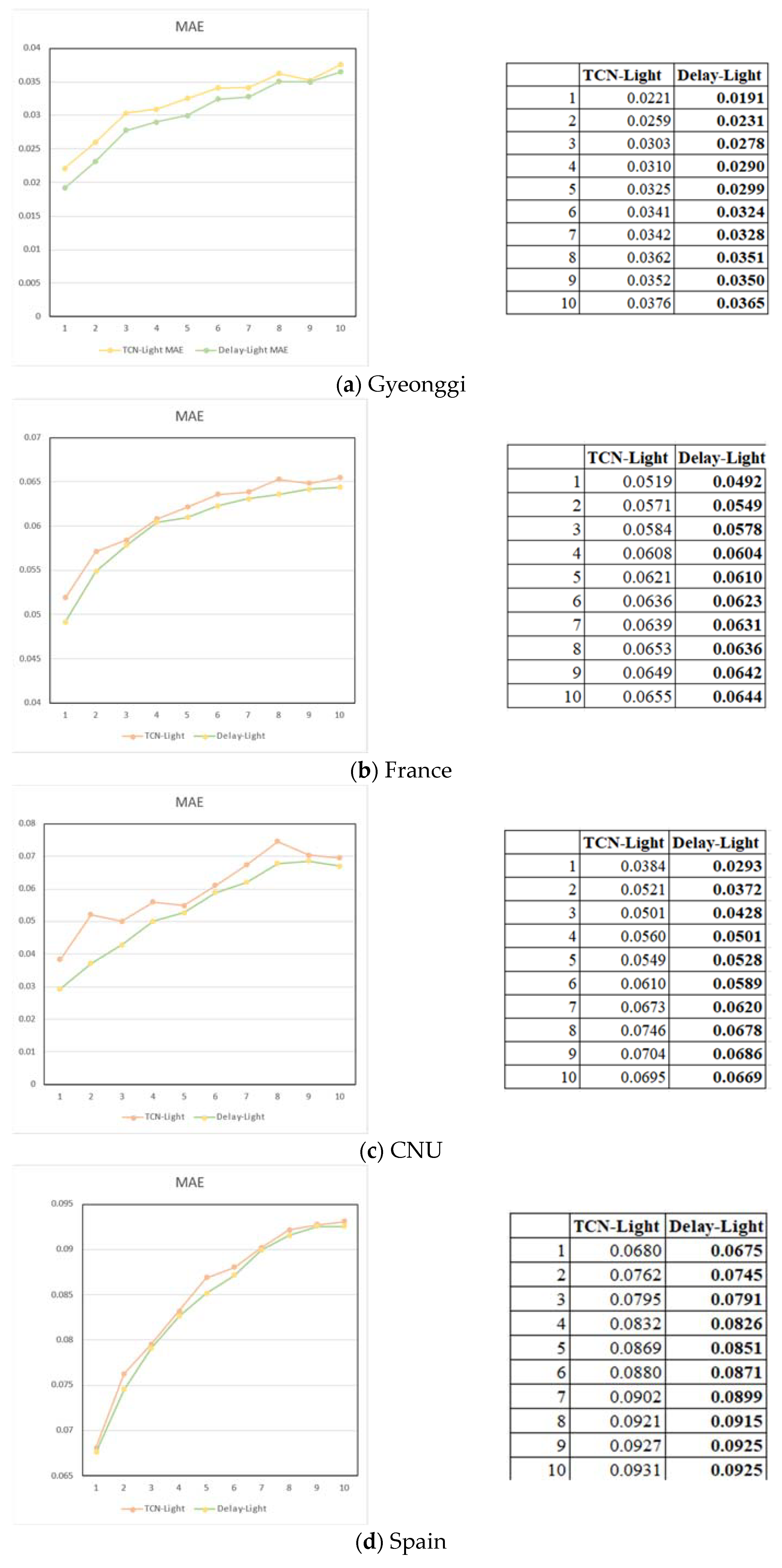
Figure 9 illustrates the MAE comparison between Light-DelayNet and Light-TCN across four datasets when predicting energy consumption for a future time horizon of 10 h. In all datasets, Light-DelayNet consistently outperforms Light-TCN in terms of forecasting error. Notably, both models exhibit an increase in prediction errors as the forecasting range extends further into the future, though the discrepancy between their performance diminishes as the time steps increase. Moreover, the performance gap between the two models becomes more recognizable when dealing with larger datasets, such as Gyeonggi and France. Specifically, the average discrepancy in MAE over the forecasting range remains at $6.26\%,$ $2.13\%,$ $10.80\%$ and $0.9\%$ for Gyeonggi, France, CNU, and Spain, respectively.

Through experiments, DelayNet exhibits remarkable adaptability in time series prediction, showcasing its prowess in forecasting over both short and extended timeframes. Drawing inspiration from TCN while surpassing its performance in simpler and more intricate cases, DelayNet is tailored for datasets of moderate size, achieving a harmonious balance between efficiency and efficacy. Furthermore, its scalability, achieved through the stacking of DelayBlocks, bolsters its suitability for addressing complex forecasting challenges. To sum up, DelayNet’s aptitude for capturing historical patterns, its flexibility across dataset sizes, and its potential for expansion make it a compelling choice for a diverse spectrum of time series forecasting applications.

5. Conclusions

While various deep learning methodologies have been applied to power consumption forecasting, they have increasingly grown in size and computational complexity. In practical applications, especially within small to medium-sized buildings, the resource constraints of computing power become a critical consideration.

To address these challenges, we have proposed a specialized deep learning model tailored for real-building power consumption prediction. Our DelayNet effectively enhances the receptive field while significantly reducing the model’s parameter count and computational complexity. This model outperforms traditional approaches, including RNN, GRU, TCN, and ARIMA, by $21.23\%$, $43.60\%,$ $17.05\%$ and $21.71\%$ in terms of MSE error.

Furthermore, we have made significant contributions by providing access to valuable datasets, such as the CNU building power usage dataset and the Gyeonggi-do building power usage dataset, which offer rich resources for future power consumption prediction research.

Future research opportunities for enhancing DelayNet include integrating external variables like weather and holidays for improved real-world predictions, fine-tuning hyperparameters to tailor the model for specific contexts, and exploring transfer learning to leverage knowledge across different datasets or domains, ultimately aiming to boost its forecasting performance and practical applicability.